Finite Element Analysis of Tunable Composite Tubes Reinforced with Auxetic Structures
Abstract
1. Introduction
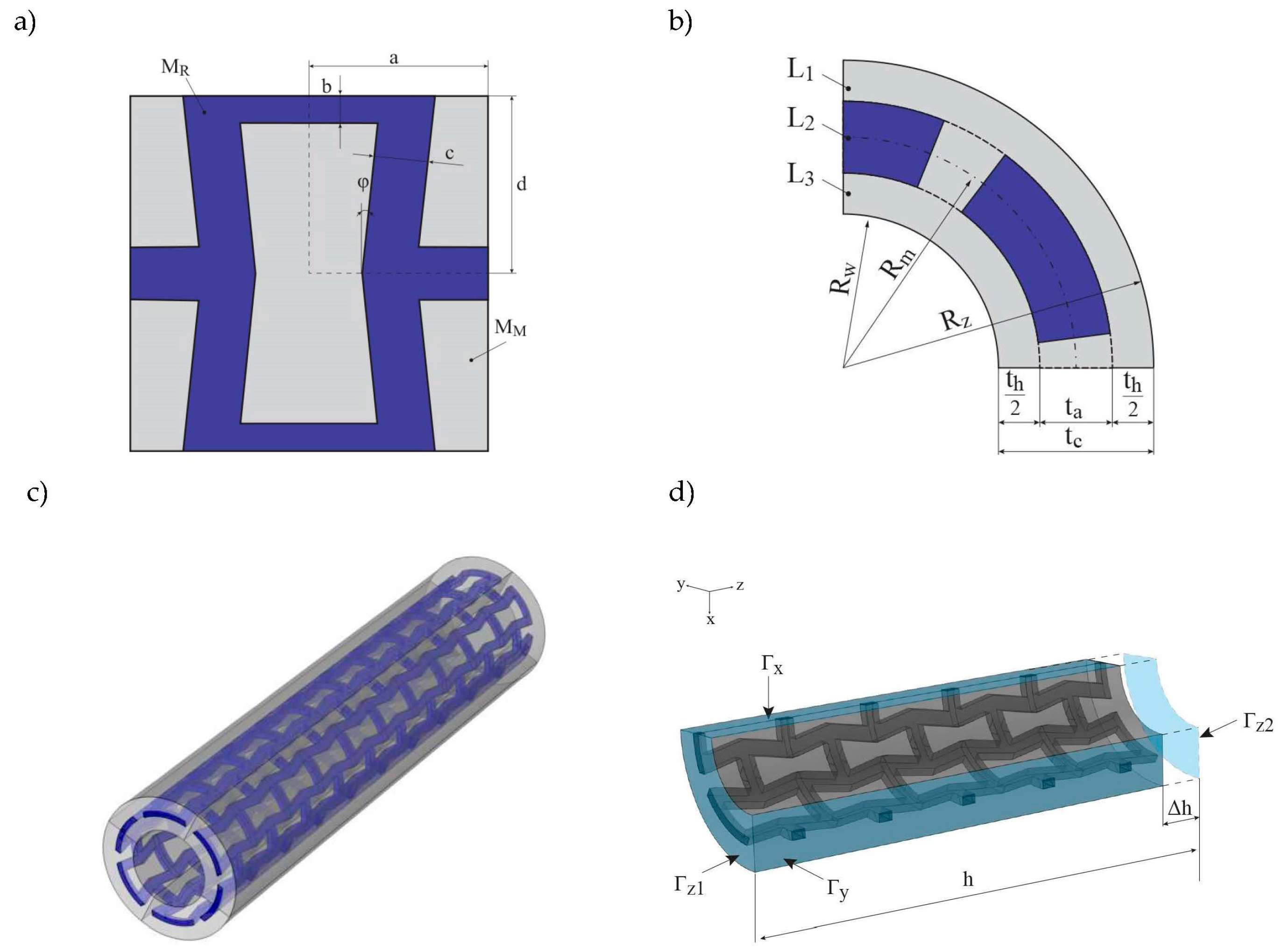
2. Composite Structure of the Tube
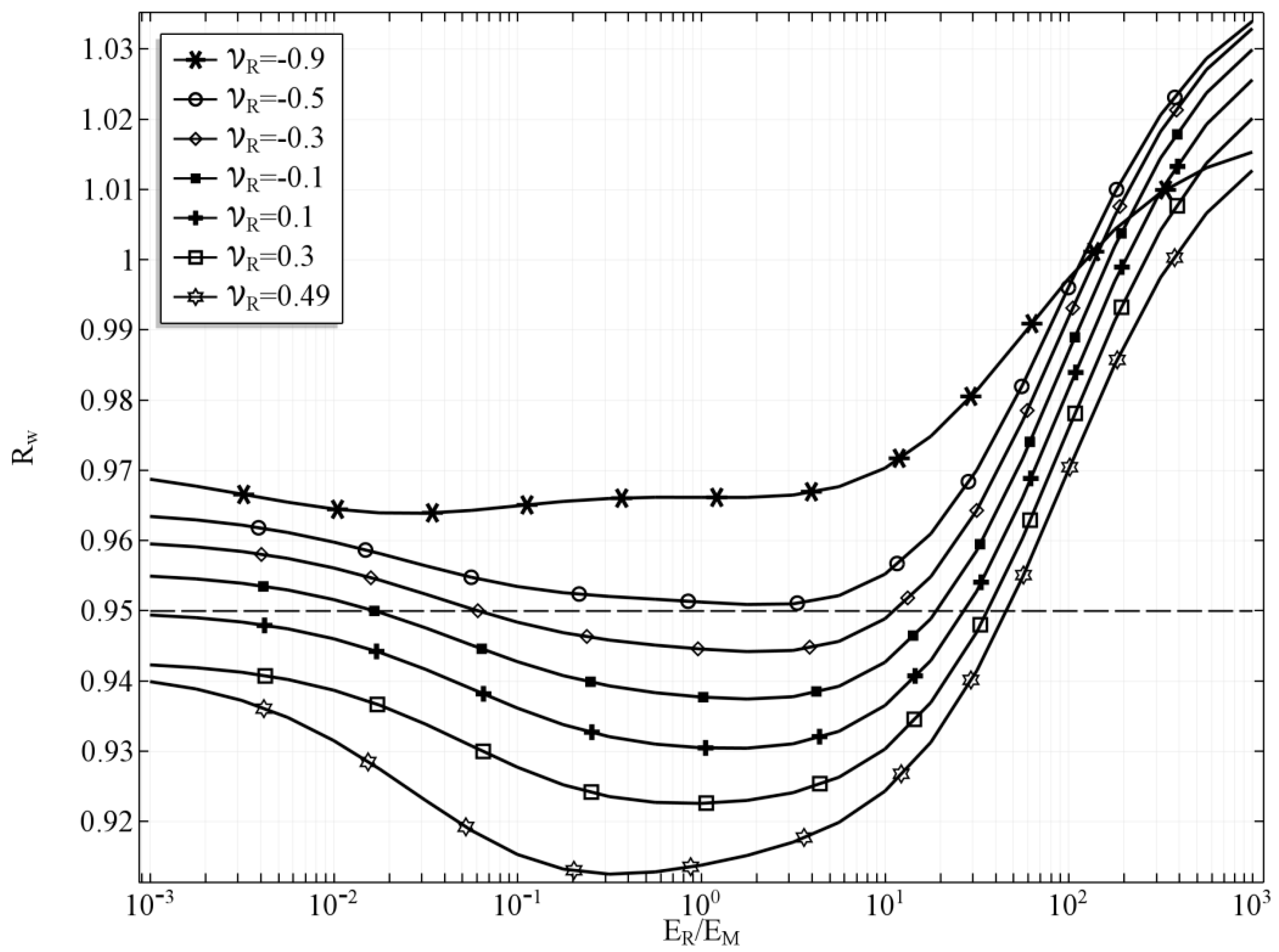
3. Results
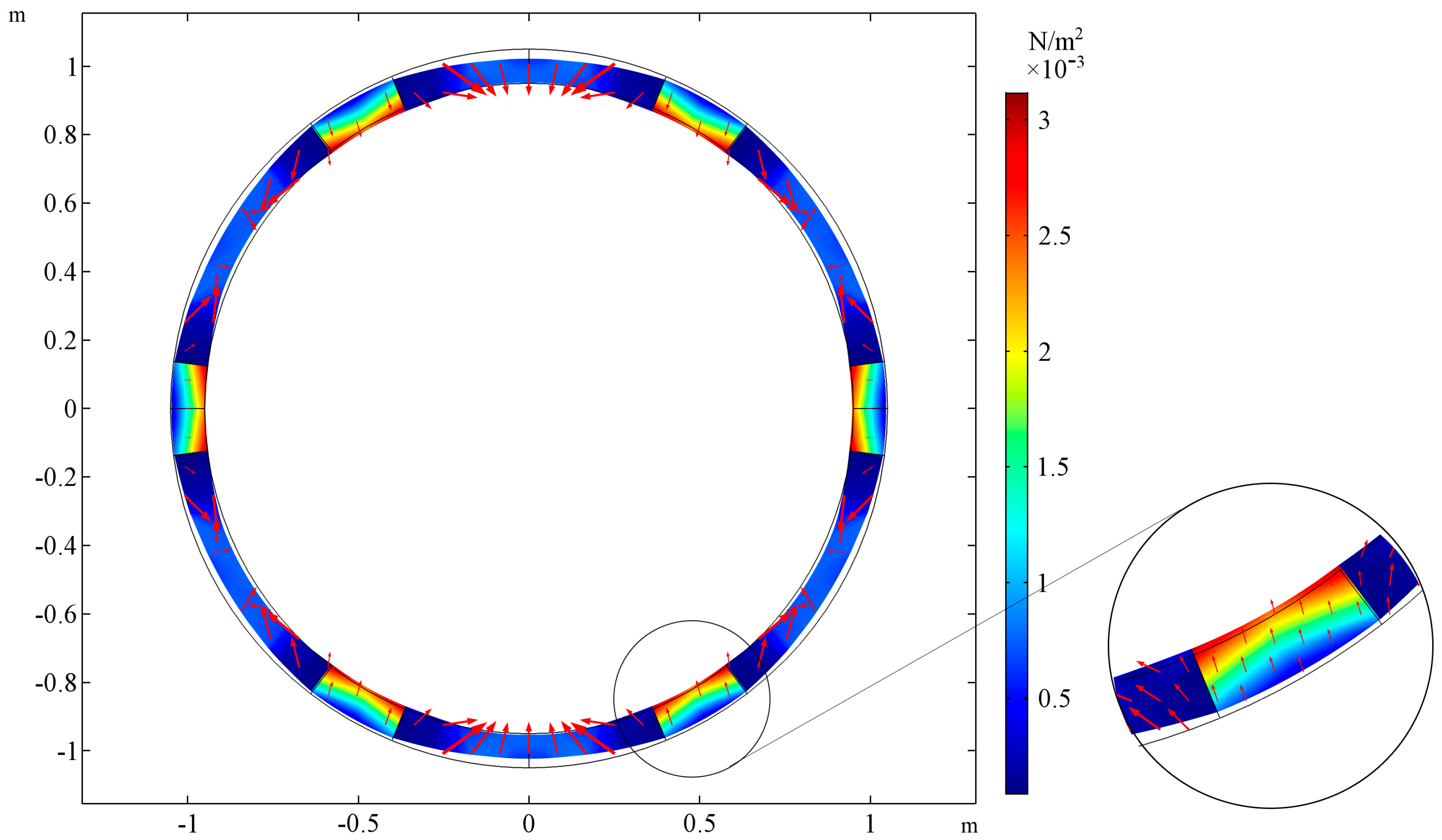
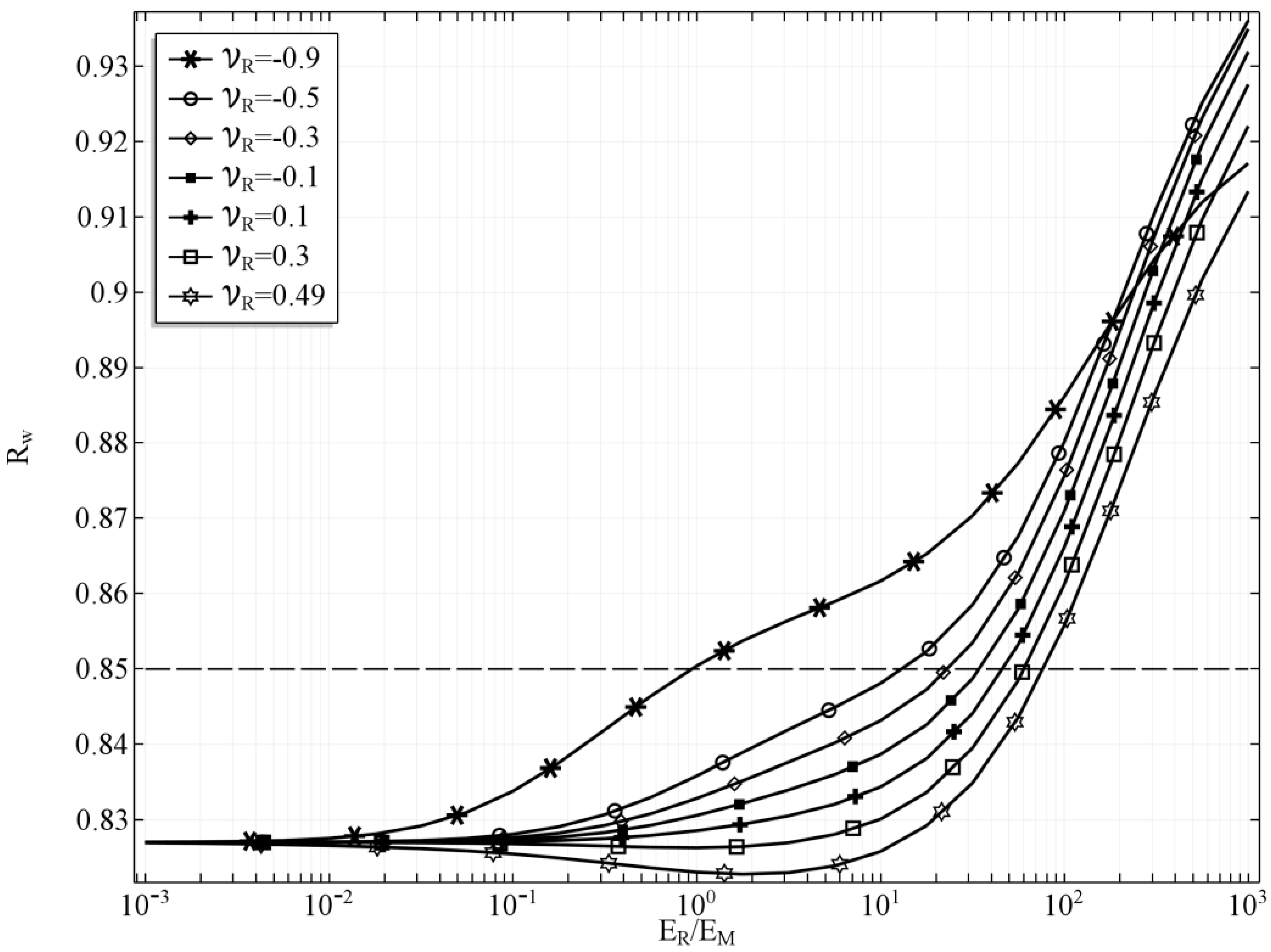
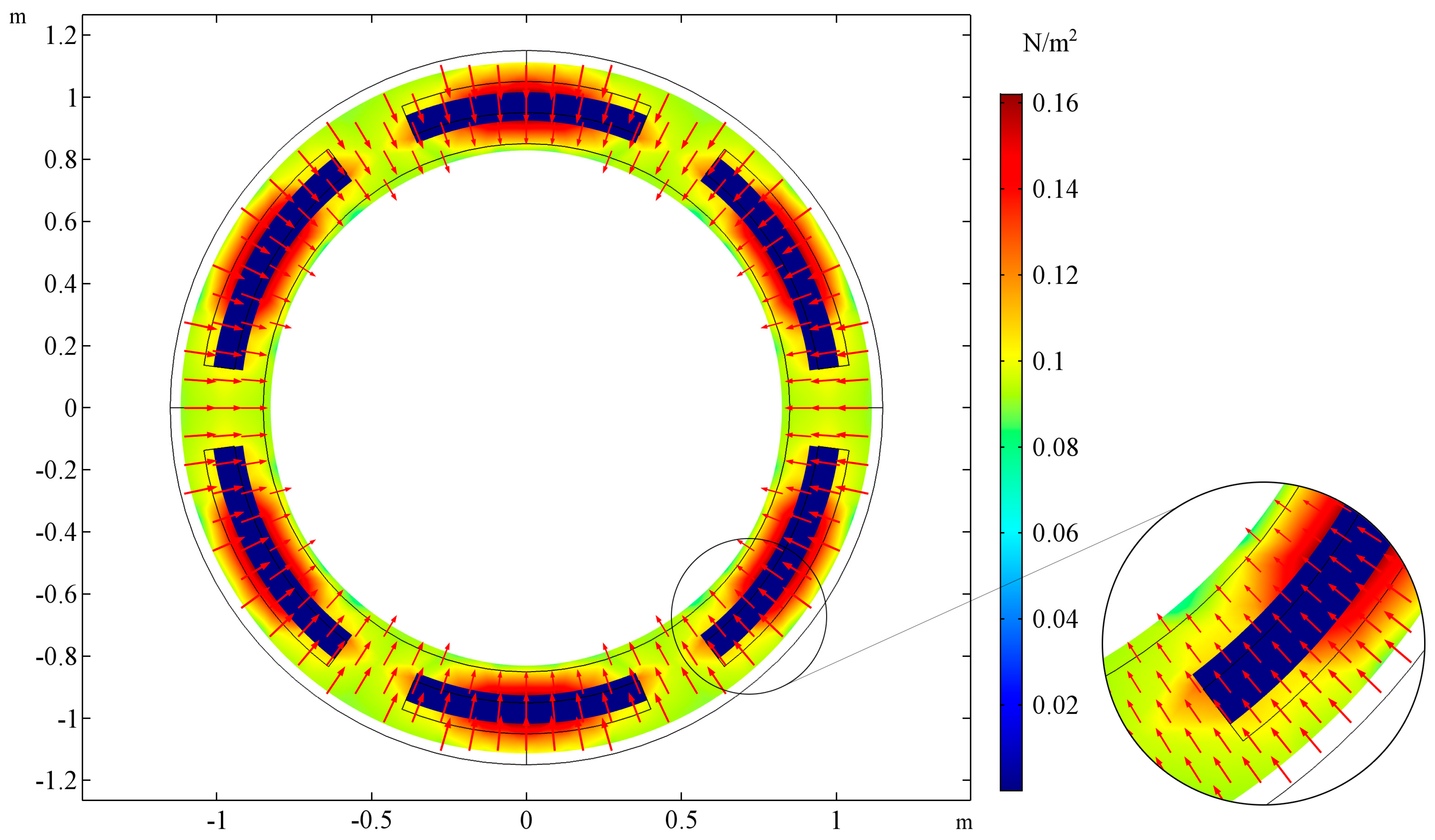
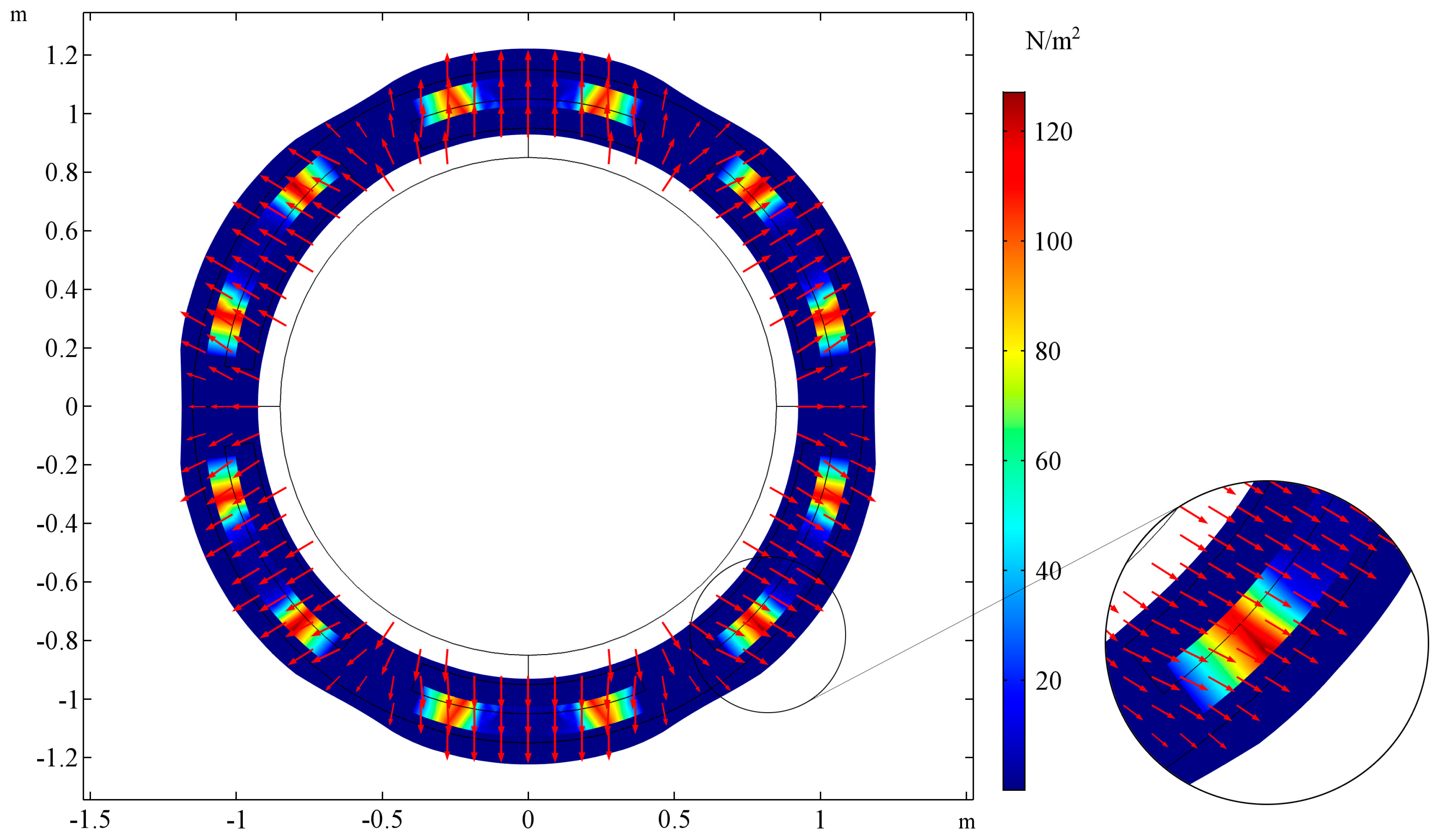
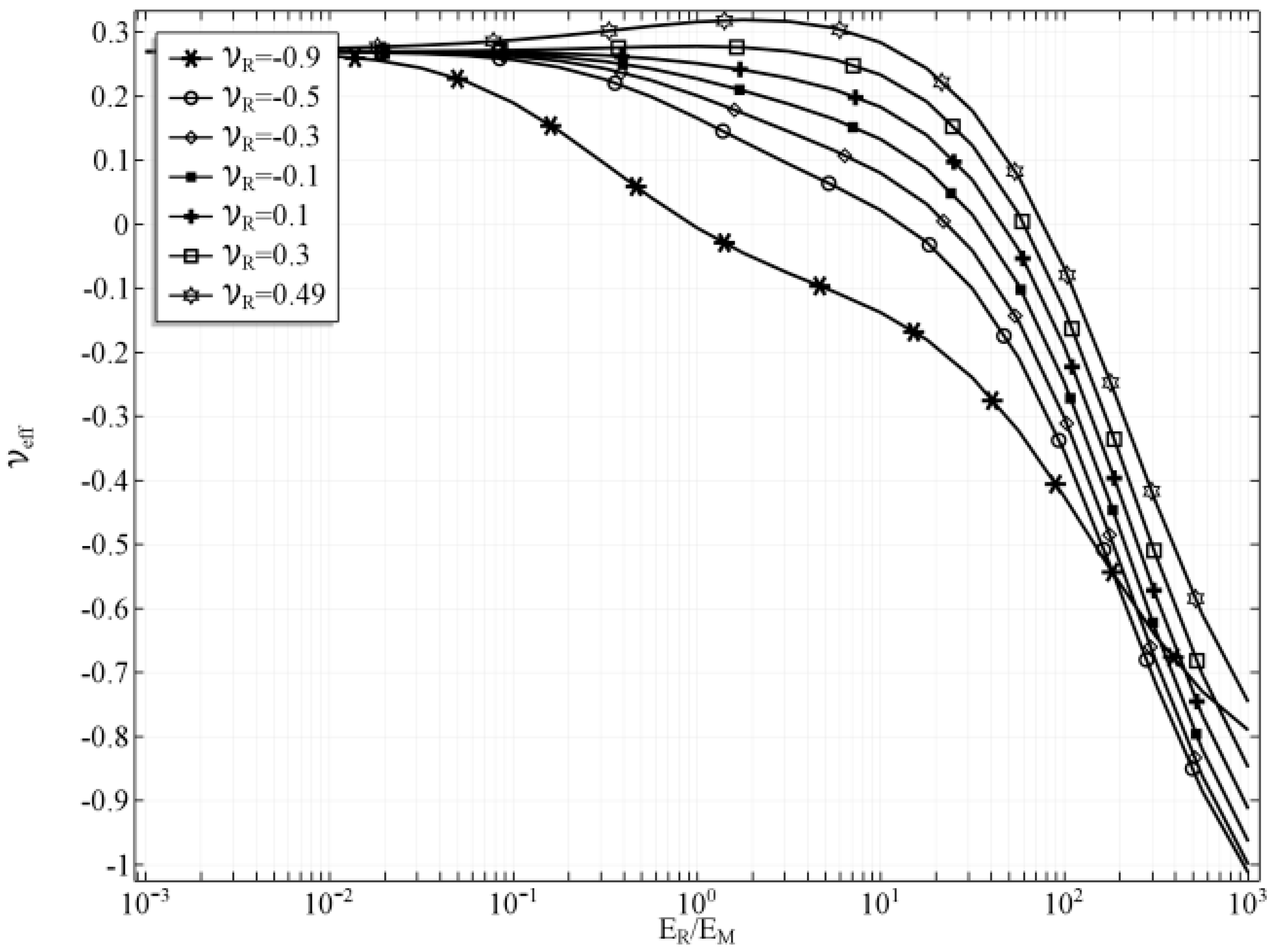
3.1. Case 1
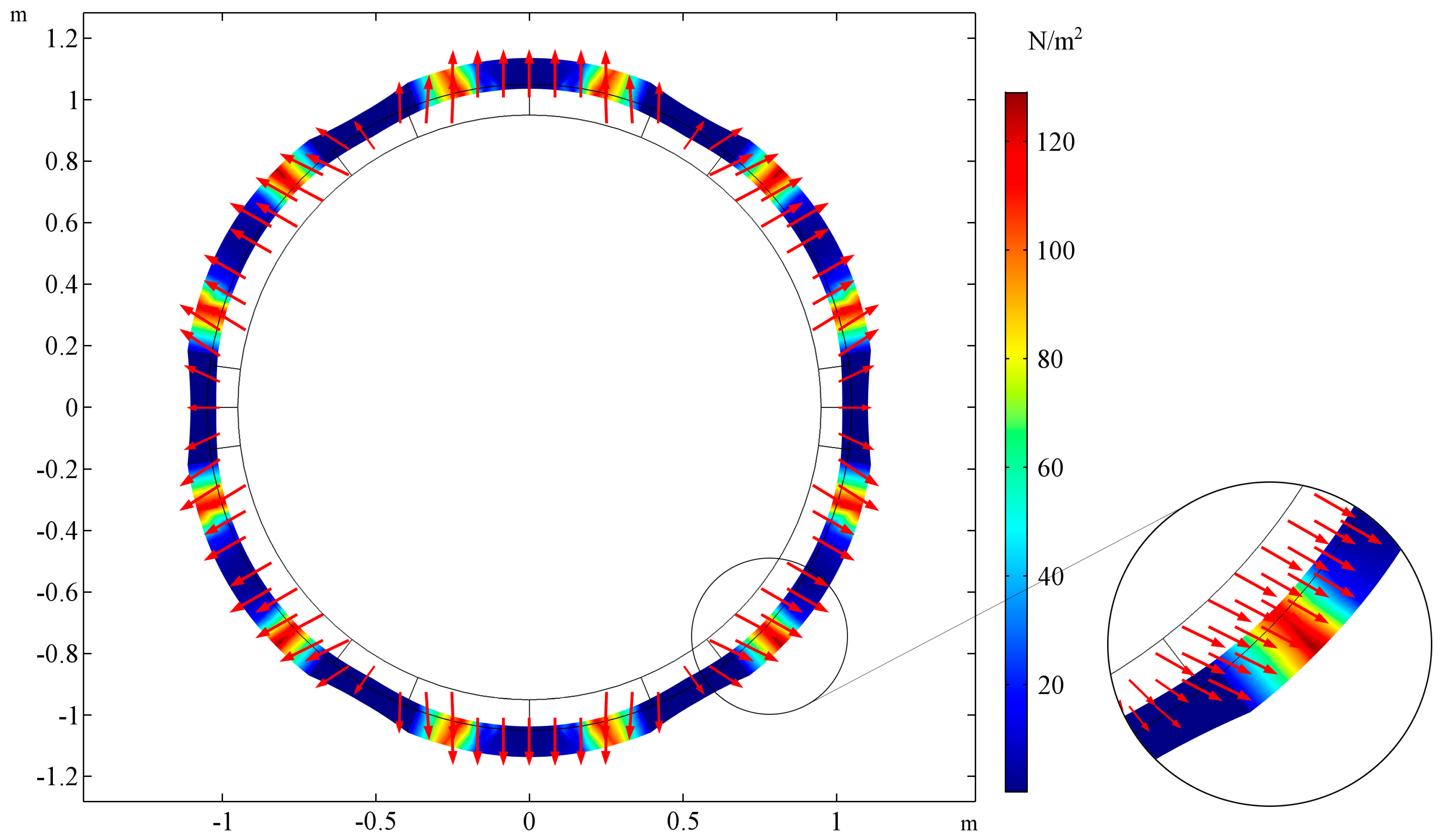
3.2. Case 2
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Kolpakov, A.G. The Determination of Averaged Characteristics for Elastic Skeletons. Prikl. Mat. Mekh. 1985, 49, 969–977. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative Poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Kang, D.; Mahajan, M.; Zhang, S.; Petschek, R.; Rosenblatt, C.; He, C.; Liu, P.; Griffin, A.C. Pretransitional behavior above the nematic-isotropic phase transition of an auxetic trimer liquid crystal. Phys. Rev. E 1999, 60, 4980–4982. [Google Scholar] [CrossRef]
- Grima, J.N.; Zerafa, C. On the effect of solvent molecules on the structure and mechanical properties of organic polyphenylacetylene auxetic re-entrant network polymers. Phys. Status Solidi B 2013, 250, 2030–2037. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Classification of cubic auxetics. Phys. Status Solidi B 2013, 250, 2038–2043. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Longitudinal elastic tension of two-layered plates from isotropic auxetics-nonauxetics and cubic crystals. Eur. J. Mech. A Solids 2017, 63, 122–127. [Google Scholar] [CrossRef]
- Lakes, R.S. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M.; Francesconi, L.; Gerendás, M.; Shanian, A.; Carson, C.; Bertoldi, K. Low porosity metallic periodic structures with negative poisson’s ratio. Adv. Mater. 2014, 26, 2365–2370. [Google Scholar] [CrossRef] [PubMed]
- Francesconi, L.; Taylor, M.; Bertoldi, K.; Baldi, A. Static and Modal Analysis of Low Porosity Thin Metallic Auxetic Structures Using Speckle Interferometry and Digital Image Correlation. Exp. Mech. 2017, 1–18. [Google Scholar] [CrossRef]
- Lakes, R.S. Deformation mechanisms in negative Poisson’s ratio materials: Structural aspects. J. Mater. Sci. 1991, 26, 2287–2292. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Farrugia, P.S. On the properties of auxetic meta-tetrachiral structures. Phys. Status Solidi B. 2008, 245, 511–520. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Non-chiral, molecular model of negative Poisson ratio in two dimensions. J. Phys. A: Math. Gen. 2003, 36, 11765–11778. [Google Scholar] [CrossRef]
- Pozniak, A.A.; Wojciechowski, K.W. Poisson’s ratio of rectangular anti-chiral structures with size dispersion of circular nodes. Phys. Status Solidi 2014, 251, 367–374. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Attard, D.; Manicaro, E.; Grima, J.N. On rotating rigid parallelograms and their potential for exhibiting auxetic behaviour. Phys. Status Solidi B 2009, 246, 2033–2044. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Idczak, E. Computational design of two-phase auxetic structures. Phys. Status Solidi 2016, 253, 1387–1394. [Google Scholar] [CrossRef]
- Jopek, H.; Strek, T. Thermal and structural dependence of auxetic properties of composite materials. Phys. Status Solidi 2015, 252, 1551–1558. [Google Scholar] [CrossRef]
- Czarnecki, S.; Lewiński, T. On material design by the optimal choice of Young’s modulus distribution. Int. J. Solids Struct. 2016, 111, 315–331. [Google Scholar] [CrossRef]
- Czarnecki, S.; Wawruch, P. The emergence of auxetic material as a result of optimal isotropic design. Phys. Status Solidi 2015, 252, 1620–1630. [Google Scholar] [CrossRef]
- Pozniak, A.A.; Wojciechowski, K.W.; Grima, J.N.; Mizzi, L. Planar auxeticity from elliptic inclusions. Compos. Part. B Eng. 2016, 94, 379–388. [Google Scholar] [CrossRef]
- Kochmann, D.M.; Venturini, G.N. Homogenized mechanical properties of auxetic composite materials in finite-strain elasticity. Smart Mater. Struct. 2013, 22, 84004. [Google Scholar] [CrossRef]
- Jopek, H. Computer simulation of bending a fibrous composite reinforced with auxetic phase. Phys. Status Solidi 2016, 253, 1369–1377. [Google Scholar] [CrossRef]
- Bilski, M.; Wojciechowski, K.W. Tailoring Poisson’s ratio by introducing auxetic layers. Phys. Status Solidi 2016, 1323, 1318–1323. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Fraska, A. Torsion of elliptical composite beams with auxetic phase. Phys. Status Solidi B 2016, 1368, 1359–1368. [Google Scholar] [CrossRef]
- Jopek, H.; Strek, T. Torsion of a two-phased composite bar with helical distribution of constituents. Phys. Status Solidi B 2017. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Ghaedizadeh, A.; Tian, H.; Xie, Y.M. Experiments and parametric studies on 3D metallic auxetic metamaterials with tuneable mechanical properties. Smart Mater. Struct. 2015, 24, 95016. [Google Scholar] [CrossRef]
- Li, D.; Dong, L.; Lakes, R.S. A unit cell structure with tunable Poisson’s ratio from positive to negative. Mater. Lett. 2016, 164, 456–459. [Google Scholar] [CrossRef]
- Li, D.; Ma, J.; Dong, L.; Lakes, R.S. A bi-material structure with Poisson’s ratio tunable from positive to negative via temperature control. Mater. Lett. 2016, 181, 285–288. [Google Scholar] [CrossRef]
- Ogden, R.W.; Steigmann, D.J. Mechanics and Electrodynamics of Magneto- and Electro-Elastic Materials; Springer Press: Vienna, Austria, 2011; ISBN 9783709107010. [Google Scholar]
- Bellan, C.; Bossis, G. Field Dependence of Viscoelastic Properties of MR Elastomers. Int. J. Mod. Phys. B 2002, 16, 2447–2453. [Google Scholar] [CrossRef]
- Liang, C.-Y.; Keller, S.M.; Sepulveda, A.E.; Bur, A.; Sun, W.-Y.; Wetzlar, K.; Carman, G.P. Modeling of magnetoelastic nanostructures with a fully coupled mechanical-micromagnetic model. Nanotechnology 2014, 25, 435701. [Google Scholar] [CrossRef] [PubMed]
- Kukla, M.; Gorecki, J.; Malujda, I.; Talaska, K.; Tarkowski, P. The Determination of Mechanical Properties of Magnetorheological Elastomers (MREs). Procedia Eng. 2017, 177, 324–330. [Google Scholar] [CrossRef]
- Varga, Z.; Filipcsei, G.; Zrínyi, M. Magnetic field sensitive functional elastomers with tuneable elastic modulus. Polymer 2006, 47, 227–233. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; McDonald, S.A.; Mottershead, B.; Nazare, S.; Withers, P.J.; Yao, Y.T. Piezomorphic materials. Macromol. Mater. Eng. 2013, 298, 318–327. [Google Scholar] [CrossRef]
- Li, Q.; Kuang, Y.; Zhu, M. Auxetic piezoelectric energy harvesters for increased electric power output. AIP Adv. 2017, 7. [Google Scholar] [CrossRef]
- Grima, J.N.; Caruana-Gauci, R.; Dudek, M.R.; Wojciechowski, K.W.; Gatt, R. Smart metamaterials with tunable auxetic and other properties. Smart Mater. Struct. 2013, 22, 84016. [Google Scholar] [CrossRef]
- Dudek, M.R.; Grabiec, B.; Wojciechowski, K.W. Molecular dynamics simulations of auxetic ferrogel. Rev. Adv. Mater. Sci. 2007, 14, 167–173. [Google Scholar]
- Dudek, M.R.; Wojciechowski, K.W.; Grima, J.N.; Caruana-Gauci, R.; Dudek, K.K. Colossal magnetocaloric effect in magneto-auxetic systems. Smart Mater. Struct. 2015, 24, 85027. [Google Scholar] [CrossRef]
- Danas, K. Effective response of classical, auxetic and chiral magnetoelastic materials by use of a new variational principle. J. Mech. Phys. Solids 2017, 105, 25–53. [Google Scholar] [CrossRef]
- Raghunath, G.; Flatau, A.B.; Wang, H.; Wu, R. Magnetoelastic auxetic-like behavior in Galfenol: Experimental data and simulations. Phys. Status Solidi 2016, 1448, 1440–1448. [Google Scholar] [CrossRef]
- Gatt, R.; Caruana-Gauci, R.; Attard, D.; Casha, A.R.; Wolak, W.; Dudek, K.; Mizzi, L.; Grima, J.N. On the properties of real finite-sized planar and tubular stent-like auxetic structures. Phys. Status Solidi Basic Res. 2014, 251, 321–327. [Google Scholar] [CrossRef]
- Duc, N.D.; Seung-Eock, K.; Tuan, N.D.; Tran, P.; Khoa, N.D. New approach to study nonlinear dynamic response and vibration of sandwich composite cylindrical panels with auxetic honeycomb core layer. Aerosp. Sci. Technol. 2017, 1, 1–9. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Ghaedizadeh, A.; Tian, H.; Xie, Y.M. A simple auxetic tubular structure with tuneable mechanical properties. Smart Mater. Struct. 2016, 25, 65012. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Two-layer tubes from cubic crystals. Dokl. Phys. 2016, 61, 604–610. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, H.; Liu, S.; Xu, B. Study of an auxetic structure made of tubes and corrugated sheets. Phys. Status Solidi Basic Res. 2013, 250, 1996–2001. [Google Scholar] [CrossRef]
- Scarpa, F.; Adhikari, S.; Wang, C.Y.Y. Nanocomposites with auxetic nanotubes. Int. J. Smart Nano Mater. 2010, 1, 83–94. [Google Scholar] [CrossRef]
- Yao, Y.T.; Alderson, A.; Alderson, K.L. Can nanotubes display auxetic behaviour? Phys. Status Solidi Basic Res. 2008, 245, 2373–2382. [Google Scholar] [CrossRef]
- Valentini, L.; Bittolo Bon, S.; Pugno, N.M. Graphene and Carbon Nanotube Auxetic Rubber Bionic Composites with Negative Variation of the Electrical Resistance and Comparison with their Nonbionic Counterparts. Adv. Funct. Mater. 2017, 27. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H. Effective mechanical properties of concentric cylindrical composites with auxetic phase. Phys. Status Solidi B 2012, 249, 1359–1365. [Google Scholar] [CrossRef]
- Ali, M.N.; Busfield, J.J.C.; Rehman, I.U. Auxetic oesophageal stents: Structure and mechanical properties. J. Mater. Sci. Mater. Med. 2014, 25, 527–553. [Google Scholar] [CrossRef] [PubMed]
- Karnessis, N.; Burriesci, G. Uniaxial and buckling mechanical response of auxetic cellular tubes. Smart Mater. Struct. 2013, 22, 84008. [Google Scholar] [CrossRef]
- Bhullar, S.K.; Ko, J.; Cho, Y.; Jun, M.B.G. Fabrication and Characterization of Nonwoven Auxetic Polymer Stent. Polym. Plast. Technol. Eng. 2015, 54, 1553–1559. [Google Scholar] [CrossRef]
- Mohsenizadeh, S.; Alipour, R.; Shokri Rad, M.; Farokhi Nejad, A.; Ahmad, Z. Crashworthiness assessment of auxetic foam-filled tube under quasi-static axial loading. Mater. Des. 2015, 88, 258–268. [Google Scholar] [CrossRef]
- Milton, G.W. Composite materials with poisson’s ratios close to-1. J. Mech. Phys. Solids 1992, 40, 1105–1137. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jopek, H. Finite Element Analysis of Tunable Composite Tubes Reinforced with Auxetic Structures. Materials 2017, 10, 1359. https://doi.org/10.3390/ma10121359
Jopek H. Finite Element Analysis of Tunable Composite Tubes Reinforced with Auxetic Structures. Materials. 2017; 10(12):1359. https://doi.org/10.3390/ma10121359
Chicago/Turabian StyleJopek, Hubert. 2017. "Finite Element Analysis of Tunable Composite Tubes Reinforced with Auxetic Structures" Materials 10, no. 12: 1359. https://doi.org/10.3390/ma10121359
APA StyleJopek, H. (2017). Finite Element Analysis of Tunable Composite Tubes Reinforced with Auxetic Structures. Materials, 10(12), 1359. https://doi.org/10.3390/ma10121359





