Anisotropic Failure Strength of Shale with Increasing Confinement: Behaviors, Factors and Mechanism
Abstract
:1. Introduction
2. Classifications on Anisotropic Failure Strength Behaviors of Shale by Experimental Results
2.1. Degree of Anisotropic Failure Strength
2.2. Laboratory Experimental Database
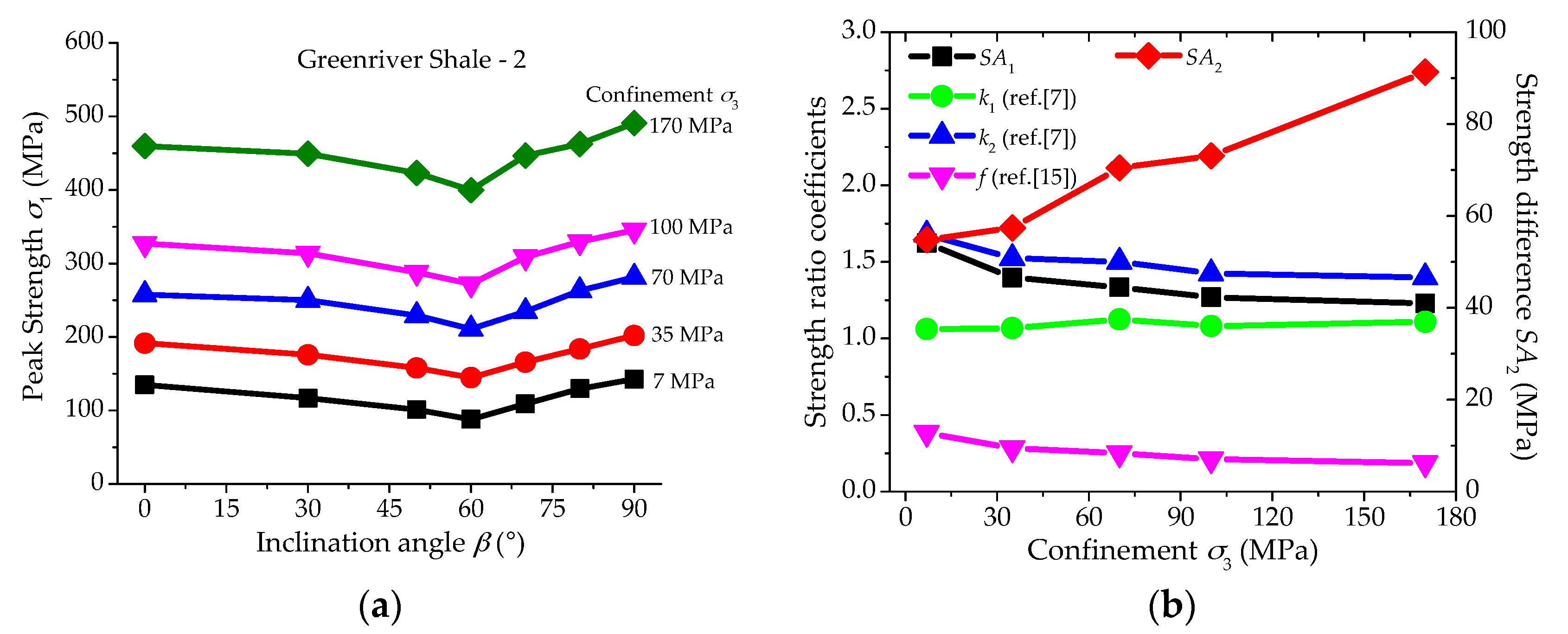
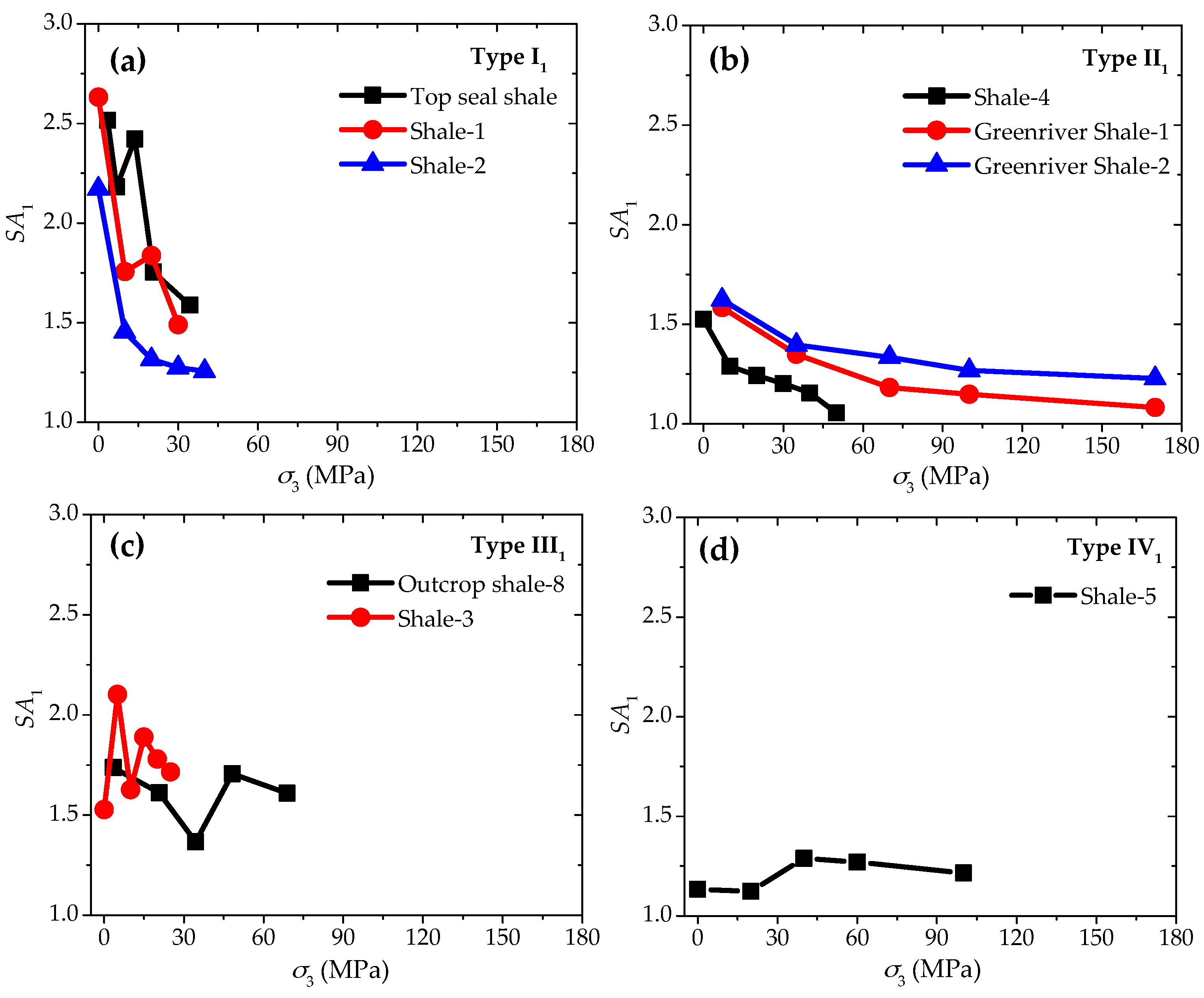
2.3. Different Types of Anisotropic Strength Behaviors Based on SA1
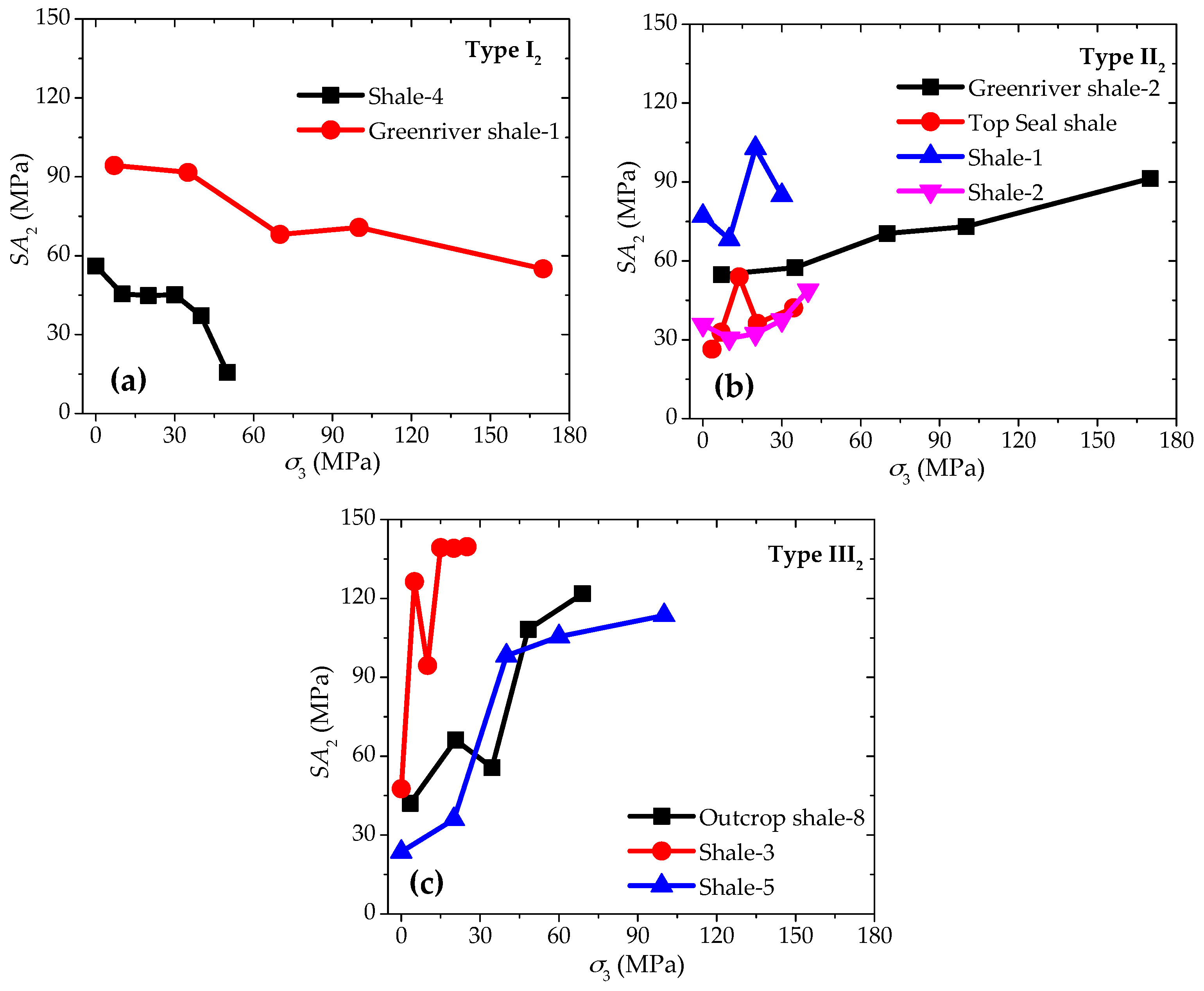
2.4. Different Types of Anisotropic Strength Behaviors Based on SA2
2.5. Discussions
3. Anisotropic Strength Behaviors Affected by Cohesion and Friction Angle of Weak Planes
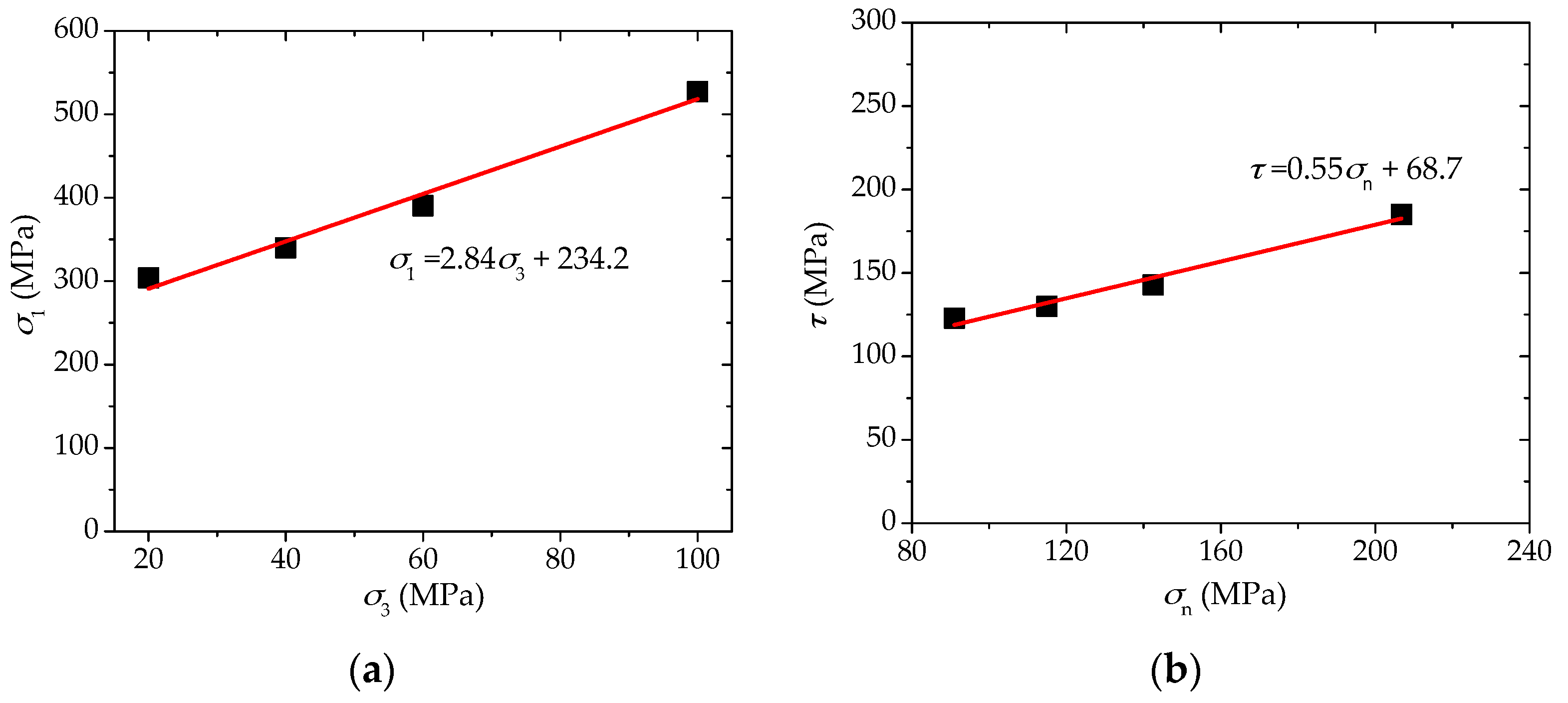
3.1. Bonded-Particle Discrete Element Modelling
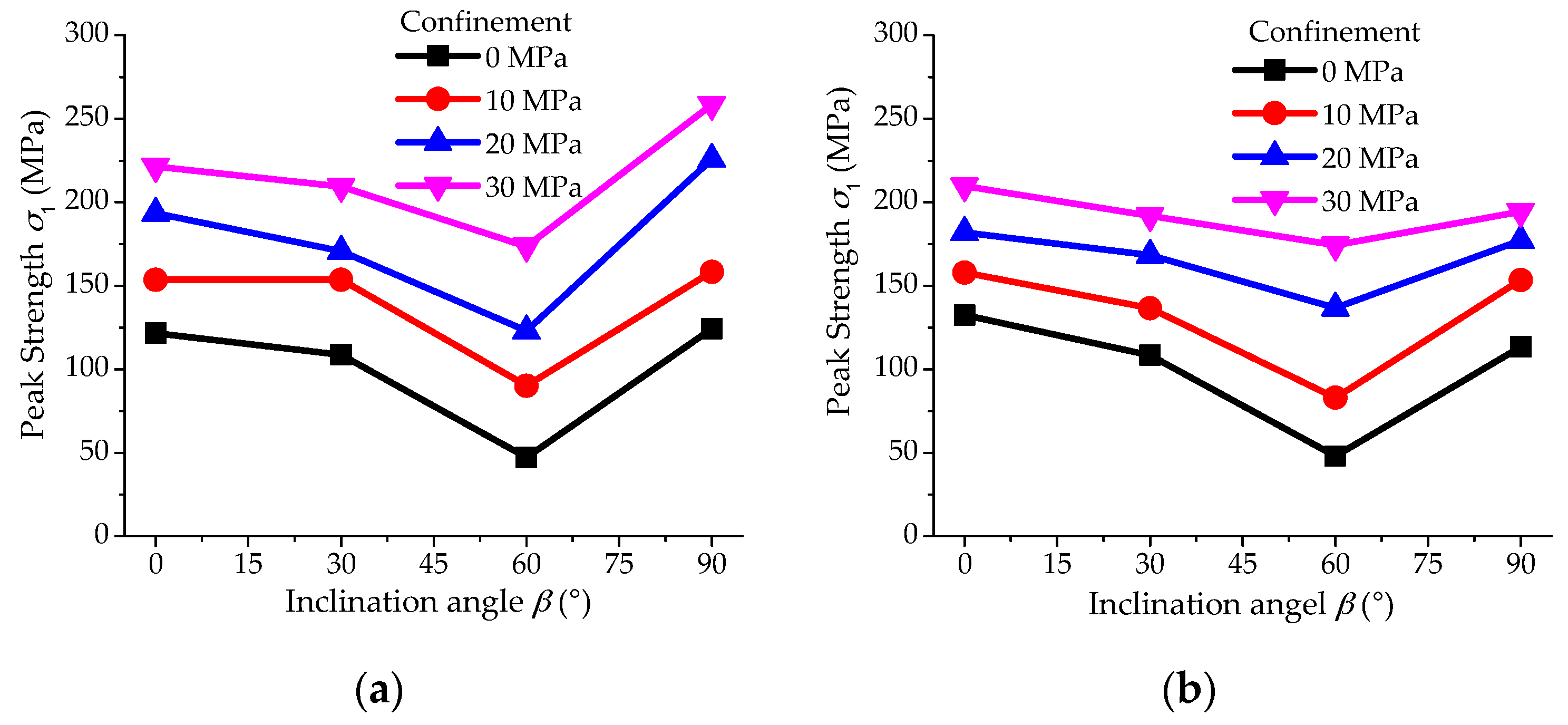
3.2. Modelling Analyses
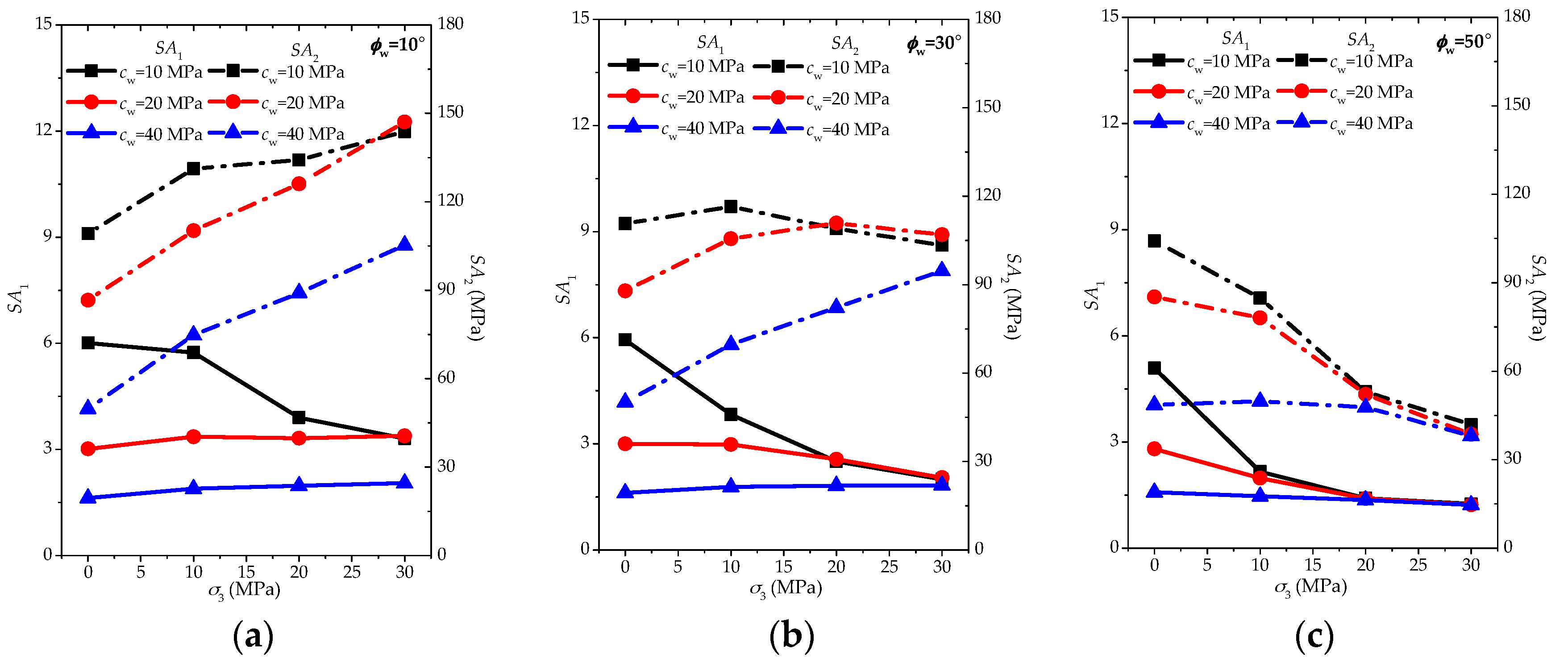
3.2.1. Influence of Cohesion of Weak Planes
- (1)
- In the case of a low to medium friction angle ( = 10° and 30°), the increase of cohesion may transfer the behaviors from significant decrease to slight decrease or even slight increase with the confinement going up;
- (2)
- For a high friction angle ( = 50°), increasing cohesion can also change the features from significant decrease to slight decrease, however, it is difficult to obtain the increasing trend of with the rise of confinement;
- (3)
- Generally speaking, the lower cohesion may be prone to lead to the significant decrease of with the increasing confinement, while the higher cohesion will weaken this trend, but whether it will be slight decrease or increase is dependent on the friction angle of the weak planes.
- (1)
- When friction angle = 10°, the increase of cohesion may lower all values under various confinements, and the increasing trend of will be more significant with the increasing confinement;
- (2)
- When friction angle = 30°, the increase of cohesion makes the slight decreasing trend of transfer to a slight or significant increase with the increasing confinement;
- (3)
- When friction angle = 50°, the increase of cohesion makes the significant decreasing trend of transfer to a slight decrease as the confinement increases.
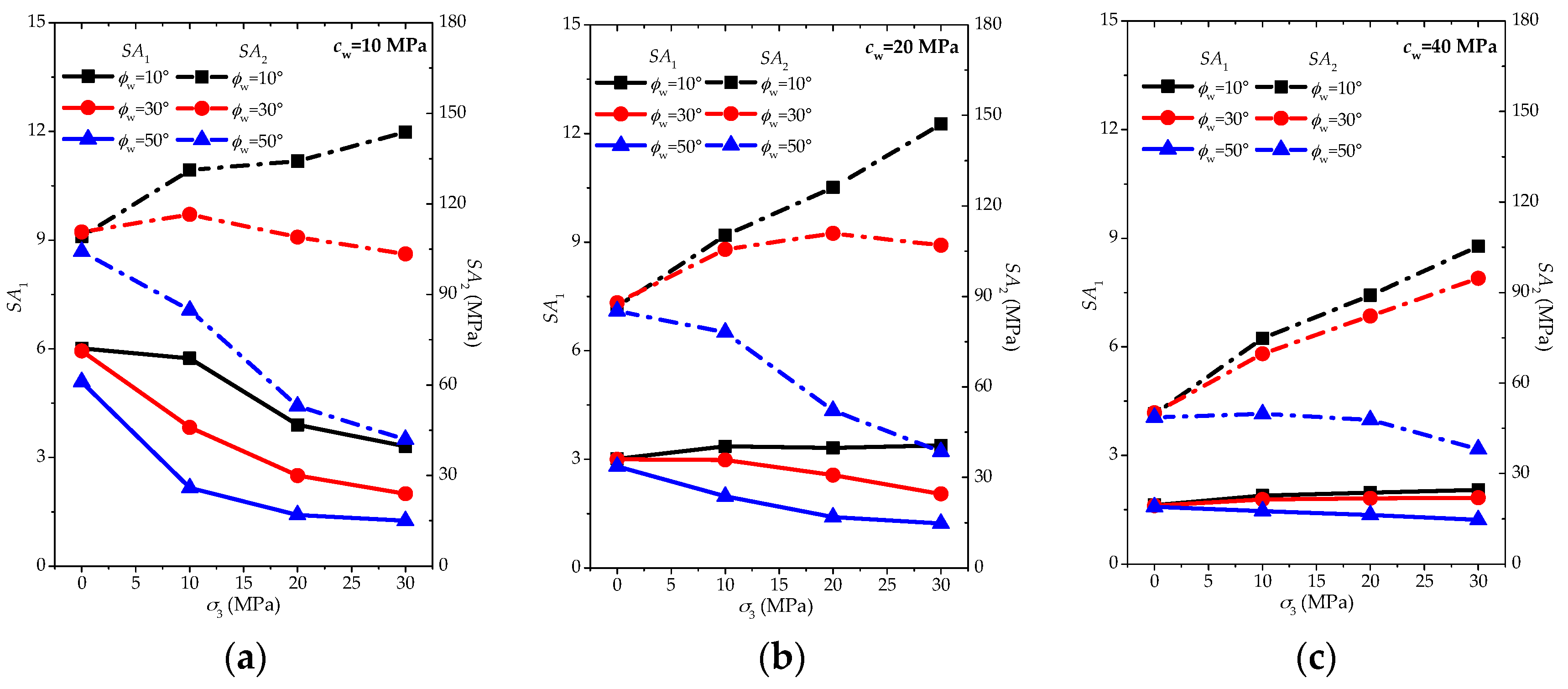
3.2.2. Influence of Friction Angle of Weak Planes
- (1)
- For lower cohesion ( = 10 MPa), the increasing friction angle can make the decreasing trend of more and more significant;
- (2)
- For medium to higher cohesion ( = 20 and 40 MPa), the increasing friction angle may transfer the slight increasing or almost constant trend of to slight increasing behaviors;
- (3)
- As the cohesion increases, the influence of friction angle on the degree of changing behaviors is more and more limited.
- (1)
- For all cases of cohesion ( = 10, 20 and 40 MPa), the increasing friction angle can induce the transferring of the trend from going up to going down with the rise of confinement;
- (2)
- As the cohesion increases, the influence of friction angle on the degree of changing behaviors is more and more limited.
3.2.3. Conjoint Analysis on Both Factors and
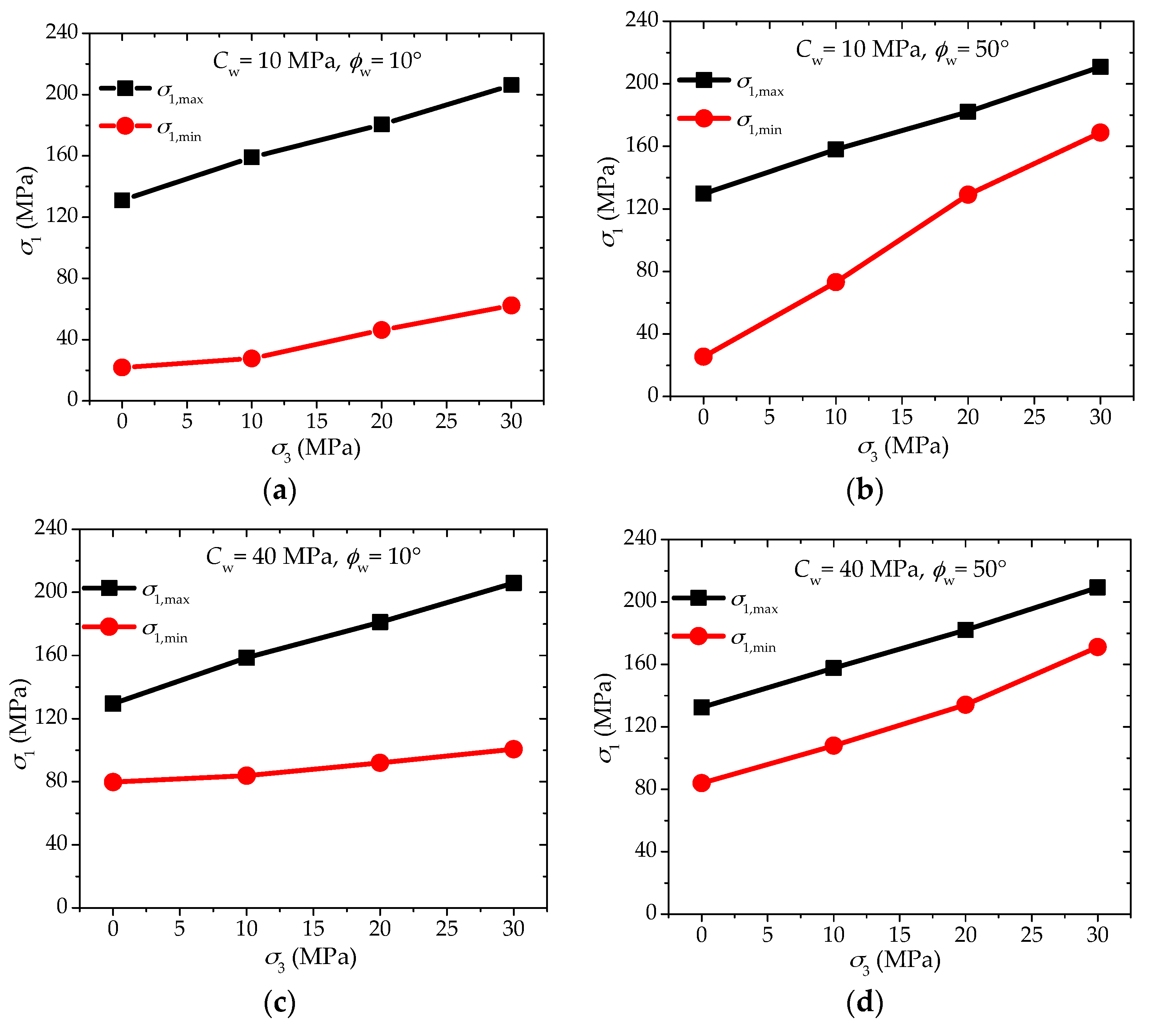
4. Discussions
- (1)
- Case I: for lower cohesion ( = 10 MPa) and lower friction angle ( = 10°), there is quite a large difference between and under lower confinement mainly resulted from the low value of , and the strength difference is also very considerable under higher confinement because the low value of cannot increase effectively with the increasing σ3. In this case, the anisotropic strength ratio may be lowered with increasing confinement, while the anisotropic strength difference may not increase or decrease significantly.
- (2)
- Case II: for lower cohesion ( = 10 MPa) and higher friction angle ( = 50°), the difference between and is again very large under lower confinement owing to the low , however, as the high value of can enhance significantly under higher confinement, the strength difference turns much smaller. In this case, both anisotropic strength ratio and anisotropic strength difference will decrease obviously with the increase of confinement.
- (3)
- Case III: for higher cohesion ( = 40 MPa) and lower friction angle ( = 10°), the difference between and is much smaller than the first two cases as the cohesion has quite a high value, while the strength difference becomes larger with the increasing confinement because the low value of leads to quite a low . In this case, the anisotropic strength ratio may remain almost constant or ever increase slightly with the increasing confinement, while the anisotropic strength difference will increase significantly.
- (4)
- Case IV: for higher cohesion ( = 40 MPa) and higher friction angle ( = 50°), there is quite a small difference between and under lower confinement attributed to the high value of , and the strength difference is also very limited under higher confinement because the high value of can increase effectively with the increasing σ3. Similar to the first case, the anisotropic strength ratio may be lowered with increasing confinement, while the anisotropic strength difference may not change significantly.
5. Conclusions
- (1)
- Two anisotropic strength parameters, from the perspective of strength ratio and from the perspective of strength difference, should both be researched for a comprehensive understanding of the anisotropic strength behaviors of shale under different confinements. is better for comparing the anisotropic strength characteristics of different shale samples as a dimensionless coefficient, while is easier to be applied to estimate the stability of a certain shale based on the strength criterion because it considers the specific values of strength differences;
- (2)
- Based on the laboratory experimental results of nine groups of different shale samples, it is found that there are four types of behaviors (significant decrease, slight decrease, generally constant, and slight increase) and three types of behaviors (gradual decrease, slight increase, and significant increase) with increasing confinement;
- (3)
- With the parallel bonded particle model simulating the rock material and smooth-joint model simulating the weak planes, the different types of anisotropic strength behaviors are well reproduced in the numerical models. By a series of systematic analyses, it is observed that cohesion and friction angle of the weak planes are two dominant factors for the anisotropic strength behaviors;
- (4)
- The increase of cohesion will change the behaviors from significant decrease to slight decrease with increasing confinement, or even slight increase if the friction angle is medium to low. Meanwhile, the decrease of friction angle are more prone to transfer behaviors from gradual decrease to slight increase with increasing confinement, or even significant increase if the cohesion is medium to high;
- (5)
- The mechanism of the anisotropic strength behaviors have been analyzed based on the well-known Jaeger’s strength criterion, as well as the laboratory and numerical test results. Under lower confinement, cohesion has more important roles as the friction angle has very limited influences on the strength. As the confinement goes up, the friction angle with different values may take different degrees of roles, while the effect of cohesion is not easy to be improved significantly. Consequently, different combinations of and may have various types of influences on the minimum failure strength with the increasing confinement, therefore different shale samples show different types of anisotropic behaviors with the increasing confinement.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ewy, R.T.; Bovberg, C.A.; Stankovic, R.J. Strength anisotropy of mudstones and shales. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010; American Rock Mechanics Association: Alexandria, VA, USA, 2010. [Google Scholar]
- Crawford, B.R.; Dedontney, N.L.; Alramahi, B.; Ottesen, S. Shear strength anisotropy in fine-grained rocks. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012; American Rock Mechanics Association: Alexandria, VA, USA, 2012. [Google Scholar]
- Ambrose, J.; Zimmerman, R.W.; Suarez-Rivera, R. Failure of shales under triaxial compressive stress. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Minneapolis, MN, USA, 1–4 June 2014. [Google Scholar]
- Fjær, E.; Nes, O.-M. The impact of heterogeneity on the anisotropic strength of an outcrop shale. Rock Mech. Rock Eng. 2014, 47, 1603–1611. [Google Scholar] [CrossRef]
- Zinszner, B.; Meynier, P.; Cabrera, J.; Volant, P. Ultrasonic, sonic ans seismic waves velocity in shale from tournemire tunnel. Impact of anisotropy and natural fractures. Oil Gas Sci. Technol. 2002, 57, 341–353. [Google Scholar] [CrossRef]
- Huang, L.C.; Xu, Z.S.; Zhou, C.Y. Modeling and monitoring in a soft argillaceous shale tunnel. Acta Geotech. 2009, 4, 273–282. [Google Scholar] [CrossRef]
- Niandou, H.; Shao, J.; Henry, J.; Fourmaintraux, D. Laboratory investigation of the mechanical behaviour of tournemire shale. Int. J. Rock Mech. Min. Sci. 1997, 34, 3–16. [Google Scholar] [CrossRef]
- Hsu, S.-C.; Nelson, P.P. Mechanical properties and failure mechanisms for clay shale masses. In Proceedings of the DC Rocks 2001, the 38th U.S. Symposium on Rock Mechanics (USRMS), Washington, DC, USA, 7–10 July 2001; American Rock Mechanics Association: Alexandria, VA, USA, 2001. [Google Scholar]
- Mese, A.; Tutuncu, A. Mechanical, acoustic, and failure properties of shales. In Proceedings of the DC Rocks 2001, the 38th U.S. Symposium on Rock Mechanics (USRMS), Washington, DC, USA, 7–10 July 2001; American Rock Mechanics Association: Alexandria, VA, USA, 2001. [Google Scholar]
- Ciz, R.; Shapiro, S.A. Stress-dependent anisotropy in transversely isotropic rocks: Comparison between theory and laboratory experiment on shale. Geophysics 2009, 74, D7–D12. [Google Scholar] [CrossRef]
- Cho, J.-W.; Kim, H.; Jeon, S.; Min, K.-B. Deformation and strength anisotropy of asan gneiss, boryeong shale, and yeoncheon schist. Int. J. Rock Mech. Min. Sci. 2012, 50, 158–169. [Google Scholar] [CrossRef]
- Hathon, L.A.; Myers, M.T. Shale rock properties: Peak strength, acoustic anisotropy and rock fabric. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012; American Rock Mechanics Association: Alexandria, VA, USA, 2012. [Google Scholar]
- Fjær, E.; Nes, O.M. Strength anisotropy of mancos shale. In Proceedings of the 47th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 23–26 June 2013; American Rock Mechanics Association: Alexandria, VA, USA, 2013. [Google Scholar]
- Park, B.; Min, K.-B. Bonded-particle discrete element modeling of mechanical behavior of transversely isotropic rock. Int. J. Rock Mech. Min. Sci. 2015, 76, 243–255. [Google Scholar] [CrossRef]
- Wu, Y.; Li, X.; He, J.; Zheng, B. Mechanical properties of longmaxi black organic-rich shale samples from south china under uniaxial and triaxial compression states. Energies 2016, 9, 1088. [Google Scholar] [CrossRef]
- McLamore, R.T.; Gray, K.E. A strength criterion for anisotropic rocks based upon experimental observations. In Proceedings of the Annual Meeting of the American Institute of Mining, Metallurgical and Petroleum Engineers, Los Angeles, CA, USA, 19–23 February 1967. [Google Scholar]
- Wu, Z.; Zuo, Y.; Wang, S.; Yi, T.; Chen, S.; Yu, Q.; Li, W.; Sunwen, J.; Xu, Y.; Wang, R.; et al. Numerical simulation and fractal analysis of mesoscopic scale failure in shale using digital images. J. Pet. Sci. Eng. 2016, 145, 592–599. [Google Scholar] [CrossRef]
- He, J.; Afolagboye, L.O. Influence of layer orientation and interlayer bonding force on the mechanical behavior of shale under brazilian test conditions. Acta Mech. Sin. 2017, 1–10. [Google Scholar] [CrossRef]
- Duan, K.; Kwok, C.Y.; Pierce, M. Discrete element method modeling of inherently anisotropic rocks under uniaxial compression loading. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 1150–1183. [Google Scholar] [CrossRef]
- Lisjak, A.; Tatone, B.S.A.; Grasselli, G.; Vietor, T. Numerical modelling of the anisotropic mechanical behaviour of opalinus clay at the laboratory-scale using fem/dem. Rock Mech. Rock Eng. 2014, 47, 187–206. [Google Scholar] [CrossRef]
- Chen, H.; Jiao, Y.; Liu, Y. Investigating the microstructural effect on elastic and fracture behavior of polycrystals using a nonlocal lattice particle model. Mater. Sci. Eng. A 2015, 631, 173–180. [Google Scholar] [CrossRef]
- Chen, H.J.; Jiao, Y.; Liu, Y. A nonlocal lattice particle model for fracture simulation of anisotropic materials. Compos. Part B Eng. 2016, 90, 141–151. [Google Scholar] [CrossRef]
- Chen, T.; Feng, X.; Zhang, X.; Cao, W.; Changjian, F.U. Experimental study on mechanical and anisotropic properties of black shale. Chin. J. Rock Mech. Eng. 2014, 33, 1772–1779. [Google Scholar]
- Sang, Y.; Yang, S.; Zhao, F.; Hou, B. Research on anisotropy and failure characteristics of southern marine shale rock. Drill. Prod. Technol. 2015, 38, 71–74. [Google Scholar]
- Jia, C.G.; Chen, J.H.; Guo, Y.T.; Yang, C.H.; Xu, J.B.; Wang, L. Research on mechanical behaviors and failure modes of layer shale. Rock Soil Mech. 2013, 34, 57–61. [Google Scholar]
- Yang, H.; Shen, R.; Fu, L. Composition and mechanical properties of gas shale. Pet. Drill. Tech. 2013, 31–35. [Google Scholar]
- Saroglou, H.; Tsiambaos, G. A modified hoek–brown failure criterion for anisotropic intact rock. Int. J. Rock Mech. Min. Sci. 2008, 45, 223–234. [Google Scholar] [CrossRef]
- Jaeger, J.C. Shear failure of anistropic rocks. Geol. Mag. 1960, 97, 65–72. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. PFC2D (Particle Flow Code in 2-Dimensions), version 4.0; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2008. [Google Scholar]
- Potyondy, D.O.; Cundall, P.A. Abonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosyst. Eng. 2015, 18, 1–28. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Wong, L.N.Y. Cracking processes in rock-like material containing a single flaw under uniaxial compression: A numerical study based on parallel bonded-particle model approach. Rock Mech. Rock Eng. 2012, 45, 711–737. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Wong, L.N.Y. Crack initiation, propagation and coalescence in rock-like material containing two flaws: A numerical study based on bonded-particle model approach. Rock Mech. Rock Eng. 2012, 46, 1001–1021. [Google Scholar] [CrossRef]
- Mas Ivars, D.; Pierce, M.E.; Darcel, C.; Reyes-Montes, J.; Potyondy, D.O.; Paul Young, R.; Cundall, P.A. The synthetic rock mass approach for jointed rock mass modelling. Int. J. Rock Mech. Min. Sci. 2011, 48, 219–244. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Hagan, P.C.; Mitra, R.; Hebblewhite, B.K. Parametric study of smooth joint parameters on the shear behaviour of rock joints. Rock Mech. Rock Eng. 2014, 48, 923–940. [Google Scholar] [CrossRef]
- Bahrani, N.; Kaiser, P.K.; Valley, B. Distinct element method simulation of an analogue for a highly interlocked, non-persistently jointed rockmass. Int. J. Rock Mech. Min. Sci. 2014, 71, 117–130. [Google Scholar] [CrossRef]
- Cheng, C.; Chen, X.; Zhang, S. Multi-peak deformation behavior of jointed rock mass under uniaxial compression: Insight from particle flow modeling. Eng. Geol. 2016, 213, 25–45. [Google Scholar] [CrossRef]
- Peng, J.; Wong, L.N.Y.; Teh, C.I. Influence of grain size heterogeneity on strength and micro-cracking behavior of crystalline rocks. J. Geophys. Res. Solid Earth 2017, 122, 1054–1073. [Google Scholar] [CrossRef]
- Han, Y.; Damjanac, B.; Nagel, N. A microscopic numerical system for modeling interaction between natural fractures and hydraulic fracturing. In Proceedings of the 46th US Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012. [Google Scholar]
- Szwedzicki, T. A hypothesis on modes of failure of rock samples tested in uniaxial compression. Rock Mech. Rock Eng. 2007, 40, 97–104. [Google Scholar] [CrossRef]
- Vervoort, A.; Min, K.-B.; Konietzky, H.; Cho, J.-W.; Debecker, B.; Dinh, Q.-D.; Frühwirt, T.; Tavallali, A. Failure of transversely isotropic rock under brazilian test conditions. Int. J. Rock Mech. Min. Sci. 2014, 70, 343–352. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Cook, N.G.W.; Zimmerman, R.W. Fundamentals of Rock Mechanics, 4th ed.; Blackwell Publishing: Hoboken, NJ, USA, 2007. [Google Scholar]






| Parameters | Descriptions | References |
|---|---|---|
| Ratio between the failure stresses in the two principal directions parallel and perpendicular to the bedding planes, respectively | [7] | |
| Ratio of the maximum to minimum failure strengths | [7] | |
| Ratio of the maximum to minimum uniaxial compressive strength (UCS) | [11] | |
| Ratio of the strength difference to the maximum strength | [15] | |
| Ratio between the UCS perpendicular to the beddings and the minimum UCS | [27] |
| Samples | Description | Inclination Angle β (°) | Confinement (MPa) | Ref. |
|---|---|---|---|---|
| Greenriver shale-1 | Light brown to light gray; highly laminated, composed of fine grained calcite and dolomite particles inter-bedded with kerogen | 0, 15, 20, 30, 45, 60, 75, 90 | 7, 35, 70, 100, 170 | [16] |
| Greenriver shale-2 | Much darker, with more oil; highly laminated, composed of fine grained calcite and dolomite particles inter-bedded with kerogen | 0, 10, 20, 30, 40, 60, 90 | 7, 35, 70, 100, 170 | [16] |
| Outcrop shale-#8 | Gray to dark, with obvious plane of anisotropy shown in the photographs | 0, 15, 30, 45, 60, 75, 90 | 3, 21, 35, 48, 69 | [2] |
| Top seal shale | - | 0, 15, 30, 45, 60, 75, 90 | 3, 7, 14, 21, 35 | [2] |
| Shale-1 | Black shale from outcrop of Longmaxi Formation in China, with laminated structures from the SEM images | 0, 30, 60, 90 | 0, 10, 20, 30 | [25] |
| Shale-2 | Cored black shale (3502.61~3508.63 m deep) of Longmaxi Formation in Sichuan, China, with planes of anisotropy | 0, 15, 30, 45, 60, 75, 90 | 0, 10, 20, 30, 40 | [24] |
| Shale-3 | Black shale at the lower part of Longmaxi Formation in Guizhou, China, with laminated structures and micro-fissures from the SEM images | 0, 45, 90 | 0, 5, 10, 15, 20, 25 | [26] |
| Shale-4 | Black shale of Niutitang Formation in China, showing obvious sedimentary rock feature from micrometer scale, with lamellar minerals | 0, 30, 45, 60, 90 | 0, 10, 20, 30, 40, 50 | [23] |
| Shale-5 | Black shale from outcrop of Longmaxi Formation in Chongqing, China, with visible planes of anisotropy | 30, 60, 90 | 0, 20, 40, 60, 100 | This study |
| Inclination Angle β (°) | Vp (m/s) | UCS (MPa) | E (GPa) |
|---|---|---|---|
| 30 | 4370 | 191.3 | 29.8 |
| 60 | 4706 | 176.6 | 32.7 |
| 90 | 4964 | 200.2 | 34.5 |
| Grain (Particles) | Cement (Parallel Bonds) | ||
|---|---|---|---|
| Ball density (kg/m3) | 2700 | Bond modulus (GPa) | 21 |
| Minimum ball radius (mm) | 0.36 | Normal bond strength (MPa) | 90 |
| Ball radius ratio Rmax/Rmin | 1.66 | S.D. 1 normal bond strength (MPa) | 15 |
| Contact modulus Ec (GPa) | 21 | Shearing bond strength (MPa) | 90 |
| Coefficient of friction | 1.0 | S.D. 1 shearing bond strength (MPa) | 15 |
| Normal to shearing stiffness ratio kn/ks | 2.5 | Normal to shearing bond stiffness ratio / | 2.5 |
| Parameters | Values |
|---|---|
| Cohesion Csj (MPa) | 20 |
| Friction angle φj (°) | 50 |
| Dilation angle ψj (°) | 0 |
| Normal stiffness kn,sj (GPa/m) | 1500 |
| Shear stiffness ks,sj (GPa/m) | 2500 |
| Tensile strength σn,sj (MPa) | 5 |
| SA1 | SA2 | ||||||
|---|---|---|---|---|---|---|---|
| = 10° | = 30° | = 50° | = 10° | = 30° | = 50° | ||
| = 10 MPa | I1 | I1 | I1 | = 10 MPa | II2 | I2 | I2 |
| = 20 MPa | III1 | II1 | II1 | = 20 MPa | III2 | II2 | I2 |
| = 40 MPa | IV1 | IV1 | II1 | = 40 MPa | III2 | III2 | I2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, C.; Li, X.; Qian, H. Anisotropic Failure Strength of Shale with Increasing Confinement: Behaviors, Factors and Mechanism. Materials 2017, 10, 1310. https://doi.org/10.3390/ma10111310
Cheng C, Li X, Qian H. Anisotropic Failure Strength of Shale with Increasing Confinement: Behaviors, Factors and Mechanism. Materials. 2017; 10(11):1310. https://doi.org/10.3390/ma10111310
Chicago/Turabian StyleCheng, Cheng, Xiao Li, and Haitao Qian. 2017. "Anisotropic Failure Strength of Shale with Increasing Confinement: Behaviors, Factors and Mechanism" Materials 10, no. 11: 1310. https://doi.org/10.3390/ma10111310
APA StyleCheng, C., Li, X., & Qian, H. (2017). Anisotropic Failure Strength of Shale with Increasing Confinement: Behaviors, Factors and Mechanism. Materials, 10(11), 1310. https://doi.org/10.3390/ma10111310




