Effective Thermal Expansion Property of Consolidated Granular Materials
Abstract
:1. Introduction
2. Mathematical Models
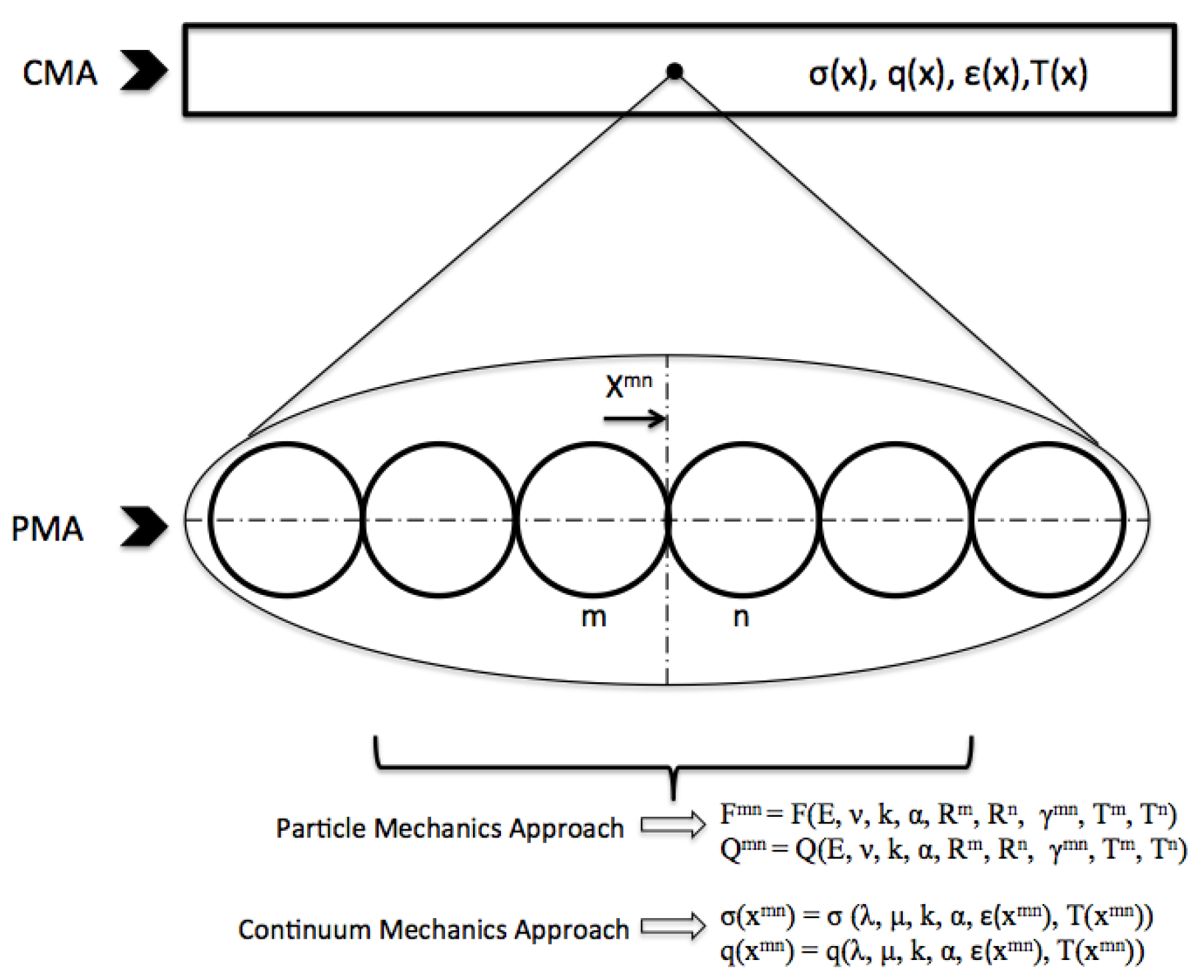
2.1. Particle Mechanics Approach
2.2. Conventional Continuum Mechanics Approach
2.3. Comparison of the Particle Mechanics Approach and the Conventional Continuum Mechanics Approach
3. Derivation of the Effective Thermal Expansion Coefficient for Thermally-Assisted Compaction of Granular Beds
An Application of the Proposed Effective Thermal Expansion Coefficient
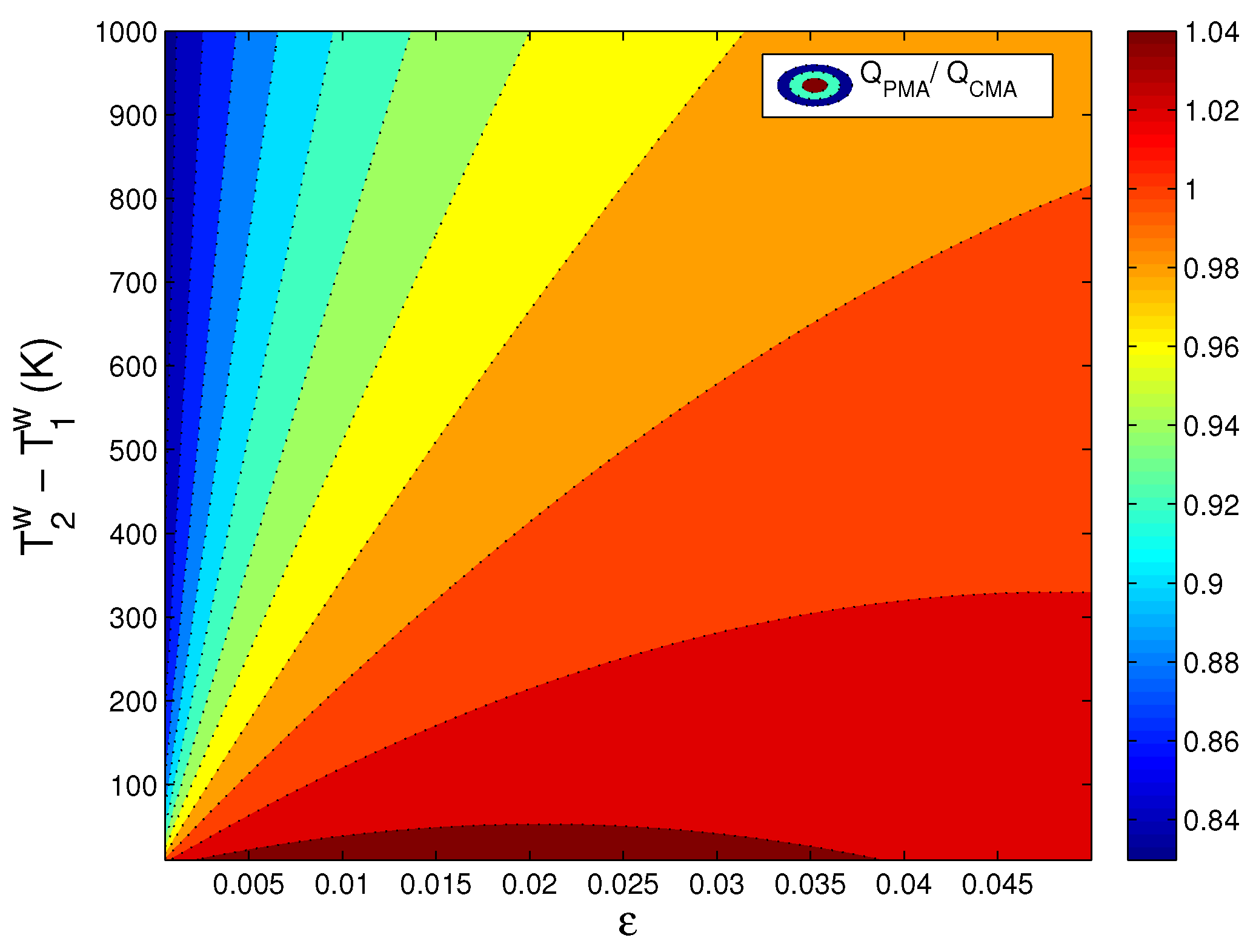
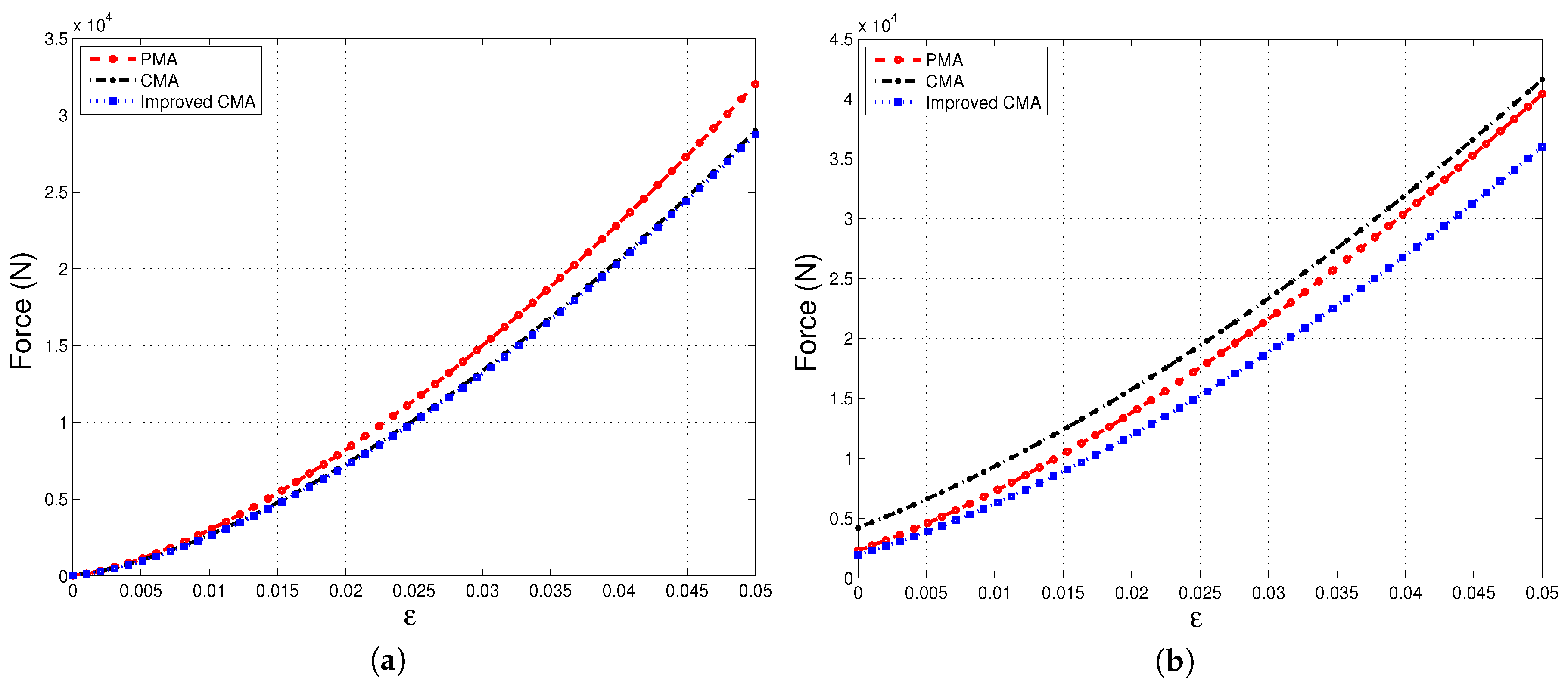
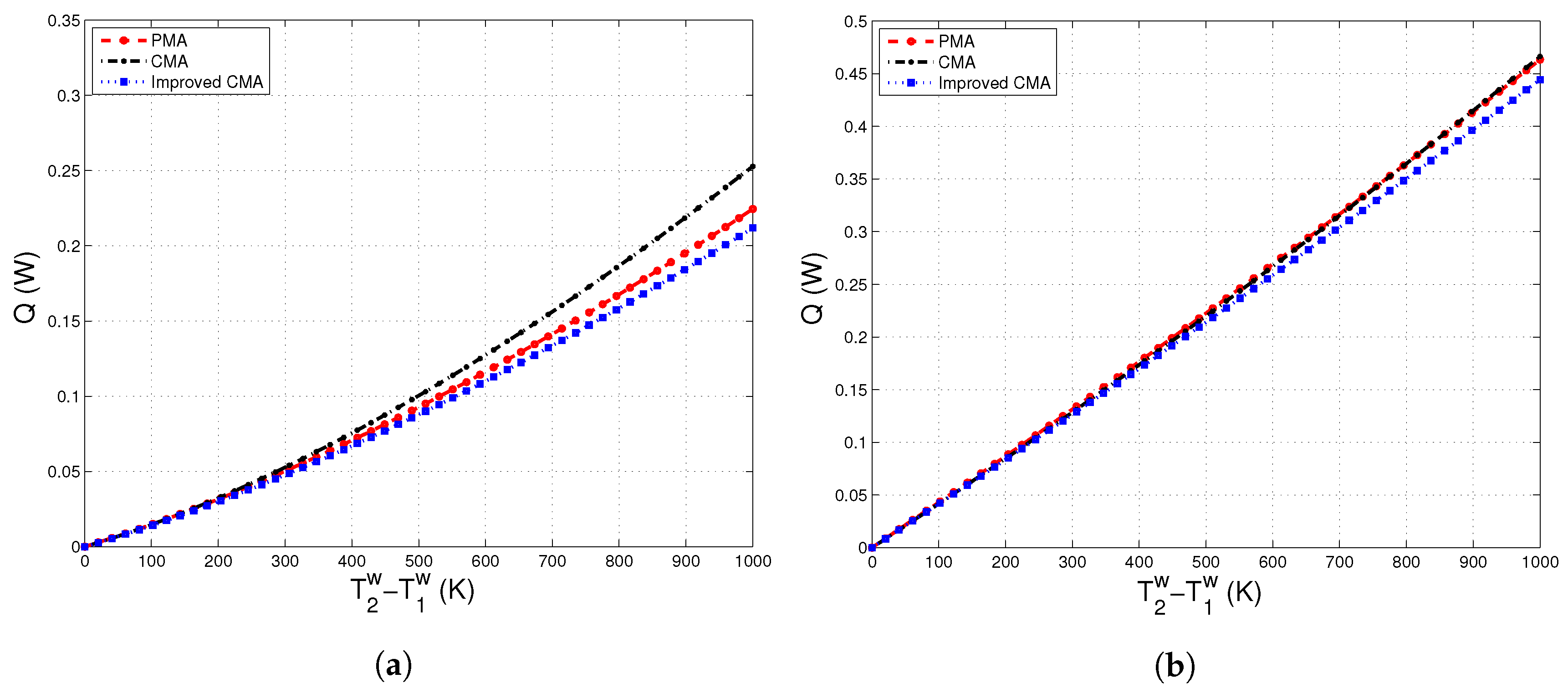
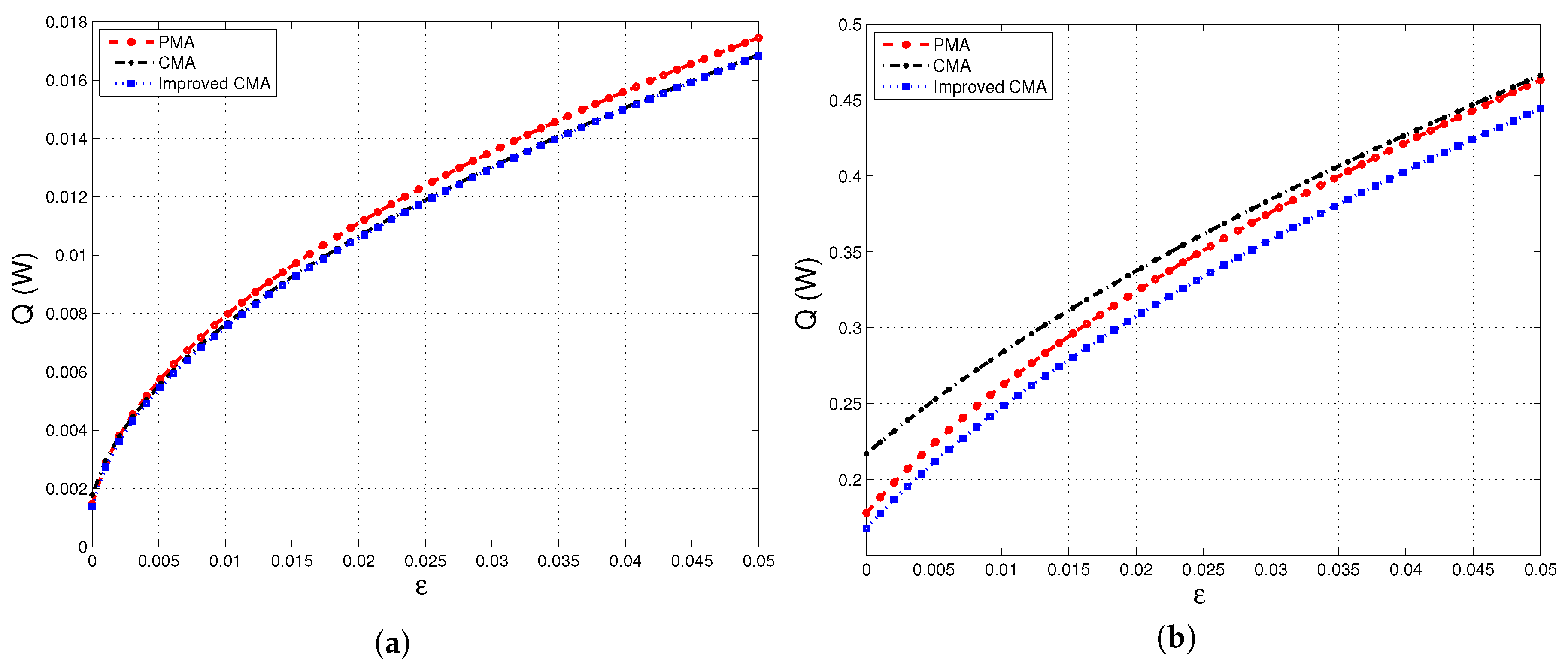
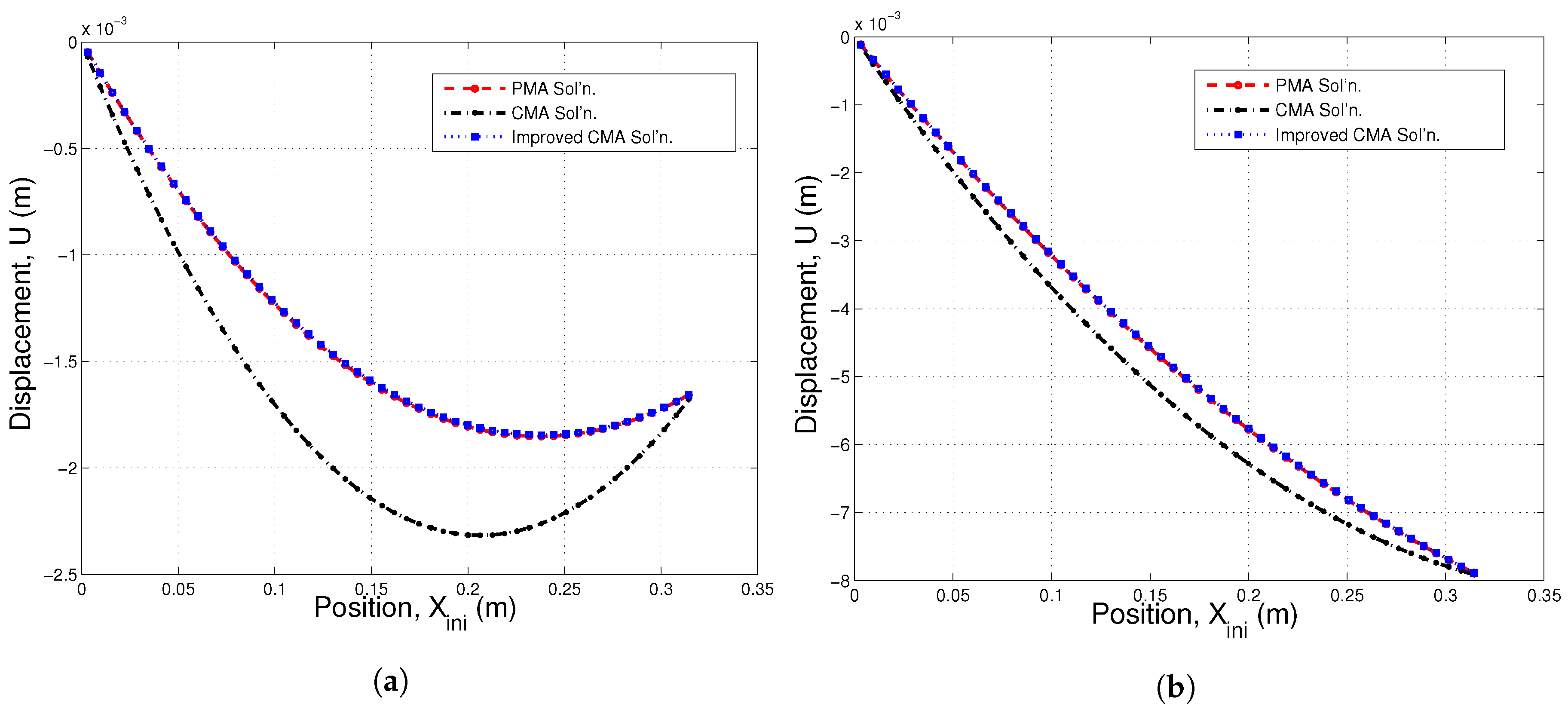
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PMA | Particle Mechanics Approach |
| CMA | Continuum Mechanics Approach |
| Symbol | |
| Young’s modulus of the individual particle m | |
| Poisson’s ratio of the individual particle m | |
| Thermal conductivity of the individual particle m | |
| Thermal expansion coefficient of the individual particle m | |
| Temperature of the individual particle m | |
| Radius of the individual particle m | |
| Hertzian contact area between the particles m and n | |
| Overlap at the contact of the particles m and n | |
| Temperature at the wall surface |
References
- Jaeger, H.M.; Nagel, S.R.; Behringer, R.P. Granular solids, liquids, and gases. Rev. Mod. Phys. 1996, 68, 1259–1273. [Google Scholar]
- Chan, C.K.; Tien, C.L. Conductance of packed spheres in vacuum. J. Heat Transf. 1973, 95, 302–308. [Google Scholar] [CrossRef]
- Kaganer, M.G. Contact heat transfer in granular material under vacuum. J. Eng. Phys. 1966, 11, 19–22. [Google Scholar] [CrossRef]
- Batchelor, G.K.; O’Brien, R.W. Thermal or electrical conduction through a granular material. Proc. R. Soc. Lond. A Math. Phys. Sci. 1977, 355, 313–333. [Google Scholar] [CrossRef]
- Hadley, G.R. Thermal conductivity of packed metal powders. Int. J. Heat Mass Transf. 1986, 29, 909–920. [Google Scholar] [CrossRef]
- Nozad, I.; Carbonell, R.G.; Whitaker, S. Heat conduction in multiphase systems—II: Experimental method and results for three-phase systems. Chem. Eng. Sci. 1985, 40, 857–863. [Google Scholar] [CrossRef]
- Shonnard, D.R.; Whitaker, S. The effective thermal conductivity for a point contact porous medium: An experimental study. Int. J. Heat Mass Transf. 1989, 32, 503–512. [Google Scholar] [CrossRef]
- Sridhar, M.R.; Yovanovich, M.M. Elastoplastic contact conductance model for isotropic conforming rough surfaces and comparison with experiments. J. Heat Transf. 1996, 118, 3–9. [Google Scholar] [CrossRef]
- Fletcher, L.S. Recent developments in contact conductance heat transfer. Am. Soc. Mech. Eng. Trans. J. Heat Transf. 1988, 110, 1059–1070. [Google Scholar] [CrossRef]
- Majumdar, A.; Tien, C. Fractal network model for contact conductance. Am. Soc. Mech. Eng. Trans. J. Heat Transf. Ser. C 1991, 113, 516–525. [Google Scholar] [CrossRef]
- Bahrami, M.; Yovanovich, M.M.; Culham, J.R. A compact model for spherical rough contacts. Trans. Am. Soc. Mech. Eng. J. Tribol. 2005, 127, 884. [Google Scholar] [CrossRef]
- Majmudar, T.S.; Behringer, R.P. Contact force measurements and stress-induced anisotropy in granular materials. Nature 2005, 435, 1079–1082. [Google Scholar]
- Yun, T.S.; Santamarina, J.C. Fundamental study of thermal conduction in dry soils. Granul. Matter 2008, 10, 197–207. [Google Scholar]
- Chen, K.; Cole, J.; Conger, C.; Draskovic, J.; Lohr, M.; Klein, K.; Scheidemantel, T.; Schiffer, P. Granular materials: Packing grains by thermal cycling. Nature 2006, 442, 257. [Google Scholar]
- Chaudhuri, B.; Muzzio, F.J.; Tomassone, M.S. Modeling of heat transfer in granular flow in rotating vessels. Chem. Eng. Sci. 2006, 61, 6348–6360. [Google Scholar] [CrossRef]
- Cook, C.A.; Cundy, V.A. Heat transfer between a rotating cylinder and a moist granular bed. Int. J. Heat Mass Transf. 1995, 38, 419–432. [Google Scholar] [CrossRef]
- Natarajan, V.V.R.; Hunt, M.L. Kinetic theory analysis of heat transfer in granular flows. Int. J. Heat Mass Transf. 1998, 41, 1929–1944. [Google Scholar] [CrossRef]
- Li, J.; Mason, D.J. A computational investigation of transient heat transfer in pneumatic transport of granular particles. Powder Technol. 2000, 112, 273–282. [Google Scholar] [CrossRef]
- Kaneko, Y.; Shiojima, T.; Horio, M. DEM simulation of fluidized beds for gas-phase olefin polymerization. Chem. Eng. Sci. 1999, 54, 5809–5821. [Google Scholar] [CrossRef]
- Hertz, H. On the contact of elastic solids. J. Reine Angew. Math. 1881, 92, 110. [Google Scholar]
- Mindlin, R.D. Compliance of Elastic Bodies in Contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar]
- Mindlin, R.D.; Deresiewicz, H. Elastic spheres in contact under varying oblique forces. J. Appl. Mech. 1953, 20, 327–344. [Google Scholar]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar]
- Feng, Y.T.; Han, K.; Li, C.F.; Owen, D.R.J. Discrete thermal element modelling of heat conduction in particle systems: Basic formulations. J. Comput. Phys. 2008, 227, 5072–5089. [Google Scholar] [CrossRef]
- Gonzalez, M.; Cuitiño, A.M. Microstructure evolution of compressible granular systems under large deformations. J. Mech. Phys. Solids 2016, 93, 44–56. [Google Scholar] [CrossRef]
- Vargas-Escobar, W.L. Discrete Modeling of Heat Conduction in Granular Media. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2002. [Google Scholar]
- Makse, H.A.; Gland, N.; Johnson, D.L.; Schwartz, L.M. Why effective medium theory fails in granular materials. Phys. Rev. Lett. 1999, 83, 5070–5073. [Google Scholar] [CrossRef]
- Makse, H.A.; Gland, N.; Johnson, D.L.; Schwartz, L. The apparent failure of effective medium theory in granular materials. Phys. Chem. Earth Part A Solid Earth Geodesy 2001, 26, 107–111. [Google Scholar] [CrossRef]
- Zheng, S.; Cuitino, A.M. Consolidation Behavior of Inhomogeneous Granular Beds of Ductile Particles using a Mixed Discrete-Continuum Approach. KONA Powder Part. J. 2002, 20, 168–177. [Google Scholar] [CrossRef]
- Koynov, A.; Akseli, I.; Cuitiño, A.M. Modeling and simulation of compact strength due to particle bonding using a hybrid discrete-continuum approach. Int. J. Pharm. 2011, 418, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, M.; Cuitiño, A.M. A nonlocal contact formulation for confined granular systems. J. Mech. Phys. Solids 2012, 60, 333–350. [Google Scholar] [CrossRef]
- Walton, K. The effective elastic moduli of model sediments. Geophys. J. R. Astron. Soc. 1975, 43, 293–306. [Google Scholar] [CrossRef]
- Vargas, W.L.; McCarthy, J.J. Heat conduction in granular materials. Am. Inst. Chem. Eng. J. 2001, 47, 1052–1059. [Google Scholar]
- Vargas, W.L.; McCarthy, J.J. Thermal expansion effects and heat conduction in granular materials. Phys. Rev. E 2007, 76, 041301. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Lu, Z.; Abdou, M.; Ying, A. 3D Micromechanical modeling of packed beds. J. Nucl. Mater. 2001, 299, 101–110. [Google Scholar] [CrossRef]
- Siu, W.W.M.; Lee, S.K. Transient temperature computation of spheres in three-dimensional random packings. Int. J. Heat Mass Transf. 2004, 47, 887–898. [Google Scholar] [CrossRef]
- Küçük, G.; Gonzalez, M.; Cuitino, A.M. Thermo-Mechanical Behavior of Confined Granular Systems. In Lecture Notes in Applied and Computational Mechanics: Innovative Numerical Approaches for Multi-Field and Multi-Scale Problems; Springer International Publishing: Cham, Switzerland, 2016; pp. 41–57. [Google Scholar]
- Markov, K.Z. Elementary micromechanics of heterogeneous media. In Heterogeneous Media; Birkhäuser: Boston, MA, USA, 2000; pp. 1–162. [Google Scholar]
- Norris, A.N.; Johnson, D.L. Nonlinear elasticity of granular media. Trans. Am. Soc. Mech. Eng. J. Appl. Mech. 1997, 64, 39–49. [Google Scholar] [CrossRef]
- Vargas, W.L.; McCarthy, J.J. Stress effects on the conductivity of particulate beds. Chem. Eng. Sci. 2002, 57, 3119–3131. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon Press: Oxford, UK, 1959. [Google Scholar]

| 0.49 | 0.49 |
| (a) | (b) |

| 0.49 | 0.49 |
| (a) H | (b) H |
| 0.46 | 0.46 |
| (a) H | (b) H |
| 0.49 | 0.49 |
| (a) h | (b) h |
| 0.49 | 0.49 |
| (a) h | (b) h |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Küçük, G.; Gonzalez, M.; Cuitiño, A.M. Effective Thermal Expansion Property of Consolidated Granular Materials. Materials 2017, 10, 1289. https://doi.org/10.3390/ma10111289
Küçük G, Gonzalez M, Cuitiño AM. Effective Thermal Expansion Property of Consolidated Granular Materials. Materials. 2017; 10(11):1289. https://doi.org/10.3390/ma10111289
Chicago/Turabian StyleKüçük, Gülşad, Marcial Gonzalez, and Alberto M. Cuitiño. 2017. "Effective Thermal Expansion Property of Consolidated Granular Materials" Materials 10, no. 11: 1289. https://doi.org/10.3390/ma10111289
APA StyleKüçük, G., Gonzalez, M., & Cuitiño, A. M. (2017). Effective Thermal Expansion Property of Consolidated Granular Materials. Materials, 10(11), 1289. https://doi.org/10.3390/ma10111289




