Techno-Economic Modeling and Analysis of Redox Flow Battery Systems

Abstract

A techno-economic model was developed to investigate the influence of components on the system costs of redox flow batteries. Sensitivity analyses were carried out based on an example of a 10 kW/120 kWh vanadium redox flow battery system, and the costs of the individual components were analyzed. Particular consideration was given to the influence of the material costs and resistances of bipolar plates and energy storage media as well as voltages and electric currents. Based on the developed model, it was possible to formulate statements about the targeted optimization of a developed non-commercial vanadium redox flow battery system and general aspects for future developments of redox flow batteries.

1. Introduction

As the contribution of renewable energy sources to power grids increases, so too does the need for energy storage [1,2]. Local electrical and electrochemical energy storages can play an important role in a variety of different tasks [3]. Redox flow batteries that store electrical energy in fluids by chemical reactions are one type of electrochemical energy store [4,5]. They allow energy and power to be independently scaled and matched to the particular demand. The energy converter consists of electrochemical cells that are assembled to form a cell stack. Most energy storage media consist of inorganic acids or bases in which metallic salts or other compounds are dissolved as redox active components. However, there are also storage media consisting of gases such as hydrogen and oxygen as well as organic substances [6]. It is the great diversity of possible chemical reactions that produces such a variety of very different cell structures in which different electrode materials can be used. In addition, catalysts can be used to accelerate reactions and so increase power densities. In the interests of research and industrial implementation and optimization, it is important to discuss which components contribute in what ways to the total cost of a battery system. It is important to know and understand the general effects of different battery parameters on system costs. From this knowledge we can draw conclusions so that we can focus work and reduce system costs in a targeted manner.

This work focuses on an easy approach to understanding relations of material choice and costs of Redox Flow Battery Systems. The main objective is the link between the cost and performance parameters of single components and the overall costs of a battery system. It is not yet fully understood which components contribute the most to final system costs. Some redox flow batteries (RFB) systems are used commercially already, whereas most of the systems are still in development. As a next step to cost-effective utilization, the price structure must be understood better so costs can be optimized. Most publications on RFB cost optimization were performed on a single technology like the work of Spellman et al. or Viswanathan et al. [7,8]. This work tries to break final system costs down into single component costs. As RFBs are the object of current research, for most components the best materials are yet to be found and there are different ways of realizing a battery system. This ranges from very small material variations for one of the cell components to various electrolyte solutions, all of which have special requirements. This leads to varying capital expenditures, operational lifetimes, specific energy, and performance costs. So far the all-vanadium redox flow battery seems to be most promising for commercial use. However, other systems are also under investigation. The model suggested in this work is not restricted to all-vanadium redox flow batteries but makes it possible to investigate and compare different systems. The model will be demonstrated in a case study about a vanadium redox flow battery with 10 kW power and 12 h storage time. As a first approximation, a simplified model was created that can be supplemented even with missing experimental data.

2. Approach

One of the biggest advantages of RFB is the mostly independent scalability of power and energy. The power is proportional to the number and size of the cells, whereas the energy can simply be scaled by the electrolyte volume (the storage media) and the concentration of the active species. For that reason the model is divided into a cost model for the system power and a cost model for the storable energy:

$$\text{RFB Costs}=C_{Power}+C_{Energy}+C_{Area\_needs}+C_{Facilities}$$

(1)

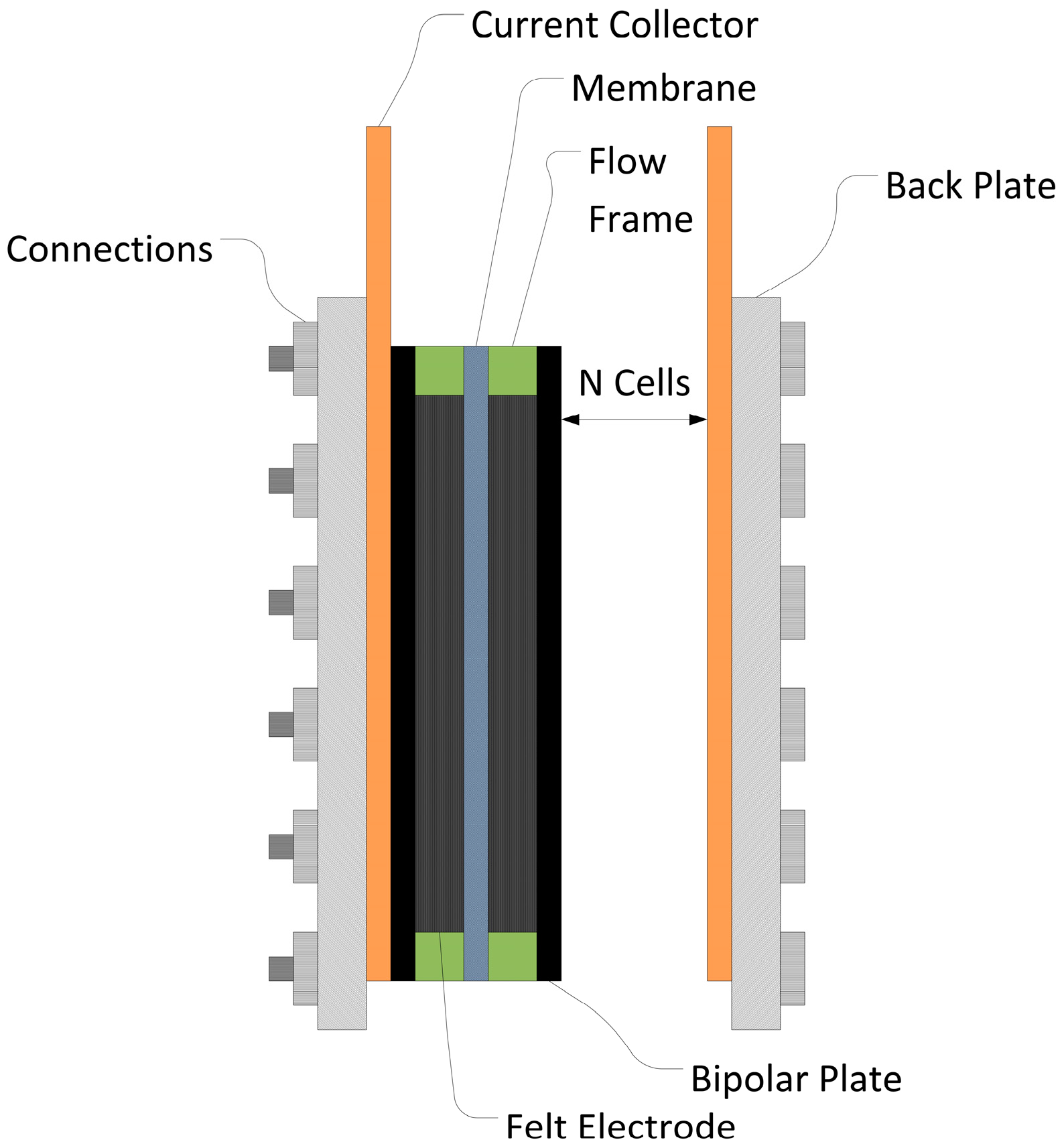
The costs for power and energy are broken down into their essential factors below. For example, the costs of the stacks were calculated from the individual components (Figure 1). Costs for power and energy were calculated depending on the output power and the storable energy. No further account was taken of the costs for the area needs (C_{Area_needs}) or housing (C_Facilities) for the whole battery installation in the subsequent analysis.

3. Model Development and Description

3.1. Cell Voltage

An understanding of the relations between single component performance parameters and overall system performance is the basis for a techno-economic model of this type, so a drawing of those relations is the starting point of the work. The working principle of redox-flow batteries can be described as a chemical reaction of two redox couples that result from the combination of two corresponding half-cell reactions, as follows:

$$\begin{array}{llll}\text{Anode}:& {\mathrm{A}}^x& \to {\mathrm{A}}^{x+z}+z{\mathrm{e}}^{-}& {\phi }_{\mathrm{A}}\\ \text{Cathode}:& {\mathrm{C}}^y+z{\mathrm{e}}^{-}& \to {\mathrm{C}}^{y-z}& {\phi }_{\mathrm{C}}\\ \text{Cell}:& {\mathrm{A}}^x+{\mathrm{C}}^y& \to {\mathrm{A}}^{x+z}+{\mathrm{C}}^{y-z}& U_{rev}={\phi }_{\mathrm{C}}-{\phi }_{\mathrm{A}}.\end{array}$$

As one important factor, the ohmic losses of a stack reduce the efficiency of the battery. The standard open circuit voltage (U_rev) can be calculated by the Nernst equation as follows:

$$U_{rev}=\left({\phi }_C^0-{\phi }_A^0\right)+\frac{RT}{zF}\ln \left(\frac{c_{C,ox}·c_{A,red}}{c_{C,red}·c_{A,ox}}\right)$$

(2)

where ${\phi }_C^0$ and ${\phi }_A^0$ are the standard redox potentials for the reaction at the positive and negative electrodes, R as the universal gas constant, T the temperature, and c_ox and c_red are the molar concentration of the oxidant and reductant. Since a cell has different kinds of losses, the effective cell voltage is calculated as the reversible cell voltage subtracted by all losses inside the cell:

$$U_{cell}=U_{rev}-U_{act}-U_{con}-U_{ohm}$$

(3)

where U_act is the activation overpotential, U_con is the concentration overpotential, and U_ohm is the ohmic overpotential. The non-linear response of the overpotential U_act with the current density can be taken into account using the Butler–Volmer equation, although this requires a knowledge of the material-dependent exchange current densities i₀ and the symmetry factors α (or β) for reactions in a complete cell or cell stack [10]. Chen et al. calculated them with Equations (4) and (5) [11], although it must be remembered that the symmetry factor α and the exchange current density i₀ are strongly electrode material dependent and usually not the same for the charge and discharge process.

$$U_{act}=\alpha \ln \left(\frac{i}{i_0}\right)$$

(4)

$$U_{con}=\frac{RT}{zF}\ln \left(\frac{i_L}{i_L-i}\right)$$

(5)

Since α, i₀, and the limiting current density i_L are difficult to obtain, U_act and U_con were left as constants in an initial approximation so as to be able to supplement the model with measured values later. The overpotentials result in all cases in heat generation, which means a loss in energy and lower battery efficiency. The ohmic losses consist of material resistances and contact resistances between the different cell components. As the choice of component directly influences the ohmic losses, this part is described in more detail with Equations (6) and (7):

$$U_{ohm}=I·\left(R_{Membrane}+2R_{Felt}+R_{BPP}+R_{Contact}+R_{Electrolyte}\right)$$

(6)

$$U_{ohm}=I·\left(\frac{b_{Membrane}}{A_{Active}·{\sigma }_{Membrane}}+2·\frac{b_{Felt}}{A_{Active}·{\sigma }_{Felt}}+\frac{b_{BPP}}{A_{Active}·{\sigma }_{BPP}}+R_{Contact}+R_{Electrolyte}\right)$$

(7)

where b is the thickness, σ is the specific conductivity, A_Active is the active cell area, and R is the ohmic resistance.

As the felt electrode is soaked with electrolyte, the conductivity will be different from the felt-only conductivity. This formula directly relates cell material performances and the current to ohmic losses. It can be seen that the ohmic losses are a function of the electric current. For this reason, the effective cell voltage can only be calculated when the current is known. Contact and electrolyte resistances were treated as constants. The resistance values for membrane, felt, and bipolar plate were broken down by thickness and specific conductivity and made scalable by a reference to the active surface area.

As the voltage is a function of the state of charge (SoC)/depth of discharge (DoD), the average cell voltage has to be calculated in the used SoC range. The effective stack voltage is calculated as the sum of the effective cell voltages:

$$\overline{U_{cell}}=\frac{1}{So{C}_{\max }-So{C}_{\min }}{\displaystyle \underset{So{C}_{\min }}{\overset{So{C}_{\max }}{\int }}{U}_{cell}dSoC}$$

(8)

$$\overline{U_{Stack}}={\Sigma }_{n=1}^N\overline{U_{Cell,n}}$$

(9)

3.2. Costs of Power Conversion

All components except the electrolyte solution and the tank are power components. The power of a battery is the energy that can be provided per unit of time. The mean power was calculated using the following equation:

$$\overline{P}=\overline{U_{Cell}}\times N\times i\times A_{Active}$$

(10)

The number of cells (N), cell voltage ($\overline{U_{Cell}}$), current density (i), and active area (A_Active) of a single cell can be varied for a modification of the power of one stack. At this step of the model, the current density (i) was supposed to be fixed. The stack voltage is the sum of single cell voltages and the current is the product of current density and active area of a single cell. The overall costs of the power components can be summarized by the following simplified formula:

$$C_{Power}=C_{Stack}+C_{Powerelectronics}+C_{Controlengineering}+C_{Fluidregulation}+C_{Power,Assembling}$$

(11)

A stack is an assembly of a certain number of cells and the heart of a redox flow battery. It is the part where electrical energy is converted into chemical energy and back. All other components are needed for the operation of the battery but are not directly involved in the energy conversion. The parts can be broken down into further components:

$$C_{Fluidregulation}=C_{Pumps}+C_{Piping}+C_{Valves}$$

(12)

$$C_{Controlengineering}=C_{Sensor}+C_{Actuator}+C_{Thermalregulation}$$

(13)

The stack components are of great interest as they directly influence the performance of the battery. In simplified terms the cost of one stack is a function of cell number (N) and cell size (A_Active):

$$\begin{array}{l}{C}_{Stack}=C_{BPP}+C_{Felt}+C_{Gasket}+C_{Membrane}+C_{Frame}+C_{Endplate}+C_{Isolationplate}\\ +C_{Currentcollector}+C_{Connections}+C_{Stack,Assembling}\end{array}$$

(14)

$$\begin{array}{l}{C}_{Stack}(N,A_{Active})=\\ C_{S,Assembling}+C_{Connections}+A_{Active}\left(2·C_{Endplate}+C_{Isolationplate}+2·C_{Currentcollector}\right)\\ +\left(N+1\right)·A_{Active}·C_{BPP}+2N·A_{Active}\left(C_{Felt}+C_{Frame}+C_{Gasket}\right)+N·A_{Active}·C_{Membrane}\end{array}$$

(15)

The production costs of the system C_P,Assembling or of the stacks C_S,Assembling could be calculated using the necessary man-hours, specific man-hour costs (costs per hour), and the specific energy costs (costs per hour):

$$C_{Assembling}=t_{manhours}\times \left(c_{manhour}+c_{Energy}\right)$$

(16)

For the configuration of a battery system, the output power of the battery is the first variable that has to be specified. The costs scale with the output power, for which a formula cost as a function of power was targeted. For a battery with one stack, the next step was to determine either the cell size (A_Active) or the number of cells.

For the configuration of a battery, some design parameters had to be specified while others were calculated based on those specifications. The output power and a design current density were determined first. Based on this, either an active cell area or the stack voltage had to be specified. These two approaches are presented below. One has to keep in mind that design values can be varied in a configured battery system. Changes in the operation of the battery will lead to different efficiencies.

3.2.1. Calculation of Costs of Power Conversion by Specification of Active Cell Area

Method 1 specified an active cell area (A_Active) and the costs could be calculated as a function of the output power. The advantage of this method was that, with a fixed current density, the current needed for the cell voltage calculation could be calculated.

$$N=\frac{\overline{P}[\mathrm{W}]}{I\times \overline{U_{cell}}}$$

(17)

$$\begin{array}{l}{C}_{Stack}\left(\overline{P}[\mathrm{W}]\right)=\\ C_{Assembling}+C_{Connections}+A_{Active,Cell}·\left(2·C_{Endplate}+C_{Isolationplate}+2·C_{Currentcollector}\right)\\ +\left(\frac{\overline{P}[\mathrm{W}]}{I·\overline{U_{Cell}}}·A_{Active,Cell}+A_{Active,Cell}\right)·C_{BPP}\\ +2·\frac{\overline{P}[\mathrm{W}]}{I·\overline{U_{Cell}}}·A_{Active,Cell}·\left(C_{Felt}+C_{Frame}+C_{Gasket}\right)\\ +\frac{\overline{P}[\mathrm{W}]}{I·\overline{U_{Cell}}}·A_{Active,Cell}·C_{Membrane}\end{array}$$

(18)

3.2.2. Calculation of Costs of Power Conversion by Specification of Stack Voltage

Method 2 specified a stack voltage which is the sum of the cell voltages. In Equations (4)–(6) it can be seen that the cell voltage changes with the current. A calculation of the active cell area at constant current density is inevitable for the calculation of the cell voltage and number of cells in a stack:

$$A_{Active,Cell}=\frac{\overline{P}[W]}{\overline{U_{Stack}}\times i}$$

(19)

$$\begin{array}{l}{C}_{Stack}\left(\overline{P}\left[\mathrm{W}\right]\right)=\\ C_{Assembling}+C_{Connections}+\frac{\overline{P}\left[\mathrm{W}\right]}{\overline{U_{Stack}}\times i}\left(2C_{Endplate}+C_{Isolationplate}+2C_{Currentcollector}\right)\\ +\left(N\frac{\overline{P}\left[\mathrm{W}\right]}{\overline{U_{Stack}}\times i}+\frac{\overline{P}\left[\mathrm{W}\right]}{\overline{U_{Stack}}\times i}\right)C_{BPP}\\ +2N\frac{\overline{P}\left[\mathrm{W}\right]}{\overline{U_{Stack}}\times i}\left(C_{Felt}+C_{Frame}+C_{Gasket}\right)+N\frac{\overline{P}\left[\mathrm{W}\right]}{\overline{U_{Stack}}\times i}{C}_{Membrane}\end{array}$$

(20)

3.3. Cost of Components

The costs of single components have to be defined in detail. As many parts of RFBs cannot be bought from the market, costs were composed of material costs (MC), either specific as costs per m² or kg, or as costs per unit, and fabrication costs (FC). Most components do not have the same size as the active cell area. One also has to take into account that parts of the material are wasted during fabrication, so a factor for the real material demand per active cell area was needed for that reason. This factor can either be proportional or fixed. In this case, the factor (X_component) was supposed to be fixed to the active cell area.

$$\begin{array}{l}{C}_{Endplate}=X_{Endplate}·\frac{M{C}_{Endplate}}{m^2}+n_{Endplate}·C_{Fabr.Endplate}\\ C_{Isolationplate}=X_{Isolationplate}·\frac{M{C}_{Isolationplate}}{m^2}+n_{Isolationplate}·C_{Fabr.Isolationplate}\\ C_{Currentcollector}=X_{Currentcollector}·\frac{M{C}_{Currentcollector}}{m^2}+n_{Current\mathrm{c}ollector}·C_{Fabr.Current\mathrm{c}ollector}\\ C_{Bipolarplate}=X_{Bipolarplate}\frac{M{C}_{Bipolarplate}}{m^2}+n_{Bipolarplate}·C_{Fabr.BipolarPlate}\\ C_{Felt}=X_{Felt}\frac{M{C}_{Felt}}{m^2}+n_{Felt}·C_{Fabr.Felt}\\ C_{Frame}=\frac{M{C}_{Frame}}{m^2}+n_{Frame}·C_{Fabr.Frame}\\ C_{Gasket}=X_{Gasket}\frac{M{C}_{Gasket}}{m^2}+n_{Gasket}·C_{Fabr.Gasket}\\ C_{Membrane}=X_{Membrane}\frac{M{C}_{Membrane}}{m^2}+n_{Membrane}·C_{Membrane}\end{array}$$

(21)

3.4. Cost of Energy Storage

The costs of energy consisted of electrolyte and tank costs:

$$C_{\text{Energy}}=C_{\text{Electrolyte}}+C_{\text{Tank}}$$

(22)

Broadly speaking, the electrolyte costs consisted of the costs of the active species, which could be more than one in some cases (e.g., Zn/Br RFBs), the costs of the solvent, the costs of additives, and the costs of fabrication:

$$C_{Electrolyte}=C_{ActiveMaterial1}+C_{ActiveMaterial2}+C_{Solvent}+C_{Additive1}+C_{ElectrolyteFabrication}$$

(23)

The costs of the electrolyte scale with the volume. The required volume is directly dependent on the energy (power for a certain time) that has to be stored. The volume of the electrolyte for the required energy capacity for one tank was calculated as follows [7]:

$$\text{Volume} V=\frac{\text{Energy} W[\text{Wh}]}{\overline{U_{cell}}\times \text{SoC range}\times \frac{Fzc}{3600}}$$

(24)

where SoC range is the usable state of charge (SoC), F is Faraday’s constant (C·mol⁻¹), z is the number of electron equivalents per mol, and c is the molar concentration of vanadium species (mol·L⁻¹).

The useable state of charge (SoC) range is a factor that takes into account the fact that the battery is never fully charged or discharged, so not all potentially available capacity can be utilized. This means that a substantial amount of the active species cannot be used for storing energy. As the calculated volume is needed for either the cathode or anode, this volume has to be multiplied by two for the calculation of the total electrolyte amount. The total electrolyte costs could be calculated by the following equation:

$$\begin{array}{l}{\mathrm{C}}_{Electrolyte}\left(\text{Energy }W\right)=2\frac{\text{Energy }W[\text{Wh}]}{\overline{U_{Cell}}\times \text{SoC range}\times \frac{F\left(z_1{c}_1+z_2{c}_2\right)}{3600}}\\ ·\left(\begin{array}{l}{M}_{ActiveMaterial1}{c}_1{\mathrm{C}}_{ActiveMaterial1}+M_{ActiveMaterial2}{c}_2{\mathrm{C}}_{ActiveMaterial2}+\\ M_{Solvent}{c}_{Solvent}{\mathrm{C}}_{Solvent}+M_{Additive1}{c}_{Additive1}{\mathrm{C}}_{Additive1}\end{array}\right)\\ {+\mathrm{C}}_{ElectrolyteFabrication}\end{array}$$

(25)

where F is Faraday’s constant, c is the molar concentration, and z is the number of electron equivalents per mol.

4. Calculations for a 10 kW/120 kWh Vanadium Redox Flow Battery System

A 10 kW vanadium redox flow battery system (VRFB) with a storage time of 12 h and 10 stacks was selected as an example. The data entered in the model are listed in

Table 1. Input values for calculating the specific costs and cost distributions of a 10 kW/120 kWh vanadium redox flow battery.

Parameter	Value	Unit	Parameter	Value	Unit
Mean power	10,000	W	Energy cost	0.3	€/kW
Storage time	12	h	Stack assembling energy	0.3	kWh/cell
Current density	50	mA/cm²	System assembling	–	–
Active area	580	cm²	Power cond. system cost	500	€/kW
Rev. cell voltage	1.255	V	Heat exchanger cost	1500	1/unit
Act. overpotential	0.005	V	Number of heat exchanger	2	unit
Conc. overpotential	0.02	V	Pump cost	1000	1/unit
Number of stacks	10	unit	Number of pumps	2	unit
Stack	–	–	Piping length	50	m
Membrane conductivity	1.44	S/m	Piping cost	20	€/m
Membrane cost	250	€/m²	Number of valves	14	unit
Membrane factor	1.5		Valve cost	30	€/unit
Felt conductivity	83.3	S/m	Number of actuators	2	unit
Felt cost	150	€/m²	Actuator cost	330	€/unit
Felt factor	1.5		Number of sensors	10	unit
BPP conductivity	5300	S/m	Sensor cost	250	€/unit
BPP cost	418	€/m²	System assembling man hour	300	h
BPP factor	1.5	–	System assembling energy	1	kW/h
Gasket cost	392	€/m²	Energy	–	–
Gasket fabr. cost	5	€/unit	Min theoretical SOC	0.2	–
Cell frame cost	100	€/m²	Max theoretical SOC	0.8	–
Cell frame fabrication cost	5	€/unit	Tank cost	1.1	–
Current collector	700	€/m²	Active species cost (Vanadium)	1.5	€/L
Current collector fabrication cost	5	€/unit	Active species concentration (Vanadium)	1.6	mol/L
Isolation plate cost	300	300 €/m²	Solvent cost (H2SO4)	0.0083	€/mol
Isolation plate fabr. cost	20	€/unit	Solvent concentration (H2SO4)	2	mol/L
End plate cost	600	€/m²	Additive 1 cost (H3PO4)	0.98	€/mol
Endplate fabr. cost	20	€/unit	Additive 1 conc. (H3PO4)	0.05	mol/L
Stack connection cost	3	€/unit	Electrolyte production cost	2.5	€/L
Stack assembling man hour	0.3	h/cell	–	–	–
Man hour cost	30	€/h	–	–	–

. All of the values were either as real as possible or were empirical values from constructed prototypes. This helped to verify the entered and calculated data for plausibility. A current density of 50 mA/cm² was assumed for the VRFB. The active area was determined as 580 cm². The theoretical value of the standard potential differences was used as the reversible cell voltage, although the actual value can be higher due to membrane potentials [12]. As described above, activation and concentration overvoltages were taken as constants in an initial approximation. The material values of the stack were taken from manufacturers where possible. The values for the costs of insulation plates, end plates, copper current collectors, gaskets, and the cell frame were taken from our own or from outsourced production. The man-hours, the average stack production time of 0.3 h/cell, and the energy consumption were estimated on the basis of empirical values. The costs of control engineering were incorporated in the sensor costs. The theoretical SOC range was assumed to be 0.2–0.8. The costs of vanadium corresponded to a high price region for vanadium pentoxide. With the calculated specific system costs, it must be remembered that these do not reflect costs that can be achieved in industry but are probably far higher, the reason being the high material costs of very small quantities and a battery system that is not optimized.

Results and Discussion

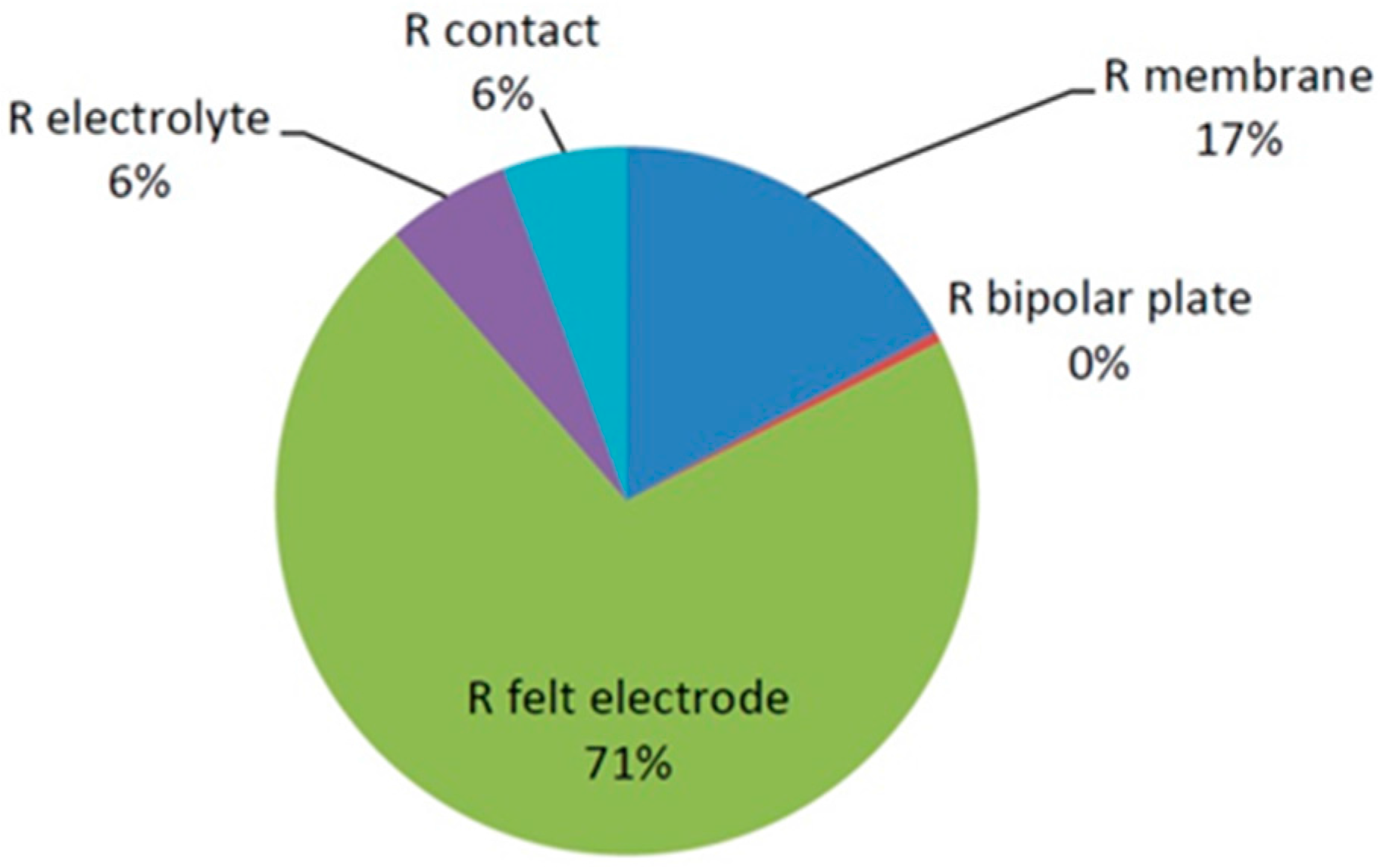
The distribution of the ohmic resistance of a typical VRFB model system is shown in Figure 2. The output values shown in

Table 2. Output values of a 10 kW/120 kWh vanadium redox flow battery.

Parameter	Value	Unit	Parameter	Value	Unit
Total cost	129,310	€	Ohmic resistance electrolyte	0.2	mΩ
Total specific cost	1078	€/kWh	Ohmic resistance contact	0.2	mΩ
Power cost	79,228	€	BPP cost	11,211	€
Power specific cost	7923	€/kWh	Felt cost	11,047	€
Energy cost	50,083	€	Frame cost	3,066	€
Energy specific cost	417	€/kWh	Membrane cost	6,656	€
Stack cost	52,648	€	Gasket cost	16,974	€
Stack specific cost	5265	€/kWh	Assembling cost	2,782	€
System assembling cost	9,000	€	End plate cost	435	€
Power electronics cost	5,000	€	Isolation plate cost	217	€
Fluid components cost	3,420	€	Current collector cost	141	€
Control engineering cost	9,160	€	Energy	–	–
Stack	–	–	Electrolyte cost	41,000	€
Effective cell voltage	1.1286	V	Volume of electrolyte	8,257	L
Number of cells	306	–	Tank cost	9,082	€
IR drop cell	0.1014	V	Active material cost	19,816	€
Ohmic resistance cell	3.5	mΩ	Solvent cost	542	€
Ohmic resistance membrane	0.60	mΩ	Additive cost	405	€
Ohmic resistance BPP	0.0017	mΩ	Fabrication cost	20,641	€
Ohmic resistance felt	2.48	mΩ	–	–	–

suggested a cell resistance of 3.5 mΩ (2.03 Ω·cm²), which roughly equates with the true values of cells and stacks. It is interesting to note that the felt electrode accounted for by far the highest share, at 71%. The wetting with electrolyte should make the felt resistance in the cell much lower than the theoretical value. The electrolyte resistance should also be different. Values for membrane, bipolar plate, and contact resistance can be assumed to be independent of wetting with electrolyte. Only the contact resistance was not specified and the activation over potential with 5 mV very low, which is why it can be assumed that the greatest share of the felt resistance and electrolyte resistance is shifted in favor of the contact resistance and the activation overpotential and the latter accounts for the main proportion of the IR loss.

The true electrolyte and felt resistances should be known so as to improve the model and calculate contact resistances; however, this proved difficult to achieve in experiments. Impedance measurements that take into account the de Levie impedances could perhaps provide experimental access to both [13]. Because the model only takes account of the total of those resistances that matched the measurements, and changes in material properties such as thickness and conductivities are incorporated linearly in the total resistance, further analyses could be undertaken.

The calculated system costs were €129,310 (C_System), or €1078/kWh (c_System) for 12 h storage time. The power-related costs were €79,228 (C_Power); the energy-related costs were €50,083, or €417/kWh (c_Energy). The general equation for the specific storage costs is:

$$c_{System}=\frac{C_{System}}{W}=\frac{C_{Power}+W·c_{Energy}}{W}$$

(26)

where W is the energy content.

This equation makes the specific storage costs significantly higher with low storage times. The same battery with 6 h of storage time (60 kWh) would cost €1738/kWh.

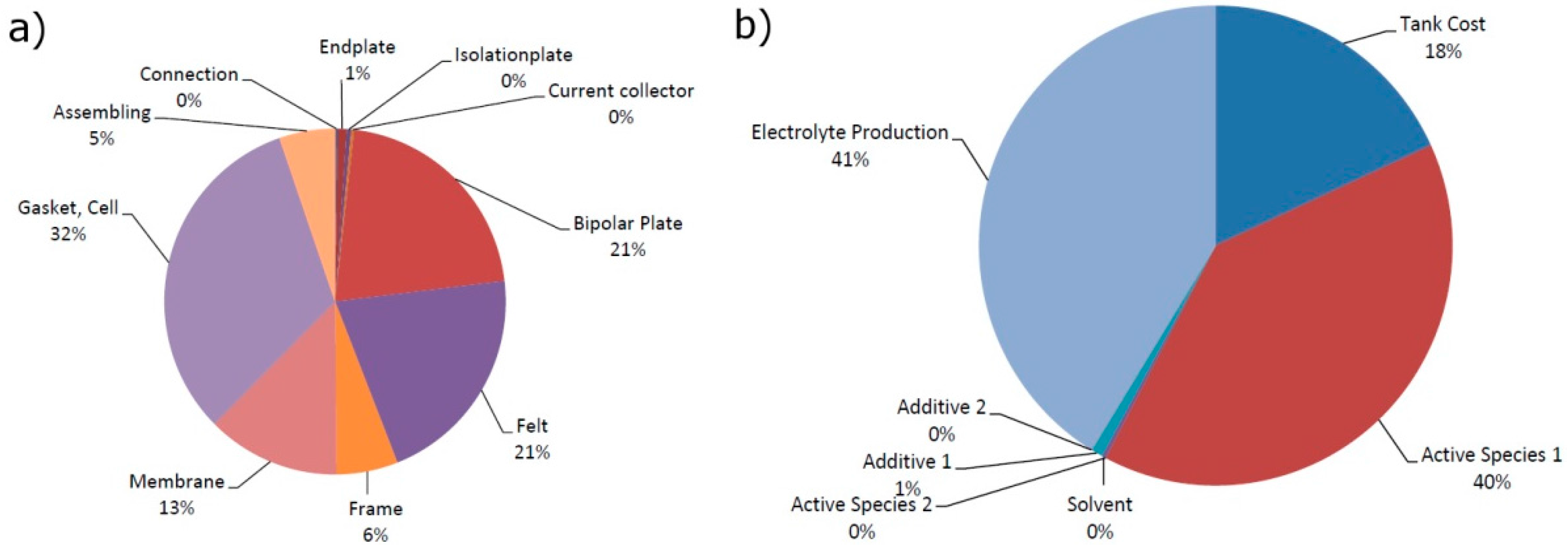
With the system costs shown in Figure 3, the stack costs accounted for the highest proportion, at 40%, followed by the electrolyte costs. Overall, the system costs were split roughly three ways into stack costs, energy costs, and peripherals.

The calculated cost breakdown of the stacks and the energy costs of the battery system are shown in Figure 4. These figures provide an overview of where decisive economies can be achieved and where there is the greatest potential for research and development. The calculated stack costs were €52,648 (€5265/kW). The gaskets had the biggest share of the costs of the stacks, at 32%. This was due to the special production method used, with cured-in-place gaskets that generated especially high material costs and could be substituted by other technologies to reduce the stack-specific costs. The gaskets were followed by the bipolar plates and felts, with a 21% share each.

The specific costs were €150/m² for felts and €418/m² for bipolar plates. Because for a stack given the same production costs per unit, twice the number of cells are needed for felts and the number of bipolar plates = the number of cells + 1, the felt costs achieved the same shares as the bipolar plate costs, at approx. €1100/kW. At over two-thirds of the stack costs, therefore, electrode and gasket costs had by far the biggest cost-cutting potential. The relatively inexpensive membrane used here—€250/m²—had a share of just 13% but increased in significance when electrode and gasket costs were reduced. Around €1000/kW of these costs, or 20% of the stack costs, could be saved just by reducing the waste of the three materials from a factor of 1.5 to 1.0. The other costs could be regarded as of secondary importance for the time being. This is particularly interesting for the production costs because at approx. €300/kW only automated production seems advisable if unit numbers are very high and the other costs are reduced.

The electrolyte costs were accounted for by almost identical percentages of vanadium costs and the production of the electrolyte. Since the vanadium costs were the costs of vanadium pentoxide, it is difficult to have any influence on these as the greatest proportion is processed in the steel industry and varies widely in consequence. It is questionable whether alternative sources such as residues of fossil fuels could bring about a reduction in the price as these would immediately compete with the steel industry again.

5. Variation in the Values of Influencing Factors

To investigate the influence of different factors, the parameters were varied and the results presented as they affected system costs. It should be remembered that all other values were left consistently constant. This does not represent a real case because changing one parameter nearly always affects the other parameters that could not be covered by this model. When material properties are changed, in particular, then in addition to changes in electrochemical properties as a result of the strictly networked behavior, there are also changes to stack costs generally, through other gasket options, labor costs, material costs, etc., so absolute values can only be achieved by the integration of values that are as real as possible. Nevertheless, it was still possible to deduce general tendencies. In the following section parameters were varied in an attempt to find answers to frequently posed questions.

5.1. Influence of Current Density and Active Material Concentration

The system costs and a breakdown by energy costs and stack costs are shown in Figure 5a. Stack costs should not be confused with power-related costs C_Power. The total of C_Stack and C_Energy was less than C_System because the peripheral costs such as power electronics, sensors, etc. were absent, but scaled linearly with the current density from a plateau caused by the constant activation and concentration over potential loss. With rising current density the system costs initially fell sharply from €2620/kWh at 10 mA/cm², to attain their minimum of approx. €915/kWh in the 100–150 mA/cm² range. The system costs increased again at current densities of over 150 mA/cm².

As the current increased, the stack costs fell asymptotically to a level of approx. €1600/kW. The energy costs had a contrary tendency and rose with current density from €390/kWh at 10 mA/cm² to €756/kWh at 300 mA/cm². The reason for the change in energy costs can be found in the cell voltage, which falls as current density rises, with the amount of electrolyte for the required 120 kWh and hence the costs increasing as a result. The reason for the increase in specific costs for decreasing current densities was the lower power per active area and thus more stacks or cells were needed to cover 10 kW power. As far as investment costs are concerned, there was generally an optimum range in which an RFB should be operated. If current densities are too low, the shares of the expensive stack predominate. With high current densities, the influence of electrolyte costs predominates, so system costs rise again.

The influence of the vanadium concentration on the current density is shown in Figure 5b. There are many reference sources that have considered increasing the vanadium concentration so as to reduce system costs, mainly by saving on area needs. In this model, however, the costs of space are initially disregarded. Nevertheless, there was a definite correlation between costs and concentration, with rising concentrations resulting in falling system costs. Concentrations below 0.5 mol/L resulted in system costs above €1500/kWh at all current densities. Concentrations above 2 mol/L achieved cost savings potential above all with higher current densities. Below 40 mA/cm², concentrations higher than 2 mol/L had hardly any impact on system costs. This was due to the fact that the power-specific costs were predominant at low current densities. The general fall in system costs as the concentration of vanadium increases was due to the effect of electrolyte production, which in this model made its impact as costs/L. The overall system costs therefore decreased as a result of increased vanadium concentrations, while production costs remained constant. It is questionable, however, whether this assumption was correct given that the costs of electrolyte production were scaled as a result of the costs of materials and electrical current, for example, which scale with the amount of vanadium. The cost degression effects shown here would therefore relativize with the increase in the active species concentration and be caused mainly by area savings.

5.2. Influence of the Bipolar Plates

One of the key questions of these investigations concerned the impact of the costs of materials—in terms of their properties—on the system costs. One of the most important materials is the carbon-based bipolar plate on which the reactions only have a secondary share but which are important for the cells’ ohmic resistance. RFBs use polymer-filled graphites or extrinsically conductive polymers, which can vary widely in their conductivities and mechanical properties. Low-filled polymers, for example, can be welded and injection molded, which allows the stack construction to be optimized, but are less conductive. The situation is exactly the opposite with highly conductive graphites, which is why there are nearly always sealing problems. The influence of conductivity and of the costs of bipolar plates on the system costs for a current density of 50 mA/cm² is shown in Figure 6. Highly conductive materials are primarily in the top right-hand area of the graph, while inexpensive carbon plastics are in the bottom left-hand area. It is interesting to note that commercial bipolar plates for fuel cells with conductivities up to approx. 5000 S/m were so effective that the IR drop they caused was entirely subsidiary to the cells’ other losses. The system costs only increased noticeably with a conductivity of 100 S/m. On the other hand, significant cost digression effects could be achieved when high-filled bipolar plates below 150 €/m² and less are available, which does not alter the material properties, however.

Inexpensive carbon plastic with conductivities of 20–40 S/m and costs of 25–75 €/m² generated the same system costs as bipolar plates with 5000 S/m and 400 €/m². With high conductivities, the system costs varied only minimally when the thickness of the plates was reduced. In this example of the model, the lower conductivities were offset by raising the number of cells, so that at 20 S/m, 344 cells instead of 306 cells at 5200 S/m were needed to achieve the required power. The most interesting area for inexpensive VRFB systems would appear to be with conductivities of 100 S/m and over and costs below €50/m², and with the bipolar plates having a thermoplastic character at the same time.

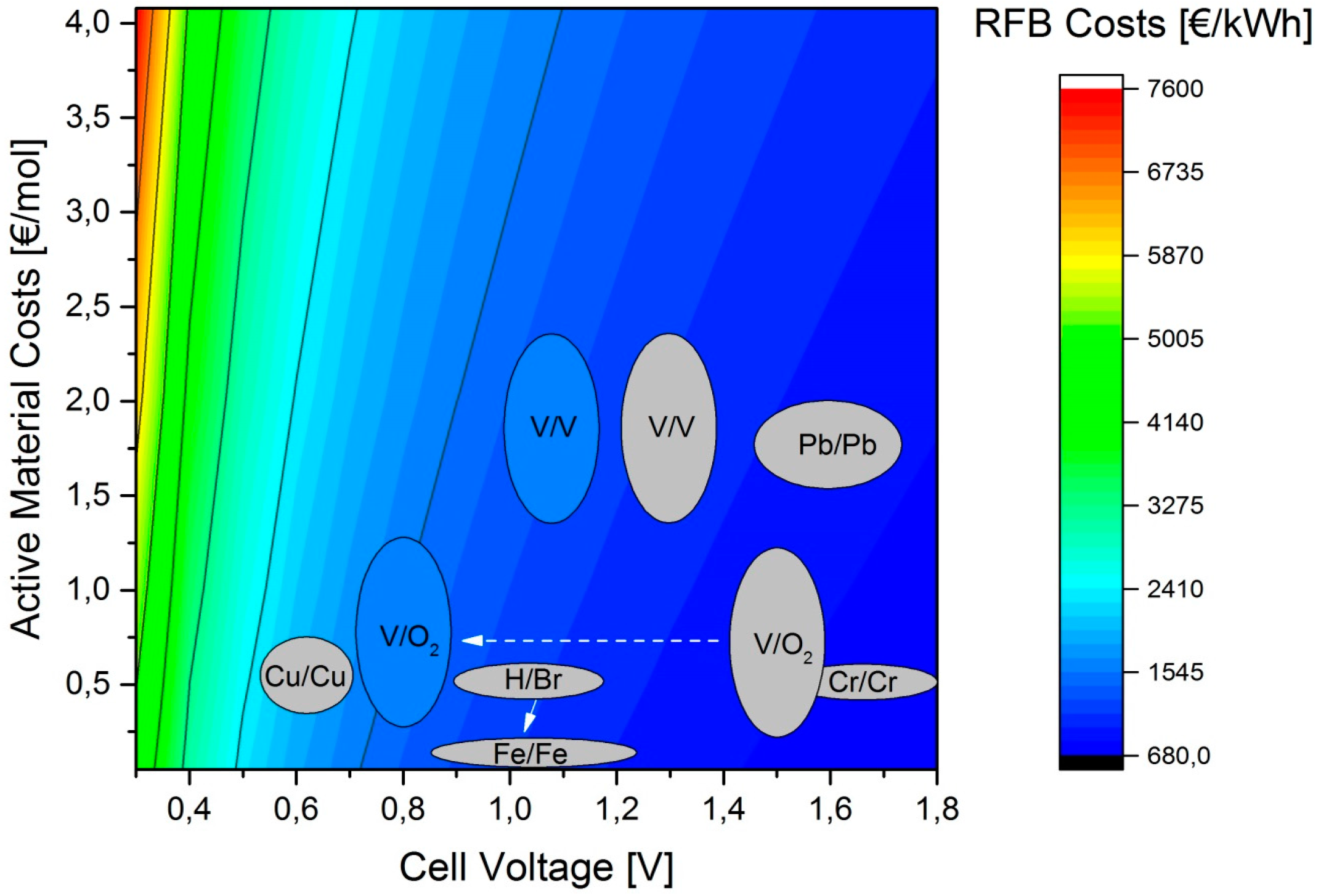
5.3. Influence of Cell Voltage and Active Material Costs

Figure 7 shows the influence of active material costs and cell voltages on system costs. As expected, the system costs decreased as material costs are reduced and cell voltage was increased.

The figure shows a number of examples of redox flow batteries at open circuit voltage, although it should be remembered that the actual values can vary due to concentration differences and membrane potentials, though this only applies to the horizontal direction. The vertical deviations can be the result of changing material prices. Basically significantly higher values for voltage and the same battery chemistry are not possible. Under operational conditions, the cell voltages will be lower as a function of kinetics and materials. At 50 mA/cm² the voltage of a V-RFB will tend towards 1.1 V. Consequently, the Pb-RFB [14], which has similar material costs, can only offer a cost advantage if it has a higher voltage than the V-RFB owing to a lower or equal cell resistance, irrespective of cycle stability. A Cu-RFB [15] has lower material costs but low voltage also. With the same cell resistance as the V-RFB, for example, Cu-RFBs struggle to compete with V-RFBs. With this type of chemistry, the power densities would have to be drastically higher to achieve similar system costs. Vanadium/air cells [16,17,18,19] offer huge potential for inexpensive storage systems by saving on electrolyte solution and their slightly higher cell voltage. However, cell resistances are so high because of the very slow oxygen reduction reaction that this potential is not currently exploited due to the resulting low cell voltage. H/Br- [20,21] and Fe-RFBs [22,23] occupied a similar position because of their similar values. Their material costs are already so low that any further reduction in material costs would have almost no impact on system costs. Here again, however, the two systems can be very different from one another because of the cell resistance. At open-circuit voltage, these two systems were on a cost par with the V-RFB due to the lower cell voltage, and could only offer advantages if their power densities exceeded those of the V-RFB. One of the oldest representatives of the RFBs, the Cr/Cr-RFB [24], was cheaper than V-RFBs for the same cell resistance, but difficult to implement for chemical and toxicological reasons.

5.4. Influence of Current Density and Cell Voltages

Another important aspect was the dependence of system costs on current density and cell voltage (see Figure 8). The calculated VRFB model system is just in the light blue band at €1078/kWh. A reduction in the current density and voltage resulted in an exponential rise in system costs due to the increasing power-related costs. As discussed previously, however, an increase in the current density without any change in cell resistances resulted in a departure from a minimum due to the necessary rise in energy storage quantities.

With low voltages it is extremely difficult to achieve economical RFB systems because power-specific and energy-specific costs have an equally negative impact on the system costs. Systems below 1 V can only be competitive when they use extremely cheap energy storage materials and have low cell resistances at the same time. In this context it is also extremely difficult to compensate for low current densities with a higher voltage. At 10 mA/cm² approx. 3 V of voltage is needed to achieve the system costs of the model system. This means that, for example, lithium ion RFBs must achieve discharge power densities of at least 30 mW/cm² for the system costs to be the same as for a VRFB. Some current lithium ion RFBs are several orders of magnitude below this value [25,26,27,28]. The current densities of commercial lithium ion batteries lie within the single-digit mA range; they only have large electrode areas—and hence acceptable volumetric power densities—because of their comparatively extremely thin construction [29]. The more expensive organic electrolyte means that the power density must be far greater, however, and this could prove to be a major obstacle for all RFBs that are based on organic electrolytes or poorly conductive separators, not least because of the poor conductivity of the electrolytes.

6. Conclusions

The techno-economic model developed in this project was used to calculate specific system costs and create a cost breakdown for a typical 10 kW/120 kWh VRFB system. One of the aims was to investigate the impact of material properties on system costs so as to be able to optimize the model in a targeted manner. It was found in particular that when nonlinear overvoltages were taken into consideration, the model displayed deficits that should be allowed for in further optimizations if there are variations in current densities, electrode material, and redox pairs. The model’s two strong points are its consideration of bipolar plates and membrane properties and the influence of cell voltage on the battery’s energy content.

For the example VRFB system, it was found that the system costs were largely influenced by the stack costs, which in turn were dominated by gasket costs, bipolar plates, and electrode felts. So far as the influence of the bipolar plates was concerned, it was found that they made a minor contribution to the ohmic losses of the cells and that the detrimental mechanical properties (gasket) were a hindrance. Materials with better mechanical properties that are less expensive would be more advantageous despite their lower conductivities.

When investigating the influence of the active material costs and the cell voltage on the system costs, it was found that it is difficult to achieve competitive systems with low cell voltages despite the lower material costs. Low cell voltages can only be effectively offset by low cell resistances and rapid redox reactions. Such a system is known as the H/Br-RFB, which can operate with high power densities at approx. 1 V cell voltage but probably contains other cost drivers.

Finally, it was shown from the influence of cell voltage and current density that it appears difficult to develop competitive organic redox flow batteries. Lithium ion RFBs, in particular, have a high open circuit voltage but they cannot use this to advantage as the electrolyte conductivities are too low, and this in turn means extremely thin flow reactors or alternatives such as percolation networks.

No competitive RFB system could be realized based on the non-commercial research example system calculated here. Nevertheless, it has become clear that stack costs will have to be significantly reduced and that the potential for this is also available if optimized production methods and alternative electrodes and membrane materials are used. On the other hand, electrolyte costs must also fall well below €100/kWh in the medium term if energy storage devices that are cheaper than lithium ion batteries are to be achieved.