Two-Layer Coordinated Optimization and Control Method for Wind Farms Considering Both Point of Common Coupling Voltage Level and Generator Terminal Voltage Security

Abstract

In large wind farms, uneven voltage distribution caused by feeder impedance and turbine spacing may pose safety hazards and reduce operational efficiency. This paper proposes a two-layer voltage coordination optimal control method for wind farms that balances both grid-connection point voltage levels and turbine-end voltage safety. The outer layer tracks voltage commands issued by the AVC master station at the point of common coupling (PCC), while the inner layer establishes a global optimization model considering generator terminal voltage safety. The second-order cone relaxation method converts nonlinear constraints into solvable convex forms. Through a two-layer iterative solution, it achieves optimal allocation of active and reactive power between wind turbines and static var compensators (SVGs) within the field, thereby enhancing the active power output at the wind farm port and increasing the system’s reactive power margin. Simulation results demonstrate that compared to conventional unified power factor control, the proposed method effectively enhances terminal voltage security, increases wind farm power generation, and boosts system reactive power reserve capacity while stably tracking PCC voltage commands.

1. Introduction

In recent years, with the transformation of the global energy landscape, renewable energy generation has experienced rapid development. As one of the primary forms of renewable energy generation, wind power has seen an increasing integration proportion into the grid, and its impact on the power system can no longer be ignored. Among the various challenges, the reactive power and voltage control of grid-connected wind farms has become a widely discussed issue. For large-scale wind farms, due to their extensive spatial distribution, significant variations in wind speed across the site, and the considerable length of internal collector lines, the terminal voltages of turbine units may still vary significantly even when the voltage at the point of common coupling (PCC) is maintained within the specified range. Under certain external disturbances, some turbine units may experience terminal voltages exceeding safe limits, leading to their disconnection from the grid and compromising both the security and economic efficiency of the system’s operation. Therefore, while addressing the voltage level at the PCC, it is also essential to implement effective control over the terminal voltages of the turbine units.

Reactive power and voltage control for wind farms can be approached from both the overall wind farm level and the individual turbine level, with utilizing the reactive power capability of the turbines being the primary consideration. Currently, most wind farms are equipped with an Automatic Voltage Control (AVC) system, which can receive dispatch commands from higher-level control centers while implementing reactive power command control for the turbines. The main functions of such systems include wind farm reactive power demand setting, allocation of reactive power commands within the wind farm, and reactive power regulation of wind turbine units.

Reference [1] proposes a control method that utilizes the reactive power output capability of the turbine units themselves to replace SVG, thereby enhancing the voltage support capability of the wind farm. References [2,3] elaborate on the reactive power regulation mechanism of doubly fed induction generators (DFIGs) and propose control strategies targeting the PCC voltage of wind farms. However, as the internal wind farm model in these studies is simplified into an equivalent representation, they fail to reflect the impact of the distribution characteristics of internal line parameters on turbine terminal voltages. References [4,5] introduce various methods for allocating reactive power commands within the farm based on the active power output status of DFIGs, taking into account the reactive power capability or margin of the units. Nevertheless, none of these studies account for the impact of unit output on their own terminal voltages, and in some cases, they even increase the deviation of turbine terminal voltages from the rated value.

Wind turbine units are interconnected through feeders in the collector system. Given that the impedance of the collector system lines cannot be neglected, the reactive power output of the units significantly influences the voltage distribution and operational loss profile along the wind farm feeders [6]. Reference [7] established a reactive power optimization model based on minimizing wind farm network losses and employed a particle swarm algorithm to solve for the optimal solution, thereby allocating reactive power commands to individual turbines. Similarly, numerous optimization studies focus on minimizing wind farm network losses, but they primarily consider only the operational economy of the wind farm. References [8,9] account for the impact of the collector system on feeder voltage distribution. The proposed reactive power allocation methods can optimize the feeder voltage profile within the farm while meeting its reactive power demand, thereby enhancing the safety margin of the turbine units. Reference [10] developed a two-layer reactive power optimization model, simultaneously considering network losses, voltage deviations, copper losses in the wind farm, as well as internal line losses, copper losses of doubly fed induction generators, and reactive power imbalance, to determine the reactive power output for each turbine. Reference [11] concurrently considers both wind farm network losses and voltage distribution, proposing a multi-objective reactive power incremental allocation optimization method for wind farms based on the sensitivity of active power losses and turbine terminal voltage to unit output. Therefore, both the feeder voltage distribution and operational losses within the wind farm are essential considerations for reactive power and voltage optimization control.

Since wind turbines operate in maximum power point tracking mode, the economic operation of a wind farm is no longer a traditional dispatch problem but rather an optimal power flow (OPF) problem [12]. For the OPF problem, apart from using DC power flow methods to approximate power flow optimization for transmission lines, the general AC grid power flow optimization remains a highly nonlinear, non-convex optimization problem that is difficult to solve within polynomial time [13,14]. For optimizing the output of wind farms, heuristic algorithms are a commonly employed class of solution methods. Reference [15] considers multiple constraints related to power sources, equipment, and processes, constructing a multi-objective mathematical model for wind farm optimization scheduling with the goal of achieving optimal economy. Reference [16] establishes a multi-mode, dual-objective scheduling model aimed at minimizing total system costs, providing decision-makers with strategies for maximizing benefits through optimal solution sets. Reference [7] utilizes the particle swarm optimization algorithm to optimize the internal reactive power of wind farms, aiming to minimize system network losses. Reference [17] proposes an optimization algorithm for grid-connected offshore wind farms based on an improved particle swarm optimization algorithm. The drawback of these heuristic optimization methods is their tendency to converge with local optima, and the obtained solutions may not necessarily be globally optimal. Thanks to advances in mathematical optimization methods, approaches that relax the original OPF problem into a convex optimization problem have emerged in recent years [18]. The main idea of convex relaxation methods is to first perform variable substitution, then relax certain non-convex constraints to form a convex optimization problem with new variables and subsequently solve for the global optimal solution of the convex optimization problem. Under exact relaxation conditions, this ensures that the global optimal solution of the original problem can be obtained within polynomial time. This approach balances both solution speed and accuracy, making it suitable for reactive power control systems within wind farms that operate on a second-level timescale.

Therefore, focusing on the safety and economy of wind farm operation, this paper establishes a global optimization model for wind farms based on second-order cone relaxation technology, taking into account the safety of turbine terminal voltages. The model optimizes the internal power flow distribution, maximizes the reactive power output of each turbine under the condition of maximum active power output, and aims to maximize the export active power and the reactive power margin of the SVG. Additionally, considering the dispatch requirements issued by the AVC master station, a two-layer control system is designed to effectively track the voltage commands at the point of common coupling (PCC). This results in a two-layer voltage coordinated optimal control method for wind farms that balances both the voltage level at the point of common coupling (PCC) and the safety of turbine terminal voltages.

2. Methodology

2.1. Voltage Issues in Wind Farms

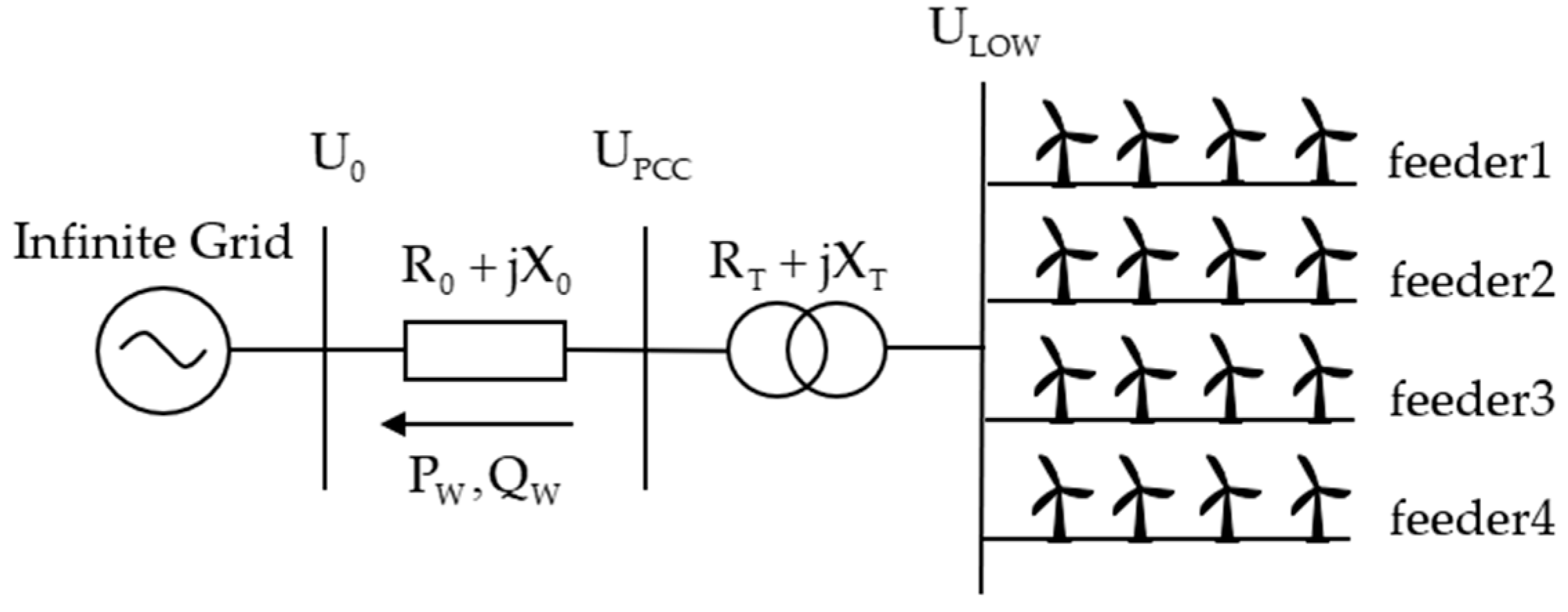
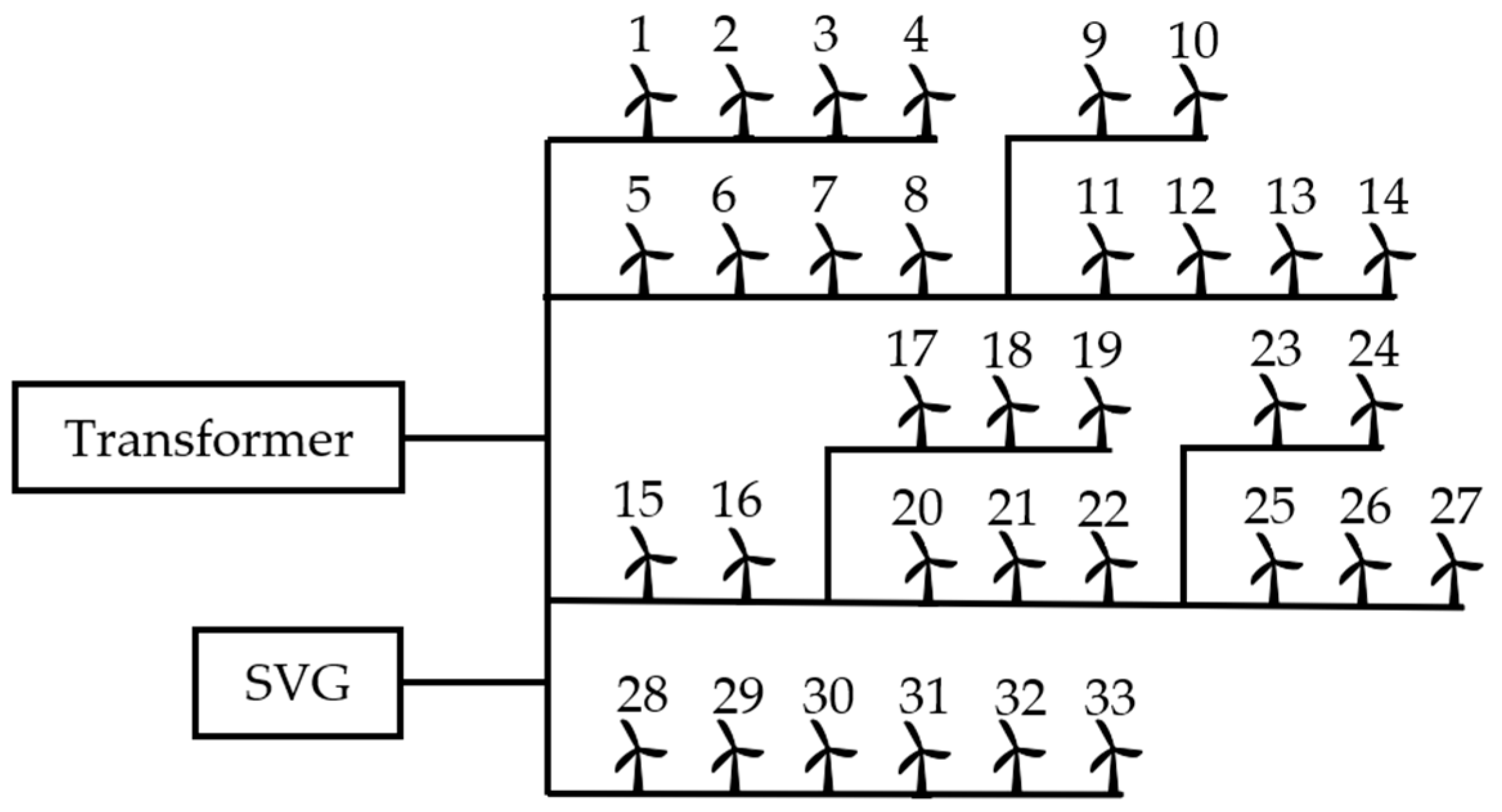
The wiring configuration of a wind farm’s collector system typically involves a single busbar or sectionalized single busbar at the low-voltage side of the farm’s step-up substation. Each busbar section supplies several feeders, where each feeder adopts a radial configuration with a trunk line to connect multiple wind turbine units. For large-scale wind farms, each feeder can typically link 10 to 12 turbine units. The high-voltage busbar of the step-up substation is connected to the main AC grid via transmission lines, as illustrated in Figure 1.

In a typical large-scale wind farm in China, there are over a hundred wind turbine units. Depending on the terrain, the distance between each unit ranges from several hundred meters to several kilometers. Consequently, the length of a feeder from start to end often spans several kilometers to several tens of kilometers. According to data measured from a specific wind farm, under heavy load conditions, the voltage difference between the low-voltage busbar at the wind farm’s step-up substation and the terminal node of a feeder can reach 5%. Therefore, reactive power and voltage control in a wind farm should not only focus on the PCC (Point of Common Coupling) voltage but also consider the internal voltage distribution within the wind farm.

First, the PCC voltage of the wind farm and its variation patterns are analyzed. Assume the wind farm contains multiple feeders connected in a radial trunk configuration, with each feeder supplying multiple wind turbine units and possibly having other branch lines, forming a radial distribution. Z₁ = R₁ + jX₁ represents the impedance of the collector line between adjacent wind turbine units (assuming equal distance between units), typically using cables for power transmission. Z_T = R_T + jX_T is the impedance of the wind farm’s step-up transformer. Z₀ = R₀ + jX₀ is the impedance of the transmission line exporting power from the wind farm, usually using overhead lines for transmission. The analysis begins with the PCC bus voltage of the wind farm. The PCC bus voltage is primarily determined by the system bus voltage U₀ and the voltage drop along the wind farm’s export line. According to the transmission line voltage drop calculation, neglecting the transverse component, the voltage at the wind farm’s point of common coupling (PCC) can be expressed as:

$${\mathrm{U}}_0={\mathrm{U}}_{\mathrm{P}\mathrm{C}\mathrm{C}}-{\displaystyle \frac{{\mathrm{P}}_{\mathrm{W}}{\mathrm{R}}_0+{\mathrm{Q}}_{\mathrm{W}}{\mathrm{X}}_0}{{\mathrm{U}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}}$$

(1)

U_PCC represents the voltage at the PCC (Point of Common Coupling) bus of the wind farm, U₀ denotes the voltage at the infinite grid bus, while P_W and Q_W are the active power and reactive power output from the wind farm node, respectively. Although the reactance of high-voltage transmission lines is typically greater than their resistance, the active power output of a wind farm is often significantly larger than its reactive power output. Therefore, it is necessary to account for the impact of fluctuations in the wind farm’s active power output on the PCC voltage. Currently, wind turbine units usually operate at a constant power factor, which can be adjusted within a certain range, either leading or lagging. Based on Equation (1), the variation pattern of the wind farm’s PCC voltage can be expressed as:

$${\displaystyle \frac{\mathsf{\partial }{\mathrm{U}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}{\mathsf{\partial }{\mathrm{P}}_{\mathrm{W}}}}\approx {\displaystyle \frac{{\mathrm{R}}_0+{\mathrm{X}}_0\tan \mathrm{\phi }}{{\mathrm{U}}_0}}$$

(2)

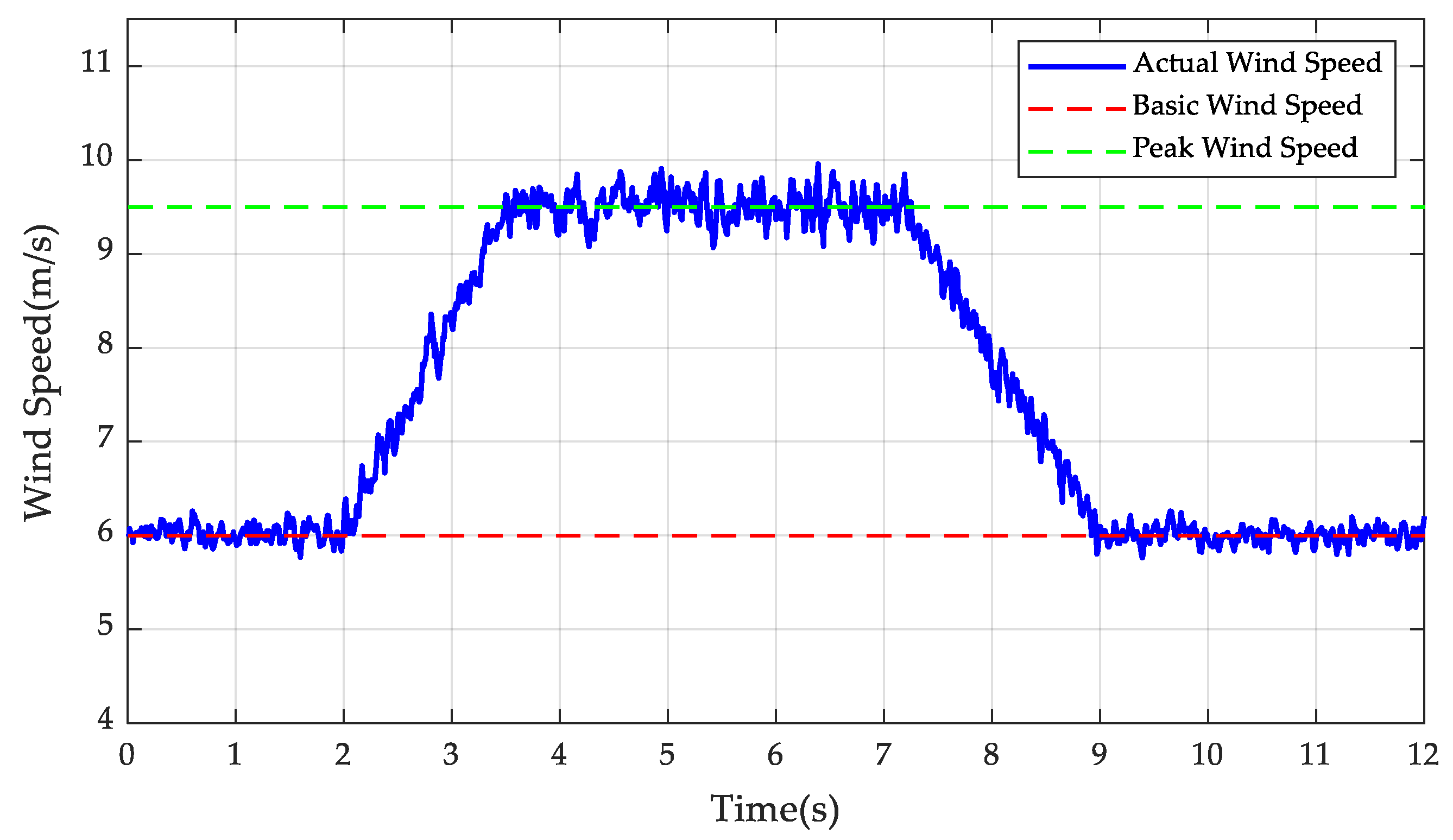
Therefore, changes in wind speed will cause fluctuations in the active power output of the wind farm. The impact of these fluctuations on the voltage at the point of common coupling (PCC) is not only related to the impedance of the transmission line but also to the operating power factor of the wind farm. By promptly adjusting the operating power factor and increasing or decreasing the reactive power output, fluctuations in the voltage at the point of common coupling (PCC) can be effectively suppressed.

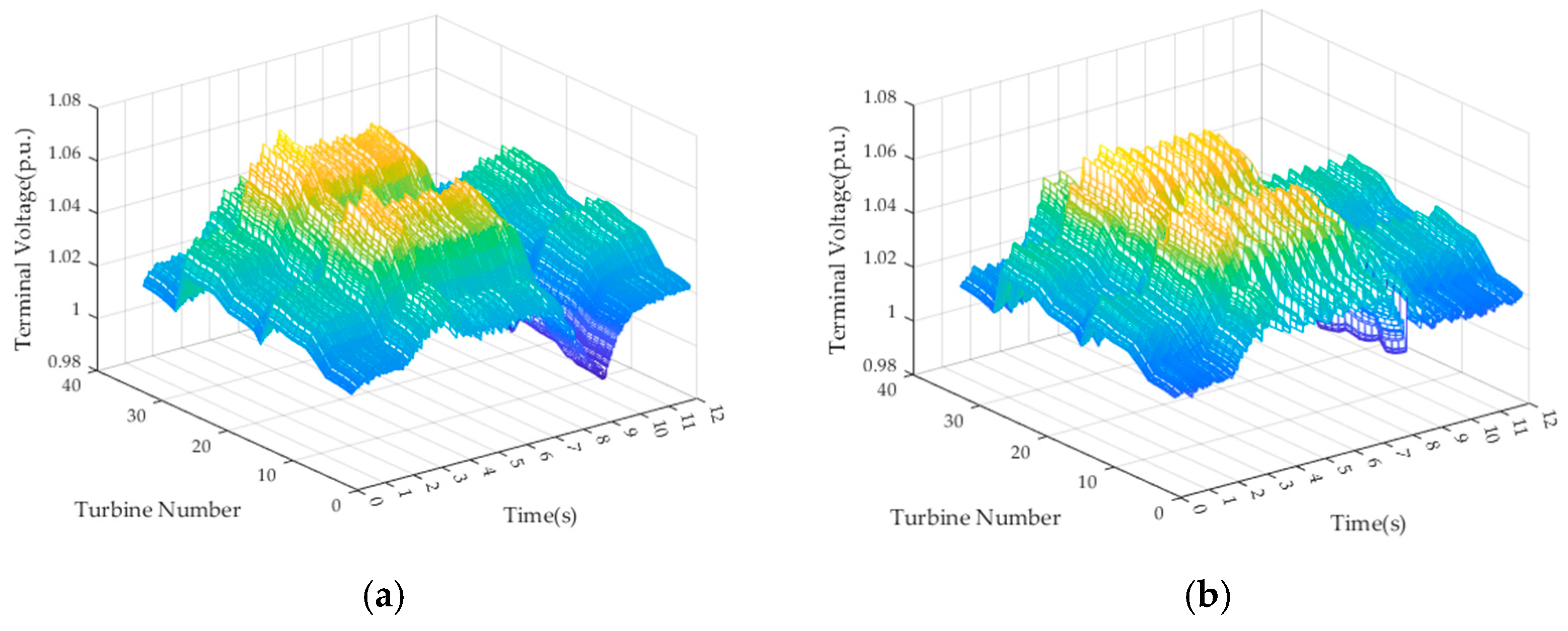
Next, the variation pattern of the terminal voltage of wind turbine units is analyzed. Based on the PCC voltage of the wind farm, the expression for the terminal voltage of each turbine unit can also be derived as follows:

$${\mathrm{U}}_{{\mathrm{G}}_{\mathrm{j}-\mathrm{i}}}={\mathrm{U}}_{\mathrm{P}\mathrm{C}\mathrm{C}}+{\displaystyle \frac{{\displaystyle \sum _{\mathrm{m}=1}^{\mathrm{i}}}\left[\left({\displaystyle \sum _{\mathrm{b}=\mathrm{m}}^{\mathrm{n}}}{\mathrm{P}}_{\mathrm{j}-\mathrm{b}}\right){\mathrm{R}}_1+\left({\displaystyle \sum _{\mathrm{b}=\mathrm{m}}^{\mathrm{n}}}{\mathrm{Q}}_{\mathrm{j}-\mathrm{b}}\right){\mathrm{X}}_1\right]}{{\mathrm{U}}_{\mathrm{L}\mathrm{N}}}}$$

(3)

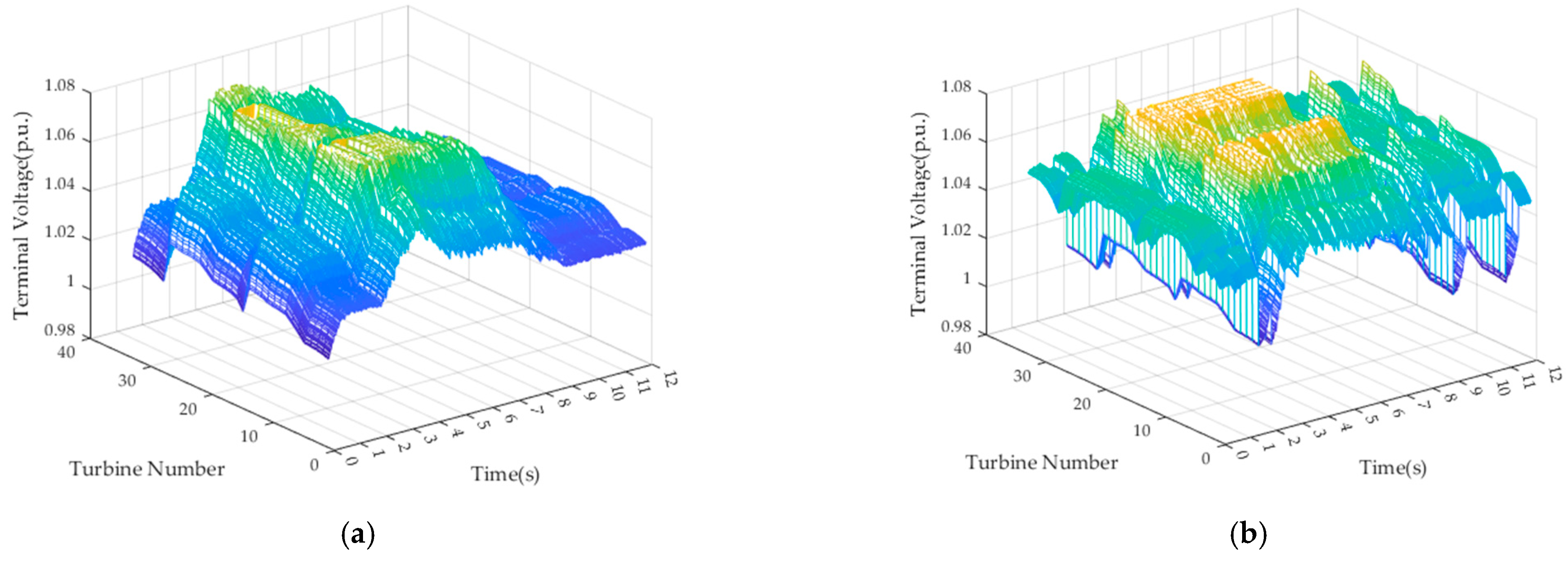
U_LN represents the rated voltage of the internal feeder network in the wind farm. By neglecting the impedance of the unit’s box-type transformer and expressing all voltage parameters in per-unit values, it can be seen that the voltage level of the wind turbine units primarily depends on the voltage of the wind farm’s PCC bus. When the PCC bus voltage is either too high or too low, the voltages of the units within the wind farm will correspondingly increase or decrease. Therefore, wind farm voltage control should first aim to keep the PCC bus voltage within a reasonable range. On the other hand, the terminal voltage of a unit is also related to its active and reactive power output. Fluctuations in power output will similarly cause fluctuations in the terminal voltage. Thus, even when the wind farm’s PCC bus voltage is controlled within a reasonable range, the terminal voltage of individual units may still deviate due to changes in the power flow distribution along the collector lines. Variations in the active power output of the units mainly originate from changes in wind speed, while the reactive power depends on the unit’s reactive power control strategy.

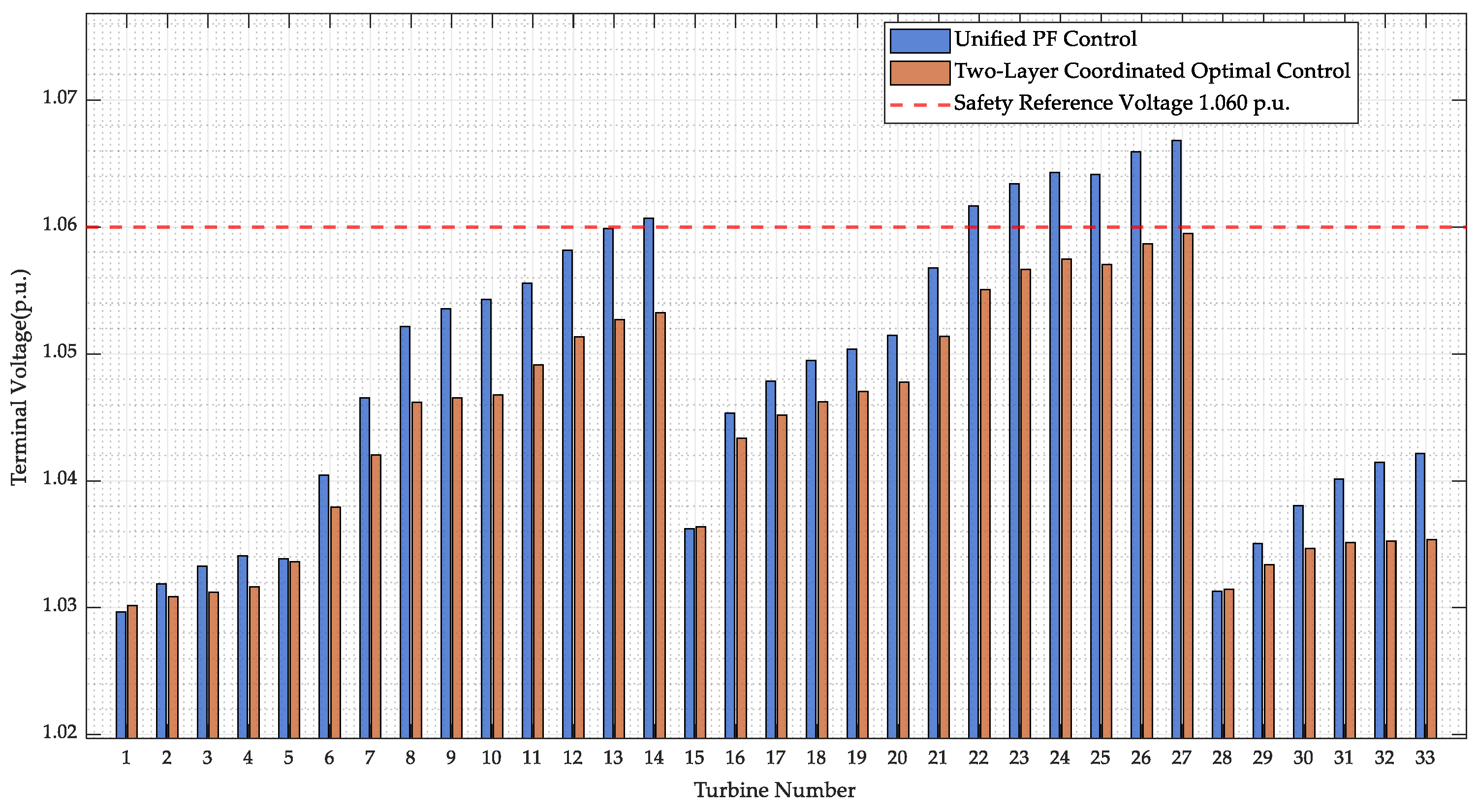
Based on the above analysis, it can be concluded that the voltage drop along the collector lines within the wind farm cannot be entirely ignored [19]. This results in a gradual increase in the voltage distribution at the nodes of the wind turbine units from the beginning to the end of the feeder. When the wind farm participates in providing auxiliary voltage support to the system, even if the voltage at the PCC is maintained within the target range, some turbine units at the end of the feeders within the farm may still experience high voltage limits. This can cause these units to either malfunction or trigger high-voltage protection actions, leading to their disconnection from the grid, thereby compromising the safe operation of the system [20].

2.2. Optimal Power Flow Problem and Second-Order Cone Relaxation Technique

The essence of reactive power optimization in wind farms is the optimal power flow problem, which is one of the most common optimization problems in power systems. It involves adjusting relevant parameters of generators or loads by controlling associated power devices, under the premise of satisfying physical constraints of the power network, such as system stable operation and security constraints, to optimize objective functions such as total generation cost and total network losses. The objective functions or constraint equations of the optimal power flow problem are typically nonlinear, and the optimization variables may be continuous or discrete. The standard form of the optimal power flow problem is as follows:

$$\left\{\begin{array}{c}\min \mathrm{f}(\mathrm{u},\mathrm{x})\\ \mathrm{s}.\mathrm{t}.\\ \mathrm{g}(\mathrm{u},\mathrm{x})=0\\ \mathrm{h}(\mathrm{u},\mathrm{x})<0\end{array}\right.$$

(4)

In Equation (4), u and x are the optimization variables; f(u, x) represents the objective function to be optimized; g(u, x) denotes the equality constraints; and h(u, x) represents the inequality constraints. The variables in the optimal power flow (OPF) problem characterize the operational state of the power system, typically including bus voltage magnitudes and phase angles, as well as variables for active and reactive power injections at the buses.

However, due to the non-convexity introduced by quadratic power flow constraints, the OPF problem is a non-convex optimization problem that is difficult to solve precisely and is prone to converging to local solutions during the solution process. Therefore, an efficient solution of the OPF problem relies on advances in convex optimization theory.

The main idea of convex relaxation methods is to transform part of the non-convex constraints into a convex optimization problem concerning new variables through variable substitution. The global optimal solution of the convex optimization problem can then be obtained. Optimization using convex relaxation methods is highly efficient, and under exact relaxation conditions, it guarantees obtaining the global optimal solution of the original problem within polynomial time. Among these, convex relaxation techniques represented by second-order cone programming relaxation have been widely applied in solving the OPF problem.

Second-order cone programming, as a special type of convex optimization problem, can be mathematically expressed as follows:

$$\left\{\begin{array}{c}\min {\mathrm{f}}^{\mathrm{T}}(\mathrm{x})\\ \mathrm{s}.\mathrm{t}.\\ \parallel {\mathrm{A}}_{\mathrm{i}}\mathrm{x}+{\mathrm{b}}_{\mathrm{i}}{\parallel }_2⩽{\mathrm{c}}_{\mathrm{i}}^{\mathrm{T}}\mathrm{x}+{\mathrm{d}}_{\mathrm{i}}\hspace{1em}\mathrm{i}=1,\cdots ,\mathrm{m}\\ \mathrm{F}\mathrm{x}=\mathrm{g}\end{array}\right.$$

(5)

In the equation, x represents the optimization variable; A_i denotes the coefficients of the second-order cone constraints. Second-order cone programming lies between linear programming and semidefinite programming, belonging to the category of convex optimization problems. When A_i = 0, the second-order cone programming problem reduces to a linear optimization problem; when c_i = 0, it transforms into a quadratically constrained quadratic programming problem.

However, its limitations primarily require a radial network topology and sensitivity to the magnitude of impedance parameters, which may result in excessive clearance or failure to solve.

2.3. Global Voltage Two Layer Optimization Method Based on Second-Order Cone Optimization

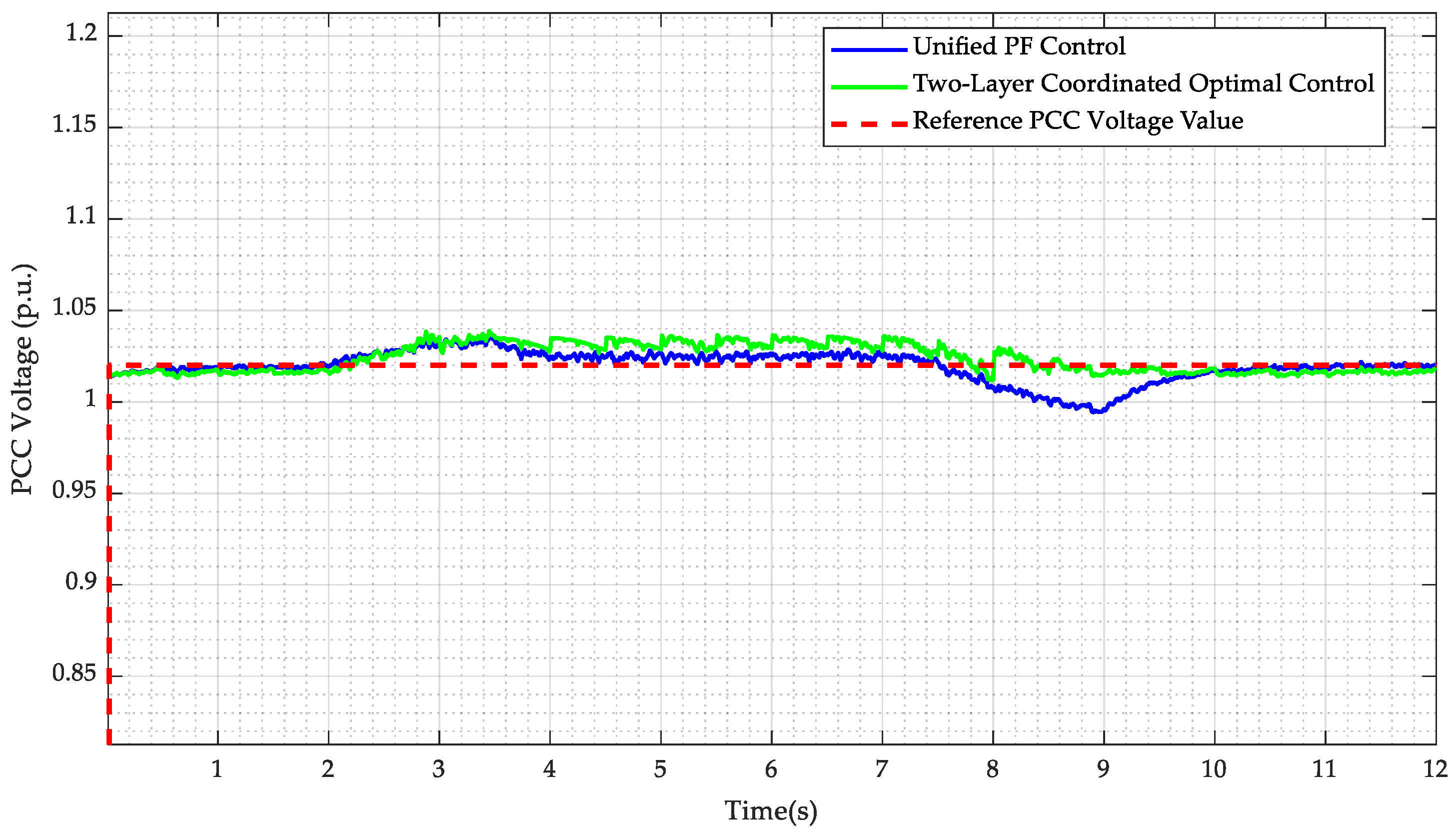
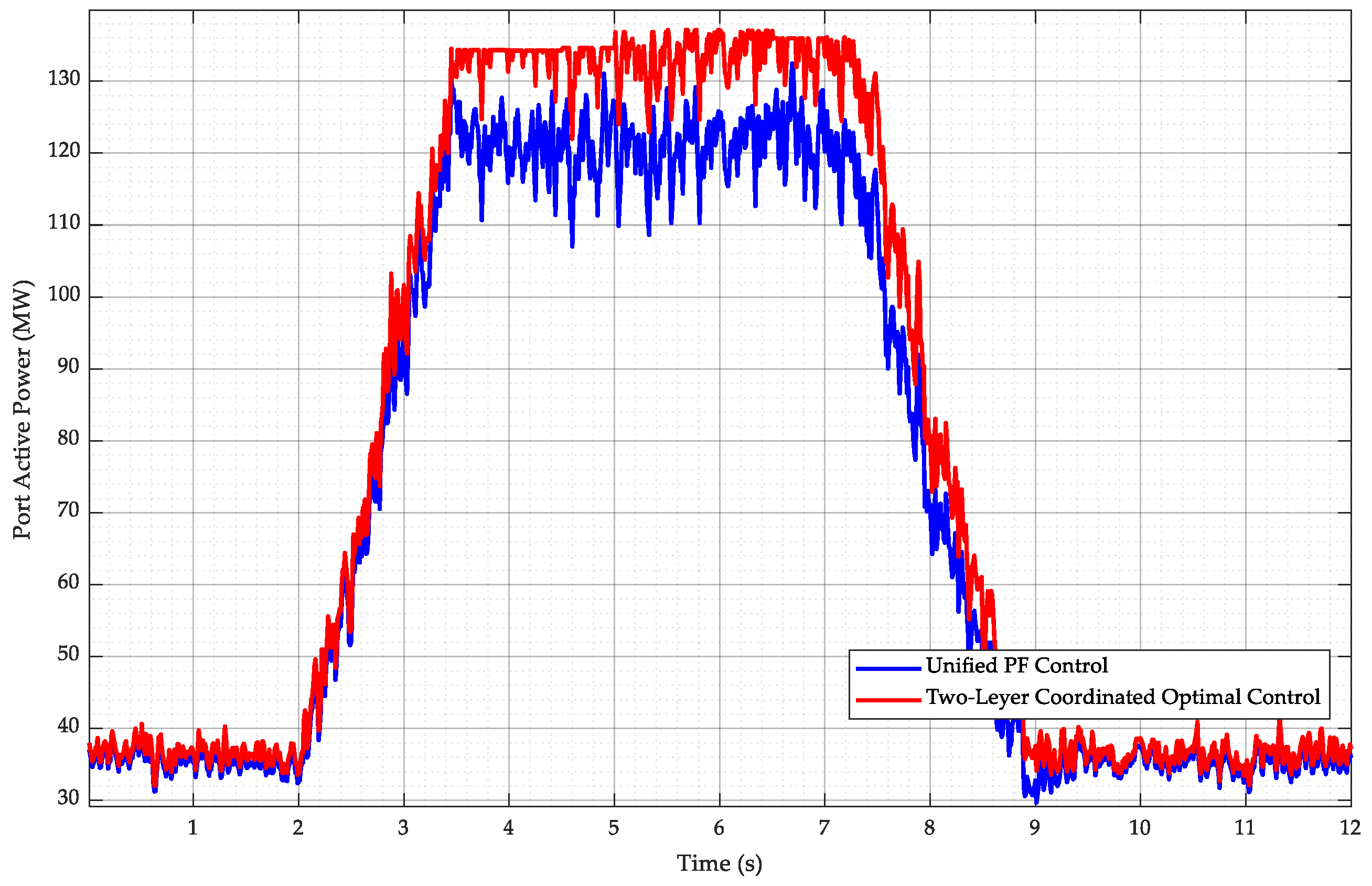
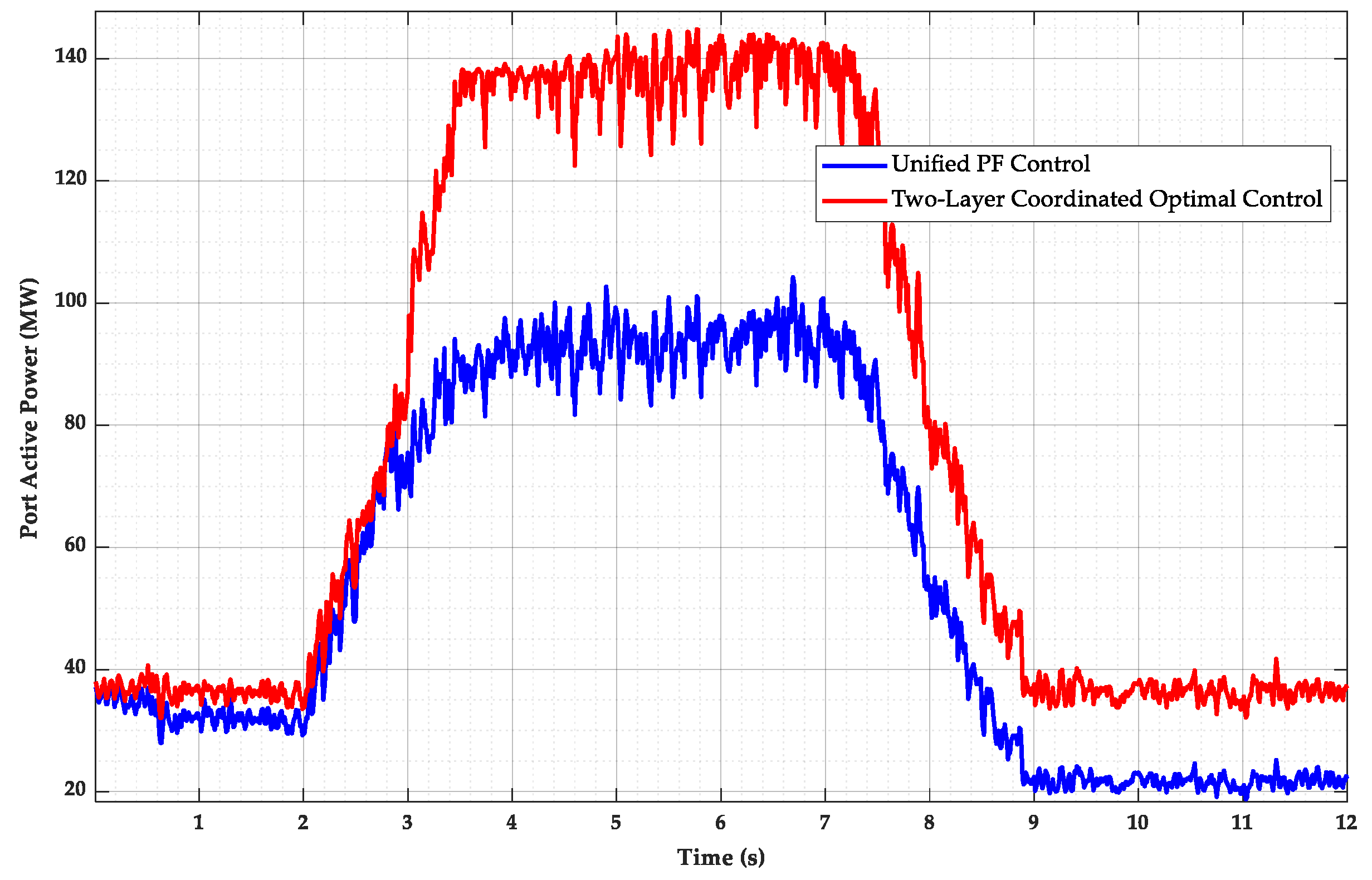
Both the voltage at the point of common coupling (PCC) and the terminal voltages of the wind turbine units within the wind farm belong to the 35 kV intra-farm voltage network. Therefore, the power flow within the farm can be optimized. The aim is to obtain the optimal distribution of active and reactive power output from the wind turbine units while ensuring intra-farm voltage security. The optimization objective is to maximize the active power output at the wind farm’s export point and the reactive power margin of the compensation devices, after accounting for the active power losses on the intra-farm collector lines. The objective function is formulated as follows:

$$\max [{\mathrm{w}}_1{\mathrm{P}}_{\mathrm{o}\mathrm{u}\mathrm{t}}-{\mathrm{w}}_2|{\mathrm{Q}}_{\mathrm{S}\mathrm{V}\mathrm{G}}|]$$

(6)

Among them, P_out represents the active power output at the wind farm’s export point, Q_SVG denotes the reactive power output of the SVG, and w₁ and w₂ represent the weighting coefficients, respectively. The weights were selected based on the operational priority: maximizing active power export (P_out) is the primary goal, followed by preserving the SVG reactive margin (|Q_SVG|). Therefore, we selected w₁ to be significantly larger than w₂.

The constraints for the global optimization include branch power flow constraints based on the linearized DistFlow model, branch current constraints, voltage constraints at the sending and receiving ends of branches, branch power constraints accounting for losses and power distribution, node power constraints, maximum rotor current constraints for doubly fed induction generators (DFIGs), upper and lower limits for active and reactive power output, node voltage security region constraints, and point of common coupling voltage constraints. These can be expressed as follows:

$$\left\{\begin{array}{c}{\mathrm{U}}_{\mathrm{j}}^2={\mathrm{U}}_{\mathrm{i}}^2-2({\mathrm{r}}_{\mathrm{i}\mathrm{j}}{\mathrm{P}}_{\mathrm{i}\mathrm{j}}+{\mathrm{x}}_{\mathrm{i}\mathrm{j}}{\mathrm{Q}}_{\mathrm{i}\mathrm{j}})+({\mathrm{r}}_{\mathrm{i}\mathrm{j}}^2+{\mathrm{x}}_{\mathrm{i}\mathrm{j}}^2){\mathrm{I}}_{\mathrm{i}\mathrm{j}}^2\hfill \\ {\mathrm{p}}_{\mathrm{j}}={\mathrm{P}}_{\mathrm{i}\mathrm{j}}-{\mathrm{r}}_{\mathrm{i}\mathrm{j}}{\mathrm{I}}_{\mathrm{i}\mathrm{j}}^2-{\displaystyle \sum _{\mathrm{k}:\mathrm{j}\to \mathrm{k}}}{\mathrm{P}}_{\mathrm{j}\mathrm{k}}\\ {\mathrm{q}}_{\mathrm{j}}={\mathrm{Q}}_{\mathrm{i}\mathrm{j}}-{\mathrm{x}}_{\mathrm{i}\mathrm{j}}{\mathrm{I}}_{\mathrm{i}\mathrm{j}}^2-{\displaystyle \sum _{\mathrm{k}:\mathrm{j}\to \mathrm{k}}}{\mathrm{Q}}_{\mathrm{j}\mathrm{k}}\\ {\mathrm{I}}_{\mathrm{i}\mathrm{j}}^2={\displaystyle \frac{{\mathrm{P}}_{\mathrm{i}\mathrm{j}}^2+{\mathrm{Q}}_{\mathrm{i}\mathrm{j}}^2}{{\mathrm{U}}_{\mathrm{i}}^2}}\end{array}\right.$$

(7)

$$\left\{\begin{array}{c}0\le {\mathrm{P}}_{\mathrm{i},\mathrm{r}\mathrm{e}\mathrm{f}}\le {\mathrm{P}}_{\mathrm{i},\mathrm{m}\mathrm{p}\mathrm{p}\mathrm{t}}\hfill \\ {\mathrm{Q}}_{\mathrm{i},\min }\le {\mathrm{Q}}_{\mathrm{i},\mathrm{r}\mathrm{e}\mathrm{f}}\le {\mathrm{Q}}_{\mathrm{i},\max }\hfill \\ 0\le {\mathrm{I}}_{\mathrm{i}\mathrm{j}}\le {\mathrm{I}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\\ {\mathrm{U}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\le {\mathrm{U}}_{\mathrm{i}}\le {\mathrm{U}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\\ \begin{array}{l}{\mathrm{V}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\le {\mathrm{V}}_{\mathrm{p}\mathrm{c}\mathrm{c}}\le {\mathrm{V}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\\ -{\mathrm{S}}_{\mathrm{S}\mathrm{V}\mathrm{G}}\le {\mathrm{Q}}_{\mathrm{S}\mathrm{V}\mathrm{G},\mathrm{r}\mathrm{e}\mathrm{f}}\le {\mathrm{S}}_{\mathrm{S}\mathrm{V}\mathrm{G}}\end{array}\end{array}\right.$$

(8)

Here, U_i and U_j represent the voltages at nodes i and j, respectively. r_ij and x_ij denote the resistance and reactance of the branch between nodes i and j. I_ij, P_ij, and Q_ij represent the current, active power, and reactive power flowing through the branch between nodes i and j. p_j and q_j represent the active and reactive power injected at node j, respectively. P_i,ref, Q_i,ref, and Q_SVG,ref denote the active power reference value of the wind turbine to be optimized, the reactive power reference value of the wind turbine, and the reactive power reference value of the SVG, respectively. P_i,mppt represents the maximum power point tracking reference value for the active power of wind turbine ii derived from the MPPT algorithm. Q_i,min and Q_i,max denote the lower and upper limits of reactive power under the current active power output, respectively. V_min and V_max represent the lower and upper safety limits of the PCC voltage, respectively. S_SVG denotes the reactive power capacity of the SVG. P_jk and Q_jk represent the active power and reactive power on the branches connected to node j, respectively.

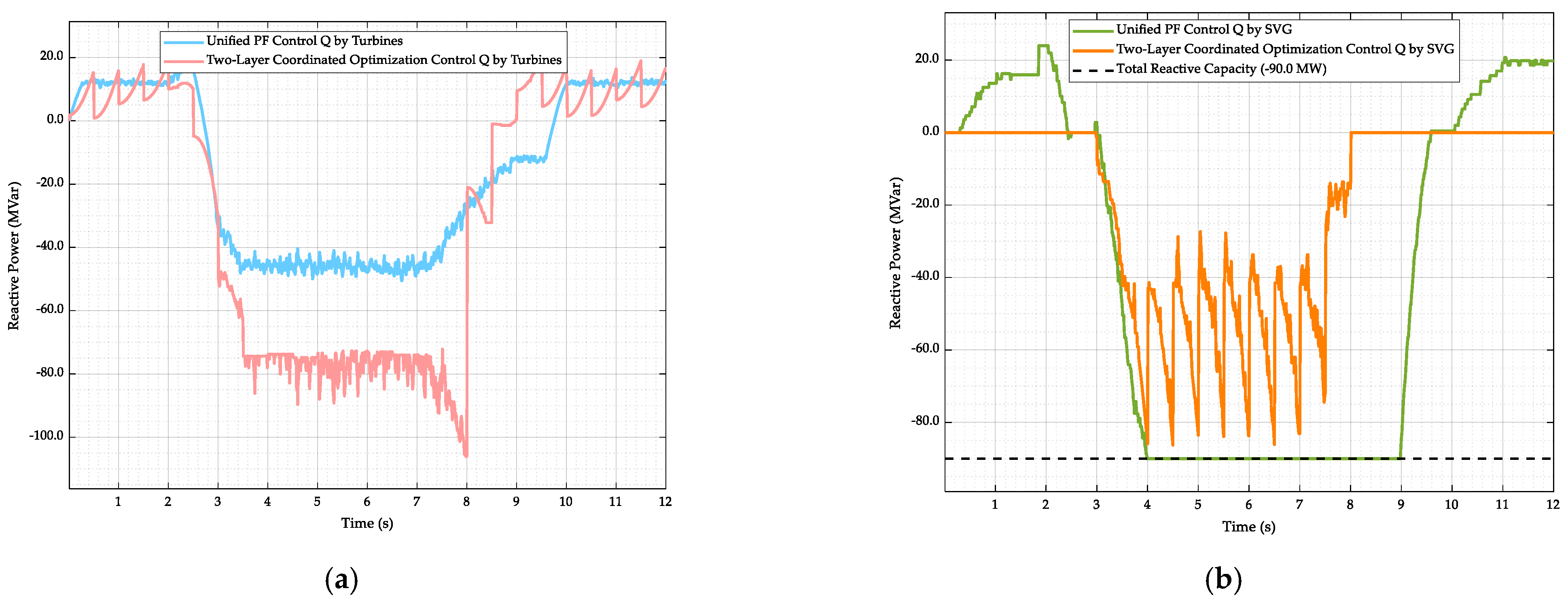
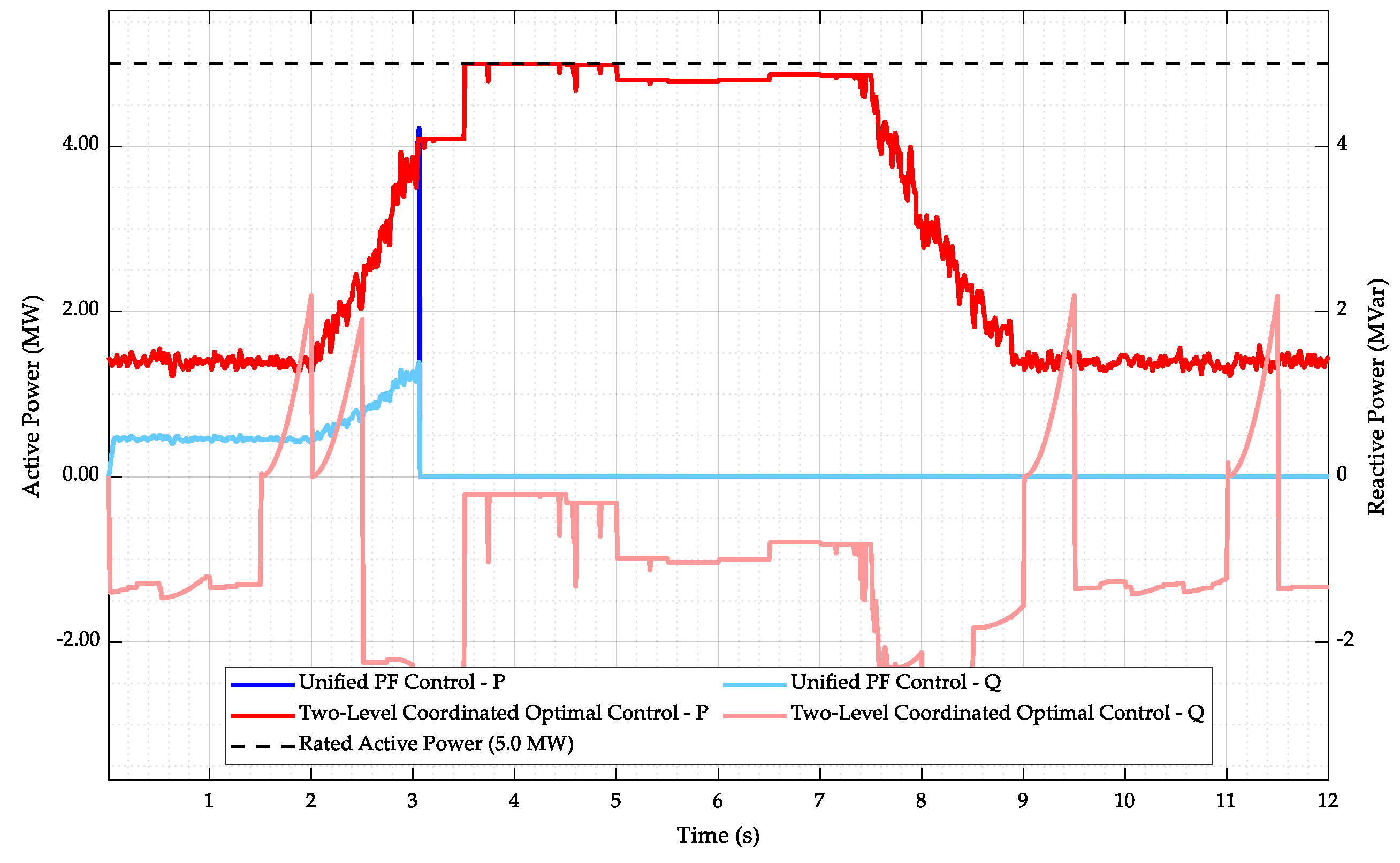
The reactive power limits on the machine side of a doubly fed induction generator (DFIG) are directly influenced by the current constraints of the stator and rotor windings, as well as the rotor-side converter. Here, the reactive power regulation capability on the grid side of the wind turbine is treated as a reactive power reserve, while only the machine-side reactive power is considered as the optimization target. The upper and lower limits of the reactive power on the machine side of the wind turbine are as follows:

$$\left\{\begin{array}{c}{\mathrm{Q}}_{\mathrm{i},\min }=-{\displaystyle \frac{3{\mathrm{U}}_{\mathrm{s}}^2}{2{\mathrm{X}}_{\mathrm{s}}}}-\sqrt{{({\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mathrm{X}}_{\mathrm{m}}}{{\mathrm{X}}_{\mathrm{s}}}}{\mathrm{U}}_{\mathrm{s}}{\mathrm{I}}_{\mathrm{rmax}})}^2-{\mathrm{P}}_{\mathrm{i},\mathrm{r}\mathrm{e}\mathrm{f}}^2}\\ {\mathrm{Q}}_{\mathrm{i},\max }=-{\displaystyle \frac{3{\mathrm{U}}_{\mathrm{s}}^2}{2{\mathrm{X}}_{\mathrm{s}}}}+\sqrt{{\left({\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mathrm{X}}_{\mathrm{m}}}{{\mathrm{X}}_{\mathrm{s}}}}{\mathrm{U}}_{\mathrm{s}}{\mathrm{I}}_{\mathrm{rmax}}\right)}^2-{\mathrm{P}}_{\mathrm{i},\mathrm{r}\mathrm{e}\mathrm{f}}^2}\end{array}\right.$$

(9)

Here, U_s denotes the stator voltage of the wind turbine, X_s and X_m represent the stator reactance and magnetizing reactance of the wind turbine, respectively, and I_rmax denotes the maximum rotor current limit of the wind turbine. U_min and U_max represent the lower and upper safety limits of the node voltage, respectively, and I_max denotes the branch current limit.

Since the power flow constraints and the upper and lower limits of the machine-side reactive power in the constraints are non-convex nonlinear constraints, they can only be solved using intelligent algorithms. However, intelligent algorithms suffer from issues such as low computational efficiency, high computational resource consumption, and susceptibility to local optima. Therefore, it is necessary to relax these nonlinear constraints to obtain second-order cone constraints that are easier for solvers to handle. The convex relaxation process via second-order cone programming is as follows: First, appropriate transformations are applied to the variables and constraints, aiming to convert the non-convex power flow equality equations into convex forms for optimized solving. During this transformation, variables or corresponding constraints can be relaxed, converting the optimization model into a convex optimization problem, thereby enabling the solution of the global optimum. Although this relaxation method expands the feasible region of the constraints, under exact relaxation conditions, the optimal solution of the original problem can be obtained at the boundary of the original feasible region.

Initially, squared variables are introduced to replace constraints involving quadratic terms, such as branch currents and node voltages, as shown in the following equations:

$$\left\{\begin{array}{c}{{\mathrm{P}}^{\prime }}_{\mathrm{i},\mathrm{r}\mathrm{e}\mathrm{f}}={\mathrm{P}}_{\mathrm{i},\mathrm{r}\mathrm{e}\mathrm{f}}\\ {{\mathrm{Q}}^{\prime }}_{\mathrm{i},\mathrm{r}\mathrm{e}\mathrm{f}}={\mathrm{Q}}_{\mathrm{i},\mathrm{r}\mathrm{e}\mathrm{f}}+{\displaystyle \frac{3{\mathrm{U}}_{\mathrm{s}}^2}{2{\mathrm{X}}_{\mathrm{s}}}}\\ {\mathrm{l}}_{\mathrm{i}\mathrm{j}}={\mathrm{I}}_{\mathrm{i}\mathrm{j}}^2\\ {\mathrm{v}}_{\mathrm{i}}={\mathrm{U}}_{\mathrm{i}}^2\end{array}\right.$$

(10)

Perform second-order cone relaxation on the nonlinear and non-convex power flow constraints; transform the maximum rotor current constraint for doubly fed induction generators into an active-reactive power output circle constraint, apply second-order cone relaxation to it, and incorporate the resulting convex second-order cone constraints into the wind farm optimization model. This can be expressed as:

$$\left\{\begin{array}{c}{‖\begin{array}{c}{{\mathrm{P}}^{\prime }}_{\mathrm{i},\mathrm{r}\mathrm{e}\mathrm{f}}\\ {{\mathrm{Q}}^{\prime }}_{\mathrm{i},\mathrm{r}\mathrm{e}\mathrm{f}}\end{array}‖}_2\le {\displaystyle \frac{3{\mathrm{U}}_{\mathrm{S}}{\mathrm{X}}_{\mathrm{m}}{\mathrm{I}}_{\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{x}}}{2{\mathrm{X}}_{\mathrm{s}}}}\\ {‖\begin{array}{c}2{\mathrm{P}}_{\mathrm{i}\mathrm{j}}\\ 2{\mathrm{Q}}_{\mathrm{i}\mathrm{j}}\\ {\mathrm{l}}_{\mathrm{i}\mathrm{j}}-{\mathrm{v}}_{\mathrm{i}}\end{array}‖}_2\le {\mathrm{l}}_{\mathrm{i}\mathrm{j}}+{\mathrm{v}}_{\mathrm{i}}\end{array}\right.$$

(11)

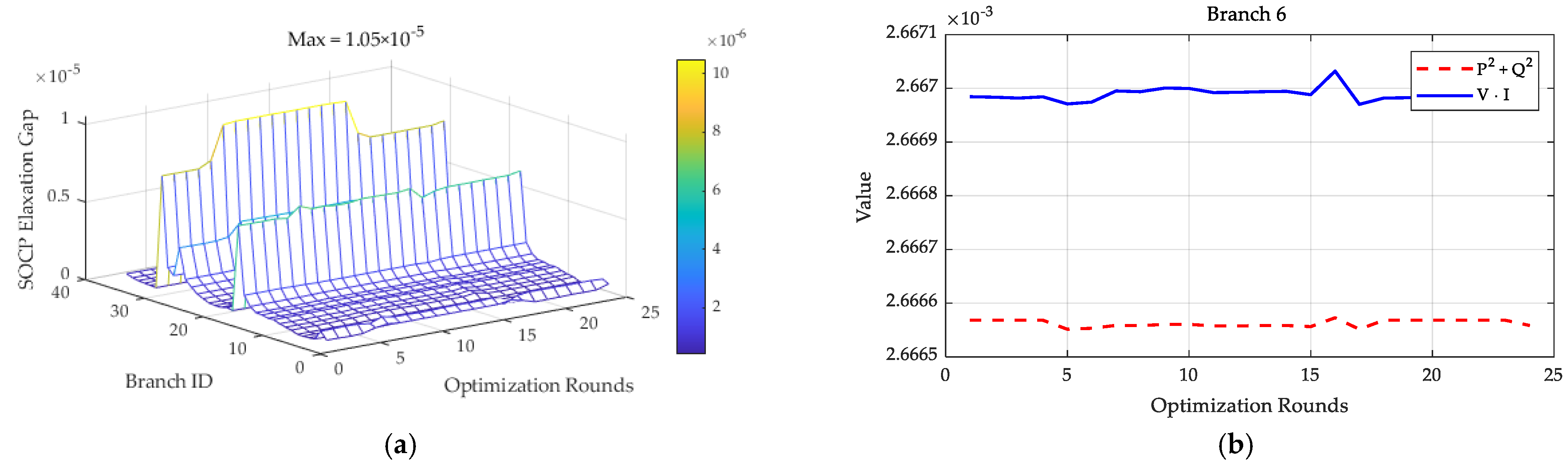
At this point, the non-convex and nonlinear constraints are transformed into a rotated second-order cone form. Research indicates that second-order cone relaxation is always tight under radial distribution network structures. Therefore, the optimal active and reactive power output of wind turbine units, as well as the corresponding terminal voltages and intra-farm power flow distribution, can be obtained by solving the optimization problem using commercial solvers. However, due to the different voltage levels between the impedance of the long-distance transmission line Z₀ = R₀ + jX₀ (connecting the infinite grid and the PCC) and the intra-farm collector line impedance Z₁ = R₁ + jX₁, which does not conform to the distribution network scenario, directly using a solver would result in an excessively large relaxation gap in the second-order cone relaxation, leading to solution failure.

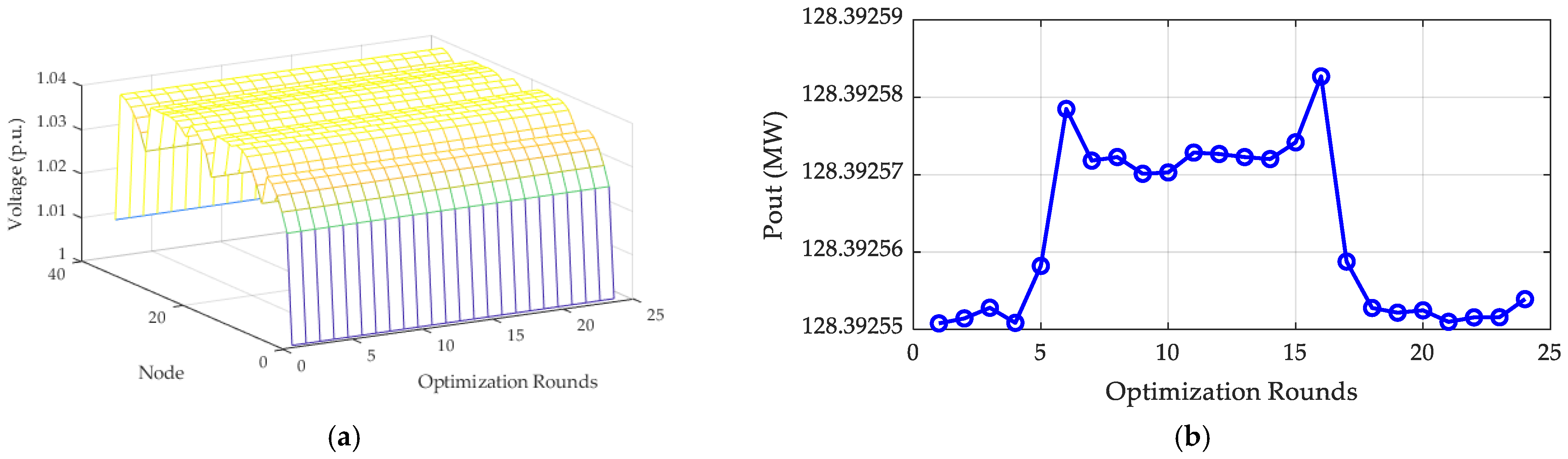
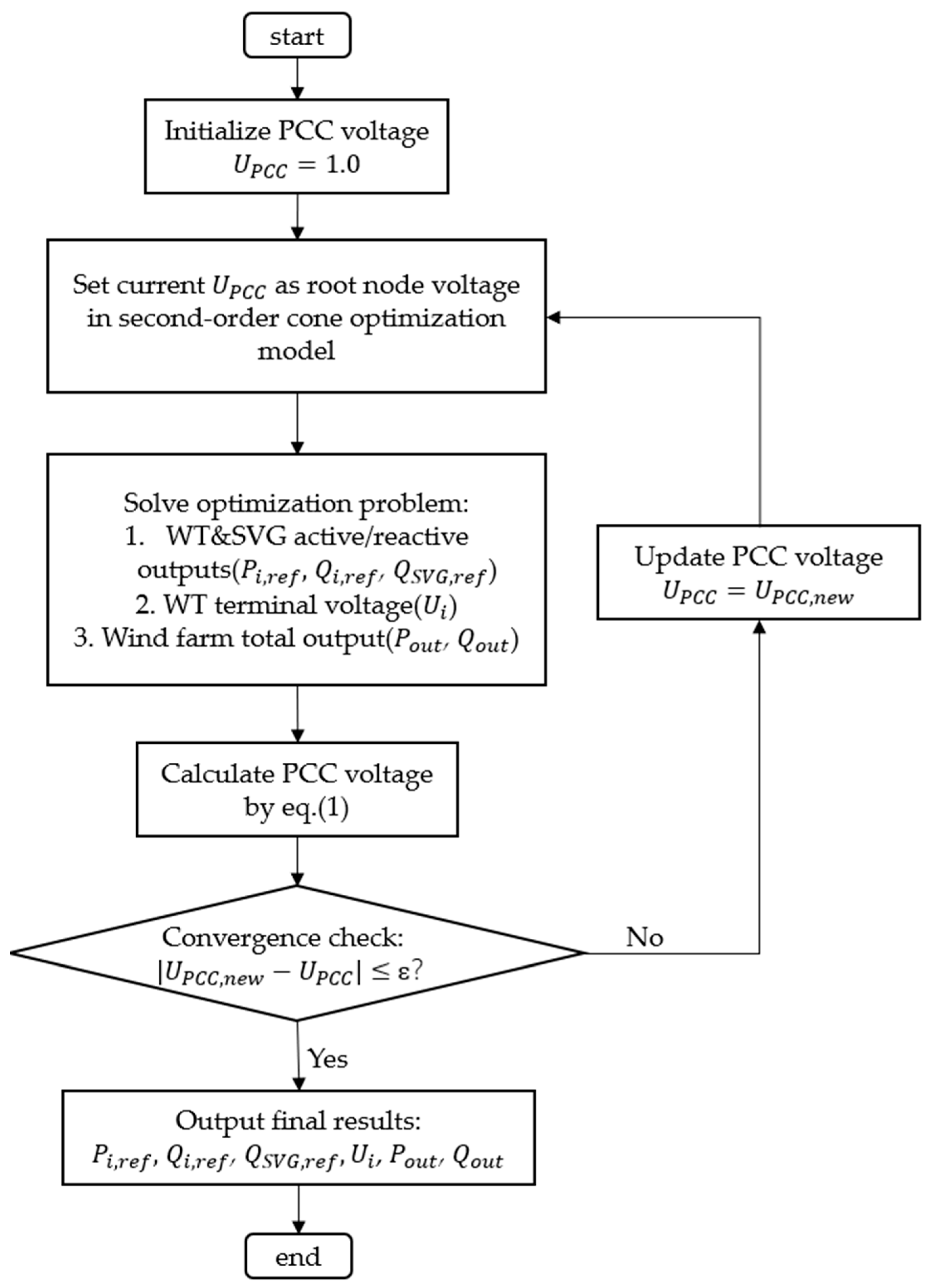
Therefore, this paper proposes a two-layer optimization. First, the per-unit PCC voltage is initialized to 1 and set as the root node voltage in the wind farm’s second-order cone optimization model to solve for the optimal active/reactive power output of the wind turbines and the corresponding terminal voltages. This yields the active power output P_out and reactive power output Q_out at the wind farm’s export point. These values are then substituted back into Equation (1) to calculate the PCC voltage U_PCC. This updated PCC voltage is iteratively fed back into the second-order cone optimization model until the difference between the PCC voltages from two consecutive iterations falls below the allowable error, at which point the iteration terminates. The iterative process is shown in Figure 2.

2.4. Wind Farm Reactive Power Demand Setting

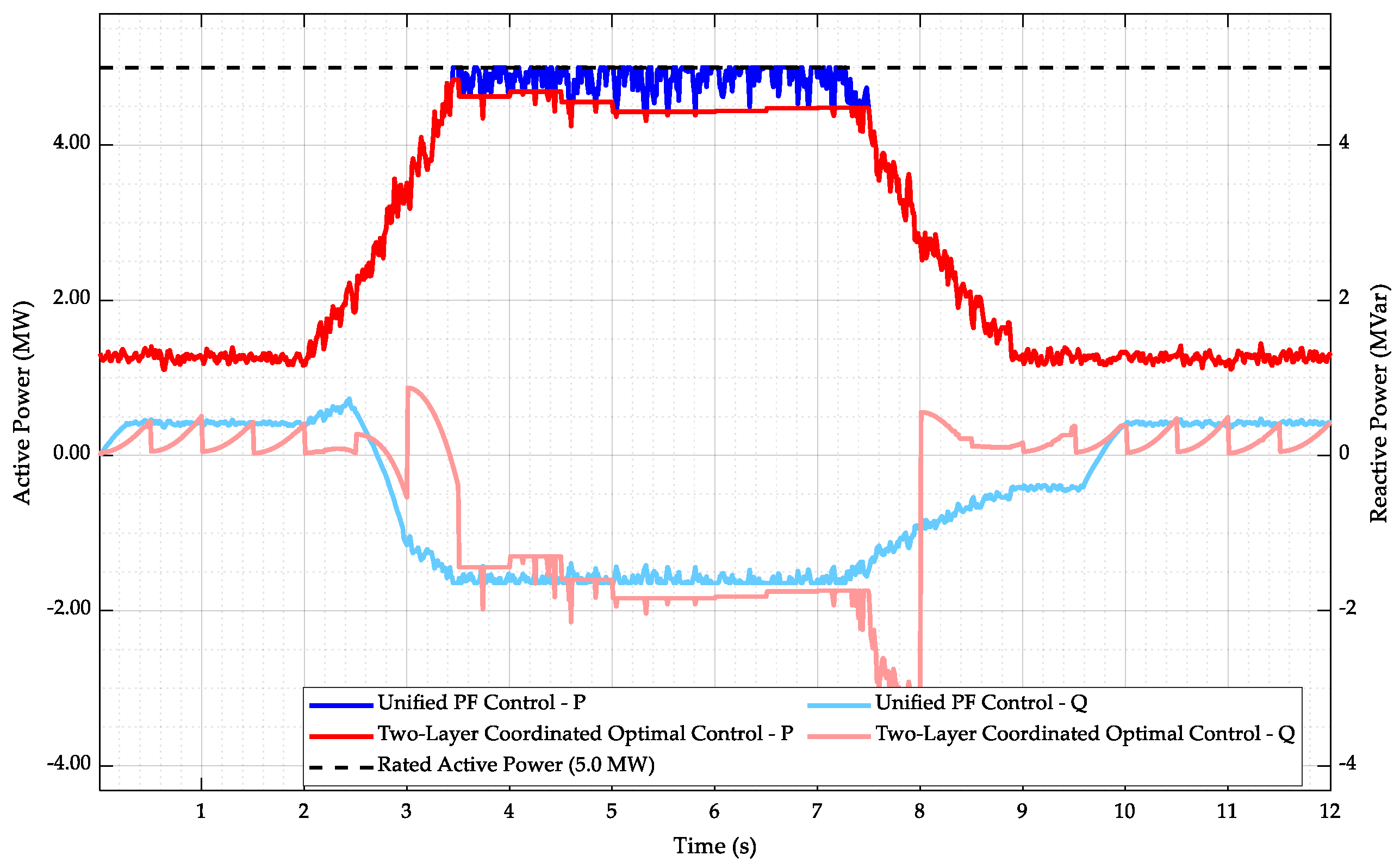
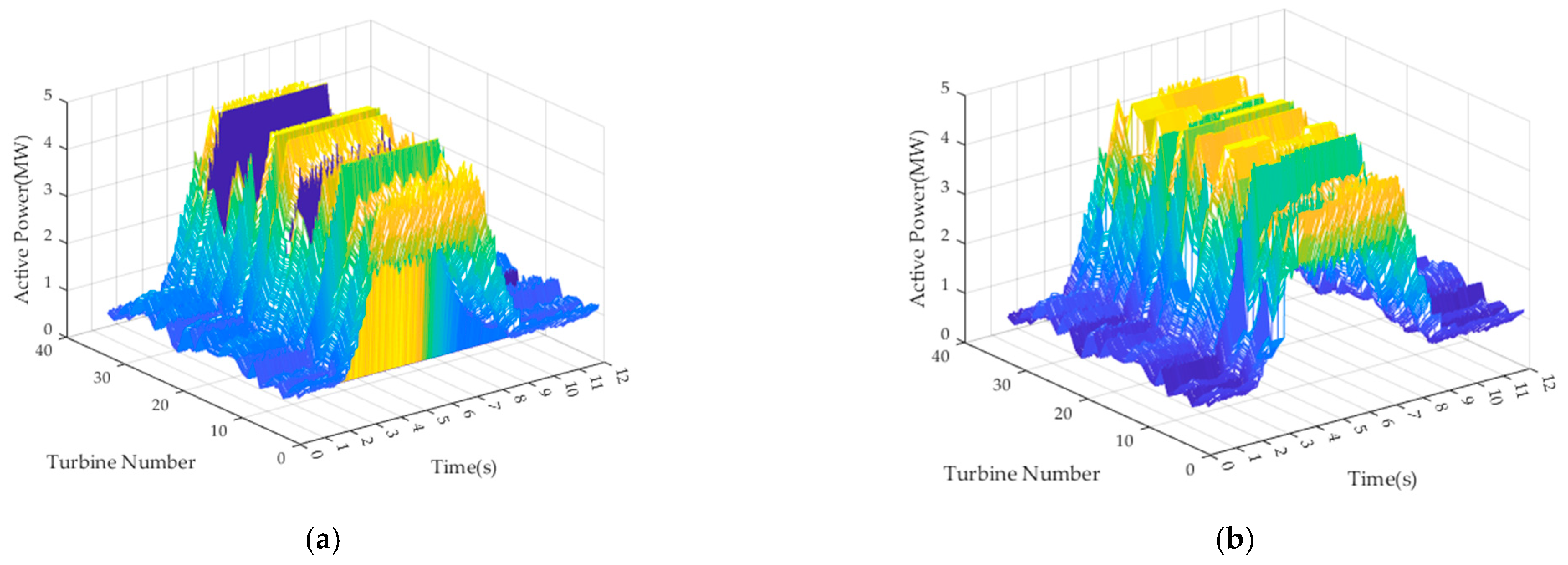
Reactive power and voltage control for the wind farm adopts a hierarchical control structure, primarily consisting of two layers: the global optimization layer and the voltage control layer. Considering the computation time required for global optimization and the fact that the time constant for adjusting the reactive power output of wind turbine units is larger than that of the SVG, the action time of the global optimization layer for wind turbines is on the order of seconds. Based on the current wind speed, this layer optimally solves for the best active and reactive power output, which is then allocated to the wind turbines and reactive power compensation devices within the farm to ensure that the terminal voltages remain within the safe range.

The voltage control layer operates on a millisecond timescale. The reactive power command generation process is shown in Figure 3. It maintains the PCC voltage at the command value from the upper-layer AVC system through PI control with a fixed voltage at the point of common coupling (PCC) when wind speed fluctuates. Within each global control cycle, the active power output of the wind turbines tracks the wind speed via the MPPT algorithm. For wind turbines that have already utilized their full reactive output capability, the active power command value set by the global optimization layer is used as the upper limit for active power output to prevent exceeding the maximum rotor current constraint during this control cycle.

Regarding the reactive power command calculated through PI control, it is first evenly distributed to each wind turbine unit. Within the limit of not exceeding the rotor current constraint, the upper limit of reactive power output is determined. The difference between the total reactive power demand and the additional reactive power generated by the turbines is treated as an additional reactive power command for the SVG. This reactive command is superimposed on the SVG command value from each global optimization cycle, which serves as a feedforward signal, and the combined total reactive command is then issued to the SVG.

3. Results

Referring to the actual conditions of current large-scale wind farms, this paper establishes a 165 MW wind farm simulation system in MATLAB 2024b. The wind farm comprises 33 doubly fed induction generators (DFIGs), each with a capacity of 5 MW. The rotor diameter is 180 m, the maximum power coefficient is 0.45, and the air density is 1.225 kg/m³. The wind farm includes four feeders, with a rated wind speed of 8.93 m/s. Among them, Feeder 2 and Feeder 3 each have one and two branch feeders, respectively, to simulate the wind farm under complex wiring conditions. The topology of this wind farm is shown in Figure 4. The feeder voltage within the wind farm is 35 kV, utilizing YJLV22-26/35-3×95 cables, with a spacing of 1 km between turbine units. The wind farm is connected to a transformer with a transformation ratio of 220 kV/35 kV for voltage step-up and then linked to the grid via a 100 km long transmission overhead line of type LGJQ-2×600. On the low-voltage busbar side of the wind farm’s step-up substation, three SVG units with a capacity of 20 MVar each are installed. The convergence tolerance ϵ for the PCC voltage iteration is set to 10⁻⁴ p.u. The maximum number of iterations is set to 10.

Two control strategies are applied to the wind farm: the proposed two-layer coordinated optimal control method and the commonly used unified power factor control method. In the two-layer coordinated optimization algorithm, the optimization period for the global layer is 0.5 s, while the control period for the voltage control layer is 0.01 s. The unified power factor control method takes the wind farm PCC voltage as the control target. The specific implementation is as follows: the active power output of the wind turbines tracks wind speed via the MPPT algorithm, and the reactive power demand is calculated through a fixed-voltage PI control at the PCC. The reactive power capability of the wind turbines is utilized first, with any shortfall compensated by the SVG. The control period is 0.01 s. We have performed a statistical analysis of the iteration process between the calculated U_PCC and the optimized P_out. The system shows stable convergence, typically requiring an average of 4 iterations. No oscillation was observed in the tested cases. We tested the algorithm on a PC with Inter i7-14600HX, 32 GB RAM. The average computation time for the global optimization is approximately 0.1–0.2 s, with a worst-case time of 0.27 s. We also validated the slack intervals in the global optimization algorithm, as detailed in Appendix A.

In a renewable energy power system, the dispatch AVC master station issues voltage commands for the PCC to the wind farm AVC slave station based on real-time system-wide conditions, aiming for safety and economy. Different voltage commands at the PCC will lead to different operating states of the units within the wind farm, requiring the AVC slave station to adjust its control strategy to enhance generation economy and operational stability.

To verify the effectiveness of control on both the PCC voltage and the unit terminal voltage under rapid wind speed fluctuations, a wind speed input profile as shown in Figure 5 is designed.

3.1. Case with the PCC Voltage Command Set to 1.02 p.u.

3.1.1. Coordinated Optimal Control Performance on PCC Voltage

First, the ability of the proposed control strategy to regulate the PCC voltage of the wind farm is examined. With the PCC voltage reference set to V_ref = 1.02 p.u., the simulation results show that fluctuations in wind speed cause variations in the active power output of the wind turbines. However, both control strategies are able to maintain the PCC voltage near the target value, ensuring a stable voltage at the grid connection point. The variation in the PCC voltage over time is shown in Figure 6.

3.1.2. Coordinated Optimal Control Performance on Wind Turbine Terminal Voltage

Figure 7 illustrates the fluctuation of terminal voltages for all turbine units within the wind farm under both control methods over the simulation period The color gradient from cool to warm represents voltage levels increasing from low to high. It can be observed that when the PCC voltage command is set to 1.02 p.u., the active power output of the wind turbines increases as wind speed rises, causing the terminal voltages of some units at the far end of the feeders to exceed 1.06 p.u. When the two-layer coordinated optimal control is applied, constraints on terminal voltages are incorporated at the global optimization layer, effectively preventing the terminal voltages of the units from exceeding the limits. As a result, the compliance rate of terminal voltages for the units within the farm is improved. Figure 8 shows the comparison of terminal voltages for wind turbines with different control methods under the same time interval.

Table 1. Comparison of Terminal Voltage Between Two Control Methods.

Method	Mean Value (p.u.)	Compliance Rate (1.06 p.u.)	Maximum Value (p.u.)
Unified PF Control	1.0347	93.87%	1.0767
Two-layer Coordinated Optimal Control	1.0355	96.56%	1.0702

shows the average fan-end voltage and voltage compliance rate under two control methods.

3.1.3. Coordinated Optimal Control Performance on Active Power

Figure 9 shows the active and reactive power output of one turbine unit within the wind farm over the entire simulation period. It can be observed that when wind speed is low, both control methods allow the unit to achieve maximum power point tracking. At higher wind speeds, the unit under unified power factor control continues to track the wind speed, whereas the unit under two-layer coordinated optimization control sacrifices a portion of its active power output to gain greater reactive power capability. This ensures that the terminal voltage does not exceed limits and optimizes the distribution of reactive power flow within the farm.

Figure 10 compares the active power output at the wind farm’s export point under the two control methods. Although the two-layer coordinated optimization control does not fully track the wind speed, it effectively reduces active power losses within the farm through optimized allocation of active and reactive power at the global optimization layer. As a result, it achieves higher active power output at the wind farm’s export point, enhancing operational economy while ensuring voltage security for the units. Over the 12 s simulation period, compared to the unified power factor control, the two-layer coordinated optimization control generated an additional 20.657 kWh of electricity, representing an 8.52% increase in power generation.

3.1.4. Coordinated Optimal Control Performance on Reactive Power

Both control methods prioritize utilizing the reactive power capability of the wind turbines. It can be seen in Figure 11. that by incorporating the maximum rotor current as a constraint in the global optimization layer, the two-layer coordinated optimization control makes greater use of the converter capacity of the wind turbines. This approach also creates conditions for sacrificing active power output to achieve higher reactive power capability, providing nearly twice the reactive power support when the unit’s active power output is near full capacity.

Furthermore, because the two-layer coordinated optimization control utilizes the reactive power output capability of the wind turbines to a greater extent, it reduces reliance on the SVG. At higher wind speeds, the three SVG units under unified power factor control have already reached their output limits, whereas those under two-layer coordinated optimization control maintain a certain margin, thereby improving the overall fault reserve level of the wind farm. Throughout the simulation period, the average reactive power margin of the SVG units under unified power factor control was 46.55%, with an average reactive power reserve of 41.895 MVar. In contrast, under two-layer coordinated optimization control, the average reactive power margin was 78.18%, with an average reactive power reserve of 70.362 MVar.

3.2. Case with the PCC Voltage Command Set to 1.04 p.u.

3.2.1. Coordinated Optimal Control Performance on Terminal Voltage Under Higher Voltage Conditions

As shown in Figure 12, after setting the PCC voltage to 1.04 p.u., the active power output of the wind turbines continues to increase as wind speed rises, leading to a further rise in terminal voltages. In the wind farm using unified power factor control, the terminal voltages of some wind turbine units exceed 1.1 p.u., causing these units to disconnect from the grid and reducing their active power output directly to 0.

Table 2. Comparison of Terminal Voltage Between Two Control Methods.

Method	Mean Value (p.u.)	Compliance Rate (1.08 p.u.)	Maximum Value (p.u.)
Unified PF Control	1.0502	95.64%	1.1047
Two layer Coordinated Optimal Control	1.0555	96.44%	1.00949

shows the average terminal voltage and voltage compliance rate under two control methods when the grid connection point voltage command is 1.04 p.u. Figure 13 shows the active power output of all wind turbines under two control methods, with colors ranging from cool to warm representing output levels from low to high.

3.2.2. Coordinated Optimal Control Performance on Active Power Under Higher Voltage Conditions

As illustrated in Figure 14 and Figure 15, under unified power factor control, Unit 24 disconnects from the grid at 3 s due to its terminal voltage exceeding 1.1 p.u., resulting in its active and reactive power output dropping to 0. In contrast, under two-layer coordinated optimization control, Unit 24 continues to operate stably. A total of five units, numbered 12, 13, 14, 22, 23, 24, 25, 26, and 27, located at the far end of the feeders and experiencing higher terminal voltages, disconnect from the grid successively, leading to a reduction in the overall active power output of the wind farm. Over the 12 s simulation period, compared to unified power factor control, the two-layer coordinated optimization control generated an additional 80.14 kWh of electricity, representing a 43.05% increase in power generation.

4. Discussion and Conclusions

This paper establishes a global optimization model for wind farms that considers the safety of generator terminal voltages. The model optimizes the internal power flow distribution and maximizes the reactive power output of each wind turbine while ensuring their maximum active power output. This approach achieves the highest possible export active power and maximizes the reactive power margin of the SVG. At the same time, considering the dispatch requirements issued by the AVC master station, a two-layer control system is designed to effectively track the voltage commands at the point of common coupling (PCC), achieving a two-layer coordinated voltage control method that balances both the PCC voltage level and the safety of the generator terminal voltages. This effectively enhances wind energy utilization efficiency, improves the economic and safe operation of the wind farm, and reduces network losses and generation loss caused by unit disconnection. Simulation results show that, compared to the traditional unified power factor control method, the proposed two-layer coordinated optimization control method for wind farms improves the safety of generator terminal voltages, increases the power generation of the wind farm, enhances the system’s reactive power margin, and strengthens the reserve capacity against potential voltage faults—all while ensuring that the PCC voltage accurately tracks the command signals. The main conclusions of this paper are as follows:

• For the nonlinear, non-convex power flow constraints and rotor current constraints in the global optimization layer, second-order cone relaxation is applied, converting them into convex second-order cone constraints that are incorporated into the wind farm optimization model. Using the commercial solver Gurobi for the solution improves both the solving speed and stability.
• Since the global optimization layer simultaneously considers both the PCC voltage and the generator terminal voltages, the significant impedance difference between the long-distance transmission lines and the internal feeders of the wind farm can easily lead to an excessively large second-order cone relaxation gap. To address this, this paper adopts a two-layer optimization structure: the inner-layer optimization model only considers the internal feeders of the wind farm, while the transmission line impedance is accounted for in the outer-layer calculation, iteratively solving for the PCC voltage and the internal power flow of the wind farm.
• A two-layer coordinated voltage optimization control structure for the wind farm is designed. Building upon the second-level global optimization, a millisecond-level PCC voltage tracking control is nested. Reactive power commands are prioritized for distribution to the wind turbine units, maximizing the utilization of the units’ reactive power capacity without exceeding their current reactive power margins. This reduces reliance on the SVG, increases the system’s reactive power reserve, and enhances its reserve capacity against potential voltage faults.