Wind–Storage Coordinated Control Strategy for Suppressing Repeated Voltage Ride-Through of Units Under Extreme Weather Conditions

Abstract

In practical engineering, large-scale wind power integration typically requires long-distance transmission lines to deliver power to load centers. The resulting weak sending-end systems lack support from synchronous power sources. Under extreme weather conditions, the rapid increase in active power output caused by high wind power generation may lead to voltage instability. In existing projects, a phenomenon of repeated voltage fluctuations has been observed under fault-free system conditions. This phenomenon is induced by the coupling of the characteristics of weak sending-end systems and low-voltage ride-through (LVRT) discrimination mechanisms, posing a serious threat to the safe and stable operation of power grids. However, most existing studies focus on the analysis of voltage instability mechanisms and the optimization of control strategies for single devices, with insufficient consideration given to voltage fluctuation suppression methods under the coordinated operation of wind power and energy storage systems. Based on the actual scenario of energy storage configuration in wind farms, this paper improves the traditional LVRT discrimination mechanism and develops a coordinated voltage ride-through control strategy for permanent magnet synchronous generator (PMSG) wind turbines and energy storage batteries. It can effectively cope with unconventional operating conditions, such as repeated voltage ride-through and deep voltage ride-through that may occur under extreme meteorological conditions, and improve the safe and stable operation capability of wind farms. Using a hardware-in-the-loop (HIL) test platform, the coordinated voltage ride-through control strategy is verified. The test results indicate that it effectively enhances the wind–storage system’s voltage ride-through reliability and suppresses repeated voltage fluctuations.

1. Introduction

In recent years, the frequency and intensity of extreme wind events have been increasing annually, leading to a rise in incidents such as sudden surges in wind turbine power generation and shutdowns triggered by excessive wind speeds. Consequently, the randomness of wind farm output has become increasingly pronounced. With the continuous growth of wind power penetration, rapid increases in active power output due to high wind power generation have resulted in voltage instability and insufficient reactive power support capability in wind farms, making the stability issues of large-scale wind power integration under grid voltage disturbances increasingly prominent [1,2,3]. Therefore, to address the dual demands of frequency stability and voltage support enhancement in this context, energy storage systems are widely deployed in wind farms to provide frequency and voltage support. The coordinated cooperation between energy storage and other power sources can effectively improve the resilience of power systems, resist extreme meteorological threats, adapt to the output randomness of renewable energy, and enhance the power grid’s capability to recover from abnormal states and faults [4]. This has prompted researchers to actively explore novel system architectures and coordinated control strategies [5,6,7].

During fault ride-through (FRT), the active power output capability of the PMSG grid-side converter (GSC) diminishes. Consequently, the key research focuses on two aspects: the absorption of unbalanced power across the DC capacitor and the control of reactive power. Ref. [8] reduces the wind energy capture of wind turbines by adjusting the pitch angle. However, the pitch angle adjustment has a relatively long response time, making it more suitable for addressing persistent faults. During faults, the dump load circuit dissipates unbalanced power through resistors. Due to its simplicity and reliability, it has become the most commonly used DC-side protection method in engineering applications [9,10]. In practical engineering, most wind farms are equipped with energy storage systems, which can respond quickly to assist wind farms in providing voltage support. Among current research on voltage control of wind farms, studies on LVRT started relatively early. Relevant methods and standards have been developed and applied in practical engineering [11].

In practical engineering, wind power integration systems generally require long-distance outgoing transmission lines, which are characterized by a relatively weak grid structure and insufficient inertia support. These systems exhibit a significantly weak sending-end power grid. This paper investigates the phenomenon of aperiodic abnormal voltage fluctuations in wind power integration systems during the actual operation of the power system. Based on fault recording data, during voltage fluctuations, wind turbines repeatedly enter the LVRT mode with no physical faults existing. The process is accompanied by corresponding fluctuations in active and reactive power. This leads to large-scale wind turbines tripping, posing a serious threat to the safe and stable operation of the system. This phenomenon is significantly different in form and mechanism from voltage fluctuations caused by random wind power fluctuations and reactive power compensation device adjustments [12,13]. Currently, there is limited literature addressing this issue, and existing studies mainly focus on mechanism analysis. Ref. [14] summarizes two typical operating conditions of abnormal voltage in distributed new energy systems: continuous LVRT and repeated LVRT. It points out that in weak power grids, the active power output of distributed new energy significantly affects its terminal voltage during LVRT, while the impact of reactive power on voltage weakens. Based on monotonic system theory, ref. [15] concludes through analysis that an excessively fast active power recovery rate after a fault will cause a dynamic voltage drop, which, in turn, leads to repeated voltage fluctuations. Ref. [16] analyzes the non-smooth bifurcation phenomenon corresponding to voltage fluctuations using bifurcation theory, and its phase diagram trajectory exhibits the switching characteristics of different control modes. Ref. [17] points out that the stable equilibrium points of the normal operation subsystem and the LVRT subsystem are different, and the system trajectory continuously switches near the LVRT threshold, triggering voltage fluctuations.

Regarding solutions, refs. [12,13] point out that two measures, increasing the LVRT exit threshold of wind turbines and maintaining a certain level of active power during the ride-through process, can suppress the phenomenon of repeated voltage fluctuations. Ref. [14] indicates that timely reactive power support during faults and slowing down the active power recovery rate after fault clearance are both conducive to avoiding repeated voltage fluctuations. Based on the stability criteria and stability indices of the common Lyapunov function, ref. [17] adopts global sensitivity analysis to identify dominant parameters and optimizes control parameters using a particle swarm optimization (PSO) algorithm to mitigate the risk of voltage fluctuations. However, existing solutions generally have problems, such as difficulty in parameter tuning and insufficient utilization of adjustable resources in wind farms, which require further research.

To address the above issues, Section 2 first introduces the basic control methods of wind–storage systems, clarifies the coordination principle of the systems during voltage ride-through and the relevant standards, and analyzes the mechanism of repeated voltage fluctuations induced by LVRT using PV curves. Section 3 classifies four different voltage ride-through modes based on the point of common coupling (PCC) voltage and formulates a coordinated voltage ride-through control strategy, which takes wind turbines, energy storage, and dump load circuit as an integrated unit. Section 4 verifies the effectiveness of the control strategy based on a HIL test platform. The results show that during voltage ride-through, the proposed strategy maintains stable system operation and responds correctly to repeated voltage ride-through conditions. Section 5 mainly conducts comparative and quantitative analysis on the adaptability of the proposed coordinated control strategy, discusses the planned application scenarios, and outlines the future development directions of this research topic.

2. Materials

2.1. Conventional Control Methods and Frameworks for Wind–Storage Systems

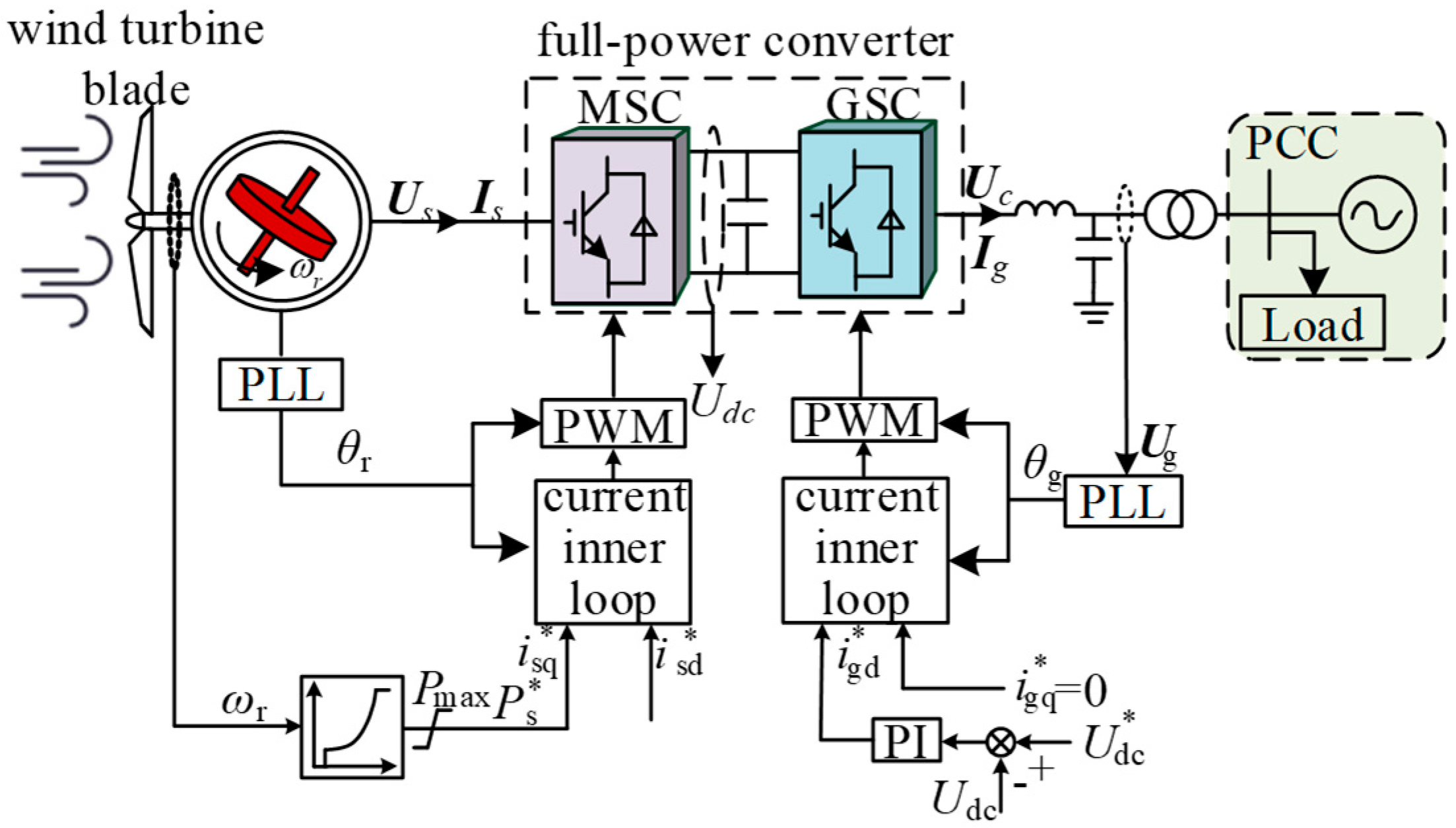
2.1.1. Overall Modeling of Wind–Storage Systems

Most energy storage systems equipped in wind farms are chemical batteries, such as lithium-ion batteries. There are two forms of coordination between energy storage batteries and wind farms. One is distributed energy storage, where a single wind turbine is directly equipped with an energy storage battery on the DC side; the other is centralized energy storage, where one or more wind farms share a single energy storage station. The capacity of each distributed energy storage unit is much smaller than that of centralized energy storage, and it has significant spatial adaptability. When some power generation equipment malfunctions, it can significantly suppress disturbances in the feeder transmission power. However, due to the lack of unified regulation among energy storage units, the station-level support capability is limited and relatively lower than that of the centralized solution. Centralized energy storage systems establish an energy management platform by integrating energy storage resources, and at the overall control level, they implement a station-level coordinated control strategy to synthesize operational parameters of all on-site units, reconcile multiple control objectives, and thereby achieve dynamic alignment between the wind farm’s output profile and grid dispatch mandates.

At the grid interaction level, they can give full play to the rapid adjustment characteristics of energy storage units, effectively improving the station-level frequency and voltage regulation capabilities [18,19]. The schematic diagram of the centralized energy storage structure is shown in Figure 1.

In summary, this study primarily conducts research on wind–storage systems based on the scenario where wind farms are equipped with centralized energy storage stations.

2.1.2. Wind Turbine Control

The machine-side converter of wind turbines typically employs the Maximum Power Point Tracking (MPPT) control strategy to effectively capture the maximum available wind energy. Based on the rotor flux-oriented d-axis current control strategy, the machine-side converter (MSC) constrains the d-axis component of the rotor current to zero (i_sd = 0), fully mapping the stator current vector to the q-axis, thereby achieving decoupled control of electromagnetic power and electromagnetic torque. The core control mechanism of the GSC lies in maintaining the stability of the DC bus voltage through the non-differential regulation of the DC voltage outer loop. In terms of AC-side control, grid voltage vector-oriented technology is used to establish a synchronous rotating coordinate system, with the d-axis dynamically aligned to the direction of the grid voltage vector, thus establishing an operating condition of unity power factor.

In the mathematical modeling of the PMSG, if the d-axis of the two-phase rotating coordinate system is aligned with the direction of the rotor flux linkage, the voltage equations of the PMSG in the dq synchronous rotating coordinate system can be expressed as the dynamic relationship between inductance parameters and flux linkage [20], which is given by

$$\left\{\begin{array}{l}{u}_{\mathrm{sd}}=R_{\mathrm{s}}{i}_{\mathrm{sd}}+L_{\mathrm{sd}}{\displaystyle \frac{\mathrm{d}{i}_{\mathrm{sd}}}{\mathrm{d}t}}-{\omega }_{\mathrm{r}}{L}_{\mathrm{sq}}{i}_{\mathrm{sq}}\\ u_{\mathrm{sq}}=R_{\mathrm{s}}{i}_{\mathrm{sq}}+L_{\mathrm{sq}}{\displaystyle \frac{\mathrm{d}{i}_{\mathrm{sq}}}{\mathrm{d}t}}+{\omega }_{\mathrm{r}}{L}_{\mathrm{sd}}{i}_{\mathrm{sd}}+{\omega }_{\mathrm{r}}{\psi }_{\mathrm{f}}\end{array}\right.,$$

(1)

where the dq-axis components of the stator terminal voltage are denoted as u_sd and u_sq; the stator resistance is recorded as R_s; the dq-axis components of the stator current are expressed as i_sd and i_sq; the dq-axis inductances of the stator are L_sd and L_sq; ω_r represents the rotor angular velocity; and the rotor permanent magnet flux linkage is denoted as ψ_f.

The machine-side converter typically adopts the MPPT control strategy to achieve effective tracking of the maximum wind energy. At this point, the expression of electromagnetic power can be given by

$$\left\{\begin{array}{l}{P}_{\mathrm{s}}=-{\displaystyle \frac{3}{2}}{u}_{\mathrm{sq}}{i}_{\mathrm{sq}}\\ Q_{\mathrm{s}}={\displaystyle \frac{3}{2}}{u}_{\mathrm{sd}}{i}_{\mathrm{sq}}\end{array}\right.,$$

(2)

$$T_{\mathrm{e}}=-{\displaystyle \frac{3}{2}}{p}_{\mathrm{n}}{\psi }_{\mathrm{f}}{i}_{\mathrm{sq}},$$

(3)

where P_s and Q_s are the electromagnetic power output by the wind turbine, and p_n is the number of pole pairs of the synchronous generator. Based on the target electromagnetic torque command value obtained by MPPT, the reference values of the dq-axis currents of the generator can be derived as follows:

$$\left\{\begin{array}{l}{i}_{\mathrm{sd}}^{\ast }=0\\ i_{\mathrm{sq}}^{\ast }=-{\displaystyle \frac{2T_{\mathrm{e}}^{\ast }}{3p_{\mathrm{n}}{\psi }_{\mathrm{f}}}}\end{array}\right.,$$

(4)

Under steady-state operating conditions, the derivatives of the dq-axis components of the stator current i_sd and i_sq are zero. In the vector control strategy, a PI controller is typically employed as the controller for the current inner loop. Based on Equation (1), the steady-state control equations of the PMSG machine-side converter can be derived as follows:

$$\left\{\begin{array}{l}{u}_{\mathrm{sd}}=(k_{\mathrm{p}1\mathrm{L}}+{\displaystyle \frac{k_{\mathrm{i}1\mathrm{L}}}{s}})(i_{\mathrm{sd}}^{\ast }-i_{\mathrm{sd}})+R_{\mathrm{s}}{i}_{\mathrm{sd}}-{\omega }_{\mathrm{r}}{L}_{\mathrm{sq}}{i}_{\mathrm{sq}}\\ u_{\mathrm{sq}}=(k_{\mathrm{p}1\mathrm{L}}+{\displaystyle \frac{k_{\mathrm{i}1\mathrm{L}}}{s}})(i_{\mathrm{sq}}^{\ast }-i_{\mathrm{sq}})+R_{\mathrm{s}}{i}_{\mathrm{sq}}+{\omega }_{\mathrm{r}}{L}_{\mathrm{sd}}{i}_{\mathrm{sd}}+{\omega }_{\mathrm{r}}{\psi }_{\mathrm{f}}\end{array}\right.,$$

(5)

where k_p1L and k_i1L are the proportional and integral adjustment gains of the current inner loop, respectively; i_sd^* and i_sq^* are the reference values of the stator currents i_d and i_q, respectively.

The core control mechanism of the GSC lies in maintaining the constancy of the DC bus voltage through the non-differential regulation of the DC voltage outer loop. In terms of the AC-side control dimension, grid voltage vector-oriented technology is adopted to construct a synchronous rotating coordinate system, dynamically aligning the d-axis with the direction of the grid voltage vector, thereby establishing an operating environment with a unity power factor.

The expressions for the grid-side instantaneous active power P_g and reactive power Q_g based on the synchronous rotating coordinate system are written as follows:

$$\left\{\begin{array}{l}{P}_{\mathrm{g}}={\displaystyle \frac{3}{2}}{u}_{\mathrm{gd}}{i}_{\mathrm{gd}}\\ Q_{\mathrm{g}}=-{\displaystyle \frac{3}{2}}{u}_{\mathrm{gd}}{i}_{\mathrm{gq}}\end{array}\right.,$$

(6)

where P_g and Q_g characterize the active power and reactive power exchanged between the GSC and the AC power grid, respectively; u_gd and u_gq correspond to the dq-axis components of the AC port voltage; and i_gd and i_gq denote the dq-axis components of the converter’s AC current, respectively. In the synchronous rotating coordinate system, the d-axis is oriented to the direction of the grid voltage vector and is mainly responsible for regulating the active power output, while the q-axis is primarily in charge of the reactive power interaction. Based on the above parameter definitions and coordinate orientation relationship, the voltage–current dynamic equations of the grid-side converter in the synchronous rotating coordinate system can be derived as follows:

$$\left\{\begin{array}{l}{L}_{\mathrm{c}}{\displaystyle \frac{\mathrm{d}{i}_{\mathrm{gd}}}{\mathrm{d}t}}=e_{\mathrm{gd}}-R_{\mathrm{c}}{i}_{\mathrm{gd}}+{\omega }_{\mathrm{g}}{L}_{\mathrm{c}}{i}_{\mathrm{gq}}-u_{\mathrm{gd}}\\ L_{\mathrm{c}}{\displaystyle \frac{\mathrm{d}{i}_{\mathrm{gq}}}{\mathrm{d}t}}=e_{\mathrm{gq}}-R_{\mathrm{c}}{i}_{\mathrm{gq}}-{\omega }_{\mathrm{g}}{L}_{\mathrm{c}}{i}_{\mathrm{gd}}-u_{\mathrm{gq}}\end{array}\right.,$$

(7)

where R_c and L_c characterize the filter resistance and filter inductance of the AC filter circuit, respectively; e_gd and e_gq are defined as the dq-axis components of the point of common coupling (PCC) voltage in the synchronous rotating coordinate system; and ω_g represents the angular velocity of the AC power grid.

The control strategy for the GSC includes two key points: first, the DC bus voltage is stabilized through constant DC voltage control. Second, for reactive power control, the q-axis current reference value is set to 0, thereby enabling the converter to operate in the unity power factor mode and effectively eliminating reactive power exchange on the AC side.

The d-axis and q-axis current reference values in the GSC control are given by Equation (8):

$$\left\{\begin{array}{l}{i}_{\mathrm{gd}}^{\ast }=(k_{\mathrm{p}2\mathrm{L}}+{\displaystyle \frac{k_{\mathrm{i}2\mathrm{L}}}{s}})(U_{\mathrm{dc}}^{\ast }-U_{\mathrm{dc}})\\ i_{\mathrm{gq}}^{\ast }=0\end{array}\right.,$$

(8)

where k_p2L and k_i2L represent the proportional and integral parameters of the PI controller in the DC voltage outer loop control; the DC voltage control output i_sd^* and the reference value i_sq^* are the reference values of the currents i_gd and i_gq, respectively. The control system adopts grid voltage vector-oriented technology, thereby forming the system constraint condition of e_gq = 0. Under steady-state operating conditions, the differential term of the DC component can be neglected, and the current inner loop performs dynamic tracking through the PI controller. Thus, the control equations of the grid-side converter can be derived from Equation (7) as follows:

$$\left\{\begin{array}{l}{u}_{\mathrm{gd}}=(k_{\mathrm{p}3\mathrm{L}}+{\displaystyle \frac{k_{\mathrm{i}3\mathrm{L}}}{s}})(i_{\mathrm{gd}}^{\ast }-i_{\mathrm{gd}})+e_{\mathrm{gd}}-R_{\mathrm{c}}{i}_{\mathrm{gd}}+{\omega }_{\mathrm{g}}{L}_{\mathrm{c}}{i}_{\mathrm{gq}}\\ u_{\mathrm{gq}}=(k_{\mathrm{p}3\mathrm{L}}+{\displaystyle \frac{k_{\mathrm{i}3\mathrm{L}}}{s}})(i_{\mathrm{gq}}^{\ast }-i_{\mathrm{gq}})-R_{\mathrm{c}}{i}_{\mathrm{gq}}-{\omega }_{\mathrm{g}}{L}_{\mathrm{c}}{i}_{\mathrm{gd}}\end{array}\right.,$$

(9)

where k_p3L and k_i3L are the proportional and integral parameters of the PI controller in the current inner loop control, respectively.

Based on the above descriptions, integrating the control strategies of the MSC and GSC yields the control structure diagram of the PMSG full-power converter shown in Figure 2.

As depicted in the diagram, the stator voltage is denoted as U_s, the stator current as I_s, the wind turbine angular velocity as ω_r, and the phase angle as θ_r. Specifically, i_sd^* and i_sq^* are the reference values for the stator currents i_sd and i_sq, respectively; i_gd^* and i_gq^* are the reference values for the currents i_gd and i_gq, respectively; and U_dc^* is the reference value for the DC voltage U_dc^*.

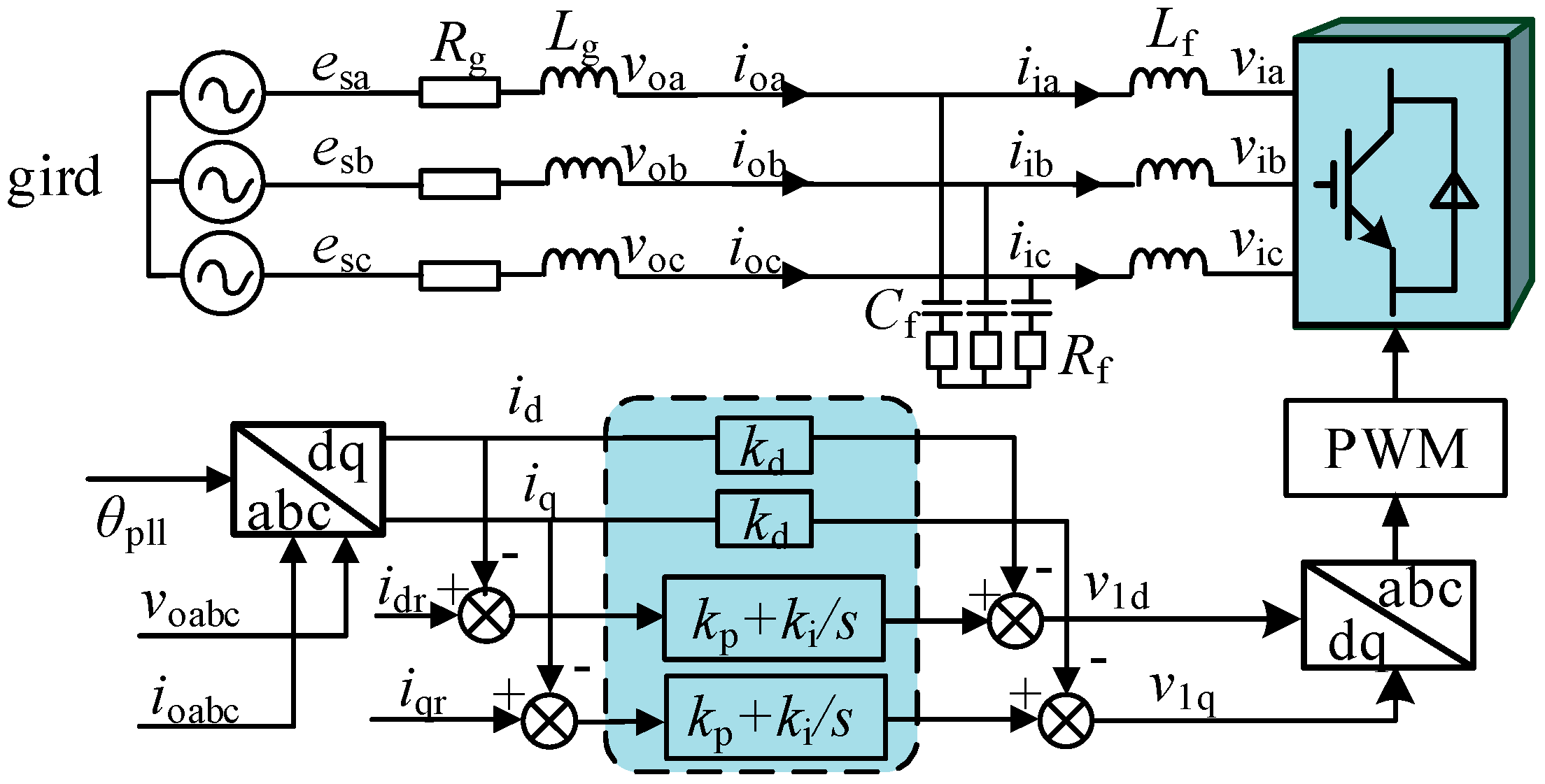
2.1.3. Energy Storage Unit Control

The grid-following energy storage converter is similar to the grid-side converter of the full-power converter, as it inverts DC into AC for grid connection. The basic control block diagram of the grid-following energy storage system is shown in Figure 3.

Among these parameters, e_sa, e_sb, and e_sc represent the three-phase grid voltages; L_g and R_g denote the grid-side inductance and resistance, respectively; L_f, C_f, and R_f stand for the filter inductance, filter capacitance, and resistance of the filter circuit, respectively; v_ia, v_ib, and v_ic are the inverter output-side voltages; v_oabc and i_oabc refer to the three-phase voltage and current at the PCC; K_d is the feedforward decoupling gain coefficient; k_p and k_i are the parameters of the current loop PI controller; k_{p_pll} and k_{i_pll} represent the parameters of the phase-locked loop (PLL) PI controller; and θ_pll is the grid phase angle obtained by the PLL.

2.2. Wind Turbine Fault Ride-Through Index Constraints and Control Characteristics

In accordance with the requirements for LVRT specified in China’s national standard [11], when the PCC voltage U_pcc is lower than the nominal voltage, wind turbines shall remain connected to the grid and operate continuously for a certain period during the voltage ride-through process. During the fault period, their dynamic reactive power support capability shall respond to changes in the PCC voltage, and the dynamic reactive current increment shall satisfy the following formula:

$$\mathrm{\Delta }{I}_{\mathrm{t}}=\left\{\begin{array}{l}{K}_1\times (0.9-U_{\mathrm{pcc}})\times I_{\mathrm{N}},(0.2⩽U_{\mathrm{t}}⩽0.9)\\ K_2\times (U_{\mathrm{pcc}}-1.1)\times I_{\mathrm{N}},(1.1⩽U_{\mathrm{t}}⩽1.3)\end{array}\right.,$$

(10)

where ∆I_t is the dynamic reactive current increment absorbed by the wind farm; K₁ and K₂ are the proportional coefficients of the dynamic reactive current of the wind farm during low-voltage and high-voltage ride-through respectively, with a value range of 1.5 to 3; U_pcc is the per-unit value of the wind farm grid-connected voltage; and I_N is the rated current of the wind farm.

The voltage ride-through process can cause instability in the DC bus voltage of wind turbines. The purpose of voltage ride-through control is to prevent wind turbines from tripping off the grid due to overvoltage and overcurrent in their components during faults. Taking LVRT as an example, when the voltage at the wind turbine’s PCC drops sharply, a constant active power will lead to a sudden current surge, which will damage components if not restricted. After triggering the grid-side low-voltage control strategy, the grid-side power output decreases; however, the power transmitted from the turbine side exhibits a certain adjustment lag, as the turbine side is still operating at the power level under the MPPT mode. The power difference between the turbine side and the grid side accumulates across the DC bus, leading to abnormal DC bus voltage fluctuations. Therefore, most existing wind turbines are equipped with a DC-side dump load circuit, which dissipates part of the power accumulated on the DC bus during the LVRT process to ensure that the DC bus voltage does not rise excessively.

During the voltage ride-through processes of wind turbines, there is a reactive power deficit in the system while active power is redundant. Therefore, it is essential to supplement reactive power to the system and adopt supplementary measures to curtail redundant active power, thereby preventing wind turbines from tripping off the grid and mitigating the risk of system instability. Meanwhile, energy storage batteries need to cooperate with wind turbines during both LVRT and high-voltage ride-through (HVRT) processes to provide voltage support during the voltage ride-through period. The schematic diagram of the wind–storage system’s automatic voltage control (AVC) is shown in Figure 4.

In the AVC control strategy, the AVC continuously collects the PCC voltage for voltage judgment. When the voltage enters the voltage ride-through range, it sends a power reduction operation signal to the machine side of the direct-drive wind turbine. When the DC voltage rises to the threshold, the dump load circuit is activated to dissipate redundant power, and the grid-side converter switches to the voltage ride-through mode. The grid-side q-axis reference command value is calculated according to Equation (10). Due to the inherent capacity limitation of the wind turbine converter, the reactive current output of the wind turbine itself cannot quickly meet the requirements of China’s national standards in many cases. Therefore, it is necessary to simultaneously send cooperative control commands to the energy storage batteries according to system conditions to implement different control strategies.

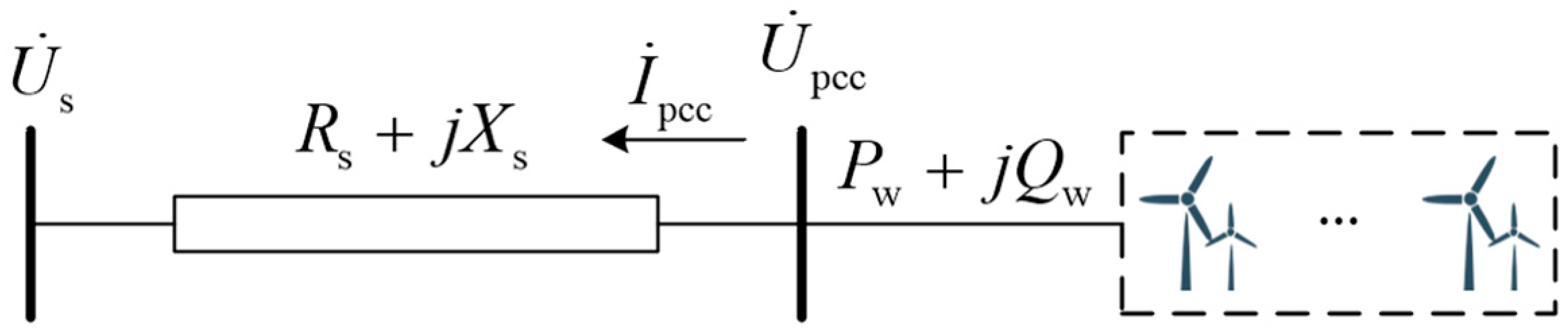
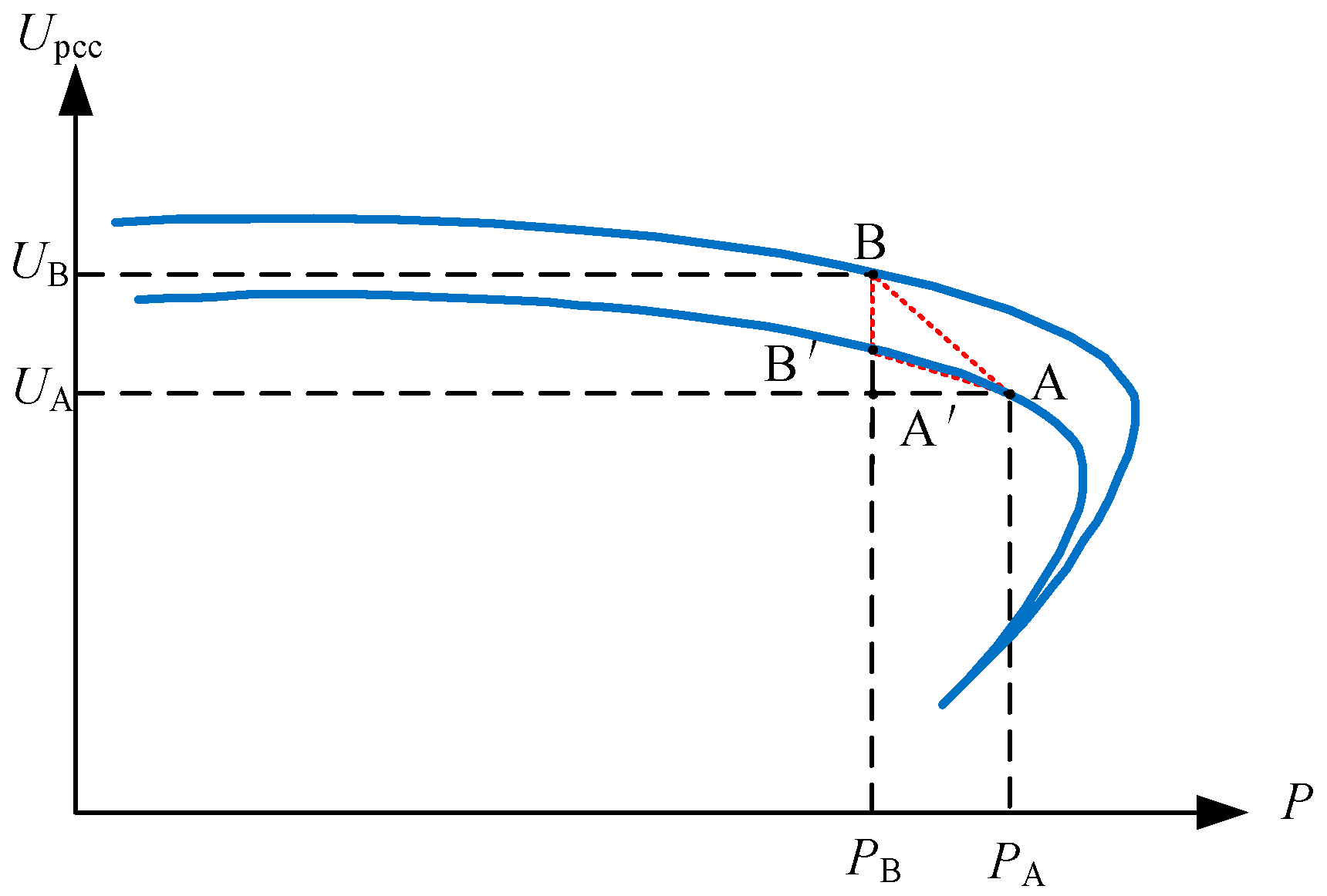
2.3. Analysis of Voltage Repeated Fluctuation Mechanism

Taking the single-machine infinite-bus equivalent system as an example, this paper analyzes the mechanism of recurrent voltage fluctuations during wind farm power output. A system model is established, and through the analysis of the system’s PV curve, the relationship between the PCC voltage and active power under different reactive power conditions is clarified. The equivalent topology of the wind farm system is shown in Figure 5.

In the topology of the equivalent system, the wind farm is equivalent to a power source; at this point, the output power of the wind farm can be expressed as

$$P_{\mathrm{w}}+j{Q}_{\mathrm{w}}=U_{\mathrm{pcc}}\angle \theta {\left({\displaystyle \frac{U_{\mathrm{pcc}}\angle \theta -U_{\mathrm{s}}\angle 0^{\circ }}{R_{\mathrm{s}}+j{X}_{\mathrm{s}}}}\right)}^{\ast },$$

(11)

where P_w and Q_w are the active power output and reactive power output of the wind farm, respectively; U_pcc and θ are the voltage and phase of the PCC; U_s is the grid voltage; and the line impedance is R_s + jX_s.

When transmitting over long distances, the resistance can be neglected. In this case, the relationship between power and voltage can be derived from the grid voltage and PCC voltage as follows:

$$\left\{\begin{array}{l}{P}_{\mathrm{w}}={\displaystyle \frac{U_{\mathrm{pcc}}{U}_{\mathrm{s}}}{X_{\mathrm{s}}}}\sin \theta \\ Q_{\mathrm{w}}={\displaystyle \frac{U_{\mathrm{pcc}}^2}{X_{\mathrm{s}}}}-{\displaystyle \frac{U_{\mathrm{pcc}}{U}_{\mathrm{s}}}{X_{\mathrm{s}}}}\cos \theta \end{array}\right.,$$

(12)

Simplifying the above equation yields

$$P_{\mathrm{w}}^2+{\left(Q_{\mathrm{w}}-{\displaystyle \frac{U_{\mathrm{pcc}}^2}{X_{\mathrm{s}}}}\right)}^2={\left({\displaystyle \frac{U_{\mathrm{pcc}}{U}_{\mathrm{s}}}{X_{\mathrm{s}}}}\right)}^2,$$

(13)

The P_w under this condition is

$$P_{\mathrm{w}}=\sqrt{{\displaystyle \frac{U_{\mathrm{pcc}}^2{U}_{\mathrm{s}}^2}{X_{\mathrm{s}}^2}}-Q_{\mathrm{w}}^2-{\displaystyle \frac{U_{\mathrm{pcc}}^4}{X_{\mathrm{s}}^2}}+{\displaystyle \frac{2Q_{\mathrm{w}}{U}_{\mathrm{pcc}}^2}{X_{\mathrm{s}}}}}=\sqrt{{\displaystyle \frac{U_{\mathrm{pcc}}^2{U}_{\mathrm{s}}^2}{X_{\mathrm{s}}^2}}-{\left(Q_{\mathrm{w}}-{\displaystyle \frac{U_{\mathrm{pcc}}^2}{X_{\mathrm{s}}}}\right)}^2},$$

(14)

Taking the derivative of Equation (14),

$${\displaystyle \frac{d{P}_{\mathrm{w}}}{d{U}_{\mathrm{pcc}}}}={\displaystyle \frac{1}{2}} · {\left({\displaystyle \frac{U_{\mathrm{pcc}}^2{U}_{\mathrm{s}}^2}{X_{\mathrm{s}}^2}}-Q_{\mathrm{w}}^2-{\displaystyle \frac{U_{\mathrm{pcc}}^4}{X_{\mathrm{s}}^2}}+{\displaystyle \frac{2Q_{\mathrm{w}}{U}_{\mathrm{pcc}}^2}{X_{\mathrm{s}}}}\right)}^{-1/2} · \left({\displaystyle \frac{2U_{\mathrm{pcc}}{U}_{\mathrm{s}}^2}{X_{\mathrm{s}}^2}}-{\displaystyle \frac{4U_{\mathrm{pcc}}^3}{X_{\mathrm{s}}^2}}+{\displaystyle \frac{4Q_{\mathrm{w}}{U}_{\mathrm{pcc}}}{X_{\mathrm{s}}}}\right),$$

(15)

The common factor is extracted from the numerator ${\displaystyle \frac{2}{X_{\mathrm{s}}^2}}{U}_{\mathrm{pcc}}\left(U_{\mathrm{s}}^2-2U_{\mathrm{pcc}}^2+2X_{\mathrm{s}}{Q}_{\mathrm{w}}\right)$ when ${\displaystyle \frac{2}{X_{\mathrm{s}}^2}}{U}_{\mathrm{pcc}}\left(U_{\mathrm{s}}^2-2U_{\mathrm{pcc}}^2+2X_{\mathrm{s}}{Q}_{\mathrm{w}}\right)=0$ (that is, when ${\displaystyle \frac{d{P}_{\mathrm{w}}}{d{U}_{\mathrm{pcc}}}}=0$), and since U_pcc > 0, we can obtain $U_{\mathrm{pcc}}=\sqrt{X_{\mathrm{s}}{Q}_{\mathrm{w}}+{\displaystyle \frac{U_{\mathrm{s}}^2}{2}}}$. This is substituted into Expression (14) for P_w, and then the corresponding result can be calculated:

$$P_{\mathrm{w}}^{\max }=\sqrt{{\displaystyle \frac{U_{\mathrm{s}}^4}{4X_{\mathrm{s}}^2}}+{\displaystyle \frac{Q_{\mathrm{w}}{U}_{\mathrm{s}}^2}{X_{\mathrm{s}}}}},$$

(16)

The function form of (14) has a clear characteristic of “first increasing and then decreasing”, and it is judged that (16) gives the maximum value of the active power generated by the wind farm within the engineering value range. It can be seen from (15) and (16) that when the system structure for wind farm power transmission remains unchanged, the grid voltage decreases as the transmitted active power increases [12,13].

Assuming a sudden increase in the active power of the wind farm, it can be derived from Equation (14) that

$$P_0={\displaystyle \frac{1}{X_{\mathrm{s}}}}\sqrt{{\displaystyle \frac{U_{\mathrm{s}}^4}{4}}+Q_{\mathrm{w}}{X}_{\mathrm{s}}{U}_{\mathrm{s}}^2-{(U_{\mathrm{t}}^2-{\displaystyle \frac{U_{\mathrm{s}}^2}{2}}-Q_{\mathrm{w}}{X}_{\mathrm{s}})}^2}.$$

(17)

Let the corresponding grid voltage at this point be U_t. The wind farm then enters the LVRT range and switches to the LVRT mode. With all conditions remaining unchanged, the LVRT mode reduces the active power and increases the reactive power, which causes the U_pcc to rise. When the U_pcc exceeds the LVRT threshold, the wind farm exits the LVRT mode and gradually returns to its power output state before LVRT, which triggers LVRT again. Consequently, such a cycle causes the wind farm to repeatedly enter the LVRT state.

As shown in Figure 6, the schematic diagram of the PV curve illustrates the repeated entry into the LVRT state caused by voltage fluctuations. The specific mechanism is explained in detail based on this schematic diagram.

First, as the active power output of the wind farm gradually increases, the system voltage decreases progressively. This process corresponds to the transition from point B to point A in the diagram, where the U_pcc drops from U_B to U_A and the active power output of the wind farm rises from P_B to P_A.

Second, the wind farm enters the LVRT range due to a voltage drop. At this point, the active power output of the wind farm decreases, while the reactive power output increases, which, in turn, causes the U_pcc to rise. Suppose the wind farm exits the LVRT state when the U_pcc reaches U_B. The system then returns to point B.

After exiting LVRT, the wind farm will gradually return to its state before LVRT, which means moving from point B back to point A. In the case where reactive power is restored immediately, and active power is restored at a specific slope after LVRT exit, the wind farm will first move from point B to point B’ and then to point A.

At this point, the voltage enters the LVRT range, and the wind farm enters LVRT again. The above process repeats continuously, which constitutes the mechanism analysis of the repeated entry into and exit from LVRT caused by voltage fluctuations.

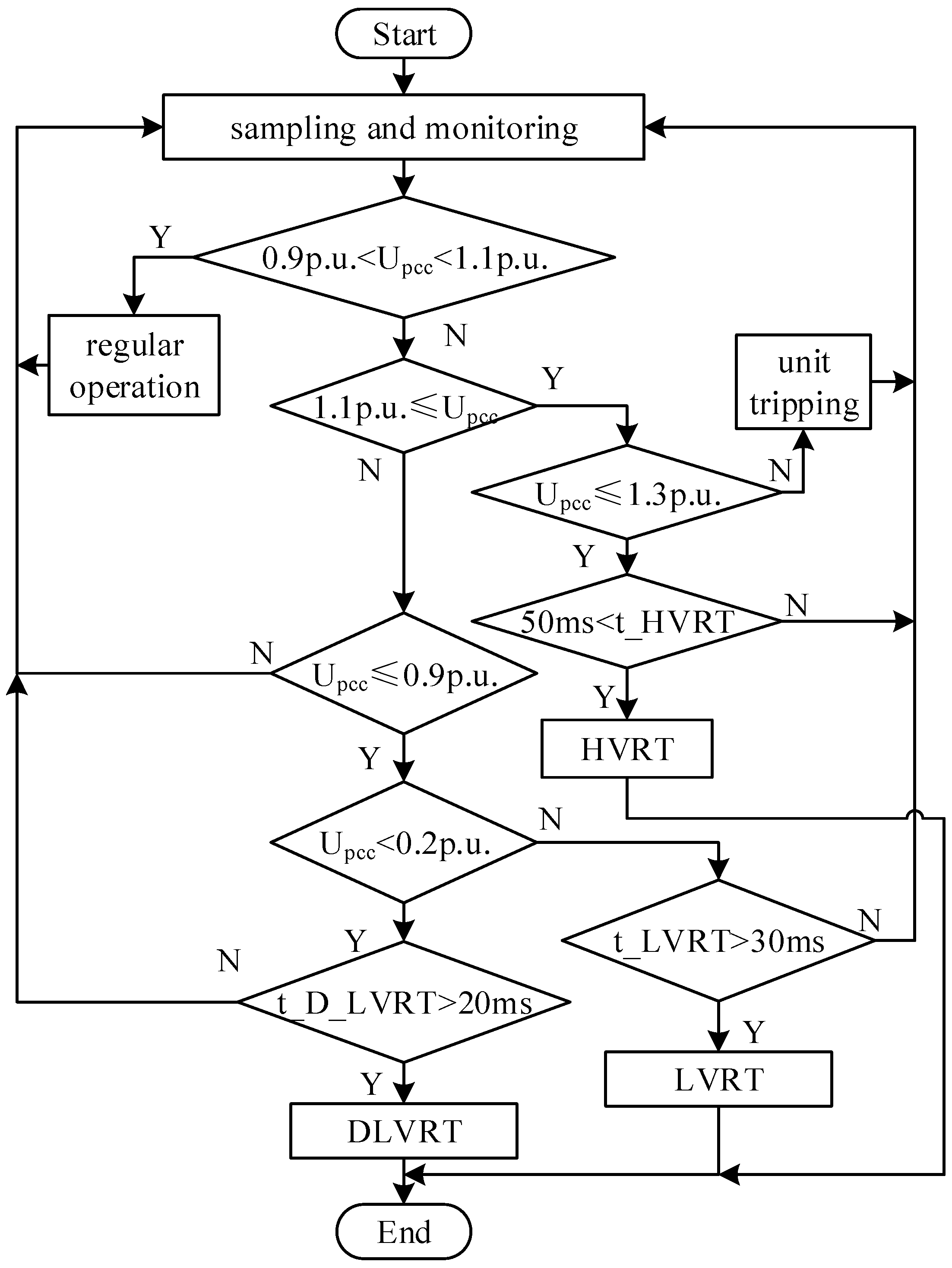
3. Methods: Wind–Storage Coordinated Voltage Ride-Through Control Strategy

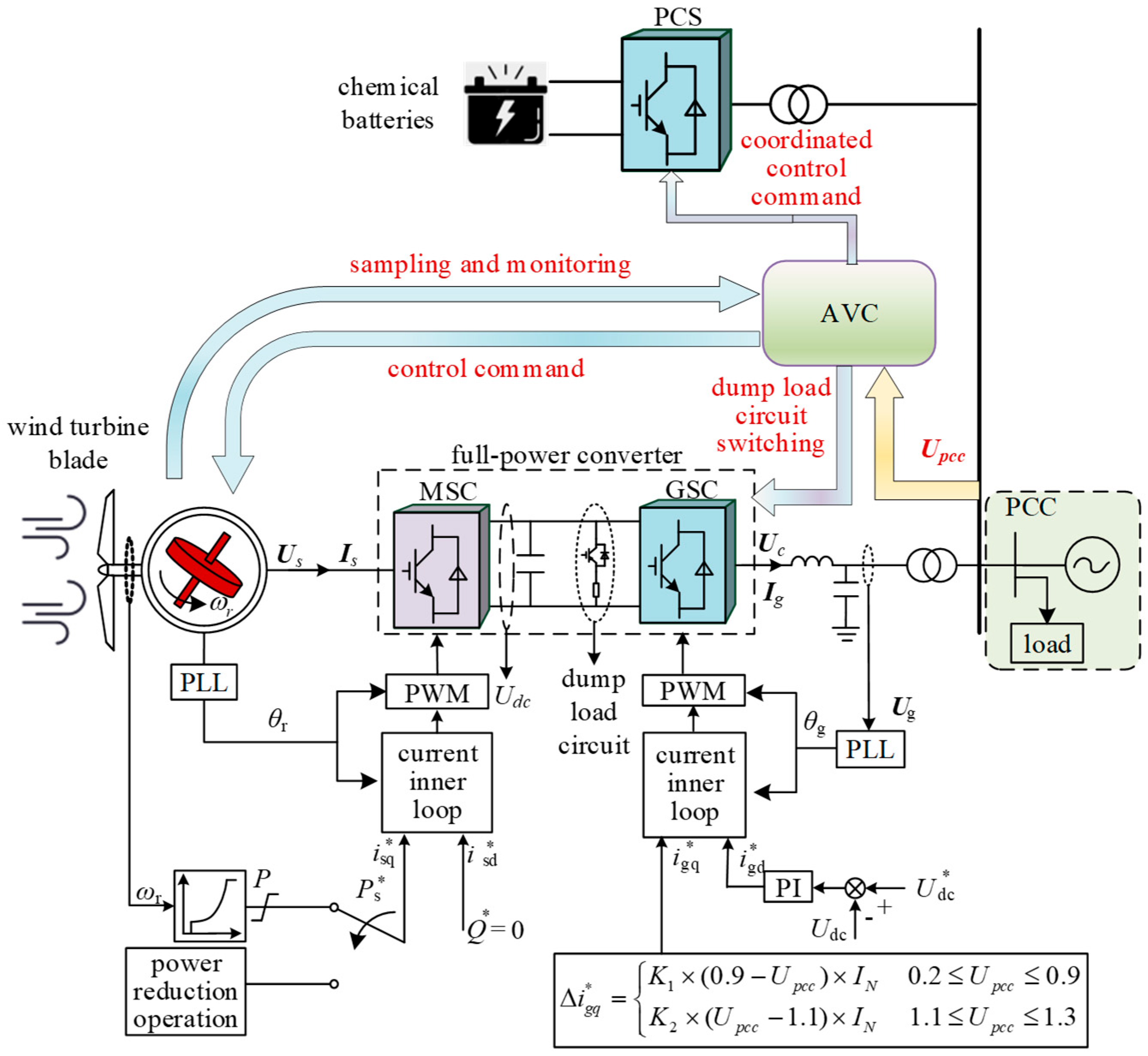
3.1. Overall Coordinated Control Framework

Building on the analysis of wind turbine voltage ride-through characteristics in the previous chapter, we found that during both high- and low-voltage ride-through processes, wind turbine systems face a reactive power deficit alongside redundant active power. In such scenarios, it is necessary to supplement reactive power to the system while implementing additional measures to reduce redundant active power, which not only prevents wind turbine tripping but also mitigates the risk of system instability. Meanwhile, the energy storage system needs to coordinate with wind turbines during the voltage ride-through process to provide voltage support, thereby addressing the aforementioned issues effectively. To enhance the stability of wind farms in the face of unconventional voltage events, such as deep voltage dips and repeated LVRT, combined with China’s national standards and practical engineering conditions [11,21,22,23], a wind–storage coordinated voltage ride-through control strategy is proposed. This strategy achieves wind farm voltage ride-through via the collaboration between the energy storage systems and voltage discrimination. The wind–storage coordinated voltage ride-through control strategy is shown in Figure 7.

As shown in the diagram, the coordinated control strategy integrated with the AVC system is activated by continuously detecting operating parameters such as U_pcc of the wind farm and conducting a voltage assessment to determine whether to enter voltage ride-through.

The voltage discrimination method in the coordinated control strategy is shown in Figure 8, which classifies voltage ride-through into three categories: high-voltage ride-through (HVRT) (1.3 p.u. ≥ U_pcc ≥ 1.1 p.u.), regular low-voltage ride-through (LVRT) (0.9 p.u. ≥ U_pcc ≥ 0.2 p.u.), and deep low-voltage ride-through (deep LVRT) (U_pcc < 0.2 p.u.).

The U_pcc is judged based on real-time voltage detection data. When the U_pcc is within the range of 0.9 p.u.~1.1 p.u., it is regarded as normal voltage fluctuation, and no strategy is triggered, which is the normal operation mode. When the U_pcc is in the range of 1.1 p.u.~1.3 p.u. and the t_HVRT is longer than 30 ms, it is in the high-voltage ride-through mode. When the U_pcc is greater than 1.3 p.u., the wind turbine will trip. When the U_pcc is in the range of 0.2 p.u.~0.9 p.u. and t_LVRT is longer than 30 ms, it is in the general low-voltage ride-through mode. When the U_pcc is less than 0.2 p.u. and t_DLVRT is longer than 20 ms, it is in the deep low-voltage ride-through mode.

3.2. Wind–Storage Coordinated LVRT

The coordinated control strategy proposed in this paper divides LVRT into two categories: one is regular LVRT within the scope of China’s national standard LVRT curve, and the other is deep LVRT under extreme conditions, where the voltage is lower than 0.2 p.u.

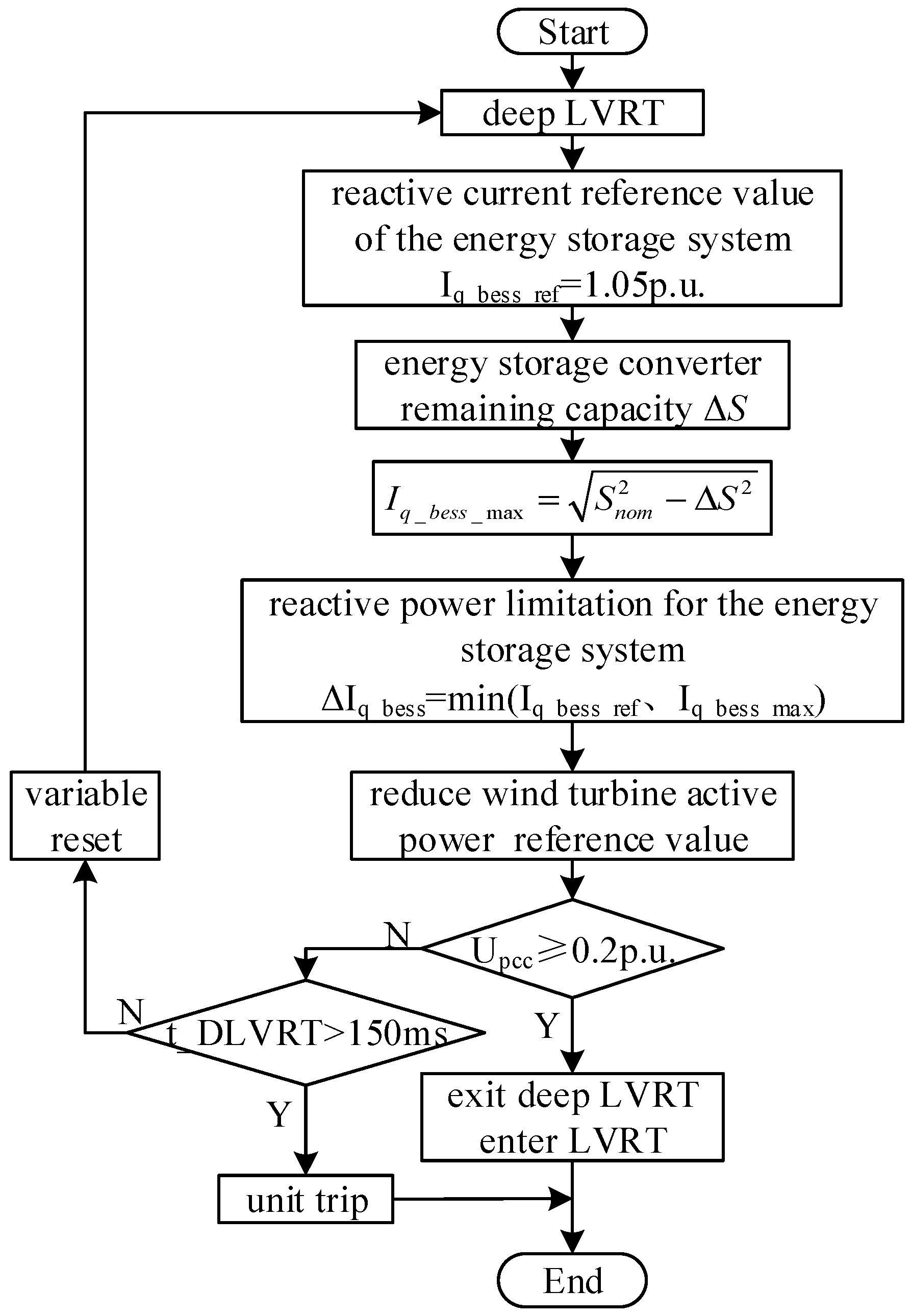
3.2.1. Deep LVRT Mode

When the U_pcc drops below 0.2 p.u., the system enters the deep LVRT mode. At this point, the voltage discrimination will activate the deep LVRT mode, and the flowchart of the deep LVRT mode is shown in Figure 9.

During deep low-voltage ride-through (deep LVRT), the energy storage reactive current reference value I_{q_bess_ref} is set to 1.05. The power output at this moment is collected to calculate the remaining power margin of the converter. The energy storage reactive current command ∆I_{q_bess} is taken as the minimum value between the reference value and the converter power margin. This value selection ensures the hardware-level safety of the equipment while considering the theoretical command of the converter.

The machine side of the wind turbine adjusts the q-axis reference current according to the depth of the voltage dip.

$$I_{\mathrm{q}\text{\_}\mathrm{m}\text{\_}\mathrm{ref}}=K_{\mathrm{r}}\times U_{\mathrm{pcc}}\times I_{\mathrm{q}\text{\_}\mathrm{MPPT}},$$

(18)

where I_{q_m_ref} represents the q-axis current command value of the wind turbine; K_r denotes the proportional coefficient of the q-axis current of the wind turbine, with a value range of 0 to 1; and I_{q_MPPT} stands for the q-axis current of the wind turbine under the MPPT mode.

The AVC system issues reactive power commands to the energy storage system. When the wind turbine enters deep LVRT, its grid-side DC voltage control is switched to a dynamic reactive current calculation mode compliant with China’s national standards, and the dump load circuit is activated.

Subsequently, the system judges whether the point of U_pcc is higher than 0.2 p.u. If yes, it exits the deep LVRT mode and enters the regular LVRT mode. If no, it further judges whether the duration of deep LVRT exceeds 150 ms. If the duration exceeds 150 ms, unit tripping is performed; if not, relevant variables are reset, and the judgment process is repeated until exiting the deep LVRT mode or unit tripping.

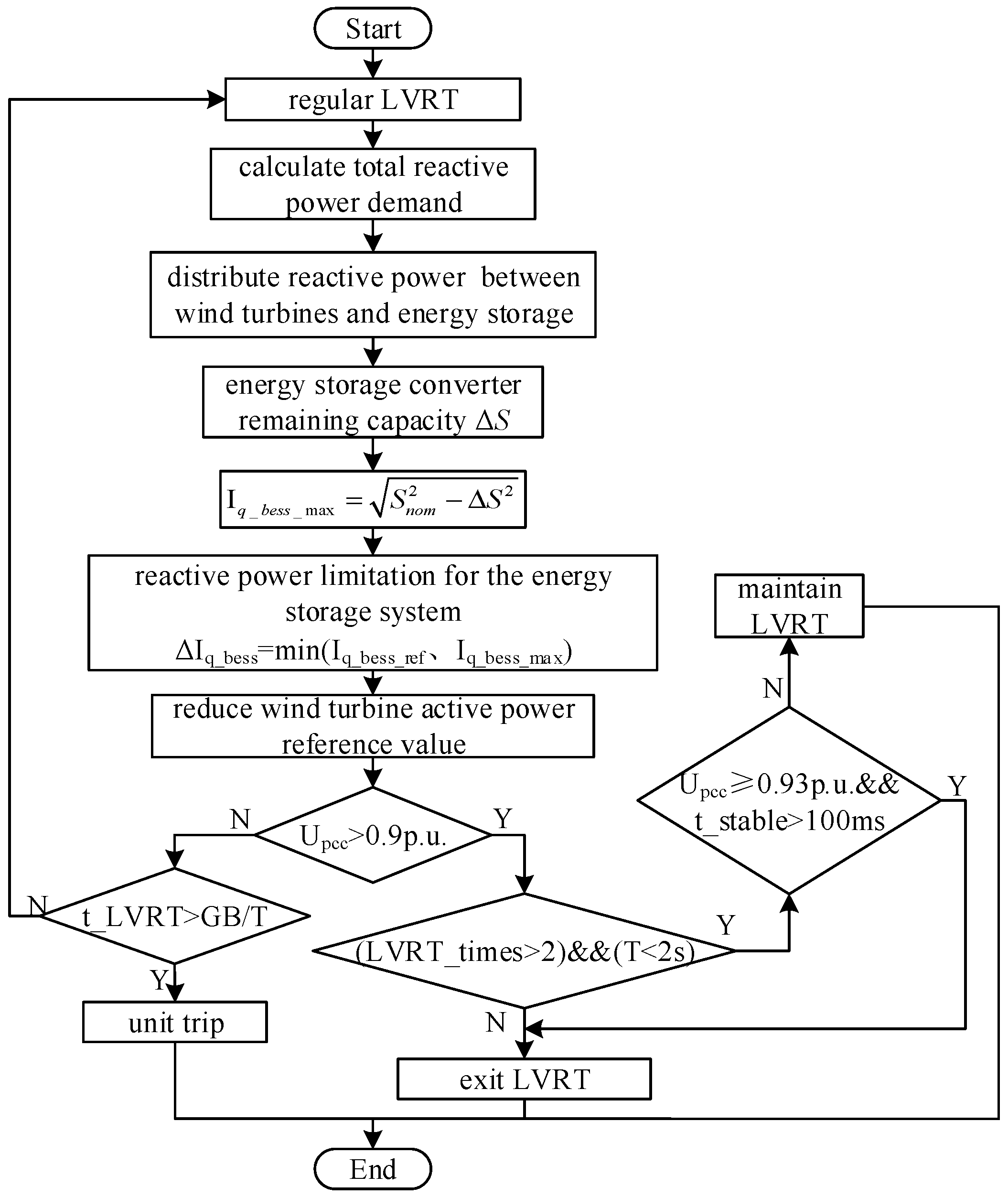
3.2.2. Regular LVRT Mode

The flowchart of the regular LVRT mode is shown in Figure 10. When the U_pcc is within the range of 0.2 p.u.~0.9 p.u., the system enters the general LVRT mode, where the strategy is formulated strictly in accordance with the requirements for LVRT specified in China’s national standards.

After entering the standard LVRT mode, the total reactive power demand of the wind farm is computed with reference to Equation (1). After deducting the reactive power of the wind turbines from the total reactive power demand, the remaining part is borne by the energy storage system. The remaining capacity of the converter is calculated, and the minimum value between the theoretical reference value of reactive current and the remaining capacity limit of the converter is taken as the reactive current command. The machine side of the wind turbine operates at reduced power following the same logic as in the deep LVRT mode, and the dump load circuit is activated to consume redundant active power.

Based on the system equivalent model established in Section 2 (as shown in Figure 5), the reactive power output expression of the wind turbine is given by Equation (12). The total apparent capacity of the wind farm is denoted as S_Farm__N. During a fault, the active power of the wind turbine drops to P_W. Under normal (non-fault) conditions, the reactive power output of the wind turbine is regarded as zero, and the maximum reactive power output of the wind turbine under the total capacity constraint is $Q_{\mathrm{W}\_\max }=\sqrt{S_{\mathrm{Farm}}^2-P_{\mathrm{w}}^2}$. Combined with the reactive power requirements specified in China’s national standards, the total reactive power demand that the wind farm needs to meet is $Q_{\mathrm{total}}=U_{\mathrm{pcc}}{I}_{\mathrm{Farm}\_\mathrm{N}}\left[K_1\times (0.9-U_{\mathrm{pcc}})\right]$. The actual total reactive power that the wind turbine can output is Q_W, so the total reactive power that needs to be supplemented by the energy storage system is Q_total − Q_w. When the total supplementary reactive power is evenly distributed among energy storage units, the reactive power command for a single energy storage unit is

$$Q_{\mathrm{bess}}=\min \left[{\displaystyle \frac{Q_{\mathrm{total}}-Q_{\mathrm{w}}}{n}}, \sqrt{S_{\mathrm{nom}}^2-P_{\mathrm{bess}}^2} \right],$$

(19)

In a wind farm, the rapid increase in active power caused by a high wind power output, coupled with the drop in the U_pcc due to the PV characteristics of the power transmission system, triggers voltage ride-through [13]. During this process, when the voltage recovers to the voltage threshold, the AVC system judges that the voltage has recovered according to conventional logic and exits the LVRT mode. However, the subsequent reactive power imbalance causes the voltage to enter the voltage ride-through range again, and the relevant devices re-enter the voltage ride-through mode until the voltage recovers. Such a cycle results in voltage fluctuations around the threshold.

Differentiating Equation (13) gives

$${\displaystyle \frac{d{U}_{\mathrm{pcc}}}{d{P}_{\mathrm{w}}}}={\displaystyle \frac{-\frac{X_{\mathrm{s}}^2{P}_{\mathrm{w}}}{\sqrt{\sigma }}}{\sqrt{\frac{U_{\mathrm{s}}^2}{2}+Q_{\mathrm{w}}{X}_{\mathrm{s}}+\sqrt{\sigma }}}}, \sigma ={\displaystyle \frac{U_{\mathrm{s}}^4}{4}}-X_{\mathrm{s}}^2{P}_{\mathrm{w}}^2+Q_{\mathrm{w}}{X}_{\mathrm{s}}{U}_{\mathrm{s}}^2,$$

(20)

During the repeated fluctuation process, the voltage fluctuation amplitude is

$$d{U}_{\mathrm{AB}}=U_{\mathrm{B}}-U_{\mathrm{A}}=d{U}_{{\mathrm{A}}^{\prime }{\mathrm{B}}^{\prime }}+d{U}_{\mathrm{B}{\mathrm{B}}^{\prime }} ,$$

(21)

where dU_A^′B^′ can be regarded as the voltage amplitude increment caused by an active power reduction; dU_B^′B^′ is the voltage amplitude increment caused by a reactive power increase. Thus,

$$d{U}_{ {\mathrm{A}}^{\prime }{\mathrm{B}}^{\prime }}\approx {\left.{\displaystyle \frac{d{U}_{\mathrm{pcc}}}{d{P}_{\mathrm{w}}}}\right|}_{P_{\mathrm{w}}=P_{\mathrm{A}}}{P}_{\mathrm{A}};$$

(22)

$$d{U}_{{\mathrm{BB}}^{\prime }}\approx {\left.{\displaystyle \frac{d{U}_{\mathrm{pcc}}}{d{Q}_{\mathrm{w}}}}\right|}_{Q_{\mathrm{w}}=Q_{{\mathrm{B}}^{\prime }}}{Q}_{{\mathrm{B}}^{\prime }}.$$

(23)

According to China’s national standards, $Q_{{\mathrm{B}}^{\prime }}=U_{{\mathrm{B}}^{\prime }}{k}_{\mathrm{c}}(0.9-U_{{\mathrm{B}}^{\prime }})$. For the scenario of a shallow voltage dip under non-fault conditions, the reactive power variation of the wind farm is small, so $d{U}_{{\mathrm{BB}}^{\prime }}\ll d{U}_{{\mathrm{A}}^{\prime }{\mathrm{B}}^{\prime }}$, and thus, $d{U}_{\mathrm{AB}}\approx d{U}_{{\mathrm{A}}^{\prime }{\mathrm{B}}^{\prime }}$.

In weak grid scenarios, the value of X_S is relatively large. Assuming P_A remains unchanged, the operating point A is closer to the static voltage stability limit of the system, so ${\left|{\displaystyle \frac{d{U}_{\mathrm{pcc}}}{d{P}_{\mathrm{w}}}}\right|}_{P_{\mathrm{w}}=P_{\mathrm{A}}}$ increases significantly, which, in turn, leads to an increase in dU_A^′B^′.

It can be seen that in the weak grid context, the repeated voltage fluctuation phenomenon caused by the interaction between wind turbine state switching and the system PV curve will be more obvious, with a larger voltage fluctuation amplitude, posing a more serious threat to the safe and stable operation of the system. If the LVRT exit threshold is increased so that U_B in Figure 5 is lower than the exit threshold of the wind turbine, the turbine can be prevented from exiting low-voltage ride-through, thereby mitigating repeated voltage fluctuations. To prevent repeated entry into LVRT due to voltage fluctuations at the threshold, an assessment criterion is set: if the voltage enters LVRT more than twice within 2 s, it is judged as a voltage fluctuation. At this time, the threshold value of LVRT is set to 0.93 p.u., Then, it is determined whether the stabilization time during which the voltage is more than 0.93 p.u. exceeds 100 ms. If this condition is satisfied, the LVRT mode is exited. Meanwhile, it is judged whether the voltage and time of LVRT meet the range required by China’s national standards. If it exceeds the standards, the unit will be tripped to ensure equipment safety.

3.3. Wind–Storage Coordinated HVRT

Similarly, the flowchart of the HVRT mode is shown in Figure 11. When the U_pcc is within the range of 1.1 p.u.~1.3 p.u., the system enters the HVRT mode. The total reactive power demand to be absorbed is calculated using the dynamic reactive current formula specified in China’s national standards, which is based on Equation (1). The reactive power reference value of energy storage is obtained by calculating the difference between the total reactive power demand and the reactive power output of the wind turbines. Subsequently, the reactive capacity margin of the available capacity of the energy storage converter is calculated according to its operating status. Finally, the reactive power command is determined based on both the remaining reactive capacity and the reactive power reference value.

To prevent repeated entry into HVRT due to voltage fluctuations at the threshold, an assessment criterion is set: if the voltage enters HVRT more than twice within 2 s, it is judged as a voltage fluctuation. At this time, the threshold value of HVRT is set to 1.07 p.u. Then, it is determined whether the stabilization time during which the voltage is less than 1.07 p.u. exceeds 100 ms. If this condition is satisfied, the HVRT mode is exited. Meanwhile, it is judged whether the voltage and time of HVRT meet the range required by China’s national standards. If it exceeds the standards, the unit will be tripped to ensure equipment safety.

4. Results

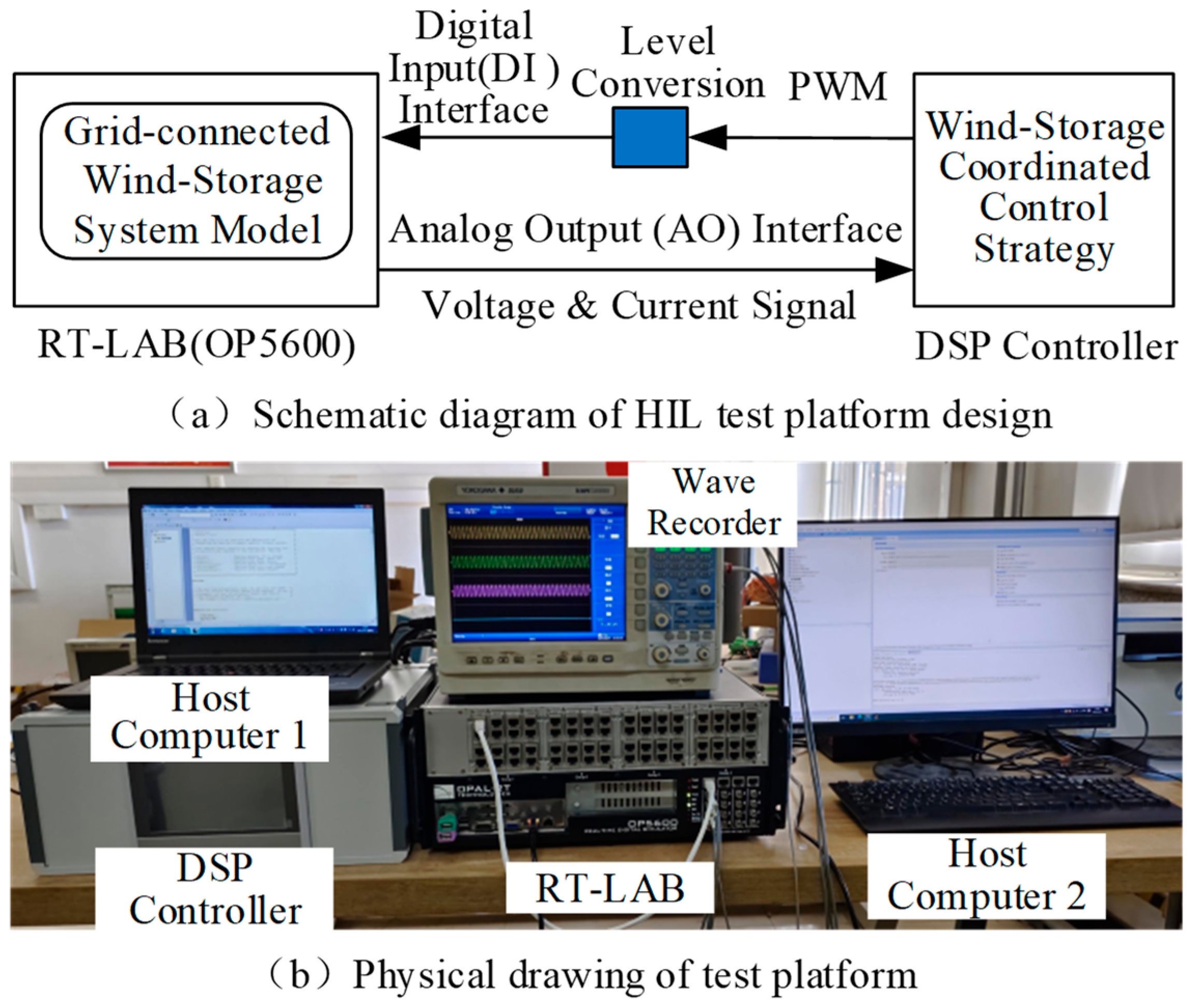
4.1. HIL Simulation Test Platform

To verify the effectiveness of the wind–storage coordinated control strategy proposed in this paper, a HIL test platform based on the OP5600 real-time simulator and a DSP actual controller is built, as shown in Figure 12. RT-LAB is used to simulate the main circuit of the system, while the proposed control strategy is implemented in the DSP controller. Typical operating conditions are set to validate the coordinated control strategy, and an oscilloscope is employed to record and monitor variables such as frequency and voltage under various operating conditions.

Figure 12a shows the HIL test schematic diagram based on RT-LAB (Version 10.7; developer: OPAL-RT Technologies, Montreal, QC, Canada). The coordinated control strategy is implemented in the DSP controller (model: TMS320F28335; developer: Texas Instruments, Dallas, TX, USA), and the RT-LAB real-time simulator realizes the simulation of the main circuit model of the wind–storage system.

Sampled signals such as voltage and current are transmitted to the DSP controller through the AO interface, and PWM control signals are transmitted to RT-LAB through level conversion to complete converter control. Voltage events in the main circuit are set. The controller detects voltage changes at the PCC, executes the coordinated control strategy for voltage support, and transmits the observed variables in the main circuit of the OP5600 real-time hardware to the waveform recorder (model: DL850; developer: Yokogawa Electric Corporation, Tokyo, Japan) via miniBNC-to-BNC to realize the observation of variables such as voltage and current at each point. It should be noted that the main circuit model of the wind–storage system is built and compiled using MATLAB/Simulink (Version 2018a, developer: MathWorks, Natick, MA, USA) before being deployed to the OP5600 real-time simulator via RT-LAB. Finally, measured data points are collected by the waveform recorder to plot the variation curves of the observed variables for analysis. The modeling data of the wind farm adopted in this study are derived from a wind farm in northern China, as detailed in

Table 1. HIL simulation parameters.

PMSG Model Parameters	Values	BESS Model Parameters	Values
Rated capacity/MVA	1.5	Rated capacity/MVA	1
Total wind farm rated power/MW	18	Total wind farm rated power/MW	3
Rated wind speed/(m/s)	11	Rated capacity per unit/MWh	1.25
DC bus voltage/V	1200	DC bus voltage/V	1200
Converter switching frequency/kHz	10	Converter switching frequency/kHz	10
Grid-side filter inductance/mH	15	Filter inductance/mH	10
Grid-side filter capacitance/μF	50	Filter capacitance/μF	40
Machine-side converter current loop PI (kp, ki)	0.9, 22	Converter current loop PI (kp, ki)	2.5, 10
Grid-side converter current loop PI (kp, ki)	0.5, 150	SOC operating range	20–90%
Reactive current coefficient during LVRT	2	Reactive current coefficient during LVRT	3

.

4.2. Test Results

In accordance with the LVRT requirement range specified in China’s national standard GB/T 19963.1-2021 mentioned earlier, the voltage dip test control strategy on the source side and the response of the wind–storage system are configured [11]. For wind turbines, the machine-side converter operates at reduced power during voltage ride-through, and the q-axis current reference value of the grid-side current loop is set to the reactive power increment calculated by the formula required in the national standard as the reference value [11]. A dump load circuit is configured. When the DC voltage exceeds the threshold, the dump load circuit is activated to limit the DC voltage, consume redundant power in the system, and ensure system safety.

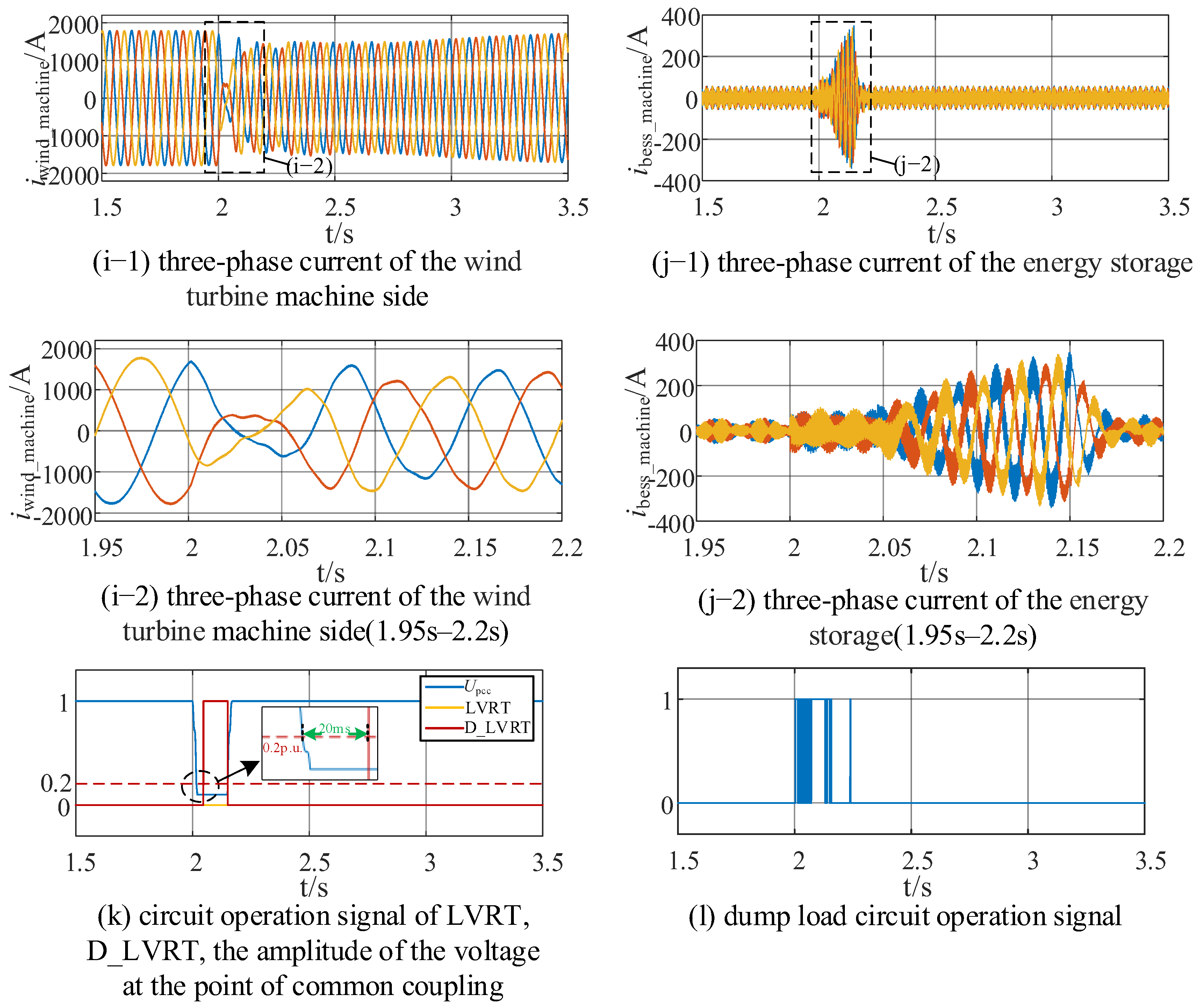
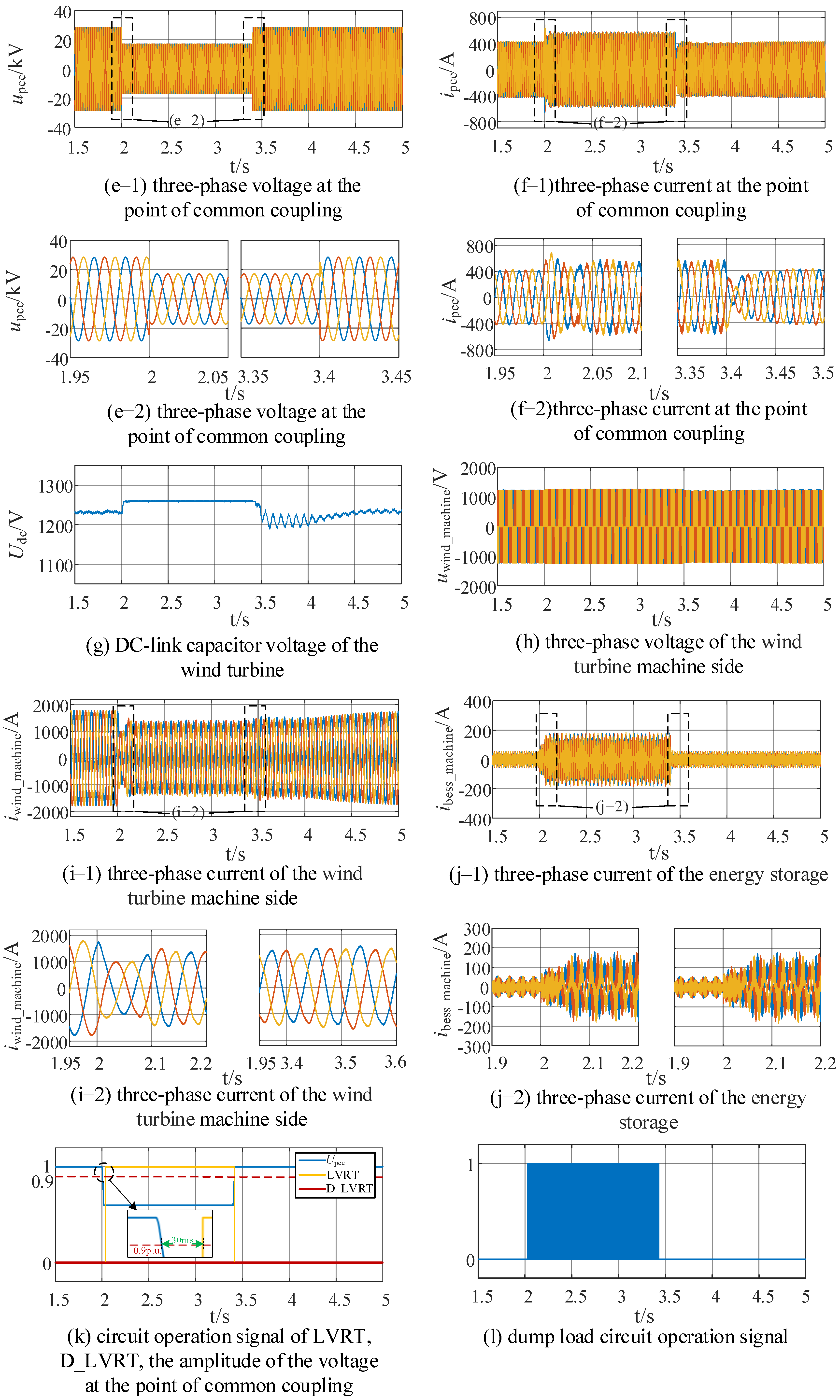
4.2.1. Deep LVRT

A voltage dip of 0.1 p.u. with a duration of 150 ms is set on the source side to simulate a deep-voltage-dip condition. At this point, the voltage dip exceeds the lower limit standard of 0.2 p.u. for LVRT. The response results of the wind–storage system are shown in Figure 13.

Figure 13a illustrates the active power response of the wind turbine, which is operating in the power reduction mode at this time; Figure 13b presents the energy storage active power curve. When the voltage dip recovers, the active power curve exhibits a response caused by system coupling factors; Figure 13c shows the reactive power of the wind turbine. Due to the short duration of the deep LVRT, the reactive power fails to respond in time; Figure 13d displays the reactive power generated by the energy storage system. Since the voltage is in a deep dip that exceeds the lower limit of the LVRT standard, the energy storage system generates as much reactive power as possible. Figure 13e–l illustrate the grid-side (PCC) three-phase (abc) voltages and currents, the DC-side voltage of the wind turbine, the machine-side voltages and currents of the wind turbine, the current of the energy storage system, the activation status of deep LVRT, and the operation status of the dump load circuit. It can be observed that all physical quantities recover to normal values relatively quickly after the deep voltage dip. The deep LVRT mode is activated after a predefined delay, the unloading circuit operates normally, and the DC voltage quickly recovers after only a short over-limit period. In Figure 13k, 20 ms after PCC voltage dips below 0.2 p.u., the deep LVRT mode initiates with the delayed startup designed in Figure 8, correctly responding to the deep sag of PCC voltage.

As shown in Figure 14, a deep voltage dip of 0.1 p.u. with a duration of 25 ms is set to simulate a lightning strike condition.

Operating conditions are set in accordance with the requirements for voltage dips caused by lightning strikes, as specified in GB/T 17626.11-2023, GB/T 30137-2024, and GB/T 39269-2020 [21,22,23]. From the PCC voltage curve in Figure 14a, it can be seen that an extremely short-term voltage dip occurs at 2 s. Due to the short duration, it is difficult for the control system to respond effectively. Therefore, in the control strategy, this situation is regarded as an interference and is no longer responded to. Similar to Figure 13, Figure 14e–l illustrate the variations under this operating condition. It can be observed that all physical quantities recover to normal values relatively quickly after the simulated lightning disturbance. Herein, as shown in Figure 14k, the deep LVRT mode does not activate as the predefined delay is not reached, and the strategy is executed correctly.

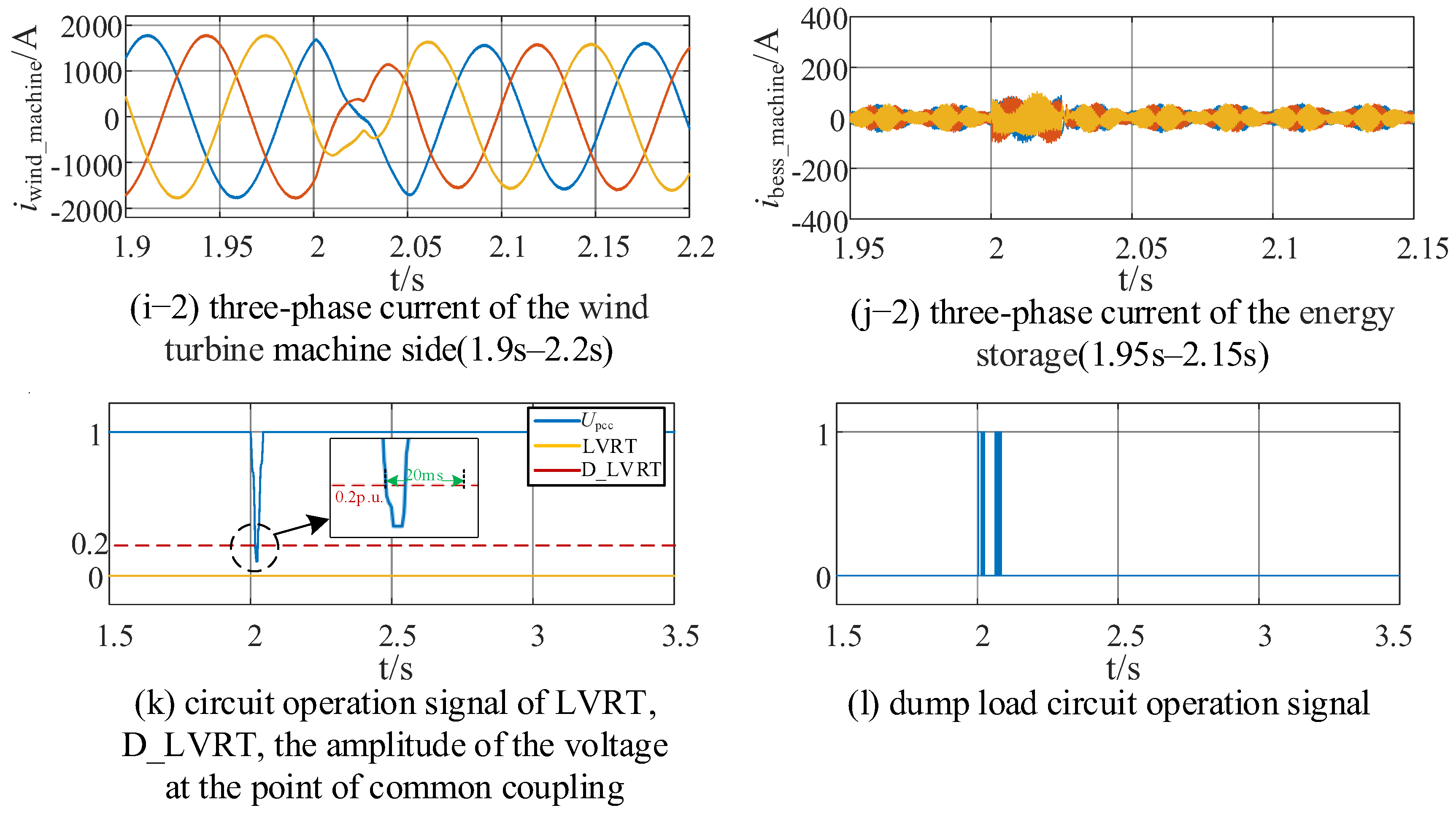
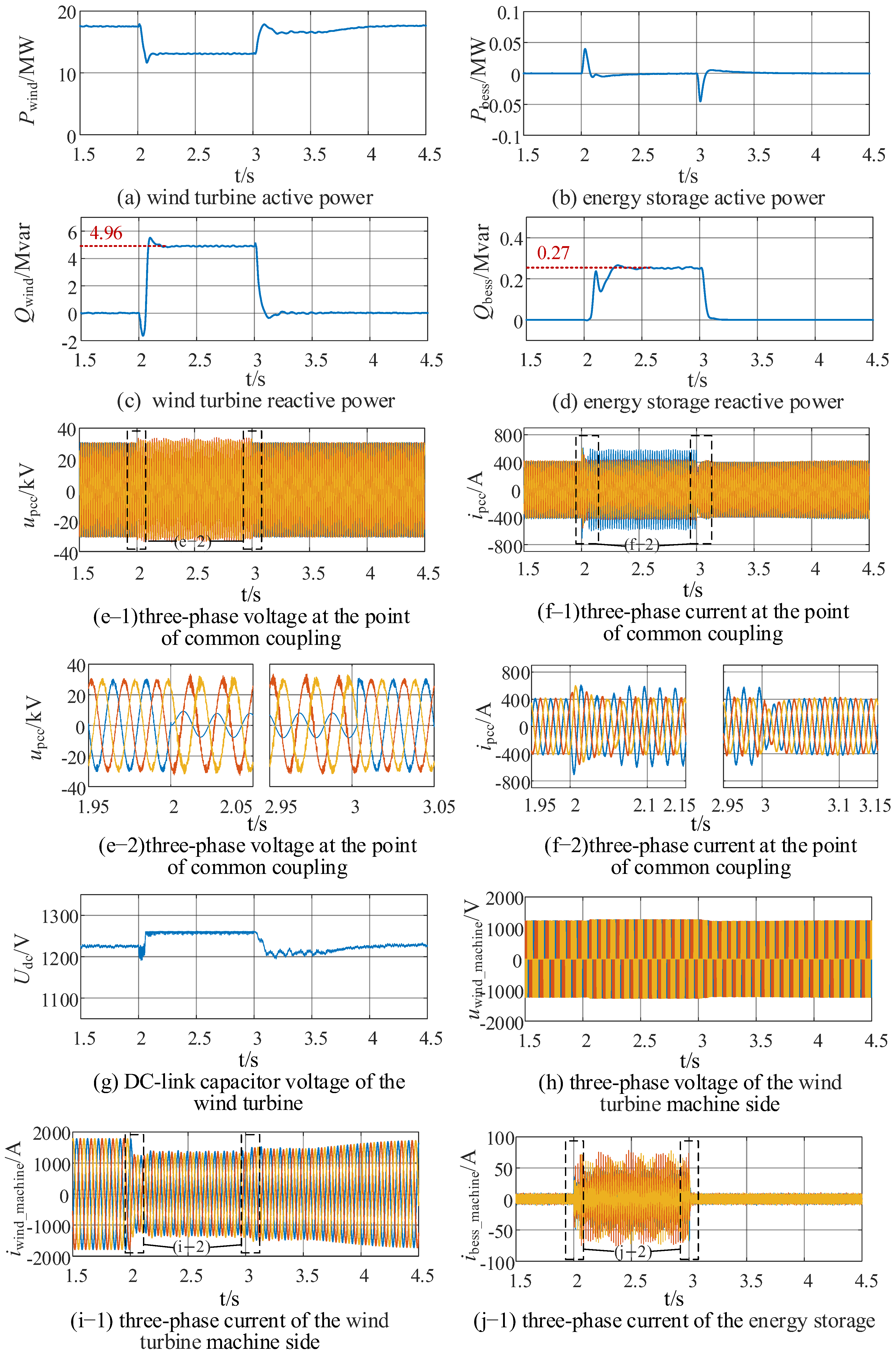
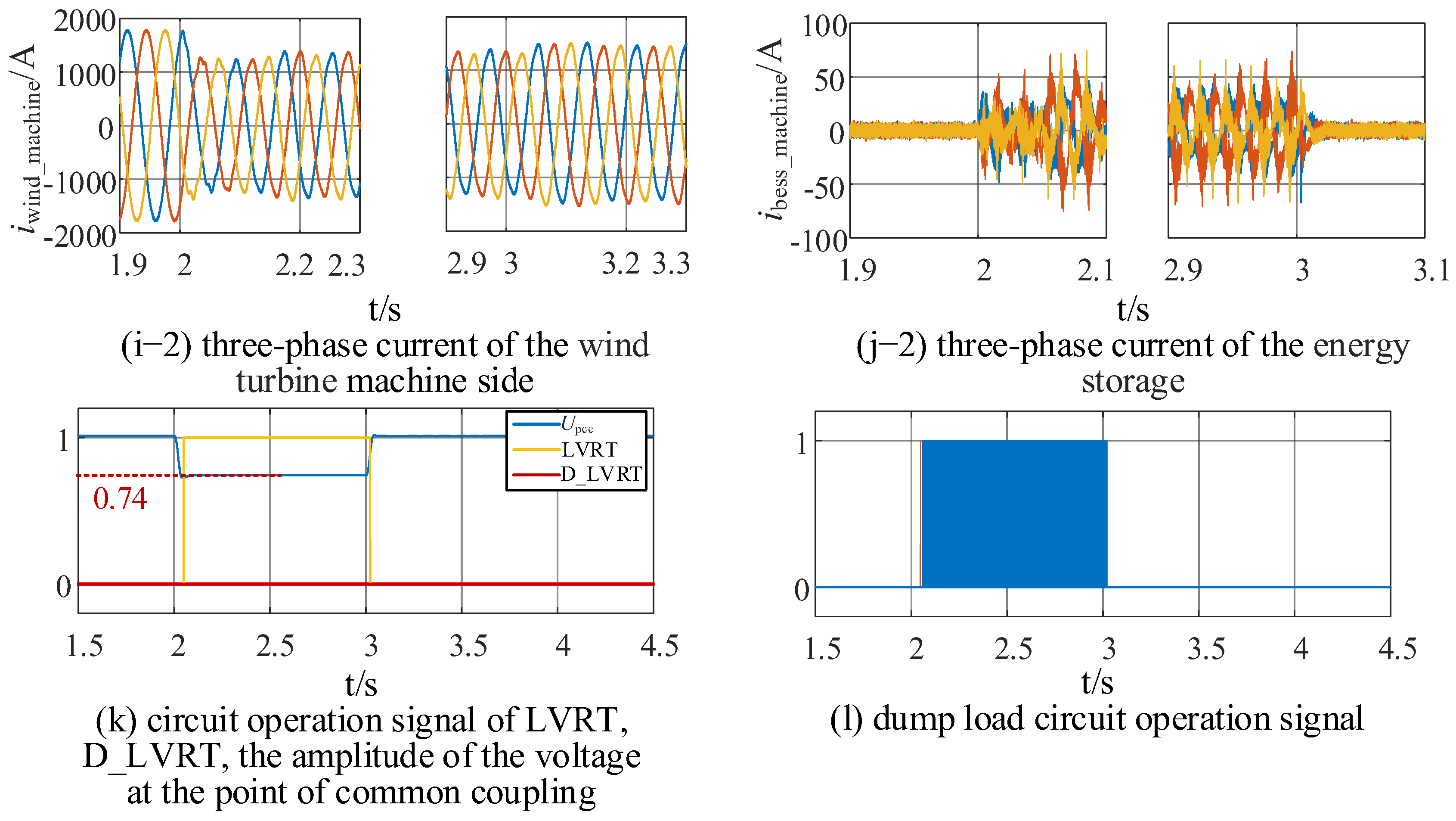
4.2.2. Regular LVRT

A voltage dip to 0.6 p.u. with a duration of 1.4 s is configured, and the effectiveness of the proposed control strategy is validated through the LVRT responses of the wind turbine and energy storage system. The response curves of the wind–storage system are presented in Figure 15.

As can be seen from the power response curves in Figure 15, during the LVRT process, when the voltage dips to 0.6 p.u., the total reactive power demand of the wind turbine can be calculated using the minimum reactive current formula required by China’s national standards. With K₁ set to 2, the total reactive power to be generated is 10.8 Mvar. As shown in Figure 15c, the reactive power output of the wind turbine in LVRT mode is 8.6 Mvar, resulting in a reactive power deficit of 2.2 Mvar. Thus, a single energy storage unit needs to generate 0.733 Mvar of reactive power. When the reactive power of the wind turbine fails to meet the requirements, if the wind turbine and energy storage calculate and inject reactive power independently in the traditional way, according to the formula for the reactive current of energy storage under low-voltage conditions, with the coefficient K set to 3, the reactive power reference value is 0.6 Mvar. If the energy storage outputs reactive power according to this reference value, there will still be a reactive power deficit in the system. Therefore, the strategy proposed in this paper can provide voltage support based on the reactive power deficit of the wind turbine, and the comparison diagram of the test results is shown in Figure 15d. Figure 15a corresponds to the active power curve of the wind turbine. It decreases during the fault period and recovers after the fault is cleared, which serves as the active power response of the wind turbine to the fault. Figure 15b refers to the active power curve of the energy storage system. Since the core of the proposed strategy is reactive power regulation, the energy storage is not scheduled to inject or absorb active power. Thus, the active power of the energy storage only shows acceptable, small, transient fluctuations caused by voltage transients and remains at 0 during the fault period. This is consistent with the design requirements of the proposed strategy.

Similar to Figure 13, Figure 15e–l illustrate the variations under this operating condition. During the regular LVRT period, both the energy storage units and the wind turbine’s unloading circuit start normally, and all physical quantities recover relatively quickly after the voltage is restored. Among them, for Figure 15i, the machine-side current of the wind turbine has a slightly slower response speed due to factors such as the mechanical adjustment of the machine-side MPPT, and it recovers to the normal value at 5 s. In Figure 15k, 30 ms after the PCC voltage drops below 0.9 p.u., the LVRT mode initiates with the delayed startup designed in Figure 8.

To verify the adaptability of the proposed strategy to unbalanced voltage dips, a phase-a ground fault is set at the PCC with a transition resistance of 1 ohm, and the fault is cleared after 1 s. Figure 16 shows the response of the wind–storage system under this operating condition.

Under this operating condition, the proposed strategy in this paper extracts the positive sequence component of PCC voltage, with Figure 16k showing the positive sequence component. In accordance with the requirements for unbalanced sags specified in GB/T 19963.1-2021 and using the same formula as Equation (1), the strategy regulates the wind turbine and energy storage to inject reactive power (see Figure 16c,d,k). At this dip depth, the total reactive power demand is 5.76 Mvar, the reactive power injected by the wind turbine is approximately 4.96 Mvar, and each energy storage unit requires 0.267 Mvar. The verification results are consistent with the power allocation command, confirming that the proposed strategy responds correctly to the unbalanced dip condition. Similar to Figure 15, Figure 16a is the wind turbine’s active power curve: it decreases during the fault and recovers post-fault, corresponding to the turbine’s active response to the fault. Figure 16b refers to the energy storage’s active power curve. Given that the proposed strategy prioritizes reactive power regulation (with no active power scheduling for the energy storage), its active power only shows acceptable, small, transient fluctuations caused by voltage transients and remains at 0 during the fault, which is consistent with the strategy’s design requirements.

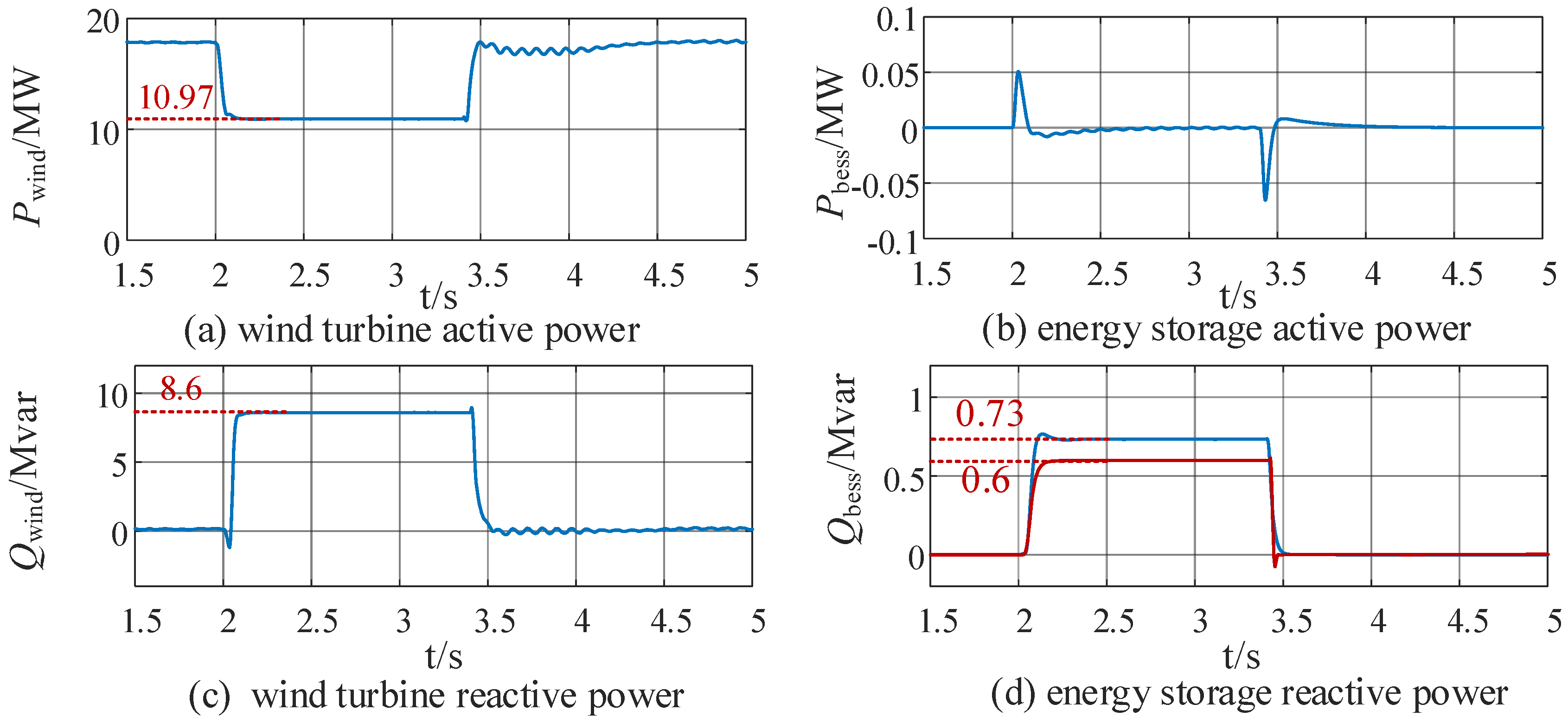
4.2.3. Voltage Fluctuation

In practical engineering, voltage fluctuations tend to occur at the LVRT threshold (i.e., 0.9 p.u.), causing the system to repeatedly enter and exit the LVRT state. To tackle this issue, the strategy proposed in this paper modifies the LVRT exit regulation when the system enters LVRT multiple times within 2 s. The system will exit the LVRT boundary only when the U_pcc exceeds 0.93 p.u. and maintains stability for 100 ms. The comparison diagram of the test results is presented in Figure 17.

Figure 17a shows the verification curves when the voltage ride-through threshold remains unchanged, where the wind turbine repeatedly enters and exits the LVRT mode, leading to frequent switching of control logic, which poses a significant threat to the safe operation of the system.

As can be seen from the comparative curve in Figure 17b, the U_pcc dips to 0.7 p.u. at 1 s, recovers to 0.91 p.u. at 1.3 s, and exits LVRT at this point. It re-enters LVRT at 1.6 s and exits again at 1.9 s, marking the end of the second LVRT process. It enters LVRT for the third time at 2.1 s, and the exit threshold of LVRT is adjusted to 0.93 p.u. at this moment. It can be observed that the threshold is reached at 2.609 s, and the LVRT state returns to 0 at 2.703 s. A delay of approximately 100 ms is successfully achieved, which verifies that the adjusted strategy maintains system stability under the condition of repeated LVRT entry caused by voltage fluctuation near the boundary value. Figure 17c shows the situation where the voltage stabilizes around 0.90. After entering the voltage ride-through for the third time, the voltage ride-through exit threshold is adjusted in accordance with the proposed strategy. At this point, the voltage may stabilize below 0.93 due to factors such as the wind farm maintaining its active power, which allows it to remain in the voltage ride-through state for a short time, maintain system stability, and similarly avoid repeated LVRT.

5. Discussion

Firstly, based on the analysis results in the Results Section, we compared the proposed coordinated control strategy with the traditional LVRT strategy, and the specific results are shown in

Table 2. Comparison between the proposed coordinated control and the traditional LVRT control under different test conditions.

Test Condition	Proposed Coordinated Control Strategy	Traditional LVRT Control Strategy	Comparison Effect
Upcc dip: 0.1 p.u.; 150 ms	PMSG maintains grid integration and provides reactive power support	PMSG trip	Enhanced adaptability to extreme operating conditions
Upcc dip: 0.1 p.u.; 25 ms	PMSG maintains grid integration	PMSG trip
Upcc fluctuation	Suppresses repeated LVRT within 2 s	Repeated LVRT
Upcc dip: 0.6 p.u.; 1.4 s	BESS reactive power support: 0.733 Mvar	BESS reactive power support: 0.6 Mvar	Improved reactive power support

. It can be seen that the proposed coordinated control strategy significantly improves the grid-connected stable operation capability of the wind farm under extreme operating conditions, such as deep voltage sags and repeated fluctuations. Meanwhile, under normal operating conditions, it fully utilizes the reactive power response capability of the energy storage system. Compared with the traditional energy storage control and standalone PMSG control, the reactive power support capability of the coordinated control is improved by more than 22%, which meets the requirements of China’s national standards.

In this paper, the modeling data of the wind farm are referenced from a wind farm in Northern China. From the perspectives of wind farm operation and complete wind turbine manufacturing, the proposed method only requires modifying the wind turbine control programs and the on-site AVC strategy, enabling it to address the aforementioned extreme operating conditions without adding new equipment. Compared with the direct tripping of wind turbines in practical operation, it also ensures the stability of the wind farm’s active power output. Under normal operating conditions, the wind–storage coordinated control can improve the utilization rate of the energy storage system and reduce long-term operating costs, serving as an effective improvement and supplement to the traditional LVRT and AVC strategies. Currently, the proposed strategy requires further verification in small-scale experimental scenarios equipped with complete wind turbines.

In addition, this method has certain limitations. For instance, it only implements suppression after the occurrence of repeated LVRT phenomena and cannot perform online analysis of network parameters and power prediction data to proactively assess the risk of voltage fluctuations and implement advanced suppression. Regarding improving the timeliness of the transient voltage fluctuation suppression method at the wind farm’s PCC, further research is required in the future.

6. Conclusions

To address unconventional voltage events such as repeated LVRT and deep voltage sags that are prone to occur in wind power cluster systems under extreme weather conditions, while efficiently utilizing the energy storage resources configured in wind farms, this study proposes a wind–storage coordinated voltage ride-through control strategy and completes relevant verifications. The specific research results are as follows:

(1)

This study classifies different operating modes based on voltage levels and designs an anti-fluctuation control logic. Compared with the traditional LVRT strategy, the multi-condition performance of the proposed strategy is significantly optimized. Under the extreme condition where the voltage drops to 0.1 pu, the traditional strategy will trigger wind turbine tripping, while the proposed strategy enables wind turbines to remain grid-connected and provide reactive power support. Under the condition of repeated voltage fluctuations induced by the coupling of weak power grids and active power fluctuations, the proposed strategy can suppress repeated LVRT within 2 s and avoid cyclic jumps of the system operating point along the PV curve. Under normal faults, the proposed strategy increases the reactive power support of the energy storage system from 0.6 Mvar (of the traditional strategy) to 0.733 Mvar, with an improvement rate of 22.2% under test conditions. This not only meets the requirements of China’s national standards but also avoids the problem of insufficient reactive power caused by the independent regulation of wind turbines and energy storage systems.

(2)

Engineering application value of the strategy: The proposed strategy does not require additional hardware equipment and only needs to optimize the wind turbine control program and the wind farm’s AVC strategy. On the one hand, it replaces the “direct turbine tripping” operation in practical operation and maintenance, ensuring the stability of the wind farm’s active power output and improving the wind farm’s adaptability to extreme weather; on the other hand, it improves the energy storage utilization rate under normal operating conditions and reduces the long-term operation cost of the wind–storage system, serving as an effective improvement to the traditional LVRT and AVC strategies.

(3)

Validation effectiveness of the strategy: This study established a HIL test environment based on RT-LAB OP5600 and completed verifications for working conditions such as deep LVRT, normal LVRT, and voltage fluctuations. The test results show that the proposed strategy can accurately match reactive power demands and effectively solve the problem of repeated LVRT caused by voltage fluctuations, which fully verifies the effectiveness of the wind–storage coordinated voltage ride-through control strategy and improves the wind farm’s adaptability to unconventional voltage events under extreme weather.