Cloud-Edge Collaboration-Based Data Processing Method for Distribution Terminal Unit Edge Clusters

Abstract

Distribution terminal units (DTUs) play critical roles in smart grid for supporting data acquisition, remote monitoring, and fault management. A single DTU generates continuous data streams, imposing new challenges on data processing. To tackle these issues, a cloud-edge collaboration-based data processing method is introduced for DTU edge clusters. First, considering the load imbalance degree of DTU data queues, a cloud-edge integrated data processing architecture is designed. It optimizes edge server selection, the offloading splitting ratio, and edge-cloud computing resource allocation in a collaboration mechanism. Second, an optimization problem is formulated to maximize the weighted difference between the total data processing volume and the load imbalance degree. Next, a cloud-edge collaboration-based data processing method is proposed. In the first stage, cloud-edge collaborative data offloading based on the load imbalance degree, and a data volume-aware deep Q-network (DQN) is developed. A penalty function based on load fluctuations and the data volume deficit is incorporated. It drives the DQN to evolve toward suppressing the fluctuation of load imbalance degree while ensuring differentiated long-term data volume constraints. In the second stage, cloud-edge computing resource allocation based on adaptive differential evolution is designed. An adaptive mutation scaling factor is introduced to overcome the gene overlapping issues of traditional heuristic approaches, enabling deeper exploration of the solution space and accelerating global optimum identification. Finally, the simulation results demonstrate that the proposed method effectively improves the data processing efficiency of DTUs while reducing the load imbalance degree.

1. Introduction

With the development of the smart grid, distribution terminal units (DTUs) have been largely deployed at substations, ring main units, and switchgear cabinets to realize data acquisition, remote monitoring, and fault management [1]. A single DTU generates continuous streams of line parameters, harmonics, equipment status signals, and protection measurements, causing new challenges in data processing. Local data processing can reduce transmission latency, but the amount of processed data is constrained by the limited computing and storage capabilities of terminals [2,3]. On the other hand, centralized cloud processing, despite its powerful computing resources, suffers from transmission latency, bandwidth limitations, and security issues [4]. To overcome these limitations, cloud-edge collaboration has emerged as a feasible solution by integrating the abundant resources of cloud with edge clusters. It enables edge-side execution of time-critical tasks while enabling data aggregation from multiple DTUs for advanced data analysis [5,6]. This novel architecture of data processing ensures low latency and high reliability while further improving data processing efficiency and resource utilization levels [7].

In the cloud-edge collaboration architecture, the load imbalance degree and the volume of processed data are two key indicators for measuring system performance. The load imbalance degree reflects the non-uniformity of the distribution of data queue backlogs among edge nodes and is typically defined as the standard deviation or coefficient of load variation on each node [8,9]. A lower load imbalance degree can prevent some nodes from being overloaded while others remain idle [10,11], thereby improving the overall data processing efficiency [12,13]. On the other hand, the volume of processed data directly reflects the real-time data processing capability of DTU edge clusters. A larger volume of processed data means higher computing throughput, which can support more complex analysis tasks, such as fault detection and power quality analysis. Scholars have determined how to reduce the load imbalance degree [14]. In [15], Binh et al. proposed a load-balanced routing algorithm for wireless mesh networks based on software-defined networking (SDN). By dynamically monitoring node loads and introducing transmission quality constraints, the algorithm achieved low-latency and high-reliability data transmission through multi-objective optimization, significantly reducing network load imbalance and resource utilization. In [16], Chen et al. proposed a two-stage intelligent load imbalance method for multi-edge collaboration scenarios in wireless metropolitan area networks. This method combined centralized deep neural networks (DNNs) for global task prediction and distributed deep Q-networks (DQNs) for local dynamic adjustment, effectively reducing system response latency. In [17], Yang et al. proposed a task offloading algorithm based on traditional deep Q-networks. By using reinforcement learning to selectively offload computing tasks to the optimal edge nodes or servers, the algorithm optimized task offloading and resource allocation. However, most existing research predominantly focuses on individually optimizing either load imbalance reduction or processed data volume, lacking a coordinated optimization.

Cloud-edge collaboration provides an effective solution for the efficient processing of data from DTUs, with its core lying in jointly optimizing the selection of edge servers, the decision on data offloading splitting ratios, and the allocation of computing resources to enhance system performance. Firstly, rational selection of edge servers can minimize network transmission latency while balancing the load distribution within the edge cluster. Secondly, optimizing the data offloading splitting ratio involves dynamically adjusting the proportion of raw data processed at the edge layer versus the cloud. This approach not only fully utilizes the real-time advantages of edge computing but also leverages the powerful batch processing capabilities of the cloud. Lastly, precise allocation of computing resources, through the rational distribution of resources such as CPU and memory, can significantly improve task processing efficiency and reduce energy consumption. However, the aforementioned optimization problem involves high-dimensional discrete variables and complex constraints, making it difficult for traditional convex optimization methods to solve effectively. There is an urgent need to introduce intelligent optimization algorithms to achieve efficient decision-making.

Multi-agent deep reinforcement learning (DRL) has gained widespread application in edge data processing due to its strong environment perception and decision-making capabilities. In terms of server selection, in [18], Bai et al. proposed a federated learning-based edge server selection method for dynamic edge networks, achieving efficient server-terminal matching by jointly optimizing communication link quality and computing resources utilization. In [19], Liu et al. introduced a mobile edge computing server selection algorithm based on DRL, which realized optimal server selection in dynamic mobile environments through the design of a multi-dimensional state space and reward functions. Regarding data offloading, in [20], Yan et al. proposed a joint optimization framework for task offloading and resource allocation in edge computing environments. By solving the optimal offloading splitting ratio and computing resource allocation simultaneously through mixed-integer nonlinear programming, this method reduced the system’s total processing delay while ensuring task dependency constraints. In [21], Alam et al. introduced a dynamic data offloading mechanism based on DRL. By designing a state prediction module containing a long short-term memory (LSTM) network, this method accurately predicted network congestion levels and edge node load states and used a double-delay deep deterministic policy gradient algorithm to optimize offloading decisions. However, traditional DRL methods, such as DQN, suffer from overestimation of Q-values and struggle to handle multi-dimensional continuous action spaces involving server selection, offloading splitting ratio decisions, and resource allocation simultaneously.

Genetic algorithms have demonstrated strong potential in the field of computing resource allocation optimization. Liu et al. proposed an improved genetic algorithm for multi-user computing offloading and resource allocation optimization in heterogeneous 5G mobile edge computing (MEC) networks [22]. In [23], Laili et al. proposed a cloud-edge-end collaborative computing resource allocation algorithm based on differential evolution. By combining genetic algorithms, deep learning, and differential evolution, this method achieved efficient task offloading and resource scheduling optimization. Zhu et al. introduced a genetic algorithm-based elastic resource scheduling method to optimize resource allocation of multi-stage stochastic tasks in hybrid cloud environments [24]. Farahnakian et al. proposed a genetic algorithm-based energy-efficient virtual machine consolidation scheme [25]. Utilizing time series analysis to predict future host loads, this scheme optimizes cloud computing resource allocation through multi-dimensional chromosome encoding and dynamic mutation mechanisms. However, traditional genetic algorithms suffer from slow convergence and a tendency to fall into local optima, making them inadequate for meeting the real-time optimization needs of cloud-edge collaboration.

Despite the progress made in the aforementioned studies, several issues remain. Firstly, traditional data processing architectures for DTU edge clusters do not consider the dynamic data processing queue evolution of the terminal, edge, and cloud sides. There is a lack of effective coordination between DTU local processing, edge cluster processing, and cloud processing. Second, in environments where data from multiple DTUs are processed concurrently, the load states fluctuate significantly across different time slots. Traditional DQN-based data offloading strategies are mostly optimized based on static reward functions, failing to account for dynamic load evolution characteristics. This results in a high load imbalance degree and a large data volume deficit accumulation over consecutive time slots. Last but not least, traditional genetic algorithms are prone to falling into local optima due to gene overlap issues. New genes generated during the mutation process overlap with existing ones, leading to slower convergence and inferior resource allocation performance.

To address the aforementioned challenges, this paper focuses on solving the following three problems:

Problem 1: How to establish an efficient data coordination processing mechanism in a cloud-edge integrated DTU edge cluster. The mechanism must be able to collaboratively optimize high-dimensional short-term decisions and satisfy long-term performance constraints to overcome the load imbalance and low efficiency caused by resource fragmentation and coupled decisions in traditional approaches.

Problem 2: How to maintain system stability under fluctuating distribution terminal loads. The mechanism must dynamically track load variations and virtual-queue evolution to link real-time offloading decisions with long-term stability constraints, thereby suppressing load oscillations and ensuring stable system performance, particularly the required total data-processing throughput.

Problem 3: How to achieve efficient resource allocation in a large-scale, dynamic cloud-edge environment. The key challenge is to overcome the tendency of traditional methods to become trapped in local optima. The objective is to enable globally efficient solutions for resource allocation strategies, thereby enhancing scheduling performance and resource utilization in dynamic scenarios.

To address the above three problems, we propose a cloud-edge collaboration-based data processing framework for DTU edge clusters. First, a cloud-edge integrated data processing architecture is established, promoting seamless collaboration among the data acquisition layer, DTU layer, edge cluster layer, and cloud server layer. Second, to enhance data processing capability and avoid load imbalance, a joint optimization problem is established. The objective is to maximize the weighted difference between the total data processing volume and the weighted load imbalance degree by jointly optimizing edge server selection, the offloading splitting ratio, and edge-cloud computing resource allocation. Then, by leveraging virtual queue theory, the long-term constraint of data processing volume is decoupled, and the original problem is decomposed into a data offloading selection subproblem and a cloud-edge resource allocation subproblem. Finally, a cloud-edge collaboration-based data processing algorithm for DTU edge clusters is proposed to address the decoupled subproblems. Unlike traditional DQN-based approaches, which exhibit significant fluctuations in load imbalance degree and long-term data volume constraint violations, the proposed algorithm incorporates load imbalance degree and data volume awareness to improve data offloading performance. It also incorporates adaptive differential evolution to enhance cloud-edge resource utilization efficiency. Extensive simulation experiments are carried out to confirm its effectiveness. The primary contributions are outlined below.

Cloud-edge integrated data processing architecture. The proposed architecture employs a collaboration mechanism between DTU local processing, edge cluster proximate processing, and cloud remote processing. The collected data are intelligently stored, split, offloaded, and parallel processed to combine the rapid response characteristics of the edge cluster and powerful computing capacities of cloud server.

Cloud-edge collaborative data offloading based on load imbalance degree and data volume-aware DQN. A penalty function based on load fluctuations and data volume deficit is incorporated into the reward function design. This drives DQN to evolve toward suppressing the fluctuation of load imbalance degree across time slots and ensures the satisfaction of differentiated long-term data volume constraints.

Cloud-edge computing resource allocation based on adaptive differential evolution. We incorporate an adaptive mutation scaling factor, which is dynamically adjusted during the iterative optimization process. This overcomes the gene overlapping issues of traditional heuristic approaches, enabling deeper exploration of the solution space and accelerating global optimum identification.

2. System Model

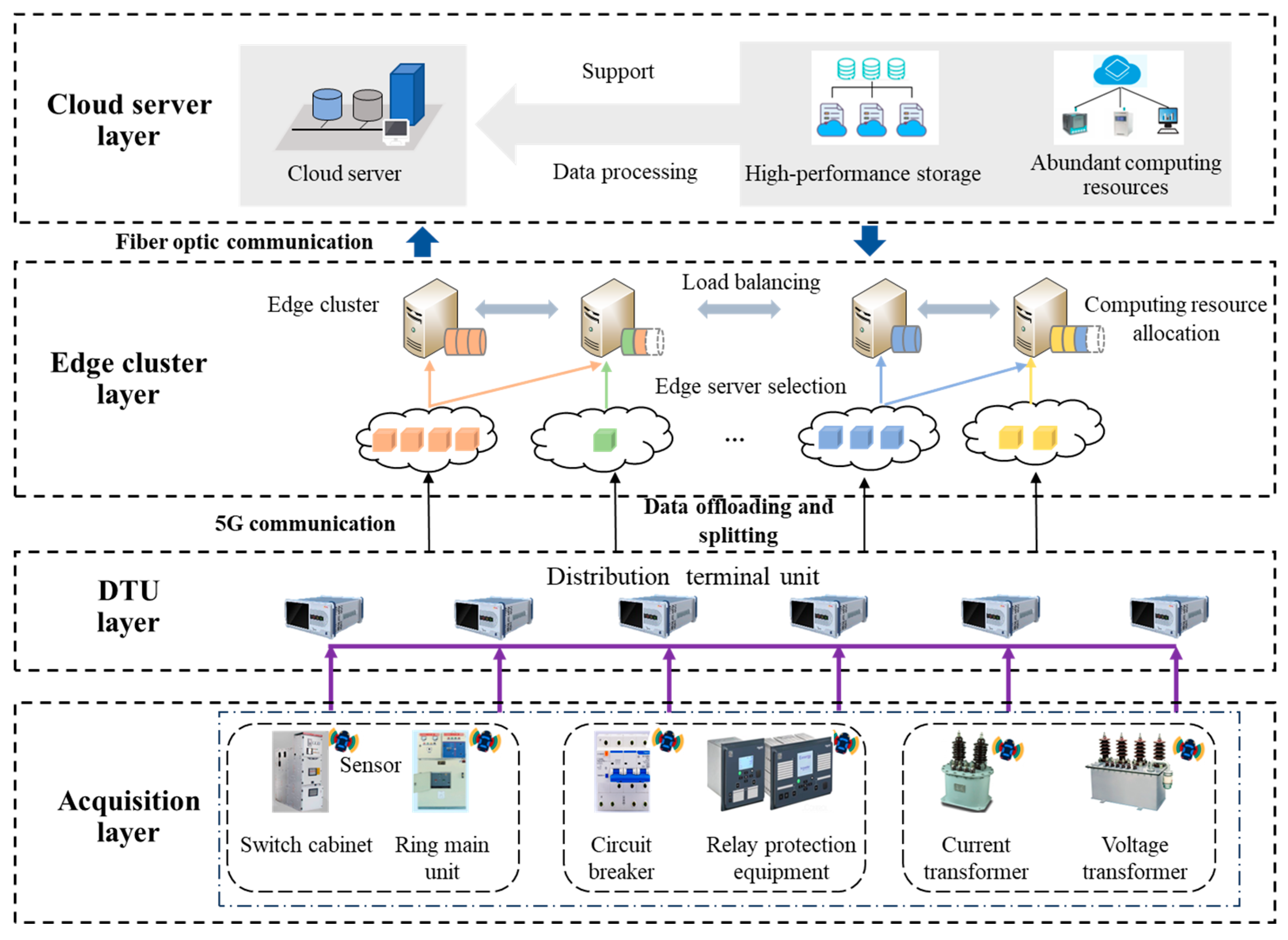
The cloud-edge integrated data processing architecture for DTU edge clusters is illustrated in Figure 1, comprising the acquisition layer, DTU layer, edge cluster layer, and cloud server layer. The acquisition layer includes various electrical equipment such as switchgear, current transformers, and voltage transformers. Each DTU is deployed on electrical equipment, receiving operational status data from the acquisition layer. The collected data are locally processed on each DTU or uploaded to the edge cluster layer and cloud server layer for further processing. The set of DTUs is denoted as $D=\left\{d_1,\cdots ,d_m,\cdots ,d_M\right\}$. The edge cluster layer consists of edge clusters and 5G base stations. The 5G base stations provide communication support for data interaction among the DTU layer, edge cluster layer, and cloud server layer. The edge clusters integrate multiple edge servers, which can assist DTUs in data processing. The set of edge servers is denoted as $S=\left\{s_1,\cdots ,s_k,\cdots ,s_L\right\}$. The cloud server layer includes a master station and cloud server $s_0$. The cloud servers possess abundant storage and computing resources, enabling rapid processing of uploaded data.

The optimization period is partitioned into $T$ slots, each with a duration $\tau$. Each slot includes four processes, namely, data acquisition, edge server selection, data offloading splitting ratio selection, and collaborative processing between the edge cluster and cloud server. During the data acquisition process, DTUs receive operational status data from the acquisition layer and await transmission. In the edge server selection process, DTUs make edge server selection decisions to determine which edge server to collaborate with. In the data offloading splitting ratio selection process, DTUs make decisions on the ratio of data offloading to the edge cluster and cloud server. During the edge cluster–cloud server collaborative processing, the edge cluster and cloud server utilize their computing resources to collaboratively process the data uploaded by the DTUs.

2.1. Edge Cluster–Cloud Server Collaboration Model

We introduce the edge cluster collaboration splitting ratio and cloud server collaboration splitting ratio to partition the data collected by DTUs. A portion of the data is retained at DTU for local processing, while another portion is offloaded to the edge layer for processing by edge clusters. The remaining data are then offloaded to the cloud layer for processing by cloud servers.

A DTU receives operational status data from the acquisition layer and awaits transmission. Subsequently, the DTU makes decisions regarding edge server selection and data offloading splitting ratio selection. The edge server selection decision variable is defined as $x_{m,k}\left(t\right)\in \left\{0,1\right\}$, with $x_{m,k}\left(t\right)=1$ indicating that DTU $d_m$ chooses the edge server $s_k$ for collaborative data processing.

During the data offloading splitting ratio selection process, the data offloading splitting ratios are discretized into L levels, denoted as $\left\{{\phi }_1,\cdots {\phi }_l,\cdots ,{\phi }_L\right\}$. The data offloading decision of DTU $d_m$ during slot $t$ is denoted by $Y_m\left(t\right)=\left\{{\phi }_m^{\mathrm{D}}\left(t\right),{\phi }_m^{\mathrm{E}}\left(t\right),{\phi }_m^{\mathrm{C}}\left(t\right)\right\}$, satisfying ${\phi }_m^{\mathrm{D}}\left(t\right)+{\phi }_m^{\mathrm{E}}\left(t\right)+{\phi }_m^{\mathrm{C}}\left(t\right)=1$. Here, ${\phi }_m^{\mathrm{D}}\left(t\right)$ represents the local offloading splitting ratio of DTU $d_m$. ${\phi }_m^{\mathrm{E}}\left(t\right)$ denotes the edge cluster offloading splitting ratio of $d_m$, representing the proportion of data offloaded to edge clusters, and ${\phi }_m^{\mathrm{C}}\left(t\right)$ signifies the cloud server offloading splitting ratio of $d_m$, reflecting the proportion of data offloaded to cloud servers.

2.2. DTU Local Computing Model

This section aims to establish the dynamic update rules for the local data queues of DTUs and the calculation method for local data processing volume. This provides a foundation for the subsequent cloud-edge collaborative data processing model while also laying a quantitative basis for the optimal allocation of computing resources.

Let the data queue maintained locally by DTU $d_m$ at slot $t$ be denoted as $Q_m^{\mathrm{D}}\left(t\right)$, which is updated as

$$Q_m^{\mathrm{D}}\left(t+1\right)=Q_m^{\mathrm{D}}\left(t\right)-U_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right)+{\widehat{A}}_m\left(t\right)+\max \left\{U_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right){\phi }_m^{\mathrm{D}}\left(t\right)-U_m^{\mathrm{D}}\left(t\right),0\right\}$$

(1)

where ${\widehat{A}}_m\left(t\right)$ represents the amount of newly arrived data at $d_m$ during slot $t+1$. $U_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right)$ represents the total amount of data offloaded by DTU $d_m$. $U_m^{\mathrm{D}}\left(t\right)$ represents the amount of data processed locally by $d_m$.

The local processing data volume $U_m^{\mathrm{D}}\left(t\right)$ of $d_m$ depends on its computing capability, denoted as

$$U_m^{\mathrm{D}}\left(t\right)=\min \left\{{\displaystyle \frac{\tau f_m^{\mathrm{D}}\left(t\right)}{{\lambda }_m}},U_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right){\phi }_m^{\mathrm{D}}\left(t\right)\right\}$$

(2)

where ${\lambda }_m$ represents the computing complexity of data processing, indicating the CPU cycles required per bit of data processed. $f_m^{\mathrm{D}}\left(t\right)$ represents the computing resources allocated by $d_m$ for local data processing.

2.3. Edge Cluster Data Processing Model

The data transmission rate between DTU $d_m$ and edge server $s_k$ is given by

$$R_{m,k}^{\mathrm{D},\mathrm{E}}\left(t\right)=B_{m,k}\left(t\right)\log \left(1+{\displaystyle \frac{P_{m,k}\left(t\right)G_{m,k}\left(t\right)}{{\delta }_{m,k}\left(t\right)+{\delta }_0}}\right)$$

(3)

where $B_{m,k}\left(t\right)$, $P_{m,k}\left(t\right)$, and $G_{m,k}\left(t\right)$ represent the communication bandwidth, transmission power, and channel gain, respectively. ${\delta }_{m,k}\left(t\right)$ represents the electromagnetic interference, and ${\delta }_0$ represents the noise power.

When making data offloading decisions, $d_m$ must ensure that all data offloaded to the edge server $s_k$ can be completely uploaded within the current slot; that is,

$$\tau R_{m,k}^{\mathrm{D},\mathrm{E}}\left(t\right)\ge x_{m,k}\left(t\right)U_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right){\phi }_m^{\mathrm{E}}\left(t\right)$$

(4)

Let the data queue maintained by the edge server $s_k$ for DTU $d_m$ at slot $t$ be denoted as $Q_{m,k}^{\mathrm{E}}\left(t\right)$, which is updated as

$$\begin{array}{l}{Q}_{m,k}^{\mathrm{E}}\left(t+1\right)=Q_{m,k}^{\mathrm{E}}\left(t\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +x_{m,k}\left(t\right)U_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right){\phi }_m^{\mathrm{E}}\left(t\right)-U_{m,k}^{\mathrm{E}}\left(t\right)\end{array}$$

(5)

where $U_{m,k}^{\mathrm{E}}\left(t\right)$ represents the amount of data processed by $s_k$ for $d_m$.

The amount of data that an edge server can process during slot $t$ is specifically expressed as

$$U_{m,k}^{\mathrm{E}}\left(t\right)=\min \left\{Q_{m,k}^{\mathrm{E}}\left(t\right)+x_{m,k}\left(t\right)U_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right){\phi }_m^{\mathrm{E}}\left(t\right),{\displaystyle \frac{\tau f_{m,k}^{\mathrm{E}}\left(t\right)}{{\lambda }_m}}\right\}$$

(6)

where $f_{m,k}^{\mathrm{E}}\left(t\right)$ represents the computing resources provided by $s_k$ for processing data of $d_m$.

Define the total computing resources available at the edge server $s_k$ during slot $t$ as $f_k^{\mathrm{E},\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right)$. Accordingly, the computing resources constraint of $s_k$ can be expressed as

$${\displaystyle \sum _{m=1}^M{f}_{m,k}^{\mathrm{E}}\left(t\right)}\le f_k^{\mathrm{E},\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right)$$

(7)

2.4. Cloud Server Data Processing Model

Fiber optics is used for data transmission between DTU $d_m$ and cloud server $s_0$. Fiber optic communication is unaffected by electromagnetic interference, offering higher stability and reliability. For simplicity, the fiber optic data transmission rate is set as $R_m^{\mathrm{D},\mathrm{C}}\left(t\right)$. Compared to edge servers, cloud servers possess more abundant storage and computing resources.

Similarly, when making data offloading decisions, $d_m$ must ensure that all data offloaded to $s_0$ can be completely uploaded within the current slot; that is,

$$\tau R_m^{\mathrm{D},\mathrm{C}}\left(t\right)\ge U_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right){\phi }_m^{\mathrm{C}}\left(t\right)$$

(8)

Let the data queue maintained by $s_0$ for $d_m$ at slot $t$ be denoted as $Q_m^{\mathrm{C}}\left(t\right)$, which is updated as

$$Q_m^{\mathrm{C}}\left(t+1\right)=Q_m^{\mathrm{C}}\left(t\right)+U_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right){\phi }_m^{\mathrm{C}}\left(t\right)-U_m^{\mathrm{C}}\left(t\right)$$

(9)

where $U_m^{\mathrm{C}}\left(t\right)$ represents the amount of data processed by $s_0$ for $d_m$ at slot $t$.

Considering the cloud server offloading splitting ratio ${\phi }_m^{\mathrm{C}}\left(t\right)$, the amount of data that the cloud server can process during slot $t$ is specifically expressed as

$$U_m^{\mathrm{C}}\left(t\right)=\min \left\{Q_m^{\mathrm{C}}\left(t\right)+U_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right){\phi }_m^{\mathrm{C}}\left(t\right),{\displaystyle \frac{\tau f_m^{\mathrm{C}}\left(t\right)}{{\lambda }_m}}\right\}$$

(10)

where $f_m^{\mathrm{C}}\left(t\right)$ represents the computing resources provided by $s_0$ for processing data of $d_m$.

2.5. Processed Data Volume Model

The total volume of processed data includes the amount of data processed locally, the amount of data processed by the edge cluster, and the amount of data processed by the cloud server, which is expressed as

$$U_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)=U_m^{\mathrm{D}}\left(t\right)+U_m^{\mathrm{C}}\left(t\right)+{\displaystyle \sum _{k=1}^K{U}_{m,k}^{\mathrm{E}}\left(t\right)}$$

(11)

2.6. Load Imbalance Degree Model

To ensure the timeliness of data processing, the data queues should be as balanced as possible across DTUs, edge clusters, and the cloud server. The load imbalance degree is employed to quantify the imbalance level of data queues. The load imbalance degrees for $d_m$ are, respectively, expressed as

$${\sigma }_m^{\mathrm{D}}\left(t\right)={\displaystyle \frac{\left|w_m{Q}_m^{\mathrm{D}}\left(t\right)-\frac{1}{M}{\displaystyle \sum _{m=1}^M{w}_m{Q}_m^{\mathrm{D}}\left(t\right)}\right|}{\frac{1}{M}{\displaystyle \sum _{m=1}^M{w}_m{Q}_m^{\mathrm{D}}\left(t\right)}}}$$

(12)

$${\sigma }_m^{\mathrm{E}}\left(t\right)={\displaystyle \frac{\left|{\displaystyle \sum _{k=1}^K{w}_m}{Q}_{m,k}^{\mathrm{E}}\left(t\right)-\frac{1}{M}{\displaystyle \sum _{m=1}^M{\displaystyle \sum _{k=1}^K{w}_m}{Q}_{m,k}^{\mathrm{E}}\left(t\right)}\right|}{\frac{1}{M}{\displaystyle \sum _{m=1}^M{\displaystyle \sum _{k=1}^K{w}_m}{Q}_{m,k}^{\mathrm{E}}\left(t\right)}}}$$

(13)

$${\sigma }_m^{\mathrm{C}}\left(t\right)={\displaystyle \frac{\left|w_m{Q}_m^{\mathrm{C}}\left(t\right)-\frac{1}{M}{\displaystyle \sum _{m=1}^M{w}_m{Q}_m^C\left(t\right)}\right|}{\frac{1}{M}{\displaystyle \sum _{m=1}^M{w}_m{Q}_m^C\left(t\right)}}}$$

(14)

where $w_m$ represents the queue backlog weight used to balance the magnitude of queue backlogs among various DTUs.

Therefore, the weighted load imbalance degree of $d_m$ is expressed as

$${\sigma }_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right)={\mu }_m^{\mathrm{D}}{\sigma }_m^{\mathrm{D}}\left(t\right)+{\mu }_m^{\mathrm{E}}{\sigma }_m^{\mathrm{E}}\left(t\right)+{\mu }_m^{\mathrm{C}}{\sigma }_m^{\mathrm{C}}\left(t\right)$$

(15)

where ${\mu }_m^{\mathrm{D}}$, ${\mu }_m^{\mathrm{E}}$, and ${\mu }_m^{\mathrm{C}}$ represent the load imbalance weight coefficients for DTU, edge cluster, and cloud server, respectively.

2.7. Long-Term Data Processing Volume Model

Constraints are imposed on the long-term data processing volume of DTUs, ensuring that the data processing requirements of various power services are satisfied. Defining the minimum tolerable average data processing volume of $d_m$ as $U_m^{\min }$, the long-term data processing volume constraint is expressed as

$$\underset{T\to \infty }{\lim }{\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T{U}_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)}\ge U_m^{\min }$$

(16)

3. Problem Formulation and Transformation

To meet differentiated processing requirements of various power services for DTUs and avoid load distribution imbalance among data queues of different DTUs, this paper balances data processing efficiency and load imbalance on the basis of satisfying the long-term data processing volume constraint of DTUs. Specifically, it maximizes the average value of the difference between total data processing volume and weighted load imbalance over $T$ time slots, which essentially achieves the collaborative optimization of data processing efficiency improvement and load imbalance reduction. The optimization variables include edge server selection, data offloading splitting ratio selection, and cloud-edge collaborative computing resource allocation. The optimization problem is formulated as follows:

$$\begin{array}{l}\mathbf{P}\mathbf{1}:\underset{\left\{x_{m,k}\left(t\right)\right\},\left\{Y_m\left(t\right)\right\},\left\{f_{m,k}^{\mathrm{E}}\left(t\right)\right\},\left\{f_m^{\mathrm{C}}\left(t\right)\right\}}{\max }{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{m=1}^M{U}_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)-\vartheta {\sigma }_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right)}}\\ \mathrm{s.t.} C_1:{\displaystyle \sum _{k=1}^K{x}_{m,k}\left(t\right)}=1,\forall d_m\in D,\forall s_k\in S\\ \hspace{1em} C_2:\left\{\begin{array}{l}{x}_{m,k}\left(t\right)\in \left\{0,1\right\}\\ {\phi }_m^{\mathrm{D}}\left(t\right),{\phi }_m^{\mathrm{E}}\left(t\right),{\phi }_m^{\mathrm{C}}\left(t\right)\in {\left\{{\phi }_1,\cdots {\phi }_l,\cdots ,{\phi }_L\right\}}^{\prime }\end{array}\right.\\ \hspace{1em}\hspace{1em}\hspace{1em}\forall d_m\in D,\forall s_k\in S\\ \hspace{1em} C_3:{\phi }_m^{\mathrm{D}}\left(t\right)+{\phi }_m^{\mathrm{E}}\left(t\right)+{\phi }_m^{\mathrm{C}}\left(t\right)=1,\forall d_m\in D,\forall s_k\in S\\ \hspace{1em} C_4:{\displaystyle \sum _{m=1}^M{f}_{m,k}^{\mathrm{E}}\left(t\right)}\le f_k^{\mathrm{E},\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right),\forall d_m\in D,\forall s_k\in S\\ \hspace{1em} C_5:\underset{T\to \infty }{\lim }{\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T{U}_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)\ge U_m^{\min },}\forall d_m\in D,\forall s_k\in S\end{array}$$

(17)

where $\vartheta$ is a weighting parameter that balances the trade-off between reducing the load imbalance degree and improving the data processing efficiency. $C_1$ restricts each DUT $d_m$ to select at most one edge server. $C_2$ defines the value range constraints for the local, edge, and cloud offloading splitting ratios. $C_3$ ensures that the sum of the splitting ratios for data allocated to the local, edge, and cloud equals 1. $C_4$ limits the amount of computing resources processed by an edge server to not exceed its maximum processing capacity. $C_5$ ensures that the long-term average data processing volume of DTU $d_m$ is not lower than the minimum tolerable average processing volume $U_m^{\min }$.

In the optimization problem $\mathbf{P}\mathbf{1}$, the long-term data processing volume constraint $C_5$ is mutually coupled with short-term decisions within a single time slot. This renders $\mathbf{P}\mathbf{1}$ unsolvable directly by traditional convex optimization methods, requiring transformation and decomposition into subproblems. Therefore, we employ Lyapunov optimization to construct dynamic virtual queues, converting $C_5$ into a stability constraint on virtual queues. The virtual deficit queue associated with $C_5$ is defined as $Z_m\left(t\right)$, which evolves dynamically as follows:

$$Z_m\left(t+1\right)=\max \left\{Z_m\left(t\right)-U_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)+U_m^{\min },0\right\}$$

(18)

where $Z_m\left(t\right)$ represents the deviation between the actual amount of processed data of $d_m$ and the required data processing constraint. According to the virtual queue theory, when the virtual deficit queue for processed data remains stable, the long-term average processed data volume will exceed $U_m^{\min }$, thus satisfying $C_5$.

On this basis, the optimization problem $\mathbf{P}\mathbf{1}$ is transformed into optimization problem $\mathbf{P}\mathbf{2}$. $\mathbf{P}\mathbf{2}$ converts the long-term constraint of $\mathbf{P}\mathbf{1}$ into a short-term observable virtual queue state, enabling the optimization problem to be solved sequentially on a per-time-slot basis and laying the foundation for subsequent decomposition into subproblems, which can be expressed as

$$\begin{array}{l}\mathbf{P}\mathbf{2}:\underset{\left\{x_{m,k}\left(t\right)\right\},\left\{Y_m\left(t\right)\right\},\left\{f_{m,k}^{\mathrm{E}}\left(t\right)\right\},\left\{f_m^{\mathrm{C}}\left(t\right)\right\}}{\max }\begin{array}{c}\Theta \left(t\right)={\displaystyle \sum _{m=1}^M{U}_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)-\vartheta {\sigma }_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right)}\\ \hspace{1em}\hspace{1em}\hspace{1em} -V{Z}_m\left(t\right)\left[U_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)-U_m^{\min }\right]\end{array}\\ \mathrm{s.t.} C_1\sim C_4\end{array}$$

(19)

where $V$ is a weight coefficient used to balance the trade-off between the optimization objective and the stability of the virtual deficit queue.

$\mathbf{P}\mathbf{2}$ can be categorized into mutually independent decision variables and resource variables. Therefore, $\mathbf{P}\mathbf{2}$ can be decomposed into a data offloading decision subproblem $\mathbf{P}\mathbf{3}$ and a cloud-edge collaborative computing resource allocation subproblem $\mathbf{P}\mathbf{4}$. $\mathbf{P}\mathbf{3}$ aims to determine the edge server selection and data offloading splitting ratios for DTUs, thereby providing the demand basis for subsequent resource allocation. $\mathbf{P}\mathbf{3}$ is formulated as follows:

$$\begin{array}{l}\mathbf{P}\mathbf{3}:\underset{\left\{x_{m,k}\left(t\right)\right\},\left\{Y_m\left(t\right)\right\}}{\max }\Theta \left(t\right)\\ \mathrm{s.t.} C_1\sim C_3\end{array}$$

(20)

Building upon the offloading splitting ratios determined by $\mathbf{P}\mathbf{3}$, $\mathbf{P}\mathbf{4}$ is responsible for computing resource allocation, thus ensuring timely data processing and thereby preventing congestion in the edge queues. $\mathbf{P}\mathbf{4}$ is formulated as follows:

$$\begin{array}{l}\mathbf{P}\mathbf{4}:\underset{\left\{f_{m,k}^{\mathrm{E}}\left(t\right)\right\},\left\{f_m^{\mathrm{C}}\left(t\right)\right\}}{\max }\Theta \left({\widehat{x}}_{m,k}\left(t\right),{\widehat{Y}}_m\left(t\right)\right)\\ \mathrm{s.t.} C_4\end{array}$$

(21)

where ${\widehat{x}}_{m,k}\left(t\right)$ and ${\widehat{Y}}_m\left(t\right)$ represent the decisions on edge server selection decisions and data offloading splitting ratios selection decisions, respectively.

4. Cloud-Edge Collaboration-Based Data Processing Method for DTU Edge Clusters

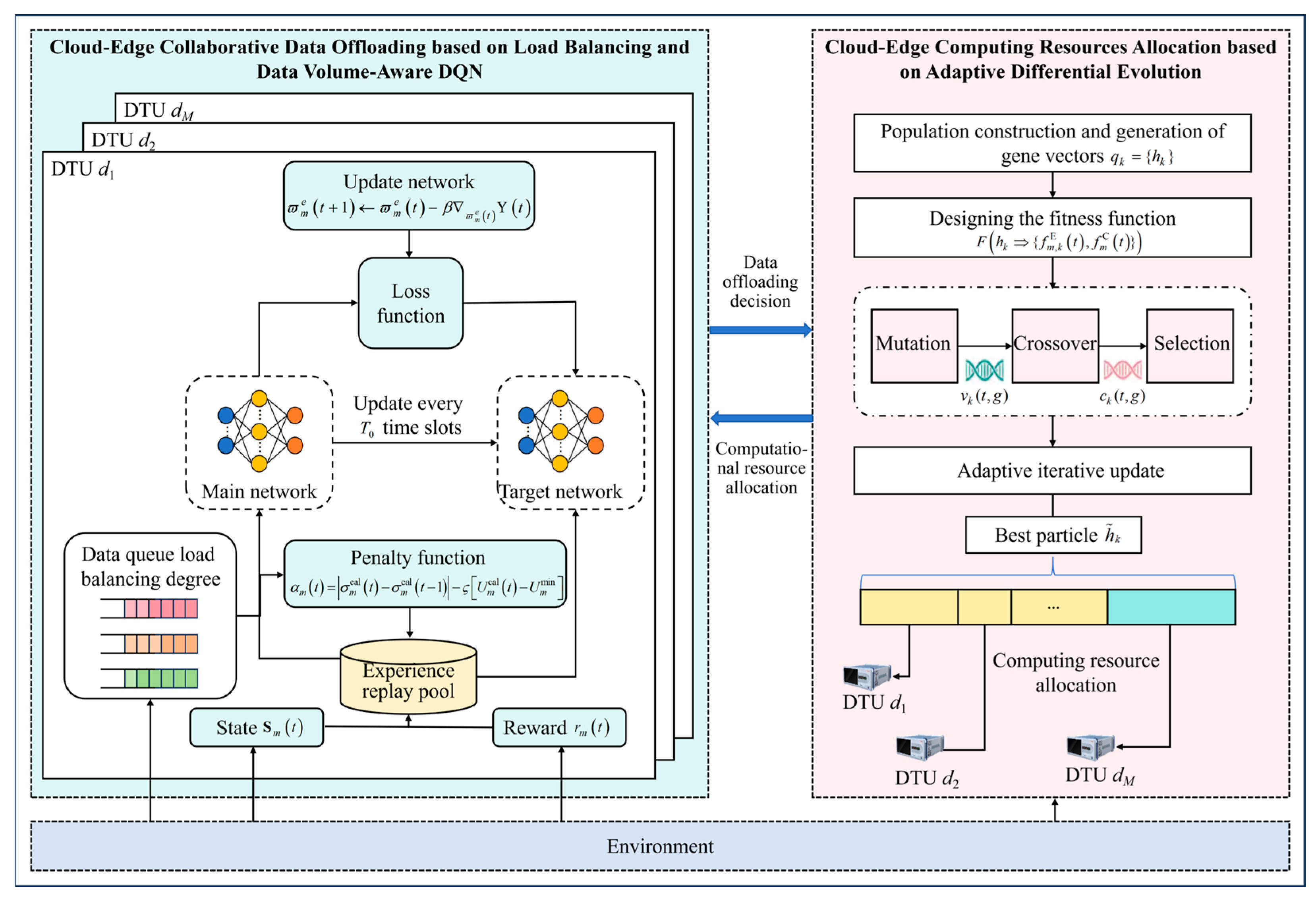
We propose a cloud-edge collaboration-based data processing method for DTU edge clusters, with its overall framework corresponding to optimization objective $\mathbf{P}\mathbf{1}$, as illustrated in Figure 2. The framework decomposes $\mathbf{P}\mathbf{1}$ into two key subproblems: the left part of Figure 2 is used to determine the edge server selection and offloading splitting ratio, corresponding to optimization subproblem $\mathbf{P}\mathbf{3}$, and demonstrates the process of solving $\mathbf{P}\mathbf{3}$ using load imbalance degree and data volume-aware DQN. The right part of Figure 2 is employed to match computing resources with data volume demands, corresponding to optimization subproblem $\mathbf{P}\mathbf{4}$, which is solved via an adaptive differential evolution algorithm. Specifically, the algorithm is divided into two stages. In the first stage, considering the load imbalance degree of DTUs across different time slots and the dynamic changes in virtual queues, a penalty function is constructed based on the fluctuation in load imbalance degree among time slots and the deficit of total processed data volume. This drives the DQN to evolve toward maximizing the reward function and minimizing the penalty function, thereby suppressing fluctuations in the load imbalance degree across different time slots and ensuring that the long-term constraint on the total processed data volume in cloud-edge collaboration is met. In the second stage, an adaptive mutation scaling factor is introduced during the mutation phase, which dynamically adjusts as the iterative optimization of cloud-edge computing resources’ collaborative allocation progresses. This enables more effective exploration of the solution space and the discovery of the global optimal solution in a shorter time, achieving efficient utilization and allocation of cloud-edge computing resources for DTUs. The algorithm execution flow is shown in Algorithm 1, with details provided below.

Algorithm 1: Cloud-Edge Collaboration-based Data Processing Method for Distribution Terminal Unit Edge Clusters

Input: $\left\{Q_m^{\mathrm{D}}\left(t\right),Q_m^{\mathrm{E}}\left(t\right),Q_m^{\mathrm{C}}\left(t\right)\right.\left.,{\sigma }_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t-1\right),Z_m\left(t-1\right),{\widehat{A}}_m\left(t\right)\left|\forall m\right.\right\}$. Output:$\left\{x_{m,k}(t),Y_m\right.(t),f_{m,k}^{\mathrm{E}}(t),f_m^{\mathrm{C}}(t)\left|\forall m\right.,\forall k\}$. 1: For $t=1,2,\dots ,T$ do Stage 1: Cloud-Edge Collaborative Data Offloading based on Load Imbalance Degree and Data Volume-Aware DQN 2:   $d_m$ selects action ${\widehat{O}}_m\left(t\right)$ based on (25). 3:   $d_m$ executes action and calculates the reward $r_m\left(t\right)$ and penalty ${\alpha }_m\left(t\right)$ based on (24) and (26). 4:      $d_m$ updates $S_m\left(t\right)$ to $S_m\left(t+1\right)$, and store the experience data $\left.\left[S_m\left(t\right),{\widehat{O}}_m\left(t\right),r_m\left(t\right),{\alpha }_m\left(t\right),S_m\left(t+1\right)\right.\right]$ into the experience buffer ${\mathcal{P}}_m\left(t\right)$. 5:   $d_m$ calculates the loss function of ${\varpi }_m^e\left(t\right)$ based on (27) and (28). 6:   $d_m$ updates ${\varpi }_m^e\left(t\right)$ and ${\varpi }_m^o\left(t\right)$ based on (29) and (30). Stage 2: Cloud-Edge Computing Resource Allocation based on Adaptive Differential Evolution 7:    Map the cloud-edge collaborative computing resource allocation to chromosome $h_k$ based on $q_k=\left\{h_k\Rightarrow \{f_{m,k}^{\mathrm{E}}\left(t\right),f_m^{\mathrm{C}}\left(t\right)\}\right\}$. 8:   For $g=1,2,\dots ,G$ do 9:     Randomly select three particles $q_{r1}(t,g)$, $q_{r2}(t,g)$, and $q_{r3}(t,g)$ to generate corresponding mutated gene $v_k(t,g)$ based on (32) and (33). 10:      Perform crossover between $q_k(t,g)$ and $v_k(t,g)$ based on (34). 11:      Select the optimal particle between the current and historical best particles using the greedy strategy based on (35). 12:     End For 13: End For

4.1. Cloud-Edge Collaborative Data Offloading Based on Load Imbalance Degree and Data Volume-Aware DQN

The DQN is a deep neural network model based on reinforcement learning. It learns the optimal mapping strategy between states and actions through a trial-and-error feedback mechanism and employs three key techniques-experience replay, target networks, and gradient descent optimization to achieve stable and efficient training. Traditional DQN approaches overlook the perception of load imbalance degree and data volume across different time slots for DTUs, leading to significant fluctuations in load imbalance degree and difficulty in meeting the long-term constraint on the total processed data volume. To address this issue, we construct a penalty function based on the fluctuation of load imbalance degree and the deficit of total processed data volume in cloud-edge collaboration, in addition to the traditional reward function. This drives the DQN to evolve toward maximizing the reward function and minimizing the penalty function, thereby suppressing fluctuations in load imbalance degree across different time slots and ensuring the long-term constraint.

The load imbalance degree and data volume-aware DQN algorithm in this paper adopts a dual-network architecture combined with a scenario-specific experience replay pool. This allows the primary network to learn from experiences that integrate scenario-specific information, while the target network ensures stable training through periodic parameter synchronization. The DQN topology follows a three-layer “input-hidden-output” structure. Each layer is responsible for quantizing local load states, queue backlogs, and data volume, extracting relevant features, and evaluating offloading action values, respectively. Through the close collaboration of these components, the system effectively suppresses load imbalance and ensures long-term data processing requirements are met.

Based on the trial-and-feedback decision-making mechanism, we formulate the subproblem $\mathbf{P}\mathbf{3}$ as a Markov decision process (MDP) [26], which includes three components: actions, states, and rewards. Specifically, interactions among the cloud server layer, edge cluster layer, and DTUs are used to obtain rewards, aiming to optimize the edge server selection and data offloading splitting ratio selection. The detailed algorithmic procedure is presented as follows.

MDP Problem Modeling:

(1)

State $S_m\left(t\right)$. To maximize the total data processing volume and avoid load imbalance, at the start of each slot, DTUs perceive real-time information, such as data queue backlog, load imbalance degree, virtual queue status, and collected data volume. This information is used to construct the state space $S_m\left(t\right)$, expressed as

$$S_m\left(t\right)=\left\{Q_m^{\mathrm{D}}\left(t\right),Q_m^{\mathrm{E}}\left(t\right),Q_m^{\mathrm{C}}\left(t\right)\right.\left.,{\sigma }_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t-1\right),Z_m\left(t-1\right),{\widehat{A}}_m\left(t\right)\right\}$$

(22)

(2)

Action $O_m\left(t\right)$. At the start of slot $t$, the DTU $d_m$ determines the data offloading decision based on the state space, specifically expressed as

$$O_m\left(t\right)=\left\{X_m\left(t\right);Y_m\left(t\right)\right\}$$

(23)

where $X_m\left(t\right)=\left\{x_{m,k}\left(t\right)\mid \forall d_m\in D,\forall s_k\in S\right\}$ represents the edge server selection decision. $Y_m\left(t\right)=\left\{Y_m\left(t\right)\mid \forall d_m\in D\right\}$ represents the data offloading splitting ratio decision, including the local offloading splitting ratio, edge server offloading splitting ratio, and cloud server offloading splitting ratio.

(3)

Reward $r_m\left(t\right)$. The reward value for $d_m$ is defined as the objective function of $\mathbf{P}\mathbf{3}$, expressed as

$$\begin{array}{l}{r}_m\left(t\right)=U_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)-\vartheta {\sigma }_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right)\\ \hspace{1em}\hspace{1em} -V{Z}_m\left(t\right)\left[U_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)-U_m^{\min }\right]\end{array}$$

(24)

Algorithm Solution:

$d_m$ simultaneously maintains two neural networks, namely, the primary network and the target network, with their respective parameters denoted as ${\varpi }_m^e\left(t\right)$ and ${\varpi }_m^o\left(t\right)$. The proposed algorithm consists of three main steps: selection of DTU action, state transition and experience storage, and experiential learning and network updates. The detailed description is as follows.

(1)

Selection of DTU Action

At the beginning of time slot $t$, the DTU $d_m$ inputs the current time slot’s state space $S_m\left(t\right)$ into the primary network ${\varpi }_m^e\left(t\right)$ to obtain the Q-values corresponding to different actions within the time slot. Based on these Q-values, action ${\widehat{O}}_m\left(t\right)$ is selected, expressed as

$${\widehat{O}}_m\left(t\right)=\underset{O_m\left(t\right)}{\mathrm{argmax}}Q\left.\left[S_m\left(t\right),O_m\left(t\right)\mid {\varpi }_m^e\left(t\right)\right.\right]$$

(25)

(2)

State Transition and Experience Storage

To avoid the issues of unsatisfied constraints and drastic fluctuations in weighted load imbalance degree, we construct a penalty function ${\alpha }_m\left(t\right)$ based on the fluctuations in load imbalance degree between time slots and the deficit in the total processed data volume, expressed as

$${\alpha }_m\left(t\right)=\left|{\sigma }_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)-{\sigma }_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t-1\right)\right|-\varsigma \left[U_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)-U_m^{\min }\right]$$

(26)

where $\varsigma$ represents the weighting coefficient. During the optimization process, the DQN network evolves in the direction of minimizing the penalty function, thereby suppressing fluctuations in the load imbalance degree, reducing the cumulative data processing deficit, and ensuring the long-term constraint.

The DTU $d_m$ executes action ${\widehat{O}}_m\left(t\right)$, calculates the reward $r_m\left(t\right)$ and penalty ${\alpha }_m\left(t\right)$, updates the state space to $S_m\left(t+1\right)$, and stores the experience data $\left.\left[S_m\left(t\right),{\widehat{O}}_m\left(t\right),r_m\left(t\right),{\alpha }_m\left(t\right),S_m\left(t+1\right)\right.\right]$ into the experience buffer ${\mathcal{P}}_m\left(t\right)$.

(3)

Experiential Learning and Network Updates

The DTU randomly samples $H$ experience data from the experience pool ${\mathcal{P}}_m\left(t\right)$ and calculates the mean squared error loss function of the main network, expressed as

$$\mathrm{{\rm Y}}\left(t\right)={\displaystyle \frac{1}{H}}\sum _{h=1}^H[Q_m^h\left(t\right)-Q\left(S_m\left(t\right),{\widehat{O}}_m\left(t\right)\mid {\varpi }_m^e\left(t\right)\right)]$$

(27)

where $Q_m^h\left(t\right)$ represents the target $\mathrm{Q}$-value obtained by the target network ${\varpi }_m^o\left(t\right)$ based on the $h$-th group of experience data, specifically expressed as

$$Q_m^h\left(t\right)=r_m\left(t\right)-{\alpha }_m\left(t\right)+\gamma Q\left(S_m\left(t+1\right),{\widehat{O}}_m\left(t+1\right)\mid {\varpi }_m^o\left(t\right)\right)$$

(28)

where $\gamma \in \left.\left[0,1\right.\right]$ is used to measure the influence of the next slot’s reward on the current action decision.

The main network parameters are updated based on the gradient descent method, expressed as

$${\varpi }_m^e\left(t+1\right)\leftarrow {\varpi }_m^e\left(t\right)-\beta {\nabla }_{{\varpi }_m^e\left(t\right)}\mathrm{{\rm Y}}\left(t\right)$$

(29)

where $\beta$ is the learning rate. ${\nabla }_{{\varpi }_m^e\left(t\right)}$ denotes the Hamiltonian operator, a vector differential operator used to compute the gradient of the primary network’s loss function with respect to network parameters, enabling iterative updates of these parameters [27]. The meaning of the entire formula is as follows: update the primary network parameters ${\varpi }_m^e\left(t\right)$ in the opposite direction of the loss function’s gradient to minimize the loss function $\mathrm{{\rm Y}}\left(t\right)$, ultimately allowing the DQN to learn the optimal offloading decision strategy.

The target network is synchronized with the primary network every $T_0$ slots. The update process can be expressed as

$${\varpi }_m^o\left(t+1\right)=\left\{\begin{array}{cc}{\varpi }_m^e\left(t+1\right),\hfill & t\hspace{0.33em}\mathrm{mod}\hspace{0.33em}{T}_0=0\\ {\varpi }_m^o\left(t\right),\hfill & \mathrm{else}\end{array}\right.$$

(30)

where $t\hspace{0.33em}\mathrm{mod}\hspace{0.33em}{T}_0$ represents the remainder of $t$ divided by $T_0$.

Leveraging the DQN network’s robust perception and precise decision-making capabilities, the proposed algorithm constructs a penalty function based on the fluctuation of the DTU load imbalance degree between time slots and the deficit in the total processed data volume. During the optimization process, it continuously perceives the load imbalance degree of DTUs and data volume, evolving toward suppressing fluctuations in load imbalance degree across different time slots and reducing the deficit in the total processed data volume of cloud-edge collaboration.

4.2. Cloud-Edge Computing Resource Allocation Based on Adaptive Differential Evolution

Although traditional genetic algorithms can solve non-convex optimization problems like $\mathbf{P}\mathbf{4}$, they may generate new genes during the mutation process that overlap with existing genes in the population, leading to a high likelihood of falling into local optima in the later stages of optimization. To address these issues, we propose a cloud-edge computing resource allocation algorithm based on adaptive differential evolution. Built upon the evolutionary framework of genetic algorithms, the algorithm introduces an adaptive mutation scaling factor to mitigate its tendency to converge to local optima. Specifically, an adaptive mutation scaling factor is incorporated during the mutation phase. This factor dynamically adjusts as iterations proceed, enabling a more efficient exploration of the solution space and facilitating the identification of the global optimum within a shorter timeframe. The detailed workflow of the proposed adaptive differential evolution algorithm is outlined in Stage 2 of Algorithm 1. We consider a total of $G$ iterations, with the specific algorithm flow as follows.

Population Construction:

There are $K$ particles in the population, and their set is denoted as $\mathcal{Q}=\left\{q_1,\cdots ,q_k,\cdots ,q_{\mathrm{K}}\right\}$. $q_k$ represents the gene vector of particle $k$, denoted as $q_k=\left\{h_k\Rightarrow \{f_{m,k}^{\mathrm{E}}\left(t\right),f_m^{\mathrm{C}}\left(t\right)\}\right\}$, which maps the cloud-edge computing resource allocation of data processing tasks onto chromosome $h_k$. $h_k$ consists of multiple genes, denoted as $h_k=\left\{h_k^1,\cdots ,h_k^m,\cdots ,h_k^M\right\}$, where $h_k^m$ represents the computing resources allocated by edge server $s_k$ and cloud server $s_0$ to DTU $d_m$.

Fitness Function Design:

The fitness function can measure a particle’s adaptation to the environment. Since the essence of the adaptive differential evolution algorithm is to stochastically search for the minimum value, the fitness function of the differential evolution algorithm is defined as the optimization objective of $\mathbf{P}\mathbf{4}$, expressed as

$$\begin{array}{l}F\left(h_k\Rightarrow \{f_{m,k}^{\mathrm{E}}\left(t\right),f_m^{\mathrm{C}}\left(t\right)\}\right)=\\ {\displaystyle \sum _{m=1}^M{U}_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)-\vartheta {\sigma }_m^{\mathrm{a}\mathrm{l}\mathrm{l}}\left(t\right)}-V{Z}_m\left(t\right)\left[U_m^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)-U_m^{\min }\right]\end{array}$$

(31)

Population Initialization:

The main task of population initialization is to assign values to the chromosomes and genes of each particle. Taking particle $k$ as an example, the gene $h_k$ on its chromosome $h_k^m$ should be greater than or equal to 0 and must satisfy the constraint $C_4$.

Adaptive Differential Evolution:

Differential evolution demonstrates robust performance in non-convex optimization through mutation, crossover, and selection operations. Building upon the traditional differential evolution algorithm, this study introduces an adaptive mutation scaling factor during the mutation phase. This factor dynamically adjusts as the iterative optimization of cloud-edge computing resource allocation progresses, enabling more effective exploration of the solution space and accelerating identification of the global optimum.

(1)

Adaptive Genetic Mutation

Let $q_k(t,g)$, $v_k(t,g)$, and $c_k(t,g)$ denote the original gene, mutated gene, and crossover gene of particle $k$ in the $g$-th iteration, respectively. In the gene mutation phase, three randomly selected particles from the same generation are used to generate a corresponding mutated gene for each particle, denoted as

$$v_k(t,g)=q_{r1}(t,g)+\xi (g)\left[q_{r2}(t,g)-q_{r3}(t,g)\right]$$

(32)

where $r1, r2, r3\in \{1\dots k\dots K\}$ represent the identifiers of different particles, and $\xi$ is the adaptive mutation rate factor, denoted as

$$\xi (g)={\xi }_0{2}^{e^{\left(1-{\displaystyle \frac{G}{1+G-g}}\right)}}$$

(33)

where ${\xi }_0\in \left(0,1\right)$ represents the preset constant mutation rate factor. During the early stages of iteration, $\xi$ is relatively large, which helps maintain population diversity and enhances the global search capability. As the number of iterations increases, $\xi$ gradually decreases, preserving the valuable information of the population, preventing the destruction of the optimal solution, and improving convergence speed. This leads to the effective utilization and allocation of cloud-edge computing resources for the DTU.

(2)

Dynamic Gene Crossover Recombination

Crossover refers to the replacement of original genes with their mutated counterparts under a certain probability, with the specific crossover position randomly determined, expressed as

$$c_k\left(t,g\right)=\left\{\begin{array}{l}{q}_k\left(t,g\right), \\ \mathrm{random}\left(0,1\right)<\mathrm{CR} \mathrm{or} \mathrm{randint}\left(0,K\right)=e\\ v_m\left(t,g\right), \mathrm{else}\end{array}\right.$$

(34)

where $\mathrm{CR}$ represents the crossover probability, and $e$ is a random integer.

(3)

Greedy-based Optimal Particle Selection

In each iteration of the proposed algorithm, the best particle is selected and compared with the best particle from previous iterations stored in the population. The individual with the higher fitness is retained. Let variable ${\tilde{h}}_k$ denote the current best particle, and a greedy strategy is used to select the optimal particle as follows:

$${\tilde{h}}_k=\left\{\begin{array}{l}{c}_k\left(t,g\right), \\ F\left(\left\{c_k\left(t,g\right)\Rightarrow \{f_{m,k}^{\mathrm{E}}\left(t\right),f_m^{\mathrm{C}}\left(t\right)\}\right\}\right)\\ >F\left(\left\{{\tilde{h}}_k\Rightarrow \{f_{m,k}^{\mathrm{E}}\left(t\right),f_m^{\mathrm{C}}\left(t\right)\}\right\}\right)\\ {\tilde{h}}_k, \mathrm{else}\end{array}\right.$$

(35)

(4)

Adaptive Differential Iteration

Let $g=g+1$, repeat steps (1) and (3), and continuously perform adaptive differential evolution iterations until the $G$-th iteration is completed.

5. Simulation

We construct a simulation area for the distribution network with dimensions of 300 m × 300 m, deploying eight DTUs randomly distributed on power equipment. These units collect voltage, current, and equipment status data at a frequency of 12.8 kHz. The edge server cluster consists of six edge servers with a time slot length of 1 s, and the unit data arrival rate follows a Poisson distribution. Additional simulation parameters are presented in

Table 1. Simulation parameters.

Parameter	Value	Parameter	Value
$I$	8	${\delta }_0$	−114 dBm
$T$	400	$f_{m,k}^{\mathrm{E}}\left(t\right)$	[2.5, 4] GHz
$P_{m,k}\left(t\right)$	[0.2, 0.4] W	$f_m^{\mathrm{C}}\left(t\right)$	[10, 20] GHz
$B_{m,k}\left(t\right)$	1 MHz	$f_m^{\mathrm{D}}\left(t\right)$	[0.5, 1] GHz
$\tau$	1 s	${\delta }_{m,k}\left(t\right)$	[−30, −14] dBm
$V$	5	${\lambda }_m$	500
$\beta$	0.001	${\xi }_0$	0.9
$K$	50	${\widehat{A}}_m\left(t\right)$	[5, 10] Mbits

[28,29].

We validate the performance improvement of the proposed algorithm by comparing it with two traditional algorithms, which are configured as follows. Baseline 1 is a task offloading algorithm based on the traditional DQN. By using reinforcement learning to selectively offload computing tasks to optimal edge nodes or servers, it optimizes resource allocation and task offloading while minimizing system latency and resource consumption [17]. However, Baseline 1 does not consider the awareness of the load imbalance degree and data volume across different time slots or data offloading splitting ratio selection. Baseline 2 is a cloud-edge-terminal computing resource allocation algorithm based on differential evolution. By combining genetic algorithms with differential evolution, it achieves efficient task offloading and resource scheduling optimization, improving scheduling stability and the accuracy of resource allocation [23]. However, Baseline 2 does not consider adaptive factors. Meanwhile, the simulation parameter settings and optimization objectives of both baseline algorithms are the same as that of the proposed algorithm, but neither consider the load imbalance degree.

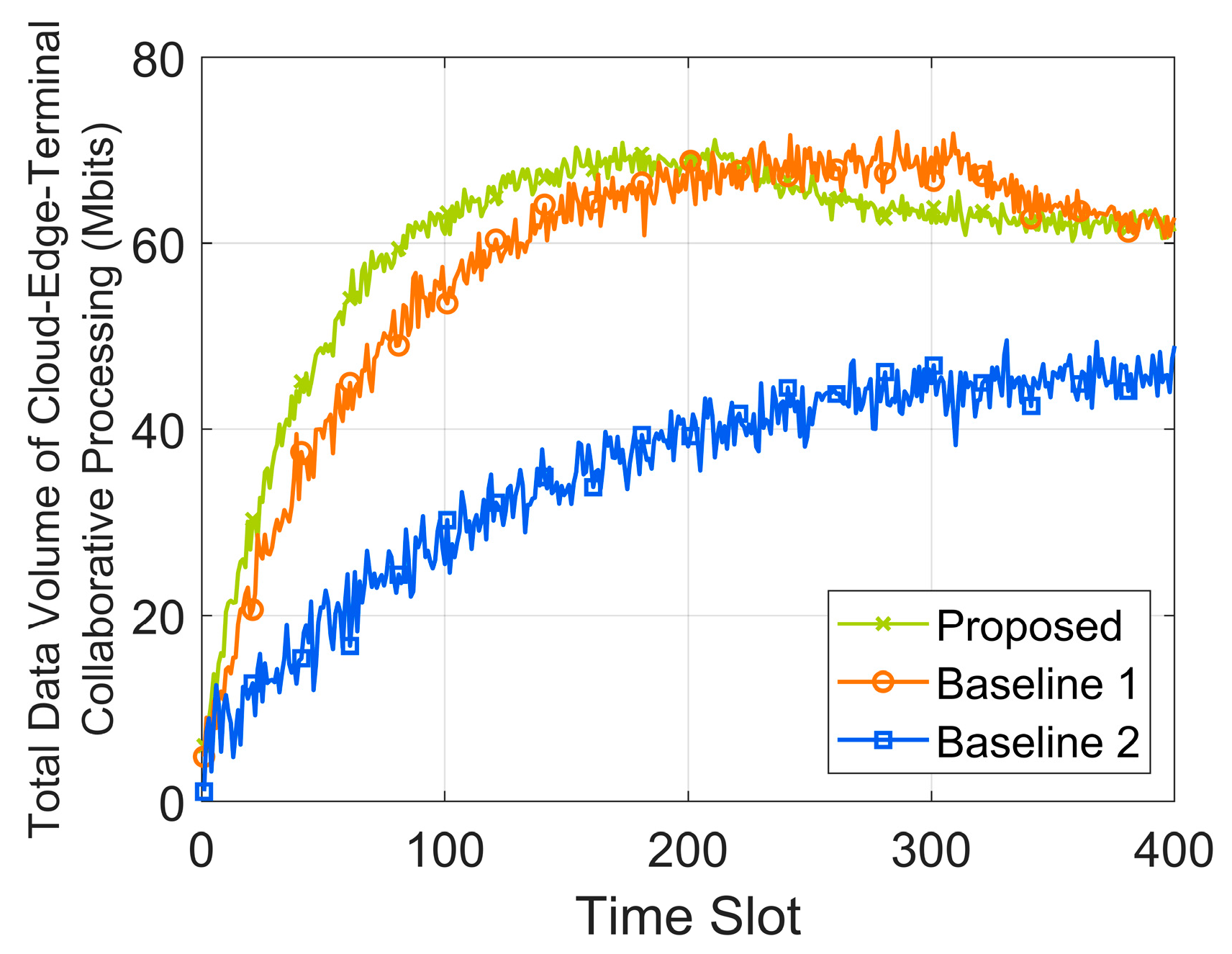
Figure 3 shows the data volume of cloud-edge-terminal collaborative processing over time slots. Compared to Baseline 2, the proposed algorithm improves the total data volume processed by cloud-edge collaboration by 45.7%. The reason is that the proposed algorithm considers the long-term data volume constraints of DTUs and dynamically adjusts strategies based on load imbalance degree across different time slots and virtual queue variations. A penalty function is introduced into the DQN network to maximize the network reward function. Under the premise of ensuring long-term constraints on the total data volume, it jointly optimizes edge server selection, data offloading splitting ratios, and cloud-edge computing resource allocation, thereby maximizing the total data volume.

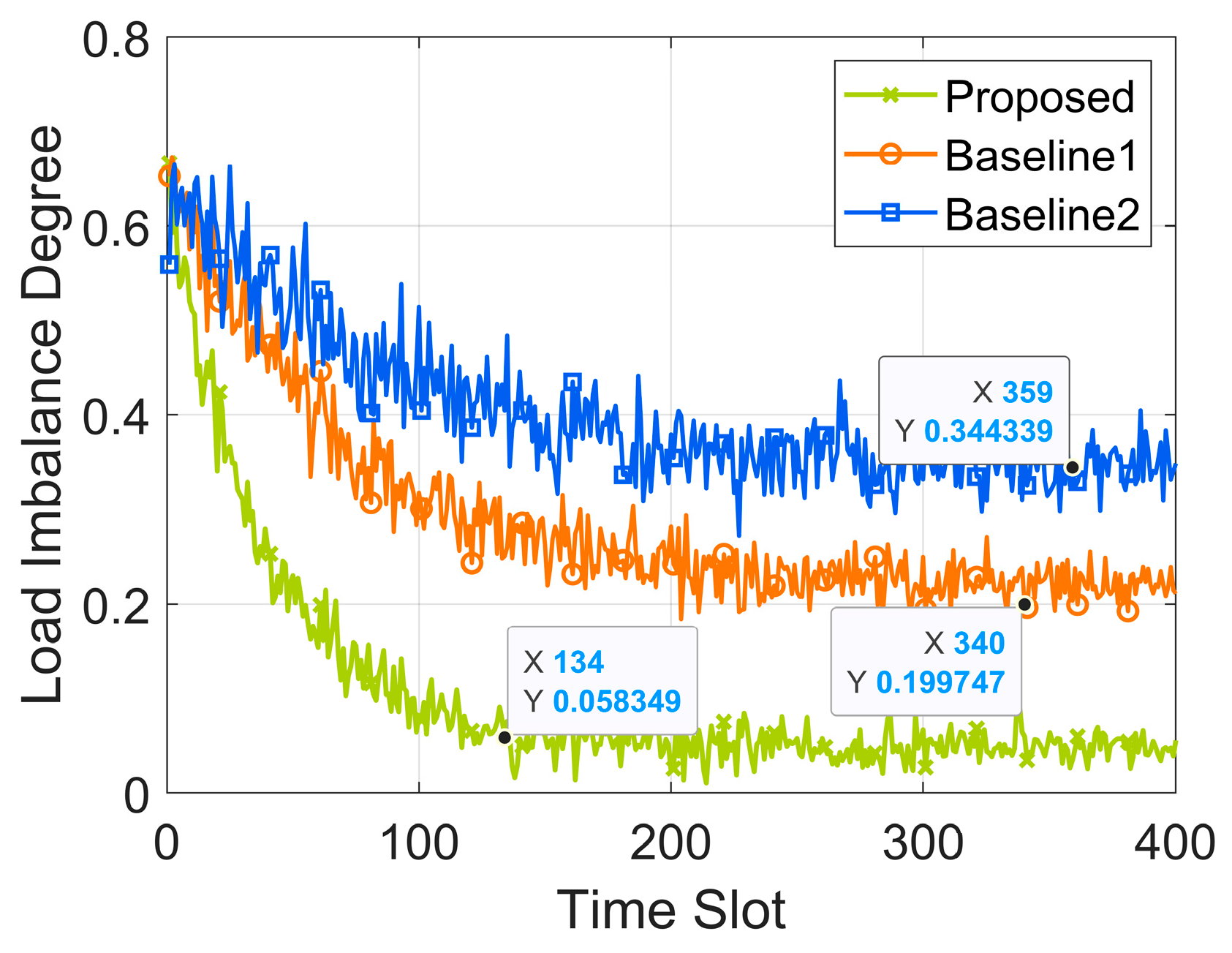
Figure 4 compares the load imbalance degree over time slots. The proposed algorithm demonstrates superior performance in reducing the load imbalance degree, with its average load imbalance degree stabilizing between 0.02 and 0.08. Compared to Baseline 1 and Baseline 2, the average load imbalance degree is reduced by 28.6% and 85.3%, respectively. This is because a penalty function related to load imbalance degree fluctuations is considered during Q-value updates, thereby promptly correcting the learning direction of the DQN agent and improving the stability of the load imbalance degree. Additionally, the proposed algorithm incorporates an adaptive mutation scaling factor in differential evolution, enhancing the global search capability during the initial stages of computing resource allocation policy iteration and avoiding local optima in the later stages.

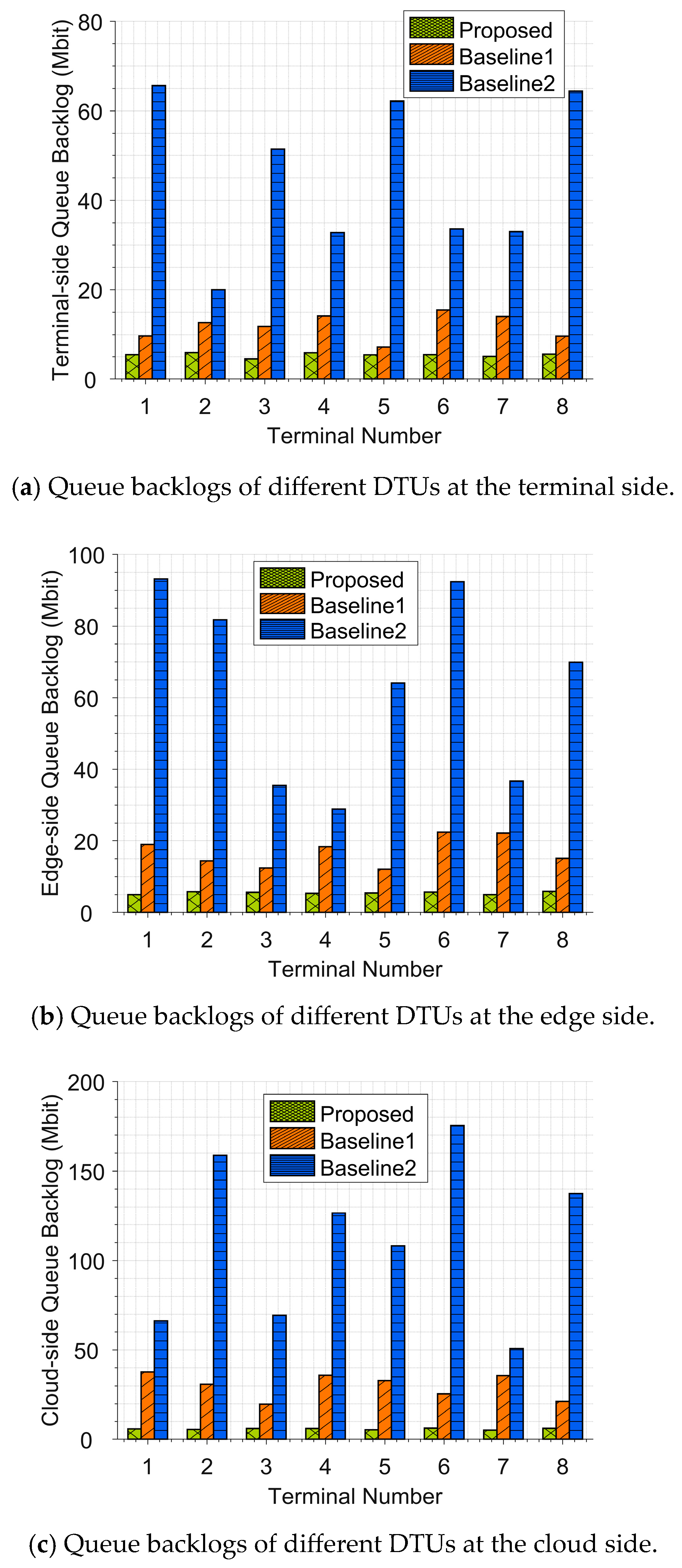
Figure 5 illustrates queue backlogs of different DTUs at time slot 400. The figure indicates that, compared with Baseline 1 and Baseline 2, the proposed algorithm achieves the most stable queue backlog. As indicated by the results in Figure 4, the proposed algorithm achieves optimal performance, ensuring balanced distribution of queue backlogs across DTUs, edge clusters, and the cloud server.

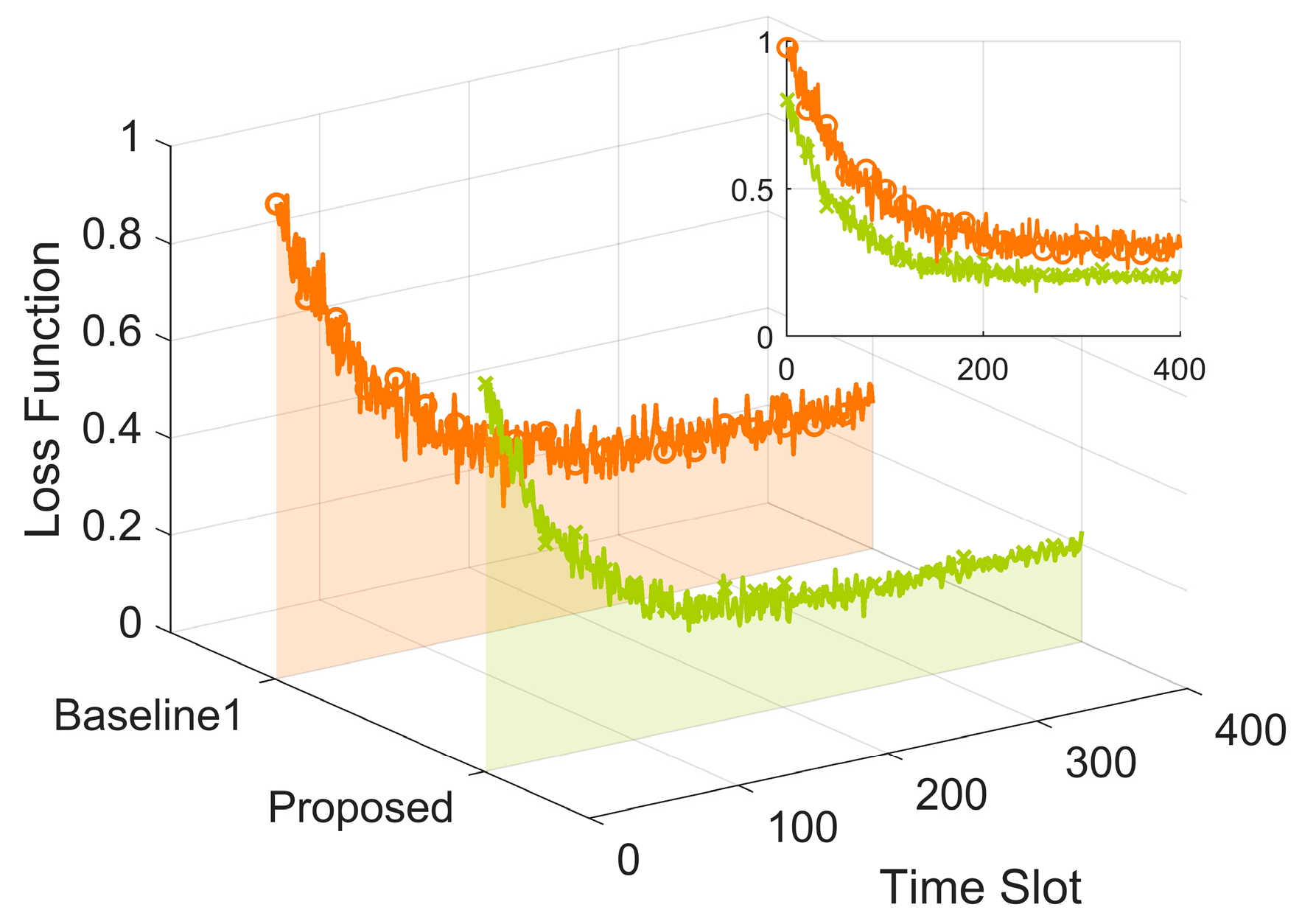
Figure 6 presents the variation in loss function values over time slots. The proposed algorithm demonstrates the fastest convergence speed and the least volatility in loss function values, significantly outperforming Baseline 1. This is attributed to the proposed algorithm’s use of penalty terms to promptly correct the learning direction of the DQN agent, enabling the algorithm to quickly converge to optimal edge server selection decisions and data offloading splitting ratio decisions.

In summary, the comparison of performance indicators of different algorithms is summarized in

Table 2. Comparison of performance indicators of different algorithms.

Performance Indicator (t = 400)	Proposed	Baseline 1	Baseline 2	Performance Improvement vs. Baseline 1, 2
Total data volume of cloud-edge-terminal collaborative processing	61.9 Mb	61.4 Mb	47.8 Mb	0.8%/29.5%
Convergence load imbalance degree	0.05	0.19	0.34	28.6%/85.3%
Average terminal-side queue backlog	5.4 Mb	11.8 Mb	45.4 Mb	54.2%/88.1%
Average edge-side queue backlog	5.5 Mb	17.1 Mb	62.8 Mb	67.8%/91.2%
Cloud-side queue backlog	5.8 Mb	11.6 Mb	30.0 Mb	50.3%/80.7%
Convergence speed	211	310	Unconvergence	31.9%/-
Convergence loss function	0.18	0.23	/	21.7%/-

.

Table 3. Comparison of indicators of different algorithms in various scenarios.

Key Metrics (Average)	8 DTUs + 6 Edge Servers	30 DTUs + 15 Edge Servers	50 DTUs + 20 Edge Servers
Total data volume of cloud-edge-terminal collaborative processing	61.9 Mb	174.8 Mb	230.3 Mb
Convergence load imbalance degree	0.05	0.08	0.12
Convergence speed	211	233	251

shows the comparison of indicators of different algorithms in various scenarios. As the scale increases, the average data volume, load imbalance degree, and convergence speed increase approximately linearly without significant performance degradation. This indicates that the proposed algorithm’s load fluctuation penalty mechanism can still work effectively in large-scale nodes. On the other hand, the state dimension of the DQN in large-scale scenarios has expanded from the original “8 × 3 (DTU queue) + 6 × 8 (edge queue)” to “50 × 3 + 20 × 50”. However, through experience replay and target network soft updates, the accuracy of Q-value estimation can still be maintained.

6. Conclusions

To address the issues of inadequate cloud-edge integration, high load imbalance degree, and low efficiency in data processing for DTU edge clusters, we proposed a cloud-edge collaboration-based data processing method for DTU edge clusters. The formulated joint optimization problem was decomposed into a cloud-edge collaborative data offloading subproblem and a cloud-edge computing resource allocation subproblem. The first one is solved by the load imbalance degree and data volume-aware DQN, which can suppress the fluctuation of the load imbalance degree and guarantee differentiated long-term data volume constraints. The second one is solved by adaptive differential evolution, which facilitates deeper exploration of the solution space and accelerates global optimum identification by overcoming the gene overlapping issues. Compared to Baseline 1 and Baseline 2, the proposed method increases the total cloud-edge collaborative data processing volume by 10.2% and 15.4%, respectively, and reduces the average load imbalance degree by 35.1% and 23.7%, respectively.

The proposed algorithm addresses existing issues in DTU edge cluster data processing, such as insufficient cloud-edge integration, high load imbalance, and low processing efficiency. However, its optimization focuses solely on improving data processing efficiency and reducing load imbalance. It does not consider the grid energy management among electrical equipment, nor does it quantify the correlation between computing resource allocation and carbon emissions. In future research, we will develop a coupled grid energy management and carbon-emission model for collaborative edge servers and DTUs. This model will reveal how computing resource allocation affects grid energy management and carbon emissions. We will then improve the DQN algorithm by designing an intelligent reward function. This function will integrate data processing efficiency, energy scheduling strategies, and carbon emissions. A multi-objective electricity-carbon optimization framework will be established. It will enhance the algorithm’s adaptive decision-making under electric-carbon constraints. Ultimately, this will support low-carbon and intelligent distribution network operation.