A New Paradigm for Physics-Informed AI-Driven Reservoir Research: From Multiscale Characterization to Intelligent Seepage Simulation

Abstract

Characterizing and simulating complex reservoirs, particularly unconventional resources with multiscale and non-homogeneous features, presents significant bottlenecks in cost, efficiency, and accuracy for conventional research methods. Consequently, there is an urgent need for the digital and intelligent transformation of the field. To address this challenge, this paper proposes that the core solution lies in the deep integration of physical mechanisms and data intelligence. We systematically review and define a new research paradigm characterized by the trinity of digital cores (geometric foundation), physical simulation (mechanism constraints), and artificial intelligence (efficient reasoning). This review clarifies the core technological path: first, AI technologies such as generative adversarial networks and super-resolution empower digital cores to achieve high-fidelity, multiscale geometric characterization; second, cross-scale physical simulations (e.g., molecular dynamics and the lattice Boltzmann method) provide indispensable constraints and high-fidelity training data. Building on this, the methodology evolves from surrogate models to physics-informed neural networks, and ultimately to neural operators that learn the solution operator. The analysis demonstrates that integrating these techniques into an automated “generation–simulation–inversion” closed-loop system effectively overcomes the limitations of isolated data and the lack of physical interpretability. This closed-loop workflow offers innovative solutions to complex engineering problems such as parameter inversion and history matching. In conclusion, this integration paradigm serves not only as a cornerstone for constructing reservoir digital twins and realizing real-time decision-making but also provides robust technical support for emerging energy industries, including carbon capture, utilization, and sequestration (CCUS), geothermal energy, and underground hydrogen storage.

1. Introduction

1.1. Background: Classical Challenges and Digital Revolution in Reservoir Research

The study of fluid flow and heat transfer within porous media is fundamental to many industrial and environmental applications. One of the most important aspects of this research is the development of oil and gas reservoirs [1], but traditional research tools, such as experimental studies, numerical simulations, etc., have inherent bottlenecks in terms of cost, efficiency, and accuracy [2]. Macrosimulation methods, while simplifying micro-level interactions, are unable to accurately model the multiscale and non-homogeneous nature of reservoirs, especially in fractured media [3]. Furthermore, geological formations often lack explicit scale separation, making classical theories such as homogenization ineffective or inapplicable [4]. This limitation is particularly evident when attempting to characterize reservoir properties under real in situ conditions [2,4]. This challenge becomes even more acute as research shifts to unconventional resources such as shale gas and tight oil [5]. The large number of micro- and nanopores in reservoirs creates a complex multiscale void structure, which triggers unique physical phenomena that are different from conventional predictions [5]. Within such confined spaces, molecular-level interactions between fluids and minerals dominate, giving rise to complex scenarios of non-Darcy flow, slip flow, and phase transitions, which require more precise physical formulations [4]. An accurate understanding of these multiscale, multiphysics transport processes, ranging from molecular competitive adsorption to pore-scale flow, is critical for effective exploration and development of hydrocarbon resources [6].

To address these challenges, the digital revolution, fueled by increased computing power, high-resolution imaging, and the explosion of multi-source data, has led to new ways of conducting research [4]. Purely data-driven models can have drawbacks such as poor generalization or physical consistency, which are addressed by the “physical-data” dual-drive approach [7,8]. Combining machine learning with traditional numerical methods and physically based models is emerging as a new tool to break through existing constraints [1,3]. Using large volumes of information from subsurface measurements and experiments, ML can enhance the level of data analysis, create efficient proxy models, and make predictions more accurate and interpretable [8]. The synergy of training artificial neural networks (ANNs) with physically based feature extraction, for example, can lead to better yield predictions and a deeper understanding of complex reservoir systems [5,7]. This integrated framework is important for connecting data and simulations across different scales and is expected to improve the accuracy of reservoir simulations, increase efficiency, and improve development strategies to address the current low recovery rates of about 25% for shale gas and 5% for shale oil [3,4].

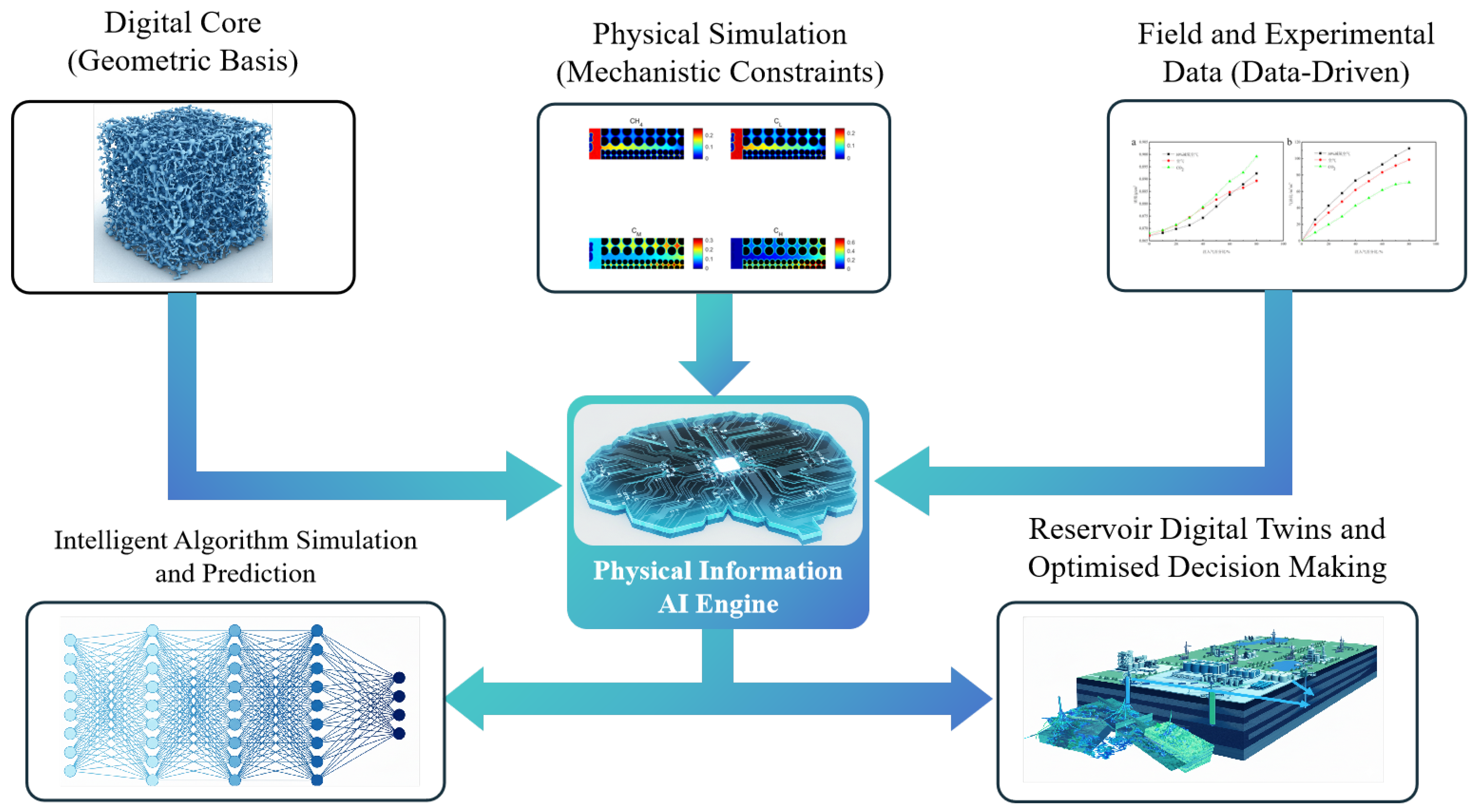
1.2. New Paradigm: The Trinity of Physical Mechanisms Plus Data Intelligence

Traditional reservoir research methods face challenges from two aspects. The first is the approach of modeling based on physical mechanisms alone, which, despite its theoretical rigor, often sacrifices accuracy in practical applications due to the need for a large number of simplifying assumptions and is inefficient due to the complexity of the computational process. The second approach is data-driven artificial intelligence (AI) methods, which can handle and fit large amounts of data well, but the “black-box” nature of the models leads to a lack of physical interpretation [9]. For example, in predicting reservoir porosity and permeability from well logging data, some early artificial neural network models were able to make predictions without a priori knowledge of petrophysics, which was seen as an advantage in some applications but also showed the risk of violating basic physical laws [9].

To break through the above bottlenecks, there is a growing consensus in academia and industry that there is an urgent need to deeply integrate traditional physical modeling methods with advanced machine learning techniques to solve complex scientific and engineering challenges [10]. In this context, a new research paradigm of “Physical Mechanisms + Data Intelligence” has emerged, and a new frontier in the field of fluid dynamics, “Digital Fluid Dynamics” has emerged [11]. For example, Raissi et al. pioneered the incorporation of the Navier–Stokes equations (N-S equations) into a neural network as a priori knowledge, and learned the hidden velocity and pressure fields from the visualization of the flow field alone, which is a typical example of the power of this integration paradigm. The main idea is to use data as the foundation and intelligent algorithms as the core, adding physical information, expert experience, and other a priori knowledge to the overall process of creating a model to create a “data + physics” dual-dynamic model with high modeling flexibility, speed, and accuracy [11]. Such models, built with data + physics dual dynamics, exhibit high flexibility, speed, and accuracy [11]. Earlier studies have attempted to integrate geological and geophysical information using linear regression and neural networks to predict geological parameters such as porosity [9,12,13].

Therefore, in this paper, it is believed that, to achieve end-to-end technological innovation from static reservoir characterization to dynamic seepage prediction, as shown in Figure 1, the key path is the fusion of digital cores (geometrical foundation), physical simulation (mechanism constraints), and AI (highly efficient reasoning). In this trinity framework, digital cores provide the foundation for finely delineating the complex microgeometric structure of the reservoir, numerical simulations based on physical mechanisms provide high-fidelity data and physical-law constraints for AI model training, and AI acts as an efficient inference engine, embedding physical laws into the model architecture or learning process to achieve fast and accurate prediction of complex seepage processes. Crucially, unlike previous studies that predominantly focused on the loose coupling of these elements, where AI serves merely as a static surrogate model, the distinctive advance of the proposed paradigm lies in its closed-loop integration. By unifying these components into an automated generation–simulation–inversion workflow, this framework overcomes the data isolation problem inherent in traditional methods, transforming reservoir characterization from a one-way prediction task into a self-evolving system. This fusion model is seen as the path to the next generation of intelligent reservoir prediction platforms [10].

While the individual concepts of digital cores, physical simulations, and AI have been explored in the literature over the past 5–7 years, existing research has predominantly focused on the loose coupling of these elements. In such established frameworks, AI typically serves merely as a static surrogate model to accelerate specific solvers, which suffer from two main limitations: (1) poor generalizability, as models often require retraining when physical parameters change (the zero-shot challenge); and (2) a lack of rigorous physical consistency, leading to the black box problem. The novelty of this work lies in systematically defining a shift from this loose coupling to a deep fusion paradigm. Unlike previous reviews, this paper clearly articulates the methodological evolution from simple surrogates to physics-informed neural networks and, crucially, to neural operators that learn the solution operators themselves. Furthermore, we propose an automated generation–simulation–inversion closed-loop workflow that transcends traditional unidirectional prediction. This closed-loop system integrates geometric characterization, mechanism constraints, and intelligent reasoning to solve the data isolation bottleneck, offering a clearer technical pathway for the next generation of intelligent reservoir research.

2. AI-Enabled Multiscale Intelligent Characterization of Digital Cores

2.1. Limitations of Traditional Digital Core Reconstruction Techniques

Obtaining accurate three-dimensional models of the pore structure of reservoir rocks is the basis for subsequent flow simulation and physical property prediction, and pore-scale modeling is one of the core techniques [11,14]. High-resolution imaging, such as X-ray micro-computed tomography (micro-CT), is generally required to obtain the internal microstructure of rocks [15]. However, conventional digital core construction methods have inherent shortcomings in terms of efficiency, accuracy, and representativeness.

A central challenge lies in established multiscale imaging techniques, which suffer from a trade-off between resolution and the field of view (FOV) [16]. Finding an appropriate compromise between computational cost and model retention is particularly difficult for geological bodies such as carbonates with complex pore textures and heterogeneity across multiple scales [16]. High-resolution imaging (e.g., FIB-SEM) can reveal minute pore-throat details, but its field of view is extremely small, while micro-CT techniques, which are capable of obtaining centimeter-scale representative volumes (REVs), are often insufficiently resolved to capture the critical pore-throat channels that control fluid flow [17]. Such limitations make flow simulations performed in digitized cores on a single, small volume only representative of that particular portion of the rock volume and limit their scalability to real cores or larger scales [17].

In addition, traditional image processing and numerical reconstruction processes are inefficient and have a limited ability to characterize cores under complex physicochemical conditions. For example, the process of creating a grid model from a CT image can be cumbersome, and researchers have been searching for more general yet easily implemented approaches [18]. In dense reservoirs such as shales, it is critical to accurately identify pore types, although traditional analysis is limited by the low resolution of mineral maps [19]. More importantly, it is difficult for static imaging techniques to directly capture and characterize the dynamic changes in pore structure that occur under actual reservoir temperature and pressure conditions or during fluid-rock interactions (e.g., dissolution or precipitation of minerals) [20]. When modeling CO₂ sequestration or acidification, for example, the reaction between fluids and calcite cement constantly changes the pore space, and accurately predicting the impact of this process on macroscopic parameters such as permeability places very high demands on the fidelity of the initial pore geometry model [20]. Together, these limitations drive the need for smarter and more efficient digital core characterization techniques.

2.2. AI-Driven Innovation in Core Characterization: From Image Processing to Physical Reality Reconstruction

AI, particularly deep learning, is driving a paradigm shift in digital core characterization, i.e., from labor-intensive, semi-automated analyses to efficient, accurate, physically consistent automated workflows. It not only improves efficiency, but also radically enhances the ability to characterize the non-homogeneity of reservoir rocks with complex 3D geometry and topology. The key advances are mainly in three areas—intelligent segmentation, generative modeling, and super-resolution reconstruction.

2.2.1. Intelligent Segmentation and Analysis: 3D-CNN Applications and Topological Challenges

Unlike traditional methods that can only process one 2D slice at a time, 3D-CNN, with its 3D convolutional kernel, can learn spatial dependencies and complex topological features directly from inside the voxel model of a rock [21]. These features, which are critical for permeability, such as pore connectivity, tortuosity, and throat distribution, are not comparable to 2D networks [21]. Among the many network architectures, the encoder–decoder structure represented by 3DU-Net performs particularly well, which is capable of understanding the global context of an image while preserving high-resolution local details [22]. This intelligent analysis relying on 3D features forms a solid foundation for the later creation of highly accurate predictive models of macrophysical attributes such as permeability.

The two core challenges for the application of 3D-CNN in segmentation tasks are as follows: first, the computational resource bottleneck—the memory consumption and computational load of 3D-CNN grow cubically with the size of the input voxels [22]. The amount of data in a high-resolution digital core sample (e.g., 1024³ voxels) usually far exceeds the memory limit of a typical graphics processing unit (GPU), which prompts researchers to use a patch-based approach for model training and inference. Second, the topological inconsistency caused by the patch-based approach—although the patch-based strategy removes the computational bottleneck, it cuts off the overall structure of the core, and the model achieves the high accuracy of pixel-level segmentation within each individual patch, but this does not guarantee that the pores or throats across the patch boundaries are physically connected. This paradox is critical because studies have shown that even when the accuracy of voxel-level segmentation of a model exceeds 95%, the inferred pore connectivity and permeability can still deviate by 1–2 orders of magnitude from the ground truth [23]. Specifically, a single topological artifact (e.g., a falsely disconnected throat) in a critical flow path can reduce the computed permeability by over 90%, rendering pixel-wise metrics meaningless [24]. Therefore, asserting ‘high-fidelity’ characterization solely based on image segmentation is insufficient; it is imperative to introduce uncertainty quantification (UQ) to assess the probability of these topological errors [25]. This topological inconsistency can lead the model to misjudge the effective pore network and the preferred channel for seepage. For example, treating isolated pores as effective pore space [26] or over-segmenting the pore space can lead to large and unquantifiable errors in predicting macroscopic properties like permeability [21].

2.2.2. Generative Reconstruction: Application of GAN and Physical Fidelity Challenges

Generative models, especially generative adversarial networks (GANs), have opened up a new path for digital core reconstruction as a viable option for reconstructing pore-scale models [27,28]. These deep learning methods are able to create digital core models that closely resemble real ones in terms of statistical properties with limited 2D or 3D data [29]. The key mechanism is that a generator network learns to create 3D pore structure voxel models from random noise or low-dimensional data (e.g., 2D slices), while another discriminator network learns the characteristics of real rock samples and “evaluates” the authenticity of the generators. The other discriminator network learns the characteristics of the real rock samples, then “evaluates” the realism of the generators and guides the generators in the direction of improvement [27,30]. Using this adversarial training, the model can produce synthetic samples that are very close to real cores in terms of statistical and physical properties such as porosity, pore size distribution, multipoint connectivity and even permeability [29,31,32]. This capability is valuable both for expanding CT imaging datasets, which are scarce and costly to acquire [33,34], and for generating rock models with specific attributes based on user-given a priori information such as porosity [28]. It is worth noting that while recently emerged generative models, such as diffusion models, have demonstrated superior capabilities in high-quality digital rock reconstruction and property estimation [35,36], they are not adopted in this paradigm. This decision is driven by the specific engineering requirement for computational efficiency. Diffusion models typically rely on iterative denoising processes to generate a single sample, which leads to prohibitive computational costs when reconstructing large-scale 3D porous media (e.g., ${512}^3$ or ${1024}^3$ voxels). Even recent attempts focusing on 3D reconstruction often require complex latent space mappings to manage these dimensions [37]. In contrast, GANs enable one-shot generation, offering orders-of-magnitude faster inference speeds essential for high-throughput reservoir characterization workflows. Furthermore, advanced GAN variants (such as WGAN-GP) employed in this study effectively mitigate mode-collapse issues, ensuring a balanced trade-off between geometric fidelity and computational feasibility.

However, despite their power in mimicking the texture and statistical distribution of rocks, GANs still face two major problems, which directly affect the physical reliability of the simulation results.

The first is the topological infidelity (TI) challenge. For GANs, the structures they generate should have physically appropriate topological features, such as the connectivity of the pore network [31]. Many studies have used the Eulerian characteristic number, pore throat geometry, and connectivity as key metrics when evaluating generative models [28]. This is because a topologically flawed model, even if its voxel-level statistics such as porosity are correct, may contain a large number of unrealistic isolated pores or artificially created “seepage shortcuts,” resulting in predictions of macroscopic seepage properties, such as permeability, that are far from the real situation [29]. It has been pointed out that traditional quantitative assessment metrics tend to flatten spatial data into vectors, thus ignoring the crucial spatial and topological relationships in the data [33]. Therefore, significant effort has focused on improving the architecture of GANs, such as adding new loss functions or network modules, to allow GANs to better detect and reproduce 3D pore structures, and to ensure that the generated samples have comparable connectivity and physical transport properties as real rocks [27,29,38].

Secondly, there is the risk of mode collapse. When the geological application scenario contains inhomogeneous reservoirs with many different lithologies, it is difficult for the GAN model to learn all the rock features, and it will only generate the most common rock structure or rock structures [30]. For shales or complex carbonates with complex structures, high anisotropy, and obvious fractures, GAN and its variants still face challenges in generating satisfactory pore structures [27,28]. This inability to generate less representative structures (e.g., fracture networks, dissolution pores, etc.) that have a significant impact on overall fluid flow greatly limits the generalization ability of the model and the reliability of geological applications [30]. Therefore, ensuring that the generated model can capture and reproduce the geological diversity of the whole reservoir is a problem that must be solved to make the approach practical.

Regarding the selection of generative architectures, recent advancements have demonstrated that diffusion models offer superior capabilities in capturing complex pore structures and enhancing image resolution compared to traditional methods [35,36]. For instance, Naiff et al. introduced controlled latent diffusion models that achieve state-of-the-art reconstruction quality for 3D porous media [37]. However, these diffusion-based approaches typically require iterative denoising steps, which impose significant computational costs for real-time applications. To balance generation quality with the inference speed required for the closed-loop system, this paradigm retains the generative adversarial network framework due to its efficient one-shot generation capability. To specifically mitigate the ‘mode collapse’ issue inherent in GANs—especially for heterogeneous lithologies—advanced variants such as the Wasserstein GAN with gradient penalty (WGAN-GP) are employed. This approach stabilizes the training dynamics and ensures that the generator captures the full diversity of topological features, offering a practical trade-off between the high fidelity of diffusion models and the computational efficiency required for engineering workflows.

2.2.3. Super-Resolution Reconstruction: Trade-Off Between “Fidelity” and “Illusion” in Scale

Deep learning-based super-resolution (SR) techniques, especially convolutional neural network (CNN)-based architectures such as EDSR, U-Net, etc., aim to overcome the inherent trade-off between the field of view (FOV) and resolution in current imaging technologies, thereby addressing this problem [39,40,41]. In practice, obtaining higher resolution 3D core images implies a small FOV, and large-FOV scanning to increase the field of view will inevitably result in a loss of resolution, which limits the characterization and analysis of heterogeneous and multiscale pore systems [42,43].

The SR technique digitally enhances the quality of LR images by learning the mapping relationship from low-resolution (LR), large-field-of-view images to high-resolution (HR), small-field-of-view images [41,44]. Its greatest value is the ability to recover the details of microscopic orifices and throats that are blurred or even missing in LR images, but are important for controlling fluid flow, providing a better database for subsequent image segmentation and flow simulation [39,45]. For example, SR techniques have been applied to enhance shale FIB-SEM images, enabling clear observation of pores smaller than 10 nm and providing support for more accurate pore network modeling (PNM) [46]. AI models not only improve the resolution of individual imaging modes but also enable conversion between different imaging modes, e.g., from low-contrast transmission X-ray microscopy (TXM) images to high-contrast focused ion beam-scanning electron microscopy (FIB-SEM) images in three dimensions. This capability makes it possible to use non-destructive imaging data to perform accurate flow simulations [47]. These techniques allow the development of multiscale models of fluid dynamics from pore to core [43].

However, the application of SR techniques also faces a core challenge—the balance between “fidelity” and “illusion”. Essentially, SR involves “guessing” missing details based on existing information. These microstructures “hallucinated” by the model may be visually very similar to real high-resolution images, even appearing indistinguishable from real images. These model ‘hallucinated’ microstructures may visually resemble real high-resolution images and even excel in metrics such as edge sharpness, but their physical accuracy cannot be fully guaranteed. Studies have shown that a decrease in image resolution leads to an average enlargement of pore and throat dimensions, which can grossly overestimate single-phase permeability [48]. Once an SR model mistakenly “creates” a connectivity channel at one location, or “fails to recover” the fact that a connectivity channel actually exists, even small topological differences can lead to differences in predicted permeability of several times or even orders of magnitude. Interestingly, however, it has also been found that images generated by SR, although differing in porosity and other metrics, may be more accurate than the original LR images in predicting fluid flow through them [48], which suggests that the distinction between fidelity and physical validity can be subtle. There is a complex balance between “fidelity” and “physical validity”.

Due to the “illusion” problem, the validation of SR models cannot be conducted by visual similarity or traditional image quality metrics (e.g., PSNR, SSIM), which are not strongly correlated with the assessment of the physical properties of rocks [45]. Therefore, the research consensus in the field is shifting toward a more rigorous verification of physical realism, which makes it necessary to put SR-generated digital cores through a complete analytical process by extracting their pore-network topological parameters and directly performing numerical simulations of single-phase or multiphase flow (e.g., the lattice Boltzmann method). These simulations enable correlation of computed macrophysical properties such as porosity, permeability, and macroscopic capillary pressure curves with experimental measurements. The resulting macroscopic physical properties, such as porosity, permeability, and capillary pressure profiles, are compared with experimental measurements or results from high-resolution image simulations [47,48]. This ensures that the microstructure reconstructed by the SR model is physically reliable and faithful, which is the biggest difficulty and key to moving this technique from qualitative image enhancement to reliable quantitative analysis.

Although standard metrics like PSNR and SSIM are widely used, they are fundamentally insufficient for reservoir characterization because they quantify pixel-wise or structural differences rather than the topological connectivity of pore networks, which dictates fluid flow [45]. Consequently, a high PSNR score does not guarantee accurate permeability predictions. Therefore, the research consensus in the field is shifting toward a more rigorous verification of physical realism. This requires integrating SR-generated digital cores into a complete analytical process by directly performing numerical simulations of single-phase or multiphase flow (e.g., the lattice Boltzmann method). Specifically, the computed macrophysical properties such as porosity, permeability, and capillary pressure curves must be strictly compared with experimental measurements or results from high-resolution ground-truth simulations [47,48]. This ensures that the microstructure reconstructed by the SR model is physically reliable and faithful, which is the critical step in moving this technique from qualitative image enhancement to reliable quantitative analysis.

3. Physical Mechanism-Driven Seepage Modeling: Sources of Constraints

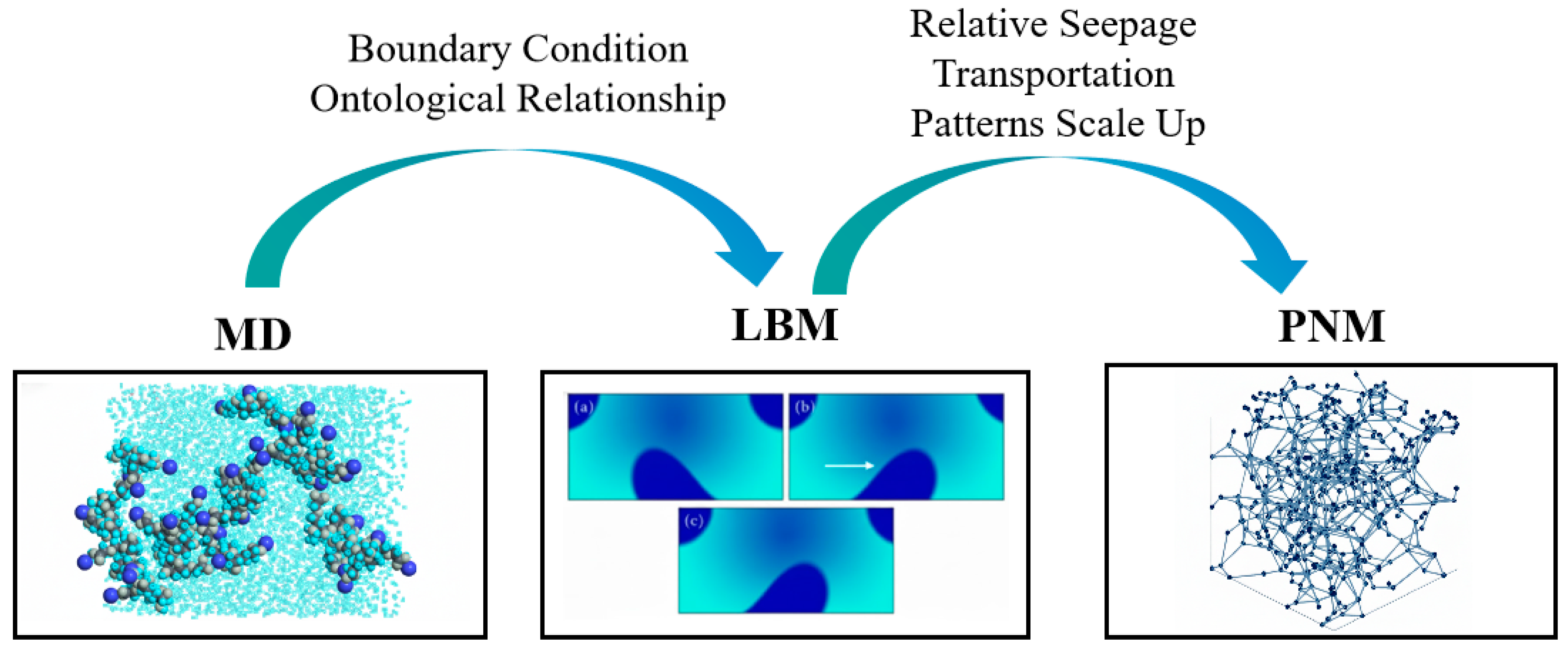
3.1. Core Modeling Approach: From Molecules to Cores

To accurately portray the complex physicochemical processes in reservoirs across a variety of spatial and temporal scales, researchers have created a multiscale simulation methodology from microscopic molecular interactions to macroscopic core seepage [49]. This bottom-up approach, as shown in Figure 2, is rooted in the main simulation methods at each scale, providing solid mechanistic constraints for physics-informed AI models.

At the most microscopic level, molecular dynamics (MD) is used to probe fundamental physicochemical mechanisms at the nanoscale [51]. MD simulations can reveal fluid–solid interactions at the atomic and molecular levels, including the selectivity of oil and gas adsorption on pore walls composed of different materials (e.g., organic matter and inorganic minerals) in tight reservoirs such as shale [52], the evolution of fluid phase behavior, and the effect of ion aggregation in brines in high-salinity formations on oil–water–rock three-phase wettability, among others [53]. These insights gained from the molecular level provide essential constitutive relationships and boundary conditions for mesoscopic and macroscopic scale models, such as the determination of slip lengths and adsorbed layer thicknesses for nanoconfined fluids [52]. The intermediate level connecting the molecular scale and the continuous medium scale is the lattice Boltzmann method at the mesoscopic level, which is currently the main method used to simulate fluid flow within the complex geometries of porous media [54].

The lattice Boltzmann method (LBM) is an intermediate method between molecular dynamics and conventional computational fluid dynamics (CFD), which allows the flow field to be directly simulated on a digital core. It therefore provides a practical way to solve [55]. It can easily simulate complex pore-solid wall boundaries and capture non-Darcy flows such as slip flow and diffusion. And the Chapman–Enskog multiscale extension can restore its governing equations to the macroscopic Navier–Stokes equations, making the LBM physically consistent [54]. LBM has been widely used to simulate complex multiphase flow phenomena in reservoirs, such as the snap-off phenomenon during gas–liquid displacement [56], and the effects of wettability and contact angle hysteresis on the dynamic behavior of droplets [56,57], oil–water phase separation and transport within pores, etc. It can also be coupled with other modules such as heat transfer and chemical reactions for simulating complex processes such as geothermal mining or evaporative cooling in porous media [58].

To improve the simulation efficiency and link to the macroscopic Darcy’s law, the pore network model is then used as a bridge from microscopic simulation to core-level seepage analysis [42]. It simplifies the complex 3D pore space into a network containing pore bodies (nodes) and connections (throats) [55]. This simplification makes it possible to reduce the computational cost considerably, thus allowing effective modeling of seepage properties at larger scales, such as the core level, but the effectiveness of the predictions made by the PNM is entirely dependent on two important factors: firstly, whether the topology of the pore network used as input is accurate or not, and secondly, whether the physical rules of the flow assigned to the pore and the throat are realistic and reliable [42]. For example, whether jamming occurs in the throat, how the fluid advances at the leading edge, etc., all of these need to be supported by physical results obtained from more fundamental LBM or MD simulations, so the value of the PNM lies in its ability to efficiently scale up complex physical laws (non-Darcy effect, relative permeability in multiphase flow) obtained from microscale simulations and then predict the macroscopic seepage parameters.

3.2. Physical Constraints, Realization Paths, and Challenges

When constructing a physics-informed AI model, the key to success is how to accurately incorporate multiscale physical mechanisms into the model, which involves three challenges—cross-scale coupling, unconventional seepage modeling, and scale upgrading.

The creation of a coupled molecular dynamics–lattice Boltzmann method–pore network model simulation system that links the molecular, pore, and macroscopic scales is a major technical challenge today. For example, at the microscopic level, by comparing molecular dynamics, LBM, and computational fluid dynamics, researchers have found that molecular-scale effects in some cases (e.g., capillary filling processes) can lead to results that differ from those of continuum models. This finding reflects the necessity of using MD simulations to determine parameters such as nanopore wall slip length, wetting angle, and other interfacial properties and to use these parameters as boundary conditions for the LBM [59]. On this basis, LBM can accurately simulate the complex fluid distribution and flow behavior in pores [60,61]. However, LBM is difficult to apply at larger scales due to its high computational cost. Thus, a combination of LBM and the computationally fast pore network model has been proposed [62]. That is, LBM is first used to simulate individual pore-throat structures extracted from digital cores (e.g., scanning electron microscope maps) and to calculate their key flow parameters, such as critical capillary pressure and phase permeability–saturation relationships, which are used as inputs to the PNM to efficiently simulate flow on a larger scale [62].

For unconventional reservoirs such as shale oil and gas, the traditional Darcy’s law has revealed obvious shortcomings, and it is necessary to develop a set of non-Darcy seepage equations that can accommodate a series of complex physical processes, such as stress sensitivity, boundary slip, adsorption and desorption, and multi-component diffusion [61,63]. When studied at the pore level, it can be recognized that the topology of the fluid (like oil droplets or clusters in isolation) plays a crucial role in the macroscopic behavior of multiphase fluids. For example, using fast X-ray microtomography and LBM simulations, it has been found that the mobilization of captured non-wetting-phase oil clusters can make a significant contribution to the total flux and that fluid topology can undergo extremely large changes even when the overall system remains at a constant saturated state, which is one of the fundamental reasons for hysteresis. This suggests that in macroscopic models, in addition to saturation, parameters describing phase connectivity—such as interfacial area and the Euler characteristic number—must also be taken into account. Moreover, pore-scale direct simulations show that, at high flow speeds, capillary pressure exhibits a pronounced dynamic effect—deviating from the static capillary pressure–saturation curve—and that this dynamic effect is sensitive to wettability and should be incorporated into a more accurate flow model [64]. Regarding the specific governance of unconventional reservoirs, the PINN formulation in this paradigm explicitly embeds multi-physical mechanisms beyond standard fluid mechanics. To address the slip effects in nanopores, the standard no-slip boundary condition is replaced by the Maxwell slip model or second-order slip boundary conditions in the loss function. For adsorption phenomena in organic-rich shale, a source/sink term governed by the Langmuir isotherm is integrated into the mass transport PDE. Additionally, for scale-up simulations, non-Darcy flow characteristics are captured by incorporating the Forchheimer inertial terms (or the Barree–Conway model) into the momentum conservation constraints, ensuring that the AI model accurately reflects the complex flow behaviors typical of unconventional resources.

How to smoothly “scale-up” nano- or pore-scale physical discoveries to the core or even reservoir scale is currently a major methodological bottleneck, which is directly related to whether the physical constraints can be accurately conveyed in macroscopic models [63,64]. The traditional Darcy-law extension model has a number of shortcomings when simulating immiscible two-phase flow, and one improvement is to create new upscaling equations using pore-scale flow patterns (i.e., topological distributions of the flow phases). It has been shown that classical Darcy’s law only holds under certain operating conditions, and for modes like clustered flow (ganglia flow), additional terms must be introduced [63]. Applying parameters such as dynamic capillary pressure profiles calculated from pore-scale models (e.g., LBM or direct simulation based on SEM images) to reservoir-scale numerical simulators allows for accurate transfer of physical information.

4. The Core Engine: A Fusion Paradigm and Technology Path for Physics-Informed AI

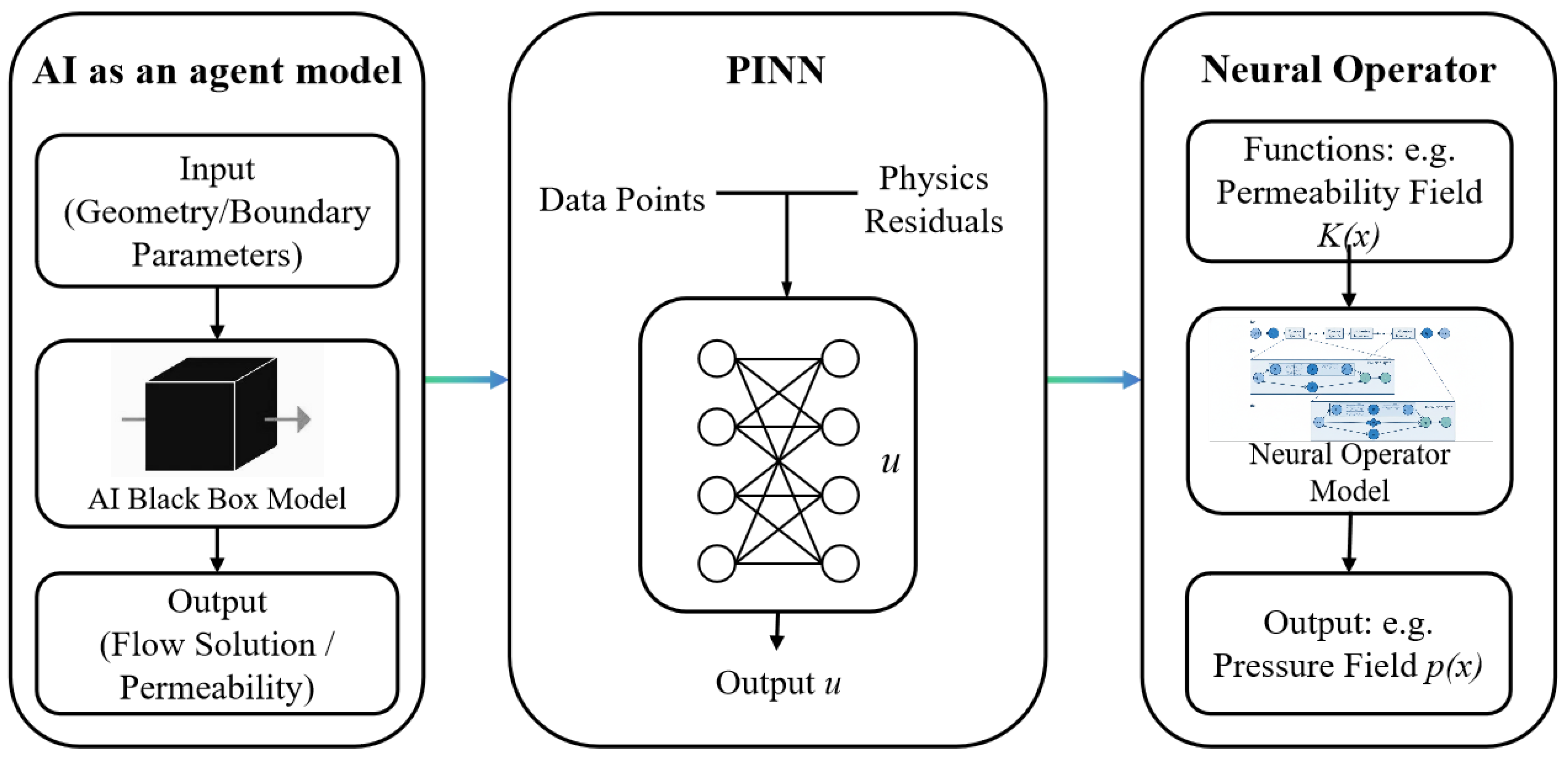
4.1. Methodological Evolution: From Substitution to Fusion to Operator Learning

The methodological evolution of physics-informed AI in reservoir modeling and seepage simulation, as shown in Figure 3, follows a clear path from efficient substitution to mechanism fusion to operator learning. Early research treated AI as an efficient surrogate model (surrogate model) for replacing computationally expensive physical simulations [65]. Subsequently, techniques such as PINNs have incorporated the laws of physics as strong constraints in training, allowing for the initial fusion of data and mechanisms [66]. However, the limitations of PINNs in dealing with challenging problems such as parameter space exploration and real-time optimization have led to a shift toward the neural operator paradigm, where the goal is to learn the solution operator of a physical process itself, which is expected to revolutionize the role of traditional numerical solvers.

4.1.1. Phase 1: AI as an Efficient Agent Model

In the original paradigm, AI models were trained to learn end-to-end mappings between “inputs and outputs” of complex physical systems, thus avoiding the large computational resources required to solve complex physical equations [68]. The typical workflow is to generate a large database of image-properties or parameter-solutions using high-fidelity numerical simulations (e.g., LBM or CFD) [69,70]; this database is then used to train deep neural networks, and convolutional neural networks and their variants (e.g., U-Net, ResNet) are the preferred architectures due to their strong image processing capabilities [71]. Researchers have utilized this approach to rapidly predict permeability [34,71,72], and even predict fracture physical parameters [73], as well as to simulate the dynamics of underground hydrogen storage [74,75], competitive CO₂ adsorption [76,77], and unsteady heat transfer processes [78]. The key advantage of this paradigm is its extremely high computational efficiency, with predictions thousands to millions of times faster than conventional simulations [79], providing a fast means for sensitivity analysis, uncertainty quantification, and scenario optimization [75].

4.1.2. Phase 2: Deep Integration of Data and Physical Mechanisms with PINNs

Although the agent model has made an orders-of-magnitude leap in computational efficiency, it is disconnected from physical principles; thus, it may produce solutions that do not conform to physical laws, and the model’s performance also relies heavily on a large amount of labeled data. To overcome the above problems, physics-informed neural networks have been developed. The basic idea of PINNs is to treat the partial differential equations (PDEs) of the control system as physical constraints, which are directly embedded into the loss function of the neural network [1]. The loss function of the neural network [80,81]. By minimizing a combined loss function that encompasses the data-fitting error and physical residuals (i.e., the degree of violation of the governing equations, boundary conditions, and initial conditions), the neural network is guided to learn a solution that satisfies both the data model and the laws of physics [79]. Specifically, the physical constraints derived from MD or LBM are encoded into the AI models through a hybrid mechanism consisting primarily of loss terms and data-driven inductive bias.

Firstly, in the physics-informed neural network modules, governing equations (e.g., Navier–Stokes equations recovered from LBM) are explicitly incorporated as regularization terms in the loss function:

$${\mathcal{L}}_{total}={\mathcal{L}}_{data}+\lambda {\mathcal{L}}_{physics}$$

(1)

where ${\mathcal{L}}_{data}$ represents the supervised loss from ground truth data, ${\mathcal{L}}_{physics}$ denotes the residuals of the governing PDEs (ensuring the gradients satisfy physical laws), and $\lambda$ is a weighting coefficient used to balance the data fitting and physical consistency.

Secondly, for neural operators (e.g., FNO), the physical constraints are implicitly encoded through architecture bias and high-fidelity training data. By training on massive datasets generated by MD/LBM simulations, the network architecture learns the underlying solution operators and inherently respects the conservation laws embedded within the data distribution. Such an approach of integrating data-driven and physical mechanisms has great potential to significantly improve model generalization and reduce data dependence when simulating single-phase flow in porous media [82], turbulence [83], and gas–liquid two-phase flow [84]. However, applying PINNs to complex scenarios such as multiphase flow in reservoirs or fractured media is not as simple as putting the standard Navier–Stokes equations into the loss function, but instead requires researchers to carefully design the network structure and loss function according to the specific physical challenges.

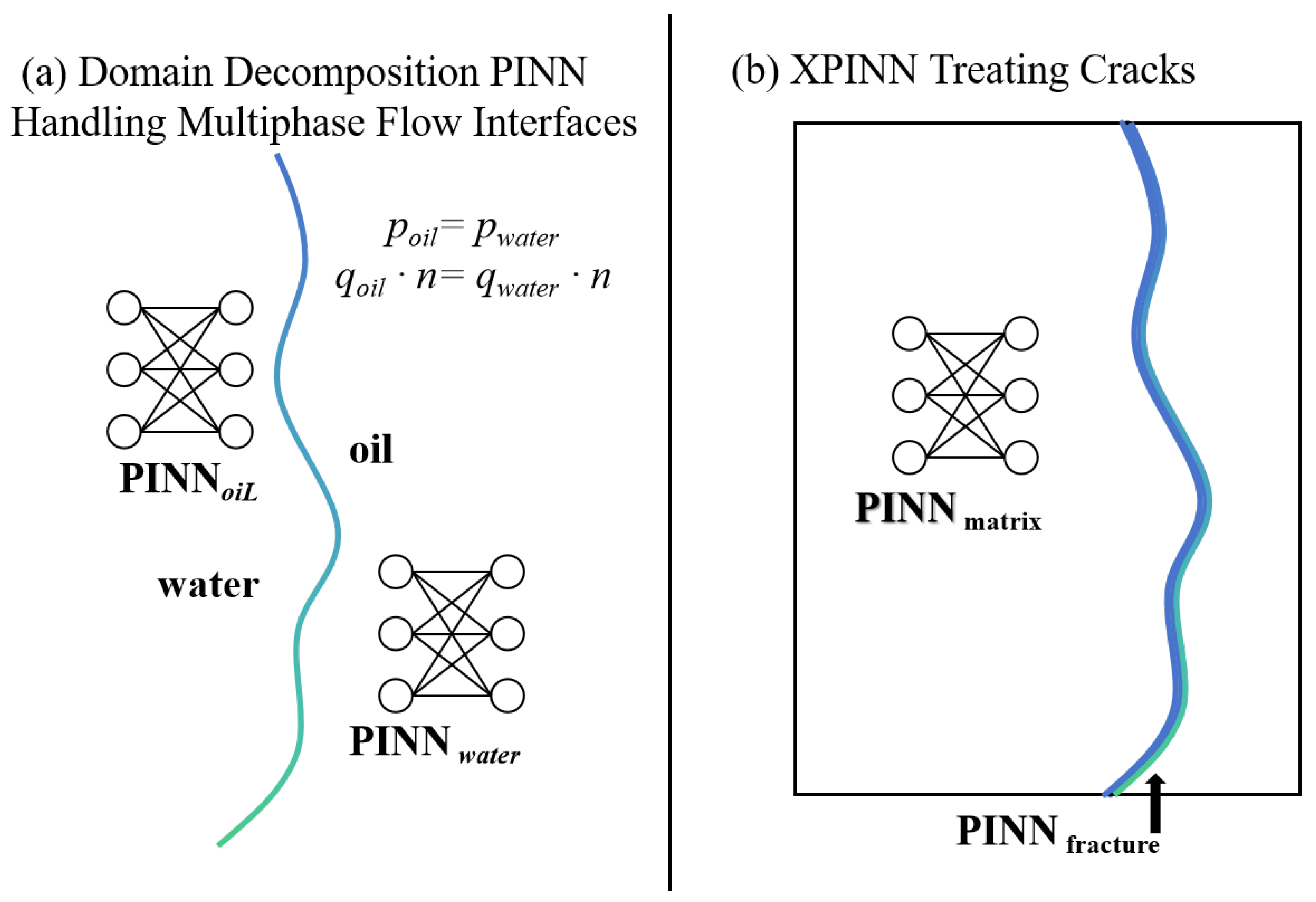
• Advanced applications and challenges for multiphase flow problems:

For problems such as oil–water two-phase flow, there must be multiple physical residual terms in the loss function of the PINN, such as losses corresponding to the total pressure equation and the saturation equation, respectively. At the oil–water interface, there is a sharp discontinuity in the saturation field and a jump in capillary pressure, and it is difficult for standard, essentially continuous, neural networks to learn this strong discontinuity directly. To address this challenge, researchers have explored various strategies, one of which is a domain-decomposition PINN that dynamically divides the computational domain into oil-phase and water-phase regions, as shown in Figure 4. For each region, a separate PINN is trained, and at the boundary shared by the two networks (i.e., the phase interface), pressure continuity and flow continuity are enforced through the loss function. This coupling can better cope with interface discontinuities, but it requires the algorithm to accurately and dynamically track the position of the phase interface.

• Advanced applications and challenges for cracked media problems:

Cracks are discontinuities, and the flow laws of fluids in crack networks and matrix systems are obviously different; thus, standard neural networks with continuous function characteristics cannot directly represent the discontinuous behaviors triggered by geometrical and physical mutations. To address this problem, researchers have proposed corresponding solutions:

• Extended PINN (eXtended PINN, XPINN): This method divides the whole simulation region into matrix and crack subdomains, deploys a regular PINN in each matrix subdomain, and uses a low-dimensional PINN to specifically address flow in the cracks. Finally, with the help of a coupling term describing fluid exchange between the matrix and cracks in the total loss function (the form of the coupling term can be found in classical models such as Warren–Root), the two systems are coupled.
• Physical knowledge-enhanced input features: This strategy modifies the input layer of the network by adding spatial coordinates (x, y), as well as one or more a priori features describing geometrical discontinuities, such as a “distance function to the nearest crack,” which help the network identify whether a point is inside the crack, close to it, or in the matrix region away from it. This a priori knowledge can help the network distinguish different physical behavior patterns inside the crack, near the crack, and in the matrix region away from the crack, which can be regarded as an implementation of physics-guided neural networks (PgNNs) [66].

Jang, et al. also used domain decomposition in their treatment of turbulence on porous media to distinguish between porous and non-porous regions, which allows the reconstruction of complex flow fields due to flow mutations with less training data [83].

Despite these advanced applications, PINNs still encounter serious challenges in problems such as complex reservoir simulation. First, it is difficult to train PINNs. The loss function of a PINN consists of multiple objectives (physical residuals, boundary/initial conditions, data points), and balancing the weights of each objective is an extremely difficult task. This often leads to optimization problems, such as vanishing or exploding gradients, and affects convergence speed and final accuracy. For this reason, researchers have proposed methods such as adaptive weighting, which enables the network to focus on difficult regions (e.g., boundary points) during training to improve accuracy [79].

A more fundamental limitation is that PINNs are neural-network structures designed to solve “rigid” forward problems [83]. For each specific physical scenario (i.e., a fixed set of parameters and boundary conditions), a completely different neural network needs to be trained to approximate a solution. That is, when facing the large number of flow equations commonly solved for reservoirs under different parameter settings, such as various injection pressures and core permeabilities, the network needs to be retrained every time the input parameters are changed [85]. This also leads to the extreme inefficiency of PINNs in the aforementioned fields. To overcome this bottleneck, scientific machine learning methodologies have evolved toward approaches that can handle parameterized systems, such as neural operators [66].

4.1.3. Phase 3: The Revolution from “Data Interpolation” to “Operator Learning” with Neural Operators

The latest frontier of methodological evolution is to overcome the “rigid” solution limitation of PINNs by learning not the “parameter-to-solution” mapping but the solution operator itself, which maps PDEs to their solutions. Some architectures, represented by the neural operator (NO), aim to learn mapping operators from permeability-field functions to pressure-field solution functions, e.g., directly from a function such as the permeability field, which represents the properties of the medium, to a solution function such as the pressure field. This is a fundamental departure from the finite-dimensional parameter-to-solution mapping learned in traditional neural networks and PINNs and a fundamental leap from data interpolation to operator learning. The fundamental leap from “data interpolation” to “operator learning” has been achieved [66]. The revolutionary feature of neural operators is their “train once, use many” capability, which directly addresses the key problem encountered by PINNs. A pre-trained neural operator can accept as input any new initial conditions, boundary conditions, or medium property field functions within the range of the training data distribution, and can solve this function at “zero cost” [66], function as input, and make zero-shot instantaneous predictions of that solution function. This is a disruptive efficiency advantage for tasks that traditionally require thousands of simulations for uncertainty analysis or optimization of reservoir development scenarios.

Nonetheless, neural operators are not entirely free from their own challenges and limitations, and their generalization ability is highly dependent on the range of physical scenarios contained in the training dataset. When encountering new problems with function distributions that are too different from those of the training set, the prediction accuracy may plummet. To mitigate this, advanced training strategies such as physics-informed neural operators (PINOs) have been proposed, which embed the governing PDE residuals directly into the loss function. By constraining the operator with physical laws, the model can better extrapolate to out-of-distribution permeability fields or unseen fracture networks, even when such samples are absent from the training set. Moreover, training a high-caliber neural operator also requires a large volume of data generated by a traditional high-precision simulator, so the computational cost invested upfront remains significant. Although specific applications in the field of reservoir simulation are still in the early stages, the operator learning paradigm pioneered by neural operators does open up great possibilities for truly real-time, high-frequency interactive simulation of complex physical systems [66].

As shown in

Table 1. Comparison of the evolution of physics-informed AI methodologies.

Feature Dimension	Phase 1: Surrogate Model	Phase 2: Physics-Informed Neural Network (PINN)	Phase 3: Neural Operator
Core Idea	Train AI to learn the end-to-end mapping between the “input–output” of a complex physical system to replace high-cost physical modeling.	Embed the partial differential equations (PDEs) of the control system into the loss function of the neural network as a physical constraint.	Learn the solution operator for solving PDEs itself, that is, learn the mapping from function to function.
Learning Goal	A specific solution under specific parameters. (Mapping relationship: parameters → solution)	A specific solution under specific parameters. Solved through regularization with physical equations.	The operator of the problem itself. Mapping relationship: function (e.g., permeability field) → function (e.g., pressure field)
Main Advantages	Extremely high inference efficiency: Prediction speed can be thousands to millions of times faster than traditional numerical solutions, suitable for uncertainty quantification and solution optimization.	Reduced data dependency: The introduction of physical constraints improves the model’s generalization ability and reduces the reliance on massive labeled data.	“Train once, use multiple times”. Can achieve “zero-cost” instantaneous prediction for new parameters, with disruptive efficiency advantages in tasks such as uncertainty analysis.
Core Challenges	1. Lack of physical consistency: Prediction results may violate physical laws. 2. Reliance on massive data: Model performance heavily depends on large-scale datasets that ensure the generation of true solution data.	1. Training difficulty: The weights of the loss function are difficult to balance, and the optimization process is unstable. 2. “Rigid” solution: Once the parameters are changed, the network theoretically needs to be retrained, which is not suitable for optimization tasks that require repeated solving.	1. Limited generalization ability: For new problems outside the training set (out-of-distribution), the accuracy may drop significantly. 2. High training cost: In the early stage, a large amount of high-precision numerical solution data is still required to train the operator.
Applicable scenarios	Scenarios that require a large number of repetitive and rapid predictions for a fixed physical model, such as preliminary sensitivity analysis, parameter optimization, etc.	Solving forward and inverse problems where data is sparse but the physical equations are known. For example, inferring the complete flow field from sparse observation points.	Scenarios that require exploring system responses under a large number of different parameters (e.g., different permeability fields), such as oil reservoir development plan optimization, real-time decision support, etc.

, the methodology of physics-informed AI exhibits a clear evolutionary path from agent models as efficient computational tools to PINNs, which integrate the laws of physics deeply, to neural operators, which are designed to learn the problem-solving operators themselves. Each new paradigm emerges to address the key bottlenecks of the previous generation of technologies in terms of physical consistency, data dependency, training efficiency, or application flexibility.

4.2. Innovations in Technical Routes and Closed-Loop Systems

To turn the potential of physics-informed AI from theory into a practical tool, researchers have made many innovations in the technological route, not only changing the model architecture but also aiming to construct a closed-loop system for automatic parameter tuning, model tuning, and even multiscale information transfer.

First, from the perspective of parameter optimization and calibration, AI methods offer a new way to improve the accuracy and efficiency of physics simulators. Traditional physics simulators, such as LBM, often contain important parameters, such as the relaxation time, and the choice of these parameters directly affects the stability and accuracy of the simulation. Manual tuning is cumbersome and experience-dependent. To address this problem, researchers have started to use machine learning and optimization algorithms to perform automated parameter optimization. Some studies have integrated machine learning models with optimization algorithms, such as particle swarms, to automatically optimize key control parameters in LBM multiphase flow models, thereby addressing instability in elastostatic flow simulations at low capillarity and greatly improving simulation accuracy and efficiency. Similarly, data-driven models such as random forests (RFs) and support vector machines (SVMs) have been used to identify the effects of individual relaxation parameters in multiple-relaxation-time LBMs (MRT-LBMs) on convergence and explore their decision boundaries, thereby selecting optimal parameter combinations that can suppress numerical bias and improve simulation accuracy [86,87]. Furthermore, the automatic differentiation (AD)-based microscopic LBM (AD-LBM) has also shown its power in inverse problems by establishing an end-to-end gradient from the simulation results to the model parameters, which can efficiently and accurately infer unknown physical parameters such as fluid viscosity, medium permeability, and boundary conditions [71]. In addition, AI can improve the simulation process. For example, researchers have trained a convolutional neural network to quickly generate an approximation of the steady-state flow field as the starting condition for an LBM simulation, which reduces the computation time required to obtain an accurate solution by an order of magnitude [88].

Secondly, the construction of an automated closed-loop system of “generation–simulation–inversion” is a major innovation in the current technological line, which aims to achieve full automation from structural characterization to parameter inversion. The core concept is to create a large number of digital core structures with generative AI models such as GAN, and then use high-fidelity physical simulators such as LBM to do forward simulation to obtain macroscopic response results, such as permeability, pressure drop, and so on, and then use AI’s proxy models or inversion algorithms to do the parameter calibration and optimization of the model. Crucially, the convergence of this closed-loop system is governed by a hybrid metric. The optimization algorithm minimizes a composite objective function that includes the data mismatch (the error between the AI-predicted macroscopic responses and field observations) and the physical residuals (the degree of violation of mass or momentum conservation laws), ensuring that the inverted parameters are both data-consistent and physically rigorous. AI can play many roles in this. On the one hand, it can be trained as a deep learning model and used as an effective proxy forward model to replace original physical simulations that take a long time, thereby greatly improving computational speed in history-matching or inversion frameworks. For example, in large-scale geological carbon sequestration projects, researchers have created deep learning-based proxy models to quickly predict changes in pressure and saturation. Embedding such models into the data assimilation process greatly reduces the time required for inverse modeling [89]. Similarly, an agent model (flow–net–DP) integrating a dual-porosity model with a data-driven flow-network model utilizes algorithms such as ensemble smoothing and multiple data assimilation (ES–MDA) to achieve history matching of model parameters and production optimization more than five times faster than full-order models [90]. On the other hand, AI has been used in direct problem-solving (i.e., inversion) approaches. For example, some studies have combined kernel regression with artificial neural networks (ANNs), coupled machine learning with an optimization framework, and constructed reservoir permeability fields consistent with logging and well-testing data. These approaches perform better than traditional kriging interpolation methods [91].

It is important to achieve efficient cross-scale information transfer, which is a key component in ensuring the physical consistency of macroscopic predictions, as shown in Figure 5. It is impossible to simulate all microphysical effects at the macro scale, so researchers use AI as a bridge to efficiently transfer the laws obtained from micro- and nanoscale physical simulations as a priori knowledge to coarser models. For example, researchers can use very little MD-simulation data to train a machine-learning surrogate model, and this surrogate can make accurate predictions of adsorption effects at different temperatures, pressures, and pore widths at a rate seven orders of magnitude faster than MD simulations. These upscaled parameters can then be embedded seamlessly into coarser-scale models to predict adsorption effects. This agent can accurately predict adsorption effects at different temperatures, pressures, and pore widths up to seven orders of magnitude faster than MD, and then embed these up-scaled parameters seamlessly into the pore-scale LBM simulations, which successfully builds a bridge between the two scales. Similarly, the results of microscopic reactive transport simulations are fed into a neural network for training, which is then integrated into a macroscopic Darcy-scale simulation code, which is computationally more efficient and memory-intensive than the traditional approach [92]. Transfer learning (TL) technology also plays a key role. Some researchers have used the knowledge gained from TL in the simulation of high-resolution, small field of view images to solve the low-resolution, large FoV core domain, and succeeded in accurately predicting the permeability of larger-sized samples, which better handles the contradiction between resolution and FoV encountered in the digital core dissection [92]. The paradox between resolution and FoV encountered in digital core dissection is better handled [93]. Ideas such as cross-scale coupling have also been applied, such as simulating a large number of individual throats with LBMs and then using them to train ANNs, replacing the time-consuming operations necessary for subsequent pore network modeling [94], or training neural networks with data from LBMs to predict effective transport coefficients in the mesoscopic range, which can then be incorporate them into macroscopic heat and mass transfer models [95]. The core of these approaches is to use the data generated from the multiscale model to train a better deep learning mapping so that it can better approximate the physical reality at fine scales [88].

However, implementing this ambitious generation–simulation–inversion closed-loop system faces practical challenges that must be addressed to ensure feasibility. First, regarding data requirements, training robust AI models necessitates large-scale, high-fidelity datasets, often requiring thousands of initial LBM simulations, which imposes a high upfront computational cost. Second, while the online inference is fast, the offline training phase is resource-intensive. Third, uncertainty management remains a critical hurdle; geometric deviations in GAN-generated cores may propagate errors to the simulation and inversion stages. Therefore, future implementations must integrate uncertainty quantification modules into the loop to monitor error propagation and ensure the reliability of the decision-making process.

4.3. Scientific Validation and Model Credibility

Scientific validation of physics-informed AI models is a critical part of ensuring that their predictions are correct and ultimately establishing their credibility in engineering applications. The most direct way to validate the value of physical constraints is to comprehensively compare the physical constraints model with the pure data-driven model. It has been shown that a dual-driven agent model incorporating oil and gas seepage theory on top of a pure data-driven model can maintain high prediction accuracy even when the training data are very sparse, and its robustness is better than that of a pure data-driven model [96]. A study on a physical information constrained neural network based on a small amount of data was able to achieve an average accuracy of more than 95% in predicting the rock mechanical parameters of shale reservoirs, and the PINN model used in the study significantly outperforms the traditional purely data-driven models, such as ANN, RF, and XGBoost [97]. The inclusion of physical constraints significantly improves the generalization ability of the model. For example, take a transmission field–coefficient–convolutional neural network (TFC–CNN) platform that has been trained on spherical filled structure data, it predicts well six porous media with different topological features including irregular, fibrous, foamy structures, etc., whereas a purely data-driven CNN model that relies purely on data falls short of generalizability, and a model that has been trained on a sandstone sample for the biological tissue-like samples would be highly biased in terms of property prediction, and that the predictive extrapolation performance of graph neural networks can be optimized to reduce prediction bias using online physical corrections such as forcing adherence to the partial equilibrium equations at the microscopic level during the inference session [98]. The above comparisons show that physical constraints are of central importance in improving model accuracy, robustness, and generalization capabilities.

To further enhance the credibility of the model in practical engineering applications, it is necessary to design a joint training and validation scheme that can integrate experimental and multiscale simulation data. An innovative workflow is to first train a physical information neural network by combining laboratory measurements (e.g., permeability, density, ultrasonic response of coal samples under different stresses) with physical simulation data (e.g., fluid flow, elastic wave propagation) [99]. The model output permeability trends are then calibrated with in-situ permeability test data from the field at a certain depth, turning the predicted trends into absolute permeability profiles over the entire layer. Such a method of fusing real-world observations for calibration greatly improves the reliability of model predictions. Similarly, comparing the results of reservoir compressibility evaluation based on physics-informed AI prediction with the actual daily oil recovery at the field site demonstrates the reliability of this intelligent evaluation approach [100]. Similarly, combining many conventional logging data (like gamma, density, resistivity, etc.) with permeability data from direct core measurements to train and validate machine learning models is also an effective means of creating reliable predictive models with real observations [101]. To substantiate the paradigm’s practical value with quantitative evidence, recent illustrative use-cases have confirmed that physics-informed AI can achieve order-of-magnitude acceleration without compromising fidelity. For instance, Tang et al. demonstrated that a multi-fidelity Fourier Neural Operator could reduce data generation costs by 81% in large-scale geological carbon storage modeling while maintaining high accuracy [102]. Similarly, Lee et al. reported that a nested Fourier-DeepONet framework improved training efficiency by two times and reduced GPU memory usage by 80% compared to standard models [103]. Regarding precision, Lyu et al. achieved a 99% modeling accuracy using transfer learning-based operators, significantly outperforming low-fidelity baselines [104], and Stankevicius et al. validated that deep learning solvers can accelerate Darcy flow simulations by orders of magnitude without loss of accuracy in heterogeneous fields [105]. With this mixture of simulated and real-world data, the models can be well calibrated and validated to bridge the gap between theoretical models and engineering reality.

4.4. Data Governance and Missing Parameter Prediction

To give high-quality data input for the training of physics-informed AI models, especially large models, which is a prerequisite for their successful application, the data generated during oil and gas exploration and development are of different sources, formats, and scales, so it is necessary to establish a standardized process of data integration and governance [106]. An important technical approach is to generate high-fidelity unified datasets with the help of multi-source data fusion. For example, by using deep generative adversarial networks, researchers can fuse high-resolution 2D scanning electron microscope (SEM) images with 3D micro-CT images, so as to reconstruct multiscale digital cores that contain macroscopic fields of view and microscopic details. Similarly, by fusing high spatial resolution RGB images and multispectral data, artificial neural networks can improve the spatial resolution of rock outcrop images from 30 m to the 1 m level and achieve 97.23% accuracy in classification tasks, providing better supporting data for geological interpretation work later [107]. These data are not only integrated with field data but also with outputs from geological interpretation work. In addition to the integration of real data, the creation of large datasets with the help of data augmentation and simulation generation is also considered a feasible data management solution. In related investigations, a large number of synthetic seismic traces were generated using a rock physics model (RPM) and statistical data from neighboring wells for pre-training convolutional neural networks, and the networks were then fine-tuned with real data via transfer learning. Using this RPM-based workflow, the P-impedance prediction achieved 96.5% R², which far exceeds traditional theory-driven pre-stack seismic inversion (81.5%) and a deep neural network (DNN) (86.2%); 97.5% R² was measured on blind wells [106]. In the geothermal context, data enhancement techniques have also been used to create large-scale and multiscale production temperature datasets to address the challenge of sparse real data when training deep learning models [42].

Oilfield field data are often sparse, mutilated, or incomplete, which poses a significant challenge to the accurate solution of physical models and the reliable training of data-driven models [108]. Methods that integrate physical mechanisms and machine learning provide a powerful solution for intelligent complementation and parameter prediction from small or trace amounts of data. Physics-informed neural networks have great potential in this regard, utilizing control equations (e.g., Navier–Stokes equations) and boundary conditions as part of the loss function to force the network output to satisfy physical consistency, thus allowing for the extrapolation of complete, high-precision flow fields based on sparse observations alone [109,110]. One of the pioneering works in this field is the ‘hidden fluid mechanics’ (HFM) framework proposed by Raissi et al., which successfully inverted the complete velocity and pressure fields using only sparse visualization of passive scalars (e.g., dyes) in the flow field, which demonstrates the effectiveness of PINN in solving the problem of sparse data. The power of PINN in solving the inverse problem with sparse data. It has been shown that even if the training data is very sparse, the presence of physical information constraints can make the model’s prediction accuracy much better than that of a purely data-driven neural network [111], and He et al. have shown that the more physical variables are jointly inverted during the data assimilation process, the higher the parameter estimation accuracy will be [110]. Similarly, the PointNet model, which relies on physical information, can accurately predict the entire fluid velocity and pressure fields at the pore scale from only sparse pressure observations in porous media [112]. It has also been argued that theory-guided neural networks (TgNNs), when optimized, can be trained efficiently based entirely on the theory of physics, even in the absence of labeled data. This type of approach has been well documented in other fields. Researchers have used generative adversarial networks to fill in large missing swaths of global total electron content (TEC) maps of the ionosphere, and have used the addition of sparse real-state updates to recurrent neural networks to enable the prediction of chaotic systems over ultra-long time horizons, thus highlighting the value of combining physical a priori and machine learning in data patching and prediction [111].

5. Engineering Applications: From Digital Platform to Digital Twin

5.1. Construction of an Integrated Digital Platform for Exploration and Development

The final outcome of the in-depth application of AI technology in the oil and gas industry is expected to be a professional software platform and an integrated intelligent system that responds to the actual needs of E&P [113]. Such a platform is expected to create automated software modules such as “in-situ pore digitization → full-phase parameter prediction → conventional/non-conventional seepage simulation,” thus forming an integrated intelligent analysis platform for E&P [114]. At its core is the creation of a series of integrated intelligent workflows, such as combining core analysis with machine learning for rock typing [115] or combining logging data with advanced algorithms to improve permeability and pore pressure prediction [116].

The construction of the platform relies on strong digital capabilities, which can be attributed to three main functions—data integration, data analysis, and data productization [117]. One of the key technical challenges in achieving data-driven decision support systems is how to automate the integration of fragmented data from different sources and formats [118]. Such platforms are often viewed as decision support systems (DSSs) or digital twins for oilfield development [119,120], and their effectiveness relies heavily on high-quality data management [120]. By embedding predictive models for different scenarios, such as production forecasting [121], equipment failure prediction [122,123], and operational risk assessment [124], the platform can support managers in making timely decisions to improve the safety and efficiency of oilfield operations.

To optimize the spreading ability and prediction accuracy of the model, it is inevitable to use data from multiple fields or blocks to perform collaborative modeling. In practice, some studies have used multiple wells and decades of production history data to train models, confirming the necessity of diversified data to improve model performance [125]. However, in the highly competitive scenario of the global oil and gas market, data sharing among various entities is constrained by a number of practical factors [114]. Therefore, the development of technological architectures that can perform collaborative modeling while protecting the privacy of each party’s data is extremely important to better leverage multi-source data and further improve the overall intelligent analytics platform.

5.2. Toward Real-Time Decision-Making: The Reservoir Digital Twin

Using efficient and highly accurate AI models of physical information as the core engine is a key path toward reservoir digital twins [126]. Reservoir digital twins create real-time interactions and feedback mechanisms between physical reservoirs and high-fidelity virtual models [127], which in turn enable intelligent risk prediction and control of subsurface systems. A step toward digital twins is the concept of a Digital Shadow, which fuses physically based simulations and data collected by in situ sensors in multiple modalities (e.g., time-shifted seismic, logging data) to continuously track the state of the subsurface CO₂ plume (e.g., saturation, pressure) and quantify its uncertainty [128].

This AI-centric paradigm can provide timely decision support for efficient and intelligent development of oilfields, such as by creating agent models that can accurately predict the dynamic parameters of the injection and extraction system, and working with algorithms such as particle swarm optimization, perform multi-objective optimization of the injection model, taking into account the physical and operational constraints, to increase the oil production while maintaining the gas-oil ratio, and finally achieve more than 10% oil increase [121]. These intelligent tools, relying on deep neural networks, can effectively judge complex reservoirs (e.g., unconventional), thereby replacing cumbersome numerical simulations and speeding up and improving development planning [129].

This technology also has a promising application in new energy scenarios such as carbon capture, utilization, and storage (CCUS), geothermal development, and underground hydrogen storage (UHS) [75]. In the case of CCUS, the development of machine learning techniques has made storage projects more secure and reliable [100]. Researchers have used deep learning models such as the Fourier neural operator (FNO) to create proxy models, reducing the coupled flow and geomechanical simulation time, which would have taken thousands of hours to complete, to less than twenty minutes, thereby enabling rapid multi-objective optimization of the CO₂ injection strategy, with the aim of both maximizing the amount of sequestration and minimizing the geomechanical risks of microseismicity and surface uplift triggered by the injection [130]. Geomechanical risks such as microseismicity and ground uplift can be induced by injection. This combination of intelligent modeling and optimization is seen as the key to developing optimal development scenarios for large-scale geological storage and utilization projects. Proxy models have also been used to efficiently predict and assess uncertainties in geomechanical responses, such as ground uplift and rock breakout risk, to inform the assessment of the long-term sealing of the reservoir. This technique is not just applicable to the reservoir itself but could potentially be applied to the entire CO₂ pipeline system, allowing for reliable, efficient, and cost-effective operation of the entire chain [126]. Similarly, when integrating the complex scenarios of CO₂ storage and geothermal mining, proxy models can efficiently perform sensitivity analyses of key parameters to guide the design of the scenarios [131].

6. Current Challenges, Opportunities, and Frontiers

6.1. Key Bottlenecks

Despite significant progress in fusing physics and AI, there are still several key bottlenecks that hinder the widespread application and development of the paradigm in reservoir engineering. These challenges revolve around the physics-mechanism-data gaps, the inherent limitations of current AI models in terms of interpretability and generalization, and the significant computational costs involved.

Mechanism-data gap: A major challenge lies in bridging the gap between complex physical phenomena and the data on which they are modeled. In terms of cross-scale transfer bottlenecks in physical mechanisms, there is a lack of mature theoretical frameworks for treating nanoscale slip effects or pore-scale non-Darcy flows (obtained through LBM simulations) as physical constraints for macroscopic AI models such as PINN or neural operators. Simply averaging out the microscopic parameters loses important nonlinear coupling effects, and adding complex terms directly to the macroscopic equations makes the training of PINN very unstable [132]. In terms of multi-source data mismatch, the integration of data from a variety of multiscale, multi-physical fields, and multi-data sources has to be handled to make the model successful. A central issue is the development of frameworks that can accurately predict reservoir state from sparse measurements [133]. Traditional proxy models that rely heavily on data may fail when faced with insufficient data samples [134]. Furthermore, even in online learning scenarios aimed at optimizing models, determining which new data samples should be selected for retraining remains a challenging problem [135].

Interpretability and generalization capabilities: The credibility and applicability of AI models in critical decision-making are constrained by their inherent limitations. The lack of transparency and physical interpretability of complex machine learning models due to their “black-box” nature is a recognized problem that hinders their wider application in areas such as oil and gas production forecasting. Ensuring that models can generalize across different reservoir types and operating conditions is a prerequisite for their engineering applications. While state-of-the-art architectures like GNNs and theory-guided networks have demonstrated excellent generalization capabilities on new grid configurations, boundary conditions, or permeability statistics [136,137], achieving robust generalization capabilities to avoid overfitting to specific datasets is still the core goal. Some agent models perform well in optimization tasks, where they generate results higher than values in the range of the training data, which is indicative of a strong generalization capability [138].

Computational power and cost: The training and deployment of large-scale, high-precision physics-informed AI models are usually accompanied by high computational requirements. Many reservoir engineering tasks, such as automated history fitting, inverse modeling, and field development optimization, are inherently very time-consuming, as these operations often involve many numerical simulations. For example, solving the inversion of two flow equations might require the simulator to do hundreds of head-on runs, which makes the workload enormous. For the kind of large-sized reservoirs that contain millions of grid-dependent parameters, huge computational and storage overheads are required for large reservoirs with millions of grid-based parameters, even if spatial features are extracted using methods such as convolutional neural networks [139]. Such computational overheads have been a major driver in the development of deep learning-based agent models that attempt to greatly accelerate these processes [132]. Creating these agent models is not without cost, as it can require a large number of manual trial-and-error [140] as well as many highly accurate simulations to initially train them [138]. Nonetheless, these agent workflows have been shown to significantly reduce costs—in some cases by more than 45% [135], 75% [138], and even down to 5% of the cost of the original simulation process [141], while achieving comparable results. to address the root of this obstacle, work has been carried out to accelerate the physics simulators themselves, such as the exponential acceleration of lattice Boltzmann simulations using GPUs and OpenACC programming [142].

6.2. Future Frontier Technology Directions

To cope with the growing complexity in reservoir simulation and to take full advantage of the opportunities presented by massive amounts of data, research in physics-informed AI is evolving toward more advanced architectures, more trustworthy decision-making, and more ambitious modeling paradigms.

Next-generation AI architectures: Future research is exploring next-generation AI architectures like Transformer, graph neural networks, and neural operators to make breakthroughs in dealing with complex spatiotemporal flow field prediction problems. Among them, the Transformer architecture, which originated in the field of natural language processing, has shown great potential in the field of geoscience due to its advantages in capturing long-distance dependencies [143]. Researchers have begun to build specialized Transformer-based models, such as the “Seismic foundation model” [143] for processing massive seismic data, and the “SpectralGPT”. The SpectralGPT [144] is also used for hyperspectral remote sensing image analysis. Meanwhile, the Vision Transformers backbone network is also used to process image-based data from Earth observation satellites and Earth system models. Geoscience [27], and together, these explorations suggest that the Transformer architecture holds great promise for application in the geosciences.

Explainable AI (XAI): As models become more and more complex, opening the “black box” of AI to improve the explainability and physical consistency of models has become a major challenge to enhance the credibility of models in critical engineering decisions. While most of the current research focuses on model performance, some studies have begun to focus on model “truthfulness” measures, such as the truthfulness of large language model (LLM) outputs, which has become a consideration for specific tasks in the oil and gas domain [145]. In the future, the development of interpretable AI techniques that can demonstrate the physical basis of model decisions will be critical to bridging the trust gap between AI predictions and engineering applications and to ensuring the security and reliability of model deployment.

Quantum computing: Quantum computing and simulation processes information by virtue of its own quantum mechanical principles, which offer revolutionary possibilities for solving scientific problems that are difficult to solve with traditional computers [146]. In the field of reservoir simulation and fluid dynamics, quantum computing may dramatically accelerate computational processes such as CFD, reservoir simulation, and seismic inversion, thereby driving innovation in energy technology [146]. The main potential lies in accelerating the solution of partial differential equations (PDEs), which are the basis for the study of fluid flow and seepage in porous media. One of the main research frontiers is the writing of quantum algorithms for the Navier–Stokes equations describing fluid motion [147,148]. To allow quantum computers to perform fluid simulations, researchers are exploring the “quantization” of classical numerical methods such as the lattice Boltzmann method [147,149,150]. In addition to solving PDEs directly, solving large-scale linear systems of equations is another key area, as this task arises after discretizing reservoir flow equations using finite element or finite difference methods [151,152]. For example, the variational quantum linear solver has been initially applied to solve discrete reservoir flow equations [151], and quantum algorithms for FEM may also offer polynomial-level speedups [152]. Despite the promise, these applications are in a nascent stage; most algorithms are validated by running quantum simulators on classical computers [149], and the size of the lattice that can be simulated is very small due to current quantum hardware limitations. Nevertheless, continued research advances, from the optimal design of quantum circuits [153] to algorithmic implementations in quantum software development frameworks [154], are paving the way for the future application of quantum computing in the field of fluid simulation [49].

Foundation models in geosciences: Drawing on the successes in natural language processing and computer vision, building pre-trained foundation models in geosciences has become a clear frontier [143]. The paradigm attempts to use a large amount of unlabeled geoscience data (e.g., 192 3D seismic datasets collected globally containing more than two million 2D images) for pre-training, such as self-supervised learning, to obtain a large-scale generic model that can generate generic features for a variety of tasks, and thus to solve the problems of the traditional AI models that have a poor generalization ability, require a large number of labels and repeated training [143]. Once these models are built, they can be quickly empowered for many downstream tasks, such as seismic denoising, parameter inversion, reservoir fracture prediction [155], segmentation [144], and now basic models specifically for domains such as seismic and remote sensing have emerged [143]. Researchers have merged large-scale language models with GIS tools to develop intelligent assistants (e.g., GeoGPT) that can autonomously understand and perform geospatial tasks [27]. This “basic model + expertise” model is considered to be an effective way to build the next generation of general-purpose geoscience AI systems.

7. Conclusions

In this paper, we have systematically reviewed the theory, methodology, and cutting-edge practice of physics-informed AI in the field of reservoir multiscale modeling and seepage simulation. This study demonstrates that the in-depth integration of data-driven “intelligence” and physically driven “mechanism” is the core path to break through the bottleneck in efficiency and accuracy inherent in traditional reservoir research. By taking physical consistency as an intrinsic constraint, this emerging paradigm not only significantly improves the generalization ability and prediction accuracy of models but also achieves an order of magnitude leap in computational efficiency, which represents an inevitable trend for the future development of this field.

This review clearly outlines a technical route of “geometric representation → mechanistic constraints → intelligent reasoning → closed-loop optimization”. Firstly, the research starts with AI-enabled multiscale in situ digital core characterization, which provides an unprecedented high-fidelity geometric basis for fine depiction of complex reservoir microstructures through generative models and super-resolution algorithms. Secondly, cross-scale physical simulations centered on molecular dynamics and the lattice Boltzmann method provide first-principle insights into complex seepage mechanisms at the nano and pore scales, and the simulation results constitute key physical a priori knowledge and high-fidelity data that constrain the AI model. On this basis, the methodology of physics-informed AI has undergone a profound evolution from agent models as efficient computational tools to physics-informed neural networks that incorporate the laws of physics as strong constraints in the training process and ultimately to neural operators that aim to learn the problem-solving operators themselves. The culmination of these technologies is the construction of an automated closed-loop system of generation–simulation–inversion, which integrates the entire process from core generation and forward simulation to parameter inversion and provides an innovative automated solution for solving real engineering problems. This series of technological breakthroughs has provided strong theoretical and practical support for effectively addressing core challenges in reservoir research, such as a lack of data, complex mechanism coupling, and difficulty in scaling up.

Looking into the future, it is essential to delineate the current maturity of this paradigm. While the methodology has been proven effective for multiscale characterization and accelerated pore-scale simulations (as discussed in Section 4), its application to complex field-scale scenarios—such as reservoir digital twins and carbon sequestration—remains a prospective vision that requires further validation. Nonetheless, the potential strategic significance is profound. This technology is expected to serve as a key cornerstone for realizing real-time monitoring and intelligent optimization of subsurface reservoirs, and to provide a core driving force for emerging green energy industries, including carbon capture, utilization, and storage, geothermal energy, and underground hydrogen storage.