A Parallel Dual LLC Resonant Converter with Wide Output Voltage Range for Energy System Applications

Abstract

This paper proposes a half-bridge parallel dual LLC resonant converter with wide output voltage range. The proposed converter uses a conventional parallel double half-bridge LLC resonant converter. On the primary side of the converter, only one of the two half bridges is used to control the two resonant loops. Due to the resonance of the converter, the active switches can achieve ZVS (zero-voltage switching), and the rectifier diode can also achieve ZCS (zero-current switching), and thus the switching loss is reduced. The current stress can be reduced and power can be distributed on both of the primary side and/or the secondary side. A voltage regulation circuit is designed on the secondary side to achieve the function of wide output voltage. The operation and analysis of the proposed converter are described in detail. The experiments were carried out on a circuit prototype, which is a converter with DC input voltage of 384 V and output voltage of 24–40 V and operating at a switching frequency of 107 kHz. The feasibility and performance of the proposed converter were verified by simulation and experimental results.

1. Introduction

DC–DC converters, such as the buck, boost, flyback, and forward converters, are widely used in low- to medium-power applications due to their simple topology and low cost [1,2]. However, the system power continues to rise, and even in high-power applications, voltage spikes may occur during switching due to the freewheeling problem caused by the inductors of the power converter. The higher the system power, the greater the voltage spike. Thus, a half-bridge isolated LLC converter appears to adapt to higher-output-power applications [3].

The traditional half-bridge LLC converter is operated by two power switches on the primary side, and a sinusoidal wave current is generated in the resonant circuit by complementary switching. The voltage gain is determined by the converter and the transformer. Thus, a stable output voltage is obtained by adjusting the switching frequency according to the input voltage.

The resonant current is a sinusoidal wave provided that the switches can be turned on at zero voltage. If the frequency is adjusted properly, the rectifier on the secondary side can be turned off at zero current. Therefore, the switching loss is significantly reduced and the efficiency is improved.

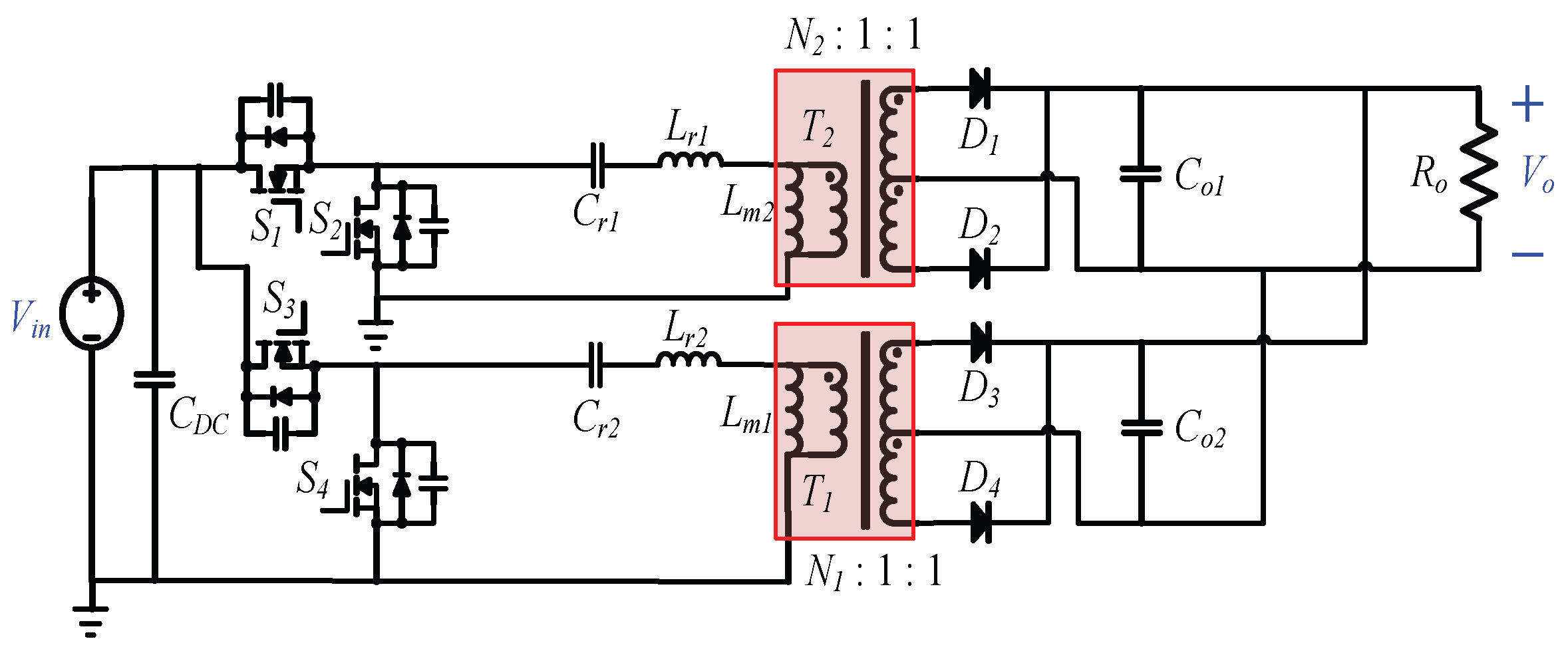
In [4], a converter with two parallel half-bridge resonant circuits was proposed, as shown in Figure 1. The proposed converter can improve the output power of the converter and reduce the power stress of the components. Several different parallel topologies have been reported. The use of fly capacitors to equalize the resonant current of a parallel two-phase circuit was proposed in [5]. However, the equalization performance was poor. In [6,7,8,9,10,11], two half bridges were connected in parallel on the primary side and the outputs in series on the secondary side. In [12], a TL DC–DC converter using phase-shift control was studied. Nevertheless, the circulating current problem cannot be ignored.

In [13], a converter with a six-switch dual active bridge and a series transformer, which connected series on the primary side and the secondary side, was proposed. However, it can only reduce the voltage stress of upper and lower switches.

In the converters of [14,15], the magnetizing inductance of the transformer can be changed to reduce the conduction loss. In [16,17,18,19,20,21,22], the hybrid bridge structure of the primary side or topology morphing method was applied on an LLC converter. However, the current stress on the secondary side could not be effectively reduced.

In [23], the converter combined an interleaved boost circuit and a full-bridge resonant circuit on the primary side to narrow the voltage gain range and reduce the voltage stress of the switch. However, this made the circuit complicated, and the power stress on the secondary side could not be further reduced. In [24], a traditional half-bridge LLC converter was used and PFM and APWM methods were adopted for the switching operation. Although this was able to narrow the switching frequency range, the zero-voltage switching (ZVS) condition sometimes disappeared.

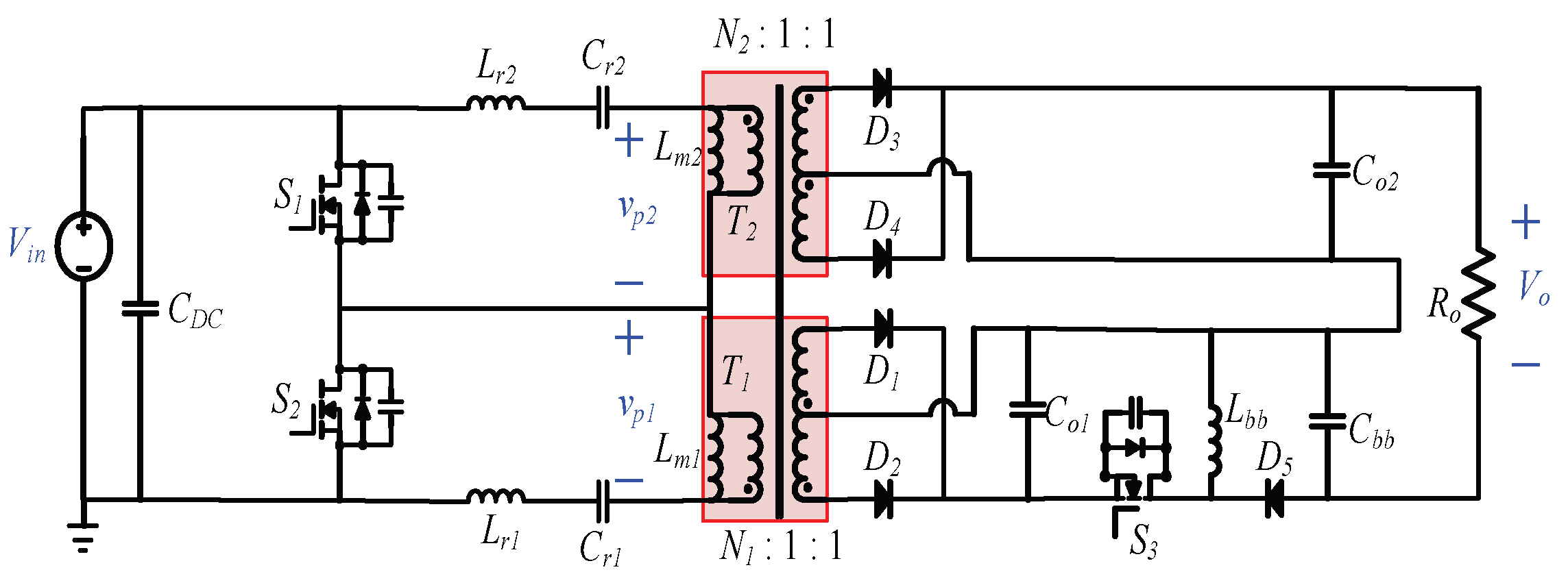
This paper proposes an LLC converter with parallel dual half-bridge resonant circuits. The dual circuits are used to distribute power to reduce the power stress of components and improve the power capacity of the proposed converter. The proposed converter is consisted of an LLC part and buck–boost part. The LLC part operates in a DCX state and the switching frequency is fixed at a resonant frequency. Moreover, the primary side switches and the secondary side diodes of the LLC part can satisfy the conditions of ZVS and zero-current switching (ZCS), respectively. The buck–boost part can achieve a wide output voltage range with pulse-width modulation (PWM).

Compared with the traditional parallel dual half-bridge resonant converter, the proposed converter shown in Figure 2 saves two active switches. Thus, the additional conduction loss and switching loss caused by the two switches are reduced. The design of magnetic components becomes simple due to fixed-frequency operation. An experimental prototype with input voltage of 384 V, output voltage of 24–40 V, and power of 80 W was established and tested. The experimental results are provided to verify the system’s performance.

2. Principle of Operation

A parallel dual half-bridge resonant LLC converter with a wide range of output voltages, as shown in Figure 2, is proposed in this paper. The primary side of the proposed converter consists of two parallel half-bridge structures with shared switches S₁ and S₂. The LLC resonant tanks are constructed by the resonant elements L_r1, L_r2, C_r1, and C_r2 and the magnetizing inductances of transformers L_m1 and L_m2. Center-tapped transformers are used as T₁ and T₂. S₃, L_bb, and D₅ are combined to form the buck–boost part. The buck–boost part is operated in continuous conduction mode (CCM) and regulates the output voltage of the proposed converter with pulse-width modulation (PWM). The switching frequency of S₃ is not equal to the switching frequencies of S₁ and S₂.

In order to simplify the analysis of the proposed converter, the following assumptions will be considered to describe the converter operation and steady-state analysis.

• The duty cycle of switches S₁ and S₂ in the primary side is fixed at 0.45.
• All switches have parasitic capacitances and bypass diodes, and transformers have certain magnetizing inductance, regardless of leakage inductance.
• The primary side switches S₁ and S₂ have a dead time.
• Each output capacitor in the secondary side is large enough to keep the output voltage constant.
• All capacitors, inductors, and diodes are ideal components.

Based on the above assumptions, there are six modes during one period of the operation of the proposed converter. The operation modes and key waveforms of the converter are shown in Figure 3 and Figure 4, respectively.

2.1. Operation Principle

There are six modes in one period of the converter operation.

Mode 1 [t₀–t₁]: As shown in Figure 3a, at t = t₀, S₂ is turned off, D₁ and D₄ turn into conduction mode, and the converter enters dead time. At this time, the resonant current i_Lr1 is negative and i_Lr2 is positive, and thus the parasitic capacitance of S₂ (C_oss2) begins to charge until it reaches V_in and then S₂ turns off, and the parasitic capacitance of S₁ (C_oss1) begins to discharge. S₃ remains turned off and L_bb continually releases energy to load through D₅. Since the magnetizing inductance does not participate in the resonance, the magnetizing current of L_m1 and L_m2 rises and falls linearly, respectively. This mode ends when V_coss2 is charged to V_in and V_coss1 is discharged to 0 V.

Mode 2 [t₁–t₂]: As shown in Figure 3b, at t = t₁, S₁ is turned on with ZVS. i_Lm1 and i_Lm2 are increasing and decreasing, respectively, in this mode. S₂ is completely turned off. At this time, due to the freewheeling of the resonant currents i_Lr1 and i_Lr2, they flow through S₁. The resonant current i_Lr1 rises, and i_Lr2 falls as the sinusoidal waveform. The energy is delivered to the load through D₁ and D₅.

Mode 3 [t₂–t₃]: As shown in Figure 3c, at t = t₂, S₃ turns on, L_bb stores energy through D₁, and the current of D₅ is decreased to zero. At this time, the resonant current i_Lr1 begins to turn into a positive current, and i_Lr2 begins to turn into a negative current. This mode ends when i_Lr1 is equal to i_Lm1 and i_Lm2 is equal to i_Lr2.

Mode 4 [t₃–t₄]: As shown in Figure 3d, at t = t₃, D₁ and D₄ are turned off with ZCS. Since the magnetizing inductances L_m1 and L_m2 represent part of the resonance with L_r1, C_r1, L_r2, and C_r2, i_Lr1 is the same as i_Lm1 and the difference between i_Lm2 and i_Lr2 is zero. V_in cannot deliver energy to load through D₁ or D₄ during this mode. i_Lbb increases continually due to C_o1 supplying energy to L_bb, while C_o2 and C_bb provide energy to the load. When S₁ is turned off, this mode ends and enters the negative cycle of operation of the proposed converter.

Mode 5 [t₄–t₅]: As shown in Figure 3e, at t = t₄, S₁ is turned off, D₂ and D₃ are conducted, and the converter enters dead time. V_in is delivering energy to load and L_bb through D₂ and D₃. At this time, the resonant current i_Lr1 is positive and i_Lr2 is negative, and thus the parasitic capacitor of S₁ starts to charge until it reaches V_in and the parasitic capacitor of S₂ begins to discharge. This mode ends when V_coss2 is discharged to 0 V and V_coss1 is charged to V_in.

Mode 6 [t₅–t₆]: As shown in Figure 3f, at t = t₅, S₂ turns on with ZVS. At this time, the resonant current i_Lr1 begins to turn into a negative current and i_Lr2 begins to turn into a positive current. The input energy is sent to the load through D₃. After the end of mode 6, i_Lr1 is equal to i_Lm1 and i_Lm2 is equal to i_Lr2.

2.2. Parameter Calculation

The input voltage of the proposed converter is 384 V, the output voltage is from 24 V to 40 V, the maximum output power is 80 W, and the switching frequency is 107 kHz. Since the output voltage is determined by the buck–boost circuit on the secondary side, the output of the LLC resonant tank is 12 V.

The voltage gain of the LLC resonant circuit is obtained from the equivalent impedance of the circuit, and the formula is expressed as follows.

$$\begin{array}{l}G\left(Q,m,Fx\right)={\displaystyle \frac{2N{V}_o}{V_{in}}}\\ ={\displaystyle \frac{{Fx}^2\times \left(m-1\right)}{\sqrt{{\left(m\times {Fx}^2-1\right)}^2+{Fx}^2\times {\left({Fx}^2-1\right)}^2\times {\left(m-1\right)}^2\times Q^2}}}\end{array}$$

(1)

If the gain G is 1, the turn ratio is 16 from (1), and F_x is the frequency ratio. In order to keep the gain G at 1, the resonance frequency selected is 107 kHz, which is the same as the switching frequency.

$$F_x={\displaystyle \frac{f_s}{f_r}}$$

(2)

The resonant frequency can be obtained from Equation (3). Since 107 kHz is selected as the resonant frequency, the resonant inductor and resonant capacitor can be obtained. Thus, the resonant inductance is 81.04μH and the resonant capacitance is 27.3 nF.

$$f_r={\displaystyle \frac{1}{2\pi \sqrt{L_r\times C_r}}}$$

(3)

In addition, m is the inductance ratio, which is designed to be 11 and makes the ratio of L_m/L_r = 10. The larger the inductance ratio, the smaller the resonant inductance value can be, thereby reducing the volume and loss of the resonant inductance.

The ratio cannot be too large: otherwise, the leakage inductance of the transformer may be greater than the resonant inductance, resulting in a different circuit from the original design.

$$m={\displaystyle \frac{L_m}{L_r}}$$

(4)

Q is the quality factor for the circuit. In order to keep a stable current gain on the secondary side, the quality factor selected is 0.134. This may make the voltage gain curve slightly steep and the range of variation wider than usual. Fortunately, the range of variation in input voltage is between −10 V and 10 V, which is acceptable.

$$\mathrm{Q}={\displaystyle \frac{\sqrt{L_r/C_r}}{R_{eq}}}$$

(5)

The equivalent impedance R_eq in (5) is expressed as follows.

$$R_{eq}={\displaystyle \frac{8}{{\pi }^2}}\times {\displaystyle \frac{N_P^2}{N_s^2}}\times R_L$$

(6)

Figure 5 shows the gain curves of different quality factors (Q). It can be seen that the gain curve with Q = 0.134 is the steepest. This can be reserved for future adjustment if the voltage regulation circuit is removed, which would mean the range would be adjustable by frequency modulation only.

3. Simulation Results

To verify the performance of the proposed converter, simulations are carried out on a parallel dual half-bridge LLC resonant converter under different conditions.

Table 1. The parameters of the proposed converter.

Items		Values
Input Voltage (Vin)		384 V
Output Voltage (Vo)		24 V–40 V
Rated Output Power (Po)		80 W
Switching Frequency (fs)	S1 and S2	107 kHz
	S3	57 kHz
Resonant Frequency of LLC Resonant Tank (fr)		107 kHz
Resonant Inductors (Lr1, Lr2)		81.04 μH
Resonant Capacitors (Cr1, Cr2)		27.3 nF
Magnetizing inductance (Lm)		810.4 μH
Buck–Boost Inductor (Lbb)		20 μH
Transformer Turn Ratio (N1, N2)		16
Diodes (D1–D5)		DSSS30
Switches	S1 and S2	SCT3120AL
	S3	IRFB4227
Core of Transformers		PQ40/40 PC47

lists the circuit specifications and component parameters for the converter.

Figure 6 shows the driving signals, the waveforms of switches S₁ and S₂ on the primary side when the output voltage is fully loaded with 24 V. Figure 7 shows the waveforms of the resonant currents i_Lr1 and i_Lr2 of the resonant circuits and the magnetizing current i_Lm1 and i_Lm2 in the transformer when the output voltage is fully loaded at 24 V.

Figure 8 shows the waveforms for the voltages and currents of the secondary side rectifier diodes when the output voltage is 24 V at full load. Figure 9 shows the waveforms of the voltage and the current of the switches S₁ and S₂ on the primary side when the output voltage is fully loaded at 40 V. Figure 10 shows the waveforms of the voltages and the currents of the secondary side rectifier diode when the output voltage is fully loaded at 40 V. From these waveforms, regardless of whether the output voltage is 24 V or 40 V, the primary side switch can achieve ZVS and the secondary side rectifier diode can achieve ZCS. Soft switching is also achieved for the proposed converter under light-load and half-load conditions, as shown in Figure 11, Figure 12 and Figure 13.

4. Experimental Results

To verify the simulation results of the proposed converter, an experimental prototype of a dual half-bridge LLC resonant converter was constructed and tested with different output voltages, as shown in Figure 14. The circuit specifications are: V_in = 384 V, V_o = 24–40 V, and P_o = 80 W. A TSM320F28335 DSP controller from Texas Instruments was used for the system control.

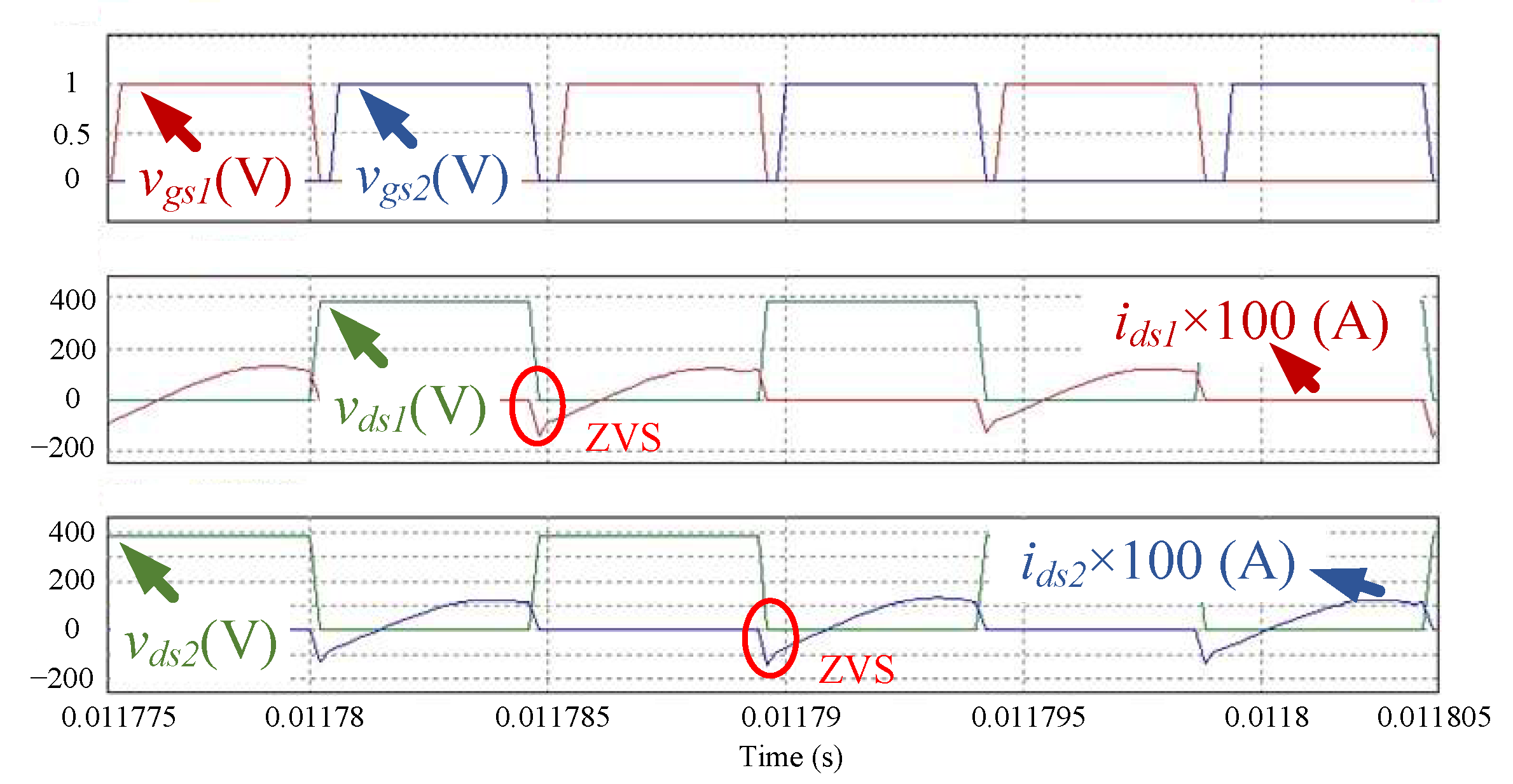
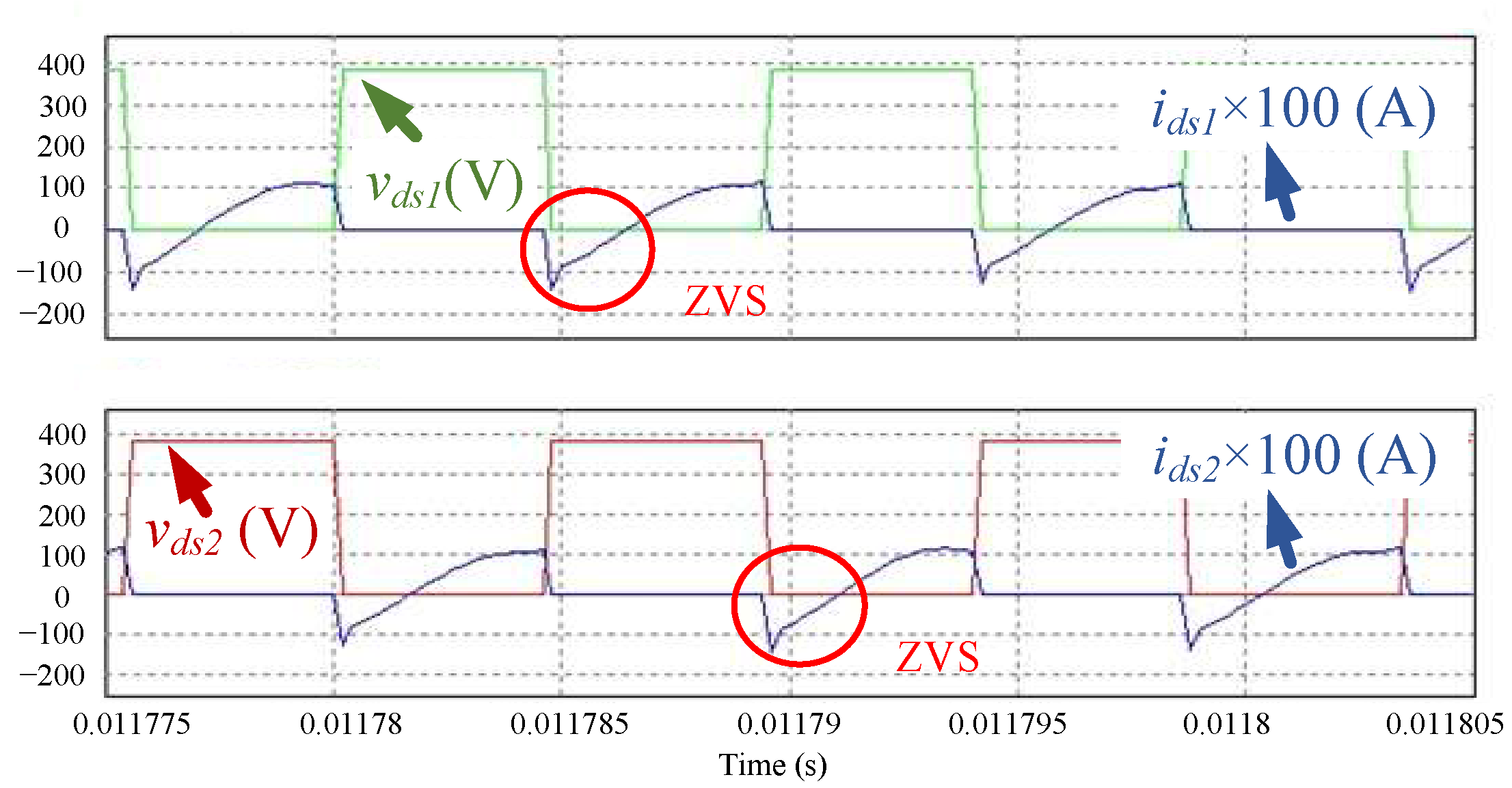
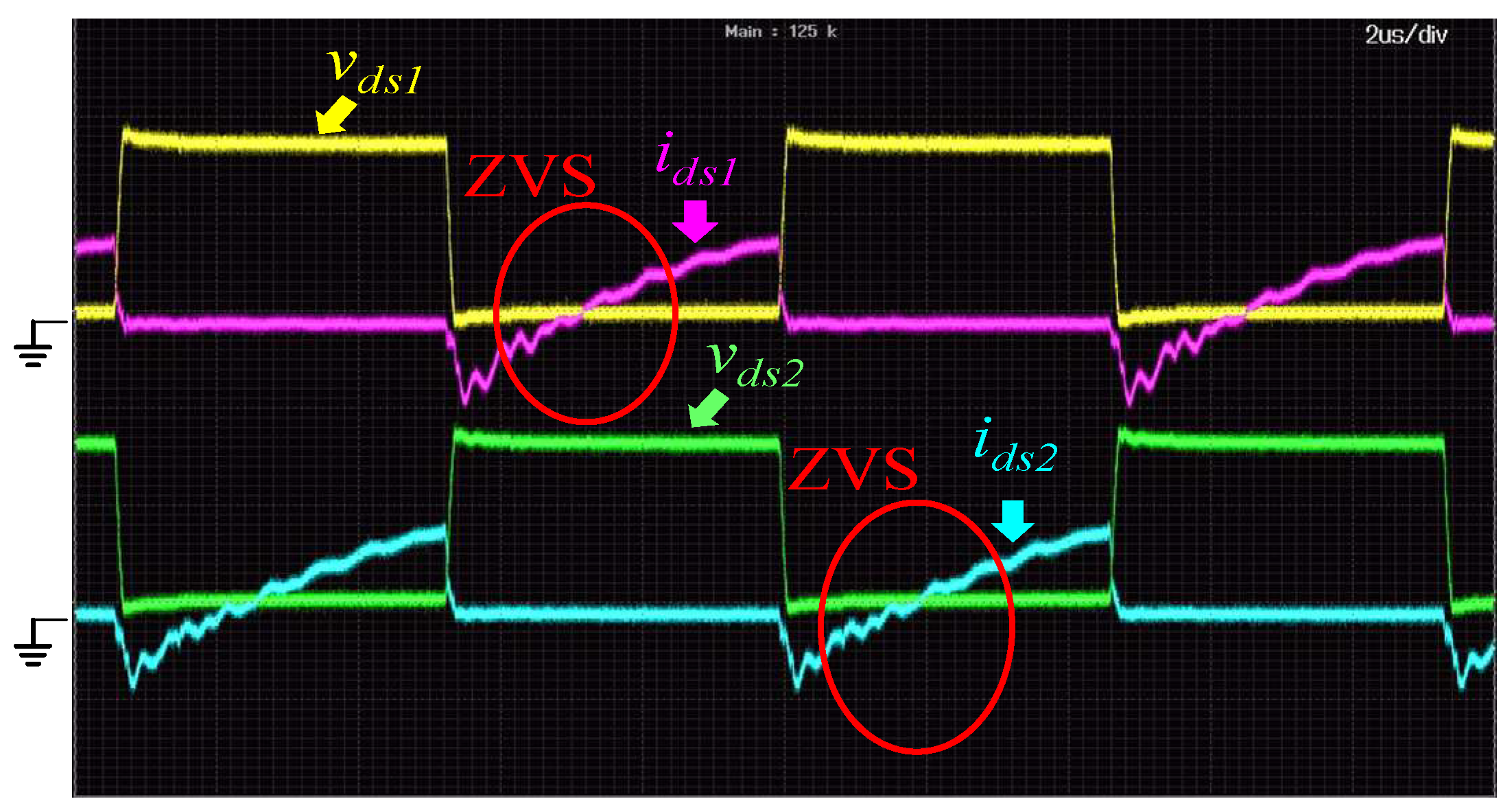
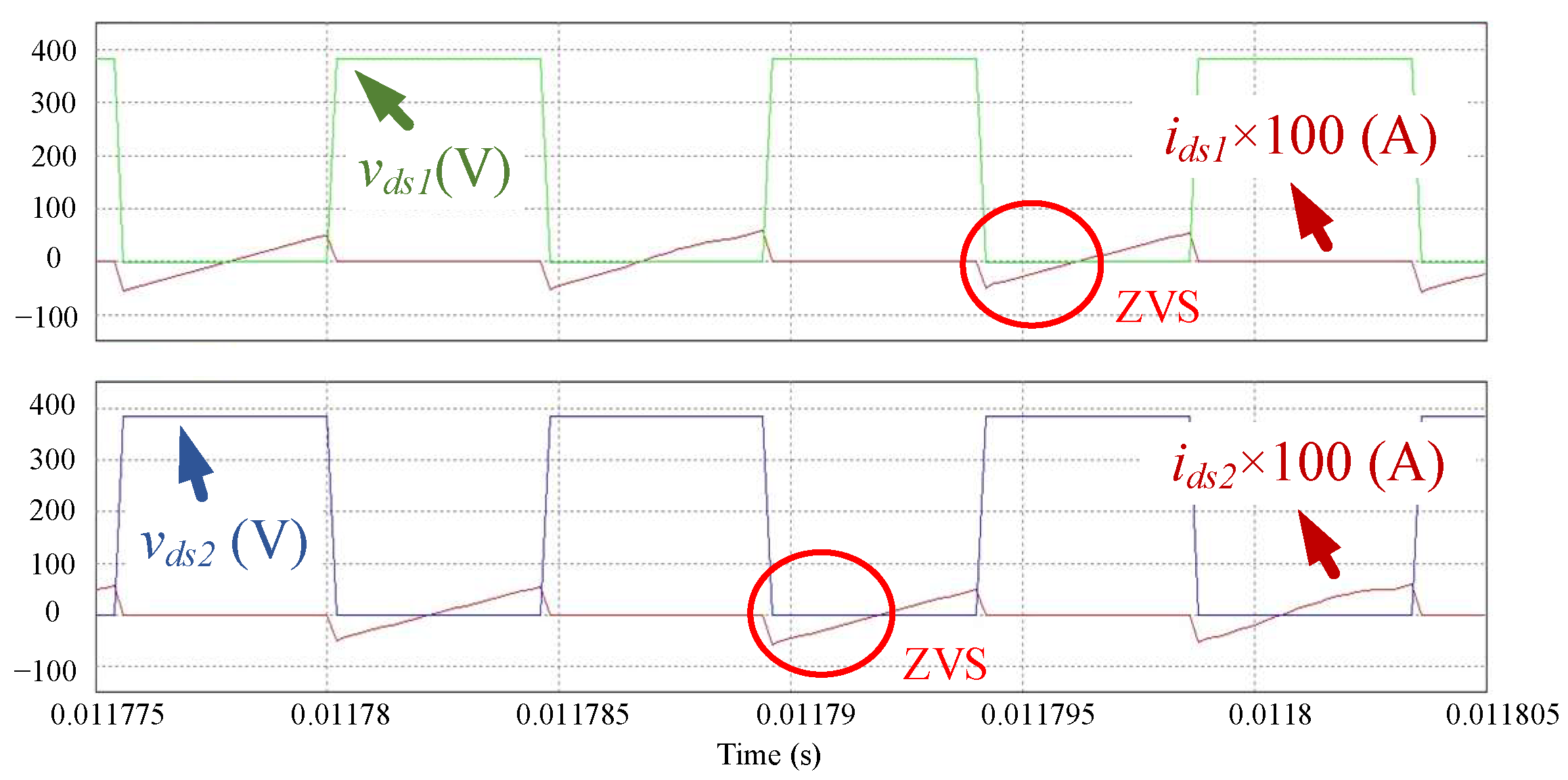
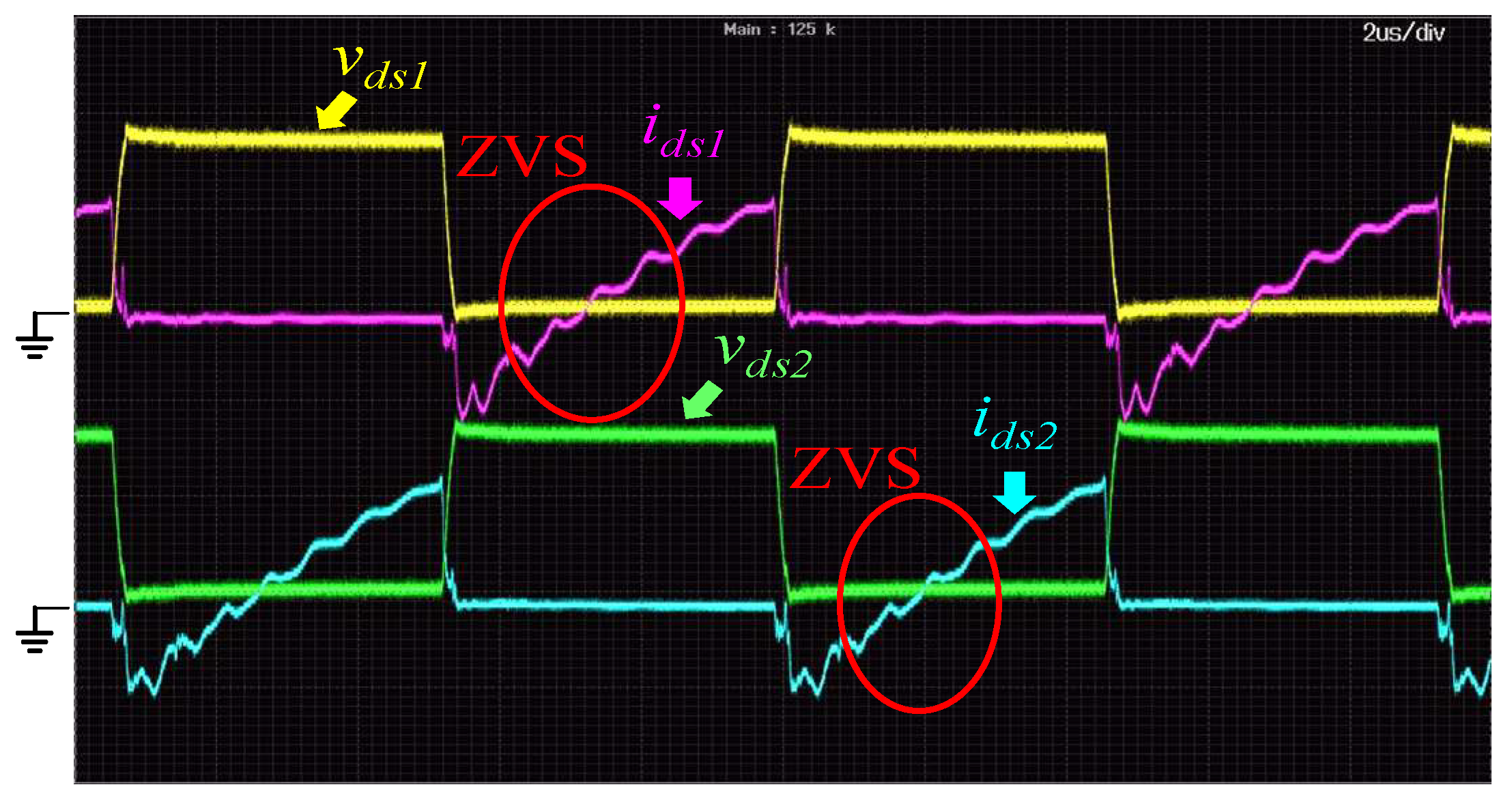
Figure 15 shows the measured waveforms of the primary side switches S₁ and S₂ when the input voltage is 384 V and the output is 10% of rated load. Figure 16 shows the measured waveforms of the primary side switches S₁ and S₂ when the input voltage is 384 V and the output is 50% rated load. Figure 17 shows the measured waveforms of the primary side switches S₁ and S₂ when the input voltage is 384 V and the output is 100% rated load. It can be found from the measured waveforms that ZVS turn-on of the proposed converter is achieved for the light-load, half-load, and full-load conditions.

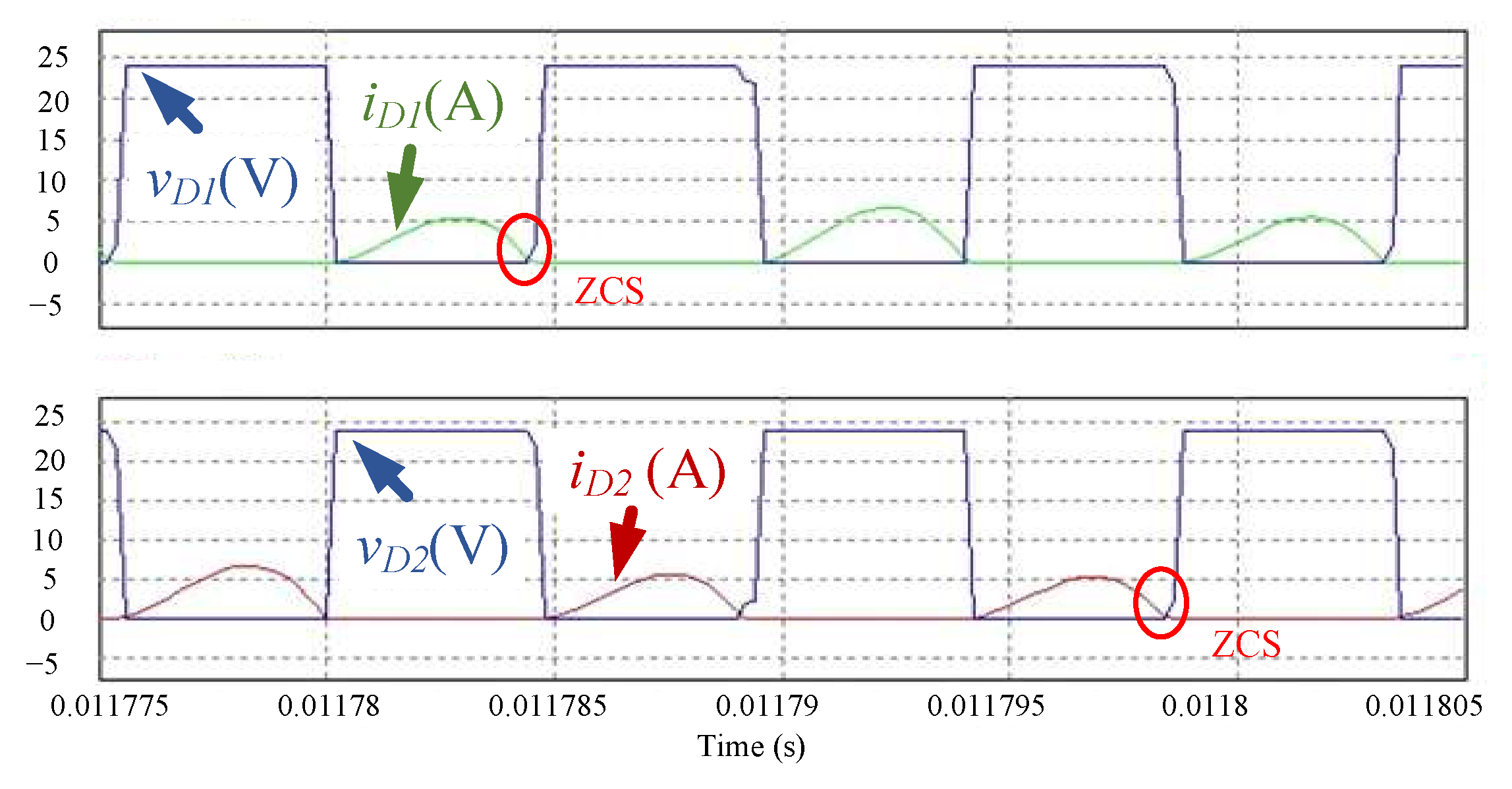
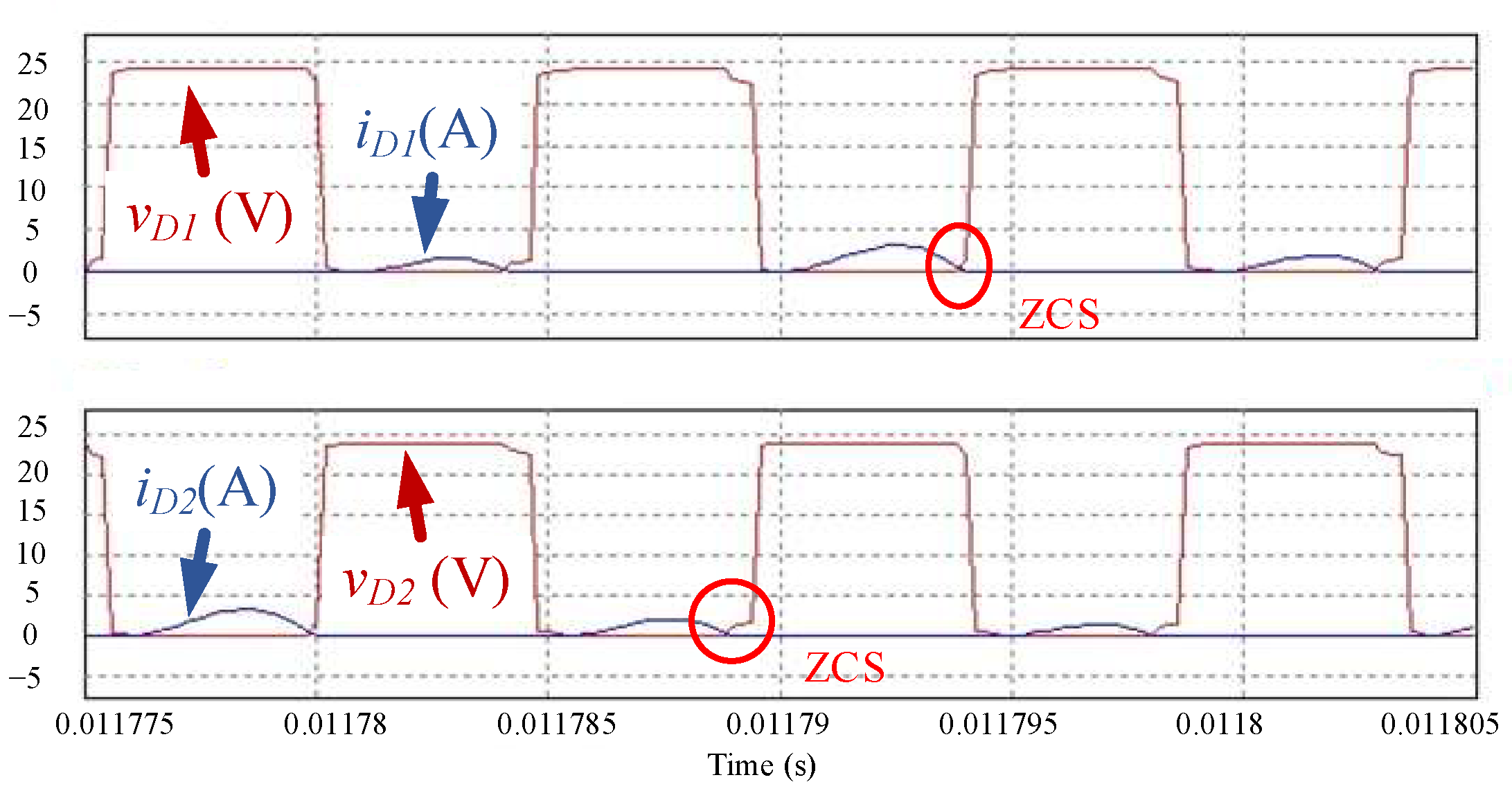
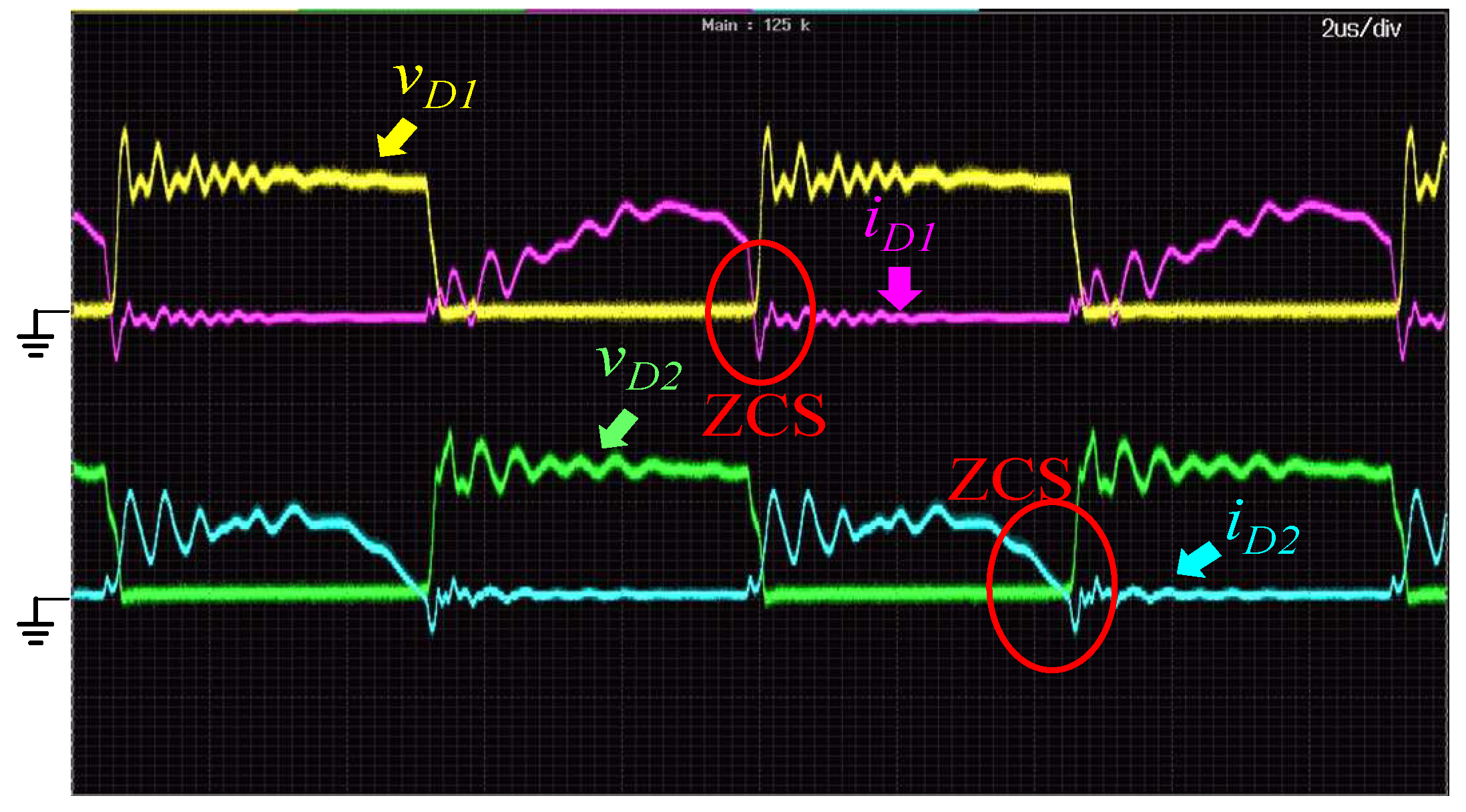
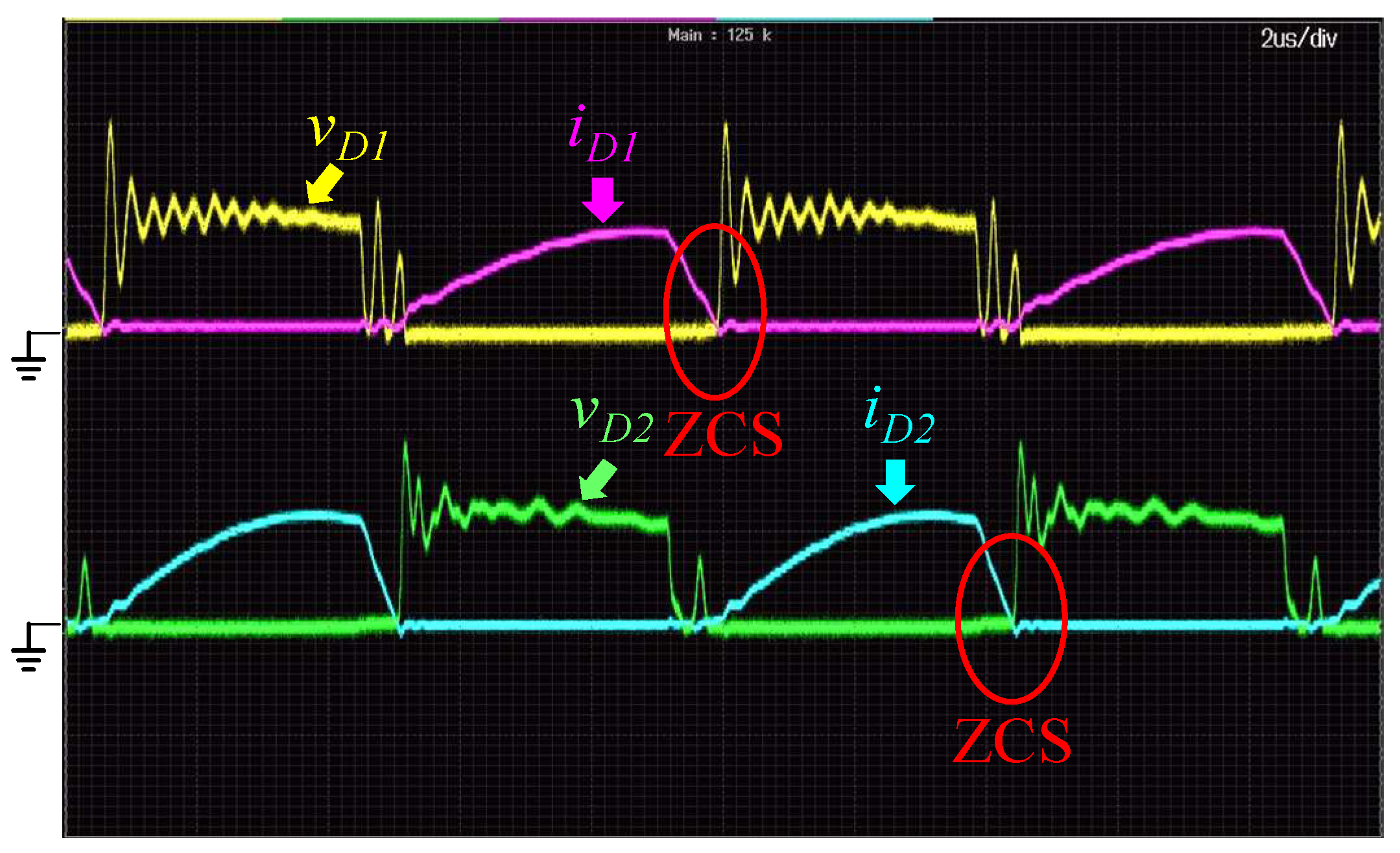
Figure 18 shows the measured waveforms of the rectifier diodes D₁ and D₂ on the secondary side, and the output is 10% rated load. Figure 19 shows the measured waveforms of the rectifier diodes D₁ and D₂ on the secondary side, and the output is 50% rated load. Figure 20 shows the measured waveforms of the rectifier diodes D₁ and D₂ on the secondary side, and the output is 100% rated load. Zero-current switching (ZCS) is achieved under light-load, half-load, and full-load conditions. The excellent performance of the proposed converter is verified by the experimental results. 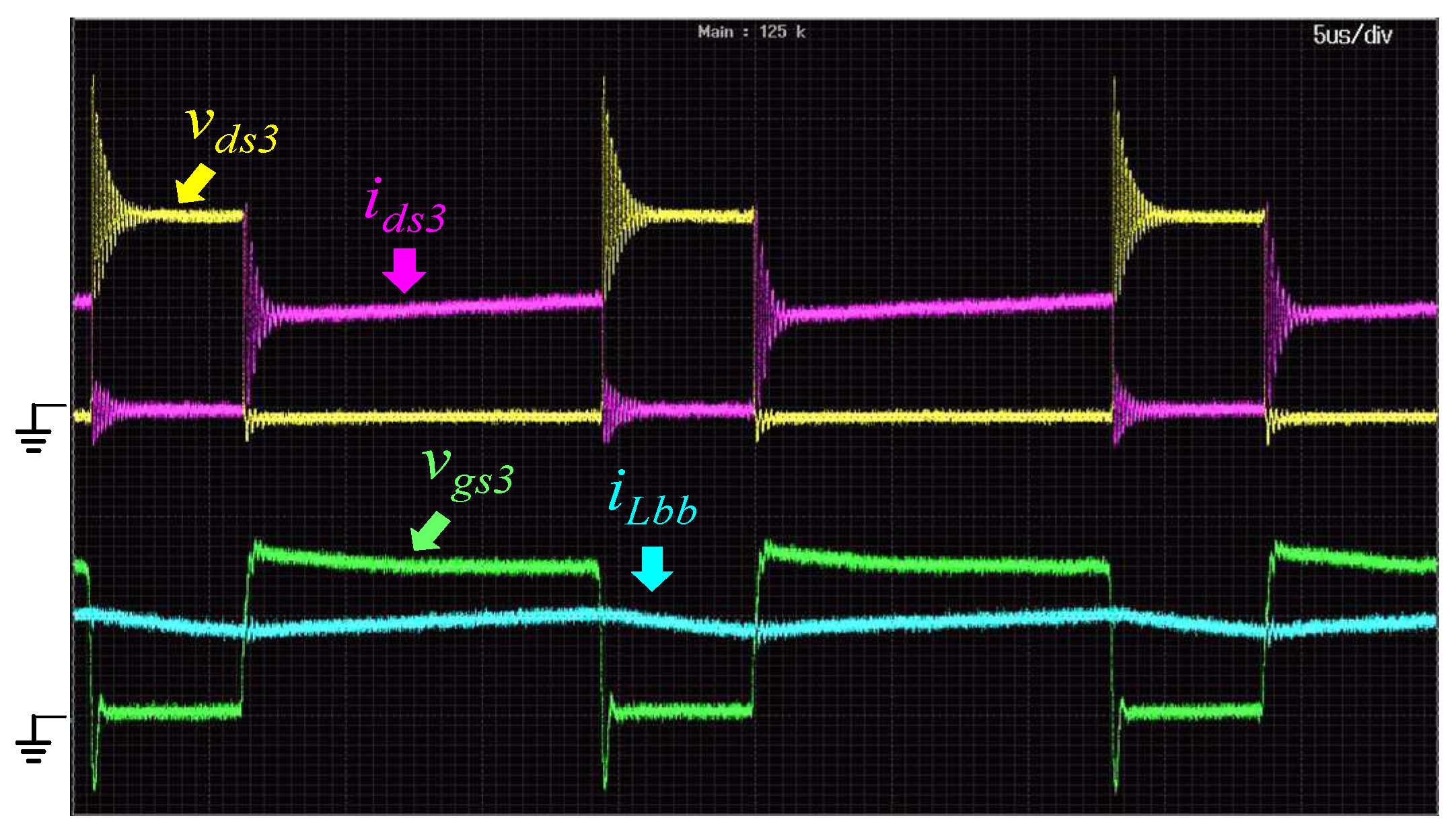It is obvious from Figure 21 and Figure 22 that the storage inductors are both operating in continuous conduction mode (CCM). In Figure 23a, if the duty ratio of switch S₃ is 0.5, the output voltage is 24 V. Figure 23b shows that the output voltage is 40 V when the duty ratio is 0.7.

Since the proposed converter can achieve ZVS turn-on at S₁ and S₂ and ZCS turn-off at D₁–D₄, power loss analysis for the converter can be divided into several main components, namely the conduction loss, switching loss of S₃, turn-off loss of S₁ and S₂, reverse recovery loss of D₅, and transformer loss. The conduction loss of the switching device P_{S_cond} and diode P_{D_cond} can be expressed as the following:

$$P_{S\_cond}=I_{rms}^2\times R_{DS\left(ON\right)}$$

(7)

$$P_{D\_cond}=I_{rms}^2{r}_D+V_F{I}_{avg}$$

(8)

where r_D and R_DS(ON) are the internal resistance of the diode and switch, respectively, I_rms is the effective value of the switch or diode current, I_avg is the average current of the diode, and V_F is the forward voltage drop of the diode.

Practically, the capacitors have equivalent series resistance (ESR) and the inductors have direct current resistance (DCR). Therefore, the conduction loss of capacitors P_{C_cond} and inductors P_{L_cond} must be considered in total power loss of the proposed converter. P_{C_cond} and P_{L_cond} can be calculated as (9) and (10), respectively:

$$P_{C\_cond}=I_{C\_rms}^2\times ESR$$

(9)

$$P_{L\_cond}=I_{L\_rms}^2\times DCR$$

(10)

where I_{C_rms} and I_{L_rms} are the rms current of capacitors and inductors, respectively, ESR is the equivalent series resistance of capacitors, and DCR is direct current resistance of inductors.

The switching loss of the power switch P_sw can be expressed as the following formula:

$$P_{sw}={\displaystyle \frac{1}{2}}{\times V}_{DS}\times I_{DS}\times t_{overlap}{\times f}_s$$

(11)

where V_DS is the DS terminal voltage of the switch, I_DS is the current of the switch, f_s is the switching frequency, and t_overlap is the overlapping time between v_DS and i_DS of the switch, as shown in Figure 24. The turn-off loss of S₁ and S₂ can also be calculated by (11).

Because of the characteristics of soft switching only being achieved at D₁–D₄, D₅ will generate reverse recovery loss P_rr when it is turned off. The formula of P_rr can be obtained as:

$$P_{rr}={\displaystyle \frac{1}{2}}{\times V}_r\times I_{rr}\times t_{rr}{\times f}_s$$

(12)

where V_r is the reverse voltage of the diode, I_rr is the reverse recovery current of the diode, and t_rr is the reverse recovery time of the diode.

Transformer loss includes winding loss P_{T_w} and core loss P_{T_core}. Since the calculation of winding loss is similar to (10), P_{T_w} will not be mentioned here. Core loss can be estimated using the Steinmetz equation:

$$P_{core}=K\times f_s^{\alpha }\times {∆B}^{\beta }$$

(13)

where K, α, and β are coefficients from the datasheet of core material and ∆B is the magnetic flux variation of transformer.

The overall converter efficiency η can be obtained by the following formula:

$$\eta ={\displaystyle \frac{P_o}{P_o+P_{loss}}}$$

(14)

where P_o is the output power and P_loss is the total power loss.

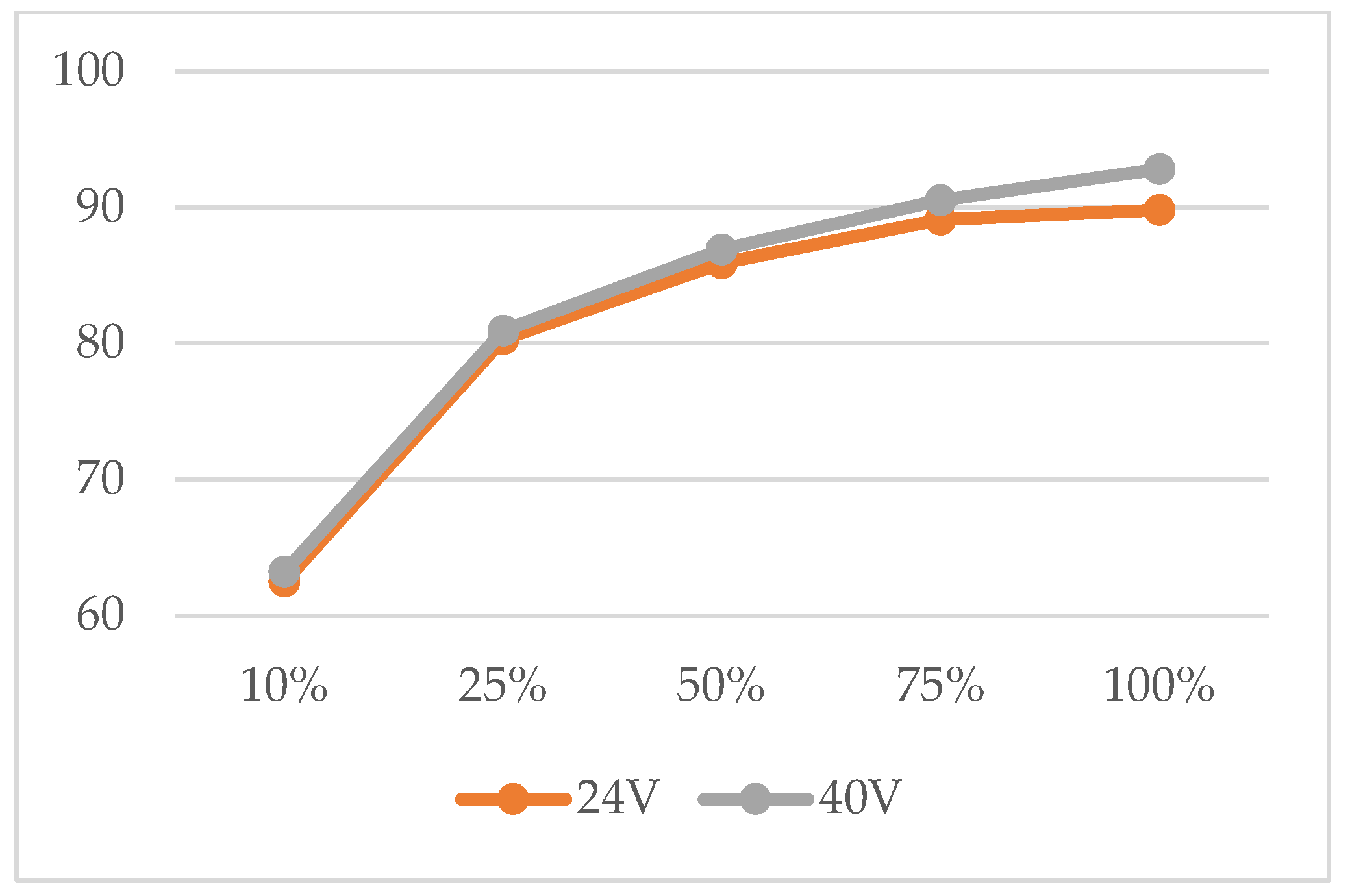
Figure 25 shows the efficiency curves of the converter at different output voltages. It can be observed in the curves that the highest efficiency reaches 92.8% at 80 W. The efficiency of the converter decreases directly proportional to the load.

Figure 26 shows the sum of different power losses of the proposed converter when the output voltage is 40 V at full load, including the switching loss of switches, the conduction loss of switches, the reverse recovery loss of diodes, the conduction loss of diodes, the conduction loss of resonant and magnetic components, the core loss, and the winding loss. As Figure 26 shows, the total power loss of the proposed converter is obtained at 6.21 W, and the LLC part is around 66.49% of the entire power loss. In the power loss of the LLC part, the core loss is the majority loss and the conduction loss of S₁ and S₂ is the minority loss. Most of the loss in the buck–boost part is due to the conduction loss of L₃. On the contrary, the reverse recovery loss of D₅ is the lowest.

Table 2. Comparison of the proposed converter and 3 other converters.

Topologies	Proposed	[5]	[6]	[14]
Efficiency (%)	92.8	97.3	94.3	95.2
Number of Switches	3	8	4	4
Number of Diodes	5	0	4	0
Number of Relays	0	0	0	1
Number of Transformers	2	2	2	2
Soft Switching	√	√	√	√
Modulation	PWM	PFM	PSM	PFM
Input Voltage (V)	384	400	260–340 (1.3)	127–190 (1.5)/ 254–380 (1.5)
Output Voltage (V)	24–40 (1.67)	12	48	16.5
Po (W)	80	600	240	60

gives a performance comparison for the proposed converter with three different converters. As Table 2 shows, the proposed converter and other converters in [5,6,14] used two transformers and achieved the ability of soft switching. The proposed converter uses the fewest switches compared with [5,6,14]. Moreover, ref. [14] is the only converter that used the relay in Table 2. The converter using pulse-frequency modulation (PFM) regulates voltage by varying the switching frequency and requires a wide switching frequency range [5,14,25]. However, the wide switching frequency range increases the difficulty of the design of the magnetic component. Pulse-width modulation (PWM) and phase-shift modulation (PSM) are the fixed-frequency modulations that simplify the magnetic component design. The voltage range of the proposed converter is wider than the other converters in Table 2 even when the proposed converter is not the best in terms of efficiency. Therefore, the proposed converter is a good choice in medium- or low-power applications.

5. Conclusions

This paper has presented a dual half-bridge parallel LLC resonant converter with a wide range of output voltages. The converter efficiencies at all load ranges are improved by zero-voltage switching and zero-current switching. The proposed converter reaches the highest efficiency of 92.8% at full load when the output is 40 V. The simulation and experimental results demonstrate that when the output voltage of the proposed converter is 40 V, ZVS is achieved for the primary side switch of the converter in heavy-load, half-load, or light-load conditions. ZCS is achieved for the secondary diode at full load and light load. The performance of the converter is verified. The proposed converter is very suitable and attractive for medium- or low-power applications with a wide range of output voltages.