Robust Stability Analysis of Grid-Forming Converter-Dominated Grids Using Grey-Box Modelling Approach
Abstract
1. Introduction
- Generic modelling of the GFM converter is provided considering all the possible implementations of the synchronization, the voltage profile management, and the inner voltage and current control loops by assuming only rough and non-detailed knowledge of the converters control system.
- The generic modelling considers the DC link dynamics, which make it suitable to model hybrid AC/DC grids.
- A proper definition of uncertainties for each uncertain control loop is discussed to be able to consider all the possible implementations.
- Stability analysis of GFM converter-dominated grids using robust control theory is conducted by studying the stability margin for different operating conditions of the grid.
- Sensitivity analysis of the uncertain control loops is also investigated in order to determine which of the control loops have a significant impact on the stability of GFM converter-dominated grids.
2. Power Converters Control System Uncertainties and Their Modelling
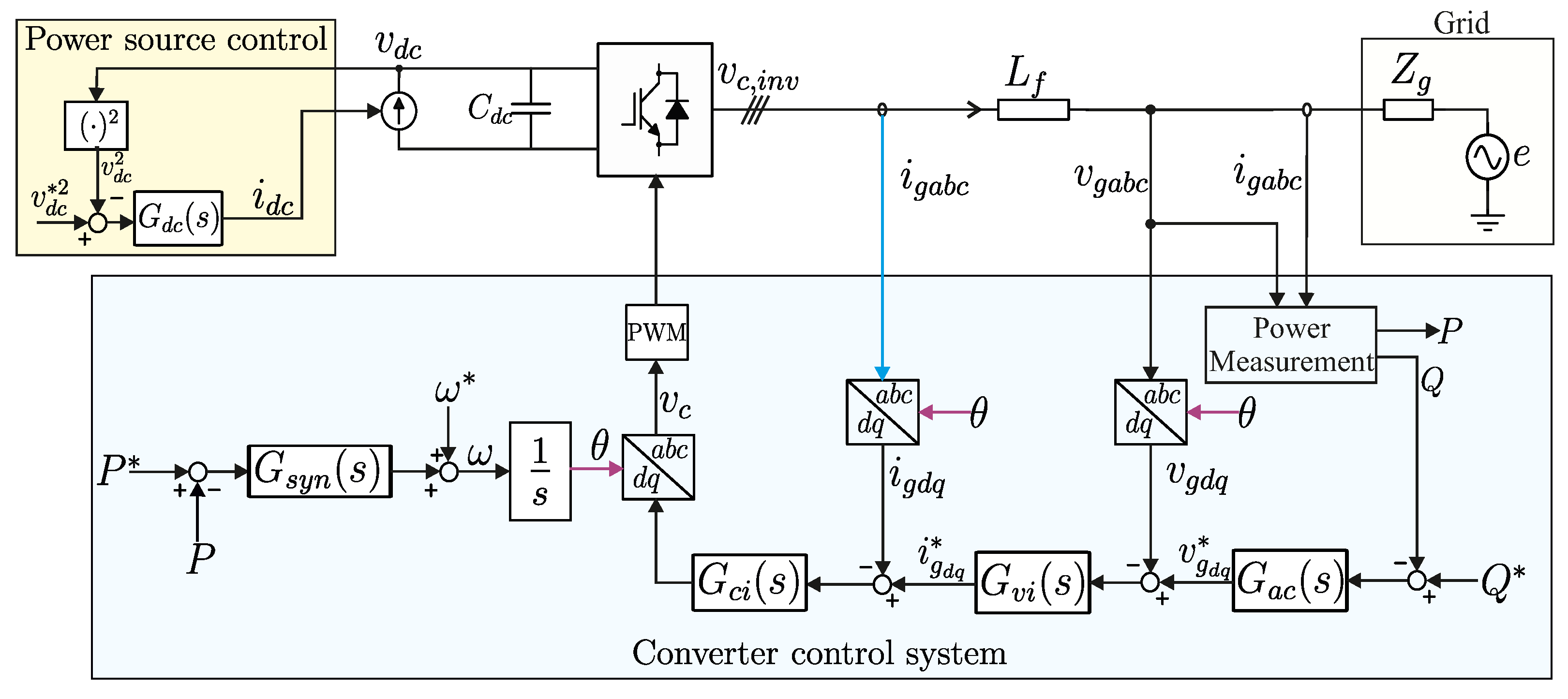
2.1. Generic Modelling of GFM Converters
2.1.1. Synchronization Loop Modelling
2.1.2. Reactive Power AC Voltage Loop Modelling
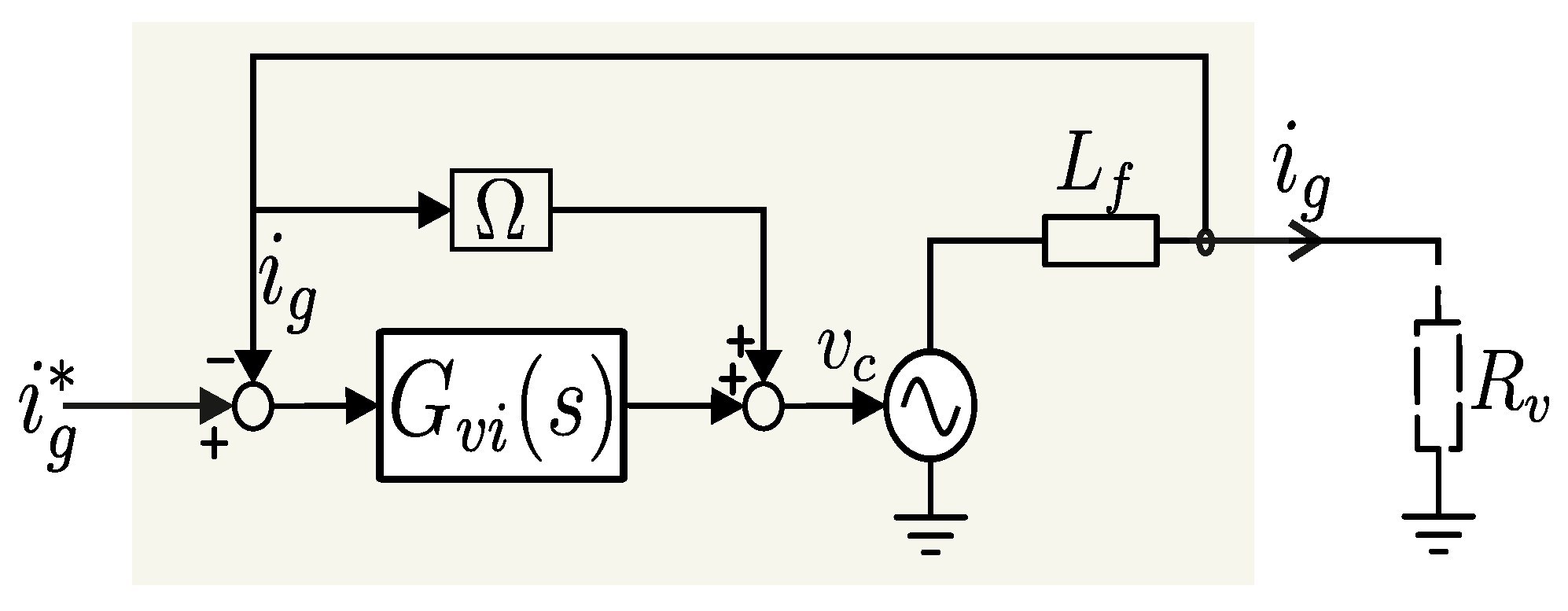
2.1.3. Cascaded Voltage and Current Control Loop Modelling
2.1.4. DC Voltage Control Loop Modelling
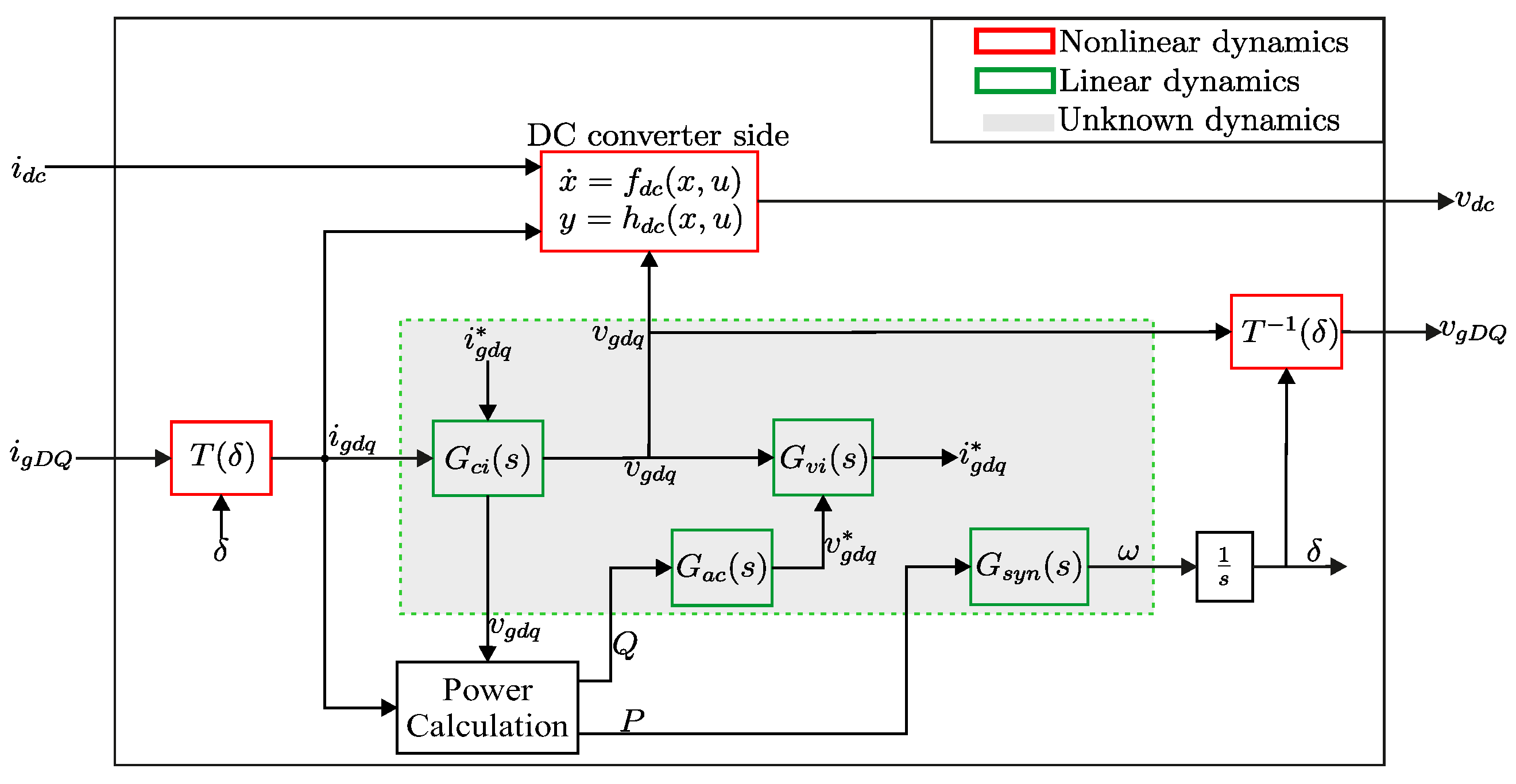
2.2. Grey-Box Non-Linear Modelling of GFM Converter
2.3. Multiplicative Uncertainty Formulation
- is the real plant transfer function.
- is the transfer function of the nominal control loop implementations. In this case, the control loop parameters and implementations are totally unknown, so the nominal control loop is chosen by the initial guess made with the generic knowledge about the converter.
- is the uncertainty transfer function for which the real plant is deviated from the initial guess . For instance, if a higher deviation is expected in the real implementations of the control loop, then can be chosen as a high-pass filter. The unknown frequency-dependent transfer function can be defined using a MATLAB 2023b command with norm of unitary and can be used to shape the frequency response of the uncertain function.
- is a scalar constant which quantifies the amount of uncertainty.
2.4. Quantitative Design of the Uncertainty in the Converter Control System
2.4.1. Synchronization Loop
2.4.2. Reactive Power AC Voltage Loop
2.4.3. Inner Voltage Control Loop
2.4.4. Inner Current Control Loop
2.4.5. DC Voltage Control Loop
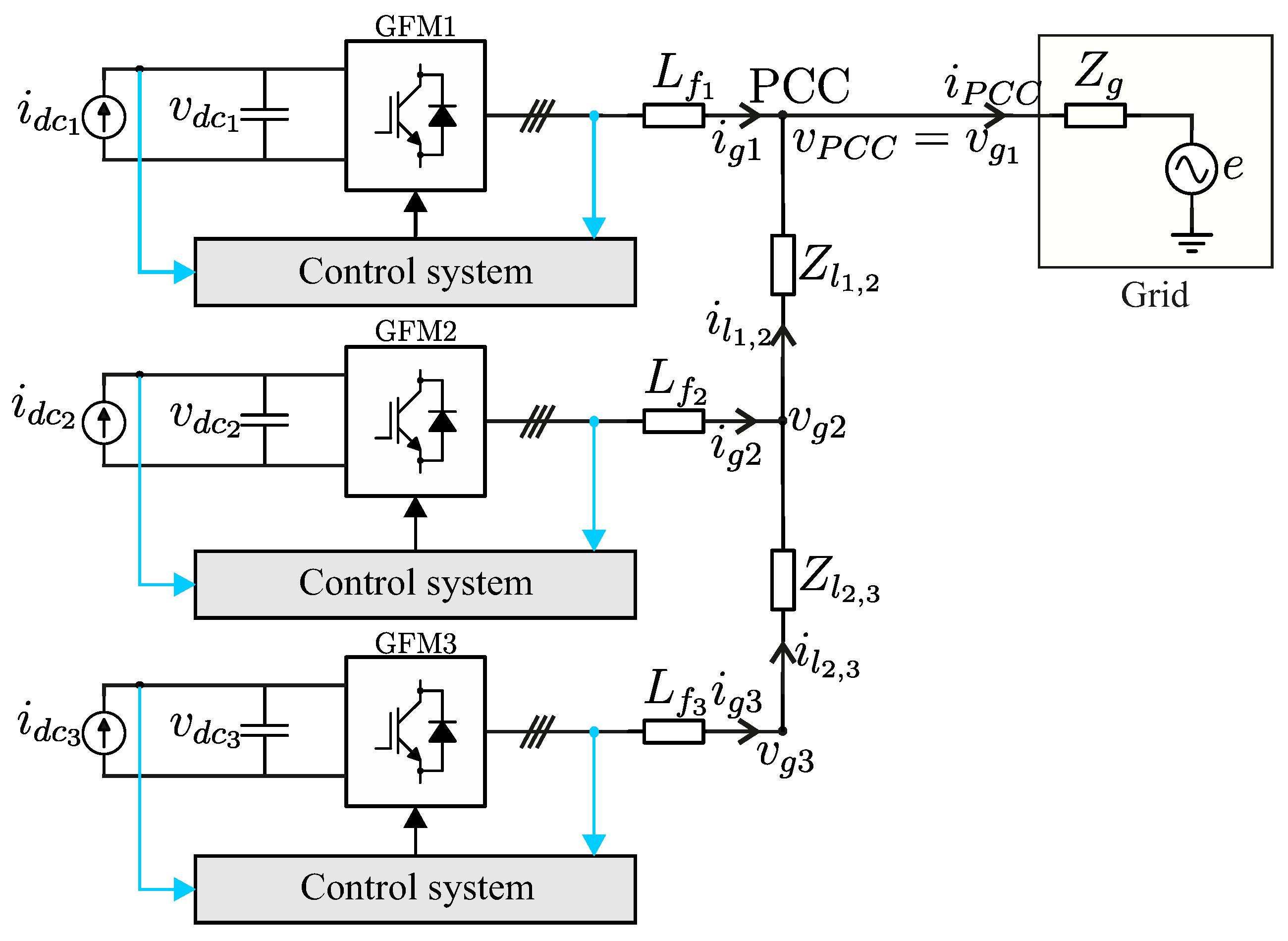
3. Non-Linear Grey-Box State-Space Model of Converter-Dominated Grids
Non-Linear Interconnection with the Power Grid
4. Robust Stability Analysis
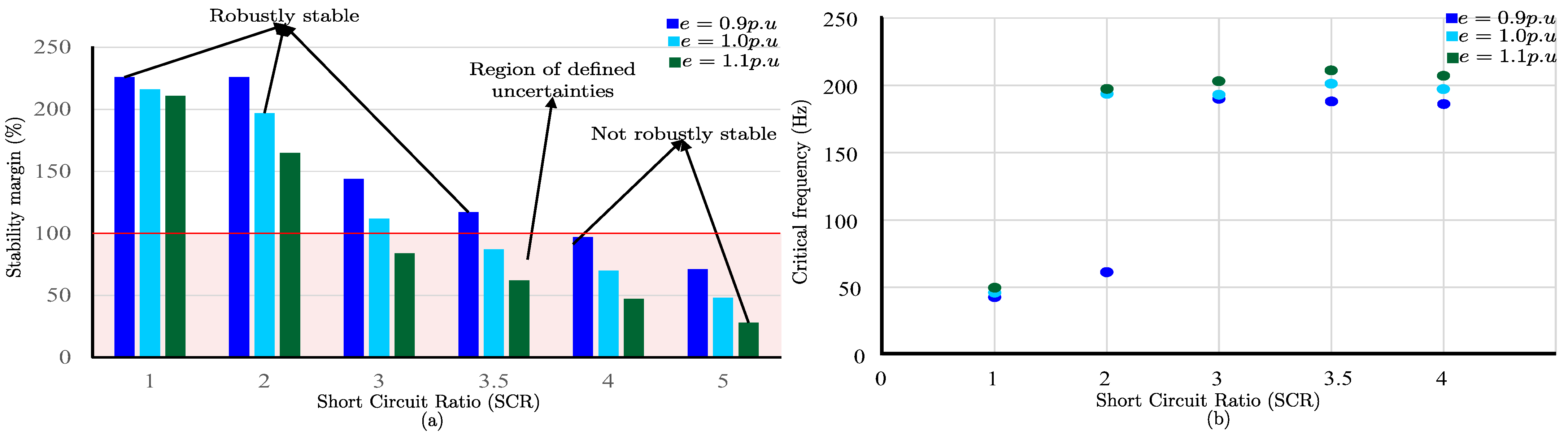
4.1. Robust Stability Analysis of the Grid with Single GFM Converter
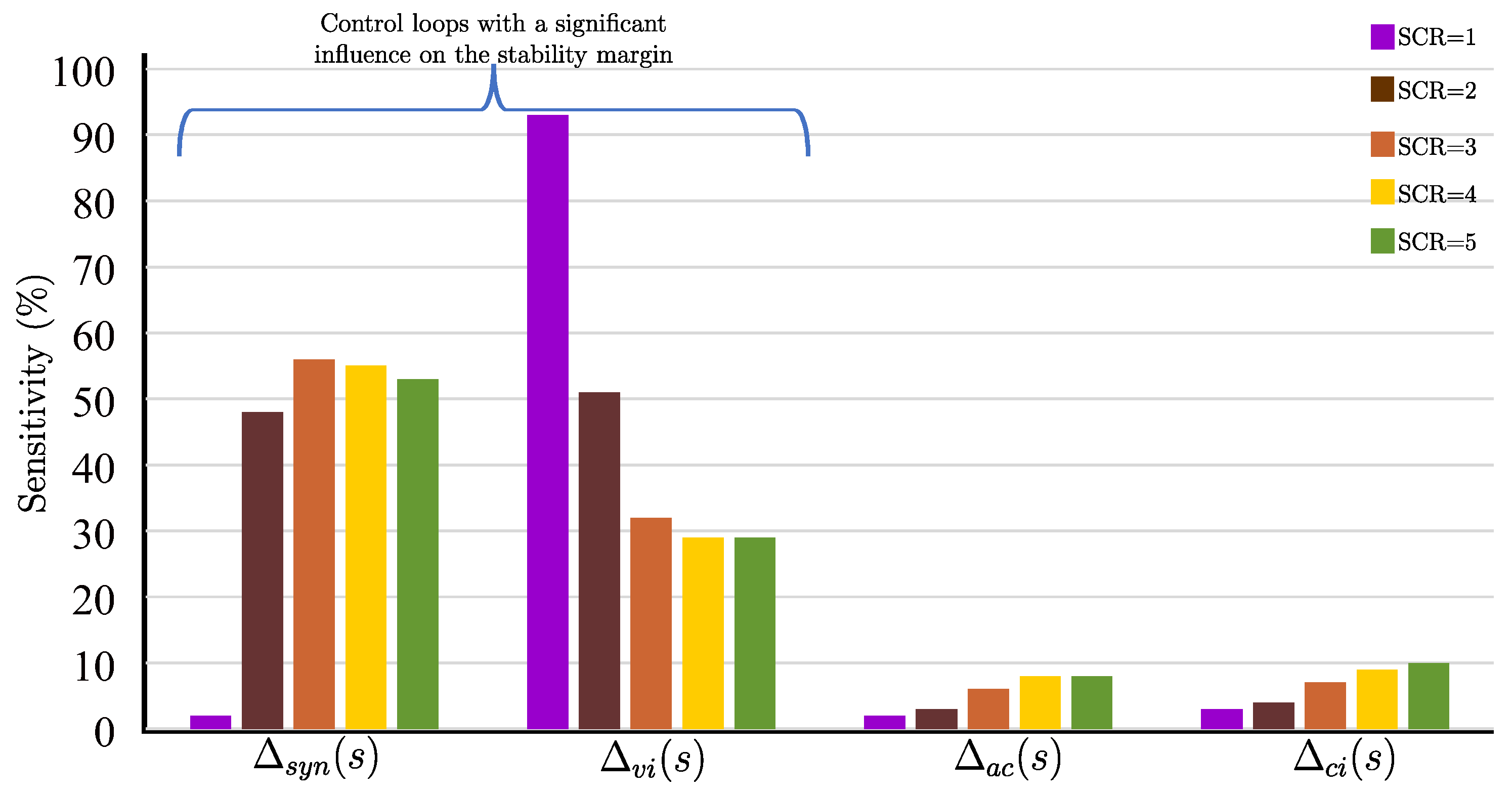
4.2. Sensitivity Analysis of the Control Loops
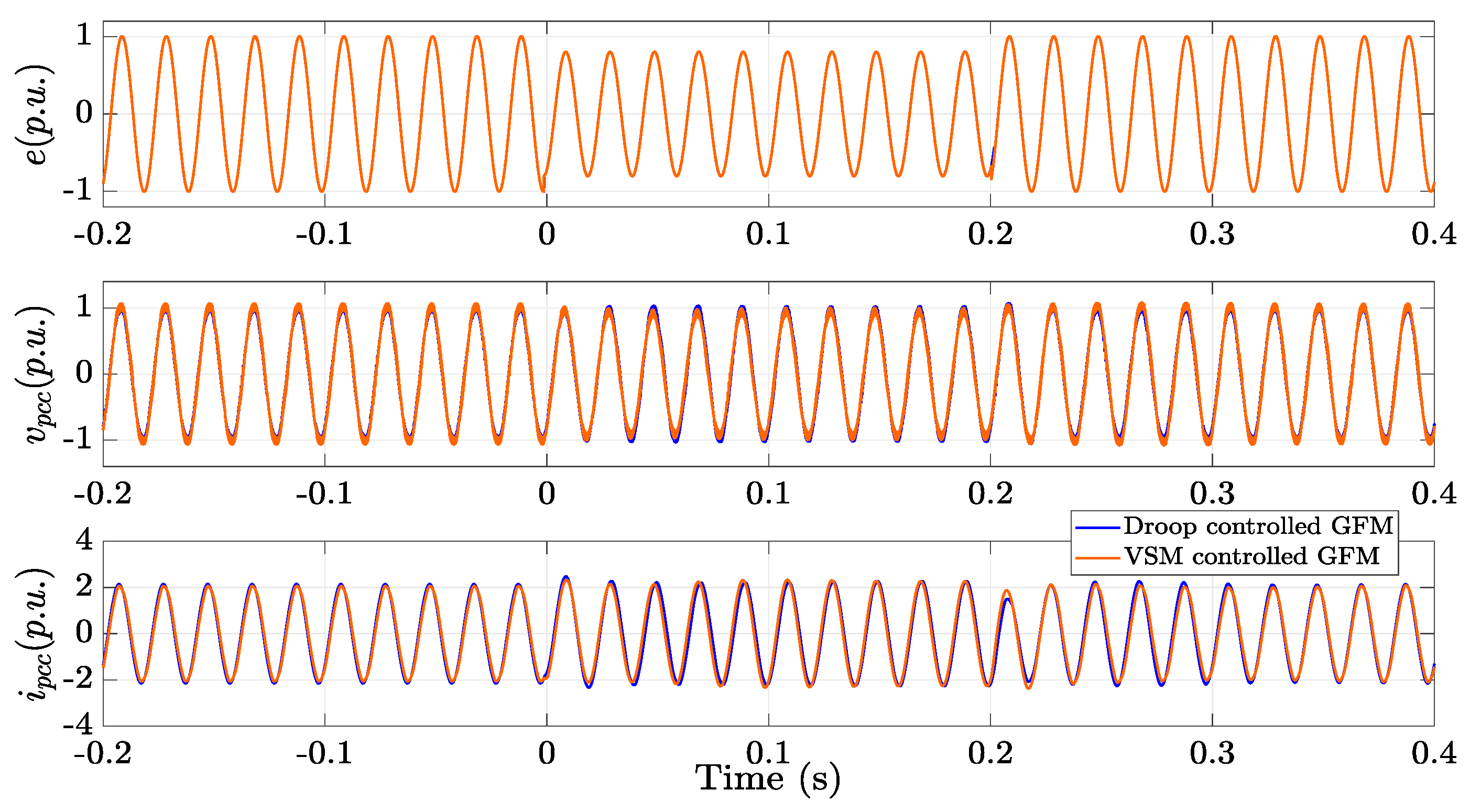
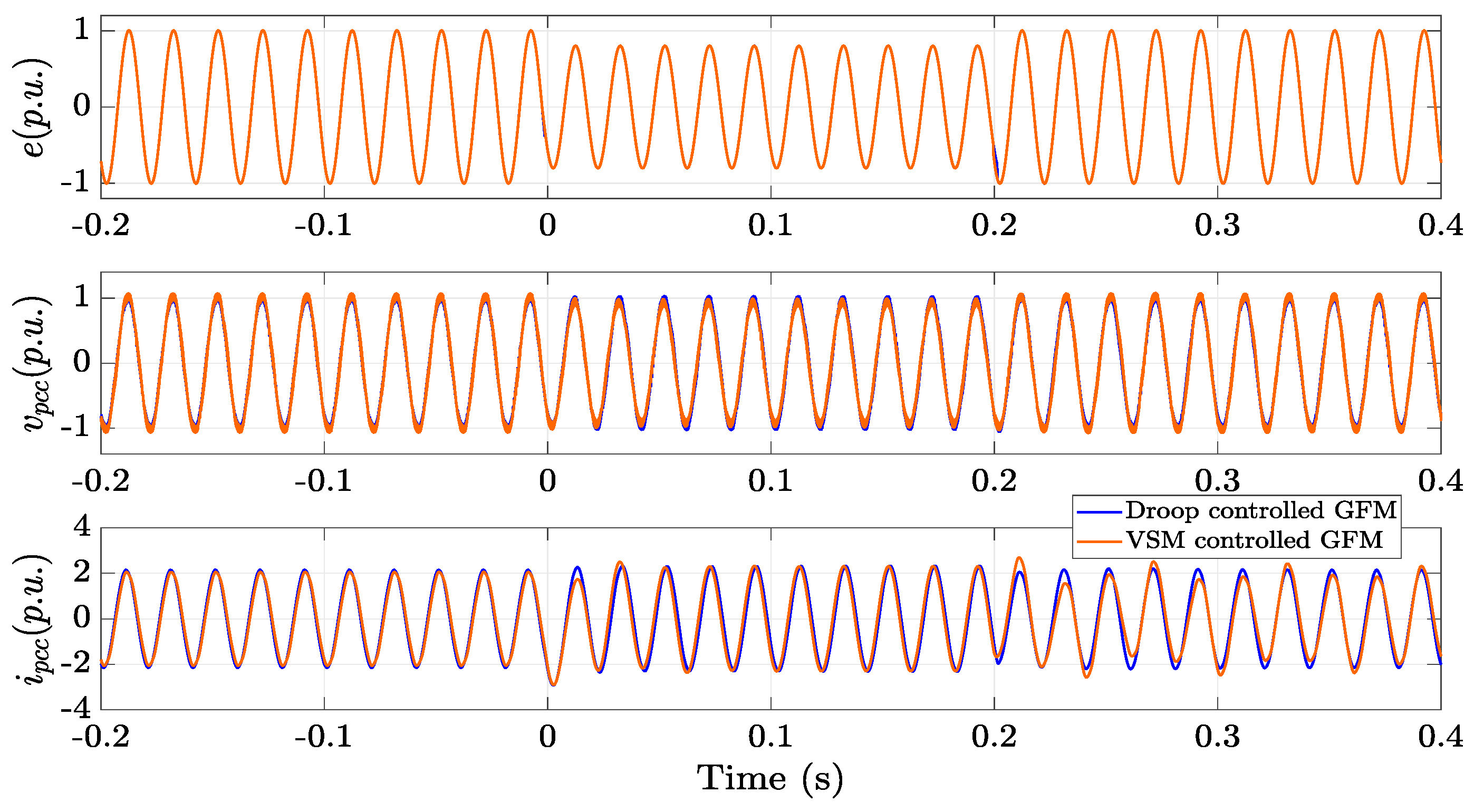
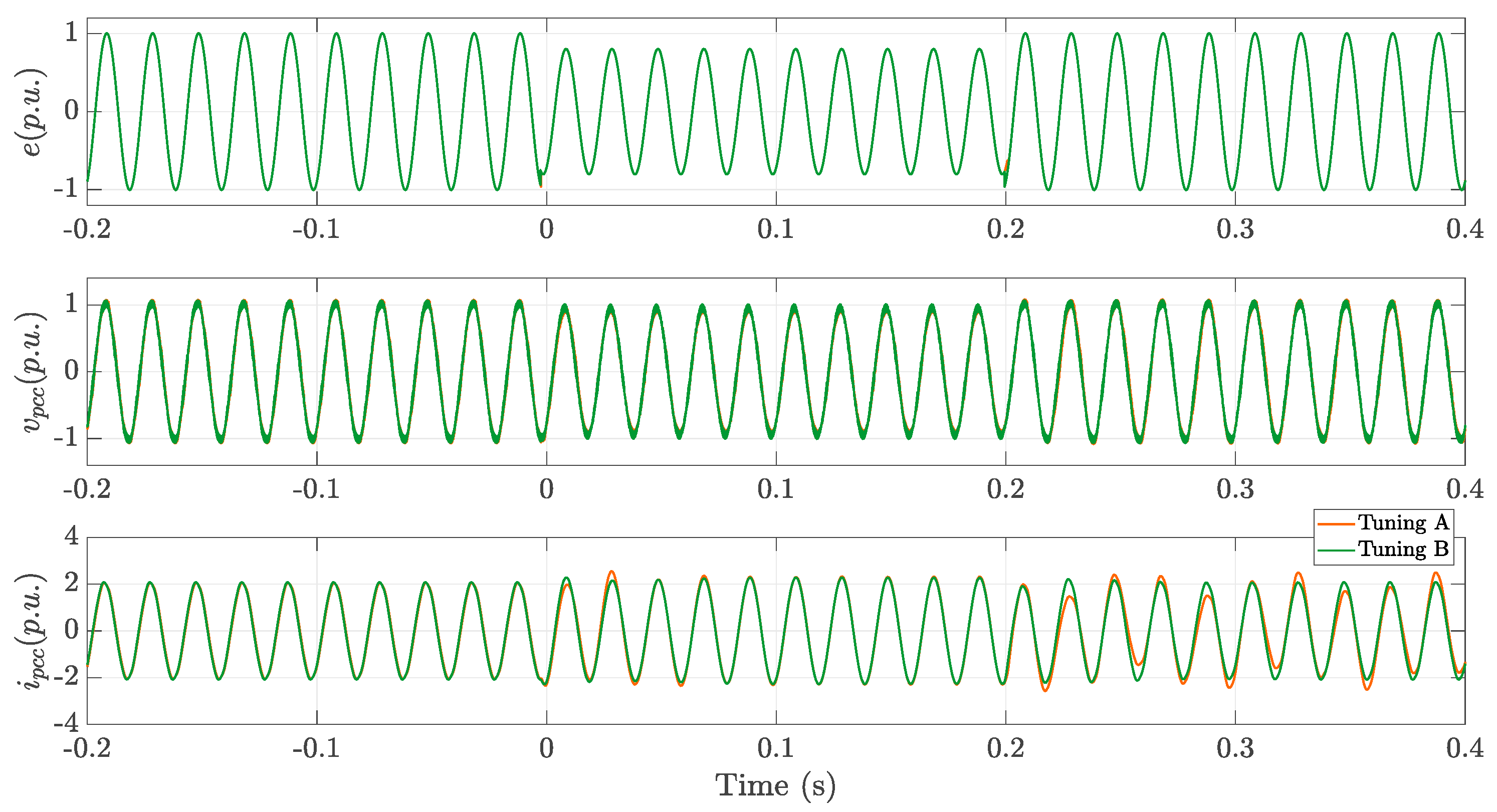
5. Hardware-in-the-Loop (Hil) Results
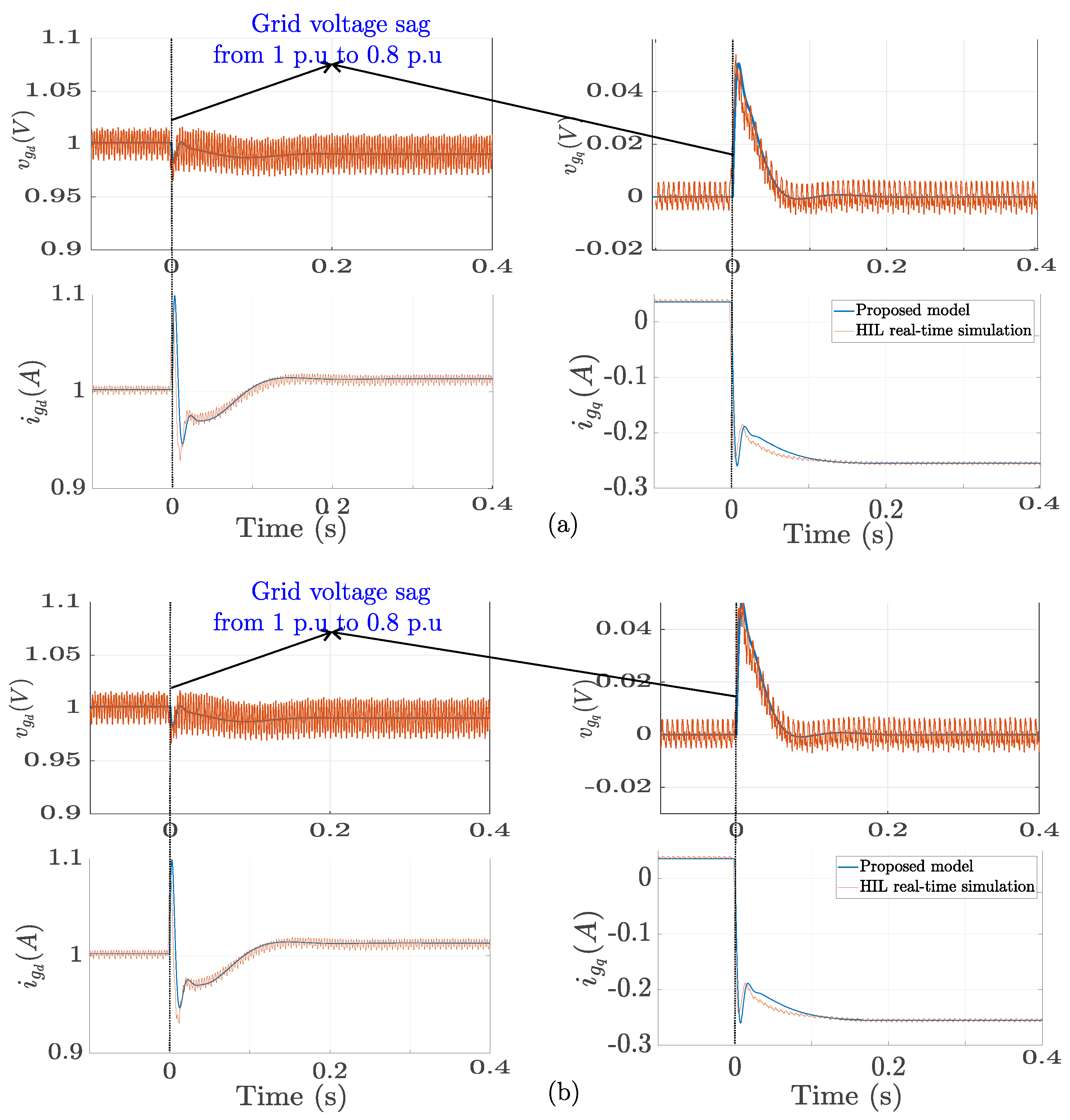
5.1. Model Validation with Hil Real Time Simulation
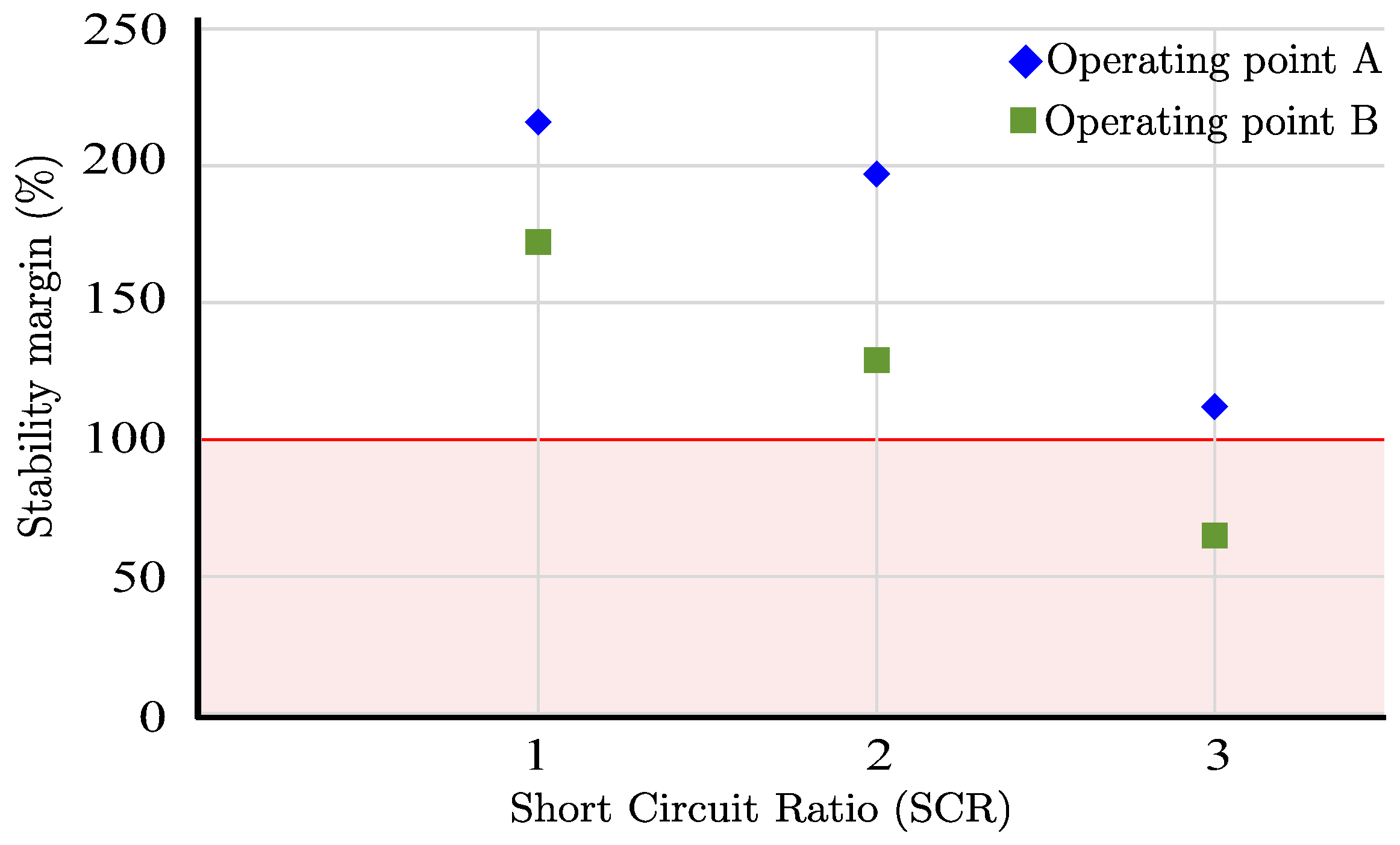
5.2. Robust Stability Analysis Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pishbahar, H.; Blaabjerg, F.; Saboori, H. Emerging grid-forming power converters for renewable energy and storage resources integration—A review. Sustain. Energy Technol. Assessments 2023, 60, 103538. [Google Scholar] [CrossRef]
- Zhang, H.; Xiang, W.; Lin, W.; Wen, J. Grid Forming Converters in Renewable Energy Sources Dominated Power Grid: Control Strategy, Stability, Application, and Challenges. J. Mod. Power Syst. Clean Energy 2021, 9, 1239–1256. [Google Scholar] [CrossRef]
- Liao, Y.; Wu, H.; Wang, X.; Ndreko, M.; Dimitrovski, R.; Winter, W. Stability and Sensitivity Analysis of Multi-Vendor, Multi-Terminal HVDC Systems. IEEE Open J. Power Electron. 2023, 4, 52–66. [Google Scholar] [CrossRef]
- Arévalo-Soler, J.; Nahalparvari, M.; Groß, D.; Prieto-Araujo, E.; Norrga, S.; Gomis-Bellmunt, O. Small-Signal Stability and Hardware Validation of Dual-Port Grid-Forming Interconnecting Power Converters in Hybrid AC/DC Grids. IEEE J. Emerg. Sel. Top. Power Electron. 2024. [Google Scholar] [CrossRef]
- Navarro-Rodríguez, Á.; García, P.; Gómez-Aleixandre, C.; Blanco, C. Cooperative Primary Control of a Hybrid AC/DC Microgrid Based on AC/DC Virtual Generators. IEEE Trans. Energy Convers. 2022, 37, 2837–2850. [Google Scholar] [CrossRef]
- Hu, P.; Li, Y.; Yu, Y.; Blaabjerg, F. Inertia estimation of renewable-energy-dominated power system. Renew. Sustain. Energy Rev. 2023, 183, 113481. [Google Scholar] [CrossRef]
- Saha, S.; Saleem, M.I.; Roy, T.K. Impact of high penetration of renewable energy sources on grid frequency behaviour. Int. J. Electr. Power Energy Syst. 2023, 145, 108701. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Sepehr, A.; Pournazarian, B.; Catalão, J.P.S. Control of power electronics-based synchronous generator for the integration of renewable energies into the power grid. Int. J. Electr. Power Energy Syst. 2019, 111, 300–314. [Google Scholar] [CrossRef]
- Liao, Y.; Li, Y.; Chen, M.; Nordstr, L.; Wang, X.; Mittal, P.; Poor, H.V. Neural network design for impedance modeling of power electronic systems based on latent features. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 5968–5980. [Google Scholar] [CrossRef] [PubMed]
- Suryani, A.; Sulaeman, I.; Rosyid, O.A.; Moonen, N.; Popović, J. Interoperability in Microgrids to Improve Energy Access: A Systematic Review. IEEE Access 2024, 12, 64267–64284. [Google Scholar] [CrossRef]
- Paolone, M.; Gaunt, T.; Guillaud, X.; Liserre, M.; Meliopoulos, S.; Monti, A.; Van Cutsem, T.; Vittal, V.; Vournas, C. Fundamentals of power systems modelling in the presence of converter interfaced generation. Electr. Power Syst. Res. 2020, 189, 106811. [Google Scholar] [CrossRef]
- Rasheduzzaman, M.; Mueller, J.A.; Kimball, J.W. Reduced-order small-signal model of microgrid systems. IEEE Trans. Sustain. Energy 2015, 6, 1292–1305. [Google Scholar] [CrossRef]
- Lai, N.B.; Baltas, G.N.; Rodriguez, P. Small-Signal Modeling of Grid-Forming Power Converter. In Proceedings of the 2022 IEEE 13th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Kiel, Germany, 26–29 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Bryant, J.S.; McGrath, B.; Meegahapola, L.; Sokolowski, P. Small-Signal Modeling and Stability Analysis of a Droop-Controlled Grid-Forming Inverter. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Mattavelli, P.; Burgos, R.; Shen, Z. Impedance-based analysis of grid-synchronization stability for three-phase paralleled converters. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 1233–1239. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Riccobono, A.; Mirz, M.; Monti, A. Noninvasive online parametric identification of three-phase ac power impedances to assess the stability of grid-tied power electronic inverters in lv networks. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 629–647. [Google Scholar] [CrossRef]
- Cecati, F.; Liserre, M. Interoperability Specifications for Multi Vendor Converter-Dominated Grid: A Robust Stability Perspective. TechRxiv 2024. [Google Scholar] [CrossRef]
- Fazal, S.; Haque, M.E.; Arif, M.T.; Gargoom, A. Droop control techniques for grid forming inverter. In Proceedings of the 2022 IEEE PES 14th Asia-Pacific Power and Energy Engineering Conference (APPEEC), Melbourne, Australia, 20–23 November 2022; pp. 1–6. [Google Scholar]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-Synchronization Control of Grid Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Nguyen, P.-L.; Ma, Z.; Sheng, W. Self-synchronized synchronverters: Inverters without a dedicated synchronization unit. IEEE Trans. Power Electron. 2013, 29, 617–630. [Google Scholar] [CrossRef]
- Rodríguez, P.; Citro, C.; Candela, J.I.; Rocabert, J.; Luna, A. Flexible Grid Connection and Islanding of SPC-Based PV Power Converters. IEEE Trans. Ind. Appl. 2018, 54, 2690–2702. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-Forming Converters: Control Approaches, Grid-Synchronization, and Future Trends—A Review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
- Cecati, F.; Zhu, R.; Liserre, M.; Wang, X. State-feedback-based Low-Frequency Active Damping for VSC Operating in Weak-Grid Conditions. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 4762–4767. [Google Scholar] [CrossRef]
- Cecati, F.; Zhu, R.; Liserre, M.; Wang, X. Nonlinear Modular State-Space Modeling of Power-Electronics-Based Power Systems. IEEE Trans. Power Electron. 2022, 37, 6102–6115. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Pogaku, N.; Prodanovic, M.; Green, T.C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef]
- Cavazzana, F.; Caldognetto, T.; Mattavelli, P.; Corradin, M.; Toigo, I. Analysis of Current Control Interaction of Multiple Parallel Grid Connected Inverters. IEEE Trans. Sustain. Energy 2018, 9, 1740–1749. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control; Prentice Hall: Upper Saddle River, NJ, USA, 1998; Volume 104. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- D’Arco, S.; Suul, J.A. Equivalence of virtual synchronous machines and frequency droops for converter-based microgrids. IEEE Trans. Smart Grid 2013, 5, 394–395. [Google Scholar] [CrossRef]
- Gao, X.; Zhou, D.; Anvari-Moghaddam, A.; Blaabjerg, F. Stability Analysis of Grid Following and Grid-Forming Converters Based on State-Space Model. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022- ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 422–428. [Google Scholar] [CrossRef]
- Li, C.; Huang, Y.; Wang, Y.; Monti, A.; Wang, Z.; Zhong, W. Modelling and small signal stability for islanded microgrids with hybrid grid-forming sources based on converters and synchronous machines. Int. J. Electr. Power Energy Syst. 2024, 157, 109831. [Google Scholar] [CrossRef]
- Milano, F. An open source power system analysis toolbox. IEEE Trans. Power Syst. 2005, 20, 1199–1206. [Google Scholar] [CrossRef]
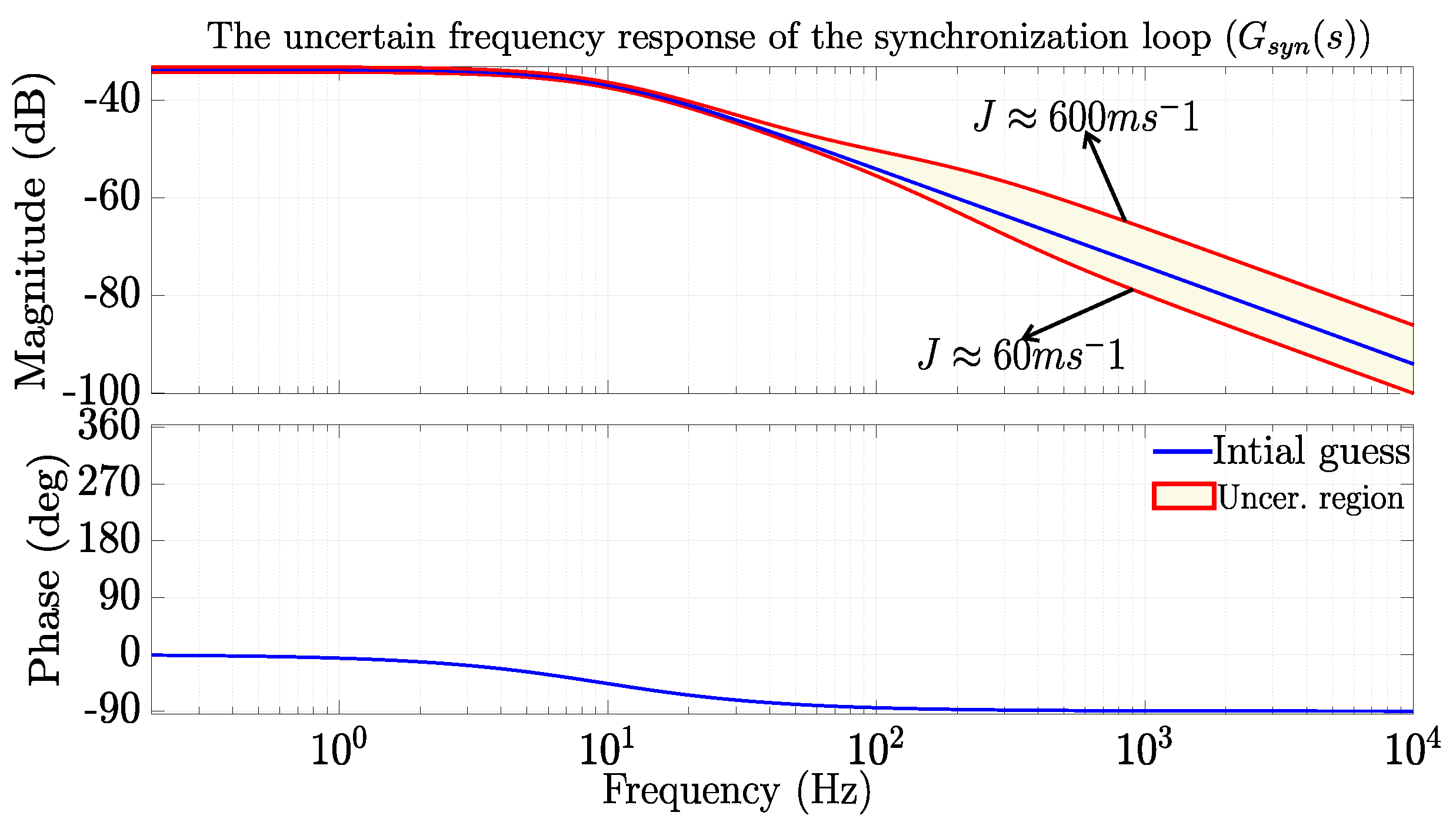
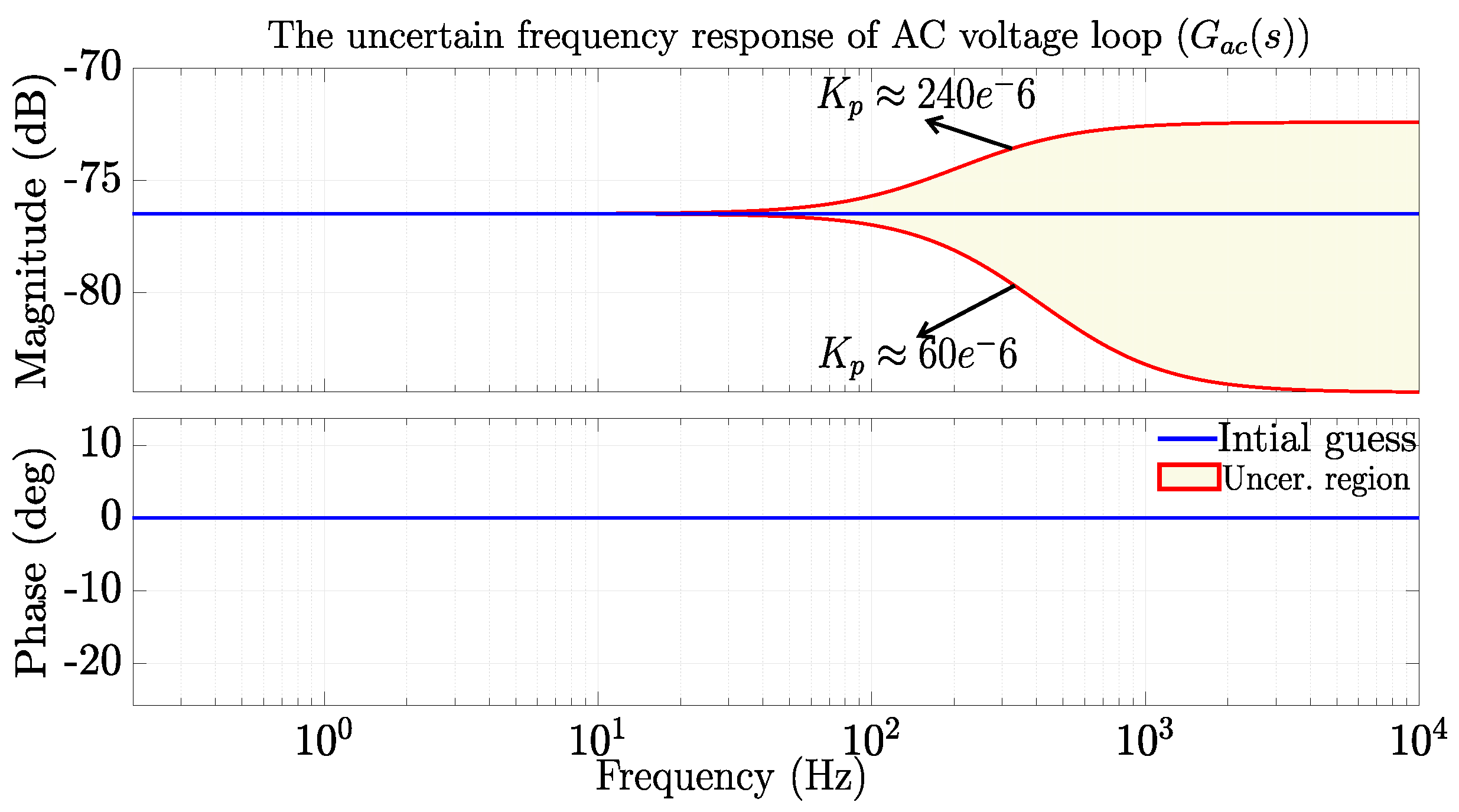
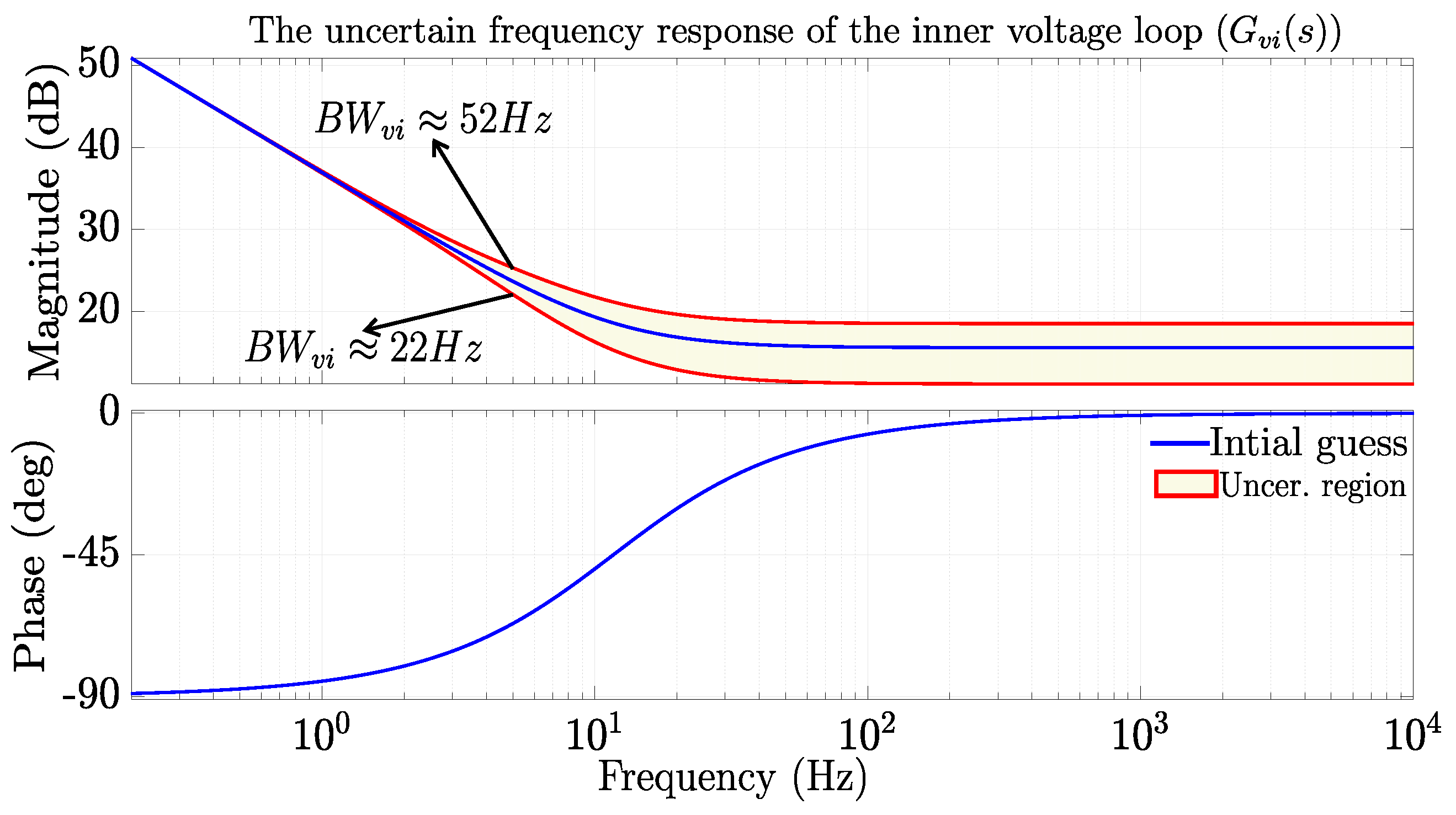
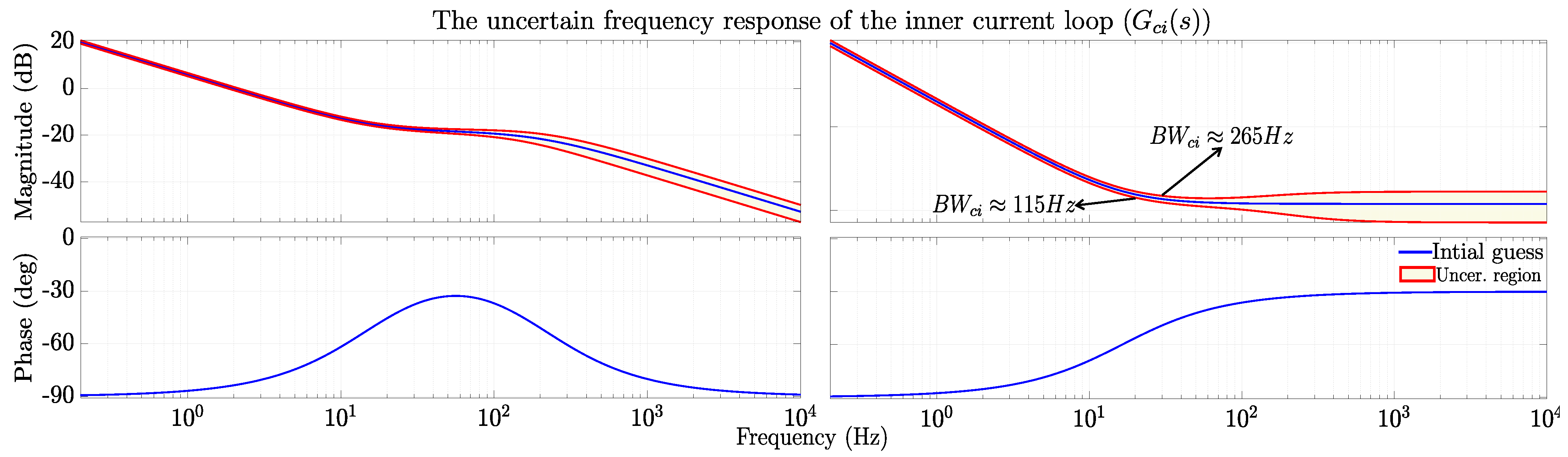

| Control Loop | Parameters for Uncertainty |
|---|---|
| Synchronization loop | , |
| AC voltage loop | |
| Inner voltage loop | |
| Inner current loop | , |
| Steady State Var. | |||||
|---|---|---|---|---|---|
| (p.u.) | 0.91 | 0.986 | 0.987 | 0.981 | |
| 0.9 | (deg) | 39.79 | 15.42 | 10 | 7.41 |
| P (p.u.) | 1 | 1 | 1 | 1 | |
| Q (p.u.) | 0.33 | 0.052 | 0.049 | 0.07 | |
| (p.u.) | 0.958 | 1.024 | 1.032 | 1.033 | |
| 1 | (deg) | 32.7 | 14.02 | 9.17 | 6.83 |
| P (p.u.) | 1 | 1 | 1 | 1 | |
| Q (p.u.) | 0.158 | −0.089 | −0.122 | −0.125 | |
| (p.u.) | 0.993 | 1.06 | 1.08 | 1.088 | |
| 1.1 | (deg) | 28.68 | 12.89 | 8.5 | 6.35 |
| P (p.u.) | 1 | 1 | 1 | 1 | |
| Q (p.u.) | 0.027 | −0.235 | −0.30 | −0.33 |
| Op. Point | Op. Point A | Op. Point B | ||||
|---|---|---|---|---|---|---|
| Steady state var. | SCR = 1 | SCR = 2 | SCR = 3 | SCR = 1 | SCR = 2 | SCR = 3 |
| (p.u.) | 0.958 | 1.024 | 1.032 | 0.93 | 1.03 | 1.04 |
| (deg) | 32.7 | 14.02 | 9.17 | 35.2 | 13.8 | 9.02 |
| P (MW) | 1 | 1 | 1 | 1.5 | 1.5 | 1.5 |
| 0.158 | −0.089 | −0.122 | 0.25 | −0.12 | −0.15 | |
| Grid and Converter Parameters | Nominal Values | For RS Analysis |
|---|---|---|
| Line-to-line grid voltage (V) | 690 | 690 |
| Short Circuit Ratio | 1.5 | variable |
| R/X ratio | 0.4 | 0.4 |
| DC-link capacitor (mF) | 22 | 22 |
| Converters Control Parameters | Nominal Values | For RS Analysis |
| Active power reference (MW) | 1 | 1 |
| Switching frequency (kHz) | 2 | 2 |
| DC-link voltage reference (V) | 1100 | 1100 |
| DC voltage time constant (ms) | 100 | 100 |
| AC voltage controller gain | 150 × 10−6 | unknown |
| Bandwidth of the synchronization loop (rad/s) | 540 | unknown |
| Bandwidth of the inner voltage loop (rad/s) | 460 | unknown |
| Bandwidth of the inner current loop (rad/s) | 1200 | unknown |
| Control Systems | Initial Guess | Tuning A | Tuning B | Rationale for Selection |
|---|---|---|---|---|
| AC voltage controller gain | 150 × 10−6 | 150 × 10−6 | 55 × 10−6 | To study grid stability with a weak control for voltage regulation |
| Bandwidth of the inner current loop (rad/s) | 1200 | 1200 | 445 | To study grid stability with slowest current dynamics |
| Bandwidth of the synchronization loop (rad/s) | 540 | 200 | 540 | To study grid stability with low damping |
| Bandwidth of the inner voltage loop (rad/s) | 460 | 170 | 460 | To study grid stability with a slow response to the grid reactive power requirement |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almawu, E.D.; Cecati, F.; Liserre, M. Robust Stability Analysis of Grid-Forming Converter-Dominated Grids Using Grey-Box Modelling Approach. Energies 2025, 18, 587. https://doi.org/10.3390/en18030587
Almawu ED, Cecati F, Liserre M. Robust Stability Analysis of Grid-Forming Converter-Dominated Grids Using Grey-Box Modelling Approach. Energies. 2025; 18(3):587. https://doi.org/10.3390/en18030587
Chicago/Turabian StyleAlmawu, Endalkachew Degarege, Federico Cecati, and Marco Liserre. 2025. "Robust Stability Analysis of Grid-Forming Converter-Dominated Grids Using Grey-Box Modelling Approach" Energies 18, no. 3: 587. https://doi.org/10.3390/en18030587
APA StyleAlmawu, E. D., Cecati, F., & Liserre, M. (2025). Robust Stability Analysis of Grid-Forming Converter-Dominated Grids Using Grey-Box Modelling Approach. Energies, 18(3), 587. https://doi.org/10.3390/en18030587








