Optimal Solutions of Economic Lot Scheduling Problem with Energy and Power Costs

Abstract

This paper proposes a new planning method for a cyclic production of many different products with steady demand and variable production rates, which minimises energy consumption while reducing and equalising power demand. The problem is modelled as the Economic Lot Scheduling Problem (elsp), with a common production cycle for all products. This paper shows that the problem can be optimally solved by a general-purpose mathematical programming solver in a short time by reformulating the general non-linear model into a Mixed-Integer Quadratically Constrained Programming (miqcp) model. This way, there is no need to develop a specialised algorithm, which requires a high level of expertise and is very labour-intensive. The proposed approach is also the only method that allows finding optimal solutions for the general case of the common-cycle elsp with variable production rates. For a problem instance known from the literature, the optimal solution ensured a reduction in the power demand cost by 10.7%, and in the total cost by 3.3%. Moreover, experiments proved that production rate lower bounds are critical for the choice of solution.

1. Introduction

Energy use and power demand are major cost factors in modern manufacturing. In the United States, the manufacturing sector was responsible for about 76% of all industrial energy use in 2022 [1]. Because many production processes are energy-intensive, even small efficiency improvements may ensure significant cost savings.

Electricity costs for factories depend not only on the total amount of energy consumed but also on the highest level of power used at any time. If production leads to sudden peaks in power demand, these short spikes can increase costs for months afterwards. This makes it important for plants to not only reduce overall energy use but also smooth out their power demand. Managing both factors, energy and power, helps companies lower costs and increase their flexibility in how they run their operations.

Recent price trends make energy management even more critical. In Europe, industrial electricity prices rose sharply during the 2021–2022 energy crisis and remain above pre-crisis levels despite some stabilisation [2]. Companies that improve efficiency and manage their power use are more resilient to such volatility. Climate policies impose additional pressure.

In this context, coupling production planning with energy and power management is a promising approach. Traditional production planning methods focus on scheduling activities, balancing workload and capacity, and minimising material, labour, transport, and inventory costs. This paper presents a method for optimally solving the Economic Lot Scheduling Problem (elsp), extended to take into account both energy consumption and power demand.

The elsp is one of the fundamental production planning models. Its goal is to determine a cyclic plan, lot sizes, and their schedule for several items produced on a single machine. It assumes that the demand and production rate are constant, the planning horizon is infinite, and the objective is to minimise average machine set-up costs and inventory holding costs per unit of time.

In the classic elsp, production rates are known and can not be changed; here, however, they are variables that have an impact not only on machine utilisation and inventory increment but also on power demand. Moreover, it is assumed that changes in production rates are limited only by the maximum allowed power demand and do not generate any additional unit costs or costs related to product quality or waste [3].

A broad review of research on energy-efficient production planning is presented in [4]. Most researchers consider various machine scheduling problems, in which the sizes of production lots are fixed in advance; the decision-maker must only assign production activities to machines and determine their sequence and timing. For example, Masmoudi et al. [5] propose integer linear programming models for the job-shop scheduling problem, which minimise energy costs while ensuring that power demand does not exceed a predefined upper bound. Böning et al. [6] propose a metaheuristic algorithm for the flexible job-shop problem, which minimises the power peak costs.

There are only two papers considering the energy-efficient elsp. Beck et al. [7] considered the common-cycle elsp with energy cost and developed a heuristic algorithm. Ferretti et al. [8] extended this model with variable production rates and power demand costs. They presented a general Mixed-Integer Non-Linear Programming (minlp) model, noted that even its subproblem is non-convex, and concluded that “it is not possible to determine a closed form that permits obtaining the optimal value of T [cycle length] and $p_j$ [production rates]”. They determined a heuristic solution with a Matlab solver.

The literature on the Economic Lot Scheduling Problem (elsp) is very rich [9,10]. However, only a few papers consider variable production rates, in which researchers propose specialised algorithms for special cases [11]. For example, Silver [12] proposed a specialised algorithm for the case where machine operating costs are non-zero and constant, increasing production rates and reducing production times and costs. The optimisation approach proposed in this paper is the first method for the common-cycle elsp with variable production rates that provides an optimal solution in a general case.

In the past, only some elsp subproblems were solved using mathematical programming methods [9,13]. Recently, Ferretti et al. [8] made an attempt to solve a general minlp model of the common-cycle elsp using a general-purpose solver, but they built a straightforward general minlp model, which is hard to solve, and applied a solver that can not guarantee optimal solutions. Kaczmarczyk [14] also considered a special case of the common-cycle elsp but reformulated its model into an miqcp model so that it could be optimally solved using a general-purpose solver.

There are many general-purpose solvers for the minlp problems. However, globally optimal solutions for non-convex non-linear problems may ensure solvers that use the spatial branch-and-bound algorithm. It makes a complete search of the entire decision space and branches the problem on continuous variables, to enable better approximation of non-convex non-linear constraints. Such solvers are built on top of the Mixed-Integer (Linear) Programming (mip) solvers [15], and they also apply piecewise relaxation techniques, bilinear programming techniques, and several other techniques specific to non-linear problems.

This paper attempts to apply a similar approach to a problem that takes into account energy and power costs. It shows how to reformulate the general minlp model proposed by Ferretti et al. [8] into an miqcp model, which may be solved optimally with a general-purpose solver. Computational experiments prove that this approach ensures better production schedules, mainly thanks to a lower and better-levelled power demand.

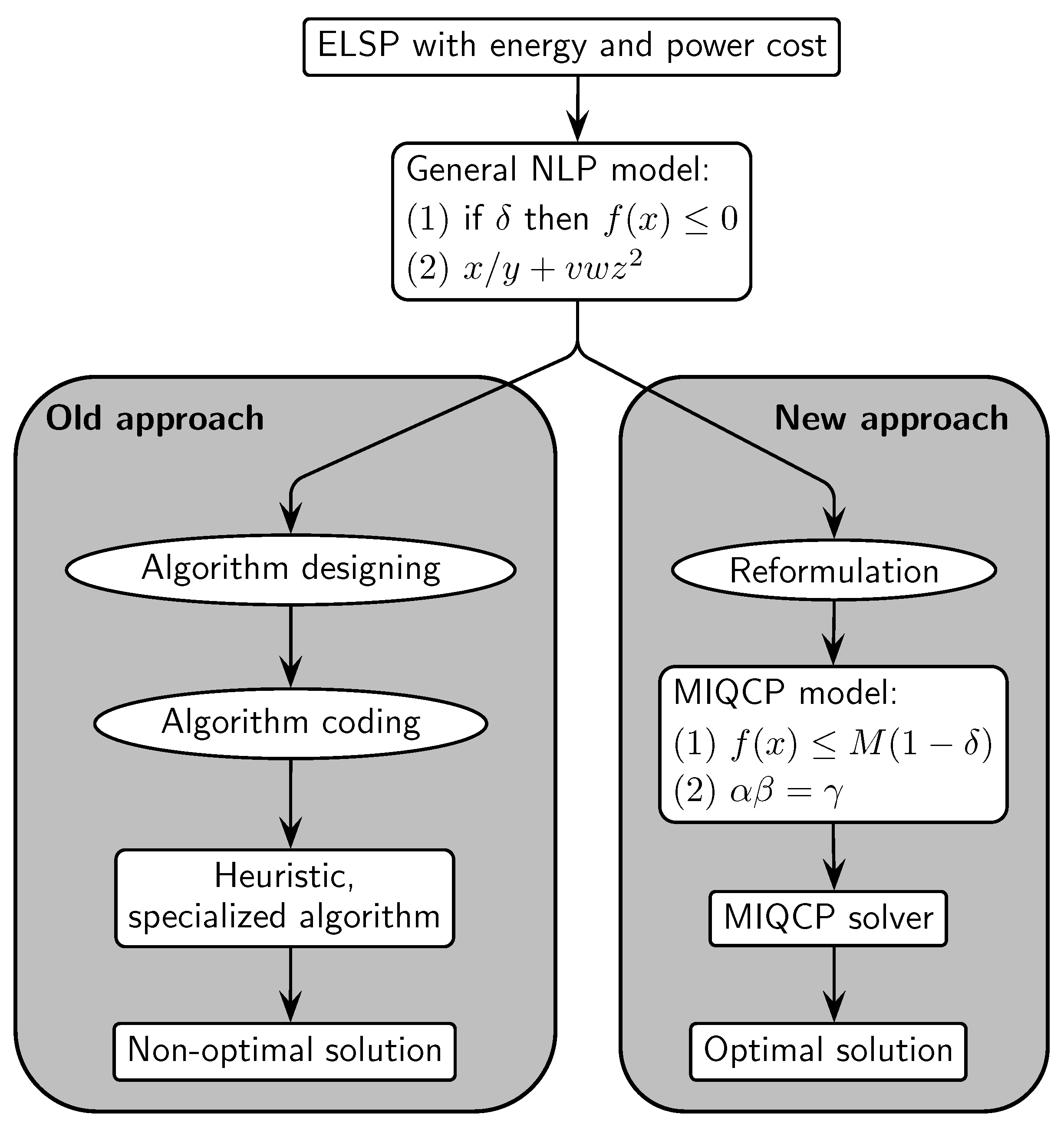
Figure 1 illustrates the framework proposed in this paper to solve the elsp with energy and power costs [8]. In the old approach, if researchers had to solve a new extended version of the elsp, they designed and coded a new specialised algorithm dedicated solely to this problem, which requires a high level of expertise and is very labour-intensive. Moreover, developed algorithms are, in most cases, heuristic; that is, they do not ensure optimal solutions [9,10], which can lead to significantly higher costs.

The new approach [14] applied in this paper is to reformulate the elsp model so that a general-purpose solver can be used. Currently, general-purpose procedures for the miqcp models are much faster and more effective than for the general minlp models. Therefore, in this paper, the minlp model of the elsp with energy and power costs [8] is reformulated into an miqcp model.

For this purpose, general logical conditions should be described using binary variables and so-called big M constraints, e.g., $(\delta =1)\Rightarrow ({\sum }_j{a}_j{x}_j\le b)$ must be replaced by ${\sum }_j{a}_j{x}_j-b<=M(1-\delta )$. Moreover, general non-linear expressions, like $x/y+vw{z}^2$ (where $x,y,v,w$, and z are variables), must be replaced by quadratic expressions like $\alpha \beta =\gamma$ (where $\alpha ,\beta$, and $\gamma$ are new auxiliary variables). Most expressions describing energy consumption and peak power demand required such reformulation.

The rest of this article is organised as follows: Section 2 describes the elsp following the common-cycle approach, taking into account variable production rates, costs of energy consumption, and power demand. Section 3 and Section 4 present the known minlp model proposed in [8] and the new miqcp model, respectively. Section 5 presents the results of the computational experiments. Section 6 gives the summary.

2. Problem Description and Notation

Several products j with a constant and deterministic demand rate $r_j$ are produced on a single machine at a rate $p_j$. Before changing the product being made, the machine must be set up, which takes some time $A_j$ and cost $s_j$, both independent of the sequence of products. The inventory holding cost is proportional to the inventory level and unit holding cost $h_j$. The goal is to set the production rates $p_j$ and the cycle length T, which uniquely determines the size of production lots equal to $r_{j}T$. The lists below present all lot-sizing parameters and variables of the considered problem:

Lot-sizing parameters:

• $\mathcal{N}$ = $\{1,\dots ,n\}$—Set of products, where n is their number;
• $r_j$—Demand rate of item j [units/h];
• $A_j$—Set-up cost of item j [USD/set-up];
• $s_j$—Set-up time of item j [h/set-up];
• $h_j$—Unit inventory holding cost of item j [USD/h/unit].

Lot-sizing variables:

• T—Length of the production cycle;
• $p_j$—Production rate of product j [units/h].

The modelling of energy and power costs in production planning models [7,8] is based on several assumptions. When the machine is idle, not processing any products and not being prepared for processing, but is in "ready for production" mode, then it requires constant power W [16]. When the machine is idle long enough, it may be shut down to save energy. However, it is profitable only if the machine’s shutdown and start-up take less time and energy than the considered idle time interval in ready mode. A sufficiently long idle time interval is called a break-even duration [17] and depends on the actual production rates $p_j$. The ratio g of the power required during the machine’s shutdown and start-up to the idle power W is constant [17]. The power required to process one unit of product j is a sum of the constant element, the idle state power W, and a variable element linearly depending on the production rate $p_j$ [18]. The ratio $f_j$ of the power needed to set up the machine for product j to the idle state power W is constant but product-dependent [19]. The list below presents all parameters and variables related to energy and power management:

Energy- and power-related parameters:

• e—Unit cost of energy consumption [USD/kWh];
• $e^p$—Unit cost of maximal power [USD/kW/h];
• $L^S$—Total duration of shutdown and start-up of the machine [h];
• $\overline{P}$—Maximum possible power [kW];
• W—Standby power (power required when the machine is idle) [kW];
• g—Ratio of power required during the shutdown and start-up of the machine to the standby power W [–];
• $f_j$—Ratio of the power required during the machine’s set-up for product j to the standby power W [–];
• $v_j$—Energy needed to process one unit of item j [kWh/unit];
• ${\underline{p}}_j$, ${\overline{p}}_j$—Minimum and maximum permissible production rate [units/h], where ${\underline{p}}_j>r_i$;
• $\underline{T},\overline{T}$—Lower and upper bounds of the cycle length T.

Auxiliary variables:

• C—Total cost;
• $c^S$, $c^H$, $c^E$, $c^P$—Total set-up, inventory, energy, and power costs;
• $L^B$—Break-even duration for the actual production rates;
• x—Machine’s idle time at the end of the production cycle [USD/h/unit];
• z = 1 if the idle time x is shorter than the break-even duration $L^B$; otherwise, $z = 0$.

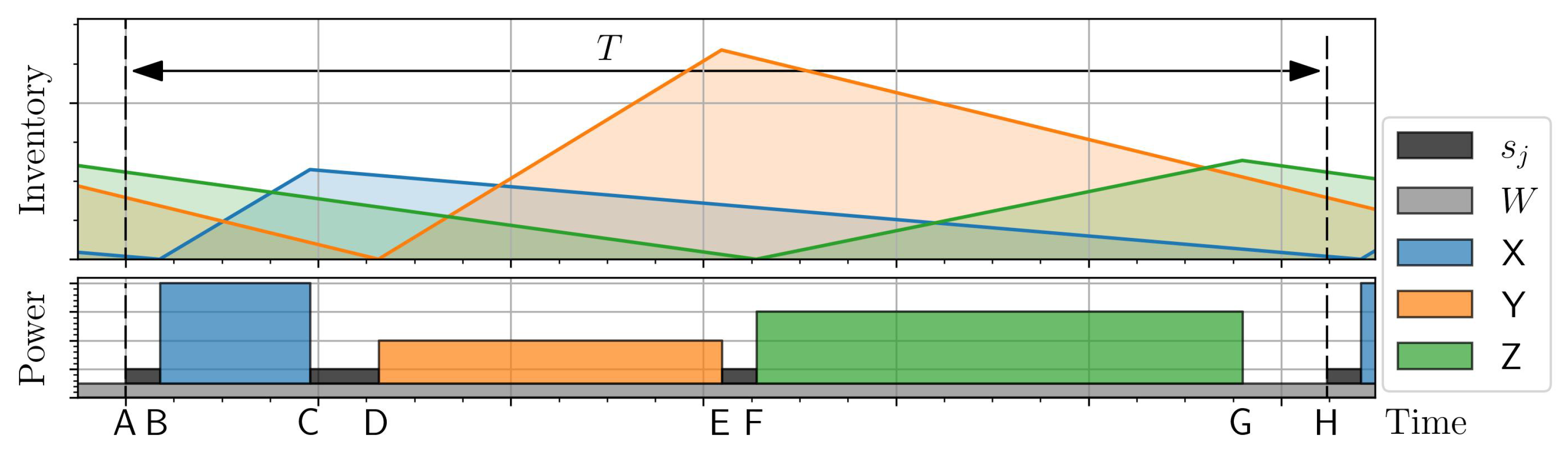
Figure 2 presents an example of an elsp schedule with power demand. A single cycle T stretches between points A and H on the time axis. Before point A ends the previous cycle, and after H starts the next cycle. During the interval AB, the set-up activity before product X is executed, of duration $s_{\mathsf{X}}$. During the interval BC, product X is processed, and its inventory rises to a level that ensures the demand will be satisfied until the end of the entire cycle. Similarly, during intervals CD and EF, the machine is set up for products Y and Z, which are processed during intervals DE and FG. During the interval GH, the machine remains idle but in a standby mode.

The lower part of the chart shows the power demand on the vertical axis. The light grey rectangle represents the standby power demand W. The set-up activities require the power $f_{j}W$; here, $f_j=2$, and the processing of products requires the power $W+v_j{p}_j$. In the standby mode, the machine needs only power W. At a constant cycle length T, increasing the production rate $p_j$ results in shorter processing times and increased power demand; decreasing the production rate has the opposite effect.

3. minlp  Model

The common-cycle elsp with the model of energy consumption costs proposed by Beck et al. [7], and with the model of power demand peak costs proposed by Ferretti et al. [8], may be described as the following minlp model:

minimise

$$C(T,p_j)=c^S+c^H+c^E+c^P$$

(1)

subject to

$$\sum _{j\in \mathcal{N}}{\displaystyle \frac{A_j}{T}}=c^S$$

(2)

$$\sum _{j\in \mathcal{N}}{\displaystyle \frac{1}{2}}{h}_j{r}_j\left(1-{\displaystyle \frac{r_j}{p_j}}\right)T=c^H$$

(3)

$$(x<L^B)\Rightarrow (z=1)$$

(4)

$$\begin{array}{cccc}\hfill \hfill & & \hfill \sum _{j\in \mathcal{N}}(W+v_j{p}_j){\displaystyle \frac{r_j}{p_j}}e+\sum _{j\in \mathcal{N}}{\displaystyle \frac{s_j{f}_{j}We}{T}}& +\hfill \\ & & \hfill +z{\displaystyle \frac{xWe}{T}}+(1-z){\displaystyle \frac{L^{S}gWe}{T}}& =c^E\hfill \end{array}$$

(5)

$$max\left\{\underset{j\in \mathcal{N}}{max}(W+v_j{p}_j),zW+(1-z)gW\right\}{e}^p=c^P$$

(6)

$$T-\sum _{j\in \mathcal{N}}{s}_j-\sum _{j\in \mathcal{N}}{\displaystyle \frac{r_j}{p_j}}T=x$$

(7)

$$\underline{T}\le T\le \overline{T}$$

(8)

$${\underline{p}}_j\le p_j\le {\overline{p}}_j,j\in \mathcal{N}$$

(9)

$$L^B,x\ge 0$$

(10)

$$z\in \{0,1\}$$

(11)

where the break-even duration $L^B$, depending on actual production rates $p_j$, equals

$$L^B=\left\{\begin{array}{cc}g{L}^S,\hfill & {\displaystyle \mathrm{if}\underset{j\in \mathcal{N}}{max}(W+v_j{p}_j)\ge gW}\hfill \\ g{L}^S+{\displaystyle \frac{{\displaystyle \left(gW-\underset{j\in \mathcal{N}}{max}(W+v_j{p}_j)\right)e^{p}T}}{eW}},\hfill & {\displaystyle \mathrm{if}\underset{j\in \mathcal{N}}{max}(W+v_j{p}_j)<gW}\hfill \end{array}\right.$$

(12)

and the production rate bounds are equal:

$$\begin{array}{cc}\hfill {\underline{p}}_j\hfill & =r_j+1\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\overline{p}}_j\hfill & ={\displaystyle \frac{\overline{P}-W}{v_j}}\hfill \end{array}$$

(14)

In Model (1)–(14), there are two decision variables (one scalar variable T, and one continuous vector variable $p_j$) and three auxiliary scalar variables (one binary z, and two continuous $L^B$ and x). The objective function (1) determines the average total cost per unit of time. Equation (2) provides the machine set-up costs, and (3) determines the inventory holding cost.

Inequality (4) ensures that the binary variable z equals one when the idle time x at the end of the production cycle is shorter than the break-even duration $L^B$, which, in turn, is determined by function (12) [7,17]. “The break-even duration $L^B$ is used to decide on whether the machine should be switched off or be kept in the idle mode” [17]. “The machine should be shut down (…) if the energy required to shut the machine down and start it up again is lower than the energy required to keep the machine in the idle state” [8]. Detailed derivation of (12) is presented in two papers. Beck et al. [7] derived the formula for $L^B$ considering only the energy consumption costs. Ferretti et al. [8] added the power demand cost.

Equation (5) sums four kinds of energy costs, using their average values per unit of time. The first element, product j’s processing cost, is determined as the product of the power demand $W+v_j{p}_j$ and cycle fraction $r_j/p_j$ necessary to meet demand during the entire cycle. The second element is the cost of machine set-up before processing product j. When the idle time is shorter than the break-even duration $L^B$, the binary variable $z=1$, the machine is idle during the time interval x, and the third element of Equation (5) determines the standby cost. When $z=0$, the machine will be shut down for some time interval, and the fourth element of (5) determines the cost of the energy needed to start the machine after a shutdown.

Equation (6) gives the cost of the maximum required power, depending on the variable production rates. This may be either the power necessary to process products, the standby power, or the power needed to start the machine after a shutdown.

Constraint (7) ensures that the sum of the total set-up time, machine workload, and idle time does not exceed the cycle length. Constraints (8)–(11) define the domains of all variables. Equations (13) and (14) set bounds for production rates. The lower and upper bounds of the cycle length bound, $\underline{T}$ and $\overline{T}$, are hard to set. Therefore, they may be set fully arbitrarily by managers based on their experience and expertise. The lower bound ${\underline{p}}_j$ is derived from constraint (7), and the upper bound is due to the maximum possible power demand $\overline{P}$.

4. miqcp  Model

Taking an example from [14], Model (1)–(14) may be solved optimally after reformulation to a Mixed-Integer Quadratically Constrained Programming (miqcp) model. To do this, it is necessary to reformulate all non-linear and non-quadratic terms into linear or quadratic ones. Several constraints in Model (1)–(14) contain division by T or $p_j$, along with products of three or four variables. All of them may be reformulated into an miqcp model using bilinear constraints [15]. Moreover, function (12) must be reformulated using an additional binary variable to represent two cases of this function.

A function $f(x,y)$ is bilinear if it is linear in x when y is fixed and linear in y when x is fixed. The square of a variable is a quadratic term, but not a bilinear one. A quadratic term does not have to be bilinear, but each bilinear term is quadratic.

The number of bilinear and quadratic expressions in the model should be minimised, as they are much harder to handle by the solver than the linear terms. To do this, auxiliary variables are necessary, aggregating many variables before multiplying them by another variable.

Additional derived parameters:

• $\overline{\alpha },\overline{L}$ —Upper bounds used in big M constraints, linking binary and continuous variables.

Additional variables:

• $T^R$ = $1/T$—Inverse of cycle length;
• $p_j^R$—Inverse of production rate of product j [h/unit]; that is, the processing time for one unit of product;
• $\delta$—Binary variable used to model the break-even duration $L^B$ function (12);
• $L^B$—Break-even duration for the actual production rates;
• V =${max}_{j\in \mathcal{N}}(W+v_j{p}_j)$—The maximal required power, an auxiliary variable necessary to build a minimax constraint;
• $\alpha ,\beta ,\gamma ,\mu ,\nu ,\omega$—Auxiliary variables used to reduce the order of polynomials and reduce the number of quadratic terms.

The common-cycle elsp with costs of energy consumption and power demand peaks describes the following miqcp model, where the hash sign precedes the comments:

minimise

$$C(T,p_j)=c^S+c^H+c^E+c^P$$

(15)

subject to

              # Inverse variables:

$$T{T}^R=1$$

(16)

$$p_j{p}_j^R=1,j\in \mathcal{N}$$

(17)

              # Set-up cost:

$$\sum _{j\in \mathcal{N}}{A}_j{T}^R=c^S$$

(18)

              # Inventory holding cost:

$$\sum _{j\in \mathcal{N}}\frac{1}{2}{h}_j{r}_j\left(1-r_j{p}_j^R\right)=\gamma$$

(19)

$$\gamma T=c^H$$

(20)

              # Energy consumption costs:

$$z{T}^R=\mu$$

(21)

$$x\mu =\nu$$

(22)

$$\begin{array}{cc}\hfill \sum _{j\in \mathcal{N}}(W{r}_j{p}_j^R+v_j{r}_j)e+\sum _{j\in \mathcal{N}}{s}_j{f}_{j}W{T}^{R}e+& \\ \hfill +\nu We+(T^R-\mu )L^{S}gWe=& c^E,\hfill \end{array}$$

(23)

              # Break-even duration:

$$v_i{p}_j\le V,j\in \mathcal{N}$$

(24)

$$gW-(W+V)=\alpha$$

(25)

$$T\alpha \le \beta$$

(26)

$$\alpha \le \overline{\alpha }\delta$$

(27)

$$L^{S}g+\frac{e^p}{eW}\beta \delta =L^B$$

(28)

              # Power demand costs:

$$L^B-x\le \overline{L}z$$

(29)

$$(W+V)e^p\le c^P$$

(30)

$$(1-z)gW{e}^p\le c^P$$

(31)

              # Machine workload:

$${\sum }_{j\in \mathcal{N}}{r}_j{p}_j^R=\omega$$

(32)

$${\sum }_{j\in \mathcal{N}}{s}_j+\omega T+x=T$$

(33)

              # Variables’ domains:

$$\underline{T}\le T\le \overline{T}$$

(34)

$$1/\overline{T}\le T^R\le 1/\underline{T}$$

(35)

$${\underline{p}}_j\le p_j\le {\overline{p}}_j,j\in \mathcal{N}$$

(36)

$$1/{\overline{p}}_j\le p_j^R\le 1/{\underline{p}}_j,j\in \mathcal{N}$$

(37)

$$\alpha ,\beta ,\in \mathbb{R}$$

(38)

$$L^B,V,x,\gamma ,\mu ,\nu ,\omega \ge 0$$

(39)

$$z,\delta \in \{0,1\}$$

(40)

where the upper bounds equal:

$$\overline{\alpha }=gW-(W+\underset{j\in \mathcal{N}}{max}{v}_j{\underline{p}}_j)$$

(41)

$$\overline{L}=g{L}^S+{\displaystyle \frac{\overline{\alpha }}{eW}}{e}^p\overline{T}$$

(42)

The objective function (15) is linear and does not have to be modified. Bilinear constraints (16) and (17) couple the new variable $T^R$ with T and $p_j^R$ with $p_j$. The set-up cost (18) and inventory holding cost (19) are determined using the new inverse variables. Determining the inventory holding cost is split into two constraints (19) and (20), to prevent multiplying each $p_j^R$ variable by T separately. The first one (19) aggregates all of the $p_j^R$ variables into one $\gamma$ variable, to have only one quadratic (bilinear) expression in the second one (20). A similar approach is applied to reformulate the energy cost constraint (5). Bilinear constraints (21) and (22) reduce the order of the polynomial in (23), which determines the average energy costs. Substituting in (23) for $T^R$, $\mu$, and $\nu$, the expressions from (17), (21), and (22), after some reformulation, one obtains (5).

Constraints (24)–(28) replace function (12). The minimax constraint (24) determines the ${max}_j{v}_j{p}_j$. Constraints (25) and (26) reduce the order of polynomials. The big M constraint (27) determines the binary variable $\delta$ necessary to describe the two cases of the break-even duration in (28). The big M parameter for constraint (27) is defined in (41).

The big M constraint (29) defines the value of the binary variable z. Its big M parameter $\overline{L}$ is explicitly defined in (42), as an upper bound for the second value in (12) for any feasible values of variables $p_j$ and T. Constraints (30) and (31) ensure that the maximum power will be equal to or higher than the power needed during any period of the schedule. The constraint (7), ensuring that the workload does not exceed capacity, is here split into two equations (32) and (33) to reduce the number of quadratic terms.

Constraints (34)–(40) define the domain of the variables. Two variables, $\alpha$ and $\beta$, are unconstrained. The cycle length bounds, $\underline{T}$ and $\overline{T}$, should be set by managers based on their experience and expertise. Bounds of production rates are given in (13) and (14).

5. Experiments and Results

The new Model (15)–(42) was tested on a problem instance proposed by Beck et al. [7] and Ferretti et al. [8], based on a real case of a metal stamping process described by Bomberger [20], which researchers often use to evaluate new optimisation methods for the elsp.

A decrease in production rates by 50% or an increase by 200% may be unrealistic. The original rate bounds, described by Equations (13) and (14), practically do not limit the solution. Therefore, four additional problem instances have been solved using the miqcp Model (15)–(42), with production rate changes bounded to $\pm 10\%$, $\pm 20\%$, $\pm 30\%$, and $\pm 40\%$.

All cases were solved with the help of the Gurobi 11.0.3 solver on an Intel Core i9-7900X processor with a 3.3 GHz clock speed, 16 GB RAM, 10 physical cores, and 20 logical processors, utilising up to 20 threads, with a time limit of 60 s.

5.1. Parameters of the Problem Instance

Table 1. Problem instance data [7,8,20].

(a) Product-Related Parameters
j	$p_j^0$	$r_j$	$h_j\left[{10}^{-5}\right]$	$A_j$	$s_j$	$f_j$	$v_j$
1	3750.0	50.0	0.033854	15	1.00	1.25	0.005
2	1000.0	50.0	0.924479	20	1.00	1.50	0.040
3	1187.5	100.0	0.664063	30	2.00	2.50	0.010
4	937.5	200.0	0.520833	10	1.00	1.25	0.025
5	250.0	10.0	14.505208	110	4.00	3.00	0.065
6	750.0	10.0	1.393229	50	2.00	2.50	0.030
7	300.0	3.0	7.812500	310	8.00	1.50	0.020
8	162.5	42.5	30.729167	130	4.00	2.75	0.050
9	250.0	42.5	4.687500	200	6.00	1.75	0.070
10	1875.0	50.0	0.208333	5	1.00	2.00	0.015
(b) Other Parameters
e	0.15
$e^p$	0.1
$L^S$	2
$\overline{P}$	200
W	50
g	4

contains all parameters of the considered problem instance [7,8,20], where $p_j^0$ is the original production rate [7,20]. The cycle length bounds were set to $\underline{T}=1$ and $\overline{T}=1000$ days. To improve the scaling of the model, all monetary values ($A_j$, $h_j$, e, $e^p$) were multiplied by 100, i.e., expressed in cents, not USD [15].

5.2. Results for Basic Case

To solve the basic case, the solver explored 51,475 nodes (159,908 simplex iterations) in 1.18 s (0.34 work units).

Table 2. Comparison of solutions obtained with various methods.

(a) Total Cost C, Cycle Length T, and Machine Utilisation u.
Model	$\mathbf{C}$	$\Delta \mathbf{C}$	$\mathbf{T}$	$\mathbf{u}[\%]$
classic	24.60	0.00	342.0	97.0
energy	24.59	−0.04	422.0	95.4
power	23.26	−0.45	376.0	98.0
miqcp	22.50	−8.54	384.4	100.0
(b) Component Costs
	Model		Difference
Cost	power	miqcp	[%]
$c^S$	2.34	2.28	−2.6
$c^H$	2.99	3.09	3.3
$c^E$	10.39	10.38	−0.1
$c^P$	7.54	6.73	−10.7

a compares results obtained with four methods: the classic elsp optimal solution, ignoring energy or power costs; the energy method, optimising only energy costs, proposed in [7]; the power method, optimising both energy and power costs, proposed in [8]; and the new miqcp Model (15)–(42). The experiments confirmed all results presented in [7,8]. The classic and energy methods use the original production rates $p_j^0$ [7,20], while in the power and miqcp methods, the production rates are optimised.

Column C presents the total cost, including costs of energy consumption and power demand peaks. The miqcp model delivered an optimal solution that ensures a total cost 3.27% lower than that of the power method.

In the miqcp solution, the cycle length T is slightly longer than in the power solution. More interestingly, in the miqcp solution, the machine is fully utilised; that is, the machine utilisation u, determined as the sum of the set-up and processing times divided by the cycle length, equals 100%.

Table 2b presents the components of total costs for the two methods, optimising both energy and power. The decrement in set-up costs $c^S$ and increment in inventory holding costs $c^H$ practically offset each other, which may be explained by the increment in cycle length and machine utilisation. Most importantly, the new model decreased the power demand costs by 10.7%.

Table 3. Production rates and power demand.

	Production Rate		Production Rate		Power
	[Units/h]		Increment [%] †		Demand [kW]
$\mathbf{j}$	power	$\mathbf{miqcp}$	power	$\mathbf{miqcp}$	power	$\mathbf{miqcp}$
1	3540	3461	−5.6	−7.7	67.70	67.30
2	452	433	−54.8	−56.7	68.08	67.30
3	1808	1730	52.3	45.7	68.08	67.30
4	723	692	−22.9	−26.2	68.08	67.30
5	278	266	11.2	6.5	68.07	67.30
6	603	577	−19.6	−23.1	68.09	67.30
7	904	865	201.3	188.4	68.08	67.30
8	220	248	35.4	52.5	61.00	62.39
9	258	247	3.2	−1.1	68.06	67.30
10	1696	1154	−9.5	−38.5	75.44	67.30

† Compared to the original production rates $p_j^0$ from Table 1.

compares the production rates and power demand obtained with the power and miqcp methods. The production rates $p_j$ in the miqcp solution are lower than in the power solution reported in [8], except for product 8, which explains the longer production cycle.

The decrement in production rates, compared to the original values $p_j^0$, for most products in both solutions is very high, which ensures reductions in power demand and cost. For the second product, the production rates are decreased by 54.8% and 56.7%. Interestingly, in the miqcp solution, the power needed to produce is the same for all products, again except for product 8. Moreover, the power demand peak in the miqcp solution is 10.8% lower than in the power solution, explaining the decrease in power costs. Thanks to the new miqcp model, the power demand is lowered and equalised more effectively.

Figure 3 shows the changes in the power demand in three solutions. In the classic solution, the highest power demand is 60.7% higher than the lowest; in the power solution [8], it is 23.7% higher; and in the miqcp solution, obtained using the proposed Model (15)–(42), it is only 7.9% higher. The new model almost perfectly equalises the power demand.

5.3. Results for Tight Bounds of Production Rates

The results for production rate changes bounded to $\pm 10\%$, $\pm 20\%$, $\pm 30\%$, and $\pm 40\%$ are presented in

Table 4. Cycle length and cost increments [%] caused by production rate bounds compared to the solution with the original bounds (13) and (14).

Bound	T	${\mathit{c}}^{\mathit{S}}$	${\mathit{c}}^{\mathit{H}}$	${\mathit{c}}^{\mathit{E}}$	${\mathit{c}}^{\mathit{P}}$	C
$\pm 10\%$	392.6	−2.1	−7.4	−0.1	27.8	7.0
$\pm 20\%$	405.0	−5.1	−7.4	−0.3	21.8	4.9
$\pm 30\%$	403.0	−4.6	−11.1	−0.3	15.9	2.6
$\pm 40\%$	414.2	−7.2	−7.5	−0.4	9.9	1.0

. The cycle length T increases and set-up costs $c^S$ decrease when the rate increment bounds become wider. The inventory holding costs $c^S$ and energy consumption cost $c^E$ change moderately. Most importantly, when the rates may change only by $\pm 10\%$, the power costs $c^P$ are 27.8% higher than in the case with the original bounds, and they decrease for wider bounds. The total cost C is 7% higher for bounds $\pm 10\%$, and it decreases when the bounds become wider.

6. Summary

This paper shows how to determine a globally optimal solution for a basic production planning model—the common-cycle Economic Lot Scheduling Problem (elsp)—that takes into account the costs of energy consumption and power demand. The problem is formulated as a Mixed-Integer Quadratically Constrained Programming (miqcp) model and solved using a general-purpose miqcp solver. This new approach ensures optimal solutions, better than solutions known from the literature [8], thanks to more effective levelling of power demand during the production of various products. It is the first method to optimally solve the common-cycle elsp with variable production rates without any simplifying assumptions.

Experiments have shown that the optimal solution to the considered problem instance provides a 3.3% lower total cost compared to the solution obtained using a heuristic algorithm [8]. Furthermore, sensitivity analysis has shown that the allowable scale of changes in production rates is critical for the choice of the solutions.

A general-purpose solver solves the new model very quickly, which should make it easier to extend the model in the future. First, it should be adapted to the extended basic period approach, allowing for different cycles for different products, which may increase the quality of the solutions. Second, it should be extended to account for non-linear cost increases in production rates due to deteriorations in product quality, increased energy consumption, processing costs, environmental pollution, or waste amounts [3].