AI-Assisted Adaptive Sliding Mode Control for Pseudo-Resonance Suppression in Dynamic Capacitive Wireless Charging Systems
Abstract
1. Introduction
- -
- A critical analysis and demonstration of the “pseudo-resonance” limitation in conventional ESMC, formally framing the control problem for a system with time-varying coupling capacitance.
- -
- The development of a dual-loop control architecture: An inner loop uses a computationally efficient RLS observer for real-time estimation of , while an outer ASMC loop uses this estimate to dynamically regulate the inverter’s switching frequency.
- -
- A rigorous stability analysis for the closed-loop system using Lyapunov theory, incorporating a projection operator to ensure bounded parameter estimates.
2. System Overview and Problem Formulation
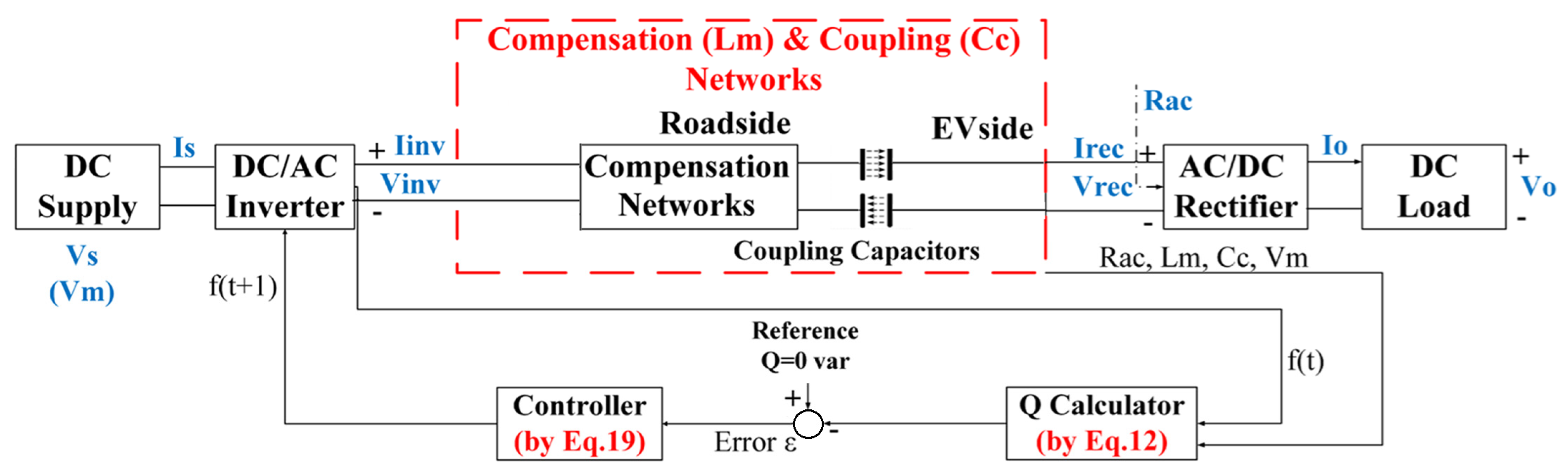
2.1. The Role of Compensation Networks in CWPT
2.2. Operational Challenges: Frequency Sensitivity and Dynamic Misalignment
2.3. Problem Formulation
- A-
- Convergence of reactive power to zero:
- B-
- Tracking of the true resonant frequency:
- C-
- Maximization of active power transfer to the load under dynamic misalignment.
3. System Modeling and Power Expressions
3.1. Active and Reactive Power Expressions
3.2. Resonance Condition and Power Extrema
3.3. Expression for
3.4. Remarks
- Equations (5) and (6) show explicitly that forcing is necessary but not sufficient to guarantee full active power transfer unless the controller ensures the zero of the numerator in (6) is the same zero that minimizes the imaginary term in the denominator, i.e., the controller must place at the true resonance . This observation explains the pseudo-resonance problem: a controller that drives the measured to zero using incorrect or stale parameter values can still end up off the true resonance and thus yield severely reduced .
- The derivative (Equation (10)), and, in particular, its resonant value (Equation (11)), is used in the conventional-SMC/ASMC laws to relate frequency adjustments to changes in (see Section 4). The positive, closed-form resonant value (11) simplifies the design and tuning of gains near .
4. Controller Design Methodology
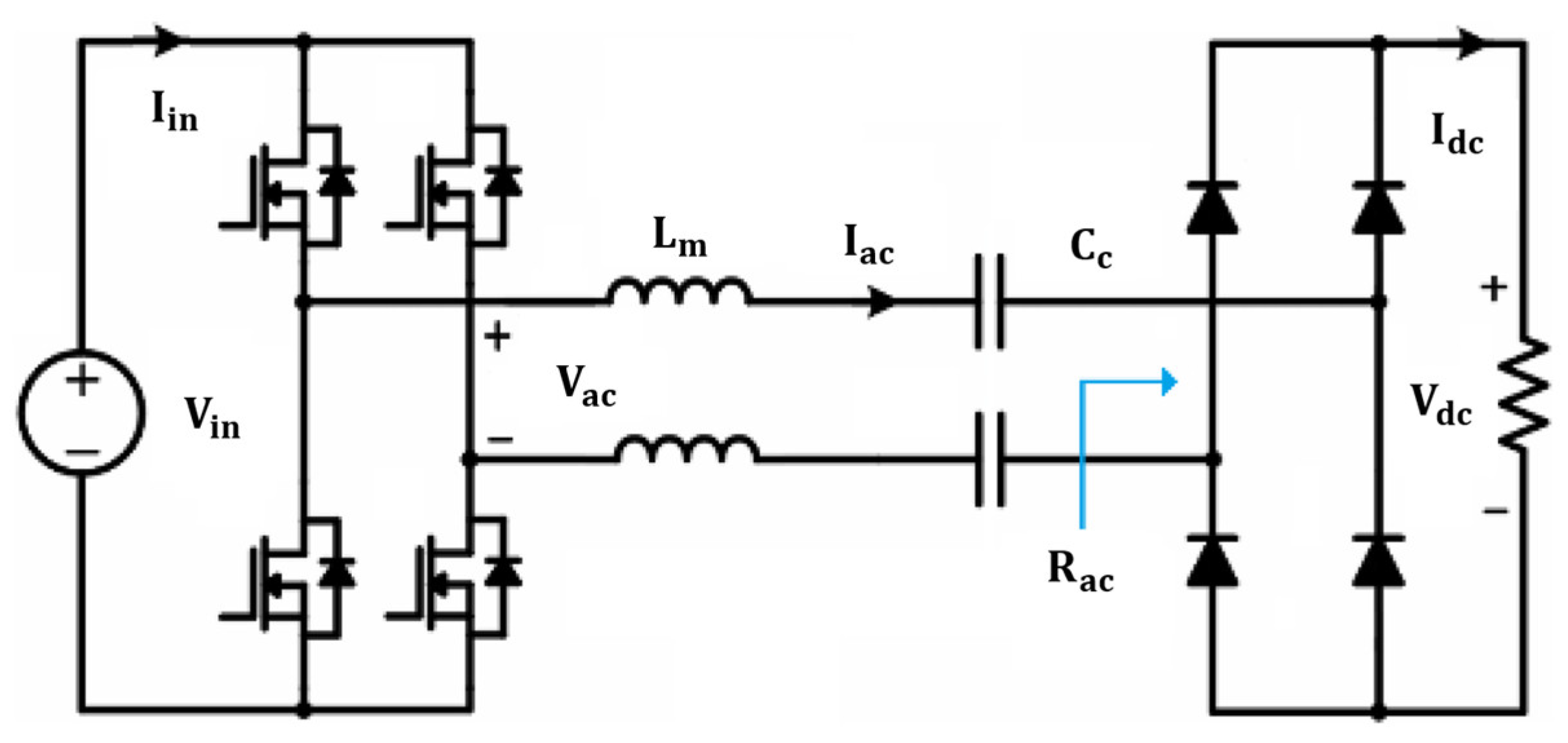
4.1. L-Type Matching CWPT Topology
4.2. Sliding Mode Control Design
4.3. Online Capacitance Estimation Using AI-Based RLS Observer
4.3.1. RLS Formulation
4.3.2. RLS Update Law
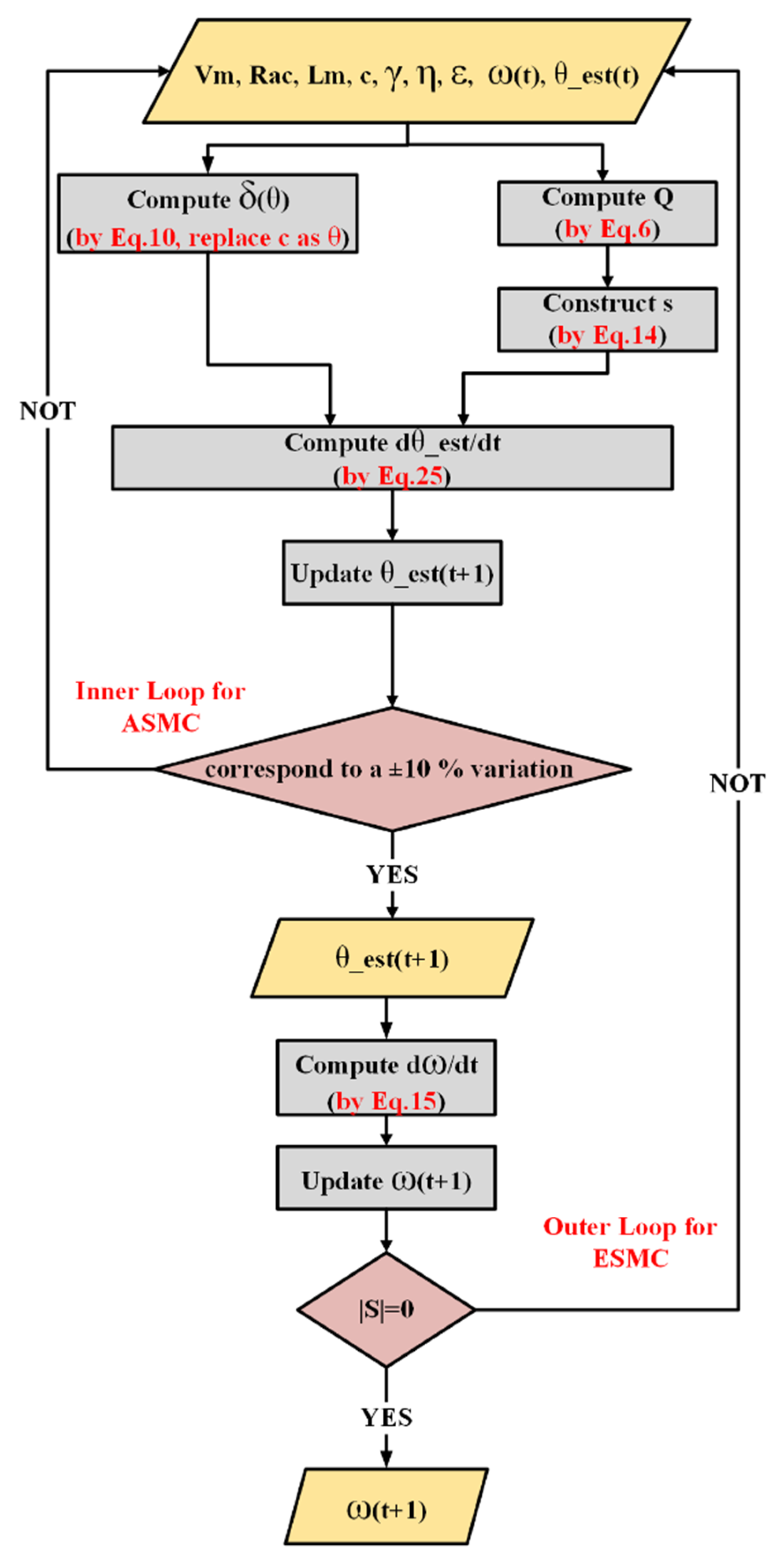
4.4. ASMC Design
4.4.1. Adaptive Law Derivation
4.4.2. Projection Operator
4.4.3. Dual-Loop Control Architecture
4.4.4. Remarks on Applicability to Other Compensation Topologies and Scope
- Simple LC-based compensator (single additional LC): If the compensator topology is modified but the overall resonant behavior can still be represented by a single dominant resonant mode whose frequency depends on the coupling capacitance (i.e., effective is a monotonic function of the coupler geometry), then the ASMC–RLS architecture remains applicable with minimal modification: the estimator should be set to identify the equivalent capacitance (or equivalent reactance) relevant to that dominant mode, and the outer sliding law will then track the mode in the same manner as for the L-type case.
- Higher-order LCLC (cascaded) compensator: Higher-order networks typically exhibit multiple resonant modes (both series and parallel modes) and modal behavior that is not necessarily uniquely determined by the coupling capacitance. In particular, some resonant modes are mainly determined by local LC elements and are relatively insensitive to the coupling change; other modes result from interaction between transmitter/receiver tanks and depend strongly on the coupling coefficient. As a result:
- -
- can have multiple zeros (multiple candidate frequencies), and driving → 0 alone does not guarantee convergence to the desired power-transfer mode (risk of converging to an undesired zero).
- -
- A single scalar estimator for the coupling capacitance is generally insufficient because modal frequencies and coupling coefficients jointly determine the resonance condition.
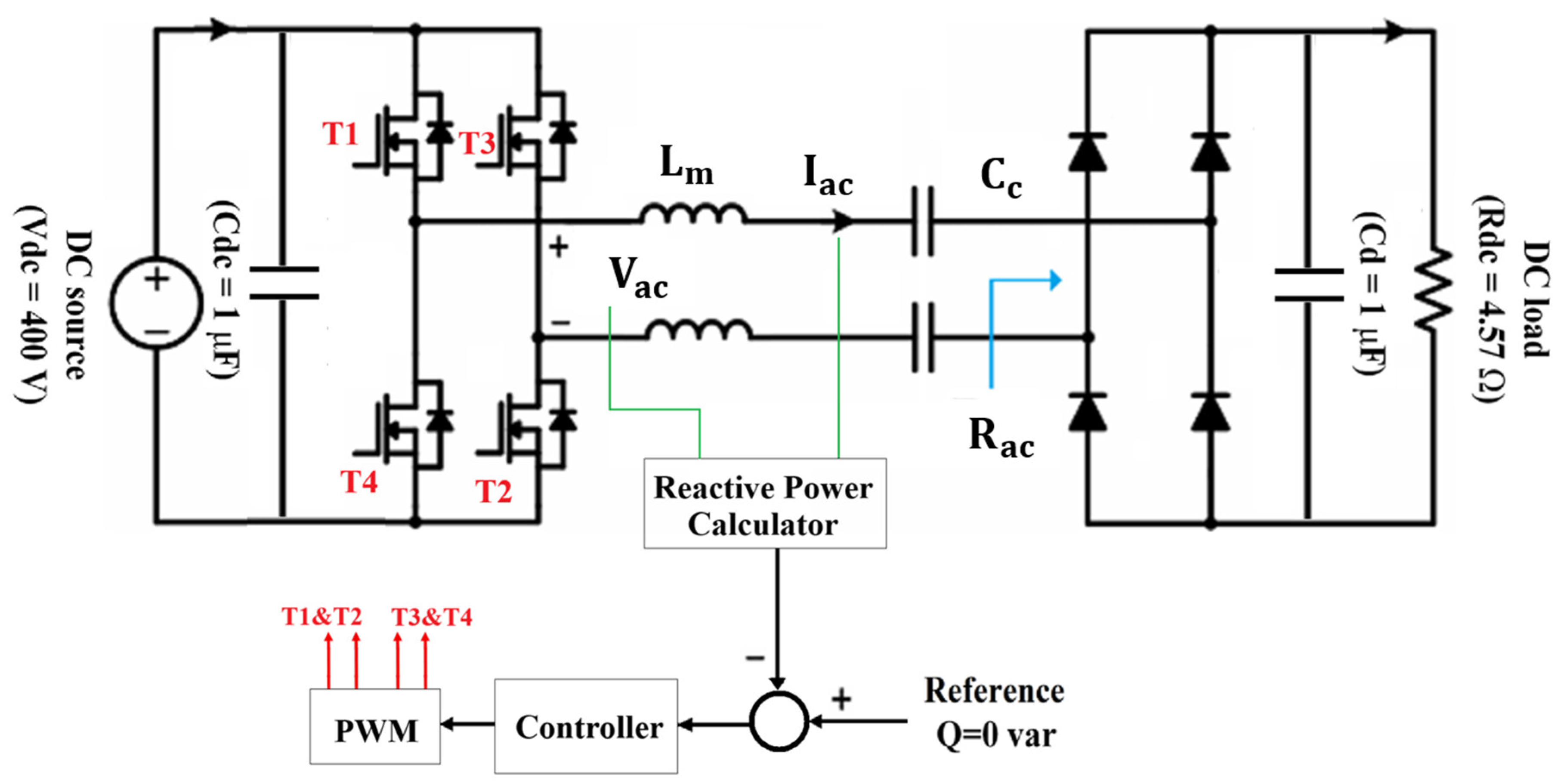
5. Simulation Results and Discussion
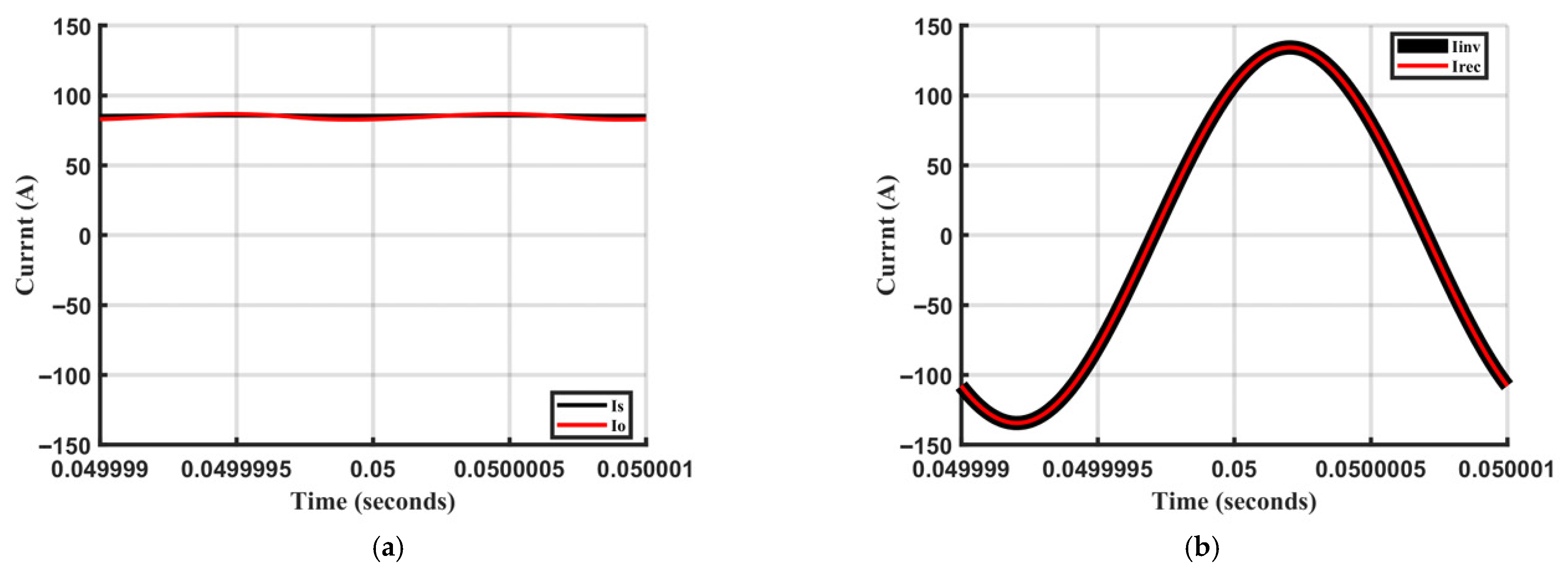
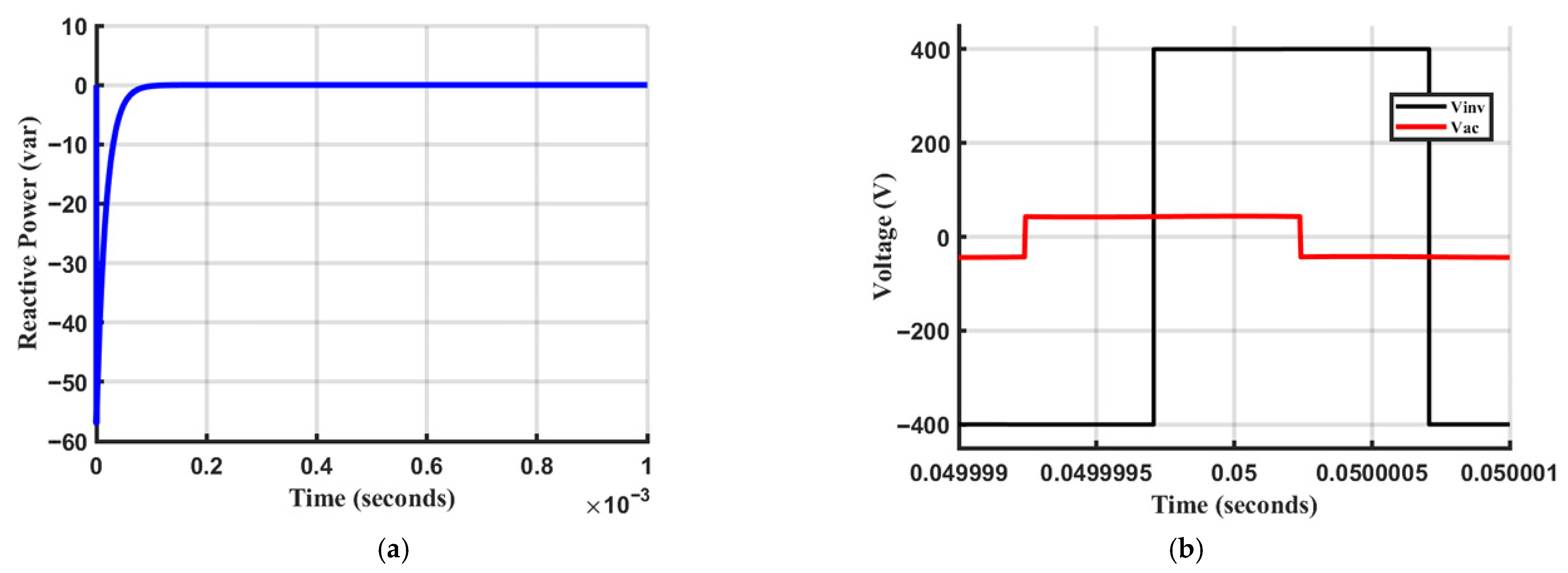
5.1. Steady-State Performance
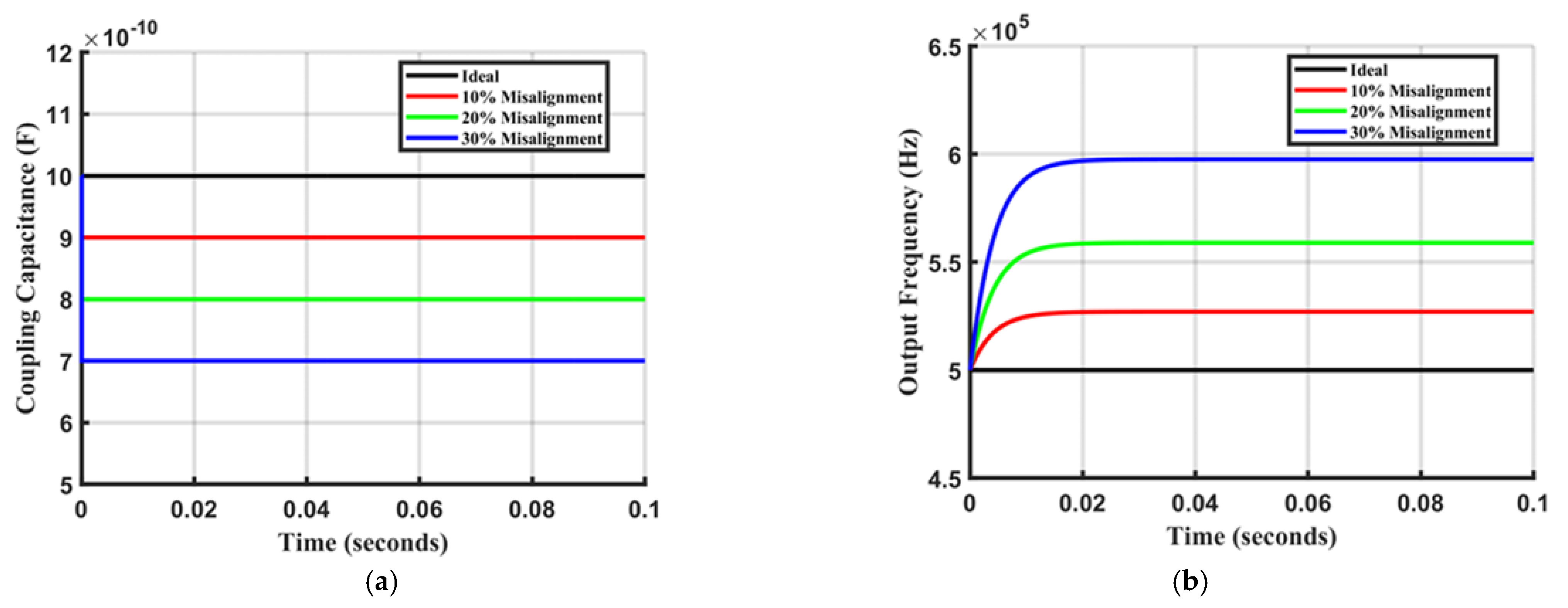
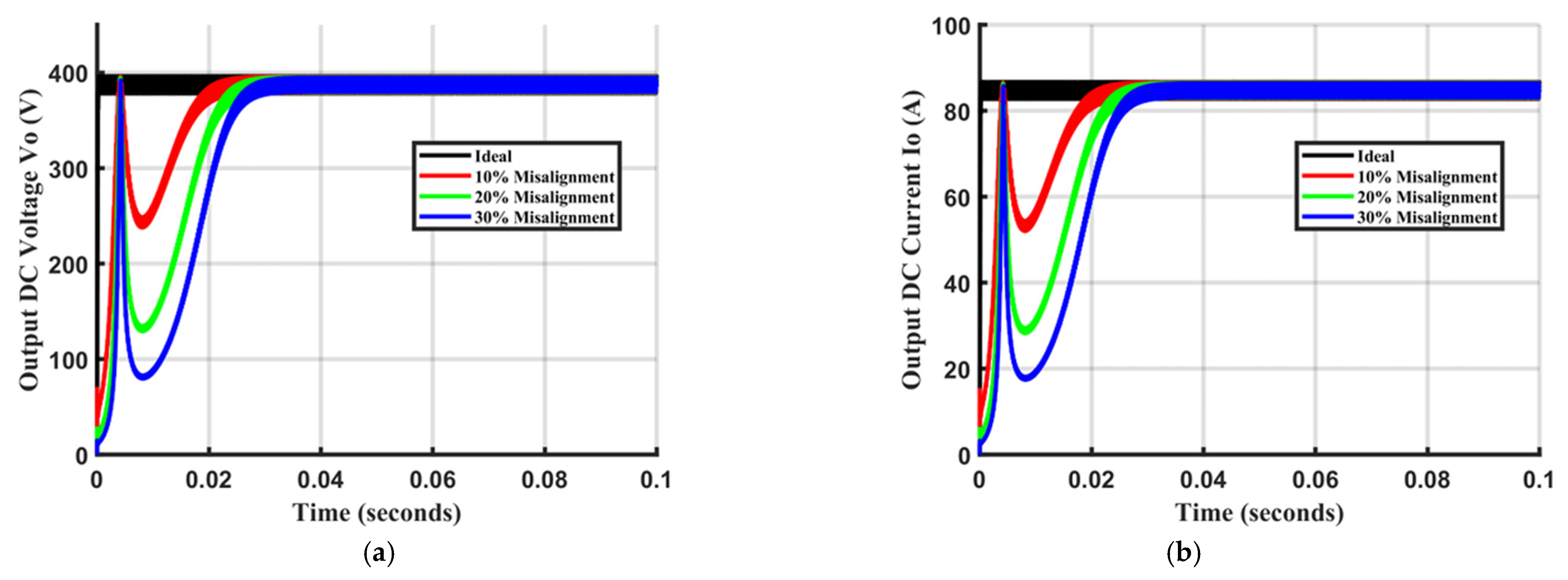
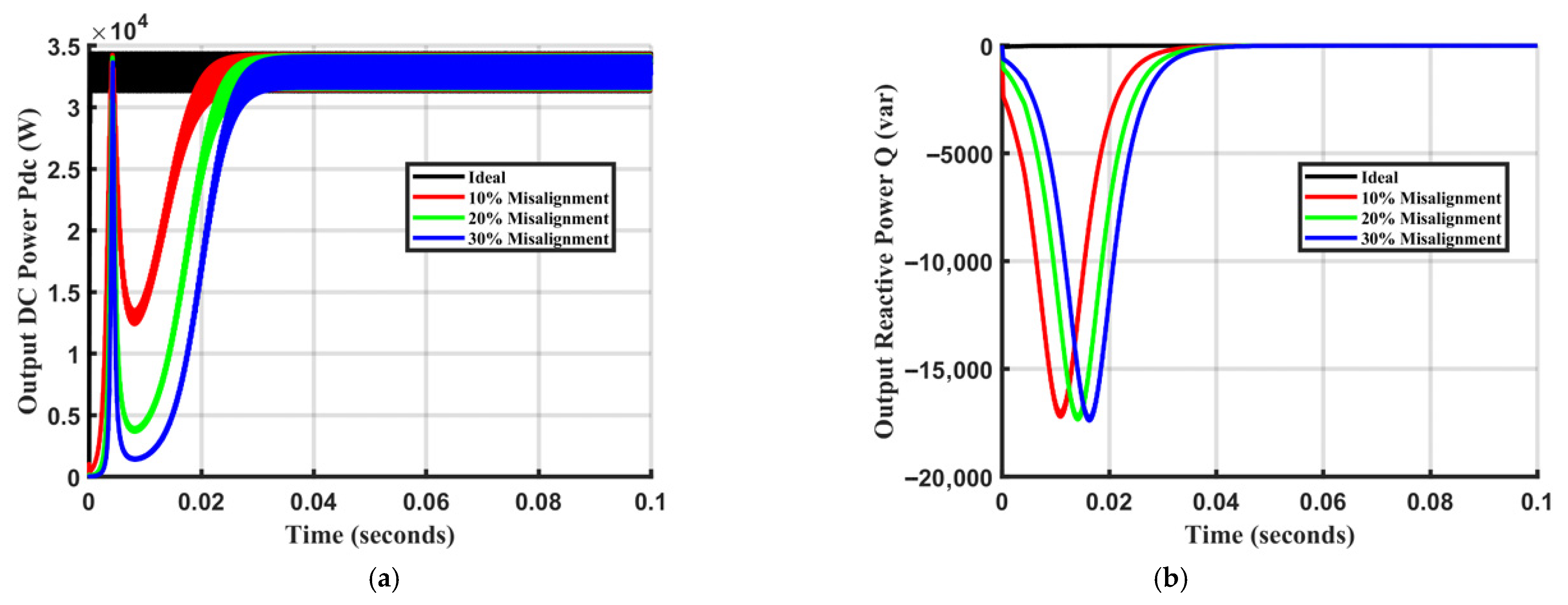
5.2. Transient Misalignment Response Characteristics
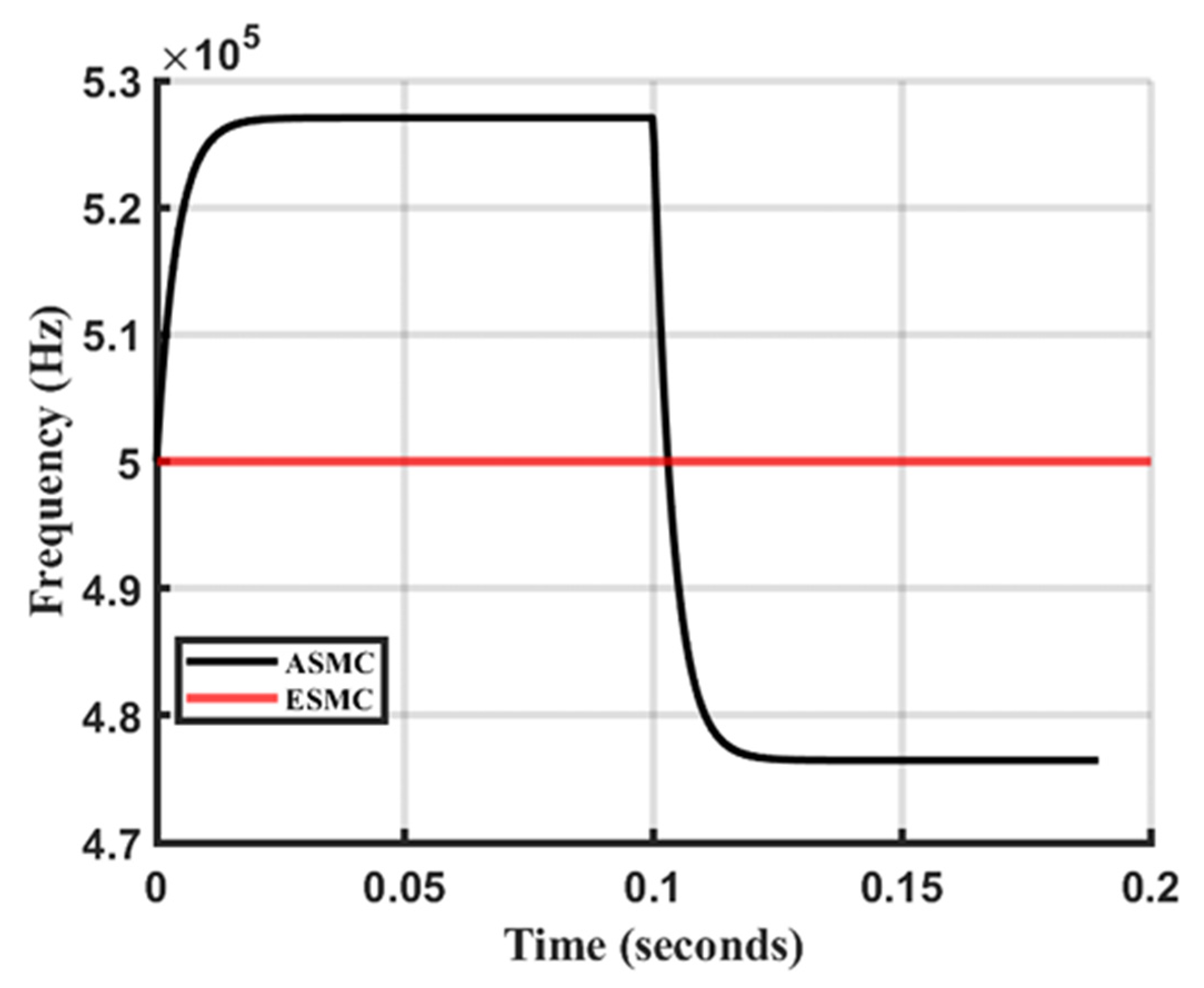
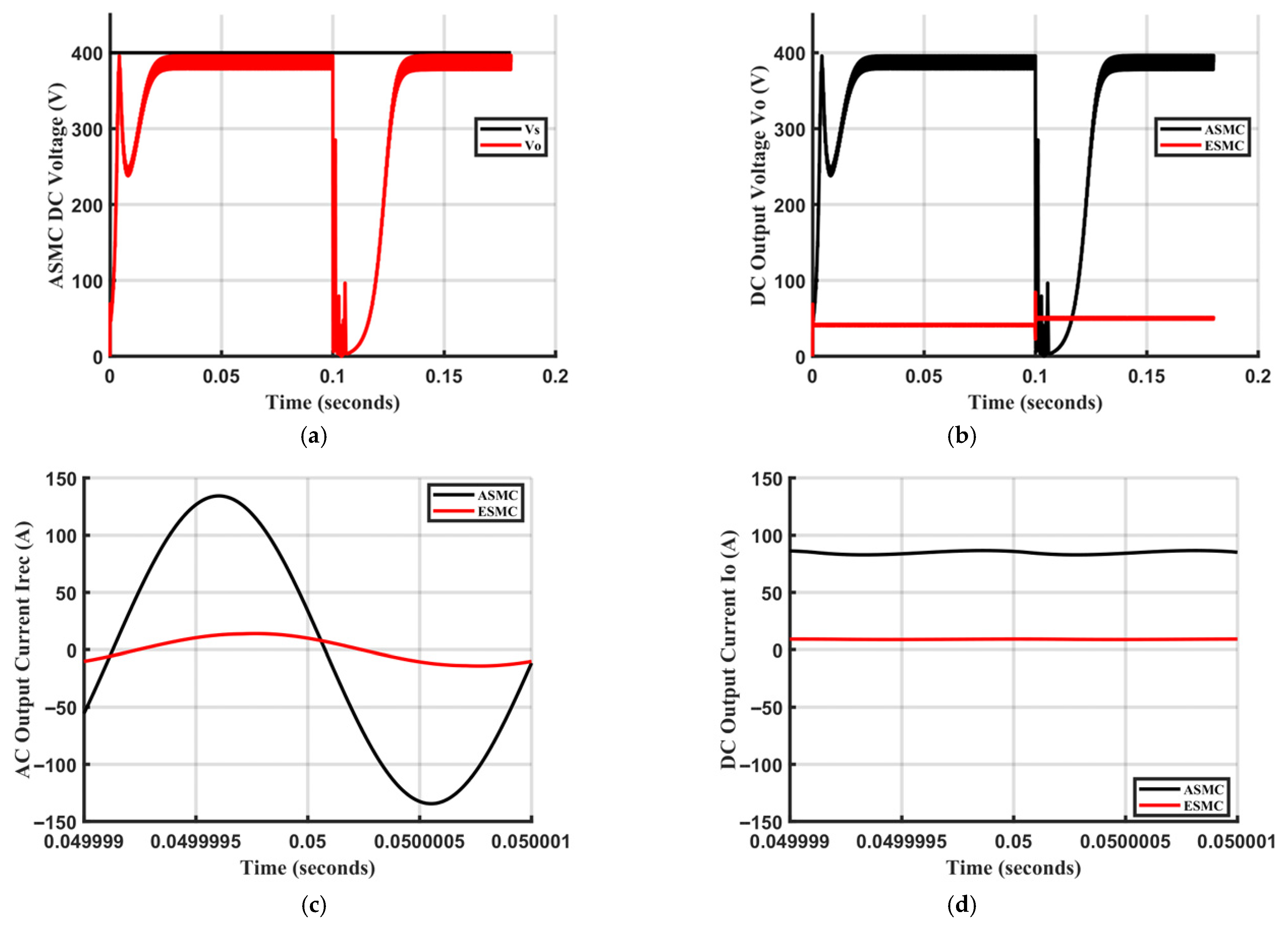
5.3. Performance Analysis of the Proposed ASMC with Conventional SMC Under Step Changes in Coupler Capacitance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Pang, H.; Georgiadis, A.; Cecati, C. Wireless Power Transfer—An Overview. IEEE Trans. Ind. Electron. 2019, 66, 1044–1058. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Deng, J.; Nguyen, T.D.; Mi, C.C. A Double-Sided LCC Compensation Network and Its Tuning Method for Wireless Power Transfer. IEEE Trans. Veh. Technol. 2015, 64, 2261–2273. [Google Scholar] [CrossRef]
- Mi, C.C.; Buja, G.; Choi, S.Y.; Rim, C.T. Modern Advances in Wireless Power Transfer Systems for Roadway Powered Electric Vehicles. IEEE Trans. Ind. Electron. 2016, 63, 6533–6545. [Google Scholar] [CrossRef]
- Covic, G.A.; Kissin, M.L.G.; Kacprzak, D.; Clausen, N.; Hao, H. A bipolar primary pad topology for EV stationary charging and highway power by inductive coupling. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 1832–1838. [Google Scholar]
- Thrimawithana, D.J.; Madawala, U.K.; Neath, M. A Synchronization Technique for Bidirectional IPT Systems. IEEE Trans. Ind. Electron. 2011, 60, 301–309. [Google Scholar] [CrossRef]
- Huang, L.; Hu, A.P.; Swain, A.; Ren, Y.; Jeong, S.S. Efficiency Analysis of Capacitive Power Transfer System with a Shielded Power Track. IEEE Trans. Power Electron. 2019, 34, 615–625. [Google Scholar]
- Lu, M.; Thrimawithana, D.J.; Madawala, U.K.; Phan, B.T.T. A Matrix Coupler for Three-Phase Capacitive Power Transfer Systems. IEEE Trans. Power Electron. 2021, 36, 2637–2648. [Google Scholar]
- Ciric, K.N.M.; Liu, S.; Regensburger, G.R.; Chen, X. A Comparative Study of Capacitive and Inductive Coupling for Wireless Power Transfer. In Proceedings of the 2020 IEEE Wireless Power Transfer Conference, Seoul, Republic of Korea, 15–19 November 2020; pp. 445–448. [Google Scholar]
- Diekhans, T.; De Doncker, R.W. A Dual-Side Controlled Inductive Power Transfer System Optimized for Large Coupling Factor Variations and Partial Load. IEEE Trans. Power Electron. 2015, 30, 6320–6328. [Google Scholar] [CrossRef]
- Zhong, W.X.; Hui, S.Y.R. Analysis of LCLC Resonant Converters with Capacitive Output Filter for Inductive Power Transfer. IEEE Trans. Power Electron. 2018, 33, 4271–4282. [Google Scholar]
- Su, Y.; Dai, X.; Jiang, C.; Qahouq, J.A.A. A Review of Recent Developments in Capacitive Wireless Power Transfer Technology. IEEE Trans. Power Electron. 2022, 37, 2475–2492. [Google Scholar]
- Miller, J.M.; Jones, P.T.; Li, J.M.; Onar, O.C. ORNL Experience and Challenges Facing Dynamic Wireless Power Charging of EV’s. IEEE Circuits Syst. Mag. 2018, 18, 40–53. [Google Scholar] [CrossRef]
- Shadmand, M.B.; Balog, R.S.; Abu-Rub, H. Model Predictive Control of a Capacitive Power Transfer System for Optimal Efficiency and Power Transfer. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition, Long Beach, CA, USA, 20–24 March 2016; pp. 2537–2542. [Google Scholar]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA—The Instrumentation, Systems, and Automation Society: Research Triangle Park, NC, USA, 2006. [Google Scholar]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Birkhäuser: Basel, Switzerland, 2014. [Google Scholar]
- Salimi, M.; Asef, P. Dynamic Wireless Charging Using Dynamic Frequency Tuning with Sliding Mode Control. In Proceedings of the ECCE Europe 2025, Birmingham, UK, 31 August–4 September 2025; IEEE: New York, NY, USA. [Google Scholar]
- Haykin, S.S. Adaptive Filter Theory, 5th ed.; Prentice Hall: Hoboken, NJ, USA, 2014. [Google Scholar]
- Ljung, L. System Identification. In Wiley Encyclopedia of Electrical and Electronics Engineering; Wiley: Hoboken, NJ, USA, 2015; pp. 1–19. [Google Scholar]
- Lian, J.; Qu, X. An LCLC-LC-Compensated Capacitive Power Transferred Battery Charger with Near-Unity Power Factor and Configurable Charging Profile. IEEE Trans. Ind. Appl. 2021, 58, 1053–1060. [Google Scholar] [CrossRef]
- Salimi, M.; Asef, P. Next-Generation EV Charging: Innovative Capacitive Wireless Power Transfer Through Harmonic Utilization. In Proceedings of the 2025 IEEE 19th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Antalya, Türkiye, 20–22 May 2025; pp. 1–7. [Google Scholar] [CrossRef]
- Gaudio, J.E.; Annaswamy, A.M.; Lavretsky, E.; Bolender, M.A. Parameter Estimation in Adaptive Control of Time-Varying Systems Under a Range of Excitation Conditions. IEEE Trans. Autom. Control 2021, 67, 5440–5447. [Google Scholar] [CrossRef]




| Constant | Value | Unit |
|---|---|---|
| Input () | 400 | V |
| DC Load () | 4.57 | Ω |
| AC Equivalent Load () | 2.285 | Ω |
| Ideal Output () | 35 | kW |
| Ideal AC Voltage Amplitude () | 400 | V |
| Initial Switching Frequency () | 0.5 | MHz |
| Mutual Inductance () | 101.32 | μH |
| Reference Coupling Capacitance () | 1000 | pF |
| Reference Angular Frequency () | rad/s | |
| Initial Estimated () | pF−1 | |
| Convergence Rate () | 250 | – |
| Switching Gain () | 1.5 | – |
| Boundary Layer Thickness () | 0.05 | – |
| Adaptive Gain () | 150 | – |
| Initial Covariance Matrix () | 1000 | – |
| Forgetting Factor () | 0.97 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, S.; Dong, Q.; Asef, P.; Salimi, M. AI-Assisted Adaptive Sliding Mode Control for Pseudo-Resonance Suppression in Dynamic Capacitive Wireless Charging Systems. Energies 2025, 18, 6052. https://doi.org/10.3390/en18226052
Cai S, Dong Q, Asef P, Salimi M. AI-Assisted Adaptive Sliding Mode Control for Pseudo-Resonance Suppression in Dynamic Capacitive Wireless Charging Systems. Energies. 2025; 18(22):6052. https://doi.org/10.3390/en18226052
Chicago/Turabian StyleCai, Shuchang, Qing Dong, Pedram Asef, and Mahdi Salimi. 2025. "AI-Assisted Adaptive Sliding Mode Control for Pseudo-Resonance Suppression in Dynamic Capacitive Wireless Charging Systems" Energies 18, no. 22: 6052. https://doi.org/10.3390/en18226052
APA StyleCai, S., Dong, Q., Asef, P., & Salimi, M. (2025). AI-Assisted Adaptive Sliding Mode Control for Pseudo-Resonance Suppression in Dynamic Capacitive Wireless Charging Systems. Energies, 18(22), 6052. https://doi.org/10.3390/en18226052








