Performance Evaluation and Structure Optimization of a New Type of Shell-and-Tube Heat Exchanger with Embedded Louver Segmental Baffle Support
Abstract
1. Introduction
2. Numerical Method
2.1. Geometric Model
2.2. Mathematic Model and Boundary Condition Setting
2.3. Grid Generation
2.4. Data Processing
2.5. Model Verification
3. Results and Discussion
3.1. Performance Comparison of the Two Kinds of Heat Exchanger
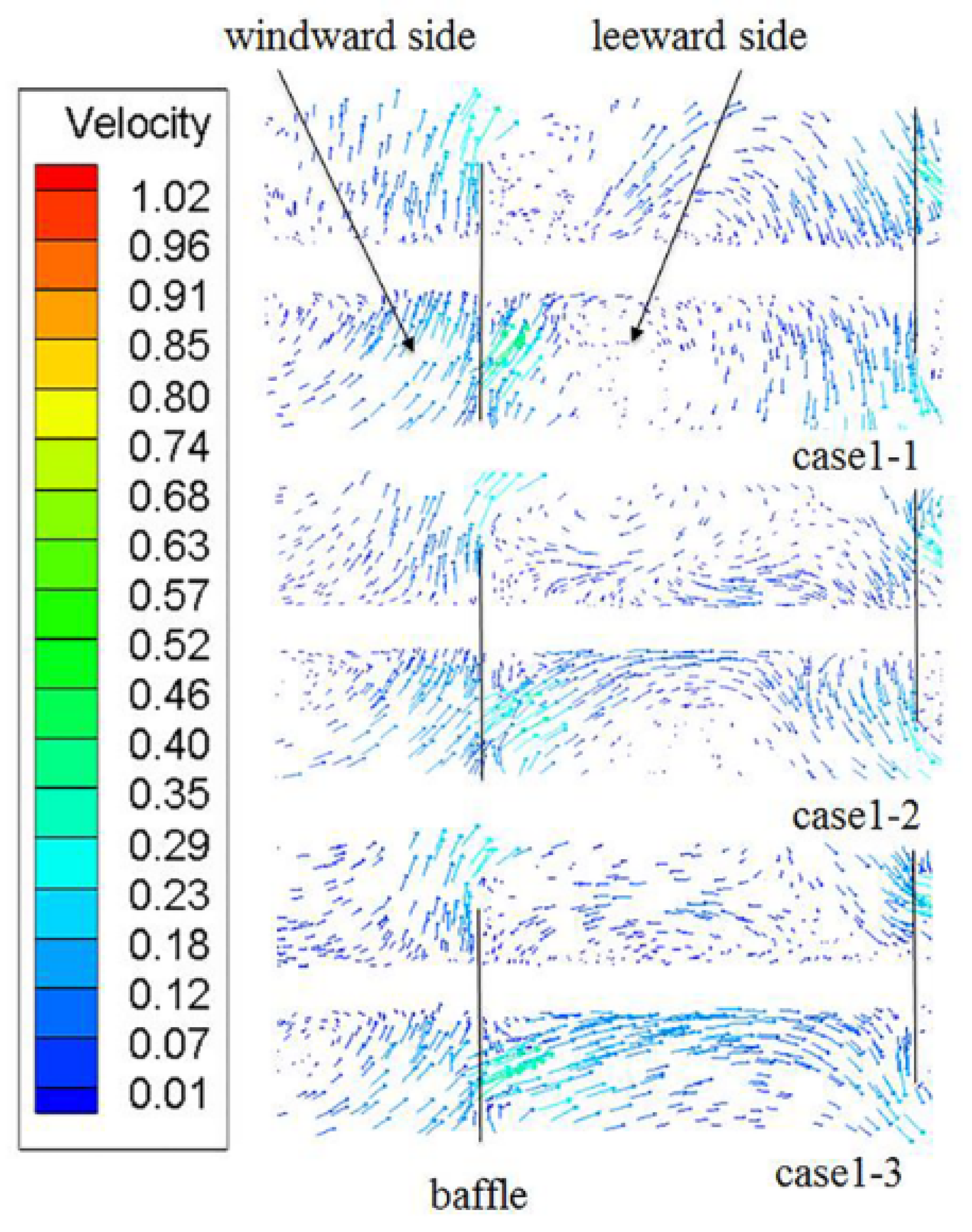
3.1.1. Velocity Distribution
3.1.2. Temperature Distribution
3.1.3. Pressure Distribution
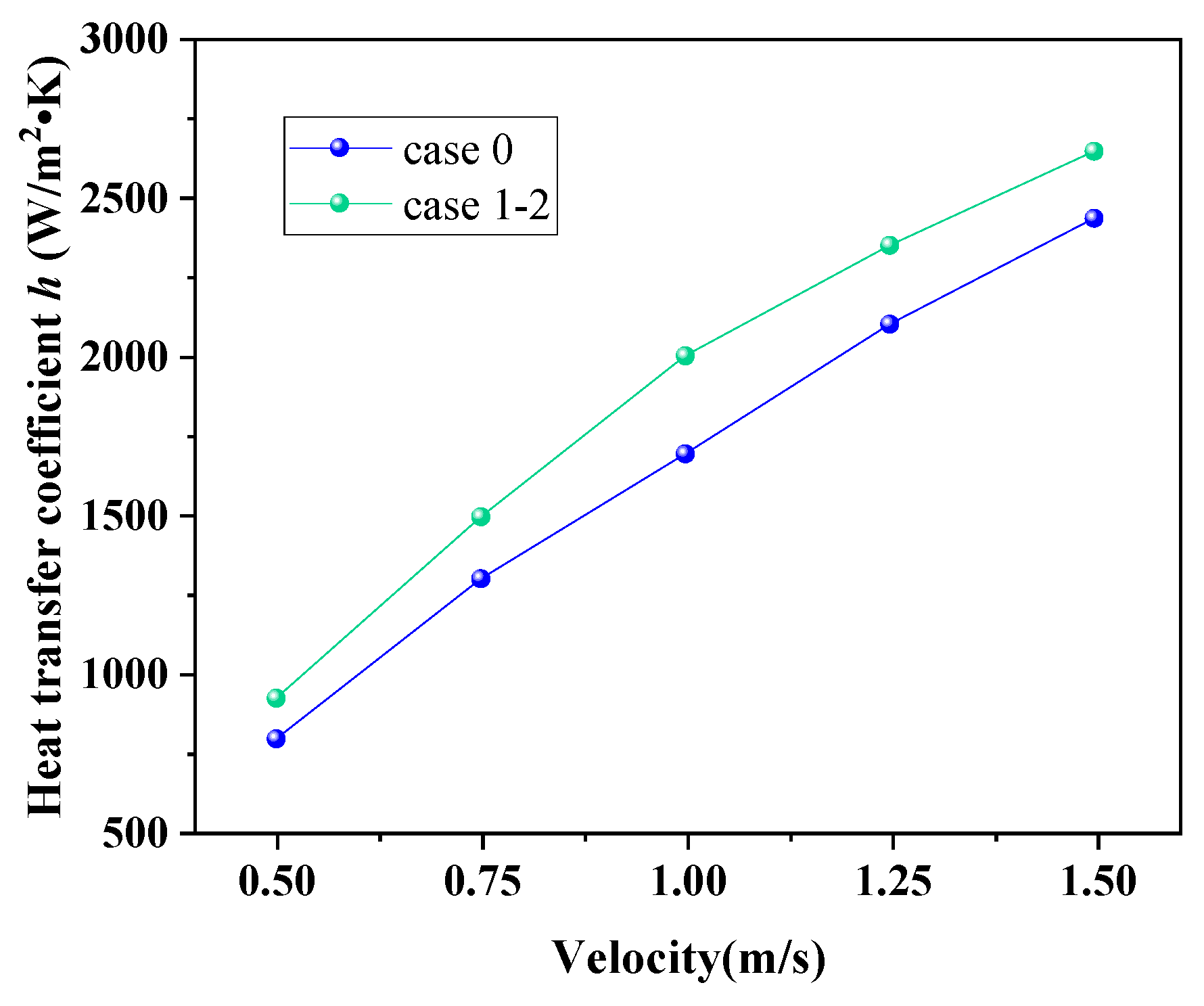
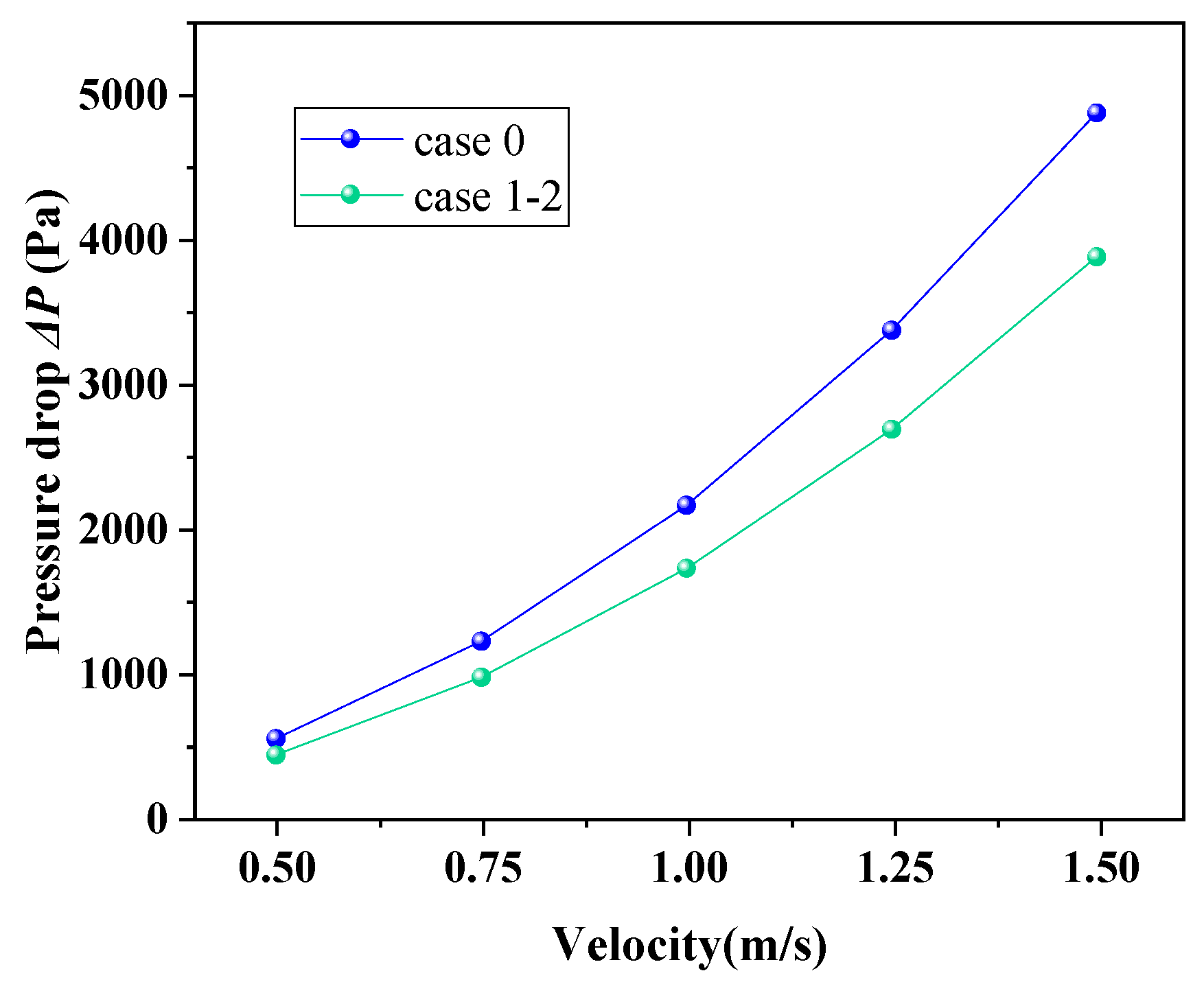
3.1.4. h and ∆P
3.2. Effect of Structural Parameters on the Performance of ELB-STHX
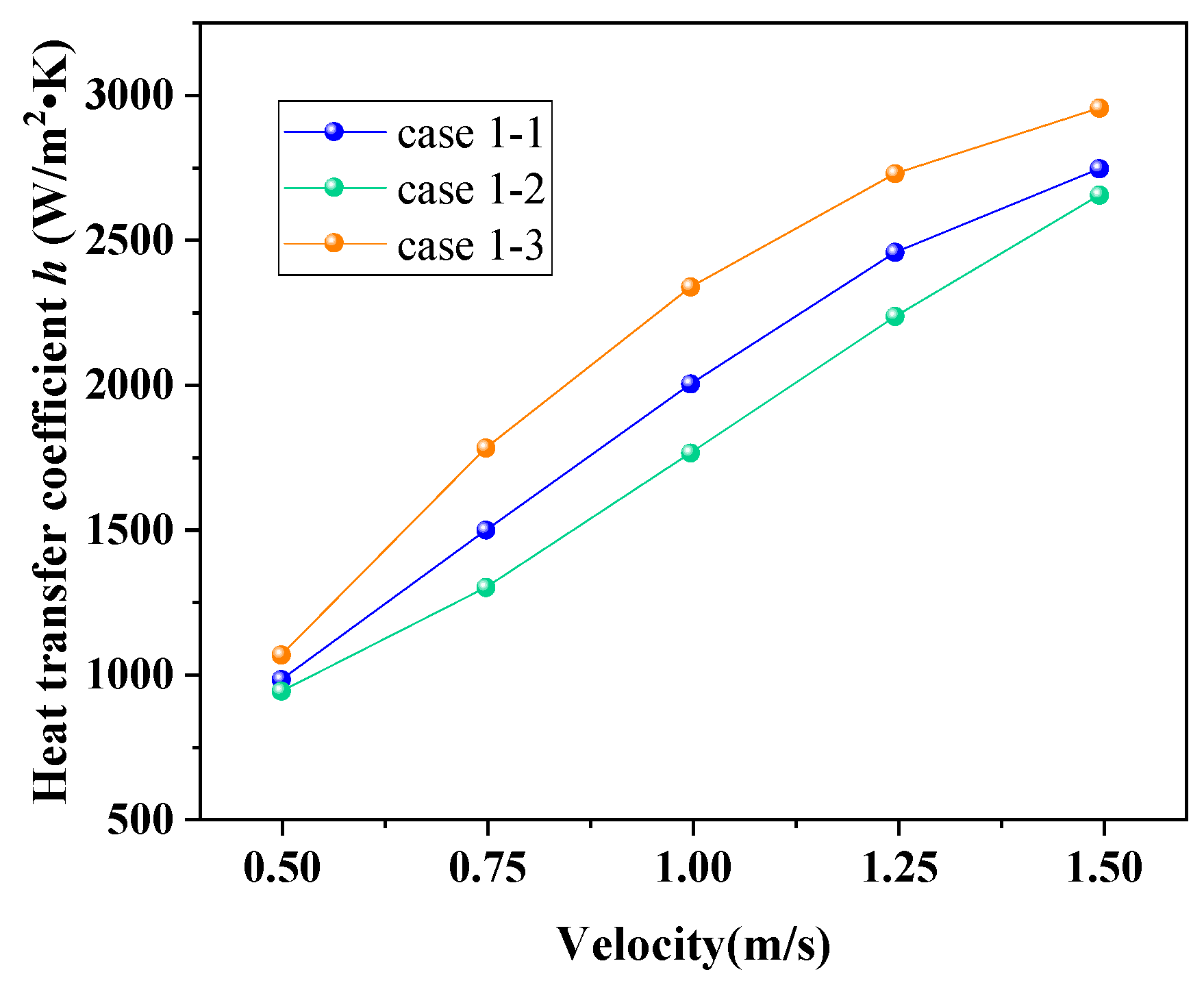
3.2.1. The Effects of θ on h
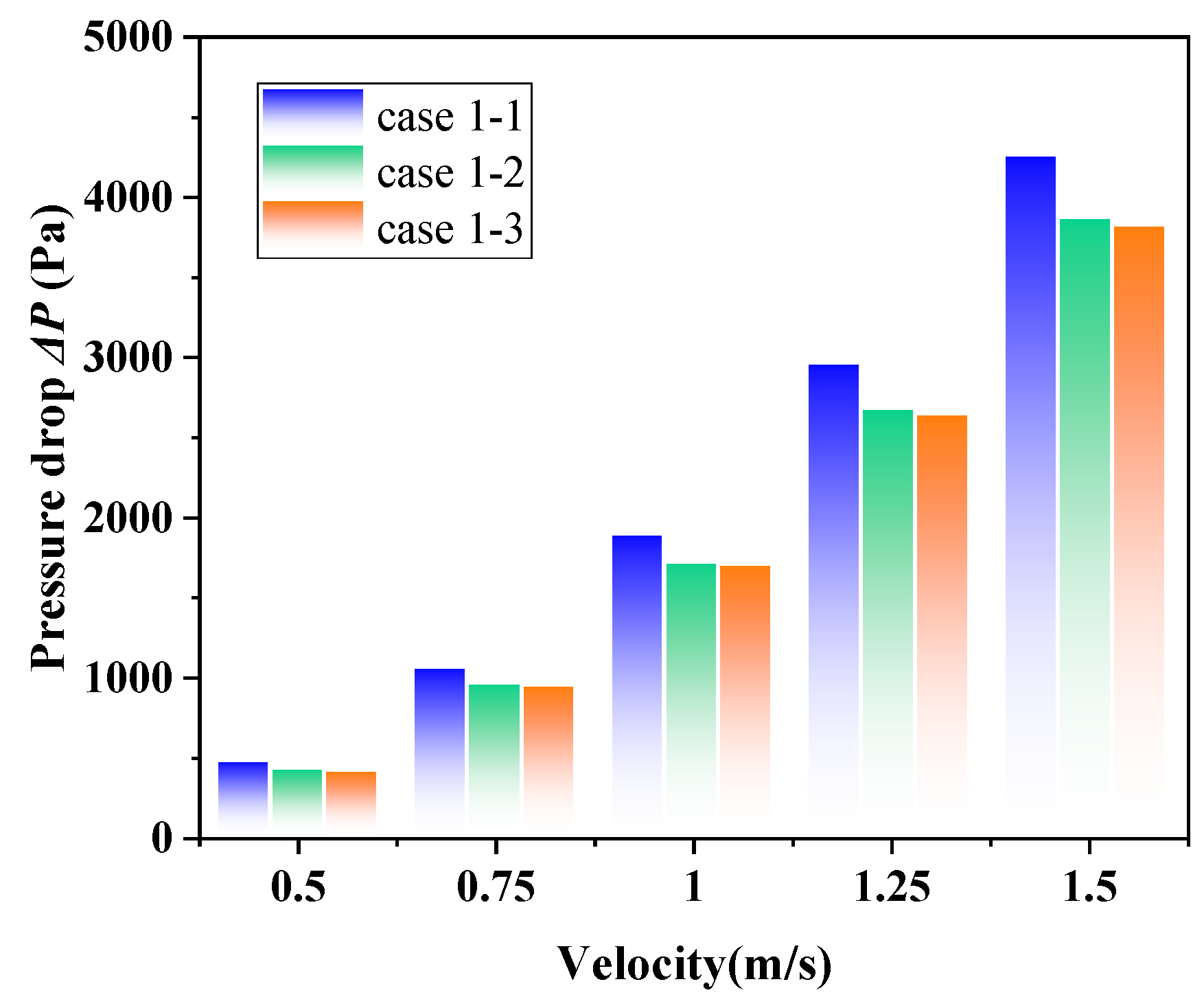
3.2.2. The Effects of θ on ∆P
3.2.3. The Effects of θ on φ
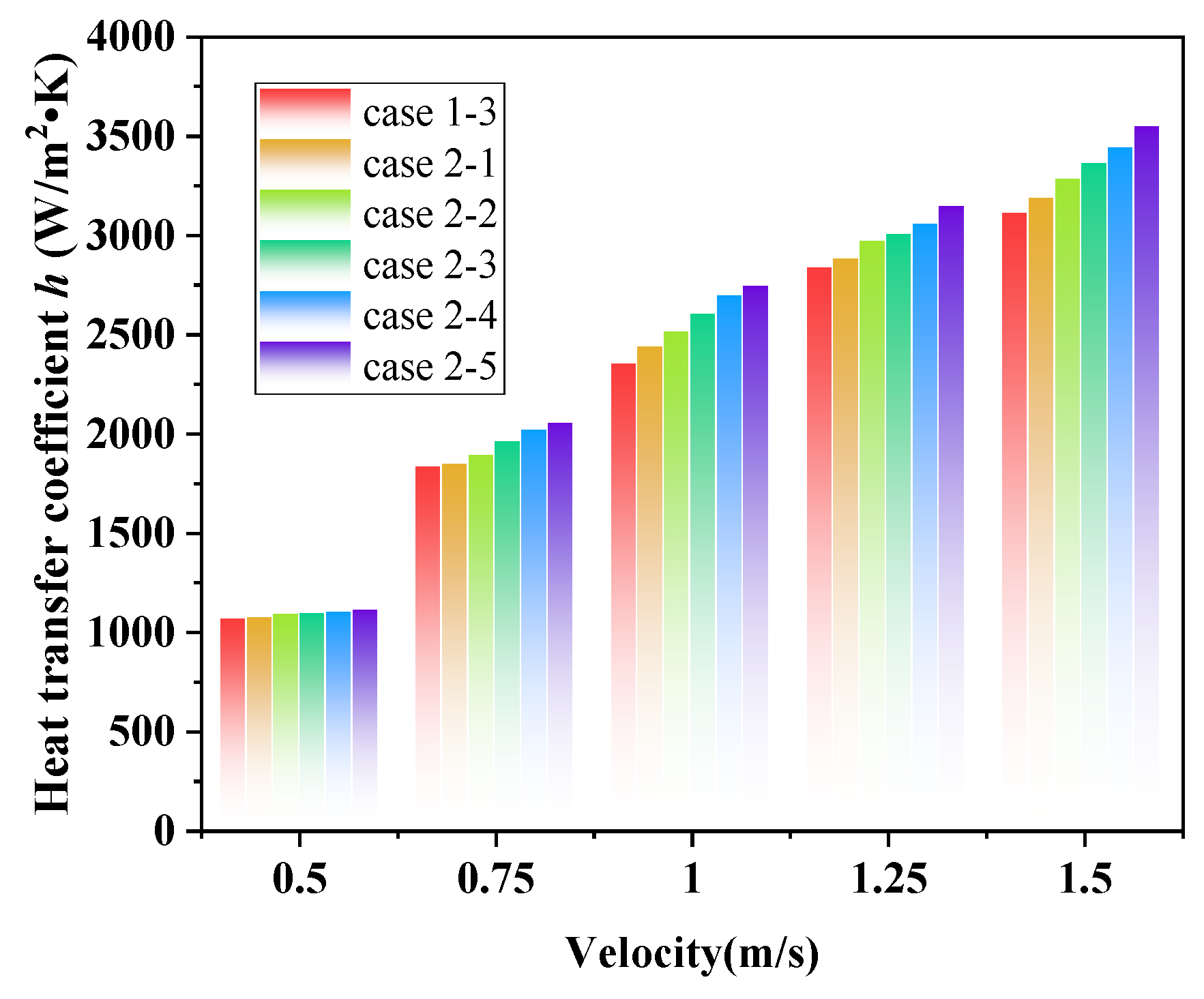
3.2.4. The Effects of l on h
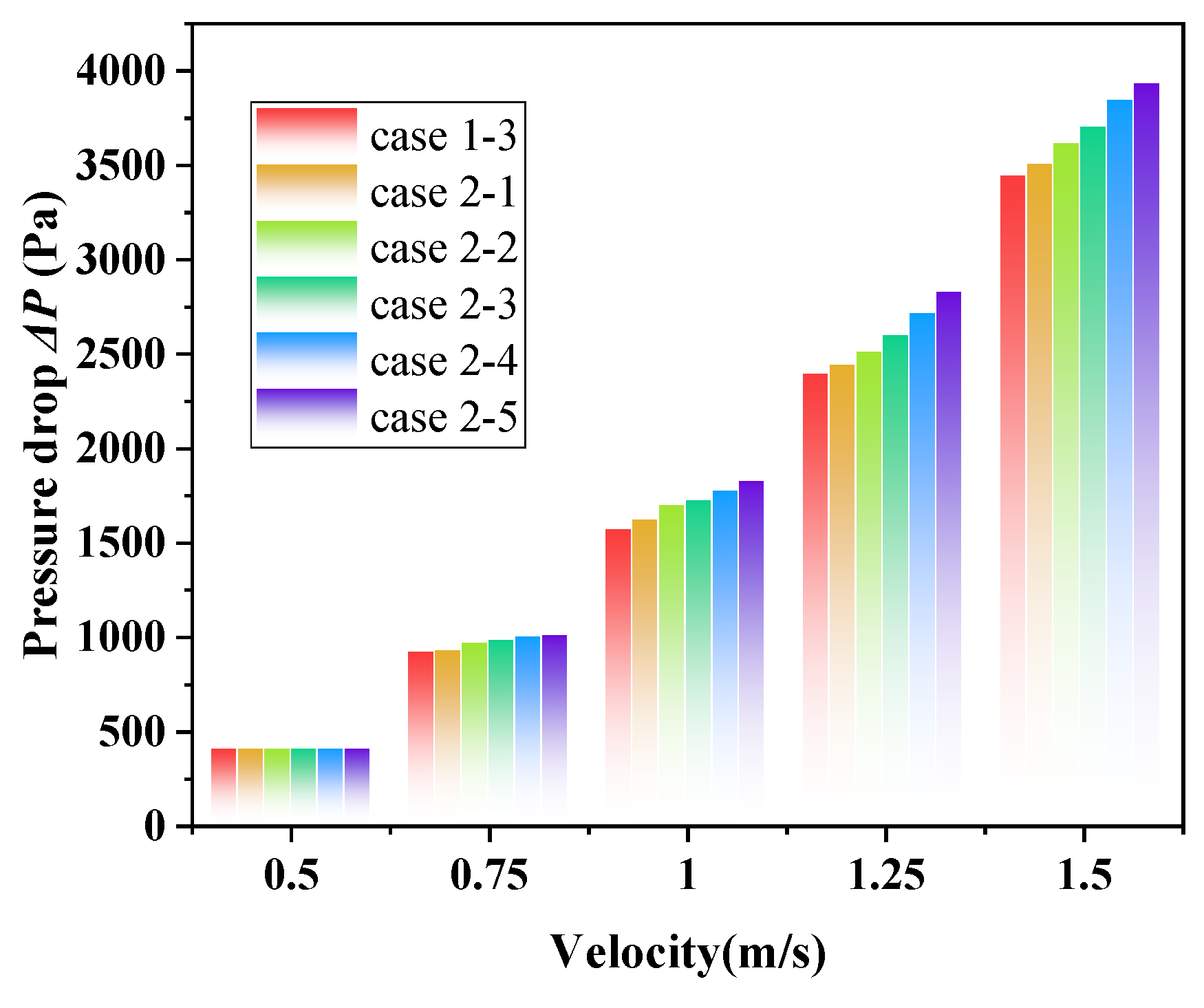
3.2.5. The Effects of l on ∆P
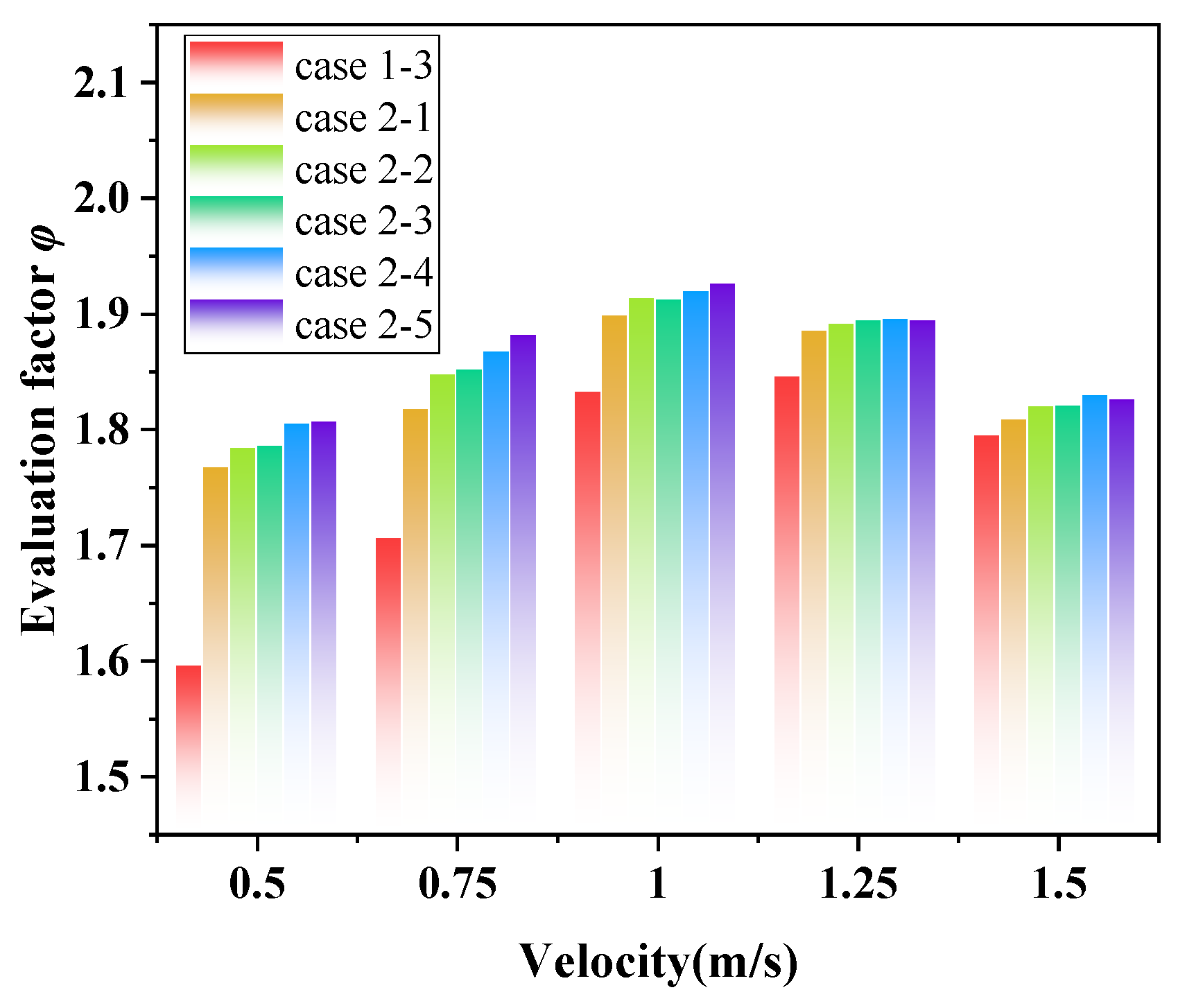
3.2.6. The Effects of l on φ
4. Conclusions
- (1)
- This improved baffle structure changes the “Z” flow of the shell side fluid of the CSB-STHX into a coexisting form of “Z” and circular arc flow, which effectively reduces the area of the flow dead zone and enhances fluid disturbance in the leeward side of the baffle.
- (2)
- In the ELB-STHX, the temperature gradient on both sides of the baffles is relatively small. At the inlet, the outlet of shell side fluid, and the middle section of the heat exchange equipment, the average fluid temperatures are 0.34 °C, 2.12 °C, and 3.08 °C higher, respectively, compared to those in the CSB-STHX.
- (3)
- The guiding effect of the louvers ensures a continuous pressure variation between the windward and leeward sides of the baffles, resulting in a lower shell side pressure loss compared to the CSB-STHX.
- (4)
- Under the same fluid velocity, compared to the CSB-STHX, the ELB-STHX increases the h by 8.75% to 16.4% while reducing pressure loss by 20.5% to 21.3%.
- (5)
- As the louver angle increases, the h initially rises and then declines, while the shell side ∆P decreases monotonically. The comprehensive evaluation factor reaches its maximum when the louver angle is 60°.
- (6)
- Increasing the louver length leads to a simultaneous rise in both the h and ∆P. However, when the louver length is extended from 1/7 to 1/3 of the distance between adjacent baffles, the improvement in the comprehensive evaluation factor is minimal. Therefore, a louver length of 1/7 the distance between adjacent baffles is the optimal design choice.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature/Abbreviations
| Nomenclature | |||
| θ | Louver angle (°) | Q | Heat flow rate (W/m2) |
| l | Louver length (mm) | Tin | Inlet temperature of shell side fluid (K) |
| D | Diameter of shell (mm) | Vin | Inlet velocity of shell side fluid (m/s) |
| din (out) | Diameter of shell inlet (outlet) (mm) | Ttube | Temperature of the tube (K) |
| L | Tube length (mm) | h | Heat transfer coefficient (W/m2∙K) |
| dtube | Outer diameter of tube (mm) | ∆P | Pressure drop (Pa) |
| n | Number of tubes | A | Effective heat transfer area (m2) |
| Z | Distance between adjacent tubes (mm) | ∆Tm | Log-mean temperature difference (K) |
| N | Number of baffles | M | Flow rate (kg/s) |
| H | Cut ratio of baffle | Tout | Outlet temperature of shell side fluid (K) |
| B | Distance between adjacent baffles (mm) | Pin | Inlet pressure of the shell fluid (Pa) |
| ρ | Liquid density (kg/m3) | Pout | Outlet pressure of the shell fluid (Pa) |
| c1, c2 | Constant | φ | Comprehensive evaluation factor |
| cμ | Function of rotation rates and mean strain | hELB | Heat transfer coefficients of ELB-STHX (W/m2∙K) |
| λ | Thermal conductivity (W/m⋅K) | hCSB | Heat transfer coefficients of CSB-STHX (W/m2∙K) |
| ν | Kinematic viscosity coefficient (m2/s) | ∆PELB | Shell side pressure drop of ELB-STHX (Pa) |
| Pr | Prandtl Number | ∆PCSB | Shell side pressure drop of CSB-STHX (Pa) |
| Cp | Specific heat capacity (J/kg⋅K) | ||
| Abbreviations | |||
| STHX | shell-and-tube heat exchanger | ||
| THB-STHX | shell-and-tube heat exchangers with trefoil-hole baffles | ||
| CBSTT-STHX | shell-and-tube heat exchanger with clamping antivibration baffles and square twisted tubes | ||
| SGCT-STHX | shell-and-tube heat exchanger with segmental baffles and cylindrical tubes | ||
| ELB-STHX | shell-and-tube heat exchanger with embedded louver segmental baffle support | ||
| CSB-STHX | shell-and-tube heat exchanger with common segmental baffle | ||
References
- Stehlík, P.; Wadekar, V.V. Different Strategies to Improve Industrial Heat Exchange. Heat Transf. Eng. 2010, 23, 36–48. [Google Scholar] [CrossRef]
- Abbasian Arani, A.A.; Moradi, R. Shell and tube heat exchanger optimization using new baffle and tube configuration. Appl. Therm. Eng. 2019, 157, 113736. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, Y.; Wu, Y. Study on the performance of a novel sinusoidal staggered shell and tube heat exchanger without baffle with experiment verification and CFD modeling. J. Energy Storage 2025, 114, 115832. [Google Scholar] [CrossRef]
- Sundén, B. Computational Fluid Dynamics in Research and Design of Heat Exchangers. Heat Transf. Eng. 2007, 28, 898–910. [Google Scholar] [CrossRef]
- Kücük, H. The effect of minichannels on the overall heat transfer coefficient and pressure drop of a shell and tube heat exchanger: Experimental performance comparison. Int. J. Therm. Sci. 2023, 188, 108217. [Google Scholar] [CrossRef]
- Shoaei, M.; Kowsary, F. Multi-objective optimization of geometrical parameters of a pipe with internal baffle using artificial neural networks and genetic algorithm. Appl. Therm. Eng. 2025, 262, 125212. [Google Scholar] [CrossRef]
- Marzouk, S.A.; Al-Sood, M.M.A.; El-Fakharany, M.K.; El-Said, E.M.S. A comparative numerical study of shell and multi-tube heat exchanger performance with different baffles configurations. Int. J. Therm. Sci. 2022, 179, 107655. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, X.; Li, J.; Lu, H. CFD analysis of mist/air film cooling on a flat plate with different hole types. Numer. Heat Transf. Part A Appl. 2017, 71, 1123–1140. [Google Scholar] [CrossRef]
- Wang, Q.; Zeng, M.; Ma, T.; Du, X.; Yang, J. Recent development and application of several high-efficiency surface heat exchangers for energy conversion and utilization. Appl. Energy 2014, 135, 748–777. [Google Scholar] [CrossRef]
- Dogan, S. Baffle angle optimization of a typical shell and tube heat exchanger. Phys. Fluids 2025, 37, 015165. [Google Scholar] [CrossRef]
- Shabani Samghabadia, A.; Abbasian Arani, A.A.; Yosofvand, H. Thermo-hydraulic efficiency enhancing: Optimized ladder fold baffle structure with cam and circle tube bundle. Int. J. Therm. Sci. 2024, 196, 108680. [Google Scholar] [CrossRef]
- Al-darraji, A.R.; Marzouk, S.A.; Aljabr, A.; Almehmadi, F.A.; Alqaed, S.; Kaood, A. Enhancement of heat transfer in a vertical shell and tube heat exchanger using air injection and new baffles: Experimental and numerical approach. Appl. Therm. Eng. 2024, 236, 121493. [Google Scholar] [CrossRef]
- Marzouk, S.A.; Abou Al-Sood, M.M.; El-Said, E.M.S.; Younes, M.M.; El-Fakharany, M.K. A comprehensive review of methods of heat transfer enhancement in shell and tube heat exchangers. J. Therm. Anal. Calorim. 2023, 148, 7539–7578. [Google Scholar] [CrossRef]
- El Maakoul, A.; Laknizi, A.; Saadeddine, S.; El Metoui, M.; Zaite, A.; Meziane, M.; Abdellah, A.B. Numerical comparison of shell-side performance for shell and tube heat exchangers with trefoil-hole, helical and segmental baffles. Appl. Therm. Eng. 2016, 109, 175–185. [Google Scholar] [CrossRef]
- You, Y.; Fan, A.; Lai, X.; Huang, S.; Liu, W. Experimental and numerical investigations of shell-side thermo-hydraulic performances for shell-and-tube heat exchanger with trefoil-hole baffles. Appl. Therm. Eng. 2013, 50, 950–956. [Google Scholar] [CrossRef]
- Saad, M.; Munir, A.; Kamran, M.A. Numerical Simulations of Shell and Tube Heat Exchanger with Segmental, Trefoil and Segmented Trefoil Baffles for Performance Comparison. Heat Transf. Eng. 2022, 44, 702–719. [Google Scholar] [CrossRef]
- Ma, L.; Wang, K.; Liu, M.; Wang, D.; Liu, T.; Wang, Y.; Liu, Z. Numerical study on performances of shell-side in trefoil-hole and quatrefoil-hole baffle heat exchangers. Appl. Therm. Eng. 2017, 123, 1444–1455. [Google Scholar] [CrossRef]
- Rezwan, A.A.; Hossain, S.; Rahman, S.M.A.; Islam, M.A. Heat Transfer Enhancement in an Air Process Heater Using Semi-Circular Hollow Baffles. Procedia Eng. 2013, 56, 357–362. [Google Scholar] [CrossRef]
- Dong, Q.W.; Wang, Y.Q.; Liu, M.S. Numerical and experimental investigation of shellside characteristics for RODbaffle heat exchanger. Appl. Therm. Eng. 2008, 28, 651–660. [Google Scholar] [CrossRef]
- Xianhe, D.; Songjiu, D. Investigation of Heat Transfer Enhancement of Roughened Tube Bundles Supported by Ring or Rod Supports. Heat Transf. Eng. 1998, 19, 21–27. [Google Scholar] [CrossRef]
- You, Y.; Zhang, F.; Fan, A.; Dai, F.; Luo, X.; Liu, W. A numerical study on the turbulent heat transfer enhancement of Rodbaffle heat exchanger with staggered tubes supported by round rods with arc cuts. Appl. Therm. Eng. 2015, 76, 220–232. [Google Scholar] [CrossRef]
- Tan X-h Zhu D-s Zhou G-y Yang, L. 3D numerical simulation on the shell side heat transfer and pressure drop performances of twisted oval tube heat exchanger. Int. J. Heat Mass Transf. 2013, 65, 244–253. [Google Scholar] [CrossRef]
- Peng, B.; Wang, Q.; Zhang, C.; Xie, G.; Luo, L.; Chen, Q.; Zeng, M. An Experimental Study of Shell-and-Tube Heat Exchangers With Continuous Helical Baffles. J. HEAT Transf.-Trans. ASME 2007, 129, 1423–1431. [Google Scholar] [CrossRef]
- Nagaeswara Rao, B.; Pavanu Sai, J. Numerical investigation of thermo-hydraulic ability of STHX with continuous helical baffles on the shell side. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Naqvi, S.M.A.; Wang, Q. Numerical Comparison of Thermohydraulic Performance and Fluid-Induced Vibrations for STHXs with Segmental, Helical, and Novel Clamping Antivibration Baffles. Energies 2019, 12, 540. [Google Scholar] [CrossRef]
- Zhang, J.-F.; He, Y.-L.; Tao, W.-Q. 3D numerical simulation on shell-and-tube heat exchangers with middle-overlapped helical baffles and continuous baffles–Part II: Simulation results of periodic model and comparison between continuous and noncontinuous helical baffles. Int. J. Heat Mass Transf. 2009, 52, 5381–5389. [Google Scholar] [CrossRef]
- Duan, Z.; Shen, F.; Cao, X.; Zhang, J. Comprehensive effects of baffle configuration on the performance of heat exchanger with helical baffles. Nucl. Eng. Des. 2016, 300, 349–357. [Google Scholar] [CrossRef]
- Kumar, R.; Chandra, P. Thermal analysis, pressure drop and exergy loss of energy efficient shell, and triple meshed helical coil tube heat exchanger. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 42, 1026–1039. [Google Scholar] [CrossRef]
- Dong, C.; Chen, Y.-P.; Wu, J.-F.; Cao, R.-B. Performance Study of a Circumferential Overlap Trisection Helical Baffle Heat Exchanger at the Shell Side. Heat Transf. Eng. 2015, 36, 1132–1143. [Google Scholar] [CrossRef]
- Dong, C.; Chen, Y.P.; Wu, J.F.; Cao, R.B. Numerical Investigation on Circumferential Overlap Trisection Helical Baffle Heat Exchanger. Appl. Mech. Mater. 2013, 389, 1035–1040. [Google Scholar] [CrossRef]
- Sun, Y.; Li, D.; Ji, J.; Hua, Z. Numerical study of structural parameters of perforated baffle on heat transfer enhancement in coiled elastic copper tube heat exchanger. Appl. Therm. Eng. 2025, 260, 124993. [Google Scholar] [CrossRef]
- Gu, X.; Li, N.; Chen, C.; Zhang, Q.; Wang, G.; Wang, Y. Analysis of fluid retention zones in heat exchangers with segmental baffle and helical baffle. Int. J. Chem. React. Eng. 2022, 20, 681–696. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, R.; Chen, D.; Chen, L.; Du, T.; Yu, H. Performance investigation and multi-objective optimization of helical baffle heat exchangers based on thermodynamic and economic analyses. Int. J. Heat Mass Transf. 2021, 176, 121489. [Google Scholar] [CrossRef]
- Lei, Y.; Li, Y.; Jing, S.; Song, C.; Lyu, Y.; Wang, F. Design and performance analysis of the novel shell-and-tube heat exchangers with louver baffles. Appl. Therm. Eng. 2017, 125, 870–879. [Google Scholar] [CrossRef]
- Sun, Y.; Li, D.; Ji, J.; Hua, Z. Numerical analysis on heat transfer performance of spiral elastic copper tube heat exchanger with helical defectors. Appl. Therm. Eng. 2024, 248, 123298. [Google Scholar] [CrossRef]
- Ji, J.; Pan, Y.; Zhang, J.; Shi, B.; Bao, L. Numerical study on the effect of baffle structure on the heat transfer performance of elastic tube bundle heat exchanger. Appl. Therm. Eng. 2024, 238, 122220. [Google Scholar] [CrossRef]
- Aslam Bhutta, M.M.; Hayat, N.; Bashir, M.H.; Khan, A.R.; Ahmad, K.N.; Khan, S. CFD applications in various heat exchangers design: A review. Appl. Therm. Eng. 2012, 32, 1–12. [Google Scholar] [CrossRef]
- Alqarni, M.M.; Ibrahim, M.; Assiri, T.A.; Saeed, T.; Mousa, A.A.A.; Ali, V. Two-phase simulation of a shell and tube heat exchanger filled with hybrid nanofluid. Eng. Anal. Bound. Elem. 2023, 146, 80–88. [Google Scholar] [CrossRef]
- Gerhardt, F.L.C.; Salvo, R.d.V.; Marchi Neto Id Lima RSd Silva, R.C.d. Computational modeling of a thermal energy storage tank coupled to a water-cooled household refrigerator. J. Energy Storage 2021, 41, 102961. [Google Scholar] [CrossRef]
- Tan X-h Zhu D-s Zhou G-y Zeng, L.-d. Heat transfer and pressure drop performance of twisted oval tube heat exchanger. Appl. Therm. Eng. 2013, 50, 374–383. [Google Scholar] [CrossRef]
- Ambekar, A.S.; Sivakumar, R.; Anantharaman, N.; Vivekenandan, M. CFD simulation study of shell and tube heat exchangers with different baffle segment configurations. Appl. Therm. Eng. 2016, 108, 999–1007. [Google Scholar] [CrossRef]
- Zhang, X.; Han, D.; He, W.; Yue, C.; Pu, W. Numerical simulation on a novel shell-and-tube heat exchanger with screw cinquefoil orifice baffles. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, P.; Wang, Q.; Zeng, M. Experimental Investigation of Shell-Side Performance and Optimal Design of Shell-and-Tube Heat Exchanger with Different Flower Baffles. Heat Transf. Eng. 2020, 42, 613–626. [Google Scholar] [CrossRef]
- Zeyninejad Movassag, S.; Nemati Taher, F.; Razmi, K.; Tasouji Azar, R. Tube bundle replacement for segmental and helical shell and tube heat exchangers: Performance comparison and fouling investigation on the shell side. Appl. Therm. Eng. 2013, 51, 1162–1169. [Google Scholar] [CrossRef]
- Roetzel, W.; Lee, D.W. Effect of baffle shell leakage flow on heat transfer in shell-and-tube heat exchangers. Exp. Therm. Fluid Sci. 1994, 8, 10–20. [Google Scholar] [CrossRef]
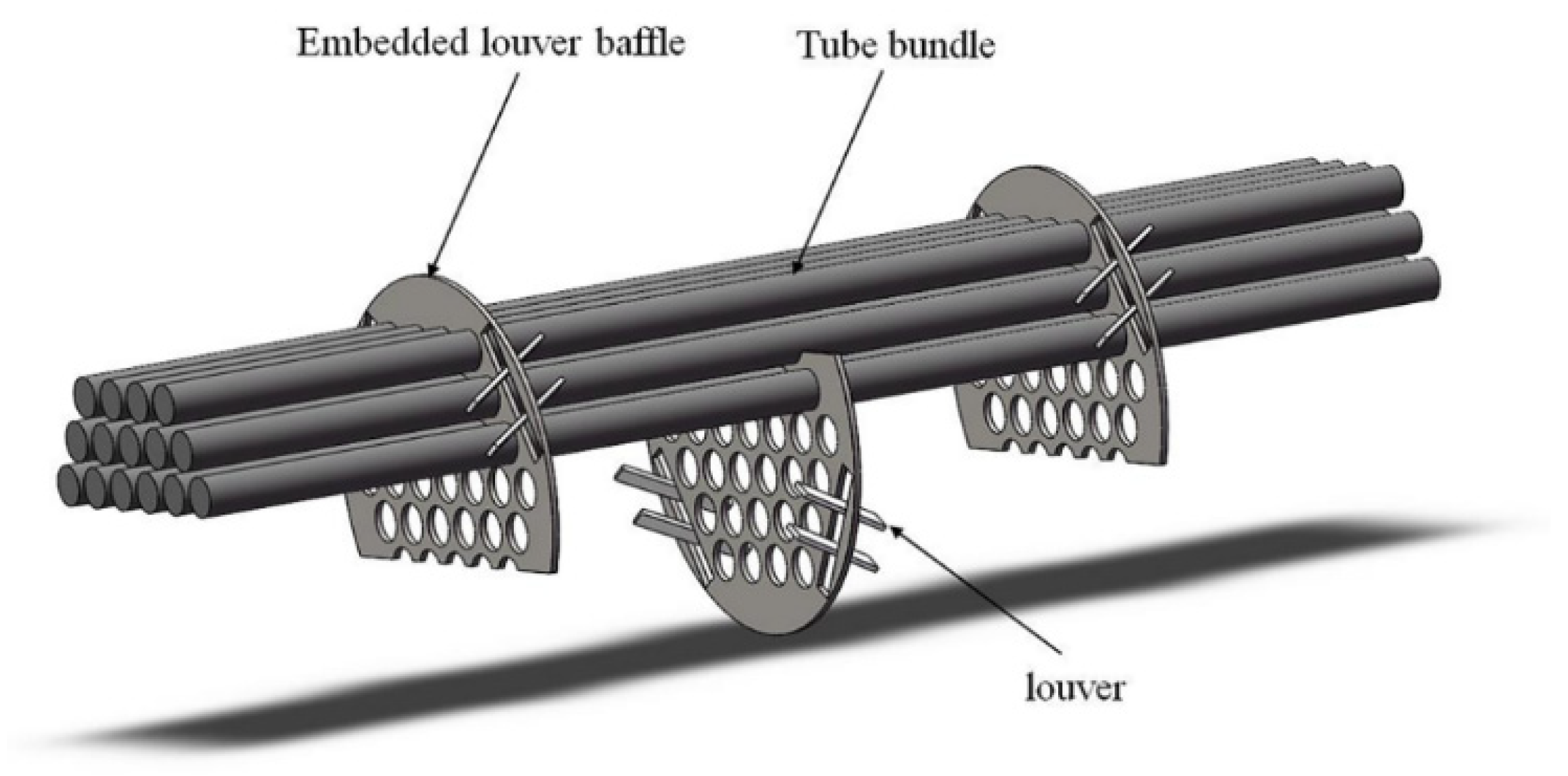

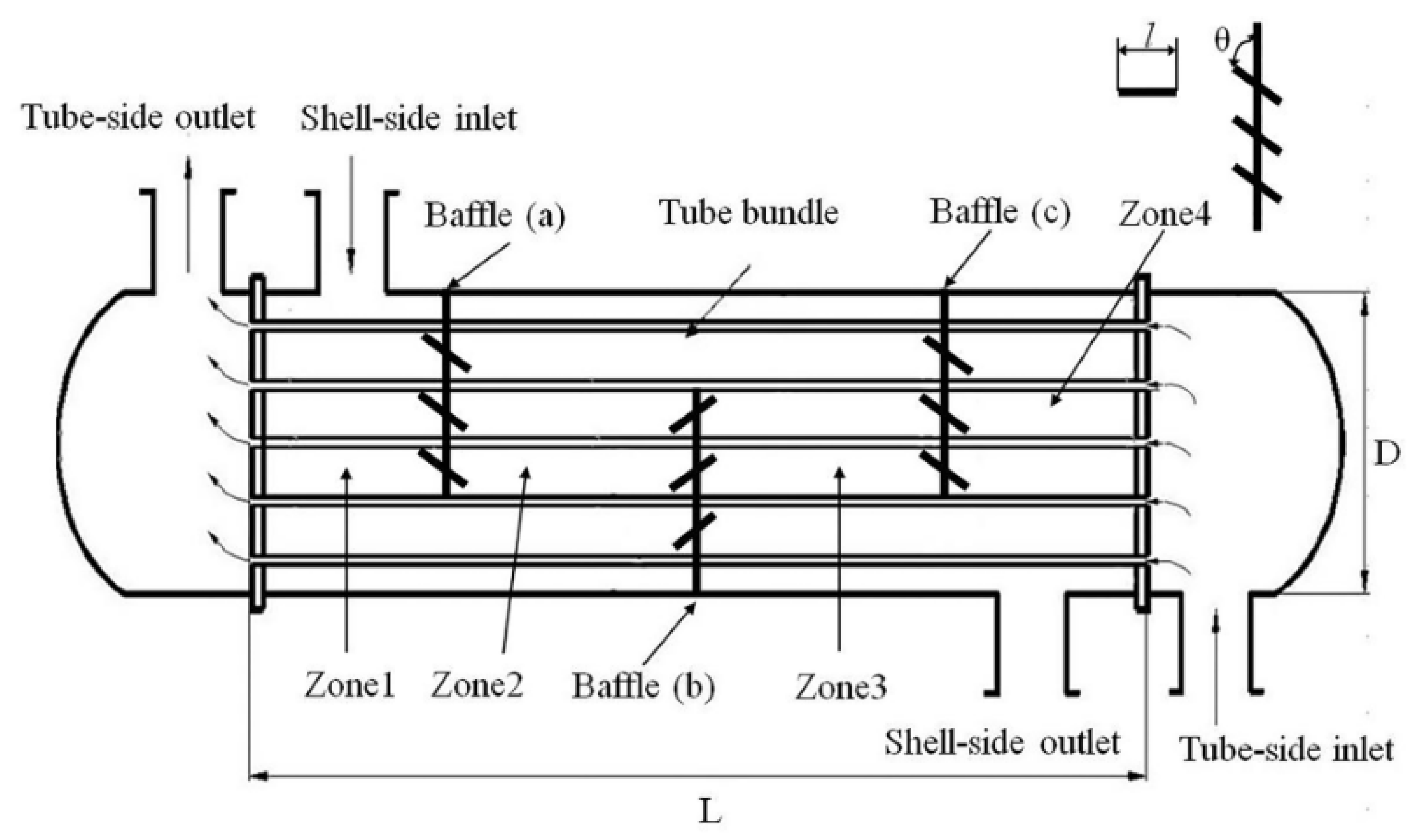
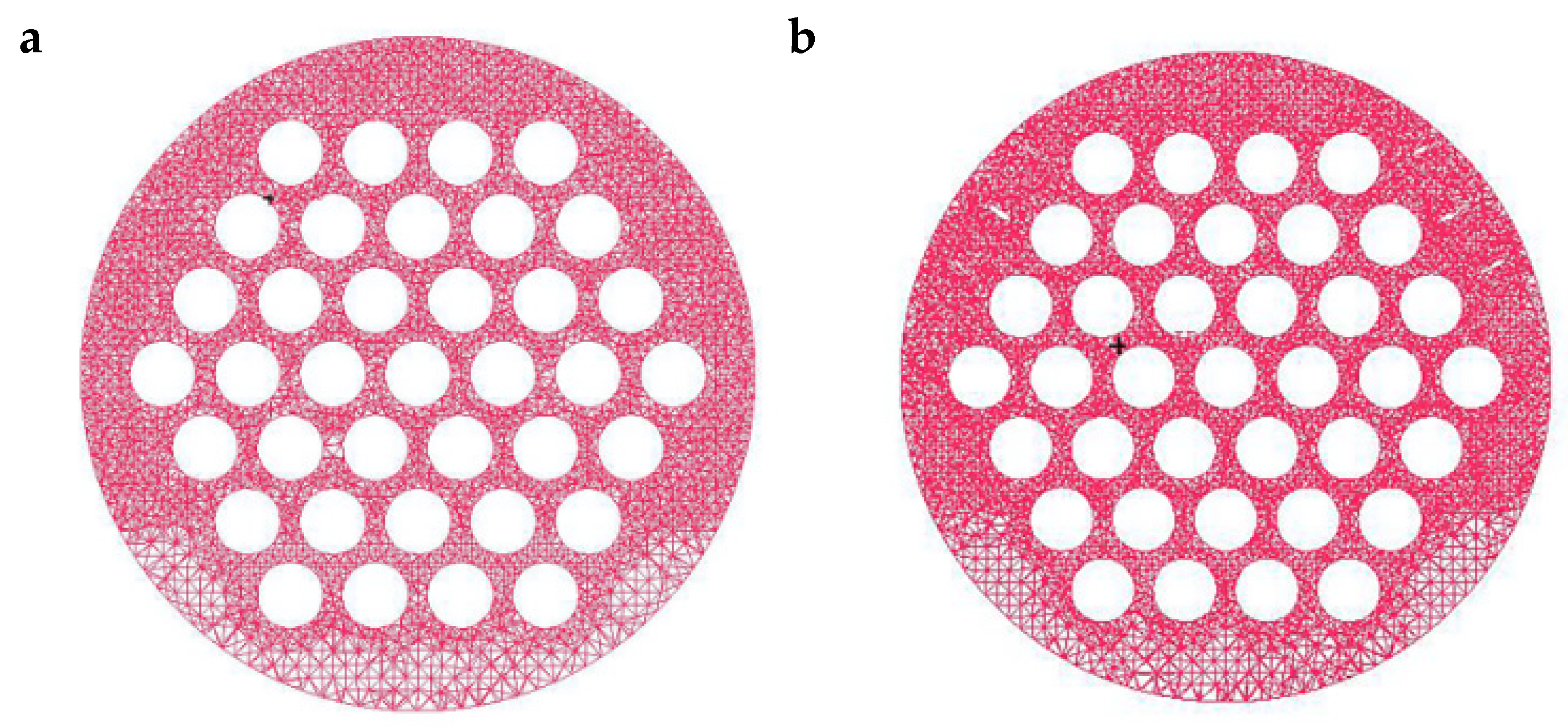

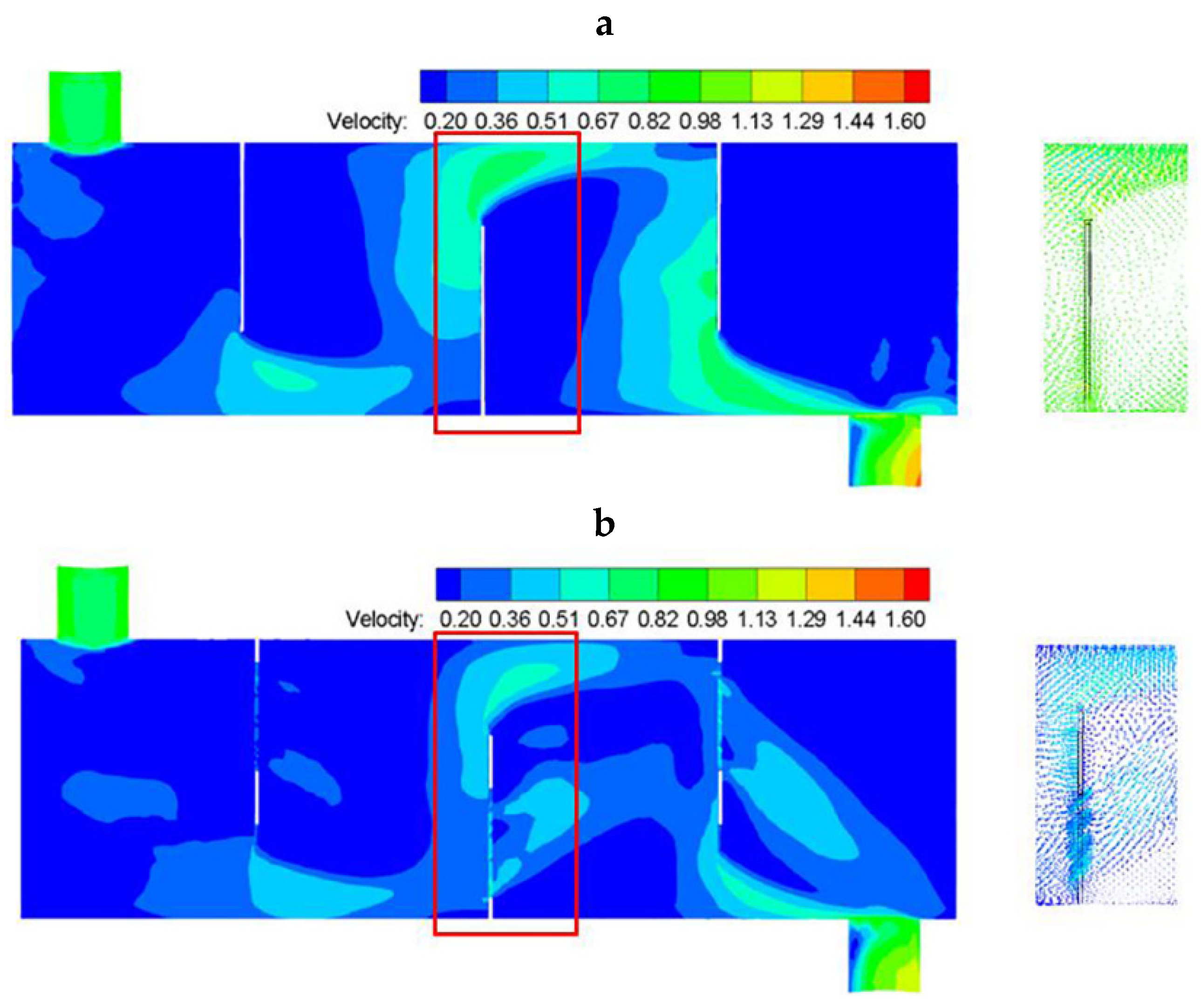




| Item | Detail |
|---|---|
| Diameter of shell D (mm) | 380 |
| Diameter of shell inlet (outlet) din(out)(mm) | 100 |
| Tube length L (mm) | 1300 |
| Outer diameter of tube dtube (mm) | 38 |
| Number of tubes n | 37 |
| Distance between adjacent tubes Z (mm) | 48 |
| Number of baffles N | 3 |
| Cut ratio of baffle H | 30% |
| Distance between adjacent baffles B (mm) | 325 |
| Classification | Working Condition Setting | Angle of Louvers θ (°) | Length of Louvers l (mm) | Velocity of Shell Side Fluid (m/s) | ||||
|---|---|---|---|---|---|---|---|---|
| CSB-STHX | Case 0 | – | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | |
| ELB-STHX | Case 1–1 | 30 | 40 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 |
| Case 1–2 | 45 | 40 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | |
| Case 1–3 | 60 | 40 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | |
| Case 2–1 | 60 | 46 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | |
| Case 2–2 | 60 | 54 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | |
| Case 2–3 | 60 | 65 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | |
| Case 2–4 | 60 | 82 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | |
| Case 2–5 | 60 | 108 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | |
| Item | Detail |
|---|---|
| ρ | 999.8 kg/m3 |
| λ | 0.668 W/m⋅K |
| ν | 1.5142 × 10−6 m2/s |
| Pr | 7.02 |
| Cp | 4195 J/kg⋅K |
| Item | Boundary Condition Applied | Detail Setting |
|---|---|---|
| Shell wall | Adiabatic boundary condition | Q = 0 W/m2 |
| Shell side inlet | Velocity boundary condition | Tin = 278.5 K, Vin = 0.5–1.5 m/s |
| Shell side outlet | Outflow boundary condition | / |
| Tube bundle wall boundary | Fixed temperature boundary condition | Ttube = 308.5 K |
| Tube side inlet wall | Adiabatic boundary condition | Q = 0 W/m2 |
| Tube side outlet wall | Adiabatic boundary condition | Q = 0 W/m2 |
| Baffle/Louver boundary | Adiabatic boundary condition | Q = 0 W/m2 |
| The CSB-STHX | The ELB-STHX | ||||
|---|---|---|---|---|---|
| Grid Number (Million) | Pressure Drop of Shell Side (Pa) | Relative Error (%) | Grid Number (Million) | Pressure Drop of Shell Side (Pa) | Relative Error (%) |
| 0.753 | 2033.01 | – | 0.687 | 1648.49 | – |
| 1.285 | 2116.92 | 4.13 | 1.167 | 1688.73 | 2.44 |
| 2.044 | 2166.67 | 2.35 | 2.106 | 1719.38 | 1.81 |
| 2.524 | 2203.41 | 1.70 | 2.693 | 1748.89 | 1.72 |
| 3.103 | 2181.89 | 0.98 | 3.062 | 1729.44 | 1.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Hu, R.; Zhao, Z.; Zhang, Y.; Zhang, Y. Performance Evaluation and Structure Optimization of a New Type of Shell-and-Tube Heat Exchanger with Embedded Louver Segmental Baffle Support. Energies 2025, 18, 5971. https://doi.org/10.3390/en18225971
Yang X, Hu R, Zhao Z, Zhang Y, Zhang Y. Performance Evaluation and Structure Optimization of a New Type of Shell-and-Tube Heat Exchanger with Embedded Louver Segmental Baffle Support. Energies. 2025; 18(22):5971. https://doi.org/10.3390/en18225971
Chicago/Turabian StyleYang, Xiao, Rui Hu, Zheng Zhao, Yuanyuan Zhang, and Yu Zhang. 2025. "Performance Evaluation and Structure Optimization of a New Type of Shell-and-Tube Heat Exchanger with Embedded Louver Segmental Baffle Support" Energies 18, no. 22: 5971. https://doi.org/10.3390/en18225971
APA StyleYang, X., Hu, R., Zhao, Z., Zhang, Y., & Zhang, Y. (2025). Performance Evaluation and Structure Optimization of a New Type of Shell-and-Tube Heat Exchanger with Embedded Louver Segmental Baffle Support. Energies, 18(22), 5971. https://doi.org/10.3390/en18225971






