Study of the Thermal Performance of Oil-Cooled Electric Motor with Different Oil-Jet Ring Configurations
Abstract
1. Introduction
2. High-Fidelity Modeling Approach and Experimental Validation
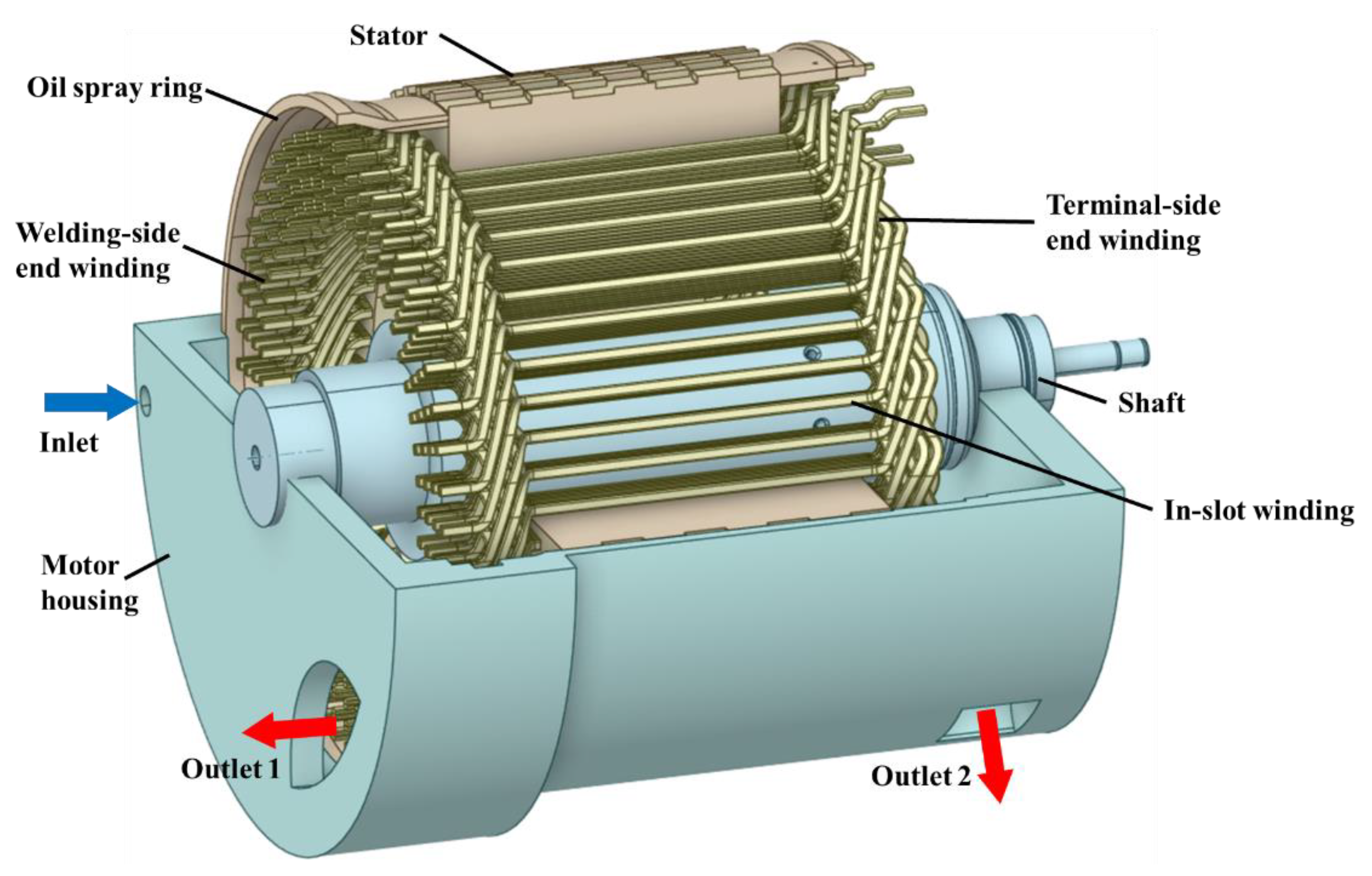
2.1. High-Fidelity Geometric Modeling Approach
- (1)
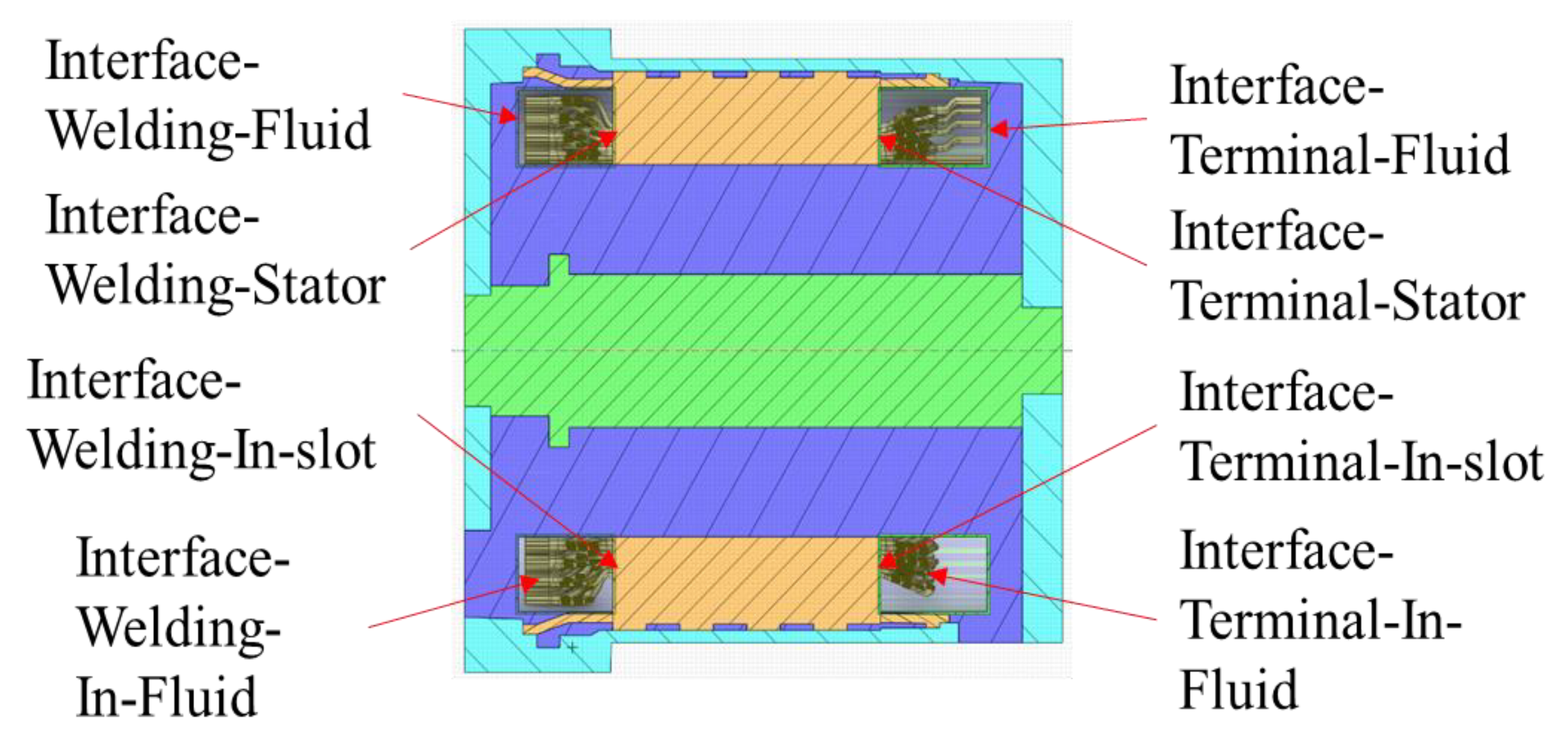
- The interfaces between the fluid and the terminal-side/welding-side end windings.
- (2)
- The interface between the in-slot winding and adjacent end windings.
- (3)
- The inner/outer fluid interfaces of the spray ring.
- (4)
- The interface between the spray-ring fluid and the stator surface.
2.2. Governing Equations and Heat Source Specification
2.3. Boundary Conditions
- (1)
- The influence of electromagnetic field transients is neglected; the motor operates under steady-state conditions.
- (2)
- The lubricating oil is modeled as an incompressible, single-phase continuous medium. Phase change phenomena such as evaporation and cavitation are ignored.
- (3)
- Thermophysical properties of all materials are considered constant and evaluated at room temperature.
- (4)
- Internal heat sources in the windings are treated as uniformly distributed volumetric heat sources derived from electromagnetic losses.
2.4. Mesh Generation and Grid Independence Verification
2.5. Numerical Validation
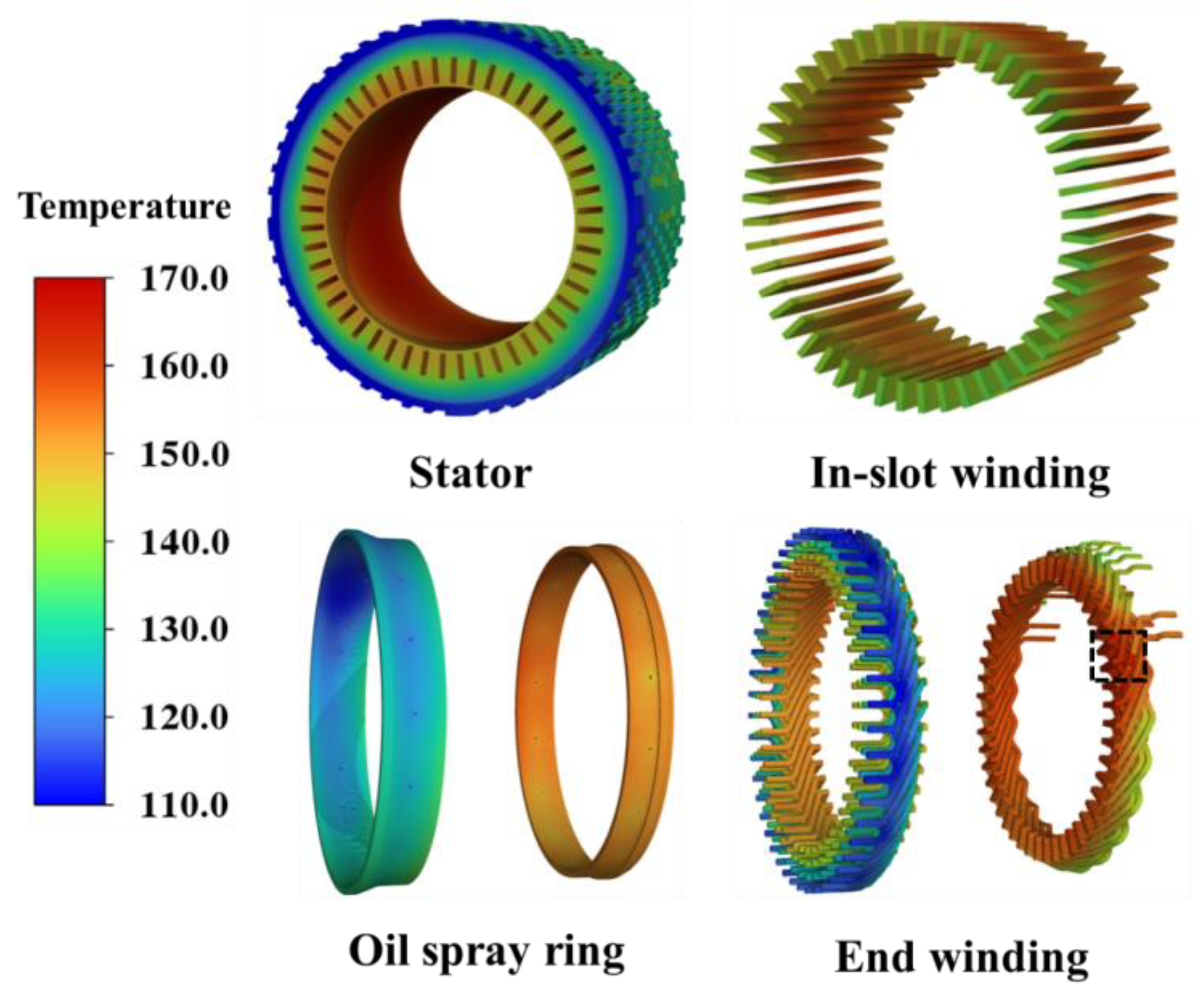
3. Results and Discussion
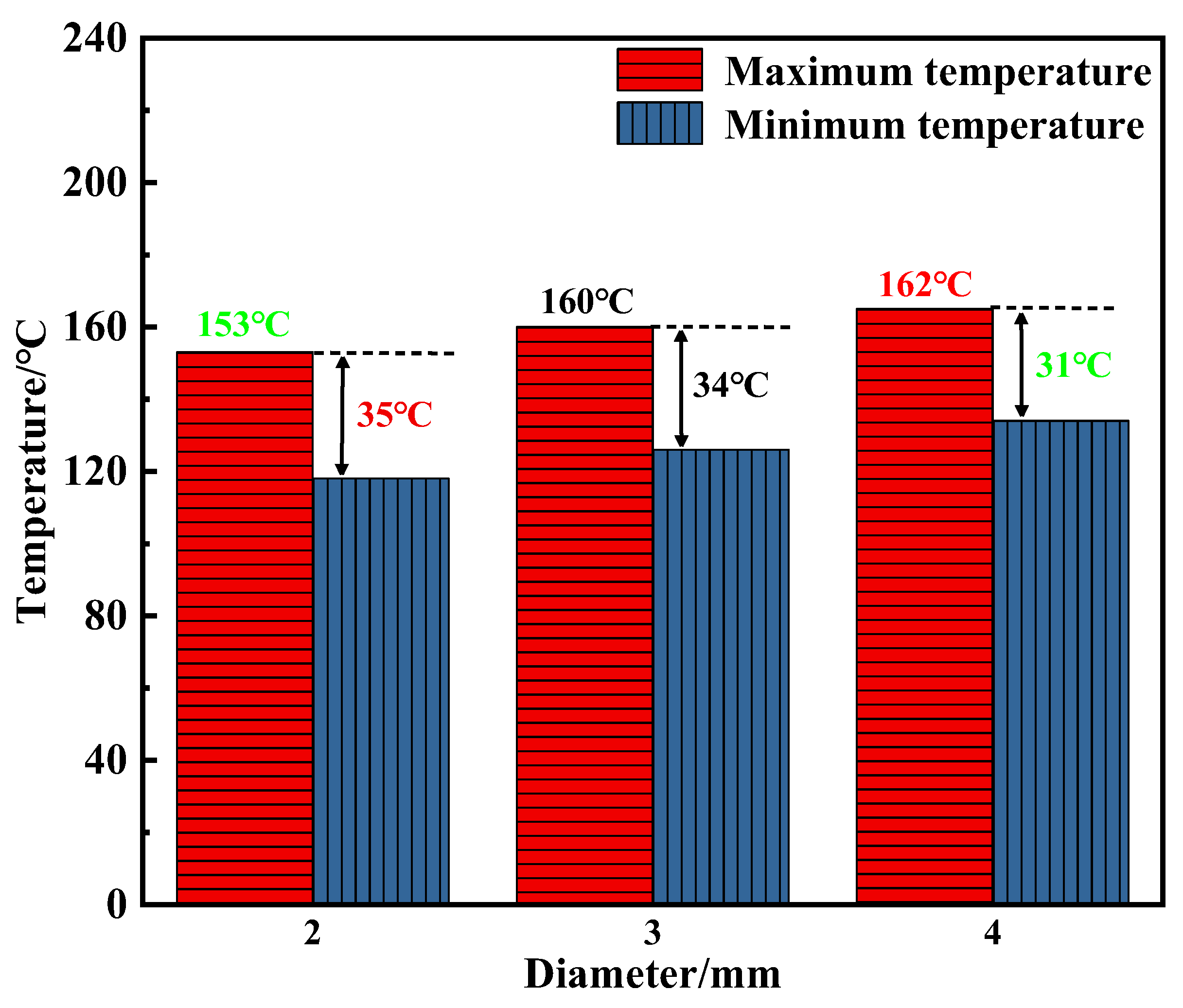
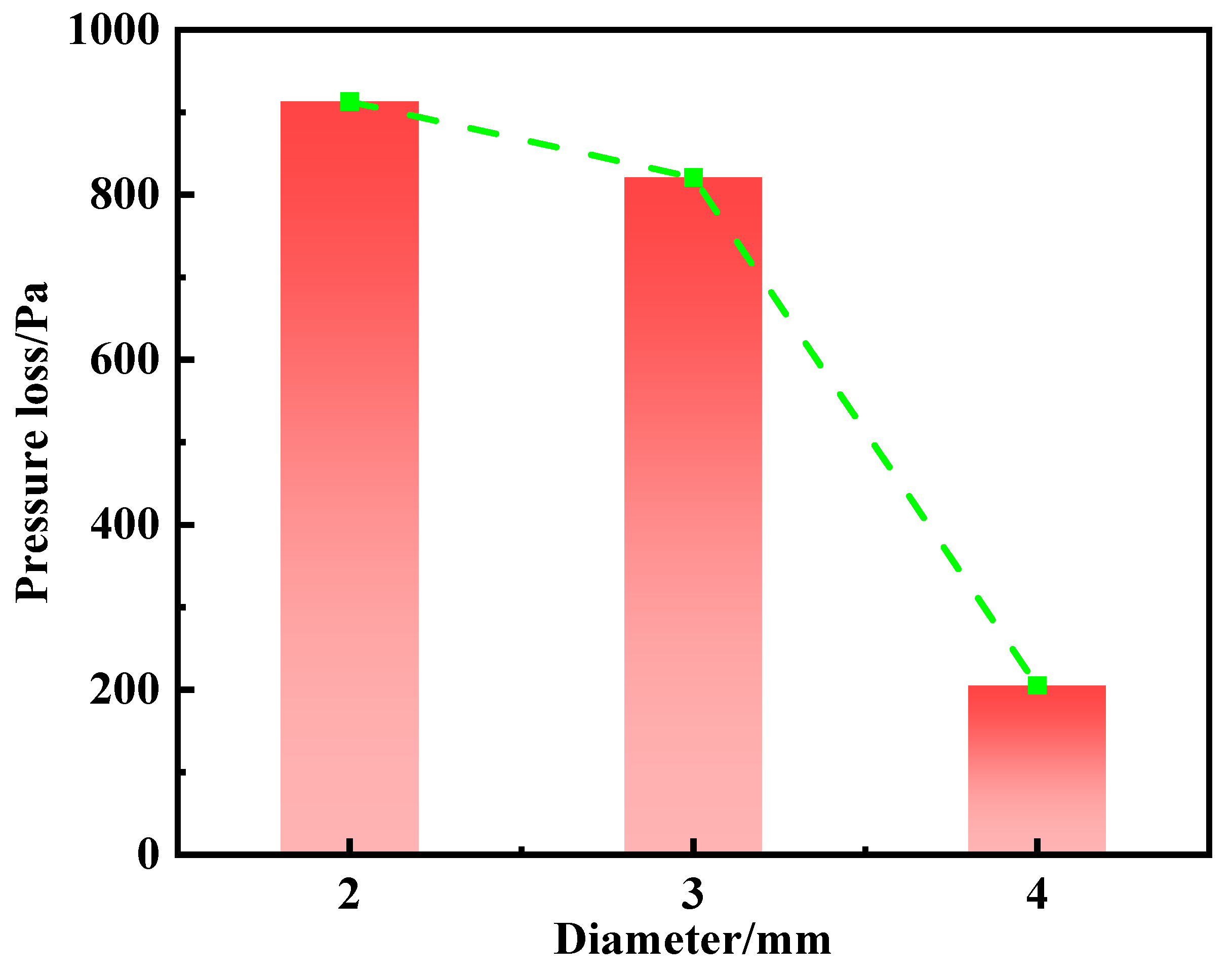
3.1. Effect of Nozzle Diameter on Winding Thermal Performance
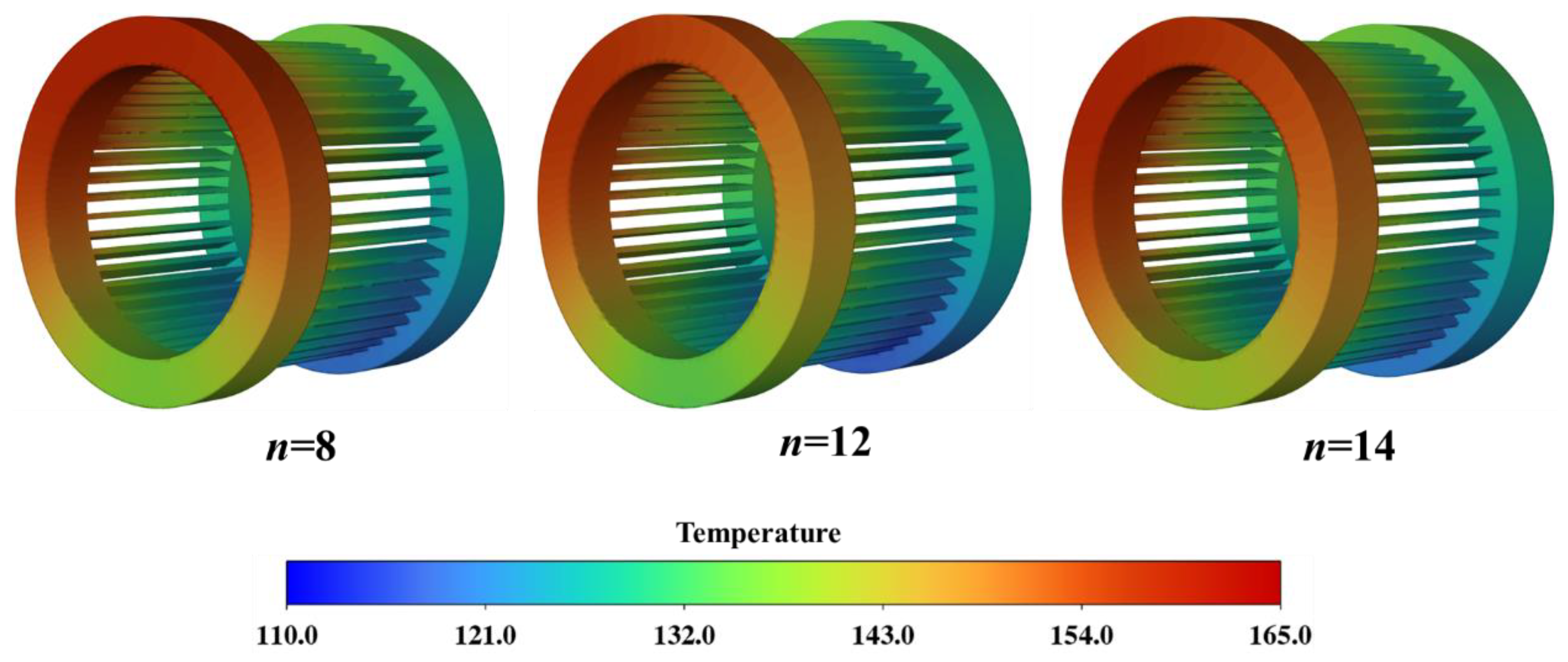
3.2. Effect of Spray Hole Number on Winding Thermal Performance
3.3. Effect of Cooling Oil Parameters on Winding Thermal Performance
3.3.1. Influence of Inlet Oil Temperature
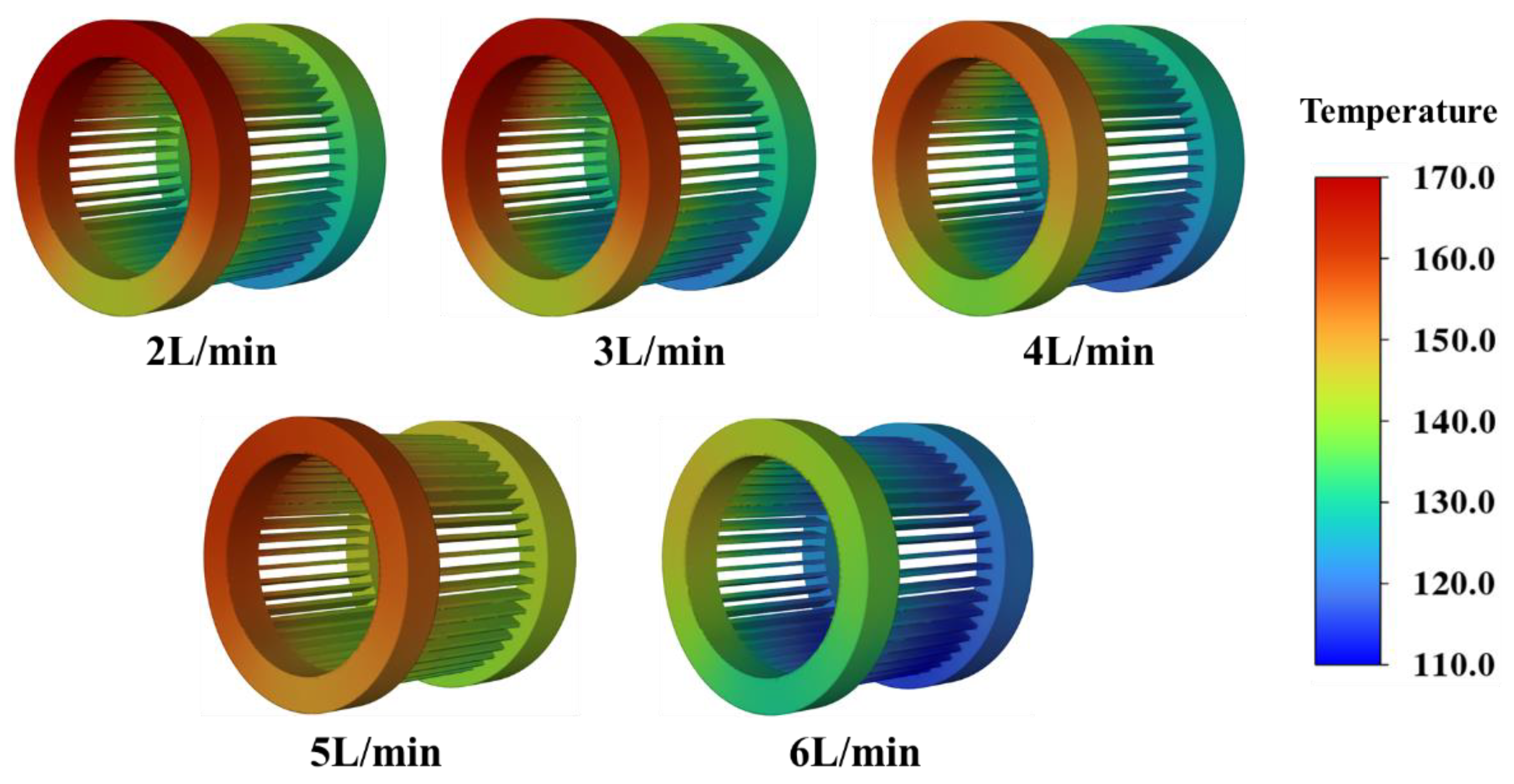
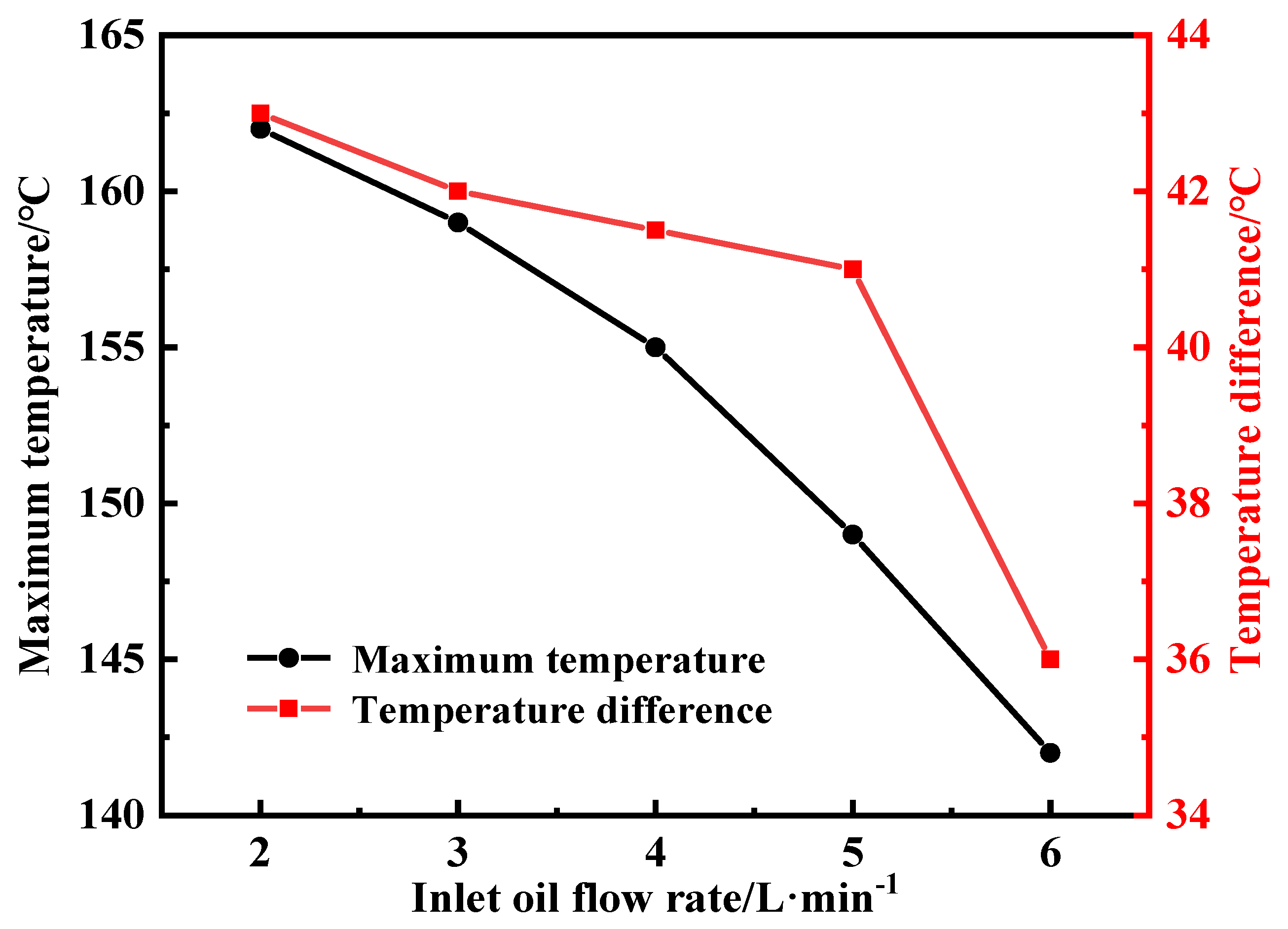
3.3.2. Influence of Inlet Oil Flow Rate
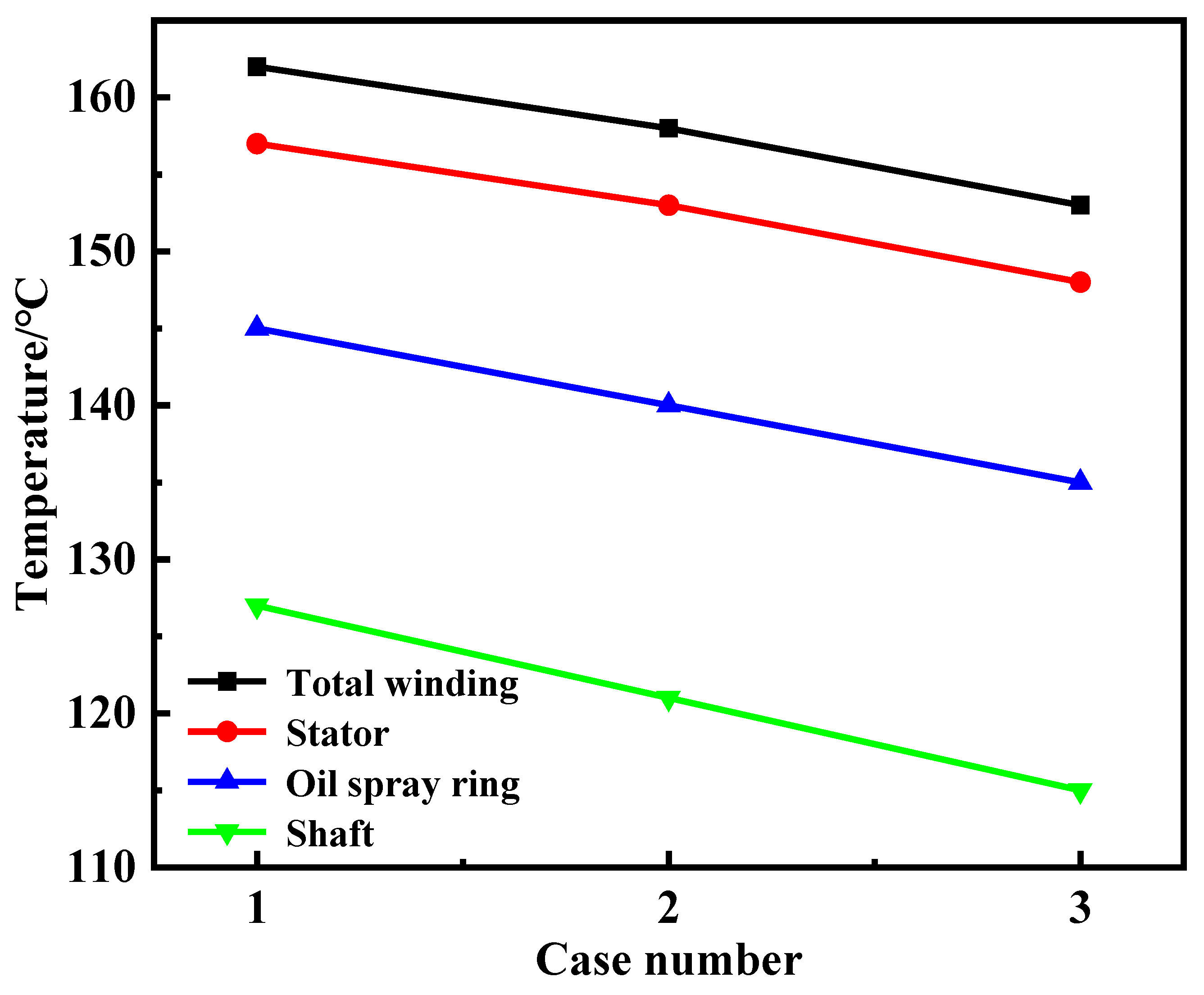
3.4. Improved Design of Spray Ring Structures
4. Conclusions
- (1)
- Smaller nozzles (2 mm) enhance local impingement cooling, effectively reducing peak winding temperatures, albeit at the cost of increased system pressure drop. Larger diameters (4 mm) promote better temperature uniformity but compromise local heat extraction efficiency.
- (2)
- A configuration with 12 holes was found to yield the best trade-off between thermal uniformity and maximum temperature control (155 °C), outperforming both the under-designed (8 holes) and over-designed (14 holes) cases.
- (3)
- Lower inlet temperatures improve peak heat removal but increase temperature gradients; higher flow rates (6 L/min) significantly reduce overall temperatures and improve spatial uniformity, though with greater energy consumption due to flow resistance.
- (4)
- A non-uniform orifice distribution (Case 3) tailored to the asymmetric heat flux between terminal and welding sides further reduced maximum component temperatures by 5.6–9.2% compared to the baseline symmetric layout. While pressure drop increased from 907 Pa to 1410 Pa, the design achieved superior cooling balance and thermal consistency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, J.; Naini, S.S.; Miller, R.; Rizzo, D.; Sebeck, K.; Shurin, S.; Wagner, J. A Hybrid Electric Vehicle Motor Cooling System—Design, Model, and Control. IEEE Trans. Veh. Technol. 2019, 68, 4467–4478. [Google Scholar] [CrossRef]
- Dai, H.; Yang, C.; Zhang, F.; Liao, G.; Zhang, B.; E, J. Transient heat dissipation performance investigation on the battery thermal management system based on S-CO2 immersion cooling. Energy 2025, 318, 13465. [Google Scholar] [CrossRef]
- Hou, J.; Xie, B. Present Situation and Future Prospects of Motor Cooling System. Recent Pat. Eng. 2024, 18, 103–115. [Google Scholar]
- Gronwald, P.-O.; Kern, T.A. Traction Motor Cooling Systems: A Literature Review and Comparative Study. IEEE Trans. Transp. Electrif. 2021, 7, 2892–2913. [Google Scholar] [CrossRef]
- Akawung, A.F.; Fujimoto, Y. Design and Thermal Analysis of Cooling System for High-Power Density Motor Based on Air-Flow. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019. [Google Scholar]
- Garud; Sandip, K.; Hwang, S.-G.; Han, J.-W.; Lee, M.-Y. Performance Characteristics of the Direct Spray Oil Cooling System for a Driving Motor of an Electric Vehicle. Int. J. Heat Mass Transf. 2022, 196, 123228. [Google Scholar] [CrossRef]
- Gundabattini, E.; Mystkowski, A.; Idzkowski, A.; Singh, R.R.; Solomon, D.G. Thermal Mapping of a High-Speed Electric Motor Used for Traction Applications and Analysis of Various Cooling Methods—A Review. Energies 2021, 14, 1472. [Google Scholar]
- Chang, C.-C.; Cheng, C.-H.; Ke, M.-T.; Chen, S.-L. Experimental and Numerical Investigations of Air Cooling for a Large-Scale Motor. Int. J. Rotating Mach. 2009, 2009, 612723. [Google Scholar]
- Dong, H.; Ruan, L.; Wang, Y.; Yang, J.; Liu, F.; Guo, S. Performance of Air/Spray Cooling System for Large-Capacity and High-Power-Density Motors. Appl. Therm. Eng. 2021, 192, 116925. [Google Scholar] [CrossRef]
- Hyeon, S.; Kim, C.; Lee, K.-S. Thermal Enhancement of an Air-Cooled Motor with a Flow Guide. Int. J. Heat Mass Transf. 2022, 183, 122228. [Google Scholar] [CrossRef]
- Madhavan, S.; PB, R.D.; Konda, Y.R.; Gundabattini, E.; Mystkowski, A.; Palka, R.; Wardach, M.; Prajzendanc, P. Thermal Management Analyses of Induction Motor through the Combination of Air-Cooling and an Integrated Water-Cooling System. Sci. Rep. 2023, 13, 10125. [Google Scholar]
- Keuter; Johannes, R.; Niebuhr, F.; Nozinski, M.; Krüger, E.; Kabelac, S.; Ponick, B. Design of a Direct-Liquid-Cooled Motor and Operation Strategy for the Cooling System. Energies 2023, 16, 5319. [Google Scholar] [CrossRef]
- Geng, W.; Zhu, T.; Li, Q.; Zhang, Z. Windings Indirect Liquid Cooling Method for a Compact Outer-Rotor Pm Starter/Generator with Concentrated Windings. IEEE Trans. Energy Convers. 2021, 36, 3282–3293. [Google Scholar]
- Chen, A.; Xu, F.; Liu, X.; He, Y.; Wu, Z.; Zhu, Y.; Han, Z.; Li, L. Sub-Cooled Liquid Nitrogen Test System for Cooling Hts Synchronous Motor. IEEE Trans. Appl. Supercond. 2011, 22, 4701304. [Google Scholar] [CrossRef]
- Baeten, A.; Barm, S.; Reitenberger, J.; Fackler, M. Parameterized Pre-Dimensioning of a Winding-Integrated Cryogenic Hydrogen Cooling System in an Axial Flux Motor for Ship Propulsion Systems. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Ottawa, ON, Canada, 19–23 June 2023. [Google Scholar]
- Hara, S.; Iwami, Y.; Kawasaki, R.; Matsumoto, T.; Shirai, Y.; Shiotsu, M.; Kobayashi, H.; Naruo, Y.; Nonaka, S.; Inatani, Y.; et al. Development of Liquid Hydrogen Cooling System for a Rotor of Superconducting Generator. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Kim, K.; Hahn, S.; Min, B.; Sim, K.-D.; Kim, Y.; Kim, S. Liquid Hydrogen Cooling System for 100 Kw-Class Hts Rotor Thermal Design. IEEE Trans. Appl. Supercond. 2024, 34, 1–5. [Google Scholar]
- Fujita, H.; Itoh, A.; Urano, T. Newly Developed Motor Cooling Method Using Refrigerant. World Electr. Veh. J. 2019, 10, 38. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Chen, Z.; Wang, C.; Xing, Z. Numerical Research on Refrigerant Injection for Motor Cooling of Screw Compressor for Heat Pump with Large Temperature Lift. Appl. Therm. Eng. 2024, 253, 123837. [Google Scholar] [CrossRef]
- Ghahfarokhi, P.S.; Podgornovs, A.; Kallaste, A.; Cardoso, A.J.M.; Belahcen, A.; Vaimann, T. The Oil Spray Cooling System of Automotive Traction Motors: The State of the Art. IEEE Trans. Transp. Electrif. 2022, 9, 428–451. [Google Scholar]
- Maddumage, W.; Ouenzerfi, S.; Harmand, S.; Cairns, A.; Paykani, A. Thermal Management of Hairpin Winding Traction Motors in Electric Vehicles: Parametric Evaluation of Impinging Oil Jet Cooling Using Cfd Simulations. Appl. Therm. Eng. 2025, 273, 126414. [Google Scholar] [CrossRef]
- Shewalkar, A.G.; Dhoble, A.S.; Thawkar, V.P. Review on Cooling Techniques and Analysis Methods of an Electric Vehicle Motor. J. Therm. Anal. Calorim. 2024, 149, 5919–5947. [Google Scholar] [CrossRef]
- Karim, A.; Ambri, Z.; Mohd Yusoff, A.H. Cooling System for Electric Motor of an Electric Vehicle Propulsion. Adv. Mater. Res. 2014, 903, 209–214. [Google Scholar] [CrossRef]
- Konovalov, D.; Tolstorebrov, I.; Eikevik, T.M.; Kobalava, H.; Radchenko, M.; Hafner, A.; Radchenko, A. Recent Developments in Cooling Systems and Cooling Management for Electric Motors. Energies 2023, 16, 7006. [Google Scholar] [CrossRef]
- Beom, T.; Kim, Y.; Ha, T.W.; Lee, S.W.; Hwang, I.G.; Kim, D.K. Development of a Coefficient of Performance to Evaluate the Oil Cooling Methods in Electric Vehicle Motors. Case Stud. Therm. Eng. 2025, 71, 106194. [Google Scholar] [CrossRef]
- Jiang, Y.; Lu, Y.; Chen, L.; Zheng, E.; Wang, C.; Luo, Z.; Shi, Y.; Wang, X.; Hu, L.; Zhao, S. Modeling, Analysis, and Optimization of the Asymmetric Cooling System for a Hybrid Oil-Cooled Motor. Appl. Therm. Eng. 2025, 270, 126215. [Google Scholar] [CrossRef]
- Thangaraju, S.K.; Munisamy, K.M.; Rajoo, S. Numerical Investigation on Cooling Performance of Oil Cooled Pmsm Jacket Design with Vertical Straight Fin Design. Int. J. Thermofluids 2022, 16, 100209. [Google Scholar] [CrossRef]
- Feng, J.; Sun, P.; Wei, D.; Shi, W.; Yang, S.; Zhao, Z. Study on Radial Oil Spray Cooling of End Windings with Hairpin Motors. Case Stud. Therm. Eng. 2025, 65, 105675. [Google Scholar]
- Rocca, L.; Salvatore; Pickering, S.J.; Eastwick, C.N.; Gerada, C.; Ronnberg, K. Numerical Study on the Impact of End Windings Porosity on the Fluid Flow and Heat Transfer in a Totally Enclosed Fan-Cooled Electrical Machine. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019. [Google Scholar]
- Gundabattini, E.; Mystkowski, A. Combinations and Thermal Analysis (Experimental and Analytical) of a Permanent Magnet Synchronous Motor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 655–668. [Google Scholar] [CrossRef]
- Han; Gu, N.; Lee, H.L.; Kim, R.H.; Beom, T.Y.; Kim, Y.K.; Ha, T.W.; Lee, S.W.; Kim, D.K. Thermal Analysis of the Oil Cooling Motor According to the Churning Phenomenon. Appl. Therm. Eng. 2023, 220, 119791. [Google Scholar]
- Rocca, L.; Salvatore; Pickering, S.J.; Eastwick, C.N.; Gerada, C.; Rönnberg, K. Fluid Flow and Heat Transfer Analysis of Tefc Machine End Regions Using More Realistic End-Winding Geometry. J. Eng. 2019, 2019, 3831–3835. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar]













| Parameter | Specification |
|---|---|
| Motor Type | PMSM |
| Number of Slots/Poles | 48/8 |
| Rated Power | 38 kW |
| Max. Power/Max. Torque | 75 kW/120 Nm |
| Base Speed/Max. Speed | 4400 rpm/12,000 rpm |
| Nominal Voltage | 380 V |
| Winding Type | 8-layer hairpin |
| Cooling Type | Rotational oil-spray cooling |
| Region | Total Heat Loss (W) | Distribution | Volumetric Heat Source (W/m3) |
|---|---|---|---|
| Stator | 1281 | Uniform | 600,415.8 |
| Welding-Side Winding | 823 | Uniform | 663,502.6 |
| Terminal-Side Winding | 687 | Uniform | 553,859.4 |
| Slot Winding | 1708 | Uniform | 1,376,989.6 |
| Permanent Magnets | 77 | Neglected | - |
| Component | Density (kg/m3) | Specific Heat (J/kg·K) | Thermal Conductivity (W/m·K) |
|---|---|---|---|
| Housing | 2700 | 900 | 201 |
| Stator | 7600 | 450 | λx = 6, λy = λz = 19.6 |
| Spray Ring | 2719 | 871 | 202.4 |
| Windings | 8933 | 385 | 390 |
| Shaft | 7800 | 470 | 46 |
| Fluid | Density (kg/m3) | Specific Heat (J/kg·K) | Thermal Conductivity (W/m·K) | Viscosity (Pa·s) |
|---|---|---|---|---|
| Air | 1.225 | 1066.43 | 0.0242 | 1.7894 × 10−5 |
| Cooling Oil | 803.74 | 2140 | 0.132 | 6.4 × 10−3 |
| Region | Location | Depth | Texp (°C) | Tsim (°C) | ΔT (°C) | Error (%) |
|---|---|---|---|---|---|---|
| Welding | 1 | Outer | 135.8 | 139.4 | 3.6 | 2.6 |
| Welding | 1 | Middle | 151.0 | 152.3 | 1.3 | 0.9 |
| Welding | 1 | Inner | 154.4 | 154.3 | −0.1 | −0.1 |
| Welding | 2 | Outer | 117.0 | 117.3 | 0.3 | 0.2 |
| Welding | 2 | Middle | 136.6 | 135.0 | −1.6 | −1.2 |
| Welding | 2 | Inner | 121.1 | 139.5 | 18.4 | 15.2 |
| Welding | 3 | Outer | 112.9 | 115.5 | 2.6 | 2.3 |
| Welding | 3 | Middle | 124.0 | 125.7 | 1.7 | 1.4 |
| Welding | 3 | Inner | 119.7 | 135.8 | 16.1 | 13.4 |
| Welding | 4 | Outer | 121.4 | 119.9 | −1.5 | −1.3 |
| Welding | 4 | Middle | 159.1 | 145.8 | −13.2 | −8.3 |
| Welding | 4 | Inner | 157.0 | 150.2 | −6.8 | −4.3 |
| Welding | 5 | Outer | 131.0 | 129.7 | −1.3 | −1.0 |
| Welding | 5 | Middle | 129.6 | 128.8 | −0.9 | −0.7 |
| Welding | 5 | Inner | 124.6 | 135.4 | 10.8 | 8.7 |
| Terminal | 1 | Outer | 126.7 | 132.6 | 6.0 | 4.7 |
| Terminal | 1 | Middle | 132.9 | 136.4 | 3.5 | 2.6 |
| Terminal | 1 | Inner | 131.1 | 147.9 | 16.8 | 12.8 |
| Terminal | 2 | Outer | 132.2 | 135.8 | 3.6 | 2.7 |
| Terminal | 2 | Middle | 133.3 | 138.1 | 4.9 | 3.6 |
| Terminal | 2 | Inner | 130.8 | 146.2 | 15.4 | 11.7 |
| Terminal | 3 | Outer | 133.9 | 134.9 | 1.0 | 0.8 |
| Terminal | 3 | Middle | 132.3 | 139.5 | 7.2 | 5.4 |
| Terminal | 3 | Inner | 129.6 | 145.6 | 16.0 | 12.4 |
| Terminal | 4 | Outer | 134.6 | 136.5 | 1.9 | 1.4 |
| Terminal | 4 | Middle | 134.8 | 139.4 | 4.6 | 3.4 |
| Terminal | 4 | Inner | 129.5 | 143.7 | 14.2 | 11.0 |
| Terminal | 5 | Outer | 133.6 | 143.4 | 9.8 | 7.3 |
| Terminal | 5 | Middle | 134.5 | 134.6 | 0.1 | 0.1 |
| Terminal | 5 | Inner | 130.5 | 145.5 | 15.0 | 11.5 |
| Design Parameter | Value Range (mm) | Case 1 | Case 2 | Case 3 |
|---|---|---|---|---|
| Oil Injection Hole Diameter at Welding End | 1 ≤ d1 ≤ 4 | 2 mm | 1.5 mm | 1 mm |
| Oil Injection Hole Diameter at Outlet End | 1 ≤ d2 ≤ 4 | 2 mm | 3 mm | 4 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Wu, F.; Fu, J.; Zeng, J.; Fu, X.; Zhai, G.; Zhang, F. Study of the Thermal Performance of Oil-Cooled Electric Motor with Different Oil-Jet Ring Configurations. Energies 2025, 18, 4302. https://doi.org/10.3390/en18164302
Yang H, Wu F, Fu J, Zeng J, Fu X, Zhai G, Zhang F. Study of the Thermal Performance of Oil-Cooled Electric Motor with Different Oil-Jet Ring Configurations. Energies. 2025; 18(16):4302. https://doi.org/10.3390/en18164302
Chicago/Turabian StyleYang, Hao, Fan Wu, Jinhao Fu, Junxiong Zeng, Xiaojin Fu, Guangtao Zhai, and Feng Zhang. 2025. "Study of the Thermal Performance of Oil-Cooled Electric Motor with Different Oil-Jet Ring Configurations" Energies 18, no. 16: 4302. https://doi.org/10.3390/en18164302
APA StyleYang, H., Wu, F., Fu, J., Zeng, J., Fu, X., Zhai, G., & Zhang, F. (2025). Study of the Thermal Performance of Oil-Cooled Electric Motor with Different Oil-Jet Ring Configurations. Energies, 18(16), 4302. https://doi.org/10.3390/en18164302







