AI-Integrated Smart Grading System for End-of-Life Lithium-Ion Batteries Based on Multi-Parameter Diagnostics
Abstract
1. Introduction
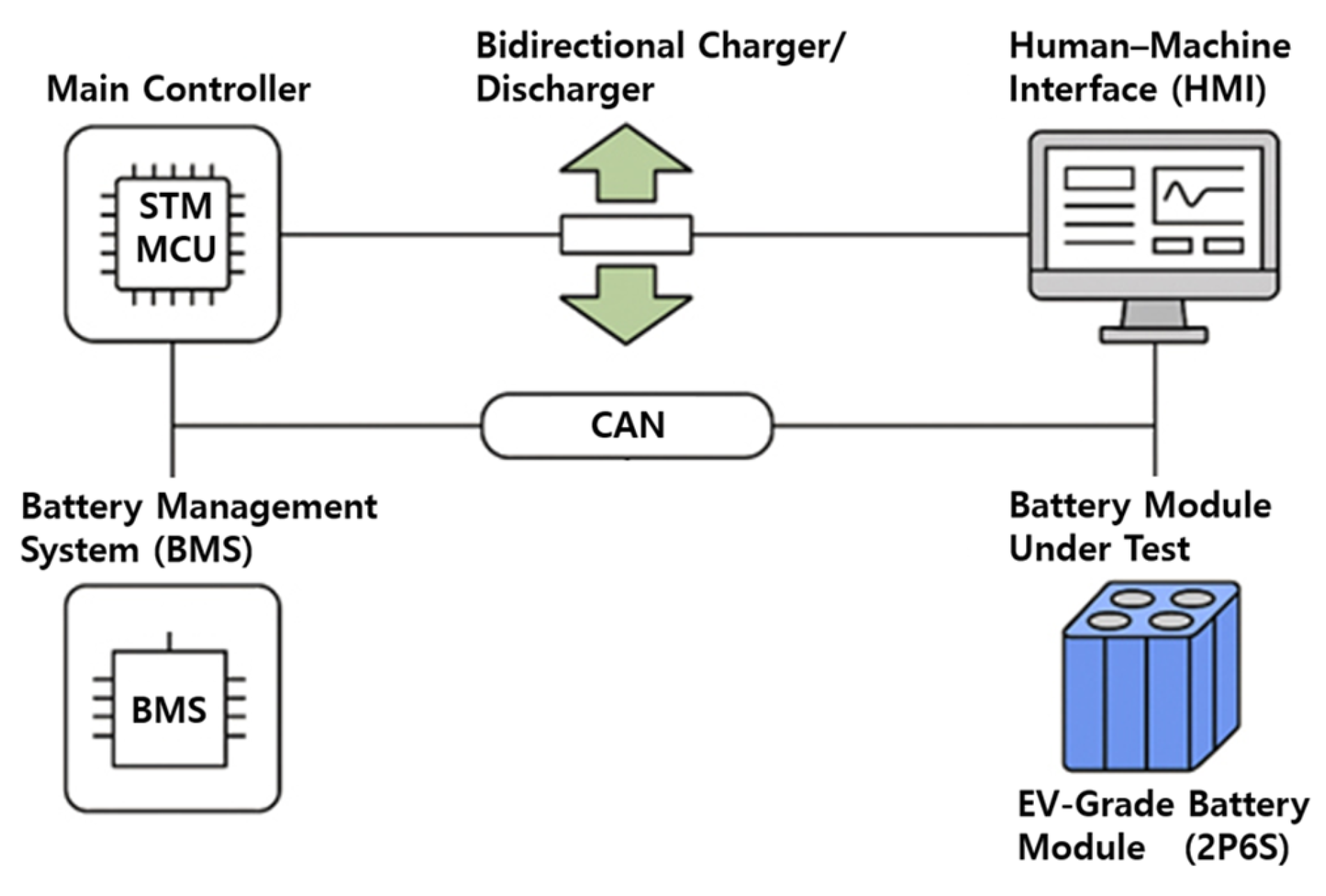
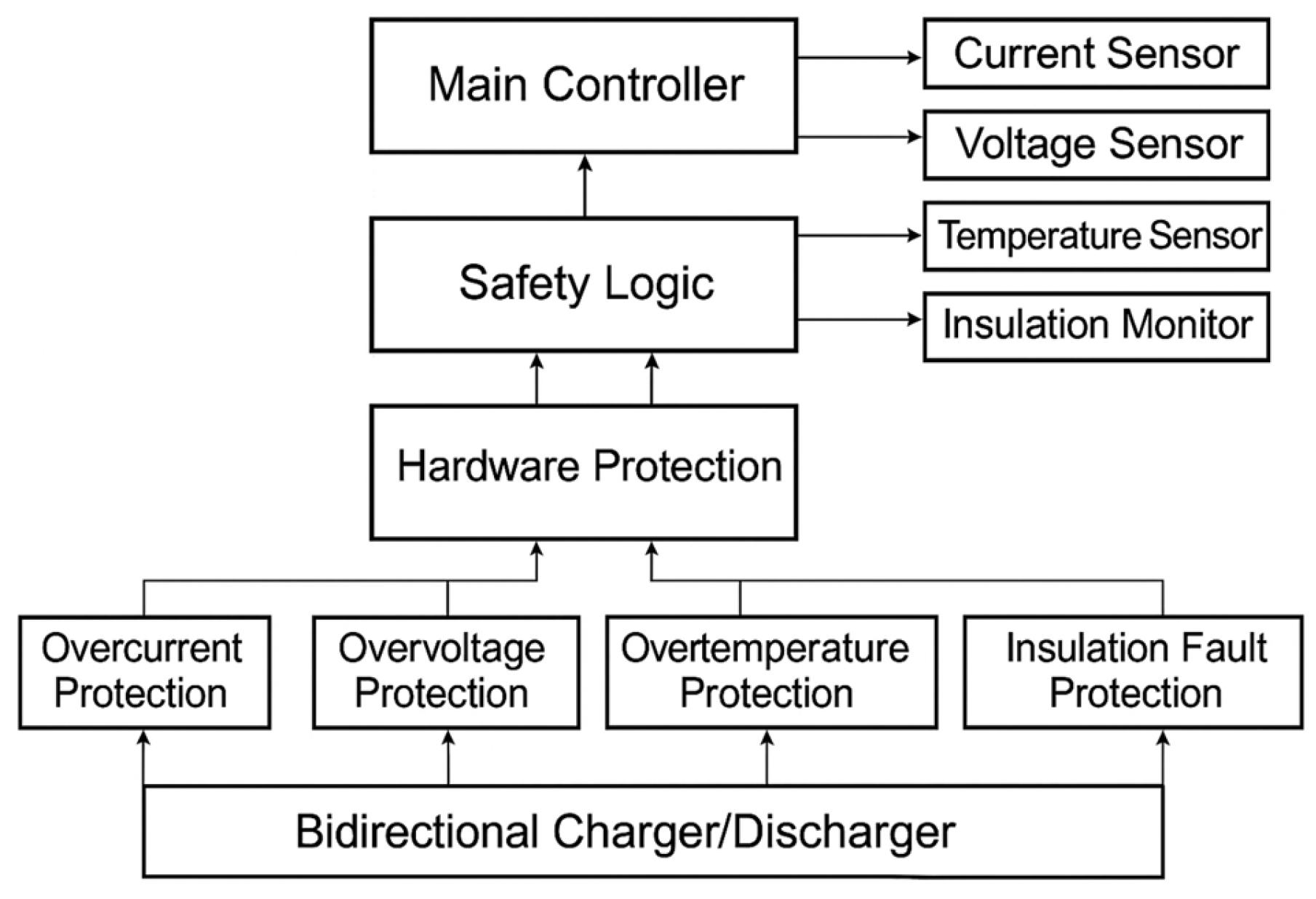
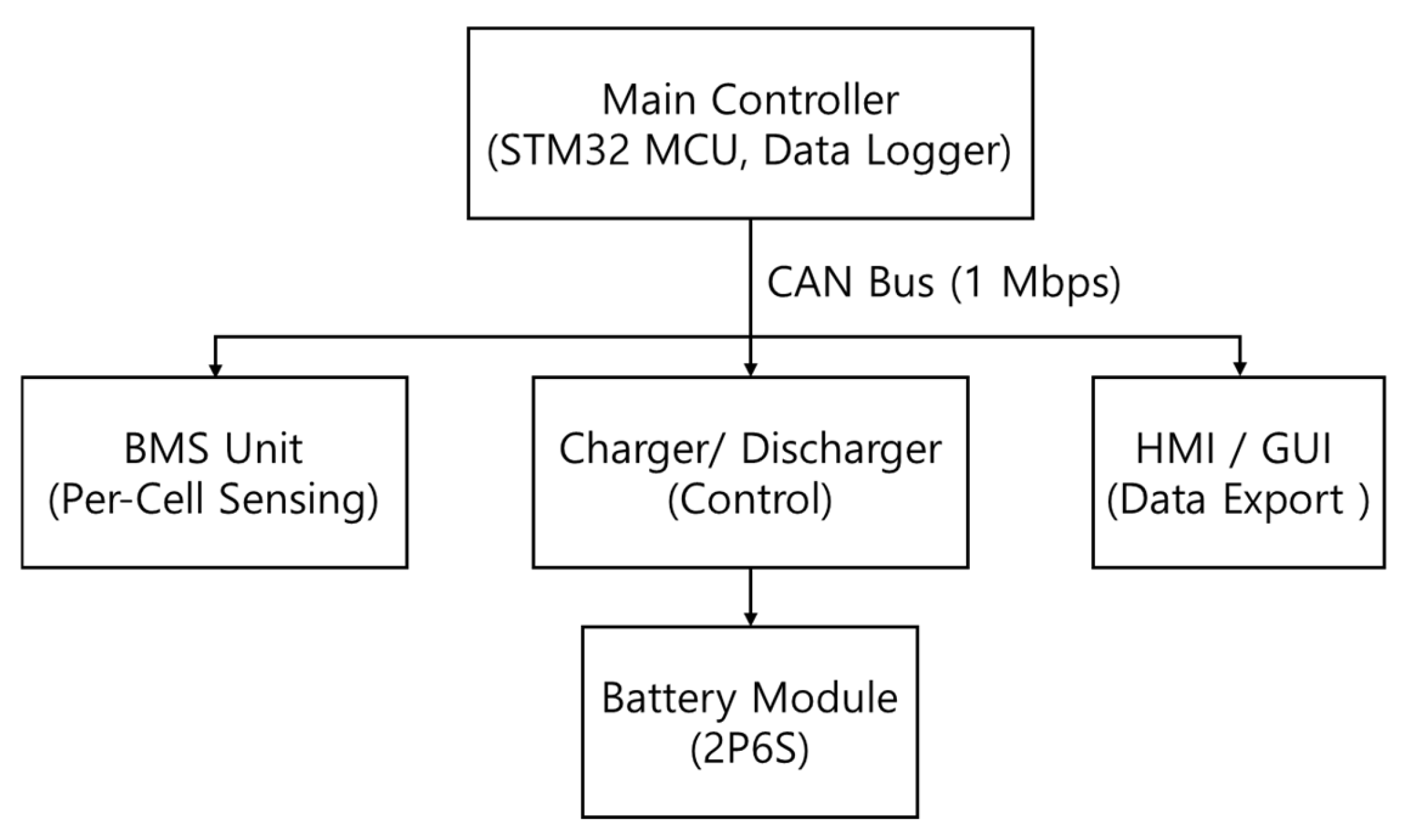
2. System Architecture
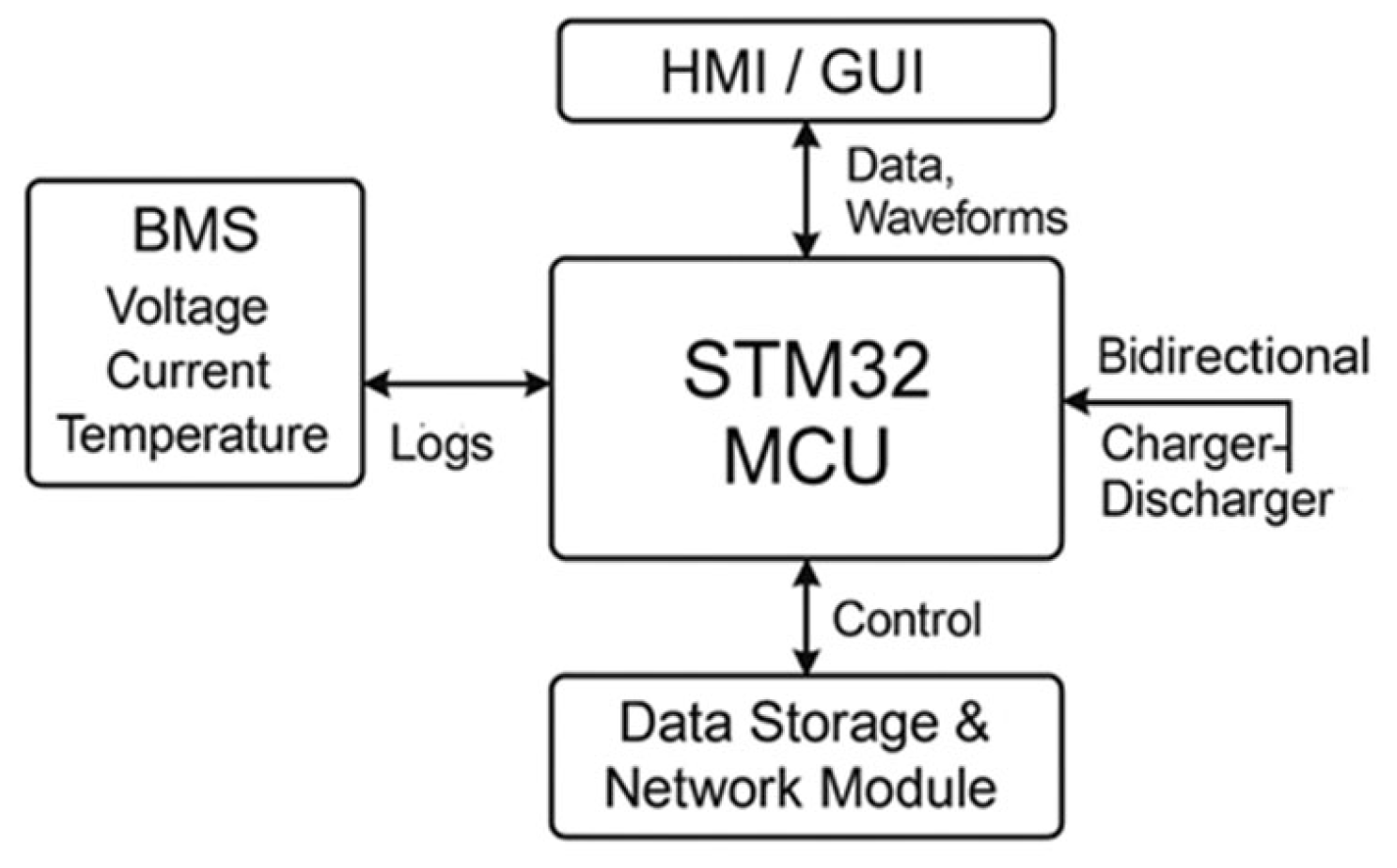
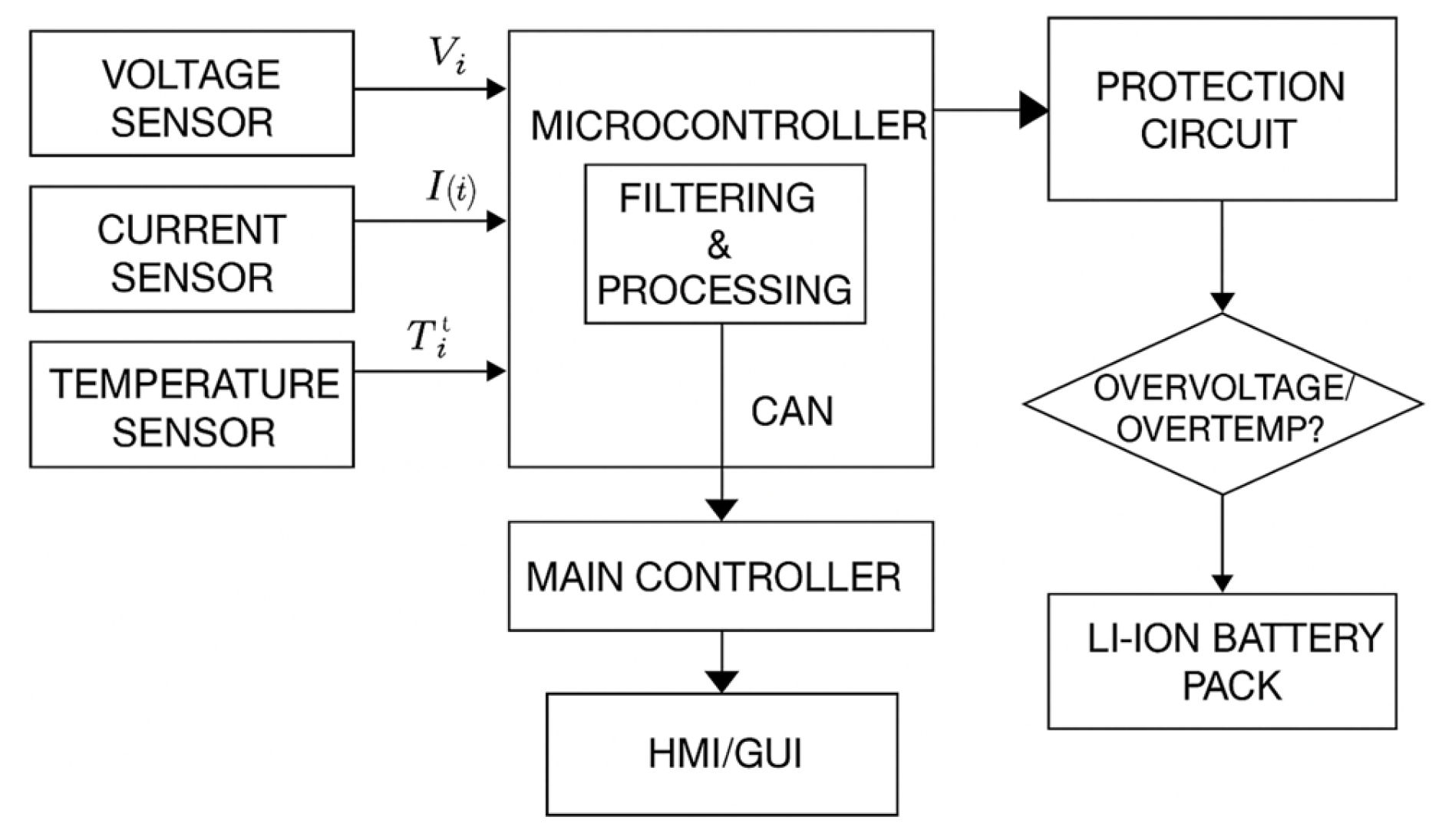
2.1. Main Controller
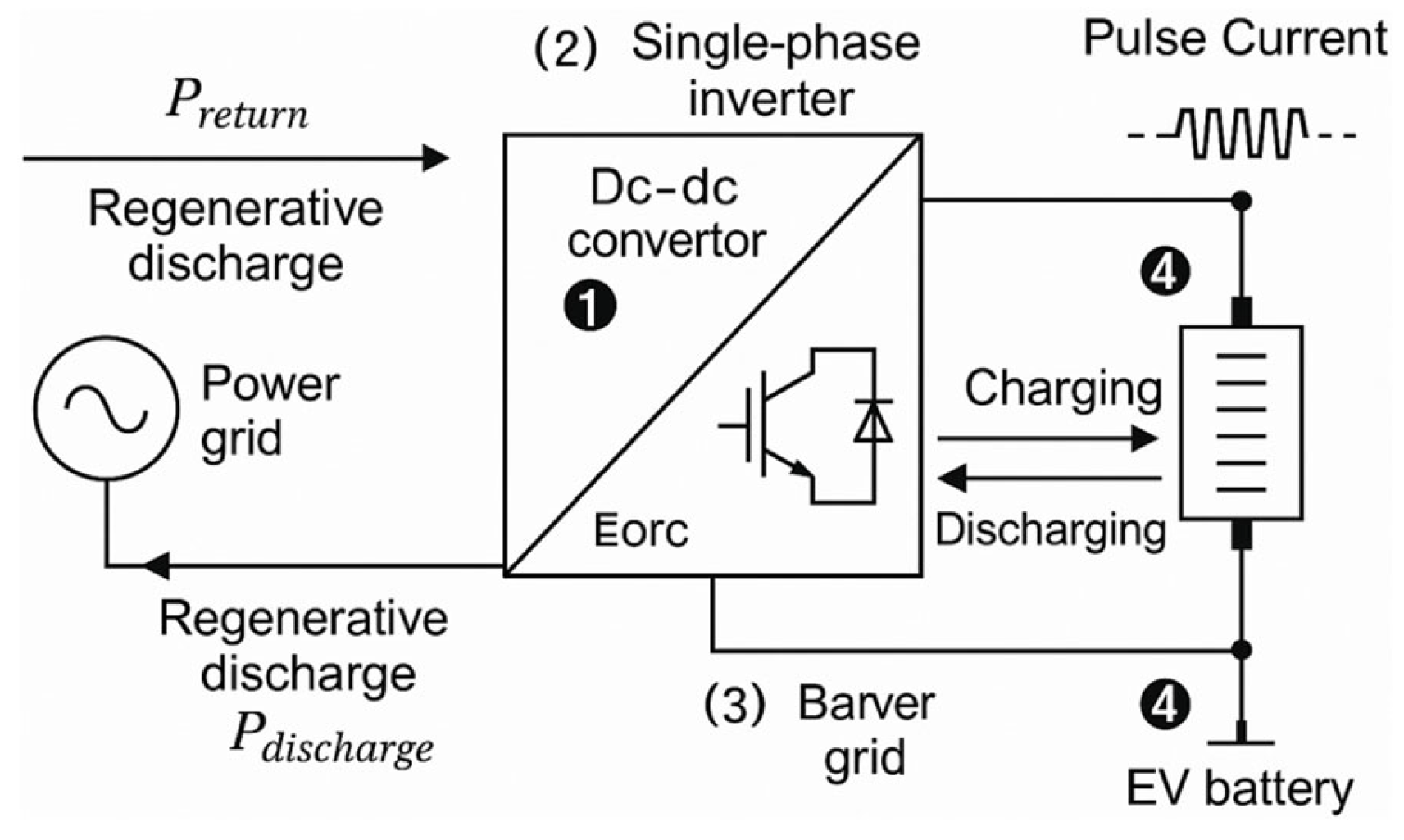
2.2. Bidirectional Charger/Discharger
- ▪
- During charging or discharging, if the current exceeds the preset limit , a hardware cutoff circuit (MOSFET + Hall sensor) immediately disconnects the circuit.
- ▪
- High-frequency sampling (>10 kHz) allows real-time detection of transient overcurrent events, and in short-circuit conditions, the circuit is interrupted within 10 μs. The protection logic is defined by Equation (9):
- ▪
- A double relay and parallel MOSFET topology is adopted to enhance cutoff reliability.
- ▪
- Each cell voltage is continuously measured by the BMS. If it exceeds the upper or lower threshold, the system automatically halts operation.
- ▪
- According to IEC 62619, the protection limits are defined as:
- ▪
- NTC thermistors are attached to each cell and MOSFET surface. When the temperature exceeds , PWM control is immediately suspended.
- ▪
- A thermal diffusion model is employed to predict the temperature rise () as follows:
- ▪
- An Insulation Monitoring Device (IMD) continuously measures the leakage resistance between the positive/negative terminals and ground during charging.
- ▪
- The insulation resistance drops below 100 kΩ, charging is immediately terminated. If the leakage current exceeds 5 mA, a warning message is displayed on the HMI interface [18].
- ▪
- This feature is critical for high-voltage modules (>60 Vdc) to prevent electric shock or fire hazards [19].
| Algorithm 1. Real-Time Safety Monitoring. |
| INPUTS: I (A), Vcell[] (V), T (°C), Riso (Ω) PARAMS: I_MAX, V_MAX, V_MIN, T_MAX, DT_MAX, RISO_MIN PERIOD: 1 ms // 1 kHz safety scan loop every 1 ms: read I, Vcell[], T, Riso if abs(I) > I_MAX: stop_power_stage(); raise_alarm("Over-current"); continue for v in Vcell: if v > V_MAX or v < V_MIN: stop_power_stage(); raise_alarm("Cell over/under-voltage"); break if T > T_MAX or dT_dt(T) > DT_MAX: stop_power_stage(); raise_alarm("Over-temperature"); continue if Riso < RISO_MIN: stop_power_stage(); raise_alarm("Insulation fault"); continue // safe state clear_alarm(); continue end loop |
2.3. Battery Management System, BMS
- ▪
- Each cell voltage is measured using a high-resolution Analog-to-Digital Converter (ADC) with a resolution of 1 mV. across all series-connected cells is calculated according to Equation (9):
- ▪
- A non-contact Hall effect sensor is employed to minimize electrical noise during current measurement. The measured current is used to dynamically calculate the SOC according to Equation (10):
- ▪
- Each cell or cell block is equipped with NTC thermistors capable of measuring temperature with a precision of ±0.5 °C. If the temperature exceeds the threshold value of , the charge/discharge operation is automatically halted. Additionally, when the temperature rise rate exceeds , a pre-warning signal is generated to prevent potential thermal runaway events.
- ▪
- All measurement data are transmitted to the main controller via a CAN protocol operating at 1 Mbps, following the message frame structure defined in Equation (2). This communication architecture minimizes data loss and enhances transmission reliability. The BMS also contains an integrated 8 MB flash memory, which automatically stores up to one hour of recent operational data for redundancy and uploads it to the cloud server for long-term monitoring.
- ▪
- Passive Balancing: dissipates excess charge as heat through a resistor network.
- ▪
- Active Balancing: transfers charge between adjacent cells using inductor- or capacitor-based energy transfer circuits.
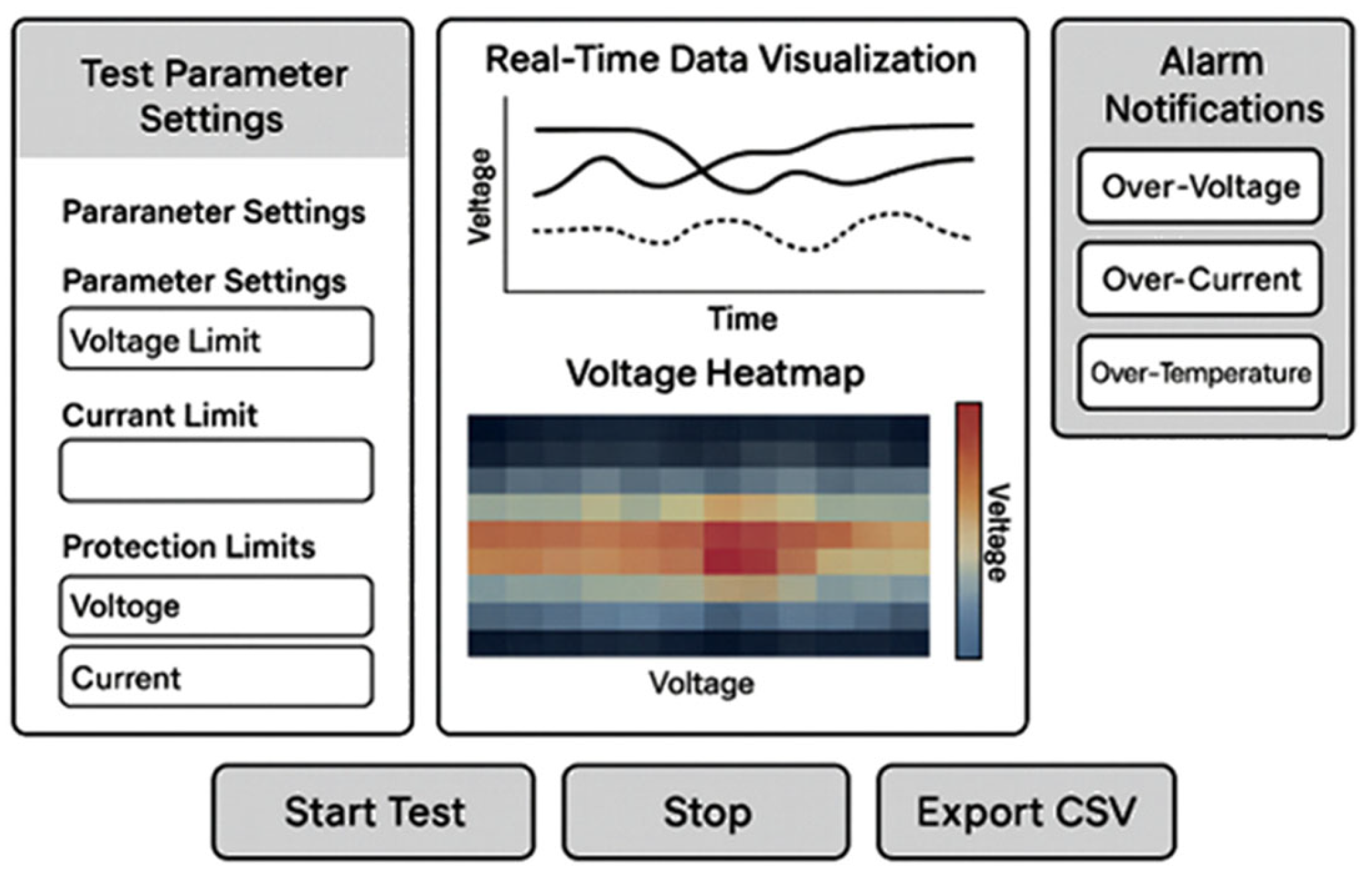
2.4. Human–Machine Interface, HMI/GUI
2.5. Battery Module Under Test
- ▪
- Cell Voltage Uniformity ()—The voltage deviation among cells, used to evaluate charge imbalance and degradation level, is calculated by Equation (20):
- ▪
- Temperature Uniformity ()—The thermal gradient across the module, measured using NTC temperature sensors attached to cell surfaces, is determined by Equation (21):
- ▪
- SOH—To quantify cell degradation, the measured capacity is compared with the initial capacity , as defined in Equation (22):
- ▪
- DCIR—Derived from the pulse charge–discharge test, this metric measures the voltage response to a change in current (ΔI) as defined in Equation (1). DCIR serves as a quantitative indicator of electrode resistance growth and electrolyte degradation, both of which directly correlate with aging and capacity loss.
2.6. CAN-Based Communication
3. Methodology
3.1. Test Sequence
- ▪
- Charging Phase (S100)—During the charging phase, a CC–CV mode is applied. Each cell is charged under the following conditions, as defined in Equation (27):
- ▪
- Discharging Phase (S110)—In the discharging phase, each cell is discharged under CC conditions down to 2.50 V. The discharge current is fixed at 1.0 C, and the instantaneous energy efficiency is computed using Equation (28):
- ▪
- Stabilization Phase (S130)—After charging and discharging, a 10 min rest period is introduced to allow for electrochemical equilibrium within each cell. Stabilization is considered complete when the temperature rate satisfies . The equilibrium voltage obtained during this phase serves as the initial reference voltage () for subsequent DCIR calculations.
- ▪
- Pulse Test (S140)—To precisely evaluate the DCIR and reaction kinetics, a pulse current test is performed. In this study, a 10 A current pulse was applied for 10 s, and the resulting voltage response was used to calculate DCIR as per Equation (1) [39]. In Equation (1), represents the instantaneous voltage drop after pulse application, and denotes the change in current. The voltage recovery profile obtained afterward provides insights into electrode interfacial reaction rates and electrolyte ion conductivity.
- ▪
- Feature Extraction (S160)—From the data collected during charging, discharging, and pulse testing, key diagnostic parameters were extracted as summarized in Table 2.
- ▪
- Grading Phase (S170)—In this final stage, each cell’s diagnostic indicators are first compared against predefined threshold values for preliminary classification. The normalized parameter vector is then fed into a DNN Classifier.
| Algorithm 2. Battery Grading Logic Based on State of Health (SOH). |
| \text{Grade} = |
| \begin{cases} |
| A, & \text{if } \text{reusable (SOH > 90\%)} |
| B, & \text{if } \text{repurposable (70\% ≤ SOH ≤ 90\%)} |
| C, & \text{if } \text{recyclable (SOH < 70\%)} \end{cases} |
| \end{cases} |
3.2. Extraction and Processing of Diagnostic Parameters
- ▪
- The DCIR is determined from the voltage response corresponding to a current pulse and reflects the electrochemical reaction rate and internal loss resistance [43]. During the pulse test (S140), DCIR is calculated from the applied current pulse () and corresponding voltage drop () using Equation (1), where is the instantaneous voltage change, and is the current difference. A lower DCIR indicates higher conductivity and more efficient electrode reactions. The evaluation thresholds are summarized in Table 3.
3.3. Data Preprocessing and Quality Control
4. Deep Learning-Based Grading Model
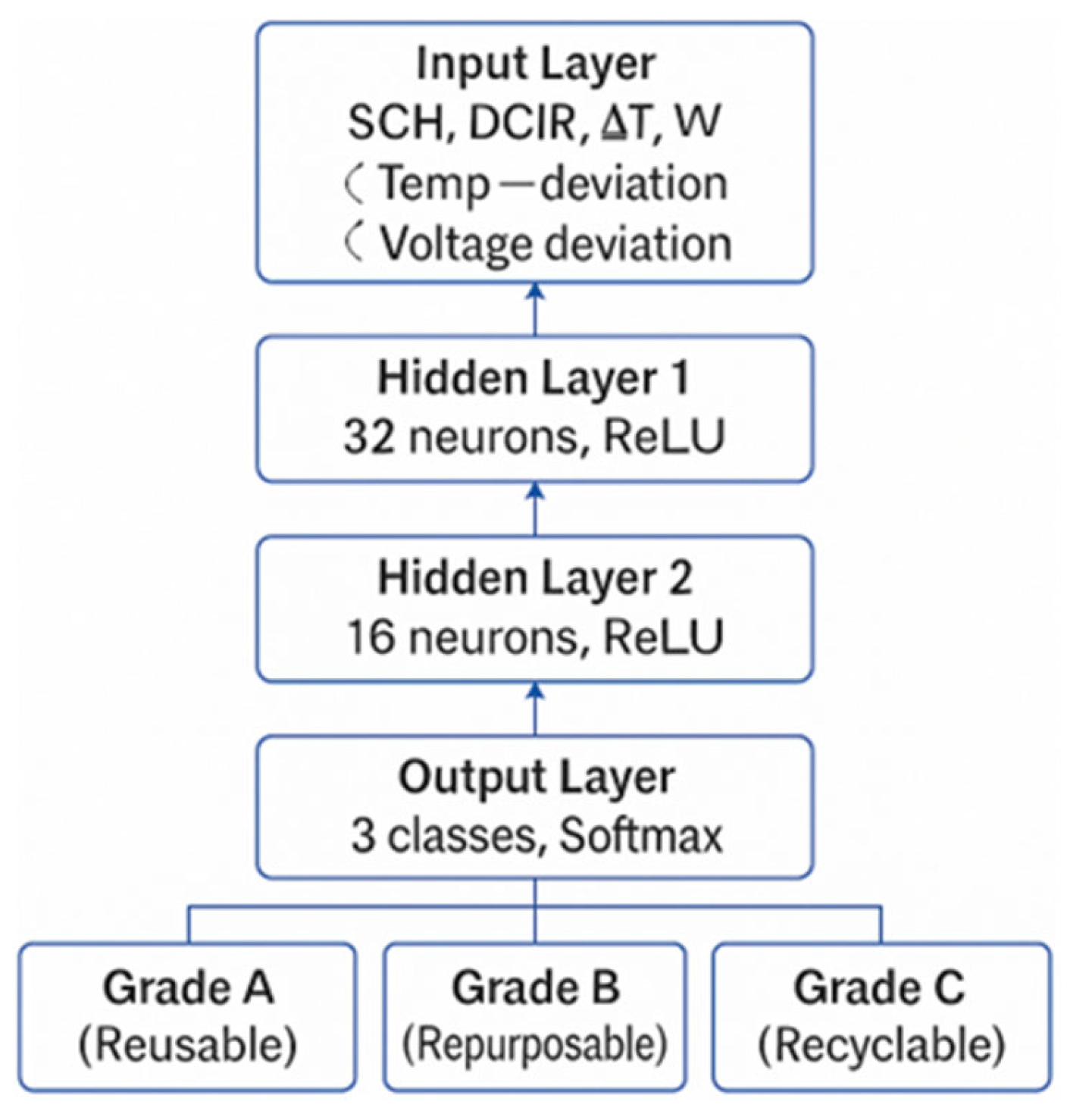
4.1. Concept Overview
4.2. Diagnostic Parameter Calculation
4.3. Model Training and Performance Evaluation
| Algorithm 3. Training Procedure for the DNN-Based Battery Grading Framework. |
| Input: Dataset D = {(x_i, y_i)}, i = 1 … N Initialize weights W and biases b for epoch = 1 to E do Shuffle D and split into mini-batches for each batch (x_batch, y_batch) do Forward propagate through layers Compute loss L using cross-entropy Backpropagate gradients ∂L/∂W Update W, b using Adam optimizer end for Evaluate validation loss L_val if L_val has not improved for 25 epochs: Stop training end for Return trained model parameters Θ* |
4.4. Model Interpretability
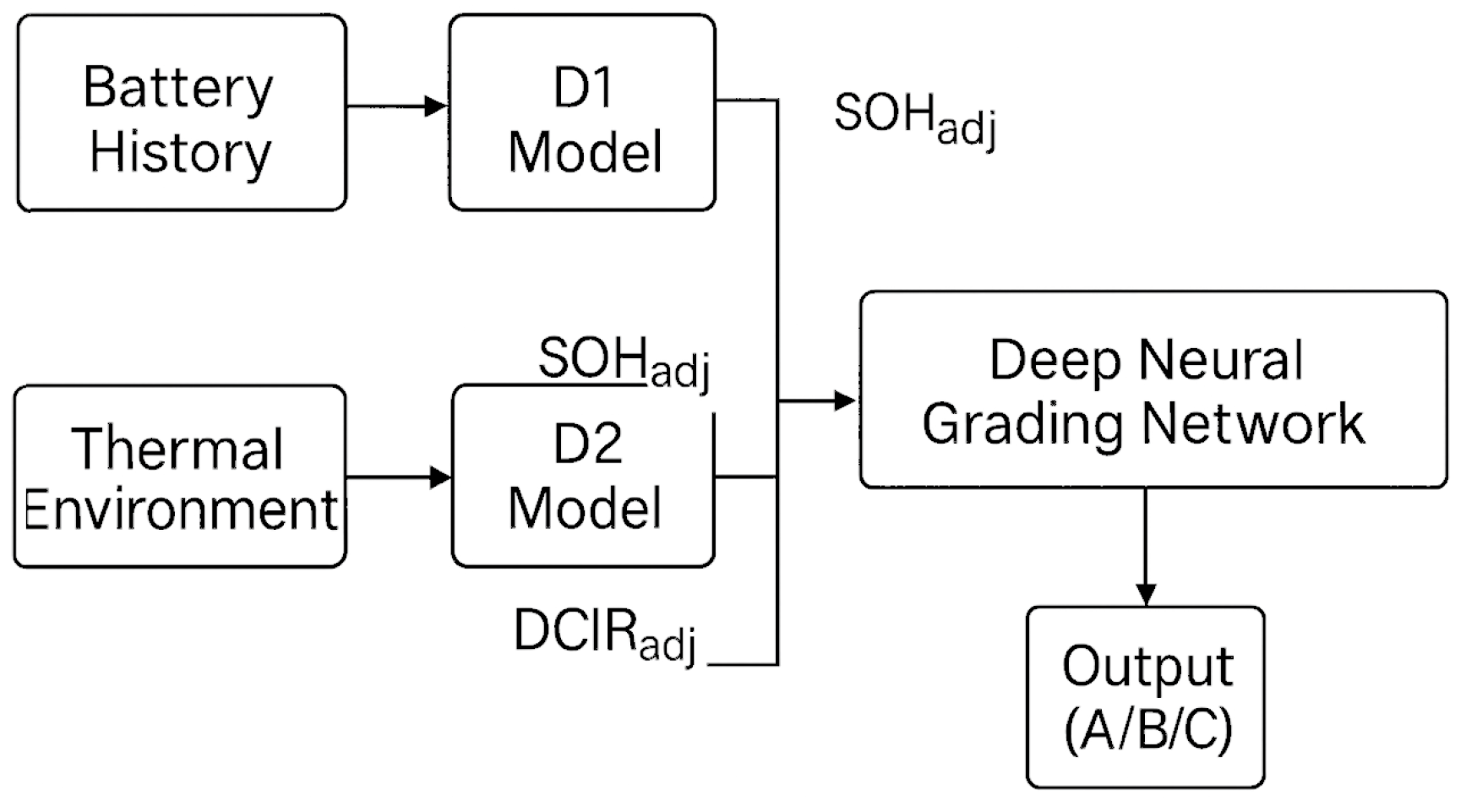
5. Adaptive Correction Models
5.1. Model D1—Life-History-Based SOH Threshold Refinement
5.2. Model D2—Temperature-Compensated DCIR Adjustment
5.3. Integration and Experimental Validation
6. Results and Discussion
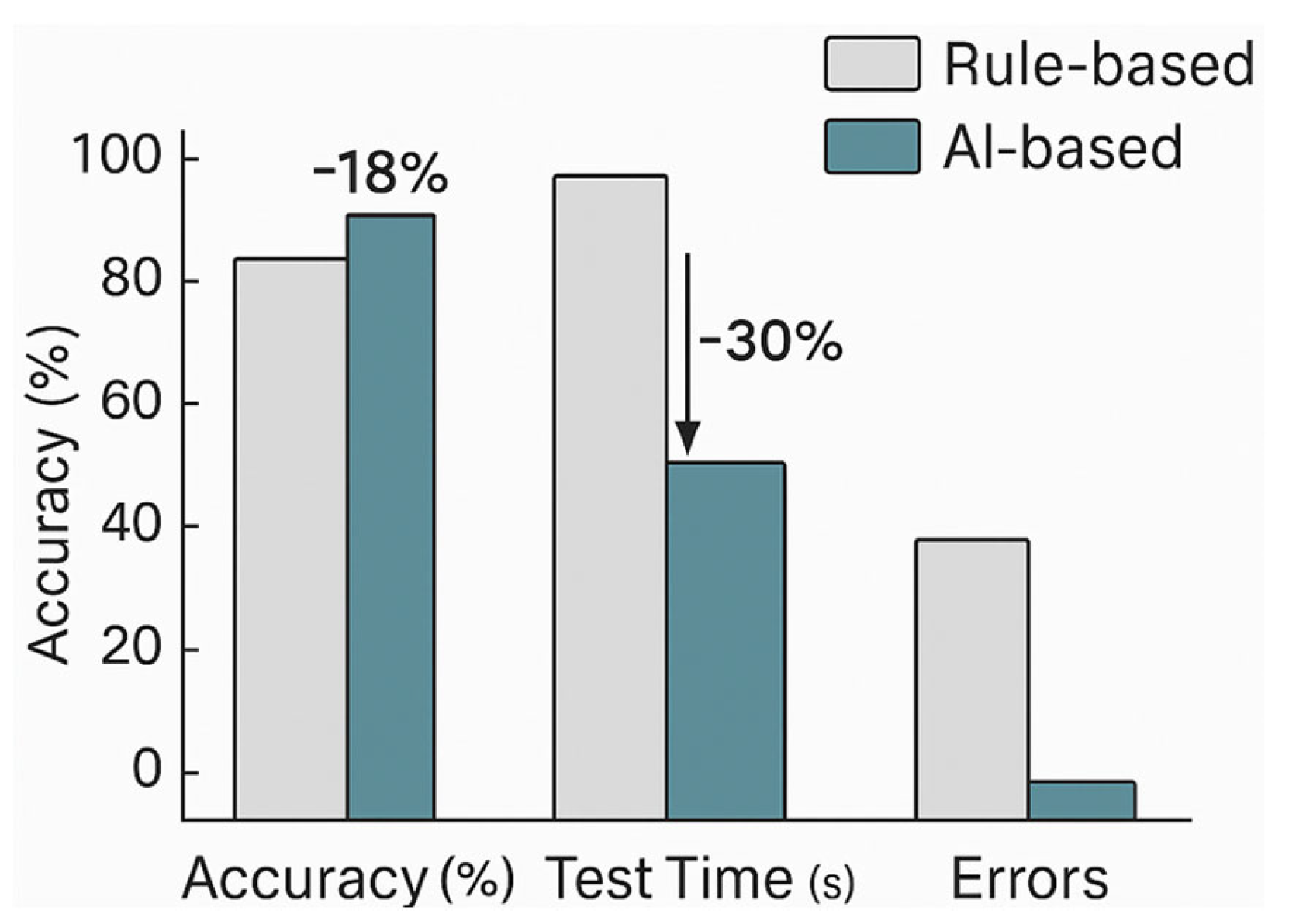
6.1. Overall Grading Accuracy and Efficiency
6.2. Statistical Significance Analysis
6.3. Visualization and Operator Awareness
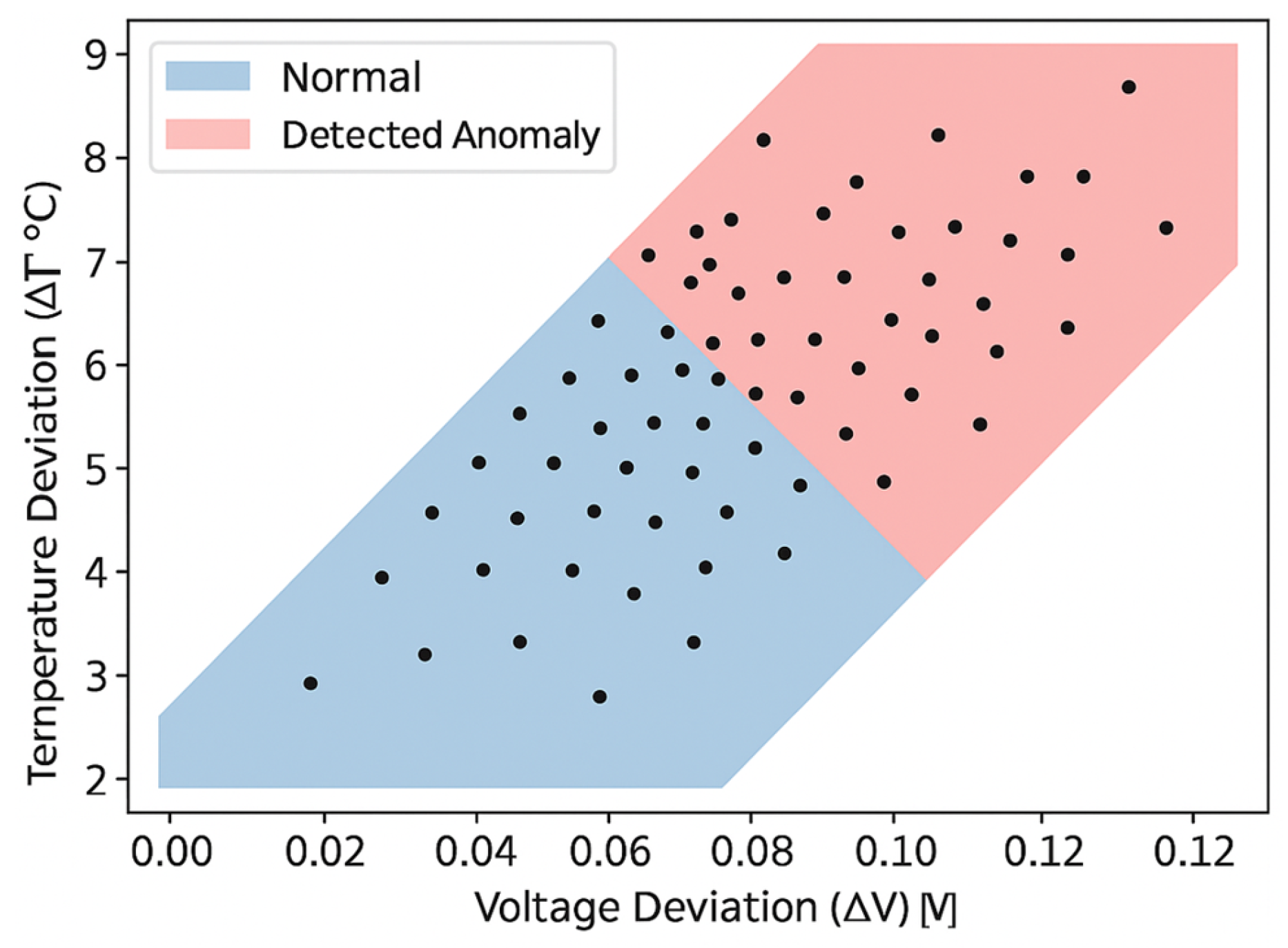
6.4. Uniformity-Based Early Anomaly Detection
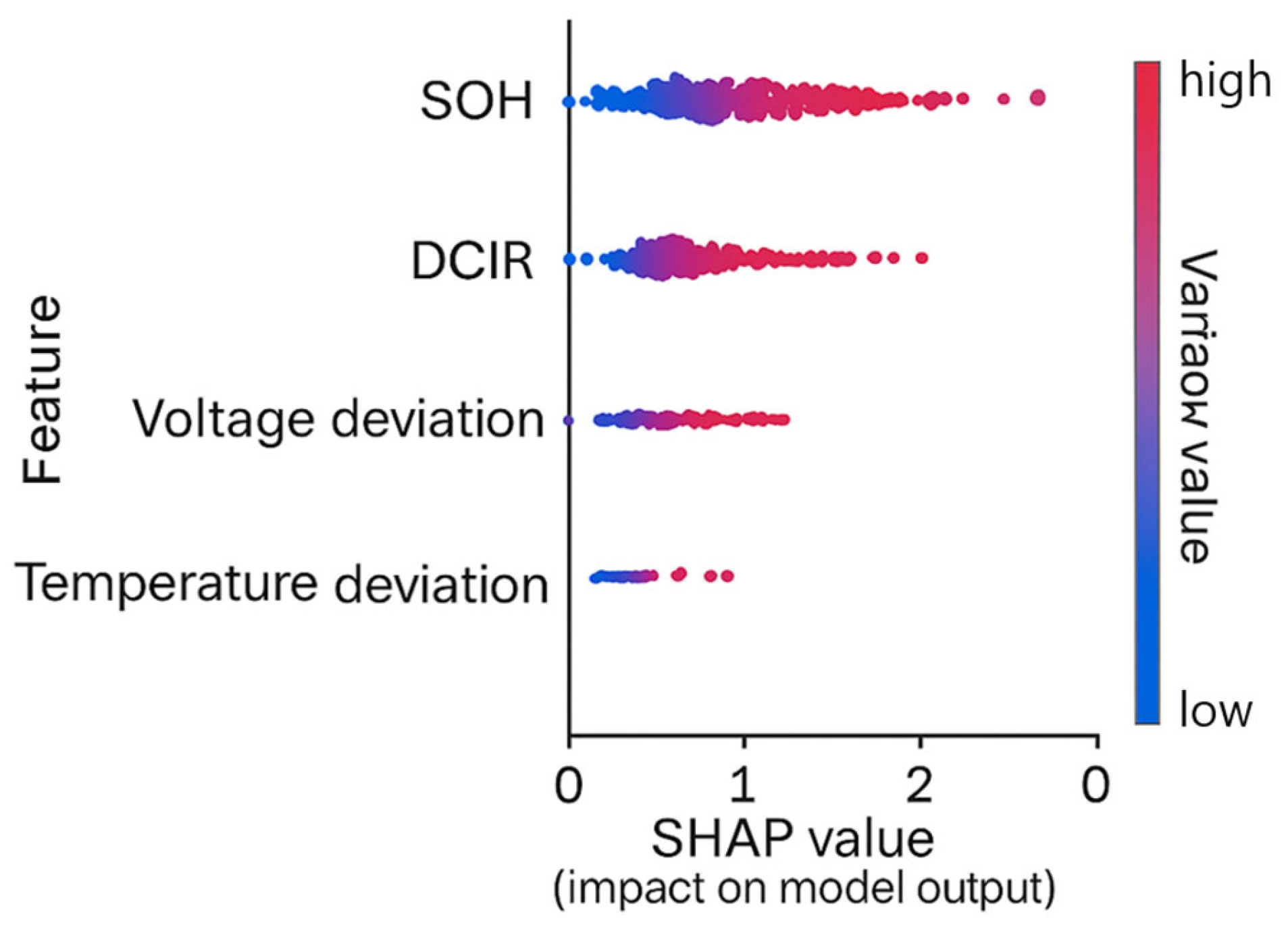
6.5. SHAP-Based Model Interpretation
6.6. Limitations and Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. Securing Supplies for an Electric Future; International Energy Agency: Paris, France, 2022. [Google Scholar]
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Harper, G.; Sommerville, R.; Kendrick, E.; Driscoll, L.; Slater, P.; Stolkin, R.; Walton, A.; Christensen, P.; Heidrich, O.; Lambert, S.; et al. Recycling lithium-ion batteries from electric vehicles. Nature 2019, 575, 75–86. [Google Scholar] [CrossRef]
- Balasingam, B.; Ahmed, M.; Pattipati, K. Battery management systems—Challenges and some solutions. Energies 2020, 13, 2825. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Peng, Q.; Zhang, C. A brief review on key technologies in the battery management system of electric vehicles. Front. Mech. Eng. 2019, 14, 47–64. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, Z.; Shu, X.; Shen, J.; Lei, Z.; Zhang, Y. State of health estimation for lithium-ion batteries based on hybrid attention and deep learning. Reliab. Eng. Syst. Saf. 2023, 232, 109066. [Google Scholar] [CrossRef]
- Renold, A.P.; Kathayat, N.S. Comprehensive review of machine learning, deep learning, and digital twin data-driven approaches in battery health prediction of electric vehicles. IEEE Access 2024, 12, 43984–43999. [Google Scholar] [CrossRef]
- Buchanan, W.J. Some Studies on CAN Specification. In Fieldbus Technology: Industrial Network Standards for Real-Time Distributed Control; Springer: Berlin/Heidelberg, Germany, 2003; pp. 519–529. [Google Scholar] [CrossRef]
- Wu, H.; Yan, Y.; Chen, B.; Hou, F.; Sun, D. FADA: A cloud-fog-edge architecture and ontology for data acquisition. IEEE Trans. Cloud Comput. 2020, 10, 1792–1805. [Google Scholar] [CrossRef]
- Monteiro, V.; Afonso, J.A.; Afonso, J.L. Bidirectional power converters for ev battery chargers. Energies 2023, 16, 1694. [Google Scholar] [CrossRef]
- Youssfi, A.; El Kadi, Y.Y. A New Advanced Strategy for Controlling the Charging and Discharging of a Storage Unit in a Microgrid Using a Finite Control Set Predictive Model. Sol. Energy Sustain. Dev. J. 2024, 14, 38–52. [Google Scholar] [CrossRef]
- Ma, X.; Wu, D.; Rebich, R. Optimizing Grid-interactive Efficient Building Designs with Stacked Value Streams. In Proceedings of the 2024 IEEE Power & Energy Society General Meeting (PESGM), Seattle, WA, USA, 21–25 July 2024; IEEE: New York, NY, USA, 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Li, Y.; Huang, X.; Meng, J.; Shi, K.; Teodorescu, R.; Stroe, D.I. State of Health Estimation for Lithium-Ion Battery Based on Sample Transfer Learning under Current Pulse Test. Batteries 2024, 10, 156. [Google Scholar] [CrossRef]
- Dubarry, M.; Yasir, F. Big data for the diagnosis and prognosis of deployed energy storage systems. In Proceedings of the 2024 IEEE Electrical Energy Storage Application and Technologies Conference (EESAT), San Diego, CA, USA, 29–30 January 2024; IEEE: New York, NY, USA, 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, W.; Gao, S.; Yan, W. Comparison-transfer learning based state-of-health estimation for lithium-ion battery. J. Electrochem. Energy Convers. Storage 2024, 21, 041013. [Google Scholar] [CrossRef]
- Guzek, M.; Jackowski, J.; Jurecki, R.S.; Szumska, E.M.; Zdanowicz, P.; Żmuda, M. Electric vehicles—An overview of current issues—Part 2—Infrastructure and road safety. Energies 2024, 17, 495. [Google Scholar] [CrossRef]
- Teliz, E.; López-Vázquez, C.; Díaz, V. Degradation study for 18650 NMC batteries at low temperature. Electrochim. Acta 2024, 475, 143540. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. International Standard Norme Internationale; IEC Edition; International Electrotechnical Commission: Geneva, Switzerland, 2015; Volume 3. [Google Scholar]
- Bais, L.R.; Singh, S.K.; Dubey, A. Novel Techniques of High Voltage Detection and its Application for Enhancing Safety in Extra High Voltage System Operation and Maintenance. In Proceedings of the 2024 23rd National Power Systems Conference (NPSC), Indore, India, 14–16 December 2024; IEEE: New York, NY, USA, 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Che, Y.; Zheng, Y.; Forest, F.E.; Sui, X.; Hu, X.; Teodorescu, R. Predictive health assessment for lithium-ion batteries with probabilistic degradation prediction and accelerating aging detection. Reliab. Eng. Syst. Saf. 2024, 241, 109603. [Google Scholar] [CrossRef]
- de França, A.A.; Villanueva, J.M.M.; de Macêdo, E.C.T. Cloud Battery Management System Development. In Proceedings of the 2024 8th International Symposium on Instrumentation Systems, Circuits and Transducers (INSCIT), Joao Pessoa, Brazil, 2–6 September 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, K.; Xiong, R.; Qu, S.; Zhang, B.; Shen, W. Electrochemical impedance spectroscopy: A novel high-power measurement technique for onboard batteries using full-bridge conversion. IEEE Trans. Transp. Electrif. 2024, 10, 10073–10082. [Google Scholar] [CrossRef]
- Pavković, D.; Kvaternik, K.; Cipek, M.; Krznar, M. State-of-charge estimator design and experimental verification for a lithium-titanate battery cell. Clean Technol. Environ. Policy 2025, 27, 1599–1615. [Google Scholar] [CrossRef]
- Pradeep, K.; Amaragatti, A.V.; Yugendra, G.L.; Manohar, P.; Kulkarni, S.V.; Ramanujan, K.S. Real Time Battery Monitoring and Protection System with CAN Bus Communication and Data Logging. In Proceedings of the 2024 IEEE 4th International Conference on Sustainable Energy and Future Electric Transportation (SEFET), yderabad, India, 31 July–3 August 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Samanta, A.; Sharma, M.; Locke, W.; Williamson, S. Cloud-Enhanced Battery Management System Architecture for Real-Time Data Visualization, Decision Making, and Long-Term Storage. IEEE J. Emerg. Sel. Top. Ind. Electronics 2025, 6, 1700–1711. [Google Scholar] [CrossRef]
- Khaleghi, S.; Hosen, M.S.; Karimi, D.; Behi, H.; Beheshti, S.H.; Van Mierlo, J.; Berecibar, M. Developing an online data-driven approach for prognostics and health management of lithium-ion batteries. Appl. Energy 2022, 308, 118348. [Google Scholar] [CrossRef]
- Devi, B.; Kumar, V.S.; Karthick, T.; Balasundar, C. Deep learning based IoT and cloud-integrated state of charge estimation for battery powered electric vehicles. J. Energy Storage 2024, 100, 113622. [Google Scholar] [CrossRef]
- Zhang, X.; Beram, S.M.; Haq, M.A.; Wawale, S.G.; Buttar, A.M. Research on algorithms for control design of human–machine interface system using ML. Int. J. Syst. Assur. Eng. Manag. 2022, 13 (Suppl. S1), 462–469. [Google Scholar] [CrossRef]
- Verani, A.; Di Rienzo, R.; Nicodemo, N.; Baronti, F.; Roncella, R.; Saletti, R. Modular battery emulator for development and functional testing of battery management systems: Hardware design and characterization. Electronics 2023, 12, 1232. [Google Scholar] [CrossRef]
- Nováková, K.; Pražanová, A.; Stroe, D.I.; Knap, V. Second-life of lithium-ion batteries from electric vehicles: Concept, aging, testing, and applications. Energies 2023, 16, 2345. [Google Scholar] [CrossRef]
- Sarrafan, K.; Sutanto, D.; Muttaqi, K.M. An electric circuit based EV battery model for runtime prediction and state of charge tracking. In Proceedings of the 2017 IEEE Transportation Electrification Conference (ITEC-India), Pune, India, 13–15 December 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Gawde, S.; Patil, S.; Kumar, S.; Kotecha, K. A scoping review on multi-fault diagnosis of industrial rotating machines using multi-sensor data fusion. Artif. Intell. Rev. 2023, 56, 4711–4764. [Google Scholar] [CrossRef]
- Conard, J.W. Services and protocols of the data link layer. Proc. IEEE 2005, 71, 1378–1383. [Google Scholar] [CrossRef]
- Bosch, R.G. CAN specification version 2.0: Robert Bosch GmbH. In Systems und Products for Car Manufacturer; Rheinmetall AG: Düsseldorf, Germany, 1991. [Google Scholar]
- Corrigan, S. Introduction to the Controller Area Network (CAN); Application Report SLOA101; Texas Instruments: Dallas, TX, USA, 2002; pp. 1–17. [Google Scholar]
- Shah, M.B.N.; Husain, A.R.; Aysan, H.; Punnekkat, S.; Dobrin, R.; Bender, F.A. Error handling algorithm and probabilistic analysis under fault for CAN-based steer-by-wire system. IEEE Trans. Ind. Inform. 2016, 12, 1017–1034. [Google Scholar] [CrossRef]
- Maletić, F.; Deur, J.; Erceg, I. A multitimescale kalman filter-based estimator of li-ion battery parameters including adaptive coupling of state-of-charge and capacity estimation. IEEE Trans. Control Syst. Technol. 2022, 31, 692–706. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Bao, Y.; Dong, W.; Wang, D. Online internal resistance measurement application in lithium ion battery capacity and state of charge estimation. Energies 2018, 11, 1073. [Google Scholar] [CrossRef]
- Madani, S.S.; Shabeer, Y.; Fowler, M.; Panchal, S.; Chaoui, H.; Mekhilef, S.; Dou, S.X.; See, K. Artificial Intelligence and Digital Twin Technologies for Intelligent Lithium-Ion Battery Management Systems: A Comprehensive Review of State Estimation, Lifecycle Optimization, and Cloud-Edge Integration. Batteries 2025, 11, 298. [Google Scholar] [CrossRef]
- Long, B.; Gao, X.; Li, P.; Liu, Z. Multi-parameter optimization method for remaining useful life prediction of lithium-ion batteries. IEEE Access 2020, 8, 142557–142570. [Google Scholar] [CrossRef]
- Remmlinger, J.; Buchholz, M.; Meiler, M.; Bernreuter, P.; Dietmayer, K. State-of-health monitoring of lithium-ion batteries in electric vehicles by on-board internal resistance estimation. J. Power Sources 2011, 196, 5357–5363. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, S.J.; Lee, J.M.; Cho, B.H. A new direct current internal resistance and state of charge relationship for the Li-ion battery pulse power estimation. In Proceedings of the 2007 7th Internatonal Conference on Power Electronics, Daegu, Republic of Korea, 22–26 October 2007; IEEE: New York, NY, USA, 2007; pp. 11173–11178. [Google Scholar] [CrossRef]
- Liu, X.; Ai, W.; Marlow, M.N.; Patel, Y.; Wu, B. The effect of cell-to-cell variations and thermal gradients on the performance and degradation of lithium-ion battery packs. Appl. Energy 2019, 248, 489–499. [Google Scholar] [CrossRef]
- Zhang, X.; Gong, A.; He, W.; Cao, Y.; He, H. A lithium battery health evaluation method based on considering disturbance belief rule base. Batteries 2024, 10, 129. [Google Scholar] [CrossRef]
- Ma, X.; Ding, X.; Tian, C.; Tian, C.; Zhu, R. Estimation of Lithium-Ion Battery State of Health-Based Multi-Feature Analysis and Convolutional Neural Network–Long Short-Term Memory. Sustainability 2025, 17, 4014. [Google Scholar] [CrossRef]
- Oh, S.; Kim, J.; Moon, I. Hybrid data-driven deep learning model for state of charge estimation of Li-ion battery in an electric vehicle. J. Energy Storage 2024, 97, 112887. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Etem, T. Interpretable machine learning for battery health insights: A LIME and SHAP-based study on EIS-derived features. Bull. Pol. Acad. Sci. Tech. Sci. 2025, 73, e155033. [Google Scholar] [CrossRef]
- Wen, P.; Ye, Z.S.; Li, Y.; Chen, S.; Xie, P.; Zhao, S. Physics-informed neural networks for prognostics and health management of lithium-ion batteries. IEEE Trans. Intell. Veh. 2023, 9, 2276–2289. [Google Scholar] [CrossRef]
- Shu, X.; Chen, Z.; Shen, J.; Guo, F.; Zhang, Y.; Liu, Y. State of charge estimation for lithium-ion battery based on hybrid compensation modeling and adaptive H-infinity filter. IEEE Trans. Transp. Electrif. 2022, 9, 945–957. [Google Scholar] [CrossRef]
- Lakshmi, V.S.G.; Rani, M.D.; Bhavana, K. AI-Improved Battery-Powered Automobile Battery Diagnostics. In Proceedings of the 2024 7th International Conference on Circuit Power and Computing Technologies (ICCPCT), Kollam, India, 8–9 August 2024; IEEE: New York, NY, USA, 2024; Volume 1, pp. 1500–1505. [Google Scholar] [CrossRef]
- Nourani, V.; Dehghan, M.; Baghanam, A.H.; Kantoush, S.A. Dual purpose of Shapley Additive Explanation (SHAP) in model explanation and feature selection for artificial intelligence-based digital twin of wastewater treatment plant. J. Water Process Eng. 2025, 75, 107947. [Google Scholar] [CrossRef]

| Classification | Standard No. |
|---|---|
| IEC 62619:2022 | Safety requirements for industrial and stationary secondary lithium-ion cells and batteries |
| UL 1973:2023 | Safety evaluation for batteries used in stationary and motive applications (energy storage systems) |
| UL 1973:2023 | Electrical safety requirements for high-voltage systems in electric vehicles |
| IEC 61557-8:2019 | Performance standards for insulation monitoring devices (IMDs) in ungrounded systems |
| Parameter | Symbol | Description |
|---|---|---|
| State of Health | Ratio of remaining capacity to initial capacity | |
| DC Internal Resistance | Internal resistance of the cell | |
| Thermal Uniformity | Difference between maximum and minimum cell temperatures | |
| Voltage Uniformity | Deviation in voltage distribution among cells |
| Condition | DCIR (mΩ) | Description |
|---|---|---|
| Healthy | Normal electrochemical response | |
| Moderate Degradation | Beginning of electrode resistance increase | |
| Severe Degradation | Possible internal damage |
| Metric | A Grade | B Grade | C Grade |
|---|---|---|---|
| SOH (%) | >90 | 70–90 | <70 |
| DCIR Δ (%) | <50 | 50–100 | >100 |
| Temp Δ (°C)/Volt Δ (V) | <5∕<0.05 | 5–10/0.05–0.1 | >10∕>0.1 |
| Parameter | Optimal Value |
|---|---|
| Batch Size | 32 |
| Epochs | 600 |
| Dropout Rate | 0.3 |
| Validation Split | 0.2 |
| Early Stopping Patience | 25 epochs |
| Metric | Value |
|---|---|
| Accuracy | 97.4% |
| Precision | 96.8% |
| Recall | 95.9% |
| F1-Score | 0.96 |
| Pred A | Pred B | Pred C | |
|---|---|---|---|
| True A | 141 | 3 | 0 |
| True B | 2 | 129 | 4 |
| True C | 0 | 5 | 118 |
| Metric | Before Correction | After D1/D2 Applied | Improvement |
|---|---|---|---|
| Cross-Temperature Accuracy (%) | 81.4 | 93.2 | +11.8 |
| Life-History Consistency (%) | 78.5 | 91.7 | +13.2 |
| DCIR Stability (Std. Dev.) | 0.42 mΩ | 0.27 mΩ | −35.7% |
| Metric | Rule-Based Method | Proposed DNN System | Improvement |
|---|---|---|---|
| Accuracy (%) | 79.2 | 93.7 | +18.3% |
| F1-Score | 0.78 | 0.94 | +0.16 |
| Average Test Time (min/module) | 28.5 | 19.8 | −30.5% |
| Operator Error Rate (%) | 7.2 | 1.3 | −81.9% |
| Early Anomaly Detection (%) | 63.5 | 91.8 | +28.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, S.; Kim, H. AI-Integrated Smart Grading System for End-of-Life Lithium-Ion Batteries Based on Multi-Parameter Diagnostics. Energies 2025, 18, 5915. https://doi.org/10.3390/en18225915
Cho S, Kim H. AI-Integrated Smart Grading System for End-of-Life Lithium-Ion Batteries Based on Multi-Parameter Diagnostics. Energies. 2025; 18(22):5915. https://doi.org/10.3390/en18225915
Chicago/Turabian StyleCho, Seongsoo, and Hiedo Kim. 2025. "AI-Integrated Smart Grading System for End-of-Life Lithium-Ion Batteries Based on Multi-Parameter Diagnostics" Energies 18, no. 22: 5915. https://doi.org/10.3390/en18225915
APA StyleCho, S., & Kim, H. (2025). AI-Integrated Smart Grading System for End-of-Life Lithium-Ion Batteries Based on Multi-Parameter Diagnostics. Energies, 18(22), 5915. https://doi.org/10.3390/en18225915








