Grid-Connected Bidirectional Off-Board Electric Vehicle Fast-Charging System
Abstract
1. Introduction
- A complete dynamic model of an integrated system comprising a three-phase AC/DC rectifier with an LCL filter and a four-phase interleaved bidirectional DC/DC converter is presented, explicitly capturing the coupling dynamics through the DC-link.
- A hierarchical control framework is developed and is enhanced with a battery current feedforward scheme to actively mitigate DC-link instability during transients.
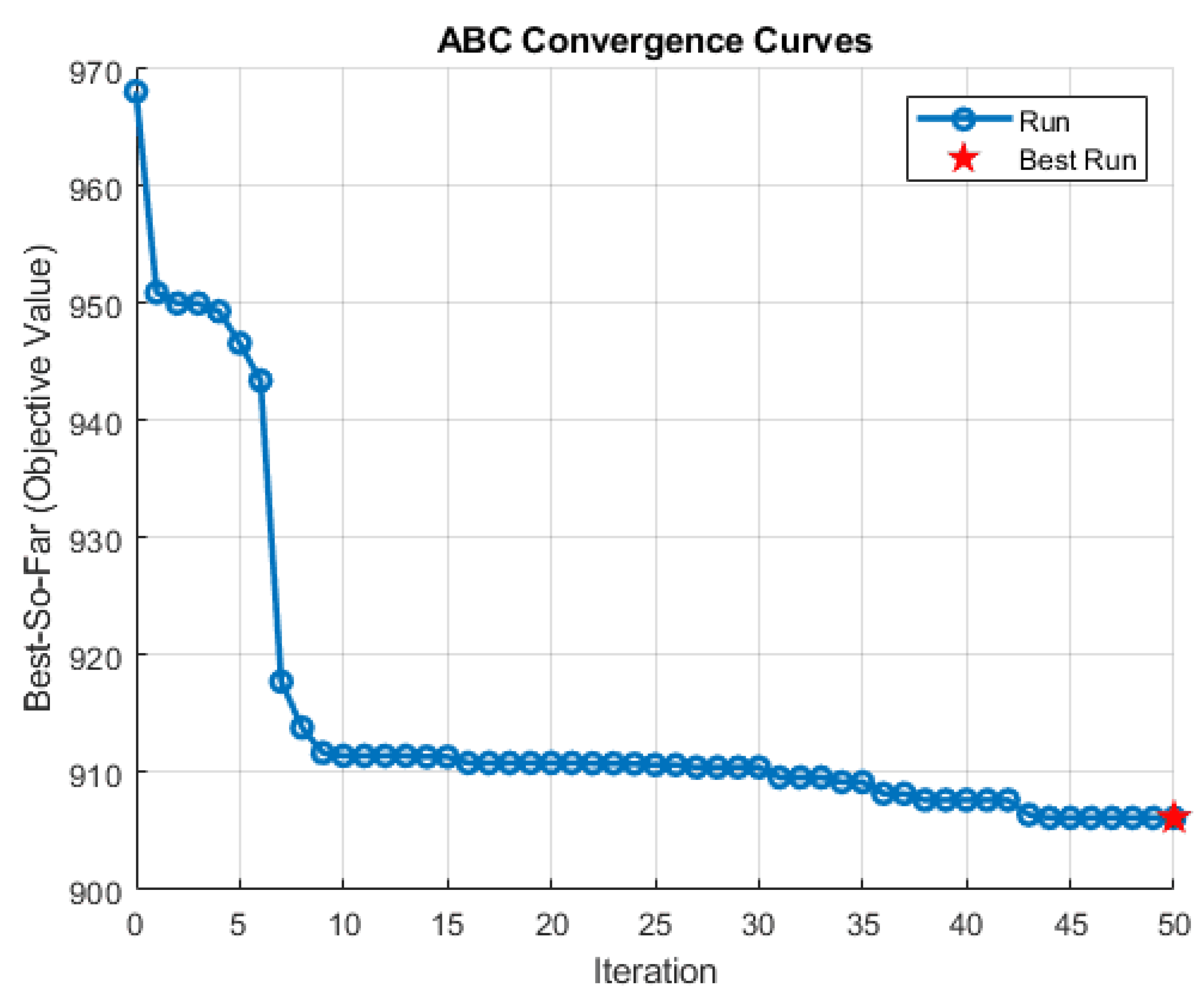
- The Artificial Bee Colony (ABC) algorithm is implemented to perform a system-wide optimization of all Proportional–Integral (PI) controller gains, moving beyond sub-optimal independent tuning to achieve a critically damped, high-performance response across both power stages.
- Through detailed simulation studies, a quantitative comparative analysis is provided, demonstrating the performance evolution from a baseline analytical design, to a feedforward-enhanced system, and finally to the fully optimized system, highlighting the significant improvements in transient response and power quality.
2. System Configuration and Modeling
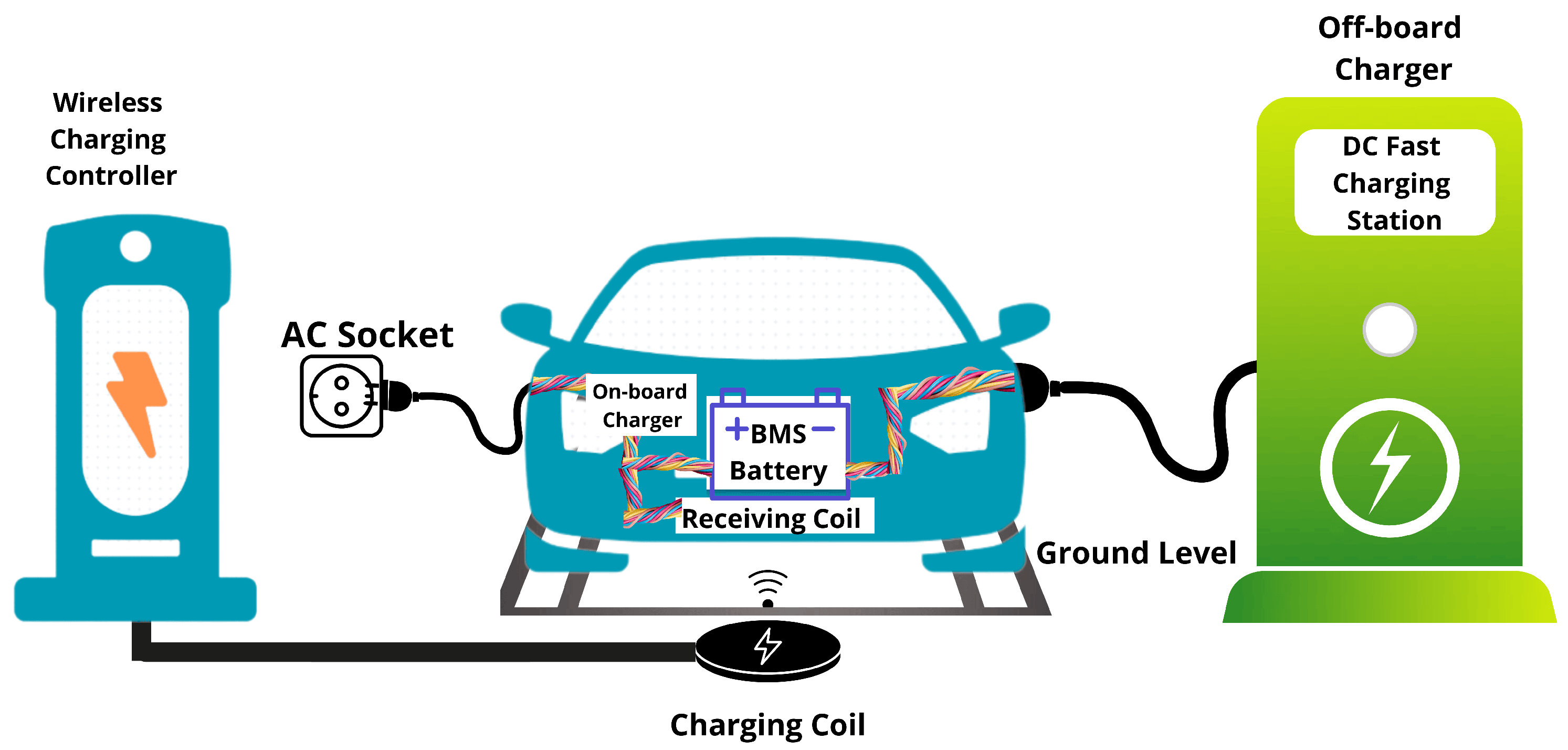
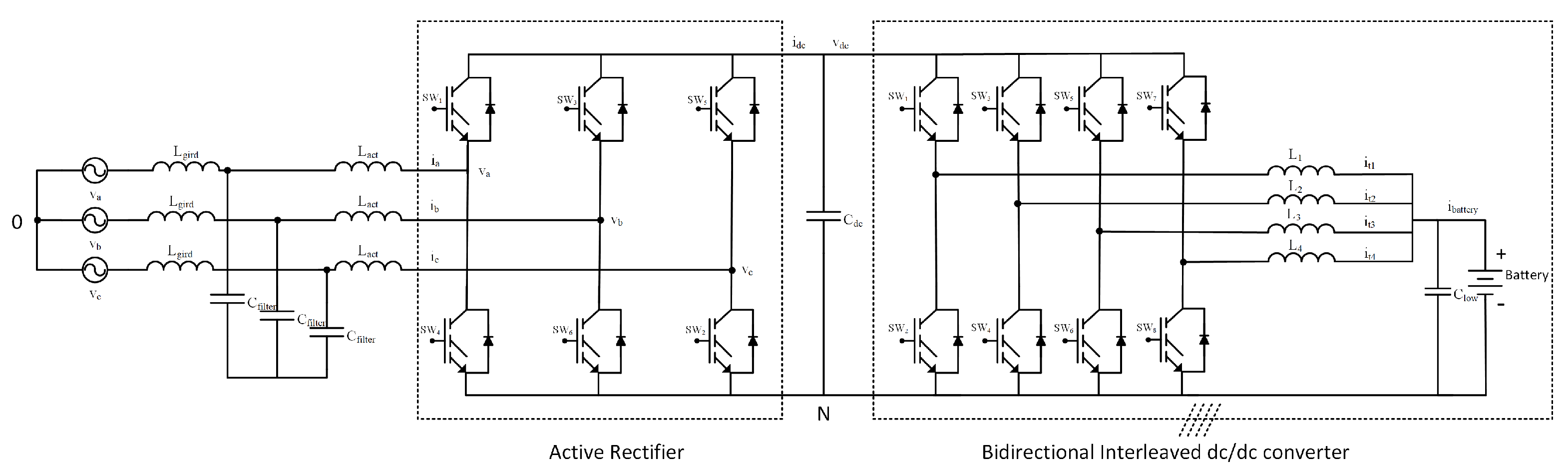
2.1. Overall System Configuration
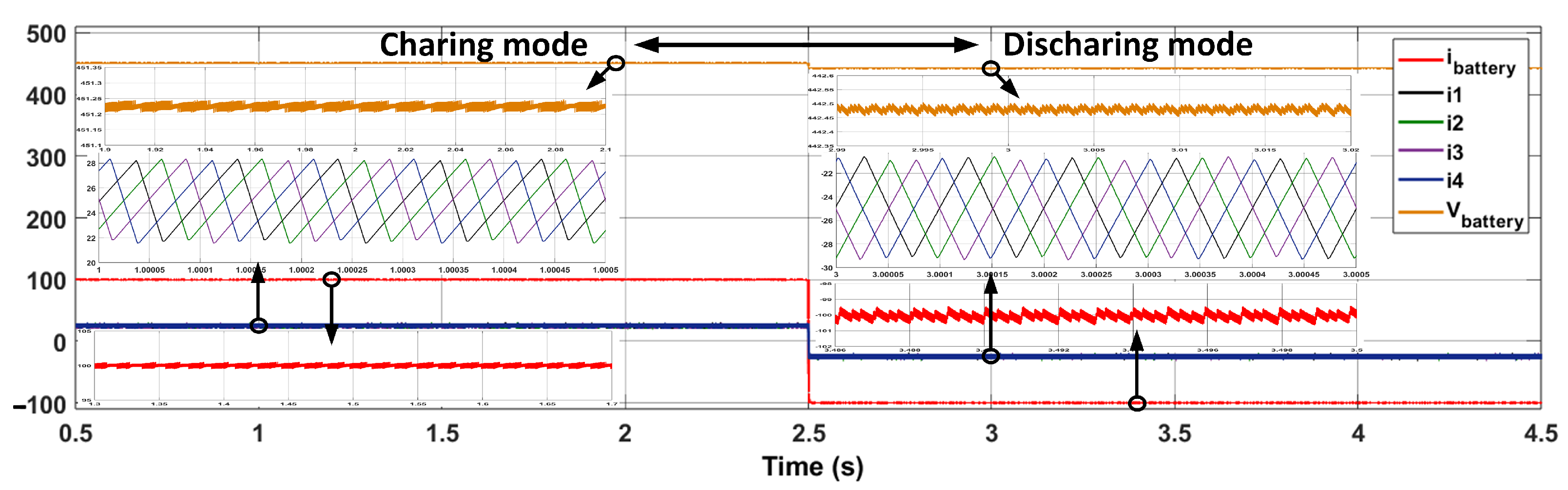
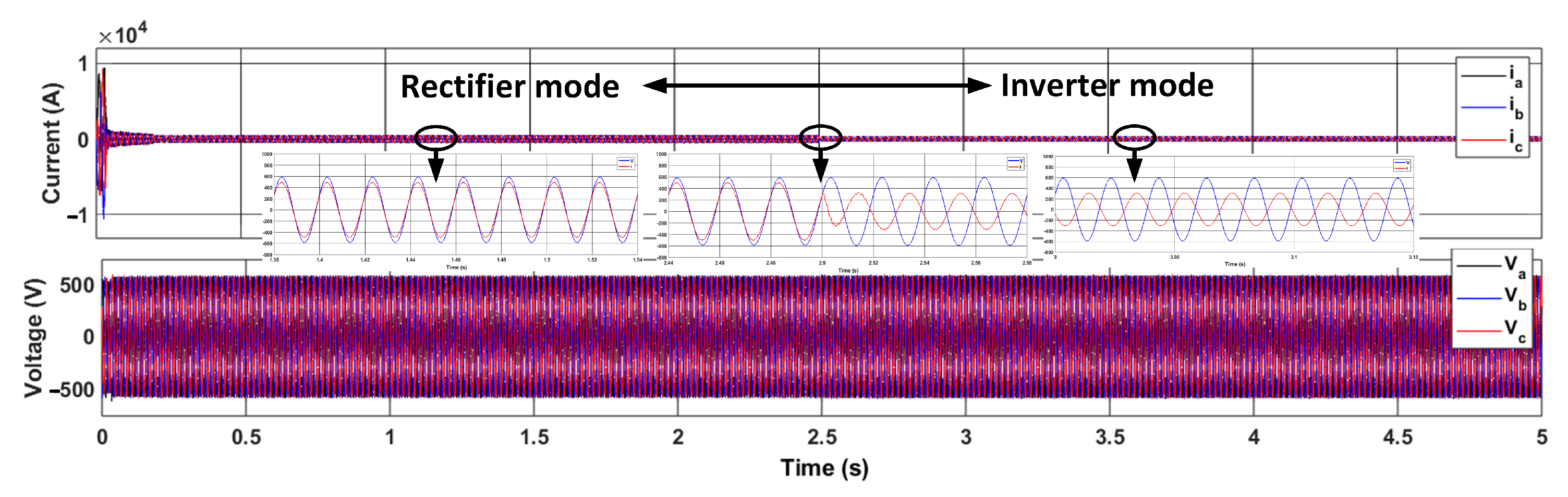
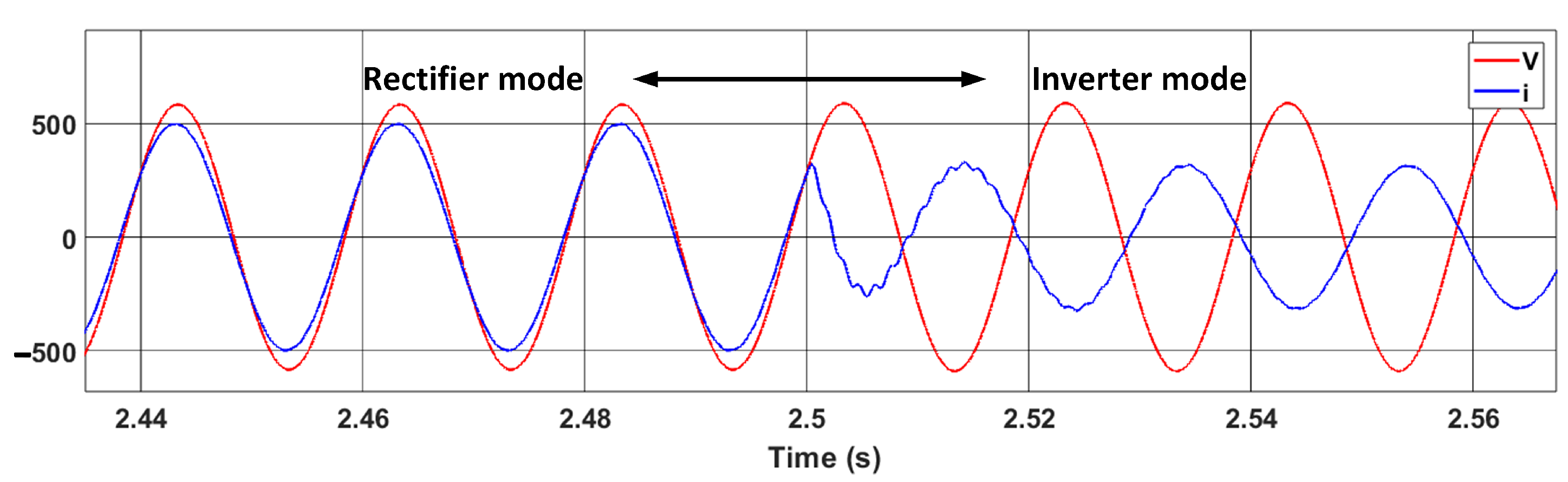
- Charging: where the AC/DC stage operates as an active rectifier to maintain a constant DC-link voltage, while the DC/DC stage operates in buck mode to regulate the battery charging current.
- Discharging: where the DC/DC stage operates in boost mode to elevate the battery voltage, and the AC/DC stage operates as an inverter to inject power back into the grid, all while maintaining DC-link voltage stability.
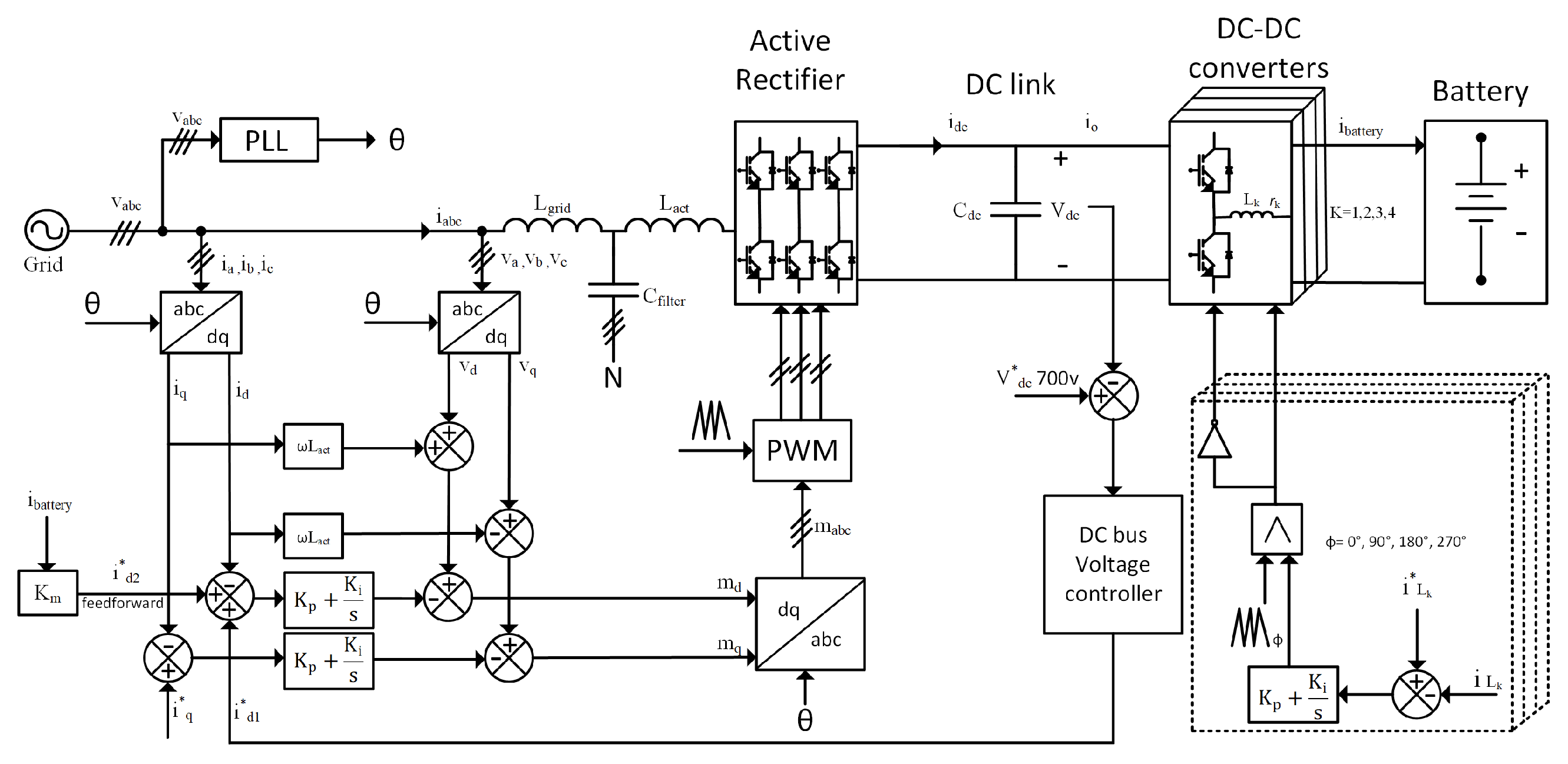
2.2. Modeling of the Grid-Connected AC/DC Converter Stage
2.3. Modeling of the Interleaved Bidirectional DC–DC Converter
2.4. DC-Link Power Balance and System Coupling
2.5. Fundamental Current and Power Relationships
2.6. Efficiency Analysis and Power Loss Calculation
2.7. Voltage and Current Stress Analysis on Power Switches
3. Control Strategy Design and Optimization
3.1. Inner Current Control Loops
3.2. Outer DC-Link Voltage Regulation
3.3. Grid Synchronization Using PLL
3.4. Feedforward Compensation for Transient Enhancement
3.5. Control of the Interleaved DC-DC Converter
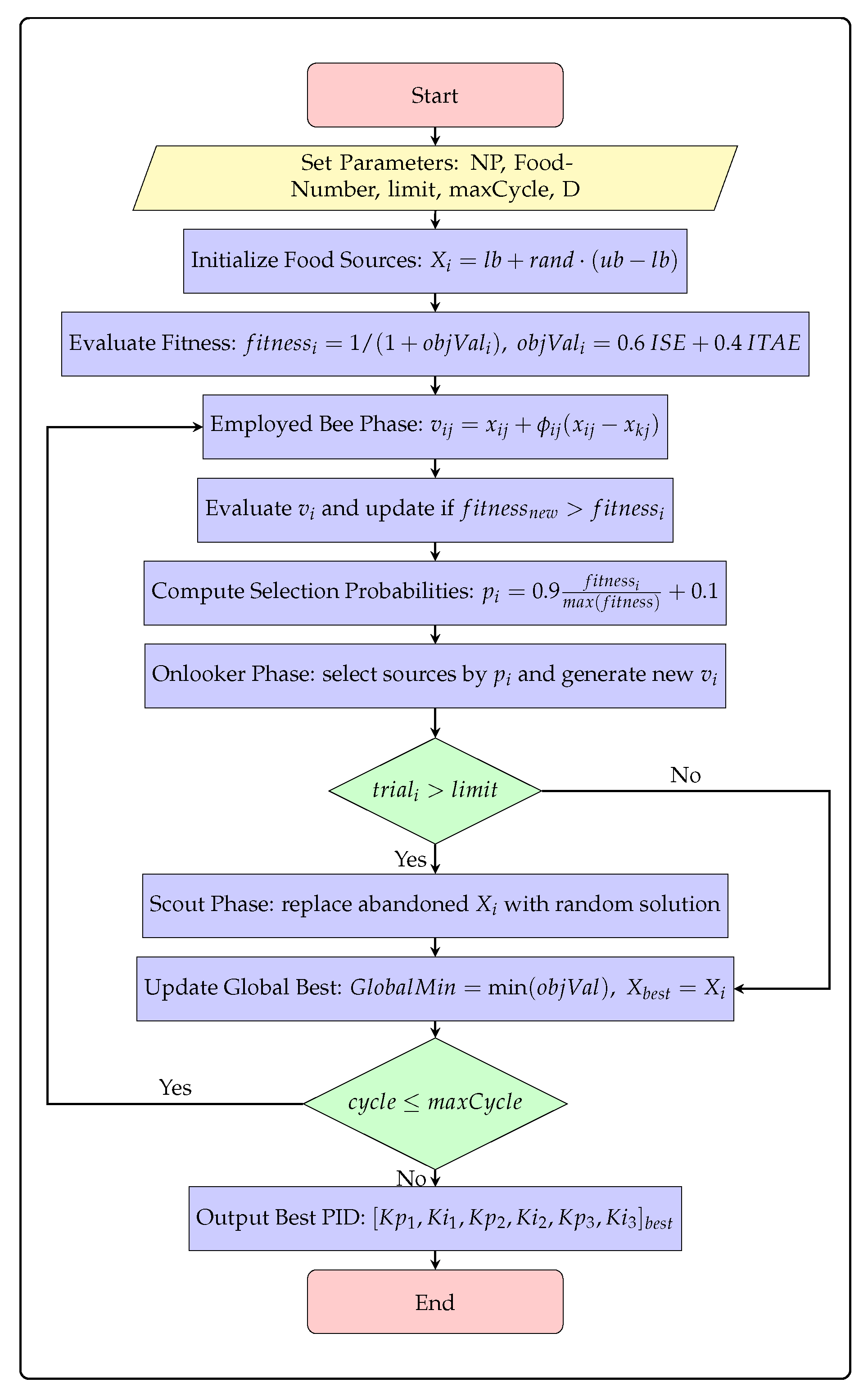
3.6. Optimization of PI Controllers Using ABC Algorithm
4. Systematic Design of Circuit Elements and Controller Parameters
4.1. Analytical Controller Design
4.2. Optimization-Based Refinement
5. System Performance Evaluation, Results and Discussion
5.1. Active Rectifier Performance Evolution
5.1.1. Baseline Performance Without Feedforward
5.1.2. Enhanced Performance with Feedforward Compensation
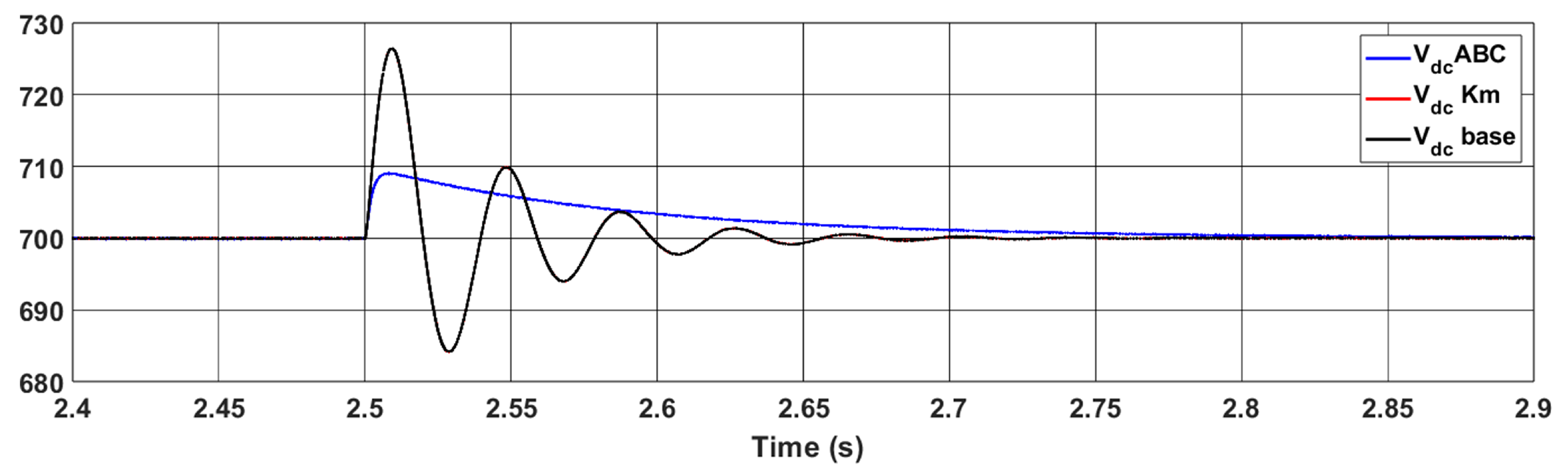
5.2. Optimized System with ABC Algorithm
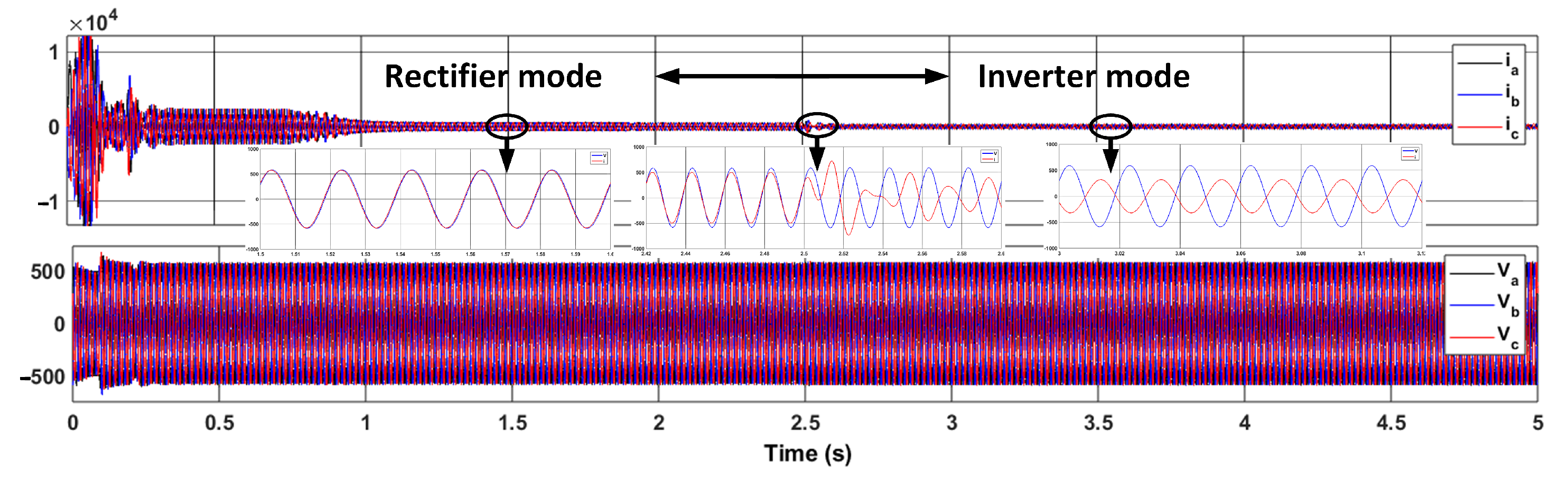
5.3. Subsystem-Level Signal Verification
6. Comparative Analysis with State-of-the-Art Topologies and Controllers
| Ref. | Year | Topology | Control Method | Key Performance | Power | Limitations |
|---|---|---|---|---|---|---|
| [22] | 2005 | Active rectifier + LCL | PI cascade | THD ∼3%, low harmonics | 4.1 kW | Passive damping losses, no V2G test |
| [16] | 2009 | VSC + LCL filter | VOC + active damping | THD <5%, fast response | 50 kVA | Grid distortion sensitivity, no battery link |
| [47] | 2014 | Single-phase AC/DC | Dual PI + feedforward | THD ∼4.3%, PF 0.991 | Proto. | Single-phase only, zero-crossing distortion |
| [29] | 2017 | 3-phase VSC | Unified droop | 18 ms settling, unity PF | 2 kW | Aircraft-specific, tuning-dependent |
| [23] | 2020 | 3-phase AC/DC + L-filter | Double PI + feedforward | THD 1.1–2.1%, 178–260 ms settling | 80 kW | Poor low-power behavior, complex tuning |
| [48] | 2023 | 3-phase VSC + LCL | VOC + PI + observer | THD 2.62–2.71%, stable | 16 kVA | Observer sensitivity, limited scalability |
| [49] | 2025 | 3-phase PWM + LCL | SMC + PI | THD ∼4.5%, 130/60 ms settling | kW-scale | High complexity, no discharging validation |
| This work | 2025 | 3-phase VSC + LCL + 4-phase IBBC | ABC-optimized PI + FF | THD 0.59%, zero V2G settling, 0.08–0.20 V ripple | 50 kW | Higher component count, global optimization effort |
| Ref. | Year | Topology | Control Method | Key Performance | Power | Limitations |
|---|---|---|---|---|---|---|
| [15] | 2007 | 3-phase interleaved | ZVS soft-switching | ∼98% efficiency, high density | 100 kW | No grid interface, DC/DC only |
| [51] | 2018 | 3-phase interleaved + coupled inductors | Phase-decoupled control | Low ripple, fast transient response | 180 W | Parameter sensitivity, complex structure |
| [50] | 2020 | Multiphase interleaved + coupled inductors | Phase-shifted PWM | >98% efficiency, low ripple | 4.5 kW | Hard switching, complex magnetics |
| This work | 2025 | 4-phase interleaved bidirectional buck–boost | Optimized PI current control | >95% efficiency, <0.6 A battery ripple | 50 kW | Requires multi-phase gate drivers |
7. Conclusions
Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, A.P.; Li, S.; Xie, D.; Wang, Y.; Li, Z.; Hu, P.J.H.; Zhang, Q. Hydrogen as the nexus of future sustainable transport and energy systems. Nat. Rev. Electr. Eng. 2025, 2, 447–466. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, L.; Hou, K.; Zhou, Y.; Zhao, R.; Jia, H. A State-similarity-based fast reliability assessment for power systems with variations of generation and load. IEEE Trans. Power Syst. 2024, 1–13. [Google Scholar] [CrossRef]
- Yoro, K.O.; Daramola, M.O. CO2 emission sources, greenhouse gases, and the global warming effect. In Advances in Carbon Capture; Elsevier: Amsterdam, The Netherlands, 2020; pp. 3–28. [Google Scholar]
- Kabir, M.; Habiba, U.E.; Khan, W.; Shah, A.; Rahim, S.; De los Rios-Escalante, P.R.; Farooqi, Z.U.R.; Ali, L.; Shafiq, M. Climate change due to increasing concentration of carbon dioxide and its impacts on environment in 21st century: A mini review. J. King Saud-Univ.-Sci. 2023, 35, 102693. [Google Scholar] [CrossRef]
- Habib, S.; Khan, M.M.; Abbas, F.; Sang, L.; Shahid, M.U.; Tang, H. A comprehensive study of implemented international standards, technical challenges, impacts and prospects for electric vehicles. IEEE Access 2018, 6, 13866–13890. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Karagiannopoulos, P.S.; Tsekouras, G.J.; Kanellos, F.D. Integration of renewable energy and electric vehicles in power systems: A review. Processes 2023, 11, 1544. [Google Scholar] [CrossRef]
- Masrur, M.A.; Skowronska, A.G.; Hancock, J.; Kolhoff, S.W.; McGrew, D.Z.; Vandiver, J.C.; Gatherer, J. Military-based vehicle-to-grid and vehicle-to-vehicle microgrid—System architecture and implementation. IEEE Trans. Transp. Electrif. 2017, 4, 157–171. [Google Scholar] [CrossRef]
- Habib, S.; Khan, M.M.; Abbas, F.; Tang, H. Assessment of electric vehicles concerning impacts, charging infrastructure with unidirectional and bidirectional chargers, and power flow comparisons. Int. J. Energy Res. 2018, 42, 3416–3441. [Google Scholar] [CrossRef]
- Savio Abraham, D.; Verma, R.; Kanagaraj, L.; Giri Thulasi Raman, S.R.; Rajamanickam, N.; Chokkalingam, B.; Marimuthu Sekar, K.; Mihet-Popa, L. Electric vehicles charging stations’ architectures, criteria, power converters, and control strategies in microgrids. Electronics 2021, 10, 1895. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, X.P.; Wang, J.; Li, J.; Wu, C.; Hu, M.; Bian, H. A review on electric vehicle charging infrastructure development in the UK. J. Mod. Power Syst. Clean Energy 2020, 8, 193–205. [Google Scholar] [CrossRef]
- Vagropoulos, S.I.; Balaskas, G.A.; Bakirtzis, A.G. An investigation of plug-in electric vehicle charging impact on power systems scheduling and energy costs. IEEE Trans. Power Syst. 2016, 32, 1902–1912. [Google Scholar] [CrossRef]
- Singh, A.K.; Pathak, M.K. Single-phase bidirectional ac/dc converter for plug-in electric vehicles with reduced conduction losses. IET Power Electron. 2018, 11, 140–148. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S.; Colicelli, A. Overview on battery charging systems for electric vehicles. Electronics 2023, 12, 4295. [Google Scholar] [CrossRef]
- Mastoi, M.S.; Zhuang, S.; Munir, H.M.; Haris, M.; Hassan, M.; Usman, M.; Bukhari, S.S.H.; Ro, J.S. An in-depth analysis of electric vehicle charging station infrastructure, policy implications, and future trends. Energy Rep. 2022, 8, 11504–11529. [Google Scholar] [CrossRef]
- Zhang, J.; Lai, J.S.; Kim, R.Y.; Yu, W. High-power density design of a soft-switching high-power bidirectional dc–dc converter. IEEE Trans. Power Electron. 2007, 22, 1145–1153. [Google Scholar] [CrossRef]
- Jalili, K.; Bernet, S. Design of LCL filters of active-front-end two-level voltage-source converters. IEEE Trans. Ind. Electron. 2009, 56, 1674–1689. [Google Scholar] [CrossRef]
- Zhou, Z. Unity Power Factor Active Rectifier and DC Bus Controller. Ph.D. Thesis, University of Sussex, Brighton, UK, 2003. [Google Scholar]
- Uppara, R.; Priya, S. Analysis of Interleaved Bidirectional DC/DC Converter for Battery Charging & Discharging Applications. In Proceedings of the 2024 International Conference on Smart Systems for applications in Electrical Sciences (ICSSES), Tumakuru, India, 3–4 May 2024; pp. 1–6. [Google Scholar]
- Singh, B.; Kushwaha, R. A PFC based EV battery charger using a bridgeless isolated SEPIC converter. IEEE Trans. Ind. Appl. 2019, 56, 477–487. [Google Scholar] [CrossRef]
- Ertekin, D. ARVIN converter: A bidirectional DC/DC converter for grid-connected G2V/V2G energy storage and electrification approaches. Electr. Eng. 2024, 106, 5485–5505. [Google Scholar] [CrossRef]
- Esfahani, A.G.; Adib, E. Very high step-down coupled inductor two-phase buck converter with single magnetic element and inherent clamp voltage capability. IET Power Electron. 2024, 17, 640–648. [Google Scholar] [CrossRef]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and control of an LCL-filter-based three-phase active rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Han, J.; Zhou, X.; Lu, S.; Zhao, P. A Three-Phase Bidirectional Grid-Connected AC/DC Converter for V2G Applications. J. Control Sci. Eng. 2020, 2020, 8844073. [Google Scholar] [CrossRef]
- Zmood, D.N.; Holmes, D.G. Stationary frame current regulation of PWM inverters with zero steady-state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar] [CrossRef]
- Golestan, S.; Freijedo, F.D.; Guerrero, J.M. A systematic approach to design high-order phase-locked loops. IEEE Trans. Power Electron. 2014, 30, 2885–2890. [Google Scholar] [CrossRef]
- Abdalgader, I.A.; Kivrak, S.; Özer, T. Power performance comparison of SiC-IGBT and Si-IGBT switches in a three-phase inverter for aircraft applications. Micromachines 2022, 13, 313. [Google Scholar] [CrossRef]
- Vishnuram, P.; Narayanamoorthi, R.; Suresh, P.; Vijayakumar, K.; Bajaj, M.; Khurshaid, T.; Nauman, A.; Kamel, S. A comprehensive review on EV power converter topologies charger types infrastructure and communication techniques. Front. Energy Res. 2023, 11, 1103093. [Google Scholar] [CrossRef]
- Umegami, H.; Harada, T.; Nakahara, K. Performance Comparison of Si IGBT and SiC MOSFET Power Module Driving IPMSM or IM under WLTC. World Electr. Veh. J. 2023, 14, 112. [Google Scholar] [CrossRef]
- Zheng, X.; Gao, F.; Ali, H.; Liu, H. A droop control based three phase bidirectional AC-DC converter for more electric aircraft applications. Energies 2017, 10, 400. [Google Scholar] [CrossRef]
- Mounica, V.; Obulesu, Y. A comprehensive review on non-isolated bidirectional dc-dc converter topologies for electric vehicle application. In Proceedings of the International Conference on Automation, Signal Processing, Instrumentation and Control, Vellore, India, 27–28 February 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 2097–2108. [Google Scholar]
- Prabhala, V.A.K.; Fajri, P.; Gouribhatla, V.S.P.; Baddipadiga, B.P.; Ferdowsi, M. A DC–DC converter with high voltage gain and two input boost stages. IEEE Trans. Power Electron. 2015, 31, 4206–4215. [Google Scholar] [CrossRef]
- Middlebrook, R.D.; Cuk, S. A general unified approach to modelling switching-converter power stages. In Proceedings of the 1976 IEEE Power Electronics Specialists Conference, Cleveland, OH, USA, 8–10 June 1976; pp. 18–34. [Google Scholar]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Qi, Q.; Ghaderi, D.; Guerrero, J.M. Sliding mode controller-based switched-capacitor-based high DC gain and low voltage stress DC-DC boost converter for photovoltaic applications. Int. J. Electr. Power Energy Syst. 2021, 125, 106496. [Google Scholar] [CrossRef]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics: Converters, Applications, and Design; John wiley & sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Beşkardeş, A.; Hameş, Y.; Kaya, K. A comprehensive review on fuzzy logic control systems for all, hybrid, and fuel cell electric vehicles. Soft Comput. 2024, 28, 8183–8221. [Google Scholar] [CrossRef]
- Hakam, Y.; Gaga, A.; Tabaa, M.; El Hadadi, B. Enhancing electric vehicle charger performance with synchronous boost and model predictive control for vehicle-to-grid integration. Energies 2024, 17, 1787. [Google Scholar] [CrossRef]
- Hao, X.; Chen, Y.; Wang, H.; Wang, H.; Meng, Y.; Gu, Q. A V2G-oriented reinforcement learning framework and empirical study for heterogeneous electric vehicle charging management. Sustain. Cities Soc. 2023, 89, 104345. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Saleh, R.A.; Akay, R. Artificial bee colony algorithm with directed scout. Soft Comput. 2021, 25, 13567–13593. [Google Scholar] [CrossRef]
- Khan, M.A.; Li, X.; Yousaf, M.Z.; Mustafa, A.; Wei, M. Metaheuristic Based Solution for the Non-Linear Controller of the Multiterminal High-Voltage Direct Current Networks. Energies 2021, 14, 1578. [Google Scholar] [CrossRef]
- Fathy, A.; Kassem, A.; Zaki, Z.A. A robust artificial bee colony-based load frequency control for hydro-thermal interconnected power system. Sustainability 2022, 14, 13569. [Google Scholar] [CrossRef]
- Mahboob Ul Hassan, S.; Ramli, M.A.; Milyani, A.H. Robust load frequency control of hybrid solar power systems using optimization techniques. Front. Energy Res. 2022, 10, 902776. [Google Scholar] [CrossRef]
- Singh, S.; Gao, D.W. Comparison amongst Lagrange, firefly, and ABC algorithms for low-noise economic dispatch and reactive power compensation in islanded microgrids. Energies 2023, 16, 5119. [Google Scholar] [CrossRef]
- IEEE Std 519-1992; IEEE Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems. Institute of Electrical and Electronics Engineers, Inc.: New York, NY, USA, 1993; p. 1.
- IEEE Std 519-2022 (Revision of IEEE Std 519-2014); IEEE Standard for Harmonic Control in Electric Power Systems. IEEE: New York, NY, USA, 2022; pp. 1–31. [CrossRef]
- Su, M.; Li, H.; Sun, Y.; Xiong, W. A high-efficiency bidirectional AC/DC topology for V2G applications. J. Power Electron. 2014, 14, 899–907. [Google Scholar] [CrossRef]
- Tasnim, M.N.; Ahmed, T.; Dorothi, M.A.; Ahmad, S.; Shafiullah, G.; Ferdous, S.; Mekhilef, S. Voltage-oriented control-based three-phase, three-leg bidirectional AC–DC converter with improved power quality for microgrids. Energies 2023, 16, 6188. [Google Scholar] [CrossRef]
- Hisar, C.; Balta, G.; Sefa, I.; Altin, N. Sliding Mode-Based Active Damping Control of LCL-Filtered Three-Phase PWM Rectifier. Arab. J. Sci. Eng. 2025, 50, 17845–17862. [Google Scholar] [CrossRef]
- Mayer, R.; El Kattel, M.B.; Oliveira, S.V.G. Multiphase interleaved bidirectional DC/DC converter with coupled inductor for electrified-vehicle applications. IEEE Trans. Power Electron. 2020, 36, 2533–2547. [Google Scholar] [CrossRef]
- Pan, T.; Wang, Y.; Qu, Z.; Tao, W. Topology optimisation and current sharing strategy of interleaved bidirectional dc/dc converter with coupling technique. IET Power Electron. 2018, 11, 2470–2480. [Google Scholar] [CrossRef]


| Research Focus | Key Advancements | Persistent Limitations |
|---|---|---|
| Power Topologies | Soft-switching converters [15], interleaved DC-DC designs [18], active front-end rectifiers [19], and advanced bidirectional DC-DC converters (e.g.,common-ground quadratic SEPIC [20] and coupled-inductor two-phase buck [21]) | Isolated component optimization; lack of co-design leading to DC-link stability issues during power flow transitions; limited exploration of system-level integration for novel high-gain topologies. |
| Grid Interface | LCL filter designs [16,22], harmonic mitigation techniques [23] | Performance analysis under idealized grid conditions, neglecting real-world transients and imbalances |
| Control Strategies | Cascaded PI control [17], voltage-oriented control(VOC) [24], synchronous reference frame phase-locked loops(SRF-PLL) [25] | Sluggish transient response; insufficient exploration of advanced, coordinated multi-loop tuning methods |
| System Integration | Bidirectional power flow capability [14], V2G service provision | Independent subsystem optimization; absence of a unified control framework addressing dynamic cross-stage interactions |
| Symbol | Description | Unit |
|---|---|---|
| Grid voltages (Phase-to-neutral voltages) | V | |
| Grid currents | A | |
| dq-axis components | A, V | |
| Grid line-to-line voltage | V | |
| Peak phase voltage | V | |
| Per-phase RMS voltagee | V | |
| Reference current values | A | |
| Feedforward control gain | – | |
| Grid frequency | Hz | |
| Grid source resistance | ||
| Equivalent grid inductance | H | |
| Grid-side inductance (LCL filter) | H | |
| Converter-side inductance (LCL filter) | H | |
| LCL filter capacitor | F | |
| Angular switching frequency | rad/s | |
| Switching frequency | Hz | |
| Current output from active rectifier (AR) | A | |
| Current output of AR after | A | |
| DC-link capacitor | F | |
| DC-link voltage (actual, reference) | V | |
| Phase inductance of Buck–Boost converter | H | |
| ESR of phase inductance | ||
| Battery current (from IBBC) | A | |
| Interleaving phase shift | ° | |
| Current in each phase of Buck–Boost | A | |
| Battery-side capacitor | F |
| Parameter | Value/Range |
|---|---|
| Colony size () | 20–50 |
| Number of parameters (D) | 6 |
| Maximum cycles () | 1000 |
| Abandonment limit () | |
| search range | [0, 10] |
| Random number (r) | [0, 1] |
| Objective function (J) | Weighted ISE + ITAE |
| Description | Parameter | Value | Description | Parameter | Value |
|---|---|---|---|---|---|
| System Specifications | |||||
| DC-link voltage | 700 V | Grid line-to-line voltage | 415 V | ||
| Grid frequency | 50 Hz | Per-phase RMS grid voltage | 239.6 V | ||
| Rated grid current | 400 A | Rated converter power | 41.5–45 kW | ||
| Battery voltage window | 415–450 V | Battery capacity | 38 Ah | ||
| Passive Components | |||||
| Conv.-side filter inductance | 0.112 mH | Grid-side inductance | 0.107 mH | ||
| Total filter inductance | 0.219 mH | Filter capacitor | 0.4465 mF | ||
| Damping resistor | 0.12 | DC-link capacitor | 95.5 mF | ||
| Interleaving phases | N | 4 | Per-phase inductor | 2 mH | |
| Inductor ESR | 2.5 | Low-side capacitor | 130 µF | ||
| High-side capacitor | 95.5 mF | Switching frequency | 10 kHz | ||
| Target ripple (design) | 40 A | LCL resonance frequency | 1.02 kHz | ||
| Analytical Controller Parameters | |||||
| Current PI (idc) | 0.7027 | 6.283 | |||
| DC-link PI (vdc) | 6.576 | 4131.8 | |||
| PLL gains | 0.555 | 43.2 | |||
| DC/DC PI gains | 0.00785 | 12.26 | |||
| ABC-Optimized Controller Parameters | |||||
| Current PI (idc) | 840.7 | 129.9 | |||
| DC-link PI (vdc) | 81.35 | 869.2 | |||
| PLL gains | 2.57 | 1.52 | |||
| ABC algorithm params | 20–50 | 1000 | |||
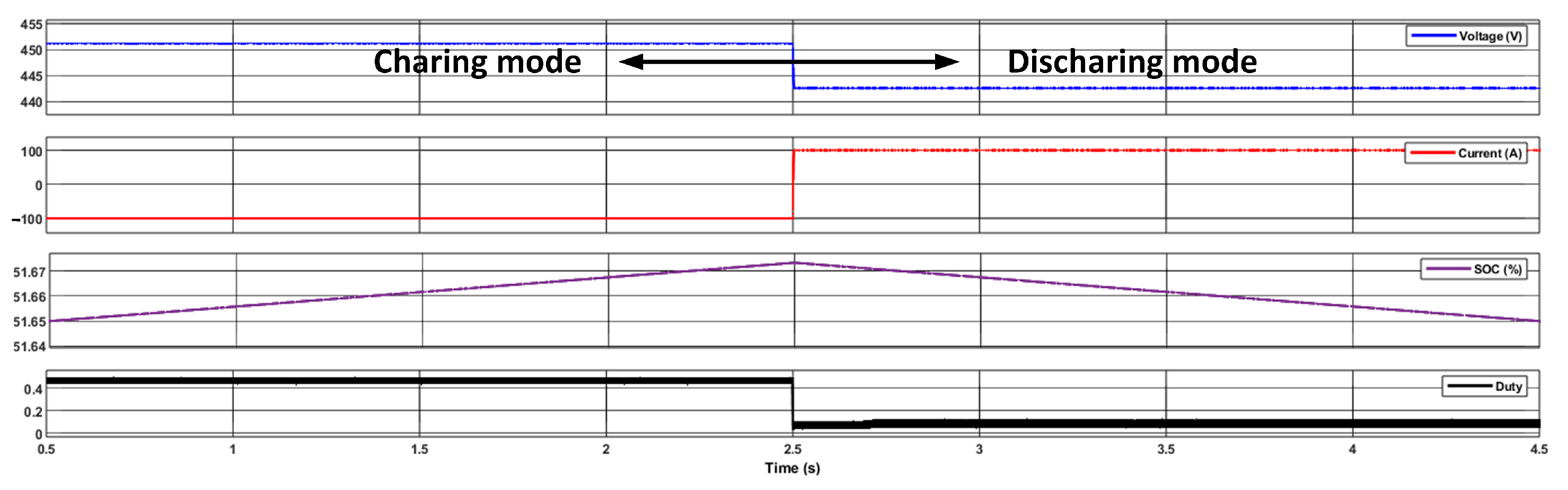
| Parameter | Charging | Discharging | Unit |
|---|---|---|---|
| Settling Time | 0.323 | 0.004292 | s |
| Battery mean voltage | 451.2 | 442.5 | V |
| Battery mean current | 100 | −100 | A |
| Battery power | 45,120 | 44,250 | W |
| Single phase mean Current | 25.03 | −24.84 | A |
| Single phase Current ripple | 6.516 | 8.625 | A |
| Battery Total Current ripple | 0.3269 | 0.554 | A |
| Overshoot Total Current | 0.695 | 0.944 | A |
| Efficiency | High | High |
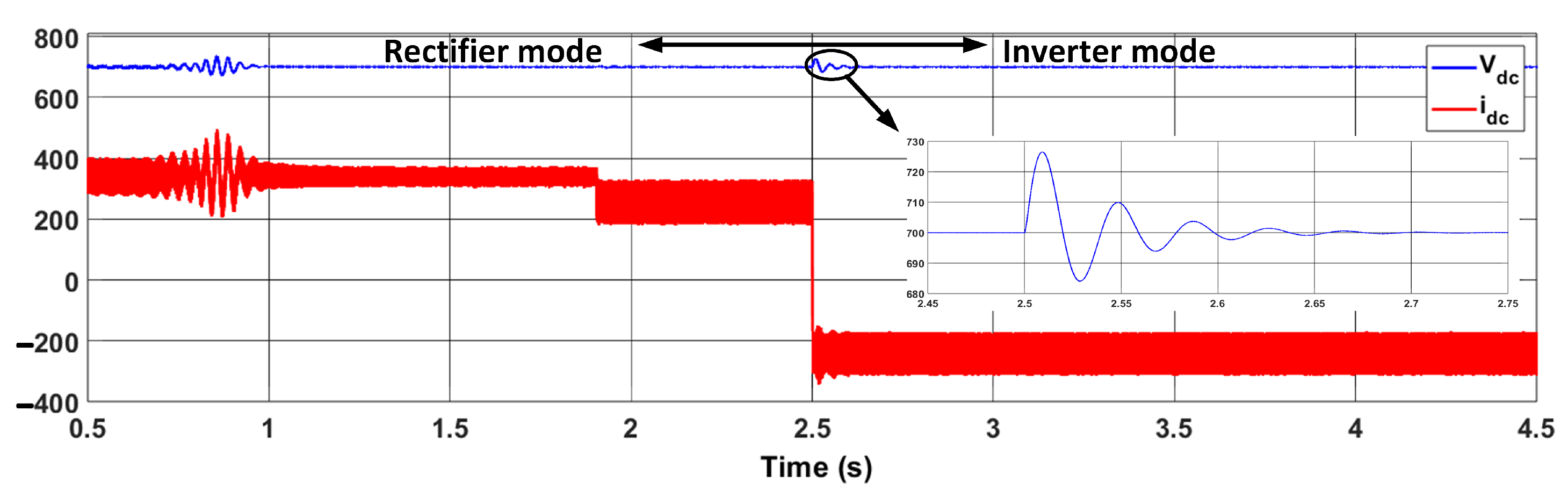
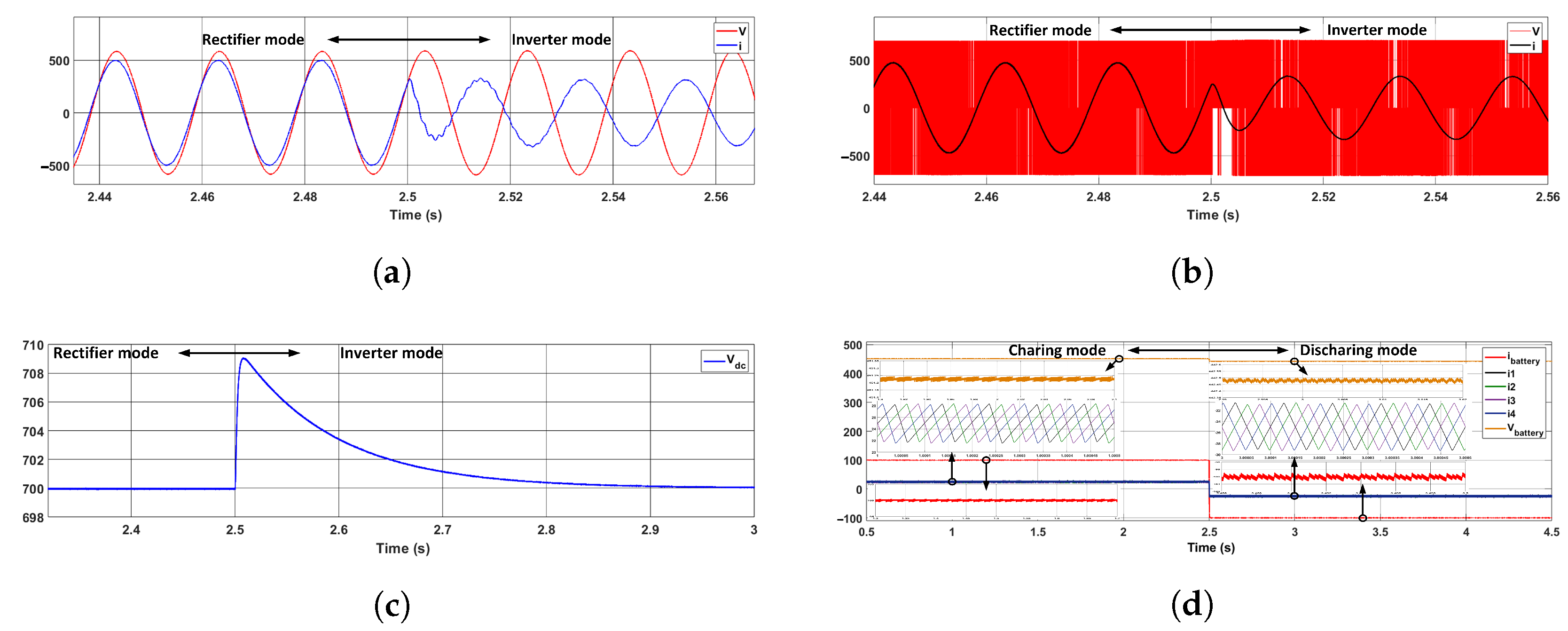
| Metric | Without Feedforward | With Feedforward | Unit | ||
|---|---|---|---|---|---|
| Charge | Discharge | Charge | Discharge | ||
| DC Link Voltage ripple | 0.2171 | 0.1787 | 0.2157 | 0.161 | V |
| Current THD | 1.77 | 0.49 | 1.63 | 0.48 | % |
| DC Link Voltage Overshoot | 138.17 | 3.70 | 138.14 | 3.67 | % |
| DC Link Voltage Undershoot | 71.71 | 2.30 | 71.43 | 2.33 | % |
| DC Link Settling time | 920 | 48.745 | 919 | 48.521 | ms |
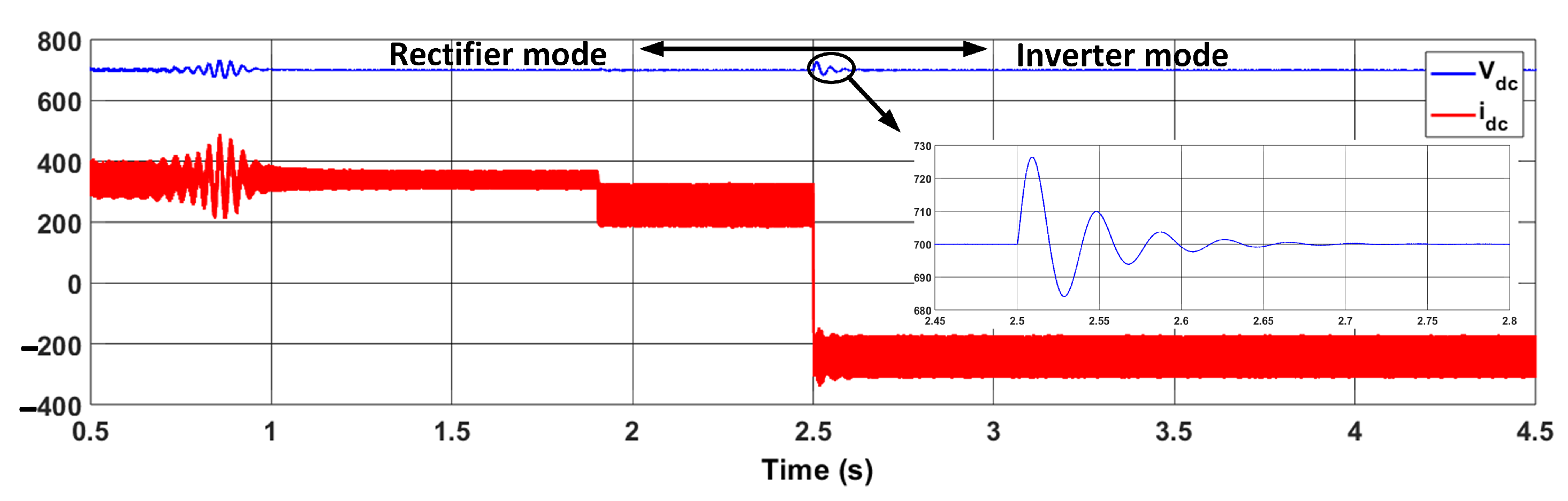
| Metric | Charge | Discharge | Unit |
|---|---|---|---|
| DC Link Voltage ripple | 0.2002 | 0.08224 | V |
| Current THD | 1.27 | 0.59 | % |
| DC Link Voltage Overshoot | 24.57 | 1.24 | % |
| DC Link Voltage Undershoot | 0 | 0 | % |
| DC Link Voltage Settling time | 238 | 0 | ms |
| Domain | Parameter | Charging Operation Mode | Discharging Operation Mode | Standard Limit/Target | Compliance | Reference/Note |
|---|---|---|---|---|---|---|
| Grid Interface | Current THD (Total) | 1.127% | 0.59% | ≤5% | Achieved | IEEE Std 519-2022 [45,46] |
| Current THD (Max. Phase) | 0.62% | 0.31% | ≤5% | Achieved | IEEE Std 519-2022 [45,46] | |
| Active Front-End (AFE) | DC-Link Voltage Ripple | 0.20 V | 0.08 V | <1% of (7 V) | Achieved | Typical stability target |
| DC-Link Overshoot (Transition) | 24.57% | 1.24% | <10% | Achieved | Industry best practice | |
| DC-Link Settling Time | 238 ms | ∼0 ms | <920 ms | Achieved | Improved control bandwidth | |
| Battery Interface | Battery Current Ripple | 0.33 A | 0.55 A | <1 A | Achieved | OEM target for battery longevity |
| System Operation | Switching Frequency | 10 kHz | 10 kHz | Design value | Achieved | Consistent with thermal and loss design |
| Performance Metric | Measured Value | Unit | Engineering Significance |
|---|---|---|---|
| DC-link voltage ripple (Charging/Discharging Operation Mode) | 0.20/0.08 | V | Minimizes DC-link capacitor stress and enhances system reliability |
| Grid current total harmonic distortion (THD) (Charging/Discharging Operation Mode) | 1.127/0.59 | % | Well below IEEE-519 limits, ensuring power quality compliance |
| Aggregated battery current ripple | 0.33/0.55 | A | Effective ripple cancellation, reducing battery stress and prolonging lifespan |
| Phase current sharing imbalance | <2% | — | Uniform thermal distribution, preventing localized overheating |
| Transient settling time (Charging Operation Mode) | 238 | ms | Rapid DC-link stabilization under dynamic conditions |
| Power factor (Charging/Discharging Operation Mode) | 1.0/1.0 | — | Optimal grid utilization with negligible reactive power |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haidar, A.; Macaulay, J.; Zhou, Z. Grid-Connected Bidirectional Off-Board Electric Vehicle Fast-Charging System. Energies 2025, 18, 5913. https://doi.org/10.3390/en18225913
Haidar A, Macaulay J, Zhou Z. Grid-Connected Bidirectional Off-Board Electric Vehicle Fast-Charging System. Energies. 2025; 18(22):5913. https://doi.org/10.3390/en18225913
Chicago/Turabian StyleHaidar, Abdullah, John Macaulay, and Zhongfu Zhou. 2025. "Grid-Connected Bidirectional Off-Board Electric Vehicle Fast-Charging System" Energies 18, no. 22: 5913. https://doi.org/10.3390/en18225913
APA StyleHaidar, A., Macaulay, J., & Zhou, Z. (2025). Grid-Connected Bidirectional Off-Board Electric Vehicle Fast-Charging System. Energies, 18(22), 5913. https://doi.org/10.3390/en18225913






