Generalized Lissajous Trajectory Image Learning for Multi-Load Series Arc Fault Detection in 220 V AC Systems Considering PV and Battery Storage
Abstract
1. Introduction
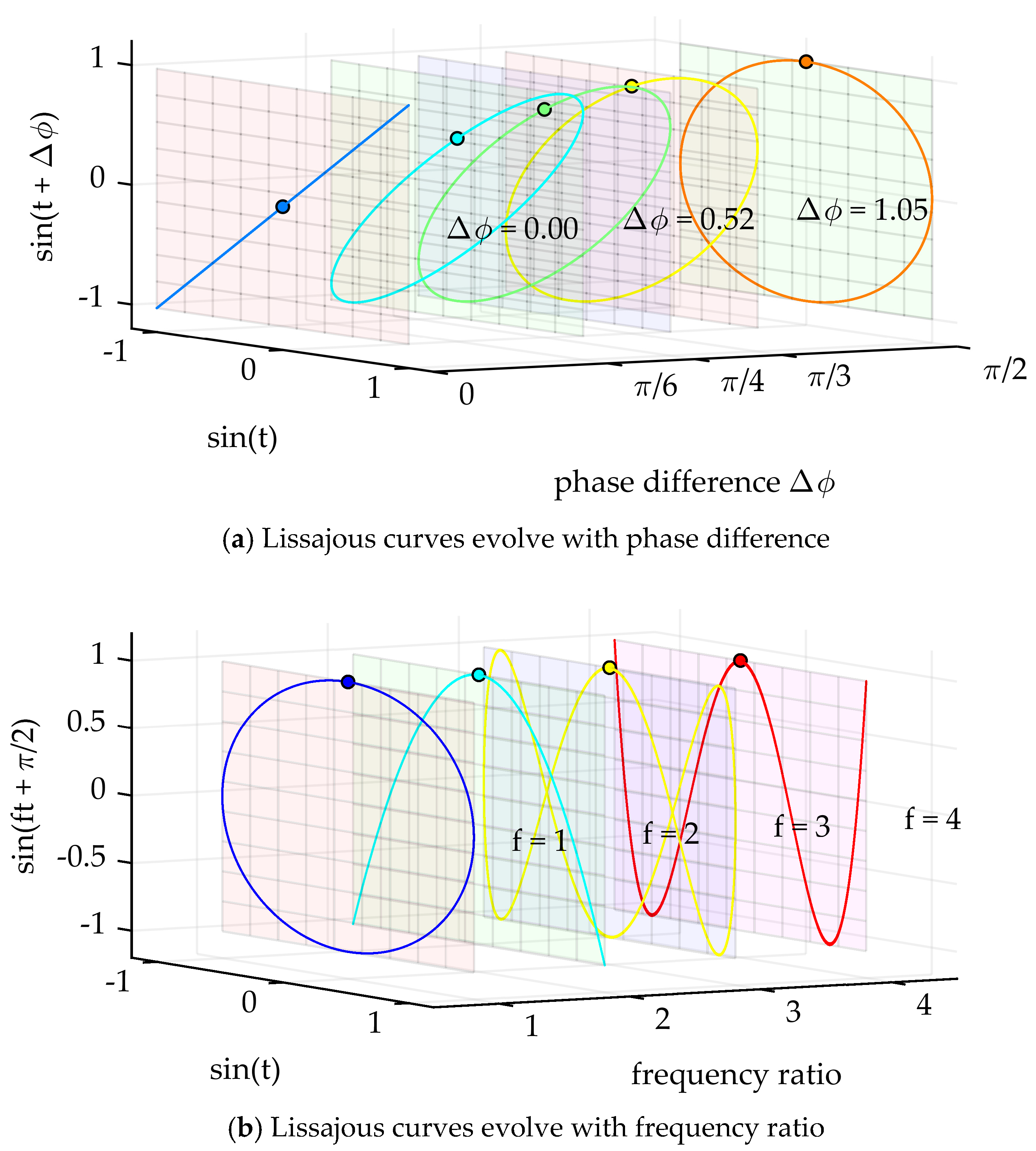
2. Generalized Lissajous Trajectory and Current Visualization
2.1. Generalized Lissajous Trajectory (GLT)
- (1)
- Signal dimension: Only a single channel of the time-domain signal is needed to generate trajectories.
- (2)
- Signal class: Compatible with non-simple harmonic periodic/quasi-periodic signals (e.g., current waveforms containing harmonic distortion, pulses, or zero-rest features), overcoming the limitations of the classical Lissajous for two-channel simple harmonic signals.
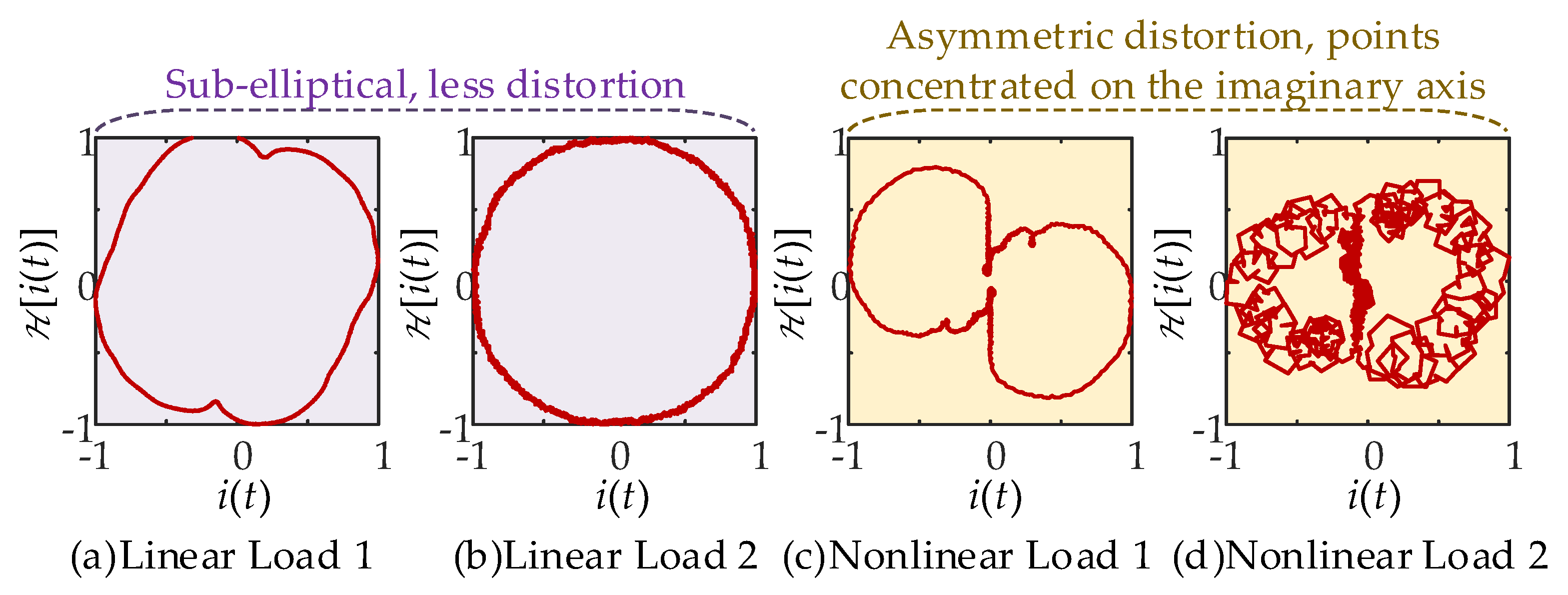
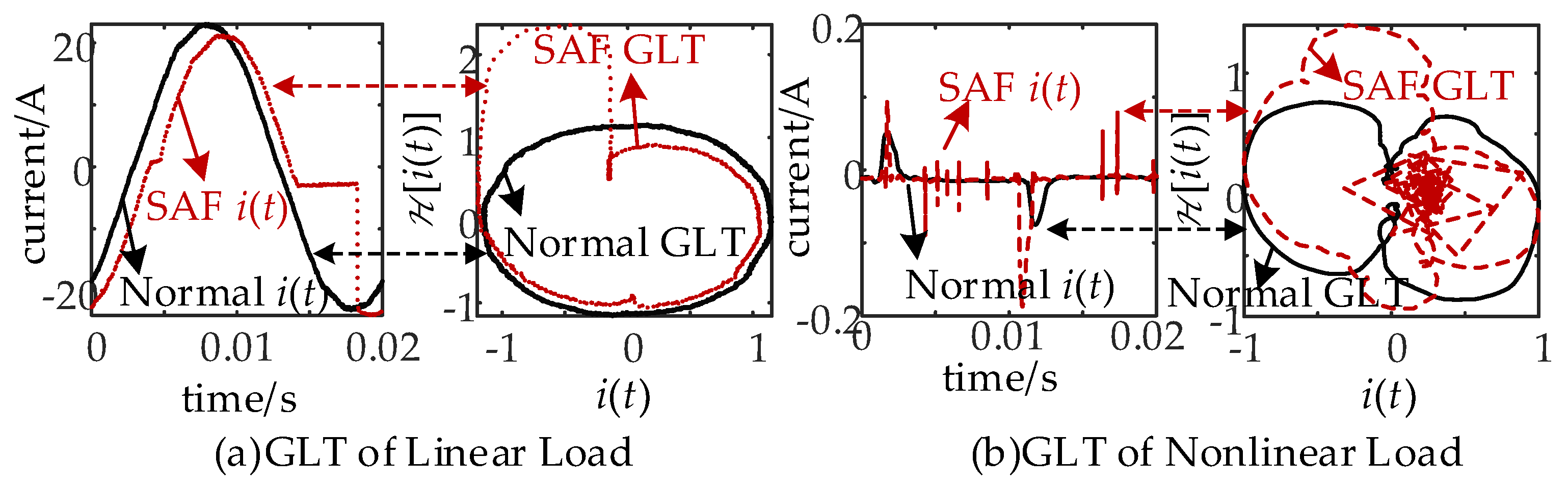
2.2. Characteristics of Current GLT Images
3. Arc Fault Experiment and Modeling of Fault Current
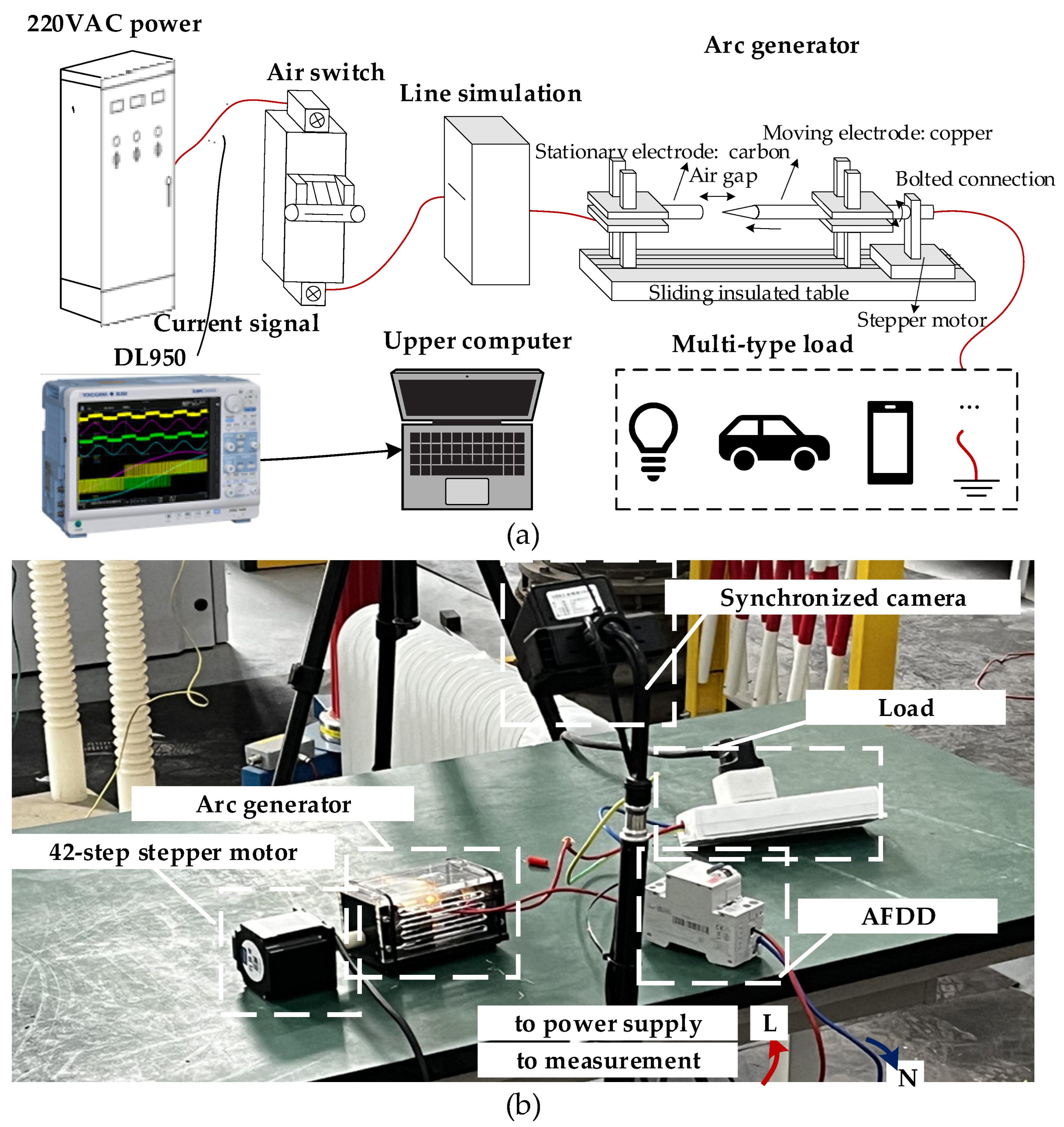
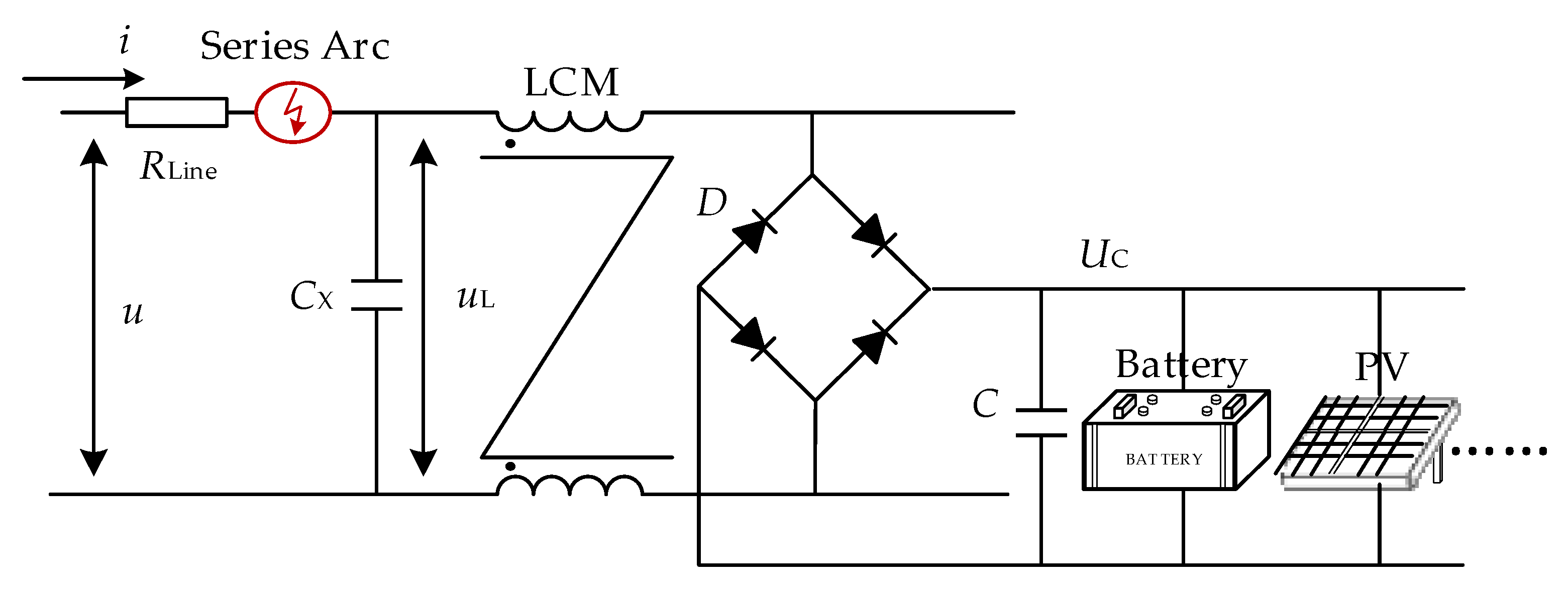
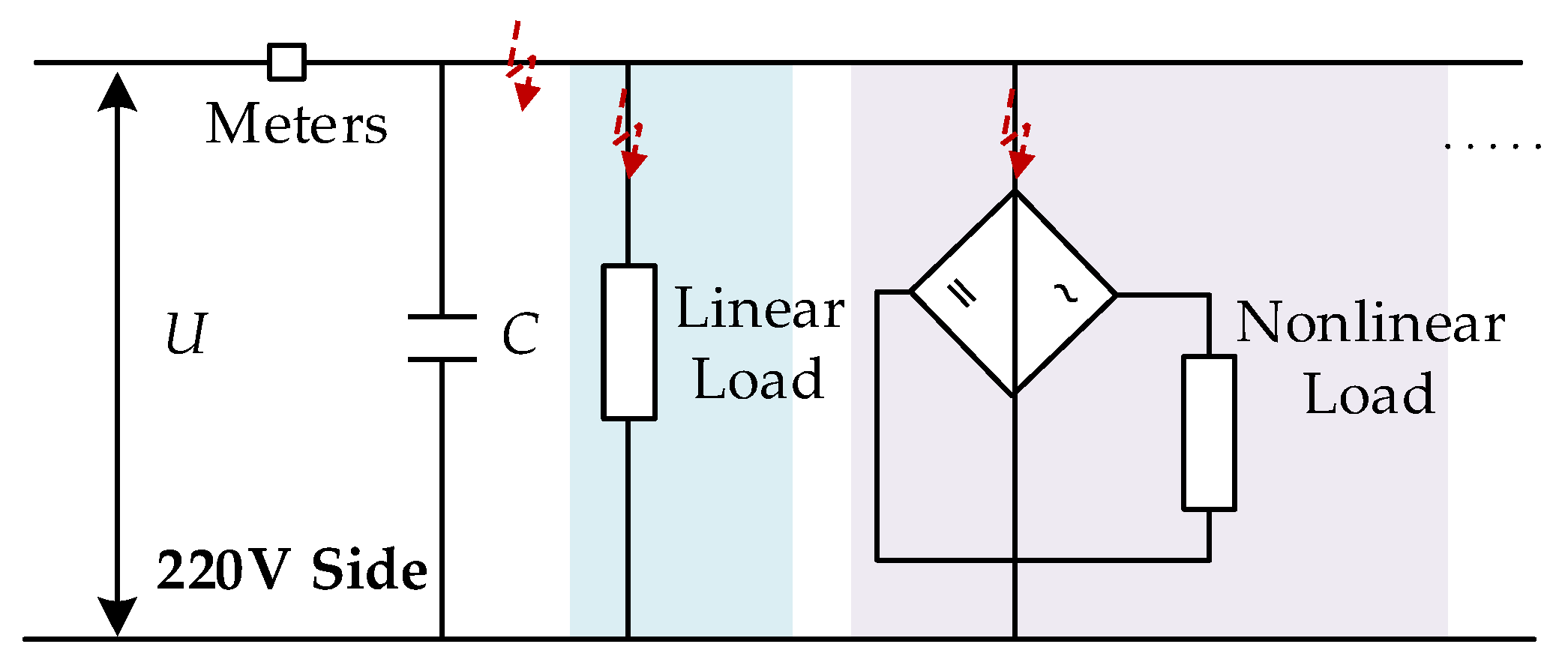
3.1. Arc Fault Experiment Platform Setup
3.1.1. Experimental Setup and Equipment Selection
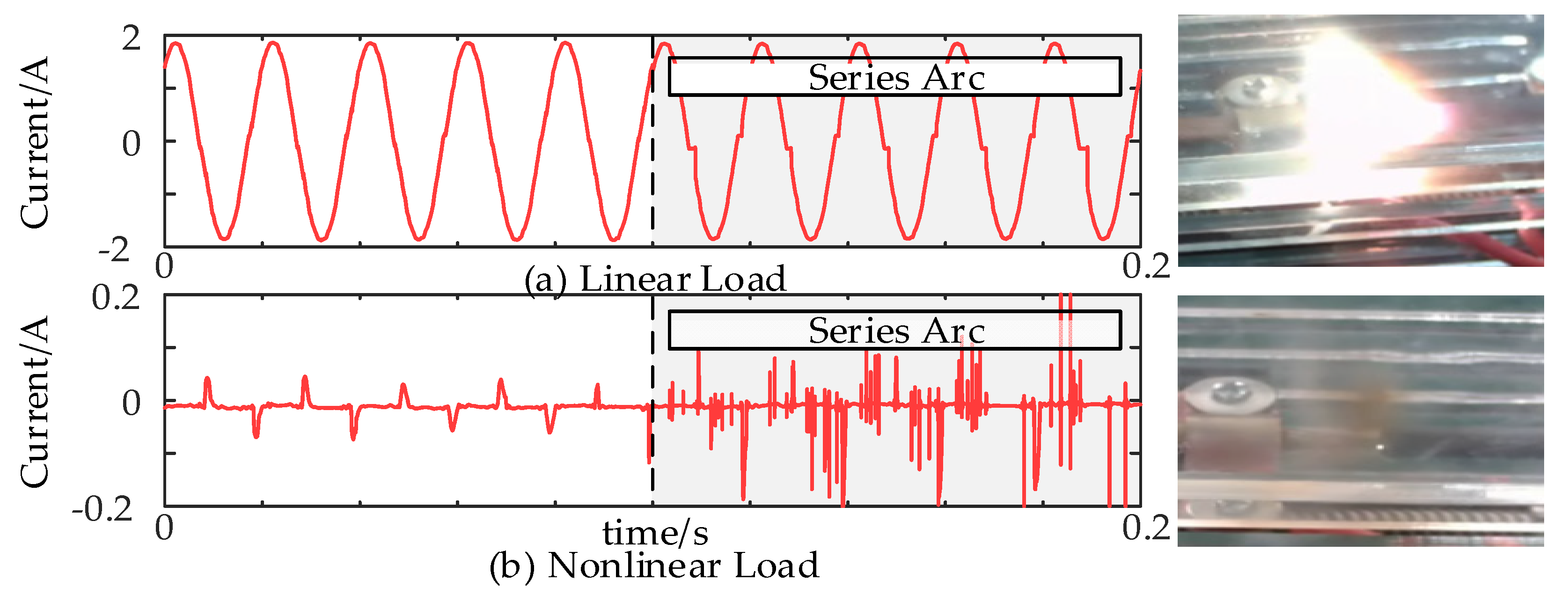
3.1.2. Arc Fault Current Measurement
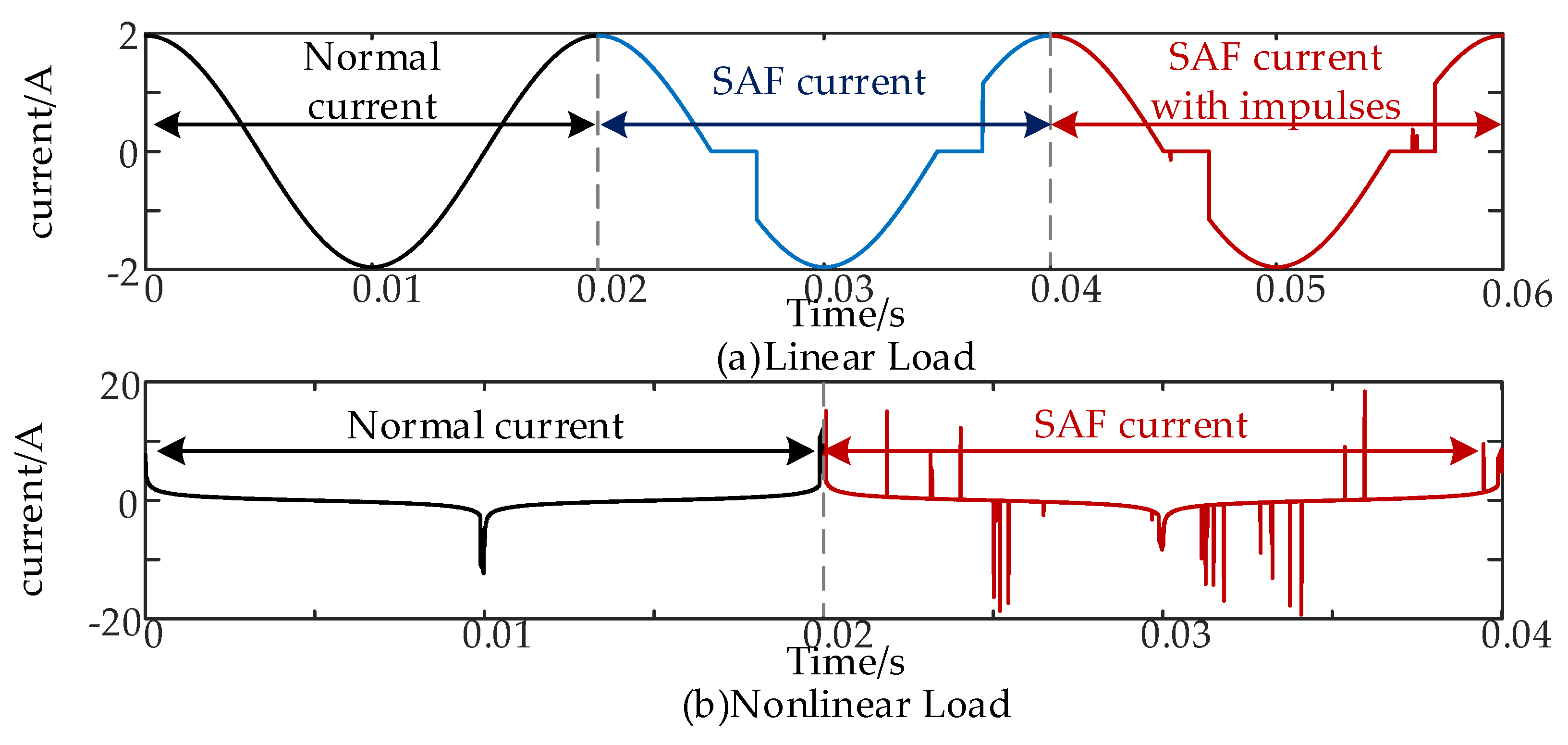
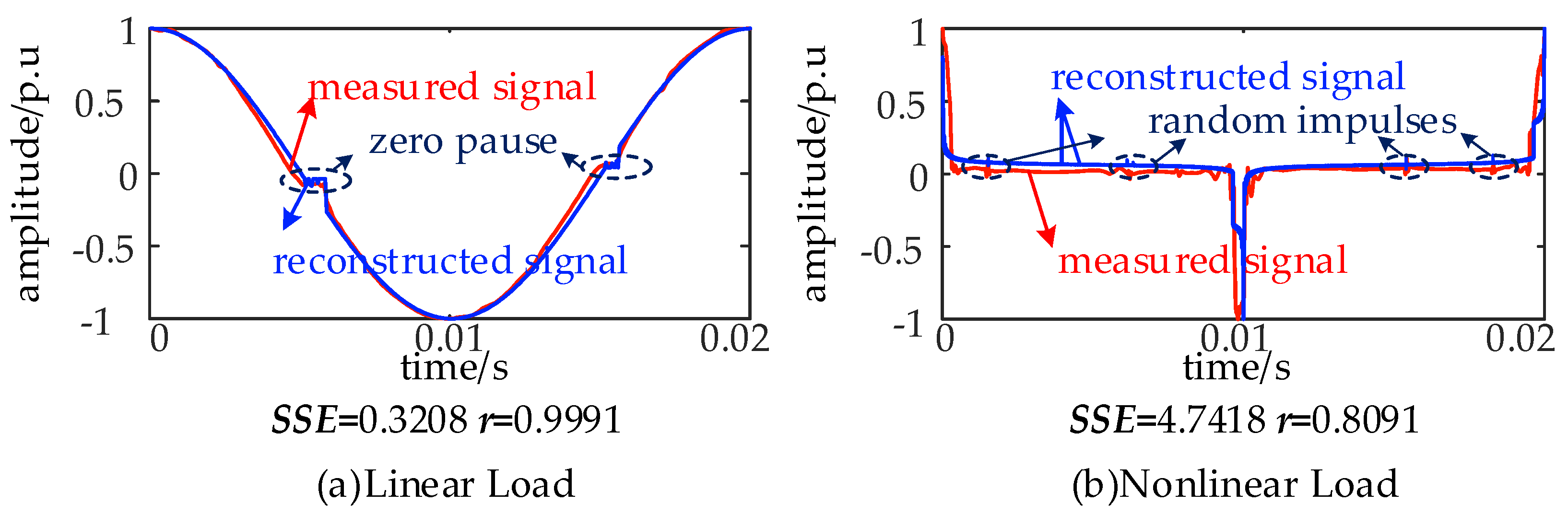
3.2. Modeling of Measured Fault Current
3.2.1. Analytical Mathematical Modeling of Two Different Types of Load Currents
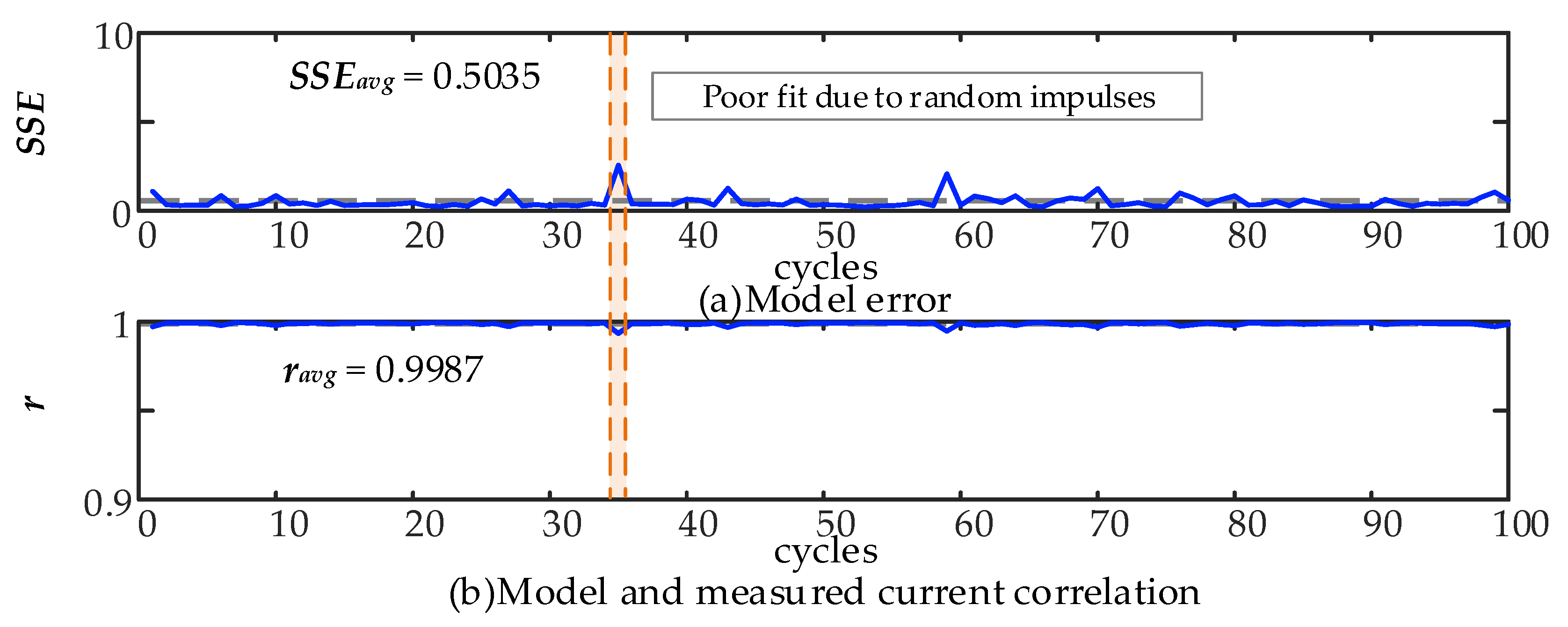
3.2.2. Particle Swarm Optimization to Verify Model Universality
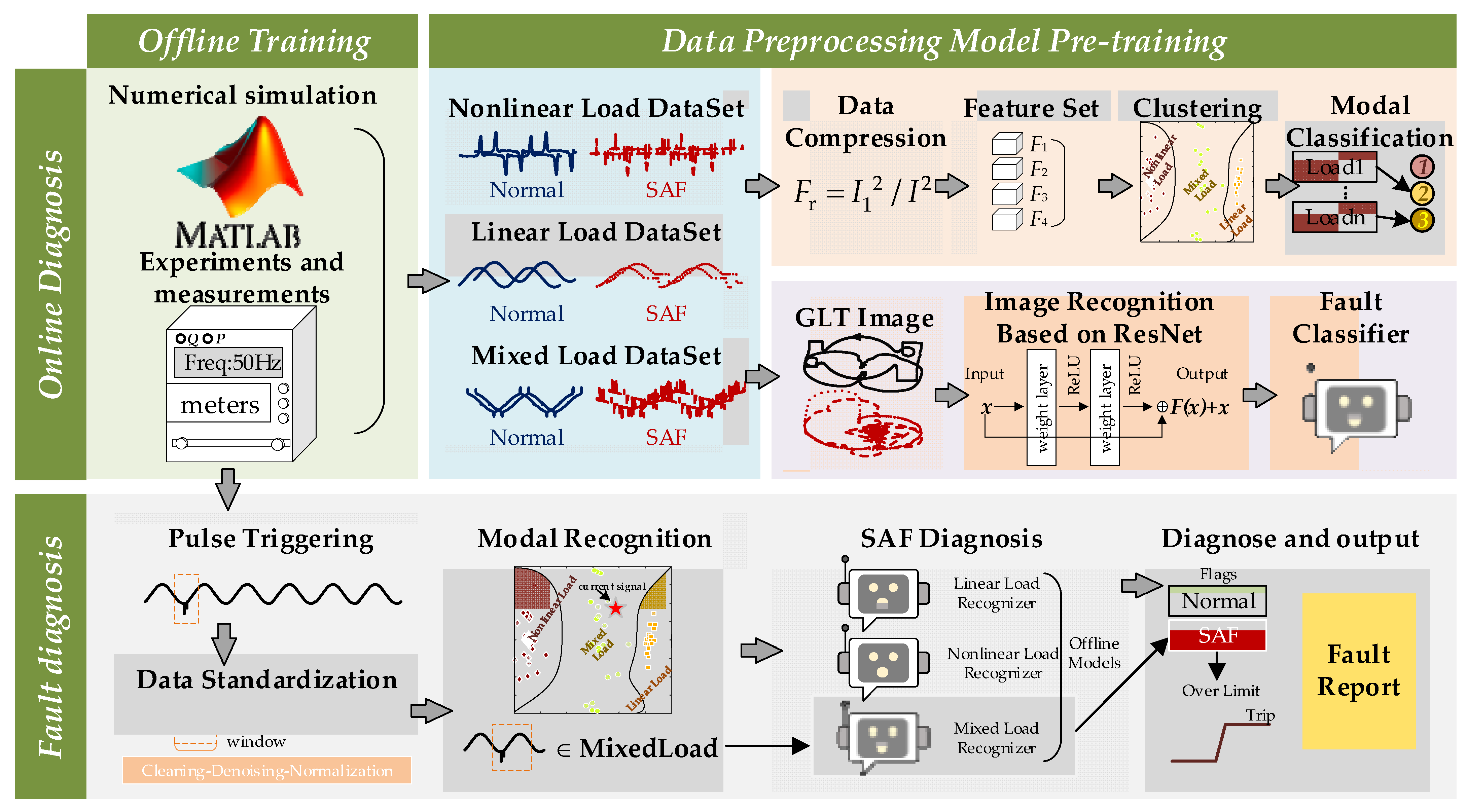
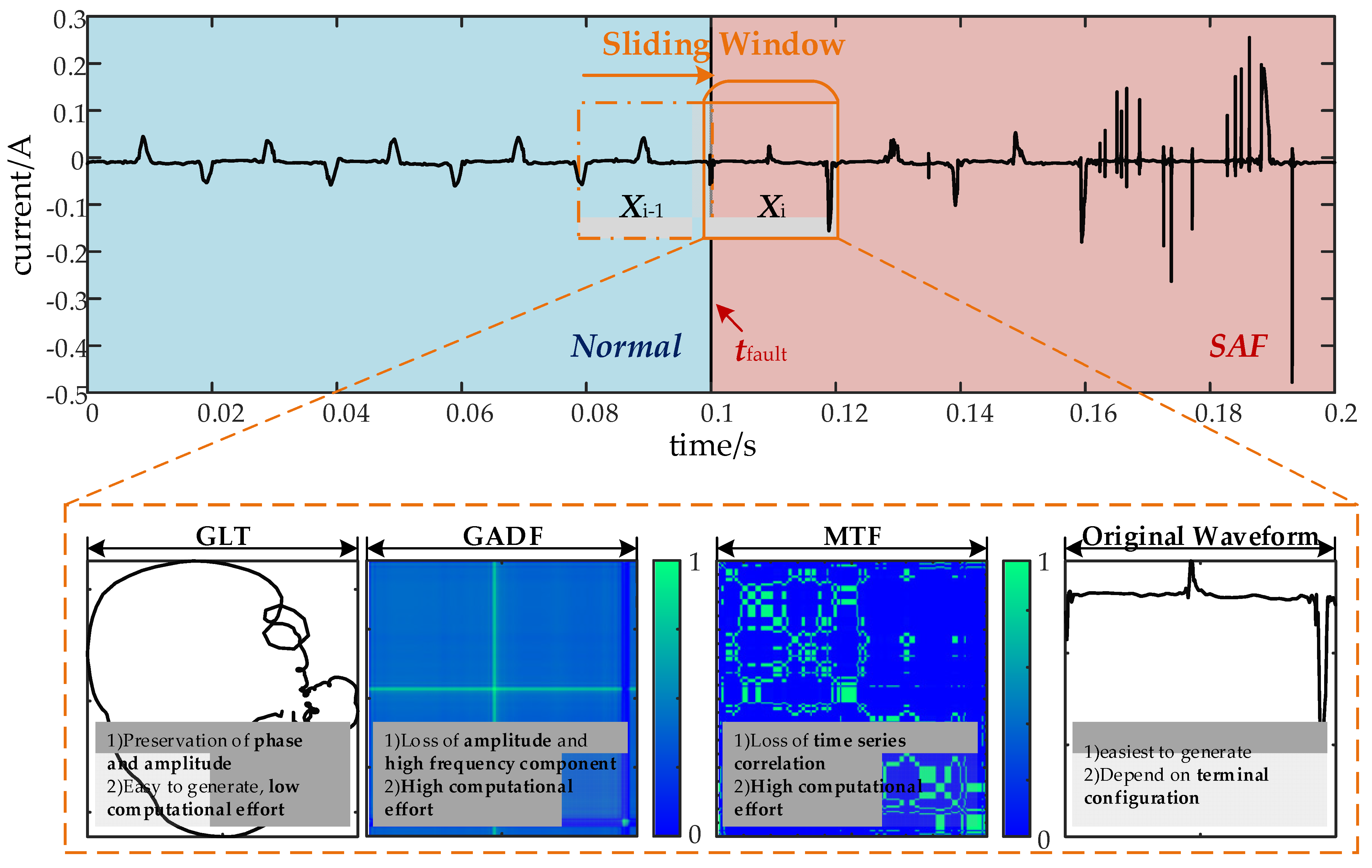
4. Proposed SAF-GLT Learning Methods
4.1. Sample Generation and Model Training
4.2. Load Modal Identification via K-Means Algorithm
4.3. Complete SAF-GLT Image-Based Detection Algorithm
5. Implementation Assessment and Method Analysis
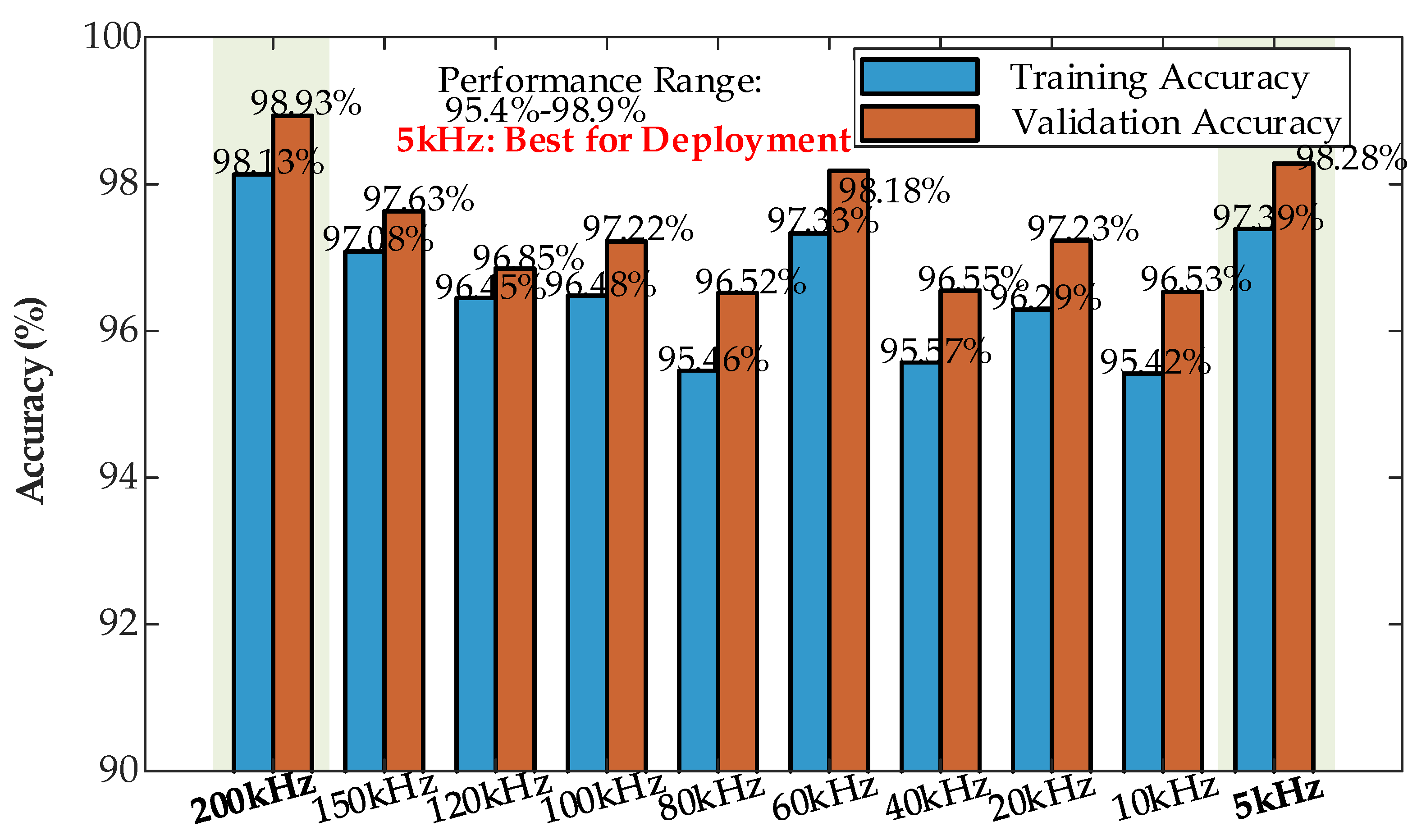
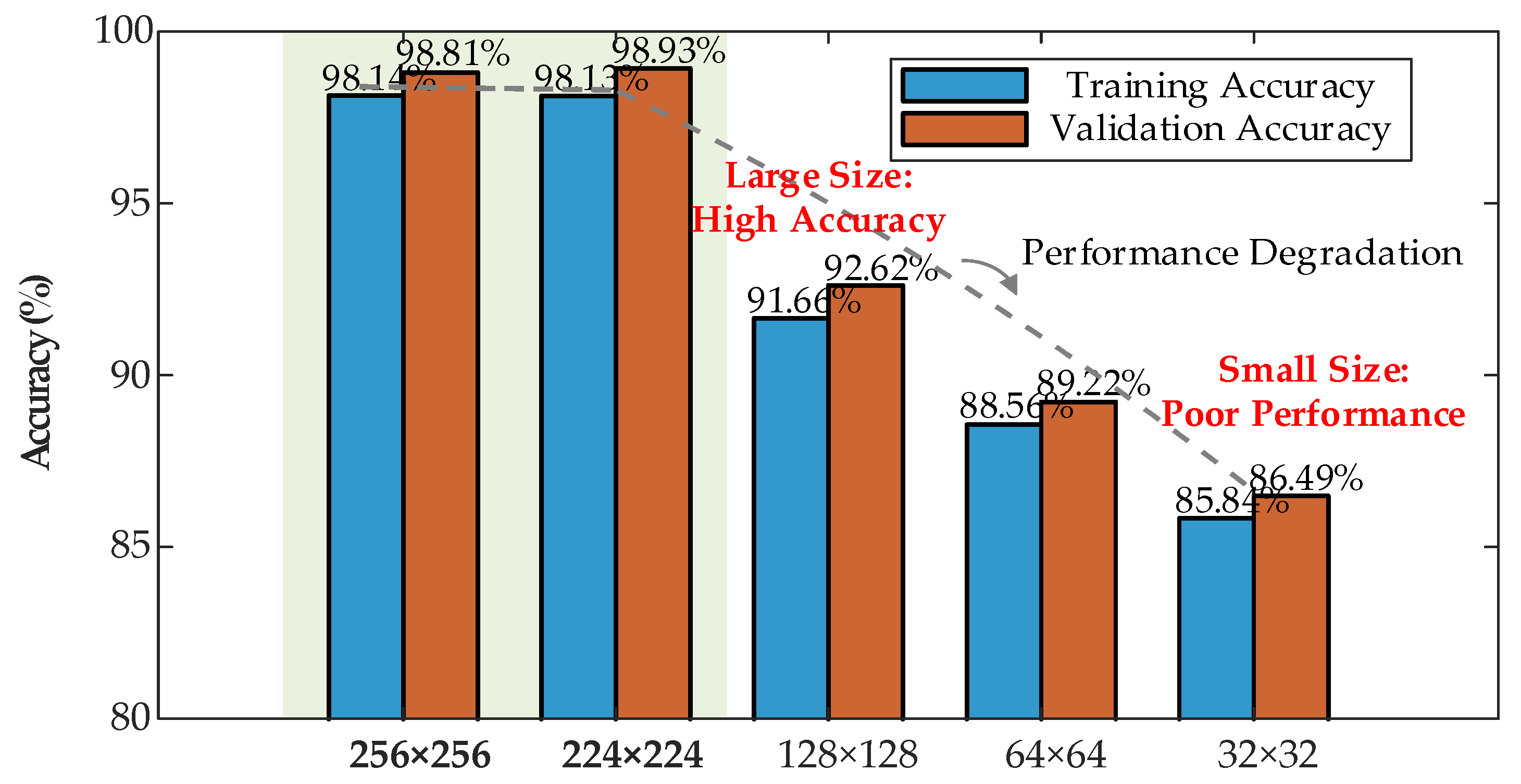
5.1. Sample Rate Sensitivity Analysis
5.2. Image Quality Compression Experiment Analysis
5.3. Trajectory Characterization Methods Comparison
5.4. Discussion and Future Work of Proposed Method
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SAF | Series Arc Fault |
| GLT | Generalized Lissajous Trajectory |
| ECG | Electrocardiogram |
| H transform | Hilbert Transform |
| PSO | Particle Swarm Optimization |
| SSE | Sum of Squares Due to Error |
| PV | Photovoltaic |
| ResNet | Residual Network |
References
- Paul, K.C.; Waldmann, D.; Chen, C.; Wang, Y.; Zhao, T. Artificial Intelligence for DC Arc Fault Detection in Photovoltaic Systems: A Comprehensive Review. IEEE Access 2025, 13, 90766–90794. [Google Scholar] [CrossRef]
- KIM, C.J. Electromagnetic radiation behavior of low voltage arcing fault. IEEE Trans. Power Deliv. 2009, 24, 416–423. [Google Scholar] [CrossRef]
- Mamis, M.S.; Meral, M.E. State-space modeling and analysis of fault arcs. Electr. Power Syst. Res. 2005, 76, 46–51. [Google Scholar] [CrossRef]
- Lee, D.; Kim, J. Empirical Modeling of Arc Faults Based on Recent Experimental Data and Field Studies. IEEE Trans. Ind. Electron. 2024, 71, 7942–7953. [Google Scholar]
- Sidhu, T.S.; Sagoo, G.S.; Sachdev, M.S. Multisensor secondary device for detection of low-level arcing faults in metal-clad MCC switchgear panel. IEEE Trans. Power Deliv. 2002, 17, 129–134. [Google Scholar] [CrossRef]
- Kizilcay, M.; Koch, K.H. Numerical fault arc simulation based on power arc tests. Euro. Trans. Electr. Power 1994, 4, 177–185. [Google Scholar] [CrossRef]
- Andrea, J.; Schweitzer, P.; Tisserand, E. A new DC and AC arc fault electrical model. In Proceedings of the 56th IEEE Holm Conference on Electrical Contacts, Charleston, SC, USA, 4–7 October 2010; pp. 1–6. [Google Scholar]
- Schavemaker, P.H.; Vander, S.L. An improved Mayr-type arc model based on current-zero measurements [circuit breakers]. IEEE Trans. Power Deliv. 2000, 15, 580–584. [Google Scholar] [CrossRef]
- Hooshmand, R.A.; Banejad, M.; Esfahani, M.T. A new time model domain model for electric arc furnace. J. Electr. Eng. 2008, 59, 195–202. [Google Scholar]
- Yao, X.; Herrera, L.; Huang, Y.; Wang, J. The detection of DC arc fault: Experimental study and fault recognition. In Proceedings of the APEC on 27th Annual IEEE, Orlando, FL, USA, 5–9 February 2012; IEEE: New York, NY, USA, 2012; pp. 1720–1727. [Google Scholar]
- Tisserand, E.; Lezama, J.; Schweitzer, P.; Berviller, Y. Series arcing detection by algebraic derivative of the current. Electr. Power Syst. Res. 2015, 119, 91–99. [Google Scholar] [CrossRef]
- Lee, W.-J.; Sahni, M.; Methaprayoon, K.; Kwan, C.; Ren, Z.; Sheeley, J.M. A novel approach for arcing fault detection for medium-/low-voltage switchgear. IEEE Trans. Ind. Appl. 2009, 45, 1475–1483. [Google Scholar]
- Lai, T.M.; Lo, W.C.; To, W.M.; Lam, K. RMS percent of wavelet transform for the detection of stochastic high impedance faults. In Proceedings of the 2012 IEEE 15th International Conference on Harmonics and Quality of Power, Hong Kong, China, 17–20 June 2012; pp. 823–828. [Google Scholar]
- Yang, G.; Li, T.; Zhang, X. Review of Arc Fault Detection Methods and the Application of Mayr Model in Electrical Arc Fault Detection. IEEE Trans. Power Electron. 2024, 39, 5398–5410. [Google Scholar]
- He, X.; Kawaguchi, T.; Hashimoto, S. Intelligent Identification Method of Low Voltage AC Series Arc Fault Based on Using Residual Model and Rime Optimization Algorithm. Energies 2024, 17, 4675. [Google Scholar] [CrossRef]
- Paul, K.C.; Zhou, J.L.; Chen, S.-E.; Zhao, T. PV Arc Fault Circuit Interrupter with Knowledge Distillation-Based Lightweight Convolutional Neural Network and SSCB Integration. IEEE Trans. Power Electron. 2025, 40, 18189–18201. [Google Scholar] [CrossRef]
- Dai, W.X.; Zhou, X.; Sun, Z.G.; Zhai, G. Series AC arc fault detection method based on spectrogram and deep residual network. Microelectron. Reliab. 2025, 170, 115756. [Google Scholar] [CrossRef]
- Jiang, J.; Wen, Z.; Zhao, M.; Bie, Y.; Li, C.; Tan, M.; Zhang, C. Series arc detection and complex load recognition based on principal component analysis and support vector machine. IEEE Access 2019, 7, 47221–47229. [Google Scholar] [CrossRef]
- Shang, T.; Wang, W.; Peng, J.; Xu, B.; Gao, H.; Zhai, G. Series arc fault identification based on complete ensemble empirical mode decomposition with adaptive noise and convolutional neural network. Int. J. Metrol. Qual. Eng. 2022, 13, 11. [Google Scholar] [CrossRef]
- Gong, Q.; Peng, K.; Gao, Q.; Feng, L.; Xiao, C. Series arc fault identification method based on wavelet transform and feature values decomposition fusion DNN. Electr. Power Syst. Res. 2023, 221, 109391. [Google Scholar] [CrossRef]
- Wu, C.J.; Liu, Y.W. Smart detection technology of serial arc fault on low-voltage indoor power lines. Int. J. Eletr. Power 2015, 69, 391–398. [Google Scholar] [CrossRef]
- Qi, P.; Jovanovic, S.; Lezama, J.; Schweitzer, P. Discrete wavelet transform optimal parameters estimation for arc fault detection in low-voltage residential power networks. Electr. Power Syst. Res. 2017, 143, 130–139. [Google Scholar] [CrossRef]
- Jiang, R.; Zheng, Y. Series Arc Fault Detection Using Regular Signals and Time-Series Reconstruction. IEEE Trans. Ind. Electron. 2023, 70, 2026–2036. [Google Scholar] [CrossRef]
- Yang, K.; Chu, R.; Zhang, R.; Xiao, J.; Tu, R. A Novel Methodology for Series Arc Fault Detection by Temporal Domain Visualization and Convolutional Neural Network. Sensors 2020, 20, 162. [Google Scholar] [CrossRef]
- Dai, W.; Zhou, X.; Sun, Z.; Miao, Q.; Zhai, G. Series AC Arc Fault Detection Method Based on L2/L1 Norm and Classification Algorithm. IEEE Sens. J. 2024, 24, 16661–16672. [Google Scholar] [CrossRef]
- Denis, S.; Angela, D.; Cornel, I.; Alexandru, S. A Novel Approach for Characterization of Transient Signals Using the Phase Diagram Features. In Proceedings of the 2021 IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS), Tel Aviv, Israel, 1–3 November 2021; pp. 299–304. [Google Scholar]
- Denis, S.; Angela, D.; Cornel, I.; Alexandru, S. Transient power grid phenomena classification based on phase diagram features and machine learning classifiers. In Proceedings of the 2022 30th European Signal Processing Conference (EUSIPCO), Belgrade, Serbia, 29 August–2 September 2022; pp. 1676–1680. [Google Scholar]
- Koziy, K.; Gou, B.; Aslakson, J. A Low-Cost Power-Quality Meter with Series Arc-Fault Detection Capability for Smart Grid. IEEE Trans. Power Deliv. 2013, 28, 1584–1591. [Google Scholar] [CrossRef]
- Jiang, J.; Li, W.; Wen, Z.; Bie, Y.; Schwarz, H.; Zhang, C. Series Arc Fault Detection Based on Random Forest and Deep Neural Network. IEEE Sens. J. 2021, 21, 17171–17179. [Google Scholar] [CrossRef]
- Jia, C.; Li, Z.; Zhang, Y.; Cao, J.; Chen, H.; Zhao, X.; Du, Y.; Cheng, Q.S.; Ma, N.; Qiu, F. Serial Arc-Fault Restriction Survey with Standard-Listed Products in the Chinese Market. IEEE Trans. Ind. Appl. 2023, 59, 7453–7461. [Google Scholar] [CrossRef]
- Izadi, M.; Mohsenian-Rad, H. A Synchronized Lissajous-Based Method to Detect and Classify Events in Synchro-Waveform Measurements in Power Distribution Networks. IEEE Trans. Smart Grid 2022, 13, 2170–2184. [Google Scholar] [CrossRef]
- Karacor, D.; Nazlibilek, S.; Sazli, M.H.; Akarsu, E.S. Discrete Lissajous Figures and Applications. IEEE Trans. Instrum. Meas. 2014, 63, 2963–2972. [Google Scholar] [CrossRef]
- Underwriters Laboratories Inc. UL Standard for Arc-Fault Circuit-Interrupters, 2nd ed.; Underwriters Laboratories Inc.: New York, NY, USA, 2011. [Google Scholar]
- GB 14287.4-2014; Electrical Fire Monitoring System—Part 4: Arcing Fault Detectors. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China & Standardization Administration of the People’s Republic of China (published by Standards Press of China): Beijing, China, 2014.
- Wang, Y.; Zhang, F.; Zhang, X.; Zhang, S. Series AC Arc Fault Detection Method Based on Hybrid Time and Frequency Analysis and Fully Connected Neural Network. IEEE Trans. Ind. Inf. 2019, 15, 6210–6219. [Google Scholar] [CrossRef]
- Li, Y.; Amari, S.; Cichocki, A.; Ho, D.; Xie, S. Underdetermined blind source separation based on sparse representation. IEEE Trans. Signal Process 2006, 54, 423–437. [Google Scholar]
- Liu, H.; Li, J.; Wang, W.; Lu, S. Arc-1DCNN: An enhanced model for series arc fault detection. Measurement 2024, 234, 114814. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.; Xiao, W.; Zhang, S.; Xiao, X. Identification of electrical breakdown faults in shunt capacitor bank elements using instantaneous negative sequence current. Int. J. Eletr. Power 2025, 170, 110962. [Google Scholar] [CrossRef]
- Shi, L.; Weng, Y.; Cui, Q.; Zheng, X.; Li, W.; Li, J. Intrinsic and Extrinsic Learning Framework for Multi-Equipment Incipient Fault Detection and Classification. IEEE Trans. Ind. Appl. 2025, 61, 1511–1522. [Google Scholar] [CrossRef]
- Shi, L.; Cui, Q.; Weng, Y.; Zhang, Y.; Chen, S.; Li, J.; Li, W. Learning Power Systems Waveform Incipient Patterns Through Few-Shot Meta-Learning. IEEE Open Access J. Power Energy 2024, 11, 532–545. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
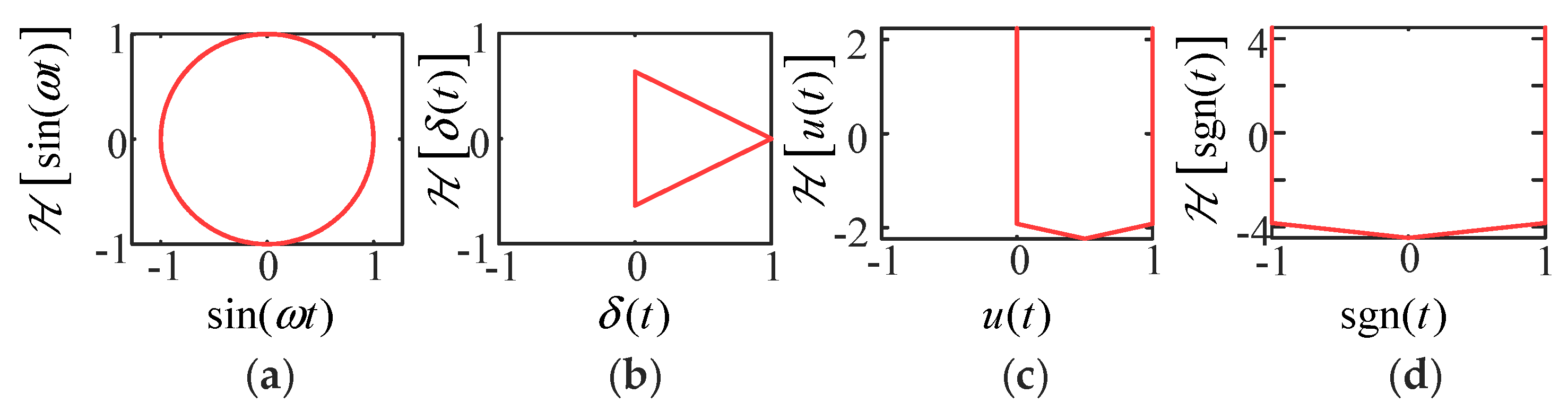

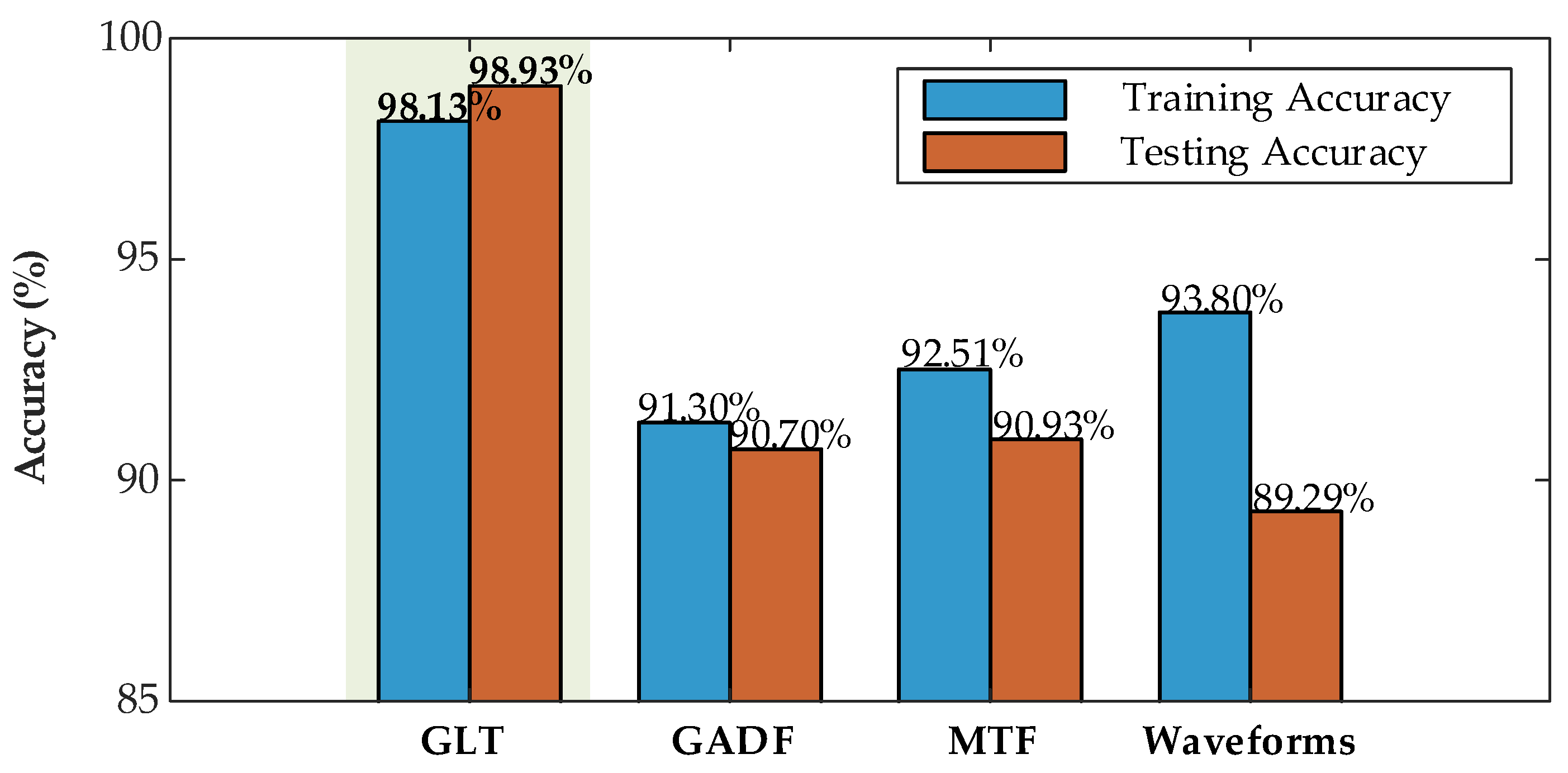
| Original Signal | Imaginary Part | Analysis Signal |
|---|---|---|
| Fault Condition | Configuration 1 | SNR (dB) | Sample Size | |
|---|---|---|---|---|
| SAF | linear load | 25, 35, 50 | 30,000 each | |
| nonlinear load | ||||
| mixed load | ||||
| trouble-free | linear load | |||
| nonlinear load | ||||
| mixed load | ||||
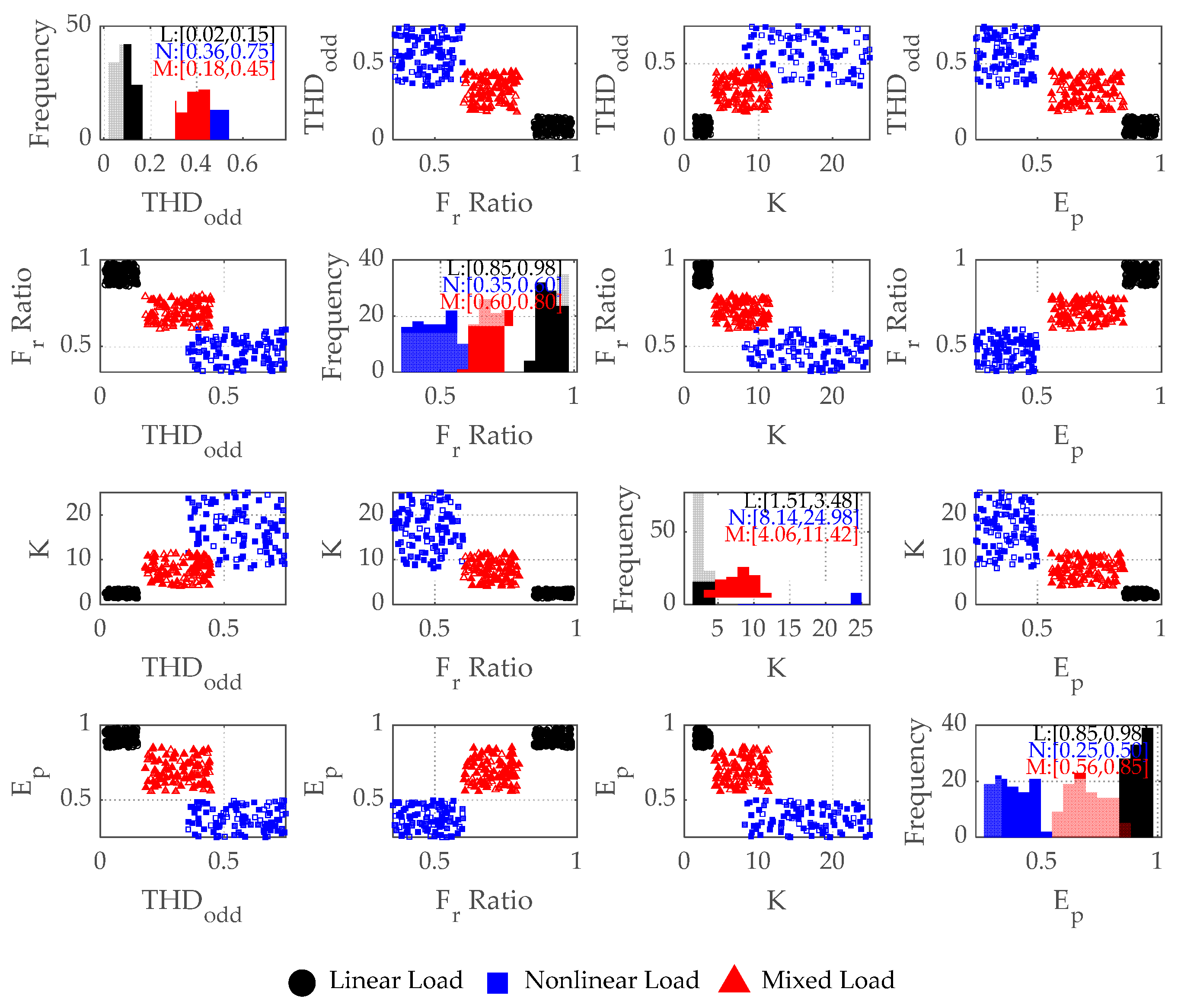
| Feature Type | Formula | Physical Meaning | |
|---|---|---|---|
| Frequency Domain | Odd Harmonic Distortion Ratio | Odd harmonics dominate in nonlinear loads | |
| Fundamental Ratio | Load energy concentration | ||
| Time Domain | Kurtosis | Current pulse sharpness | |
| Trajectory | Ellipticity | Degree to which the trajectory is nearly elliptical | |
| Different Sample Sets | Acctrain | Accval | Preval | Recallval | F1val | |
|---|---|---|---|---|---|---|
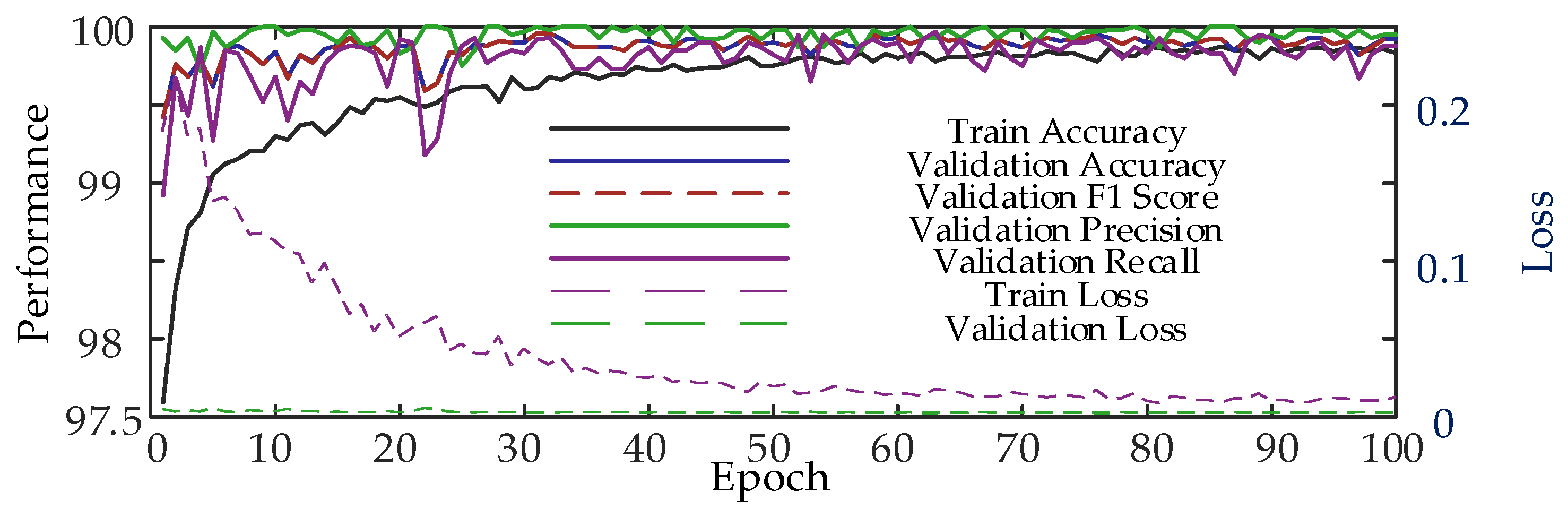
| Specific conditions for training | Linear Load | 99.83% | 99.81% | 99.95% | 99.88% | 99.92% |
| Nonlinear Load | 98.13% | 98.93% | 98.72% | 99.15% | 98.94% | |
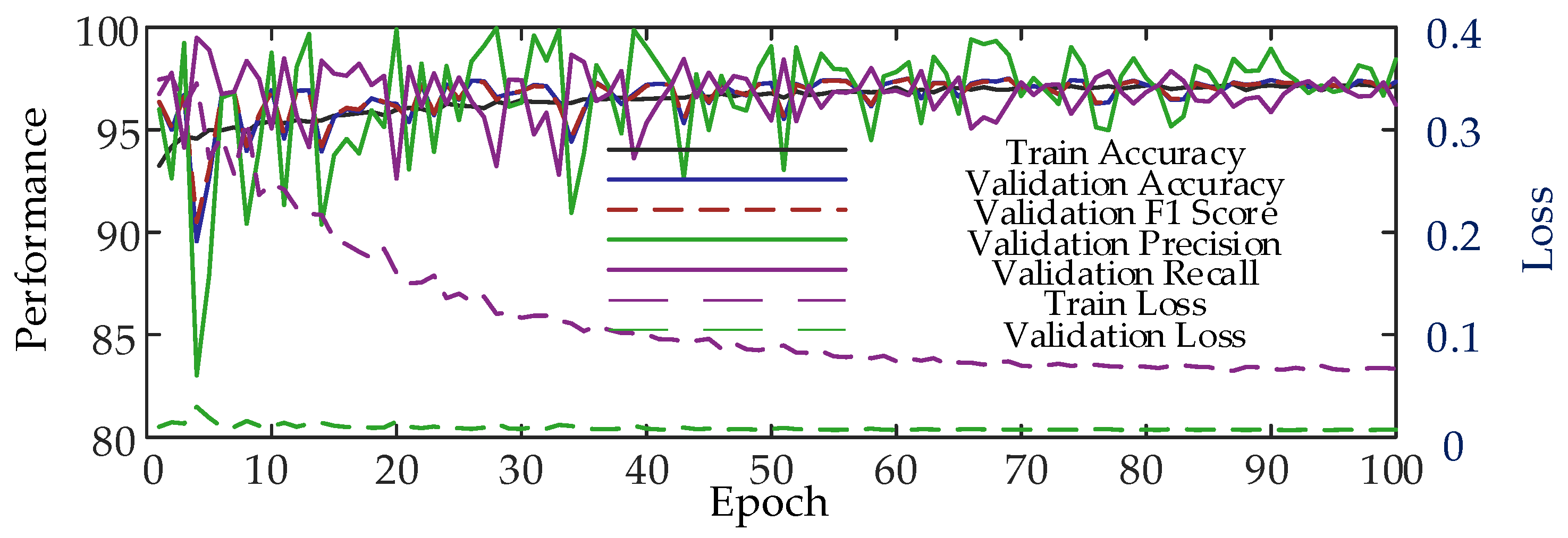
| Mixed Load | 97.11% | 97.33% | 98.43% | 96.22% | 97.31% | |
| Mixed data 1 | 92% | 93% | 93% | 94% | 94% | |
| Linear Load 1 | Predicted Normal | Predicted Abnormal |
|---|---|---|
| True Normal | 5919 (98.65%) | 81 (0.68%) |
| True Abnormal | 127(1.06%) | 5873 (97.88%) |
| Nonlinear Load 1 | Predicted Normal | Predicted Abnormal |
|---|---|---|
| True Normal | 5952 (99.20%) | 48 (0.40%) |
| True Abnormal | 236 (1.97%) | 5764 (96.07%) |
| Mixed Load 1 | Predicted Normal | Predicted Abnormal |
|---|---|---|
| True Normal | 5866 (97.77%) | 134 (1.12%) |
| True Abnormal | 1376 (11.47%) | 4624 (77.07%) |
| Methods | Acctr | Accval | Note |
|---|---|---|---|
| GLT | 98.13% | 98.93% | Simple pre-processing with accurate results |
| MTF | 91.3% | 90.7% | Complex calculations and loss of phase information |
| GADF | 92.51% | 90.93% | Complex calculations and high sampling rate requirements |
| Original Waveforms | 93.80% | 89.29% | Performance depends on terminal configuration |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Tang, R.; Wu, J.; Chen, Y.; Yang, C.; Zhang, S. Generalized Lissajous Trajectory Image Learning for Multi-Load Series Arc Fault Detection in 220 V AC Systems Considering PV and Battery Storage. Energies 2025, 18, 5916. https://doi.org/10.3390/en18225916
Zhang W, Tang R, Wu J, Chen Y, Yang C, Zhang S. Generalized Lissajous Trajectory Image Learning for Multi-Load Series Arc Fault Detection in 220 V AC Systems Considering PV and Battery Storage. Energies. 2025; 18(22):5916. https://doi.org/10.3390/en18225916
Chicago/Turabian StyleZhang, Wenhai, Rui Tang, Junjian Wu, Yiwei Chen, Chunlan Yang, and Shu Zhang. 2025. "Generalized Lissajous Trajectory Image Learning for Multi-Load Series Arc Fault Detection in 220 V AC Systems Considering PV and Battery Storage" Energies 18, no. 22: 5916. https://doi.org/10.3390/en18225916
APA StyleZhang, W., Tang, R., Wu, J., Chen, Y., Yang, C., & Zhang, S. (2025). Generalized Lissajous Trajectory Image Learning for Multi-Load Series Arc Fault Detection in 220 V AC Systems Considering PV and Battery Storage. Energies, 18(22), 5916. https://doi.org/10.3390/en18225916






