Experimental and Numerical Study of a Towing Test for a Barge-Type Floating Offshore Wind Turbine

Abstract

Several experimental and numerical studies have been conducted on the towing behavior of floating offshore wind turbines (FOWTs); however, these studies mainly focus on tension-leg platform (TLP) and semi-submersible designs with cylindrical features. The University of Maine’s VolturnUS+ concept is a cruciform-shaped barge-type FOWT with distinctive hydrodynamic properties that have not been characterized in previous research. This study presents basin-scale experiments that characterize the hydrodynamic drag properties of the VolturnUS+ platform, as well as observing the motion behavior of the platform and added resistance during towing in calm water and waves. The towing experiments are conducted in two towing configurations, with differing platform orientations and towline designs. The basin experiments are supplemented with a numerical study using computational fluid dynamic (CFD) simulations to explore flow-induced motion (FIM) on the platform during towing. In both the experiments and the CFD simulations, it was determined that the towing configuration significantly impacted the drag and motion characteristics of the platform, with the cruciform shape producing FIM phenomena. Observations from the towing tests confirmed the feasibility of towing the VolturnUS+ platform in the two orientations. The results and observations developed from the experimental and numerical towing studies will be used to inform numerical models for planning towing operations, as well as develop informed recommendations for towing similar cruciform-shaped structures in the future.

1. Introduction

1.1. Background

The floating offshore wind industry is set to expand in the coming years, with more commercial opportunities and emerging technologies all around the world. According to the Offshore Wind Market Report: 2024 Edition [1], new capacity for global floating offshore wind energy projects nearly doubled to 231.4 MW in 2023, and the global pipeline for floating offshore wind energy increased to 104,399 MW. The installation costs associated with an offshore wind project are a considerable portion of the overall capital expenses (CapEx), especially with floating offshore wind. The Cost of Wind Energy Review: 2024 Edition [2] estimates that the installation of a floating offshore wind system makes up 14.4% of the CapEx, as shown in the chart in Figure 1.

One of the most important marine operations related to offshore wind is towing. The safety and cost of a towing operation are highly dependent on the choice of suitable tug vessels, towing speeds, and allowable sea states in which these operations are performed. With emerging novel ideas and designs in floating offshore wind turbine (FOWT) technology comes increased size and more unique foundation shapes [3]. A comprehensive understanding of the towing resistance, towline loads, and towing dynamics is vital to efficient and safe marine operations.

Currently, limited data is available on full-scale towing operations of FOWTs, primarily due to a lack of technological maturity and the scarcity of publicly accessible information from the few deployed projects. Calculating forces on a towing system can require complex models and significant computational resources. During early-stage calculations, when high-fidelity simulations are not required, simple drag-based methods are available but may overlook important towing forces and dynamic effects, and they rely on drag coefficients that must be either pre-measured or estimated.

There have been efforts to develop general methodology recommendations for simplified towing force calculations, such as the U.S. Navy Towing Manual [4] and Det Norske Veritas (DNV) guidelines [5,6,7]. These references are useful for estimating mean loads on the towed object but typically require known drag coefficients or offer basic estimation methods based on simplified geometry. As a result, they may not accurately account for complex geometric shapes. Basin-scale experimental testing is a valuable method that allows for controlled variability and detailed observations, facilitating the measurement and calculation of key parameters such as drag coefficients.

1.2. Literature Review

There have been several scale-model towing tests conducted to study the towing behavior of FOWTs. Hyland et al. [8] and Mas-Soler et al. [9] investigated towing with different tension leg platform (TLP) designs, the GICON TLP and the CENTEC -TLP. In both studies, the structure was towed with different towline configurations and orientations. The orientation of the platform relative to the tow direction was changed, along with the use of a single towline or a towline bridle in different test configurations. Notable differences were observed between towing configurations in both studies, with complex flow interactions affecting the towing performance. Towing tests were performed in waves to determine the added towing resistance and to observe the platform motions.

Buttner et al. [10] performed similar towing experiments with the OrthoSpar FOWT concept, a unique structure made from slender piles and a hanging counterweight. They focused on seakeeping-related platform motions and towline loads, observing significant platform motions and towline loads at certain wave frequencies and wave directions. The platform rotational motions in pitch and roll were of notable interest, especially at resonant frequencies where large magnitudes were observed.

A key area of interest in many towing tests was the comparison of experimental and numerical results. Scale-model towing tests were used to validate numerical tools for use in planning towing operations. Adam et al. [11] compared ANSYS-AQWA (Version 14.5) [12] simulations to platform motions observed during towing experiments of the GICON TLP, finding good agreement with the numerical models but identifying some discrepancies due to complex flow effects in the experiments. Le et al. [13] used an experimental tow test of two scale-model submerged floating offshore wind turbines (SFOWTs) to validate numerical models used to conduct parametric studies on platform motions and towing forces. Ramachandran et al. [14] investigated towing the DeepCwind OC4 [15] semi-submersible FOWT design using both experimental towing tests and towing numerical methods. Both methods showed good agreement with the experiments, but differences were found between the experimental and numerical results at larger wave heights and faster towing speeds due to nonlinear effects not captured in simulations.

Chen et al. [16] used a combination of numerical techniques to model the towing of the OC4 semi-submersible with a single tugboat. The dynamic responses of the towing system were evaluated, considering the tow speed and environmental loads during towing.

Roberts et al. [17] presented experimental tow tank testing of a 1:70 Froude scaled model of the 15 MW VolturnUS-S [18] semi-submersible design. Towing test runs were performed at a range of tow speeds and irregular wave cases. Two different towing conflagrations were used, where in one arrangement the model was towed from a single leg and in the other it was towed from two legs. The experimental results were supplemented with numerical results from a ship simulator developed by the Maritime Simulation Laboratory at the University of Plymouth. The ship simulator uses hydrostatics, hydrodynamic, and aerodynamic data from physical experiments and numerical models to derive coefficients for describing the FOWT and tugboat behavior. The coefficients were input into the ship simulator towing model to simulate the motions and forces of the FOWT–towline–tugboat system.

A description of the Maritime Simulation Laboratory’s ship simulator was introduced by Le Pivert et al. (2024) [19] and is used for towing simulations of the VolturnUS-S platform for routing optimization. Further VolturnUS-S towing simulations using the ship simulator are conducted by Le Pivert et al. (2025) [20] to optimize the scheduling of towing between the assembly port and installation location.

In addition, unique physics such as flow-induced motions (FIMs) and vortex-induced motions (VIMs) appeared throughout many of the experimental tow tests. Hyland et al. [8] and Ramachandran et al. [14] observed oscillatory sway motions of their respective platforms, leading to towing instabilities such as fishtailing and galloping. Yin et al. [21] performed scale-model towing tests with the INO WINDMOOR [22] semi-submersible design, specifically focusing on the FIM due to the cylindrical columns of the structure. The FIM was found to influence the sway and yaw motion of the structure, and coupled motions were observed. It was determined that the towline configuration can mitigate some of the FIM, leading to stabilized towing motions.

The FIM and VIM have been an area of interest for numerical and experimental studies of other offshore structures and floating hulls. To date, most research has primarily concentrated on FOWT platforms with vertical columns, such as semi-submersible designs. The vortex-induced motions (VIMs) of floating structures emerged as an area of interest with the oil and gas industry. Waals et al. [23] performed an experimental study on a multi-column TLP, Gonca̧lves et al. [24,25] and Liu et al. [26] studied a semi-submersible structure with four square columns. Gonca̧lves et al. later focused studies on the FIM of FOWT structures with cylindrical columns [27,28], including the DeepCwind OC4 design.

Numerical studies of the VIM of floating structures have been conducted using computational fluid dynamics (CFD). Recent studies have focused specifically on the VIM of FOWTs. Liu et al. [29] performed CFD simulations to model the VIM responses of the DeepCwind OC4 semi-submersible FOWT using OpenFOAM [30]. The results showed that there are considerable VIM responses over a range of current conditions, which should be important considerations for the design stage of FOWTs. Jiang et al. [31] used CFD to model the VIM of the INO WINDMOOR semi-submersible. The varying effects of VIM in different current conditions are presented.

1.3. Research Gaps and Novelty

The VolturnUS+ concept is a uniquely shaped barge-type FOWT foundation with distinctive hydrodynamic properties that have not been characterized in previous publicly available research. Previous scale model towing tests and numerical simulations mainly focus on designs with multiple vertical columns, while the VolturnUS+ is a cruciform-shaped barge-type design.

Without useful data from previous towing operations or experiments, there was a need for a study to take place. Each unique foundation shape requires investigations into the shape-specific properties and the potential different towing configurations. Therefore, in this work, basin-scale model testing of the FOWT platform is used to determine the towing characteristics of the novel VolturnUS+ model. Numerical simulations are used to supplement the model tests and investigate FIM and other complex flow characteristics further.

A more comprehensive understanding of the platform during towing gained during experimental and numerical testing allows for more informed and safer decisions for towing operations. In April 2025, the University of Maine launched and towed a 1:4 scale model of the VolturnUS+ design in the Gulf of Maine [32,33]. These marine operations necessitated accurate calculation of towing forces to support the design and planning process.

The objectives of this research were as follows: conduct experimental basin towing tests in two towing configurations to (a) calculate the drag coefficients of the FOWT in calm water at a range of tow speeds, (b) compare the tow forces and motions of the FOWT in the two towing configurations, and (c) characterize the added tow resistance in different regular and irregular wave cases.

In addition, CFD was used to model the towing of the FOWT in order to (a) compare numerical results to the experimental data, and (b) observe flow-induced motions (FIM) on the FOWT during the towing operation. The overall experimental and numerical methodology is illustrated in Figure 2.

2. Methods

2.1. Basin Facility

The towing tests took place in the Alfond W2 Ocean Engineering Lab in the Advanced Structures and Composites Center (ASCC), located at the University of Maine. The basin within the W2 lab is 30 m long and 9 m wide, and has a depth of 4.5 m. A tow carriage is positioned above the basin and moves using an electric motor on rails that run along each side. The tow carriage allows for towing tests to be conducted at a constant known speed. A paddle-type wave maker is located on one end of the basin, and a sloped beach wall on the opposite side to absorb the waves. The W2 is equipped with a wind generator, but wind speed was not considered for this study [34].

The tow distance in this study was limited to a distance of about 20 m within the basin due to depth constraints on the beach end and the wind generator wall and instrumentation bridge located on the other end. Figure 3 shows a diagram of the basin layout during the towing trials.

2.2. FOWT Model

The experiments in this study were designed based on a towing operation for the intermediate-scale concrete VolturnUS+ 1:4 FOWT. A 1:15 Froude-scaled model of the VolturnUS+ 1:4 design was used for the basin experiments. Froude scaling factors, denoted by $\lambda$, are shown in

Table 1. Froude Scaling Factors.

Parameters	Scale Factor Symbolic
Length	$\lambda$
Angle	1
Velocity	${\lambda }^{0.5}$
Frequency	${\lambda }^{-0.5}$
Force	${\lambda }^3$
Time	${\lambda }^{0.5}$

for key parameters. The basin model was ballasted to a representative transit draft, including the tower and wind turbine. A steel weight was installed at the top of the model tower to represent the mass properties of the rotor-nacelle assembly (RNA), while the aerodynamic properties of the RNA were not included in the basin model. Key properties of the basin-scale VolturnUS+ model during the towing tests are provided in

Table 2. Properties of VolturnUS+ basin model.

Properties
Mass	63.25 kg
Draft	0.143 m
Freeboard	0.113 m
Platform Width	1.08 m
Platform Material	Aluminum

.

Due to the unique cruciform shape of the barge-type VolturnUS+ design and the placement of the mooring fairleads, there are two orientations for the FOWT to be towed. In the first towing orientation one of the legs of the platform is oriented in line with the direction of the tow velocity, as shown in Figure 4. This orientation represents 0° rotation and was tested using a single towline attached to the front leg mooring attachment point. This towing setup is labeled the plus configuration. In the second orientation, the FOWT is rotated 45°. The second orientation allows for a towline bridle to be attached to the mooring line attachment points on the two leading legs. This towing setup is labeled the cross configuration.

The towlines used in the experiment were made from a synthetic polymer line. The stiffness of the towline in the plus configuration was 938 N/m, and the stiffness of the cross configuration towline that included the bridle was 1065 N/m. A spring with a stiffness value $k=1281$ N/m was added to the end of the towline to act as a shock absorber. The towline and spring stiffnesses were directly measured using known masses and by measuring the elongation.

2.3. Instrumentation

The towline tension, 6DoF motions, tow speed, and a visual video feed were collected during each tow trial. Towline tension was measured using an in-line load cell attached to the underside of the tow carriage at the end of the towline. The 6DoF motions of the FOWT were recorded using Qualysis (Qualisys AB, Göteborg, Sweden) motion capture cameras. The motion capture cameras were located on top of the tow carriage to capture detailed motions relative to the towing velocity. The wave heights within the basin were measured using capacitance wave probes located on the instrumentation bridge in the basin. The video cameras were positioned above the FOWT on the tow carriage and in fixed locations on the side of the basin. A layout of the instrumentation used during the lab testing is shown in Figure 5. The multiple cameras allowed for multiple detailed views of the wake and motions during the tow tests, providing physical insights into the resistance behavior of the platform in the two tested towing configurations.

2.4. Tested Towing Environments

2.4.1. Calm Water

The calm water tests involved towing the FOWT at seven tow speeds in both configurations. Three repeating towing trials were conducted at each tow speed to analyze the repeatability and mitigate errors in individual trials. The calm water trial tow speeds are given in

Table 3. Tow speeds for towing test experiments.

	Model Scale	Intmd. Scale
Label	Tow Speed [m/s]	Tow Speed [m/s]	Tow Speed [kt]
S1	0.196	0.75	1.46
S2	0.268	1.02	1.99
S3	0.395	1.51	2.94
S4	0.467	1.78	3.47
S5	0.539	2.06	4.01
S6	0.612	2.34	4.55
S7	0.667	2.55	4.96

.

The main goal of the calm water trials was to measure the resistance of the FOWT at each tow speed and determine the drag coefficients of the FOWT in the two towing configurations. In these towing tests, tow resistance refers to the drag force on the platform, measured as the towline tension by the load cell. In an actual towing operation, the total tow resistance would also include the drag force on the tugboat in addition to the platform, but since no tugboat is present in these tests, tow resistance only refers to the platform.

The drag coefficient of the platform shape was calculated for both orientations at each tow speed. The measured towline tension is equivalent to the towing resistance of the FOWT. The towing drag coefficient ($C_D$) is calculated using Equation (1).

$$C_D={\displaystyle \frac{R}{\frac{1}{2}\rho A_P{v}^2}}$$

(1)

where R is the tow resistance of the towed object, $\rho$ is the density of the water, $A_R$ is the submerged reference area of the towed object, and v is the tow speed. The tow resistance of the FOWT was determined by taking the average of the towline tension measured at each tow speed.

The motion data collected during the calm water tow runs was analyzed and compared to observe how tow speed, orientation, and towline configuration influence the behavior of the FOWT. Time series data from individual runs was compared, and statistical values were computed to characterize the motions of the turbine at each tow speed and in the two orientations.

2.4.2. Wave Environments

Tow test trials were conducted in different wave environments, involving regular and irregular waves. The regular wave cases included four different combinations of wave height (H) and period (T). The wave parameters of the regular wave cases are given in

Table 4. Regular wave cases for towing tests.

	Model Scale		Intmd. Scale
Wave Case Label	$\mathit{H}$ [m]	$\mathit{T}$ [s]	$\mathit{H}$ [m]	$\mathit{T}$ [s]
RW1	0.034	1.31	0.5	5
RW2	0.103	1.31	1.5	5
RW3	0.034	0.65	0.5	2.5
RW4	0.103	0.65	1.5	2.5

.

The irregular wave cases included six different combinations of JONSWAP wave spectra [35], defined by significant wave height ($H_s$) and peak wave period ($T_p$). The wave parameters of the irregular wave cases are given in

Table 5. Irregular wave cases for towing tests.

	Model Scale		Intmd. Scale
Wave Case Label	${\mathit{H}}_{\mathit{s}}$ [m]	${\mathit{T}}_{\mathit{p}}$ [s]	${\mathit{H}}_{\mathit{s}}$ [m]	${\mathit{T}}_{\mathit{p}}$ [s]
IRW1	0.021	0.65	0.3	2.5
IRW2	0.034	1.83	0.5	7
IRW3	0.068	1.31	1.0	5
IRW4	0.068	2.35	1.0	9
IRW5	0.103	1.83	1.5	7
IRW6	0.137	1.57	2.0	6

.

For all wave cases, regular and irregular, towing trials were conducted in both configurations and at two different tow speeds. The tow speeds chosen for the wave cases were S2 and S3, as shown in Table 3, due to their choice as a target tow speed for the intermediate VolturnUS+ tow operation. Three repetition towing trials were performed for each wave case at both speeds.

The goals of the towing trials in wave environments were to determine the added resistance in waves and to observe the effects on the FOWT motions. The added resistance in waves is a measure of the extra resistance experienced by the FOWT due to wave-induced effects. The added resistance in waves ($R_{AW}$) was determined by subtracting the calm water tow resistance (R) from the average tow resistance measured during the wave trails (${\overline{R}}_{wave}$) [14], as shown in Equation (2).

$$R_{AW}={\overline{R}}_{wave}-R$$

(2)

2.4.3. Wave Encounter Frequency

When a marine vessel is traveling at a constant speed in waves, its motion relative to the waves affects how frequently it encounters wave crests. Wave encounter frequency is the rate at which a moving vessel encounters successive wave crests, influenced by both the vessel’s speed and the wave properties. It is typically higher than the actual wave frequency when the vessel moves into the waves and lower when moving with them. The equation for calculating the wave encounter frequency (${\omega }_e$) is given in Equation (3).

$${\omega }_e=\omega -{\displaystyle \frac{{\omega }^{2}Ucos\mu }{g}}$$

(3)

where $\omega$ is the wave frequency, U is the tow velocity, $\mu$ is the wave heading angle (180° in head seas), and g is the acceleration due to gravity [36].

In the towing tests in this study, the FOWT model is moving into the waves for all cases, so the wave encounter periods ($T_e$) will be smaller than the actual wave periods. In

Table 6. Encounter wave periods at tow speeds S2 and S3.

Wave Case Label	$\mathit{T},{\mathit{T}}_{\mathit{p}}$ [s]	${\mathit{T}}_{\mathit{e}}^{\mathit{S}2}$ [s]	${\mathit{T}}_{\mathit{e}}^{\mathit{S}3}$ [s]
RW1	1.31	1.16	1.10
RW2	1.31	1.16	1.10
RW3	0.65	0.51	0.47
RW4	0.65	0.51	0.47
IRW1	0.65	0.51	0.47
IRW2	1.83	1.67	1.61
IRW3	1.31	1.16	1.10
IRW4	2.35	2.19	2.12
IRW5	1.83	1.67	1.61
IRW6	1.57	1.41	1.35

, the wave encounter periods are given for each regular and irregular wave cases at both tow speeds. Because the FOWT is experiencing the wave encounter periods during towing, these periods will be more accurate in determining the wave environment’s influence on the structure motions.

2.4.4. Decay Tests and Natural Periods

Decay tests were conducted on the FOWT model within the basin to determine the natural periods of the heave, pitch, and roll motions. The natural periods measured are given in

Table 7. Natural periods from free decay tests.

	Plus Configuration	Cross Configuration
DOF	${\mathit{T}}_{\mathit{n}}$ [s]	${\mathit{T}}_{\mathit{n}}$ [s]
Heave	1.20	1.20
Pitch	2.42	2.46
Roll	2.46	2.46

.

Sway motions are of particular interest in this study due to the potential of transverse FIM. The natural period of sway in a towing configuration is dependent on the tow speed and towline properties [21]. The sway stiffness of the towed system is given in Equation (4).

$$k_{sway}={\displaystyle \frac{R}{L_t}}$$

(4)

where $L_t$ is the length of the towline.

Based on the sway stiffness, the natural period of the structure in sway can be calculated using Equation (5).

$$T_{n,sway}=2\pi \sqrt{{\displaystyle \frac{m+m_A}{k_{sway}}}}$$

(5)

where m is the mass of the structure and $m_A$ is the added mass.

2.5. CFD Modeling

A numerical study was conducted on the VolturnUS+ floating offshore wind turbine (FOWT) model using computational fluid dynamics (CFD) to analyze flow-induced motion (FIM) in the sway direction during towing. The objective was to replicate and evaluate the FOWT’s dynamic behavior under calm water towing conditions at three tow speeds consistent with those used in basin model experiments.

The geometry of the VolturnUS+ FOWT, scaled to match the basin model, was created using Salome [37], while OpenFOAM [30] served as the CFD solver. Transient simulations were performed using the pressure-based solver pimpleFoam, which is suitable for incompressible flow. The solver was run with a convergence criterion for residuals set to ${10}^{-5}$ for pressure, velocity, and turbulence quantities. An adjustable time step was used to maintain numerical stability and ensure accuracy, and each simulation ran for a total of 180 s of simulated time.

The 3D CFD simulation domain represented the submerged hull of the FOWT in a steady current, with no free surface modeled. The mesh domain was a rectangular prism with dimensions 12 m × 6 m × 3.143 m. The domain size was refined to minimize computational expense while maintaining the features of interest. The FOWT was positioned 2 m downstream from the inlet and centered horizontally within the domain. An overhead view of the final meshes for both the plus and cross configurations is provided in Figure 6. The mesh was generated using the snappyHexMesh tool within OpenFOAM, with significant refinement around the hull geometry and behind the FOWT to capture near-body flow and downstream wake features. Coarser cells were used in the other regions of the domain to reduce computational cost.

The boundary conditions applied to each face of the CFD domain were defined as follows:

• The inlet (front face) was assigned a fixed flow velocity to match the tow speeds used in the experiments.
• The outlet (rear face) used a zero-gradient boundary condition for pressure, appropriate for an outlet where velocity is prescribed at the inlet.
• Symmetry boundary conditions were applied on the side faces under the assumption that the FOWT’s wake does not interact with the domain boundaries, while also reducing computational cost.
• Because the free surface was not modeled, the top face was treated as a slip wall, allowing tangential flow with no shear stress while removing wall-normal velocity.
• The bottom surface was treated as a no-slip wall, although the domain was deep enough that its influence on the flow around the FOWT was negligible.

A Reynolds-Averaged Navier Stokes (RANS) k-$\omega$ SST turbulence model [38] was used in the simulation. The turbulence properties represented low-turbulence inlet conditions to model towing through calm water.

To capture the FIM response of the FOWT, dynamic mesh motion with rigid body dynamics was used. The FOWT was allowed to move freely in the sway direction while being constrained in all other degrees of freedom. The solver calculated rigid body motion at each time step, and the mesh was dynamically morphed to accommodate the movement of the FOWT. A spring force was applied in the sway direction to represent the sway stiffness provided by the towline at each tow speed, calculated using Equation (4). The boundary condition of the FOWT model was no-slip walls that accounted for the moving wall velocity at each time step.

A mesh convergence test was conducted for the CFD simulations for both configurations. The convergence of the average force on the FOWT body in the x-direction ($F_x$) was considered.

Table 8. Mesh Sizes for the Convergence Test.

	Plus Config.	Cross Config.
Mesh	Number of Cells
Mesh 1	2495	2388
Mesh 2	10,673	9803
Mesh 3	72,809	67,388
Mesh 4	200,032	413,937

gives the number of cells in each of the four mesh sizes considered for both configurations. Figure 7 shows the values of $F_x$ for the four meshes. The mesh was considered sufficiently converged for Mesh 3, so that was the mesh size used for the CFD study.

3. Results and Discussion

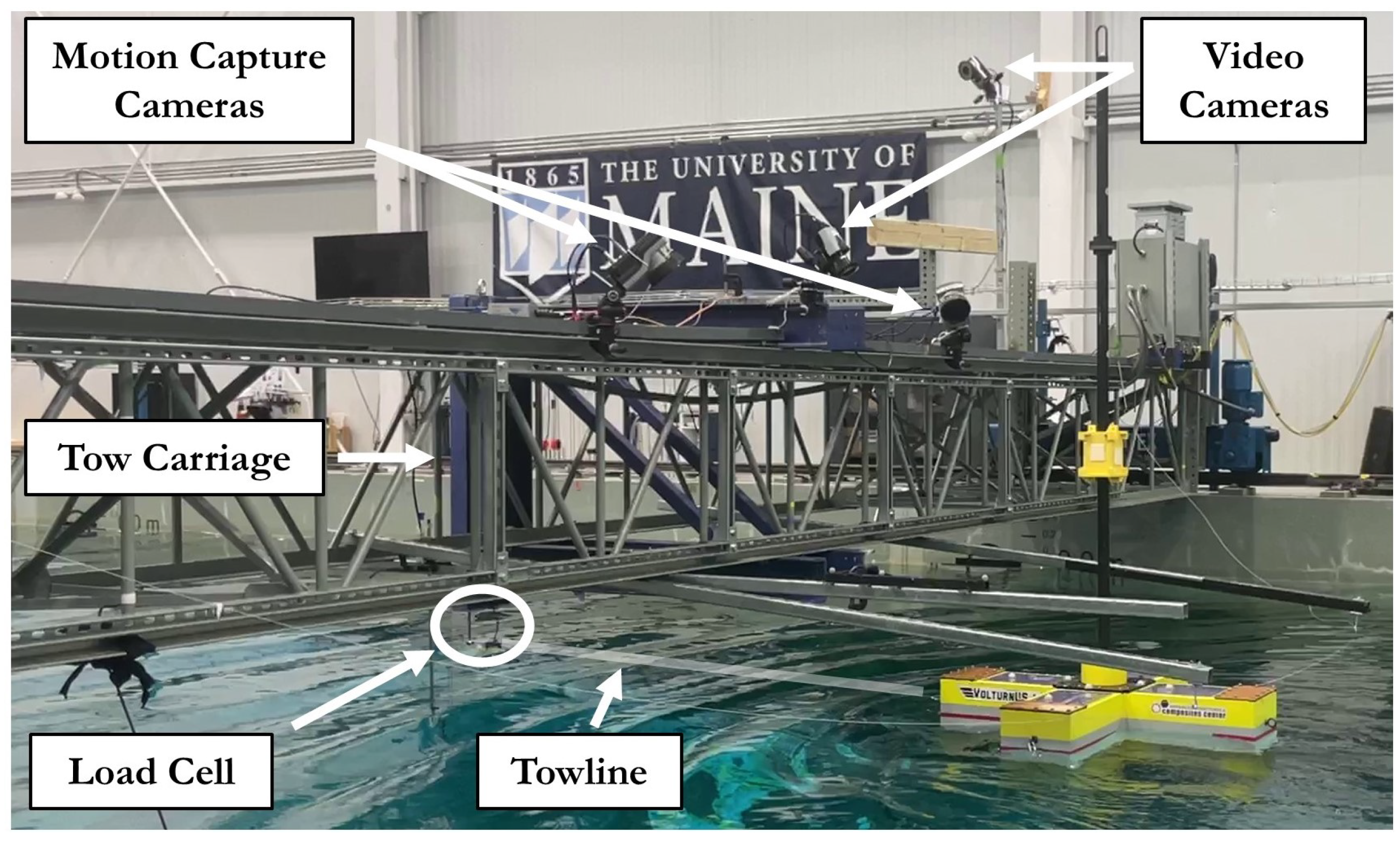
3.1. Calm Water Resistance: Experiments

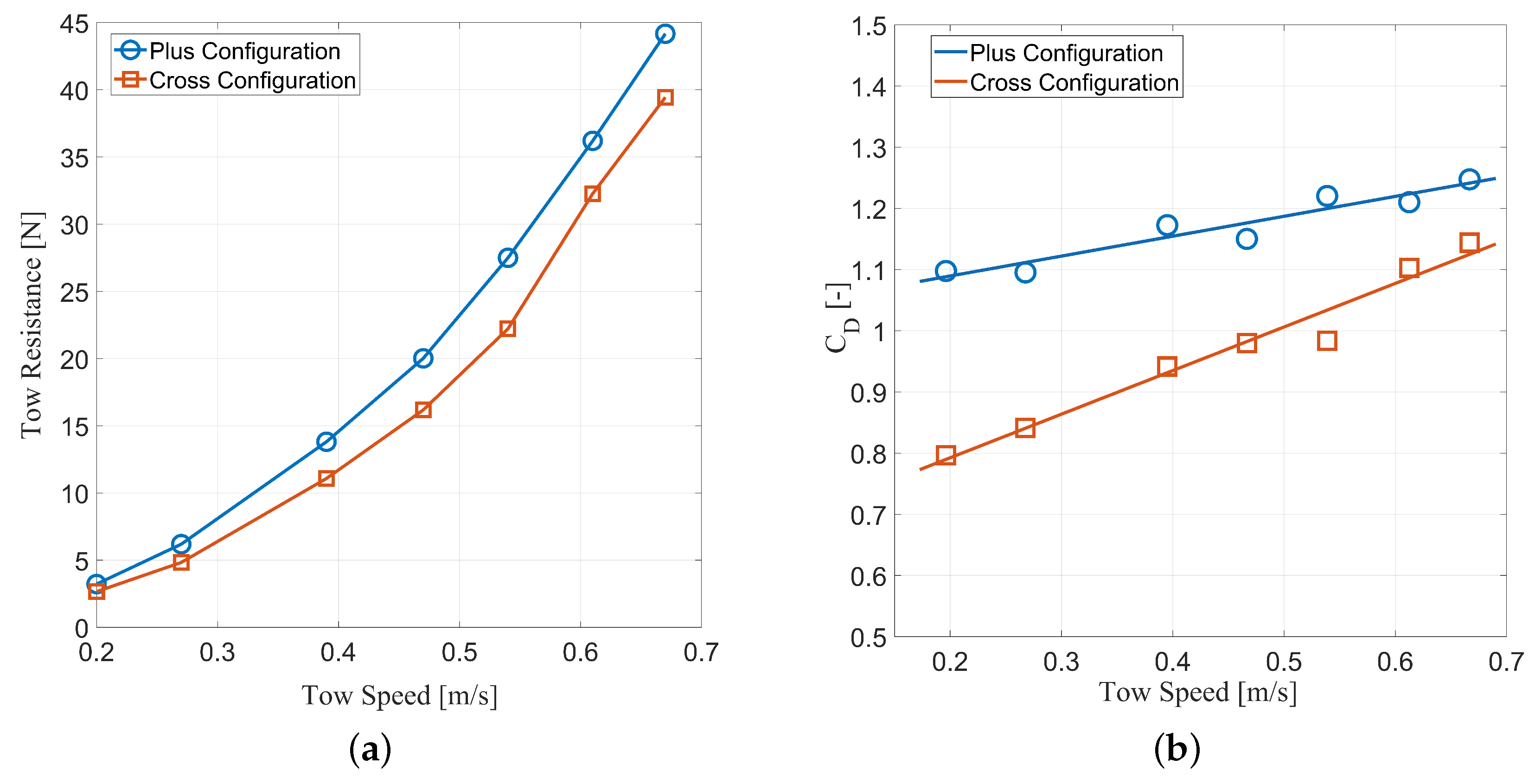
The calm water tow resistance of the FOWT at each tow speed was determined by averaging the measured towline tension for each run. The time series measurements for each run included areas of transient tow speeds at the start, when the model was accelerating up to speed, and at the end, when the model was slowing down. These areas were removed from the time series averaging to only capture areas at a steady tow speed. Each time series was visually inspected and manually trimmed to retain only the steady-state tow speed sections, identified as the regions where the velocity signal remained qualitatively constant. The tow resistances in both configurations are plotted at the range of tested tow speeds, as shown in Figure 8a.

The drag coefficients of the FOWT at each tow speed were calculated using the average tow resistances. The drag equation was used to calculate the drag coefficients in both configurations using the same reference area, tow speed, and water density. The drag coefficients in both configurations are plotted at the range of tested tow speeds in Figure 8b.

The tow resistance tests revealed that the plus configuration exhibited an average of 20% greater tow resistance than the plus configuration across the tow speeds. Consequently, the calculated drag coefficients were greater for the plus configuration. The cross configuration exhibited smaller tow resistances and drag coefficients for all tow speeds. These differences indicate that the orientation of the cruciform shape played a significant role in the drag behavior of the two configurations.

The drag coefficient values calculated for both configurations revealed an interesting trend related to the tow speed. For both configurations, the experimental drag coefficients exhibit a positive trend with increasing tow speed. The plus configuration drag coefficient increased from about 1.10 to 1.25 as the tow speed increased. The cross configuration’s drag coefficient range was found to be 0.80 to 1.15.

Similar behavior was exhibited in the towing tests performed by Mas-Soler et al. [9] where a bow wave was observed to form during the towing tests, resulting in an additional contribution to the resistance at greater tow speeds. The increase in calculated drag coefficient as the tow speed increases may be explained by the formation of a bow wave in front of the FOWT, resulting in an additional contribution to the tow resistance. A visualization of the bow wave formation in the cross configuration is shown in Figure 9. For comparison, the plus configuration appeared to produce a smaller bow wave with less impact on the model, as shown in Figure 10. The larger range of the drag coefficients in the cross configuration may be explained by the different geometry representing the “bow” of the FOWT, meaning that in this orientation of the shape, the bow wave has a greater effect on the tow resistance.

3.2. Calm Water Motions

The calm water pitch motion responses for the plus and cross configurations are shown in Figure 11a,b, respectively. The maximum, mean, and minimum pitch angles are exhibited for each tow speed. The maximum, mean, and minimum values represent the average of the parameters across all the trials at each tow speed. A positive pitch angle represents an angle towards the front of the structure where the towline is connected.

In both configurations, the average pitch angle increased as the tow speed increased. This is expected due to the hydrodynamic force acting on the model increasing with tow speed, resulting in a greater moment on the structure, which induces a greater pitch angle. The cross configuration exhibited a greater average pitch angle for all tow speeds. This may be explained by the effects due to the collection of water between the legs of the model, as the formation of a larger and more focused bow wave in the cross configuration may induce a greater pitch angle on the structure. The collection of water at the bow of the cross configuration can be observed between the model and the red line in Figure 9.

The cross configuration has smaller magnitude pitch deviations to the maximum and minimum until the fastest two tow speeds. For the cross configuration, the trend of the maximum pitch angle continually moves further from the mean with the increased tow speed, while in the plus configuration, the maximum pitch angle appears to converge to a relatively constant offset from the mean, even decreasing between the last two tow speeds.

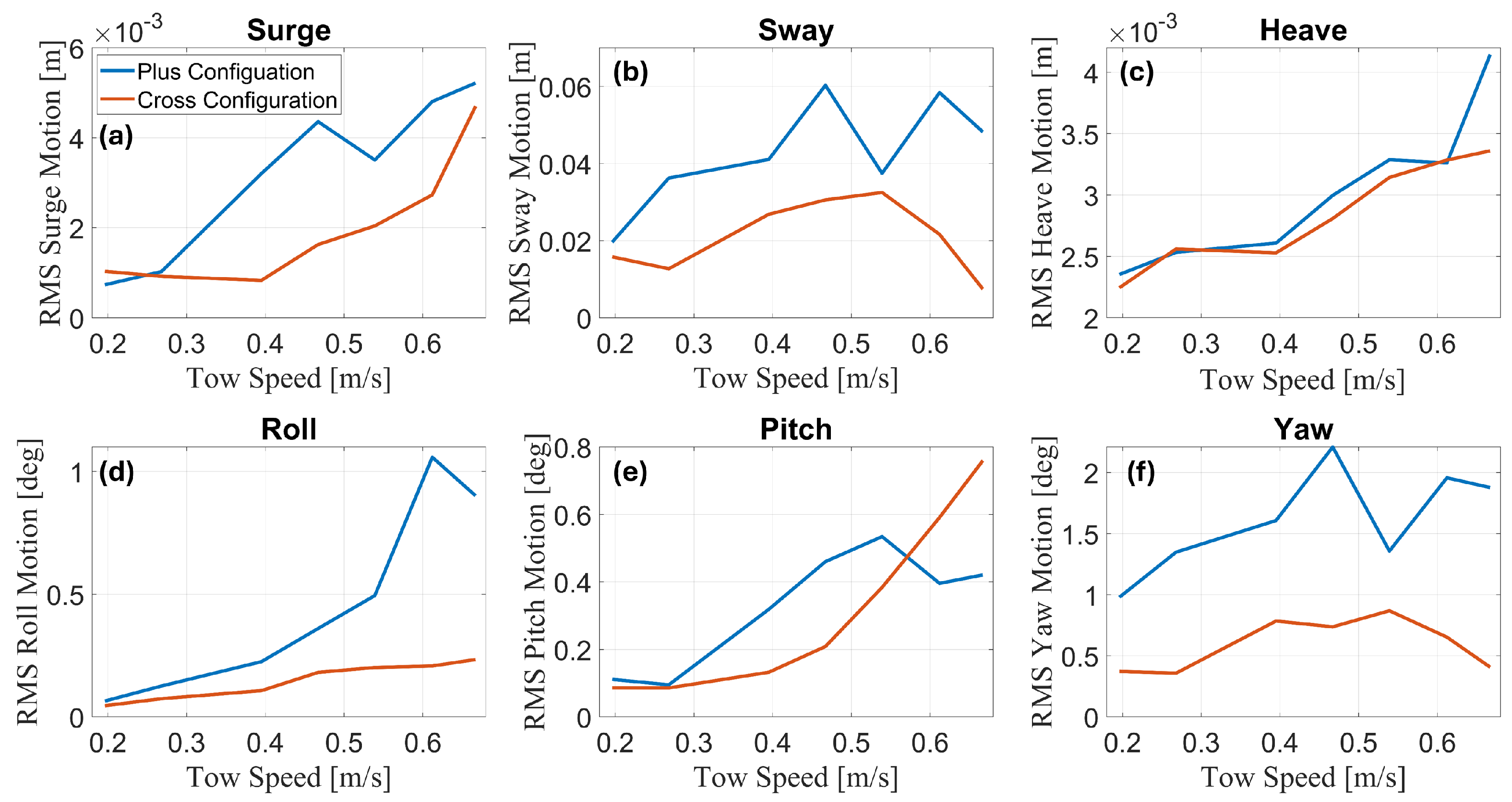
To compare the platform motions across different sea conditions and towing configurations, the root mean square (RMS) of the motion time series was used. The RMS provides a representative value for the amplitude of the motions that can easily be used for comparison. Each time series was mean-subtracted to isolate the fluctuating components, and the RMS of these deviations was calculated. As a result, only oscillatory behavior is captured in the RMS values, and steady offsets, such as a mean pitch angle, are not captured in the comparison. The calm water RMS motion responses are shown in Figure 12. For all degrees of freedom, the values shown represent the RMS of the deviating components of the motion data.

The RMS surge motions in calm water are small for both configurations, as shown in Figure 12a, only reaching a maximum of 5 mm at the fastest tow speed. The plus configuration consistently had slightly higher RMS motions, but the difference was only 2 mm at most. Figure 12c shows that the heave motions were small and of similar magnitudes for both configurations, although the plus configuration had a slightly higher RMS heave at the largest tow speed.

The sway motion of the plus configuration was larger than that of the cross configuration at all tow speeds, as seen in Figure 12b. The inclusion of the towline bridle lines in the cross configuration may contribute to the reduced sway motions. The sway motion observed during the tow trials had long periods, some of which may not have been fully resolved periods due to the size constraints of the basin. Ramachandran et al. [14] observed that during the calm water towing tests, oscillatory motion induced by the flow was observed. In their study, the towing configuration with a bridle exhibited reduced FIM. This is the same trend that is observed in this study and indicates that the increased sway motion may be FIM. A more detailed comparison of individual sway time series is given in the following section involving CFD.

The yaw motion of the plus configuration was consistently much larger than the motion in the cross configuration at all tow speeds, as seen in Figure 12f. The reduced yaw motion in the cross configuration is clearly seen in the experimental data, where the cross had a 0.5–1.0° reduction in sway motion when compared to the plus. Any difference due to the orientation of the FOWT shape on the yaw motion would require further testing with identical towline setups for both orientations. In the tow test conducted by Yin et al. [21], the roll and yaw motions were also observed to be much smaller in the configuration with a towline bridle, indicating that the bridle contributes to increased rotational stiffness, stabilizing the motions in these degrees of freedom. The sway and yaw motions were also observed to be coupled in their study, which is consistent with the sway and yaw trends observed in this study.

Figure 12d shows the RMS roll motions of the model. In the plus configuration, the roll angles increased significantly with increased tow speed, reaching a larger RMS value than the cross configuration at all tow speeds. While the towline differences should not directly affect the roll stiffness in the two configurations, the increased motions in other degrees of freedom and other hydrodynamic effects may result in the larger roll angles for the plus configuration. The cross configuration remained stable for all tow speeds, with the largest RMS roll angle reaching about 0.25°.

Following the analysis of the maximum, mean, and minimum pitch angles in both configurations, the RMS motions reveal more insight into the pitch behavior of the FOWT. The RMS pitch motions, as shown in Figure 12e, are similar at the lowest tow speeds, and as tow speed increases, the pitch motion of the plus becomes larger than the cross. The RMS pitch motion for the plus reaches a maximum of 0.5° at a tow speed of 0.54 m/s and then decreases for the next two tow speeds. The cross RMS pitch motion continues to increase as the tow speed increases, eventually exceeding the plus.

3.3. Calm Water CFD Comparison

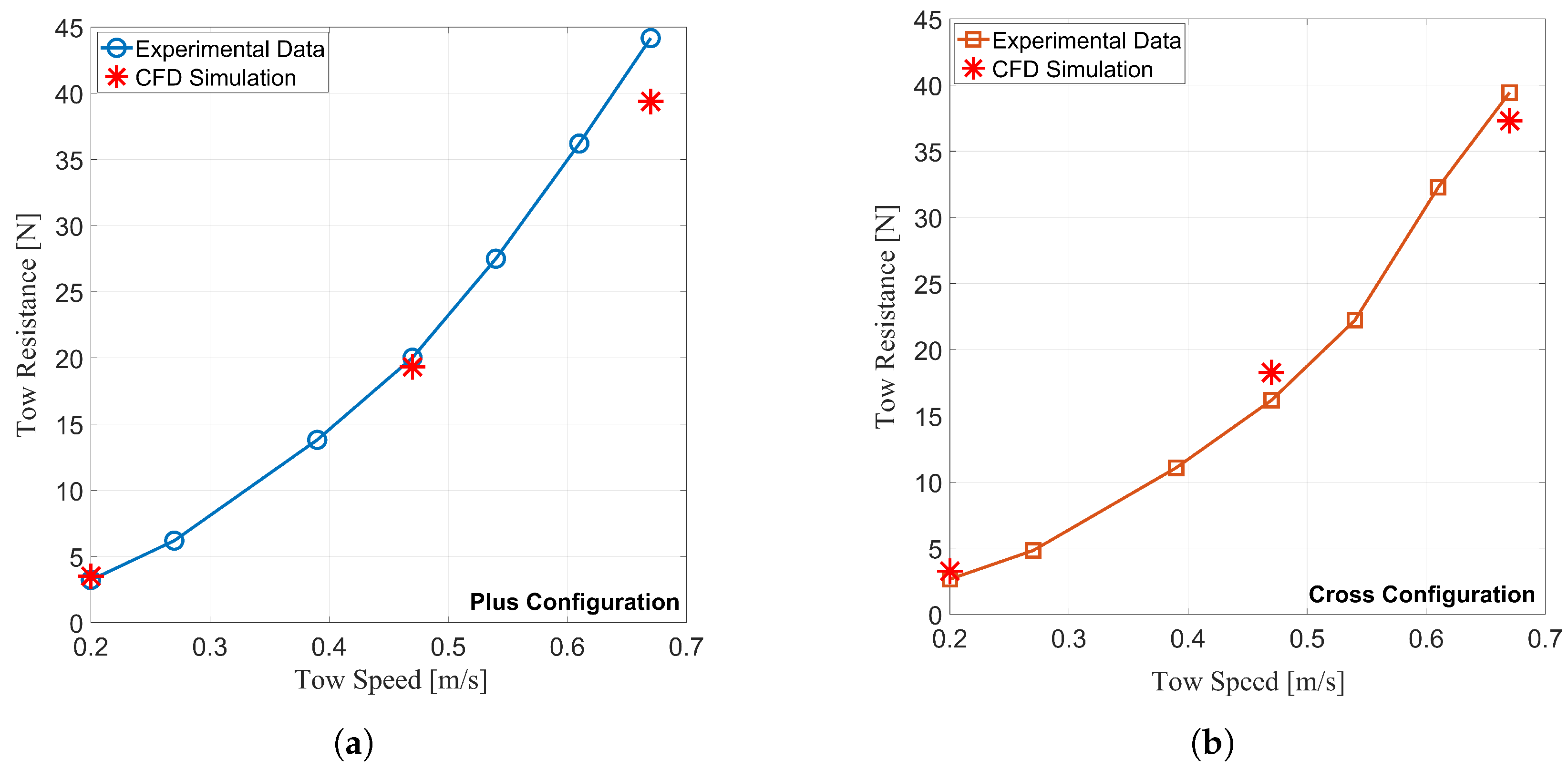
The experimental tow resistances for the plus and cross configurations are shown in Figure 13a,b, respectively, with three points representing tow speeds at which CFD simulations were conducted. The tow resistance value from the CFD tests is determined by the calculated force on the CFD body in the flow direction (x-direction).

The CFD showed good agreement with the experimental tests for both configurations, within the limitations of the modeling approach without a free surface. In both configurations, the CFD simulation over-predicted the tow resistance at the lowest tow speed and under-predicted the resistance at the highest tow speed. The trend shown by the differences between the experimental and CFD resistance values may support the claim that the formation of a bow wave is contributing to larger tow resistances at higher tow speeds. The formation of a bow wave cannot occur in the CFD model used for this study, as there is no free surface modeling, so any added resistance due to this phenomenon would not be captured.

During the experimental testing of the plus configuration, large sway motions were observed at multiple tow speeds. The structure would begin moving in sway and continually drift in the same direction, resulting in large sway offsets. The sway motion was of low frequency, with the sway motion appearing as drifting motion rather than oscillations, but this could be attributed to the limited towing distance during the tests. The same behavior was not observed during the cross configuration trials. The magnitudes of sway offsets were significantly smaller and were not visually noticeable. The time series data showed that the sway motion in the cross configuration was small and oscillatory rather than the large drifting motion observed in the plus configuration. Increased sway motions can lead to greater towing resistance, as described by Yin et al. in their experiments [21]. Large sway offsets can also lead to side-loading on the towline attachment points, leading to structural damage and unsafe motions during towing.

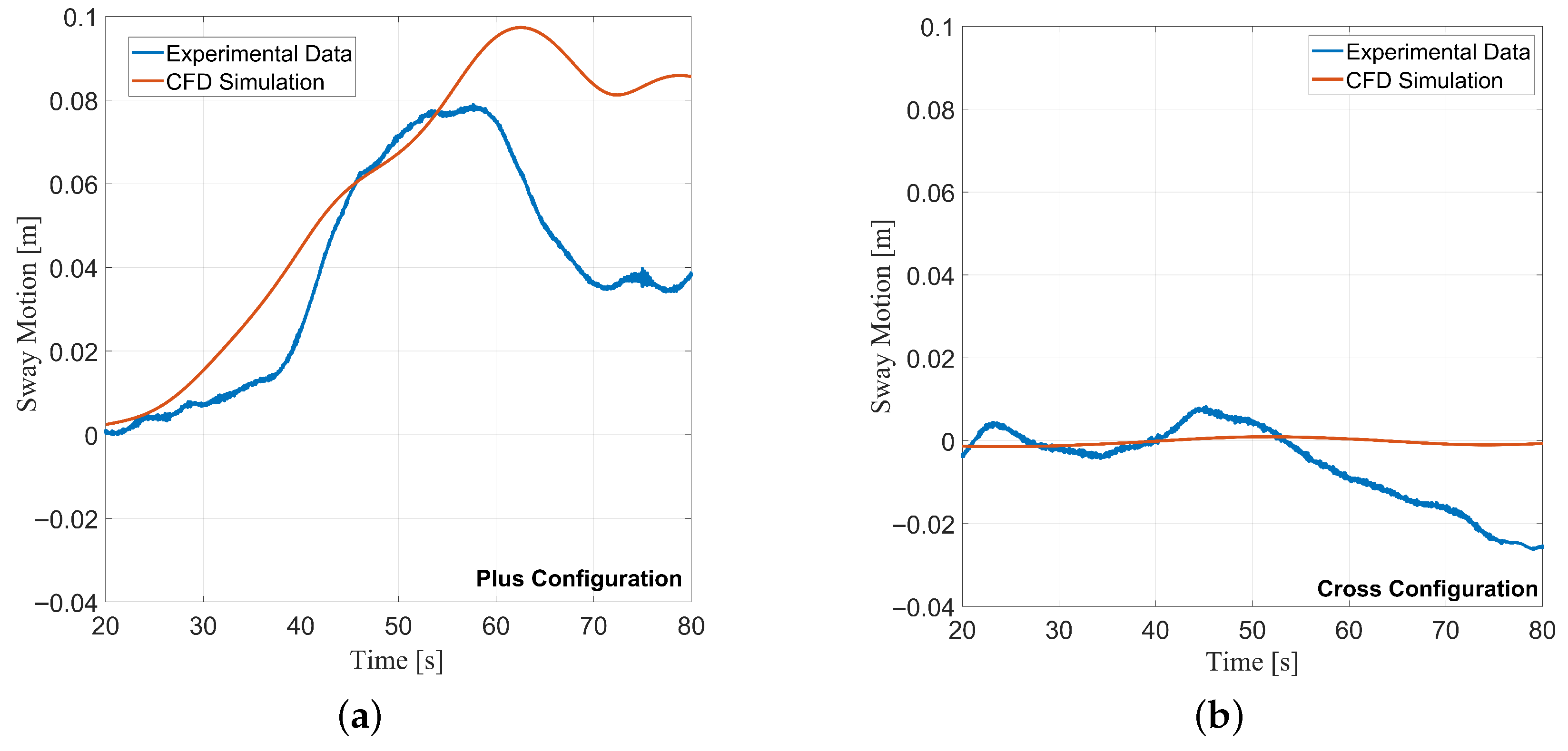
In the CFD simulations of the FOWT, the body motion was limited to only sway motion. All other body degrees of freedom were fixed. In the sway direction, the body had a stiffness value equivalent to the sway stiffness provided by the towline in both configurations. Figure 14a,b provide time series comparisons of the CFD with experimental data in the plus and cross configurations, respectively.

The position of the body calculated in the CFD simulations revealed similar drifting sway motion in the plus configuration. The trend and shape of the sway motion time series from CFD simulation are long-period oscillations, similar to the time series measurements from the drifting events during experimental testing. The cross configuration sway motions in CFD were low-magnitude offsets and oscillatory about zero, matching the behavior seen in experimental testing. The similarities observed indicate that the drifting sway motion may be due to flow effects captured by the CFD model. 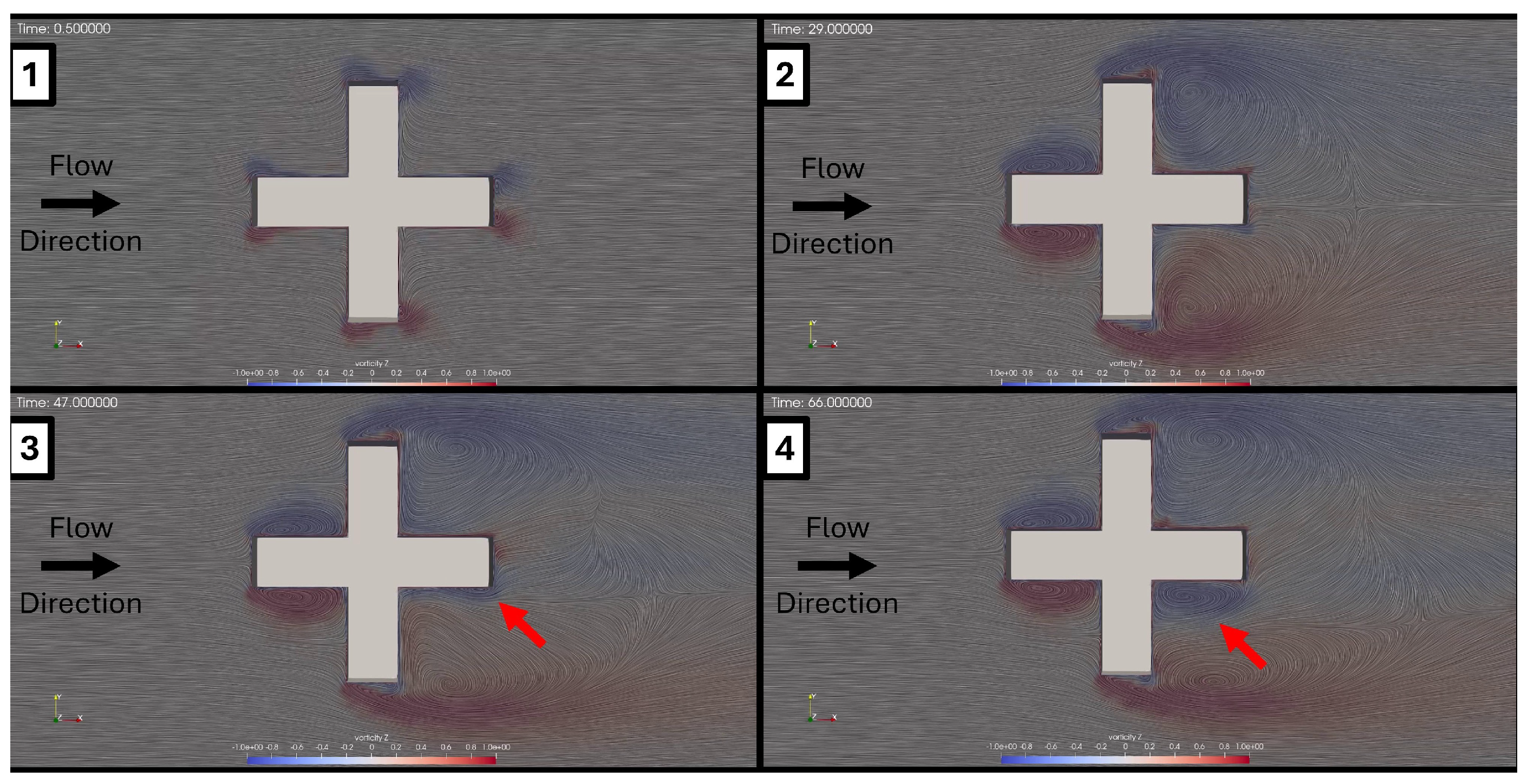Figure 15 shows how, during the plus configuration simulations, an asymmetric vorticity formation appears in frames 3 and 4, which are related to the drifting sway behavior of the model. These asymmetric vorticity features were not present in the simulations in the cross configuration.

To assist in visualizing the sway motions observed in both the basin experiments and the CFD simulations, Figure 16 overlays the initial position of the platform (red) with the peak sway offset (blue) in the plus configuration. The red and blue crosses on each image represent the centerline of the platform legs.

3.4. Added Resistance from Regular Waves

To determine the added resistance from waves two trials were performed at a range of regular wave cases with defined wave heights and periods. Trials at two different tow speeds were performed for each regular and irregular wave case. The towline tension was recorded for each trial, and each individual time series was trimmed to exclude the transient periods at the beginning and end of the trials. The towline tension was averaged for each trial, and then averages were calculated for each wave case at each tow speed to represent the average wave resistance. The added resistance in waves was calculated by subtracting the calm water resistance from the average wave resistance. 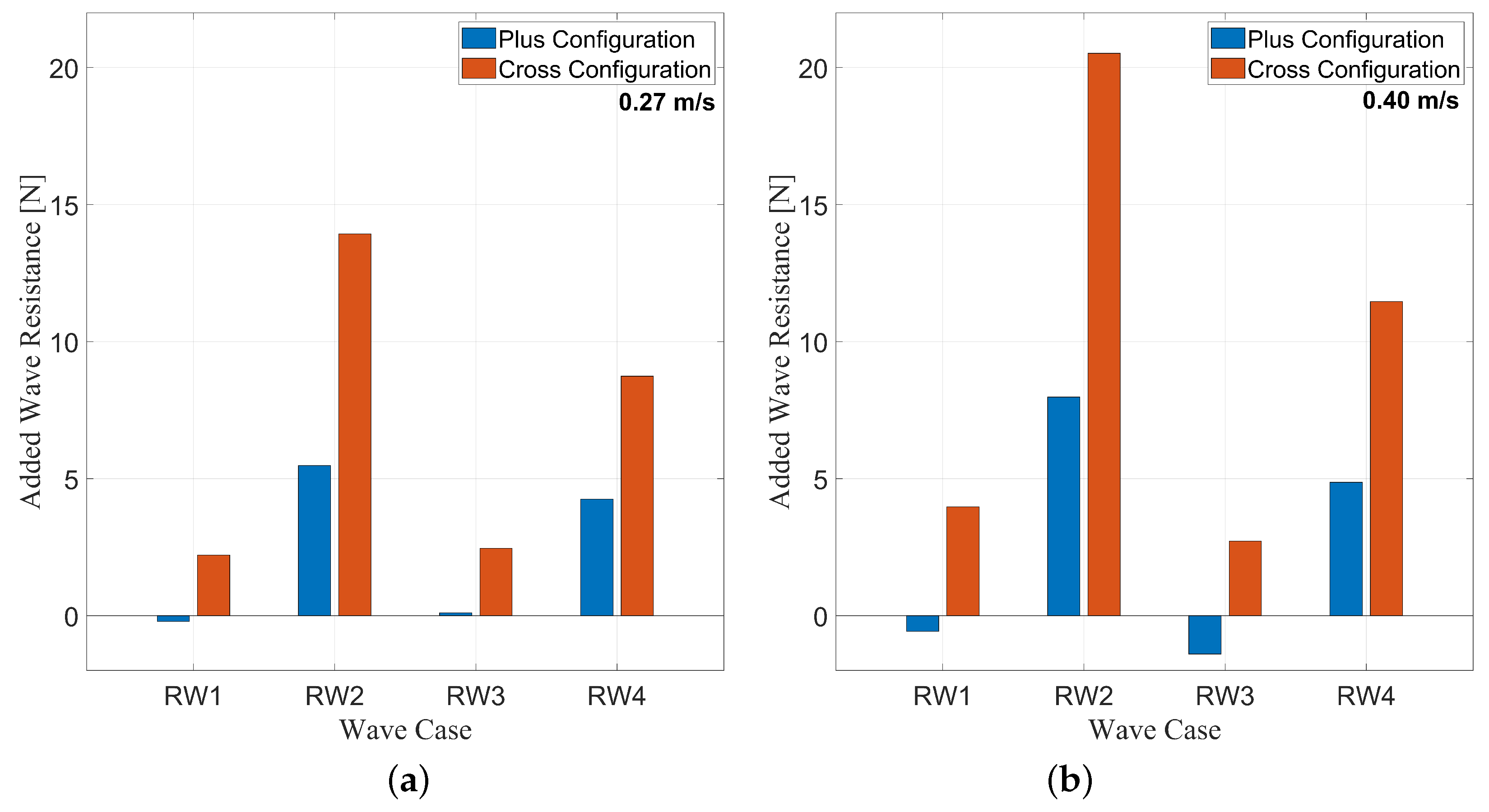Figure 17a,b provide the added resistance in regular wave cases at tow speeds of 0.27 m/s and 0.40 m/s, respectively.

Regular wave cases RW1 and RW3 show relatively small added resistance in waves as compared to cases RW2 and RW4. Cases RW2 and RW4 represent the cases with the higher wave height. The results indicate that wave height had a more significant impact on added wave resistance than the wave period in these cases.

In the regular wave cases, the cross configuration exhibited greater total wave resistances in all cases. The calm water resistance in the cross configuration was less than that in the plus configuration, so the added resistance in waves is higher in the cross configuration in all cases. In cases RW2 and RW4, the cross configuration exhibited significantly greater added wave resistance than the plus configuration, indicating that greater wave heights may amplify the effects, causing greater wave resistance in the cross configuration.

Hyland et al. [8] observed that a bow wave system formed in the towing configuration with a greater added resistance in one of the wave cases, leading to the conclusion that the bow wave interaction with the regular waves may be a cause of greater towing resistance. The results of this study indicate that the cross orientation may form a more significant bow wave, leading to more complex flow and wave interactions and causing the increased added resistance in waves.

In multiple cases, the plus configuration exhibited lower total wave resistances than the calm water resistance, meaning there was negative added wave resistance. A similar phenomenon was observed by Mas-Soler et al. [9], where the experiments showed a negative added resistance in some of the wave tests. The authors hypothesized that the negative added resistance is due to the fact that, at certain encounter frequencies, the harmonic pressure field from the waves reduces flow separation, therefore reducing the resistance of the platform. In this study, the phenomenon was only observed in the plus configuration, further indicating that it may be a flow-related effect that is dependent on the shape of the structure. Further investigation of this phenomenon is needed in the future.

3.5. Regular Waves Motions

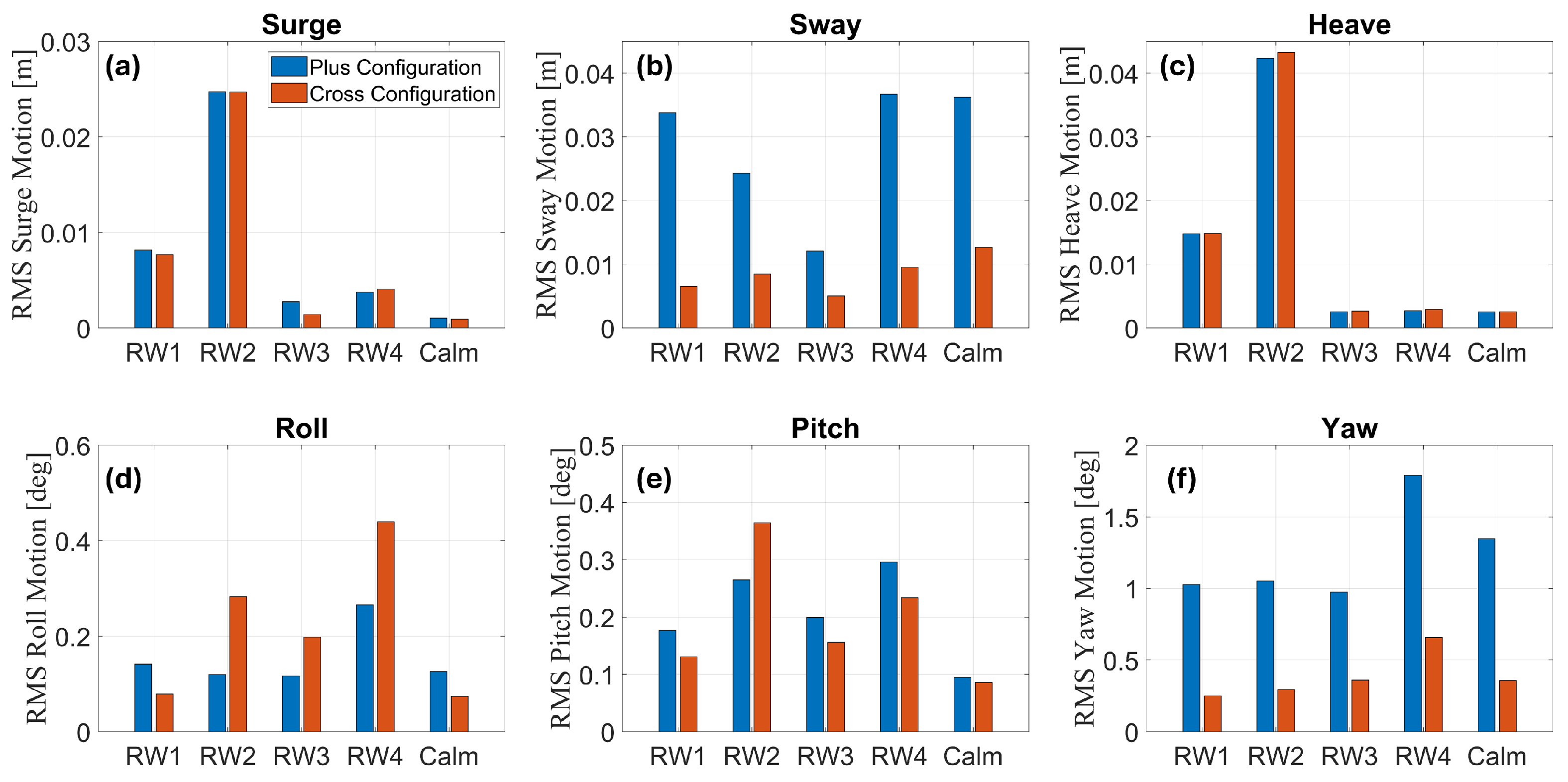
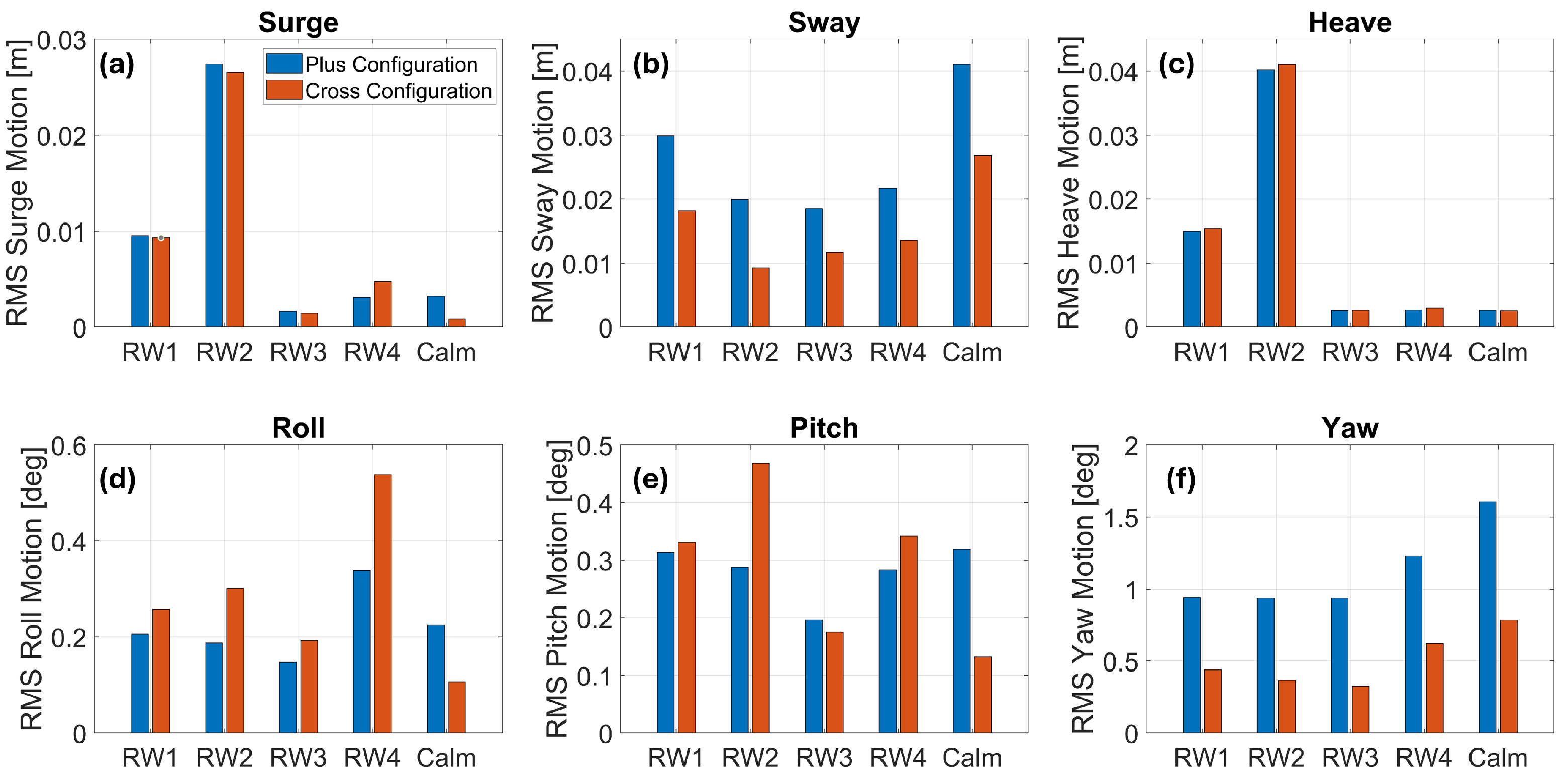
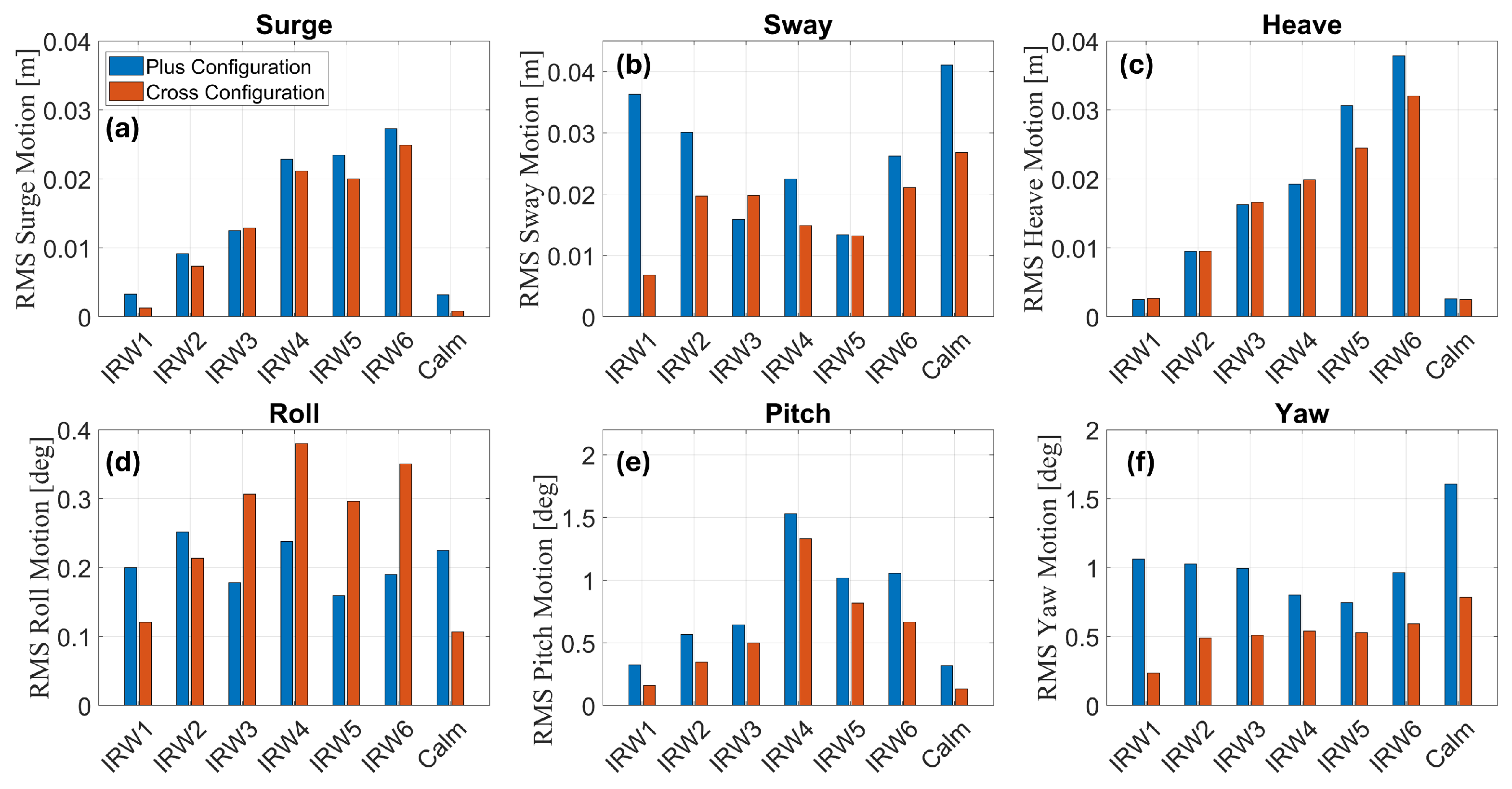
The mean-subtracted RMS values of the platform motions are presented for each wave case. Figure 18 provides the motions in all degrees of freedom at a tow speed of 0.27 m/s, while Figure 19 provides the same motions at a tow speed of 0.40 m/s.

Surge: The RMS surge motion is similar between the plus and cross configurations for all regular wave cases, as seen in Figure 18a and Figure 19a. The surge motions were the greatest in RW2, featuring the largest wave heights and longest wave periods. Increasing the tow speed slightly increased the surge motions for both configurations. The surge motions in waves were significantly larger than the motions observed during the calm water trials.

Sway: Sway motions of the model are shown in Figure 18b and Figure 19b. The sway motion of the plus configuration was larger than that of the cross configuration and similar to the calm water tests. The RMS sway motion decreased in some of the regular wave cases compared to the calm trials. The decrease is most significant in regular wave cases, RW3, at the lower speed of 0.27 m/s. At the faster tow speed of 0.40 m/s, all the regular wave cases showed notably smaller sway motions than the calm water trials. Hyland et al. [8] observed that in the calm water tests, oscillating sway motions were observed to be generated by unsteady flow attachment at the cylindrical bodies. In the regular wave tests, the VIMs were no longer significant, likely because the waves disrupted the periodic flow separation that drives VIMs. The harmonic pressure field reduced flow separation, which in turn mitigated the sway motion, similar to the negative added resistance effect.

Heave: The heave motions of the FOWT were in similar magnitudes between the two configurations in all regular wave cases, as seen in Figure 18c and Figure 19c. Regular wave cases RW1 and RW2 showed the largest responses, as the encounter periods of these wave cases (1.16 s, 1.10 s) were near the natural period of the model in heave (1.20 s). The RMS response showed a linear increase with wave height between wave cases RW1 and RW2. The heave responses were not significantly greater than the calm water response in regular wave cases RW3 and RW4.

Roll and Pitch: The roll and pitch motions were relatively small in the regular wave cases for both configurations, generally only slightly increasing from the calm water values in magnitude. As shown in Figure 18d and Figure 19d, the largest roll motions occurred in the regular wave case RW4 at both tow speeds. The cross configuration exhibited slightly higher roll responses in each case, with the exception of the regular wave case RW1 and the slower tow speed. This trend is opposite to what was observed in the calm water trials. Pitch motions are shown in Figure 18e and Figure 19e. The larger pitch responses were mixed between the two configurations but were the greatest in the regular wave case RW2 in the cross configuration at both tow speeds. The pitch responses were slightly higher at the lower tow speed. Neither of the wave periods in the regular wave cases was near the roll and pitch natural frequencies, resulting in the small responses.

Yaw: Yaw motions are shown in Figure 18f and Figure 19f. As with the calm water trials, the yaw motion of the cross configuration was significantly smaller in all regular wave cases due to the towline bridle. In many of the regular wave cases, especially at the faster tow speed, the yaw motion was reduced from what was observed during the calm water test. The reduced motion may once again be explained by the harmonic pressure field from the waves mitigating FIM.

3.6. Added Resistance from Irregular Waves

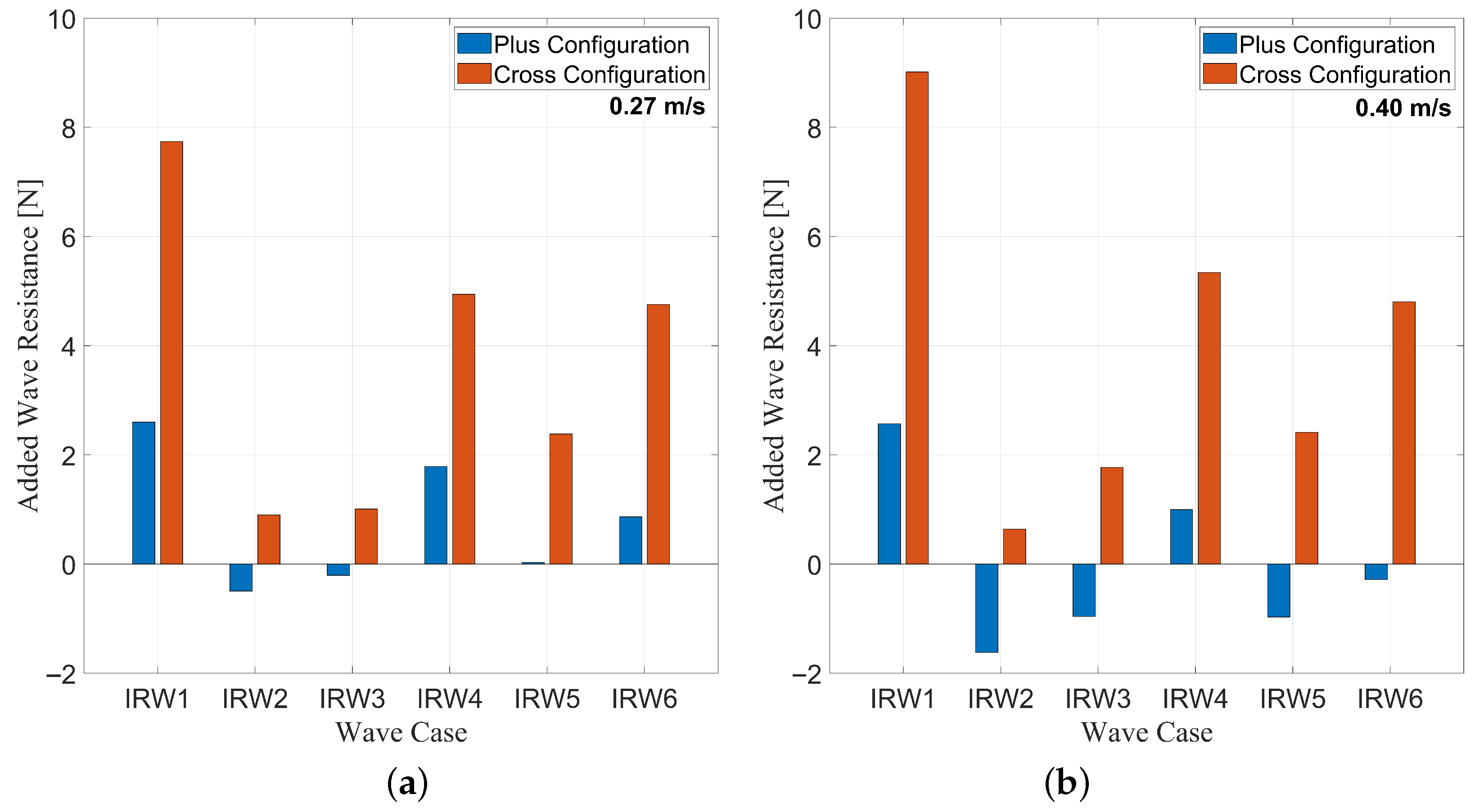
For the irregular wave cases, the added resistance is once again calculated. The added resistances in the plus and cross configurations are provided in Figure 20a and Figure 20b, respectively.

In the irregular wave cases, the cross configuration exhibited greater added resistance in waves for all cases, as compared to the plus configuration. In cases IRW1 and IRW2 at both tow speeds, the total wave resistance was relatively similar for both orientations. In cases IRW3-IRW6, the cross orientation exhibited greater total wave resistance at both tow speeds.

Added wave resistance in irregular waves generally trended positively with increased significant wave height. The exception to this trend was between case IRW3 and case IRW5. The added resistance was smaller in case IRW5 than in case IRW3 in both orientations and at both speeds, meaning that the difference in peak wave period between the two cases was more significant. The effect of changing peak wave period can also be observed between case IRW3 and case IRW4. In both orientations and at both tow speeds, the added resistance in case IRW3 was greater than that in case IRW4, with case IRW3 having a smaller peak wave period.

The negative added resistance phenomenon was once again observed in the irregular wave cases. The phenomenon occurred in cases IRW1, IRW2, and IRW4 in the plus configuration at both tow speeds. Once again, this only occurred in plus configuration trials.

The added resistance values, especially in the cross configuration, show that there was relatively little change in added resistance between the tow speeds. This result indicates that the dependence on tow speed for added wave resistance is small in the cross configuration for irregular waves. Tow speed has a more significant effect on added wave resistance in the plus configuration.

3.7. Irregular Waves Motions

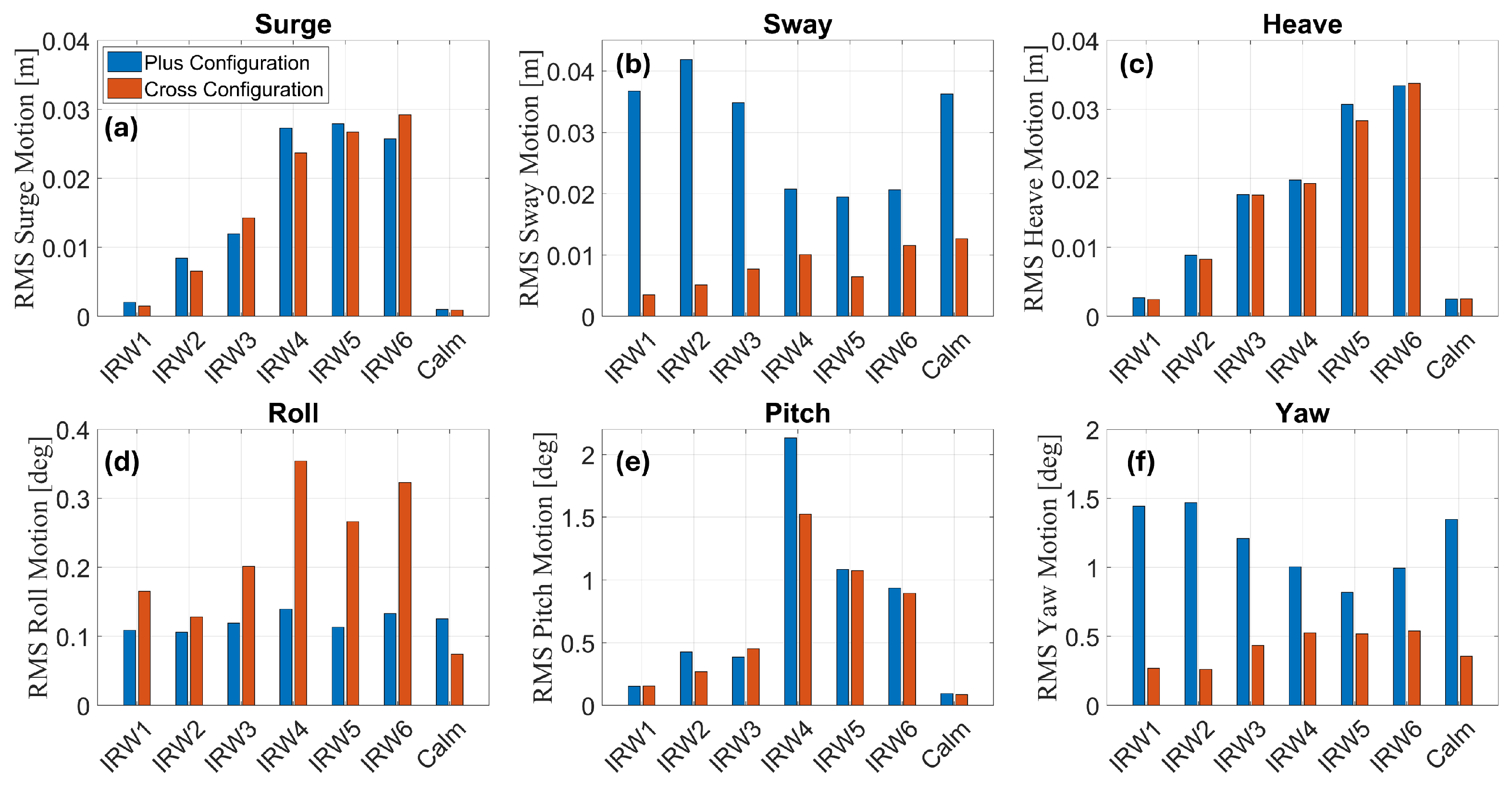
The mean-subtracted RMS motions are presented again for the irregular wave cases. The motions at a 0.27 m/s tow speed are shown in Figure 21 and at a 0.40 m/s tow speed in Figure 22.

Surge: The surge response trended positively with both significant wave height and peak wave period, as shown in Figure 21a and Figure 22a. The trend with wave height can be seen most clearly between IRW2 and IRW3. Between these two cases, the significant wave height increases and the peak wave period decreases, while the surge motion response increases. The trend with peak wave period can be seen between IRW3 and IRW4, where the significant wave height remains the same and the peak wave period increases, resulting in the surge motion increasing.

Sway and Yaw:Figure 21b and Figure 22b show that sway motions were generally larger in the plus configuration in the irregular wave cases. Yaw motions were once again much larger for the plus configuration in all irregular wave cases due to no towline bridle, as shown in Figure 21f and Figure 22f. The sway and yaw motions appear to be coupled for the irregular wave cases. As with the regular waves, the sway and yaw motions decreased from the calm water values in some of the irregular wave cases, indicating wave interaction with FIM.

Heave: As with the regular waves, the heave responses are similar in magnitude for the two configurations, as shown in Figure 21c and Figure 22c. There are two observed exceptions in IRW5 and IRW6, where the plus configuration had slightly larger heave motions than the cross. The magnitude of the RMS heave motion tends to increase roughly linearly with significant wave height. There does not appear to be significant resonant motion on the heave response, which would be expected to occur in IRW3 due to the encounter peak wave period being near the heave natural period.

Roll and Pitch: The roll and pitch motions in both configurations exhibit resonance during IRW4, which has peak wave encounter periods of 2.19 s at the lower tow speed and 2.12 s at the higher tow speed. These encounter periods are near the roll and pitch natural periods of 2.42 s and 2.46 s, respectively. Figure 21d and Figure 22d show that the roll responses were once again generally larger in the cross configuration than the plus configuration, opposite to the behavior of the configurations in calm water. The pitch responses shown in Figure 21e and Figure 22e were generally similar between the configurations, with the plus exhibiting slightly larger angles in most cases. The roll angles were larger at the higher speed, while the pitch angles were higher at the lower speed. The RMS pitch angle reached a maximum of just above 2° during IRW4 in the plus configuration.

4. Conclusions and Future Work

Scale-model basin towing tests of the VolturnUS+ design were successfully conducted to evaluate drag coefficients, motion responses, and added resistance in waves across two towing configurations. Flow-induced towing motion behavior was observed during the experiments and further investigated using supplemental CFD simulations. The results of the towing tests provided key insights that informed the prediction and modeling of larger-scale towing operations for the VolturnUS+ platform. The tests also confirmed the feasibility of towing operations in both configurations, as no uncontrollable or dangerous behavior was observed. The following conclusions were drawn from the towing experiments:

• The drag coefficients of the model were calculated at a range of tow speeds in the two towing configurations. The cross configuration exhibited a smaller towing resistance at all tow speeds, therefore having smaller drag coefficient values. The drag coefficients in both configurations were observed to increase as tow speed increased, leading to the conclusion that bow wave effects may be contributing to added towing resistance at larger speeds.
• The cross configuration exhibited larger mean pitch angles during testing, possibly due to water collection and a more significant bow wave formation due to the orientation of the platform. The magnitude of pitch angle is an important parameter when considering the transport of wind turbines and should be taken into account when determining transit configurations. The towline bridle in the cross configuration increased the yaw stiffness of the platform, leading to smaller yaw motions compared to the plus configuration.
• Observations of the motions in calm water testing showed evidence of FIM on the platform. Significant sway drift and oscillatory yaw motions were observed for the plus configuration, while the motions in these degrees of freedom were significantly smaller in the cross configuration. CFD simulations supported the claim that FIMs are the cause of the larger sway motions in the plus configuration.
• The observed FIM motions are not necessarily indicative of poor behavior and could even offer advantageous effects such as reducing tugboat propeller wake interactions during towing. When planning and performing various towing operations, these motion behaviors should be considered to determine the best towing configurations. More analysis is needed to describe the flow effects on the motions of the platform in different configurations.
• Towing tests in waves revealed that the added resistance of the cross configuration is greater in all regular and irregular wave cases. The more significant bow wave formed in this configuration may interact with the oncoming waves, resulting in larger added resistance. Negative added resistance values were observed in the plus configuration. Evidence points towards the harmonic pressure field of the waves mitigating flow separation, therefore reducing the towing resistance.
• Pitch and roll motions significantly increased when the encounter peak wave periods were near the natural periods of the platform. Heave motions exhibited resonance in regular waves but were relatively unaffected by the peak wave period in irregular waves. Sway and yaw motions of the plus configuration were reduced in some wave cases, leading to the conclusion that the harmonic pressure field of the waves may also mitigate FIM. For a more comprehensive explanation of this phenomenon, more investigations are needed.
• Each towing configuration presents potential distinct advantages. The plus configuration’s reduced average pitch angles suggest suitability for transport with the turbine RNA attached, while the cross configuration’s lower resistance and increased stability favor smaller tugs or operations, requiring greater maneuverability. The sway offset observed in the plus configuration may also reduce resistance with larger tugboats by displacing the platform from the propeller wake. Further analysis is required to determine more robust engineering guidance.

Future Work

While this research has investigated key towing properties of the cruciform-shaped VolturnUS+ foundation, it also revealed opportunities for further exploration. Further analysis is needed of complex flow effects causing sway and yaw motion of the model during towing. The negative added wave resistance phenomenon and the reduced motion oscillations in some wave cases require further investigation, potentially with higher-fidelity CFD simulations that include free surface effects and wave interactions. The flow field details from high-fidelity CFD simulations may further verify the harmonic wave pressure field interactions with the model. Future work may also include an evaluation of the influence of towing tank length on the quality of experimental results during towing tests.