Abstract
The growing complexity of electric vehicle charging station (EVCS) operations—driven by grid constraints, renewable integration, user variability, and dynamic pricing—has positioned reinforcement learning (RL) as a promising approach for intelligent, scalable, and adaptive control. After outlining the core theoretical foundations, including RL algorithms, agent architectures, and EVCS classifications, this review presents a structured survey of influential research, highlighting how RL has been applied across various charging contexts and control scenarios. This paper categorizes RL methodologies from value-based to actor–critic and hybrid frameworks, and explores their integration with optimization techniques, forecasting models, and multi-agent coordination strategies. By examining key design aspects—including agent structures, training schemes, coordination mechanisms, reward formulation, data usage, and evaluation protocols—this review identifies broader trends across central control dimensions such as scalability, uncertainty management, interpretability, and adaptability. In addition, the review assesses common baselines, performance metrics, and validation settings used in the literature, linking algorithmic developments with real-world deployment needs. By bridging theoretical principles with practical insights, this work provides comprehensive directions for future RL applications in EVCS control, while identifying methodological gaps and opportunities for safer, more efficient, and sustainable operation.
1. Introduction
1.1. General
The accelerating adoption of electric vehicles (EVs) is reshaping both the transportation and energy sectors, particularly through the growing demand for electric vehicle charging stations (EVCSs) [1,2,3]. As countries pursue decarbonization and sustainable mobility, EVCSs have become essential infrastructure, enabling broader EV integration by ensuring convenient and reliable access to charging. This accessibility plays a vital role in encouraging consumers to shift away from fossil fuel transportation [4]. However, incorporating EVCSs into existing power distribution networks presents several technical challenges, such as load balancing, managing peak demand, and optimizing infrastructure planning [5,6,7,8,9]. As a result, the effective deployment, coordination, and operation of EVCSs has become a key concern for urban planners, utility operators, and policymakers working toward smarter and more sustainable cities [10,11,12].
In the early stages, EVCS control relied on basic rule-based methods—such as immediate charging upon connection or simple time-of-use (TOU) schedules—which, while straightforward, lacked the flexibility to adapt to real-time grid and user dynamics [13]. As EV usage increased, such approaches began to show clear limitations, including grid stress, inefficient energy usage, and a lack of responsiveness [14]. This led to the emergence of more advanced control strategies, such as optimization-based techniques—including linear programming and offline scheduling approaches [15,16]—followed by the adoption of model predictive control (MPC), which enables forecasting within a predefined horizon to anticipate and adjust for future events [17,18,19,20,21]. However, the reliance on accurate system models and their computational complexity stimulated interest toward more flexible, learning-based approaches [22,23]. In this context, novel machine learning (ML) methods, particularly those capable of adaptive, intelligent control, emerged as promising tools for managing the uncertainty, variability, and scale of EVCS systems [24,25,26,27].
Reinforcement learning, a subfield of ML, has attracted significant attention as a key approach for adaptive control due to its ability to learn optimal decision policies through direct interaction with dynamic environments [28,29]. Unlike traditional approaches, RL does not require explicit modeling of system behavior—instead, it learns from experience by trial and error, optimizing for long-term cumulative rewards. Such methodology has been successfully applied in numerous contexts, devastated by complex, uncertain dynamics, such as building energy management [30,31,32], demand response [33,34], traffic control [35,36,37,38], and robotic navigation [39,40]. In the EVCS domain, RL appears particularly effective due to its ability to adapt to uncertainties such as variable user behavior, unsteady electricity prices, and periodic renewable generation [41,42,43]. Its strength in handling complex, multi-agent environments also renders it suitable for EVCS control, where numerous interconnected decisions need to take place in real time [44,45,46,47,48].
When compared to conventional methods like rule-based control (RBC) or MPC, RL offers considerable advantages in adaptability, scalability, and handling system nonlinearity and stochasticity [49,50]. It is particularly well-suited to managing large-scale, heterogeneous EVCS networks with minimal reliance on precise modeling. Moreover, RL agents may be tailored to optimize multiple, often competing objectives—such as user satisfaction, grid stability, and energy cost—by continuously adjusting charging strategies in response to real-time operational data [51,52,53]. RL-based control also supports integration with vehicle-to-grid (V2G) technologies [54,55,56], renewable energy sources (RESs) [57,58], and shared infrastructure scenarios [59]. Such features position RL as a powerful tool for next-generation EVCS management, especially in contexts where traditional optimization methods struggle to scale or adapt effectively [11]. In particular, in cases where adaptive control, such as RL, is integrated as a hybrid control scheme, methodological advances further demonstrate the potential of optimization and decision-making as concerns complex, non-linear domains [60,61].
Despite its potential, though, RL faces several challenges. For instance, long training times, sample inefficiency, and potential instability during the learning process [6,31] may prohibit the efficient control procedure. Additionally, ensuring explainability and safety is crucial in critical infrastructure applications such as EVCSs. Another limitation concerns the heavy reliance on simulation environments, with limited real-world implementation to date—raising valid questions about generalizability and robustness under real-world conditions [6,11]. Moreover, designing effective state and action representations, reward functions, and coordination mechanisms in multi-agent settings remains complex, particularly in the absence of standardized benchmarks and frameworks tailored to EVCSs [45]. Overcoming these challenges requires an elaborate understanding of RL behavior in diverse operational scenarios, along with a careful balance of performance trade-offs.
1.2. Motivation
With growing interest in using RL for EVCS control, a wide range of studies has emerged, demonstrating both the potential of RL and the challenges involved in its practical application. The current paper review responds to that momentum by offering a focused, RL-specific analysis of the field. After introducing the different EVCS types and key mathematical RL concepts relevant to EVCSs, this paper maps out and categorizes the most influential frameworks developed over the past decade. Given the diversity of RL methods-spanning algorithms, agent structures, state–action representations, reward designs, and evaluation practices—there is a clear need for systematic synthesis. This review addresses that need by identifying common patterns, open challenges, and research gaps through a structured statistical analysis of high-impact studies. To this end, this paper is intended as a resource for researchers, practitioners, and system designers interested in the current state and future direction of RL-based EVCS control. By organizing the literature into a consistent comparison framework and highlighting practical insights, this paper aims to help readers understand the technical landscape and support the informed development of future, real-world-ready solutions.
1.3. Previous Works
The academic literature includes numerous review studies examining EVCSs, each focusing on distinct frameworks and methodologies. Abdullah et al. [62] conducted a focused review on the application of RL in EV charging coordination. The paper emphasized the shortcomings of traditional RBC and centralized optimization approaches under uncertainty, advocating for decentralized RL methods as a scalable and adaptive alternative. Such a study discussed the integration of vehicle-to-grid (V2G) capabilities and categorized RL strategies, though it did not delve into algorithmic details or benchmark environments. In a broader context, Al-Oagili et al. [63] explored EV charging control strategies through scheduling, clustering, and forecasting approaches. While not specific to RL, this work contributed valuable insights into data-driven coordination techniques and distinguished between probabilistic and AI-based methodologies. The proposed work identified practical implementation challenges that added to the real-world applicability of the findings. Similarly, Shahriar et al. [64] examined various machine learning approaches for predicting EV charging behavior, covering supervised, unsupervised, and deep learning techniques. Although RL was not the primary focus, such work underscored the importance of user behavior modeling and high-quality data for effective EVCS control—laying the groundwork for the integration of predictive analytics with real-time RL systems. More recently, Zhao et al. [65] presented a comprehensive and systematic review dedicated to RL-based scheduling for EV charging. The analysis covered different RL algorithms, agent configurations, training methodologies, and evaluation metrics across diverse stakeholder objectives. By mapping technical advances, identifying challenges, and highlighting future research avenues, the work provided a thorough exploration of the role in EVCS optimization.
1.4. Novelty and Contribution
This review offers a comprehensive and methodologically structured analysis of RL applications in the control and optimization of EVCSs, setting itself apart from prior surveys by focusing exclusively on RL-based frameworks tailored for intelligent EV charging management. Unlike broader reviews that address AI in energy systems or general EV infrastructure planning, this study concentrates specifically on RL techniques designed to improve EVCS operational efficiency, enhance user satisfaction, and strengthen grid integration. A key contribution of this paper lies in its large-scale, in-depth evaluation of RL-based EVCS control strategies. It systematically summarizes and categorizes a wide range of high-impact publications from the past decade (including more than fifty impactful papers), with inclusion based on academic influence (more than 30 citations, or a minimum of 5–15 for recent studies), as indexed in Scopus. Such rigorous filtering ensures the relevance and quality of the analyzed content, enabling a focused synthesis of the most significant research developments and insights into how RL has evolved to address the growing complexity of EVCS control. The review begins by outlining the foundational theory of EVCS and RL algorithms commonly used in EVCS applications, followed by detailed tables that summarize key studies—highlighting their algorithmic structures, evaluation methods, and control objectives. Beyond a general overview, this work introduces a structured classification scheme that evaluates RL frameworks along critical dimensions—algorithm type (value-based, policy-based, actor–critic), agent structure (single vs. multi-agent), forecast horizon and control intervals, baseline methods, datasets, performance indexes, deployment settings (e.g., residential, public, fleet-based), and power grid interaction features such as V2G or renewable energy integration. By synthesizing results from a wide array of studies, this review not only highlights the most impactful approaches, but also identifies major challenges, emerging trends, and outlines future directions for advancing RL-driven EVCS control. Table 1 presents a detailed comparison matrix highlighting this review’s contributions in relation to existing surveys in the literature:

Table 1.
Contribution comparison between current and previous works on RL for EVCSs, based on key evaluation attributes.
At a glance, the current review makes five distinct contributions beyond prior surveys. More specifically, this review achieves the following:
- Covers a large number of RL applications for EV charging stations, achieving a scope not reached by earlier surveys. It systematically captures algorithmic design details such as explicit state, action, and reward formulations; the choice of forecast horizons and control time steps; and the baseline control strategies (rule-based, greedy, MILP, MPC, etc.) against which RL methods are compared. This focus allows not only a high-level overview but also a reproducible and technical understanding of how RL has been implemented across diverse studies.
- Introduces a new unified evaluation schema that classifies the literature along multiple dimensions—algorithmic family (value-based, policy-based, actor–critic, hybrid), agent structure (single vs. multi-agent), state space variables and action definitions, reward design principles, forecast horizon and control time step, baseline methodology, deployment environment (residential, workplace, public, depot, highway, renewable-integrated), smart grid interaction features (V2G, bidirectional, renewable integration, connectivity), type of data and simulation platforms used, and the performance metrics reported. These dimensions are consolidated into comprehensive key attribute tables and concise per-paper summaries, enabling transparent cross-comparison of results and establishing a standardized template for reporting future work.
- Derives practical deployment insights by explicitly mapping charger categories and their smart grid features to feasible control cadences, communication requirements, and V2G or renewable integration readiness. By linking the operational characteristics of EVCSs to the RL state–action–reward choices and control horizons, the review highlights what control designs are viable in practice, what simulation assumptions break down in real deployments, and where the main research gaps remain for achieving safe, scalable, and grid-friendly RL-based charging management.
1.5. Paper Structure
As illustrated in Figure 1, this review is structured to guide the reader from foundational concepts to advanced methodological analysis and synthesis:
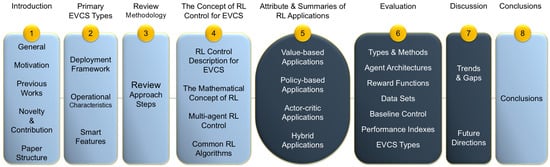
Figure 1.
Paper structure.
- Section 1 introduces the general status of RL for EVCSs, the motivation for this review, previous contributions, and the paper structure.
- Section 2 presents the methodological approach adopted for the literature analysis, describing the sequential steps undertaken to integrate the relevant studies.
- Section 3 presents a classification of EVCS types across multiple dimensions, including deployment framework, operational characteristics, and smart features, offering a foundational taxonomy for understanding control requirements.
- Section 4 illustrates a step-by-step description for RL control in BEMS while also providing the mathematical framework of RL methodologies for EVCSs.
- Section 5 illustrates the tables considering the different key attributes and the summaries of the integrated RL applications.
- Section 6 conducts a comprehensive review and evaluation of RL-based EVCS studies published between 2015–2025, synthesizing them in terms of their control strategies, agent design, reward formulations, baselines, datasets, performance indexes, and deployment index.
- Section 7 synthesizes the identified emerging trends and methodological gaps, and proposes future directions toward scalable, explainable RL systems for EVCSs.
- Section 8 concludes this paper by summarizing the key contributions and outlining the implications for both research and practice.
2. Review Methodology
To provide a structured and in-depth synthesis of existing research, the reviewed studies are systematically categorized based on the type of RL approach—value-based, policy-based, actor–critic, or hybrid—alongside agent configurations (single-agent or multi-agent systems) and specific smart charging objectives. Further dimensions such as reward design, baseline control strategies, datasets, performance evaluation metrics, and deployment contexts are also examined to ensure a holistic understanding of RL-driven EVCS optimization:
- Study Selection: A rigorous study selection protocol was followed to ensure the quality and relevance of the included works (see Figure 2. Only peer-reviewed articles and top-tier conference papers indexed in Scopus and Web of Science were considered. An initial screening yielded over 200 publications, from which a refined subset was chosen for full-text analysis based on a combination of quality and thematic alignment. The inclusion criteria were as follows: (a) Citation Threshold: A minimum of 30 citations was required, excluding self-citations. For recent publications (2022–2025), a relaxed threshold of 5–15 citations was applied to accommodate their growing influence. (b) Topical Relevance: Only studies directly addressing RL-based control of EVCSs were included. Papers solely focused on EV routing, mobility patterns, or market mechanisms—without an RL control component—were excluded. (c) Peer Review Status: Only peer-reviewed journal articles and reputable conference proceedings (e.g., IEEE, Elsevier, MDPI, Springer) were retained; pre-prints and non-reviewed material were excluded. (d) Methodological Transparency: Studies had to clearly define their RL framework, including state and action space design, reward formulation, and evaluation protocol. (e) Algorithmic Diversity: A balanced representation across different RL algorithm families was maintained to reflect methodological variety.
 Figure 2. Article selection process.
Figure 2. Article selection process. - Keyword Strategy: A focused keyword strategy was used to ensure that the search captured only studies relevant to RL applications in EVCSs. Core search terms included “Reinforcement Learning for Electric Vehicle Charging Stations”, “RL-based Smart EV Charging”, “Multi-agent RL for EV Charging Control”, “Deep Reinforcement Learning for EVCS Optimization”, and “Intelligent Charging Control with Reinforcement Learning”. Efforts were made to exclude unrelated domains such as electric mobility logistics, EV routing, or broader smart grid topics not involving EVCS-specific RL control.
- Data Categorization: Each selected study was systematically classified across multiple dimensions critical to RL-based EVCS control. These dimensions included the specific RL algorithm employed (e.g., Q-learning, DDPG, PPO, A2C), agent architecture (single vs. multi-agent), state and action space design, and reward modeling approach. Additional classification covered simulation or deployment environments, control time steps, prediction horizons, and the type of EVCS implementation (e.g., residential, public, workplace, fleet, mobile, depot-based, or integrated with renewables). Information about benchmark control methods—such as RBC logic, TOU strategies, greedy algorithms, offline optimization, MPC, or RL—was also collected for comparative analysis.
- Quality Assessment: To maintain analytical rigor, a quality-assessment framework was applied. Citation counts from Scopus served as a primary filter, based on the thresholds noted earlier. Beyond citation metrics, the academic standing of the authors and their institutional affiliations were also considered, particularly their contributions to RL, energy systems, or EV-infrastructure research. Studies with well-defined experimental setups, clearly justified reward structures, and comprehensive comparisons with baselines were prioritized. Emphasis was placed on works that introduced methodological or architectural innovations and reported extensive evaluations using recognized performance indicators.
- Findings Synthesis: The extracted insights were thematically synthesized to allow for cross-comparison of RL applications in EVCS control. This synthesis involved grouping studies based on RL architecture, deployment environments, interaction with the power grid (e.g., V2G or RES integration), and evaluation objectives (e.g., energy cost savings, peak load reduction, user comfort). Such a structured approach also enabled basic meta-analyses across studies, facilitating the identification of emerging trends, key limitations, and underexplored areas. The resulting framework formed a comprehensive knowledge base to support future advancements in RL-driven EVCS management.
The methodology employed for the literature analysis may be outlined in Figure 3.
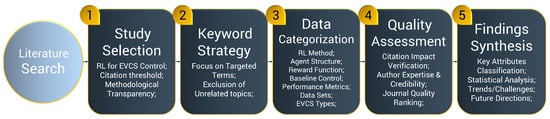
Figure 3.
Literature approach.
3. Primary EVCS Types
EVCS frameworks may be systematically categorized along three key dimensions—deployment context, operational characteristics, and smart feature capabilities. The deployment framework context defines where and for whom the charger is installed, such as residential, public, workplace, or fleet environments. The operational characteristics refer to the charger’s power level and speed—ranging from slow residential units to ultra-fast highway systems—which determine how quickly vehicles can be recharged. Lastly, the smart features and grid interaction capabilities describe the technological sophistication of the charger, including connectivity, bidirectional energy flow, renewable integration, and wireless functionality [66,67]. This three-fold classification framework is essential for understanding the technical and contextual diversity of EVCSs in both research and real-world applications. Figure 4 delivers such a three-dimensional classification of EVCS frameworks. More specifically:
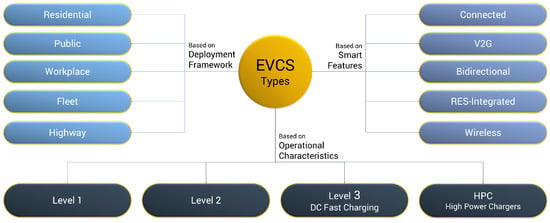
Figure 4.
Primary EVCS types based on deployment framework, smart features, and operational characteristics.
3.1. EVCS Types Based on Deployment Framework
The deployment framework of an EVCS refers to the physical setting and functional purpose of the charging infrastructure, which varies significantly based on user needs, usage behavior, and local infrastructure constraints. Different deployment contexts demand tailored design and control strategies. For instance, residential setups prioritize user convenience and integration with home energy systems, while public or fleet-based deployments require scalability, fast service, and grid coordination. Recognizing these deployment types is essential for designing effective and context-aware RL optimization strategies. Broadly, EVCS deployment categories include the following:
- Residential EVCSs: Typically installed in private homes or apartment complexes, residential chargers offer Level 1 or Level 2 charging and are intended for individual users. These systems are often part of broader smart home energy networks and are integrated into demand-side management programs [68]. A notable subset is community or shared residential charging, found in multi-unit dwellings or energy communities. These setups prioritize equitable access, cooperative scheduling, and shared infrastructure ownership among residents [69].
- Public EVCSs: These chargers are accessible to all users and are located in urban areas such as shopping malls, city centers, and public parking facilities [70]. They typically include Level 2 and DC fast-charging stations and are essential for alleviating range anxiety. An overlapping category includes workplace chargers with public access during non-business hours [71], sharing operational concerns such as pricing models, accessibility, and utilization rates.
- Workplace EVCSs: Installed at corporate campuses or business facilities, workplace chargers primarily serve employees during work hours. They support strategies like load balancing, integration with solar energy systems, and sustainability initiatives [72]. Unlike public-access chargers, these systems benefit from predictable charging patterns and controlled access.
- Fleet EVCSs: Designed for centralized, high-power charging of commercial fleets such as buses, taxis, or delivery vans, fleet EVCSs enables scheduled charging aligned with route planning and operational needs [73]. These stations play a vital role in logistics electrification and often use advanced dispatch algorithms and energy cost optimization techniques.
- Highway EVCSs: Positioned along highways or intercity routes, these fast and ultra-fast charging stations support long-distance travel. They are optimized for short dwell times, high user throughput, and wide-area-network planning [74]. Fleet operators, particularly those in freight or long-haul transport, may also use these facilities, resulting in overlap with depot-type charging infrastructure [75].
- Mobile EVCSs: Mobile EVCSs consist of portable charging units that can be rapidly deployed in temporary or emergency scenarios, including rural zones, outdoor events, or disaster recovery operations [76]. They offer unmatched flexibility and are often used as backup or supplemental charging for residential or fleet operations [77].
3.2. EVCS Types Based on Operational Characteristics
Another important classification of EVCSs relates to their operational characteristics, specifically the power output and corresponding charging speed (see Figure 5). Such factors not only influence the charger’s suitability for different contexts—residential vs. highway—but also affect energy management, grid load, and user convenience. The four primary EVCS types (See also Figure 5) vary significantly in terms of power capacity, infrastructure cost, and deployment use cases [78,79]:
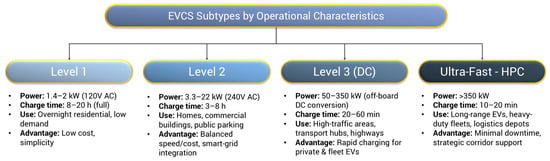
Figure 5.
EVCS subtypes based on operational characteristics.
- Level 1 Chargers: Such subtypes concern the most basic and slowest charging systems, providing 1.4–2 kW via a standard 120V AC outlet. A full charge typically takes 8 to 20 h, making them ideal for overnight residential use where charging speed is not critical [80]. Their affordability and simplicity make them suitable for households with low daily driving demands [79,80].
- Level 2 Chargers: Offering 3.3–22 kW of power through a 240 V connection, Level 2 chargers significantly reduce charging time to around 3–8 h. They are widely used in homes with higher electrical capacity, commercial buildings, and public parking areas. Balancing performance and cost, Level 2 chargers are commonly integrated into smart grid systems for improved load management [78].
- Level 3—DC Fast Chargers: These high-powered systems deliver 50–350 kW and can charge most EVs up to 80% in just 20 to 60 min. By converting AC to DC within the charging station itself, they bypass the vehicle’s onboard charger to allow rapid energy transfer [80]. DC fast chargers are typically found in high-traffic commercial areas, transportation hubs, and along highways, serving both private users and fleet vehicles [81].
- Ultra-Fast–High-Power Chargers (HPCs): Exceeding 350 kW, these next-generation chargers are designed for ultra-rapid refueling of heavy-duty or long-range EVs. HPC stations can deliver a near-full charge in just 10–20 min [82,83]. Their deployment is common along strategic transport corridors, logistics hubs, and in fleet depots where minimizing vehicle downtime is essential [83].
3.3. EVCS Types Based on Smart Features
As EVCSs evolve beyond basic power delivery, their integration into intelligent and flexible energy ecosystems has become increasingly critical. This classification dimension focuses on the smart features of EVCSs—specifically their communication, control, and interaction capabilities with users and the power grid. These features not only enhance user experience but also facilitate load balancing, renewable energy integration, and overall grid reliability. Smart-enabled EVCSs are essential building blocks for future smart cities and resilient transportation infrastructures.
- Smart-Connected EVCSs: These chargers are equipped with communication interfaces that enable real-time data exchange with users, utilities, and energy management platforms [84]. Smart functionalities may include user authentication, remote diagnostics, usage-based billing, dynamic charging schedules, and intelligent load management [85]. Such chargers play a pivotal role in demand response (DR) programs and are commonly linked to mobile applications or cloud-based control systems [86].
- V2G-Enabled EVCSs: Vehicle-to-grid (V2G)-enabled chargers allow energy to flow bidirectionally—enabling EVs not only to charge from the grid but also to return excess energy to it [87,88]. This bidirectional capability supports grid services such as frequency regulation, peak demand mitigation, and emergency power supply. V2G systems are typically implemented in scenarios where EVs function as distributed energy storage assets, enhancing grid flexibility and stability [89].
- Bidirectional EVCSs: While V2G represents a subset, the broader category of bidirectional EVCSs includes support for vehicle-to-home (V2H), vehicle-to-building (V2B), and vehicle-to-load (V2L) applications. These systems allow energy to flow between the EV and various endpoints, enabling use cases like home backup power during outages or supporting microgrid operations. Such functionality increases energy autonomy and system resilience.
- RES-Integrated EVCSs: These charging systems are coupled with on-site renewable energy sources (RESs), most commonly solar photovoltaic (PV) or small-scale wind turbines [90]. Often paired with battery energy storage systems (ESSs), RES-integrated EVCSs help mitigate renewable variability and allow EVs to be charged using clean, locally generated power [91]. This configuration is particularly valuable in eco-villages, rural areas, and sustainability-focused communities.
- Wireless EVCSs: Wireless charging stations transfer energy via inductive coupling between a ground pad and a receiver mounted beneath the vehicle [92,93]. Although still in early commercial or pilot stages, this technology eliminates the need for physical connectors, offering a seamless and automated charging experience. Wireless EVCSs are particularly promising for autonomous vehicle fleets, shared mobility hubs, and curbside urban charging, where automation and user convenience are key priorities.
4. The Concept of RL Control for EVCSs
RL presents a powerful paradigm for optimizing the operation of EVCSs, especially under dynamic and uncertain conditions. In an RL-based system, an intelligent agent learns to make sequential decisions by interacting with its environment,-comprising EV arrivals and departures, user preferences, electricity prices, grid conditions, and renewable energy availability.
At each decision step, the agent observes the current state of the environment—such as battery levels, charger occupancy, and time constraints—and selects an action, for example, when and how much to charge a vehicle. After executing this action, the environment transitions to a new state, and the agent receives a reward signal that quantifies the effectiveness of its decision. This reward may reflect objectives such as minimizing energy costs, avoiding grid overloads, maximizing renewable energy usage, or meeting user deadlines. Over time, the RL agent learns an optimal policy that balances these trade-offs, enabling real-time, adaptive control of the EV charging process.
4.1. RL Control Description for EVCSs
A step-by-step description of the RL control optimization procedure for EVCSs—along with interactions with other energy system components—is illustrated in Figure 6 and outlined as follows:
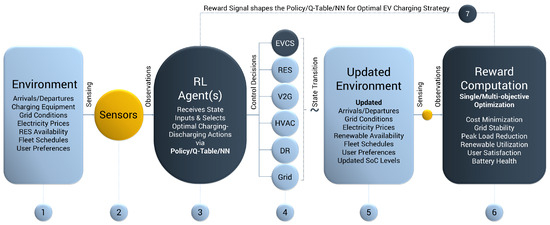
Figure 6.
Step-by-step RL control optimization procedure for EVCSs.
- Environment: The environment includes the EVCS infrastructure and its broader energy ecosystem. This encompasses EV arrivals and departures, energy availability from the grid or renewables, dynamic electricity prices, user preferences (e.g., departure time, desired state of charge), battery limitations, and possible grid-side constraints. In more complex scenarios, the environment may involve multiple stations, aggregators, and fleet operators. While the RL agent does not control the environment, it continuously adapts to its evolving state.
- Sensors and Observations: Real-time data is collected through smart meters, session logs, reservation systems, user applications, and grid communication interfaces. Observed variables include EV arrival times, current SoC, time-to-departure, energy demand, charger availability, historical usage patterns, grid signals (e.g., time-of-use tariffs, demand response events), and renewable generation levels. This data forms the observable state space for the RL agent.
- RL Agent(s): The RL agent is responsible for making optimal charging decisions. It may be centralized—controlling one or more stations—or decentralized, where each EV or charger acts independently. The agent selects actions such as which EV to charge, how much energy to deliver, or when to pause or resume charging. These decisions aim to optimize multiple objectives, including energy cost reduction, peak load mitigation, user satisfaction, and renewable energy utilization. Through continuous interaction with the environment, the agent improves its policy over time.
- Control Decision Application: Once the RL agent selects an action, it is translated into executable commands such as initiating charging, adjusting power levels, or deferring sessions. In depot or fleet contexts, this may include multi-vehicle scheduling. These actions are applied in real time through the electric vehicle supply equipment (EVSE), subject to physical constraints such as charger capacity and transformer limits.
- Environment Update: Following the action, the environment evolves naturally. Vehicles gain charge, some depart, others arrive; electricity prices fluctuate; renewable output varies; and user behavior introduces further uncertainty. This results in a new system state, which becomes the next input to the agent’s learning process.
- Reward Computation: The system computes a numerical reward that reflects how well the agent’s action aligned with predefined objectives. Reward components may include energy cost savings, success in peak shaving, alignment with renewable output, user satisfaction (e.g., full charge before departure), or penalties for poor performance. In V2G scenarios, rewards may also account for grid services provided or revenue from energy discharge.
- Reward Signal Feedback: The reward is fed back into the RL algorithm, enabling the agent to refine its policy. Algorithms such as Q-learning, DDPG, or PPO are used to guide this learning process. With each interaction cycle, the agent improves its ability to handle diverse conditions, including fluctuating prices, variable loads, and unpredictable user demands—ultimately enabling intelligent, real-time control of EV charging operations.
Through continuous learning and adaptation, RL-based EVCS control frameworks have the potential to outperform traditional rule-based or pre-scheduled methods. By dynamically responding to real-world complexities such as stochastic EV arrivals, time-varying pricing, intermittent renewable energy, and system constraints, RL enables smarter, user-centric, and grid-supportive charging strategies.
4.2. The Mathematical Concept of RL
RL models EVCS control as a Markov decision process (MDP), enabling agents to learn optimal charging strategies through continuous interaction with a dynamic environment. This formalism allows the agent to make sequential decisions under uncertainty, adapting to real-time variables such as electricity pricing, EV arrival and departure times, grid load conditions, renewable energy output, and user demand. As a model-free, data-driven approach, RL eliminates the need for manually crafted rules or pre-defined schedules, offering adaptive control that evolves over time.
The mathematical foundation of RL is defined by the MDP tuple , where
- S represents the set of environment states (e.g., SoC levels, grid load, energy prices, EV requests);
- A denotes the set of actions (e.g., charging rate adjustment, delay charging, activate V2G);
- is the transition probability to a new state from state s under action a;
- defines the immediate reward for executing action a in state s;
- is the discount factor used to balance short- and long-term rewards.
The agent aims to learn a policy that maximizes the expected cumulative return:
This leads to the definition of the state–value function:
and the action-value function:
In model-free learning approaches like Q-learning, the Q-function is iteratively updated using the following:
where denotes the learning rate that determines the step size in learning.
4.3. Multi-Agent Reinforcement Learning
While single-agent RL is suitable for isolated EVCS control, real-world scenarios often involve multiple interacting entities—EVs, chargers, aggregators, and grid operators—each with their own objectives and decision-making capabilities. In such settings, multi-agent reinforcement learning (MARL) becomes essential, enabling decentralized or distributed control via multiple coordinated RL agents.
In MARL, we define a set of agents , each operating with its own policy . The environment is modeled as a stochastic game represented by the tuple , where
- is the global state space;
- is the action space of agent i;
- is the state transition probability;
- is the reward for agent i;
- is the discount factor for future rewards.
Each agent seeks to maximize its expected return:
However, from an individual agent’s perspective, the environment becomes non-stationary as other agents simultaneously update their strategies. This complexity introduces significant challenges, necessitating specialized coordination and training mechanisms.
Value and Action Networks in MARL
In both single-agent and multi-agent RL, decision-making is commonly supported by two core components [31]:
- Value Networks (Critics): These networks evaluate the quality of a given state or state–action pair. The state-value function predicts the long-term return when following policy from state s, while the action-value function estimates the expected return when taking action a in state s. In actor–critic algorithms, the critic informs and guides policy improvement.
- Action Networks (Policies): These networks determine the agent’s actions. In discrete spaces, the policy outputs action probabilities; in continuous settings, it generates control commands (e.g., specific charging rates). Policies are optimized using signals from the critic to favor actions with higher expected returns.
In MARL environments, value and policy networks require careful design due to the presence of multiple agents and shared decision spaces. Their structure, training strategy, and coordination mechanism are critical to achieving robust and scalable learning outcomes [31,37]:
- Structure: Describes how networks are distributed or shared among agents. Common configurations include the following:
- -
- Centralized Critic with Separate Policies: A single critic observes the global state; each agent maintains an independent policy.
- -
- Fully Separate Critics and Policies: Agents operate entirely independently, which maximizes autonomy but can hinder learning stability.
- -
- Shared Critic and Policy: All agents share a common network, promoting unified control but limiting agent specialization.
- -
- Hybrid–Partially Shared: Network layers are partially shared to capture global patterns, while deeper layers remain agent-specific.
- Training: Refers to how agents update their policies and what information is available during learning. Variants include the following:
- -
- Centralized Training with Decentralized Execution (CTDE): Global information is used during training; agents act based on local data at runtime.
- -
- Fully Decentralized Training: Agents learn from their own experience only, enabling privacy but risking convergence issues.
- -
- Fully Centralized Training: A central controller manages training across agents; computationally intensive but often stable.
- -
- Hybrid Approaches: Combine centralized and local training, e.g., agents train locally with periodic global updates.
- Coordination: Focuses on how agents cooperate or share information:
- -
- Implicit Coordination: Achieved via shared objectives or rewards, without direct communication.
- -
- Explicit Coordination: Involves message exchange, negotiation, or prediction sharing.
- -
- Emergent Coordination: Cooperation arises naturally as agents learn interdependencies through interaction.
- -
- Hierarchical Coordination: Involves structured agent roles, such as leaders assigning tasks to sub-agents.
In the context of EVCSs, MARL provides the foundation for enabling decentralized yet coordinated decision-making across vehicles, stations, and energy systems, supporting intelligent, adaptive control that balances local autonomy with global optimization.
4.4. Common RL Algorithms for EVCS Control
RL algorithms used for EVCS management can be broadly categorized into three main types: value-based, policy-based, and actor–critic approaches [37]. Each class offers distinct advantages in handling control challenges related to discrete versus continuous action spaces, centralized versus decentralized control, and the presence of dynamic or stochastic environments.
4.4.1. Value-Based Algorithms
Value-based methods focus on estimating the expected return of each action and selecting the action with the highest value. These algorithms are particularly well-suited for EVCS environments involving discrete decisions, such as choosing between charging, idling, or discharging [94,95].
- Q-Learning (QL): Q-Learning is a widely used off-policy algorithm that learns the optimal action-value function independently of the current policy. It is especially effective in small-scale EVCS systems and updates the Q-values using the following:Despite its simplicity, Q-Learning struggles with scalability in large or high-dimensional EVCS networks [58].
- Deep Q-Networks (DQNs): DQN extends Q-Learning by approximating the Q-function using deep neural networks. It incorporates experience replay and target networks to stabilize training [96]:DQN has been applied in community-scale EVCS deployments and load balancing tasks where temporal variability is a key factor [97].
4.4.2. Policy-Based Algorithms
Unlike value-based methods, policy-based algorithms directly optimize the policy without explicitly estimating the value function. These are especially useful in continuous action domains, such as fine-tuning the charging rate over time.
- Proximal Policy Optimization (PPO): PPO achieves a balance between policy exploration and training stability by constraining the magnitude of policy updates [98,99]:where and is the advantage estimate. PPO has demonstrated strong performance in scalable EVCS applications, particularly under dynamic pricing conditions.
4.4.3. Actor–Critic Algorithms
Actor–critic methods combine the strengths of value-based and policy-based algorithms. The actor proposes actions, while the critic evaluates them, enabling efficient and stable learning in complex environments.
- Deep Deterministic Policy Gradient (DDPG): DDPG is well-suited for continuous control tasks, such as modulating EV charging rates. The critic and actor are updated as follows [100]:
- Soft Actor–Critic (SAC): SAC enhances exploration by adding an entropy term to the learning objective, promoting robustness in uncertain environments [101]:This algorithm has been adopted in V2G-enabled EVCS settings, where the environment is highly dynamic and unpredictable [102].
- Advantage Actor–Critic (A2C): A2C improves training efficiency and reduces variance using the advantage function [103]:A2C has been used in decentralized, multi-agent EVCS control, where minimal communication among agents is required but cooperative behavior is still essential.
Each of these RL paradigms enables EVCS control systems to autonomously learn optimal strategies that adapt to user preferences, grid constraints, and cost objectives—offering a scalable and intelligent alternative to traditional rule-based or model-driven approaches.
5. Attribute Tables and Summaries of RL Applications
This section illustrates the high impact of RL applications in EVCSs from 2015 to 2025, by offering a high-level overview of value-based, policy-based, actor–critic, and hybrid high-impact applications found in the literature. This approach allows readers to quickly identify relevant applications in the attribute tables and refer to the detailed summaries for deeper insights into their methodologies and findings.
5.1. Attribute Tables and Summaries Description
Key attribute tables, systematically illustrate each application according to key characteristics, ensuring a comprehensive understanding of the overall approach:
- Ref.: Contains the reference application, which is listed in the first column.
- Year: Contains the publication year for each research application.
- Method: Contains the specific RL algorithmic methodology applied in each application.
- Agent: Contains the agent type of the concerned methodology (single-agent or multi-agent RL approach).
- FH/TS: Illustrates the forecast horizon (FH) and the time step (TS) intervals for the RL control application considering the EVCSs.
- Baseline: Illustrates the comparison methods used to evaluate the proposed RL approach (such as RBC, MPC, greedy, fixed, MILP, or other RL-based strategies).
- Type: Contains the primary deployment type of the concerned EVCSs (e.g., residential, public, fleet, highway, etc.).
- Integration: Indicates additional energy systems and mechanisms interacting with the EVCSs (e.g., RES, ESS, HVAC, DR, V2G, main grid, etc.).
- Data: Describes the type of data used to train the RL algorithms. Studies utilizing actual measurements from real-world EVCS deployments are labeled as real; those using simulated or synthetic data are labeled as synth; and those combining both sources are marked as Both.
Moreover, the summaries are integrated in the tables that follow each key attribute table, providing a brief synopsis of the applications. More specifically:
- Author: Contains the name of the author along with the reference application.
- Summary: Contains a brief description of the research work.
The abbreviations “-” or “N/A” represent the “not identified” elements in tables and figures.
5.2. Value-Based RL Applications
The value-based RL applications for TSC and their primary attributes are integrated in Table 2, while the brief summaries of the applications are illustrated in Table 3.

Table 2.
Key attributes of value-based RL applications for EVCSs.

Table 3.
Summaries of value-based RL applications for EVCSs.
5.3. Policy-Based RL Applications
The policy-based RL applications for EVCSs and their primary attributes are integrated in Table 4, while brief summaries of the applications are illustrated in Table 5:

Table 4.
Key attributes of policy-based RL applications for EVCSs.

Table 5.
Summaries of policy-based RL applications for EVCSs.
5.4. Actor–Critic RL Applications
The actor–critic RL applications for EVCSs and their primary attributes are depicted in Table 6, while brief summaries of the applications are illustrated in Table 7:

Table 6.
Key attributes of actor–critic RL applications for EVCSs.

Table 7.
Summaries of actor–critic RL applications for EVCSs.
5.5. Hybrid RL Applications
The hybrid RL applications for EVCSs and their primary attributes are depicted in Table 8, while brief summaries of the applications are illustrated in Table 9:

Table 8.
Key attributes of hybrid RL applications for EVCSs.

Table 9.
Summary of hybrid RL applications for EVCSs.
6. Evaluation
To offer a structured and comparative overview of existing RL applications for EVCSs, the evaluation focuses on seven key attributes:
- Methodology and Type: Defines the core structure and features of each RL algorithm.
- Agent Architectures: Explores prevailing agent architectures, emphasizing multi-agent RL trends.
- Reward Functions: Analyzes reward design variations across RL control implementations.
- Baseline Control: Reviews baseline strategies used to compare and validate RL performance.
- Datasets: Reviews the utilized data types for RL implementation in EVCS frameworks.
- Performance Indexes: Identifies commonly used evaluation metrics and their characteristics.
- EVCS Types: Identifies commonly used EVCS types in research, identifying trends and limitations.
Such dimensions capture the critical factors in designing, deploying, and benchmarking RL-based controllers. Dissecting the literature along these axes helps readers understand how RL techniques align with various traffic control frameworks, design constraints, and performance objectives—supporting informed choices for different network scenarios.
6.1. RL Types and Methodologies
The analysis of RL methodologies applied to EVCS control reveals that actor–critic approaches dominate in volume, reflecting their strong capability to manage continuous action spaces, multi-agent interactions, and constraint-aware decision-making (see Figure 7—right). Techniques such as DDPG and SAC are frequently employed in grid-integrated and scalable scheduling frameworks [126,129,137,138], where they often outperform value-based methods in high-dimensional, dynamic environments (see Figure 7—left). Value-based RL algorithms—such as Q-learning and DQN—remain widely used, particularly in simpler, single-agent, or discretized scenarios where cost optimization is the primary focus [104,106,117]. In contrast, policy-based RL methods appear far less frequently in the literature, with only a few notable studies. Nevertheless, in those limited cases, policy-based strategies have demonstrated considerable promise, especially in embedding safety constraints directly into the EVCS decision-making pipeline [120,121]. Such methodological distribution reflects a broader evolution in the field—while value-based methods laid the groundwork for early EVCS control solutions, actor–critic architectures have since emerged as the dominant paradigm for managing complex, real-world, and multi-agent charging environments. More specifically:
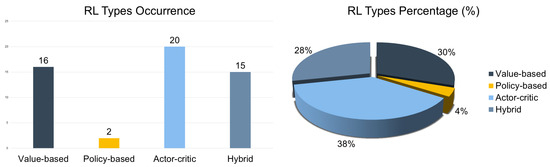
Figure 7.
(Left): RL type occurrence overall; (Right): RL type percentage (%) overall.
Value-based: The development of value-based RL in EVCS applications illustrates a clear trajectory, evolving from early model-free Q-learning toward more advanced deep and hybrid formulations that address the increasing complexity of charging systems. Initial studies, such as those using fitted Q-Iteration [104,109], validated the feasibility of batch-mode RL, enabling training from historical data and reducing the risks associated with real-world exploration. These methods proved especially effective in residential and public charging environments by offering scalability without needing detailed grid models. However, their offline learning nature limited adaptability in real-time scenarios, encouraging a shift toward online learning and function approximation. This shift became evident in studies like [108,120], where SARSA with linear approximators and deep value networks improved the responsiveness and scalability of control systems for dynamic pricing and power flow management. Meanwhile, deep Q-learning frameworks—such as those presented in [106,111,113]—incorporated temporal representation learning (e.g., LSTM networks) to model sequential patterns in charging behavior, improving forecasts and dynamic adaptability. While these innovations marked major advancements, they also introduced new challenges—deep value-based RL models required significant training data and were often sensitive to poorly shaped or sparse reward functions. Multi-agent extensions, as seen in [110,112], broadened the applicability of value-based approaches by decentralizing decision-making across multiple EVs or distributed loads. Such methods tackled issues of fairness and coordination in community-level EVCS operations, but also exposed vulnerabilities such as slow convergence and increased instability due to non-stationary learning environments. To address these, enhancements like prioritized experience replay (PER) and hierarchical coordination schemes were integrated [117].
Notably, hybrid architectures that blend value-based learning with actor–critic principles or incorporate advanced replay mechanisms (e.g., PER, HER) have shown promising results in continuous control environments [114,115,116]. These demonstrate the flexibility of value-based RL to adapt when appropriately extended. Nonetheless, persistent limitations remain—particularly in handling continuous action spaces, which often necessitate integration with policy-gradient methods [115]. Additionally, extensive reliance on simulation restricts real-world deployment potential, a challenge shared across most RL methodologies. Reward engineering remains a central obstacle. For example, while DQN-based methods such as [118] demonstrated effective cost and grid optimization, they lacked explicit modeling of long-term battery degradation or user-centric objectives. These gaps are prompting a convergence in algorithmic design, incorporating hierarchical RL, model-based components, and transfer learning to reduce data requirements and improve generalizability.
Looking ahead, value-based RL is expected to evolve from its traditional single-agent, cost-minimization role toward more sophisticated multi-agent, multi-objective frameworks that jointly optimize user satisfaction, renewable integration, and grid flexibility. Emerging works—such as the cooperative DDQN-PER model of [117] and the dynamic frameworks of [115]—have illustrated this direction. Ultimately, the next generation of value-based RL will need to bridge discrete and continuous control strategies, integrate domain-aware reward structures, and deliver scalable, real-world-ready policies.
Policy-based: Although policy-based RL approaches remain limited in EVCS literature, they have addressed key limitations of value-based and actor–critic methods by focusing on direct policy optimization and the integration of safety guarantees. For example, Ref. [121] introduced Constrained Policy Optimization (CPO) to enforce grid and operational constraints directly during training, thereby ensuring safe and constraint-compliant charging behavior without the need for post hoc corrections. In a similar direction, Ref. [120] proposed a DNN-enhanced policy-gradient framework, augmented by dynamic programming techniques for real-time power flow control. This approach demonstrated rapid convergence and scalability in complex grid environments. Collectively, these studies highlight the potential of policy-gradient methods to effectively manage continuous control tasks and embed safety-critical features within the decision-making process. However, their broader adoption remains limited, potentially due to high computational demands and relatively low sample efficiency, which constrain their scalability and implementation in larger EVCS systems.
Actor–Critic: Actor–critic RL methodologies have rapidly evolved from basic single-agent implementations to advanced multi-agent and hybrid frameworks capable of addressing large-scale coordination, grid integration, and safety-aware control. Foundational contributions—e.g., the goal representation adaptive dynamic programming (GrADP) approach by [122]—have demonstrated early on the suitability of actor–critic methods for continuous control tasks, particularly in frequency regulation and ancillary services. Building on this foundation, deterministic policy gradient algorithms like DDPG became widely adopted (see Figure 8—left) for their ability to operate in continuous action spaces without discretization overheads [123,128,132]. The integration of recurrent structures, such as LSTM, further improved temporal decision-making in applications like dynamic pricing and SoC-constrained energy scheduling.
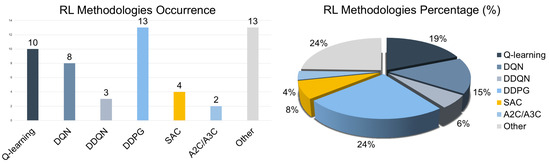
Figure 8.
(Left): RL methodology occurrence overall; (Right): RL methodology percentage (%) overall.
Scalability and decentralization have emerged as prominent research directions with the advent of multi-agent actor–critic frameworks. Studies such as [129,135] employed centralized training with decentralized execution (CTDE) architectures, leveraging mechanisms like counterfactual baselines (e.g., COMA) and game-theoretic coordination to mitigate credit assignment challenges while promoting cooperative autonomy. Similarly, in [130], researchers introduced adaptive gradient re-weighting among critics to reduce policy conflict, whereas [134] extended multi-agent DDPG for V2G-enabled frequency regulation, enabling collaborative EV decision-making in grid-supportive scenarios.
Recent advances have also prioritized constraint-aware learning. For instance, Ref. [125] incorporated second-order cone programming (SOCP) into DDPG to enforce voltage stability constraints, while [138] applied a constrained soft actor–critic (CSAC) method to embed grid and operational constraints directly into the policy-learning process. Similarly, Ref. [133] proposed a bilevel DDPG framework that combines predictive LSTM modules with safety shields, enabling feasible and reliable scheduling decisions under uncertainty. Such innovations underscored the growing emphasis on safe and risk-aware RL—an especially important consideration for real-world EVCS operations within tightly constrained grid infrastructures.
Entropy-regularized actor–critic methods such as SAC are also gaining traction due to their improved exploration capabilities and higher sample efficiency in stochastic environments [136,139]. Meanwhile, Ref. [141] combined actor–critic RL with probabilistic forecasting and metaheuristics to develop a risk-sensitive, multi-objective scheduling framework. In parallel, Ref. [131] employed TD3 to address value overestimation and improve the training stability of battery-enabled charging infrastructure. Collectively, these innovations illustrate a trajectory toward integrated, hybrid actor–critic systems that balance learning efficiency with operational safety, grid stability, and market responsiveness.
Although actor–critic RL has shown promise, several challenges still limit its practical use in EVCS control. One major issue is its high sample complexity—these methods often need millions of state–action interactions to learn effectively, which makes real-world training difficult. Another common problem is training instability: if the critic’s estimates are inaccurate, they can misguide the actor, leading to unstable or even failed learning. To tackle such challenges, several strategies have been proposed. Some studies use offline pre-training with historical charging or mobility data to give the model a strong starting point, reducing the need for extensive online learning [106,115]. Others rely on expert demonstrations or simpler rule-based/MPC controllers to guide early learning, which helps improve stability [109,127]. In addition, actor–critic models are increasingly incorporating learned models of the environment or predictive demand approximations to reduce the number of real-world interactions needed. These efforts aim to bridge the gap between data-hungry simulations and the more demanding conditions of real-world EVCS deployment, where efficiency and stability are key.
Furthermore, multi-agent actor–critic models often suffer from non-stationarity and increased coordination overhead in large-scale networks—a limitation only partially addressed through hierarchical control decomposition [124] or federated learning architectures [126]. Going forward, future research should prioritize the integration of hierarchical actor–critic schemes, safety-focused RL, and hybrid decision-making frameworks informed by predictive modeling, in order to bridge the persistent gap between simulation-based learning and real-world deployment in EVCS systems.
Hybrids: Hybrid RL approaches have also emerged as a prominent direction in EVCS control research, representing a significant evolution of RL by integrating complementary methodologies to overcome the individual limitations of model-free RL, mathematical optimization, and forecasting. Early contributions, such as [142], combined multi-step Q() learning with multi-agent coordination to enhance convergence speed and scalability in mobile EVCS scheduling under dynamic grid conditions. Likewise, Ref. [143] proposed a hybrid of model-based and model-free RL, using value iteration for rapid policy initialization followed by Q-learning refinement—thereby reducing exploration overhead while preserving adaptability.
According to evaluation, hybrid RL schemes are predominantly characterized by combinations of RL with mathematical optimization techniques—such as MILP, ILP, BLP, SP, and game theory—for feasibility and constraint satisfaction [149,151] (see Figure 9—left and right). This hybridization illustrates how the real-time adaptability of RL can be effectively fused with the rigor of optimization frameworks to yield high-quality, feasible charging strategies. For instance, Ref. [149] integrated multi-agent DQN with MILP post-optimization to enable decentralized agents to learn local policies, while MILP ensured coordinated scheduling across battery-swapping and fast-charging stations. Similarly, Ref. [151] used RL in conjunction with MILP to maintain grid-compliant station operations, and [152] merged RL with LSTM-based forecasting and ILP for adaptive yet constraint-respecting V2G scheduling. Additional works have explored RL in tandem with game-theoretic models [145] or surrogate optimization [153], and hybridized RL with metaheuristics like GA, DE, WOA, and MOAVOA to support large-scale planning and global search tasks [148,156]. A smaller subset of hybrid studies also focused on algorithmic coordination and matching: for instance, Ref. [143] demonstrated how local RL decisions can be augmented through tailored global coordination schemes.
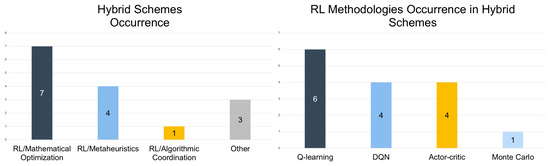
Figure 9.
(Left): Hybrid RL scheme occurrence; (Right): RL methodology occurrence as a counterpart in hybrid schemes.
Recent developments in hybrid RL have expanded into multi-agent and actor–critic combinations. For example, Ref. [150] combined soft actor–critic (SAC) for virtual power plant (VPP) energy trading with TD3 for EVCS-level scheduling in a cooperative, multi-agent setting—demonstrating how hybrid RL can co-optimize grid-scale operations and local EV management. Similarly, Ref. [154] introduced a two-level P-DQN-DDPG architecture that integrates discrete booking decisions with continuous pricing control, a particularly valuable advancement for real-time, market-driven EVCS operations. These multi-layered frameworks signal a broader trend in hybrid RL: toward holistic, multi-agent, multi-objective, and multi-level optimization across operational, economic, and grid-interactive domains. In addition, surrogate modeling and simulation-based planning have been incorporated into hybrid RL designs. For instance, Ref. [153] fused Monte Carlo RL with surrogate optimization to solve large-scale EVCS siting problems, while [146] combined DQN with binary linear programming for efficient fleet and charger coordination. These innovations illustrate the potential of hybrid RL to act as an orchestrator—merging data-driven learning with analytical models to enhance convergence speed, policy quality, and scalability.
Overall, hybrid RL has matured into a unifying framework in which RL is no longer treated as a standalone controller, but as the intelligent core of integrated decision-making systems. This paradigm shift effectively addresses challenges such as scalability, safety, and multi-objective optimization in EVCS management, while paving the way for real-world deployment. Future research is expected to build on these foundations by exploring risk-aware scheduling strategies [141], scalable multi-agent architectures [155], and hierarchical RL–optimization pipelines that support real-time, grid-interactive EVCS control.
6.2. Agent Architectures
MARL has emerged as a critical trend in EVCS control, addressing the scalability and coordination challenges posed by large-scale EV integration. As illustrated in Figure 10 (right and center), MARL methodologies have seen widespread adoption across EVCS-related research. Early decentralized Q-learning studies, such as [110,112], demonstrated how independent agents can learn charging policies based solely on local observations, enabling scalable and modular control architectures without the need for centralized oversight. However, such fully decentralized frameworks often suffer from suboptimal global coordination, leading to the rise of centralized training with decentralized execution (CTDE) paradigms.
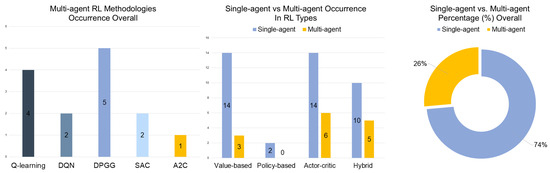
Figure 10.
(Left): Multi-agent applications by RL methodology; (Center): single-agent vs. multi-agent distribution by RL type; (Right): overall percentage of single-agent vs. multi-agent applications.
Recent works such as [129,130,134,150,155] employed shared critics with decentralized policy networks, allowing agents to access global grid-level knowledge during training while preserving execution autonomy. Moreover, advanced designs such as the non-cooperative game-theoretic MARL framework by [135] introduced spatially discounted rewards to balance local competitiveness with system-level coordination. Hybrid MARL frameworks have also emerged—for instance, the integration of MILP post-optimization in [149] and the hierarchical Kuhn-Munkres matching algorithm in [145]—showcasing how optimization techniques can enhance MARL to ensure grid compliance and infrastructure-wide efficiency. Overall, MARL research in EVCS control is clearly progressing toward hierarchical, hybrid, and cooperative architectures capable of addressing diverse objectives such as grid stability, fairness, and renewable energy integration.
An essential consideration in MARL control lies in the clear identification and implementation of three foundational elements: Structure, Training, and Coordination, as introduced in Section 3. These dimensions are crucial, as they define how knowledge is shared, how policies are learned, and how agent collaboration is orchestrated across the system. A well-defined strategy for each of these dimensions directly impacts scalability, learning stability, and adaptability to complex, dynamic environments like EVCS systems. A closer look reveals the following:
- Structure: Analysis of structural choices in MARL for EVCSs shows a clear dominance of architectures using a shared centralized critic with separate policy networks (see Figure 11—left). This configuration, adopted in studies such as [129,130,134,150], enables agents to benefit from a global value function during training while preserving decentralized policy execution for scalability. In contrast, architectures with fully independent critics and policies, as found in [110,112], prioritize agent autonomy and implementation simplicity at the cost of coordinated global optimization. Partially shared or hybrid structures are rare, appearing in only a few studies such as [142], with most research favoring CTDE-compatible architectures due to their balance of coordination and independence. Some advanced variants, like [130], further enhanced MARL scalability by employing multi-critic architectures with adaptive gradient re-weighting to mitigate inter-agent policy conflict.
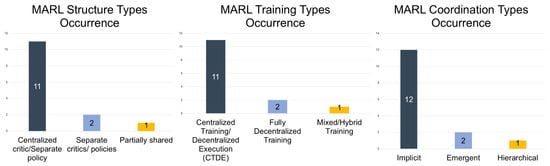 Figure 11. (Left): MARL structure-type occurrence in EVCS frameworks; (Center): MARL training-type occurrence in EVCS frameworks; (Right): MARL coordination-type occurrence in EVCS frameworks.
Figure 11. (Left): MARL structure-type occurrence in EVCS frameworks; (Center): MARL training-type occurrence in EVCS frameworks; (Right): MARL coordination-type occurrence in EVCS frameworks. - Training: Centralized Training with Decentralized Execution has become the prevailing training paradigm in MARL-based EVCS control (Figure 11—Center), enabling agents to incorporate global system information during learning while executing actions locally [126,135,155]. CTDE effectively mitigates non-stationarity in multi-agent settings and promotes stable convergence. Fully decentralized training appears mainly in simpler settings involving tabular or basic function-approximation Q-learning [110,112]. Some studies also explored mixed training schemes—such as [145], which combines decentralized Q-learning with periodic centralized matching—demonstrating how hybrid paradigms can enable scalable yet coordinated scheduling.
- Coordination: Implicit coordination has dominated the MARL landscape for EVCS control (see Figure 11—right), relying on shared reward functions or centralized critics to align agent behaviors without direct communication [129,134,150]. Such an approach may reduce communication overhead and simplify implementation, making it ideal for scalable and deployable systems. Emergent coordination—cases where agents collaborate through shared interactions with the environment—have been observed in decentralized frameworks like [110,112]. Explicit or hierarchical coordination mechanisms remain relatively rare; for example, Ref. [145] used a Kuhn-Munkres algorithm to coordinate agents periodically for efficient V2V charging. The general absence of explicit communication-based coordination reflects a broader focus on lightweight, communication-efficient MARL solutions tailored to real-world EVCS deployment.
Overall, MARL remained relatively underexplored in EVCS control, with only 14 of 52 studies (26% percentage—see Figure 10—right) employing decentralized or distributed RL methodologies despite its suitability for large-scale, decentralized charging coordination. Current applications, such as decentralized Q-learning [110,112] and CTDE-based actor–critic methods [129,130,134], demonstrated MARL’s potential to manage grid-constrained, multi-agent environments while enabling scalable cooperation among EVs, aggregators, and grid entities. However, potential challenges, including non-stationarity, high sample complexity, and coordination overheads, seem to prohibit a broader adoption. Future research is anticipated to deploy MARL research more intensively, focusing specifically on hierarchical coordination mechanisms [145], federated and privacy-preserving training schemes [126], and the integration with forecasting and optimization layers [149,155] to improve convergence, safety, and real-world deployability. Such advancements may promote MARL as the next-generation EVCS control, enabling self-organizing, grid-interactive, and fairness-aware charging ecosystems.
6.3. Reward Functions
Reward design concerns a foundational element in RL-based EVCS control, as it directly shapes agent behavior and learning convergence. A clear trend in recent literature reveals a shift toward multi-objective reward formulations, which have become significantly more prevalent than single-objective designs (see Figure 12—right). Only a limited subset of studies—such as [104,108,110,113,114,123,127,131,135,136,144,145,148,151]—have relied on single-objective rewards, often focused on isolated goals such as economic optimization or specific grid performance metrics (see Figure 12—right). In contrast, the majority of RL implementations adopted composite reward functions that integrated multiple objectives considering economic, grid, user experience, battery health, environmental sustainability, and fairness-related penalties, reflecting the complexity of modern EVCS ecosystems.
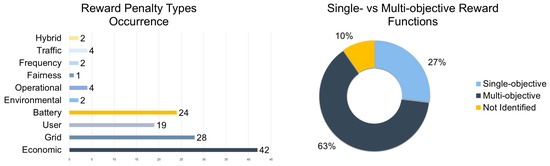
Figure 12.
(Left): Frequency of Reward Components in Overall RL Applications; (Right): Percentage of Single vs. Multi-objective Reward Functions.
Among these objectives, economic-oriented terms concern the most widely utilized penalties; see Figure 12—left). Such penalties typically aim to minimize charging costs or maximize operational profit through dynamic pricing strategies and energy arbitrage mechanisms [104,105,114,136,150] (see Figure 12—left). However, recent work has increasingly paired these with grid-supportive components—such as transformer overload mitigation, load balancing, and voltage/frequency stabilization—to enhance alignment with distribution network performance and reliability [109,110,117,134,137,152].
In parallel, user-centric reward terms have gained traction. These include penalties for unmet SoC targets, excessive waiting times, or high levels of range anxiety [106,112,118,129,130]. Additionally, some studies incorporate battery degradation costs to ensure the long-term health of EV batteries, an increasingly relevant concern for both fleet operators and private users [117,129,131]. Though less common, environmental-oriented rewards—particularly those targeting CO2 reduction and renewable energy utilization—are beginning to emerge, highlighting a growing emphasis on sustainability and carbon neutrality in EVCS design [155,156].
Despite this increasing sophistication in reward structures, several critical challenges remain. Sparse reward environments—such as those described in [115]—may significantly prohibit learning convergence, particularly in complex or sequential decision-making tasks. Additionally, linear weighting schemes used in multi-objective formulations—e.g., [135,152]—are often sensitive to hyperparameter-tuning, potentially introducing bias in the prioritization of objectives. Penalty-based constraint handling also dominates the field, which can lead to transient constraint violations during training [138].
Another notable trend acquired by the evaluations is that, despite the prevalence of multi-objective formulations, almost all existing EVCS RL studies ultimately relied on scalarized rewards through weighted sums or penalties [106,112,115,116,121,129,135,139,155,156]. To this end, almost no work has been found to employ genuine multi-objective RL methods, such as Pareto front learning, multi-objective policy gradients, or separate critics per objective. Such a trend highlights a significant research opportunity to move beyond ad-hoc weighting schemes toward principled frameworks that can capture diverse trade-offs and provide more robust charging policies.
Looking ahead, the development of more nuanced reward mechanisms is essential. Promising directions include risk-aware and probabilistic reward shaping strategies, such as those demonstrated in [141], where penalties are dynamically weighted based on uncertainty or event severity. Hierarchical or modular reward architectures may also offer greater clarity and flexibility, enabling agents to independently learn sub-policies for economic efficiency, grid compliance, and user satisfaction, while maintaining coherence at the system level. Finally, the integration of real-world feedback, particularly in federated or decentralized learning setups [126]—will be vital in ensuring that reward functions are practically grounded, robust, and capable of generalization to large-scale EVCS deployment scenarios.
6.4. Baseline Control
The analysis of baselines employed across RL-based EVCS studies reveals clear patterns regarding how researchers benchmark their approaches, reflecting both methodological maturity and evolving expectations in the field. RBC strategies, typically based on Time-of-Use (TOU) pricing or immediate charging policies, remain among the most widely adopted baselines [104,109,137] (see Figure 13—left). These methods are computationally simple, forecasting-free, and reflect legacy charging practices, making them ideal for demonstrating how RL can dynamically adapt to real-time pricing signals and grid conditions. Particularly in residential and public charging scenarios, outperforming RBC allows RL to establish its relevance in moving from static heuristics to context-aware optimization [118,140]. Another frequently used—yet simplistic—heuristic concerns the greedy or charge-when-plugged strategy, where EVs immediately draw maximum available power upon connection until fully charged [105,118,152]. Despite its lack of intelligence, this baseline provides a clear lower bound for evaluating RL effectiveness, especially in minimizing peak demand, transformer stress, and overall charging costs in single-agent and residential settings [106,118,137,138]. Together with fixed control strategies, these heuristic approaches constitute the dominant form of baseline control in current literature (see Figure 13—right).
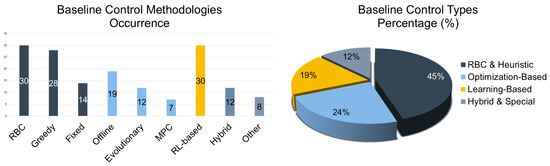
Figure 13.
(Left): Occurrence of baseline methodologies in overall RL applications; (Right): percentage of baseline control types used.
Offline optimization methods—particularly mixed-integer linear programming (MILP)—have also been widely used to benchmark RL against theoretically optimal schedules with perfect foresight (see Figure 13—left). Such approaches may offer a valuable upper bound for assessing cost minimization, load balancing, and constraint satisfaction [106,149,151]. For instance, Ref. [116] compared a cooperative DDQN framework with MILP optimization assuming full future knowledge to highlight RL’s capacity to approximate optimal solutions in real-time settings. Similarly, Refs. [111,118] employed offline MILP or deterministic optimization to quantify the performance gap between centralized planning and RL-based adaptive control. These comparisons reinforce RL’s advantage in uncertain or computationally constrained environments where offline methods may be impractical.
Evolutionary algorithms, including genetic algorithms (GAs), particle swarm optimization (PSO), and differential evolution (DE), were also present as comparative benchmarks, particularly in large-scale or multi-objective EVCS problems [112,155,156]. While these methods provide near-optimal offline solutions, their computational complexity and inability to adapt in real time make them unsuitable for operational use. Comparing RL to such baselines allows researchers to demonstrate that RL can deliver comparable (or superior) performance while adapting to dynamic conditions without repeated re-optimization. For example, Ref. [112] used GA as a baseline for microgrid-level MARL scheduling, and [155] contrasted MOAVOA-MADDPG against a standalone MOAVOA, showcasing RL’s advantage under uncertainty. Similarly, Ref. [156] benchmarked DE against an RL-based mobile EVCS planner, emphasizing RL’s superior adaptability.
MPC baselines, although less common, were employed in advanced studies involving grid-integrated and community-level charging systems [106,115,125]. MPC offers strong performance under forecastable environments by optimizing over a receding horizon; however, its reliance on accurate models and high computational cost renders it impractical for large-scale, real-time EVCS operation [115,128]. Consequently, many studies position RL as a scalable and model-free alternative, capable of achieving similar or better outcomes under stochastic conditions and incomplete information [106,115,125,128].
A particularly important trend involves the increasing use of learning-based baselines, which mark a methodological shift from feasibility demonstration to algorithmic refinement (see Figure 13—right). Many studies benchmarked new RL schemes against existing state-of-the-art RL variants to showcase improvements in learning speed, convergence, and robustness. For instance, Ref. [117] evaluated their cooperative DDQN model against standard Q-learning, DQN, and prioritized replay variants, highlighting gains in cost reduction and convergence rate. Similarly, Ref. [150] demonstrated that their hybrid SAC–TD3 architecture outperformed both SAC and TD3 independently, showing the benefits of hybridization. In hierarchical RL research, Ref. [126] benchmarked a federated SAC framework against standard SAC, A2C, and TOU-based RBC baselines, validating superior economic and user satisfaction performance. Moreover, hybrid learning baselines—e.g., integrating forecasting into RL—have gained traction. For example, Ref. [141] evaluated their WOAGA-RL approach against DDPG and traditional ML forecasting methods (LSTM, DeepAR), establishing the value of incorporating predictive modeling into decision-making. This trend indicates that RL-based baselines are now central to performance benchmarking, highlighting the maturity of the field and its shift toward intra-RL comparisons across algorithm families.
Finally, some studies employed hybrid or metaheuristic baselines—such as MOAVOA, WOAGA, or stochastic MILP—particularly in mobile EVCS deployment and multi-objective optimization contexts [141,155,156]. Such comparisons illustrate the growing emphasis on robustness, sustainability, and real-world applicability, placing RL within the broader paradigm of hybrid and integrative control frameworks. In summary, the evolution of baseline methodologies—from simplistic heuristics to sophisticated optimization and learning-based frameworks—signals a broader transition in EVCS research. Rather than merely establishing feasibility, RL methods are increasingly validated through comparisons with state-of-the-art optimization and learning systems. This shift underscores RL’s maturity and its growing potential to serve as a scalable, intelligent control strategy for next-generation EVCS infrastructure.
Across the surveyed studies, baseline hyperparameter-tuning practices were inconsistent and often under-documented. In many cases, authors tuned only their proposed method while leaving baselines at default settings. For example, Ref. [106] provides extensive details on their DQN architecture but does not report whether the MPC forecast models or FQI baseline were re-tuned for fairness. Similarly, Refs. [130,150] benchmarked their approaches against multiple RL algorithms (DQN, SAC, PPO, and MADDPG) but did not disclose search ranges or tuning budgets for those comparators. A second common pattern noticed was the reuse of hyperparameters from prior work or standard toolboxes without re-validation under the current problem setting. For instance, in [126,127], researchers compare against actor–critic and Q-learning baselines but adopt fixed parameters, noting that they follow configurations from earlier studies. Finally, several works give insufficient detail for reproducibility, simply listing baselines such as MPC [125], offline MILP optimization [151], or TOU-based RBC [137,138], but without specifying solver tolerances, forecast model retraining, or parameter sweeps. Such variability creates the risk that poorly tuned baselines may inflate the reported advantages of new methods, a concern already raised in reinforcement learning more broadly. To mitigate such issues, current work strongly recommends the adoption of a common hyperparameter optimization (HPO) protocol: allocate equal tuning budgets across all methods, define and report search spaces for key hyperparameters, apply a consistent optimization strategy to both proposed and baseline algorithms, and disclose solver settings for MPC or offline optimization baselines. Such practices would improve reproducibility and prevent inflated performance claims due to poorly tuned baselines.
6.5. Datasets
The evaluation of recent literature reveals a significant reliance on synthetic data generated via simulation environments or heuristic modeling, primarily due to their flexibility in supporting large-scale scenario testing and controlled policy evaluation [104,108,114,151,154] (see Figure 14—left and Right). These synthetic datasets, while not dominant, are often constructed using pricing signals, grid topology models, and stochastic vehicle arrival distributions, allowing researchers to train and validate RL agents in highly customizable settings devoid of real-world noise and variability. However, the larger share of studies has shifted toward using real-world datasets—or combinations of real and synthetic data, to enhance policy generalizability and align training environments with practical operating conditions (see Figure 14—right). For instance, Ref. [106] employed real-world EV usage patterns and electricity market prices to train DQN agents, while [109] leveraged ElaadNL’s real charging session data to evaluate multi-agent grid load management. Likewise, Ref. [137] used residential microgrid datasets to optimize charging with DDPG, and [118] combined real-world EV mobility profiles with simulation-based grid models to bridge user and infrastructure perspectives. Recent works such as [132,141,152] even integrated hardware-in-the-loop and historical datasets, emphasizing a growing shift toward data-driven RL frameworks where real-world information underpins deployment-ready policy design.
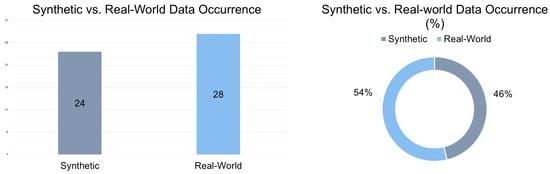
Figure 14.
(Left): Occurrence of synthetic vs. real-world data in RL applications; (Right): percentage distribution of data type usage.
Broadly, datasets used in RL-based EVCS research may be categorized into five groups: EV-centric, grid and market-related, renewable and storage-related, mobility and traffic, and contextual data. Each serves a distinct role—from capturing charging flexibility and grid dynamics to incorporating renewable integration and external environmental factors [106,112,125,141]. This diversity reflects the increasing system-level complexity of EVCS frameworks and underscores the need for RL agents capable of learning within interconnected energy and mobility domains.
EV-centric data form the foundation of nearly half the reviewed studies, as they capture vehicle-level behavior and constraints—especially relevant in decision-making around scheduling and flexibility (see Figure 15—right). Among the most commonly used features are EV arrival/departure times and state-of-charge (SoC) levels, which define the temporal and operational constraints of RL agents [104,105,106,118] (see Figure 15—left). Such features enable intelligent scheduling aligned with user objectives and grid availability. In multi-agent frameworks, additional parameters such as booking data and aggregated charging demand are often used to coordinate resources fairly and minimize congestion [109,117]. While the field remains focused on optimizing EV–infrastructure interaction, future directions may potentially involve fleet-level coordination and multi-agent systems and thus, demand more granular and scalable EV datasets [129,145].
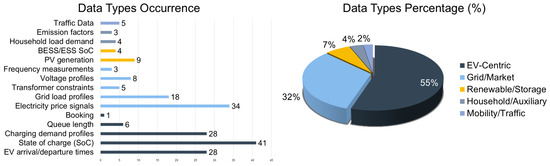
Figure 15.
(Left): Data-type occurrence in overall RL applications; (Right): data-type percentages (%) in the overall RL applications.
Grid and market-related data are critical for embedding RL-based EVCS control into power system operations. Grid-related variables, including transformer capacity, voltage stability, and feeder constraints, were commonly used to ensure grid-compliant charging decisions [108,125,137] (see Figure 15—left). For instance, transformer loading profiles informed Q-learning agents managing residential EV clusters [110], while voltage thresholds were incorporated into actor–critic schemes for community-scale DER coordination [141]. Price signals (TOU, real-time, or dynamic pricing) were widely adopted as reward elements or state inputs, allowing RL agents to respond adaptively to market conditions [106,118,152]. Although less common, frequency-related data have also been explored—especially in studies focused on V2G services for frequency regulation [134,140].
Renewable generation and energy storage data have gained prominence in recent years as EVCS research moves toward integrated energy systems. Photovoltaic (PV) profiles were widely used in residential and community-scale studies to align charging with solar availability, reducing peak demand and improving self-consumption [112,115,137] (see Figure 15—left). Similarly, state-of-charge (SoC) data for battery energy storage systems (BESSs) were essential for hybrid RL models, supporting co-optimization of EV charging and stationary storage [131,138]. Actor–critic algorithms—and particularly SAC and DDPG—were frequently deployed in this context due to their ability to handle continuous action spaces and real-time power modulation [126,141]. The growing use of such data indicates a shift toward RL-enabled control strategies that support dynamic coordination among EVs, distributed storage, and renewable assets.
Data related to mobility and traffic were primarily utilized in emerging research on public and fleet-based EVCSs. Such data proved essential for bridging the gap between transportation and power networks, allowing RL agents to not only optimize charging costs but also reduce travel distances and alleviate congestion. To this end, traffic flow, road network topology, and queue length datasets were incorporated in hybrid RL frameworks to support location-aware charging station recommendations and navigation strategies [111,135,147]. Such applications relied mostly on graph-based deep RL or MARL coordination, particularly in vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) contexts [135,145]. Although still a niche area, the inclusion of traffic data signals a future direction where EVCS scheduling will be co-optimized with intelligent transportation systems for city-scale electrification strategies.
Auxiliary data such as household load demand and emission factors appeared less frequent but increasingly relevant in advanced multi-objective RL research (see Figure 15—left and right). Household load demand was typically included in residential energy management studies, where EVCS operation needs to be coordinated with other appliances to minimize peak demand and user costs [112,124]. Emission factors, used in hybrid RL frameworks like WOAGA-RL [141] and multi-objective MARL [155], represent a growing effort to internalize environmental impacts into RL training, allowing EVCS policies to optimize not only cost and grid stability but also carbon footprint. Although such data types remained relatively underutilized, their presence marks an important step toward sustainability-aware EVCS scheduling that aligns with future energy transition goals.
6.6. Performance Indexes
Several categories of performance indexes were observed across the literature, spanning economic, grid-related, operational, user-centric, energy-oriented, environmental, and specialized domains. Each category served to evaluate distinct aspects of RL-based EVCS control, collectively contributing to a comprehensive assessment of policy effectiveness, scalability, and real-world applicability. More specifically:
Cost-related performance indexes dominated the field, providing direct evaluation of the economic feasibility of RL policies from both EVCS operator and end-user perspectives (see Figure 16—left and right). Such metrics included total charging cost, dynamic pricing responsiveness, revenue maximization, and investment indicators such as net present value (NPV) and Levelized Cost of Storage [104,114,131]. For example, cost minimization in day-ahead or real-time market scenarios was used to assess the efficiency of RL agents in exploiting temporal price variations for arbitrage. Revenue-related metrics, meanwhile, often captured aggregator profits or V2G revenues in grid-interactive contexts [118,152]. Hybrid frameworks that incorporated forecasting (e.g., WOAGA-RL) further introduced financial risk indicators, such as market imbalance penalties, to evaluate robustness under uncertainty [141]. The most frequently used economic metric across studies was total charging cost [104,113,128], while revenue metrics were more common in advanced or multi-agent frameworks involving grid services or market participation [118,131,152]. These cost indicators serve not merely as measures of monetary expenditure but also as proxies for the adaptability and decision-making granularity of RL algorithms under volatile pricing conditions—effectively capturing the economic intelligence of RL-driven EVCS control.
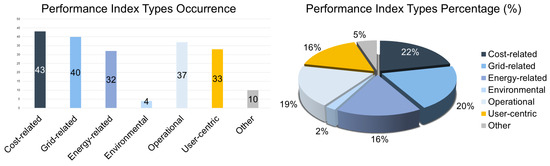
Figure 16.
(Left): Performance-index type occurrence in RL-based EVCS studies; (Right): percentage distribution of performance-index types.
Grid-related metrics were similarly prevalent, focusing on evaluating the impact of RL-based scheduling on power system stability and distribution network health (see Figure 16—left and right). Among these, peak load reduction was the most widely adopted index, serving as a key measure of load smoothing and transformer stress mitigation [109,125]. Other commonly used indicators included load variance, transformer loading frequency, and peak-to-valley ratios [110,152]. Recent studies extended such evaluations to include voltage stability margins and penalty-based constraint violations, particularly in actor–critic or hybrid methods dealing with real-world grid constraints [137,141]. For example, transformer overload frequency was used in decentralized MARL frameworks to assess coordination effectiveness across agents in shared grid environments [110]. Additionally, frequency deviation metrics—such as the RMS of frequency variation—were applied in V2G scenarios to evaluate system-level support capabilities [134]. Thus, grid-related metrics extend beyond purely technical evaluation: they quantify how effectively RL-based EVCS strategies function as flexibility enablers within broader smart grid ecosystems.
Energy-related performance indexes focused on the integration of EVCS scheduling with distributed energy resources (DERs) and local energy flows. These include PV self-consumption ratios [112], BESS utilization [131], energy arbitrage efficiency, and bidirectional power flow in V2G-enabled systems. Among these, PV self-consumption emerged as a key metric in energy-oriented research aiming to align EV charging with RES generation [112,131]. In RES-integrated microgrids, such metrics quantified how effectively RL agents synchronized charging with solar peaks to minimize grid imports [112]. Other studies leveraged battery energy throughput and SoC stability metrics to assess the long-term sustainability of storage-integrated strategies [138]. Overall, energy-related indices served as indicators of how well RL-based EVCS control can be embedded within broader energy management frameworks, signaling a shift from cost-centric scheduling to energy-autonomous paradigms.
Environmental performance metrics have remained relatively underexplored, despite the growing global emphasis on decarbonization (see Figure 16—left and right). Such metrics typically include CO2 emissions, emission reductions compared to baseline strategies [155], and carbon footprint minimization for mobile renewable-integrated charging stations [156]. Unlike cost or grid indexes, environmental metrics often depend on exogenous variables such as grid carbon intensity, requiring RL agents to adapt to context-aware, carbon-optimized operation. For instance, hybrid optimization approaches [141] integrated forecasted grid emission profiles into RL scheduling to achieve environmentally conscious arbitrage. The inclusion of environmental metrics marks a paradigm shift where EVCS control is evaluated not just in terms of economic or technical performance, but also by its contribution to systemic sustainability. However, their limited adoption underscores a significant research gap, highlighting the need for life-cycle-aware emission modeling, carbon-sensitive reward functions, and environmentally coupled policy learning in future RL frameworks [141,155,156].
Operational performance metrics were also widely used to assess both algorithmic performance and system-level viability of RL strategies (see Figure 16—left and right). While early studies emphasized algorithm speed or convergence, recent literature expanded this scope to include real-time feasibility, robustness under uncertainty, and implementation overhead. These metrics included convergence speed and training stability [127,150], station utilization, queue length reduction, and runtime efficiency [115,153]. For example, policy convergence rates in DRL settings [129] were used to validate the applicability of complex models under large state–action spaces. In MARL settings, additional operational indicators such as Pareto front hypervolume and spacing [155] were employed to assess the effectiveness of multi-objective planning. Battery degradation cost was also occasionally tracked as a constraint or secondary metric [133], closing the gap between algorithmic outcomes and hardware durability. Among operational metrics, convergence speed emerged as the most commonly used, consistently deployed to ensure both training stability and applicability in real-time EVCS environments [127,150].
User-related performance indexes were prevalent in the literature (see Figure 16—left and right), as they directly connect RL-driven EVCS policies to service quality and user satisfaction. These include SoC at departure, charging completion rates, waiting time, and fairness across heterogeneous EV fleets [109,128]. Fairness metrics, for instance, were used to ensure equitable resource allocation, preventing bias toward early-arriving vehicles [109], while SoC constraints ensured user satisfaction was not compromised for grid objectives [138]. In mobile or reservation-based settings, additional metrics such as booking acceptance rate [154] and average navigation energy [135] extended the scope of user evaluation to mobility-aware decision-making. Collectively, these metrics reflect the increasing importance of human-centric design in RL frameworks, aiming to bridge algorithmic optimization with perceived service quality. Among them, charging delay was the most frequently reported, used as a proxy for temporal satisfaction and system responsiveness [115,128].
Beyond these dominant categories, RL-based EVCS studies also introduced specialized or “other” performance metrics that captured nuances not fully addressed by standard cost, grid, or operational indexes. For example, forecasting accuracy indicators—such as prediction interval coverage probability and average interval score, were adopted in hybrid RL-forecasting models to evaluate decision robustness under uncertainty [141,149]. Optimization-specific metrics, including hypervolume, spacing, and inverted generational distance (IGD), were employed to benchmark Pareto front quality and diversity in multi-objective planning scenarios [155]. Additional metrics, such as reward variance and policy stability, quantified robustness in stochastic environments [150]. Mobility-oriented indicators like average road speed [147] and congestion-aware queuing metrics extended the evaluation to power-transportation coupling. Lastly, emerging considerations such as pricing stability [114] and real-time responsiveness [140] further expanded the performance landscape. These “other” metrics function as higher-order tools for assessing RL models’ scalability, uncertainty handling, and system-wide integration capabilities—critical for advancing toward holistic, real-world EVCS control solutions.
Across the surveyed works, no study systematically applies a formal fairness index such as Jain’s, Gini, or Theil to quantify equity among EV users. The single mention of “fairness among EVs” in [109] lacks a defined formula or reproducible metric, making it incomparable across studies. Instead, most papers rely on proxies that only partially reflect fairness, such as departure SoC as a minimum satisfaction guarantee [128,129,138], waiting time or queue length to capture service accessibility [115,130,147], or the number of users successfully served [136]. While these proxies provide indirect evidence of equitable allocation, they do not reveal distributional disparities (e.g., whether some users consistently pay more, wait longer, or depart undercharged). This highlights a systematic gap in the EVCS RL literature: fairness remains underexplored and is seldom quantified using standardized, interpretable metrics
6.7. EVCS Types
The analysis of RL-based EVCS applications reveals distinct methodological patterns across different deployment types, shaped by the associated objectives, agent architectures, and system complexities. More specifically:
Residential EVCS deployments primarily focused on cost minimization, demand response integration, and renewable energy utilization. These scenarios predominantly employed single-agent deep RL methods—particularly DQN and DDPG—due to their capacity to operate efficiently within limited-scale environments [106,112,128] (see Figure 17—left and right). Residential-focused studies often utilized real-world datasets to align EV charging with PV generation and dynamic tariff structures, optimizing for metrics such as charging delay and SoC satisfaction. More recent research extended to multi-agent RL, enabling household-level coordination and transformer load balancing in distribution networks [110].
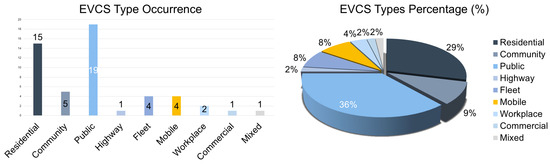
Figure 17.
(Left): EVCS-type occurrence in the overall RL applications; (Right): EVCS-type percentage (%) in the overall RL applications.
In contrast, public and workplace EVCSs represented the most commonly studied category (see Figure 17—left and right), with a greater focus on grid-interactive coordination and congestion mitigation. Value-based RL techniques such as FQI and SARSA, along with hybrid RL–optimization frameworks, have been employed to manage peak load and flatten demand profiles [104,108,154]. Multi-agent actor–critic models were particularly prominent in this space, addressing large-scale urban deployments where metrics such as station utilization, user waiting time, and booking acceptance rate are central [135,139]. Due to the inherent complexity of mobility-grid coupling, these applications often relied on simulation-based environments, including tools like SUMO, to facilitate mobility-aware EVCS scheduling [147].
Community EVCS scenarios often incorporate distributed energy resources such as ESS and V2G capabilities. Such setups leveraged advanced actor–critic algorithms like SAC and TD3 [137,141], with MARL gaining traction for coordinating among aggregated chargers and distributed resources [129,150]. Research in this domain frequently utilizes hybrid RL–optimization models that simultaneously address economic, grid-supportive, and environmental objectives. The result is a transition toward multi-objective, carbon-aware planning that better aligns with emerging smart community infrastructure paradigms.
Mobile and fleet-based EVCSs constituted a more recent and rapidly evolving application domain, often characterized by dynamic topology and mobility constraints. Mobile and fleet-based studies predominantly employed hybrid RL strategies that combine Q-learning with evolutionary optimization or stochastic decision-making for charging location planning and route optimization [142,156]. Multi-agent RL architectures were commonly applied in V2V and vehicle-to-infrastructure (V2I) coordination schemes [135,145], where cooperative agent behavior was necessary to minimize travel distance, reduce waiting times, and alleviate traffic or grid congestion.
Lastly, emerging research on highway- and mixed-type EVCSs has begun to integrate high-power charging infrastructure with renewable energy and storage systems. These contexts typically adopt hybrid frameworks—such as RL combined with MILP, AVOA, or other metaheuristic optimizers—to meet long-horizon planning and scalability requirements [151,155]. Such approaches were aimed at balancing cost efficiency with grid stability, often under uncertain mobility demand and renewable generation profiles.
Overall, while residential and public EVCS applications are relatively mature and frequently utilize single-agent value-based or actor–critic RL methods, recent trends clearly point toward hybrid and multi-agent frameworks for community, fleet, and mobile deployments. This transition reflects the growing complexity and interdependence of modern EVCS ecosystems, where coordination, multi-objective optimization, and grid-supportive behavior are vital for scalable and real-world deployments.
7. Discussion
Numerous trends and research gaps have been examined in detail in Section 5, with a focus on the key attributes of RL-based control strategies for EVCSs. This section synthesizes those findings, providing a consolidated overview of the most significant trends and limitations that emerged throughout the review. Based on this synthesis, the subsequent subsection proposes actionable future directions aimed at addressing the identified challenges, thereby charting a structured pathway for the advancement of RL in EVCS control toward more efficient, scalable, and sustainable applications.
7.1. Trends and Gaps Identification
- Methodological Shift from Value-Based to Actor–Critic and Hybrid RL: The evolution of RL techniques for EVCS control has shown a clear methodological transition. Initial efforts were dominated by value-based methods—particularly Q-learning and DQN—which proved effective for single-agent scheduling problems focused on cost optimization in discrete action spaces [104,109]. As EVCS scenarios became increasingly complex—featuring continuous control, energy integration, and participation in grid services—research has progressively shifted toward actor–critic methods such as DDPG, SAC, and TD3 [123,137,138]. In parallel, hybrid approaches that combine RL with mathematical programming (e.g., MILP, ILP) or metaheuristics (e.g., GA, DE, WOA) gained traction [149,156], illustrating a broader trend toward integrated decision frameworks that combine RL’s adaptiveness with the constraint-handling strengths of optimization.
- Lack of Safety, Explainability, and Transparency: Despite these algorithmic advancements, most RL models—particularly deep actor–critic and hybrid designs—remain opaque, offering limited interpretability. Only a few studies, such as those employing CSAC [138], explicitly address safety guarantees. Approaches involving explainability, formal verification, or transparent reward shaping are notably underrepresented, posing a significant barrier to real-world deployment in safety-critical EVCS environments.
- Limited Adoption of Multi-Agent RL: Multi-agent RL (MARL) remains relatively underutilized, appearing in just 26% of reviewed studies. The majority of these adopt centralized training with decentralized execution (CTDE) combined with implicit coordination. However, explicit communication, hierarchical structures, or coordination strategies tailored for heterogeneous EVCS systems remain scarce [129,135]. Most MARL implementations have not been stress-tested at large scales (hundreds or thousands of agents), and few incorporate techniques to address non-stationarity, such as opponent modeling or policy distillation. Fully decentralized MARL remains confined to relatively simple applications [110,112], highlighting the need for improved scalability and coordination mechanisms.
- Evolution of Reward Functions Toward Multi-Objective Design: Reward design in EVCS research has evolved significantly. Approximately 80% of studies employ multi-objective reward functions, typically placing cost or profit at the core, with grid, environmental, and user-centric goals represented as secondary or penalty terms [131,155].
- Economic Bias in Reward Design: This design bias risks steering policies toward market-optimized behaviors at the expense of systemic optimization. Balanced, stakeholder-inclusive reward structures—with structured weighting schemes and robustness testing—are largely absent. Encouragingly, recent studies have started to incorporate additional objectives such as grid stability (e.g., peak shaving), user satisfaction (e.g., SoC at departure, waiting time), and, in fewer cases, environmental impacts like emission reduction [131,155].
- Increasing Use of Real-World and Mixed Datasets: The use of real-world data has expanded, with many studies integrating historical charging logs, market prices, and grid metrics into their training pipelines [132,137]. Nevertheless, a substantial proportion (46%) of studies still rely primarily on synthetic data. Increasing the use of real-world data is vital for enhancing model robustness and ensuring realistic policy behavior in deployment settings.
- Scarcity of Real-World Validation: Most RL applications remain confined to simulated environments [104,108,114,154], limiting their exposure to real-world uncertainties. A handful of studies bridge this gap: Ref. [132] validated bidirectional charging with real building and EV hardware, while Refs. [106,137] utilized real market and microgrid data. Hardware-in-the-loop evaluations, as demonstrated in [120,152], further reinforce the importance of hybrid validation for uncovering deployment-specific issues.
- Maturing Baseline Comparisons and Performance Metrics: Benchmarking has matured, progressing from simplistic heuristics (e.g., RBC, greedy policies) to more rigorous comparisons against offline optimization (e.g., MPC, MILP) and alternative RL frameworks [117,150]. Evaluation metrics have similarly expanded to include grid-level, user-centric, and—albeit less frequently—environmental indicators.
- Uncertainty Modeling: Robustness to uncertainty remains an underexplored area. Few studies integrate probabilistic forecasting or adopt robust/distributional RL techniques. This omission leaves systems vulnerable to real-time volatility, forecast inaccuracies, and rare extreme events. Moreover, the lack of standardized datasets and test beds continues to hinder meaningful cross-study comparisons. Safety and interpretability, both essential for critical infrastructure control, remain largely unaddressed—except in a few constrained RL applications [138].
- Neglect of Environmental and Life-cycle Objectives: Environmental sustainability and life-cycle factors—such as carbon footprint reduction and battery degradation minimization—are rarely included in RL frameworks. The majority of studies remain focused on short-term cost or grid optimization, despite growing interest in long-term sustainability. Techniques such as transfer learning, federated RL, and meta-RL [126] hold promise for enabling scalable, context-adaptive control, but have yet to gain substantial traction.
- Minimal Cross-Domain Generalization: Current RL controllers for EVCSs are often tailored to specific sites, grid configurations, and pricing schemes, with limited ability to generalize across diverse environments [106,114]. Only a few works employ federated learning [126], transfer learning [135,150], or meta-RL. This lack of cross-domain generalization restricts scalability and imposes significant retraining costs when deploying to new locations or system contexts.
In sum, while RL for EVCS control has progressed toward more capable, integrated, and context-aware algorithms, its future trajectory hinges on moving beyond economic optimization toward holistic, safe, explainable, uncertainty-aware, and field-validated solutions that can scale across heterogeneous, real-world charging ecosystems.
7.2. Future Directions
Transitioning RL-based EVCS control from promising laboratory prototypes to robust, field-deployable systems demands controllers that are not only scalable and efficient but also safe, interpretable, and capable of operating under real-world uncertainty, regulatory constraints, and multi-stakeholder objectives. Achieving this requires the convergence of advanced RL algorithms with domain-specific knowledge from power systems, fostering solutions that go beyond performance optimization to also ensure feasibility, fairness, and long-term sustainability.
A fundamental priority lies in the development of safety-aware hybrid controllers that embed actor–critic architectures within differentiable optimization layers—such as optimal power flow (OPF) or second-order cone programming (SOCP)—to ensure all actions are inherently feasible with respect to voltage, transformer, and line constraints. Building on the foundations of constrained RL, as demonstrated in CSAC and CPO [121,138], future systems should move beyond penalty-based shaping and instead employ differentiable feasibility maps or barrier functions, optionally shielded by MPC-style fallback mechanisms [125,139]. Safety guarantees should also be maintained in two-timescale hierarchical schemes, where a high-level planner (e.g., DDPG/SAC) allocates feasible power bands, while a lower-level controller (e.g., Q-learning/SAC) executes real-time tracking with certified fallback logic [123,124,137,150].
The progression of multi-agent RL (MARL) must move beyond conventional CTDE architectures [129,135]. Advanced coordination mechanisms—such as GNN-based message passing, counterfactual baselines (COMA), and mean-field approximations—offer promising avenues for scaling MARL systems to thousands of agents while preserving local autonomy and coordination fidelity [110,130]. Incorporating explicit communication protocols and spatial discounting will be particularly valuable for heterogeneous EVCS systems, including community-level energy sharing and grid-supportive V2G applications.
In market-integrated control scenarios, future RL methods should embrace game-theoretic principles and develop market-aware agents. Multi-objective SAC or TD3 frameworks can co-optimize energy arbitrage and ancillary service participation by embedding market rules into bilevel critics, capturing the strategic interaction between EVCS agents and electricity markets [118,122,131]. Reward engineering will require greater structure—replacing ad hoc weighting schemes with Lagrangian multi-objective formulations, integrating fairness and battery health directly as optimization objectives, and potentially recovering utility functions through inverse RL [115,116,117]. Reporting full Pareto fronts, instead of single KPIs, will be essential to properly visualize trade-offs among competing objectives such as cost, grid reliability, environmental impact, and user experience.
Given the inherent uncertainty in RES generation and EV demand, robust and uncertainty-aware RL should become standard practice. This includes distributional critics, conditional value-at-risk-based objectives, and probabilistic forecasting techniques such as quantile regression or autoregressive recurrent neural networks (RNNs—DeepAR) [141,149]. Embedding ensemble forecasts within hierarchical planner/executor architectures can enhance resilience. Closing the simulation-to-reality (sim-to-real) gap will also require standardized hardware-in-the-loop frameworks and digital twins that incorporate latency, noise, and hardware constraints [106,120,132]. Progressive deployment workflows, from offline training to hardware-in-the-loop testing to staged pilots, are crucial to surface real-world issues such as communication bottlenecks, computational constraints, and user acceptance.
To support cross-site adaptability, federated RL [126], transfer learning [150], and meta-RL must be adopted to generalize across diverse topologies, DER mixes, and pricing structures. Embedding system context (e.g., feeder topology, tariff structure, renewable share) as input to policy networks will enable region-aware decision-making. Cross-site zero-shot and few-shot performance benchmarks should become standard. In hybrid frameworks, RL should specialize in adaptive, feedback-driven decisions, while discrete and combinatorial tasks—such as booking, matching, or commitment—can be delegated to MILP or metaheuristics like GA, DE, or WOA, as observed in [144,149,151,156], with learned approximations distilled into lightweight neural models suitable for edge deployment.
Interpretability and auditability will remain prerequisites for regulatory approval and operator trust. Future work should also focus on distilling deep policies into interpretable surrogates (e.g., decision trees or rule sets), employing additive explanations or local interpretable model-agnostic explanations for feature attribution, tracking constraint violations in real-time, and generating operator-facing playbooks that explain and justify agent actions [126,138]. Standardized benchmarking—including shared datasets, canonical reward structures, and stress-testing protocols (e.g., N-1 contingencies, communication failures)—should be adopted to ensure reproducibility and comparability across studies [104,106,115,154]. Moreover, to ensure fair benchmarking, we recommend that future EVCS RL studies adopt a simple HPO protocol. First, all algorithms—including baselines-should be allocated an equal tuning budget (number of trials, seeds, and epochs) to ensure parity. Second, search spaces for critical parameters (e.g., learning rate, discount factor, exploration coefficients, network depth/width) should be explicitly defined and reported. Third, a consistent optimization strategy (random/grid search or Bayesian optimization) should be applied across methods rather than selectively for the proposed model. Fourth, offline optimization and MPC baselines should also be tuned by reporting solver tolerances, horizon lengths, and forecast model parameters subject to sensitivity checks, as in Dorokhova et al. [115]. Finally, reporting standards should include mean standard deviation across multiple seeds, publication of final tuned hyperparameters, and clear disclosure if defaults are reused. Such a protocol would improve reproducibility and ensure that performance claims are grounded in fair comparisons rather than baseline under-tuning.
Finally, future EVCS control should be co-designed with transportation-energy systems integration. Graph-based RL can be leveraged to jointly optimize power flows, routing, and queuing, combining centralized assignment mechanisms (e.g., MILP or Kuhn–Munkres matching) with local RL-based dispatch [111,145,146,147]. To support long-term sustainability, RL formulations must integrate carbon and life-cycle-aware objectives—including marginal emissions, degradation-aware SoC tracking, and carbon budgets—within constrained MDP (C-MDP) formulations [141,155]. Such systems must ultimately be deployable on edge-ready platforms, featuring quantized models, communication-efficient policies, and continual learning mechanisms that adapt to non-stationary tariffs, DER profiles, and load patterns without catastrophic forgetting [127,136].
In addition to these algorithmic directions, two overarching barriers must be highlighted as decisive for real-world adoption. The significantly critical technical barrier is related to sample efficiency and safe exploration—current RL methods require large numbers of state–action interactions, which are feasible in simulation but impractical in the field where unsafe decisions risk transformer overload or unmet charging contracts. Advances in offline RL, model-based RL, and constrained safe RL are therefore indispensable to make training both data-efficient and deployment-ready. The most potentially critical non-technical barrier concerns data availability and standardization. Access to realistic charging demand, grid constraints, and user behavior data is currently fragmented and proprietary, preventing reproducibility and robust benchmarking. Building open, standardized datasets and test beds—aligned with regulatory frameworks—would enable fair comparisons across methods and accelerate regulatory trust.
Collectively, these research directions outline a comprehensive roadmap for advancing RL in EVCSs from simulation to deployment—ensuring that future controllers are not only benchmark-leading, but also robust, interpretable, scalable, and trusted within the multi-layered, dynamic landscape of real-world EVCS–grid integration.
8. Conclusions
The current review offered a focused and in-depth examination of RL methods for EVCS control, setting itself apart from previous surveys by providing a systematic, large-scale analysis of RL-specific design choices alongside a unified evaluation framework that enables detailed technical comparisons across studies. A unified evaluation framework was introduced and applied through structured key attribute and summary tables, enabling systematic cross-study comparison. By analyzing the large number of integrated influential works, the review captured detailed aspects such as algorithm design, agent architecture, reward formulation, baseline control strategies, data usage, performance metrics, and practical deployment settings. Based on this comprehensive mapping, the study identified key research trends, existing gaps, and proposed future directions to support scalability and real-world implementation.
According to the evaluation, a clear methodological shift has been observed—from early reliance on value-based algorithms for discrete, single-agent scheduling, toward actor–critic frameworks capable of handling continuous action spaces, multi-objective optimization, and participation in grid-supportive services. Hybrid RL paradigms—integrating policy learning with mathematical programming (e.g., MILP) or metaheuristics (e.g., DE, GA)—have also emerged, offering a pragmatic approach to reconcile RL’s adaptability with hard operational constraints, particularly in voltage, transformer, and line limit compliance.
Despite such advancements, several key research gaps remain. For instance, MARL remains underutilized, with most applications limited to CTDE architectures and implicit coordination schemes. Explicit communication, hierarchical organization, and large-scale scalability remain insufficiently addressed, limiting MARL’s broader applicability to heterogeneous EVCS ecosystems and V2G-enabled networks. Moreover, according to analysis, reward functions continue to exhibit a strong economic bias, with grid reliability, environmental impact, and fairness often relegated to secondary roles via penalty terms. Furthermore, while uncertainty and non-stationarity are intrinsic to EVCS environments, few studies incorporate robust RL, distributional learning, or probabilistic forecasting frameworks.
The lack of real-world validation concerns another significant limitation in RL for EVCSs. Most studies operate entirely in simulated environments, thereby failing to capture real-world constraints such as communication latency, hardware variability, or user behavior. Although a few promising examples utilize hardware-in-the-loop setups, digital twins, or partial deployment pilots, these remain the exception rather than the norm. While baseline comparisons have matured—now including MPC, MILP, and most importantly alternative RL architectures—the absence of standardized datasets, feeder models, and testing protocols continues to hinder reproducibility and cross-study benchmarking.
From this landscape analysis, several research priorities clearly emerge. The development of safety-aware hybrid controllers—particularly those incorporating differentiable optimization layers and MPC-based shielding—will be essential for trustworthy real-world operation. MARL research must progress toward explicit coordination, scalable communication, and game-theoretic interaction models. Reward engineering should shift from heuristic-weighted objectives to structured, stakeholder-driven frameworks capable of transparently managing trade-offs. The integration of uncertainty-aware RL, including distributional critics and probabilistic forecasting, is essential for resilience under volatile grid and market conditions. To bridge the sim-to-real gap, standardized pipelines, shared digital twin infrastructures, and staged deployment strategies must be established. Finally, generalization across systems will require federated RL, transfer learning, and meta-RL—ensuring policy portability across regions, tariffs, and DER configurations. Embedding life-cycle- and carbon-aware objectives will also be critical for aligning EVCS control with long-term sustainability goals.
In summary, RL for EVCS control is evolving from a conceptual innovation to a sophisticated framework for intelligent, grid-integrated decision-making. To unlock its full potential, future research must produce RL controllers that are not only high-performing but also interpretable, safe, adaptive, and validated in real-world scenarios. Through synergistic advances in algorithm design, uncertainty handling, reward formulation, and deployment strategies, RL can become a foundational tool in the realization of sustainable, scalable, and intelligent electric mobility infrastructure.
Author Contributions
Conceptualization, P.M.; methodology, P.M. and I.M.; software, P.M.; validation, all authors; formal analysis, all authors; investigation, all authors; resources, all authors; writing—original draft preparation, P.M.; writing—review and editing, all authors; visualization, all authors; supervision, P.M. and E.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results was partially funded by the European Commission HORIZON-CL5-2023-D4-01-05—Innovative solutions for cost-effective decarbonisation of build-ings through energy efficiency and electrification (IA): SEEDS—Cost-effective and replicable RES-integrated electrified heating and cooling systems for improved energy efficiency and demandresponse (Grant agreement ID: 101138211) https://project-seeds.eu/, accessed on 30 September 2025.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| AC | Actor–Critic |
| AIS | Average Interval Score |
| BESS | Battery Energy Storage System |
| BLP | Binary Linear Programming |
| CMDP | Constrained Markov Decision Process |
| CTDE | Centralized Training with Decentralized Execution |
| CVaR | Conditional Value-at-Risk |
| DDPG | Deep Deterministic Policy Gradient |
| DDQN | Double Deep Q-Network |
| DE | Differential Evolution |
| DER | Distributed Energy Resource |
| DQN | Deep Q-Network |
| DRL | Deep Reinforcement Learning |
| ESS | Energy Storage System |
| EV | Electric Vehicle |
| EVCS | Electric Vehicle Charging Station |
| FQI | Fitted Q Iteration |
| GA | Genetic Algorithm |
| GNN | Graph Neural Network |
| HIL | Hardware-in-the-Loop |
| IGD | Inverted Generational Distance |
| ILP | Integer Linear Programming |
| KM | Kuhn–Munkres Algorithm |
| LCOS | Levelized Cost of Storage |
| MILP | Mixed-Integer Linear Programming |
| MOAVOA | Multi-Objective Adaptive Vortex Optimization Algorithm |
| MPC | Model Predictive Control |
| NPV | Net Present Value |
| OPF | Optimal Power Flow |
| P-DQN-DDPG | Parametric Deep Q-Network with DDPG |
| PICP | Prediction Interval Coverage Probability |
| PPO | Proximal Policy Optimization |
| PSO | Particle Swarm Optimization |
| QL | Q-Learning |
| RES | Renewable Energy Source |
| RBC | Rule-Based Control |
| RL | Reinforcement Learning |
| SARSA | State–Action–Reward–State–Action |
| SAC | Soft Actor–Critic |
| SoC | State of Charge |
| SOCP | Second-Order Cone Programming |
| SP | Stochastic Programming |
| TD3 | Twin Delayed DDPG |
| TOU | Time-of-Use |
| V2G | Vehicle-to-Grid |
| vV2V | Virtual Vehicle-to-Vehicle |
| WOA | Whale Optimization Algorithm |
| WOAGA | WOA with Genetic Algorithm |
References
- de Quevedo, P.M.; Muñoz-Delgado, G.; Contreras, J. Impact of electric vehicles on the expansion planning of distribution systems considering renewable energy, storage, and charging stations. IEEE Trans. Smart Grid 2017, 10, 794–804. [Google Scholar] [CrossRef]
- Hakam, Y.; Gaga, A.; Elhadadi, B. Exploring the state of electric vehicles: An evidence-based examination of current and future electric vehicle technologies and smart charging stations. Energy Rep. 2024, 11, 4102–4114. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, K.; Kumar, J.A.; Thanikanti, S.B.; Nwulu, N.I. A comprehensive review and analysis of the allocation of electric vehicle charging stations in distribution networks. IEEE Access 2024, 12, 5404–5461. [Google Scholar] [CrossRef]
- Minelli, F.; Ciriello, I.; Minichiello, F.; D’Agostino, D. From net zero energy buildings to an energy sharing model-The role of NZEBs in renewable energy communities. Renew. Energy 2024, 223, 120110. [Google Scholar] [CrossRef]
- Coban, H.H.; Lewicki, W. Assessing the efficiency of hybrid energy facilities for electric vehicle charging. In Scientific Papers of Silesian University of Technology; Organization and Management Series; Silesian University of Technology Publishing House: Gliwice, Poland, 2023. [Google Scholar] [CrossRef]
- Panossian, N.; Muratori, M.; Palmintier, B.; Meintz, A.; Lipman, T.; Moffat, K. Challenges and opportunities of integrating electric vehicles in electricity distribution systems. Curr. Sustain. Energy Rep. 2022, 9, 27–40. [Google Scholar] [CrossRef]
- Rana, M.M.; Alam, S.M.; Rafi, F.A.; Deb, S.B.; Agili, B.; He, M.; Ali, M.H. Comprehensive review on the charging technologies of electric vehicles (EV) and their impact on power grid. IEEE Access 2025, 13, 35124–35156. [Google Scholar] [CrossRef]
- Coban, H.H.; Lewicki, W. Daily electricity demand assessment on the example of the Turkish road transport system–a case study of the development of electromobility on highways. Pr. Kom. Geogr. Komun. PTG 2022, 25, 52–62. [Google Scholar] [CrossRef]
- Kurucan, M.; Michailidis, P.; Michailidis, I.; Minelli, F. A Modular Hybrid SOC-Estimation Framework with a Supervisor for Battery Management Systems Supporting Renewable Energy Integration in Smart Buildings. Energies 2025, 18, 4537. [Google Scholar] [CrossRef]
- Diaz-Londono, C.; Gruosso, G.; Maffezzoni, P.; Daniel, L. Coordination strategies for electric vehicle chargers integration in electrical grids. In Proceedings of the 2022 IEEE Vehicle Power and Propulsion Conference (VPPC), Merced, CA, USA, 1–4 November 2022; pp. 1–6. [Google Scholar]
- Gnanavendan, S.; Selvaraj, S.K.; Dev, S.J.; Mahato, K.K.; Swathish, R.S.; Sundaramali, G.; Accouche, O.; Azab, M. Challenges, solutions and future trends in EV-technology: A review. IEEE Access 2024, 12, 17242–17260. [Google Scholar] [CrossRef]
- Garg, A.; Pattnaik, T.; Verma, S.R.; Ballal, M.S.; Wath, M.G.; Wakode, S.A. Addressing Challenges and Promoting Standardization in EVCS: A Review. In Proceedings of the 2023 IEEE 3rd International Conference on Smart Technologies for Power, Energy and Control (STPEC), Bhubaneswar, India, 10–13 December 2023; pp. 1–6. [Google Scholar]
- Bhatti, A.R.; Salam, Z. A rule-based energy management scheme for uninterrupted electric vehicles charging at constant price using photovoltaic-grid system. Renew. Energy 2018, 125, 384–400. [Google Scholar] [CrossRef]
- Al-Alwash, H.M.; Borcoci, E.; Vochin, M.C.; Balapuwaduge, I.A.; Li, F.Y. Optimization schedule schemes for charging electric vehicles: Overview, challenges, and solutions. IEEE Access 2024, 12, 32801–32818. [Google Scholar] [CrossRef]
- Franco, J.F.; Rider, M.J.; Romero, R. A mixed-integer linear programming model for the electric vehicle charging coordination problem in unbalanced electrical distribution systems. IEEE Trans. Smart Grid 2015, 6, 2200–2210. [Google Scholar] [CrossRef]
- Uiterkamp, M.H.S.; van der Klauw, T.; Gerards, M.E.; Hurink, J.L. Offline and online scheduling of electric vehicle charging with a minimum charging threshold. In Proceedings of the 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aalborg, Denmark, 29–31 October 2018; pp. 1–6. [Google Scholar]
- Tang, W.; Zhang, Y.J. A model predictive control approach for low-complexity electric vehicle charging scheduling: Optimality and scalability. IEEE Trans. Power Syst. 2016, 32, 1050–1063. [Google Scholar] [CrossRef]
- Michailidis, P.; Michailidis, I.; Gkelios, S.; Kosmatopoulos, E. Artificial neural network applications for energy management in buildings: Current trends and future directions. Energies 2024, 17, 570. [Google Scholar] [CrossRef]
- Michailidis, P.; Michailidis, I.; Minelli, F.; Coban, H.H.; Kosmatopoulos, E. Model Predictive Control for Smart Buildings: Applications and Innovations in Energy Management. Buildings 2025, 15, 3298. [Google Scholar] [CrossRef]
- Fernandez, V.; Pérez, V. Optimization of electric vehicle charging control in a demand-side management context: A model predictive control approach. Appl. Sci. 2024, 14, 8736. [Google Scholar] [CrossRef]
- Yang, Y.; Yeh, H.G.; Nguyen, R. A robust model predictive control-based scheduling approach for electric vehicle charging with photovoltaic systems. IEEE Syst. J. 2022, 17, 111–121. [Google Scholar] [CrossRef]
- Michailidis, P.; Pelitaris, P.; Korkas, C.; Michailidis, I.; Baldi, S.; Kosmatopoulos, E. Enabling optimal energy management with minimal IoT requirements: A legacy A/C case study. Energies 2021, 14, 7910. [Google Scholar] [CrossRef]
- Michailidis, P.; Michailidis, I.; Vamvakas, D.; Kosmatopoulos, E. Model-free HVAC control in buildings: A review. Energies 2023, 16, 7124. [Google Scholar] [CrossRef]
- Korkas, C.D.; Baldi, S.; Michailidis, P.; Kosmatopoulos, E.B. A cognitive stochastic approximation approach to optimal charging schedule in electric vehicle stations. In Proceedings of the 2017 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017; pp. 484–489. [Google Scholar]
- Lee, Z.J.; Chang, D.; Jin, C.; Lee, G.S.; Lee, R.; Lee, T.; Low, S.H. Large-scale adaptive electric vehicle charging. In Proceedings of the 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aalborg, Denmark,, 29–31 October 2018; pp. 1–7. [Google Scholar]
- Kumar, N.; Singh, H.K.; Niwareeba, R. Adaptive control technique for portable solar powered EV charging adapter to operate in remote location. IEEE Open J. Circuits Syst. 2023, 4, 115–125. [Google Scholar] [CrossRef]
- Kermansaravi, A.; Refaat, S.S.; Trabelsi, M.; Vahedi, H. AI-based energy management strategies for electric vehicles: Challenges and future directions. Energy Rep. 2025, 13, 5535–5550. [Google Scholar] [CrossRef]
- Vamvakas, D.; Michailidis, P.; Korkas, C.; Kosmatopoulos, E. Review and evaluation of reinforcement learning frameworks on smart grid applications. Energies 2023, 16, 5326. [Google Scholar] [CrossRef]
- Nerkar, M.; Mukherjee, A.; Soni, B.P. A review on optimization scheduling methods of charging and discharging of EV. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2022; Volume 2452, p. 040002. [Google Scholar]
- Lazaridis, C.R.; Michailidis, I.; Karatzinis, G.; Michailidis, P.; Kosmatopoulos, E. Evaluating reinforcement learning algorithms in residential energy saving and comfort management. Energies 2024, 17, 581. [Google Scholar] [CrossRef]
- Michailidis, P.; Michailidis, I.; Kosmatopoulos, E. Reinforcement learning for optimizing renewable energy utilization in buildings: A review on applications and innovations. Energies 2025, 18, 1724. [Google Scholar] [CrossRef]
- Michailidis, P.; Michailidis, I.; Kosmatopoulos, E. Review and Evaluation of Multi-Agent Control Applications for Energy Management in Buildings. Energies 2024, 17, 4835. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Alfaverh, F.; Denai, M.; Sun, Y. Demand response strategy based on reinforcement learning and fuzzy reasoning for home energy management. IEEE Access 2020, 8, 39310–39321. [Google Scholar] [CrossRef]
- Chu, T.; Wang, J.; Codecà, L.; Li, Z. Multi-agent deep reinforcement learning for large-scale traffic signal control. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1086–1095. [Google Scholar] [CrossRef]
- Yau, K.L.A.; Qadir, J.; Khoo, H.L.; Ling, M.H.; Komisarczuk, P. A survey on reinforcement learning models and algorithms for traffic signal control. ACM Comput. Surv. (CSUR) 2017, 50, 1–38. [Google Scholar] [CrossRef]
- Michailidis, P.; Michailidis, I.; Lazaridis, C.R.; Kosmatopoulos, E. Traffic Signal Control via Reinforcement Learning: A Review on Applications and Innovations. Infrastructures 2025, 10, 114. [Google Scholar] [CrossRef]
- Michailidis, I.T.; Manolis, D.; Michailidis, P.; Diakaki, C.; Kosmatopoulos, E.B. Autonomous self-regulating intersections in large-scale urban traffic networks: A Chania City case study. In Proceedings of the 2018 5th International Conference on Control, Decision and Information Technologies (CoDIT), Thessaloniki, Greece, 10–13 April 2018; pp. 853–858. [Google Scholar]
- Lee, M.F.R.; Yusuf, S.H. Mobile robot navigation using deep reinforcement learning. Processes 2022, 10, 2748. [Google Scholar] [CrossRef]
- Singh, B.; Kumar, R.; Singh, V.P. Reinforcement learning in robotic applications: A comprehensive survey. Artif. Intell. Rev. 2022, 55, 945–990. [Google Scholar] [CrossRef]
- Sen, S.; Sharma, A.K.; Patel, M. Real-Time Resource Allocation for Electric Vehicle Charging Stations Using Reinforcement Learning. In Proceedings of the International Conference on Advanced Informatics for Computing Research, Rohtak, India, 16–17 December 2023; Springer: Cham, Switzerland, 2023; pp. 129–140. [Google Scholar]
- Coban, H.H. Production and use of electric vehicle batteries. In Energy Systems Design for Low-Power Computing; IGI Global: Hershey, PA, USA, 2023; pp. 279–304. [Google Scholar]
- D’Agostino, D.; Mazzella, S.; Minelli, F.; Minichiello, F. Obtaining the NZEB target by using photovoltaic systems on the roof for multi-storey buildings. Energy Build. 2022, 267, 112147. [Google Scholar] [CrossRef]
- Qian, T.; Shao, C.; Li, X.; Wang, X.; Chen, Z.; Shahidehpour, M. Multi-agent deep reinforcement learning method for EV charging station game. IEEE Trans. Power Syst. 2021, 37, 1682–1694. [Google Scholar] [CrossRef]
- Liu, L.; Huang, Z.; Xu, J. Multi-agent deep reinforcement learning based scheduling approach for mobile charging in internet of electric vehicles. IEEE Trans. Mob. Comput. 2024, 23, 10130–10145. [Google Scholar] [CrossRef]
- Cappiello, M.; D’Agostino, D.; Minelli, F.; Minichiello, F. Towards zero-emission building mall: Hybrid multi-criteria decision-making approach. In Proceedings of the 19th SDEWES (Sustainable Development of Energy, Water and Environment Systems) Conference, Rome, Italy, 8–12 September 2024; pp. 1–14. [Google Scholar]
- Michailidis, I.T.; Manolis, D.; Michailidis, P.; Diakaki, C.; Kosmatopoulos, E.B. A decentralized optimization approach employing cooperative cycle-regulation in an intersection-centric manner: A complex urban simulative case study. Transp. Res. Interdiscip. Perspect. 2020, 8, 100232. [Google Scholar] [CrossRef]
- Gong, J.; Fu, W.; Kang, Y.; Qin, J.; Xiao, F. Multi-agent deep reinforcement learning based multi-objective charging control for electric vehicle charging station. In Proceedings of the Chinese Conference on Swarm Intelligence and Cooperative Control, Nanjing, China, 24–27 November 2023; Springer: Singapore, 2023; pp. 266–277. [Google Scholar]
- Fonseca, T.; Ferreira, L.L.; Cabral, B.; Severino, R.; Nweye, K.; Ghose, D.; Nagy, Z. EVLearn: Extending the cityLearn framework with electric vehicle simulation. Energy Inform. 2025, 8, 16. [Google Scholar] [CrossRef]
- Michailidis, I.T.; Michailidis, P.; Rizos, A.; Korkas, C.; Kosmatopoulos, E.B. Automatically fine-tuned speed control system for fuel and travel-time efficiency: A microscopic simulation case study. In Proceedings of the 2017 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017; pp. 915–920. [Google Scholar]
- Zhao, Q.; Wu, W.; Cheng, N.; Guo, G.; Han, Y. A Deep Reinforcement Learning-Based Multi-Objective Charging Scheduling Method for Electric Vehicle Charging Station. IEEE Internet Things J. 2025, 12, 28925–28936. [Google Scholar] [CrossRef]
- Coban, H.H. Smart steps towards sustainable transportation: Profitability of electric road system. Balk. J. Electr. Comput. Eng. 2023, 11, 88–99. [Google Scholar] [CrossRef]
- D’Agostino, D.; Minelli, F.; Minichiello, F.; Ruocco, V.; Saccone, M. HVAC system energy retrofit for infection risk mitigation—A Multi-Objective Optimization and Multi-Criteria Decision-Making approach. In Proceedings of the 41st UIT International Heat Transfer Conference, Naples, Italy, 19–21 June 2024; pp. 1–8. [Google Scholar]
- Maeng, J.; Min, D.; Kang, Y. Intelligent charging and discharging of electric vehicles in a vehicle-to-grid system using a reinforcement learning-based approach. Sustain. Energy Grids Netw. 2023, 36, 101224. [Google Scholar] [CrossRef]
- Fonseca, T.; Ferreira, L.; Cabral, B.; Severino, R.; Praça, I. EnergAIze: Multi Agent Deep Deterministic Policy Gradient for Vehicle-to-Grid Energy Management. In Proceedings of the 2024 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Oslo, Norway, 17–20 September 2024; pp. 232–237. [Google Scholar]
- D’Agostino, D.; Minelli, F.; D’Urso, M.; Minichiello, F. Fixed and tracking PV systems for Net Zero Energy Buildings: Comparison between yearly and monthly energy balance. Renew. Energy 2022, 195, 809–824. [Google Scholar] [CrossRef]
- Sun, F.; Diao, R.; Zhou, B.; Lan, T.; Mao, T.; Su, S.; Cheng, H.; Meng, D.; Lu, S. Prediction-based EV-PV coordination strategy for charging stations using reinforcement learning. IEEE Trans. Ind. Appl. 2023, 60, 910–919. [Google Scholar] [CrossRef]
- Rani, G.A.; Priya, P.L.; Jayan, J.; Satheesh, R.; Kolhe, M.L. Data-driven energy management of an electric vehicle charging station using deep reinforcement learning. IEEE Access 2024, 12, 65956–65966. [Google Scholar] [CrossRef]
- Shin, M.; Choi, D.H.; Kim, J. Cooperative management for PV/ESS-enabled electric vehicle charging stations: A multiagent deep reinforcement learning approach. IEEE Trans. Ind. Inform. 2019, 16, 3493–3503. [Google Scholar] [CrossRef]
- Shaikh, M.S.; Zheng, G.; Wang, C.; Wang, C.; Dong, X.; Zervoudakis, K. A classification system based on improved global exploration and convergence to examine student psychological fitness. Sci. Rep. 2024, 14, 27427. [Google Scholar] [CrossRef] [PubMed]
- Shaikh, M.S.; Raj, S.; Abdul Latif, S.; Mbasso, W.F.; Kamel, S. Optimizing transmission line parameter estimation with hybrid evolutionary techniques. IET Gener. Transm. Distrib. 2024, 18, 1795–1814. [Google Scholar] [CrossRef]
- Abdullah, H.M.; Gastli, A.; Ben-Brahim, L. Reinforcement learning based EV charging management systems—A review. IEEE Access 2021, 9, 41506–41531. [Google Scholar] [CrossRef]
- Al-Ogaili, A.S.; Hashim, T.J.T.; Rahmat, N.A.; Ramasamy, A.K.; Marsadek, M.B.; Faisal, M.; Hannan, M.A. Review on scheduling, clustering, and forecasting strategies for controlling electric vehicle charging: Challenges and recommendations. IEEE Access 2019, 7, 128353–128371. [Google Scholar] [CrossRef]
- Shahriar, S.; Al-Ali, A.R.; Osman, A.H.; Dhou, S.; Nijim, M. Machine learning approaches for EV charging behavior: A review. IEEE Access 2020, 8, 168980–168993. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, C.K.; Yan, X.; Wang, H. Reinforcement learning for electric vehicle charging scheduling: A systematic review. Transp. Res. Part E Logist. Transp. Rev. 2024, 190, 103698. [Google Scholar] [CrossRef]
- Yousuf, A.; Wang, Z.; Paranjape, R.; Tang, Y. An in-depth exploration of electric vehicle charging station infrastructure: A comprehensive review of challenges, mitigation approaches, and optimization strategies. IEEE Access 2024, 12, 51570–51589. [Google Scholar] [CrossRef]
- Yousuf, A.; Wang, Z.; Paranjape, R.; Tang, Y. Electric vehicle charging station infrastructure: A comprehensive review of technologies, challenges, and mitigation strategies. In Proceedings of the 2023 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Regina, SK, Canada, 24–27 September 2023; pp. 588–592. [Google Scholar]
- Al Momin, K.; Sadri, A.M.; Muraleetharan, K.K.; Campos, R.; Harvey, P.S. Application of multi-criteria decision analysis for optimal siting of electric vehicle charging stations in Oklahoma. Transp. Eng. 2025, 20, 100325. [Google Scholar] [CrossRef]
- Salcido, V.; Tillou, M.; Franconi, E. Electric Vehicle Charging for Residential and Commercial Energy Codes. Pacific Northwest National Laboratory. 2021. Available online: https://www.energycodes.gov/sites/default/files/2021-07/TechBrief_EV_Charging_July2021.pdf (accessed on 29 July 2022).
- Zheng, Y.; Keith, D.R.; Wang, S.; Diao, M.; Zhao, J. Effects of electric vehicle charging stations on the economic vitality of local businesses. Nat. Commun. 2024, 15, 7437. [Google Scholar] [CrossRef] [PubMed]
- Carpitella, S.; Jia, X.; Narimani, R. A review on current trends on optimal EVCS location. In Proceedings of the International Workshop on Simulation for Energy, Sustainable Development & Environment, Tenerife, Spain, 18–20 September 2024; pp. 18–20. [Google Scholar]
- Shahrier, H.; Habib, M.A. Econometric Modelling Approach to Explore the EV Adoption and Charging Opportunities at Workplace. Transp. Res. Procedia 2025, 82, 2348–2361. [Google Scholar] [CrossRef]
- Yadav, M.; Jena, S.; Panigrahi, C.K.; Naik, A.K. Comparative Analysis of Optimal EV Charging Strategies for Fleet Management, Based on Customer Perspective. In Proceedings of the 2024 3rd Odisha International Conference on Electrical Power Engineering, Communication and Computing Technology (ODICON), Bhubaneswar, India, 8–9 November 2024; pp. 1–5. [Google Scholar]
- Gönül, Ö.; Duman, A.C.; Güler, Ö. A comprehensive framework for electric vehicle charging station siting along highways using weighted sum method. Renew. Sustain. Energy Rev. 2024, 199, 114455. [Google Scholar] [CrossRef]
- Yazir, K.; Karasan, A.; Kaya, İ. Optimization of Electric Vehicle Charging Infrastructure Location for InterCity Transportation: Pre-Results and Discussion for Turkiye Case. In Proceedings of the 2024 International Conference on Green Energy, Computing and Sustainable Technology (GECOST), Miri Sarawak, Malaysia, 17–19 January 2024; pp. 416–419. [Google Scholar]
- Li, S.; Zhou, Z. A New Type of Vehicle Mounted Multifunctional Portable Charging Device Based on AI Control. In Proceedings of the 2024 6th International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 28–30 November 2024; pp. 234–237. [Google Scholar]
- Moghaddam, V.; Ahmad, I.; Habibi, D.; Masoum, M.A. Dispatch management of portable charging stations in electric vehicle networks. ETransportation 2021, 8, 100112. [Google Scholar] [CrossRef]
- Acharige, S.S.; Haque, M.E.; Arif, M.T.; Hosseinzadeh, N.; Hasan, K.N.; Oo, A.M.T. Review of electric vehicle charging technologies, standards, architectures, and converter configurations. IEEE Access 2023, 11, 41218–41255. [Google Scholar] [CrossRef]
- Dericioglu, C.; YiriK, E.; Unal, E.; Cuma, M.U.; Onur, B.; Tumay, M. A review of charging technologies for commercial electric vehicles. Int. J. Adv. Automot. Technol. 2018, 2, 61–70. [Google Scholar]
- Khan, S.; Alam, M.S.; Asghar, M.J.; Khan, M.A.; Abbas, A. Recent development in level 2 charging system for xEV: A review. In Proceedings of the 2018 International Conference on Computational and Characterization Techniques in Engineering & Sciences (CCTES), Lucknow, India, 14–15 September 2018; pp. 83–88. [Google Scholar]
- Berrehil El Kattel, M.; Mayer, R.; Ely, F.; de Jesus Cardoso Filho, B. Comprehensive review of battery charger structures of EVs and HEVs for levels 1–3. Int. J. Circuit Theory Appl. 2023, 51, 3514–3542. [Google Scholar] [CrossRef]
- Pradhan, R.; Keshmiri, N.; Emadi, A. On-board chargers for high-voltage electric vehicle powertrains: Future trends and challenges. IEEE Open J. Power Electron. 2023, 4, 189–207. [Google Scholar] [CrossRef]
- Meintz, A.; Slezak, L.; Kisacikoglu, J.; Kandula, P.; Bohn, T.; Ucer, E.; Harper, J.D.; Mohanpurkar, M. Electric Vehicles at Scale (EVs@ Scale) Laboratory Consortium Deep-Dive Technical Meetings: High Power Charging (HPC) Summary Report; Technical report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2022.
- Arsalan, A.; Papari, B.; Muriithi, G.; Scruggs, D.; Buraimoh, E.; Ozkan, G.; Edrington, C.S. A Resilient Distributed Control and Energy Management Approach for DERs and EVs with Application to EV Charging Stations. IFAC-PapersOnLine 2023, 56, 2115–2120. [Google Scholar] [CrossRef]
- Martins, J.A.; Rodrigues, J.M. Intelligent Monitoring Systems for Electric Vehicle Charging. Appl. Sci. 2025, 15, 2741. [Google Scholar] [CrossRef]
- Hafez, O.; Bhattacharya, K. Integrating EV charging stations as smart loads for demand response provisions in distribution systems. IEEE Trans. Smart Grid 2016, 9, 1096–1106. [Google Scholar] [CrossRef]
- Li, C.; Carta, D.; Benigni, A. EV charging station placement considering V2G and human factors in multi-energy systems. IEEE Trans. Smart Grid 2024, 16, 529–540. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Choi, D.H. Distributionally robust model predictive control for smart electric vehicle charging station with V2G/V2V capability. IEEE Trans. Smart Grid 2023, 14, 4621–4633. [Google Scholar] [CrossRef]
- Bilal, M.; Rizwan, M. Integration of electric vehicle charging stations and capacitors in distribution systems with vehicle-to-grid facility. Energy Sources Part A Recover. Util. Environ. Eff. 2025, 47, 7700–7729. [Google Scholar] [CrossRef]
- Nirala, P.K.; Barik, A.K.; Bhushan, R.; Jagtap, K.M.; Raushan, R. Renewable Power Integration for Electric Vehicle Charging System: A Review. In Proceedings of the 2025 IEEE 1st International Conference on Smart and Sustainable Developments in Electrical Engineering (SSDEE), Dhanbad, India, 28 February–2 March 2025; pp. 01–05. [Google Scholar]
- Neelashetty, K.; Rawat, R.; Ramesh, D.R.; Jethava, G.; Nandanka, P.V.; Natrayan, L. Energy Management for PV-Powered EV Charging With Grid Integration and Battery Energy Storage System using Dung Beetle Optimizer. In Proceedings of the 2025 5th International Conference on Trends in Material Science and Inventive Materials (ICTMIM), Kanyakumari, India, 7–9 April 2025; pp. 38–44. [Google Scholar]
- Jacob, J.J.; Abinaya, S.; Khatarkar, P.; Barno, A. Electric Vehicle Wireless Charging using RFID. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2023; Volume 399, p. 01010. [Google Scholar]
- Santhanakrishnan, T.; Vidyasagar, S. Self-Align & Wireless EV Charging System (SAW-EVCs). Solid State Technol. 2020, 63, 1002–1007. [Google Scholar]
- Velamuri, S.; Sudabattula, S.K.; Kantipudi, M.P.; Prabaharan, N. Q-learning based commercial electric vehicles scheduling in a renewable energy dominant distribution systems. Electr. Power Components Syst. 2023, 1–14. [Google Scholar] [CrossRef]
- Velamuri, S.; Kantipudi, M.P.; Sitharthan, R.; Kanakadhurga, D.; Prabaharan, N.; Rajkumar, A. A Q-learning based electric vehicle scheduling technique in a distribution system for power loss curtailment. Sustain. Comput. Inform. Syst. 2022, 36, 100798. [Google Scholar] [CrossRef]
- Erüst, A.C.; Taşcıkaraoğlu, F.Y. Spatio-temporal dynamic navigation for electric vehicle charging using deep reinforcement learning. IET Intell. Transp. Syst. 2024, 18, 2520–2531. [Google Scholar] [CrossRef]
- Adetunji, K.E.; Hofsajer, I.W.; Abu-Mahfouz, A.M.; Cheng, L. A two-tailed pricing scheme for optimal EV charging scheduling using multiobjective reinforcement learning. IEEE Trans. Ind. Inform. 2023, 20, 3361–3370. [Google Scholar] [CrossRef]
- Li, Y.; He, S.; Li, Y.; Ge, L.; Lou, S.; Zeng, Z. Probabilistic charging power forecast of EVCS: Reinforcement learning assisted deep learning approach. IEEE Trans. Intell. Veh. 2022, 8, 344–357. [Google Scholar] [CrossRef]
- Tian, D.; Zhang, H.; Huang, J.; Zhang, Z.; Yu, C. An Attention-Based Reinforcement Learning Approach For Electric Vehicle Charging Control. In Proceedings of the 2023 7th Asian Conference on Artificial Intelligence Technology (ACAIT), Jiaxing, China, 10–12 November 2023; pp. 173–182. [Google Scholar]
- Suanpang, P.; Jamjuntr, P. Optimizing electric vehicle charging recommendation in smart cities: A multi-agent reinforcement learning approach. World Electr. Veh. J. 2024, 15, 67. [Google Scholar] [CrossRef]
- Liang, Z.; Qian, T.; Hu, Q. Price-based demand response in the coupled power and transportation network via EV charging station. In Proceedings of the 2023 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Chiang Mai, Thailand, 28 November–1 December 2023; pp. 1–6. [Google Scholar]
- Lee, S.; Choi, D.H. Three-stage deep reinforcement learning for privacy-and safety-aware smart electric vehicle charging station scheduling and Volt/VAR control. IEEE Internet Things J. 2023, 11, 8578–8589. [Google Scholar] [CrossRef]
- Erüst, A.C.; Beyazıt, M.A.; Taşcıkaraoğlu, F.Y.; Taşcıkaraoğlu, A. Deep reinforcement learning-based navigation strategy for a mobile charging station in a dynamic environment. In Proceedings of the 2023 International Conference on Smart Energy Systems and Technologies (SEST), Mugla, Turkiye, 4–6 September 2023; pp. 1–6. [Google Scholar]
- Vandael, S.; Claessens, B.; Ernst, D.; Holvoet, T.; Deconinck, G. Reinforcement learning of heuristic EV fleet charging in a day-ahead electricity market. IEEE Trans. Smart Grid 2015, 6, 1795–1805. [Google Scholar] [CrossRef]
- Arif, A.; Babar, M.; Ahamed, T.I.; Al-Ammar, E.; Nguyen, P.; Kamphuis, I.R.; Malik, N. Online scheduling of plug-in vehicles in dynamic pricing schemes. Sustain. Energy Grids Netw. 2016, 7, 25–36. [Google Scholar] [CrossRef]
- Wan, Z.; Li, H.; He, H.; Prokhorov, D. Model-free real-time EV charging scheduling based on deep reinforcement learning. IEEE Trans. Smart Grid 2018, 10, 5246–5257. [Google Scholar] [CrossRef]
- Dang, Q.; Wu, D.; Boulet, B. A q-learning based charging scheduling scheme for electric vehicles. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019; pp. 1–5. [Google Scholar]
- Wang, S.; Bi, S.; Zhang, Y.A. Reinforcement learning for real-time pricing and scheduling control in EV charging stations. IEEE Trans. Ind. Inform. 2019, 17, 849–859. [Google Scholar] [CrossRef]
- Sadeghianpourhamami, N.; Deleu, J.; Develder, C. Definition and evaluation of model-free coordination of electrical vehicle charging with reinforcement learning. IEEE Trans. Smart Grid 2019, 11, 203–214. [Google Scholar] [CrossRef]
- Da Silva, F.L.; Nishida, C.E.; Roijers, D.M.; Costa, A.H.R. Coordination of electric vehicle charging through multiagent reinforcement learning. IEEE Trans. Smart Grid 2019, 11, 2347–2356. [Google Scholar] [CrossRef]
- Qian, T.; Shao, C.; Wang, X.; Shahidehpour, M. Deep reinforcement learning for EV charging navigation by coordinating smart grid and intelligent transportation system. IEEE Trans. Smart Grid 2019, 11, 1714–1723. [Google Scholar] [CrossRef]
- Xu, X.; Jia, Y.; Xu, Y.; Xu, Z.; Chai, S.; Lai, C.S. A multi-agent reinforcement learning-based data-driven method for home energy management. IEEE Trans. Smart Grid 2020, 11, 3201–3211. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Wu, F.; Tang, B.; Fan, W. Effective charging planning based on deep reinforcement learning for electric vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 542–554. [Google Scholar] [CrossRef]
- Fang, C.; Lu, H.; Hong, Y.; Liu, S.; Chang, J. Dynamic pricing for electric vehicle extreme fast charging. IEEE Trans. Intell. Transp. Syst. 2020, 22, 531–541. [Google Scholar] [CrossRef]
- Dorokhova, M.; Martinson, Y.; Ballif, C.; Wyrsch, N. Deep reinforcement learning control of electric vehicle charging in the presence of photovoltaic generation. Appl. Energy 2021, 301, 117504. [Google Scholar] [CrossRef]
- Tuchnitz, F.; Ebell, N.; Schlund, J.; Pruckner, M. Development and evaluation of a smart charging strategy for an electric vehicle fleet based on reinforcement learning. Appl. Energy 2021, 285, 116382. [Google Scholar] [CrossRef]
- Zhang, Y.; Rao, X.; Liu, C.; Zhang, X.; Zhou, Y. A cooperative EV charging scheduling strategy based on double deep Q-network and Prioritized experience replay. Eng. Appl. Artif. Intell. 2023, 118, 105642. [Google Scholar] [CrossRef]
- Hao, X.; Chen, Y.; Wang, H.; Wang, H.; Meng, Y.; Gu, Q. A V2G-oriented reinforcement learning framework and empirical study for heterogeneous electric vehicle charging management. Sustain. Cities Soc. 2023, 89, 104345. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, A.; Wang, Q.; Hu, Y.; Fang, F.; Cheng, L. Quantum Reinforcement Learning for real-time optimization in Electric Vehicle charging systems. Appl. Energy 2025, 383, 125279. [Google Scholar] [CrossRef]
- Amir, M.; Zaheeruddin; Haque, A.; Kurukuru, V.B.; Bakhsh, F.I.; Ahmad, A. Agent based online learning approach for power flow control of electric vehicle fast charging station integrated with smart microgrid. IET Renew. Power Gener. 2025, 19, e12508. [Google Scholar] [CrossRef]
- Li, H.; Wan, Z.; He, H. Constrained EV charging scheduling based on safe deep reinforcement learning. IEEE Trans. Smart Grid 2019, 11, 2427–2439. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, J.; Yan, J.; He, H. Intelligent load frequency controller using GrADP for island smart grid with electric vehicles and renewable resources. Neurocomputing 2015, 170, 406–416. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, Q.; An, D. CDDPG: A deep-reinforcement-learning-based approach for electric vehicle charging control. IEEE Internet Things J. 2020, 8, 3075–3087. [Google Scholar] [CrossRef]
- Lee, S.; Choi, D.H. Energy management of smart home with home appliances, energy storage system and electric vehicle: A hierarchical deep reinforcement learning approach. Sensors 2020, 20, 2157. [Google Scholar] [CrossRef]
- Ding, T.; Zeng, Z.; Bai, J.; Qin, B.; Yang, Y.; Shahidehpour, M. Optimal electric vehicle charging strategy with Markov decision process and reinforcement learning technique. IEEE Trans. Ind. Appl. 2020, 56, 5811–5823. [Google Scholar] [CrossRef]
- Lee, S.; Choi, D.H. Dynamic pricing and energy management for profit maximization in multiple smart electric vehicle charging stations: A privacy-preserving deep reinforcement learning approach. Appl. Energy 2021, 304, 117754. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, H.; Li, D.; Zhang, G. Smart online charging algorithm for electric vehicles via customized actor–critic learning. IEEE Internet Things J. 2021, 9, 684–694. [Google Scholar] [CrossRef]
- Li, S.; Hu, W.; Cao, D.; Dragičević, T.; Huang, Q.; Chen, Z.; Blaabjerg, F. Electric vehicle charging management based on deep reinforcement learning. J. Mod. Power Syst. Clean Energy 2021, 10, 719–730. [Google Scholar] [CrossRef]
- Park, K.; Moon, I. Multi-agent deep reinforcement learning approach for EV charging scheduling in a smart grid. Appl. Energy 2022, 328, 120111. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, H.; Wang, F.; Xu, T.; Xin, H.; Dou, D.; Xiong, H. Intelligent electric vehicle charging recommendation based on multi-agent reinforcement learning. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 1856–1867. [Google Scholar]
- Lai, C.S.; Chen, D.; Zhang, J.; Zhang, X.; Xu, X.; Taylor, G.A.; Lai, L.L. Profit maximization for large-scale energy storage systems to enable fast EV charging infrastructure in distribution networks. Energy 2022, 259, 124852. [Google Scholar] [CrossRef]
- Svetozarevic, B.; Baumann, C.; Muntwiler, S.; Di Natale, L.; Zeilinger, M.N.; Heer, P. Data-driven control of room temperature and bidirectional EV charging using deep reinforcement learning: Simulations and experiments. Appl. Energy 2022, 307, 118127. [Google Scholar] [CrossRef]
- Tan, M.; Dai, Z.; Su, Y.; Chen, C.; Wang, L.; Chen, J. Bi-level optimization of charging scheduling of a battery swap station based on deep reinforcement learning. Eng. Appl. Artif. Intell. 2023, 118, 105557. [Google Scholar] [CrossRef]
- Alfaverh, F.; Denaï, M.; Sun, Y. Optimal vehicle-to-grid control for supplementary frequency regulation using deep reinforcement learning. Electr. Power Syst. Res. 2023, 214, 108949. [Google Scholar] [CrossRef]
- Fu, L.; Wang, T.; Song, M.; Zhou, Y.; Gao, S. Electric vehicle charging scheduling control strategy for the large-scale scenario with non-cooperative game-based multi-agent reinforcement learning. Int. J. Electr. Power Energy Syst. 2023, 153, 109348. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Wang, W.; Liu, C.; Li, Y. Dynamic pricing based electric vehicle charging station location strategy using reinforcement learning. Energy 2023, 281, 128284. [Google Scholar] [CrossRef]
- Liu, D.; Zeng, P.; Cui, S.; Song, C. Deep reinforcement learning for charging scheduling of electric vehicles considering distribution network voltage stability. Sensors 2023, 23, 1618. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Jia, R.; Pan, H.; Cao, Y. A safe reinforcement learning-based charging strategy for electric vehicles in residential microgrid. Appl. Energy 2023, 348, 121490. [Google Scholar] [CrossRef]
- Lee, S.; Choi, D.H. Two-stage scheduling of smart electric vehicle charging stations and inverter-based Volt-VAR control using a prediction error-integrated deep reinforcement learning method. Energy Rep. 2023, 10, 1135–1150. [Google Scholar] [CrossRef]
- Bae, S.; Kulcsár, B.; Gros, S. Personalized dynamic pricing policy for electric vehicles: Reinforcement learning approach. Transp. Res. Part C Emerg. Technol. 2024, 161, 104540. [Google Scholar] [CrossRef]
- Li, G.; Zhang, R.; Bu, S.; Zhang, J.; Gao, J. Probabilistic prediction-based multi-objective optimization approach for multi-energy virtual power plant. Int. J. Electr. Power Energy Syst. 2024, 161, 110200. [Google Scholar] [CrossRef]
- Jiang, C.; Jing, Z.; Cui, X.; Ji, T.; Wu, Q. Multiple agents and reinforcement learning for modelling charging loads of electric taxis. Appl. Energy 2018, 222, 158–168. [Google Scholar] [CrossRef]
- Ko, H.; Pack, S.; Leung, V.C. Mobility-aware vehicle-to-grid control algorithm in microgrids. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2165–2174. [Google Scholar] [CrossRef]
- Ko, Y.D. An efficient integration of the genetic algorithm and the reinforcement learning for optimal deployment of the wireless charging electric tram system. Comput. Ind. Eng. 2019, 128, 851–860. [Google Scholar] [CrossRef]
- Li, G.; Sun, Q.; Boukhatem, L.; Wu, J.; Yang, J. Intelligent vehicle-to-vehicle charging navigation for mobile electric vehicles via VANET-based communication. IEEE Access 2019, 7, 170888–170906. [Google Scholar] [CrossRef]
- Liang, Y.; Ding, Z.; Ding, T.; Lee, W.J. Mobility-aware charging scheduling for shared on-demand electric vehicle fleet using deep reinforcement learning. IEEE Trans. Smart Grid 2020, 12, 1380–1393. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, J.; Gao, T.; Chen, S.; Wang, X.; Jiang, H.; Gao, W. Real-time fast charging station recommendation for electric vehicles in coupled power-transportation networks: A graph reinforcement learning method. Int. J. Electr. Power Energy Syst. 2022, 141, 108030. [Google Scholar] [CrossRef]
- Adetunji, K.E.; Hofsajer, I.W.; Abu-Mahfouz, A.M.; Cheng, L. An optimization planning framework for allocating multiple distributed energy resources and electric vehicle charging stations in distribution networks. Appl. Energy 2022, 322, 119513. [Google Scholar] [CrossRef]
- Tao, Y.; Qiu, J.; Lai, S.; Sun, X.; Zhao, J.; Zhou, B.; Cheng, L. Data-driven on-demand energy supplement planning for electric vehicles considering multi-charging/swapping services. Appl. Energy 2022, 311, 118632. [Google Scholar] [CrossRef]
- Wang, J.; Guo, C.; Yu, C.; Liang, Y. Virtual power plant containing electric vehicles scheduling strategies based on deep reinforcement learning. Electr. Power Syst. Res. 2022, 205, 107714. [Google Scholar] [CrossRef]
- Makeen, P.; Ghali, H.A.; Memon, S.; Duan, F. Smart techno-economic operation of electric vehicle charging station in Egypt. Energy 2023, 264, 126151. [Google Scholar] [CrossRef]
- Ren, L.; Yuan, M.; Jiao, X. Electric vehicle charging and discharging scheduling strategy based on dynamic electricity price. Eng. Appl. Artif. Intell. 2023, 123, 106320. [Google Scholar] [CrossRef]
- Zhou, Y.; Ong, G.P.; Meng, Q.; Cui, H. Electric bus charging facility planning with uncertainties: Model formulation and algorithm design. Transp. Res. Part C Emerg. Technol. 2023, 150, 104108. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, C.K.; Ren, J. A two-level charging scheduling method for public electric vehicle charging stations considering heterogeneous demand and nonlinear charging profile. Appl. Energy 2024, 355, 122278. [Google Scholar] [CrossRef]
- Abid, M.S.; Apon, H.J.; Hossain, S.; Ahmed, A.; Ahshan, R.; Lipu, M.H. A novel multi-objective optimization based multi-agent deep reinforcement learning approach for microgrid resources planning. Appl. Energy 2024, 353, 122029. [Google Scholar] [CrossRef]
- Ala, A.; Deveci, M.; Bani, E.A.; Sadeghi, A.H. Dynamic capacitated facility location problem in mobile renewable energy charging stations under sustainability consideration. Sustain. Comput. Inform. Syst. 2024, 41, 100954. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).