A Single-Phase Compact Size Asymmetrical Inverter Topology for Renewable Energy Application
Abstract
1. Introduction
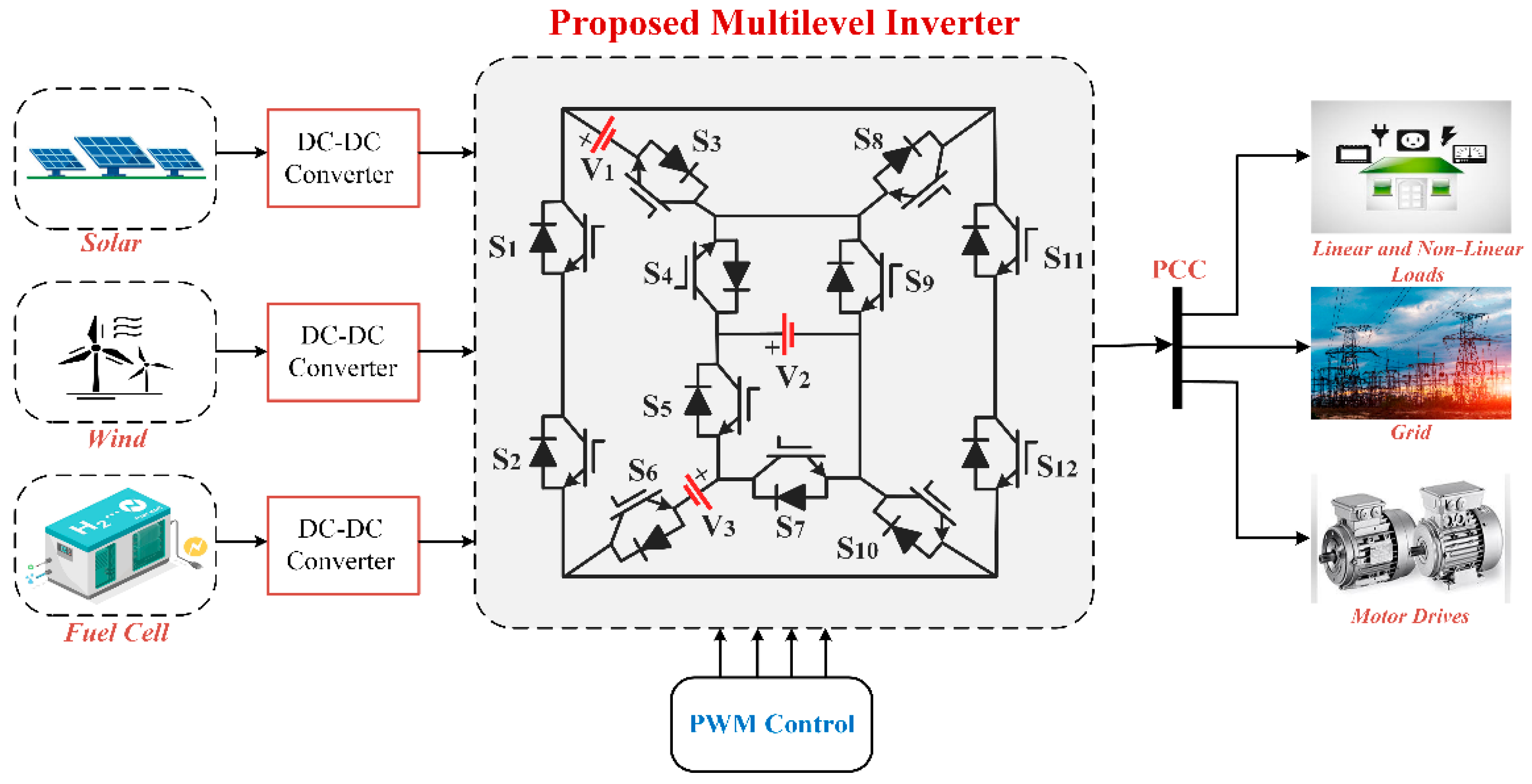
2. Description of the Proposed Topology
2.1. Circuit Configuration
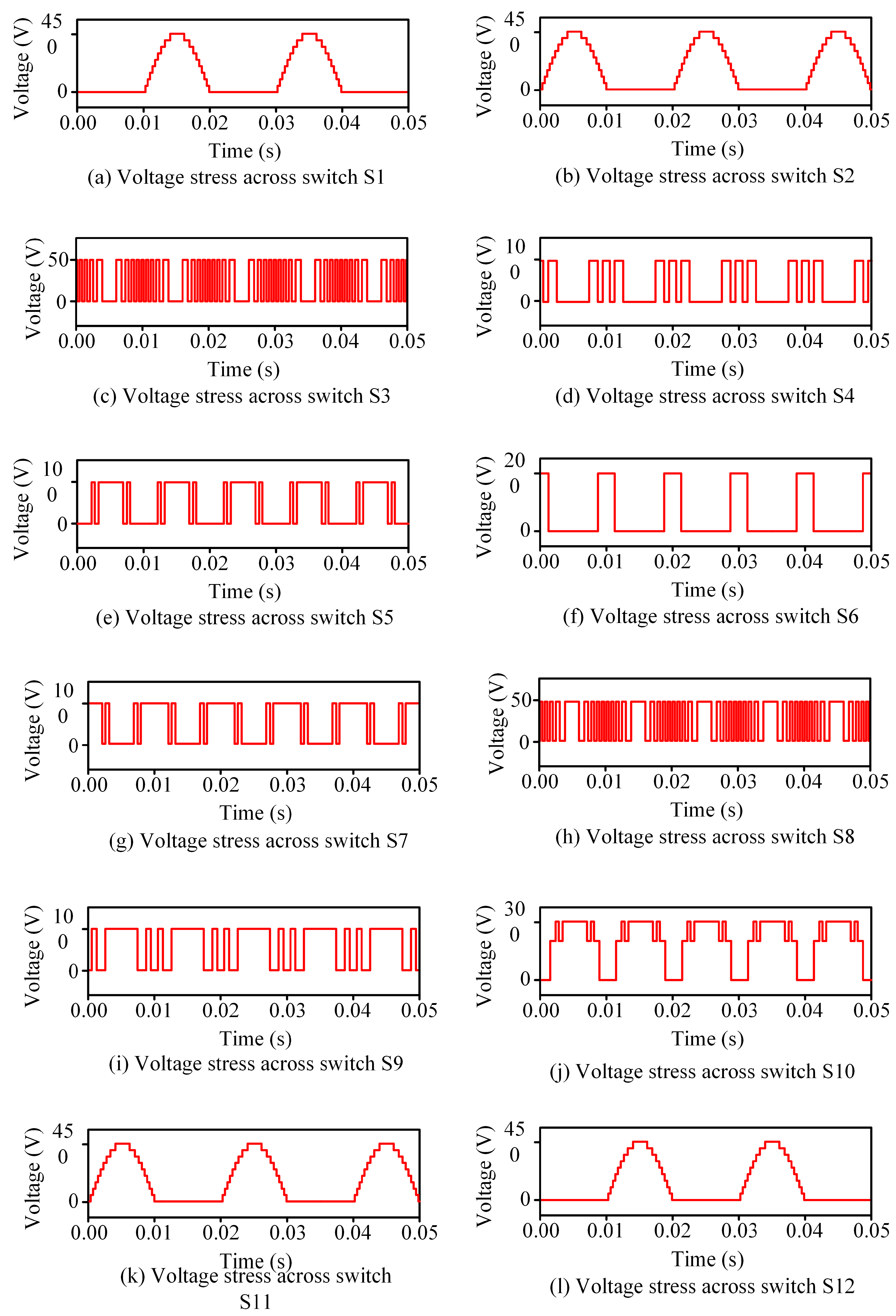
2.2. Voltage Rating of Switches
2.3. Extended Generalized Structure
2.4. Modulation Strategy
2.5. Cost Analysis
2.6. Reliability Analysis
3. Results and Discussion
3.1. Simulation Results
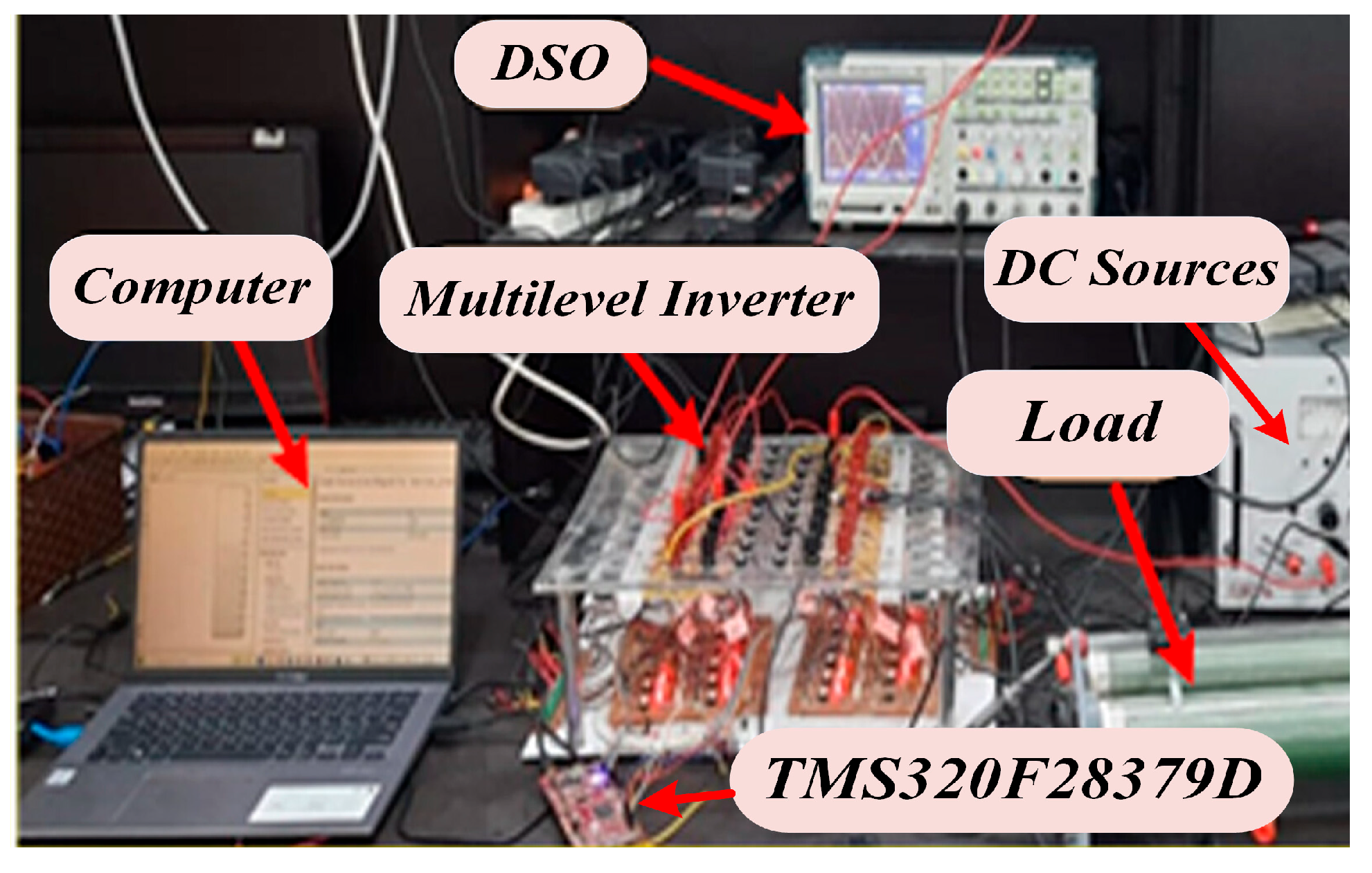
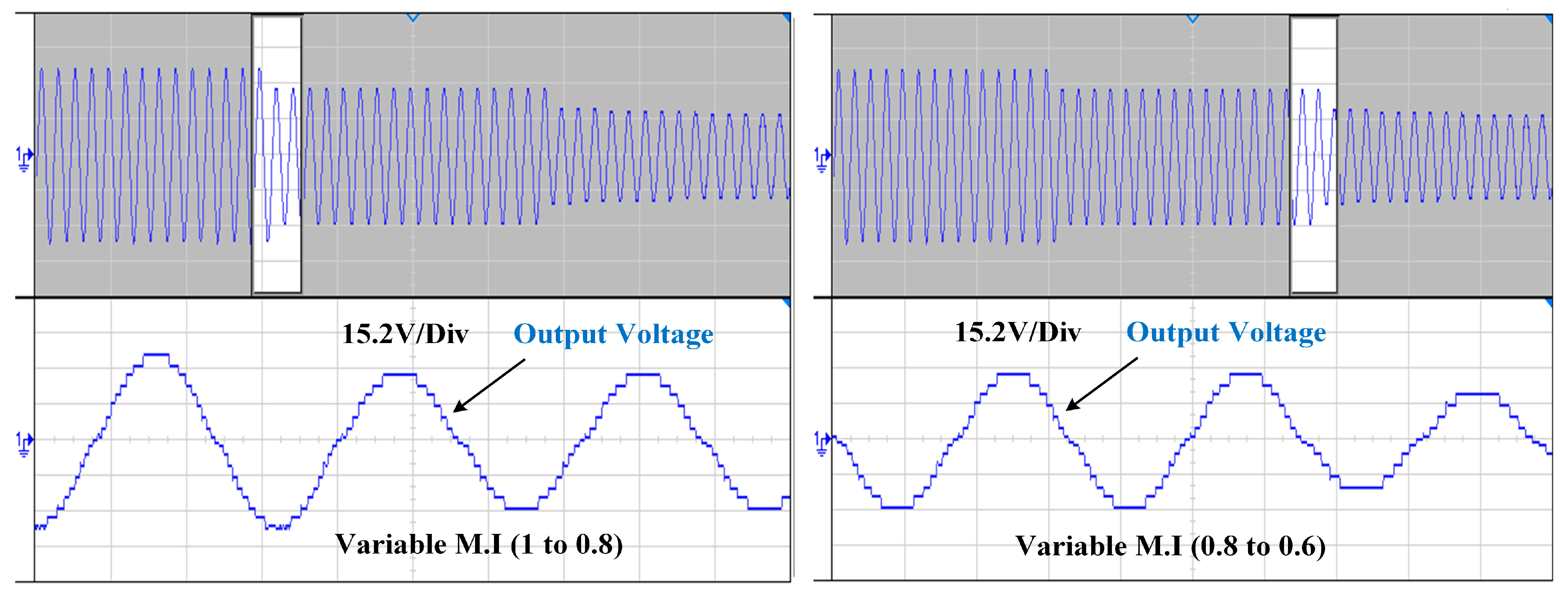
3.2. Hardware Results
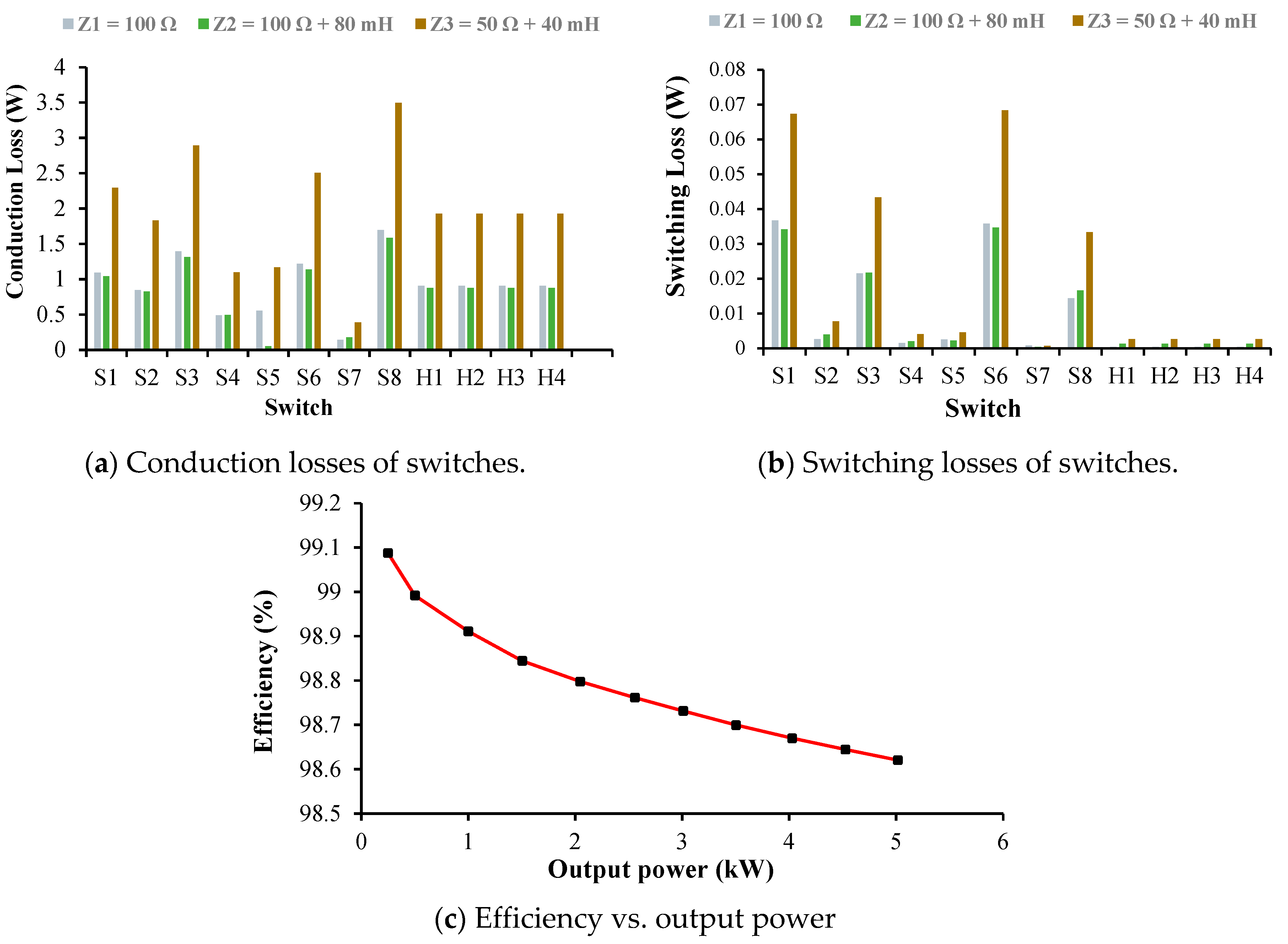
4. Power Loss Analysis
5. Comparative Analysis
6. Application of the Proposed Topology
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rodriguez, J.; Franquelo, L.G.; Kouro, S.; Leon, J.I.; Portillo, R.C.; Prats, M.A.M.; Perez, M.A. Multilevel Converters: An Enabling Technology for High-Power Applications. IEEE Proc. 2009, 97, 1786–1817. [Google Scholar] [CrossRef]
- Barzegarkhoo, R.; Forouzesh, M.; Lee, S.S.; Blaabjerg, F.; Siwakoti, Y.P. Switched-Capacitor Multilevel Inverters: A Comprehensive Review. IEEE Trans. Power Electron. 2022, 37, 11209–11243. [Google Scholar] [CrossRef]
- Mukundan, N.; Sangeetha, V.; Jayaprakash, P.; Asokan, O.V.; Al-Durra, A.; Zeineldin, H.; El-Fouly, T.H. A New Multilevel Inverter Based Grid Connected Reliable Solar Power Transfer Unit with Power Quality Enhancement. IEEE Trans. Ind. Appl. 2023, 59, 1887–1900. [Google Scholar] [CrossRef]
- Anand, V.; Singh, V.; Mekhlief, S. Power electronics for renewable energy systems. Renew. Energy Sustain. Growth Assess. 2022, 5, 81–117. [Google Scholar]
- Ramasamy, S.; Sivasubramaniyam, V.; Gatto, G.; Kumar, A. DC link voltage control based energy management strategy for standalone solar PV fed hybrid system. In Proceedings of the 2023 AEIT International Conference on Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Modena, Italy, 17–19 July 2023; IEEE: Piscataway, NY, USA, 2023. [Google Scholar]
- Rajender, B. A dissertation submitted in partial fulfillment of the requirements for the award of the degree of Master of Technology in Electrical Engineering with specialization in Electric Drives and Power Electronics. Indian Inst. Technol. Roorkee 2011. [Google Scholar]
- Akbari, A.; Ebrahimi, J.; Jafarian, Y.; Bakhshai, A. A Multilevel Inverter Topology with an Improved Reliability and a Reduced Number of Components. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 553–563. [Google Scholar] [CrossRef]
- Gupta, K.K.; Ranjan, A.; Bhatnagar, P.; Sahu, L.K.; Jain, S. Multilevel inverter topologies with reduced device count: A review. IEEE Trans. Power Electron. 2016, 31, 135–151. [Google Scholar] [CrossRef]
- Vemuganti, H.P.; Sreenivasarao, D.; Ganjikunta, S.K.; Suryawanshi, H.M.; Abu-Rub, H. A survey on reduced switch count multilevel inverters. IEEE Open J. Ind. Electron. Soc. 2021, 2, 80–111. [Google Scholar] [CrossRef]
- Samadaei, E.; Sheikholeslami, A.; Gholamian, S.A.; Adabi, J. A Square T-Type (ST-Type) Module for Asymmetrical Multilevel Inverters. IEEE Trans. Power Electron. 2018, 33, 987–996. [Google Scholar] [CrossRef]
- Samadaei, E.; Kaviani, M.; Bertilsson, K. A 13-levels module (K-type) with two DC sources for multilevel inverters. IEEE Trans. Ind. Electron. 2019, 66, 5186–5196. [Google Scholar] [CrossRef]
- Ounejjar, Y.; Al-Haddad, K.; Gregoire, L.-A. Packed U cells multilevel converter topology: Theoretical study and experimental validation. IEEE Trans. Ind. Electron. 2011, 58, 1294–1306. [Google Scholar]
- Gupta, K.K.; Jain, S. A novel multilevel inverter based on switched DC sources. IEEE Trans. Ind. Electron. 2014, 61, 3269–3278. [Google Scholar]
- Nair, R.V.; Gopakumar, K.; Franquelo, L.G. A Very High Resolution Stacked Multilevel Inverter Topology for Adjustable Speed Drives. IEEE Trans. Ind. Electron. 2018, 65, 2049–2056. [Google Scholar] [CrossRef]
- Jena, K.; Kumar, D.; Kumar, B.H.; Janardhan, K.; Singh, A.R.; Naidoo, R.; Bansal, R.C. A Single DC Source Generalized Switched Capacitors Multilevel Inverter with Minimal Component Count. Int. Trans. Electr. Energy Syst. 2023, 2023, 3945160. [Google Scholar] [CrossRef]
- Kumari, M.; Siddique, M.D.; Sarwar, A.; Tariq, M.; Mekhilef, S.; Iqbal, A. Recent trends and review on switched-capacitor-based singlestage boost multilevel inverter. Int. Trans. Elect. Energy Syst. 2021, 31, 3. [Google Scholar] [CrossRef]
- Behara, S.; Sandeep, N.; Yaragatti, U.R. Design and Implementation of Transformer-Based Multilevel Inverter Topology with Reduced Components. IEEE Trans. Ind. Appl. 2018, 54, 4632–4639. [Google Scholar] [CrossRef]
- Thangapandi, A.K.; Kumar, A.; Karthigeyan, D.; Ramasamy, S.; Arumugam, V.; Gatto, G. A novel artificial neural network based selection harmonic reduction technique for single source fed high gain switched capacitor coupled multilevel inverter for renewable energy applications. Heliyon 2024, 10, 19. [Google Scholar] [CrossRef]
- Thiyagarajan, V.; Somasundaram, P. Simulation of New Symmetric and Asymmetric Multilevel Inverter Topology with Reduced Number of Switches. In Proceedings of the 2018 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 7–9 February 2018; pp. 315–319. [Google Scholar]
- Siddique, M.D.; Mustafa, A.; Sarwar, A.; Mekhilef, S.; Shah, N.B.M.; Seyedamahmousian, M.; Stojcevski, A.; Horan, B.; Ogura, K. Single phase symmetrical and asymmetrical design of multilevel inverter topology with reduced number of switches. In Proceedings of the 2018 IEEMA Engineer Infinite Conference, New Delhi, India, 13–14 March 2018; IEEE: Piscataway, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Barzegarkhoo, R.; Moradzadeh, M.; Zamiri, E.; Kojabadi, H.M.; Blaabjerg, F. A new boost switched-capacitor multilevel converter with reduced circuit devices. IEEE Trans. Power Electron. 2018, 33, 6738–6754. [Google Scholar] [CrossRef]
- Arif, M.S.B.; Mustafa, U.; Ayob, S.B.M.; Rodriguez, J.; Nadeem, A.; Abdelrahem, M. Asymmetrical 17-Level inverter topology with reduced total standing voltage and device count. IEEE Access 2021, 9, 69710–69723. [Google Scholar] [CrossRef]
- Shehu, G.S.; Kunya, A.B.; Shanono, I.H.; Yalçınöz, T.A. Review of Multilevel Inverter Topology and Control Techniques. Int. J. Autom. Control. 2016, 4, 233–241. [Google Scholar] [CrossRef][Green Version]
- Sarwer, Z.; Sarwar, A.; Zaid, M.; Hussan, M.R.; Tariq, M.; Alamri, B.; Alahmadi, A. Implementation of a Novel Variable Structure Nearest Level Modulation on Cascaded H-Bridge Multilevel Inverter. IEEE Access 2021, 9, 133974–133988. [Google Scholar] [CrossRef]
- Ahmad, M.F.; Arif, M.S.B.; Abdelrahem, M.; Rodriguez, J. A high gain and compact size asymmetrical 17-level inverter for medium-and high-power applications. Int. J. Circuit Theory Appl. 2023, 52, 2741–2759. [Google Scholar] [CrossRef]
- Mustafa, U.; Arif, M.S.B.; Kennel, R.; Abdelrahem, M. Asymmetrical eleven-level inverter topology with reduced power semiconductor switches total standing voltage and cost factor. IET Power Electron. 2022, 15, 395–411. [Google Scholar] [CrossRef]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An Industry Based Survey of Reliability in Power Electronic Converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Alavi, O.; Hooshmand Viki, A.; Shamlou, S. A Comparative Reliability Study of Three Fundamental Multilevel Inverters Using Two Different Approaches. Electronics 2016, 5, 18. [Google Scholar] [CrossRef]
- US Department of Defense. US Department of Defense: MIL-HDBK-217F (NOTICE 2), Military Handbook Reliability Prediction of Electronic Equipment; Defense Technical Information Center: Alexandria, VI, USA, 1995. [Google Scholar]
- Thakre, K.; Mohanty, K.B.; Chatterjee, A.; Kommukuri, V.S. A modified circuit for symmetric and asymmetric multilevel inverter with reduced components count. Int. Trans. Electr. Energy Syst. 2019, 29, e12011. [Google Scholar] [CrossRef]
- Alishah, R.S.; Hosseini, S.H.; Babaei, E.; Sabahi, M. A new general multilevel converter topology based on cascaded connection of submultilevel units with reduced switching components, DC sources, and blocked voltage by switches. IEEE Trans. Ind. Electron. 2016, 63, 7157–7164. [Google Scholar] [CrossRef]
- Ngo, B.; Nguyen, M.; Kim, J.; Zare, F. Single-phase multilevel inverter based on switched-capacitor structure. IET Power Electron. 2018, 11, 1858–1865. [Google Scholar] [CrossRef]
- Dhanamjayulu, C.; Prasad, D.; Padmanaban, S.; Maroti, P.K.; Holm-Nielsen, J.B.; Blaabjerg, F. Design and implementation of seventeen level inverter with reduced components. IEEE Access. 2021, 9, 16746–16760. [Google Scholar] [CrossRef]
- Seifi, A.; Hosseini, S.H.; Hagh, M.T.; Hosseinpour, M. New multilevel inverter based on reduced switch basic cell for high voltage levels. IET Power Electron. 2024, 17, 551–563. [Google Scholar] [CrossRef]
- Babaei, E.; Laali, S.; Bayat, Z. A Single-Phase Cascaded Multilevel Inverter Based on a New Basic Unit with Reduced Number of Power Switches. IEEE Trans. Ind. Electron. 2015, 62, 922–929. [Google Scholar]
- Meraj, S.T.; Yahaya, N.Z.; Hasan, K.; Masaoud, A. Single phase 21 level hybrid multilevel inverter with reduced power components employing low frequency modulation technique. Int. J. Power Electron. Drive Syst. 2020, 11, 810. [Google Scholar]
- Dargahi, V.; Sadigh, A.K.; Abarzadeh, M.; Pahlavani, M.R.A.; Shoulaie, A. Flying capacitor reduction in an improved double flying capacitor multicell converter controlled by a modified modulation method. IEEE Trans. Power Electron. 2012, 27, 3875–3887. [Google Scholar] [CrossRef]
- Babaei, E.; Laali, S.; Alilu, S. Cascaded Multilevel Inverter with Series Connection of Novel H-Bridge Basic Units. IEEE Trans. Ind. Electron. 2014, 61, 6664–6671. [Google Scholar] [CrossRef]
- Hosseini Montazer, B.; Olamaei, J.; Hosseinpour, M.; Mozafari, B. A generalized diode containing bidirectional topology for multilevel inverter with reduced switches and power loss. Int. J. Circ. Theor. Appl. 2021, 49, 2959–2978. [Google Scholar] [CrossRef]
- Bana, P.R.; Panda, K.P.; Naayagi, R.T.; Siano, P.; Panda, G. Recently developed reduced switch multilevel inverter for renewable energy integration and drives application: Topologies, comprehensive analysis and comparative evaluation. IEEE Access 2019, 7, 54888–54909. [Google Scholar] [CrossRef]
- Mittal, S.; Singh, A.; Chittora, P. Design and development of Reduced Switch Five Level Inverter for interfacing renewable energy sources and EV charger. Electr. Eng. 2024, 107, 6735–6749. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, S.; Ma, J.; Jiang, Y.; Wang, P.; Liu, T.; Yang, Y. An Asymmetric Hybrid Phase-Leg Modular Multilevel Converter with Small Volume, Low Cost, and DC Fault-Blocking Capability. IEEE Trans. Power Electron. 2025, 40, 5336–5351. [Google Scholar] [CrossRef]
- Gao, S.; Chen, Y.; Song, Y.; Yu, Z.; Wang, Y. An Efficient Half-Bridge MMC Model for EMTP-Type Simulation Based on Hybrid Numerical Integration. IEEE Trans. Power Syst. 2024, 39, 1162–1177. [Google Scholar] [CrossRef]
- Rong, Q.; Hu, P.; Yu, Y.; Wang, D.; Cao, Y.; Xin, H. Virtual External Perturbance-Based Impedance Measurement of Grid-Connected Converter. IEEE Trans. Ind. Electron. 2025, 72, 2644–2654. [Google Scholar] [CrossRef]
- Rong, Q.; Hu, P.; Wang, L.; Li, Y.; Yu, Y.; Wang, D.; Cao, Y. Asymmetric Sampling Disturbance-Based Universal Impedance Measurement Method for Converters. IEEE Trans. Power Electron. 2024, 39, 15457–15461. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Kong, X.; Zhou, J.; Shi, G.; Zang, J.; Wang, J. A Novel Multiple-Medium-AC-Port Power Electronic Transformer. IEEE Trans. Ind. Electron. 2024, 71, 6568–6578. [Google Scholar] [CrossRef]
- Li, N.; Zhang, C.; Liu, Y.; Zhuo, C.; Liu, M.; Yang, J.; Zhang, Y. Single-Degree-of-Freedom Hybrid Modulation Strategy and Light-Load Efficiency Optimization for Dual-Active-Bridge Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 3936–3947. [Google Scholar] [CrossRef]
- Li, S.; Zhou, J.; Zhou, F.; Niu, F.; Deng, W. A Reduced Current Ripple Overmodulation Strategy for Indirect Matrix Converter. IEEE Trans. Ind. Electron. 2025, 72, 3768–3777. [Google Scholar] [CrossRef]
- Lu, G.; Lin, Q.; Zheng, D.; Zhang, P. Online Degradation Fault Prognosis for DC-Link Capacitors in Multistring-Connected Photovoltaic Boost Converters Subject to Cable Uncertainties. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 1107–1117. [Google Scholar] [CrossRef]
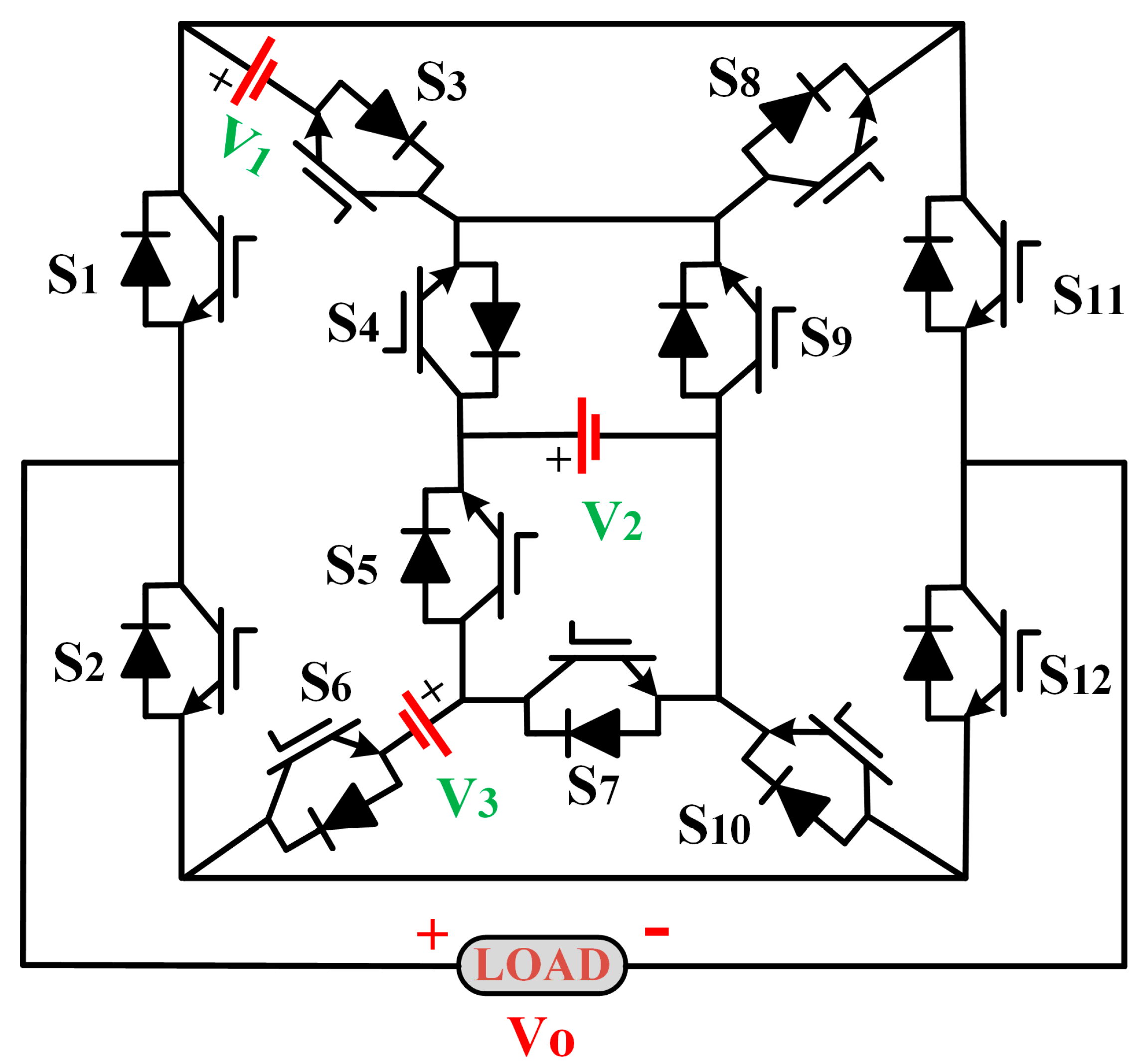

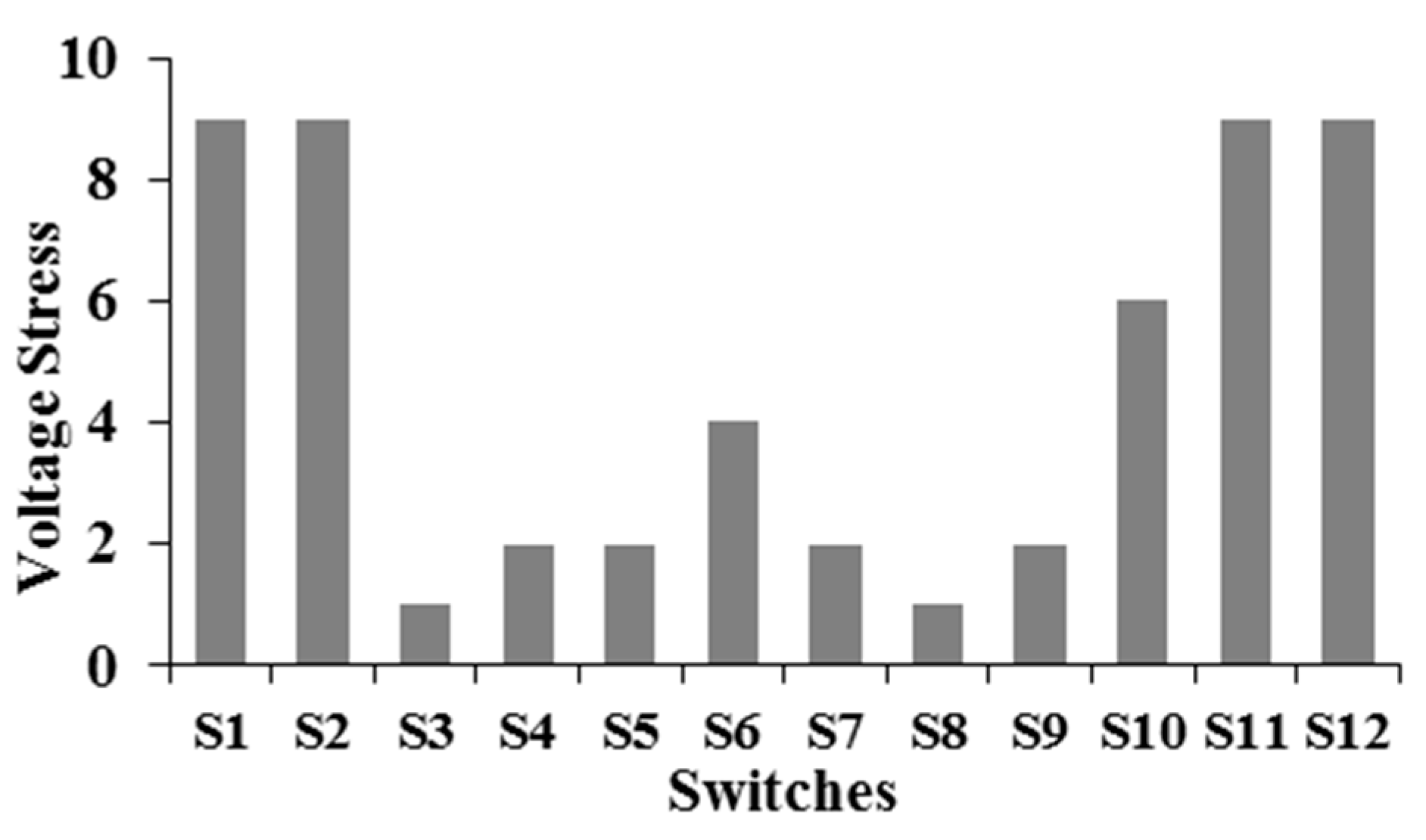
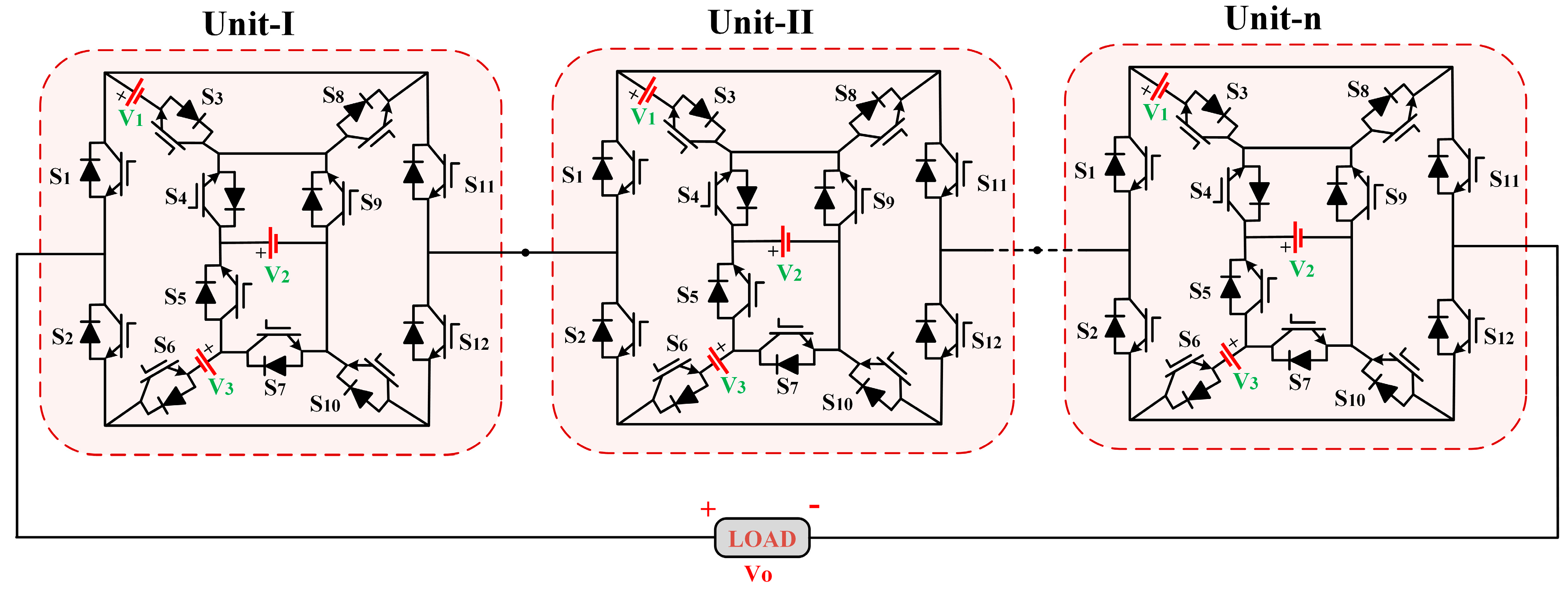

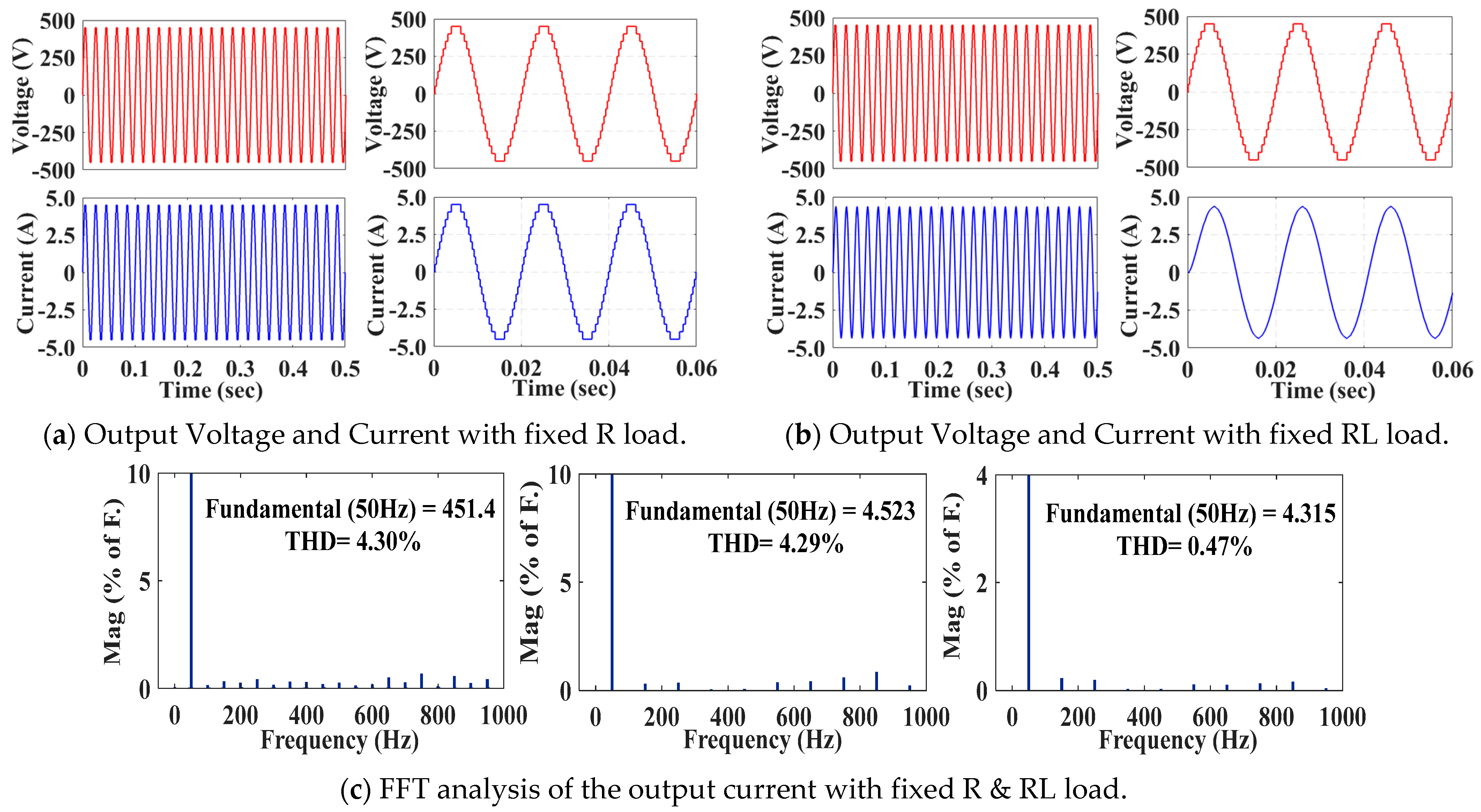


| Vo | Switches States | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | |
| +1 V | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| +2 V | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| +3 V | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| +4 V | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| +5 V | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| +6 V | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| +7 V | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| +8 V | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| +9 V | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 V | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| −1 V | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| −2 V | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| −3 V | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| −4 V | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| −5 V | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| −6 V | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| −7 V | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| −8 V | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 |
| −9 V | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| Parameters | Values |
|---|---|
| 0.00074 | |
| θjc | 1 °C/W |
| θca | 64 °C/W |
| Ta | 30 °C/W |
| 1.5 | |
| 1 | |
| 1 | |
| 1 | |
| Vs | 0.6 |
| Parameters | Values |
|---|---|
| Voltages | V1 = 50 V, V2 = 100 V, V3 = 300 V |
| Switching frequency | 50 Hz |
| Switch | IGBT |
| Resistive load | 50 Ω, 100 Ω |
| Inductive load | 40 mH, 80 mH |
| Modulation index (MI) | 1, 0.8, 0.6 |
| Parameters/Device | Values |
|---|---|
| DC source voltages | V1 = 4.5 V, V2 = 9 V, V3 = 27 V |
| Switching frequency | NLC-PWM @ 50 Hz |
| Switch | IGBT/FGA25N120/1200 V, 25 A |
| Controller | TMS320F28379D |
| Gate Driver IC | TLP250H |
| Resistive load | 40 Ω, 80 Ω |
| Inductive load | 90 mH, 120 mH |
| Modulation index (MI) | 1, 0.8, 0.6 |
| Topology | NL | NIGBT | NIGBT/NL | Ngd | Ndc | TSVp.u. | NC | CF/NL (α = 0.5) | CF/NL (α = 1.5) |
|---|---|---|---|---|---|---|---|---|---|
| [31] | 17 | 12 | 0.70 | 10 | 4 | 6 | 0 | 1.7 | 2.05 |
| [32] | 17 | 12 | 0.70 | 12 | 2 | 6.6 | 3 | 1.9 | 2.28 |
| [33] | 17 | 16 | 0.94 | 14 | 4 | 6.5 | 4 | 2.42 | 2.8 |
| [34] | 17 | 18 | 1.05 | 18 | 8 | 6.5 | 0 | 2.77 | 3.16 |
| [31] | 17 | 12 | 0.70 | 10 | 4 | 6 | 0 | 1.69 | 2.05 |
| [35] | 21 | 16 | 0.76 | 16 | 7 | 6.7 | 0 | 2.01 | 2.33 |
| [36] | 21 | 10 | 0.47 | 10 | 6 | 4 | 0 | 1.33 | 1.52 |
| [37] | 19 | 18 | 0.94 | 18 | 2 | 4.9 | 4 | 2.33 | 2.59 |
| [38] | 19 | 18 | 0.94 | 18 | 6 | 4 | 0 | 2.31 | 2.52 |
| [39] | 19 | 11 | 0.57 | 10 | 5 | 6.25 | 0 | 1.53 | 1.86 |
| Proposed | 19 | 12 | 0.63 | 12 | 3 | 6.22 | 0 | 1.58 | 1.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, M.F.; Arif, M.S.B.; Bhardwaj, A.; Waseem, A.; Rodriguez, J.; Abdelrahem, M. A Single-Phase Compact Size Asymmetrical Inverter Topology for Renewable Energy Application. Energies 2025, 18, 5121. https://doi.org/10.3390/en18195121
Ahmad MF, Arif MSB, Bhardwaj A, Waseem A, Rodriguez J, Abdelrahem M. A Single-Phase Compact Size Asymmetrical Inverter Topology for Renewable Energy Application. Energies. 2025; 18(19):5121. https://doi.org/10.3390/en18195121
Chicago/Turabian StyleAhmad, Mohd Faraz, M Saad Bin Arif, Abhishek Bhardwaj, Ahsan Waseem, Jose Rodriguez, and Mohamed Abdelrahem. 2025. "A Single-Phase Compact Size Asymmetrical Inverter Topology for Renewable Energy Application" Energies 18, no. 19: 5121. https://doi.org/10.3390/en18195121
APA StyleAhmad, M. F., Arif, M. S. B., Bhardwaj, A., Waseem, A., Rodriguez, J., & Abdelrahem, M. (2025). A Single-Phase Compact Size Asymmetrical Inverter Topology for Renewable Energy Application. Energies, 18(19), 5121. https://doi.org/10.3390/en18195121










