Influence of Web-Perforated Cold-Formed Steel Studs on the Heat Transfer Properties of LSF External Walls
Abstract
1. Introduction
2. Methodology
2.1. Model Validation
2.2. Studied Cases—Thermal Resistance of LSF Wall and Structural Capacity of CFS Stud
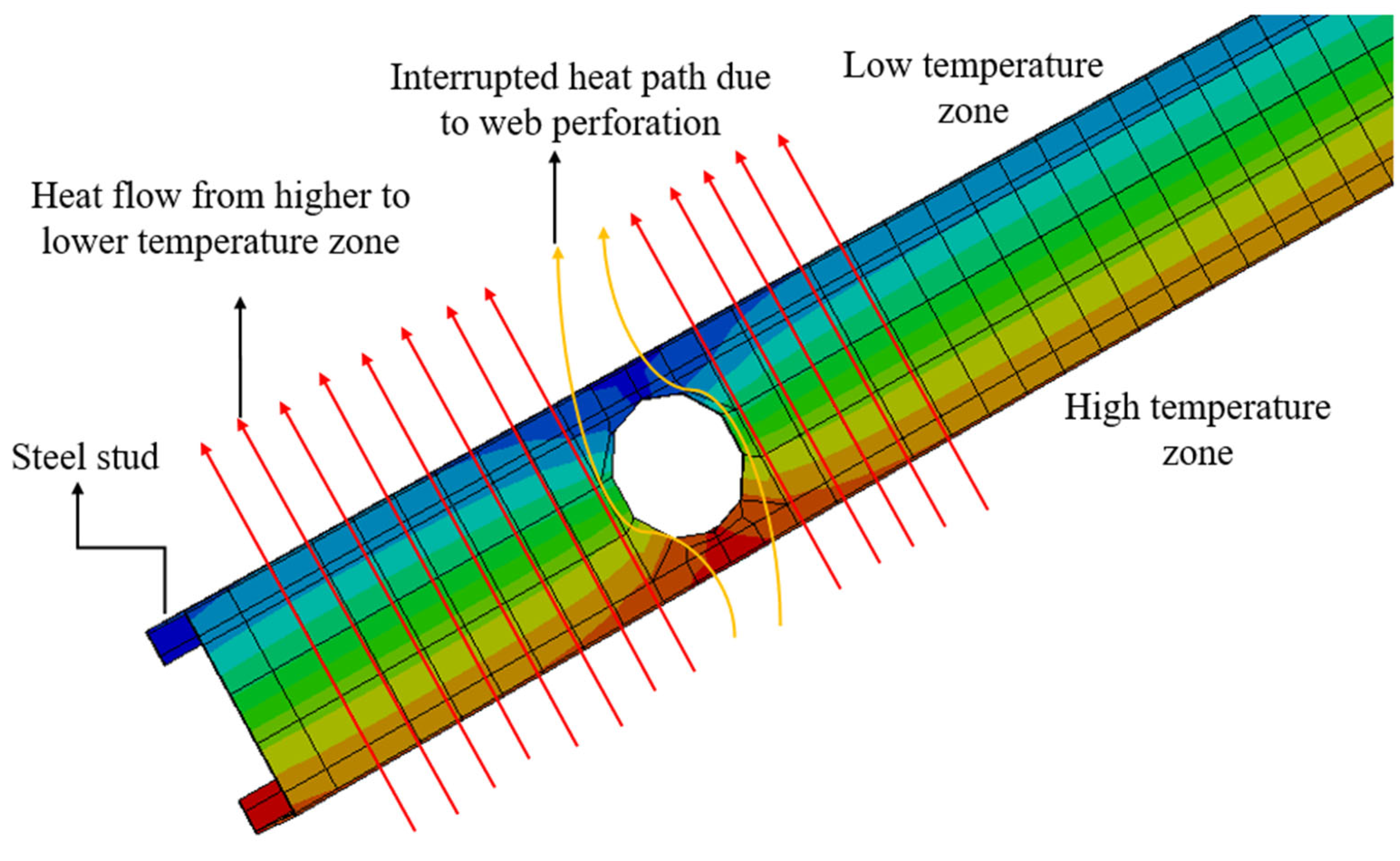
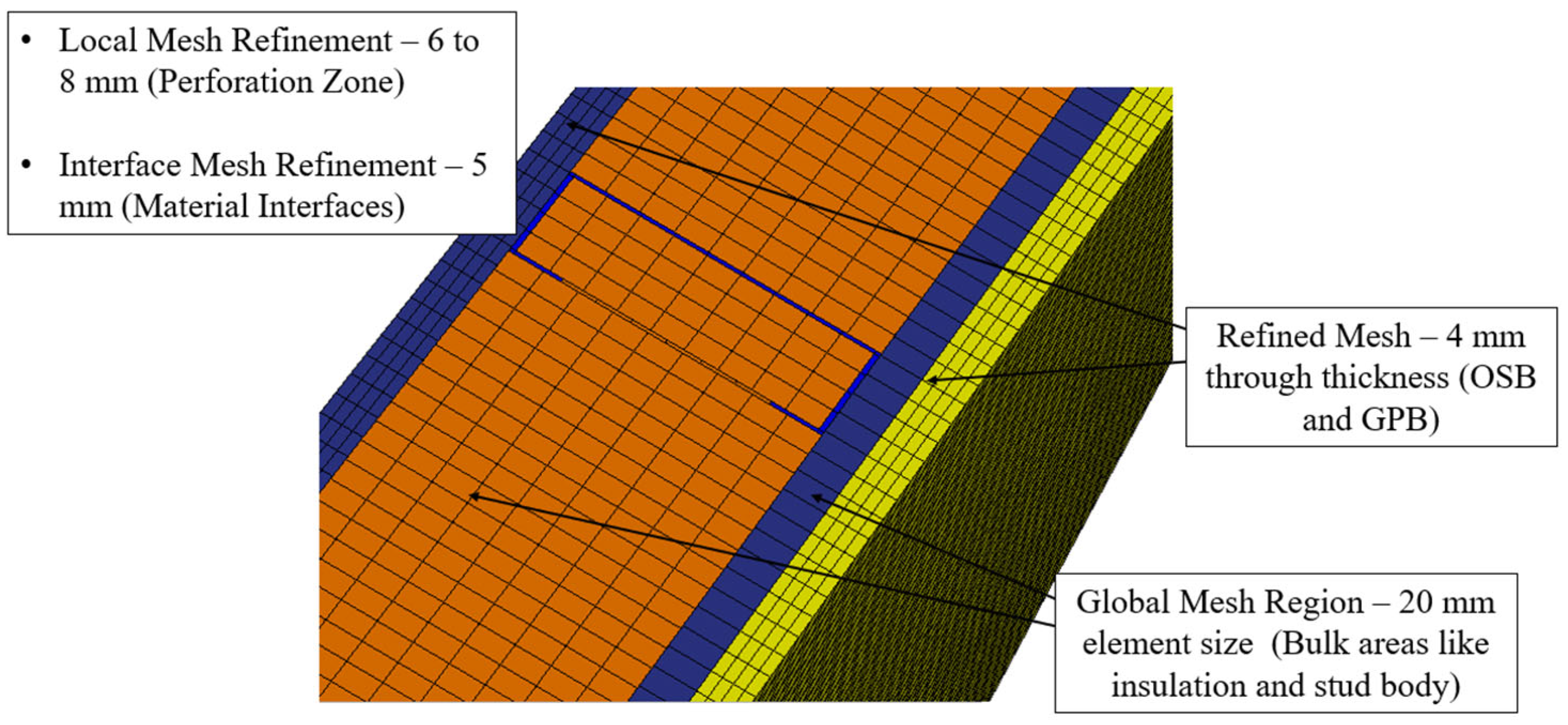
3. Three-Dimensional Heat Transfer Simulation Using Abaqus Finite Element Models
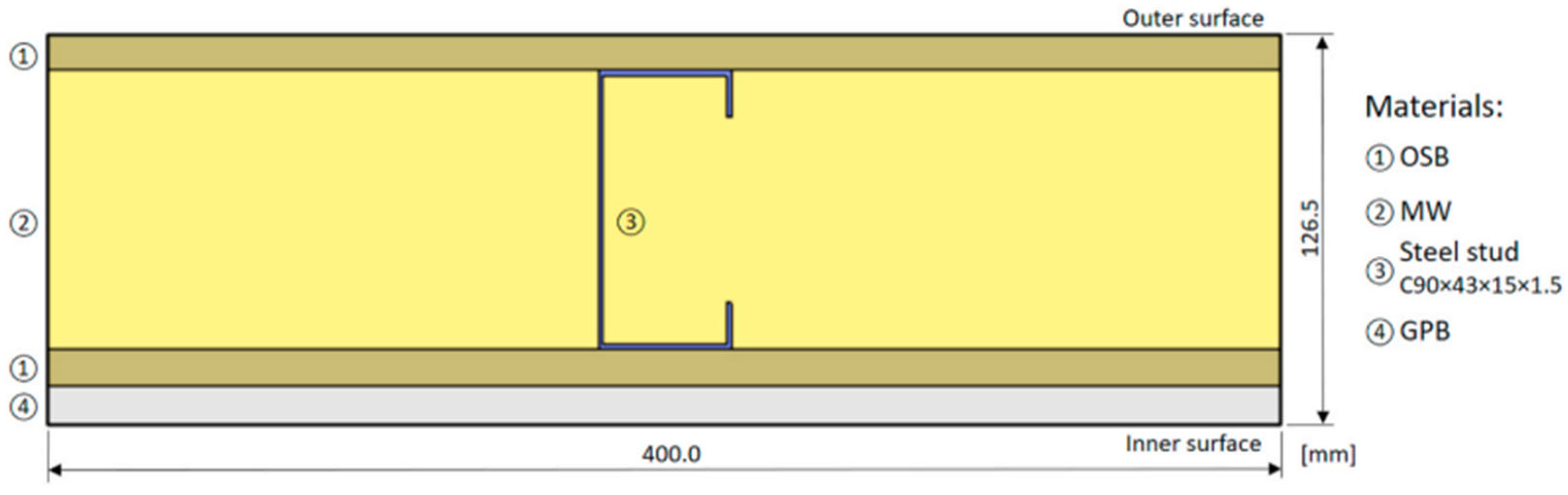
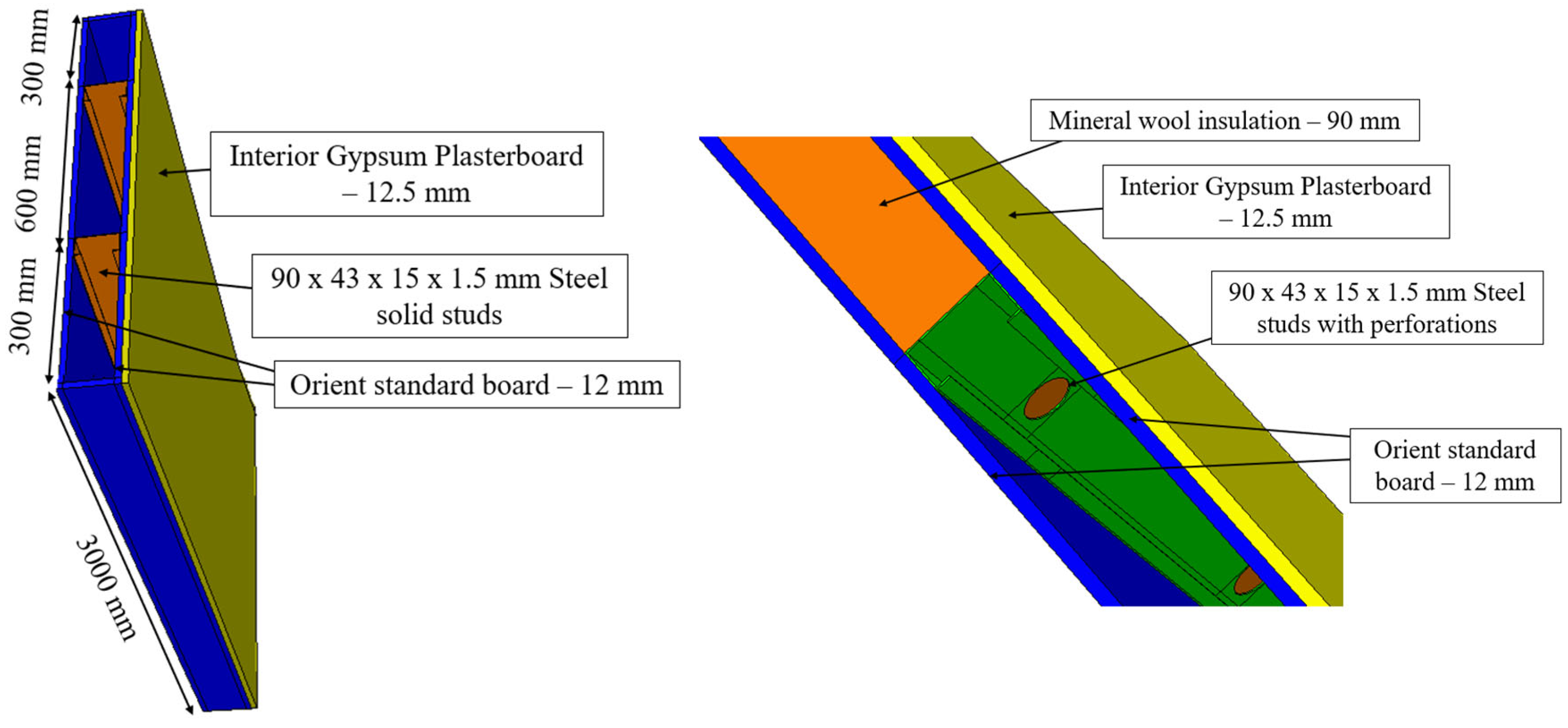
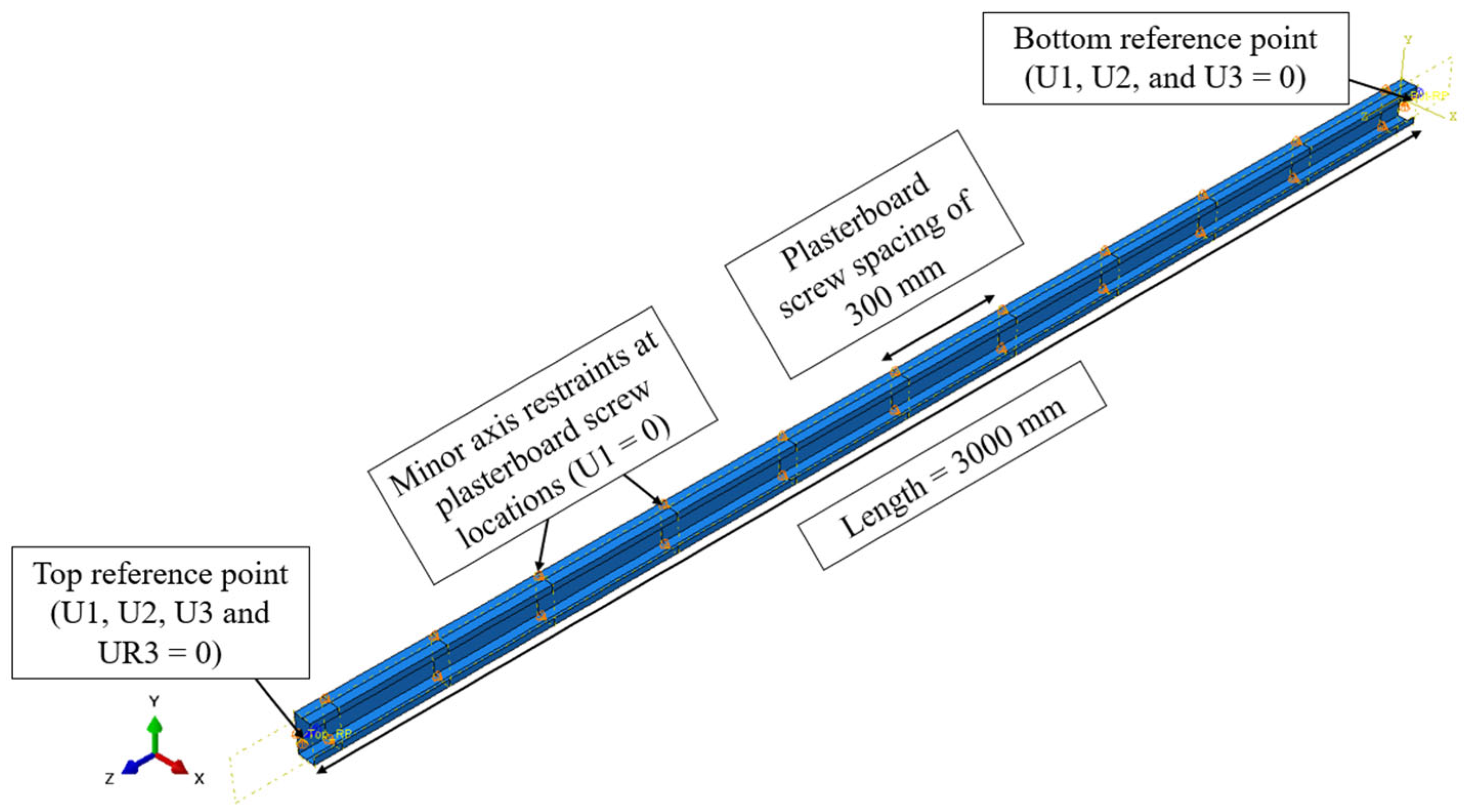
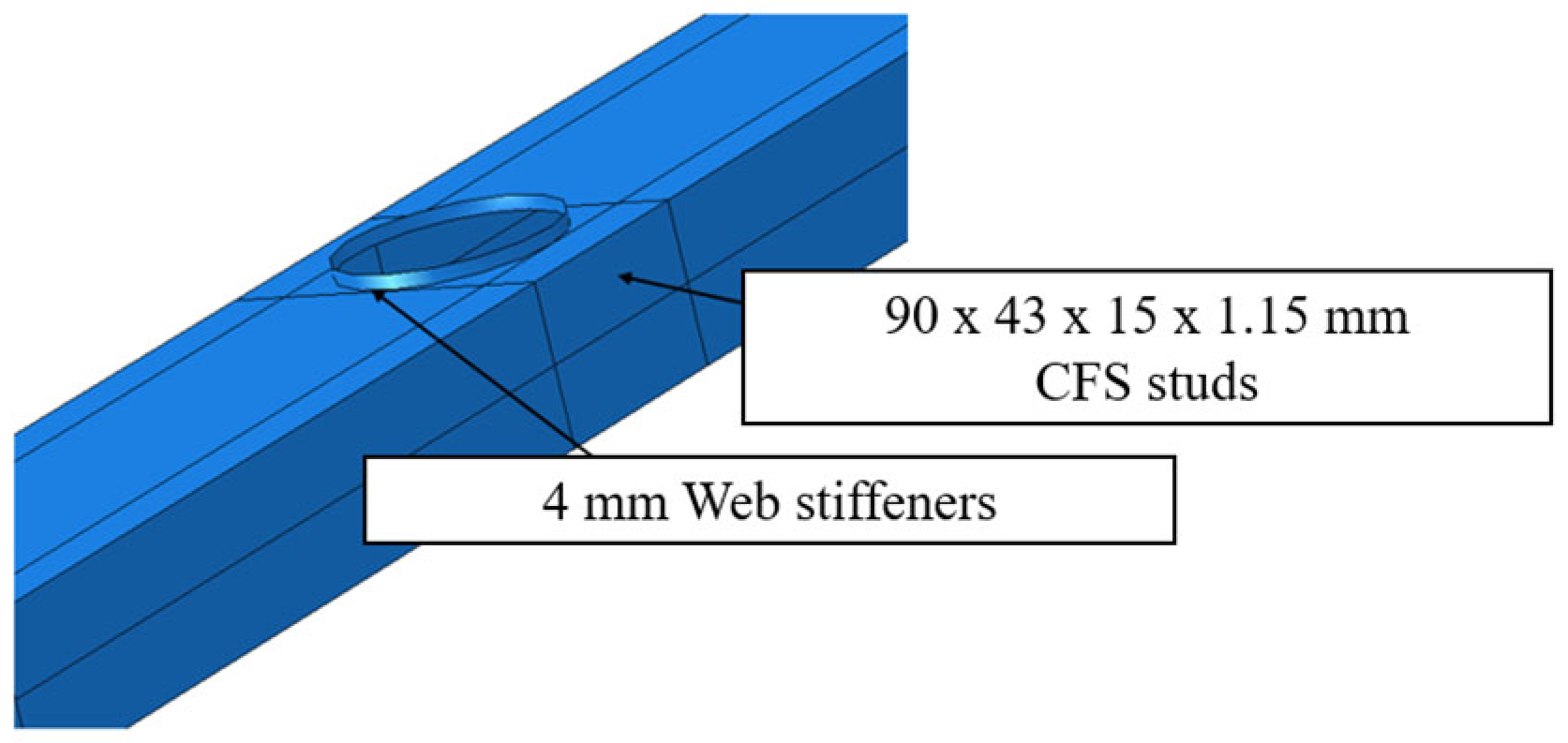
3.1. Model Description
3.2. Constraints, Boundary Conditions and Contact Interactions
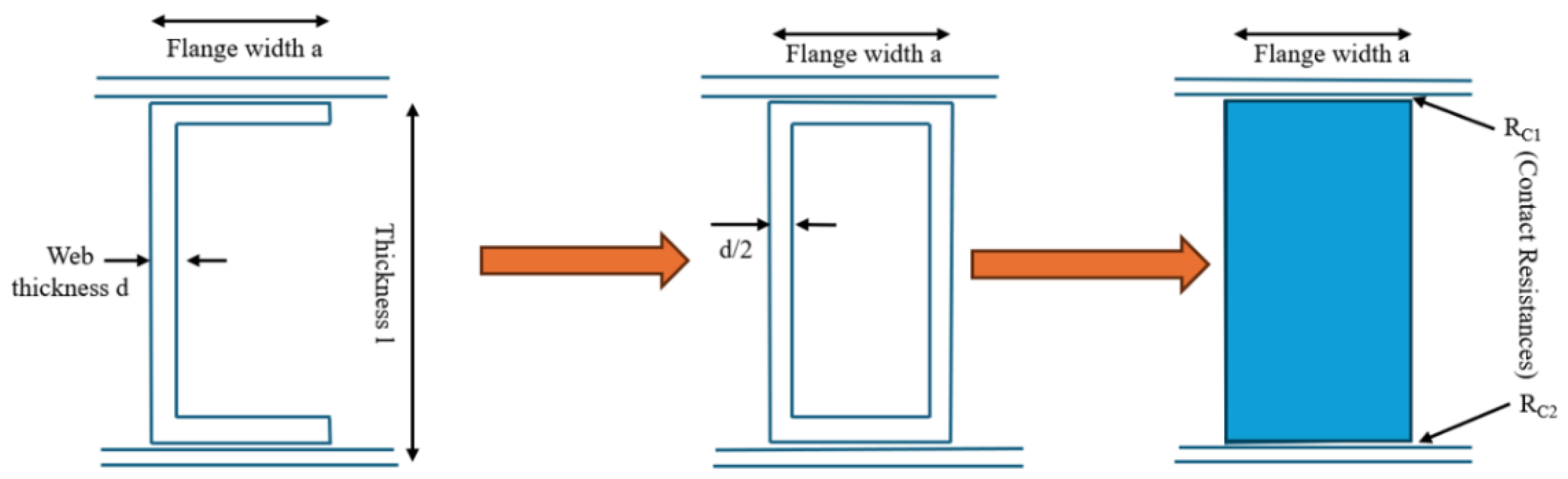
3.3. Thermal Resistance Calculation Using Heat Flux Measurement
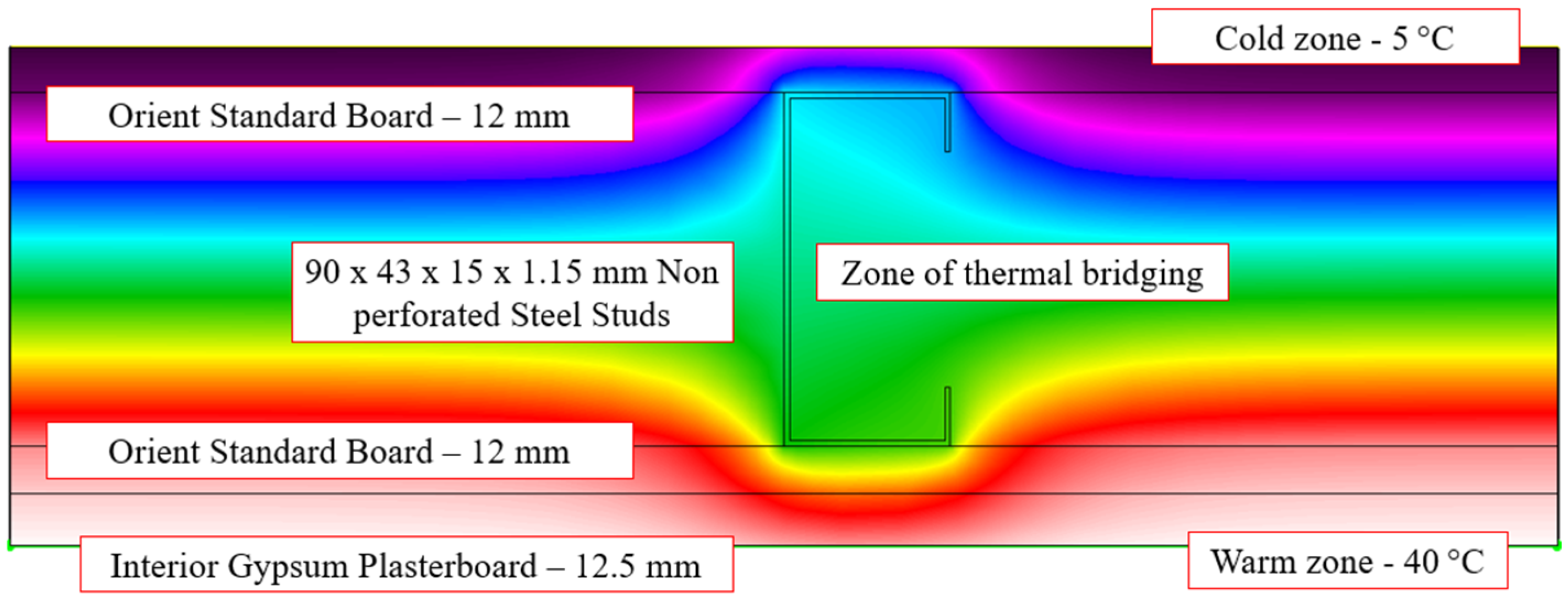
4. Two-Dimensional Thermal Modelling of Load-Bearing LSF Walls Using THERM
5. Modified Analytical Methods for Calculating Thermal Resistance of LSF Walls with Web-Perforated Studs
5.1. Model-Based Validation of R-Values for Web-Perforated LSF Walls Using the NZS 4214 Analytical Framework
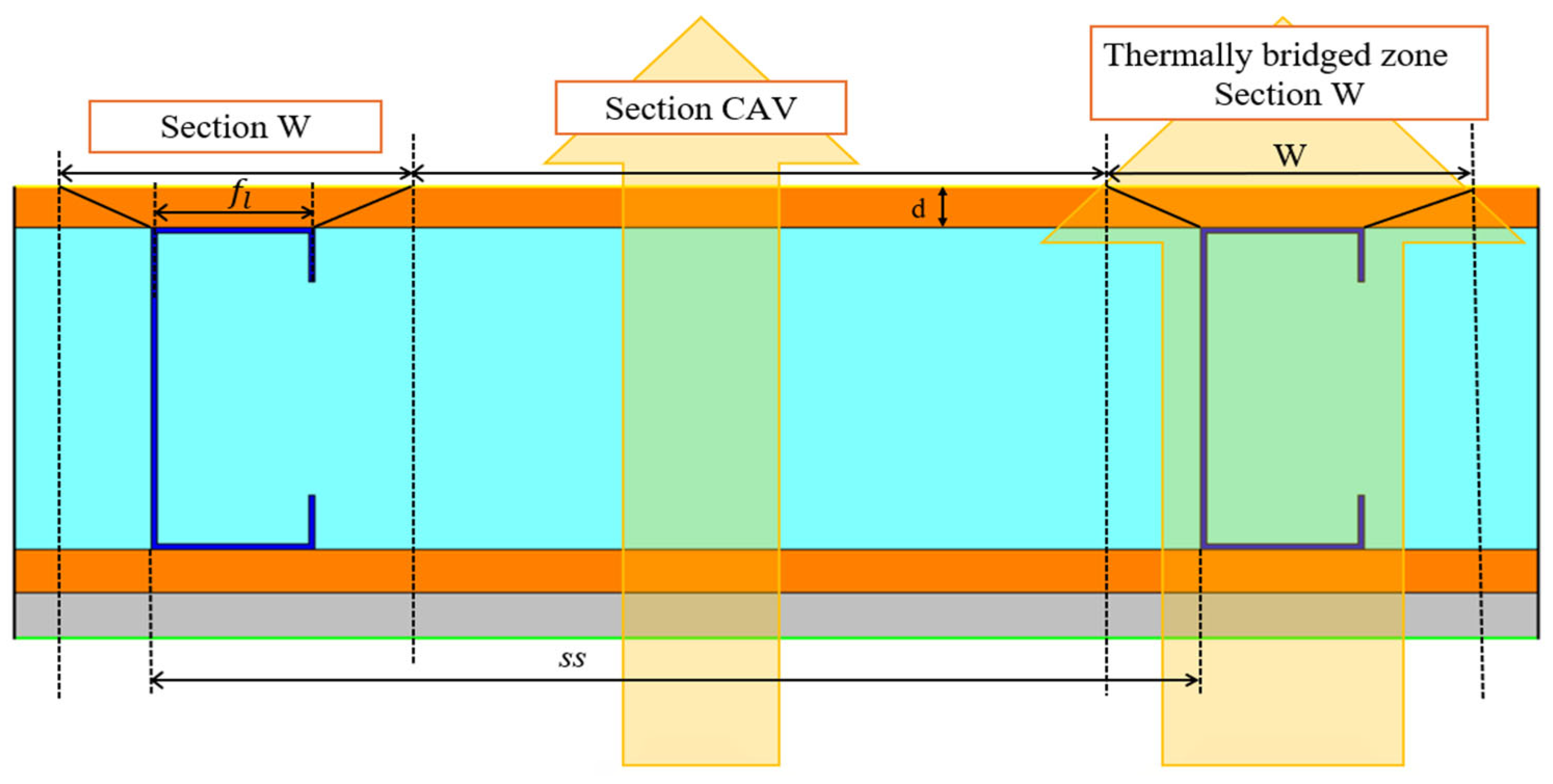
5.2. Modified ASHRAE Zone Method Incorporating Perforation-Based Heat Flux and Area Corrections
6. Analysis of Results
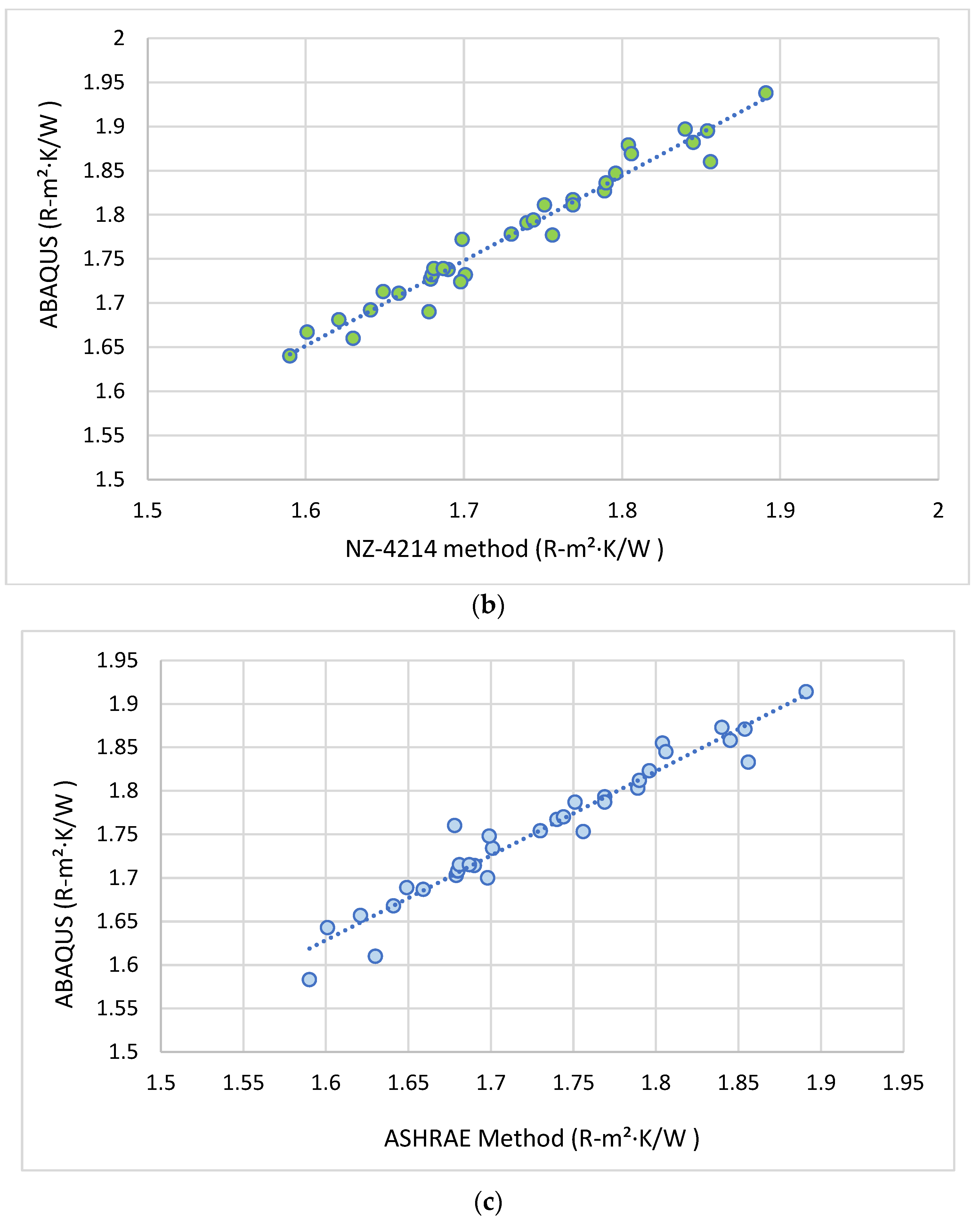
6.1. Validation of Numerical Models
6.2. Thermal Resistance Enhancement in LSF Walls with Perforated Studs
6.3. Thermal Performance of 3 m High LSF Walls
6.3.1. Walls with Non-Perforated Steel Studs
6.3.2. Walls with Perforated Steel Studs
6.4. Thermal Performance of External LSF Walls with Fire-Rated Facades and Web-Perforated Studs
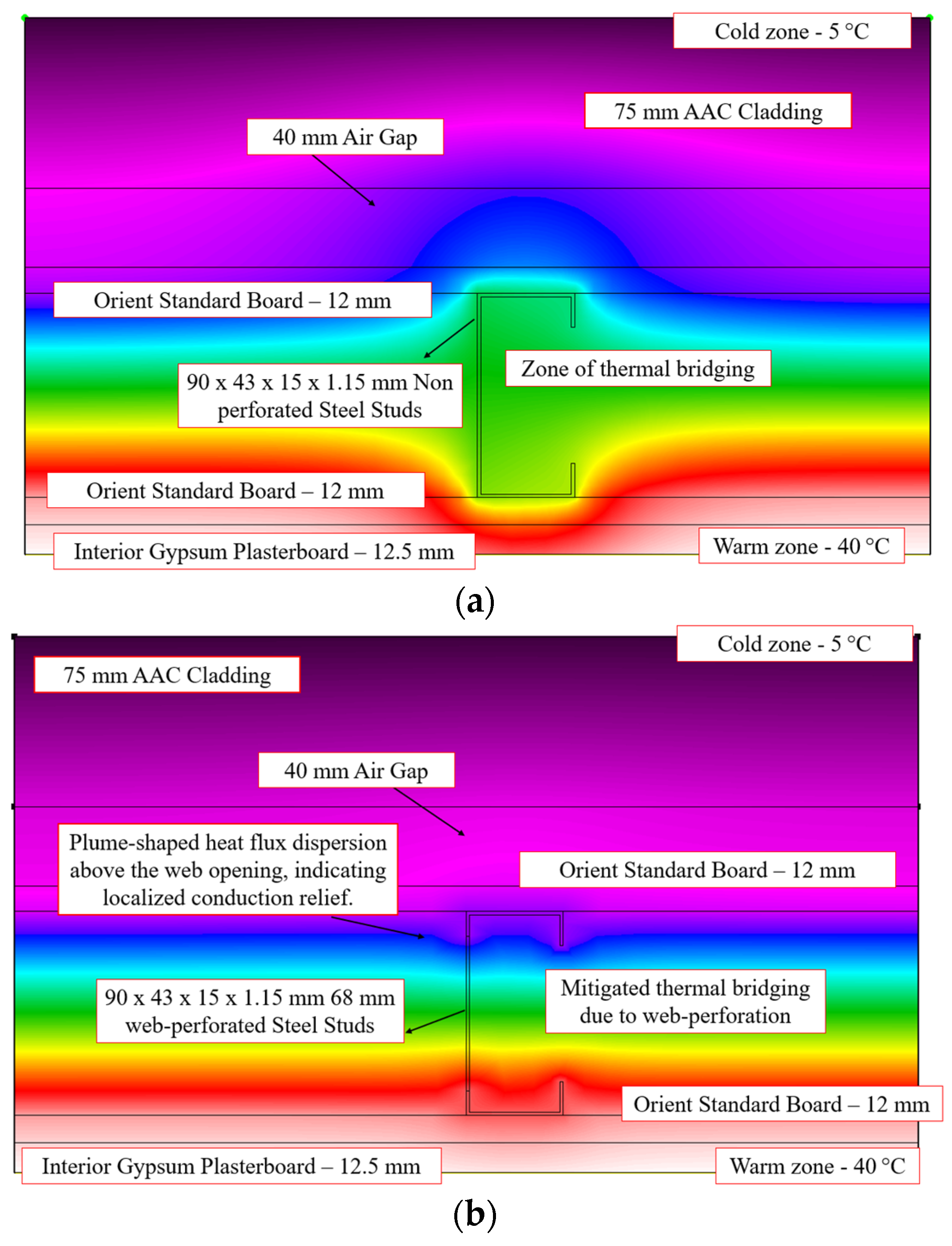
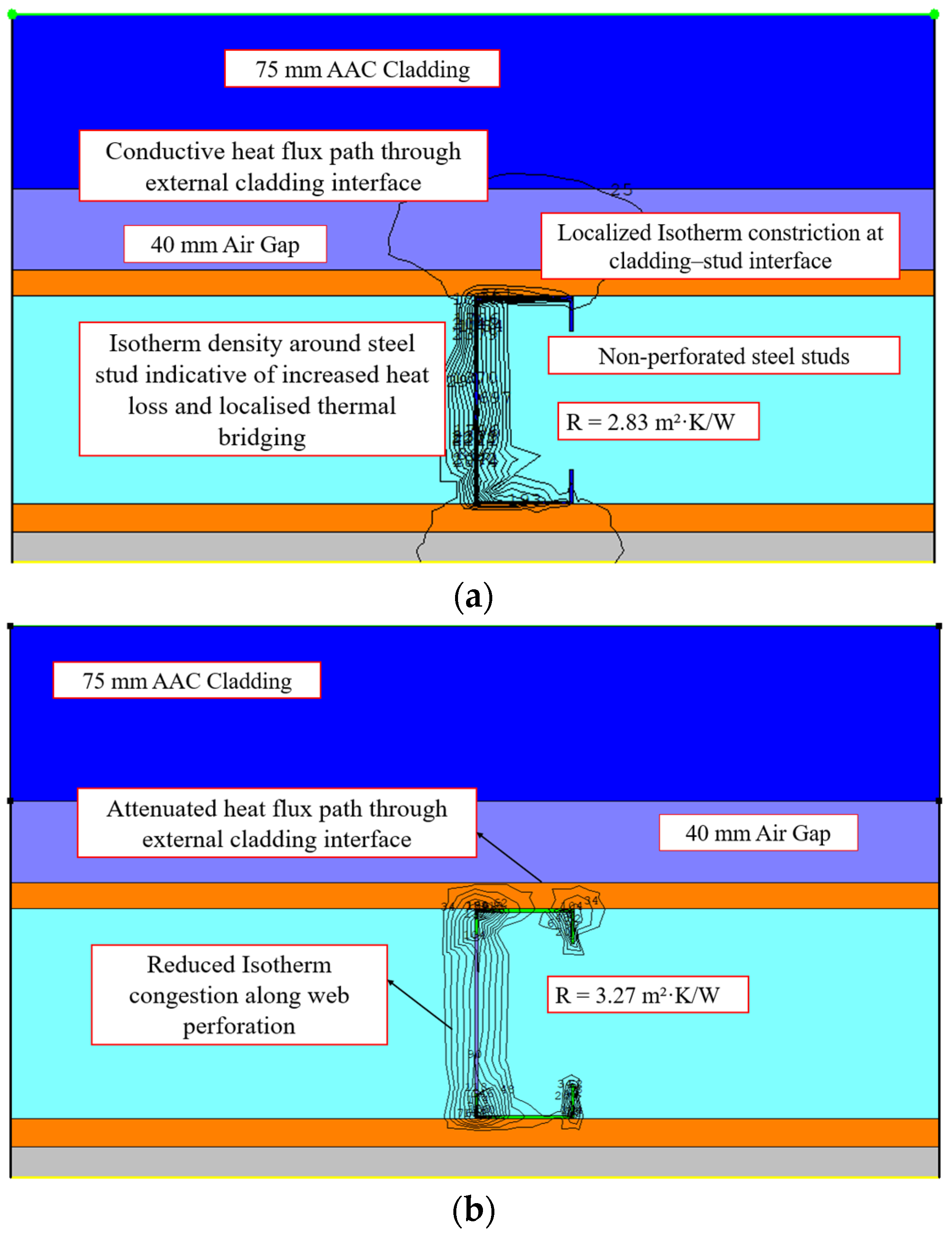
6.4.1. External LSF Wall with AAC External Cladding
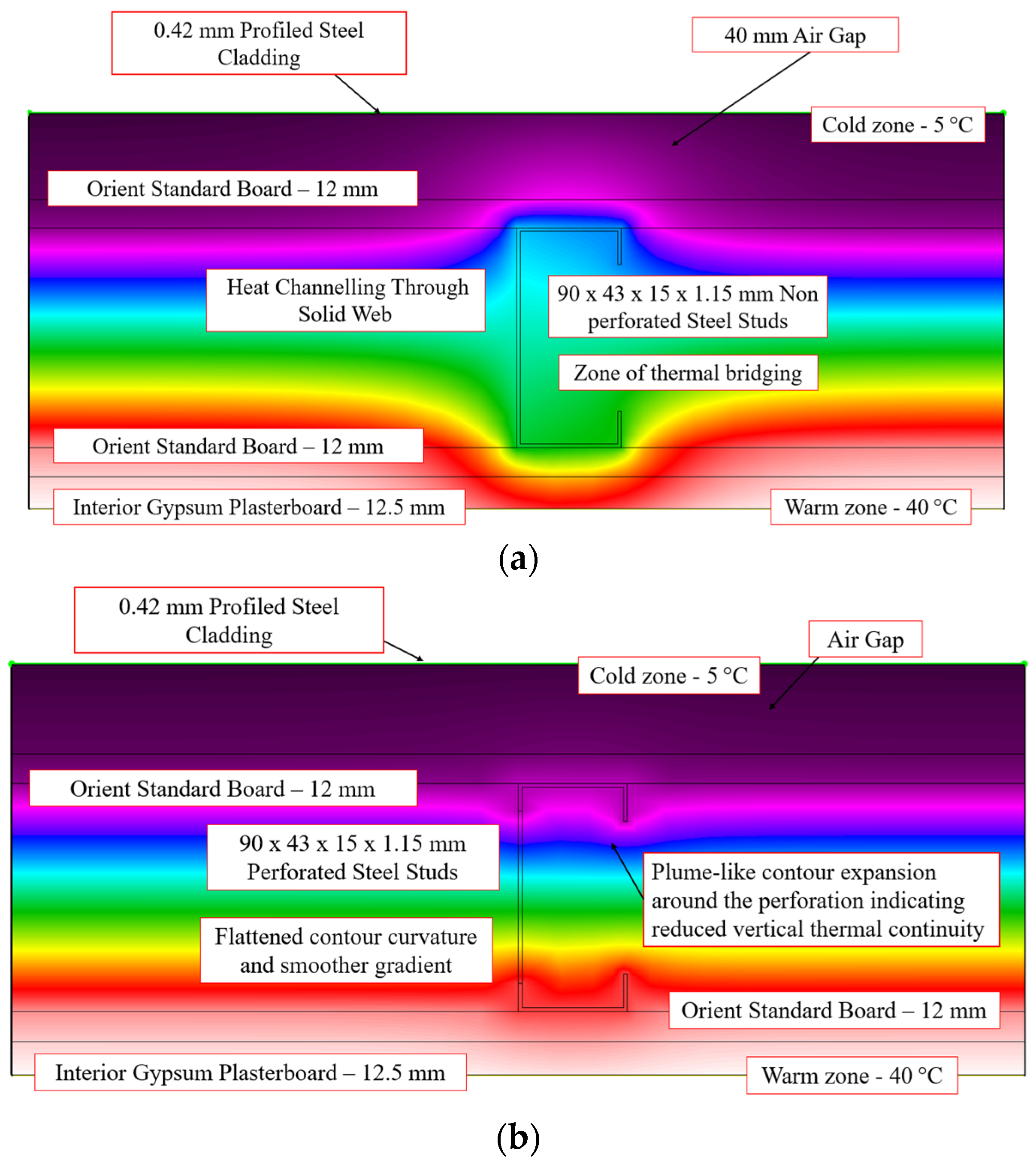
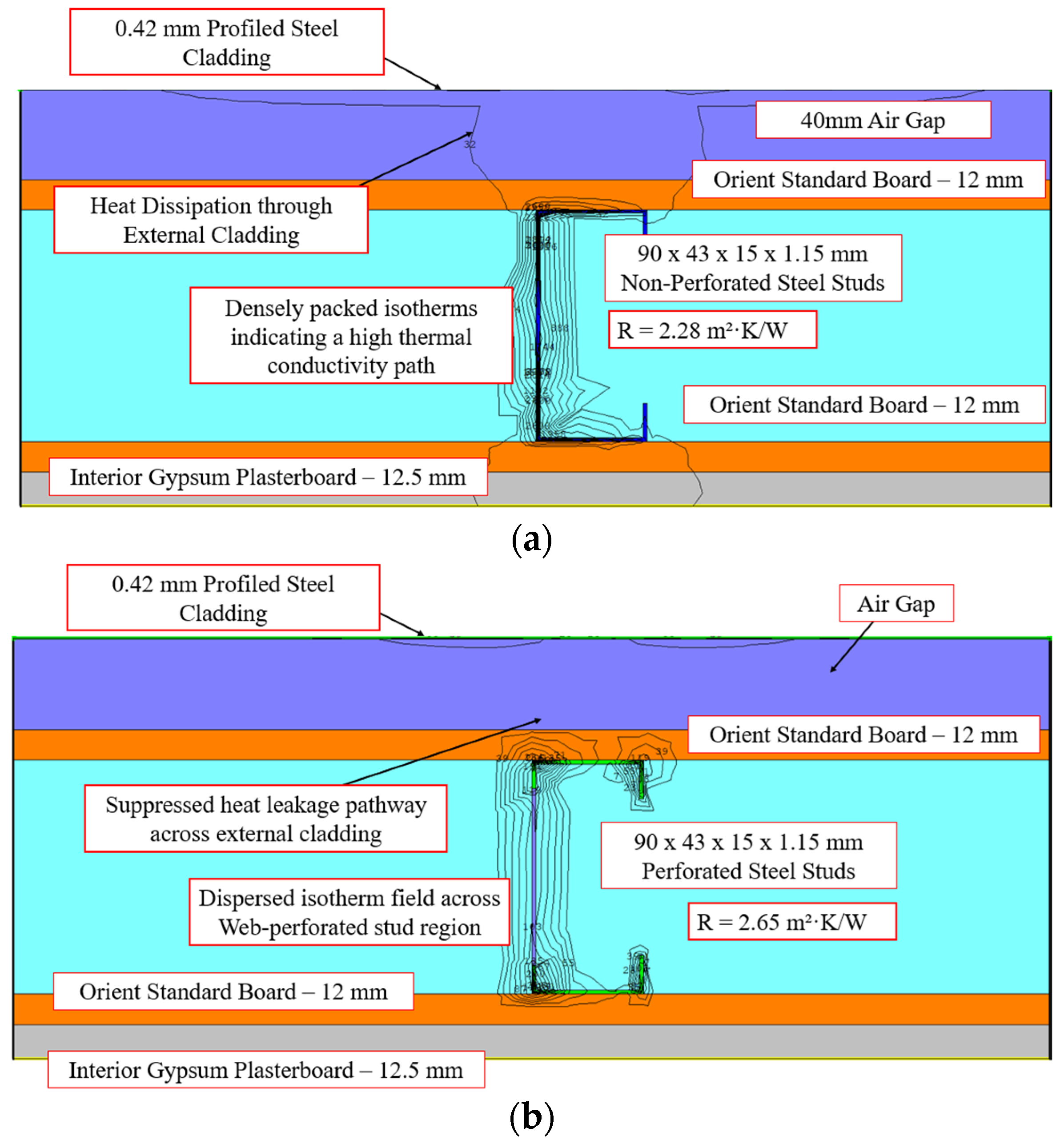
6.4.2. External LSF Wall with 0.42 mm Profiled Steel Cladding
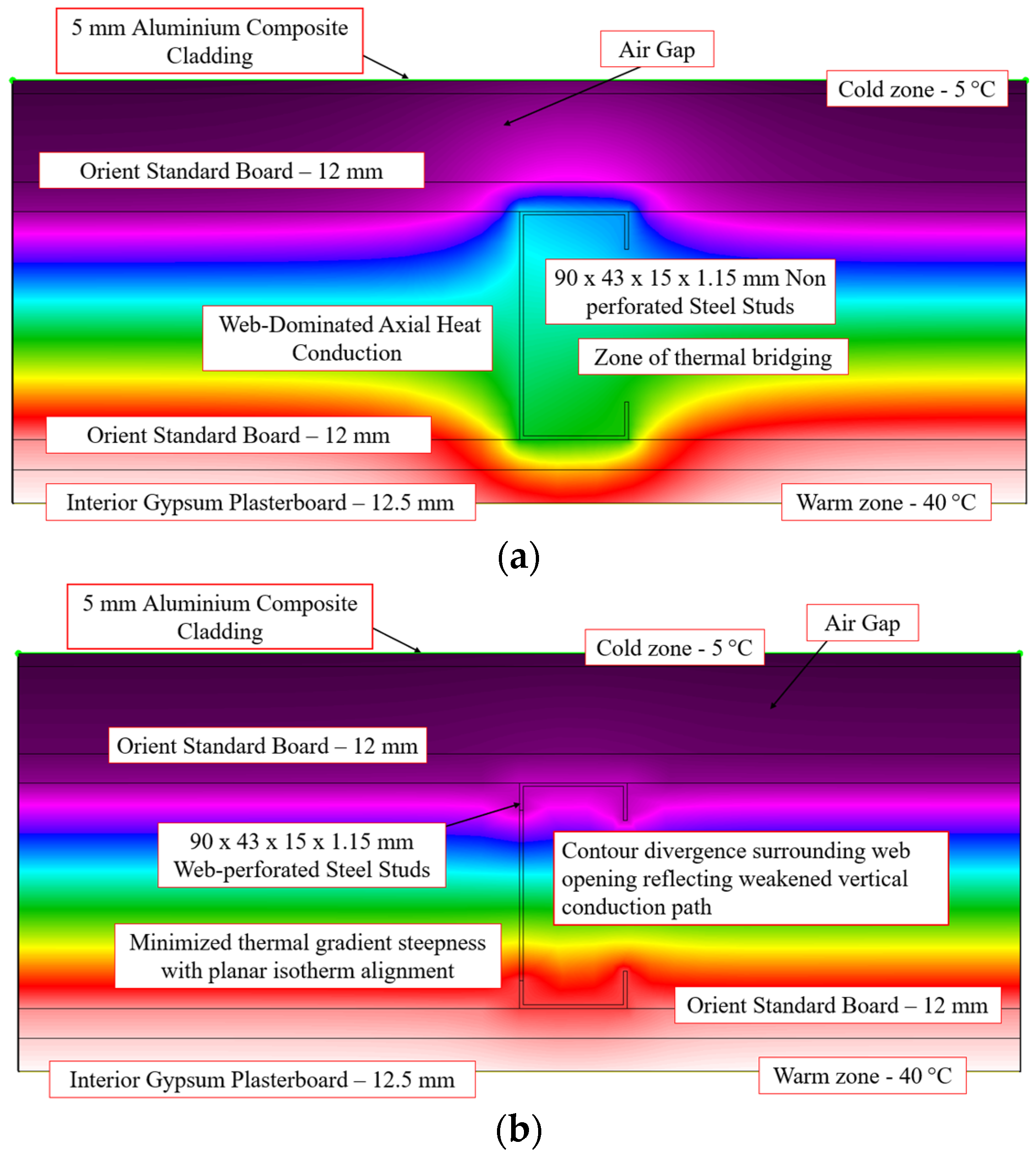
6.4.3. External LSF Wall with 5 mm Aluminium Composite Panel (ACP) Cladding
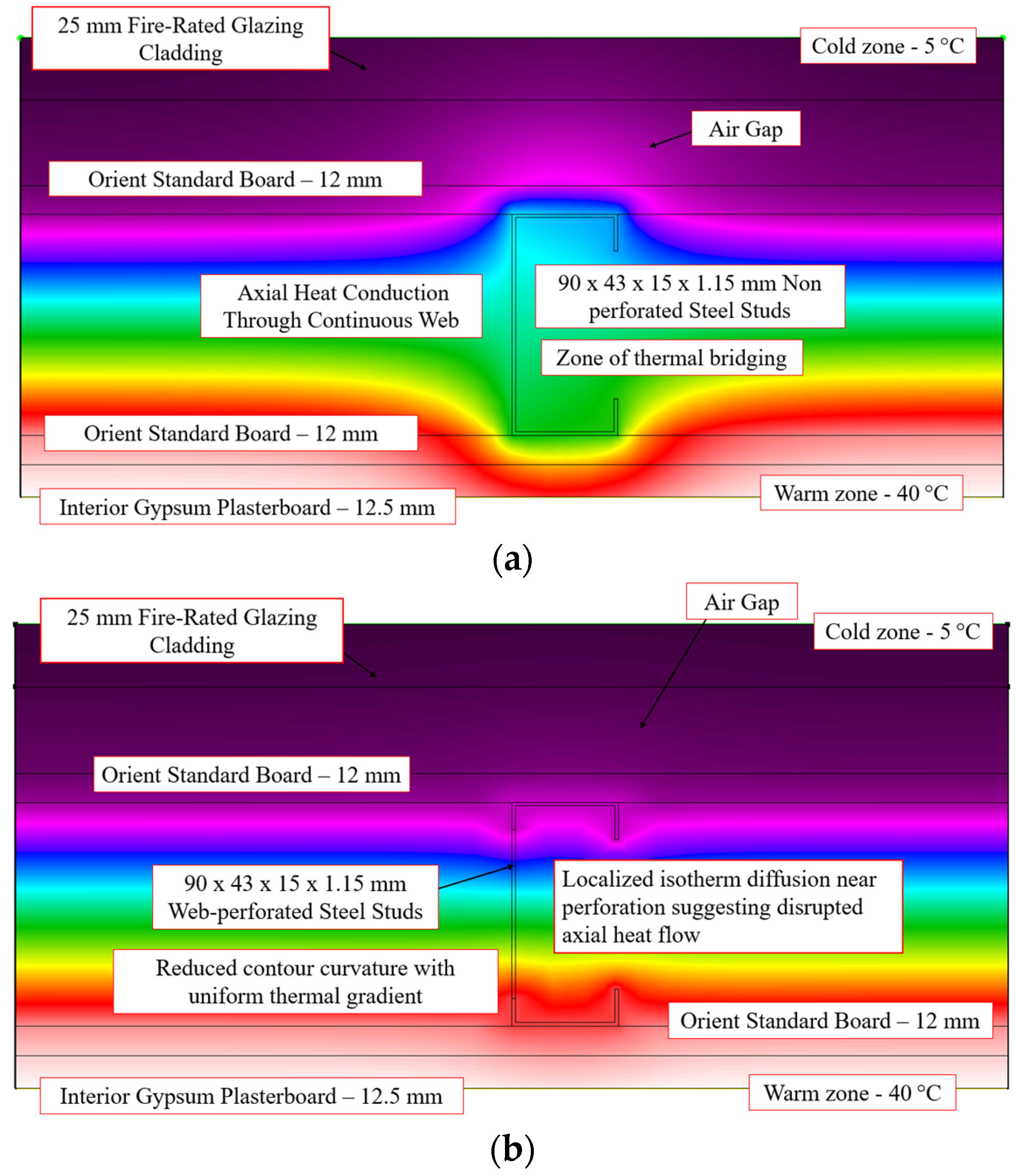
6.4.4. External LSF Wall with 25 mm Fire-Rated Glazing Cladding
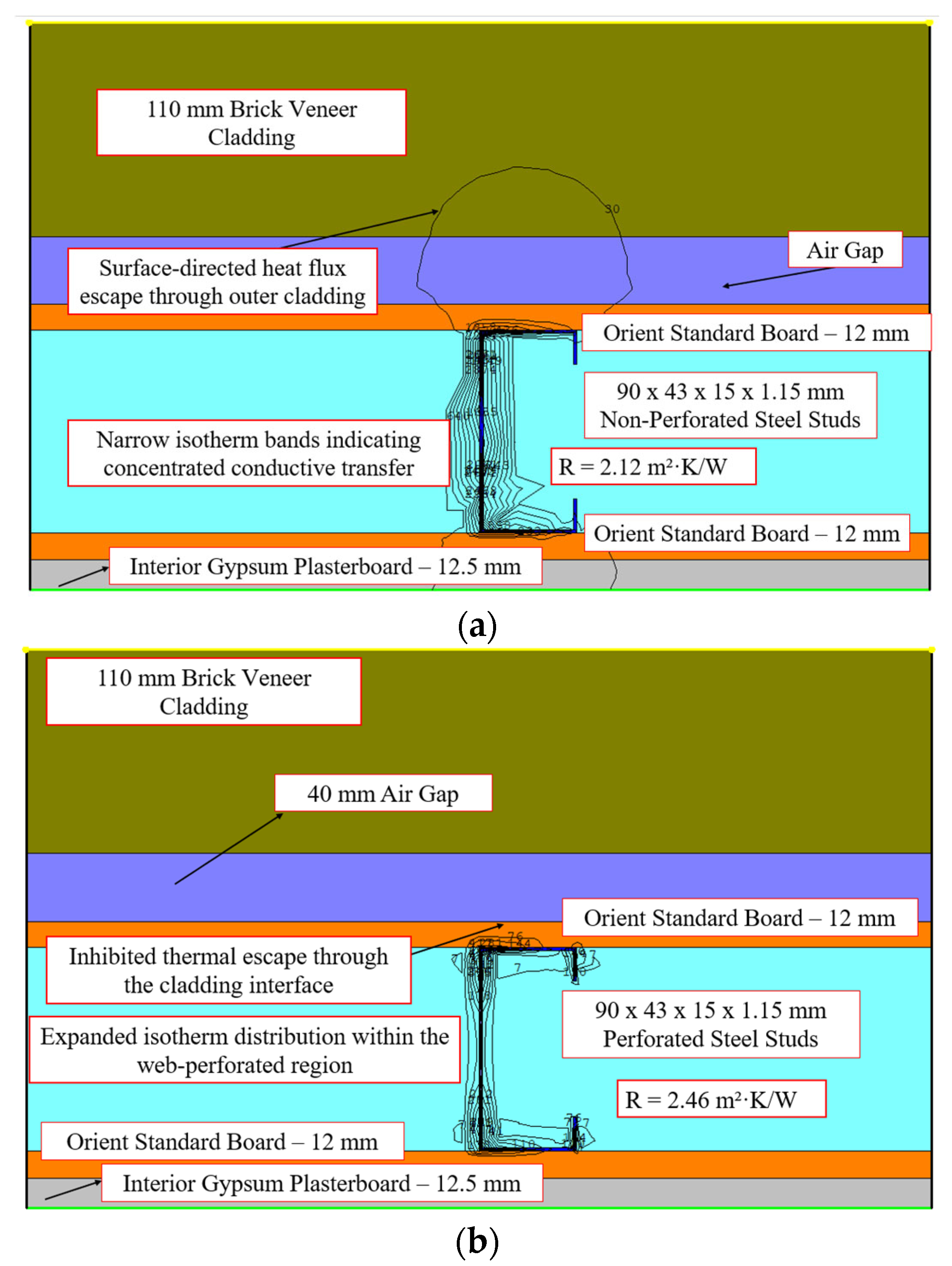
6.4.5. External LSF Wall with 110 mm Brick Veneer Cladding
7. Heat Transfer Modulation Through Web Perforations in Previously Published LSF Wall Assemblies
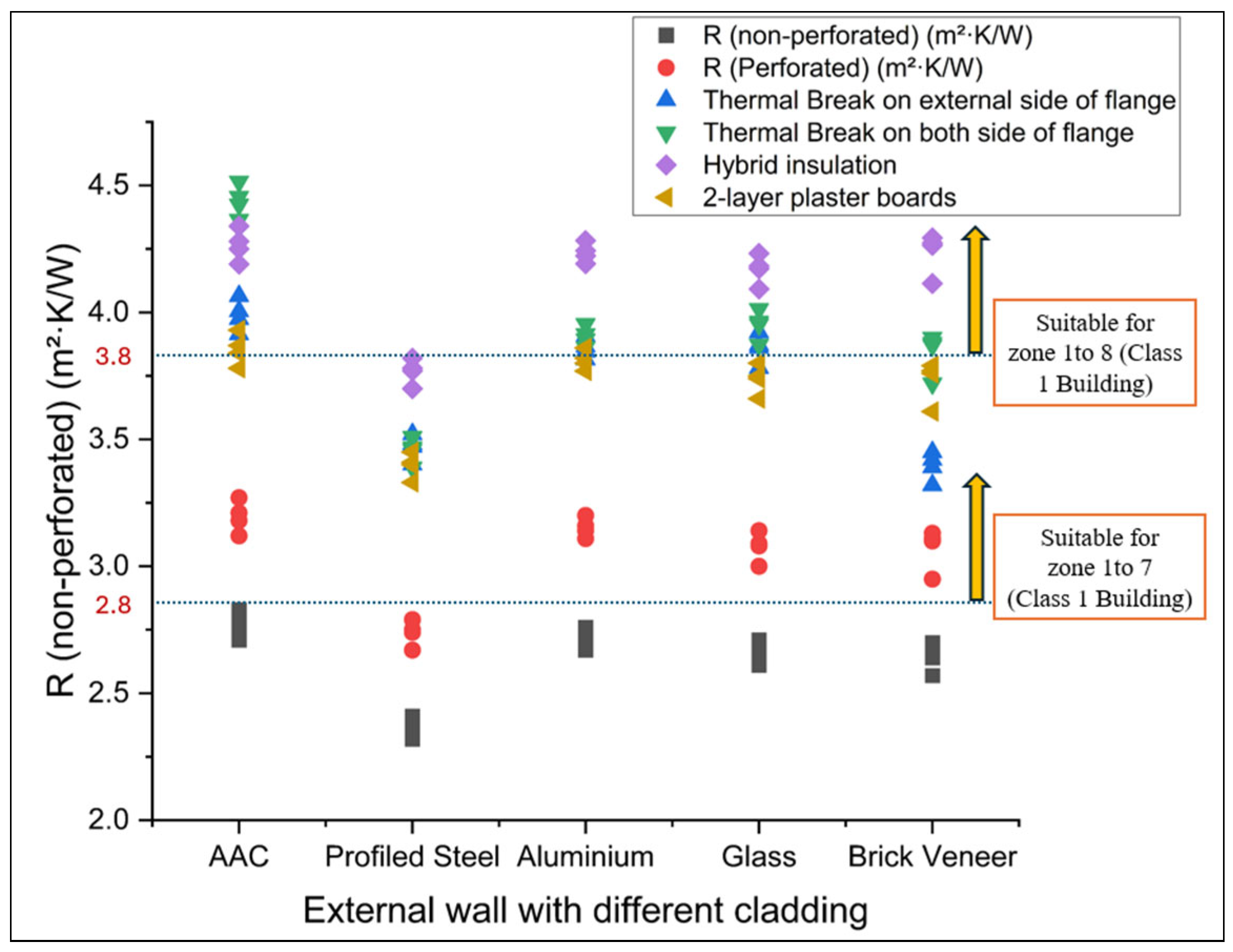
8. Climate Zoning Assessment of Enhanced Web-Perforated LSF Wall Systems
9. Conclusions
- Web perforations in CFS studs function as a passive thermal optimization strategy, delivering consistent R-value enhancements of 14.79 to 20.06% across all tested wall systems. R-values increased from 2.57–2.83 m2·K/W (non-perforated) to 2.95–3.27 m2·K/W (perforated), with a peak gain of 0.54 m2·K/W in AAC-clad walls.
- By reducing the steel web cross-sectional area, perforations interrupted the continuous through-stud conduction path and promoted lateral heat flux redistribution into the insulation. Heat flux vectors along the stud web decreased by 23.6–37.5%, with 2D and 3D isotherm analyses in THERM and Abaqus confirming flux redistribution and attenuated thermal bridging.
- The maximum R-value of 1.892 m2·K/W was achieved in a 3 m wall with 68 mm diameter holes at 200 mm spacing, improving thermal resistance by 20.06%.
- Although the axial compression capacity reduced by 29.51% in perforated studs (from 82.13 to 57.1 kN), it was restored to within 3.2% of the non-perforated stud capacity using 4 mm long edge stiffeners around the holes (78.31 kN).
- Web-perforated studs increased thermal resistance across all façade systems, with perforations alone sufficient to satisfy NCC 2022 R-value thresholds in several zones. As NCC mandates thermal breaks (R ≥ 0.2) for metal-framed external walls and roofs where cladding and lining are directly fixed, combined systems with 19 mm thermal breaks or hybrid insulation achieved 4.2–4.5 m2·K/W, ensuring compliance across all climate zones (Z1–Z8).
- Adapted NZS 4214 and ASHRAE Modified Zone methods accurately predicted the R-values of perforated walls using frame fraction and flux correction adjustments.
- Across selected façade systems, web-perforated LSF wall designs achieved R-values of 3.14 to 3.27 m2·K/W, demonstrating that in certain climates, thermal breaks can be excluded where cladding or insulation sufficiently limits heat transfer.
- Heat flux correction factors (Cf= 0.52 to 0.89) derived from the 120 Abaqus models allow accurate R-value estimation without full 3D FE simulations, supporting practical design and compliance with NCC, ASHRAE, and ISO 6946.
- Furthermore, the climate zoning analysis demonstrated that web-perforated LSF wall systems, either alone or in combination with moderate enhancements such as thermal breaks or hybrid insulation, satisfied the NCC 2022 R-value requirements across all Australian climate zones (Z1–Z8).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, J.-H.; Kim, H.-W. Performance Evaluation of Low Thermal Bridging Drywall System with Separating Clips for C-Studs. Buildings 2024, 14, 3032. [Google Scholar] [CrossRef]
- Qi, X.; Tan, Y.; Tan, J.; Li, X. Methods for improving the thermal performance of thermal bridges of lightweight steel-framed buildings. PLoS ONE 2024, 19, e0314634. [Google Scholar] [CrossRef]
- Soares, N.; Santos, P.; Gervásio, H.; Costa, J.J.; da Silva, L.S. Energy efficiency and thermal performance of lightweight steel-framed (LSF) construction: A review. Renew. Sustain. Energy Rev. 2017, 78, 194–209. [Google Scholar] [CrossRef]
- Soares, N.; Martins, C.; Gonçalves, M.; Santos, P.; da Silva, L.S.; Costa, J.J. Laboratory and in-situ non-destructive methods to evaluate the thermal transmittance and behavior of walls, windows, and construction elements with innovative materials: A review. Energy Build 2019, 182, 88–110. [Google Scholar] [CrossRef]
- Santos, P.; Poologanathan, K. The importance of stud flanges size and shape on the thermal performance of lightweight steel framed walls. Sustainability 2021, 13, 3970. [Google Scholar] [CrossRef]
- Santos, P. Energy Efficiency of Lightweight Steel-Framed Buildings. In Energy Efficient Buildings; InTech: London, UK, 2017. [Google Scholar] [CrossRef]
- Rajanayagam, H.; Upasiri, I.; Poologanathan, K.; Gatheeshgar, P.; Sherlock, P.; Konthesingha, C.; Nagaratnam, B.; Perera, D. Thermal Performance of LSF Wall Systems with Vacuum Insulation Panels. Buildings 2021, 11, 621. [Google Scholar] [CrossRef]
- Francis, E.; Gatheeshgar, P.; Santos, P. Thermal transmittance of single and double stud LSF walls: Parametric study and simplified models. J. Build. Eng. 2025, 102, 111939. [Google Scholar] [CrossRef]
- Martins, C.; Santos, P.; da Silva, L.S. Lightweight steel-framed thermal bridges mitigation strategies: A parametric study. J. Build. Phys. 2016, 39, 342–372. [Google Scholar] [CrossRef]
- Santos, P.; Abrantes, D.; Lopes, P.; Mateus, D. Experimental and Numerical Performance Evaluation of Bio-Based and Recycled Thermal Break Strips in LSF Partition Walls. Buildings 2022, 12, 1237. [Google Scholar] [CrossRef]
- Gorgolewski, M. Developing a simplified method of calculating U-values in light steel framing. Build Environ. 2007, 42, 230–236. [Google Scholar] [CrossRef]
- Chandrasiri, D.; Gatheeshgar, P.; Ahmadi, H.M.; Simwanda, L. Numerical Study of Thermal Efficiency in Light-Gauge Steel Panels Designed with Varying Insulation Ratios. Buildings 2024, 14, 300. [Google Scholar] [CrossRef]
- Santos, P.; Lemes, G.; Mateus, D. Analytical Methods to Estimate the Thermal Transmittance of LSF Walls: Calculation Procedures Review and Accuracy Comparison. Energies 2020, 13, 840. [Google Scholar] [CrossRef]
- Sovetova, M.; Calautit, J.K. Thermal and energy efficiency in 3D-printed buildings: Review of geometric design, materials and printing processes. Energy Build. 2024, 323, 114731. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, L.; Nan, B.; Wei, S. Thermal Performance of Slotted Light Steel-Framed Composite Wall. Energies 2023, 16, 2482. [Google Scholar] [CrossRef]
- Alekperov, R.; Aksenov, I. Decrease of cold-formed slotted studs heat conductivity by slots shape modification. E3S Web Conf. 2019, 97, 06009. [Google Scholar] [CrossRef]
- Langner, M.; Soares, T.A.; Figueiredo, A.; Almeida, R.M.S.F.; Vicente, R. Parametric Analysis of Steel Studs to Reduce Thermal Bridges in Light Steel Framing Construction Systems. Buildings 2025, 15, 194. [Google Scholar] [CrossRef]
- Höglund, T.; Burstrand, H. Slotted steel studs to reduce thermal bridges in insulated walls. Thin-Walled Struct. 1998, 32, 81–109. [Google Scholar] [CrossRef]
- BS EN ISO 6946:2017; Building Components and Building Elements. Thermal Resistance and Thermal Transmittance. Calculation Methods. British Standards Institute: London, UK, 2017.
- NCC 2022 Volume Two—Building Code of Australia Class 1 and 10 Buildings. Available online: http://ncc.abcb.gov.au/editions/ncc-2022/adopted/volume-two (accessed on 1 April 2025).
- Liang, H.; Roy, K.; Fang, Z.; Lim, J.B.P. A Critical Review on Optimization of Cold-Formed Steel Members for Better Structural and Thermal Performances. Buildings 2022, 12, 34. [Google Scholar] [CrossRef]
- 2021 International Energy Conservation Code (IECC) and ANSI/ASHRAE/IES Standard 90.1-2022. Available online: https://www.energycodes.gov/sites/default/files/2024-02/Standard_90.1-2022_Final_Determination_TSD.pdf (accessed on 1 March 2025).
- ASHRAE. Handbook of Fundamentals, American Society of Heating; Refrigeration and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2021. [Google Scholar]
- European Commission. Directive (EU) 2018/844 on the Energy Performance of Buildings (EPBD). Off. J. Eur. Union 2018, L156, 75–91. [Google Scholar]
- NZS 4214; Methods of Determining the Total Thermal Resistance of Parts of Buildings. New Zealand Standard: Wellington, New Zealand, 2006.
- Santos, P.; Ribeiro, T. Thermal Performance of Double-Pane Lightweight Steel Framed Walls with and without a Reflective Foil. Buildings 2021, 11, 301. [Google Scholar] [CrossRef]
- Kempton, L.; Kokogiannakis, G.; Green, A.; Cooper, P. Evaluation of thermal bridging mitigation techniques and impact of calculation methods for lightweight steel frame external wall systems. J. Build. Eng. 2021, 43, 102893. [Google Scholar] [CrossRef]
- A Review of Thermal Bridging Mitigation Provisions and Thermal Break Provisions NCC 2022. Available online: https://www.abcb.gov.au/sites/default/files/resources/2023/LittleShrub%20Report%20-%20Thermal%20Bridging%20and%20Thermal%20Break.pdf (accessed on 1 February 2025).
- Department of Climate Change, Energy, the Environment and Water. Trajectory for Low Energy Buildings; Department of Climate Change, Energy, the Environment and Water: Canberra, Australia, 2019.
- ationwide House Energy Rating Scheme. Software Accreditation Protocol—New Homes 2025. Available online: https://www.nathers.gov.au/sites/default/files/2025-02/Software%20Accreditation%20Protocol%20-%20New%20Homes%2020250227.pdf (accessed on 1 March 2025).
- Santos, P.; Mateus, D. Experimental assessment of thermal break strips performance in load-bearing and non-load-bearing LSF walls. J. Build. Eng. 2020, 32, 101693. [Google Scholar] [CrossRef]
- Gunalan, S.; Kolarkar, P.; Mahendran, M. Experimental study of load bearing cold-formed steel wall systems under fire conditions. Thin-Walled Struct. 2013, 65, 72–92. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- ISO 10211:2017; Thermal Bridges in Building Construction—Heat Flows and Surface Temperatures—Detailed Calculations. International Organization for Standardization: Geneva, Switzerland, 2017.
- Vy, S.T.; Mahendran, M.; Ariyanayagam, A. Numerical modelling and investigation of CFS built-up stud walls in fire. Fire Saf. J. 2024, 144, 104102. [Google Scholar] [CrossRef]
- AS/NZS 4600:2005; Cold-Formed Steel Structures. Standards Australia: Sydney, Australia; Standards New Zealand: Wellington, New Zealand, 2018.
- Clayton, T.G. Design of Steel Wall Studs with Service Holes; Senior Research Engineer, BlueScope Steel Research. Available online: https://www.nash.asn.au/wp-content/uploads/2022/04/303_1330395018.pdf (accessed on 1 April 2023).
- ABAQUS; Dassault Systèmes: Providence, RI, USA, 2023.
- Keerthan, P.; Mahendran, M. Thermal Performance of Composite Panels Under Fire Conditions Using Numerical Studies: Plasterboards, Rockwool, Glass Fibre and Cellulose Insulations. Fire Technol. 2013, 49, 329–356. [Google Scholar] [CrossRef]
- Perera, D.; Upasiri, I.R.; Poologanathan, K.; Gatheeshgar, P.; Sherlock, P.; Hewavitharana, T.; Suntharalingam, T. Energy performance of fire rated LSF walls under UK climate conditions. J. Build. Eng. 2021, 44, 103293. [Google Scholar] [CrossRef]
- Auwerda, G.J.; Zheng, Y.H.; Kloosterman, J.L.; Lathouwers, D. Comparison of 2D and 3D heat transfer models around the coolant channels in the HTR-PM side reflector. Nucl. Eng. Des. 2014, 271, 465–471. [Google Scholar] [CrossRef]
- Peiris, M.; Mahendran, M. Behaviour of cold-formed steel lipped channel sections subject to eccentric axial compression. J. Constr. Steel Res. 2021, 184, 106808. [Google Scholar] [CrossRef]
- Santos, P.; Lopes, P.; Abrantes, D. Thermal Performance of Lightweight Steel Framed Facade Walls Using Thermal Break Strips and ETICS: A Parametric Study. Energies 2023, 16, 1699. [Google Scholar] [CrossRef]
- Roque, E.; Santos, P. The Effectiveness of Thermal Insulation in Lightweight Steel-Framed Walls with Respect to Its Position. Buildings 2017, 7, 13. [Google Scholar] [CrossRef]










| Climate Zone | Class of Building | ||
|---|---|---|---|
| 1 | 2, 5, 6, 7, 8 or 9b or 9a Excluding Ward Area | 3 or 9c or 9a Ward Area | |
| 1 | 2.8 | 2.4 | 3.3 |
| 2 | 2.8 | 1.4 | 1.4 |
| 3 | 2.8 | 1.4 | 3.3 |
| 4 | 2.8 | 1.4 | 2.8 |
| 5 | 2.8 | 1.4 | 1.4 |
| 6 | 2.8 | 1.4 | 2.8 |
| 7 | 2.8 | 1.4 | 2.8 |
| 8 | 3.8 | 1.4 | 3.8 |
| Study Component | Details | Scope/Configurations | Purpose |
|---|---|---|---|
| Model Validation | Reference LSF wall by Santos & Mateus [31] (guarded hot-box) | 1 wall (R = 1.558 m2·K/W)—Heat transfer model | Benchmark validation of LSF wall using Abaqus and THERM |
| Gunalan et al. [32] 3 m lipped channel CFS stud | 1 stud (81 kN vs. 79 kN (experimental).)—Structural capacity model | Structural validation of CFS stud model in Abaqus | |
| Numerical Study | Validated LSF walls with and with-out web-perforated CFS studs | THERM (2D), Abaqus (3D), and analytical methods (NZS 4214, ASHRAE) | Evaluate the role of web-perforations in thermal capacity enhancement |
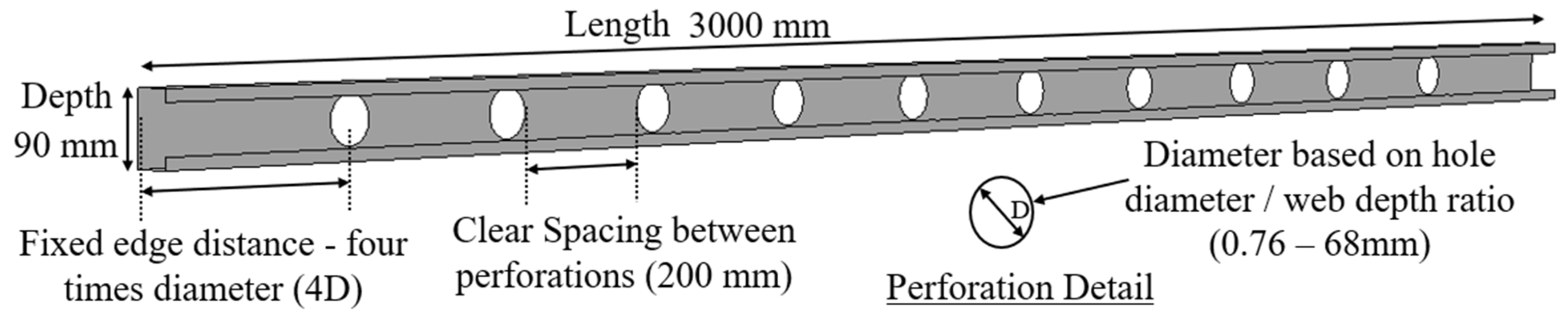
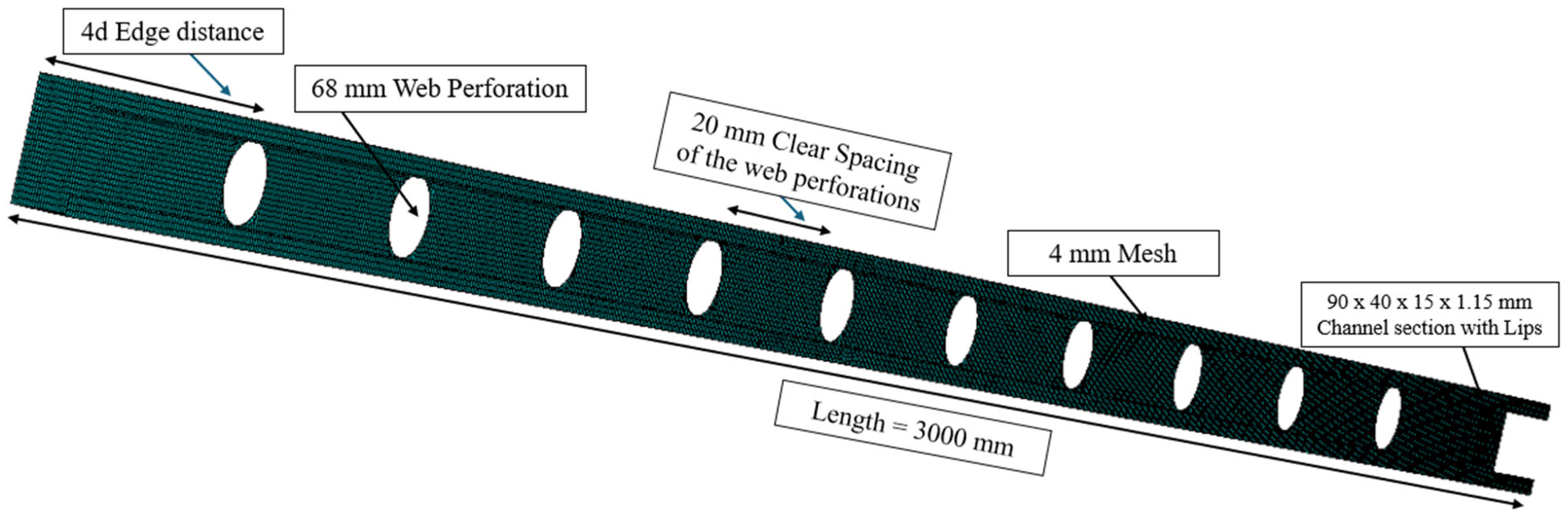
| Parametric Study (CFS studs) | Lipped channel stud 90 × 40 × 15 × 1.15 mm, 3 m height | 120 CFS studs: Hole Ø 36–68 mm, spacing 120–450 mm (d/h = 0.40–0.76) | Evaluate thermal R-values and load capacity |
| Edge stiffeners (4 mm plates) | 1 CFS stud with 68 mm Ø holes with 200 mm clear spacing | Restore structural capacity of perforated studs | |
| Analytical Methods | Modified NZS 4214 & ASHRAE MZM | Compared with Abaqus & THERM | Develop reliable predictive models |
| Façade Systems (External Walls) | AAC panels | 1 case (THERM (2D), Abaqus (3D), and analytical methods (NZS 4214, ASHRAE)) | High thermal mass façade |
| Corrugated steel sheeting | 1 case (THERM (2D), Abaqus (3D), and analytical methods (NZS 4214, ASHRAE)) | Lightweight, high conductivity façade | |
| Aluminium composite panels (ACP) | 1 case (THERM (2D), Abaqus (3D), and analytical methods (NZS 4214, ASHRAE)) | Insulated lightweight façade | |
| Fire-rated glass façade | 1 case (THERM (2D), Abaqus (3D), and analytical methods (NZS 4214, ASHRAE)) | Transparent, fire-resistant façade | |
| Ventilated brick veneer | 1 case (THERM (2D), Abaqus (3D), and analytical methods (NZS 4214, ASHRAE)) | Brick veneer with ventilated cavity | |
| Enhancements | Thermal breaks | Applied in all external walls considered in study | Reduce thermal bridging |
| Hybrid insulation (partial cavity fill + sheathing) | Applied in all external walls considered in study | Improve thermal efficiency | |
| Double plasterboard | Applied in all external walls considered in study | Increase thermal mass & fire performance | |
| Climate Zone Analysis | NCC 2022 Australian climate zones (Z1–Z8) | Applied in all external walls considered in study | Demonstrate compliance with R-value requirements |
| Method | R Value–Non-Perforated LSF Walls (m2·K/W) | Deviation from Experiment (%) |
|---|---|---|
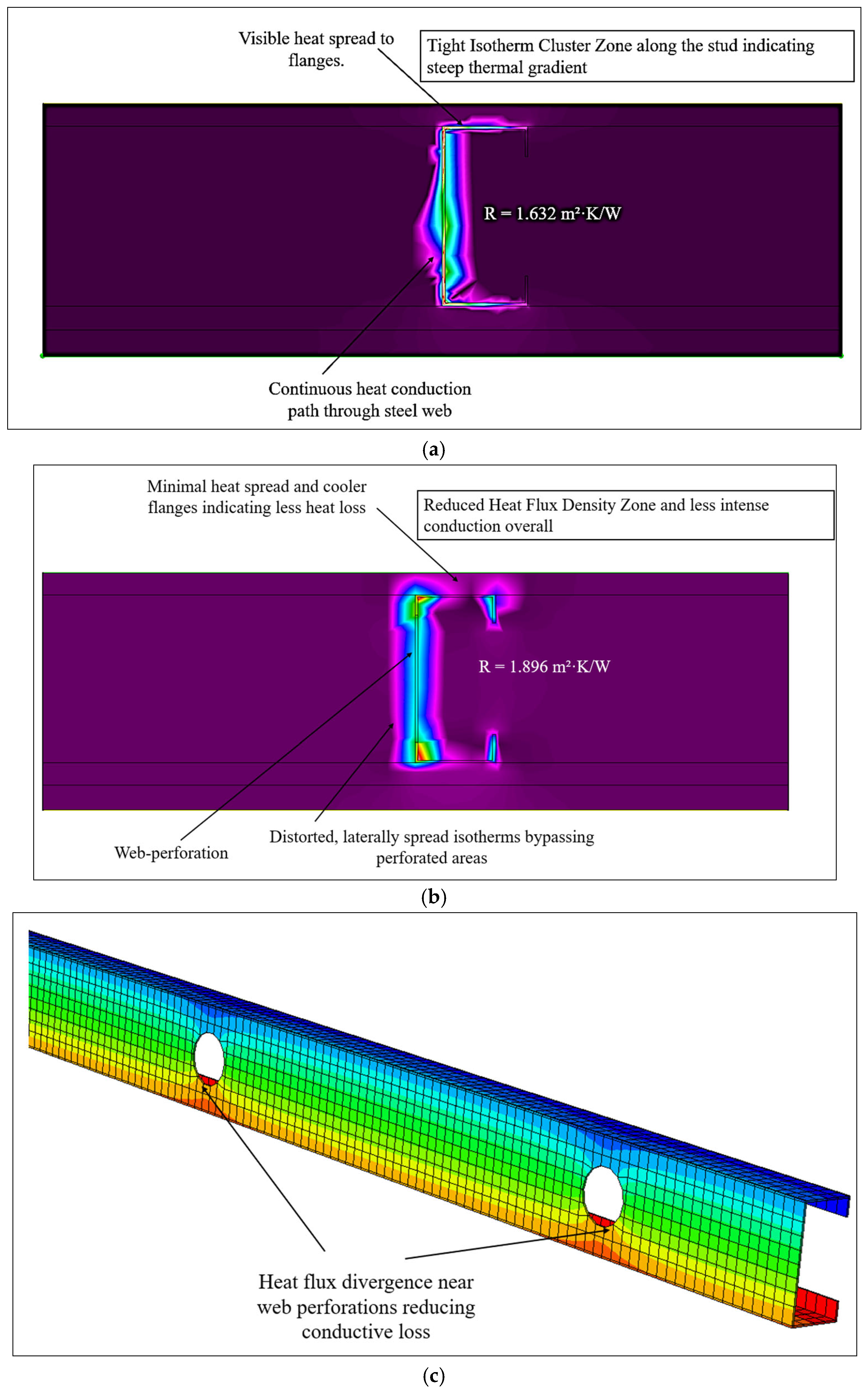
| Experimental reference | 1.558 | — |
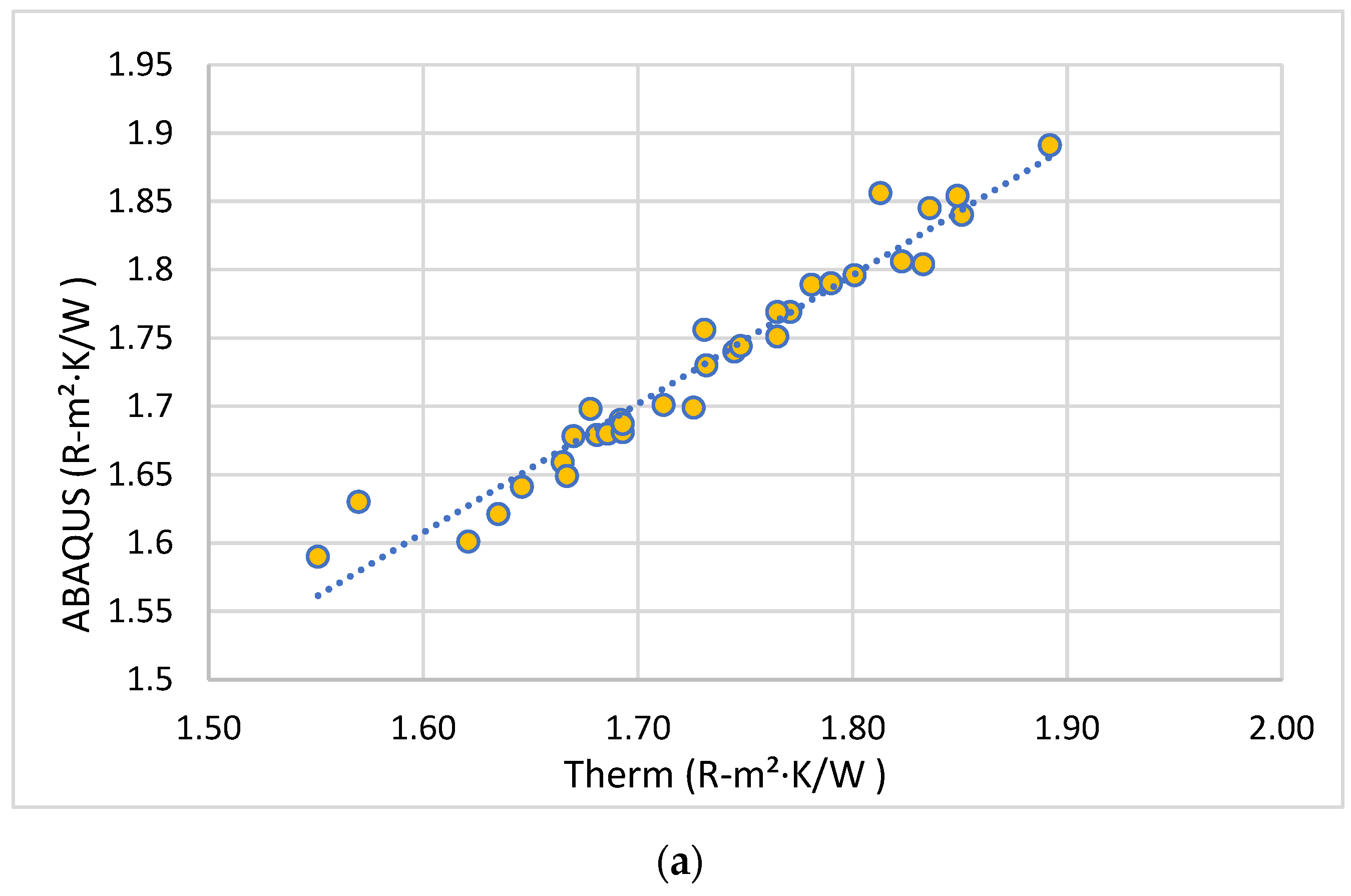
| Abaqus | 1.570 | 0.77% |
| THERM | 1.632 | 4.75% |
| NZS 4214:2016 | 1.591 | 2.12% |
| ASHRAE Modified Zone method | 1.579 | 1.35% |
| Method | R Value–Web-Perforated LSF Walls (m2·K/W) | % Improvement of R Value Due to Web-Perforation |
|---|---|---|
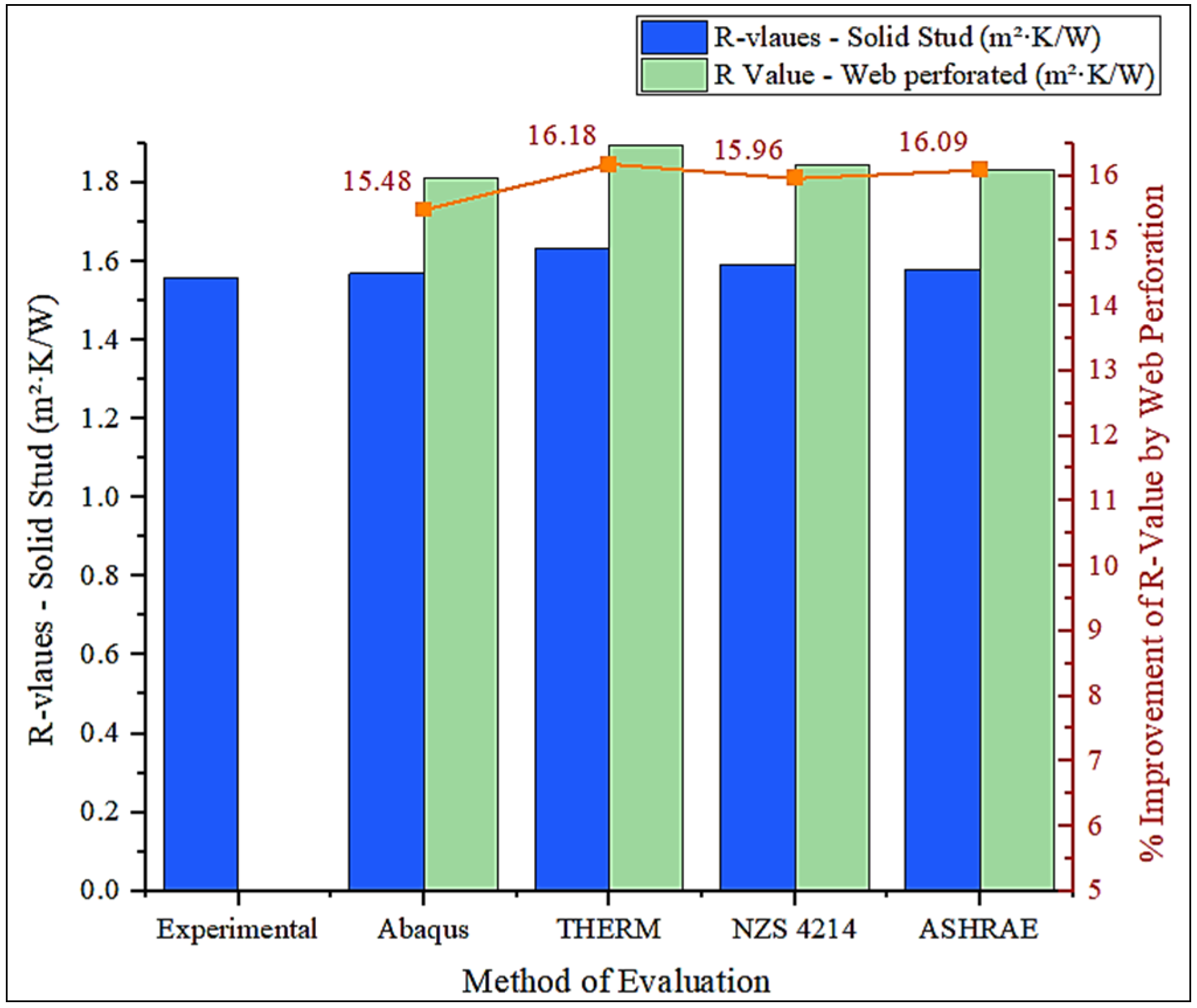
| Abaqus | 1.813 | 15.48% |
| THERM | 1.896 | 16.18% |
| NZS 4214 | 1.845 | 15.96% |
| ASHRAE Modified Zone | 1.833 | 16.09% |
| Material | Description | Thickness (mm) | Thermal Conductivity (W/m·K) |
|---|---|---|---|
| AAC | Lightweight cellular concrete panel | 75 | 0.14 |
| Profiled Steel Cladding | Zinc-coated profiled steel cladding (BMT 0.42 mm) | 0.42 | 51 |
| ACP | Non-combustible A1-grade panel with mineral core | 5.0 (total) | 0.40 (effective) |
| Fire-Rated Glazing | Laminated fire-resistive glass with intumescent core | 25 | 1.0 (overall) |
| Brick Veneer | External clay brick masonry | 110 | 0.7 |
| External Wall Type | Method | R (Non-Perforated) (m2·K/W) | R (Perforated) (m2·K/W) | % Improvement |
|---|---|---|---|---|
| AAC Cladding | Abaqus | 2.71 | 3.12 | 15.13 |
| THERM | 2.83 | 3.27 | 15.50 | |
| NZS 4214 | 2.77 | 3.21 | 15.88 | |
| ASHRAE Modified Zone | 2.73 | 3.18 | 16.48 |
| External Wall Type | Method | R (Non-Perforated) (m2·K/W) | R (Perforated) (m2·K/W) | % Improvement |
|---|---|---|---|---|
| Profiled Steel Cladding | Abaqus | 2.32 | 2.67 | 15.09% |
| THERM | 2.41 | 2.79 | 15.77% | |
| NZS 4214 | 2.35 | 2.75 | 17.02% | |
| ASHRAE Modified Zone | 2.33 | 2.74 | 17.60% |
| External Wall Type | Method | R (Non-Perforated) (m2·K/W) | R (Perforated) (m2·K/W) | % Improvement |
|---|---|---|---|---|
| ACP Cladding | Abaqus | 2.68 | 3.109 | 15.99% |
| THERM | 2.76 | 3.2 | 15.94% | |
| NZS 4214 | 2.71 | 3.16 | 16.61% | |
| ASHRAE Modified Zone | 2.67 | 3.14 | 17.60% |
| External Wall Type | Method | R (Non-Perforated) (m2·K/W) | R (Perforated) (m2·K/W) | % Improvement |
|---|---|---|---|---|
| Fire-Rated Glazing Cladding | Abaqus | 2.61 | 3 | 14.94% |
| THERM | 2.71 | 3.14 | 15.87% | |
| NZS 4214 | 2.65 | 3.09 | 16.60% | |
| ASHRAE Modified Zone | 2.61 | 3.08 | 17.62% |
| External Wall Type | Method | R (Non-Perforated) (m2·K/W) | R (Perforated) (m2·K/W) | % Improvement |
|---|---|---|---|---|
| Fire-Rated Glazing Cladding | Abaqus | 2.57 | 2.95 | 14.79% |
| THERM | 2.70 | 3.13 | 15.93% | |
| NZS 4214 | 2.67 | 3.11 | 16.48% | |
| ASHRAE Modified Zone | 2.64 | 3.10 | 17.42% |
| Wall Configuration | R (Non-Perforated) (m2·K/W) | R (Perforated) (m2·K/W) | % Improvement | Source |
|---|---|---|---|---|
| 12.5 mm gypsum plasterboard (both sides) + 90 mm mineral wool + single C90 stud (400 mm spacing) | 1.78 | 2.06 | 15.73% | Francis et al. [8] Journal of Building Engineering, 2025. |
| 12.5 mm gypsum plasterboard (both sides) + 90 mm mineral wool + back-to-back C90 studs (400 mm spacing) | 1.45 | 1.64 | 13.10% | Francis et al. [8] Journal of Building Engineering, 2025, |
| 12.5 mm gypsum + 12 mm OSB + 90 mm mineral wool + C90 × 43 × 15 × 1.5 mm stud (400 mm spacing) + 50 mm EPS + ETICS finish (no Thermal breaks -TBS) | 3.204 | 3.648 | 13.87% | Santos et al. [43] Energies, 2023. |
| 12.5 mm gypsum + 12 mm OSB + 90 mm mineral wool + C90 × 43 × 15 × 1.5 mm stud + 1 TBS (10 mm, λ = 7.5 mW/m·K) + 50 mm EPS + ETICS finish | 3.842 | 4.487 | 16.78% | Santos et al. [43] Energies, 2023. |
| 12.5 mm gypsum + 12 mm OSB + 90 mm mineral wool + C90 × 43 × 15 × 1.5 mm stud + 2 TBS (5 mm each, λ = 7.5 mW/m·K) + 50 mm EPS + ETICS finish | 4.444 | 5.219 | 17.43% | Santos et al. [43] Energies, 2023. |
| 12.5 mm gypsum plasterboard + 90 mm mineral wool + single C90 stud (600 mm spacing) + 15 mm flange indentation filled with aerogel | 1.906 | 2.135 | 12.00% | Santos et al. [5] Sustainability, 2021. |
| 12.5 mm gypsum + 90 mm MW + C90 (600 mm) + 15 mm indentation (aerogel) + ETICS | 3.499 | 3.954 | 13.00% | Santos et al. [5] Sustainability, 2021. |
| 12.5 mm gypsum + 90 mm MW + C150 (600 mm) + 15 mm indentation (aerogel) + ETICS | 4.301 | 5.032 | 17.00% | Santos et al. [5] Sustainability, 2021. |
| 12.5 mm gypsum + 90 mm MW + C90 (400 mm) + 15 mm indentation (aerogel) + ETICS | 3.203 | 3.812 | 19.00% | Santos et al. [5] Sustainability, 2021. |
| 12.5 mm plasterboard + 10 mm OSB + 150 mm RW between steel studs + 15 mm OSB + 5 mm ETICS (C1—Cold Construction) | 2.317 | 2.595 | 12.00% | Santos et al. [44] Buildings, 2017. |
| 12.5 mm plasterboard + 10 mm OSB + 150 mm steel studs + 15 mm OSB + 75 mm RW (internal) + 75 mm EPS (external) + 5 mm ETICS (H1—Hybrid Construction) | 3.744 | 4.249 | 13.50% | Santos et al. [44] Buildings, 2017. |
| 12.5 mm plasterboard + 10 mm OSB + 150 mm steel studs + 15 mm OSB + 150 mm EPS (fully external) + 5 mm ETICS (W1—Warm Construction) | 4.779 | 5.496 | 15.00% | Santos et al. [44] Buildings, 2017. |
| External Wall Type | Method | R (Non-Perforated) (m2·K/W) | R (Perforated) (m2·K/W) | Web-Perforated + Thermal Break (External Flange)—R (m2·K/W) | Web-Perforated + Thermal Break (Both Flanges)—R (m2·K/W) | Web-Perforated + Hybrid Insulation—R (m2·K/W) | Web-Perforated + Double Plasterboards—R (m2·K/W) |
|---|---|---|---|---|---|---|---|
| AAC | Abaqus | 2.71 | 3.12 | 3.915 | 4.365 | 4.19 | 3.78 |
| THERM | 2.83 | 3.27 | 4.065 | 4.515 | 4.34 | 3.93 | |
| NZS 4214 | 2.77 | 3.21 | 4.005 | 4.455 | 4.28 | 3.87 | |
| ASHRAE Mod. Zone | 2.73 | 3.18 | 3.975 | 4.425 | 4.25 | 3.84 | |
| Profiled Steel | Abaqus | 2.32 | 2.67 | 3.401 | 3.389 | 3.7 | 3.33 |
| THERM | 2.41 | 2.79 | 3.521 | 3.509 | 3.82 | 3.45 | |
| NZS 4214 | 2.35 | 2.75 | 3.481 | 3.469 | 3.78 | 3.41 | |
| ASHRAE Mod. Zone | 2.33 | 2.74 | 3.471 | 3.459 | 3.77 | 3.4 | |
| ACP | Abaqus | 2.68 | 3.109 | 3.815 | 3.863 | 4.192 | 3.769 |
| THERM | 2.76 | 3.2 | 3.906 | 3.954 | 4.283 | 3.86 | |
| NZS 4214 | 2.71 | 3.16 | 3.866 | 3.914 | 4.243 | 3.82 | |
| ASHRAE Mod. Zone | 2.67 | 3.14 | 3.846 | 3.894 | 4.223 | 3.8 | |
| Fire-Rated Glass | Abaqus | 2.61 | 3 | 3.782 | 3.873 | 4.0923 | 3.66 |
| THERM | 2.71 | 3.14 | 3.922 | 4.013 | 4.2323 | 3.8 | |
| NZS 4214 | 2.65 | 3.09 | 3.872 | 3.963 | 4.1823 | 3.75 | |
| ASHRAE Mod. Zone | 2.61 | 3.08 | 3.862 | 3.953 | 4.1723 | 3.74 | |
| Brick Veneer | Abaqus | 2.57 | 2.95 | 3.32 | 3.72 | 4.114 | 3.61 |
| THERM | 2.7 | 3.13 | 3.45 | 3.9 | 4.294 | 3.79 | |
| NZS 4214 | 2.67 | 3.11 | 3.42 | 3.88 | 4.274 | 3.77 | |
| ASHRAE Mod. Zone | 2.64 | 3.1 | 3.39 | 3.87 | 4.264 | 3.76 |
| External Wall Type | R (Non-Perforated) | Zones | R (Perforated) | Zones | Thermal Break-Ext | Zones | Thermal Break-Both | Zones | Hybrid Insulation | Zones | Double Plasterboards | Zones |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AAC | 2.71–2.83 | Z1–7 | 3.12–3.27 | Z1–7 | 3.9–4.1 | Z1–8 | 4.4–4.5 | Z1–8 | 4.19–4.34 | Z1–8 | 3.78–3.93 | Z1–8 |
| ACP | 2.67–2.76 | Not suitable for any zone | 3.10–3.2 | Z1–7 | 3.8–3.9 | Z1–8 | 3.9–3.95 | Z1–8 | 4.19–4.3 | Z1–8 | 3.769–3.86 | Z1–8 |
| Brick Veneer | 2.57–2.7 | Not suitable for any zone | 2.95–3.13 | Z1–7 | 3.3–3.5 | Z1–7 | 3.72–3.9 | Z1–8 | 4.1–4.3 | Z1–8 | 3.61–3.79 | Z1–8 |
| Fire-Rated Glass | 2.61–2.71 | Not suitable for any zone | 3.00–3.14 | Z1–7 | 3.8–3.9 | Z1–8 | 3.9–4.0 | Z1–8 | 4.1–4.2 | Z1–8 | 3.66–3.8 | Z1–8 |
| Profiled Steel | 2.32–2.41 | Not suitable for any zone | 2.67–2.79 | Not suitable for any zone | 3.4–3.5 | Z1–8 | 3.39–3.5 | Z1–8 | 3.7–3.82 | Z1–8 | 3.33–3.45 | Z1–8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilango, S.; Ariyanayagam, A.; Mahendran, M. Influence of Web-Perforated Cold-Formed Steel Studs on the Heat Transfer Properties of LSF External Walls. Energies 2025, 18, 5103. https://doi.org/10.3390/en18195103
Ilango S, Ariyanayagam A, Mahendran M. Influence of Web-Perforated Cold-Formed Steel Studs on the Heat Transfer Properties of LSF External Walls. Energies. 2025; 18(19):5103. https://doi.org/10.3390/en18195103
Chicago/Turabian StyleIlango, Saranya, Anthony Ariyanayagam, and Mahen Mahendran. 2025. "Influence of Web-Perforated Cold-Formed Steel Studs on the Heat Transfer Properties of LSF External Walls" Energies 18, no. 19: 5103. https://doi.org/10.3390/en18195103
APA StyleIlango, S., Ariyanayagam, A., & Mahendran, M. (2025). Influence of Web-Perforated Cold-Formed Steel Studs on the Heat Transfer Properties of LSF External Walls. Energies, 18(19), 5103. https://doi.org/10.3390/en18195103








