Influence of Long-Term and Short-Term Solar Radiation and Temperature Exposure on the Material Properties and Performance of Photovoltaic Panels: A Comprehensive Review

Abstract

This review provides a comprehensive synthesis of the coupled effect of temperature and solar radiation on photovoltaic (PV) module performance and lifespan. Although numerous investigations have examined these stressors in themselves, this research addresses their interrelationship and evaluates the way climatic conditions affect short-term performance fluctuation and long-term degradation mechanisms. The assessment consolidates outcomes from model strategies, laboratory tests, and field monitoring studies. Through the presentation of these findings in a narrative form, the paper identifies recurring difficulties in terms of the absence of shared assessment metrics and the low level of standardisation of long-term test regimes. Second, it underlines the importance of predictive modelling and live monitoring as important management tools for coupled stressors. Finally, the review points out research gaps and underscores future research avenues, including ongoing work towards the development of a coupling index, a composite measure being piloted in individual studies, and advancements in materials technology, predictive methodology, and durability testing.

1. Introduction

Globally, photovoltaic renewable energy plays an important role in mitigating the adverse effects of fossil fuel extraction. There has been an exponential rise in interest in green energy in recent years [1] through solar photovoltaic technology and due to increased efficiency in recent times and also due to large-scale production at reduced costs, easy installation, and lower maintenance costs [1,2].

It is noted that the photovoltaic technology market is experiencing significant growth [3]; from 2010 to 2019 alone, the global installed capacity increased from 40.3 GW to 580.2 GW [4], and in 2022, the installed solar energy capacity reached 1185 GW, with photovoltaics accounting for 70% of total additions, which is around 348 GW [5]. According to experts’ projections, the world must install more than 75 TW of photovoltaic energy by 2050 to achieve its climate decarbonization targets [6]. Crystalline silicon (c-Si) photovoltaic technology has a conversion efficiency of 27.6% [7], which highlights the need for improvement in order to ensure greater competitiveness [8].

As photovoltaic systems spread worldwide, uncertainties regarding their long-term reliability and performance under various climates are also growing [9]. It is extremely important to predict the energy yield of photovoltaic systems over their life cycle to understand degradation rates [10], as well as many underlying factors that impact their efficiency, such as meteorological parameters [11], particularly solar radiation, ambient temperature, dust storms, wind speed [3], the effect of shading, orientation, and the geographical location of solar panels [12].

It has also been shown that climatic stresses can lead to degradation through hydrolysis, thermomechanical degradation, photodegradation, and the rate at which degradation occurs when temperature, humidity, and ultraviolet irradiation are combined [9]. The factors affecting the efficiency of photovoltaic systems are shown in Figure 1.

Experiments conducted in open spaces [13], be it accelerated or lengthy and laborious [14], help to reduce degradation rates in photovoltaic systems as well as potential failures, as they provide information on performance throughout the life cycle [13]. Climatic and environmental conditions [11,15,16] are the main causes of the degradation of photovoltaic modules over their useful life cycle [17,18]. Degradation rate is one of the main variables that has influenced the price of electricity for photovoltaic systems over a 25-year life cycle, with some manufacturers designing a 30-year service life as a way to reverse the issue [19].

The solar cell has multiple equivalent electrical circuits, comprising mainly the single diode model, which is defined by five parameters (Iph, Isd, n, Rs, Rsh) [20,21,22]. The degradation of the photovoltaic cell affects its I–V characteristic, which eventually influences the five parameters of the solar cell [14,23], proving the dependence of these parameters on the long-term effect of temperature and radiation. Several researchers have discussed at length the influence of temperature on the operating characteristics of photovoltaic modules [24].

A variety of techniques are used to detect defects in photovoltaic modules, such as electrical characterisation, electroluminescence (EL), visual inspection, thermal imaging, and electrical insulation testing [25]. Statistical techniques used to estimate the degradation rate include linear regression (LE), ordinary least squares (OLS), locally weighted scatterplot smoothing (LOESS), classical seasonal decomposition (CSD), year-over-year (YOY) and robust principal component analysis, and integrated autoregressive moving average (ARIMA) [26,27,28].

This article presents an analytical approach to various studies on the effects of the relationship between temperature and solar radiation on the performance and conversion efficiency of photovoltaic solar modules. At the same time, it highlights environmental factors and provides tools that quantify thermal and solar radiation fluctuations, seeking a futuristic view of trends and highlighting various technological strategies and innovative solutions for mitigating the effects of these parameters on solar systems subject to diverse environmental conditions.

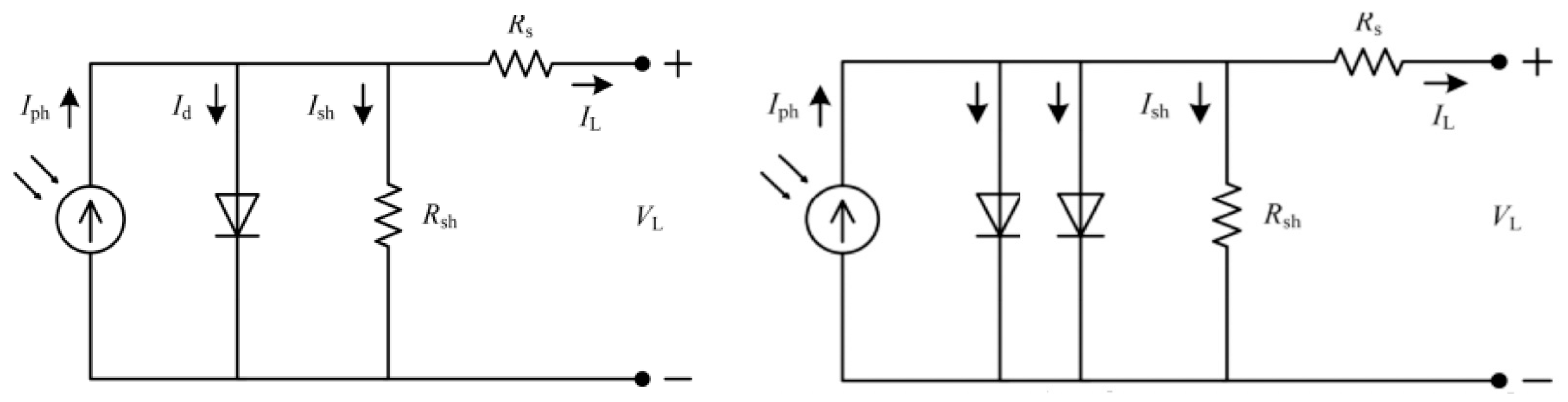
2. Fundamentals of Solar Cell Operation

2.1. Characteristic I–V Curves

A solar cell operates based on the photoelectric effect, in which the solar radiation of a particular frequency is absorbed in an intrinsic region, resulting in an electron–hole pair. Due to the presence of the electric field forces of the p–n junction, they are directed to opposite sides, creating a high potential difference in the semiconductor [29,30].

To describe the operating principle of a solar cell, a model in the form of an equivalent electrical circuit is generally used, comprising mainly the single diode model (SDM) [31] and the double diode model (DDM) [22], which illustrates the non-linear P–V characteristics and I–V characteristics [32,33]. These models are configured to contain a diode (Isd, n) or two (Isd1, n1, Isd2, n2) in parallel with a shunt resistance (Rsh) to understand the effect of PN junction leakage current, and associated with a series resistance (Rs) to consider its internal resistance, and with a photogenerated current (Iph), as shown in Figure 2 [34,35,36].

The general characteristic equations for a photovoltaic device using the equivalent electrical circuits of the single diode and double diode models are given, respectively, by the following equations [20,36]:

$$I_L=I_{ph}-I_{sd}\left[exp\left({\displaystyle \frac{V_L+I_L\times R_s}{{nV}_t}}\right)-1\right]-{\displaystyle \frac{V_L+I_L\times R_s}{R_{sh}}},$$

(1)

$$I_L=I_{ph}-I_{sd1}\left[exp\left({\displaystyle \frac{V_L+I_L\times R_s}{{n1V}_t}}\right)-1\right]-I_{sd2}\left[exp\left({\displaystyle \frac{V_L+I_L\times R_s}{{n2V}_t}}\right)-1\right]-{\displaystyle \frac{V_L+I_L\times R_s}{R_{sh}}},$$

(2)

where V_L is the cell output voltage. I_sd, I_sd1, I_sd2 are the saturation currents; n, n1, and n2 are the ideal diode factors. V_t = kT/q represents the junction thermal voltage, which is expressed in function of k the Boltzmann’s constant, q the electron charge, and T the temperature.

To extract the parameters of the characteristic curve in the SDM, it is necessary to create an objective function to verify the congruence of the established model with the real model [32]; and to facilitate, in several cases, an approximation or adjustment is performed to simplify the complexity of the problem, since the output current and photovoltaic equations do not follow a linear relationship and are implied [37]. The accuracy of various methods in the SDM depends on the precision of the approximations, simplifications, adjustment algorithm, and initial inputs fed into the algorithm. The extraction scheme is also affected by measurement accuracy and errors incorporated in numerical differentiation and by the error function defined by the operator [37].

2.2. Main Photovoltaic Technologies

The main photovoltaic solar technologies can be classified based on their materials and production technology, and in this case can be categorised according to their technological progress over time, as shown in Figure 3.

3. Effects of Temperature on the Performance of Photovoltaic Modules

Temperature variation has a significant impact on the electrical properties of photovoltaic cells, influencing performance control and efficiency [45]. The band gap is attenuated with increasing temperature, causing an increase in electron energy at very high temperatures [46].

The operating temperature of the photovoltaic module is defined by the energy balance, where the absorbed solar energy is partially converted into thermal energy (which is dissipated by the heat transfer mechanism adjustment) and partially into electrical energy that will be removed from the cell through the external circuit. The photovoltaic energy balance can be expressed mathematically as follows [47]:

$$\left(\tau \alpha \right)G_T={\eta }_c{G}_T+U_L(T_c-T_a),$$

(3)

where

$\tau \alpha$—effective transmittance–absorption product on and from the photovoltaic panel [%].

$G_T$—solar radiation hitting the photovoltaic panel [kW/m²].

${\eta }_c$—electrical conversion efficiency of the photovoltaic array [%].

$U_L$—heat transfer coefficient to the surrounding environment [kW/m² °C].

$T_c$—photovoltaic cell temperature [°C].

$T_a$—ambient temperature [°C].

Solving Equation (3) for the cell temperature, we obtain

$$T_c=T_a+G_T\left({\displaystyle \frac{\tau \alpha }{U_L}}\right)\left(1-{\displaystyle \frac{{\eta }_c}{\tau \alpha }}\right),$$

(4)

As it is difficult to measure the parameter $\left({\displaystyle \frac{\tau \alpha }{U_L}}\right)$ directly, manufacturers chose to present the nominal operating temperature of the cell (NOCT), cell or module temperature, resulting from an incident radiation of 800 W/m², ambient temperature of 20 °C, with a wind speed of 1 m/s, and operation without load (η_c = 0) [47]. Under NOCT conditions, we can express the equation as follows:

$$\left(\tau \alpha \right)G_{T,NOCT}= U_{L,NOCT}(T_{c,NOCT}-T_{c,NOCT}),$$

(5)

The cell temperature can be determined at any ambient temperature using the following expression:

$${\displaystyle \frac{T_c-T_a}{T_{C,NOCT}-T_{a,NOCT}}}={\displaystyle \frac{G_T }{G_{NOCT} }}{\displaystyle \frac{U_{L,NOCT}}{U_L}}\left[1-{\displaystyle \frac{{\eta }_c}{\left(\tau \alpha \right)}}\right],$$

(6)

$$T_c=T_a+\left({\displaystyle \frac{G_T }{G_{NOCT}}}\right)\left({\displaystyle \frac{U_{L,NOCT}}{U_L}}\right)(T_{C,NOCT}-T_{a,NOCT})\left[1-{\displaystyle \frac{{\eta }_c}{\left(\tau \alpha \right)}}\right],$$

(7)

where $G_{NOCT}$—solar radiation for which NOCT is defined [0.8 kW/m²].

$T_{a,NOCT}$—ambient temperature at which NOCT is defined [20 °C].

$T_{C, NOCT}$—nominal operating temperature of the cell [°C].

Assuming an estimate of 0.9 for the product ($\tau \alpha$) and because the term ${\displaystyle \frac{{\eta }_c}{\left(\tau \alpha \right)}}$ is small in comparison with the unit, knowing that Equation (7) does not take into account the variation in cell temperature with wind speed, an approximation can be made by replacing the term with the convection coefficient under the conditions (h) NOCT and under the actual operating conditions, being [47]

$$h=5.7+3.8 V,$$

(8)

then,

$${\displaystyle \frac{T_c-T_a}{T_{C,NOCT}-T_{a,NOCT}}}={\displaystyle \frac{G_T }{G_{NOCT} }}{\displaystyle \frac{9.5}{(5.7+3.8V)}}\left[1-{\displaystyle \frac{{\eta }_c}{\left(\tau \alpha \right)}}\right],$$

(9)

3.1. Impact of Temperature Variation on Photovoltaic Cells

The main impact of temperature variation is on the saturation current, as it is associated with the intrinsic concentration of carriers, which causes the V_OC to decrease as the temperature increases. The dependence of this parameter on band gap energy means that smaller band gaps result in a higher concentration of intrinsic carriers. Furthermore, the energy of the carriers also plays an important role, since high temperatures cause an increase in the concentration of intrinsic carriers [48]. The overall efficiency of the cell tends to decrease with high temperatures, affecting the FF due to resistive losses within the cell [49].

It has been established that the output power of a photovoltaic solar module can decrease by approximately 0.4 W for every degree Celsius increase in temperature, which demonstrates the close dependence between energy conversion efficiency and temperature [50], exacerbated in climates with high temperatures where performance can decrease even further due to thermal losses and reduced V_OC [51].

This relationship between the electrical performance of photovoltaic cells and temperature is described by temperature coefficients, which quantify the decrease in efficiency as temperature increases [52].

3.2. Temperature Coefficient

The specific value of the temperature coefficient not only depends on the material used in the production of photovoltaic solar cells, but is also associated with the reference temperature [53], i.e., the fundamental loss mechanisms and additional losses are dependent on the temperature of the device, and the efficiency of the modules is a function of temperature. The temperature coefficients of short-circuit current density (α), output power (γ), and open-circuit voltage (β) are normally analysed, with the latter being responsible for the overall temperature sensitivity of solar cells [54,55]. In general, the temperature coefficients are given by the following equations [56,57,58]:

$$\beta ={\displaystyle \frac{1}{V_{oc}}}{\displaystyle \frac{d{V}_{oc}}{dT}}={\displaystyle \frac{1}{V_{oc}}}{\displaystyle \frac{1}{T_c}}\left(V_{oc}-{\displaystyle \frac{E_{g\left(0\right)}}{q}}-{\gamma }_r{\displaystyle \frac{k{T}_c}{q}}\right),$$

(10)

where ${\gamma }_r$ represents the recombination processes in the cell, and $E_{g\left(0\right)}$ is the bandgap of the semiconductor linearly extrapolated to a temperature of 0 K.

$$\alpha ={\displaystyle \frac{1}{I_{sc}}}{\displaystyle \frac{d{I}_{sc}}{dT}}={\displaystyle \frac{1}{I_{sc,ideal}}}{\displaystyle \frac{d{I}_{sc,ideal}}{{dE}_g}}{\displaystyle \frac{{dE}_g}{dT}}+{\displaystyle \frac{1}{f_c}}{\displaystyle \frac{{df}_c}{dT}},$$

(11)

where $f_c$ is the collection fraction

$$\delta ={\displaystyle \frac{1}{FF}}{\displaystyle \frac{dFF}{dT}}=\left(1-1.02{FF}_o\right)\left({\displaystyle \frac{1}{V_{oc}}}{\displaystyle \frac{d{V}_{oc}}{dT}}-{\displaystyle \frac{1}{T}}\right)-{\displaystyle \frac{R_s}{\left(\frac{V_{oc}}{I_{sc}}-R_s\right)}}\left({\displaystyle \frac{1}{R_s}}{\displaystyle \frac{d{R}_s}{dT}}\right),$$

(12)

$${FF}_o={\displaystyle \frac{V_{oc}-\mathrm{l}\mathrm{n}(V_{oc}+0.72)}{V_{oc}+1 }},$$

(13)

In the photovoltaic module performance research, the maximum power coefficient is used to correct the module power. And as the variation in parameters ($V_{oc},I_{sc}, FF$) is approximately linear with temperature, the theoretical value of the coefficient can be determined by separating its sensitivity to temperature from the module performance by adding the respective coefficients [56,59].

$$\gamma =\beta +\alpha +\delta ,$$

(14)

The table below shows the temperature coefficients of different solar technologies based on certain research, where it can be seen that solar cells with technologies based on monocrystalline and polycrystalline silicon have high values, justified by their low efficiency at high temperatures when compared to others. Since thin-film cells have relatively low coefficients, it makes them more stable in hot climates; with heterojunction cells and perovskites having the best thermal stability, it makes them more promising for new applications in hot climates.

Comparing temperature coefficients in

Table 1. Solar cell temperature coefficients.

Solar Technology	Temp. of Coef. [%/°C]	Observation
Monocrystalline Silicon (c-Si)	−0.44 till −0.50 [60]	With increasing temperature, efficiency decreases due to reduction in VOC and FF [61,62].
Polycrystalline Silicon (p-Si)	−0.44 till −0.48 [61]	The decrease in performance is attributed to the increase in series resistance and the decrease in shunt resistance with increasing temperature [63].
Amporphous Silicon (a-Si)	−0.20 till −0.234 [64,65]	Efficiency decreases significantly with increasing temperature, and it is interesting to note that VOC decreases while JSC shows the opposite trend, increasing slightly, making the interaction between temperature and overall efficiency more complex [66].
Heterojunction (HTJ)	−0.26 till −0.32 [64,67]	They benefit from low processing temperatures, contributing to reduced degradation and improved temperature coefficients [68], which leads to high VOCs, improving overall performance [69]; and performance is also influenced by its microstructure and surface morphology, affecting thermal stability and efficiency [70].
Copper Indium Gallium Selenide (CIGS)	−0.32 till −0.36 [60,64]	Although their performance remains relatively stable in the face of rising temperatures, they suffer efficiency losses due to thermal effects [71].
Cadmium Telluride (CdTe)	−0.23 till −0.28 [64,72]	Moderate temperature sensitivity makes it suitable for high-temperature environments, although efficiency decreases as temperature increases [73], with it being less sensitive to temperature fluctuations than many photovoltaic materials [74].
Perovskite Solar Cells	−0.08 till −0.17 [75,76]	They can maintain better efficiency, although their performance may vary depending on the composition of the perovskite and the architecture [77].

reveals varying trends for PV technologies. Conventional crystalline silicon modules (polycrystalline and monocrystalline) are most sensitive (−0.44 to −0.50%/°C), which explains their commonly reported temperature-influenced losses in thermal performance at high temperatures. Amorphous silicon products are less sensitive (−0.20 to −0.23%/°C), although overall efficiency is poor and the response is counteracting VOC and JSC shifts. Heterojunction cells are in an intermediate band (−0.26 to −0.32%/°C) with structural stability and high VOC advantages, and these improve the cells’ resistance to thermal stress. Among the thin-film options, CIGS modules degrade from −0.32 to −0.36%/°C, whereas CdTe modules are superior at −0.23 to −0.28%/°C and hence well adapted to high-temperature regions. Perovskite solar cells demonstrate the lowest reported coefficients (−0.08 to −0.17%/°C), which show great thermal potential but remain subject to the constraint of lower long-term stability in practical implementation. These comparisons as a group demonstrate the trade-offs among maturity, efficiency, and thermal stability, and the need for a material innovation and durability strategy particularly adapted to these requirements.

3.3. Thermal Modelling

The temperature variation in a module can be treated as a statistical function, but as it changes abruptly, the effect of the material’s thermal capacity cannot be ruled out because it affects the temperature variation in relation to the output parameters [78]. This behaviour is investigated based on the concept of thermal modelling, which helps to understand and predict the performance of the various existing solar technologies. Thermal models for photovoltaic cells can be divided into static models (steady states) and dynamic models [79]:

• Static or steady-state models: Assume environmental and operational conditions (irradiance and ambient temperature) as independent parameters with respect to time [79]. These models are widely used in research that provides an estimate of temperature as a function of average environmental conditions such as solar radiation, ambient temperature, and wind speed [80]. The nominal operating cell temperature (NOCT) model is the most commonly used model in studies for simple estimates of module temperature. It is given by the linear relationship [81,82]:

  $$T_m=T_a+\left({\displaystyle \frac{G}{800 \mathrm{W}/{\mathrm{m}}^2}}\right)\times (NOCT-20 °\mathrm{C}),$$

  (15)
• Dynamic models: Consider variations in environmental conditions through differential equations over time. Using the principle of the heat transfer mechanism [79] to establish the total energy balance in the module [83,84], the energy balance for each layer of material can be included in the model [85], by considering every module [86]. This total energy balance can be determined by Equation (16) [86]:

  $$C_{mod}{\displaystyle \frac{{dT}_{mod}}{dt}}=Q_{sun}-Q_{cond}-Q_{conv}-Q_{rad}-P_e,$$

  (16)

  where $Q_{sun}$ represents the net solar irradiance reaching the front surface of the module. $Q_{cond}$, $Q_{conv}$, $Q_{rad}$ are losses due to heat transfer to the environment. $P_e$ represents the electrical energy produced by the module.

Table 2. Thermal models.

Period	Authors	Thermal Model
1970–1980	Ross [87]	$T_{PV}=T_a+k{G}_T$
	Rauschenbach [88]	$T_{PV}=T_a+{\displaystyle \frac{G_T}{G_T^{NOCT}}} \left(T_{PV}^{NOCT}-T_a^{NOCT}\right)\left(1-{\displaystyle \frac{{\eta }_{PV}}{\tau \alpha }}\right)$
1980–1990	Risser e Fuentes [89]	$T_{PV}=3.81+0.0282\times G_{T}1.31\times T_a-1.65V_w$
	Severant [90]	$T_{PV}=T_a+\alpha \left(1+\beta T_a\right)\left(1-\gamma V_w\right)G_T$
	Schott [91]	$T_{PV}=T_a+0.028\times G_T-1$
	Ross e Smokler [92]	$T_{PV}=T_a+{\displaystyle \frac{G_T}{G_T^{NOCT}}} \left(T_{PV}^{NOCT}-T_a^{NOCT}\right)$
1990–2000	Lasnier e Ang [93]	$T_{PV}={30.006+0.0175\left(G_T-300\right)+1.14(T}_a-25)$
	King [94]	$T_{PV}=T_a+{\displaystyle \frac{G_T}{1000}}({0.0712V}_w^2-{2.411V}_w+32.96)$
	King [95]	$T_{PV}=T_a+{\displaystyle \frac{G_T}{1000}}(19.6e^{{-0.223V}_w}+11.16)$
2000–2010	TamizhMani et al. [96]	$T_{PV}=0.943T_a+0.028G_T-1.528{\displaystyle \frac{G_T}{G_T^{NOCT}}}+4.3$
	King et al. (I) [94]	$T_{PV}=T_a+G_T{e}^{{-3.56-0.0750V}_w}$
	King et al. (II) [94]	$T_{PV}=T_a+G_T{e}^{{-3.47-0.0594V}_w}$
	Duffie end Beckman [47]	$T_{PV}=T_a+\left({\displaystyle \frac{9.5}{5.7+3.8V_w}}\right){\displaystyle \frac{G_T}{G_T^{NOCT}}} \left(T_{PV}^{NOCT}-T_a^{NOCT}\right)\left(1-{\displaystyle \frac{{\eta }_{PV}}{\tau \alpha }}\right)$
	Chenni et al. [97]	$T_{PV}=0.943T_a+0.028G_T-1.528V_w+4.3$
	Mondol et al. [91]	$T_{PV}=T_a+0.031G_{T }end$ $T_{PV}=T_a+0.031G_T-0.058$
	Faiman [98]	$T_{PV}=T_a+{\displaystyle \frac{G_T}{h}}{h=U}_0+U_1\times v$
	Skoplaki et al. (I) [99]	$T_{PV}=T_a+{\displaystyle \frac{0.25}{5.7+3.8V_w}}{G}_T$
	Skoplaki et al. (II) [99]	$T_{PV}=T_a+{\displaystyle \frac{0.32}{8.91+2V_w}}{G}_T$
	Sandia [94]	$T_{PV}=T_a+G_T{e}^{{(a+bV}_w)}$
	Mattei et al. [100]	$T_{PV}={\displaystyle \frac{{h\times T}_a+G_T\times \left[\alpha \tau -\eta \times \left(1+{\gamma }_T\times T_{a,STC}\right)\right]}{h-\left({\gamma }_T\times \eta \times G_T\right)}}$ ${h=u}_0+u_1\times v$
2010–2020	Mazuthik [101]	$T_{PV}={0943T}_a+0.0195G_T-1.528V_w+03529$
	Ren et al. [102]	$T_{PV}=T_a+\left[{\displaystyle \frac{\alpha \tau \times G_T\times \left(1-\eta \right)}{h}}\right]$ ${h=u}_0+u_1\times v$
	Segado et al. [103]	$T_{PV}=T_a+0.022G_T(1+0.009T_a)\times (1-0.063\times v)$
	Kamuyu et al. [92]	$T_{PV}={09458T}_a+0.0215G_T-1.2376V_w+2.0458$
	Duffie end Beckman [47]	$T_c=T_a+\left({\displaystyle \frac{h_{NOCT}}{h}}\right){\displaystyle \frac{G_T}{G_{NOCT}}} \left(T_{NOCT}-T_a^{NOCT}\right)$ ${h=u}_0+u_1\times v$
	Jacques [82]	$T_{PV}=T_a+\left[{\displaystyle \frac{\alpha \tau \times G_T\times \left(1-\eta \right)}{2h}}\right]$ ${h=u}_0+u_1\times v$
	PVSyst [104]	$T_{PV}=T_a+G_T{\displaystyle \frac{\alpha (1-{\eta }_m)}{u_0+u_1\times v}}$

shows different thermal models for treating module temperature variation.

3.4. Experimental Studies

Temperature fluctuations have a significant effect on output parameters [17,105]. Experimental studies that have been conducted demonstrate this dependence, such as the following:

An experimental and simulative study conducted in Malaysia, with a monocrystalline panel under constant irradiation of 458.2 W/m² with an operating temperature between 25° and 60°, proved that the reduction in the energy gap in the solar cell is a consequence of the increase in temperature and affects the electrical output parameters [106]. The study shows that an increase in temperature linearly reduces Pmax and V_OC causes a slight increase in ISC, with temperatures between 25° and 35 °C being the best for solar cell performance [106].

Another similar study was conducted in Malaysia by using the PVsyst software to evaluate the design of the output parameters. In the experimental part, the PROVA 200 analyser was used to measure and record the electrical parameters of the module, with sensors on the rear side to record the average temperature and a FLIR thermal camera on the front side to capture the temperature distribution. In both methods, it was concluded that with an increase in temperature, even with an increase in output current, there was no efficient production of output power due to the reduction in voltage, which caused the quality of the operation to be increasingly minimal [107].

The effect of temperature on the efficiency of the photovoltaic module was also investigated under climatic conditions in Turkey, where the photovoltaic module was placed inside a closed glass chamber, with temperatures fixed at four values using an electric heater and a vapour compression refrigeration cycle system coupled to a PID control mechanism to maintain the desired temperatures. The results obtained experimentally in this configuration based on several tests, regardless of the variation in the zenith angle, conclude that as the temperature increases, the efficiency of the photovoltaic module decreases, affecting the electrical output parameters [108].

Ebhota, W. S. and Tabakov, P.Y. [109] used an ambient temperature range between −10 °C and 50 °C with intervals of 5 °C to analyse the influence on the performance of a photovoltaic system, taking into account c-Si and CIGs technologies. The specialised software tool PVsyst was used in the design and simulation of the 6 kW rooftop system, which was subjected to the same conditions. The results showed that, in all three technologies, performance is inversely proportional to ambient temperature and, at 50 °C, CIGs modules achieved higher temperatures compared to Si-mono and Si-poly technologies [109]. Although CIGs modules had a higher temperature, lower module losses were recorded, which shows that they perform better when compared to mono-Si and poly-Si technologies.

It has been estimated that the efficiency of silicon cells decreases by approximately 0.4% [110], 0.5% to 0.65% [111,112], for each increase in degree Celsius [110]. This temperature sensitivity was confirmed in a study by Chander et al., with silicon cells in series and parallel configurations showing significant variations in performance with changes in temperature, in accordance with Kirchhoff’s laws [113]. Furthermore, Ukwenya et al. highlight in their study that the performance of perovskite cells can be optimised by the operating temperature, with simulation results showing a drop in performance at high temperatures [111].

In a study by Garg and Arun, they detected an increase in energy yield with increasing temperature, justified by certain climatic conditions where high temperatures can have a positive impact on overall performance [114]. The impact of climatic conditions on solar cell performance beyond temperature has been extensively studied. The interaction between temperature, radiation, and other environmental factors further complicates the issue of solar cell performance.

Experimental research has shown that performance can also vary depending on the composition of the materials and the design of the cells. Nowsherwan et al. point out that incorporating hole transport materials into organic solar cells can optimise performance under different temperatures [115]. The study by Kumar et al. reinforces the idea that as the surface temperature of photovoltaic modules increases, there is a noticeable drop in their performance, demonstrating the importance of thermal management in solar photovoltaic systems [116].

4. Effect of Solar Radiation on the Performance of Solar Modules

Solar radiation is a critical factor that directly influences the performance of photovoltaic technologies, affecting their energy production efficiency. The intensity and type of solar radiation are related to electricity production in solar cells. Higher intensity is related to the output power in photovoltaic solar technologies, but with a greater impact on the current produced, as it has a minimal impact on voltage [117]. There is a direct proportional relationship between solar radiation and output current, as well as in the efficiency of solar panels, whereby an increase in solar radiation causes an increase in output current, improving its efficiency. Conversely, this increase in radiation is followed by an increase in the temperature of the photovoltaic cell, causing a negative effect on the parameters [118]. Abdel-Aziz et al. found that intense solar radiation increases cell temperature, affecting energy conversion efficiency [119].

The panels are tested to determine their maximum efficiency under standard conditions (STC) with an irradiance of 1000 W/m² at a temperature of 25 °C and AM 1.5 [120]. However, in reality, there are often deviations from these standards due to adverse environmental conditions and the location in which the panels are operated, influencing their conversion efficiency.

Existing solar technologies react differently to the wavelengths of the solar spectrum. For example, Hudisteanu et al., in their research, conclude that monocrystalline silicon cell technology performs better than polycrystalline technology because of its higher performance across a broader spectrum of sunlight [121]. Solar photovoltaic production also depends on the spectral distribution of radiation, which can vary depending on geographical location, time of year, and atmospheric conditions [122]. Knowledge of spectral distribution can contribute to improving the design of photovoltaic systems, allowing manufacturers to select materials with the capacity to maximise the capture of available solar radiation.

Recent photovoltaic solar system technologies rely on the photoconductive effect in semiconductor materials to convert solar energy into electrical energy, which is significantly affected by the type and intensity of solar radiation they receive [123,124,125]. Understanding the differences between the solar radiation that reaches terrestrial surfaces, mainly direct and diffuse radiation, has a major influence on the optimisation of solar systems, as both affect the efficiency of solar panels.

When solar radiation reaches the Earth’s atmosphere, part of its incident energy is removed by scattering or absorption [111]. The light that travels in a straight line from the sun to the solar panel without being scattered or absorbed by the atmosphere is called direct radiation, while diffuse radiation is the radiation received from the sun after its direction has been altered by scattering through the atmosphere, resulting in a soft and uniform distribution of light [47]. To achieve high efficiency in photovoltaic solar panels, direct solar radiation is vital, as it contributes mainly to the energy that photovoltaic cells need to convert into electricity.

Direct radiation is most effective when solar panels are oriented towards the sun, as they maximise the amount of energy captured and operate more efficiently if they receive direct sunlight throughout the day [126,127]. Furthermore, Diez et al. point out that choosing an ideal angle of inclination for the panels significantly improves their performance by maximising the capture of direct solar radiation [128], since the angle at which sunlight hits the solar panels significantly affects the intensity of the direct radiation received. And with the incorporation of solar trackers, the amount of direct solar radiation can be increased, boosting their overall energy conversion efficiency [129].

The role of direct solar radiation goes beyond simple exposure; it also interacts with parameters such as temperature and configuration to affect the output of the photovoltaic module [130]. The amount of solar radiation received is in line with the progress of new solar photovoltaic technologies, increasing their energy conversion rate. This is supported by recent technologies that use optical devices in smaller, high-efficiency solar cells to concentrate sunlight, which increases the density of direct solar radiation and can influence conversion efficiency that exceeds that of conventional solar technologies by a factor of several times [127].

Optimising exposure to direct solar radiation is a fundamental principle based on the operational dynamics of photovoltaic technologies. Several studies encourage the integration of solar-tracking technologies and ideal angles in more advanced systems in order to maximise the capture of direct solar radiation, as this is fundamental to improving the short-term performance and long-term sustainability of these technologies.

Unlike direct radiation, diffused solar radiation is the result of scattering by molecules and particles in the atmosphere. It is distributed more evenly and can illuminate panels from all directions, making it ideal in cloudy or urban environments where direct solar radiation is obstructed by buildings [131]. Kumar et al. indicate in their research that although diffuse radiation normally contributes less to overall energy conversion than direct radiation, it is essential for sustaining a more consistent energy supply, particularly as direct solar radiation fluctuates [132]. Buildings equipped with solar photovoltaic systems integrated into their construction could, in a way, benefit from the use of diffuse radiation through their facades and panel materials [133].

The interaction between direct and diffuse radiation contributes to the overall energy yield in solar systems. This can be seen in systems that use bifacial solar panels because they capture light on both sides, as they are designed to use both types of radiation in a more optimised way. These types of panels improve overall efficiency by capturing diffuse radiation reflected by the ground and other surrounding surfaces [134]. Optimisation to maximise exposure to both types of radiation can be achieved by choosing the ideal angle of inclination for the solar panels, as different angles favour direct light at a certain time of day while also capturing diffuse radiation throughout the day [135].

The effects discussed show that photovoltaic systems require more careful consideration when exposed to the surrounding physical environment. At the same time, the integration of advanced modelling techniques is advocated to predict how solar radiation interacts with different installation layouts, enabling good design strategies for the implementation of photovoltaic systems [136].

Solar Radiation Estimation Models

Measuring solar radiation is extremely important due to the various applications of the information. To design a system that uses solar energy, you need extensive knowledge about the capacity available in a given region and the amount that reaches a given surface, which is possible through long-term measurements. However, due to the costs involved in maintaining and calibrating the measuring devices, several studies have opted to develop estimation methods using various factors.

Empirical models are based on astronomical, geographical, physical, and meteorological factors [108]. In solar systems, empirical models for estimating solar radiation correlate with meteorological factors [137] and, depending on the input parameters, can be grouped into models based on sunlight, temperature, cloud cover, and other meteorological parameters [137,138]. Notwithstanding these, there are those based on the day of the year [139]. The use of parameters in combination to create models makes correlation difficult, but in some cases it is possible [140].

Table 3. Empirical models for estimating solar radiation for solar systems.

Models	Authors/Reference	Model Equation	Features/Limitations
Based on sunlight	Angstrom [141]	${\displaystyle \frac{H}{H_C}}=\left[a+b\left({\displaystyle \frac{S}{S_o}}\right)\right]$	It is a linear relationship between the average monthly–daily radiation ratio and the clear day radiation at the location and the insolation rate.
	Angstrom and Prescott [137]	${\displaystyle \frac{H}{H_o}}=\left[a+b\left({\displaystyle \frac{S}{S_o}}\right)\right]$	Based on linear regression, it is useful in locations with little data and dependent on the quality of the insolation period, requiring calibration of coefficients on site for greater accuracy and less efficient on cloudy days.
	Ögelman et al. [142]	${\displaystyle \frac{H}{H_o}}=a+b\left({\displaystyle \frac{S}{S_o}}\right)+c{\left({\displaystyle \frac{S}{S_o}}\right)}^2$	It incorporates a quadratic structure in the insolation ratio, which facilitates the adjustment of real data, basically where the relationship between the insolation duration and radiation is not linear, but requires calibration with local meteorological data through statistical regression.
	Glower and McCulloch [143]	${\displaystyle \frac{H}{H_o}}=a\cos \phi +b\left({\displaystyle \frac{S}{S_o}}\right)$	It is a parameterisation that incorporates the influence of the latitude of the location and the duration of insolation to improve accuracy, basically in diverse topographical areas and atmospheric conditions.
	Coppolino [144]	${\displaystyle \frac{H}{H_o}}=\mathrm{e}\mathrm{x}\mathrm{p}(a){\left({\displaystyle \frac{S}{S_o}}\right)}^b$	An exponential power law dependence between normalised solar radiation and relative duration of insolation, which is used on horizontal surfaces, where the constants are adjusted by the least squares of the local meteorological data.
	Ampratwum and Dorvlo [145]	${\displaystyle \frac{H}{H_o}}=a+b\times log\left({\displaystyle \frac{S}{S_o}}\right)$	Logarithmic transformation allows working with large variations in solar radiation data, making it perfect for data modelling. When the insolation period increases, the logarithmic transformation of the insolation ratio favours the capture of decreasing returns in the increase in radiation.
Based on temperature	Bristow and Campbell [146]	${\displaystyle \frac{H}{H_o}}=a\left[1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-b{∆T}^C\right)\right]$	It explores the temperature range of the time of day and the intensity of the radiation reaching the surface.
	Hargreaves [147]	${\displaystyle \frac{H}{H_o}}=a\sqrt{T_{max}-T_{min}}$	It uses daily temperature extremes correlated with solar radiation, requiring the coefficient to be calibrated on site and in areas where there are significant atmospheric changes so it can be less efficient.
	Annandale et al. [148,149]	${\displaystyle \frac{H}{H_o}}=a\left(1+2.7\times {10}^{-5}Z\right)\left(\sqrt{T_{max}-T_{min}} \right)$	It integrates the effect of reduced altitude and atmospheric thickness into the Hargreaves–Samani model, which makes it crucial for mountainous regions and the intrinsic dependence of temperature extremes on radiation estimation.
	Allen [150]	${\displaystyle \frac{H}{H_o}}=k_r\sqrt{T_{max}-T_{min}}$	It considers Kr as a function of altitude and clarifies the effect of elevation on the volumetric heat capacity of the atmosphere.
	Thornton and Running [151]	${\displaystyle \frac{H}{H_o}}={\tau }_{t, max}.{\tau }_{f,max}$	Based on the Bristow–Campbell model, it uses the daily and monthly temperature range to obtain the atmospheric transmissivity coefficient.
	Chen et al. [152]	${\displaystyle \frac{H}{H_o}}=a \mathrm{l}\mathrm{n}(T_{max}-T_{min})+\mathrm{b}$	Based on the regression of radiation and temperature variations, it incorporates the logarithmic function of the daily temperature range to reflect the effects of solar radiation on temperature change and, because it excludes other environmental factors, makes it less accurate in certain regions.
	Li et al. [153]	${\displaystyle \frac{H}{H_o}}=(a\times T_{max}+b\times T_{min})+c$	It adopts the coefficient of the Hargreaves and Samani model as a linear function of the average temperature in the modified Chen model and performs best in regions where the diurnal temperature range correlates reliably with solar radiation.
Based on Cloud Cover	Badeseu [154]	${\displaystyle \frac{H}{H_o}}=a+bC$ ${\displaystyle \frac{H}{H_o}}=a+bC+c{C}^2$ ${\displaystyle \frac{H}{H_o}}=a+bC+c{C}^2+c{C}^3$	It introduces cloud cover and is based on the brightness of the sky to estimate radiation on a horizontal surface; and in the situation where unusual weather conditions are encountered, it becomes less reliable and proposes some correlations to be more flexible in matching solar radiation data.
	Black [155]	${\displaystyle \frac{H}{H_o}}=a+bC+c{C}^2$	It facilitates more flexible arrangements by including quadratic terms in cloudiness or insolation, and is useful in locations with variable cloud cover.
	Angstrom and Savinov [156]	${\displaystyle \frac{H}{H_o}}=\left[1-(1-k)\right]C$	It relates average cloudiness to global solar radiation by applying the transmission of radiation inside the clouds, depending on latitude, and performs best in regions with a stable climate.
Based on other parameters	Swartman and Ogunlade [157]	${\displaystyle \frac{H}{H_o}}=a{\left({\displaystyle \frac{S}{S_o}}\right)}^{b}R{H}^c$	The non-linear model is more flexible than the linear model when it comes to adapting to changing environmental situations, making it easier to incorporate local climatic conditions into the estimation of solar radiation and is very useful in regions where fluctuations in relative humidity play a role.
		${\displaystyle \frac{H}{H_o}}=a+b \left({\displaystyle \frac{S}{S_o}}\right)+cRH$
	Hunt et al. [158]	$H=a(T_{max}-T_{min}{)}^{0.5}{H}_o+b{T}_{max}+cP+d{P}^2+e$	Multivariate and more comprehensive, it allows for the influence of precipitation and considers the combination of meteorological parameters that interfere with solar radiation.
	Garg and Garg [159]	${\displaystyle \frac{H}{H_o}}=a+b \left({\displaystyle \frac{S}{S_o}}\right)+cw$ $w=0.0049RH\left[{\displaystyle \frac{\mathrm{e}\mathrm{x}\mathrm{p}(26.23-5416/T_k}{T_k}}\right]$	They present a double linear relationship for estimating the average daily–monthly global solar radiation, which requires the coefficients to be calibrated on site.

shows the empirical models for estimating solar radiation for solar systems.

5. Interaction Between Temperature and Solar Radiation and Their Long-Term Effects

The interaction between solar radiation and temperature has a significant impact on the performance of solar systems installed in various regions of the world, which are influenced by different meteorological and environmental conditions. The sensitivity of solar technologies to temperature is particularly pronounced when high levels of solar radiation are recorded, which can lead to efficiency losses due to increased heat. The increase in open-circuit voltage and short-circuit current is caused by increased solar radiation under variable environmental conditions, which can create fluctuations in maximum output power (Pmax) [160]. However, optimal performance is achieved when solar radiation reaches its peak and the temperature on the surface of the solar panels remains low [161,162].

The performance of solar photovoltaic technologies in tropical regions, due to high temperatures and radiation levels, can deteriorate more easily when compared to temperate regions [163]. In Africa, where the climate is quite turbulent, ranging from arid regions to tropical zones, the impact of solar radiation and temperature is visible in solar systems. In these regions, the increase in extreme temperatures, exacerbated by climate change, poses challenges for the conversion efficiency of photovoltaic systems [164].

Hudisteanu et al., in an experimental study in Asia with monocrystalline and polycrystalline panels under controlled conditions, demonstrated that high operating temperatures negatively influence open-circuit voltage, reducing conversion efficiency even in situations of high irradiance [121]. In a seasonal study, it was shown that solar radiation, even though it is the biggest driver of solar production, when combined with high temperatures significantly influences efficiency [165]. Choo and Wei found that solar panels can experience a drop of about 7.5% to 22.5% in their conversion efficiency rate under conditions of excessive heat during peak solar hours [166].

For Europe, the interaction between temperature and radiation, divided by geographical and climatic variety, is more complex. The performance of solar technologies is related to the harmony of parameters such as solar radiation and temperature. Some regions benefit from high solar irradiance combined with relatively moderate temperatures, leading to ideal operating conditions, while other regions with high irradiance and temperature may experience drops in efficiency, requiring specific models for performance [61,167]. For silicon panels, when there is an increase in temperature, their efficiency decreases when compared to other technologies under the same conditions because of the specific thermal sensitivity that characterises them [168].

Zhang Mingzhu, Liu Wanfu, and Qi Wuqin [165] conducted a study on the impact of two simultaneous factors, namely temperature and radiation, on photovoltaic energy production, based on a 1 kW independent photovoltaic production system installed at Tianjin University of Commerce over a period of one week. Data was recorded in two ways, firstly, using an air temperature metre and a TES-1333R Solar Power Metre for radiation, and secondly, using averages obtained from the Meteorological Data Centre. Based on physical systems and experimental values evaluated in SPSS and DPS and the multiple non-linear regression analysis model, the results show that when the factors are combined, there is a proportional trend towards higher energy production, which differs when both factors diverge, especially when low radiation conditions are observed. This reveals that there are optimal maximums for both in photovoltaic energy production.

Bhavani, Munipally et al. [167] conducted a simulated study in MATLAB with a production of 100 kW, which aimed to estimate the inverter efficiency through the effects of solar temperature and photovoltaic radiation in different climatic seasons in an on-grid system. Overall losses were obtained through inverter efficiency, where it was possible to verify the waveforms produced from the inverter’s efficiency, which reflected the variation in irradiation and temperature at the inverter’s output in the on-grid system. When the ambient temperature was 47 °C and irradiance reached 863.5 W/m², the inverter’s energy conversion capacity was 0.06%, with inverter efficiency falling to 3.8%, showing in this case that its efficiency in summer decreases and only increases slightly with the increase in irradiance.

Studies show that the combined effects of temperature and solar radiation are multifaceted, leading us to develop innovative techniques to integrate into photovoltaic solar technologies in order to control or regulate adverse environmental fluctuations, so as to maintain optimal operating standards.

5.1. I–V Curve Under Different Temperature and Irradiation Conditions

Photovoltaic solar systems can be characterised by the current and voltage (I–V) curves they generate, which are severely influenced by temperature and solar radiation conditions. For this reason, it is necessary to understand the extent to which these parameters affect the performance of photovoltaic solar systems in order to optimise their design.

Temperature affects the I–V characteristics of photovoltaic solar cells, and according to Coftas et al., the open-circuit voltage (Voc) decreases with increasing temperature, as it is completely associated with the thermal sensitivity of the energy gap, which decreases with increasing temperature, causing the intrinsic concentration of available carriers [61]. When the temperature increases, the short-circuit current (Isc) shows an increasing behaviour, while Voc shows a decreasing behaviour [169]. These effects of temperature on the I–V characteristics are already encoded by manufacturers in the temperature coefficients of the various solar technologies on the market.

Exposure of panels to different levels of irradiation further complicates the I–V relationships in photoconductive materials. I–V curves under different irradiations, for example, may exhibit different behaviour in some ways. Normally, high irradiance generates higher currents, maintaining Voc values until saturation is reached with high light levels [170]. The general shape of the I–V curve can be altered by the fact that irradiance affects the effective series resistance in solar devices, presenting apparent interactions that can somewhat confuse optimal performance analyses.

Studies conducted by He et al. prove that the interaction between temperature and radiation leads to a considerable deviation in the I–V curves of standard test conditions (STC), making it necessary to use high-precision sensors to locate parameters in real operating contexts [171]. The introduction of maximum power point tracking (MPPT) algorithms is crucial in mitigating panel performance losses due to fluctuations in solar radiation and temperature. MPPT technologies continuously regulate the electrical load to satisfy the maximum output power, optimising the system even in periods with unfavourable environmental parameters [172].

Improving knowledge about the correlation between temperature and solar radiation in I–V characteristics in various solar technologies is a crucial factor in optimising solar systems. In practice, it is essential to use on-site measurements that help in the development of I–V curve plots, which facilitate more accurate and rapid recognition of the parameters of a solar panel [173], or even incorporate advanced methods that use non-contact measurement practices for temperature and radiation, enabling real-time monitoring of I–V characteristics [174], resulting in a diagnosis that adjusts for fluctuations in environmental parameters in operational situations.

5.2. Theoretical and Experimental Models

The combination of theoretical and experimental models, or models that integrate theoretical insights with experimental approaches to radiation and temperature applied to photovoltaic systems, is extremely important, as these parameters have a direct influence on efficiency and production. And when incorporated into models that study the variation in temperature resulting from the absorption of solar radiation intensity on different surfaces, they can help monitor and prevent the accuracy of solar photovoltaic system performance. The following

Table 4. Studies with theoretical and experimental models.

Reference	Description
[175]	In this study, the relationship between temperature and solar radiation intensity was examined, emphasising that when solar radiation exceeds 3 kW/m2, it correlates with the performance of the solar system due to the influence of temperature.
[176]	This study discussed the challenges to the efficiency of photovoltaic systems related to radiation intensity and temperature, focusing on MPPT and the issue of shading, using a theoretical model where the results of the Honey Badger Optimisation Algorithm (HBO) are compared with conventional methods such as Perturb and Observe (P&O), Whale Optimisation Algorithm (WOA), and Flying Squirrel Search Optimisation (FSSO), using MATLAB.
[177]	This study estimates the efficiency of solar cells influenced by temperature and solar radiation parameters using computational models with single and double diode configurations.
[178]	This study explains how the variation in the output power of photovoltaic solar panels is affected by the direct relationship between solar radiation intensity and temperature, using the Elman theoretical model.
[179]	They refine thermal management strategies using an experimental and theoretical model through numerical modelling of temperature distributions in photovoltaic modules, validating them with experimental measurements.
[180]	To demonstrate the prediction of production efficiency in photovoltaic systems, an experimental and theoretical method was used, integrating artificial neural networks in modelling the relationship between temperature and solar radiation intensity.
[181]	To evaluate more efficient monitoring of temperature and solar radiation, the authors used interpolation techniques, demonstrating the importance of these parameters in the output power of solar panels.
[182]	To help understand and optimise production in photovoltaic systems, models that integrate variations in solar radiation intensity and cell temperature have been developed to study the dynamics of solar radiation and its impact on photovoltaic solar energy production.
[183]	They emphasise the application of mathematical models to estimate the energy production generated by solar photovoltaic systems, using historical radiation and temperature data, and in a way serving to aid in forecasting.
[184]	They use experimental tests, through modelling the impacts of solar radiation, to assess the performance of photovoltaic modules, adjusting theoretical modelling approaches to prevent photovoltaic solar energy production.

illustrates some studies.

The conclusions of various studies involving model development demonstrate the relevance of applying them to solar technologies for understanding the solar radiation–temperature relationship, as well as for monitoring and preventing performance losses and improving the efficiency of solar systems. Theoretical models play an important role in understanding radiation intensity and its effects on temperature, which in turn highlights the importance of using empirical data to validate predictions, thereby increasing model effectiveness. On the experimental side, the relationship between these parameters can be assessed through direct measurements and statistical regressions. The combination of these models provides a more robust framework for analysing these factors.

One of the most notable trends in the quantitative development of technology, taking crystalline silicon cells as an example and using efficiency as the performance index metric, is that in recent decades there have been major advances in overall performance, representing world market dominance in photovoltaic solar energy. Efficiency in 1978 was around 12% and has evolved to 27.8% today [38].

This significant evolution was due to the introduction of innovations, starting with the Passivated Emitter Rear Cell (PERC) format and Interdigitated Back Contacts (IBCs), which substantially reduce recombination losses [185]. The incorporation of silicon heterojunction further boosted efficiency, and new trends were also applied to cells, such as polycrystalline silicon on oxide (POLO), the ion implantation technique and tunnel oxide passivating contacts (TopCon) [186], and bifacial technology.

Recent studies propose light management and anti-reflective coatings to increase conversion rates, thereby extending the limits of current efficiency [187]. The continuous refinement of production mechanisms, the integration of advanced materials, the improvement of physical properties, and doping make the evolutionary trajectory of silicon technology more robust in the solar photovoltaic energy market.

5.3. Photochemical Degradation and Long-Term Effects of Temperature and Radiation

Long-term performance, efficiency and durabilty of photovoltaic panel technolgies are important issues to address long-term energy policies and economical investments axed on sustainibilty. Therefore, it is necessary to understand the long-term effects of exposure to high temperatures, as they respond differently to thermal stress. Much attention has been given to research highlighting the detrimental impact on the longevity of panels due to their exposure to high temperatures.

The long-term exposure of the panels is contextualised by slow production losses during their operational lifespan, which is generally between 25 and 30 years, caused by continuous thermal stresses, which lead to degradation and manifest themselves in a progressive loss of performance estimated at 0.5 to 1% per year, and which are associated with the cumulative ageing of materials [188]. While short-term exposure of the panels is characterised by infrequent thermal events with immediate consequences related to load peaks or rapid environmental stresses such as temperatures close to the phase transition temperature, which cause very sudden changes and can cause degradation through a single factor, namely an increase in temperature [189]. The degradation of solar panels due to long-term exposure is a cumulative process that requires the entire thermal history, while changes due to short-term exposure are concentrated at the upper end of the temperature distribution curve [189].

The longevity of photovoltaic solar panels is compromised in some ways when they are subjected to high temperatures, aggravating the degradation of materials, such as physical and chemical changes in the module components, such as microcracks, and delamination characterised by loss of adhesion in the encapsulation and rear sheets, which can cause a shorter operational life [24,190,191].

At ambient temperatures of around 85 °C, it can affect output power, reducing it by almost 30% due to the increase in panel temperature [192,193]. Liu et al. suggest that in crystalline silicon panels, a 10 °C increase in operating temperature can lead to a doubling of the degradation rate, due to the critical influence of thermal conditions on solar photovoltaic performance, as well as aggravating the urban heat island effect in large installations [24].

The consequences of high temperatures go beyond direct efficiency losses. The use of materials that mitigate losses, such as phase change materials (PCMs), tend to reduce energy losses caused by high operating temperatures, as they reduce the operating temperature of solar panels by around 7 °C, introducing uniformity in cell temperature [194].

The impact of solar radiation on the photochemical degradation of solar panels is a constant concern for researchers, as it is a decisive factor in the longevity and efficiency of photovoltaic solar systems. The photochemical degradation of solar panels is understood as the deterioration of materials caused by chemical reactions induced by the exposure to light, particularly in the presence of ultraviolet (UV) radiation, causing changes in the molecular structure of components [195,196]. In general, this exposure to solar radiation has an impact on photostability, triggering photochemical reactions, altering their photophysical properties and introducing additional traps and recombination sites, leading to a reduction in energy production efficiency over the long term [195,197].

Specific degradation processes may differ due to the various solar technologies used. Organic-based technologies are susceptible to photochemical degradation due to their dependence on organic materials that can undergo bond breaking under high-energy photon irradiation [198]. Manser et al. highlight that panels based on metal halide perovskites are praised for their efficiency but are vulnerable to environmental stress factors, including ultraviolet radiation, heat, and humidity [199]. Similarly, the stability of organic–inorganic hybrid perovskites is compromised by prolonged exposure to light, which can considerably vary their output characteristics, thus affecting their overall performance [200]. This differs from silicon-based technologies, which have different degradation rates, predominantly influenced by environmental factors and installation conditions [201]. Several studies demonstrate the dependence of degradation rates on the light spectrum, operating temperature, and characteristics of the materials used [196], which can vary in the order of average rates of −0.4% till −2% per year, although these may be exacerbated in adverse environmental conditions in different regions [202].

Environmental factors such as temperature fluctuations, humidity, and dust accumulation can exacerbate degradation by ultraviolet rays due to interaction with photochemical degradation. The presence of dust not only reduces the efficiency of the panel by obstructing direct sunlight, but can also cause hot spots, which in turn increase degradation rates when combined with exposure to ultraviolet radiation [203].

The impact of UV radiation on photovoltaic solar panels goes beyond visible degradation; it has notable effects on long-term energy production. There is a need to create strategies to protect against UV-induced degradation, such as the use of nanocomposite coatings (zinc oxide), which have been shown to mitigate the effects of photochemical degradation [204]. Praveena et al. emphasise that the continuous evaluation of emerging technologies and materials is fundamental to maximising the efficiency of solar cells, prolonging their operational life cycle in real-world situations [205].

The degradation discussed from a photochemical perspective helps to improve the resilience of existing solar technologies against environmental stresses, thus ensuring their viability and performance in the short and long term. As argued by Patil et al., degradation significantly influences efficiency and, naturally, overall sustainability when these technologies are subjected to solar radiation over time [206]. Ultimately, progress in solar energy sustainability depends on more comprehensive analyses, considering environmental and economic aspects, to aid decision-making in solar photovoltaic projects [207,208].

6. Technological Perspectives and Mitigating Solutions for the Effects of Temperature and Radiation

To mitigate the effects of temperature and solar radiation intensity on solar photovoltaic systems, it is important to integrate advanced technologies and innovative solutions. Methods such as phase change materials, cooling technologies, coating technologies, bifacial technologies, and other advanced technologies can be used for thermal and radiation management.

Cooling systems can be active or passive [110], which aims to improve the efficiency and performance of photovoltaic systems under high operating temperatures, where the reduction in solar cell temperature through active cooling can be up to 7.5 °C greater than than through passive cooling [110]. Active cooling incorporates mechanical or electrical components to directly remove heat from photovoltaic panels. However, relying on additional energy for these systems can lead to a decrease in overall system efficiency, as the energy required for operation can offset some of the gains obtained through cooling. Hybrid systems that are described use forced ventilation by fans or water to maintain optimal temperatures [209], and can also use residual heat in thermal applications, contributing positively to the overall efficiency of the system if well executed [210].

Systems that use microchannel heat sinks through nanofluids are gaining greater prominence for their thermal management efficiency in photovoltaic systems. Silicon carbide (SiC) nanofluids present better thermal efficiency performance when compared to common coolants such as pure water and aqueous alumina, standing out for their particle type in the heat transfer dynamics in microchannels [211]. This confirms previous studies that show that nanoparticles in nanofluids help reduce thermal resistance by decreasing temperature differences in configurations that use microchannels, improving heat transfer efficiency with fluids by approximately 10% [212].

Systems that use passive cooling generally utilise natural phenomena to improve thermal management, thus avoiding additional energy consumption. These systems use heat sinks, phase change materials, and natural convection [213].

In a comparative analysis, while systems that use active cooling immediately balance the temperature, improving performance, passive cooling stands out for its low operating costs and energy independence. The table below shows several strategies coupled with different technologies to mitigate the effects of temperature and radiation on the performance of photovoltaic systems.

Table 5. Technological strategies and solutions to mitigate the effects of temperature and solar radiation.

Technologies
Technique/Type	Description	Results	Reference
Passive cooling	They use natural convection or radiation, such as fins or reflective materials, for heat dissipation.	They increase efficiency and can reduce operating temperatures, but are less efficient than active systems.	[214,215]
Active cooling	With the aid of water pumps, fans or even evaporative cooling, they actively remove heat from photovoltaic solar modules.	Efficiency and output power in high temperature conditions are improved when cooling begins at the maximum permitted temperature, reducing the temperature by an average of 18.26% and increasing energy production by 10.14% when used in conjunction with reflectors.	[216]
Heat pipe cooling	They are passive devices that use the vapour–liquid phase change process in thermal management, with high thermal conductivity.	Maintains the operating temperatures of photovoltaic systems, leading to improved efficiency even under high radiation rates, and when combined with other technologies, increases thermal management capacity.	[217,218,219]
PV/T hybrid systems	To optimise energy generation, they control the temperature of the cells and convert excess heat into thermal energy through a combination of photovoltaic and thermal systems.	They maintain low temperatures in the cells and simultaneously generate thermal energy, substantially improving electrical efficiency.	[220,221]
Anti-reflective coating	They reduce light reflection on the surface of the cells, increasing absorption and efficiency in the conversion of solar energy.	The application of these coatings on photovoltaic solar panels increases their performance.	[222,223]
Infrared reflective coatings	They act as infrared radiation reflectors, thereby reducing heat build-up and alleviating the drop in efficiency associated with the thermal effect.	These radiative cooling strategies, through these coatings, demonstrate reduced heat loss and longer operational life for the systems, increasing efficiency, especially in high solar irradiance.	[224,225]
Bifacial	They are vertical or inclined bifacial panels that increase the capture of direct or reflected solar radiation from the ground, i.e., from both the front and rear surfaces.	They produce more energy than monofacial panels due to their shape, providing optimal performance in variable irradiation conditions. Their production increases by between 10% and 20% depending on the albedo and angle of inclination, and can reach around 32%.	[226,227]
Bifacial + reflectors	They have different reflector designs incorporated into bifacial modules which direct additional solar radiation to the panels.	They improve energy capture in variable temperature and radiation conditions, increasing the albedo effect, with an increase of around 35% in annual electricity generation when installed in conditions of reflectivity greater than 50% and with a rate of transparent space greater than 30%.	[228,229]
Bifacial with tracking	They adjust the orientation in the sun’s path, maximising sun exposure throughout the day.	In regions with higher albedo, annual production is higher than that of monofacial systems, with a gain of 15% to 25%, minimising losses from the angle of incidence.	[230]

Table 5. Technological strategies and solutions to mitigate the effects of temperature and solar radiation.

Technologies
Technique/Type	Description	Results	Reference
Passive cooling	They use natural convection or radiation, such as fins or reflective materials, for heat dissipation.	They increase efficiency and can reduce operating temperatures, but are less efficient than active systems.	[214,215]
Active cooling	With the aid of water pumps, fans or even evaporative cooling, they actively remove heat from photovoltaic solar modules.	Efficiency and output power in high temperature conditions are improved when cooling begins at the maximum permitted temperature, reducing the temperature by an average of 18.26% and increasing energy production by 10.14% when used in conjunction with reflectors.	[216]
Heat pipe cooling	They are passive devices that use the vapour–liquid phase change process in thermal management, with high thermal conductivity.	Maintains the operating temperatures of photovoltaic systems, leading to improved efficiency even under high radiation rates, and when combined with other technologies, increases thermal management capacity.	[217,218,219]
PV/T hybrid systems	To optimise energy generation, they control the temperature of the cells and convert excess heat into thermal energy through a combination of photovoltaic and thermal systems.	They maintain low temperatures in the cells and simultaneously generate thermal energy, substantially improving electrical efficiency.	[220,221]
Anti-reflective coating	They reduce light reflection on the surface of the cells, increasing absorption and efficiency in the conversion of solar energy.	The application of these coatings on photovoltaic solar panels increases their performance.	[222,223]
Infrared reflective coatings	They act as infrared radiation reflectors, thereby reducing heat build-up and alleviating the drop in efficiency associated with the thermal effect.	These radiative cooling strategies, through these coatings, demonstrate reduced heat loss and longer operational life for the systems, increasing efficiency, especially in high solar irradiance.	[224,225]
Bifacial	They are vertical or inclined bifacial panels that increase the capture of direct or reflected solar radiation from the ground, i.e., from both the front and rear surfaces.	They produce more energy than monofacial panels due to their shape, providing optimal performance in variable irradiation conditions. Their production increases by between 10% and 20% depending on the albedo and angle of inclination, and can reach around 32%.	[226,227]
Bifacial + reflectors	They have different reflector designs incorporated into bifacial modules which direct additional solar radiation to the panels.	They improve energy capture in variable temperature and radiation conditions, increasing the albedo effect, with an increase of around 35% in annual electricity generation when installed in conditions of reflectivity greater than 50% and with a rate of transparent space greater than 30%.	[228,229]
Bifacial with tracking	They adjust the orientation in the sun’s path, maximising sun exposure throughout the day.	In regions with higher albedo, annual production is higher than that of monofacial systems, with a gain of 15% to 25%, minimising losses from the angle of incidence.	[230]

The use of technologies that mitigate the effects of temperature and radiation on photovoltaic solar panels, as shown in Table 5, depends on factors such as estimated operating costs, system life, and operating and maintenance requirements, since each of them has different details in terms of application and necessary components. Those that use active cooling techniques have an estimated installation cost of $0.05–0.20/W and a levelised cost of energy (LCOE) of 0.018–0.032 $/kW and require little maintenance, but periodic monitoring. Active cooling systems, on the other hand, require regular equipment maintenance and have an estimated installation cost of 0.15–0.30 $/W and an LCOE of 0.045–0.075 $/kW [231]. In systems with hybrid technology, the installation cost is equal to the LCOE of between 0.025 and 0.040 $/W [231]. In bifacial systems or those associated with reflectors or tracking systems, initial costs are high when compared to cooling systems, and due to the complexity of the mechanical systems, adjustments and inspections must be performed regularly.

Continuous improvement in research to address the performance challenges of solar photovoltaic systems should contribute to the longevity and reliability of these systems, which are subject to a variety of environmental conditions. The integration of bifacial and cooling technologies and other innovative solutions to mitigate the effects of temperature and radiation on solar photovoltaic systems show considerable gains in conversion efficiency and thermal fluctuation management but also require a careful approach due to their particularities in installation and economic viability and long-term maintenance.

7. Discussion and Final Considerations

The performance of photovoltaic solar modules is directly and significantly influenced by environmental factors, particularly photovoltaic converters, which are affected by the relationship between temperature and solar radiation, as they play a key role in energy production and in optimising the energy efficiency of photovoltaic solar systems.

The main catalyst for photovoltaic solar energy production is radiation. It determines the magnitude of the photocurrent and, as a consequence, drives the overall energy production of the entire system [232]. On the other hand, it is known that part of the radiation through the photovoltaic effect serves to convert solar energy into electrical energy, and a large part is converted into thermal energy, contributing to the temperature balance of the surface of the photovoltaic panels, negatively affecting the photoelectric conversion efficiency [233]. Fluctuations in radiation throughout the day lead to intermittent energy production, making it necessary to incorporate dynamic forecasting and analysis models in order to manage the fluctuations that affect solar energy production [234].

However, as the temperature rises, it typically causes a reduction in efficiency of 0.4–0.5% per degree Celsius above 25 °C and in the power output of photovoltaic modules in hotter climates [235]. The operating temperature of the solar module is limited by the balance between the heat generated and the heat lost to the environment [235].

Understanding the relationship between temperature and radiation is essential, as solar photovoltaic technologies perform best under high radiation and moderate temperatures. Optimising the performance of these systems requires a balance between these parameters, introducing intelligent management language with integrated models and real-time monitoring in order to adapt the system to environmental fluctuations. At the same time, new technological approaches and innovative solutions for mitigating the effects of temperature and solar radiation must be taken into account in order to bring to the market systems that are more efficient and resilient to environmental fluctuations, capable of maintaining their performance throughout their useful life cycle.

Limitations in the Literature and Future Perspectives

Despite significant advances in understanding the relationship between solar radiation and temperature, there are several published studies on the effects, but they require more comprehensive exploration. As these are critical parameters that impact the performance of solar modules, they should provide a more detailed approach to the complex and dynamic interaction between them under various environmental conditions. This fact is corroborated by Kotz et al., who provide evidence of continuous changes in temperature fluctuations as a consequence of palpable anthropogenic climate change, which in turn requires discussion through localised assessments [236].

Many studies focus on standard approaches, often overlooking the complex and dynamic interaction between radiation and temperature under different environmental conditions. In turn, future considerations should include the development of research outside the operational scope, aimed at creating increasingly interactive and comprehensive mathematical models with various variables, incorporating the factor of reliability and long-term maintenance, the influence of microclimatic effects on temperature profiles and performance, as well as spectral variations in radiation in field situations in various solar technologies.

Future research should prioritise the development and validation of a coupling index capable of making quantitative evaluations of the joint effect of temperature and solar irradiance on photovoltaic (PV) module performance. Such a metric would provide a rational basis for comparing different technologies, climates, and operating conditions, while also providing a foundation for system-level predictive modelling and optimisation. Meanwhile, research must address the particular challenges facing each photovoltaic route. Even mature crystalline silicon modules require new thermal management approaches, innovative cooling, and improved encapsulant materials, to lessen efficiency losses attributed to heat. CIGS modules could benefit from improved protective and barrier layers in order to buffer against their sensitivity to humidity and thermal variations. The most urgent developments are needed by the perovskite technologies, with priority areas being long-term material stabilisation, scalable encapsulation methods, and compositional engineering in order to withstand joint UV and thermal stress. Beyond these technology-specific developments, overarching innovations in multifunctional materials in the form of nanocomposites and phase-change layers and in standardised long-term tests are essential. Together, these efforts, supported by the development of a tested and validated coupling index, will accelerate innovation, increase robustness, and allow fair comparisons among technologies in support of broad deployment.

There is evidence of success in the development of new materials that are less sensitive to thermal fluctuations, which have a positive impact on conversion efficiency and performance over the long term and in extreme environmental conditions. On the other hand, industries must begin to incorporate these technologies, as well as cooling and maximum power point tracking (MPPT) algorithms, in an integrated manner into solar technologies as a way to reverse the issue of thermal management, which causes significant losses in the long term, degrading and reducing the useful life of the systems. Due to the growing demand for renewable technologies, it is essential for industries to bring together market trends with a view to new innovative technological research that impacts long-term conversion efficiency, and mitigating losses resulting from adverse environmental conditions, preventing premature degradation of modules and maintaining systems operational throughout their life cycle.

8. Conclusions

Photovoltaic (PV) module performance is dynamically regulated by the interaction between solar radiation and temperature, which remain important parameters for system efficiency optimisation and technological advancement. Effective control of these variables entails the integration of predictive modelling into field monitoring systems for the minimization of performance losses, ensuring stable operation.

Several significant challenges still exist in the field: (i) high operating temperatures worsen material degradation and efficiency losses, (ii) ultraviolet-induced photochemical degradation compromises long-term stability, particularly in new PV technologies, (iii) absence of a standard metric for quantifying the combined influence of temperature and irradiance makes inter-study comparison problematic, and (iv) insufficiently standardised long-term test protocols limits confidence in degradation data.

Looking ahead, a quantitative coupling index to integrate performance assessment—a tool we are actively developing in a follow-up study through simulation and validation—must be a research priority going forward. Additional efforts are justified to develop state-of-the-art materials (e.g., nanocomposite coatings, multifunctional encapsulants, and thermal-regulating layers) to withstand coupled stressors, integrate AI-enabled predictive models and digital twins for real-time monitoring, and standardise accelerated testing protocols across technologies. Advances in this direction will increase the competitiveness, lifetime, and sustainability of PV systems for their long-term service to the world’s energy transition.