Creation of a Synthetic Rural Alaskan Microgrid Model

Abstract

Power system models of electric systems are crucial in system planning for operations, economics, and expansion analyses. However, as these models contain critical infrastructure data, they are not publicly available. This poses challenges in future expansion scenarios and evaluating technological advancements in an electric grid. Synthetic models are realistic power system models, both topologically and operationally. However, since the electrical network is typically produced using statistical data and often uses machine learning, it does not contain propriety information. This allows researchers to evaluate system behavior under various operating conditions and as test cases for emerging technologies. These test cases are particularly important in highly evolving electric grids and areas of high renewable energy integration such as Alaska. Currently, no publicly available benchmark power system models of rural Alaskan island microgrids exist. This paper presents a rural Alaskan microgrid synthetic power system model and the methodology adopted to develop the model. The performance of the developed synthetic grid was assessed through steady state and positive-sequence dynamic simulations under various operating conditions.

1. Introduction

Realistic power system benchmark models are critical for evaluating new technologies and controls in electrical grids. Due to electric utility data being Critical Energy Infrastructure Information, there is significant, if not prohibitive, risk for utilities including those in Alaska, to share power system models [1]. In the absence of real utility models, researchers and industry have used benchmark test cases, such as IEEE and CIGRE test cases IEEE 118 and CIGRE (Nordic) 32 [2]. However, most of these test cases are not built on the basis of real power systems nor designed to represent a specific, real power system. The development of synthetic power system test cases has opened the door for realistic representations of systems to more credibly evaluate technologies and strategies while removing confidentiality risks.

Synthetic power system test cases are fictional but realistic power system models. Often leveraging machine learning, synthetic power system test cases use real utility models and data to create transmission and/or distribution electric grids overlaid on geographical footprints [3,4,5,6]. Synthetic power system test cases have been developed to represent large interconnected electrical grids of the continental United States or Europe. Synthetic power system models have been developed for transmission [7] and distribution grids [6] in the U.S. and Europe [3,4,5]. These synthetic power system models have been developed and used to study economic dispatch [8,9], transient stability [10,11,12], load modeling [13,14], and for simulation of interactions with natural gas systems [15] or transportation networks [16].

Some of the regions of the United States with the highest penetrations of inverter-based resources (IBRs) are in the isolated remote microgrids of Alaska [17] and the Hawaiian islands [18]. These permanently islanded power systems exhibit unique network layouts, dynamic stability phenomena, including low inertia and low system strength, and furthermore, since they lack connection to a bulk power system, must internally generate all necessary grid services. These systems have long been of interest to researchers and industry as high impact areas for advancements in IBRs and controls due to high IBR penetration and also high energy burden [19].

In particular, the cost of electricity in rural Alaskan microgrids can exceed USD 1/kWh [17]. Development of synthetic power system test cases for these remote isolated or islanded microgrids can have considerable benefit to both researchers and industry to test proof of concepts and reduce burden and risk on partnering utilities. Recently, a transmission synthetic model of the Hawaiian island of Oahu was developed [7,20]. However, there are no synthetic models or public realistic test cases of the islanded microgrids in Alaska, nor methods or assessment metrics to develop such islanded synthetic microgrid models.

This paper presents a rural Alaskan microgrid synthetic power system model. This synthetic microgrid will increase the ability of researchers and industry to evaluate energy solutions for these types of communities using a synthetic microgrid model that more realistically represents the network and stability issues found in rural Alaskan microgrids than currently available models. The network and steady-state model was developed using data-based methods similar to those used in [3,4,5,6], by using data collected from several isolated microgrids in Alaska. Dynamic models were added for model completeness; however, due to lack of real operational data these dynamic models were based on generic dynamic models that do not necessarily represent the dynamic behavior of these isolated microgrids. The contribution of this paper is the introduction of a new publicly available rural Alaskan microgrid synthetic power system model whose network design and steady-state model parameters represent real Alaskan microgrid characteristics.

2. Rural Alaskan Microgrid Characteristics

Rural Alaskan microgrids have unique characteristics when compared to distribution systems in the contiguous United States. Unlike distribution systems in the contiguous United States, 240 rural Alaskan microgrids are isolated and permanently islanded. Communities are tens to hundreds of miles apart and have small loads (<1 MW peak load), resulting in only a few communities being close enough for connection to each other to be economically viable [21]. Therefore, these systems must provide all the energy requirements for reserves and ancillary services, which is normally provided by the transmission system in the contiguous United States. Examples of some characteristics that are unique to rural Alaskan microgrids include the following: sensitivities to individual loads such as washeterias or ‘laundromats’, the amount of unbalance between phases, and combinations of three and single phase systems.

One of the biggest challenges for rural Alaskan microgrids is the lack of comprehensive system design. Distribution systems in the contiguous United States, particularly newer systems, have had the benefit of planned comprehensive design. Instead, Alaskan microgrids evolve and grow in piece-meal sections as needed with severely limited budgets. These rural Alaskan utilities often start with low budgets, low power levels, and low voltages. Initially, power plants are located in the center of a community, and distribution is limited to single phase lines extending radially to supply customers. This construction method has cost savings benefits but establishes the initial problem of unbalanced phases, which are sometimes severe. Additionally, voltage drop is a common issue in distribution systems due to distribution lines being continually extended with undersized conductors resulting in low voltages. As the community evolves, existing infrastructure is adapted and upgraded. Three-phase distribution lines are constructed as needed when modern larger facilities are constructed. However, the redesign of these distribution systems is limited due to budget constraints, and the inherent issues of imbalance and overload tend to continue for extended periods of time or are simply not resolved.

A rural community with no commercial loads such as fish processing plants or saw mills, generally consists of mostly small single-phase residential loads. However, these communities have several large loads that must be accommodated. Large and important loads include modern K-12 schools, community stores with large refrigerators, and hospitals. The community washeteria or ‘laundromat’ is a daily cyclic load that is planned for power plant operations and dispatch, often requiring additional generators to be turned on at certain times of the day. These larger customers often require three-phase connections, and their location within the existing distribution system determines what amount of additional infrastructure is needed for connection.

Integrating large renewable energy projects into the existing distribution infrastructure also poses challenges to remote Alaskan communities. Often, these resources are located large distances from the power plant, and the required power level to be transferred cannot be supported by any existing distribution lines. Therefore, installation of these projects requires budgeting for new three-phase power lines.

These unique features are important considerations for modeling and analysis and understanding the unique network layout and load driven stability challenges of these systems. The statistics and validation metrics calculated from real Alaskan microgrid data, that are included in this paper, capture many of these characteristics.

3. Rural Alaskan Microgrid Data and Metrics

Traditionally, there was little need to create power system models of small, radial, and diesel generation-based microgrids. Hence, there is limited existing power system data for rural Alaskan microgrids. The need for power system models and analysis has arisen as IBRs have been integrated into these systems. Examples are outlined in [22] of how some of these communities have been on the forefront of integrating wind energy into isolated Alaskan microgrids.

Rural Alaskan microgrid data were collected for several communities, either provided by the local electric utilities or public sources such as the Alaska Energy Authority’s Remote Alaska Communities Energy Efficiency Challenge (RACEE) data [23]. The collected data included power system models in various formats, supervisory control and data acquisition (SCADA) data, one-line diagrams, and generator information.

The compiled data were used to generate microgrid validation metrics, similar to how characteristic and validation metrics for synthetic electric grid models have been derived from other distribution and transmission systems [4,24]. However, due to the unique characteristics of isolated microgrids previously mentioned, some metrics typically used for transmission systems and only some for distribution systems are applicable and necessary for understanding rural Alaskan microgrids. This is despite all Alaskan microgrids only having equipment that is classified as distribution equipment based on voltage. The metrics generated for rural Alaska in this paper have been compared against the metrics from the contiguous United States [4,24] as shown in

Table 1. Synthetic power system model validation metrics comparison between contiguous U.S. and rural Alaska [4,24].

Validation Metric	Contiguous U.S. Criteria	Rural AK Criteria
Percent of substation with buses in kV range	200 kV, 85–100% 201 kV, 7–25%	12.47 kV, 90–100% 24.9 kV, 0–10%
Generation capacity per load	1.2–1.6	Mean: 2.9, Range: 1.5–6.5
Substation with generation	5–25%	12.47 kV, 0.5–35% 24.9 kV, 0–0.5%
Generation capacities	25–200 MW, 40+%, 200+ MW, 5–20%	0.4–2.5 MW, 50+% 2.5+ MW, 5–30%

.

Significant differences are found between the metrics of rural Alaska and that of the contiguous United States, which signifies that synthetic models of the distribution system built for the contiguous United States do not provide a good representation for rural Alaska microgrids. The metrics and methodology used to develop the synthetic Alaskan microgrid model introduced in this paper could be useful for developing additional synthetic models to represent additional rural Alaskan communities.

4. Network Generation

A specific community was selected to provide a realistic layout for the synthetic microgrid network. However, the identity of the selected community used for network layout creation is kept anonymous in this paper for confidentiality reasons. Open access software tools and data were utilized to create the synthetic network of the selected microgrid. The road network was accessed from Open Street Map, a free map tool, while QGIS was utilized for geospatial data including estimation of building size. Publicly available building footprint data from [25] was used to estimate building load. The general procedure of the network generation is outlined here.

4.1. Inputs

The following publicly available data on the selected microgrid were inputs to the network model:

• GIS building data, including estimated building size and location [25];
• Location of city powerhouse;
• Road network [26];
• Estimated load statistics see Section 3;
• General characteristic data, see Section 3, including the following:

  –

  Transformer kVA limits;

  –

  Maximum distance from distribution transformer to load;

  –

  Distribution feeder limits.

4.2. Methods

Building footprints were collected from the USA Structures dataset from [25], and building loads were estimated based on average peak electric demand of houses of various sizes (small, medium, and large) [27]. The building location, square footage, and estimated load were then combined to create a points layer in QGIS, called the ‘Building Layer’. The road network data from Open Street Maps [26], the ‘Road Layer’, was added to the same QGIS project as the Building Layer. A line layer, ‘Driveway Layer’, was then constructed containing a line from each point in the Building Layer to the closest point on the Road Layer. The Road, Driveway, and Building Layers were merged into a single layer, the ‘Road Driveway Building Layer’.

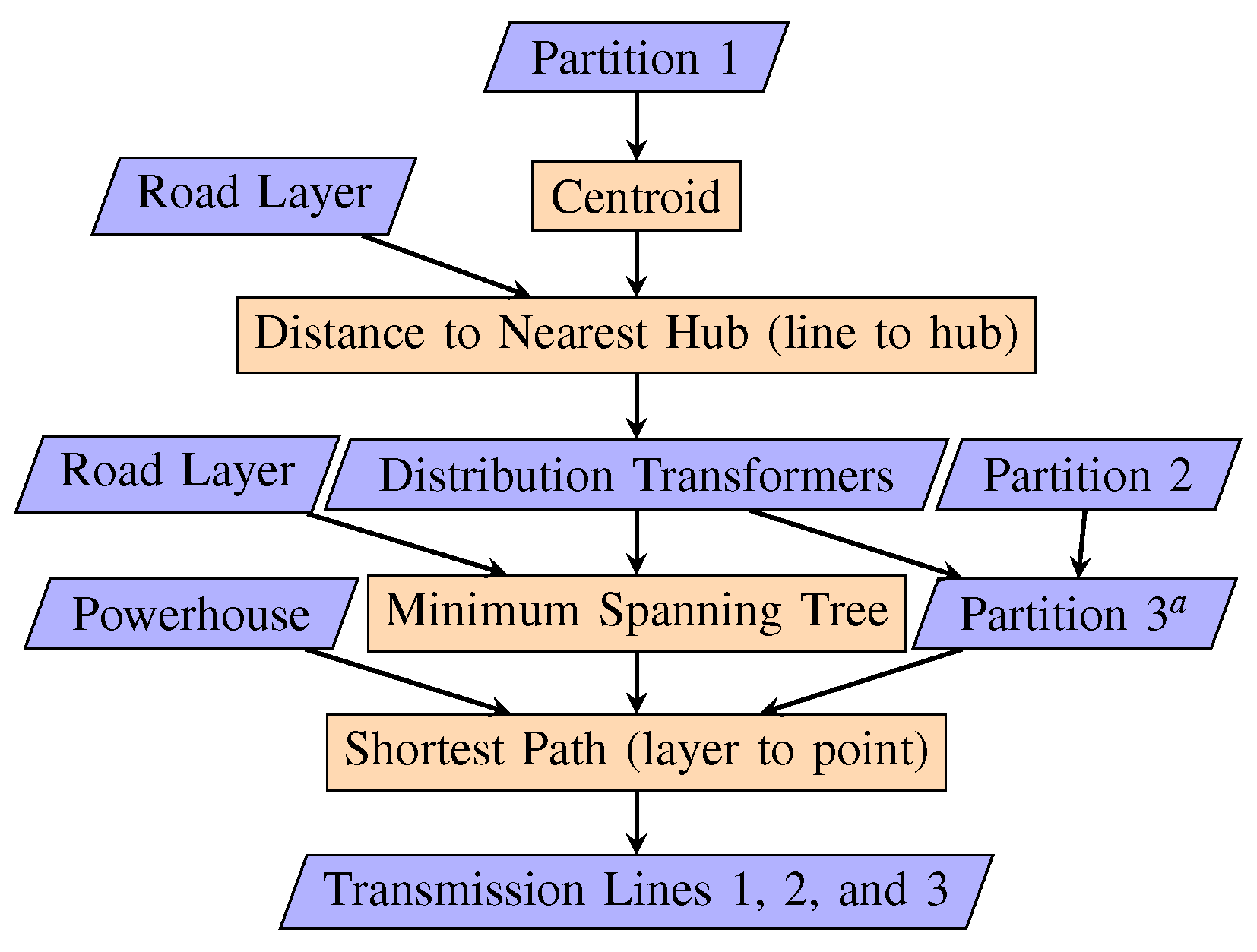
The Python packages, using python version 3.11, GeoPandas [28], Momepy [29], NetworkX [30], and SciPy [31] were implemented to produce two partitions of the Building Layer. A flow diagram illustrating the method is shown in Figure 1, where the ‘SciPy’ node represents two SciPy functions for hierarchical clustering. The first one, ‘linkage’, produces a matrix of clusters and a dendrogram to select the cut height for the next function, ‘fcluster.’ The ‘ward’ method was chosen for linkage [31]. Different cut heights (denoted ‘t’ in SciPy documentation) for fcluster were selected to produce two partitions of the Building Layer. The cut height determines the maximum inter-cluster distance allowed [31]. Partition 1, generated using a cut height of 300 m, was used to place synthetic distribution transformers and assign each building a synthetic transformer. The algorithm was rerun with a cut height of 2.3 km to generate Partition 2. Given the transformer assignments from Partition 1, Partition 2 was used to place single-phase synthetic feeders, which the transformers were assigned to (see Figure 2). The resulting network generated three single-phase feeders that start at the powerhouse and extend along roads. Manual adjustments were included to create the final model (see Section 5).

5. Synthetic Microgrid: Power System Model

The DIgSILENT PowerFactory power system modeling software was utilized to develop a synthetic microgrid model of a remote Alaskan community. The software was selected because of its ability to perform both positive-sequence or root mean square (RMS) and electromagnetic transient (EMT) simulations. The Alaskan microgrid characteristics and metrics served as inputs in determining the appropriate feeder voltage levels, component sizing and configuration, and phase assignments. PowerFactory generic library dynamic models of generators and transformers were used due to the unavailability of datasheets for real Alaskan generators and transformers. The models that best matched the frequency, voltage levels, and power ratings of the generators and transformers found in rural Alaska were selected from these generic library models.

Two load seasons, summer peak (SP) and winter peak (WP), were created as two separate test cases in the model. However, the generators, transformers, lines capacities, and initial system performance were selected based on the WP peak-load scenario as Alaska systems are winter-peaking systems.

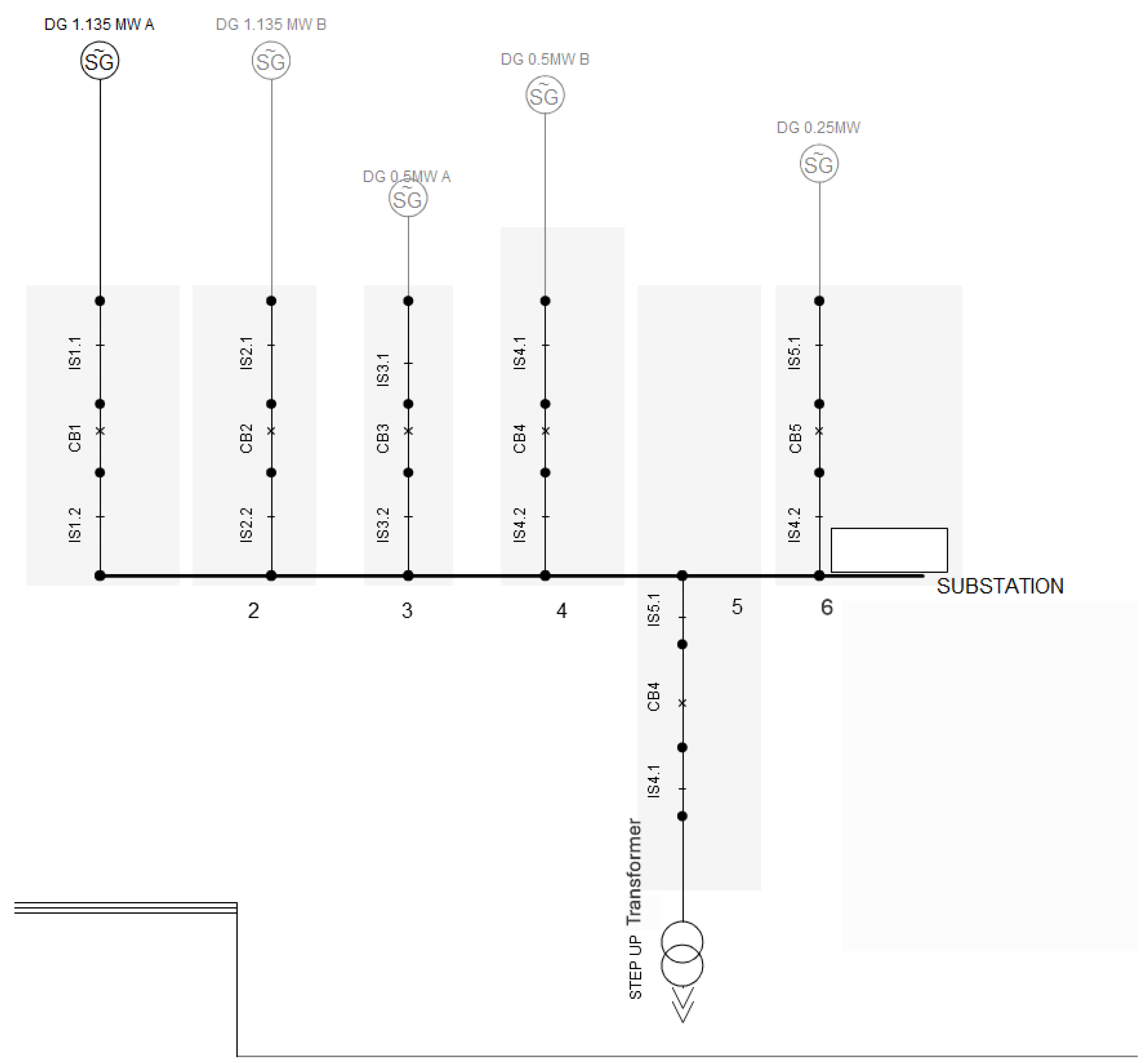
The initial network layout made assumptions on the placement and number of single-phase distribution lines. The final synthetic microgrid model incorporates manual adjustments to the system (based on engineering judgment as described in the next section) and is composed of single- and three-phase feeders. Figure 3 shows the initial and final one-line diagrams of the model.

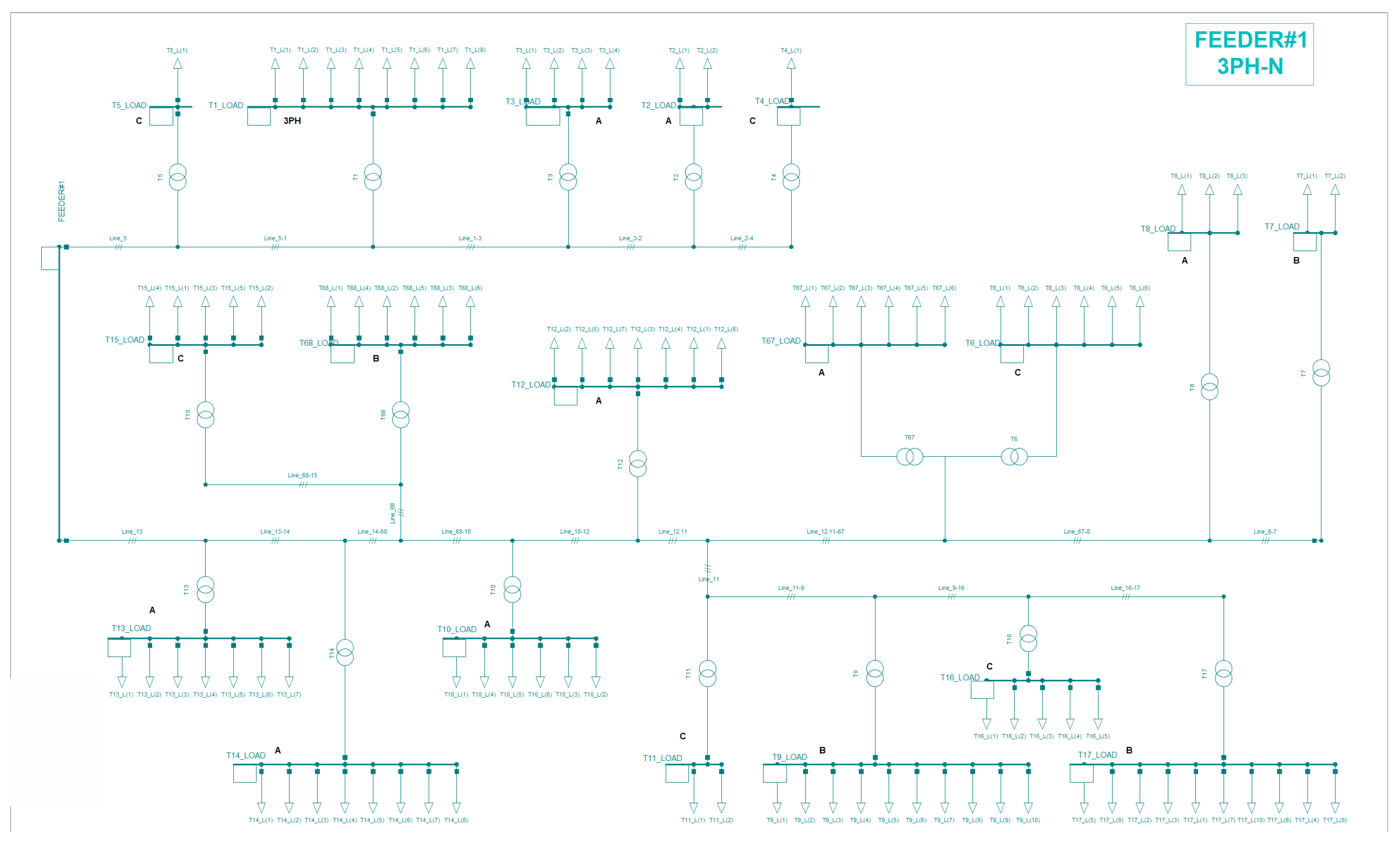
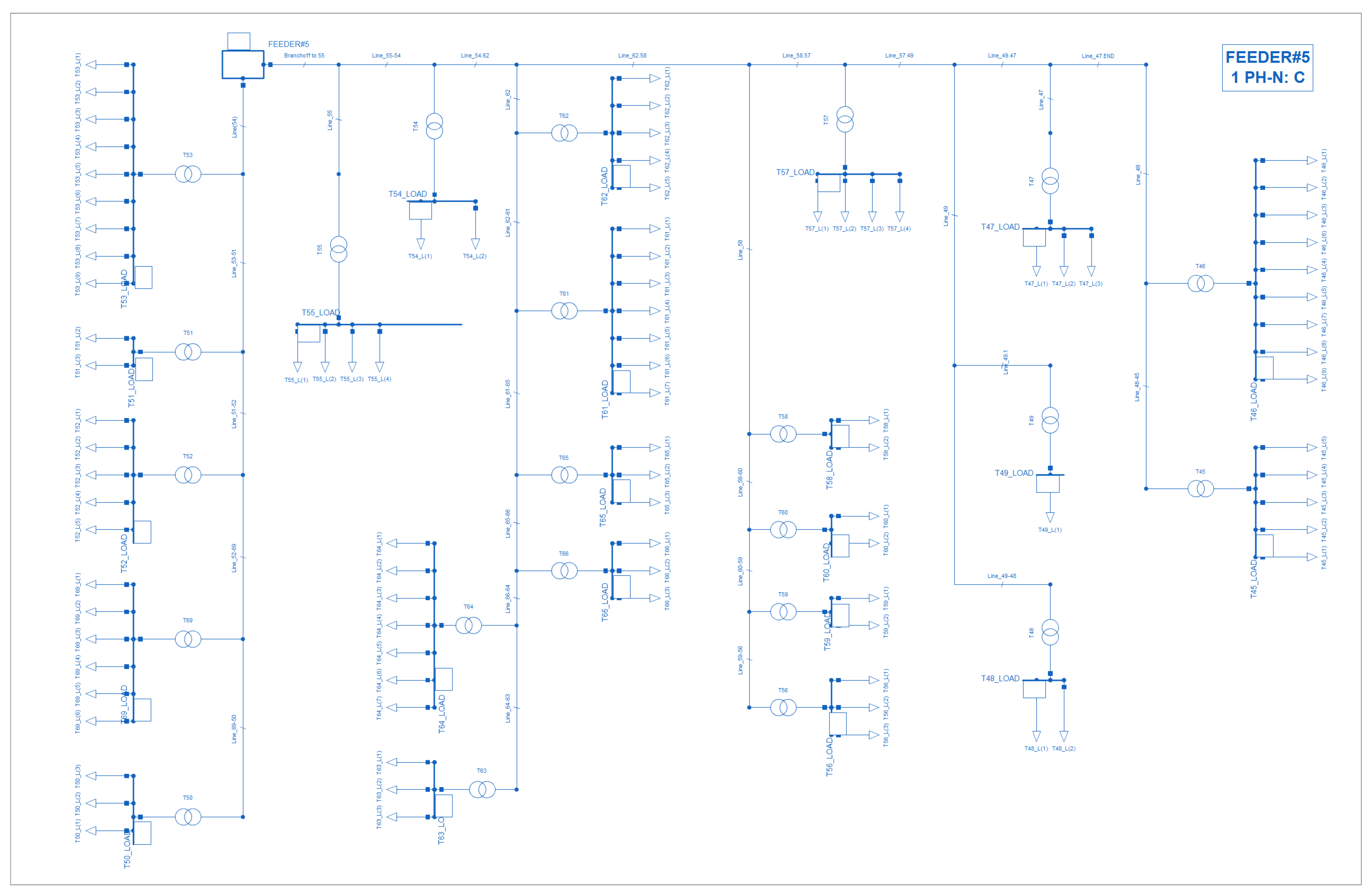
The generation substation and the single- and three-phase feeder diagrams are illustrated in Figure 4, Figure 5 and Figure 6.

The methodology of developing the final synthetic microgrid model is discussed in the following sections.

5.1. Distribution Feeders

All feeder voltages, single and three phase, were set to 12.47 kV line–line. The system was initially configured to contain three feeders, with the original Feeder #2 being a three-phase feeder to serve large motor loads and/or critical loads (e.g., school and hospital) along the path. Due to practical constraints and simplicity, it was deemed more feasible to split Feeder #2 into two primary sections: one north and one south of the powerplant. The south section was converted to the single-phase Feeder #3 (see Figure 3), while the north section includes the three-phase Feeder #2 and single-phase Feeder #4. The three-phase feeder provides power to the three-phase loads as well as single-phase loads along its path, and Feeder #4 branches off the end of Feeder #2. This configuration eliminates the need of longer three-phase sections and additional wires, while also allowing flexibility on phase assignment to Feeders #3 and #4 and the single-phase loads.

In addition, the original Feeder #1, which splits off into two distinct areas and includes the largest single-phase transformers, was converted to three phase due to the feeder containing the largest loads in the system. Transformers above 37.5 kVA were converted to three phase.

The final model contains five feeders: 2 three-phase feeders (Feeders 1 and 2) and 3 single-phase feeders (Feeders 3, 4, 5). See Figure 3 for the comparison of the initial vs. the final model configuration.

5.2. Overhead Lines

Conductors in rural AK microgrids are typically Aluminum Conductor Steel Reinforced (ACSR) and range from #4 AWG to 4/0, with phase and neutral conductors often using the same size. To appropriately size the conductors, the feeder currents were calculated from the estimated loads (ignoring losses). The conductor #4 AWG 7/1 Swanate was selected as the phase and neutral conductors for the feeders. The #4 AWG ampacity was sufficient for the largest estimated feeder current of 29.88 A [32]. Additional consideration of snow and ice loading and accumulation on lines led to the selection of the 7/1 Swanate conductor, which offered a higher rated strength of 2360 lbs compared to the 6/1 Swan conductor’s 1860 lbs [32].

To model the feeders as overhead lines, tower types for the single-phase and three-phase towers were constructed, which included the pole geometry and conductor type parameters. The #4 AWG conductor was modeled as tubular, and the electric parameters from the cable manufacturing company General Cable [33] were utilized. The number of line circuits corresponded to the number of conductors in a feeder: two for the phase-to-neutral (PH-N) and four for the four-wire three-phase-to-neutral (ABC-N) configuration. The line towers were modeled according to the pole specifications outlined in the Rural Utility Service (RUS) electric standards [34], which Alaskan utilities commonly follow. The towers were modeled according to the conductor spacing, utility pole length, and pole settling depth of the standard utility pole assemblies for 12.5 KV/7.2 KV line constructions [34,35]. A single support (A1.1P) and single support on crossarms (C1.11) with post insulators were selected for the single-phase and three-phase standard assemblies, respectively, with pole heights of 40 ft. tall.

5.3. Transformers

Three types of transformers were utilized in the model: a 0.480/12.47 kV step-up transformer to step up the voltage from the generator to the feeder voltages, and the step-down transformers 12.47/0.208 kV for three-phase and 7.2 kV LN/0.24 kV LL split-phase or center-tapped configuration. The distribution transformers were configured to match the nominal service voltage of residential loads on a 120/240 V split-phase load and 208 V for three-phase loads.

The kVA ratings of the distribution transformers were determined by calculating the load current and the primary (HV side) current of the transformers. The load currents and kVA rating of each transformer were calculated from the standard three-phase and single-phase power equations. The size of the generator step-up (GSU) transformers were determined by calculating the root mean square (RMS) current on the HV side of the transformer. Standard transformers with the appropriate voltage and current ratings were then selected [27]. In some cases, the calculated load current, which did not factor no-load losses, was nearly the rated current of a standard transformer. While it is important to consider the losses, Alaska’s cold climate offers some flexibility in overloading conditions. Some rural Alaskan microgrids allow for operation above the rating of transformers during peak winter loads due to increased heat dissipation during extreme cold temperatures. Thus, the standard transformer in such cases were not upgraded and were instead allowed to overload during winter peak-load scenarios.

Table 2. Transformer types and the calculated ratings.

Transformer	kVA Rating	Current Rating (A)	No. of Transformers
Distribution: single phase 12.47/0.24 kV-LL Y/YN	10 15 25 37.5	41.67 62.5 104.2 156.3	28 21 15 4
Distribution: three phase 12.47/0.208 kV-LL D/YN	30 150 75	72.17 360.85 208.19	2 1 1
Substation: three phase 0.48/12.47 kV-LL D/YN	1500	69.45	1

summarizes the number of standard transformers and their full load current for the distribution and GSU transformers. Due to unavailability of transformer datasheets, the smallest 60 Hz PowerFactory template, 30 kVA 13.2/0.22 kV WEG, was implemented for both single- and three-phase distribution transformers. The 1.5 MVA 12/0.44 kV WEG template was used for the generator step-up transformer. The kVA ratings, winding connections, and voltage levels were modified to reflect the parameters in Table 2.

The percent difference between the calculated and power flow current results ranged between 1.61% and 5.76% on the feeders.

5.4. Loads

Buildings were modeled as individual loads with a power factor of 0.95 [36]. The single-phase loads were connected to a 240 V load bus to represent the typical residential voltage of 120/240 split-phase system, while the three-phase loads were connected to 208 V load bus. The total SP and WP loads are summarized in

Table 3. Feeder load during SP and WP and the maximum (WP) feeder current.

Feeder	SP Load (kW)	WP Load (kW)	WP Current (A)
Feeder #1	217.04	365.19	18.04
Feeder #2	131.86	221.87	11.09
Feeder #3	63.78	107.31	15.69
Feeder #4	59.67	100.41	14.68
Feeder #5	121.47	204.39	29.88
Total	593.81	999.17	–

, including the calculated maximum feeder current, ignoring losses, which occurs in the winter.

5.5. System Phase Balancing

Manual phase balancing of feeders and loads was performed to minimize the unbalance experienced by the generator(s). The single-phase feeders were assigned to the following phases: Feeder #1 to phase A, Feeder #2 to phase B, and Feeder #3 to phase C. Single-phase transformers on three-phase feeders were then reassigned phases to balance the system. Load flow analysis was performed to ensure convergence at all feeder scenarios and that load bus voltages remained within 5% of the nominal values.

Table 4. Total load on each phase and total three-phase loads at SP and WP.

Phase	SP (kW)	WP (kW)
A	169.63	257.62
B	138.39	242.52
C	166.95	299.09
Three-phase Load	118.84	199.97
Total Load	593.81	999.17

summarizes the total load for each phase from the single-phase load and the balanced three-phase load, with approximately 18% percent difference between the most lightly and heavily loaded phases. Note that the three-phase loads are recorded separately as they are modeled as balanced, and only the single-phase loads contribute to phase unbalance.

5.6. Generators

To increase resiliency and reliability, it is common and crucial for isolated microgrids to secure multiple backup generators in case of maintenance and unexpected events that disrupt normal operating conditions. Rural Alaskan microgrids employ diesel generators, which are optimized when loaded at 70–100% [37]. Generator sizes were selected to facilitate continuous operation at 80% of individual generator rated capacity.

5.6.1. Generator Sizing

Factors considered in determining the size and number of generators in the model included the SP and WP peak load and a goal of continuous operation at 80% of the generators’ rated capacity. The following conditions were considered in selecting the generator sizes: available generator data, standard generator sizes, and three redundant ways to supply the winter peak load. The final synthetic model included five generators: two 1.135 MW, two 0.5 MW, and one 0.250 MW to satisfy these considerations.

5.6.2. Dynamic Models

The 0.5 MW PowerFactory diesel genset template with the following parameters was used for all generators in the synthetic model: 625 kVA, 0.8 power factor, and 400 kV. The template was modified to reflect the diesel genset parameters employed in an Alaskan microgrid: Y-connected, 0.8 power factor, and 480 V line-line. Based on available data, the inertia constants (H) were adjusted to 0.29 s, 0.188 s, and 0.15 s for the 1135 kW, 500 kW, and 250 kW generators, respectively.

The generator control models represent the controls systems that regulate the generator’s operation. Modeling of the turbine governor and the exciter system is crucial in stability studies of a system [38]. A literature review of various dynamic models for diesel-based generators [39,40,41,42], including default values from software tools such as ANDES [43], NEPLAN [44,45], PowerWorld [46], and DIgSILENT PowerFactory [47] was conducted to determine an appropriate type and range of values for the governor and exciter models [42,43]. Based on the survey, DEGOV1 and EXAC1 were chosen as the governor and the automatic voltage regulator (AVR) models, respectively.

The default PowerFactory values for the exciter were used in the synthetic model, while the default PowerWorld governor values were implemented for the governor. The actuator derivative time constant was changed from PowerWorld’s default value of 0 s to 0.1 s to stabilize the system during dynamic simulations.

5.6.3. Generator Operation

Frequency droop is the ratio of the change in frequency setpoint based on real power output, typically expressed as percent change in frequency for per unit change in load. Frequency droop control, implemented through the generator governor model, allows generator frequencies to deviate from the reference in response to load changes according to their droop settings [38]. The contiguous United States typically employ droop load-sharing between generators, where loads are distributed among generators according to their droop settings, ranging between 3 and 5% [38], resulting in proportional load sharing. A 5% frequency droop was applied to all generators in this model.

A local controller was also implemented to control the voltage setpoint at the generator terminal. Because the generators were designed to operate in droop, the voltage Q-droop local controller was selected, where reactive power was adjusted proportionally according to the specified droop (5%) to keep the local voltage between 0.95 p.u. and 1.05 p.u.

6. Synthetic Microgrid: Performance Assessment

Typically, synthetic models undergo model and operational validations using real system data, to ensure accurate topology and high system fidelity [4,12]. This process provides confidence that study results using synthetic grids represent behaviors and results representative of real systems. However, due to the lack of operational data, it was not possible to validate the dynamic model portion of synthetic model developed in this paper. Instead, a performance assessment of the model was conducted to ensure system stability and robustness and reasonable response. Criteria utilized in other synthetic grids were consulted to evaluate the model’s steady state and dynamic performance.

6.1. Steady State

Steady state load flow analysis was executed to ensure convergence at all feeder combinations while maintaining acceptable voltage limits and reasonable component loading. The following metrics were monitored during the steady state load flow studies in both the SP and WP load scenarios:

• Loading conditions of the network components;
• Voltage profile across the synthetic grid.

Bus voltages conformed to the recommended RUS standard of voltage range between 0.95 and 1.05 per unit [48]. Additional load flow analysis criteria [4] were analyzed for each load scenario.

Table 5. Applicable operational metrics [4] applied to the synthetic model.

Parameter	Exit Target	WP	SP
		(1) 1.135 MW, (1) 250 kW	(1) 500 kW (1) 250 kW
Convergence: No. of Iterations	<20	6	5
Voltage (p.u.)	Min = 0.95 Max = 1.05	Min = 0.96 Max = 1.00	Min = 0.97 Max = 1.02
System losses (%)	<10	9.72	9.98
Overload count	<0	10	0
Undervoltage count	<0	0	0
Overvoltage count	<0	0	0
Transformer loading (%)	0–100	53.3–109.7	16.8–62.6
Voltage unbalance [49] (%)	<3	0.64	0.48

below summarizes the applicable steady state exit criteria [4] and the synthetic model results. As previously discussed, overloading was allowed during WP but was limited to 110%.

6.2. Dynamic Performance

To assess the dynamic performance of the synthetic model, unbalanced RMS dynamic studies were conducted for both WP and SP load scenarios. Power system stability is typically classified into the following buckets: angular, frequency, and voltage stability [12,50,51]. For the developed synthetic microgrid, only frequency and voltage transient operating performance was assessed. The generator rotor angles were monitored to ensure reasonable rotor angle behavior and stabilization following a transient disturbance. The following case studies were considered for the performance assessment:

• Fault disturbance tests: test the dynamic behavior of the grid in response to various fault scenarios;
• Frequency regulation: test grid response to large load variations;
• Voltage regulation: test grid response to the step voltage changes.

Table 6. Dynamic case studies.

Case Study	Objective	Description
1	Fault: single phase-G	Phase A bolted fault at HV side of GSU
2	Fault: two phase	Phase A-B bolted fault at HV side of GSU
3	Fault: three phase	Balanced bolted fault at HV side of GSU
4	Fault: three phase	Z = 0 $\Omega$ with retained voltage of 0% for 120 ms at substation
5	Fault: three phase	Z = 0.058 $\Omega$ with retained voltage of 35% for 480 ms at substation
6	Fault: three phase	Z = 0.21 $\Omega$ with retained voltage of 76% for 1 s at substation
4	Frequency Regulation	Feeder disconnection and reconnection of largest three-phase feeder: Feeder #1
5	Frequency Regulation	Feeder disconnection and reconnection of largest single phase feeder: Feeder #5
6	Voltage Regulation	Step response of ±5%

summarizes the set of case studies carried out for fault, frequency, and voltage regulation. Faults were cleared in 100 ms (6 cycles); variables were ensured to reach steady state following the initial disturbances (e.g., faults) for frequency and voltage regulation.

The following components and variables were monitored during SP and WP loadings to determine system stability under the various system disturbances listed in Table 6:

• RMS phase voltage: magnitude and angle of generation substation and feeder head;
• RMS positive sequence voltage: magnitude of load buses;
• Active Power P, reactive power Q, and internal rotor angle of generators;
• Frequency: As measured at the generation substation and feeder head, which refers to the HV side of the GSU transformer where all but Feeder #4 splits off the substation;
• Current: generators (fault events only).

Generation protection setpoints, including alarm and shutdowns, were used as guidelines to determine the acceptable transient voltage and frequencies of the generators.

Table 7. Example of generator protection system’s voltage and frequency setpoints for a small community.

PEEC Limits	Alarm	Shutdown
Undervoltage	0.9 p.u.; 10 s	0.85 p.u.; 15 s
Overvoltage	1.05 p.u.; 10 s	1.10 p.u.; 10 s
Underfrequency	57 Hz; 10 s	54 Hz; 15 s
Overfrequency	63 Hz; 10 s	66 Hz; 10 s

summarizes the envelope of acceptable frequency and voltage response for the generators that were considered in the dynamic performance of the synthetic model. During faults, generator transient voltages exceeded the limits shown in the table; however, this was expected and only lasted for the fault duration (100 ms). The system was deemed stable when the monitored variables reached steady state, which occurred within 10 s of all simulated disturbances.

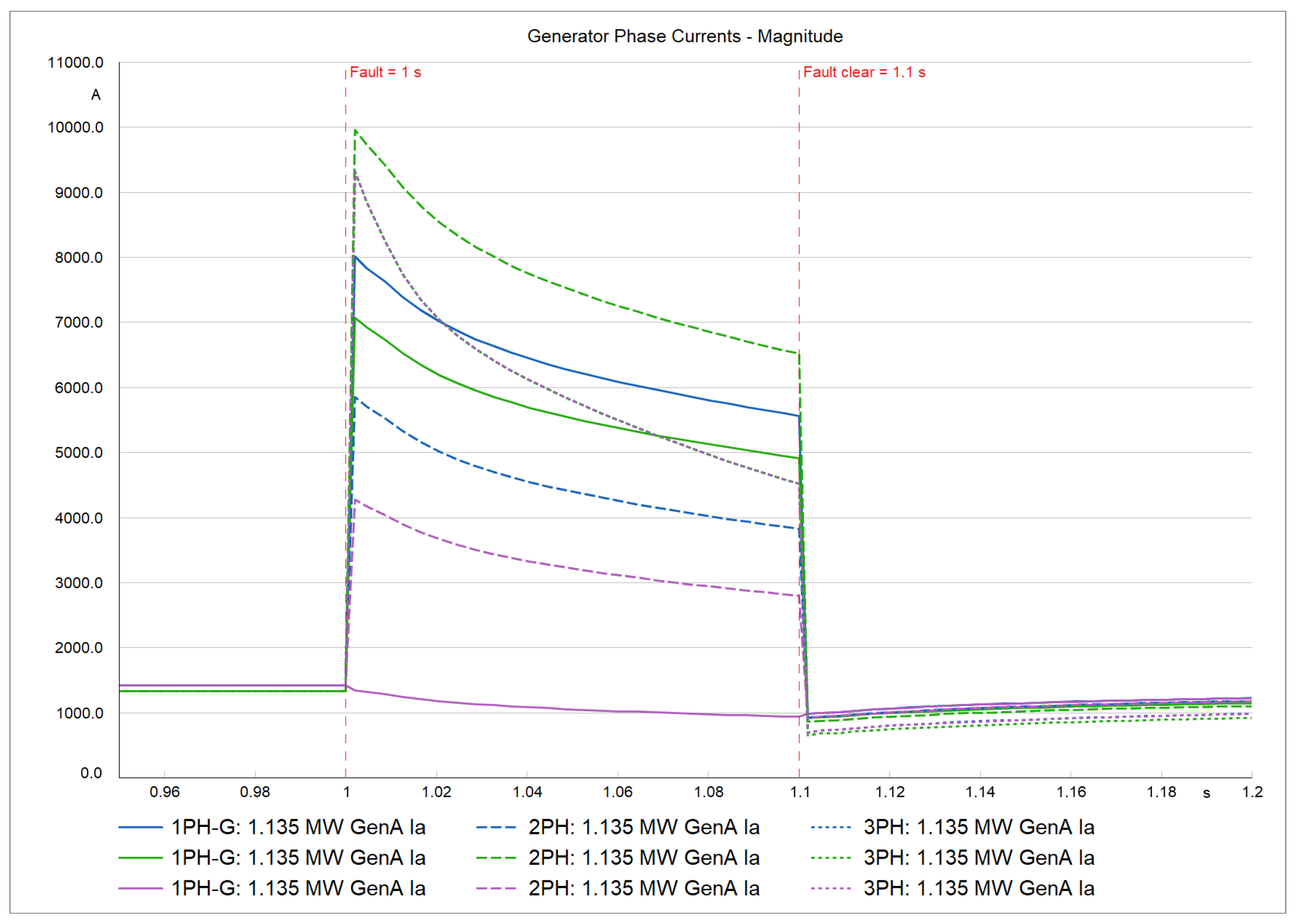
The 1.135 MW generator’s phase currents and voltage magnitudes are illustrated in Figure 7 and Figure 8, respectively, in response to the single-phase, two-phase, and three-phase bolted faults shown in Table 6. Immediately after the fault, the generator current overshoots and voltage dips close to 0.1 p.u., with the most severe cases occurring during a three-phase fault. However, the system was able to quickly recover after the fault was cleared.

Voltage and current waveforms during single-phase, two-phase, and three-phase faults are represented by solid, dashed, and dotted curves, respectively. Phases A, B, and C corresponds to blue, green, and purple curves.

7. Future Work

The developed synthetic model serves as an initial framework to facilitate power system studies of rural Alaskan microgrids without compromising confidential information from power system models. The model provides a much more realistic representation of these systems than currently available benchmark models. However, this is a progressive model and many improvements and future work could be conducted to further increase the model’s fidelity and reliability. This includes validating the model from component modeling to dynamic performance, developing isochronous load-sharing controls, integrating inverter-based resources (IBRs), and tuning controls. As rural microgrid data becomes available to researchers, whether publicly or through increased partnership and collaboration with rural microgrids’ utilities and stakeholders, the model could be further improved. Additionally, future work could include incorporating economic factors into the model to evaluate social and economic impacts.

The following factors are identified for future work using the proposed synthetic model:

• Validation/Benchmarking RMS and EMT models against real Alaskan operational data;
• Isochronous load-sharing for paralleled generators;
• System security measures;
• Controller tuning;
• Integration of IBRs;
• Economic factors.

8. Conclusions

Synthetic grids offer the benefits of allowing researchers to study a realistic power system without the use of real power system models containing critical energy infrastructure information. In this project, publicly available and community-specific data were collected and analyzed to develop a power system metric for remote Alaskan communities and utilize it to construct a realistic, but not actual, model of a selected remote Alaskan microgrid. Several studies such as faults, load steps, and voltage steps were conducted to ensure that the system was resilient under various operating conditions. The model and framework serves as a first step in developing synthetic models of power systems in Alaska. This synthetic microgrid model representing rural Alaskan microgrids can assist researchers answer unique stability and economic questions of Alaska’s rural microgrids and support efforts in reducing electricity costs in Alaska.