The Economic Optimization of a Grid-Connected Hybrid Renewable System with an Electromagnetic Frequency Regulator Using a Genetic Algorithm

Abstract

This paper presents a comprehensive economic optimization of a grid-connected hybrid renewable energy system (HRES) enhanced with an electromagnetic frequency regulator (EFR) to improve frequency stability and provide clean and continuous electricity to the Macau City Campus while reducing dependence on fossil sources. The system includes photovoltaic (PV) arrays, wind turbines, battery storage, EFR, and a backup diesel generator. A genetic algorithm (GA) is employed to optimally size these components with the objective of maximizing the net present value (NPV) over the system’s lifetime. The GA implementation was validated on standard benchmark functions to ensure correctness and was finely tuned for robust convergence. Comprehensive sensitivity analyses of key parameters (discount rate, component costs, resource availability, etc.) were performed to assess solution robustness. The optimized design ($\mathrm{PV}\approx 35\mathrm{kWp}$, $\mathrm{WT}=30\mathrm{kW}$, $\mathrm{ESS}\approx 200\mathrm{kWh}$, and $\mathrm{EFR}=30\mathrm{kW}$) achieves a highly positive net present value of BRL 1.86 M in 2015 values (BRL 3.11 M in 2025) and discounted payback in approximately 9 years. A comparative assessment with the 2015 baseline project revealed up to a 10.1% enhancement in the net present value, underscoring the economic advantages of the optimized design. These results confirm the system’s strong economic viability and environmental benefits, providing a valuable guideline for future grid-connected hybrid energy systems.

1. Introduction

The growth in energy demand, coupled with concerns about sustainability, has significantly boosted the integration of renewable sources into the electricity system. Among the most promising solutions are hybrid systems made up of solar photovoltaic generation, wind power, and battery storage [1,2]. These configurations, known as distributed generation systems, can operate autonomously or be connected to the main electricity grid, promoting greater efficiency and resilience in the supply of electricity. In order for these systems to be technically viable and economically attractive, they must be optimally sized. This means minimizing investment and operating costs, as well as greenhouse gas emissions (such as CO₂) while ensuring high levels of operational reliability. In addition, regulatory policies and charging mechanisms linked to interaction with the electricity grid, such as charging for exported energy, have become integrated components in the energy planning of hybrid systems. This reinforces the importance of broader, integrated, and multi-objective optimization approaches.

Various optimization methods have been used in the literature to achieve this balance, including heuristic algorithms such as PSO (particle swarm optimization), GA (genetic algorithms), and MILP (mixed integer linear programming), as well as specialized computational tools such as HOMER and GAMS. A notable example is the study by Ismail et al. [3], which proposes an optimization model based on genetic algorithms for designing hybrid systems composed of photovoltaic (PV) panels, microturbines (or diesel generators), and battery banks. The study’s aim is to minimize the cost of energy generated (COE), reduce polluting emissions, and ensure a continuous supply to small rural communities located in Palestine. In a similar vein, Yang et al. [4] developed a GA-based optimization model for solar–wind–battery systems, using the annualized cost of the system (ACS) as the economic metric and the loss of load probability (LPSP) as the technical criterion. The actual application of the model to a telecommunications station demonstrated consistent performance throughout the year, with an LPSP of less than 2%, reinforcing the potential of this approach for remote areas. Complementing this panorama, Dufo-López and Bernal-Agustín [5] proposed a multi-objective optimization framework for complex hybrid systems (PV, wind, diesel, hydrogen, and batteries), using the SPEA algorithm to simultaneously minimize total system cost (NPC), $C{O}_2$ emissions, and unserved load (UL). The model generates a set of Pareto solutions, offering the designer flexibility to choose between multiple technically feasible and environmentally sustainable alternatives.

Recently, Paulitschke et al. [6] proposed an optimization model that simultaneously integrates component sizing and energy management control parameters in PV–battery–hydrogen hybrid systems. The study introduces an enhanced particle swarm algorithm (EPSO), capable of dealing with the complexity and non-linearity of the problem, including invalid regions in the search space. Another approach that has been gaining prominence in recent years is the use of artificial intelligence (AI) for dimensioning in hybrid systems. For example, in [7], a new framework for optimal sizing of autonomous hybrid energy systems (photovoltaic, wind, and hydrogen) was proposed. This approach incorporates weather forecasts and a hybrid heuristic algorithm based on chaotic search, harmony search, and simulated annealing, aided by artificial neural networks for predicting solar radiation, ambient temperature, and wind speed. The study shows that combining weather forecasts via an artificial neural network (ANN) with a hybrid search algorithm significantly improves the sizing of hybrid off-grid systems. Along the same lines, Zhang et al. [8] developed an optimization approach based on hybrid simulated annealing (HCHSA), combining harmonic and chaotic search techniques, for the optimal sizing of PV/wind hybrid systems with battery and hydrogen storage. The model considers four decision variables, areas of solar collectors and wind rotors, number of batteries and hydrogen tanks, with the aim of minimizing the life cycle cost (LCC) of the system. Applied to a remote region in Iran, the study evaluated six different hybrid system configurations. The results indicated that the solar/wind combination with batteries offers the best technical-economic performance, even outperforming systems with hydrogen storage.

In remote locations such as Sabah, Malaysia, electrification still depends mostly on isolated diesel generators, which are associated with high fuel costs and significant environmental impacts. The adoption of hybrid systems with photovoltaic panels and batteries has emerged as a promising alternative to increase supply reliability, reduce emissions, and lower the levelized cost of energy (LCOE). In [9]’s study, specialized HOMER software was used to model and compare different generation scenarios, including pure diesel arrangements, PV/diesel/battery hybrid systems (in current and optimized configurations), and a 100% PV/battery-based system, with a focus on evaluating technical, economic and environmental performance. The optimized PV/diesel/battery hybrid system presents the best compromise between reliability, cost, and environmental impact. The 100% PV/battery scenario, although emission-free, is still economically unviable due to the high investment costs in PV and batteries. In addition, Sen and Bhattacharyya [10] proposed a comprehensive approach for sizing and evaluating hybrid off-grid systems in remote villages. Also, using the HOMER software, the authors modeled different combinations of micro-hydropower, solar panels, wind turbines, and biodiesel generators, seeking to identify the most technically reliable and economically viable solution.

Complementing this perspective, Gu et al. [11] proposed a techno-economic evaluation model for PV/T solar concentrators applied to the building sector in Sweden, using Monte Carlo simulation techniques to incorporate uncertainties associated with technical and financial variables. The study analyzed the combined impacts of 11 critical parameters, such as solar radiation, interest and inflation rates, collector efficiency, and cost of capital, on metrics such as levelized cost of energy (LCOE), net present value (NPV), and payback. The reference configuration analyzed achieved an average LCOE of SEK 1.27/kWh, a positive NPV of approximately EUR 1,880, and an estimated payback period of 10 years.

Based on the literature reviewed, there is a consolidated trend towards the use of genetic algorithms as an effective optimization method for sizing the components of hybrid systems, especially when it comes to selecting the most efficient configurations between components such as photovoltaic panels, wind turbines, storage systems, and auxiliary generators. Works such as those by Ismail et al. [3], Yang et al. [4], and Dufo-López and Bernal-Agustion [5] demonstrate that the GA is capable of exploring complex and non-linear solution spaces, allowing optimal arrangements to be found that minimize indicators such as the levelized cost of energy (LCOE), $C{O}_2$ emissions, and the probability of load shedding (LPSP). In addition, many of these studies consider the use of diesel generators as an integral part of hybrid solutions, not only because of their reliability but also to guarantee load service in critical scenarios, especially in isolated regions. However, arrangements that combine renewable sources with well-designed storage tend to significantly reduce the time of use and costs associated with fossil generators [9,10]. Another recurring aspect is the emphasis on maximizing net present value (NPV) as the main metric of economic attractiveness. Studies such as those by Gu et al. [11] and Zhang et al. [8] reinforce that considering discounted cash flows over the useful life of the system allows for a more realistic assessment of the viability of the project, especially when variables such as inflation, interest rates, operating costs, and climatic uncertainties are incorporated.

On the other hand, conventional wind systems connected to the grid, such as turbines with synchronous generators or double-fed generators controlled by converters, still present challenges such as high maintenance costs, degradation of power quality due to harmonics, and the complexity of power converters [1]. In this scenario, the electromagnetic frequency regulator (EFR) has emerged as an innovative alternative, with the potential to mitigate harmonics and facilitate direct hybridization with auxiliary sources via the DC bus of the inverter [1,12,13,14]. The EFR’s architecture, based on an induction machine with a rotating armature, enables the conversion of variable wind speeds into frequencies compatible with the electricity grid, promoting greater electromechanical robustness and integration with hybrid systems.

This paper proposes the sizing and technical-economic analysis of a hybrid renewable energy system (HRES) made up of photovoltaic panels, wind turbines, a diesel generator, and a battery bank (BB), to be applied to UFRN’s Macau Campus and connected to the electricity grid. Inspired by the approach of Delson et al. [15], three improvements are made to the computational model: (i) adjustment of the temperature coefficients of the PV modules and incorporation of shading and degradation losses; (ii) parameterization of the turbine power curve considering aerodynamic corrections; and (iii) hourly simulation integrated with the evolution of the state of charge (SoC) of the batteries. A genetic algorithm is then used to simultaneously optimize the installed capacity of each component in order to maximize the net present value (NPV) over 20 years. Finally, we carry out a comparative study of the results obtained with the proposed method and with the original sizing presented by Delson et al. [15], highlighting gains in cash flow accuracy and economic viability.

This article is structured as follows: Section 1 introduces the study’s motivation, objectives, and a literature review. Section 2 provides a detailed description of the grid-connected hybrid system and its components (PV modules, wind turbine, EFR, and battery bank). Section 3 formulates the mathematical model of the HRES, including generation equations and storage dynamics. Section 4 outlines the genetic algorithm employed for optimal system sizing. Section 5 defines the NPV-based objective function, detailing cash-flow formulations and constraints. Section 6 presents GA validation results using benchmark functions. Section 7 describes the simulation setup, and Section 8 reports the simulation outcomes. Section 9 examines the sensitivity analysis, while Section 10 compares the proposed design against the reference project using a unified NPV methodology. Finally, Section 11 discusses key findings, limitations, and practical implications, and Section 12 offers concluding remarks and future research recommendations.

2. Description of the Grid-Connected Hybrid Energy System

This article proposes a hybrid renewable energy generation system with the aim of providing clean and continuous electricity to the Macau City Campus while reducing dependence on fossil sources. Figure 1 shows the topology of the proposed configuration, which integrates wind turbines (WT), photovoltaic panels (PV), an energy storage system (ESS), a diesel generator (DG), an electromagnetic frequency regulator (EFR), a synchronous generator (SG), the campus load, and the connection point to the electricity grid. The system’s operation is coordinated by a centralized energy management system (EMS), which is responsible for real-time control of energy flows.

The wind turbine converts the wind’s kinetic energy into mechanical power ($P_{WT}^H$), which is transferred via a set of gears to the EFR. This electromagnetic device creates a rotating magnetic field that mechanically drives the SG, allowing the generation of alternating current ($P_{SG}^{AC}$) compatible with the AC bus. The energy produced can be directed to meet the campus load ($P_L$) or exported to the electricity grid ($P_G$).

The direct current sources, consisting of the photovoltaic modules and the battery bank, are connected to the system via a DC/AC inverter. This inverter is also responsible for regulating the rotation speed of the EFR rotor, keeping it constant to ensure the stability of the generated frequency. The EMS monitors and controls critical operating variables in real time, such as the power supplied by each source ($P_{WT}^H$, $P_{PV}$, and $P_{BSS}$), the exchange with the grid ($P_G$), and the ESS state of charge (${\rho }_{SoC}$). Based on the instantaneous operating conditions, the EMS controls the switches ($S_{w1}$ to $S_{w6}$) and the automatic transfer switch (ATS) in order to prioritize the use of renewable sources, store surplus energy, or activate auxiliary sources, depending on demand.

In addition, the system incorporates an emergency diesel generator, used exclusively in extreme conditions. This resource is activated, for example, during simultaneous failures of wind and solar generation at night, when the battery bank does not have enough energy to keep the DC bus voltage within operating limits. Therefore, the proposed system stands out for its operational flexibility, robustness in the face of adverse scenarios, and ability to efficiently integrate multiple renewable and conventional energy sources.

3. Mathematical Model of the Hybrid Renewable Energy System (HRES)

This section presents the sizing of the components of the grid-connected HRES. The actual meteorological data, such as wind speed and solar radiation, were obtained from the NASA database. Based on this information, mathematical models were developed for the main components of the system: the campus electrical loads, the photovoltaic (PV) system, the wind turbine, the EFR, and the energy storage system (ESS). These models considered input variables including climate data (wind speed and solar radiation), the energy consumption profile of the academic unit, and equipment specifications such as nominal power, efficiency, and useful life.

3.1. Load Model

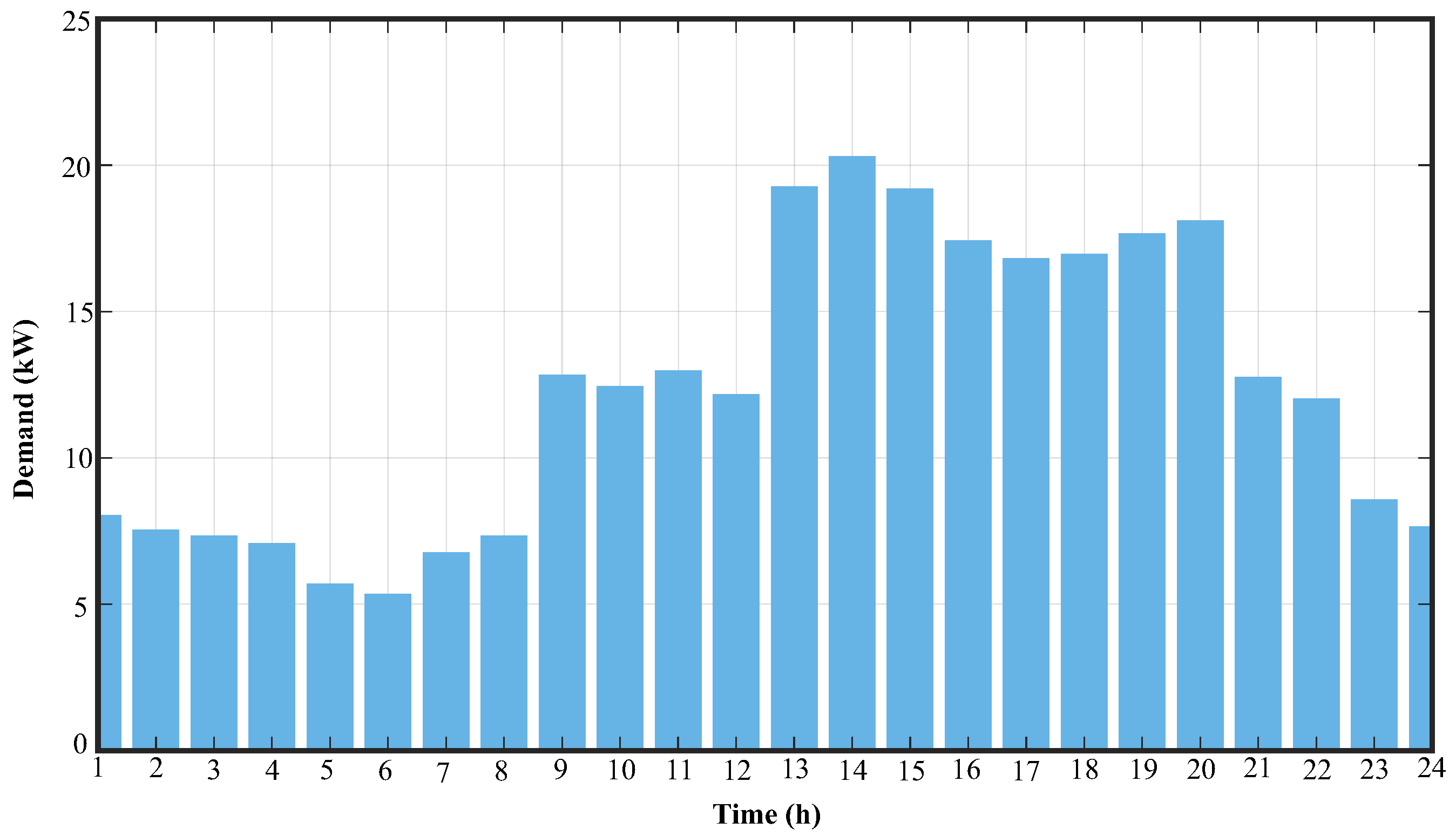
The load profile, which represents the variation in energy demand over the course of a typical day, was based on data provided by [15] and is illustrated in Figure 2. This figure shows the average hourly energy demand over a 24-h period. The daily energy consumption ($E_{load}$) is calculated by adding up the power consumed in each time interval and multiplying by the duration of that interval ($\Delta t$) [16]:

$$E_{load}\left(k\right)=\sum \left[P_{fixed}\left(k\right)+\sum _{i=1}^{N_t}{P}_i\left(k\right)\right]·\Delta t,k=1,\dots ,24.$$

(1)

In this Equation (1), $P_{fixed}\left(k\right)$ represents constant energy consumption (e.g., lighting or fixed equipment), while $P_i\left(k\right)$ corresponds to the power consumed by the i-th controllable load (e.g., appliances that can be switched on or off). The parameter $N_t$ indicates the total number of controllable loads.

3.2. Photovoltaic Model

The photovoltaic system model estimates the power generated by the solar panels, denoted as $P_{solar}\left(t\right)$, based on factors such as solar irradiance, ambient temperature, cell temperature, and equipment efficiency. The output power is probided by the following equation [17]:

$$P_{solar}\left(t\right)=I_t\left(t\right)·A_{pv}·\left[1-\psi \left(T_{mod}\left(t\right)-T_{ref}\right)\right]·{\eta }_{CC},$$

(2)

where $I_t\left(t\right)$ is the solar irradiance at the optimum tilt angle, $A_{pv}$ is the total area of the solar panels, and $\psi$ is the temperature coefficient, typically 0.5%/°C, indicating the reduction in power due to the increase in temperature [18]. ${\eta }_{CC}$ is the efficiency of the DC/DC converter that regulates the output. The module temperature $T_{mod}\left(t\right)$ is calculated based on the ambient temperature $T_{amb}\left(t\right)$ and the solar irradiance using Equation (3):

$$T_{mod}\left(t\right)=T_{amb}\left(t\right)+\left({\displaystyle \frac{\mathrm{NOTC}-T_{cr}}{0,8}}\right)·{\displaystyle \frac{I_G\left(t\right)}{I_{stc}}},$$

(3)

where $T_{amb}\left(t\right)$ is the ambient temperature at time t, NOTC is the nominal operating temperature of the cell (supplied by the manufacturer under conditions of 800 W/m² and 20 °C), and $T_{cr}$ is the reference temperature, typically 20 °C. Figure 3 presents the seasonal distribution of solar irradiance in the Macau/RN region, with hourly data collected by NASA throughout 2015, showing the variations in the intensity of sunlight during each season of the year.

3.3. Wind Turbine Model

To calculate the power generated by the wind turbine, it is necessary to adjust the measured wind speed to the turbine’s hub height, as the measuring equipment (anemometers) is typically located at different heights. The relationship between wind speed at hub height $u\left(h_2\right)$ and anemometer height $h_1$ is provided by the following:

$${\displaystyle \frac{u\left(h_2\right)}{u\left(h_1\right)}}={\left({\displaystyle \frac{h_2}{h_1}}\right)}^{\beta }.$$

(4)

In this Equation (4), $u\left(h_2\right)$ is the wind speed (in meters per second) at the height of the cube $h_2$, and $h_1$ is the height of the anemometer. The exponent $\beta$ depends on the terrain, time, and season, but it is typically around ${\displaystyle \frac{1}{7}}$, as proposed by Johnson (1985) [19].

The output power of the wind turbine $P_{wt}\left(t\right)$ depends on the wind speed $u\left(t\right)$ and is modeled as follows [20]:

$$\begin{array}{cc}\hfill P_{wt}\left(t\right)=& \left\{\begin{array}{cc}{P}_{wt,r}·{\displaystyle \frac{u^3\left(t\right)-u_{min}^3}{u_r^3-u_{min}^3}}\hfill & \mathrm{if}{u}_{min}\le u\left(t\right)\le u_r,\hfill \\ P_{wt,r}\hfill & \mathrm{if}{u}_r<u\left(t\right)<u_{max},\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.,\hfill \end{array}$$

(5)

where $P_{wt,r}$ is the turbine’s nominal power, $u\left(t\right)$ is the instantaneous wind speed, $u_{min}$ is the minimum speed for power generation, $u_r$ is the nominal speed, and $u_{max}$ is the maximum speed, above which the turbine is shut down for protection. Here, the wind speed data were obtained from the INMET database for the same period as the solar data, measuring at a height of 17.37 meters at hourly intervals, totaling 8760 data points.

The nominal power of the wind turbine $P_{wt,r}$ is calculated from the maximum power coefficient $C_{p,max}$, the air density ($\rho$), the area swept by the rotor blades (${\displaystyle \frac{\pi D_r^2}{4}}$), and the nominal wind speed $u_r$, as expressed in [20]:

$$\begin{array}{ccc}\hfill P_{wt,r}& =& C_{p,max}\left(0.5\right)\rho ({\displaystyle \frac{\pi D_r^2}{4}})u_r^3.\hfill \end{array}$$

(6)

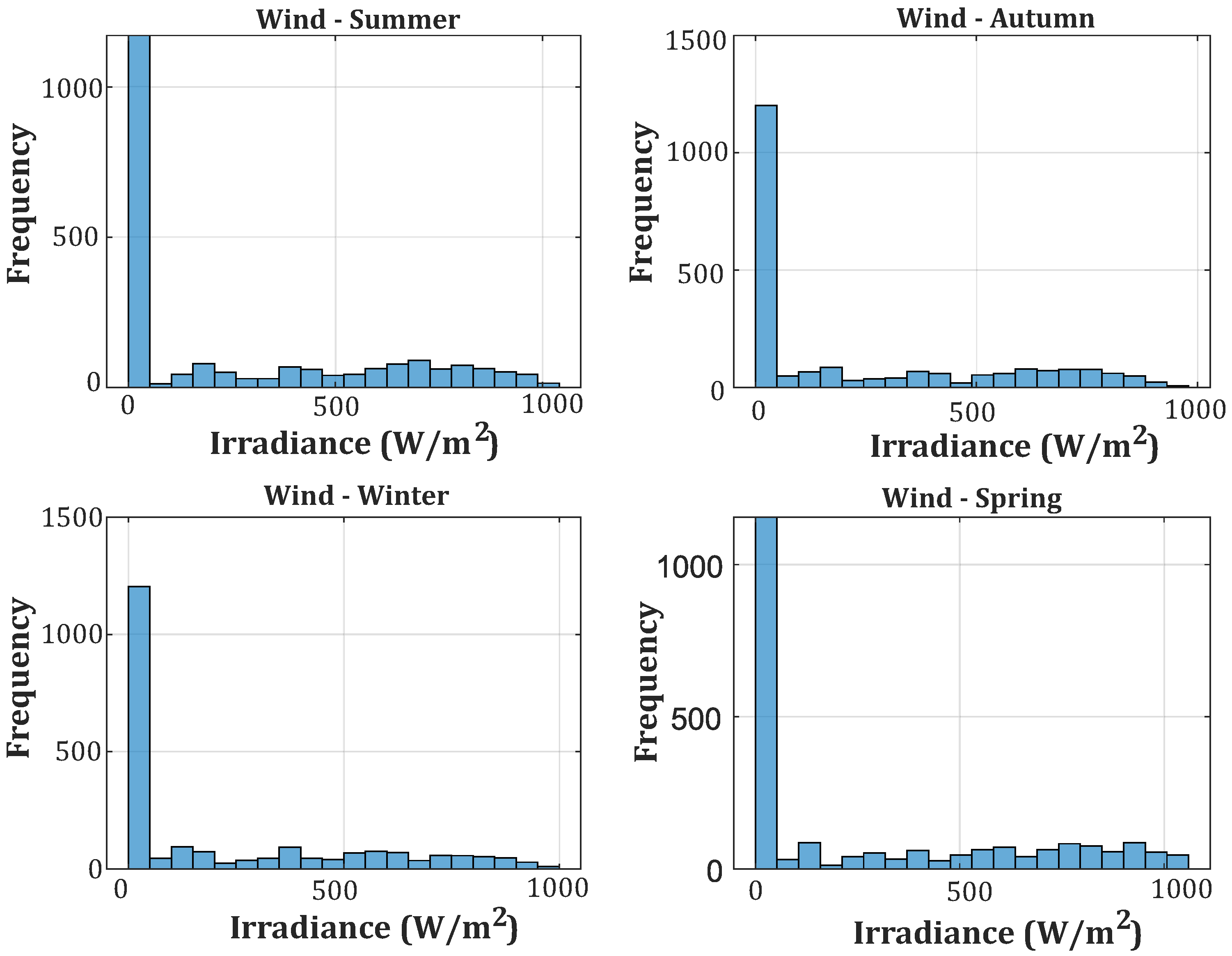
Figure 4 illustrates the seasonal distribution of wind speed in the same region and period, showing how the wind profiles behave in summer, autumn, winter, and spring.

3.4. Modeling of the Electromagnetic Frequency Regulator (EFR)

The EFR’s rated power ($P_{EFR}$) is sized equal to the wind turbine’s rated power ($P_{wt,r}$) due to its direct mechanical coupling and shared nominal rotational speed [13]. This power-matching strategy ensures torque compatibility while maximizing energy conversion efficiency, as validated experimentally in EFR-based systems (cf. [1]). Transient stability analyses further confirm this approach maintains operational integrity during wind speed fluctuations and abrupt load changes [1].

$$P_{EFR}=P_{wt,r}.$$

(7)

This relationship ensures that the EFR operates at the same angular speed as the turbine, maximizing energy conversion efficiency. This technology offers several advantages compared to conventional wind systems: (i) reduced maintenance costs, i.e., by eliminating the need for complex power converters, the EFR reduces maintenance costs and increases reliability; (ii) improved power quality, i.e., by mitigating harmonics and voltage fluctuations, this ensures compliance with grid quality standards; (iii) hybrid integration, i.e., facilitating direct hybridization with other energy sources (such as PV and ESS) through the EFR armature slip rings. Thus, the EFR works in conjunction with the wind turbine and the synchronous generator to provide AC power that can be used directly by the campus or exported to the COSERN grid in Rio Grande do Norte, Brazil.

3.5. Modeling of the Battery Energy Storage System

In hybrid renewable energy systems, the energy storage system (ESS) plays a critical role in mitigating the variability inherent in renewable sources, such as solar PV. Accurate modeling of the ESS is essential to ensure system reliability, meet load demand, and optimize economic costs. In this study, the ESS model is based on the daily energy balance between generation and demand, adopting the methodology proposed by Lai and McCulloch (2017) [21] for hybrid systems with high solar energy utilization. Thus, ESS sizing is based on the difference between PV generation and load demand over a 24-h period. For the UFRN campus in Macau/RN, the daily energy surplus was estimated at 120 kWh, as illustrated in Figure 5. This surplus ensures that the ESS can store energy during periods of high solar generation and supply it during periods of low generation or high demand, such as at night or on cloudy days. For the UFRN campus in Macau/RN, the daily energy surplus was estimated at 120 kWh, corresponding to the area under the photovoltaic curve above demand (highlighted in green in Figure 5). Note that although total daily consumption is higher than the peak generated, only the period in which PV generation exceeds load results in energy available for storage or injection into the grid. This value of 120 kWh was used as the minimum reference for storage capacity. However, the genetic algorithm applied to the sizing of the hybrid system identified an optimum storage capacity close to 200 kWh, in order to more reliably meet fluctuations in generation and demand.

The state of charge (SoC) of the battery at any time (t) is modeled by the following equation:

$$SoC\left(t\right)=SoC(t-1)+[E_{PV}\left(t\right)-{\displaystyle \frac{E_{load}}{{\eta }_{inv}}}]·{\eta }_{bat},$$

(8)

where

• $\mathrm{SoC}\left(t\right)$ is the state of charge at time (t);
• $E_{PV}\left(t\right)$ is the energy generated by the PV system at time (t) (kWh);
• $E_{\mathrm{load}}$ represents the energy demanded by the load at time (t) (kWh);
• ${\eta }_{\mathrm{inv}}$ is the inverter efficiency (typically 0.95), and ${\eta }_{\mathrm{bat}}$ is the battery efficiency.

This equation reflects the hourly dynamics of the SoC, considering the energy generated by the PV system that is directed to the battery, the output to meet demand (adjusted by the inverter efficiency), and the losses associated with battery efficiency. ESS sizing is adjusted to operate within the safe depth of discharge (DoD) limits, in this case between 20% and 80% for lithium-ion batteries, in order to maximize service life.

4. Genetic Algorithm for Optimal Sizing of HRES

Genetic algorithms (GAs) are a class of stochastic optimization methods inspired by the principles of natural evolution, as originally formulated by John H. Holland (1975) [22] and later popularized by Goldberg (1989) [23]. Such algorithms are widely used to solve complex optimization problems, characterized by multidimensional, non-linear, and often multimodal search spaces [24].

One of the most common representations in GAs is binary, where each individual is encoded as a sequence of bits (0 and 1). However, alternative representations, such as real values or permutations, are also frequently used depending on the problem [25].

The main genetic operators are as follows:

• Selection: Individuals with higher fitness, determined by an objective function, have a higher probability of being selected for reproduction. Common techniques include roulette and binary tournament [26].
• Crossover: Combines characteristics of two individuals (parents) to generate offspring. A classic example is the one-point crossover, in which segments of the parents are recombined [24].
• Mutation: Small random perturbations are introduced into the chromosomes, preserving genetic diversity and preventing premature convergence [25].

The iterative process of a GA can be summarized in the following steps [24]:

• Initialization: Random generation of an initial population.
• Evaluation: Calculation of the fitness of each individual based on the objective function.
• Selection: Selection of the fittest individuals for reproduction.
• Application of Operators: Crossover and mutation to create a new generation.
• Stopping Criterion: Verification of convergence or maximum number of generations.

GAs have been widely applied in the optimization of renewable energy systems, such as hybrid microgrids. In this context, the objective is to minimize investment and operating costs while meeting energy demand. Variables such as the number of photovoltaic panels, wind turbines, battery banks, and inverters are optimized to ensure efficiency and cost-effectiveness [27]. The objective function usually incorporates acquisition, maintenance, and operation costs, in addition to technical constraints.

In this work, a genetic algorithm is adopted as a metaheuristic technique for the optimal dimensioning of the main components of a hybrid power generation system (HPGS), including photovoltaic (PV) modules, wind turbine (WT), battery bank (BB), and electromagnetic frequency regulator (EFR). The objective of the optimization process is to maximize the net present value (NPV), as defined in Section 5. Metaheuristics are well-suited for sizing HRES due to their ability to navigate vast and complex search spaces without getting stuck in local optima. Among these, genetic algorithms (GAs) are the most prevalent.

Each individual (chromosome) of the GA is represented by a real vector x of four decision variables:

$$\mathrm{x}=[{\mathrm{C}}_{\mathrm{PV}},{\mathrm{P}}_{\mathrm{WT}},{\mathrm{C}}_{\mathrm{ESS}},{\mathrm{C}}_{\mathrm{EFR}}],$$

(9)

where

• ${\mathrm{C}}_{\mathrm{PV}}$ (kWp) is the installed capacity of photovoltaic panels;
• $P_{WT}$ (kW) is the nominal power of the wind turbine;
• ${\mathrm{C}}_{\mathrm{ESS}}$ (kWh) is the capacity of the battery bank;
• ${\mathrm{C}}_{\mathrm{EFR}}$ (kW) is the nominal power of the EFR.

The initial population of size ${\mathrm{N}}_{\mathrm{P}}$ is randomly generated within predefined lower and upper bounds for each decision variable, ensuring a broad exploration of the search space from the beginning. Thus, pairs of parents are chosen by performing binary tournaments, in which two random individuals are compared and the one with the highest fitness is selected as the parent.

For each pair of parents ${\mathbf{x}}^{\left(a\right)}$, ${\mathbf{x}}^{\left(b\right)}$, a descendant y is generated. Real uniform crossover is used, where for each gene i,

$$y_i=\alpha x_i^{\left(a\right)}+(1-\alpha )x_i^{\left(b\right)},\alpha \sim \mathcal{U}(0,1).$$

(10)

For each gene, with probability $p_m$, an adaptive Gaussian perturbation is applied:

$$y_i\leftarrow y_i+{\delta }_i,{\delta }_i\sim \mathcal{N}(0,{\sigma }_i^2),$$

(11)

where ${\sigma }_i\left(g\right)={\sigma }_{i,0}exp(-\lambda g)$ decays exponentially with generation g.

In addition, the top 5% of individuals are copied directly to the next generation, ensuring that high-performing solutions are not lost.

For each individual x in the population, the fitness value is determined by the NPV, which integrates both technical performance (energy generation and storage) and economic metrics (revenues, costs, and cash flows) over a 20-year horizon. The evaluation procedure comprises the following steps: (a) Decoding: Map the chromosome x to its physical parameters (${\mathrm{C}}_{\mathrm{PV}}$, ${\mathrm{P}}_{\mathrm{WT}}$, ${\mathrm{C}}_{\mathrm{ESS}}$, and ${\mathrm{C}}_{\mathrm{EFR}}$). (b) Simulation: Run the hybrid generation model for 20 years using hourly solar radiation, wind speed, and temperature data (NASA/INMET) alongside component models (Equations (2), (5), and (8)). (c) Cash Flow Computation: Estimate annual revenues, investment costs, and operation and maintenance expenses according to Equations (14)–(17). (d) Discounting: Apply the minimum attractive rate of return to discount all cash flows to present value, yielding the NPV (Equation (13)). (e) Fitness Assignment: Assign the computed NPV as the fitness value of the individual. The GA procedure follows the pseudocode in

Table 1. Pseudocode adapted for HRES sizing.

Step	Description
1	Initialize random seed and define search ranges: $\mathrm{PV}\_\mathrm{range}$, $\mathrm{Wt}\_\mathrm{range}$, $\mathrm{ESS}\_\mathrm{range}$, $\mathrm{Efr}\_\mathrm{range}$.
2	Initialize population Pop with ${\mathrm{N}}_{\mathrm{P}}$ individuals within the defined ranges.
3	For each generation $g=1$ through $G_{max}$:
	3.1 Evaluate the fitness of each individual ($\mathrm{Fitness}=\mathrm{NPV}\left(\mathrm{x}\right)$).
	3.2 Sort Pop in decreasing order of fitness.
	3.3 Copy the $N_{\mathrm{elite}}=\mathrm{round}(\mathrm{elitism}\_\mathrm{rate}·{\mathrm{N}}_{\mathrm{P}})$ best individuals to NewPop.
	3.4 While $\left|\mathtt{NewPop}\right|<{\mathrm{N}}_{\mathrm{P}}$:
	(a) Select two parents by binary tournament.
	(b) If $\mathrm{rand}<p_c$, apply real uniform crossover.
	(c) Apply adaptive Gaussian mutation with probability $p_m$.
	(d) Add generated children to NewPop.
	3.5 Update $\mathtt{Pop}=\mathtt{NewPop}(1:{\mathrm{N}}_{\mathrm{P}})$.
4	Return the best individual of Pop and its optimal parameters.

.

5. Objective Function

The economic feasibility analysis of energy projects is commonly performed using consolidated financial indicators, such as net present value (NPV), internal rate of return (IRR), benefit–cost ratio (B/C), and payback period. In this study, NPV was adopted as the main decision criterion, due to its wide acceptance in the literature, robust methodological basis, and ease of interpretation [28]. In addition, it was established as the objective function to be maximized, determining the ideal system configuration.

The NPV represents the net benefit of the project over its lifespan, considering a discount rate (MAT) that reflects the opportunity cost of capital or the minimum attractive rate of return (MARR). A positive NPV indicates that the project tends to generate benefits greater than costs over time, and is therefore economically viable. A negative NPV suggests financial unfeasibility, given that costs would exceed expected benefits [29].

The calculation of NPV involves three fundamental steps: (i) projection of annual cash flows ($C{F}_t$); (ii) definition of the minimum attractiveness rate of return $MARR$, usually between 7% and 15%, according to the investment risk and the macroeconomic scenario [30]; (iii) discounting the flows to the present value, subtracting the initial investment $C_0$. The general equation is expressed by the following:

$$\mathrm{NPV}=-{\mathrm{C}}_0+\sum _{t=1}^n{\displaystyle \frac{{\mathrm{CF}}_{\mathrm{t}}}{{(1+\mathrm{MAT})}^{\mathrm{t}}}},$$

(12)

where

• ${\mathrm{C}}_0$ is the initial cost of the project, including acquisition ($C_{\mathrm{aq}}$) and installation ($C_{\mathrm{inst}}$) [31];
• ${\mathrm{CF}}_{\mathrm{t}}$ is the cash flow in year t;
• MAT is the minimum attractiveness tax;
• n is the analysis horizon, defined by the useful life of the equipment.

The optimization routine in this study aims to maximize the system’s net present value (NPV) by determining the optimal combination of generation and storage capacities. Accordingly, the fitness function is formulated as follows:

$$\mathrm{Fitness}=\underset{\mathrm{x}}{\max }\mathrm{NPV}\left(\mathrm{x}\right)=-{\mathrm{C}}_0\left(\mathrm{x}\right)+\sum _{t=1}^n{\displaystyle \frac{{\mathrm{CF}}_{\mathrm{t}}\left(\mathrm{x}\right)}{{(1+\mathrm{MAT})}^{\mathrm{t}}}},$$

(13)

where

• $\mathrm{x}=\left[{\mathrm{C}}_{\mathrm{PV}},{\mathrm{P}}_{WT},{\mathrm{C}}_{\mathrm{ESS}},{\mathrm{C}}_{\mathrm{EFR}}\right]$ denotes the decision-variable vector;
• ${\mathrm{C}}_0\left(\mathrm{x}\right)$ is the initial capital outlay (acquisition + installation);
• ${\mathrm{CF}}_{\mathrm{t}}\left(\mathrm{x}\right)$ is the annual cash flow (revenue ${\mathrm{R}}_{\mathrm{t}}\left(\mathrm{x}\right)$ minus costs, Equation (14));

The net present value (NPV) is the predominant metric for assessing economic viability in energy engineering, as it synthesizes capital expenditures, operational and maintenance costs, and anticipated revenues into a single, time-discounted measure [32,33,34,35]. By employing NPV as the sole objective, the optimization framework directly targets the configuration that maximizes long-term financial returns, in accordance with established best practices for techno-economic sizing of hybrid renewable systems [36]. This focused approach simplifies the decision process and ensures comparability across studies, while still capturing the full spectrum of project cash flows over the analysis horizon.

The function ${\mathrm{CF}}_{\mathrm{t}}\left(\mathrm{x}\right)$ includes all annual revenues and expenses of the system as follows:

$${\mathrm{CF}}_{\mathrm{t}}\left(\mathrm{x}\right)={\mathrm{R}}_{\mathrm{t}}\left(\mathrm{x}\right)-{\mathrm{C}}_{\mathrm{aq}}\left(\mathrm{x}\right)-{\mathrm{C}}_{\mathrm{dem},\mathrm{t}}-{\mathrm{C}}_{\mathrm{op},\mathrm{t}}-{\mathrm{C}}_{\mathrm{man},\mathrm{t}}\left(\mathrm{x}\right),$$

(14)

where

• ${\mathrm{R}}_{\mathrm{t}}\left(\mathrm{x}\right)$ is the revenue from energy generation in year t;
• ${\mathrm{C}}_{\mathrm{aq}}\left(\mathrm{x}\right)$ is the cost of acquiring equipment;
• ${\mathrm{C}}_{\mathrm{dem},\mathrm{t}}$ is the annual cost with an increase in contracted demand;
• ${\mathrm{C}}_{\mathrm{op},\mathrm{t}}$ is the operational cost (e.g., installation labor);
• ${\mathrm{C}}_{\mathrm{man},\mathrm{t}}\left(\mathrm{x}\right)$ is the maintenance cost.

All terms, except ${\mathrm{C}}_{\mathrm{dem},\mathrm{t}}$ and ${\mathrm{C}}_{\mathrm{op},\mathrm{t}}$, depend on the decision vector x as follows: the annual revenue ${\mathrm{R}}_{\mathrm{t}}\left(\mathrm{x}\right)$, calculated from the PV/WT energy output (cf. Equation (15)); the acquisition cost ${\mathrm{C}}_{\mathrm{aq}}\left(\mathrm{x}\right)$, which scales with the installed capacities of the components; the maintenance cost ${\mathrm{C}}_{\mathrm{man},\mathrm{t}}\left(\mathrm{x}\right)$, assumed proportional to the yearly generated energy ${\mathrm{E}}_{\mathrm{g},\mathrm{year}}$ (cf. Equation (16)).

The revenue ${\mathrm{R}}_{\mathrm{t}}\left(\mathrm{x}\right)$ is obtained according to the following equation:

$${\mathrm{R}}_{\mathrm{t}}\left(\mathrm{x}\right)={\mathrm{E}}_{\mathrm{p}}\left(\mathrm{x}\right)·{\mathrm{T}}_{\mathrm{p},\mathrm{t}}+{\mathrm{E}}_{\mathrm{fp}}\left(\mathrm{x}\right)·{\mathrm{T}}_{\mathrm{fp},\mathrm{t}},$$

(15)

where

• ${\mathrm{E}}_{\mathrm{p}}\left(\mathrm{x}\right)$ is the average annual energy generated during peak hours;
• ${\mathrm{E}}_{\mathrm{fp}}\left(\mathrm{x}\right)$ is the average annual energy generated outside peak hours;
• ${\mathrm{T}}_{\mathrm{p},\mathrm{t}}$, ${\mathrm{T}}_{\mathrm{fp},\mathrm{t}}$ are the energy rates during peak and off-peak hours in year t.

Both costs and rates are updated annually, considering inflation and variations in electricity prices.

The annual maintenance costs and installation costs are calculated using Equations (16) and (17), respectively. The annual maintenance cost (${\mathrm{C}}_{\mathrm{man},\mathrm{t}}\left(\mathrm{x}\right)$) is incurred regularly throughout the project’s useful life. It is composed of a fixed annual portion and a variable portion, proportional to the amount of energy generated during the period. The installation cost is estimated as 15% of the total acquisition value of the equipment [35].

$${\mathrm{C}}_{\mathrm{man},\mathrm{t}}\left(\mathrm{x}\right)={\mathrm{C}}_{\mathrm{f}}+({\mathrm{E}}_{\mathrm{g},\mathrm{year}}\left(\mathrm{x}\right)·\mathrm{K}),$$

(16)

$${\mathrm{C}}_{\mathrm{inst}}=15\%·{\mathrm{C}}_{\mathrm{lab}},$$

(17)

where ${\mathrm{C}}_{\mathrm{f}}$ represents the annual fixed maintenance cost, ${\mathrm{E}}_{\mathrm{g},\mathrm{year}}$ is the electrical energy generated annually by the system, K is the maintenance cost coefficient per unit of energy (kWh), and ${\mathrm{C}}_{\mathrm{lab}}$ corresponds to the installation labor cost.

6. Validation of the GA with Benchmark Functions

The core parameters governing the behavior of the genetic algorithm (GA) are outlined below, covering population structure, genetic operator rates, and search boundaries. These values were selected based on well-established literature and carefully calibrated for the HRES sizing task.

Table 2. Summary of parameters used in the genetic algorithm.

Parameter	Symbol	Value / Range
Population size	${\mathrm{N}}_{\mathrm{P}}$	100
Maximum generations	$G_{max}$	200
Crossover rate	$p_c$	0.8
Mutation rate	$p_m$	0.05
Elitism rate	${\rho }_{\mathrm{elite}}$	0.05 (5%)
PV limit	$[{\mathrm{C}}_{\mathrm{PV}}^{min}-{\mathrm{C}}_{\mathrm{PV}}^{max}]$	[10–50] kWp
WT Limit	$[{\mathrm{P}}_{\mathrm{WT}}^{min}-{\mathrm{P}}_{\mathrm{WT}}^{max}]$	[10–50] kW
ESS Limit	$[{\mathrm{C}}_{\mathrm{ESS}}^{min}-{\mathrm{C}}_{\mathrm{ESS}}^{max}]$	[50–250] kWh
EFR limit	$[{\mathrm{C}}_{\mathrm{EFR}}^{min}-{\mathrm{C}}_{\mathrm{EFR}}^{max}]$	[10–50] kW
Mutation decay	$\lambda$	0.01

summarizes the GA settings employed in this study. The population size (Np = 100) was chosen to balance exploratory search and convergence speed, consistent with the recommended range of 50–100 individuals in optimization applications [37]. A crossover probability of 0.8 (pc = 0.8) and a mutation probability of 0.05 (pm = 0.05) were adopted following best practices that advocate for high crossover rates (0.6–0.8) to encourage solution recombination, paired with low mutation rates (0.02–0.1) to maintain diversity without disrupting convergence [37,38]. To further enhance performance, elitism was applied at 5% (${\rho }_{\mathrm{elite}}=0.05$), allowing the best-performing solutions to persist across generations and support faster convergence. The algorithm was set to run for a maximum of 200 generations (${\mathrm{G}}_{\max }=200$), a value determined through prior calibration to ensure optimal results within feasible computational time. This setup leverages the synergistic benefits of elitism and adaptive Gaussian mutation strategies. Finally, the search bounds for system components, namely PV, WT, ESS, and EFR, were defined to reflect realistic and commercially viable capacity ranges. This ensured that the optimization process adequately explored all feasible configurations applicable to the energy profile of the UFRN campus located in Macau.

To further assess the generality and robustness of the proposed GA configuration, two classical benchmark functions were employed [39]: Sphere

$$f_{\mathrm{Sphere}}\left(\mathrm{x}\right)=\sum _{i=1}^4{\mathrm{x}}_i^2,{\mathrm{x}}_i\in [-5.12,5.12],$$

(18)

and Rastrigin

$$f_{\mathrm{Rastrigin}}\left(\mathrm{x}\right)=10·4+\sum _{i=1}^4\left[{\mathrm{x}}_i^2-10cos(2\pi ·{\mathrm{x}}_i)\right],{\mathrm{x}}_i\in [-5.12,5.12].$$

(19)

Each function was optimized over 100 independent runs in MATLAB R2021a sing the same algorithmic settings as in Table 2: population size ${\mathrm{N}}_{\mathrm{p}}=100$, maximum generations $G_{max}=200$, crossover rate $p_c=0.8$, mutation rate $p_m=0.05$ with adaptive Gaussian mutation, elitism of 5%, and function tolerance of ${10}^{-6}$. The metrics recorded were the mean objective value $\overline{f}$, standard deviation ${\sigma }_f$, average number of generations $\overline{g}$, average runtime, and success rate (fraction of runs with $f<{10}^{-3}$), as summarized in

Table 3. GA performance on sphere and Rastrigin functions (100 Runs).

Function	$\overline{\mathit{f}}$	${\mathit{\sigma }}_{\mathit{f}}$	$\overline{\mathit{g}}$	Time (s)	Success (%)
Sphere	$4.30\times {10}^{-9}$	$1.29\times {10}^{-8}$	86.0	0.07	100
Rastrigin	$1.39\times {10}^{-1}$	$4.25\times {10}^{-1}$	107.2	0.08	89

.

The results obtained after running the GA indicate the optimal HRES configuration as follows: ${\mathrm{C}}_{\mathrm{PV}}\approx 35\mathrm{kWp}$, ${\mathrm{P}}_{\mathrm{WT}}=30\mathrm{kW}$, ${\mathrm{C}}_{\mathrm{ESS}}\approx 200\mathrm{kWh}$, and ${\mathrm{C}}_{\mathrm{EFR}}=30\mathrm{kW}$. Next, the economic and operational impact of this configuration is examined through a long-term simulation.

7. Simulation

To evaluate the technical and economic performance of the proposed hybrid system, a simulation was carried out considering a period of 20 years.

Table 4. Technical and economic parameters of the simulated system.

Parameter	Value
Simulation horizon	20 years
Average annual energy generated	217,978.80 kWh
Total energy generated (20 years)	4,359,576 kWh
Total load consumption (20 years)	2,105,590.68 kWh
Estimated initial annual revenue	BRL 74,657.74
Base rate used	BRL 0.34/kWh (2015)
Monetary update considered	67.8% (2015–2025)

presents the main data adopted.

The system was designed to generate an average of approximately 218 MWh per year, totaling approximately 4.36 GWh at the end of the period evaluated. This value is much higher than the load consumption, which totals just over 2.1 GWh in 20 years. The estimated annual revenue is based on a tariff of BRL 0.34 per kWh, according to the values practiced in 2015. To bring the results to more current values, an accumulated monetary correction of 67.8% was considered until 2025, following the inflation projection published in the Central Bank of Brazil’s Focus bulletin on 28 April 2025.

Table 5. Hybrid system component costs.

Components	Price (BRL)	Durability (Years)
EFR, 30 kW	16,026.44	20
WT, 30 kW, Height 18 m	184,253.56	20
PV 245 $W_p$, 1640 × 990 × 35 mm	156,585.00	25
ESS	110,747.00	5
Inverter nominal power 30 kW	19,380.00	15
Diesel Generator 20 kVA	36,580.00	20
Cables and Accessories	29,148.00	20
Installation Labor	78,535.80	20
Annual Maintenance Cost	18,489.11	1

shows the costs of the equipment used in the simulation, as well as the estimated useful life of each component. These data are essential for calculating the necessary investments, future replacements, and maintenance of the system.

The values include all the main elements of the system, such as turbines, solar panels, batteries, inverters, and auxiliary generators, as well as materials and installation costs. Durability was taken into account to estimate future replacements. For example, the battery bank has a useful life of 5 years, requiring replacements throughout the analysis period, while the solar panels last 25 years and do not require replacement during the horizon considered.

In addition to the main technical and economic data of the hybrid system, other parameters were considered in the simulation with the aim of making the analysis more realistic and in line with the practical implementation conditions. These data are presented in

Table 6. Additional data.

Description	Cost (BRL)
Price (2015) ($)	3.01
EFR increase (%)	20
WT discount (%)	20
PV quantity	143
WT quantity	1
Inverter quantity	1
Acquisition price (%)	15
Maintenance cost per kWh (BRL)	$0.05$
kWh rate 2015	$0.3425$

.

The dollar exchange rate considered refers to the year 2015 and was used to convert the purchase price of an industrial induction motor to the equivalent in Brazilian reais (BRL). This value served as a basis for the EFR’s estimated cost, which is derived from an induction motor with structural modifications. An increase of 20% over the original value of the motor was adopted to represent the additional adaptation costs required to transform the conventional motor into an EFR. This modification involves, for example, allowing the stator to rotate, which requires specific mechanical changes to the housing and the assembly system.

On the other hand, the proposal to use the EFR also results in savings in other components of the system. For the wind turbine, a 20% discount on the total cost was considered in relation to a conventional turbine [15]. This is justified by the elimination of equipment such as transformers, speed multipliers, and electronic converters, which become unnecessary due to the characteristics of the EFR for small systems.

Other relevant parameters include the number of photovoltaic modules (143 units), the presence of only one wind turbine and one inverter, and an estimated maintenance cost of BRL 0.05 per kWh generated. In addition, a 15% rate on the acquisition cost of all equipment, cables, and accessories was considered for estimating labor costs for installing the system. Finally, the electricity tariff adopted for revenue calculations corresponds to the value of BRL 0.3425 per kWh, as practiced in 2015, which is compatible with the historical data of the local distributor. These additional parameters were essential to improve the financial feasibility calculations and to ensure greater accuracy in obtaining the net present value (NPV) of the proposed system.

8. Results

The analysis of the simulated data allowed the assessment of the economic and financial viability of the proposed hybrid system, with emphasis on the NPV calculation, which reached BRL 1,855,971.99 in 2015 values, indicating a significant financial return over the 20 years of operation. The results are detailed in

Table 7. Annual financial indicators of the hybrid energy system (in BRL).

Year	Annual Maint.	Energy Price	Discounted Expenses	Discounted Revenues	Net Discounted Value	Payback
0	0.00	0.00	−631,255.80	0.00	−631,255.80	−631,255.80
1	−18,250.86	84,363.25	−17,217.79	79,587.97	62,370.18	−568,885.62
2	−21,287.80	107,723.43	−18,946.06	95,873.47	76,927.40	−491,958.22
3	−22,990.82	121,727.47	−19,303.54	102,204.73	82,901.20	−409,057.02
4	−24,830.09	137,552.04	−19,667.75	108,954.10	89,286.35	−319,770.67
5	−26,816.49	155,433.81	−141,635.44	116,149.19	−25,486.26	−345,256.93
6	−28,961.81	175,640.21	−20,416.94	123,819.41	103,402.48	−241,854.45
7	−31,278.76	198,473.43	−20,802.16	131,996.17	111,194.01	−130,660.44
8	−33,781.06	224,274.98	−21,194.65	140,712.90	119,518.24	−11,142.20
9	−36,483.54	253,430.73	−21,594.55	150,005.26	128,410.70	117,268.50
10	−39,400.23	286,376.72	−155,511.10	159,911.27	4400.17	121,668.67
11	−42,554.41	323,605.69	−22,417.13	170,471.44	148,054.31	269,722.98
12	−45,958.76	365,674.43	−22,840.09	181,728.99	158,888.90	428,611.88
13	−49,635.46	413,212.11	−23,271.04	193,729.96	170,458.92	599,070.80
14	−53,606.30	466,929.69	−23,710.12	206,523.45	182,813.33	781,884.13
15	−57,894.80	527,630.54	−196,398.17	220,161.79	23,763.62	805,647.75
16	−62,526.38	596,222.52	−24,613.28	234,700.78	210,087.50	1,015,735.25
17	−67,528.49	673,731.44	−25,077.68	250,199.89	225,122.21	1,240,857.46
18	−72,930.77	761,316.53	−25,550.84	266,722.52	241,171.68	1,482,029.13
19	−78,765.24	860,287.68	−26,032.93	284,336.27	258,303.34	1,740,332.47
20	−85,066.45	972,125.08	−187,473.68	303,113.19	115,639.52	1,855,971.99

, which presents, year by year, the annual maintenance costs, the energy tariff value, the updated (discounted) expenses and revenues, the annual cash flow (Total Desc.), and the accumulated cash flow (Payback).

The initial investment required to implement the system was BRL 631,255.80, reflecting installation and infrastructure costs. From the first year onwards, revenues from energy generation showed continuous growth, reaching BRL 972,125.08 in year 20, driven by the appreciation of the energy tariff. At the same time, maintenance expenses increased over time, starting at BRL 18,250.86 in year 1 and reaching BRL 85,066.45 in year 20, incorporating inflation adjustments and projected operating costs. Table 7 shows that the net cash flow (net discounted value) has positive values in the first four years, followed by a negative value in the fifth year. From the sixth year onwards, the flows become positive again, indicating greater financial stability of the system over time. However, the full return on the initial investment, as indicated by the Payback indicator, only occurs in the ninth year, when the accumulated cash flow becomes positive, totaling BRL 117,268.50.

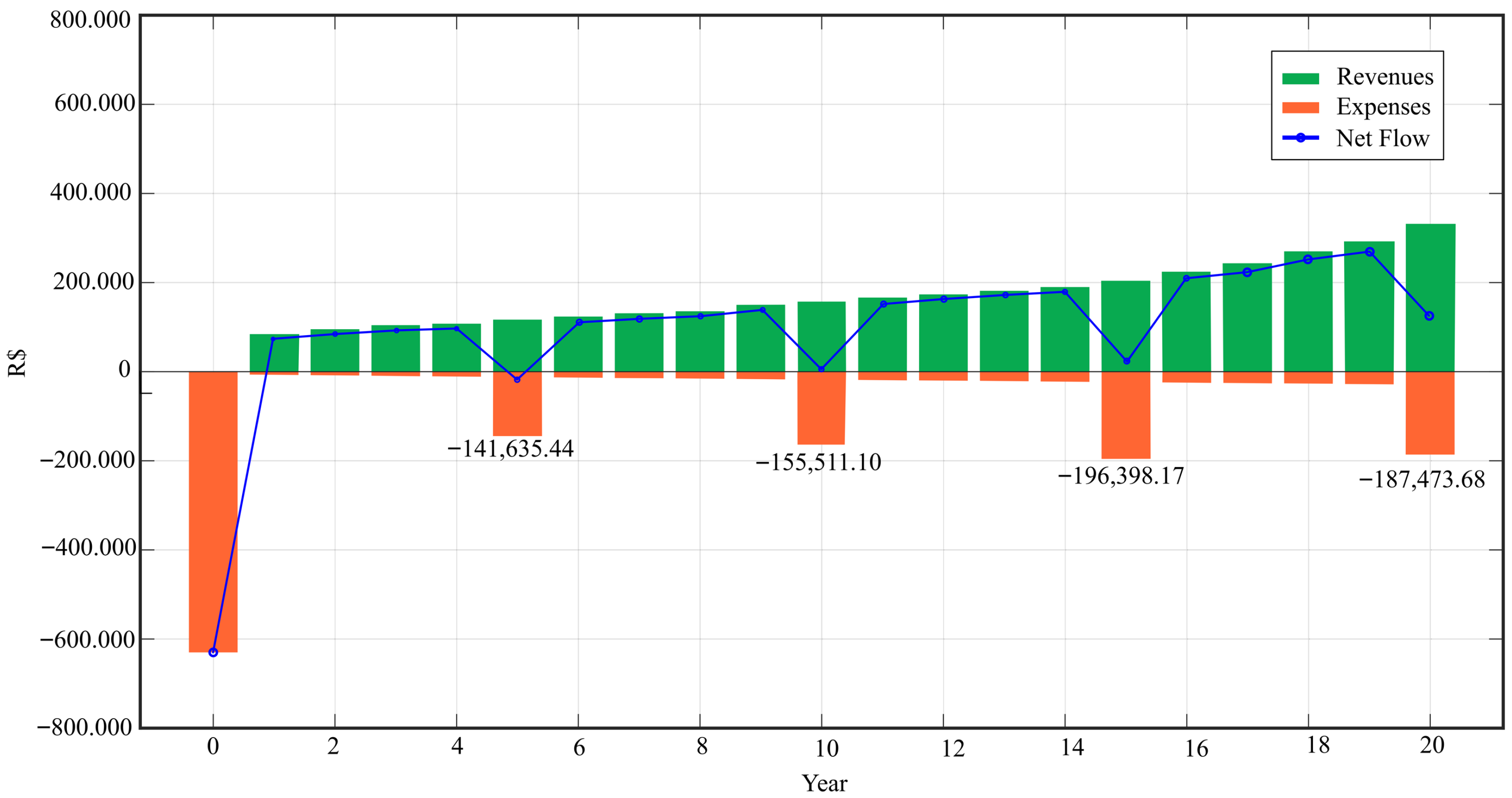
Figure 6 highlights the dynamics between revenues (green), expenses (orange), and net flow (blue) over 20 years. It can be observed that expenses presented notable peaks, such as in year 0 (-BRL 631,255.80), year 5 (-BRL 141,635.44), year 10 (-BRL 155,511.10), year 15 (-BRL 196,398.17) and year 20 (-BRL 187,473.68), reflecting initial investments and high operating costs at specific moments. The discounted revenues, in turn, grew consistently, reaching around BRL 304,000 in year 20, while net flow fluctuated but showed a recovery trend from the tenth year onwards, suggesting financial stabilization. 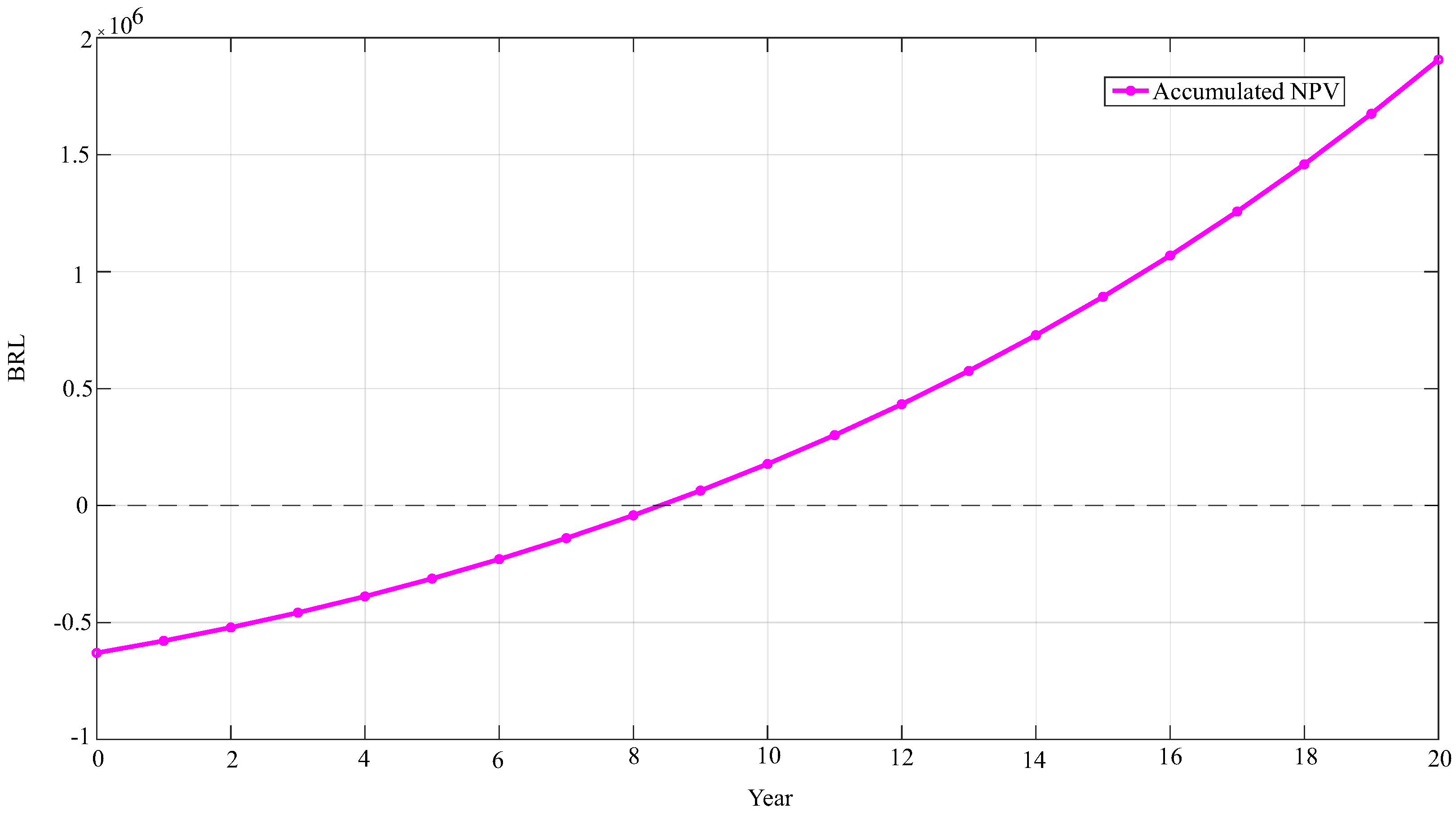Figure 7 complements this analysis by illustrating the accumulated NPV, which starts negative, crosses the break-even point around the eighth year, and reaches BRL 1,855,971.99 in year 20, demonstrating exponential growth and the economic viability of the project in the long term.

These findings corroborate the attractiveness of the proposed hybrid system. Despite the high initial costs and growing operating expenses, the balance between income and expenses, combined with the significant cumulative return, shows that the project achieves financial sustainability from the ninth year onwards, with a robust performance at the end of the analyzed horizon.

In Figure 7, there is an exponential growth in accumulated NPV from year 0, where it starts out negative, crossing the zero line around year 8 and reaching around 2 million in year 20. This indicates that the investment becomes profitable in the long term, with a significant return after the break-even point.

9. Sensitivity Analysis

The viability of HRES projects is subject to uncertainties and fluctuations in multiple economic, operational, and environmental parameters over their operational lifetime. Therefore, sensitivity analysis is a critical step to assess the robustness of the optimal sizing solution and to quantify the potential impact of these variations on the project’s financial performance metrics. This section presents the results of a comprehensive sensitivity analysis, examining how the net present value responds to $\pm 30\%$ variations in four key parameters: the electricity selling tariff, the acquisition cost of the electromagnetic frequency regulator (EFR), the cost of the wind turbine (accounting for the discount afforded by EFR integration), and the availability of climatic resources (solar irradiance + wind speed). The $\pm 30\%$ magnitude was chosen to represent aggressive scenarios, testing the project’s resilience under extreme conditions.

The reference scenario for this analysis is the optimal HRES configuration (PV ≈ 35 kWp, WT = 30 kW, ESS ≈ 200 kWh, and EFR = 30 kW), which yielded a cumulative NPV of BRL 1,855,971.99 (in 2015 values) at the end of the 20-year simulation horizon. The NPV values for each variation scenario are presented annually in

Table 8. NPV sensitivity analysis.

Year	Tariff ($\times {10}^3$)		Cost ($\times {10}^3$)		Discount ($\times {10}^3$)		Climate ($\times {10}^3$)
	−30%	30%	−30%	30%	−30%	30%	−30%	30%
0	−631.3	−631.3	−626.4	−636.1	−576.0	−686.5	−631.3	−631.3
1	−592.8	−545.0	−564.1	−573.7	−513.6	−624.2	−595.5	−509.2
2	−544.6	−439.3	−487.2	−496.8	−436.7	−547.2	−551.0	−359.3
3	−492.4	−325.8	−404.2	−413.9	−353.8	−464.3	−502.9	−198.1
4	−435.8	−203.8	−315.0	−324.6	−264.5	−375.0	−451.0	−24.9
5	−496.1	−194.4	−340.4	−350.1	−290.0	−400.5	−516.5	39.6
6	−429.8	−53.9	−237.0	−246.7	−186.6	−297.1	−456.0	239.5
7	−358.2	96.9	−125.9	−135.5	−75.4	−185.9	−390.9	454.1
8	−280.9	258.6	−6.3	−16.0	44.1	−66.4	−320.6	684.4
9	−197.5	432.1	122.1	112.5	172.5	62.0	−245.0	931.5
10	−241.1	484.4	126.5	116.9	176.9	66.4	−297.1	1062.9
11	−144.2	683.6	274.5	264.9	325.0	214.4	−209.6	1347.0
12	−39.8	897.0	433.4	423.8	483.9	373.3	−115.5	1651.5
13	72.5	1125.6	603.9	594.3	654.3	543.8	−14.4	1977.8
14	193.4	1370.4	786.7	777.1	837.2	726.6	94.2	2327.4
15	151.1	1460.2	810.5	800.8	860.9	750.4	38.6	2529.5
16	290.8	1740.7	1020.5	1010.9	1071.0	960.5	163.8	2930.4
17	440.8	2040.9	1245.7	1236.0	1296.1	1185.6	298.1	3359.6
18	602.0	2362.1	1486.8	1477.2	1537.3	1426.8	442.2	3819.0
19	775.0	2705.7	1745.1	1735.5	1795.6	1685.1	596.7	4310.6
20	799.7	2912.2	1860.8	1851.2	1911.2	1800.7	601.4	4675.6

Tariff: electricity selling tariff; cost: EFR acquisition cost; discount: wind turbine discount; climate: climate resources.

.

The electricity selling tariff constitutes the primary revenue source for the HRES, making it one of the most influential parameters on the project’s economic attractiveness. A 30% reduction in the selling tariff results in a substantially negative impact on the cumulative NPV. At the end of 20 years, the NPV falls to BRL 799,701.16, representing a decrease of approximately 56.9% relative to the base scenario (BRL 1,855,971.99). Although the project remains NPV-positive, this sharp decline underscores the high sensitivity of HRES profitability to energy tariff fluctuations and highlights the need for stable regulatory frameworks to mitigate investment risks. The payback period would also be significantly extended under this scenario; conversely, a 30% increase in the electricity selling tariff elevates the cumulative NPV to BRL 2,912,242.81 after 20 years, an increase of approximately 56.9% over the base case. This result demonstrates the substantial profit potential of the project under more favorable tariff conditions, accelerating the return on investment and enhancing financial robustness, thereby emphasizing the importance of supportive regulatory environments for renewable energy deployment.

The EFR is an innovative component designed to optimize wind turbine efficiency and reduce maintenance costs. The sensitivity analysis on its acquisition cost evaluates the influence of this investment on overall project profitability. The base cost for the 30 kW EFR is BRL 16,026.44. A 30% reduction in this cost yields a cumulative NPV of BRL 1,860,779.92 over 20 years, only a 0.26% increase relative to the base scenario. Similarly, a 30% increase in the EFR cost leads to an NPV of BRL 1,851,164.06, representing a 0.26% decrease from the base. The low sensitivity of NPV to EFR cost variations is attributed to its relatively small share of the total initial investment, dominated by larger capital items such as wind turbines, PV modules, and batteries. This suggests that, while EFR offers technical advantages such as improved power quality, harmonic reduction, and hybridization facilitation, its cost fluctuations do not constitute a primary financial risk for the project.

The wind turbine cost is one of the most significant capital investments in a hybrid renewable energy system. The base cost for the 30 kW turbine is BRL 184,253.56, already reflecting a 20% discount relative to a conventional model, justified by the elimination of auxiliary equipment (e.g., transformers and power converters) due to EFR integration. The ±30% variations reported in Table 8 refer to fluctuations around this discounted base cost. A 30% reduction in turbine cost increases the 20-year NPV to BRL 1,911,248.06, a gain of approximately 3.0% over the base case. Conversely, a 30% cost increase reduces the NPV to BRL 1,800,695.92, a decrease of about 3.0%. Although the turbine cost represents a considerable investment, the NPV sensitivity to its variations is moderate compared to tariff and climatic resource parameters. This indicates that the project can absorb significant turbine price fluctuations without fundamentally compromising viability, likely due to balanced contributions to total energy generation and cost-optimization benefits provided by the EFR.

The availability and consistency of solar and wind resources are determinants of HRES generation capacity. Variations in these resources directly affect energy output and project revenues. A 30% decrease in climatic resource availability (solar irradiance and wind speed) has the most severe impact on NPV, reducing it to BRL 601363.37 over 20 years, a decline of approximately 67.6% relative to the base scenario. While the NPV remains positive, such a scenario would necessitate a critical reappraisal of revenue projections and rigorous risk management strategies to address the inherent variability of renewable sources. Conversely, a 30% increase in resource availability boosts the cumulative NPV to BRL 4,675,634.40, a 151.9% rise over the base case. This represents the most optimistic scenario, underlining the substantial financial gains achievable under more favorable climatic conditions. It emphasizes the imperative for precise resource assessments and site selection to maximize investment returns.

Overall, the sensitivity analysis reveals that HRES NPV is most sensitive to variations in electricity selling tariffs and climatic resource availability, parameters that directly influence project revenues. Significant fluctuations in these factors can markedly alter the project’s financial attractiveness over a 20-year horizon. In contrast, acquisition cost variations for the EFR and the wind turbine exhibit moderate to low impacts on NPV. The particularly low sensitivity to EFR cost underscores that implementing this innovative technology, delivering operational and maintenance benefits, does not introduce substantial capital cost risk. The project’s robustness to equipment cost fluctuations indicates the effectiveness of the genetic algorithm in identifying an optimal configuration that balances initial investments with long-term benefits.

Even under aggressive ±30% variations, the GA-sized optimal HRES configuration demonstrates remarkable economic resilience. The project maintains a positive NPV (BRL 601,363.37) even in the most challenging scenario of reduced resource availability, confirming its fundamental viability and validating the optimization approach. This sensitivity analysis strengthens confidence in the proposed model’s applicability for real-world planning of renewable energy systems. For future work, it would be valuable to incorporate combined parameter variation scenarios and stochastic uncertainties in cost and resource projections to provide an even more comprehensive risk and opportunity assessment.

10. Comparison with Previous Project

To put the results in context, a comparison was made with a previous project, carried out in 2015 under the same conditions. The comparative data is summarized in

Table 9. Updated net present value (NPV) for the evaluated projects.

Project	NPV in 2015 (BRL)	NPV in 2025 (BRL)
Current Project	1,855,971.99	3,114,320.99
Previous Project	1,685,529.00	2,828,317.66

and

Table 10. Comparison of the main parameters between the proposed system and the project in 2015.

Parameter	Proposed System	Project 2015 (Delson et al. [15])
Wind energy generated (20 years)	2,006,460.54 kWh	1,922,800.00 kWh
PV energy generated (20 years)	2,353,115.41 kWh	5,122,453.00 kWh
Load demand (20 years)	2,105,590.68 kWh	2,105,590.68 kWh
Number of PV modules	143 (245 Wp)	504 (245 Wp)
Battery bank	91 (12 V, 220 Ah)	150 (12 V, 220 Ah)
NPV (2015)	BRL 1,855,971.99	BRL 1,685,529.00
NPV (2025)	BRL 3,114,320.99	BRL 2,828,317.66

, allowing a detailed analysis of the economic and technical performance of the proposed hybrid system of the reference project.

Table 9 shows the NPV values for both projects, in 2015 values and updated to 2025. The current project achieved an NPV of BRL 1,855,971.99 in 2015, which, adjusted for inflation, is equivalent to BRL 3,114,320.99 in 2025. In contrast, the Delson et al. [15] project recorded an NPV of BRL 1,685,529.00 in 2015, corresponding to BRL 2,828,317.66 in 2025. These results indicate that the proposed sizing technique has a superior economic performance, both in nominal terms and adjusted for inflation, showing significant improvements in the technical, operational, and financial parameters adopted in the current project.

Table 10 details the main technical and financial parameters of the two projects, allowing for a more in-depth analysis of the differences between them. The proposed system generated 2,006,460.54 kWh of wind energy over 20 years, slightly more than the project in Delson et al. [15], which produced 1,922,800 kWh. On the other hand, photovoltaic (PV) energy generation in the current project was 2,353,115.41 kWh, significantly lower than the 5,122,453 kWh of the 2015 project, which reflects a lower dependence on photovoltaic modules in the proposed hybrid system. This is corroborated by the number of PV modules used: 143 (245 Wp) in the current project, compared to 504 (245 Wp) in the project of Delson et al. Similarly, the battery bank in the proposed system consists of 91 units (12 V, 220 Ah), a reduction from the 150 units in the previous project, indicating optimization in the sizing of energy storage.

Despite the lower photovoltaic generation, the load demand met remained identical in both projects, totaling 2,105,590.68 kWh over 20 years, which suggests that the proposed system achieved greater efficiency in integrating wind and photovoltaic sources to meet the same energy needs. In addition, the higher NPV of the current project (BRL 1,855,971.99 in 2015 and BRL 3,114,320.99 in 2025) compared to the Delson et al. Project (BRL 1,685,529.00 in 2015 and BRL 2,828,317.66 in 2025) reflects better economic performance.

In summary, the comparative analysis shows that the proposed hybrid system has economic and technical advantages over the Delson et al. project, with higher efficiency in energy generation and storage, as well as a more significant financial return. These results reinforce the strategies adopted, consolidating the viability of the current project in the context of hybrid energy generation systems.

11. Discussions

The proposed optimization yielded a design favoring solar generation, supplemented by wind and appropriately sized battery storage, consistent with the site’s abundant solar resource. In this configuration, the EFR provides physical inertia, smoothing frequency fluctuations, and a higher renewable penetration without compromising stability. The optimized configuration resulted in a substantially positive NPV, indicating robust profitability over the project lifetime. These outcomes underscore the dual economic and environmental benefits of the proposed design.

Crucially, the GA algorithm was rigorously validated and tuned before application to the system model. It successfully converged using several standard benchmark functions, verifying correct implementation and convergence behavior. Key GA parameters were systematically adjusted: for example, a population of a few hundred individuals and moderate mutation/crossover rates balanced exploration with convergence speed. This careful tuning prevented premature convergence and ensured consistent attainment of high-quality solutions across multiple runs. Our use of NPV as the optimization metric follows common practice in energy system design, although multi-objective approaches (e.g., including emissions or reliability criteria) could be explored for a more comprehensive assessment.

A thorough sensitivity analysis characterized the solution’s robustness. We varied financial and technical inputs (discount rate, equipment costs, solar/wind resource levels, etc.) and observed that the optimal NPV remained positive under all tested scenarios, including ±30% variations in electricity tariff, component costs, and climatic resource availability. The NPV was most sensitive to climatic resource availability: for example, a 30% reduction in solar irradiance and wind speed resulted in $67.6\%$ drop in project NPV, underscoring the critical role of site-specific climate conditions in hybrid system planning. Financial parameters such as tariff or discount rate also had notable but comparatively smaller effects. Some limitations of the current study should be acknowledged. The optimization approach focused solely on maximizing NPV, without explicitly enforcing renewable penetration thresholds or reliability constraints. Despite these limitations, the proposed hybrid system is shown to be both economically viable and environmentally beneficial, offering practical insights for the design of future grid-connected hybrids.

12. Conclusions

The present study has demonstrated a robust methodology for the economic design of a grid-connected hybrid renewable system equipped with an electromagnetic frequency regulator. By integrating detailed component modeling with a validated GA optimizer, the optimal configuration was found to deliver strong economic performance and high renewable utilization. Specifically, the optimized system meets almost all of its load demand from PV and wind generation while yielding a high NPV (1.86 M) over the project horizon. The inclusion of the EFR was critical in achieving this result by enhancing frequency stability, which enabled the high renewable penetration. Overall, the optimized design achieves a strong economic return. The sensitivity analysis confirmed the robustness of the proposed approach under a wide range of conditions, including ±30% variations in electricity tariff, wind turbine costs, EFR acquisition costs, and climate resource availability. In all cases, the NPV remained positive, highlighting the method’s resilience to economic and environmental uncertainties. Furthermore, a comparative analysis with a 2015 reference project revealed a 10.1% increase in NPV, underscoring the economic advantages of the proposed improvements. These findings position the proposed methodology as a high-impact planning tool for hybrid energy systems in both remote and grid-connected regions, contributing meaningfully to the ongoing energy transition. Future research should investigate multi-objective optimization frameworks that jointly minimize CO₂ emissions and maximize financial returns. Additionally, the incorporation of machine learning-based climate forecasting could further enhance the accuracy and robustness of hybrid system sizing under variable meteorological conditions.