Optimal Sizing of Residential PV and Battery Systems Under Grid Export Constraints: An Estonian Case Study

Abstract

This study investigates the optimal sizing of photovoltaic (PV) and battery storage (BAT) systems for Estonian households operating under grid constraints that prevent selling surplus energy. We develop and compare three sizing models of increasing complexity, ranging from a simple heuristic to a full simulation based optimization. Their performance is evaluated using a multi-criteria decision analysis (MCDA) framework that integrates Net Present Value (NPV), Internal Rate of Return (IRR), Profitability Index Ratio (PIR), and payback period. Sensitivity analyses are used to test the robustness of each configuration against electricity price shifts and market volatility. Our findings reveal that standalone PV-only systems are the most economically robust investment. They consistently outperform combined PV + BAT and BAT-only configurations in terms of investment efficiency and overall financial attractiveness. Key results demonstrate that the simplest heuristic-based model (Model 1) identifies configurations with a better balance of financial returns and capital efficiency than the more complex simulation-based approach (Model 3). While the optimization model achieves the highest absolute NPV, it requires significantly higher investment and results in lower overall efficiency. The economic case for batteries remains weak, with viability depending heavily on price volatility and arbitrage potential. These results provide practical guidance, suggesting that for grid constrained households, a well-sized PV-only system identified with a simple model offers the most effective path to cost savings and energy self-sufficiency.

1. Introduction

Globally, installed photovoltaic (PV) capacity has soared in the past decade thanks to steep declines in panel costs, supportive policy incentives, and growing interest in self-generation and flexible demand. By the end of 2023, cumulative PV capacity worldwide topped 1 $\mathrm{T}$$\mathrm{W}$, but this rapid expansion also brought new challenges for distribution networks. Excess solar output can push voltages above safe limits, create reverse flow bottlenecks, and negative wholesale prices during sunny, low-demand hours [1,2]. In recent years, midday prices have frequently turned negative, which limits the economic benefit of PV to saving on network related charges, since electricity cannot be exported profitably.

In Estonia, total installed PV capacity has grown from under 50 $\mathrm{M}$$\mathrm{W}$ in 2018 to over 500 $\mathrm{M}$$\mathrm{W}$ by mid-2025, though a large share of this is obtained from utility-scale ground mounted plants. Residential rooftop systems accounted for around 12,000 installations by the end of 2024 [3,4]. Unlike countries that allow net-metering or generous feed-in tariffs, many Estonian low-voltage feeders cannot handle power flowing back from households. As a result, any surplus solar generation must be curtailed or stored on site. Battery storage has thus become essential not only to boost household self-consumption but also to relieve stress on the local grid.

Over the years, researchers have tested PV-battery co-sizing across a range of market designs and regulations. Foundational works focused on the techno economic impacts of tariffs and sizing ratios. For example, Khalilpour and Vassallo [2] emphasized that the gap between retail and export tariffs, rather than the tariff levels themselves, most influences the value of storage, while Luthander et al. [1] showed that pairing PV with appropriate battery capacities can significantly improve self-consumption.

More recent studies have incorporated advanced decision frameworks to address this challenge. For example, Nizami et al. [5] employed a bi-level optimization strategy that modeled real time price signals and comfort constraints, reporting cost savings of up to 51%. In a different approach, Li [6] applied a genetic algorithm, demonstrating that optimal capacities in Australia are strongly dependent on individual load profiles and tariff structures. Complementing these technical analyses, Nousdilis et al. [7] focused on policy, assessing how different incentive schemes affect NPV-optimal sizing to provide insights for both policymakers and prosumers.

Emerging research expands on these methods by incorporating multi-criteria decision analysis (MCDA) frameworks. Jiang et al. [8] provided a comprehensive review of optimization models for battery sizing, highlighting hybrid mathematical programming and heuristic approaches. Nematirad et al. [9] proposed a statistical methodology for sizing systems to reduce peak demand using Monte Carlo simulations, emphasizing robustness. Importantly, Sandelic et al. [10] evaluated simplified sizing rules against comprehensive modeling, finding that heuristic based approaches can provide robust results with much lower data complexity, a finding that supports the direction of our study.

Despite these advances, there remains a gap in applying a unified multi-criteria decision analysis (MCDA) that integrates payback period (ROI), net present value (NPV), internal rate of return (IRR), and profitability index ratio (PIR) under strict export constraints and volatile price trajectories in the Estonian context. This paper aims to determine which sizing strategies provide the most robust and economically attractive investment paths under grid export constraints and volatile price conditions in Estonia. To achieve this, we develop and compare three progressively sophisticated sizing models: a simple annual consumption heuristic; a profile-based method distinguishing key time periods; and a full hourly simulation with a brute-force search over PV and battery capacities. These models are then systematically compared using the MCDA framework. Through sensitivity analyses under diverse price scenarios, we identify which sizing approaches provide the most reliable and economically sound guidance for PV and storage investments in Estonia.

2. Data

This study relies on three primary datasets: household electricity consumption, solar irradiation, and electricity prices. These datasets are used to support the sizing models and economic analyses described in Section 3 and Section 4.

2.1. Electricity Consumption Data

We utilized real consumption data from 2023, drawn from 640,903 distinct Estonian households (Estonian electricity data from [Statistics Estonia, 2023]). The dataset spans an entire calendar year with hourly measurement intervals, ensuring a detailed temporal resolution of electricity usage.

Basic preprocessing steps included:

• Missing values: Interpolated linearly whether any household had under 24 h of missing data consecutively; otherwise, that household’s data were excluded to maintain consistency.
• Outlier removal: Extreme consumption values more than three standard deviations from the mean were clipped to the 99th percentile to prevent artificial bias in calculations.
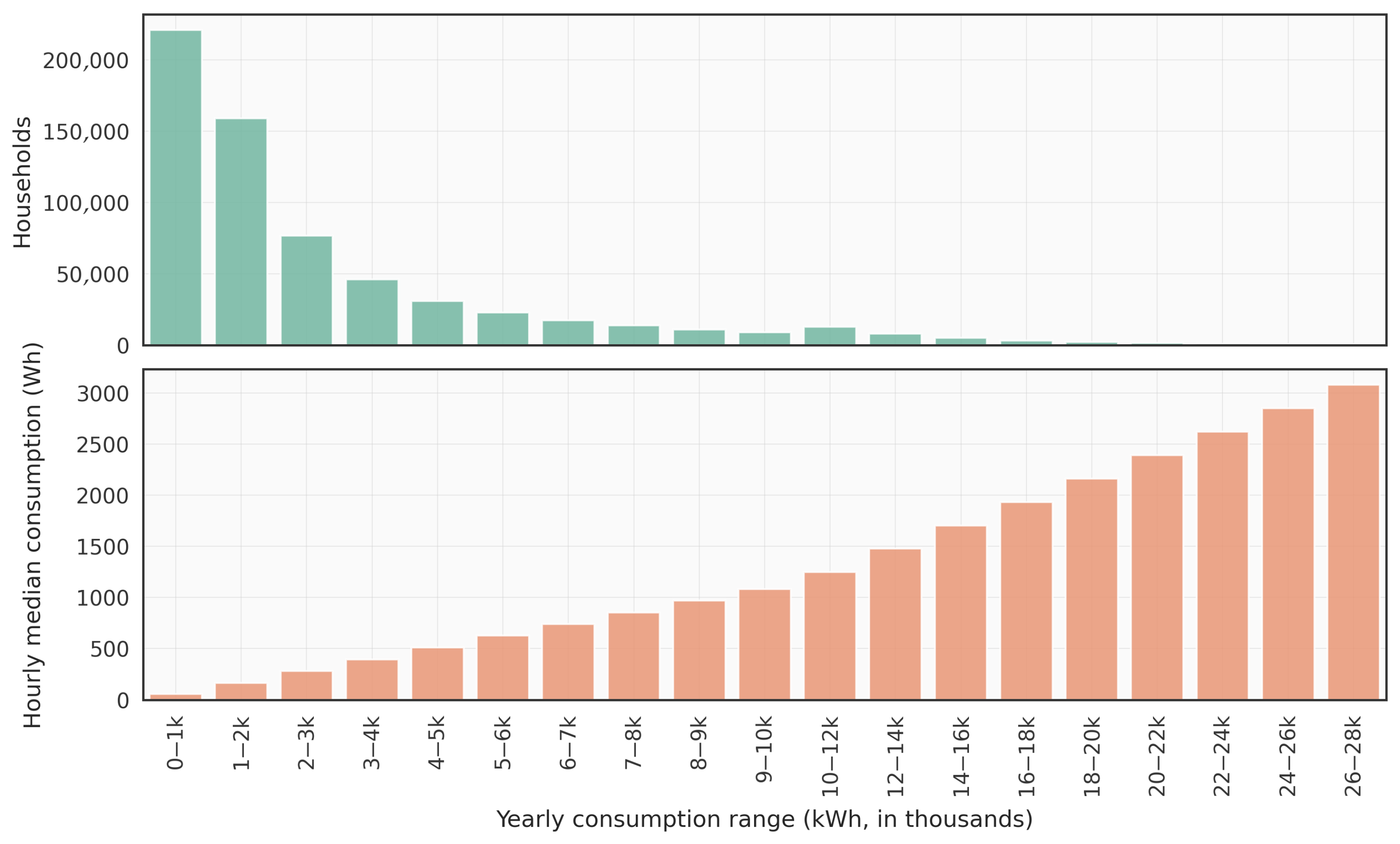
• High consumption filtering: Households with yearly consumption exceeding 28,000 kWh were removed. These cases were rare and behaved more like outliers, disproportionately skewing the consumption profiles. As shown in Figure 1, the number of households decreases sharply in higher consumption ranges.

Yearly Consumption Bins

Households were grouped into bins based on their yearly electricity consumption. The first bin (0–1000 kWh) contained many empty or seasonally occupied dwellings. Many of the included households are also apartments, which typically lack roof space or legal permission to install solar panels. This limits their suitability for PV adoption and should be considered when interpreting aggregate results. Subsequent bins increased in increments of 1000 kWh for lower consumption ranges and in larger intervals for higher ranges. Each bin contained the households whose annual consumption fell within its specified range. Figure 1 illustrates the distribution of households and shows the median hourly consumption in each bin.

2.2. Solar Irradiation Data

Solar irradiation data were obtained from the Open-Meteo Weather Forecast API [11], providing hourly GHI at Estonia’s latitude and longitude. These GHI values, together with cyclic time features, are normalized and passed through a pre-trained Random Forest regressor to predict hourly kWh outputs.

2.3. Electricity Price Data

We sourced electricity price information (real-time and historical) from the Elering API [12] that is aligned with the Nord Pool market [13]. This dataset covers the full year of 2023, capturing fluctuations and volatility across different time periods. The granularity is in hourly prices which match the resolution of the consumption data. Additionally, future scenarios are constructed by modifying these baseline prices to assess how static changes or volatility affect system economics.

3. Methodology

We developed three distinct models to determine optimal PV and battery (BAT) sizes for households that cannot sell excess electricity to the grid. Each model represents a different level of complexity and data requirement, ranging from simple heuristics to more detailed simulations.

For each annual consumption range, we applied the three models to estimate ideal sizes for PV only, battery only, and combined PV + BAT systems. These size estimates were used as inputs in our simulation framework [14].

The simulation models hourly electricity flows between generation, storage, and consumption, taking into account charging and discharging limits, state of charge constraints, battery degradation, and historical electricity prices from 2023. Each configuration is evaluated over one year to estimate cost savings, payback period, and other financial indicators. Simulations are based on average hourly consumption profiles for different household consumption ranges, reflecting typical Estonian conditions.

To compare the configurations, we use a multi-criteria decision analysis (MCDA) approach. This aggregates four financial metrics into a single score. The weighting of each metric reflects its relative importance and scale, as detailed in Section 4.1. This composite score is the main metric used to rank system configurations.

3.1. Model 1: Simple Yearly Consumption-Based Estimation

A first-order estimate based solely on a household’s annual electricity use, Model 1 is intended for quick feasibility checks when finer resolution consumption data are unavailable.

3.1.1. PV Sizing

The PV system size is determined as a direct percentage of the household’s total annual consumption. While based on a simple heuristic, the sizing factor was calibrated to ensure the model produces outputs in a realistic range compared to the more complex models, making it a pragmatic and accessible starting point for preliminary assessments. The formula is

$$P_{\mathrm{PV}}=\alpha \times E_{\mathrm{annual}},$$

(1)

where $E_{\mathrm{annual}}$ is the annual consumption in kWh and $\alpha =0.0002$. This sizing factor means the installed PV capacity in kW is 0.02% of the annual energy consumption in kWh.

3.1.2. Battery Sizing

Similarly, the battery’s energy capacity is sized to cover a fraction of the average daily load, ensuring it can meet typical needs during hours without sun. The capacity is calculated as

$$E_{\mathrm{bat}}=\beta \times {\displaystyle \frac{E_{\mathrm{annual}}}{365}},$$

(2)

with the dimensionless coefficient $\beta =0.25$. This value, drawn from [15], was validated against our more complex models to ensure it represents a reasonable baseline for storing a fraction of the daily load (approximately six hours of average consumption).

3.1.3. Advantages and Limitations

Model 1 is extremely quick and data-light, making it ideal for preliminary feasibility studies. However, it does not account for the following:

• Hourly or daily consumption variations;
• Real-time electricity prices or solar irradiation patterns;
• Load shifting opportunities afforded by batteries.

3.2. Model 2: Consumption Patterns and Peak Demand Adjustment

3.2.1. Overview

Model 2 leverages hourly load profiles and simple solar irradiance thresholds to distinguish “sunny” from “non-sunny” hours, then sizes PV and battery separately for each regime.

3.2.2. Defining Sunny Hours

We classify any hour with measured global horizontal irradiance above 200 W/m² as “sunny” [16,17]. All other hours are “non-sunny.”

3.2.3. Identifying High Consumption Periods

We identify periods of high demand by first establishing a threshold based on the 75th percentile ($Q_{75}$) of consumption during non-sunny hours. Any hour where consumption exceeds this threshold is classified as a “high-consumption” period. This filtering is performed over a rolling six-hour window to capture sustained peaks in usage.

3.2.4. Battery Sizing

The optimal battery size $B_{\mathrm{optimal}}$ is estimated by examining daily sums of these high-consumption periods during non-sunny hours:

$$B_{\mathrm{optimal}}=\mathrm{Median}\left(S_{\mathrm{peak},\mathrm{daily}}\right),$$

(3)

where

$$S_{\mathrm{peak},\mathrm{daily}}=\sum _{\mathrm{day}}{C}_{\mathrm{high},\mathrm{day}}$$

(4)

If the user wants more conservative sizing (to ensure coverage of nearly all peak events), the mean or upper percentile could be used instead of the median. This choice should align with household risk tolerance.

3.2.5. PV Sizing

The PV size $P{V}_{\mathrm{optimal}}$ is selected to meet the maximum hourly consumption during sunny hours:

$$P{V}_{\mathrm{optimal}}=max\left(C_{\mathrm{sunny}}\right)$$

(5)

where

$$C_{\mathrm{sunny}}=c_t\mid t\in \mathrm{sunny}\mathrm{periods}$$

(6)

3.2.6. Combining PV and Battery

For households that install both, a slight oversizing of the PV system can be beneficial:

$$P{V}_{\mathrm{bat}}=\gamma \times P{V}_{\mathrm{optimal}}+B_{\mathrm{optimal}}$$

(7)

where $\gamma$ is a PV oversizing factor that accounts for additional generation needed to support battery charging. While $\gamma =1.2$ is used illustratively here, its optimal value may vary depending on local climate conditions and economic parameters [18,19].

3.3. Model 3: Simulation-Based Optimal PV and Battery Sizing

3.3.1. Overview

Model 3 employs a simulation framework with a iterative search approach to jointly optimize both PV and battery sizes under realistic conditions:

• Hourly consumption;
• Hourly PV generation (based on irradiation data);
• Hourly electricity prices (no selling back to the grid permitted).

3.3.2. Simulation Framework Parameters

• Time resolution: the simulation runs on an hourly basis to align with the consumption and price datasets.
• Investment cost assumptions: battery cost approximately 300 EUR/kWh and PV cost approximately 600 EUR/kW. These estimates are for turnkey systems, inclusive of all hardware and installation costs. The figures are based on recent 2023–2024 Estonian market data, including the Auvere utility scale battery project and reports from Eesti Energia and the Estonian Renewable Energy Chamber [20,21,22].
• Battery degradation: modeled via a simplified linear approximation over the system’s lifetime, similar to [23]. The first year’s revenue is interpolated using arithmetic or geometric sequences to reflect diminishing capacity but without simulating each year in detail. The residual value of the battery is conservatively assumed to be zero at the end of its service life.
• Efficiency factors: charging/discharging efficiencies ${\eta }_{\mathrm{ch}}$ and ${\eta }_{\mathrm{dis}}$ each set at 95%. Round-trip efficiency is then 90%.
• Battery power limit: A battery can charge or discharge at 50% of its capacity in kWh. For example, a 10 kWh battery can charge or discharge at a maximum rate of 5 kW. This is a common rule of thumb for C-rate design in grid-storage applications [24].

3.3.3. Optimization Logic

We explore a range of discrete PV sizes (e.g., 1–30 kW) and battery capacities (e.g., 1–50 kWh). For each pair, the simulation:

1.

Calculates self-consumption and battery usage over a full year, given hourly prices and irradiation;

2.

Estimates total cost savings versus a baseline of buying 100% of electricity from the grid;

3.

Computes the financial metrics (ROI, NPV, IRR, PIR) considering the capital investment and operational savings.

While advanced solvers could also be used, our use of a discrete, iterative search over a defined and manageable range of system sizes was computationally feasible for this study and guarantees finding the global optimum within the specified discrete search space.

3.3.4. Objective Function and Constraints

The framework’s objective is to minimize the net cost of electricity over the project lifetime, formulated as

$$min\sum _{t=1}^T\left(p_t^{\mathrm{buy}}\times G_t^{\mathrm{in}}\right)+I,$$

(8)

where $G_t^{\mathrm{in}}$ is the energy drawn from the grid, $p_t^{\mathrm{buy}}$ is the hourly purchase price, and I is the total investment. This optimization is subject to several key operational constraints:

• No grid export: Energy sold to the grid, $G_t^{\mathrm{out}}$, must be zero for all hours t.
• Battery state of charge: $SO{C}_{min}\le SO{C}_t\le SO{C}_{max}$.
• Battery power limits: The charging and discharging power, $P_{\mathrm{ch},t}$ and $P_{\mathrm{dis},t}$, cannot exceed the battery’s maximum power ratings.
• Hourly energy balance: The household’s load ($L_t$) plus any energy used to charge the battery must be met by a combination of grid imports, PV generation ($P_{\mathrm{PV},t}$), and battery discharge: $L_t+P_{\mathrm{ch},t}=G_t^{\mathrm{in}}+P_{\mathrm{PV},t}+P_{\mathrm{dis},t}$.

4. Simulations and Sensitivity Analysis

To evaluate the economic performance and reliability of the proposed PV and BAT sizing models (Models 1–3), we performed detailed simulations and sensitivity analyses. This process included setting a baseline scenario to compare model performance and systematically varying key parameters to assess how each model responds to electricity price changes and market volatility.

4.1. Financial Metrics and Multi-Criteria Decision Analysis (MCDA)

To evaluate each system more comprehensively than just using ROI, we use four financial metrics:

• NPV [EUR]: Net Present Value, reflecting long-term profitability.
• IRR [%]: Internal Rate of Return, representing investment efficiency.
• PIR [–]: Profitability Index Ratio, a benefit-to-cost ratio.
• ROI [years]: Payback period (shorter values are preferable).

We combine these into a single score using a simple multi-criteria decision analysis (MCDA) approach. This makes it easier to compare different system configurations. Each metric is assigned a weight, and the score is calculated as

$$\mathrm{Score}=w_{\mathrm{NPV}}·\mathrm{NPV}+w_{\mathrm{IRR}}·\mathrm{IRR}+w_{\mathrm{PIR}}·\mathrm{PIR}+w_{\mathrm{ROI}}·\left({\displaystyle \frac{1}{\mathrm{ROI}}}\right),$$

(9)

with the following weights: $w_{\mathrm{NPV}}=0.0004$, $w_{\mathrm{IRR}}=0.3$, $w_{\mathrm{PIR}}=0.2$, and $w_{\mathrm{ROI}}=1.0$.

The weights are chosen to ensure the different metrics are on roughly the same scale and to reflect their importance. ROI is given the most weight, since a short payback time is often the most critical factor for households. NPV has the smallest weight because its absolute value (in euros) tends to be much larger than the other metrics. IRR and PIR help capture longer-term investment quality and profitability.

This composite score is the main decision metric used throughout the analysis.

Weighting Subjectivity

It is important to acknowledge that the choice of weights in the MCDA is inherently subjective and reflects a specific set of priorities. The weights used here represent a typical homeowner’s preference for a quick payback and strong investment efficiency. A different set of priorities (e.g., maximizing long term absolute profit) would result in a different weighting scheme and could alter the final rankings. A formal sensitivity analysis of these weights or the use of methods like the Analytic Hierarchy Process (AHP) to derive them more objectively is a valuable extension for future work but falls outside the scope of this study.

4.2. Baseline Scenario

The baseline scenario represents typical conditions in Estonia using historical electricity prices from 2023, sourced from the Nord Pool Spot market. This scenario provides a standard reference point to compare the performance of each model.

Table 1. Key parameters and assumptions for the simulation framework.

Parameter	Value/Assumption
Battery cost per kWh	300 EUR
PV cost per kW	600 EUR
Battery degradation	Simplified linear approximation
PV degradation	Simplified linear approximation
Battery charging/discharging speed	50% of capacity per hour
Simulation resolution	Hourly data
Electricity price (buy)	NPS price
Network price (buy)	0.08 EUR/kWh
Renewable energy fee	0.0128 EUR/kWh
Electricity excise duty	0.00145 EUR/kWh
Can sell	No

summarizes the key assumptions and parameters used.

We evaluated each model using financial metrics such as Net Present Value (NPV), Return on Investment (ROI), Internal Rate of Return (IRR), and Profitability Index Ratio (PIR). These results allowed us to compare each model’s performance clearly.

4.3. Sensitivity Analysis to Static Price Changes

To evaluate model robustness and adaptability under varying market conditions, we conducted a comprehensive price sensitivity analysis across electricity price changes ranging from −30% to +30% relative to the 2023 Estonian baseline. This analysis provides insights into how each sizing methodology responds to market volatility and which approaches offer the most reliable performance across different economic scenarios. The price sensitivity analysis examines two key dimensions:

• Relative impact: percentage change in performance metrics relative to baseline conditions.
• Robustness assessment: statistical measure of performance stability across price scenarios using the coefficient of variation (CV) of MCDA scores and NPV values.

For each price scenario, we calculated performance metrics across all three models and technology configurations. The price sensitivity score was computed as the coefficient of variation of MCDA scores across all price scenarios, providing a normalized measure of model robustness.

4.4. Sensitivity Analysis to Price Volatility

Given that electricity market prices frequently change, we assessed the impact of price volatility on system performance. We generated new price scenarios by applying multiplicative Gaussian noise to the 2023 hourly baseline electricity prices. This method adjusts each hourly price by a random percentage, using standard deviations of 5%, 10%, 15%, and 20% to simulate different levels of market volatility.

The goal was to understand how effectively battery systems capitalize on price arbitrage charging when prices are low and discharging when prices are high. By analyzing the resulting changes in NPV, ROI, and PIR, we can illustrate each system’s ability to manage economic risk under uncertain market conditions.

To quantify robustness across these scenarios, we calculated the coefficient of variation (CV) for each configuration. Specifically, the CV of the MCDA scores and NPV values was computed across all volatility levels. As in the static price sensitivity analysis, the CV provides a normalized measure of stability, with lower values indicating more consistent performance under variable pricing. This allows direct comparison of model robustness across different technologies and sizing approaches.

5. Results and Discussion

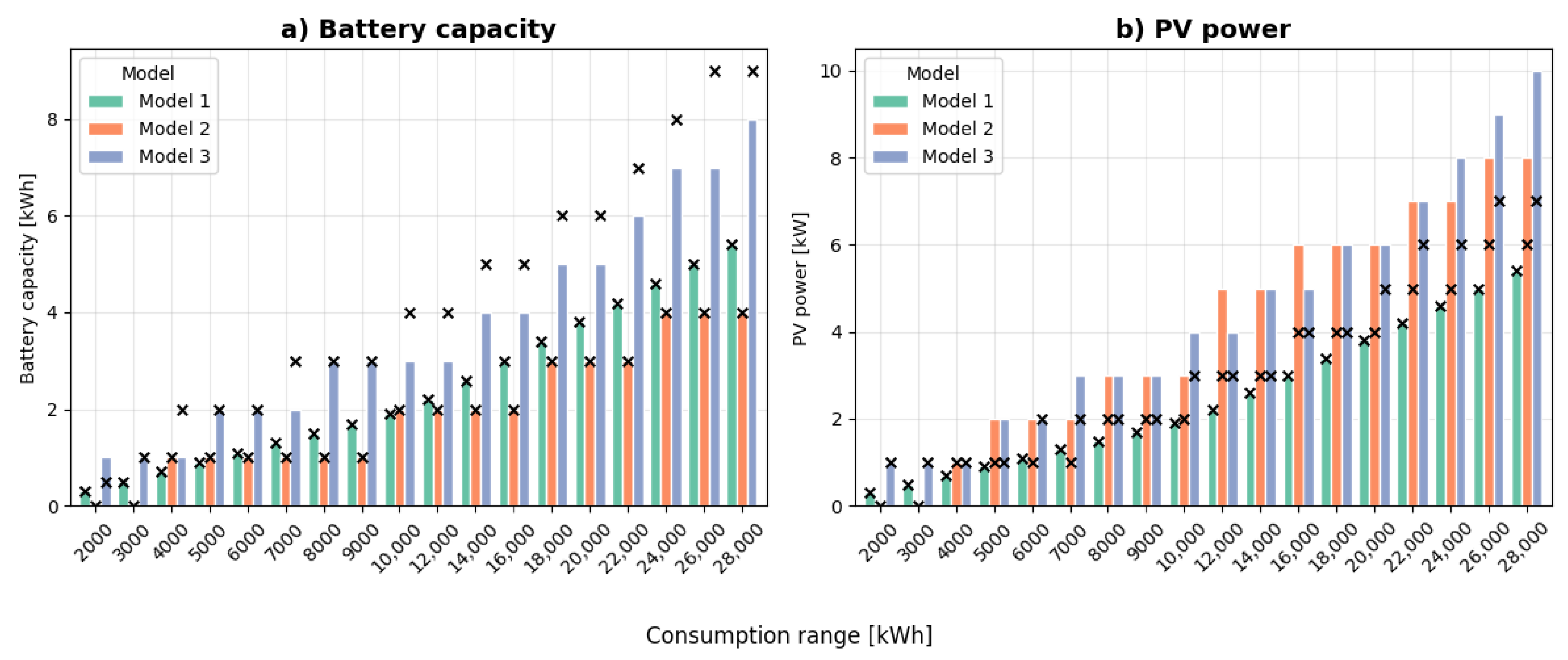
The baseline scenario uses 2023 Estonian electricity prices to evaluate three distinct sizing methodologies across different technology configurations. While all models scale their recommended capacities with household consumption, their underlying strategies result in significant differences in system configuration, investment cost, and financial performance, as demonstrated in Figure 2 and Figure 3 as well as summarized in

Table 2. Average performance by model and technology.

Technology	Model	Invest [EUR]	NPV/Invest	Profit/Invest	NPV [EUR]	IRR [%]	ROI [yrs]	PIR	MCDA	MCDA_Std
Battery	Model 1	735	0.85	0.148	625	14.0	6.6	3.02	5.20	0.11
	Model 2	583	0.92	0.154	540	14.5	6.5	3.10	5.36	0.21
	Model 3	1325	0.57	0.126	752	11.2	7.9	2.54	4.28	0.30
PV	Model 1	1470	2.24	0.260	3296	27.1	3.7	5.47	10.82	0.57
	Model 2	1667	1.96	0.237	3259	24.4	4.1	4.95	10.04	1.03
	Model 3	2000	1.69	0.216	3379	21.4	4.6	4.37	8.86	1.25
PV + Battery	Model 1	2205	1.83	0.227	4033	23.2	4.2	4.72	9.76	0.61
	Model 2	3050	1.33	0.187	4051	18.2	5.3	3.78	8.24	1.08
	Model 3	3783	1.17	0.174	4408	16.7	5.7	3.51	7.65	1.17

.

5.1. Model Sizing Strategies and Performance

Our analysis reveals three divergent sizing philosophies:

• Model 1 operates on a direct, linear scaling principle, tying PV and battery capacity directly to annual consumption. As shown in Figure 2, this approach yields unique sizing recommendations for each consumption bracket, with perfect correlation between consumption and capacity. For combined systems, it maintains a strict 1:1 ratio of PV power (kW) to battery capacity (kWh). This straightforward methodology demonstrates strong consistency across different household consumption levels (MCDA standard deviation of 0.61 for PV + Battery) and achieves the highest overall MCDA ranking (9.76), making it particularly attractive for practical implementation due to minimal data collection and computational requirements.
• Model 2 takes a fundamentally different approach, grouping households into broader categories and recommending standardized, discrete system sizes (e.g., 1, 2, or 4 kWh batteries). This methodology focuses on covering specific high consumption periods during non-sunny hours rather than total annual consumption. A notable characteristic of Model 2 is its aggressive oversizing of PV arrays when paired with batteries, maintaining an average PV/Battery ratio of 2.11 compared to Model 1’s 1.00 ratio. This strategy aims to ensure adequate battery charging even during suboptimal solar conditions, though it significantly increases upfront investment costs (EUR 3050 average for PV + Battery versus EUR 2205 for Model 1).
• Model 3 performs comprehensive optimization across all possible configurations to maximize economic returns. It consistently recommends the largest system capacities across all technology categories (Figure 2), leading to the highest absolute Net Present Value but at the cost of substantially higher initial investments. Model 3 also suggests a smaller battery in a combined system compared to a standalone battery system (15.7% smaller on average). For PV + Battery systems, Model 3 requires an average investment of EUR 3783 compared to EUR 2205 for Model 1, while delivering only marginally higher NPV (EUR 4408 vs. EUR 4033). The investment efficiency analysis reveals Model 3’s fundamental trade off: highest absolute returns but lowest NPV to investment ratio (1.17) among all approaches.

5.2. Technology Configuration Analysis

The financial performance data reveal a markedly different landscape than initially expected, with important implications for technology selection strategies. Figure 3 illustrates these performance relationships across all evaluated metrics.

PV-only systems emerge as the clear financial winners, delivering the highest MCDA scores across all three models (8.86 to 10.82) and exceptional investment efficiency. Model 1 achieves particularly strong performance with an NPV of EUR 3296, IRR of 27.1%, and rapid 3.7 year payback period. The NPV to investment ratio of 2.24 for Model 1 PV only systems significantly exceeds all other technology configurations, indicating superior capital efficiency. This performance reflects the straightforward economics of solar generation without the complexity and additional costs associated with energy storage.

PV + Battery systems show modest performance improvements over PV-only in absolute terms but suffer from reduced investment efficiency due to higher capital requirements. NPV values range from EUR 4033 to EUR 4408, representing only 23–30% improvement over PV-only systems despite requiring 50–90% additional investment. The IRR values (16.7–23.2%) are notably lower than PV-only systems (21.4–27.1%), and payback periods extend to 4.2–5.7 years. Model 1 achieves the best performance in this category with an MCDA score of 9.76, though this still falls short of its PV-only performance (10.82).

Battery-only configurations demonstrate the most challenging economics, with limited NPV potential (EUR 540–EUR 752) and extended payback periods (6.5–7.9 years). The investment efficiency ratios (0.57–0.92) indicate that these systems struggle to generate attractive returns through energy arbitrage alone. Model 2 shows marginal superiority in this category with the lowest average investment (EUR 583) and highest efficiency ratio (0.92), though the absolute performance remains modest across all metrics.

5.3. Comparative Analysis of Baseline Results

The investment efficiency analysis provides crucial insights into the relationship between system size and financial attractiveness. Table 2 reveals that Model 1 consistently achieves superior investment efficiency across all technology categories, balancing adequate system sizing with reasonable capital requirements.

For PV-only systems, Model 1’s efficiency advantage is substantial, achieving an NPV to investment ratio of 2.24 compared to 1.69 for Model 3, despite requiring 26% less capital (EUR 1470 vs. EUR 2000). This pattern suggests diminishing returns from aggressive system oversizing, where additional capacity fails to generate proportional economic benefits.

The PV + Battery category shows even more pronounced efficiency differences. Model 1’s ratio of 1.83 significantly exceeds Model 3’s 1.17 while requiring 42% less initial investment. This finding challenges the assumption that optimization algorithms necessarily deliver superior financial outcomes, highlighting the importance of balancing absolute returns with capital efficiency.

Model consistency analysis reveals additional strategic considerations. Model 1 demonstrates the most stable performance across different household consumption levels, with MCDA standard deviations consistently below 0.61. In contrast, Models 2 and 3 show greater variability, particularly for complex technology configurations, making standardized recommendations more challenging.

The conclusion that the simplest model outperforms the most complex one stems from the critical tradeoff between maximizing absolute returns and maintaining capital efficiency. Model 3, through its exhaustive optimization, successfully identifies configurations with the highest absolute NPV. However, achieving these returns requires substantial initial investments, which reduces overall investment efficiency (i.e., lower IRR, PIR, and longer ROI). In contrast, Model 1 recommends smaller, more affordable systems that deliver a better balance of returns relative to the capital invested. Our MCDA framework, which places significant weight on efficiency and rapid payback, consequently favors the more balanced and less capital intensive approach of Model 1.

5.4. Sensitivity Analysis: Static Price Shifts

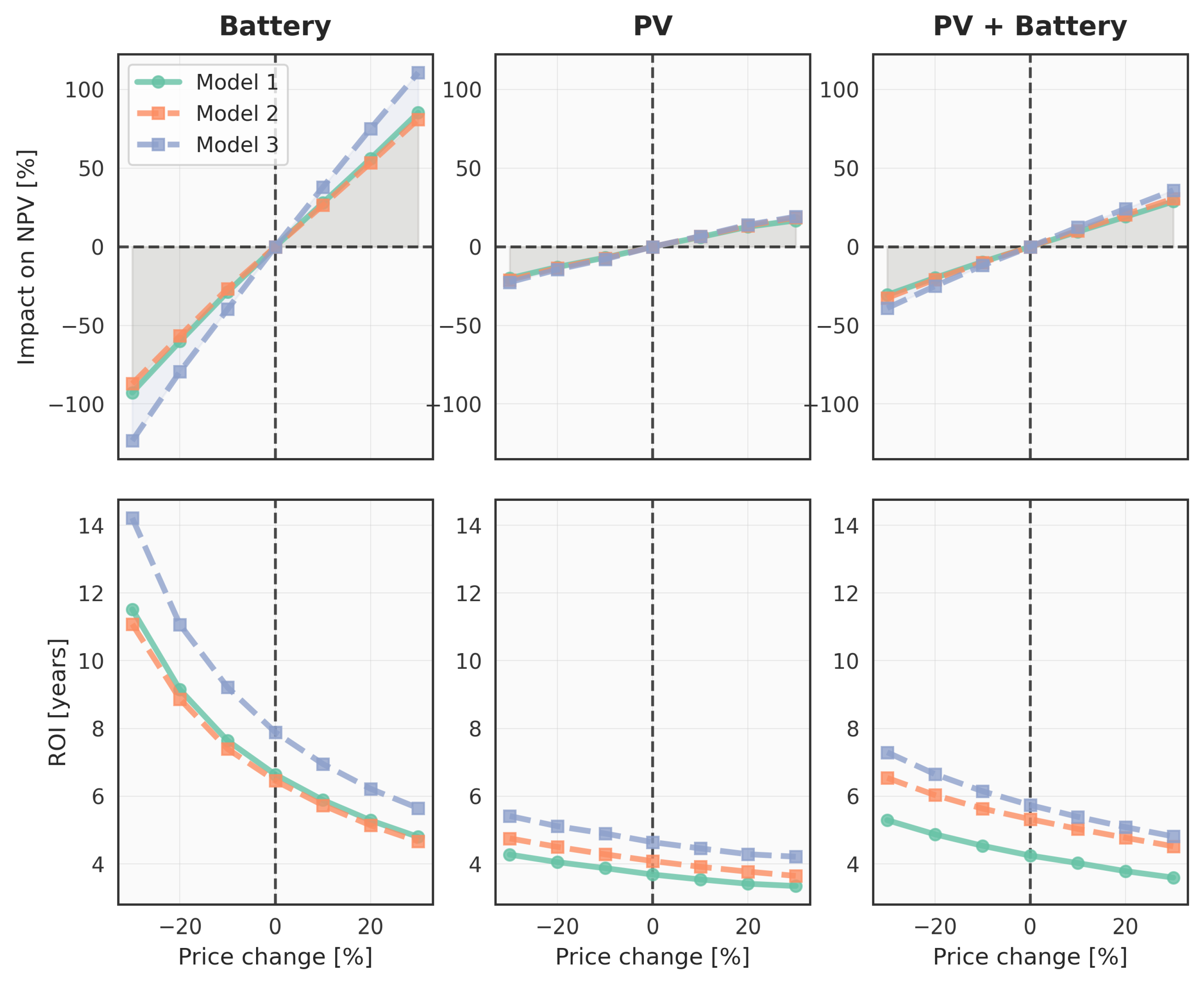
Our sensitivity analysis assesses how the financial viability of each system responds to static shifts in electricity price. As illustrated in Figure 4, the results show profound differences between the systems. The key finding is that a system’s resilience to different price conditions is driven primarily by its technology configuration, with the sizing methodology acting as a secondary, though important, factor.

5.4.1. Battery Only

Systems relying solely on battery arbitrage are the most sensitive to the baseline electricity price. This is evident in the steep slopes of the NPV curves in Figure 4 (top left panel). For instance, a 30% price decrease causes the NPV of the Model 3 battery system to plummet by 123.3%, turning a EUR 752 baseline profit into a EUR 176 net loss. This extreme financial exposure is quantified by its high NPV CV of 85.1% (

Table 3. Robustness and average performance of each system under static electricity price changes. The table reports both the mean MCDA score and NPV, alongside their CV. A higher mean indicates stronger average performance, while a lower CV suggests greater robustness to price variation.

Technology	Model	MCDA [Mean]	MCDA CV [%]	NPV [EUR]	NPV CV [%]
Battery	Model 1	5.4	39.9	1512	64.9
Battery	Model 2	5.6	37.9	1299	60.1
Battery	Model 3	4.6	49.1	1794	85.1
PV	Model 1	13.0	10.5	8788	13.3
PV	Model 2	12.6	11.0	8875	13.8
PV	Model 3	11.1	11.8	9157	15.2
PV + Battery	Model 1	12.3	16.5	10,550	20.6
PV + Battery	Model 2	11.5	16.8	11,032	20.8
PV + Battery	Model 3	10.6	20.3	11,646	25.5

). The composite MCDA score is similarly sensitive, with CVs ranging from 37.9% to 49.1%. Nevertheless, Model 3 delivers the highest average NPV (€1794), indicating its potential under favorable conditions.

5.4.2. PV Only

In contrast, PV-only systems are exceptionally resilient to changes in the electricity price level. Their NPV is far less affected by price shifts, a stability reflected in the gentle slopes of their performance curves (Figure 4, top-middle panel). This is confirmed by the very low NPV CV values, all below 16%. The stability of the holistic MCDA score is equally strong, with CVs around 11% (Table 3). Moreover, these systems maintain high mean NPV values (up to EUR 9157) and MCDA scores (up to 13.0), reinforcing their strong financial viability across all tested price scenarios.

5.4.3. PV + Battery

Combined PV + Battery systems offer a middle ground. They balance the stability of PV generation with the price dependent nature of battery arbitrage. Their performance curves in Figure 4 (right panels) are steeper than those of PV-only systems but significantly flatter than their battery only counterparts. This hybrid nature results in moderate NPV CVs between 20.6% and 25.5%. The MCDA scores show similar moderate sensitivity. Importantly, these systems achieve the highest mean NPVs overall, with Model 3 reaching EUR 11,646, and maintain MCDA scores above 10.0 in all configurations.

PV-only systems represent the most secure investment, demonstrating high average performance and low sensitivity to price fluctuations. Battery-only systems exhibit the greatest financial risk, requiring either supplementary revenue streams or a high tolerance for downside exposure to be considered viable. PV + Battery systems offer a compelling compromise: while more sensitive to price changes, they deliver the highest mean NPVs and maintain strong overall attractiveness.

5.5. Sensitivity Analysis to Price Volatility

For each configuration, simulations were performed using hourly electricity prices, generated by applying multiplicative Gaussian noise with standard deviations of 5%, 10%, 15%, and 20% to the 2023 NPS prices. The MCDA score and NPV were calculated at each noise level to evaluate how systems respond to increased market uncertainty.

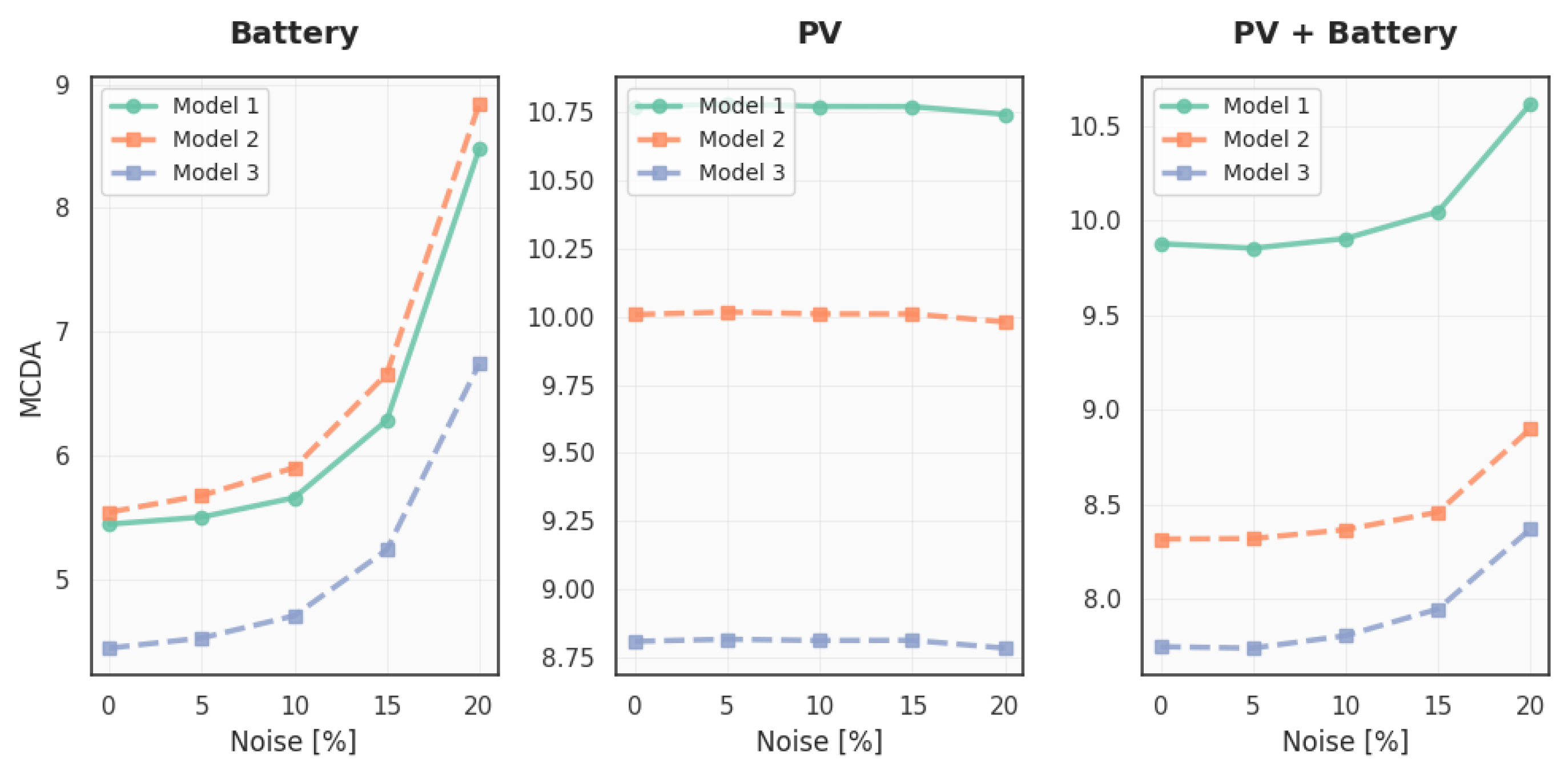
Figure 5 and Figure 6 show the progression of MCDA scores and NPV values as volatility increases. PV-only systems remained effectively constant across all scenarios, indicating that their performance is largely unaffected by short-term price fluctuations. This is expected, as PV generation is deterministic and does not directly depend on hourly price variation due to the assumed inability to sell electricity to the grid.

Battery-only systems, in contrast, demonstrated a consistent increase in both MCDA score and NPV with increasing price volatility. For instance, the average MCDA score for Model 1 increased from 5.4 at 0% volatility to 8.5 at 20%, while the corresponding NPV rose from EUR 654.8 to EUR 1353.3. This improvement is driven by enhanced price arbitrage opportunities: as volatility increases, the system can more effectively charge at low prices and discharge at high prices, improving overall economic returns.

PV + Battery systems showed intermediate behavior. While PV generation contributes a stable component to the system, the battery component still benefits from price volatility. This results in moderate but noticeable improvements in MCDA and NPV values as noise levels increase.

To compare robustness across systems, we calculated the CV for both MCDA and NPV values across all noise levels (

Table 4. Mean MCDA scores and NPV values, along with their corresponding coefficients of variation for each technology and model configuration under increasing electricity price volatility. Lower CV values indicate greater robustness to volatility.

Technology	Model	MCDA [Mean]	MCDA CV [%]	NPV Mean [EUR]	NPV CV [%]
Battery	Model 1	6.3	20.3	870.7	33.0
Battery	Model 2	6.5	20.9	748.8	33.0
Battery	Model 3	5.1	18.5	1068.3	33.1
PV	Model 1	10.8	0.1	3281.7	0.2
PV	Model 2	10.0	0.1	3245.0	0.2
PV	Model 3	8.8	0.1	3358.7	0.2
PV + Battery	Model 1	10.1	3.2	4217.5	4.9
PV + Battery	Model 2	8.5	2.9	4212.4	4.1
PV + Battery	Model 3	7.9	3.3	4643.8	5.2

). PV-only systems displayed the lowest CVs, confirming their high stability. Battery-only systems had significantly higher CVs but also showed the greatest performance gains under volatile conditions. Hybrid systems offered a compromise between robustness and volatility responsiveness.

These findings suggest that while PV-only systems offer highly predictable outcomes, battery-based systems can exploit volatile markets to improve economic performance.

6. Limitations and Future Work

The limitations of this study also highlight several areas for future work. First, our findings are specific to the Estonian context, characterized by high retail electricity prices, no feed-in tariffs, and a northern European climate. The generalizability of our results to other markets depends on the similarity of these conditions.

Second, our analysis is deterministic, using historical data for consumption, irradiation, and prices. Future work could incorporate stochastic modeling to account for uncertainty in these variables and assess the impact of forecast errors on financial outcomes.

Third, the economic analysis of batteries could be expanded. A comparative analysis against alternative investments, such as energy efficiency measures (e.g., insulation, heat pumps), would provide a more holistic view for homeowners. We also acknowledge that our model assumes a zero residual value for the battery at the end of its service life, which is a conservative assumption.

Finally, our study is based on the current regulatory framework in Estonia. Future research should explore alternative policy scenarios, such as the introduction of partial grid export allowances or feed-in tariffs, to assess how such changes would impact the economic viability of these systems. The simulation model was also not calibrated against real-world performance data from specific installations, which remains an important step for future validation studies.

7. Conclusions

This study developed and evaluated three distinct sizing models for photovoltaic (PV) and battery (BAT) systems for Estonian households operating under grid constraints that prevent the sale of surplus energy. By employing a multi-criteria decision analysis (MCDA) framework, we moved beyond simple payback metrics to assess system configurations based on a weighted balance of Net Present Value (NPV), Internal Rate of Return (IRR), Profitability Index Ratio (PIR), and Return on Investment (ROI).

Our findings reveal several key insights with practical implications for homeowners and policymakers:

1.

PV-only systems are the most robust investment. Across all models and scenarios, standalone PV systems consistently delivered the highest investment efficiency and MCDA scores. Their financial performance is resilient to shifts in electricity price levels, making them the most secure and economically attractive option for most households in the current Estonian market.

2.

Simplicity outperforms complex optimization in practical terms. While the simulation-based optimization (Model 3) identified systems with the highest absolute NPV, it did so at the cost of significantly higher initial investments and lower capital efficiency. The simple, heuristic-based approach (Model 1) consistently provided a superior balance of strong financial returns, lower investment risk, and practical simplicity, making it a highly effective tool for real-world decision-making.

3.

Batteries add value through volatility, but their economic case is challenging. Battery-only systems are highly sensitive to electricity price levels and only become financially viable under conditions of high price volatility, where they can capitalize on arbitrage opportunities. When combined with PV, batteries provide a modest increase in absolute NPV but reduce overall investment efficiency. Without additional revenue streams, such as grid services, the high capital cost of batteries makes them a less compelling investment than PV-only systems.

4.

The choice of sizing model is important. Our analysis demonstrates that different methodologies lead to vastly different system configurations and financial outcomes. Specifically, an aggressive oversizing strategy does not guarantee superior results, and a balanced approach considering both absolute returns and investment efficiency proves more effective.

In conclusion, for Estonian households unable to export surplus energy, the optimal path to energy self-sufficiency and cost savings is a well-sized, PV-only system. Simple, data-light sizing models can provide reliable and financially sound recommendations. While battery storage has future potential, its current economic viability is limited and largely dependent on market volatility, suggesting that its widespread adoption may require further cost reductions or new value streams.