Abstract
In recent years, solar energy has emerged as one of the most advanced renewable energy sources, with its production capacity steadily growing. To maximize output and efficiency, choosing the right configuration for a specific location for these installations is crucial. This study uniquely integrates detailed multi-variant fixed-tilt PV system simulations with comprehensive economic evaluation under temperate climate conditions, addressing site-specific spatial constraints and grid integration considerations that have rarely been combined in previous works. In this paper, an energy and economic efficiency analysis for a photovoltaic power plant, located in central Poland, designed in eight variants (10°, 15°, 20°, 25°, 30° PV module inclination angle for a south orientation and 10°, 20°, 30° for an east–west orientation) for a limited building area of approximately 300,000 m2 was conducted. In PVSyst computer simulations, PVGIS-SARAH2 solar radiation data were used together with the most common data for describing the Polish local solar climate, called Typical Meteorological Year data (TMY). The most energy-efficient variants were found to be 20° S and 30° S, configurations with the highest surface production coefficient (249.49 and 272.68 kWh/m2) and unit production efficiency values (1123 and 1132 kWh/kW, respectively). These findings highlight potential efficiency gains of up to approximately 9% in surface production coefficient and financial returns exceeding 450% ROI, demonstrating significant economic benefits. In economic terms, the 15° S variant achieved the highest values of financial parameters, such as the return on investment (ROI) (453.2%), the value of the average annual share of profits in total revenues (56.93%), the shortest expected payback period (8.7 years), the value of the levelized cost of energy production (LCOE) (0.1 EUR/kWh), and one of the lowest costs of building 1 MWp of a photovoltaic farm (664,272.7 EUR/MWp). Among the tested variants of photovoltaic farms with an east–west geographical orientation, the most advantageous choice is the 10° EW arrangement. The results provide valuable insights for policymakers and investors aiming to optimize photovoltaic deployment in temperate climates, supporting the broader transition to renewable energy and alignment with national energy policy goals.
1. Introduction
1.1. Global and European Trends in Renewable Energy
The share of renewable energy in the global sector is steadily increasing despite ongoing challenges. Global energy demand is rising rapidly due to economic and population growth. Fossil fuels still dominate global electricity and heat generation. For example, Turkey relies heavily on imported natural gas, threatening energy independence and increasing its current account deficit. Paper [1] investigates Turkey’s current policy system, including its strengths and shortcomings in different stages of distributed photovoltaic power generation development (DPPG) in the country.
The Global Electricity Review 2024 report indicates that, worldwide, hydropower accounted for about 14.3% of electricity produced, photovoltaics and wind power for 13.3%, and other renewable sources for about 2.6% (total renewable generation sources accounted for over 30% of global electricity in 2023) [2].
EU countries are shifting from conventional to renewable energy under the European Green Deal, a strategy focused on sustainability, climate action, and environmental protection [3]. The European Commission has proposed legislation to reduce net greenhouse gas emissions by at least 55% by 2030 compared to 1990. These measures aim for climate neutrality by 2050, though implementation may be challenging across member states. Poland, similar to other EU countries, has committed to expanding renewables, especially large-scale photovoltaic plants. Though Poland’s solar radiation is lower than southern Europe’s, favorable conditions and modern technology support efficient PV farm development in central and northern Europe. Equatorial countries receive the highest solar radiation, driving rapid growth in solar power installations recently [4,5,6]. Figure 1 shows the electricity generation potential for European countries (including Poland) using a unit power of PV installations.
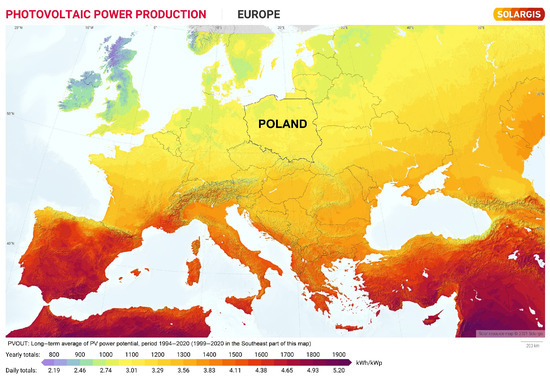
Figure 1.
Solar resource map of Europe [7].
Large-scale PV systems require extensive land, posing challenges in countries with valuable agricultural areas. Therefore, PV systems are increasingly being implemented worldwide in combination with agricultural crops: agro-photovoltaics or Agro-PV, Agri-PV, aPV. This technology was pioneered at the German Fraunhofer ISE Institute (Freiburg im Breisgau, Germany) [8].
Sun-tracking PV modules provide another approach to boosting electricity production on limited land. In 2022, the authors of [9] analyzed electricity production in power plants equipped with an east–west tracker.
1.2. Development of Large-Scale Photovoltaic Farms in Poland and Beyond
Poland’s PV farm growth has resulted from energy policy, economics, technology access, and local geographic and climatic factors. Recent sustainable energy planning highlights holistic integration of renewables, balancing technical, economic, and environmental concerns. Multi-criteria decision-making (MCDM) methods have gained prominence in optimizing renewable energy investments, incorporating regional development, environmental impact, and social acceptance [10,11]. These approaches are vital for implementing policies like the European Green Deal, aiming for carbon neutrality and sustainable development. PV farm planning is inherently multi-dimensional, requiring the balancing of solar resource availability, land use, environmental constraints, and economic viability. MCDM techniques such as Analytic Hierarchy Process (AHP), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), and Fuzzy Logic have been widely applied for site selection and system optimization [12,13,14]. These methodologies facilitate structured decision-making that integrates diverse quantitative and qualitative factors.
PV installations have surged recently after an initially slow start, reflecting significant technological progress. The intensive development of photovoltaic farms contributes to increasing the overall security of the Polish power system. Their spatial distribution prevents local grid overloads, lowering national power reserve costs. In 2023, 80 photovoltaic farms with a total power of 0.77 GW and 1417 small PV installations (from 50 kW to 1 MW) with a total power of 1.1 GW were connected in Poland. The vast majority (873 MW) was from photovoltaic farms with generation capacity above 30 MW [15]. The majority of photovoltaic installations in Poland operate in the power range of 0.5–1 MW (3510 are small PV installations, 34 are PV farms). The vast majority of PV farms in Poland (175 out of 262) operate in the power range of 1–5 MW. The highest numbers of installations (with the power provided) are in the Wielkopolskie voivodeship (701, 887.84 MW), the Warmińsko–Mazurskie voivodeship (404, 544.81 MW), and the Lubuskie voivodeship (401, 510.77 MW). In terms of the number of farms in operation, the voivodeships with the largest numbers are Warmińsko–Mazurskie (48 farms, total power 233.57 MW), Wielkopolskie (34, 307.49 MW), and Lubelskie (21, 121.11 MW) [16]. The largest photovoltaic farm in Poland, with a nominal power of 204 MW, is located in Zwartowo. Second place is occupied by the PV farm in Brudzewo (70 MW).
In 2023, the authors of [17] presented an exergoeconomic analysis of solar photovoltaic power plants (11.52 kWp in the far north of the country and the other 1.25 MWp connected to the grid in the Littoral) in different tropical zones (Maroua and Douala) in Cameroon. The authors stated that the Maroua PV plant was more efficient in terms of exergy production, but the Douala PV plant had a significantly lower production cost, making it economically favorable. Exergy losses were higher in Sahelian regions, particularly for systems with storage. Both climatic regions were suitable for PV deployment, but economic and technical optimizations should be considered based on location-specific conditions.
In paper [18], the authors analyzed the economic feasibility of developing large-scale solar photovoltaic power plants in Spain, where the average solar irradiation also reaches high values of approximately 1600 kWh∙m−2. The study evaluates solar PV systems with output power ranging from 100 MW to 400 MW and equivalent sunlight hours ranging from 800 to 1800 h/year. The analysis concludes that developing large-scale PV power plants in Spain is economically feasible, particularly in areas with higher solar irradiation and longer equivalent sunlight hours. The results suggest that large-scale solar PV projects in Spain can be economically viable, with an IRR of 11.01% and a positive NPV, indicating good profitability even with moderate electricity prices of 50–60 EUR/MWh. These findings emphasize that Spain’s favorable solar conditions (high irradiation) combined with the declining cost of solar technology make such projects financially attractive.
In Poland, further intensive development of the RES sector is combined with the recently introduced concept of sharing transmission infrastructure (cables, power lines) by various energy sources, most often renewable ones, such as wind farms and photovoltaic farms (so-called cable pooling). Analysis of cable pooling in Poland suggests that this approach can significantly reduce costs (with lower connection costs, the cost of electricity generation from renewable sources can potentially be lower), accelerate renewable energy deployment, and enhance grid integration, thus supporting Poland’s transition to a cleaner energy mix. By sharing transmission infrastructure, the need for additional land for new power lines can be reduced, which helps minimize the environmental and social impact of large-scale energy infrastructure. However, it also highlights the need for careful grid planning, coordination between stakeholders, and a supportive regulatory framework to ensure its effective implementation.
Scientific research on high-power photovoltaic installations focuses on multi-criteria analyses, which take into account a number of factors influencing the efficiency of a PV farm, such as available area, investment costs, expected payback period, geographical characteristics of the area, weather conditions, and energy policy. The process of selecting potential locations for photovoltaic projects is a key element of the global strategy, as confirmed by numerous studies [19,20,21] and organizations such as the National Renewable Energy Laboratory (NREL). The suitability of Moroccan lands for hosting Solar Power Plants was studied in [13] using the combination of the Geographic Information System (GIS) and the Analytical Hierarchy Method (AHP). A case study for Saudi Arabia was provided in [22]. The goal of the research was to evaluate and select the best location for utility-scale solar PV projects using geographical information systems (GIS) and a multi-criteria decision-making (MCDM) technique. The Fuzzy Multi-Criteria Decision-Making Method and the Delphi method were also used by the authors of [23]. The results of the study showed that the rate of solar radiation and average temperature were the most important criteria in locating a photovoltaic solar power plant. Similar activities, consisting of indicating ideal locations for the construction of large-scale wind and solar farms in Songkhla (a province in southern Thailand), were presented in [24]. The work [25] presents the most up-to-date and complete comparison of the largest existing solar PV power plants in the world.
Works by Polish authors also present analyses of the energy efficiency of photovoltaic farms with various nominal powers. In [26], the authors presented how the energy profit of a high-power 140 MW photovoltaic farm located in Siemiatycze (Podlaskie Voivodeship, Poland) changes with the change of the angle of inclination of the PV modules in the range of 20° to 25°. In work [27], the economic efficiency of 22 photovoltaic farms located in north-eastern Poland was assessed. In 2018, paper [28] presented the results of a two-year (2016–2017) analysis of the energy efficiency of a grid-connected solar power plant with a total rated power of 2.985 MW and operating in a temperate climate in eastern Poland.
The report presented in 2021 in Poland entitled IEO Photovoltaic Market in Poland 2020 [29] indicates that a 100 kW PV farm requires an investment cost of EUR 82,938. The highest cost of building a photovoltaic farm is the purchase of PV modules, which accounts for 48% of the total investment costs. The second available report [30] highlights more components, such as costs related to the preparation of design documentation (3–5%), cost of purchasing PV modules (40–45%), cost of purchasing a support structure (15–17%), other costs related to the construction of access roads, lighting, and monitoring.
Scientific publications supplemented with economic aspects are presented in [17,18,31,32,33]. In work [31], the authors compared the unit cost of electricity production (LCOE) using an 800 MW photovoltaic farm (Alkarsaah PV farm, Qatar) and the most efficient CCGT (combined cycle gas turbine) plants. The results of the analysis show that the 800 MWp Alkarsaah PV farm has a significantly lower LCOE compared to the most efficient combined cycle gas turbine (14.03 USD/MWh to 39.18 USD/MWh). This demonstrates the substantial economic benefits of large-scale PV farms, particularly in regions with abundant solar resources.
In [18], PV power plants with power between 100–400 MW and numbers of equivalent hours between 800–1600 h year−1 were considered, and the profitability analysis considered different prices of the electricity produced in the daily market (50–60 EUR/MWh−1). In [32], the construction of a 10 MW power plant in the city of Sirjan (Iran) was economically and technically analyzed. The analysis concludes that the construction of a 10 MW solar power plant in Sirjan is economically feasible with an investment of USD 16.14 million. The initial capital for the solar power plant is expected to be recouped in about four years, demonstrating a relatively quick return on investment.
A comprehensive analysis of PV farms with the same rated power for India [33] showed that Allahabad city was the most profitable site, with values of 16,686 MWh of electricity exported to the grid and 9.4 years of simple payback period. The authors concluded that Allahabad was the top location for a solar PV power plant in terms of profitability, Gorakhpur ranked second, and Varanasi was the least profitable. Agra and Kanpur were not considered suitable for the solar PV projects because they had negative values for NPV and Annual Life Cycle Savings (ALCS), indicating poor financial viability. This analysis is essential for guiding decisions on where to invest in solar PV power plants for maximum financial returns.
In 2023, the authors of [17] presented an exergoeconomic analysis of two photovoltaic systems, a 11.52 kWp power plant with storage installed at Maroua Airport (tropical dry region) and a 1.25 MWp grid-connected plant at Douala Airport (tropical humid region).
Some authors in their economic analyses also take into account the additional operating cost resulting from cleaning the surfaces of PV modules in order to increase power generating efficiency [34].
An element of economic calculation that may influence the proper determination of the payback period for the incurred investment outlays is the need to incur additional financial outlays during the facility’s operational period. In [35], the authors presented analysis that highlights the complexity of optimizing the efficiency of existing solar power plants. In the analyzed case, the research object was a 2.5 MW solar power plant in the Republic of Cuba. The authors stated that the most significant economic factor affecting the NPV of the solar power plant modernization was the price per 1 kWh. Reducing system losses from 20% to 10% led to a 2.5% increase in NPV. Solar module efficiency and inflation also significantly impacted the results, but to a lesser extent.
Researchers increasingly emphasize the importance of computer simulations and modeling, which enable precise prediction of the energy and economic efficiency of photovoltaic farms in various operating variants [26,36]. In work [37], the authors, in 2018, evaluated a large-scale, 20 MW grid-connected photovoltaic power plant (LS-PVPP) in a hot climate in Adrar, Algeria, using PVSyst software. The PVSyst program was also used to simulate performance of 100 kW grid-connected CIS photovoltaic system located in Semnan City [38]. In [9], the authors also used the PVsyst software; in this work, power plant models were developed in different modes of fixed, seasonal, north–south orientation, east–west orientation, east–west orientation with a suitable tilt angle towards the south, and biaxial movement for a power plant with technical specifications similar to the 10 MW.
Growing PV penetration challenges grid integration, especially matching generation profiles with demand. The high penetration of photovoltaic systems in modern power grids introduces significant challenges related to intermittency, voltage stability, and reverse power flows. Advanced grid management techniques—including energy storage integration, demand response, and smart grid technologies—are essential to mitigate these effects and maintain reliability [39,40,41]. Moreover, evolving grid codes and operational practices support the stable integration of distributed solar generation. The traditional approach to PV farm design focuses on maximizing energy yields by setting modules at the optimal tilt angle (around 37° for Poland). However, this can lead to excessive midday generation, contributing to grid congestion and declining electricity prices, even reaching negative values on the Day-Ahead Market. The Day-Ahead Market plays a key role in energy market operations, allowing for optimal planning of electricity production and consumption. However, the growing capacity of installed solar power exacerbates the so-called cannibalization effect—the more PV power in the system, the greater the midday energy surplus, which drives prices down and creates financial challenges for large-scale PV farms. As PV penetration grows, issues such as grid congestion, power balancing difficulties, and curtailment of large-scale solar farms become more significant.
This research aims to analyze the impact of different PV module inclination angles on both energy efficiency and grid integration of large-scale photovoltaic farms under Polish climatic conditions. The study investigates how reducing the tilt angle can alter the solar generation curve, flattening the midday peak and shifting energy production to better match demand. Additionally, a lower tilt angle allows for higher module density per unit area, partially compensating for energy losses by increasing the total installed power. This approach can lead to a more stable and grid-friendly generation profile while maintaining competitive energy yields. To ensure the feasibility of these alternative configurations, the study also includes a comprehensive economic analysis. By balancing energy efficiency with system-wide benefits and financial performance, this research provides valuable insights for optimizing large-scale PV farm designs. The conclusions can also be applied to other countries with similar solar radiation patterns, topographical conditions, and energy sector problems.
The objective of this study is to conduct a comprehensive analysis of the impact of photovoltaic module tilt angles on both the energy performance and economic feasibility of large-scale PV installations located in a temperate climate, exemplified by central Poland. The research hypothesis posits that optimizing the tilt angle—considering solar irradiation patterns, spatial constraints, and grid integration aspects—can significantly enhance the annual energy yield and cost-effectiveness of the investment. The central research question focuses on identifying the range of tilt angles that achieve the best compromise between maximizing annual electricity production, minimizing the levelized cost of energy (LCOE), and ensuring stable and grid-friendly generation profiles. Furthermore, this study evaluates the influence of module orientation (south-facing versus east–west) on these parameters, which is critical for designing efficient and economically viable PV systems.
Although many studies have analyzed optimal tilt angles and economic aspects of photovoltaic farms, this work offers a distinct contribution by combining detailed PVSyst simulations with a comprehensive economic assessment of fixed-tilt, large-scale PV installations in a temperate climate, exemplified by central Poland. Unlike prior research, which typically focused on either energy performance or financial metrics separately, this study integrates both perspectives, addressing spatial limitations and implications for grid integration. By examining multiple tilt angles and orientations (south and east–west) on a constrained land area (~300,000 m2), the research provides new insights into optimizing energy yield, cost-effectiveness, and generation profiles that better align with grid demands. Additionally, situating these findings in the context of similar temperate-zone studies helps fill an existing gap regarding PV farm design under mid-latitude climatic and regulatory conditions.
2. Materials and Methods
2.1. Designation of the Area for a Photovoltaic Farm
The aim of the analysis was to assess the energy and economic efficiency of a photovoltaic farm that could be installed, in different variants, on the same plot of limited area in central Poland. The region where the photovoltaic power plants are located is characterized by an average level of insolation compared to other parts of the country. The distribution of global horizontal irradiation and photovoltaic power potential in Poland is shown in Figure 2.
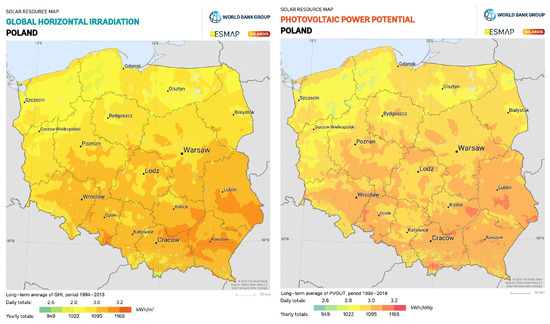
Figure 2.
Solar resource maps of Poland [7].
Due to current practical problems with connecting RES installations to the grid in Poland, the availability of land for investment, the desire to shorten the length of cable routes, and the electrical power of the photovoltaic power plant, the appropriate plot for investment was selected near the Plewiska high voltage 400/220/110 kV power station. There is one photovoltaic farm already in operation and another one under construction on the north-east side of the station (Figure 3).
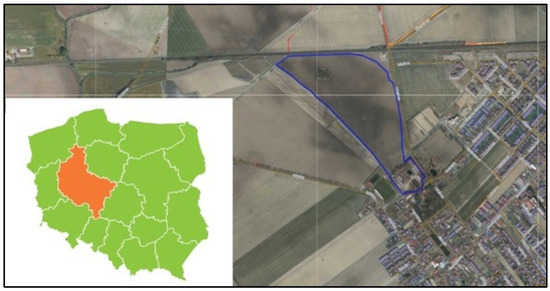
Figure 3.
View of the Plewiska Power Station with the area of plot no. 1216/3 for the location of a photovoltaic farm.
Plot no. 1216/3 is located in Wielkopolska Province, Poznań County, Komorniki Commune. The plot ID is 302107_2.0005.1216/3. The total area of the plot is 30.3795 ha. It is covered by the Local Spatial Development Plan on part of the property area.
When assessing the potential investment site, the following aspects were taken into account:
- The type of network to which the energy source would be connected;
- Presence or absence of a Local Spatial Development Plan;
- Land use classification;
- The infrastructure located on the property and the guidelines from the Local Spatial Development Plan;
- The environment and related forms of spatial nature protection;
- Presence of monuments and related conservation or archaeological works;
- The scale of flood risk in a given area;
- Presence of terrain obstacles such as areas of trees, hills, or wetlands.
2.2. Computer Software
Optimization algorithms, including genetic algorithms, particle swarm optimization, and hybrid metaheuristics, have been increasingly utilized to optimize PV system design, layout, and operation, balancing energy yield, cost, and reliability [42,43]. Integration of these algorithms with simulation tools such as PVSyst allows multi-objective optimization addressing sizing, shading, inverter loading, and grid compatibility challenges [44].
For design purposes, the BricsCAD version 24 and VirtoCAD version 1.10 programs were used. They allow for the development of the photovoltaic farm area, the layout of tables for photovoltaic modules, DC-DC switchboards, inverter–transformer stations, and the design of the farm cabling. The computer simulation of the energy nature of all analyzed variants of the photovoltaic farm was carried out using the PVSyst program version 7.4.0.
Meteorological data from the external PVGIS database, version 5.2, and the SARAH-2 model were used in the simulation analyses. PVGIS-SARAHs uses the images of the METEOSAT geostationary satellites covering Europe, Africa, and Asia (±65° longitude and ±65° latitude). The data on solar radiation come from the so-called Typical Meteorological Year (TMY).
2.3. Photovoltaic Farm Variants
The photovoltaic farm was located on a property with an area of 30.3795 ha, of which the area available for photovoltaic development was approximately equal to 19 ha. The analysis covered the inclination angles of the PV module planes relative to the ground at 10°, 15°, 20°, 25°, 30° for the south-facing farm configuration and 10°, 20°, 30° for the east–west farm configuration.
2.4. Components of a Photovoltaic Farm
In each analyzed variant, the same component devices were included in a number adequate for the possible nominal power of the photovoltaic farm in a specific installation variant. The project was based on the concept of a central inverter. The central inverter was designed to aggregate thousands of photovoltaic modules, with their series connection in the string form and then parallel.
A comprehensive solution integrating the central inverter is an inverter–transformer station. In order to adopt the right solution, a functional analysis of two selected solutions available on the market was carried out. The SMA MVPS station and the Sungrow SG3300/4400UD-MV station were considered. Due to the higher unit rated power of the variable voltage section and the compact solution with predictable parameters, the SMA MVPS 4–4.6 MVA station was adopted. The SMA MVPS inverter–transformer station consists of three main components: the Sunny Central UP central inverter, the LV/MV transformer, and the MV switchgear (Figure 4).
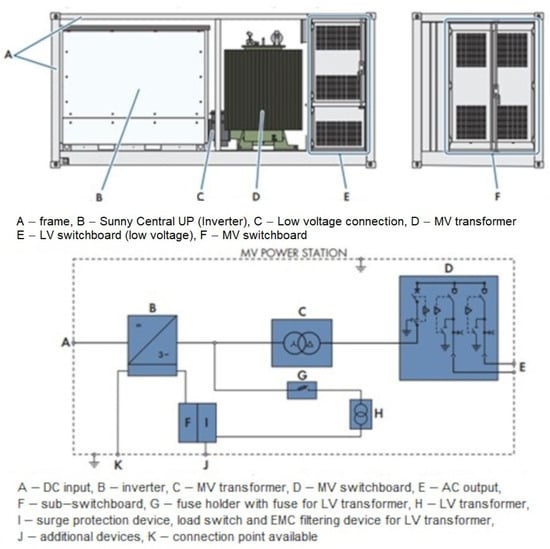
Figure 4.
The SMA MVPS transformer-inverter station with the electrical connection diagram.
The next elements of the analyzed photovoltaic farms are DC combiner boxes. DC combiner boxes are installed to connect and protect strings of PV DC modules which are then connected to the inverter. In the project, DC-DC switchboards from Weidmueller, model PV 232S0F0C15V0O1T7P015LWW, were selected.
The choice of the photovoltaic module model was based on two pillars. These are two efficiency coefficients, where the first is related to cost, while the second is related to the unit surface power. The first cost-effectiveness ratio is described by the price of one photovoltaic module related to its rated power under STC conditions. The second factor is the surface efficiency factor calculated as the unit installed power of the photovoltaic module related to the geometric dimensions. A total of 13 different models were analyzed and the parameters necessary to determine their efficiency coefficients were specified (Table 1 and Table 2). The selected model is marked in both tables.

Table 1.
Summary of PV module parameters analyzed in order to determine the cost-effectiveness ratio.

Table 2.
Summary of PV module parameters analyzed in order to determine the surface efficiency coefficient.
The selected Jinko Solar Tiger Neo Type N 60HL4-(V) 470 W PV module is characterized by the following important features:
- ▪
- The module efficiency is 21.78% for the variant with a rated power of 470 Wp in STC conditions;
- ▪
- The cell type is monocrystalline N-type semiconductor;
- ▪
- Application of SMBB technology with Hot 2.0;
- ▪
- Increased protection against power loss due to PID process;
- ▪
- Linear efficiency guarantee—in the first year the energy efficiency of the module is 99%, while the annual degradation is on average 0.4%;
- ▪
- The manufacturer provides a 30-year guarantee on linear energy efficiency and a 15-year product guarantee.
The current–voltage characteristics and power curves of the selected module are shown in Figure 5.
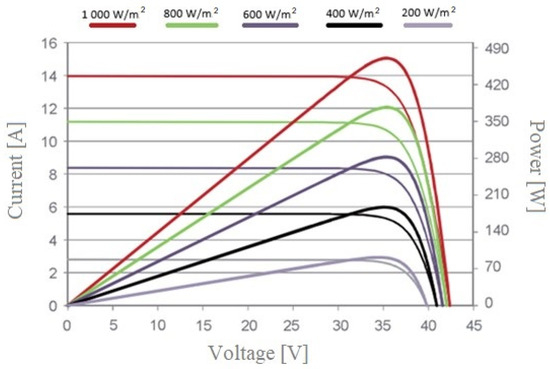
Figure 5.
Current–voltage characteristic and power curve of Jinko Tiger module.
2.5. Photovoltaic Farm Configuration
An important issue is the number of PV modules in one string. It is determined based on the voltage criterion, taking into account the open circuit voltage of the module UOC and the voltage temperature coefficient %UOC/°C. For the selected Jinko Solar Tiger Neo 470 W module, the given parameters are 42.38 V and −0.25%/°C, respectively.
For the extreme operating temperature of the cell, equal to −40 °C, the maximum voltage in one module is calculated as follows:
The open circuit voltage of the series connection of PV modules should not exceed the maximum permissible operating voltage of the PV system, which for this configuration is 1500 V due to the technical conditions of the inverter, DC-DC switchboards, or DC side cabling.
Therefore, the maximum number of PV modules in one string is:
In the next step, the parameters of the DC-DC switchboards were determined. The maximum number of inputs that can be used is determined, taking into account the current criterion. The fuses in the SMA MVPS 4000–4600 kVA inverter–transformer station can be used with a current between 200 and 500 A. The highest possible value was selected for the project. According to manufacturers of electrical equipment, a safety factor of 1.5 should be used. This safety factor value is suitable for an outside temperature of 45 °C. The fuse manufacturer also specifies the method of selecting fuses for photovoltaic systems according to the formula:
On this basis, the maximum permissible value of the current intensity in one series of connected modules for one DC input was determined:
The short circuit current ISC was determined for extreme weather conditions. The short circuit current value for STC conditions is 14.15 A and the temperature coefficient of the short circuit current is +0.046%/°C:
On this basis, the maximum number of PV module strings connected to one DC input in the inverter–transformer station was determined, and therefore it was also the maximum number of PV module strings connected to one DC-DC switchboard:
The number of PV module strings connected to one DC input in the inverter–transformer station, and thus to one DC-DC distribution board, is a maximum of 22 strings. In such a situation, in order to increase the transparency of the designed photovoltaic farm and facilitate maintenance work, it was decided to use the configuration based on 21 strings in the DC-DC switchboard as often as possible. This would allow the use of unified table structures with photovoltaic modules, based on the arrangement of 3 modules in a vertical row and 30 modules in a horizontal row. This would ensure that one module string corresponded to one horizontal row of a given table. This is an important aspect in the context of the efficiency of the PV system, for example in a shading situation.
The DC-DC switchboards selected for the project are characterized by a maximum permissible DC current per one input of 48 A. It was decided that the appropriate solution was to apply the principle that one string of PV modules would be connected to one input in the DC-DC switchboard (limiting the effects of reverse current flow).
The last aspect was the adjustment of the central inverter (inverter–transformer station). In the analyzed case, a modified connection system was used. The maximum number of DC inputs in the central inverter is 18, and 6 additional inputs are considered standard for cooperation with battery energy storage systems. However, it is possible not to use the energy storage and to extend the basic inverter function to 24 DC inputs. At the same time, the number of PV module strings connected to the DC-DC switchboard does not have to be the same for each DC input going to the inverter, because the inverter uses a busbar and the current values are summed. Therefore, the variable for adapting the changing power of the PV farm to the inverters will be the number of inputs in the DC-DC switchboard.
For the east–west farm orientation variant with an inclination angle of 10°, 54,180 PV modules were installed, on 301 photovoltaic tables, and the building area of the PV farm was 119,568 m2. The installed power was equal to 25.465 MW. Four SMA Sunny Central UP 4600 kVA inverter–transformer stations were installed with a maximum total AC output power of 18.4 MVA. The oversizing factor for the photovoltaic farm was 1.389. The total number of DC-DC switchboards was 88.
The internal distance between the rows of fixed PV panels is assumed to be 2.5 m, allowing for free access for operation and maintenance by road transport. In order to provide space for cable trenches, areas inaccessible for PV development were designated in the central part of the investment plot in the east–west direction. The analysis assumed one PV table configuration as a three-row one with 30 modules in each row.
The farm was divided into groups assigned to a given inverter–transformer station. The division into groups was made on the basis of multiples of 90 modules (Table 1) for the farm facing south and multiples of 180 PV modules for the configuration with an east–west geographical orientation. For the east–west orientation variant, 4 groups were designated (G1–G4). Groups G1 and G2 have the same number of modules (13,500), group G3 has 13,860 modules, and 13,320 modules were added to group G4. The photovoltaic system for one station consists of 22 DC-DC switchboards, of which 21 switchboards are connected to 21 PV module strings, and the last switchboard is assigned, depending on the needs of a given system, the remaining number of PV module strings. Each string consists of 30 PV modules.
Detailed data for an east–west example variant are presented in Table 3.

Table 3.
Summary of information about the photovoltaic farm project.
Figure 6 shows the structure of a photovoltaic farm with an east–west geographical orientation.
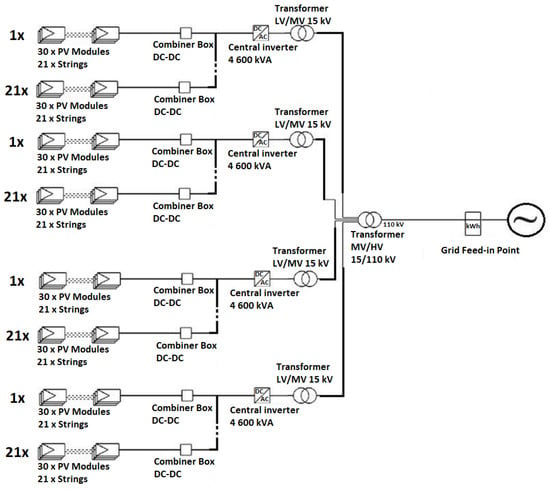
Figure 6.
Single-line diagram of a photovoltaic farm with an east–west geographic orientation and a tilt angle of 10°.
The DC/AC oversizing ratios applied in the simulations were selected to balance energy yield maximization and inverter operational constraints. For south-facing configurations, the oversizing ratio of 1.158 corresponds to the ratio between the target installed DC power and the nominal inverter capacity (4600 kVA), which aims to maximize inverter utilization while minimizing clipping losses during peak irradiance. The maximum inverter load, utilizing all 24 DC inputs, yields an oversizing factor of 1.618, representing the upper design limit under optimal conditions. For east–west oriented configurations, a slightly lower oversizing factor of 1.5 is adopted, aligning with industry recommendations to optimize performance given the smoother daily generation profiles and different shading characteristics. These oversizing choices ensure realistic simulation of system behavior in temperate climate conditions.
The division of the photovoltaic farm into connection groups is shown in Figure 7.
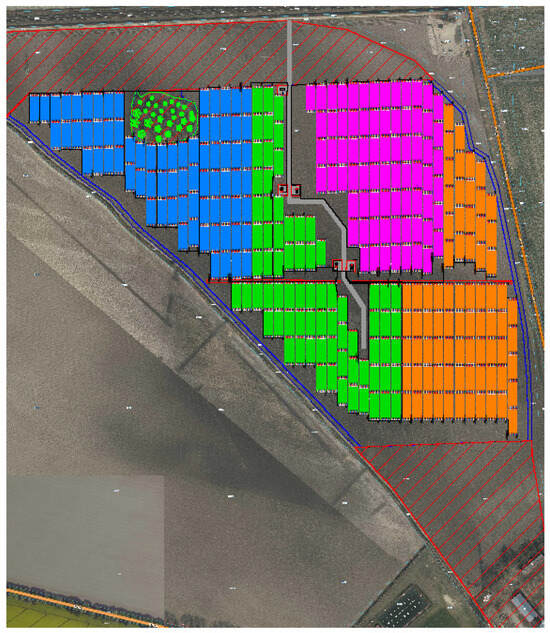
Figure 7.
The photovoltaic farm divided into four groups, each with one dedicated inverter–transformer station. The 4 colors represent the 4 connection groups of the PV modules.
2.6. Economic Analysis Tools
In terms of economic analysis, comparative indicators were calculated on the basis of the following:
- -
- LCOE indicator (ang. Levelized cost of energy) as the normalized price of producing a unit of energy, taking into account the present value of future cash flows by applying a discount rate:
- -
- Net present value (NPV)—the difference between the present value of cash inflows and the present value of cash outflows in a given period:
- ▪
- Return on investment (ROI)—the ratio of net benefits to initial investment, which measures the profitability of the system. A negative ROI indicates that the system is not profitable.
The analysis assumed real and applicable costs related to individual elements included in the photovoltaic farm at the construction stage and during its operation. The construction of a photovoltaic farm is associated with the purchase or lease of investment land, the execution of construction, implementation and as-built design. The initial assessment of the investment location consisted of selecting potential locations in the Wielkopolska Province (central Poland). On this basis, the final location of the planned photovoltaic farm was selected. Depending on the scope, the cost of such a study is approximately EUR 1927. In order to locate an investment in a given area, the right to use the land must be obtained. This is usually done by means of an agreement in the form of a land lease agreement between the property owner and the investor with the involvement of a notary. The lease period for the land is set at 25 or 30 years (in the analyzed case, 25 years). The owner is paid a fee for the lease, which can amount to 2890–3853 EUR/ha. Often, the investor intends to lease only land deemed suitable for PV development; therefore, wooded land or land with quality class 3 or higher is not covered by the agreement. In the analyzed case, the lease covered an area of 19 ha out of 30.3795 ha.
Based on the offers submitted to landowners in 2023, it was assumed that 4238 EUR/ha is offered for the lease of 1 ha of land for the purpose of building a photovoltaic farm (with 19 ha of area, the fee is EUR 80,530 /year). The one-time cost of notarial services was assumed to be EUR 1927. In the analyzed case, the costs related to the purchase of real estate were zero, because no land was purchased.
The development of the farm designs, including obtaining all necessary consents, agreements, and documents, may take about 2 years. The cost was assumed to be EUR 192,655.95, divided into the design services for the project by the design office in the amount of EUR 144,492, costs related to official fees in the amount of EUR 9632.8, the service of preparing a study of the impact of the investment on the natural environment in the amount of EUR 23,118.71, and the service of preparing an economic analysis of the planned undertaking in the amount of EUR 15,412.5.
To estimate the cost of preparatory earthworks, data on the PV development area for each variant of the photovoltaic farm and the average cost of levelling the area for construction purposes were used—this cost within the city of Poznań amounts to 1.1 EUR/m2.
The detailed cost estimation for specialized PV farm components is presented in Table 4.

Table 4.
List of materials and services for a photovoltaic farm (10° EW variant).
An example distribution of investment costs for the construction of a photovoltaic farm with an east–west geographical orientation and an inclination angle of 10° is shown in Figure 8.
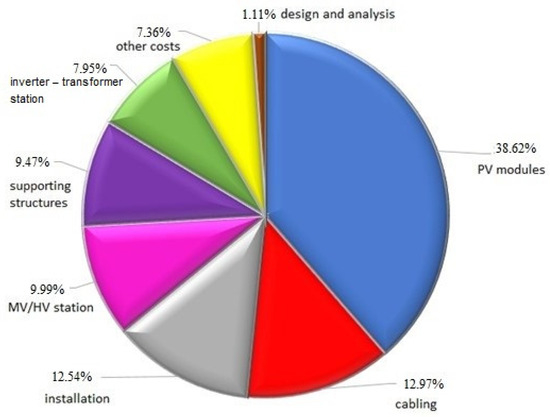
Figure 8.
Graph of the distribution of investment costs allocated to the construction of a photovoltaic farm with an east–west geographical orientation and an inclination angle of 10°.
Instead of the technique of concreting the supporting structures, the method of driving piles into the ground was adopted. The cost of the supporting structure for PV modules was set at 3413,72 EUR/pc (the unit price of the PV table is 2731 EUR/pc with a typical discount of 20%). The costs of assembling and installing the components of the photovoltaic farm were assumed to be 77 EUR/kW. The cost of assembling the inverter–transformer station was estimated at EUR 3853 per station.
Based on offers from insurance companies, the annual insurance was assumed to be 5.78 EUR/kWp, with a simultaneous one-off insurance cost of EUR 154,125 before the start of the photovoltaic farm’s operation.
Maintenance and service costs were estimated at EUR 11,559–13,486 per year per 1 MWp of installed capacity. Service and maintenance costs of 13,486 EUR/MWp per year were assumed (remuneration for service workers 9633 EUR/MW per year, repair costs EUR 2312 per year, cleaning costs 963.3 EUR/MW per year, and facility protection fees 578 EUR/MW per year). The amount of the commission for the replacement of the central inverter was calculated based on the total purchase cost of the inverter–transformer stations and the life of the device.
The analysis assumes that 50% of the energy produced Is covered by the auction system and sold at the auction price, while the remaining 50% of the energy is sold under a corporate Power Purchase Agreement (cPPA). To determine the auction price, the reference price included in the regulation of the Minister of Climate and Environment of 31 October 2022 was used [45]. For categories with total installed power exceeding 1 MW, using only solar radiation energy to generate electricity, the reference sales price of electricity is 84.12 EUR/MWh. Taking into account the fact that an offer proposing the reference price does not usually sell at auction, the price of electricity sold at auction is assumed to be EUR 5.92 lower (78.2 EUR/MWh in total). Information on the selling price at which energy companies involved in the generation of electricity sell, buy, or settle electricity in accordance with art. 49aa sec. 2 of the Energy Law Act was used to estimate the average selling price of electricity. In this case, the average quarterly sales price of electricity for Q2 2023 was 185.79 EUR/MWh. Therefore, the average total sales price of electricity produced sold through the auction system and based on the provisions of the cPPA agreement is 132.59 EUR/MWh (the sales price of electricity adopted in the first year of operation of the photovoltaic farm). Taking into account the fact that the prices of electricity sales under auctions are concluded for a period of 15 years and that in recent years the price of electricity sales on the energy market has been significantly higher than the price determined under auctions, it should be assumed that the price of electricity sales in the subsequent years of the operation of the photovoltaic farm will experience an upward trend (an average annual moderate increase in electricity sales prices of 8% over the entire life of the photovoltaic farm was assumed).
Taxes related to the operation of a photovoltaic farm are mainly property tax, VAT, and excise tax. The property tax in 2023 was 0.27 EUR/m2 per year. Excise tax applies to the sale of electricity as well as its consumption by an entity without a license. Assuming successful acquisition of a license to produce and sell electricity by the Energy Regulatory Office, the company that owns the planned photovoltaic farm is exempt from paying excise duty. Having a concession is connected with the obligation to pay a fee for the granted concession. There are three levels for this: 0.0003% of the obtained revenue, 0.0005% of the obtained revenue, and the company may be exempt from the obligation to pay it. In this case, the concession covers the generation of electricity, which is associated with the obligation of the investor (owner of the photovoltaic farm) to pay a fee for the granted concession in the amount of 0.05% of the income achieved in a given year. The company established at the initiative of the investor, which is the owner of the planned photovoltaic farm and has the status of a legal person, is charged with corporate income tax (CIT), which is 19% of the tax base.
The basic assumption In the economic analysis Is the Initial amount of cash allocated for investments (the amount of EUR 2,369,668.2 was assumed). If the investment costs exceed the initial amount, it would be necessary to take out a loan for the remaining amount needed to cover the total investment costs. It was assumed that the investment loan bears an interest rate of 5% on a fixed-interest basis throughout the entire loan period (an interest-bearing bullet loan was assumed, where annual interest on the borrowed capital is paid each calendar year throughout the loan period, and the entire repayment is made at the end of the loan period).
The operating time was determined to be 25 years, with the first year of investment operation beginning in 2024. The degree of variability of electricity production over time by the photovoltaic farm was taken into account.
The inflation level was assumed to be 3.00%, while the discount rate was assumed to be 2.00%. A fee related to determining the connection conditions was taken into account, at an amount of 7.11 EUR/kW of installed power plant capacity, but not more than EUR 577,967.9. The fee is borne in full by the investor of the project.
3. Results
3.1. Analysis of Land Available for Investment
An analysis of land availability and possible exclusions on the property was carried out. According to Polish law, land use classes marked as III and higher (in this case classes II and I) cannot be used directly for energy development [46,47]. In the analysis, after assessing the characteristics of the terrain, it was assumed that the planned investment is carried out entirely on class IV terrain.
Due to the industrial nature of the planned photovoltaic farm, it should be planned in areas designated for this purpose in the Local Spatial Development Plan.
There is a 110 kV HV power line in the northern part of plot no. 1216/3. The guidelines of the Distribution/Transmission System Operator indicate the minimum distance from the line axis, which delimits the technological area for the discussed infrastructure. According to information provided by Polskie Sieci Elektroenergetyczne (PSE), for lines with a rated voltage of 220 kV, the technological strip delineates the area at a distance of 25 m from the axis of the 220 kV HV line. In work [47], other definitions of the occupancy zone, easement zone, and protective zone are presented along with the methods for determining them. Taking into account both documents, the distance of the easement or technological area, which is necessary for the correct operation of the devices, was assumed to be 20 m, which means that the entire northern part of the plot is not suitable for PV development, so it is excluded from the analysis.
A watercourse flows along the western boundary of the property. According to the guidelines, the area 5 m from the plot boundary is marked as green/standing water. Therefore, this area should not be designated for PV development and was excluded. There was no form of nature protection in the area of plot no. 1216/3, so there were no additional exclusions. There were no monuments or related conservation or archaeological works.
Based on information from Polish Waters and the Hydroportal they run, it can be determined that there is no flood risk (a probability of occurrence below 1%).
In the northern part of the property, there is a wooded area. In the simulation analysis, the structure of the discussed wooded area was modeled, and was shown to consist of the following:
- -
- From the southwest, four trees with the following dimensions: height 20 m, crown width 8 m, trunk thickness 1.1 m;
- -
- From the south and southeast, nine trees with the following dimensions: height 15 m, crown width 6 m, trunk thickness 0.8 m;
- -
- From the north, in the center, 15 trees with the following dimensions: height 10 m, crown width 4 m, trunk thickness 0.5 m.
Figure 9 shows a view of the investment site, indicating areas excluded from photovoltaic development.
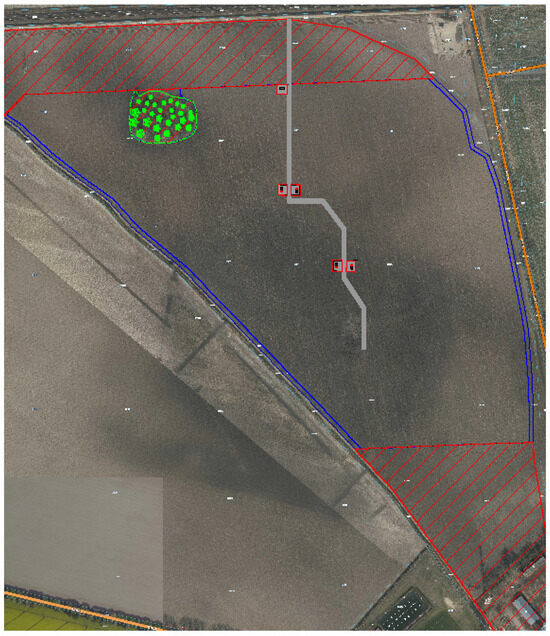
Figure 9.
Location of the photovoltaic farm installation site in various variants, excluding impossible areas. Red indicates unmanageable (crossed out) land, as noted in the drawing caption and text. Green indicates trees.
3.2. Energy Analysis of Photovoltaic Farm Variants
Table 5 presents a summary of the computer simulation results for five variants of a photovoltaic farm with the PV module plane oriented south and for three variants with the planes oriented east–west. The PR is calculated based on IEC EN61724.

Table 5.
Energy comparison of the tested variants of the planned photovoltaic farm.
Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 present a graphical interpretation of selected computer simulation results.
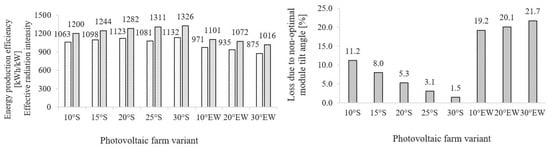
Figure 10.
Annual energy production efficiency and effective radiation intensity incident on the surface of PV modules (left) and graph of losses due to non-optimal module inclination angle (right) for the tested variants of photovoltaic farms.
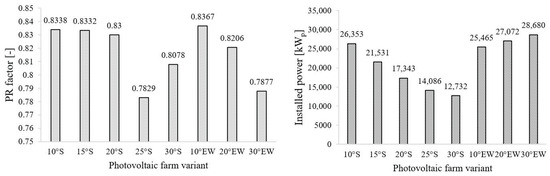
Figure 11.
The average annual PR coefficient (left) and the installed power (right).
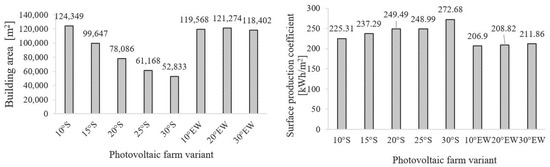
Figure 12.
Development area (left) and graph of surface production coefficient (right) for the tested variants of photovoltaic farms.
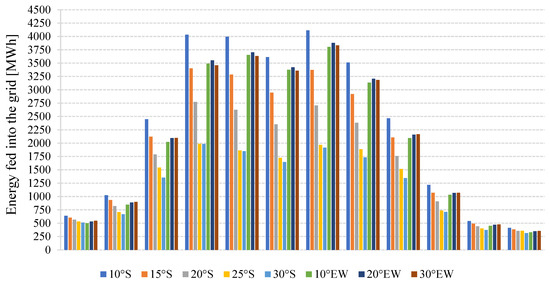
Figure 13.
Monthly amount of energy fed into the grid for all tested variants of photovoltaic farms.
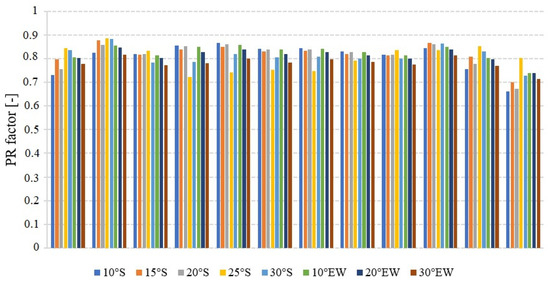
Figure 14.
Monthly PR coefficient value for all tested variants of photovoltaic farms.
3.3. Economic Analysis of Photovoltaic Farm Variants
Financial summaries for each of the eight studied variants of photovoltaic farms are presented in Table 6 and Table 7.

Table 6.
Financial summary of the studied variants of photovoltaic farms—part I.

Table 7.
Financial summary of the studied variants of photovoltaic farms—part II.
According to [48], the payback period is from 8 to 12 years. In [49], a payback period of 10 years and a profitability of 9% are indicated, assuming the use of favorable financing methods and benefiting from an attractive auction. In [50], a broad simulation of profits from a photovoltaic farm is presented where the return on investment was achieved after 10 years of operation, while, after 15 years, a profit of EUR 473,933.6 was generated. The designed system achieved a payback period of 12.7 years.
3.4. Cross-Regional Validation of Economic and Technical Results
Recent research on photovoltaic farms in northeastern Poland [27] confirms the economic viability of PV investments, reporting positive net present value (NPV) across a range of farm sizes. Payback periods varied from approximately 8.5 to 13.5 years, consistent with the 8.7- to 11.3-year range observed in our study, depending on system configuration. While larger farms generally showed higher profitability, no strict linear relationship with capacity was identified, aligning with our finding that economic efficiency is influenced by site-specific factors and farm layout. The study also emphasizes the crucial role of financial support mechanisms, supporting our assumptions regarding policy impacts on levelized cost of energy (LCOE) values of 0.10–0.13 EUR/kWh, thereby validating our economic analysis within the Polish context.
A recent investigation in southeastern Poland [51] analyzed the economic feasibility of large-scale PV installations using key metrics including ROI, payback periods, NPV, IRR, DPBT, and LCOE over a 25-year lifespan, both with and without subsidies. Results showed that all investments were profitable with subsidies (NPV > 0), whereas six installations would be unprofitable without them. Discounted payback periods ranged from 8.1 to 22 years (conservative scenario) and from 5.6 to over 15 years (optimistic scenario). Subsidies effectively halved payback times and reduced LCOE by approximately 30%. Capital expenditure ranged between 4919 and 7285 PLN/kW, higher than our study’s estimates, reflecting differences in scale and market conditions. However, their average annual productivity of 1040.98 MWh/MW closely corresponds to our results. Payback period estimates also align well, reinforcing the economic feasibility of PV farms under Polish conditions.
The technical and economic findings for the Polish temperate climate exhibit strong consistency with studies from regions of comparable climates in Central Europe. For instance, research in Southern Slovakia [52] highlights the pivotal influence of PV module tilt and azimuth angles on energy yield, identifying an optimal tilt near 34.5° and an azimuth range between −20° and 15°. This confirms the transferability of models developed for such regions to other Central European locales with similar solar and climatic conditions, supporting the broader applicability of these findings.
Similarly, economic viability has been demonstrated in northern latitudes such as the Baltic States [53], where PV systems exhibit median LCOE values between 0.08 and 0.09 EUR/kWh at a 6% discount rate. Our results for large-scale farms, with LCOE values between 0.10 and 0.13 EUR/kWh, correspond closely when considering differences in system scale and project type. This discrepancy can be attributed primarily to additional costs associated with the construction of high-voltage stations and grid connection infrastructure, which are significant capital expenditures in Poland’s temperate climate zones. Both studies underscore the dominant influence of capital expenditure (CAPEX) on economic outcomes and highlight the importance of supportive policy frameworks.
Insights from Hungary [54] further corroborate our findings. An analysis of three PV system configurations (HMKE, small-scale, and KÁT) with capacities from 50 to 500 kW found payback periods of between 7 and 9 years, closely matching our observed range. The Hungarian study also emphasizes the impact of regulatory context and system design on investment returns, confirming our observation that site-specific conditions and financing mechanisms critically shape economic performance. These results affirm that well-planned small to medium-scale PV installations can yield attractive returns, reinforcing the viability of PV investment in Central Europe’s temperate climates.
Beyond economic and technical metrics, spatial planning research in Poland [55] complements these validations by employing geoinformation and multi-criteria decision-making techniques to identify optimal PV farm locations. Key spatial factors such as terrain slope, exposure, precipitation, and grid proximity were weighted through Analytic Hierarchy Process (AHP) and entropy methods across 555 existing farms. This approach revealed that economic viability must be integrated with spatial constraints, environmental considerations, and social acceptance. Challenges in permission related to proximity to industrial and residential zones further underscore the complexity of PV deployment. These findings align with our holistic approach, suggesting that combining economic evaluation with advanced spatial planning enhances decision-making and investment feasibility in temperate climates like Poland.
3.5. Sensitivity Analysis of Economic Results
Sensitivity analysis is a crucial step in assessing the robustness and reliability of the economic outcomes of the photovoltaic farm investment. Its purpose is to evaluate how variations in key parameters influence critical economic indicators such as the levelized cost of energy (LCOE), return on investment (ROI), internal rate of return (IRR), and payback period. Conducting sensitivity analysis allows for a better understanding of the financial risks associated with the project by considering potential changes in market, technical, and regulatory conditions.
In this study, the impact of three fundamental parameters on the economic performance of the PV farm was examined:
- Discount rate, initially set at 2%, with additional scenarios tested at 1% and 3%.
- Installation costs, analyzed with a +10% increase and −5% decrease relative to the baseline assumptions.
- Electricity selling price, with a baseline value of 0.559 PLN/kWh and scenarios adjusted by +5% and −10%.
This approach provides insight into the investment’s resilience to fluctuations in the most significant economic factors and identifies which parameters exert the greatest influence on the project’s profitability.

Table 8.
Sensitivity analysis results assuming changes in the discount rate.

Table 9.
Sensitivity analysis results assuming changes in the level of installation costs.

Table 10.
Results of the sensitivity analysis assuming changes in the electricity sales price.
3.6. Limitations of the Study and Future Research Directions
While this study provides a comprehensive analysis of the energy and economic efficiency of fixed-tilt photovoltaic farms under Polish temperate climate conditions, several limitations warrant consideration.
Key economic and technical assumptions such as a fixed discount rate, static land availability, and pre-set inverter oversizing factors were applied uniformly for consistency. However, these parameters can vary dynamically with policy shifts, land-use changes, and technological advancements, which may influence the real-world performance and viability of PV projects.
The study focuses on fixed-tilt PV configurations, which limits generalizability across alternative system designs. Emerging PV technologies, including bifacial modules, single-axis trackers, and advanced inverter solutions, have the potential to improve energy yields and grid compatibility but were not explored here.
Environmental and grid integration aspects, including land use conflicts, biodiversity impacts, water runoff, and challenges such as grid congestion and curtailment, have been qualitatively mentioned but not quantitatively analyzed. These represent important factors influencing PV farm sustainability and operational feasibility.
In this context, agro-photovoltaic (Agri-PV) systems, which combine solar power generation with agricultural activities on the same land area, present a promising solution to mitigate land use conflicts and enhance land use efficiency. By allowing dual land exploitation, Agri-PV can reduce competition between energy and food production, provide shading benefits such as improving crop yields, and foster biodiversity. Incorporating Agri-PV concepts into PV farm design could thus extend the applicability and social acceptance of large-scale solar investments, especially in regions like Poland where agricultural land is valuable.
Similarly, integrating energy storage systems (such as battery storage) with PV farms addresses the intermittency and variability of solar generation, improves grid stability, and enhances the economic profile by enabling energy shifting and peak shaving. Hybrid PV + storage systems can better match supply with demand, reduce curtailment risks, and increase self-consumption, all of which are critical in temperate climates with variable insolation patterns.
Although these advanced system configurations fall beyond the scope of the current study, they represent vital directions for future research to build upon the energy and economic optimization framework presented here. Such studies will be essential to develop resilient, efficient, and sustainable PV farms capable of meeting evolving grid requirements and policy objectives.
4. Discussion
Large-scale photovoltaic farms, while providing significant renewable energy benefits, inevitably raise environmental and grid integration concerns that merit careful consideration. One critical environmental trade-off involves land use, as extensive PV installations can compete with agricultural land, natural habitats, and biodiversity. Changes in land cover can affect soil quality and water runoff patterns, potentially leading to erosion or altered local hydrology. These challenges are well documented in regional studies and highlight the importance of integrating environmental assessments into PV planning.
In addition to technical and land use considerations, environmental and social impacts play a crucial role in the sustainable deployment of photovoltaic farms. These include potential effects on local biodiversity, visual landscape changes, and community acceptance, which can significantly influence project feasibility and long-term success. Studies highlight the importance of engaging stakeholders early, conducting thorough environmental impact assessments, and integrating mitigation measures to address concerns related to habitat disruption and aesthetic integration. Accounting for these factors complements technical evaluations and ensures more holistic planning and implementation of renewable energy projects.
An emerging and promising approach to mitigate these impacts is the implementation of agro-photovoltaic (Agro-PV) systems, which combine solar energy production with agricultural activities on the same land area. Agro-PV offers multiple benefits: it enhances land use efficiency, supports biodiversity by maintaining vegetation cover, reduces soil erosion, and may even improve crop yields through shading and microclimate regulation. By leveraging dual land use, Agro-PV presents a sustainable pathway to reconcile energy generation with agricultural productivity and environmental stewardship.
In recent years, advancements in semi-transparent photovoltaic technologies, particularly those based on perovskite materials, have opened new avenues for enhancing the versatility and integration of solar energy systems. Unlike conventional PV modules, semi-transparent perovskite-based solutions enable partial transmission of light, making them especially suitable for building-integrated photovoltaics (BIPV) and agro-photovoltaic applications where maintaining natural illumination is crucial. As highlighted in [56], these innovative PV modules demonstrate promising efficiency and stability, suggesting their potential to improve land use efficiency and expand PV deployment opportunities in temperate climates similar to Poland. Incorporating such emerging technologies in future system designs could address some limitations of fixed-tilt PV farms by enabling dual-purpose land use and contributing to the aesthetic and functional diversification of solar installations.
In terms of grid integration, the high penetration of PV generation introduces operational challenges such as intermittency, curtailment, and grid congestion, especially during peak solar production periods. Our findings suggest that east–west oriented PV configurations can partially alleviate these issues by producing a smoother and more distributed daily generation profile, thus reducing midday peaks that strain the grid. Nevertheless, effective grid management solutions—including energy storage, demand response, and advanced forecasting—remain essential to fully address variability and ensure stable grid operation.
Although this study primarily focuses on energy and economic analyses, acknowledging environmental impacts and grid challenges provides a more comprehensive understanding of large-scale PV deployment in temperate climates. Future research could further quantify these effects and explore integrated solutions like Agro-PV technologies, which hold promise for sustainable solar farm development aligned with environmental and grid reliability goals.
The analysis of the eight photovoltaic farm configurations reveals clear trends in both energy performance and economic efficiency linked to module tilt angle and orientation. Among south-facing variants, the 20° and 30° tilt angles deliver the highest annual energy yields, with production efficiencies of 1123 kWh/kWp and 1132 kWh/kWp, respectively. The Performance Ratio (PR) is also highest for the 20° S variant, reaching approximately 0.83, indicating optimal system operation. However, the installed capacity nearly doubles when the tilt is reduced from 30° to 10° (from 12.7 MWp to 26.3 MWp), as lower tilt angles allow denser module placement due to reduced shading and shorter shadow length, which supports higher land utilization efficiency.
Economically, the 15° S variant stands out, achieving the shortest payback period of 8.7 years, the highest ROI of 453%, and the lowest levelized cost of energy (LCOE) at 0.10 EUR/kWh. This variant balances land use efficiency and energy generation, making it the most cost-effective option. In contrast, east–west oriented systems exhibit lower production efficiencies (e.g., 971 kWh/kWp for 10° EW) and higher LCOE values, with payback periods extending up to 11.3 years for 30° EW. East–west farms also show a smoother, more grid-friendly energy production profile with less pronounced midday peaks, which can reduce grid congestion and curtailment risk, offering operational advantages despite somewhat lower profitability.
Investment costs per MWp are inversely related to installed capacity; larger farms benefit from economies of scale, resulting in unit costs as low as ~644,000 EUR/MWp for 30° EW and ~649,000 EUR/MWp for 10° S. Conversely, smaller or more inclined farms incur higher unit costs, up to 709,000 EUR/MWp for 30° S. This cost behavior reflects the trade-off between technical design choices and economic efficiencies, reinforcing the need to optimize layout and module orientation in line with site-specific constraints.
Oversizing of inverters, particularly in higher-tilt south-facing systems with fewer inverter–transformer stations, contributes to seasonal performance variations. This strategy improves winter energy yield and grid injection predictability but can reduce efficiency during summer months. For example, the 25° S variant with significant oversizing demonstrated higher PR in winter and shoulder months but showed decreased efficiency during peak summer irradiance, emphasizing the importance of balancing inverter sizing for year-round optimal performance.
Cross-regional validation supports these findings. Studies from Southern Slovakia [52] report optimal tilt angles near 34.5°, with similar azimuth considerations, aligning closely with our 20–30° south-facing variants. Research from the Baltic States [53] confirms comparable LCOE ranges (0.08–0.09 EUR/kWh), while Hungarian analyses [54] note similar payback periods (7–9 years) and emphasize regulatory impact on investment returns, mirroring our observations on site- and policy-specific economic sensitivities. Polish spatial planning research [55] further contextualizes the study, highlighting that economic viability is strongly tied to terrain, grid proximity, and land use constraints, validating the importance of integrating geospatial factors with economic modeling.
The conducted sensitivity analysis highlights the robustness of the economic performance of the photovoltaic farm across a range of realistic variations in key parameters. Variations in the discount rate (±1%) showed expected impacts on the levelized cost of energy (LCOE), return on investment (ROI), internal rate of return (IRR), and payback period, with lower discount rates improving economic attractiveness and vice versa. Similarly, adjustments to installation costs by ±5–10% directly influenced profitability indicators, confirming the sensitivity of project economics to capital expenditures. Changes in the electricity sale price demonstrated a notable effect on all economic metrics, underscoring the critical role of market conditions and tariff structures on investment viability. Importantly, despite these parameter fluctuations, all variants maintained positive IRR values and reasonable payback periods, indicating a generally stable and resilient financial outlook for the project.
Future work should incorporate probabilistic modeling and scenario analysis to quantify the robustness of economic and energy performance outcomes under varying assumptions. Moreover, inclusion of grid impact assessments, demand-side integration, and advanced storage or tracking technologies would enrich the decision-making framework, particularly for large-scale PV farms in temperate climates facing evolving grid challenges.
In conclusion, the combined analysis of energy and economic metrics identifies the 15° S configuration as the most advantageous overall, balancing high profitability with efficient land use and acceptable energy yield. While east–west orientations offer smoother generation profiles that are beneficial for grid integration, trade-offs in profitability and LCOE must be carefully considered. The alignment of these findings with international studies underlines their broader applicability, yet continued evaluation under uncertainty and technological advancement remains essential for resilient PV farm design.
5. Conclusions
According to a report presented by the European Photovoltaic Industry Association (EPIA), net installation prices in the segment of ground-mounted photovoltaic farms with power up to 2.5 MW have fallen over recent years from the range of EUR 1.22/W–EUR 1.75/W to the range of EUR 0.98/W–EUR 1.45/W, which improves the economics of investing in large-scale photovoltaic farms.
Designing a photovoltaic farm is a long and complicated process. It is usually associated with creating many variants of land development by photovoltaic system elements and adapting the system in real time to meet the assumed goals.
This study comprehensively evaluated eight large-scale photovoltaic (PV) farm configurations in a temperate climate, focusing on module tilt angles and orientations. The results highlight the significant influence of these parameters on both energy yield and economic performance.
Among south-facing configurations, the 20° S and 30° S variants achieved the highest energy production efficiencies—1123 kWh/kWp and 1132 kWh/kWp, respectively—with the 20° S variant also exhibiting the highest Performance Ratio (~0.83). However, lower tilt angles, particularly 10° S, allow for denser module placement due to reduced shading, nearly doubling installed capacity from 12.7 MWp (30° S) to 26.3 MWp (10° S), thereby increasing land utilization efficiency.
From an economic perspective, the 15° S variant offers the most favorable balance, delivering the shortest payback period (8.7 years), highest return on investment (453%), and lowest levelized cost of energy (0.10 EUR/kWh). In contrast, east–west oriented systems, while yielding lower production efficiencies (e.g., 971 kWh/kWp for 10° EW) and longer payback periods (up to 11.3 years for 30° EW), provide smoother, more grid-friendly generation profiles, which can mitigate grid congestion and curtailment risks.
Investment costs inversely correlate with installed capacity, with larger farms benefiting from economies of scale. Unit costs ranged from approximately 644,000 EUR/MWp for the 30° EW and 10° S configurations to 709,000 EUR/MWp for smaller or more inclined setups like 30° S.
Oversizing inverters in high-tilt south-facing farms improved wintertime energy yields and grid injection stability but reduced summer efficiency, highlighting the importance of system design tailored to seasonal variability.
Cross-regional comparisons align these findings with studies from Central and Eastern Europe, confirming the robustness and broader applicability of the results.
Practical implications of this study suggest prioritizing the 15° S configuration for balanced energy output and cost-effectiveness in temperate zones, while considering east–west orientations where grid integration and generation smoothing are critical. Future research should address uncertainties through probabilistic modeling and explore advanced technologies such as tracking systems and energy storage to further optimize PV farm design.
Author Contributions
Conceptualization, D.T.; methodology, D.T.; validation, A.B.; formal analysis, W.C.; data curation, D.B.; writing—original draft preparation, A.B.; writing—review and editing, A.B.; visualization, D.T.; supervision, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cecen, M.; Yavuz, C.; Tirmikci, C.A. Analysis and evaluation of distributed photovoltaic generation in electrical energy production and related regulations of Turkey. Clean Technol. Environ. Policy 2022, 24, 1321–1336. [Google Scholar] [CrossRef]
- Energetyka24. Available online: https://energetyka24.com/oze/analizy-i-komentarze/niemal-13-energii-elektrycznej-na-swiecie-jest-zielona-a-rok-2024-bedzie-przelomowy (accessed on 15 August 2024).
- European Green Deal. Available online: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal_en (accessed on 20 March 2025).
- Ali, T.; Ma, H.; Nahian, A.J. An analysis of the renewable energy technology selection in the southern region of Bangladesh using a hybrid multicriteria decision making (MCDM) method. Int. J. Renew. Energy Res. 2019, 9, 1838–1848. [Google Scholar] [CrossRef]
- Kang, S.W.; Yoon, H.S.; Kim, S.B.; Baatarbileg, A.; Sakong, J.; Lee, G.M. Regional Generation Characteristics of MW Photovoltaic Power Plants in Jeju Island. In Proceedings of the 2018 5th International Conference on Renewable Energy: Generation and Applications (ICREGA), Al Ain, United Arab Emirates, 25–28 February 2018; pp. 52–55. [Google Scholar]
- Ouali, H.A.L.; Guechchati, R.; Moussaoui, M.A.; Mezrhab, A. Performance of parabolic through solar power plant under weather conditions of the Oujda city in Morocco. Appl. Sol. Energy 2017, 53, 45–52. [Google Scholar] [CrossRef]
- Solar Resource Map 2021 Solargis. Available online: https://solargis.com/resources/free-maps-and-gis-data?locality=europe (accessed on 20 July 2025).
- Fraunhofer ISE. Available online: https://www.ise.fraunhofer.de/en/research-projects/apv-resola.html (accessed on 12 August 2024).
- Tafazoli, M.; Salimi, M.; Zeinalidanaloo, S.; Mashayekh, J.; Amidpour, M. Techno-Economic Analysis of Electricity Generation by Photovoltaic Power Plants Equipped with Trackers in Iran. Energies 2023, 16, 235. [Google Scholar] [CrossRef]
- Abhishek, K.; Bikash, S.; Arvind, R.; Singh, Y.D.; Xiangning, H.; Praveen, K. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Choudhury, B.B.; Dhal, P.R.; Hanspal, M.S. A Comprehensive Review of Multi-criteria Decision-making (MCDM) Toward Sustainable Renewable Energy Development. Spec. Oper. Res. 2025, 2, 268–284. [Google Scholar] [CrossRef]
- Talal, A.; Waleed, A.R.; Khalifa, A.J.; Ammar, A. Solar farms suitability analysis using GIS-Based Analytic Hierarchy Process (AHP) multi-criteria: A case study of Al Duqm—Oman. Renew. Energy 2025, 241, 122295. [Google Scholar]
- Taoufik, M.; Meriem, L.; Ahmed, F. Land suitability analysis for solar farms exploitation using the GIS and Analytic Hierarchy Process (AHP)—A case study of Morocco. Energy Policy J. 2021, 24, 79–96. [Google Scholar] [CrossRef]
- Nasehia, S.; Nohegar, A. Photovoltaic Farm Site Selection using Fuzzy Multi Criteria Evolution with Emphasis on Air Quality and Environmental Conditions. Environ. Energy Econ. Res. 2025, 9, 102. [Google Scholar]
- Gramwzielone. Available online: https://www.gramwzielone.pl/energia-sloneczna/20193166/takie-instalacje-fotowoltaiczne-dominuja-w-polsce (accessed on 17 August 2024).
- Trade. Available online: https://www.trade.gov.pl/aktualnosci/fotowoltaika-w-polsce-wzrost-instalacji-o-41-w-2023-roku/ (accessed on 17 August 2024).
- Inoussah, M.; Ngoh, S.; Mboumboue, E.; Tonga, A.; Lissouck, D. Exergoeconomic analysis of solar photovoltaic power plants: Case study in differents tropicals zone (Maroua and Douala) in Cameroon. Water-Energy Nexus 2023, 10, 100206. [Google Scholar]
- Menéndez, J.; Loredo, J. Economic feasibility of developing large scale solar photovoltaic power plants in Spain. E3S Web Conf. 2019, 122, 02004. [Google Scholar] [CrossRef]
- Carrión, J.A.; Estrella, A.E.; Dols, F.A.; Toro, M.Z.; Rodríguez, N.; Ridao, A.R. Environmental decision-support systems for evaluating the carrying capacity of land areas: Optimal site selection for grid-connected photovoltaic power plants. Renew. Sustain. Energy Rev. 2008, 12, 2358–2380. [Google Scholar] [CrossRef]
- Gašparović, I.; Gašparović, M. Determining Optimal Solar Power Plant Locations Based on Remote Sensing and GIS Methods: A Case Study from Croatia. Remote Sens. 2019, 11, 1481–1498. [Google Scholar] [CrossRef]
- Luis-Ruiz, J.M.; Salas-Menocal, B.R.; Pereda-García, R.; Pérez-Álvarez, R.; Sedano-Cibrián, J.; Ruiz-Fernández, C. Optimal Location of Solar Photovoltaic Plants Using Geographic Information Systems and Multi-Criteria Analysis. Sustainability 2024, 16, 2895. [Google Scholar] [CrossRef]
- Al Garni, H.Z.; Awasthi, A. Solar PV power plant site selection using a GIS-AHP based approach with application in Saudi Arabia. Appl. Energy 2017, 206, 1225–1240. [Google Scholar] [CrossRef]
- Pour, A.K.; Shahraki, M.R.; Saljooghi, F.H. Evaluation of the Effective Factors in Locating a Photovoltaic Solar Power Plant Using Fuzzy Multi-Criteria Decision-Making Method. J. Renew. Energy Environ. 2024, 8, 16–25. [Google Scholar]
- Ali, S.; Taweekun, J.; Techato, K.; Waewsak, J.; Gyawali, S. GIS based site suitability assessment for wind and solar farms in Songkhla, Thailand. Renew. Energy 2019, 132, 1360–1372. [Google Scholar] [CrossRef]
- AlMallahi, M.N.; Swailmeen, Y.A.; Abdelkareem, M.A.; Olabi, A.G.; Elgendi, M. A path to sustainable development goals: A case study on the thirteen largest photovoltaic power plants. Energy Convers. Manag. 2024, 22, 100553. [Google Scholar]
- Walichnowska, P.; Idzikowski, A. Energy Analysis of the PV Farm with a Capacity of 140 MW. Conf. Qual. Prod. Improv. (CQPI) 2021, 3, 369–376. [Google Scholar]
- Brodziński, Z.; Brodzińska, K.; Szadziun, M. Photovoltaic Farms—Economic Efficiency of Investments in North-East Poland. Energies 2021, 14, 2087. [Google Scholar] [CrossRef]
- Zdyb, A.; Dragan, P.; Jaremek, A. The analysis of the solar power plant performance in temperate climate. J. Civ. Eng. Environ. Archit. 2018, 65, 73–79. [Google Scholar]
- Enerad. Available online: https://enerad.pl/aktualnosci/koszt-budowy-farmy-fotowoltaicznej-100-kw/ (accessed on 10 August 2024).
- Koszty Farmy Fotowoltaicznej—Od Czego Zależą? Available online: https://www.energetyka.plus/ (accessed on 10 March 2025).
- Alashqar, M.; Xue, Y.; Yang, C.; Zhang, X. Comprehensive economic analysis of PV farm—A case study of Alkarsaah PV farm in Qatar. Front. Energy Res. 2022, 10, 987773. [Google Scholar] [CrossRef]
- Makkiabadi, M.; Hoseinzadeh, S.; Taghavirashidizadeh, A.; Soleimaninezhad, M.; Kamyabi, M.; Hajabdollahi, H.; Majidi, N.M.; Piras, G. Performance Evaluation of Solar Power Plants: A Review and a Case Study. Processes 2021, 9, 2253. [Google Scholar] [CrossRef]
- Singh, S.; Alharthi, M.; Anand, A. Performance evaluation and financial viability analysis of grid associated 10 MWP solar photovoltaic power plant at UP India. Sci. Rep. 2022, 12, 22380. [Google Scholar] [CrossRef] [PubMed]
- Yang, R. Economical Analysis of the Influence of Cleaning PV modules on Power Generating Cost of Photovoltaic Power Station. In Proceedings of the 2015 International Symposium on Energy Science and Chemical Engineering (ISESCE), Guangzhou, China, 12–13 December 2015; Atlantis Press: Dordrecht, The Netherlands, 2015. [Google Scholar]
- Iakovleva, E.; Guerra, D.; Tcvetkov, P.; Shklyarskiy, Y. Technical and Economic Analysis of Modernization of Solar Power Plant: A Case Study from the Republic of Cuba. Sustainability 2022, 14, 822. [Google Scholar] [CrossRef]
- Kwaśniewski, D.; Akdeniz, C.; Durmaz, F.; Kömekçi, F. Economic Analysis of the Photovoltaic Installation Use Possibilities in Farms. Agric. Eng. 2020, 24, 47–60. [Google Scholar] [CrossRef]
- Bendaas, I.; Bouchouicha, K.; Semaoui, S.; Razagui, A.; Bouchakour, S.; Boulahchiche, S. Performance evaluation of large-scale photovoltaic power plant in Saharan climate of Algeria based on real data. Energy Sustain. Dev. 2023, 76, 101293. [Google Scholar] [CrossRef]
- Gharibshahian, I.; Sharbati, S.; Oroujia, A. The design and evaluation of a 100 kW Grid Connected Solar Photovoltaic Power Plant in Semnan City. J. Energy Res. 2017, 24, 287–293. [Google Scholar]
- Denholm, P.; Ela, E.; Kirby, B.; Milligan, M. The Role of Energy Storage with Renewable Electricity Generation; Report NREL/TP-6A2-47187; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
- Hossain, S.; Madlool, N.A.; Al-Fatlawi, A.W.; Assad, M. High Penetration of Solar Photovoltaic Structure on the Grid System Disruption: An Overview of Technology Advancement. Sustainability 2023, 15, 1174. [Google Scholar] [CrossRef]
- Maghami, M.R.; Pasupuleti, J.; Ekanayake, J. Energy storage and demand response as hybrid mitigation technique for photovoltaic grid connection: Challenges and future trends. J. Energy Storage 2024, 88, 111680. [Google Scholar] [CrossRef]
- Gusain, C.; Tripathi, M.M.; Nangia, U. Study of Meta-heuristic Optimization Methodologies for Design of Hybrid Renewable Energy Systems. Therm. Sci. Eng. Prog. 2023, 39, 101711. [Google Scholar] [CrossRef]
- Jarso, A.K.; Jin, G.; Ahn, J. Hybrid Genetic Algorithm-Based Optimal Sizing of a PV–Wind–Diesel–Battery Microgrid: A Case Study for the ICT Center, Ethiopia. Mathematics 2025, 13, 985. [Google Scholar] [CrossRef]
- Nagadurga, T.; Devarapalli, R.; Knypiński, Ł. Comparison of Meta-Heuristic Optimization Algorithms for Global Maximum Power Point Tracking of Partially Shaded Solar Photovoltaic Systems. Algorithms 2023, 16, 376. [Google Scholar] [CrossRef]
- Regulation of the Minister of Climate and Environment. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU2022000224 (accessed on 23 March 2025).
- Globenergia. Available online: https://globenergia.pl/klasa-gruntu-odrolnienie-i-dzierzawa-gruntu-pod-farme-jak-to-dzisiaj-dziala/ (accessed on 19 August 2024).
- Ongeo. Available online: https://blog.ongeo.pl/grunty-pod-fotowoltaike (accessed on 19 August 2024).
- EnergetykaPlus. Available online: https://www.energetyka.plus/koszty-farmy-fotowoltaicznej-od-czego-zaleza/ (accessed on 19 August 2024).
- Energetyka-Polska. Available online: https://www.energetyka-polska.pl/farma-fotowoltaiczna-jak-zaczac-inwestycja-krok-po-kroku/ (accessed on 19 July 2024).
- Fotowoltaikaonline. Available online: https://fotowoltaikaonline.pl/farma-fotowoltaiczna (accessed on 15 July 2024).
- Żurakowska-Sawa, J.; Gromada, A.; Trocewicz, A.; Wojciechowska, A.; Wysokiński, M.; Zielińska, A. Photovoltaic Farms: Economic Efficiency of Investments in South-East Poland. Energies 2025, 18, 170. [Google Scholar] [CrossRef]
- Božiková, M.; Bilčík, M.; Madola, V.; Szabóová, T.; Kubík, Ľ.; Lendelová, J.; Cviklovič, V. The Effect of Azimuth and Tilt Angle Changes on the Energy Balance of Photovoltaic System Installed in the Southern Slovakia Region. Appl. Sci. 2021, 11, 8998. [Google Scholar] [CrossRef]
- Lebedeva, K.; Borodinecs, A.; Palcikovskis, A.; Wawerka, R.; Skandalos, N. Estimation of LCOE for PV electricity production in the Baltic States—Latvia, Lithuania and Estonia until 2050. Renew. Sustain. Energy Transit. 2025, 7, 100110. [Google Scholar] [CrossRef]
- Zsiborács, H.; Hegedűsné Baranyai, N.; Csányi, S.; Vincze, A.; Pintér, G. Economic Analysis of Grid-Connected PV System Regulations: A Hungarian Case Study. Electronics 2019, 8, 149. [Google Scholar] [CrossRef]
- Kowalczyk, A.M.; Czyża, S. Optimising Photovoltaic Farm Location Using a Capabilities Matrix and GIS. Energies 2022, 15, 6693. [Google Scholar] [CrossRef]
- Spampinato, C.; Valastro, S.; Calogero, G.; Smecca, E.; Mannino, G.; Arena, V.; Balestrini, R.; Sillo, F.; Ciná, L.; Magna, A.L.; et al. Improved radicchio seedling growth under CsPbI3 perovskite rooftop in a laboratory-scale greenhouse for Agrivoltaics application. Nat. Commun. 2025, 16, 2190. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).