Collaborative Microgrids as Power Quality Improvement Nodes in Electricity Networks

Abstract

This paper explores the integration of microgrids within utility networks and distinguishes selfish from collaborative microgrids. Research has shown that selfish microgrids tend to increase volatility of order updates to power generators, whereas collaborative microgrids decrease that volatility, resulting in smoother, more controllable operations of networks. This paper proposes an analytical formula linking power volatility to power quality, i.e., to issues such as voltage dips, surges, and transients. These are known risks for disrupting the operation of utility grids, causing instability and jeopardising efficiency and reliability. As collaborative microgrids reduce volatility, they improve power quality. That argument is extended to propose that collaborative microgrids can act as quality improvements agents within wider networks.

1. Introduction

As concerns about the impact of climate changes are mounting [1] and as evidence that humanity has gone past planetary boundaries [2], the use of renewable energy for power generation has become the main solution to green energy generation [3]. However, it is well known that the increasing penetration of renewable energy sources poses a challenge due to intermittence [4,5]. Not only do the majority of renewable energy sources output power of lower quality [6], but they also make the balancing of supply and demand more challenging, which has an additional knock-on effect on power quality [7]. Together, uncertainty about electricity demand, uncertainty about the availability of renewable energy fuels, intermittence, and lower power quality combine to create serious challenges to the safe operations of utility grids. These issues are compounded by an expected future increase in electricity demand (from vehicle electrification, data centers, etc.) and an increased proportion of renewable energy sources.

The vast majority of countries that are proactively addressing sustainability concerns envision a significant investment in renewable energy capacity, with some countries targeting 100% renewable energy mixes. As this strategy brings many challenges to utility grids, a second, counter-acting, investment in smart grids, or self-healing grids, is required [8,9].

In this paper, we explore a different direction of research by looking at the concept of a collaborative microgrid [10,11,12], building on the original idea of Sato et al. [13] who applied the principle of Heijunka (stable, level demand), a foundational concept of lean thinking [14] to stabilise the power supply of a microgrid by using energy storage. The collaborative microgrid concept expands this application of Heijunka to stabilising the demand from the utility grid by using microgrids that make forward electricity purchase commitments. Feleafel et al. [11,12] demonstrate that this approach results in a significant decrease in order volatility to the grid and reduces carbon emissions. In other words, collaborative microgrids are a way to become more sustainable without requiring the deployment of smart grids, as uncertainty in the whole network is reduced. There is less of a need for a grid to self-repair itself if the challenge from handling uncertainty has been reduced, or eliminated, in the first place. The aim of this paper is to extend this argument to power quality, i.e., to propose that collaborative microgrids can be used as cleaning agents improving the overall power quality of electricity networks. This aim is broken down into two objectives that form the two main parts of this paper: In the first part, a model is used to compare the power quality impact of a collaborative microgrid when compared to a selfish microgrid. It shows that collaborative microgrids create less power quality issues. In the second part, the results are extrapolated by considering further energy storage solutions to discuss the role that microgrids could play as improvement nodes of power quality, by opposition to their current status as nodes deteriorating power quality within distribution grids. We start by discussing the relationship between uncertainty and power quality in the next section.

2. Uncertainty and Power Quality

Stone and Collinson [15] described power quality as in increasing concern in 2001. They explain that consumption equipment was previously insensitive to power quality fluctuations, but that as modern equipment now depends on a high level of power quality, network operators had to define adequate standards. They define a power quality issue as a voltage fluctuation from a standard, which is similar to the IEC definition [16]: “Power quality encompasses the characteristics of the electricity at a given point on an electrical system, evaluated against a set of reference technical parameters”. In practice, power quality standards are about the voltage, frequency, and waveform of electricity. High power quality results in a consistent, stable, and reliable power supply.

Table 1. Relationship between Uncertainty and Power Quality. Compiled by the authors from the following sources: [15,17,18,19].

Source of Uncertainty	Network Power Quality	Consumption Nodes Impact
Increases in demand, transitional events, energizing transformers, faults	Voltage dip	Increases in power consumption to offset drop in effective power
Faults, load switching, capacitor switching	Voltage swell	Possible damage to unprotected equipment
Rapid temporary changes in current and load/source switching	Voltage spike from transients	Equipment damage and system instability
Use of nonlinear loads, use of power electronics, overloading	Harmonics, flicker	Equipment overheating, reduced efficiency, voltage distortion, interference with equipment
Imbalance between power generation and demand, islanding operations, faults	Frequency deviation	Equipment overheating, damage, reduced efficiency

presents a summary of different types of power quality issues.

Power quality, like the power variable that it is derived from, is a property of an electricity network at a specific location and point in time. It is a system state property which is created by events within the network. The events described in Table 1 can be created either by generation nodes or by consumption nodes. This is why Ferrero [17] describes electrical networks as healthy carriers of disturbances and provides the example of a disturbance created by one customer that damages the equipment of a second customer. The increasing use of wind energy is a significant contributor to decreasing power quality, as wind is naturally unsteady. This is a well-known issue and one solution adopted by turbine manufacturers is to use power electronics modules to improve output quality. However, the use of power electronics creates harmonics. In other words, one power quality problem (voltage instability) has been replaced by another (harmonics).

As the paper’s idea of applying load levelling (Heijunka) comes from operations and supply chain management, volatility, typically measured as the standard deviation of demand or supply, is the universally used performance measure to evaluate a system’s lack of stability. Therefore, this paper aims to establish an analytical relationship between the different sources of uncertainty listed in Table 1 (left-hand side column), which are based on the electronics literature, with a higher-level general measure of volatility. An electrical system’s level of volatility is thus defined as a proxy measure for power quality. Volatility is in this case the standard deviation of power required in a network compared to its average requirement.

To better appreciate the meaning of Heijunka, consider for example a house with a constant power requirement of 3.2 kW connected to a petrol generator with the effective capacity to deliver that power. This is the most basic energy system to operate, and if petrol is steadily supplied and demand maintained, no energy management system of any sort is required, as power volatility is nil. The energy system is controlled, predictable, and deterministic. This provides the benchmark that Heijunka aims to replicate. If a volatile system is operated, can technologies be deployed to make the operations of this system more stable and more like this benchmark?

Figure 1 shows how relaxing the underlying stable conditions of operations creates power quality issues. Using the 3.2 kW house example, a number of computers may be switched on or off in the house. The increasing or decreasing load is a form of volatility, which could cause a voltage swing, but Figure 1 shows that there could be a two-way interaction between that volatility and the fact that the timing of load switching is difficult to predict. When the load switching timing and amplitude cannot be predicted and the resulting volatility of demand becomes uncertain, the house, representing here a demand node, is uncontrollable. This is where the distinction between selfish and collaborative microgrids becomes important. A selfish microgrid makes energy decisions independently (switching loads when needed). From a utility grid perspective, it makes it a volatile, unpredictable, and uncontrollable node. In contrast, a collaborative microgrid engages in joint collaborative planning (the planning scheme is described in the next section) and thus becomes a more controllable and predictable node. The aim of this paper is to demonstrate that the collaborative approach reduces volatility and therefore improves power quality.

The example of a demand node with a constant demand of 3.2 kW does not and cannot exist as real life conditions are characterised by volatile power supply and demand, creating not only the need for balancing the two in real time but for a protocol to manage dynamic conditions [7].

In the most traditional form of energy management without demand management, the volatility of power demand is taken a given, i.e., electricity network operators accept demand volatility as the aggregate result of consumers’ behaviour, and resort to forecasts of demand to flexibly plan power production. There are well-known cases where this proves to be challenging, such as predicting when individuals install and turn on Christmas lights on their houses. It is possible to predict the time window of the installation of the lights but challenging to predict the exact day within that time window. This type of uncertainty/volatility is what makes electricity grids difficult to balance and occasionally leads to supply interruption. The national blackout that took place in Spain and Portugal in May 2025 was initially blamed on volatile supply (caused by a high renewable energy content) but it later transpired that failing to predict demand was the most likely root cause. When we introduce renewable energy sources that are affected by their own sources of volatility (i.e., renewable energy volatility is not demand-related), we increase complexity as distribution networks are challenged by volatility from both demand and supply sides.

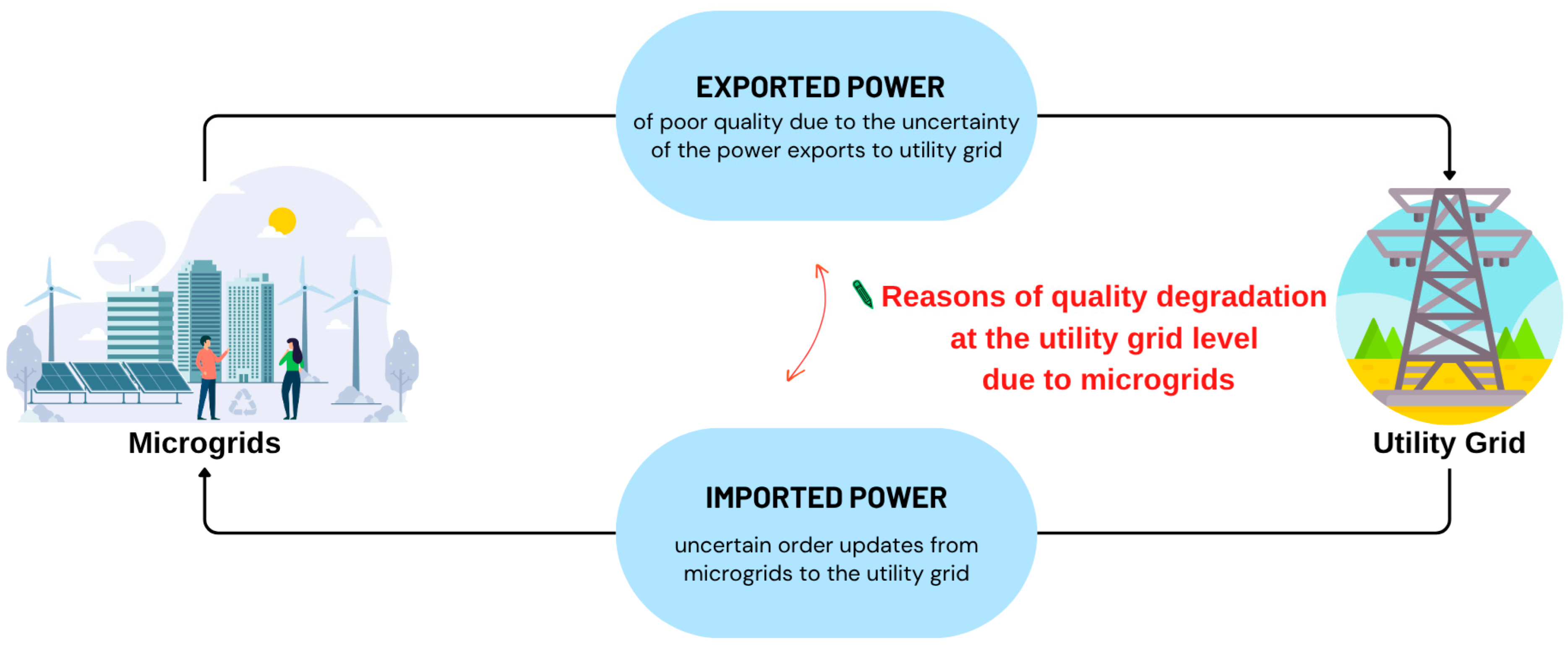
As power quality is a function of network design, supply decisions, demand decisions, location, and time, it is challenging to measure it, and especially in a general fashion (see [17] for a full technical account of the challenges of measuring power quality). In this paper, the focus is the power quality impact that a microgrid has on a utility grid, as shown in Figure 2. Our notional case study is based in the UK, hence the assumption that grid power is of good quality. The research question is: what is the impact of the microgrid on the power quality of the utility grid? Figure 2 shows that we are concerned with two impact pathways: (1) the exports by the microgrid of poor-quality power, which cause power quality degradation due to the uncertainty of exports, and (2) the degradation of power quality induced by the uncertainty of imports from the utility grid.

The motivation for the research follows Feleafel et al. [10,11,12]: we define a selfish microgrid as a grid with an energy management regime aiming to maximise autonomy and/or to minimize costs, while ordering only spot orders to the utility grid. In contrast, a collaborative microgrid places forward orders, labelled COUs (for pre-contracted order updates). With reference to Figure 1, using COUs eliminates the need for demand forecasting at the utility grid level. It also provides an opportunity for co-ordination when switching loads on or off, i.e., it provides an opportunity to control power changes. In other words, a collaborative microgrid seeks to eliminate any source of uncertainty that amount to injecting disturbances in power networks. Therefore, by definition, a collaborative microgrid use of COUs means that imported power in Figure 2 will have no impact, or very little impact, on the power quality within the utility network.

Previous research [11,13] has confirmed that a collaborative microgrid with local generation and storage can stabilise and level electricity demand (Heijunka), i.e., it can transform a volatile demand into the example of the steady 3.2 kW house. However, the references above conclude that the downside of the levelized power demand is that the microgrid has excess power which needs to be exported. The excess green power generated by the microgrid could be exported if it is economically worth doing so. Historically, power exported from microgrid received generous feed-in-tariffs, but there is evidence that similar tariffs are becoming less generous, if not a disincentive [20].

The practice of discouraging microgrids’ power exports can be explained by the fact that power exported from a microgrid is much more difficult to forecast than the traditional problem of forecasting electricity demand. Electricity demand is repeatable, seasonal, and cyclic, and therefore times series forecasting models will normally achieve very good results (e.g., [21]). Forecasting the value of power exported by a microgrid has to address three sources of uncertainty: (1) the usual demand uncertainty, (2) the uncertainty of local generation due to weather variability, and (3) the change in consumption behaviour as the microgrid adapts to weather conditions. Exports from microgrids are key culprits in terms of the source of uncertainty listed in Table 1. This is the reason why distributed generation loads are often considered to be uncontrollable nodes associated with voltage fluctuations [22,23]. The next section describes how the impact of these uncontrollable nodes is modelled in the rest of the paper.

3. Model

This paper is based on an analytical modelling based on two parts. In the first part, a microgrid model, implemented in Excel, is used to balance supply and demand. The inputs to this first model are a set daily demand profile, a one-week ahead weather forecast, and actual values of wind speed and irradiance for a period of 3 months. Different planning rules are applied within the microgrid to balance supply and demand, for example by using different energy storage tactics or forward by opposition to spot orders. The outputs of the first model are the volatility of power imported and exported by the microgrid, measured as a standard deviation.

These volatility figures become the input of the second part of the model, where volatility is converted into a measure of power quality. The following sections provide a more detailed explanation of each part of the model, starting with the specification of a measure for power quality.

3.1. Case Study and Microgrid Power Flows

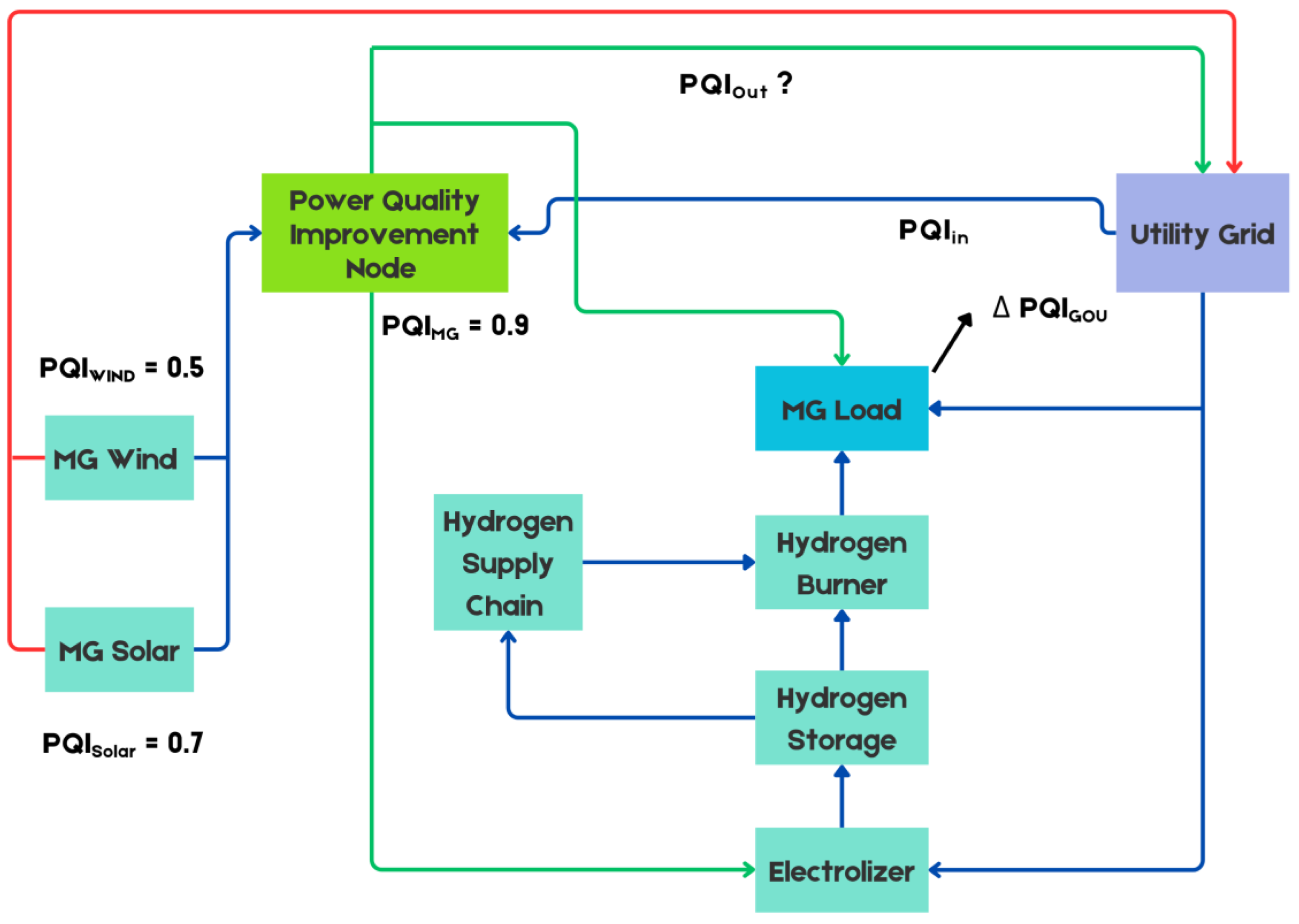
Our model is based on a notional case study of a UK-based microgrid as depicted in Figure 3. Interconnections in Figure 3 represent potential power flows and are characterised by a level of power quality measured as a composite index PQI, as shown in Equation (1).

$$\mathrm{P}\mathrm{Q}\mathrm{I}=\sum {\mathrm{w}}_{\mathrm{i}}{\mathrm{P}\mathrm{Q}}_{\mathrm{i}}$$

(1)

The power quality composite index PQI is the weighted sum of normalised individual power quality parameters PQ_i. For example, with reference to Table 1, i = 1 could be voltage dips, and i = 5, frequency deviation. The weights w1 and w5 represent the respective importance of these problems.

3.2. Estimation of Power Quality Composites Indices (PQI_i)

The microgrid is connected to a utility grid through a single interconnection, but Figure 3 displays three distinct flows to highlight the differences in planning regimes used in this paper (these regimes are described in more details in Section 3.5). The first interconnection is a power import flow into the microgrid, where we assume the power quality from the utility grid to be good. As our case study is UK based, we consider a PQI_in of 0.9. Power quality indices are not publicly available, and when they are, they are expressed as a more complex set of measures than a composite index. For example, the UK National Grid is a well-managed grid, hence the upper value of 0.9 (A PQI of 1 would represent ideal power quality). As the UK is planning to further increase its reliance on renewable energy, and especially offshore wind, we note that the value of PQI_in could decrease in the future.

Wind power is associated with lower power quality, and we estimate the value of PQI_wind based on Gala and Jaderko’s [24] assessment of the impact of a wind turbine on the power quality of a distribution network.

Table 2. Estimation of PQI_wind.

Parameter	Measured Value (From [24])	Standard Limit (IEC61000-2-2 & IEEE 519-2014)	Normalised Value PQi
Voltage total harmonic distortion (%)	1.88–3.05%	5%	2.465/5 = 0.493
Current harmonics	7.11%	8%	7.11/8 = 0.889
Voltage imbalance (%)	0.32%	2%	0.16
Flicker severity (Pst)	0.25–0.50	1	0.375

shows the measured value of power quality parameters from this source and their normalised values based on the average measurement. Using equal weights, the normalised values from Table 2 give PQI_wind = 0.479, which we round to 0.5. Estimates of power quality impact of solar PV are more difficult to find but as the intermittence issues of solar power generation are smoother than those of wind, we assume, for the sake of modelling, PQI_solar = 0.7.

Returning to the discussion of the interconnections in Figure 2, we assume that the microgrid is equipped with its own power quality solution. This is because its locally generated green power has low power quality indices, and because the power it receives from the utility grid could also be a low power quality. In Figure 3, this solution is implemented as a “black box” power quality improvement node. Although there is extensive research about how to mitigate power quality risks [25,26] and how power quality is managed within microgrids, this aspect of energy management is not central to our research question. This is because the scope of the paper is the study of the planning regime—uncertainty—power quality relationship rather than the design of power electronic systems used to improve power quality. We therefore assume that it is feasible to achieve good power quality (PG_MG = 0.9), that it is economic to do so, and therefore the equipments used in the microgrid are protected against poor power quality.

To differentiate between the selfish and the collaborative microgrid regimes, there are two export power flows shown in Figure 3. The green export interconnector is used by the collaborative microgrid to export its green energy surplus production after improving it, whereas the red export interconnector is used to export wind and solar PV power directly (i.e., with PQI_wind = 0.5 and PQI_solar = 0.7). The power quality of exported power can be computed according to Equation (2):

$${\mathrm{P}\mathrm{Q}}_{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}}=\sum _{\mathrm{i}=1}^3{\mathrm{q}}_{\mathrm{i}}{\mathrm{P}\mathrm{Q}\mathrm{I}}_{\mathrm{i}}-\mathrm{k}{\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{E}}}{∆\mathrm{t}}}$$

(2)

Indices 1 to 3 represent respectively direct wind power export, direct solar PV power export, and power exports that have gone through the local power quality improvement node. The weights ${\mathrm{q}}_{\mathrm{i}}$ are the respective proportions of these flows (for example, for a collaborative microgrid, ${\mathrm{q}}_1=0,{\mathrm{q}}_2=0,{\mathrm{q}}_3=1$). Each is associated with an overall power quality composite index PQI_i, as discussed above and in Figure 3. ${\mathrm{\sigma }}_{\mathrm{E}}$ is the volatility of exported energy (in kWh) over a period of time $∆\mathrm{t}$. The coefficient k is our master unknown and the key to answering our research question: it is the coefficient of degradation of power quality caused by the injection of power volatility (${\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{E}}}{∆\mathrm{t}}}$) in kW volatility.

The next section presents the data and models used to compute ${\sigma }_{\mathrm{E}}$. This is followed by the estimation of the coefficient k for our case study.

3.3. Derivation of ${\sigma }_E$

The microgrid has a time dependent power demand D(t). It places two types of order updates to the utility grid. Some orders are firm, pre-contracted commitments made in advance, COU(t). In our model, this is implemented as orders placed one week in advance. The use of COUs means that the responsibility of balancing supply and demand is partially transferred to the microgrid as the MG operator takes full responsibility for the commitment that was made. Examples of these commitments could be either a perfectly level order or can be a step function to accommodate for daily demand variations. In the model used in this paper, COU is an hourly commitment (an hourly step function) made one week in advance based on a weather forecast. When a step function is used, the commitment can include protocols for linear power level transitions. For this reason, the use of COUs implies k = 0; i.e., as everything is pre-planned, there are no injections of uncontrollable power flows in the grid.

Our model is based on a one-week ahead forecast but longer periods are possible. There are many variables that are considered when defining COUs levels, such as the expected local power generation. Using short periods for COUs does not make sense as it equates to forecasting weather conditions. This can only be reliable for next-day conditions, which is the current operation mode of load balancing mechanisms. The longer the time period, the more the COU level depends on a climate forecast instead of a weather forecast. As climate is the average of weather, and as it is always easier to predict an average than a spot value, it is best to set at least one-week-ahead COUs.

It is important to note that in the planning regime of the microgrid, there will be many instances where COU(t) > D(t), i.e., the microgrid orders more than it needs, and this, even in cases when local green power is generated. The flow and balancing equations of the system are shown in Section 3.5. The principle of operations is that the total amount of power available at time t is the sum of COU(t), the power from turbines Pw(t), the power from solar panels P_pv(t), and the possible use of power from the hydrogen burner when relying on the energy stored in the microgrid. Note that local generation is calculated based on real weather data rather than the forecast used to set COU(t).

If there is surplus power, it is directed to the electrolyzer in Figure 3 to be stored as hydrogen. If the storage is full, then the microgrid exports the power back to the grid. It is this part of the process that triggers power quality degradation, though k, in the utility grid. If the microgrid faces a shortage of power, then it will either consume power from the grid (called a Grid Order Update GOU) or use the hydrogen burner in Figure 3 as its backup power supply. This means at any point in time, the total supply from the utility grid to the microgrid is GOU(t) + COU(t). Only collaborative microgrids use COUs, so selfish microgrids only rely on GOUs. As GOUs are more difficult to predict than traditional power demand time series, relying on GOUs also lead to power quality degradation through ${\sigma }_{GOU}$. This impact has been taken into account as $k.{\sigma }_{GOU}$.

The efficiency of the power conversion to stored hydrogen is assumed to be 60%. The hydrogen storage capacity is defined as the maximum excess power that the microgrid can produce during a 90 days-time period (April–June), which is the time window for the case study. Feleafel et al. [12] performed a similar comparative analysis of selfish and collaborative microgrid for 8 different scenarios, concluding that the collaborative microgrid has a significant impact on reducing power volatility and that it also achieves a much lower carbon footprint. The 8 scenarios are needed to explore the carbon emissions of different planning regimes and of different backup power generation tactics. As this paper is concerned with the impact of the operations of these two types of microgrid on power quality, we only need two scenarios, based on the two greenest scenarios of the 8. In the first scenario, the utility grid remains the ultimate recourse for a microgrid experiencing a power shortage. In the second scenario, a hydrogen burner is used as the green alternative to a tradition diesel generator as the backup power source, in an attempt to eliminate the most uncontrollable part of the GOUs while remaining sustainable. This is summarised in

Table 3. Models and Scenarios.

	Scenario 1	Scenario 2
Model 1: Selfish Microgrid (COU = 0)	Any shortage of power at the microgrid is mitigated by the utility grid (no backup power)	Any shortage of power at the microgrid is addressed with the hydrogen burner
Model 2: Collaborative microgrid (use of COUs)	Any shortage of power within the microgrid is mitigated by the utility grid (no backup power)	Any shortage of power at the microgrid is addressed with the hydrogen burner

.

Another reason for selecting a hydrogen burner is to remove the constraint of locally available stored hydrogen. The hydrogen storage capacity in models 1 and 2 is fixed and the capacity decision was based on heuristics guaranteeing a good utilisation of storage: energy storage will always increase cost, and thus it can only be justified if it is utilised efficiently. It is not economically viable to store energy, say, for the 3 months of our case study, at the scale of the microgrid. This is why we assume that at any point in time, the microgrid can source hydrogen from the open market, if and when it needs to use the hydrogen burner for energy generation as a backup power source.

For both models, the power quality performance measures shown in

Table 4. Performance Measures.

	Impact of Microgrid on Distribution Network’ Power Quality
	Power Quality of Exported Power	Degradation of Power Quality from ${\mathsf{\sigma }}_{\mathrm{E}}$	Degradation of Power Quality from ${\mathsf{\sigma }}_{\mathrm{G}\mathrm{O}\mathrm{U}}$
Microgrid power quality impact	${\displaystyle \sum _{\mathrm{i}=1}^3}{\mathrm{q}}_{\mathrm{i}}{\mathrm{P}\mathrm{Q}\mathrm{I}}_{\mathrm{i}}$	$\mathrm{k}{\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{E}}}{∆\mathrm{t}}}$	$\mathrm{k}{\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{G}\mathrm{O}\mathrm{U}}}{∆\mathrm{t}}}$
Comparison: Selfish vs. Collaborative	${\mathrm{P}\mathrm{Q}\mathrm{I}}_{\mathrm{E}}^{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}\mathrm{i}\mathrm{s}\mathrm{h}}-{\mathrm{P}\mathrm{Q}\mathrm{I}}_{\mathrm{E}}^{\mathrm{C}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}$	${\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{E}}^{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}\mathrm{i}\mathrm{s}\mathrm{h}}}{{\mathsf{\sigma }}_{\mathrm{E}}^{\mathrm{C}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}}}$	N/A

are computed. The ultimate purpose of the case study is to expand the analysis of [12] to the comparative impact of selfish and collaborative microgrids on power quality.

3.4. Estimation of Coefficient of Power Quality Degradation

The degradation of power quality can be caused by voltage fluctuations ∆V which can be estimated by Equation (3), where S is the short circuit capacity in MVA at the point of connection and ${\mathsf{\sigma }}_{\mathrm{P}}$ is power volatility:

$$∆\mathrm{V}={\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{P}}}{\mathrm{S}}},$$

(3)

The change in power quality can be estimated as being proportional to ∆V, as shown in Equation (4), where ${\mathrm{s}}_{\mathrm{v}}$ is a sensitivity coefficient derived from grid codes or measurements.

$$∆{\mathrm{P}\mathrm{Q}}_{\mathrm{V}}={\mathrm{s}}_{\mathrm{v}}∆\mathrm{V}={\mathrm{s}}_{\mathrm{v}}\times {\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{P}}}{\mathrm{S}}},$$

(4)

Therefore, the coefficient of degradation k_v from voltage fluctuations can be obtained as shown in Equation (5):

$${\mathrm{k}}_{\mathrm{v}}={\displaystyle \frac{{\mathrm{s}}_{\mathrm{v}}}{\mathrm{S}}},$$

(5)

The UK Grid Code requires operators to provide short-circuit capacity at connection point. We assume that the microgrid is on a terminal node remote from high voltage substations and typical values are in the 100 to 500 MVA range. We use S = 250 MVA. As there are no available estimates of ${\mathrm{s}}_{\mathrm{v}}$ for composite power quality index, we use the following approximation: The European EN 50160 Voltage Characteristics in Public Distribution Systems defines acceptable voltage fluctuations are +/−10% of nominal voltage. We set this acceptable deviation to a PQ_i of 0.9, i.e., a 10% drop from ideal power quality, implying ${\mathrm{s}}_{\mathrm{v}}$ = 1 and ${\mathrm{k}}_{\mathrm{v}}={\displaystyle \frac{1}{\mathrm{S}}}=0.004$.

As the microgrid exported power changes the effective load, another source of degradation of power quality is the frequency deviation ∆f which can be expressed as a function of power volatility and the grid frequency response β (in MW/Hz) as shown in Equation (6):

$$∆\mathrm{f}={\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{P}}}{\mathsf{\beta }}},$$

(6)

The UK Grid code specifies that the system should not deviate by more than 0.5 Hz for loads of 300 MW to 1000 MW, so a conservative estimate of β is 300/0.5 = 600 MW/Hz. The impact of $∆\mathrm{f}$ on $∆\mathrm{P}\mathrm{Q}$ will also be subject to a sensitivity coefficient ${\mathrm{s}}_{\mathrm{f}}$. Using the same reasoning as above for ${\mathrm{s}}_{\mathrm{v}}$, we set that a ${\mathsf{\sigma }}_{\mathrm{P}}$ of 300 will be associated with an acceptable PQ_i of 0.9, giving ${\mathrm{s}}_{\mathrm{v}}=0.2$ and ${\mathrm{k}}_{\mathrm{f}}={\displaystyle \frac{{\mathrm{s}}_{\mathrm{v}}}{\mathsf{\beta }}}=0.0003$. The overall degradation coefficient is $\mathrm{k}={\mathrm{k}}_{\mathrm{v}}+{\mathrm{k}}_{\mathrm{f}}=0.004+0.0003=0.0043$ per MW of power volatility.

3.5. Specification of Models 1 and 2

The case study is set up as in [12] and is a microgrid of 70 interconnected houses (consuming a total power of 2800 kWh/day). The local energy generation comes from 1 turbine (450 kW maximum output) and 380 solar panels (320 W maximum output each, nominal efficiency of 21%).

The power in storage at time t, P_st(t) is computed as:

$${\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}\right)=\left\{\begin{array}{c}\left(\mathrm{C}\mathrm{O}\mathrm{U}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)\right) \times {\mathrm{S}\mathrm{t}}_{\mathrm{e}} \\ \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}(\mathrm{t}-1)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)<{\mathrm{S}\mathrm{t}}_{\mathrm{c}}\\ {\mathrm{S}\mathrm{t}}_{\mathrm{c}}\times {\mathrm{S}\mathrm{t}}_{\mathrm{e}} \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)>{\mathrm{S}\mathrm{t}}_{\mathrm{c}} \\ 0 \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)<0 \end{array}\right.$$

(7)

${\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}\right)=$ Where COU(t) is the precontracted grid order update at time t, P_st(t − 1) is the power in storage system at the beginning of a time period, S(t) is the power supply from wind turbine and PV panels at time t, D(t) is the aggregate demand for the interconnected households, St_c is storage capacity in kilowatts, and St_e is storage system efficiency.

D(t) is a set function capturing the typical hourly variations of demand in such a microgrid. S(t) is computed based on real weather data observations collected over a 3-month period for a specific location.

COU(t) is computed as:

$$\mathrm{C}\mathrm{O}\mathrm{U}\left(\mathrm{t}\right)=\left\{\begin{array}{c} \\ \mathrm{D}\left(\mathrm{t}\right)-{\mathrm{F}}_{\mathrm{s}}\left(\mathrm{t}\right)-{\mathrm{F}}_{\mathrm{w}}\left(\mathrm{t}\right)-{\mathrm{F}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right) \mathrm{if} \mathrm{D}\left(\mathrm{t}\right)>{\mathrm{F}}_{\mathrm{s}}\left(\mathrm{t}\right)+{\mathrm{F}}_{\mathrm{w}}\left(\mathrm{t}\right)+{\mathrm{F}}_{\mathrm{s}\mathrm{t}}(\mathrm{t}-1) \\ \\ 0 \mathrm{if} \mathrm{D}\left(\mathrm{t}\right)\le {\mathrm{F}}_{\mathrm{s}}\left(\mathrm{t}\right)+{\mathrm{F}}_{\mathrm{w}}\left(\mathrm{t}\right)+{\mathrm{F}}_{\mathrm{s}\mathrm{t}}(\mathrm{t}-1) \\ \end{array}\right.$$

(8)

where F_s(t) is the one week ahead of local solar power generation forecast, and F_w(t) is the one week ahead wind power forecast for the same location (both forecasted and actual values were collected for a 3-month period). F_st(t − 1) is the forecasted amount of energy available in storage at the beginning of a time period based on the 1-week ahead forecast (F_st is calculated using Equation (7) but considering the forecasted data from wind and solar power).

Electricity consumption from the utility grid (spot grid order updates) is calculated as GOU(t):

$$\mathrm{G}\mathrm{O}\mathrm{U}\left(\mathrm{t}\right)=\left\{\begin{array}{c}\mathrm{D}\left(\mathrm{t}\right)-\mathrm{S}\left(\mathrm{t}\right)- \mathrm{COU}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right) \\ \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)<0 \\ 0 \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)>0 \end{array}\right.$$

(9)

The power supply from the H₂ burner in kWh, P_HB(t), is calculated as follows:

$${\mathrm{P}}_{\mathrm{H}\mathrm{B}}\left(\mathrm{t}\right)=\left\{\begin{array}{c}\mathrm{D}\left(\mathrm{t}\right)-\mathrm{S}\left(\mathrm{t}\right)- \mathrm{COU}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right) \\ \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)<0 \\ 0 \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)>0 \end{array}\right.$$

(10)

This H₂ supply for the H₂ burner comes from two sources: the excess power in the system that is more than the basic storage capacity, where this power is stored in the additional storage. If the additional storage is empty, then the microgrid buys hydrogen from an external supplier. The power from the additional storage and the power from the external supplier are calculated as:

$${\mathrm{P}}_{\mathrm{H}\mathrm{B}-\mathrm{A}\mathrm{S}}\left(\mathrm{t}\right)=\left\{\begin{array}{c}{\mathrm{P}}_{\mathrm{A}\mathrm{S}}\left(\mathrm{t}\right) \mathrm{if} {\mathrm{P}}_{\mathrm{H}\mathrm{B}}\left(\mathrm{t}\right)>{\mathrm{P}}_{\mathrm{A}\mathrm{S}}\left(\mathrm{t}-1\right)\\ {\mathrm{P}}_{\mathrm{H}\mathrm{B}}\left(\mathrm{t}\right) \mathrm{if} {\mathrm{P}}_{\mathrm{H}\mathrm{B}}\left(\mathrm{t}\right)<{\mathrm{P}}_{\mathrm{A}\mathrm{S}}\left(\mathrm{t}-1\right)\\ 0 \mathrm{if} {\mathrm{P}}_{\mathrm{A}\mathrm{S}}\left(\mathrm{t}-1\right)<0\end{array}\right.$$

(11)

where, P_HB−As(t) is the power supply from the hydrogen burner that comes from the additional storage at time t in kilowatts, and P_AS(t) is stored power in the additional storage at time t.

$${\mathrm{P}}_{\mathrm{H}\mathrm{B}-\mathrm{H}\mathrm{S}}\left(\mathrm{t}\right)={\mathrm{P}}_{\mathrm{H}\mathrm{B}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{H}\mathrm{B}-\mathrm{A}\mathrm{S}}\left(\mathrm{t}\right)$$

(12)

where, P_HB−Hs(t) is the power supply from the hydrogen burner coming from the external H₂ supplier. P_AS(t) is calculated as follows:

$${\mathrm{P}}_{\mathrm{A}\mathrm{S}}\left(\mathrm{t}\right)=\left\{\begin{array}{c}\left(\mathrm{C}\mathrm{O}\mathrm{U}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)-{\mathrm{S}\mathrm{t}}_{\mathrm{c}}\right) \times {\mathrm{S}\mathrm{t}}_{\mathrm{e}} \\ \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)>{\mathrm{S}\mathrm{t}}_{\mathrm{c}}\\ 0 \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)<0 \\ 0 \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)<{\mathrm{S}\mathrm{t}}_{\mathrm{c}} \end{array}\right.$$

(13)

The volatility of the spot order updates for each scenario was measured by calculating the standard deviation for the spot order updates within the modelled time horizon as show in Equation (14):

$${\mathrm{V}}_{\mathrm{S}\mathrm{O}\mathrm{U}}=\sqrt{{\displaystyle \frac{{\sum }_{\mathrm{t}=1}^{\mathrm{N}}{(\mathrm{S}\mathrm{O}\mathrm{U}\left(\mathrm{t}\right)-\overline{\mathrm{S}\mathrm{O}\mathrm{U}})}^2}{\mathrm{N}-1}}}$$

(14)

where, V_SOU is the volatility of the spot order updates in the MG system depending on the backup generation source, $\overline{\mathrm{S}\mathrm{O}\mathrm{U}}$ is the mean of the spot order updates.

The exported power from the MG to the national grid at each hour was calculated based on the power in storage at the previous hour, the power supply from the renewables source, the contracted power supply from the national grid, the demand at that hour and the storage capacity. The exported power to national grid at each hour is shown by the Equation (15):

$${\mathrm{P}}_{\mathrm{e}\mathrm{x}\mathrm{p}}\left(\mathrm{t}\right)=\left\{\begin{array}{c}\mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)-{\mathrm{S}\mathrm{t}}_{\mathrm{c}} \\ \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)>{\mathrm{S}\mathrm{t}}_{\mathrm{c}}\\ 0 \mathrm{if} \mathrm{COU}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{s}\mathrm{t}}\left(\mathrm{t}-1\right)+\mathrm{S}\left(\mathrm{t}\right)-\mathrm{D}\left(\mathrm{t}\right)<{\mathrm{S}\mathrm{t}}_{\mathrm{c}} \end{array}\right.$$

(15)

The total exported power to the national grid in each studied time horizon is equal the sum of the exported power at each hour within this time horizon as presented in Equation (16):

$${\mathrm{T}\mathrm{P}}_{\mathrm{e}\mathrm{x}\mathrm{p}}=\sum _{\mathrm{t}=1}^{\mathrm{t}=\mathrm{N}}{\mathrm{P}}_{\mathrm{e}\mathrm{x}\mathrm{p}}\left(\mathrm{t}\right)$$

(16)

where, P_exp is the exported power to the grid at each hour, TP_exp is the total exported power to the grid within a time horizon.

4. Results

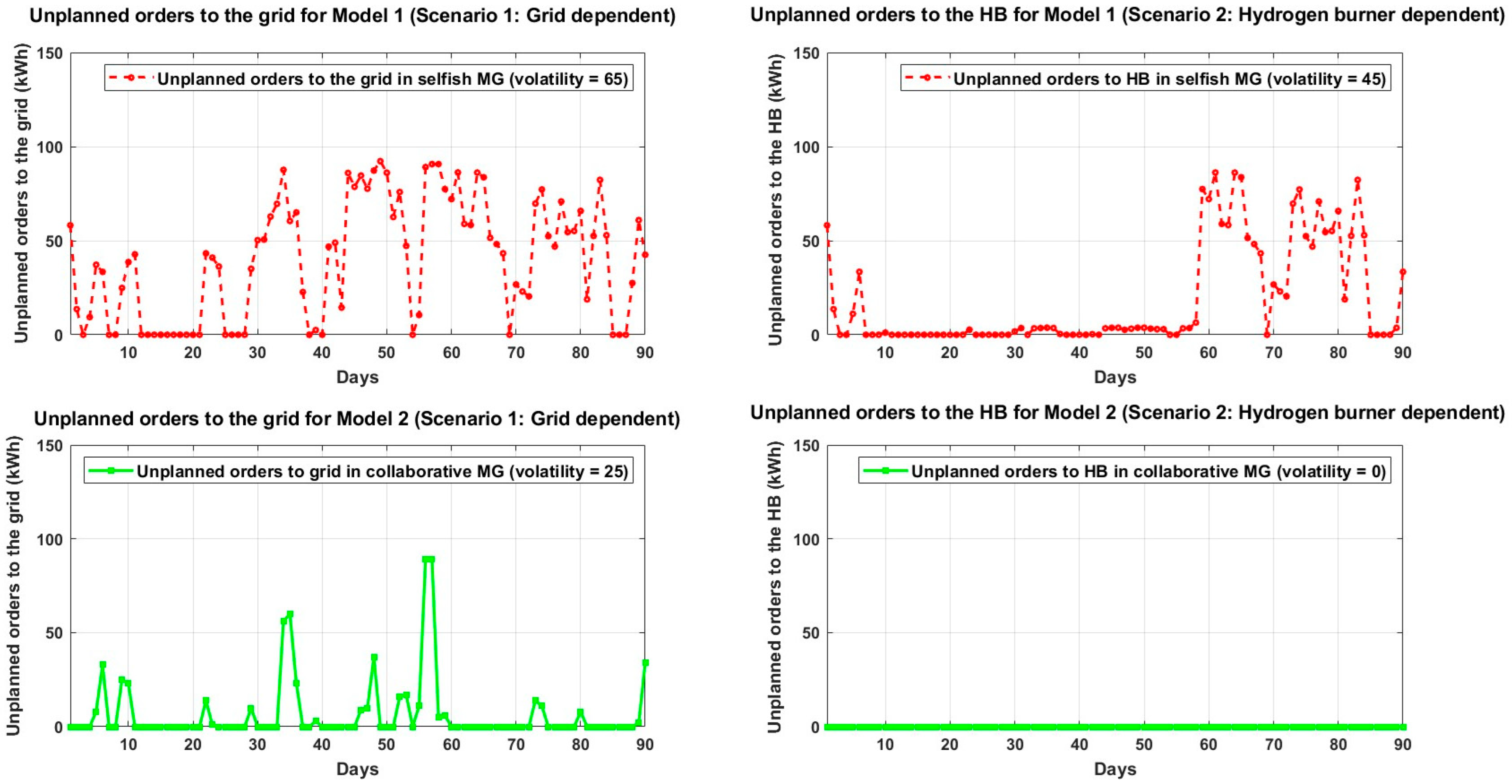
Figure 4 shows (i) unplanned orders (GOUs) to the utility grid for the first scenarios and (ii) the use of the backup power source for the second scenarios. Figure 4 shows a significant difference in volatility between the selfish microgrids and the collaborative microgrids. This volatility is completely eliminated by the collaborative microgrid when it uses the hydrogen burner as a backup power source. The volatility of orders from the selfish microgrid is itself reduced from 65 to 45 kWh-volatility but note that this reduced volatility does not affect the utility grid but hydrogen markets instead.

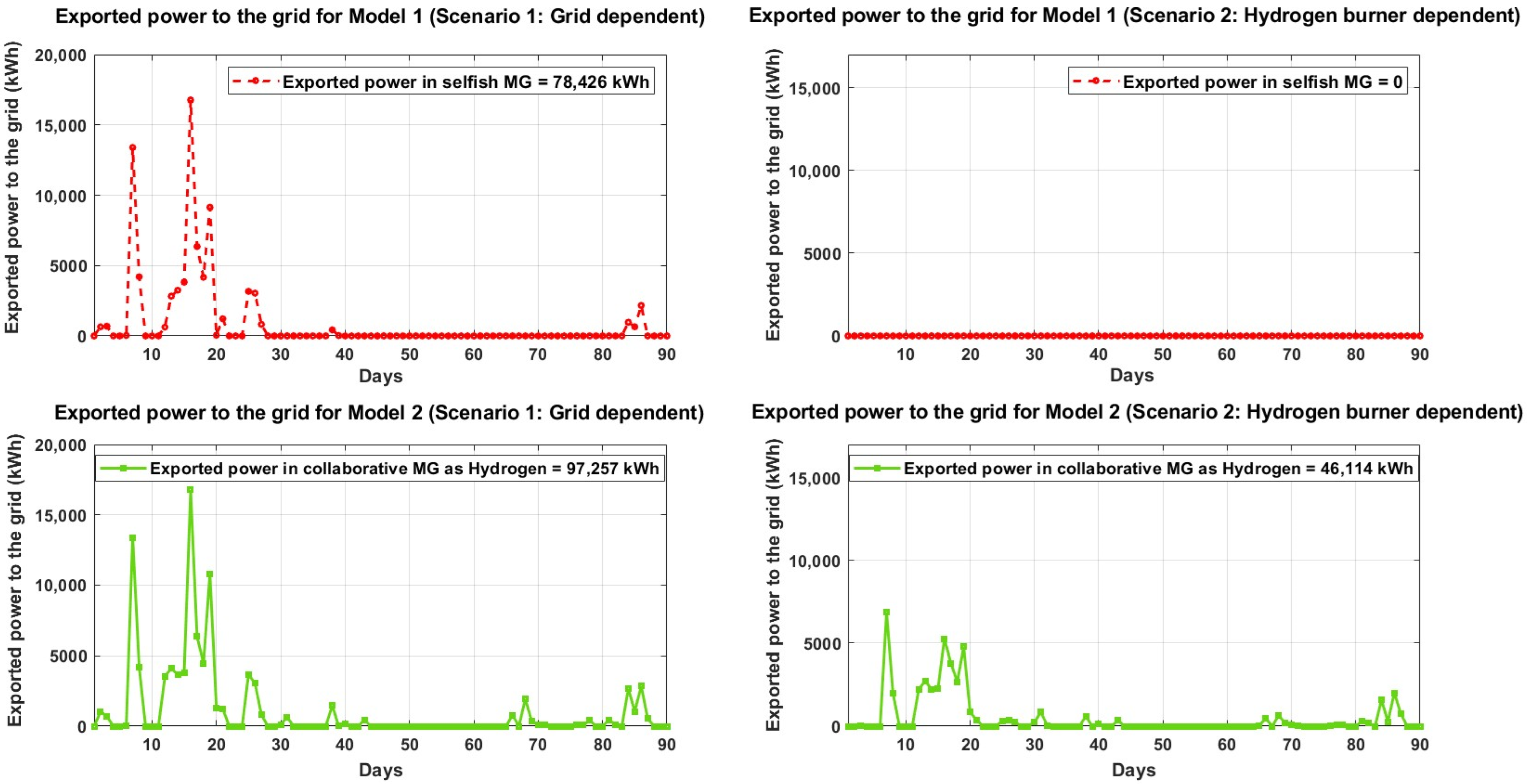
Figure 5 shows the power exported by each type of microgrid. Given the weather in the 90-day period, surplus power is available in the first 30 days. Thereafter, limited local generation means that both microgrid tend to rely on GOUs or backup generation to meet demand. Note that in the case of the collaborative microgrid in scenario 2, the exported power is as hydrogen rather than power exported in the utility grid.

Table 5. Power quality impact of the microgrids.

	Impact of Microgrid on Distribution Network’ Power Quality
	Power Quality of Exported Power	Degradation of Power Quality from ${\mathsf{\sigma }}_{\mathrm{E}}$	Degradation of Power Quality from ${\mathsf{\sigma }}_{\mathrm{G}\mathrm{O}\mathrm{U}}$
Microgrid power quality impact	${\displaystyle \sum _{\mathrm{i}=1}^3}{\mathrm{q}}_{\mathrm{i}}{\mathrm{P}\mathrm{Q}\mathrm{I}}_{\mathrm{i}}$	$\mathrm{k}{\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{E}}}{∆\mathrm{t}}}$	$\mathrm{k}{\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{G}\mathrm{O}\mathrm{U}}}{∆\mathrm{t}}}$
Model 1 (selfish) Scenario 1	PQE = 0.55	(90 days): −2.78 × 10−7 (daily max): −9.33 × 10−5	(90 days): −1.218 × 10−7 (daily max): −1.46 × 10−5
Model 1 (selfish) Scenario 2	PQE = 0.55	0	0
Model 2 (collaborative) Scenario 1	PQE = 0.9	(90 days): −2.88 × 10−7 (daily max): −9.32 × 10−5	(90 days): −5.11 × 10−8 (daily max): −1.4 × 10−5
Model 2 (collaborative) Scenario 2	PQE = 0.9	Exported as H2.	0
Comparison: Selfish vs. Collaborative (scenarios 1)	−0.35	90 days: 0.96 Daily max: 1	90 days: 2.38 Daily max: 1.03

uses the results shown in Figure 4 and Figure 5 to estimate the power quality impact of the microgrids for each scenario. The power quality degradation figures are small as they are the degradation caused by a small microgrid onto a large utility grid, in line with ratio comparisons used in Table 5. The results show that over the 90 days-time period, the degradation of power quality caused by the volatility of unplanned orders (GOUs) is twice higher for the selfish microgrid. In other words, this means that by using COUs, a collaborative microgrid can reduce power quality degradation within a utility grid by half. When the hydrogen burner is used as a backup power generator, power quality degradation issues are eliminated altogether.

The quantities of energy exported are different (97,257 kWh for the collaborative microgrid vs. 78,426 kWh for the selfish microgrid), but the volatility patterns are comparable. By relying on a supply chain of hydrogen, whereby power can be sourced or exported for either the power network or the hydrogen supply chain, both types of microgrid can eliminate these exports and the induced power quality degradation.

5. Discussion

The results confirm that the use of a collaborative approach, using pre-contracted orders to the utility grid (COUs), reduces the power quality degradation caused by the uncontrollable nature of microgeneration. If all residential households in the UK joined a microgrid like the one used in our case study, for a total of 82,000 microgrids in operations, the overall power quality degradation solely caused by ${\mathsf{\sigma }}_{\mathrm{GOU}}$ would be 2.15% (5% for selfish microgrids). This implies that microgeneration does not have to be considered as a challenge to power quality [23], provided that the right collaborative planning approaches are used.

The results also show that if microgeneration sites are considered to be a challenge to the safe and secure operations of utility grids, this challenge can be completely avoided by encouraging the use of hydrogen as a green backup power generation solution (as with the second scenarios in Table 3), where the exported power is converted to hydrogen. Returning to the example of 82,000 microgrids, the impact of ${\mathsf{\sigma }}_{\mathrm{E}}$ on the power quality composite index is a more substantial 12%. It suggests that energy exports from microgrids should be discouraged, and local backup power generation solutions preferred. Is this process of eliminating exports from microgeneration sites a good idea, when these sites will typically have invested in the ability to export power of good quality? Instead of conceptualising microgeneration sites as a power quality problem, can we consider them to be solutions to power quality issues? To answer these questions, the relationship between energy storage and power quality must be examined.

5.1. Energy Storage and Power Quality

Energy storage systems have been extensively studied and reported in published literature. Recently several reviews have been undertaken, providing a holistic overview of contemporary technologies [27,28,29]. Historically, the focus was on electrochemical energy storage systems. More recently thermal, chemical, and mechanical energy storage technologies have been gaining popularity. In addition to different technical and technological underpinnings, a vast diversity of energy storage systems is also reflected in economic and environmental considerations, as well as a range of applications and ease of implementation. Classification of energy storage systems and typical technologies are shown in

Table 6. Classification of energy storage systems and typical technologies.

Type of Energy Storage	Typical Technology
Chemical	Hydrogen Fuel cells Solar fuels
Electric	Supercapacitors Super Magnetic Energy Storage (SEMS) Electric vehicles
Electrochemical	Batteries Flow batteries
Mechanical	Pumped Hydro Energy Storage (PHES) Compressed Air Energy Storage (CAES) Flywheels
Thermal	Sensible Heat storage (SHS) Latent heat storage (LHS) Phase change materials (PCM)

.

The selection of energy storage systems depends on many factors. In addition to geological and geographical suitability and limitations, choice of a specific energy storage system is principally informed by storage capacity, the required duration of energy to be stored, nominal round-trip efficiency, and the maturity of technology. Typical values for selected energy storage systems are given in

Table 7. Main characteristics of selected energy storage systems [29,30,31,32].

Energy Storage System	Capacity (MW)	Duration	Round Trip Efficiency (%)	Maturity
CAES	200–500	6–24 h	40–70	Commercially tested
PHES	200–3000	8–36 h	70–80	Commercially proven
Batteries	1–100	1–4 h	70–95	Commercially proven
Flow batteries	1–100	4–24 h	70–80	Commercially proven
Hydrogen	1–400	hours-months	40–50	Under development

.

Due to their stability and reliability, as well as low maintenance, battery energy storage systems are generally acknowledged as the preferred choice for microgrids [33], especially when renewables are employed. High efficiency and range of capacities available, make battery energy storage systems suitable for balancing fluctuating demands with intermittent nature of renewable power systems. Whilst batteries are generally deemed to be a cost-effective energy storage solution, relatively short storage duration is also one of the main drawbacks. In contrast, hydrogen energy storage offers itself to be employed as a longer-term storage option. Whilst still in development, hydrogen energy storage is notably more expensive compared to some other energy storage technologies, although the costs are generally on the downwards trajectory [34]. Low efficiency and complex infrastructure remain the main drawbacks of hydrogen-based storage solutions.

In this paper, the microgrid is powered by wind and solar energy systems and intermittence affects the operation and relatability of the microgrid. In addition to compromising the stability and safety of the microgrid, the volatility also leads to reduced power quality [35]. It has been reported that hydrogen energy storage can improve power quality by reducing voltage sags and enhancing power system reliability [36]. Battery energy storage systems are also recognised as possible aids in improving power quality by regulating voltage and frequency [37].

Thermal energy storage systems generally cannot be used to control or influence power quality since they store heat rather than electricity. Pumped hydro energy storage provides high quality power due to its ability to deliver power of consistent quality with minimal voltage fluctuations [38]. Compressed air energy storage systems have also been seemed to be suppliers of good quality power when integrated with relevant control systems, especially when they are utilised during peak demand periods [39,40].

5.2. From Autonomy to Power Quality Services

In our case study, we considered a microgrid with the capacity to transform local green power generation into stored hydrogen. In the case of the collaborative microgrid, there are also instances where power purchased from the utility grid is stored rather than used. Choosing hydrogen as the storage medium could be criticised, as the cost of hydrogen storage is high. For the modest storage capacity that we employ (1500 kWh), it could be argued that electrochemical batteries would be a cheaper option.

However, should the local storage capacity be increased, there is a point at which it becomes more interesting to invest in hydrogen. Additionally, the fact that electricity is converted to hydrogen means that when our microgrid faces an uncontrollable power requirement, handling this exception is decoupled from the utility grid, as the microgrid can either sell or purchase hydrogen in the open market. Hydrogen storage asset provides a switching real option whose value can be modelled financially [20]. There is a need for more research to explore what can be achieved if the storage capacity of our microgrid is expanded beyond 1500 kWh to financially benefit from the underlying switching real options. Note that this would be more difficult to achieve with electrochemical batteries as the cost of scaling up would be much higher.

Each of the current benefits of the storage used in our case study can be extrapolated as follows:

• Storage is used to balance daily, or across-days, volatility of demand and supply. A higher capacity means the ability to balance supply and demand over longer time periods. Long term storage can be controversial at it implies low utilisation of the storage asset, unless storage cost is sufficiently low.
• Storage is used to switch GOUs for COUs, thereby reducing power quality degradation in the network by half. Increasing storage capacity means the ability to commit to longer, more levelled COU commitments, further reducing power degradation induced by microgeneration.
• Table 5 shows that the power quality degradation of power exports remains an issue. More storage can be used to address this issue by applying the concept of COUs in reverse, i.e., applying COUs to exported energy. If the microgrid has extra storage capacity, it can build up a green energy inventory and release it into the utility according to a pre-arranged timetable (in the case of model 2 scenario 1). This means that extra inventory can eliminate induced power quality degradation from microgrids exports.
• As low power quality also affects distribution losses [41], microgrids with energy storage could be located in the near location of large-scale wind and solar generation sites, for the main purpose of receiving low quality power, storing it, and exporting it when needed, effectively making the microgrid a cleaning agent within the network.
• Including hydrogen storage as part of the energy storage solutions used by a microgrid means that at any point in time, the balancing of power supply and demand can be managed by relying on a secondary, physical supply chain of stored hydrogen. This has important implications for managing safety stocks, including strategic safety stocks (equivalent to secret fuel depots managed by the government). The operations of a real time power network are challenging, and the risk of blackouts is almost completely mitigated by creating bridges with a hydrogen supply chain. This also has implications for countries experiencing unreliable power supply, where an optimal ratio of the dependence between maintaining a balanced power flow and a hydrogen supply chain could be explored.

5.3. Research Limitations and Direction for Future Research

The model developed in this paper is built from two parts. In the first part of the model, real weather and weather forecast data is used to compare the performance of different system load balancing rules, given a power demand function. The impact of different load balancing plans is measured as the volatility of the demand consumed from or exported to a utility grid. In the second part of the model, this volatility figure is converted into a power quality index. Although both parts of the model have their limitations, this section will focus on the second part of the model, i.e., the conversion of a volatility figure into a power quality index. Several assumptions were made: the first is that the power quality index is a weighted additive function of different factors contributing to lower power quality, as shown in Equation (1). The second is that power volatility decreases power quality through a linear function, shown in Equation (2), and that the relationship between power quality and volatility is captured through a sensitivity coefficient k. These are all simplifying assumptions used to establish a link between volatility and power quality. Verifying that these assumptions are reasonable is an important direction for future research and would involve the measurement or simulation of fault currents, frequency deviations, etc., created by volatility of power flows at the interface between the microgrid and the utility grid.

Another assumption made in the planning equations shown in Section 3 is that the COU regime consisting of a 24-step forward order function does not induce any power quality issue as the timing and amplitude of power demand changes are known in advance. More research is needed to verify if this assumption is realistic, as in practice it will imply a planned power flow change, i.e., a smoothed function rather than a mathematical, discontinuous, step function.

Finally, the idea of extending the principle of forward orders (COU) to microgrid exports by relying more on storage, as discussed in Section 5.2, is another direction for future research.

6. Conclusions

As many countries, such as the United Kingdom, are planning to invest in larger scale renewable energy generation, there is a question about the fitness for purpose of their existing energy distribution infrastructures. These were not designed with these new specifications in mind. At the time of writing this paper, these countries are planning large investments in upgrading their national grids. Whether or not these investments will lead to reliable and safe national grids remains to be seen. Typically, microgeneration is not considered to be an important part of future energy as it is often viewed as making end nodes uncontrollable, and therefore not desirable for overall system stability. For example, the International Energy Agency commented in 2022 that “many operators lack visibility and control over DERs [Distributed Energy Resources]” and that “distributed generators present another challenge to utilities in the form of bi-directional flow of power. When power flows from consumer-owned solar to the grid, it can overflow power line capacity, resulting in more frequent grid congestion” [42].

This paper used a simplified, high-level power quality performance measure that estimates power quality degradation from the power volatility created by microgeneration sites. The results show that power quality degradation can be mitigated, partially or completely, by (1) collaborative planning approaches and (2) relying on energy storage. By extrapolating the results to expanded storage capacity, it becomes possible to envision microgrids playing a pro-active role as power quality improvement agents within electricity networks, suggesting that microgrids can be power quality solutions rather than problems. This means that the current negative perception of microgrids by utility grids, and the many associated barriers preventing the growth of microgrids, are caused by the current infrastructure design and the ways in which this infrastructure is utilised. The concept of a collaborative microgrid, if deployed as described in this paper, means that it is possible to increase the number of renewables-based microgrids and microgeneration capacity while simplifying utility grids operations. This is because the management of volatility issues have been transferred to the microgrid through combining forward electricity orders and energy storage tactics.