Abstract
Accurate forecasting of energy consumption in buildings is essential for achieving energy efficiency and reducing carbon emissions. However, many existing models rely on limited input variables and overlook the complex influence of indoor environmental quality (IEQ). In this study, we assess the performance of hybrid machine learning ensembles for predicting hourly energy demand in a smart office environment using high-frequency IEQ sensor data. Environmental variables including carbon dioxide concentration (CO2), particulate matter (PM2.5), total volatile organic compounds (TVOCs), noise levels, humidity, and temperature were recorded over a four-month period. We evaluated two ensemble configurations combining support vector regression (SVR) with either Random Forest or LightGBM as base learners and Ridge regression as a meta-learner, alongside single-model baselines such as SVR and artificial neural networks (ANN). The SVR combined with Random Forest and Ridge regression demonstrated the highest predictive performance, achieving a mean absolute error (MAE) of 1.20, a mean absolute percentage error (MAPE) of 8.92%, and a coefficient of determination (R2) of 0.82. Feature importance analysis using SHAP values, together with non-parametric statistical testing, identified TVOCs, humidity, and PM2.5 as the most influential predictors of energy use. These findings highlight the value of integrating high-resolution IEQ data into predictive frameworks and demonstrate that such data can significantly improve forecasting accuracy. This effect is attributed to the direct link between these IEQ variables and the activation of energy-intensive systems; fluctuations in humidity drive HVAC energy use for dehumidification, while elevated pollutant levels (TVOCs, PM2.5) trigger increased ventilation to maintain indoor air quality, thus raising the total energy load.
1. Introduction
The construction sector is the largest consumer of energy resources worldwide, accounting for roughly 36% of global energy use and about 39% of annual CO2 emissions. These figures place buildings at the heart of the global climate agenda and necessitate actions that cut energy demand across the building life cycle, accelerate renewable integration, deploy advanced insulating materials, and implement strict performance standards and smart controls to curb losses and operating costs [1]. Although a substantial share of these emissions is generated during the operational phase, a “hidden” carbon component is also associated with raw material extraction, material production, construction, and eventual demolition. In modern buildings, operational emissions exceed 70% of the total carbon footprint; however, as operational energy consumption declines, the share of embodied carbon becomes critically important [2]. Highly energy-intensive materials—reinforced concrete, steel, and brick—can contribute 60–70% of total emissions, underscoring the need for low carbon structural solutions and sustainable construction methods [1].
Carbon dioxide (CO2) is one of the main greenhouse gases emitted as a result of anthropogenic activities such as fossil fuel combustion, cement production, and deforestation. It is a well-mixed gas in the Earth’s atmosphere with a complex removal mechanism involving physical processes like ocean absorption and chemical processes that occur over various timescales ranging from years to millennia [3,4].
Unlike reporting on net CO2 emissions, carbon dioxide equivalent (CO2-eq) is a metric developed to account for the overall warming effect of a mix of greenhouse gases. Not all greenhouse gases behave the same: gases such as methane (CH4), nitrous oxide (N2O), and various fluorinated gases exhibit different radiative efficiencies and atmospheric lifetimes compared to CO2 [5].
The CO2-eq approach involves converting emissions of non-CO2 gases into an equivalent mass of CO2 using global warming potential (GWP) factors. GWP is defined as the time-integrated radiative forcing of a pulse emission of a given gas relative to that of an equivalent mass of CO2, typically aggregated over a 100-year time horizon (GWP100) [5].
A regional perspective reveals marked heterogeneity: in China alone, buildings generate nearly 5% of global CO2 energy-related emissions, and similar proportions are evident in several developed countries where electricity supply still relies heavily on high-carbon-intensity fossil fuels [6]. Consequently, modernizing the existing building stock is among the most effective pathways to reduce energy consumption. For example, lowering air infiltration from 1.76 to 0.6 ACH in an office building saved 11% in energy costs and prevented roughly 20 t CO2-eq annually; comprehensive thermal insulation of the envelope can raise total savings to almost 45%, equivalent to 75 t CO2-eq per year [7].
Actual efficiency depends heavily on occupant behavior: deploying automated monitoring, smart controls, and energy use feedback systems delivers an additional demand reduction of up to 20% compared with design values [8]. Nonetheless, the performance gap between design and reality remains significant owing to technical constraints in the existing stock, high retrofit costs, and operational factors [8,9]. Financial barriers (capital scarcity, long payback periods, lack of incentives) and institutional fragmentation hinder large-scale adoption of best practices, while the absence of unified metrics complicates progress monitoring [9,10].
Energy efficiency forecasting is critical during design, operation, and retrofitting stages, yet the accuracy of most existing models is limited by their reliance on a small set of input variables such as outdoor temperature and time of day [11]. This simplification overlooks many internal processes and introduces systematic errors that render operational decisions sub optimal. Indoor climate emerges from nonlinear interactions among building materials, structural features, and occupant behavior [12]. These interactions include not only planned presence but also adaptive actions such as window opening, blind adjustment, and thermostat set point changes [13]. Behavioral responses are non-deterministic and vary both between different occupants and for the same individual over time, sharply reducing the applicability of uniform behavioral assumptions [14]. Outdoor temperature and time of day capture basic trends in heating and cooling loads but cannot adequately represent internal fluctuations governed by occupants. Static models based on fixed timestamps or piecewise temperature regression ignore fast feedback loops between the microclimate and occupant actions, especially during abrupt condition changes [15]. Key parameters such as humidity, CO2 concentration, and local thermal gradients are seldom incorporated [16]. High variability in occupant behavior intensifies discrepancies between models and actual consumption. Transient processes triggered by spontaneous actions generate rapid swings in thermal and internal quality loads that static timestamps fail to capture [17].
Dependence on a limited set of inputs such as outdoor temperature and time of day inevitably underestimates dynamic interactions between the indoor environment and occupant behavior. These overly simplified models cannot reflect the stochastic nature of behavioral responses, which include both adaptive and non-adaptive actions that substantially influence energy loads and indoor comfort [17]. Resulting performance gaps not only reduce the accuracy of energy consumption forecasts but also hamper optimization of building system designs and operational strategies [15].
Despite notable advances in hybrid machine learning models for energy consumption forecasting, a critical gap persists in developing and systematically evaluating multi-level hybrid architectures capable of simultaneously addressing both short- and long-term prediction horizons. Most studies focus on single models or shallow ensemble approaches without deep multi-level integration [18,19]. This deficit stems from the difficulty of combining multiple processing levels—each with distinct learning objectives and data requirements—into a unified composite structure. Convolutional neural networks effectively extract spatial features from structured sensor data or images, whereas recurrent architectures (LSTM, GRU) better capture temporal dependencies; however, coherent integration of these paradigms into a multi-level system remains a significant scientific and practical challenge [19,20].
Total volatile organic compounds (TVOC) are defined as the total concentration of volatile organic compounds (VOCs) in indoor air and serve as an aggregated measure without identifying individual chemicals. TVOC comprise a broad range of organic compounds that volatilize at room temperature, typically from C6 to C16 [21].
The main indoor sources of TVOC include building materials and finishes, adhesives, cleaning agents, paints, and various consumer products. In addition, outdoor contributions from industrial activity and vehicle emissions can increase indoor TVOC when they infiltrate through heating, ventilation, and air conditioning (HVAC) systems [22,23]. Secondary emissions also play a role; for example, spent fibrous filters in portable air cleaners can begin to release VOCs over time as equilibrium with the surrounding environment is reached [24]. Indoor TVOC concentrations vary with occupant activities, ventilation intensity, and environmental conditions such as temperature and humidity—factors that are critical for HVAC design and control [25,26].
Maintaining acceptable TVOC levels is a key objective for HVAC, as elevated concentrations are associated with adverse health effects, including airway irritation, headaches, and symptoms of sick building syndrome (SBS) [21,23]. While measurements of individual VOCs provide detailed chemical profiles, the TVOC metric offers a simplified, aggregate assessment of the overall chemical burden indoors and is convenient for rapid appraisal [22,23].
Heating, Ventilation, and Air Conditioning (HVAC) systems are designed to control indoor pollutant levels through appropriate ventilation and air filtration and, where needed, dynamic (demand-controlled) ventilation that modulates airflow in response to pollutant concentrations. TVOC measurements provide direct feedback on the effectiveness of these ventilation strategies [27,28].
The eTVOC (equivalent TVOC) parameter is introduced to standardize and normalize the output of commercial sensors, which—being miniature devices designed for continuous monitoring—often cannot accurately separate or identify individual VOCs [29,30]. eTVOC is a calculated value obtained through an internal sensor algorithm that converts raw signals (changes in the conductivity of a metal-oxide element or currents generated during photo-ionization) into a number expressed in units equivalent to the concentration of a reference gas, typically toluene [5,31].
The fundamental difference between TVOC and eTVOC lies in how the data are obtained and interpreted. TVOC is the directly measured total concentration of all volatile organic compounds present in the air, determined with precise analytical methods such as GC/MS; it reflects the actual pollutant load, as each component is quantified and their concentrations summed using individual response factors [31,32]. In contrast, eTVOC is an output parameter provided by commercial sensors via internal signal-processing algorithms. These algorithms normalize raw sensor data, converting them into units equivalent to the concentration of the selected reference compound (toluene), thereby enabling comparability across devices despite differences in design, calibration mixtures, or operating principles [31].
Existing approaches to building energy consumption forecasting primarily rely on climatic, operational, and coarse occupancy parameters. In doing so, they overlook IEQ factors, such as noise level, PM2.5 concentration, and TVOC. Although these variables have been shown to influence occupant comfort and behavior, and consequently energy demand, they see limited use as direct predictors [31,32]. Even advanced hybrid schemes that blend observation and simulation data have not yet effectively integrated these multimodal IEQ signals. As a result, the development and objective evaluation of multilayer hybrid architectures capable of effectively utilizing data on noise, PM2.5, and TVOC for energy forecasting remains an underexplored area [32,33], a gap that our research addresses.
2. Literature Review
Traditional building-energy forecasting methods rely on physical “white box” models that compute thermal and mass balances, sequentially describing all internal processes under specified conditions [34]. While this detail enables precise tracking of energy transfer mechanisms, such models poorly capture occupant behavior, which leads to significant errors and limits their usefulness for accurate load prediction [35]. A comprehensive physical model also demands a large volume of input data, and if these data are incomplete or inaccurate, the calculated results diverge from reality [36]. Educational buildings account for 10.79% of the total energy consumption of commercial buildings. Universities and colleges consume 33 billion kWh, representing 24.44% of the total energy use of educational institutions [37].
Traditional white box heat and mass balance models have gradually been strengthened with statistical regression, giving rise to black box solutions that retain acceptable accuracy while demanding only modest computational resources. A vivid example is the three-parameter heating and cooling degree model, whose key coefficients are derived from historical weather data and energy consumption records [38,39].
The earliest machine learning studies in energy consumption forecasting applied SVMs and multilayer perceptions, training them on load, weather, and calendar features. SVMs outperformed classical regression in cooling load prediction thanks to their ability to handle high-dimensional data and built-in regularization [40]. Subsequent advances introduced deep networks and LSTMs that capture temporal dynamics, markedly reducing mean absolute errors compared with traditional methods [29,41]. ML approaches offer flexibility, require minimal detailed engineering input, and can self-learn as data accumulate, which is vital amid stochastic demand fluctuations and changing occupant behavior [42].
The widespread deployment of IoT sensors now provides continuous, high-frequency measurements of temperature, humidity, occupancy, illuminance, and equipment status. These streams feed BMS and BACS platforms, supporting calibration of physics-based models and training of machine learning algorithms [43,44]. Cloud computing and standardized protocols such as BACnet have expanded analytical capabilities, enabling predictive maintenance and real-time adaptive control [45]. External meteorological variable solar radiation, wind, and air temperature are fused with indoor measurements, boosting forecast accuracy and enabling proactive responses to extreme weather swings. Sensor data has thus become a critical foundation for flexible energy strategies, underpinning both physics-based and data-driven approaches [45,46].
When data are limited or noisy, individual ML models tend to overfit, so hybrid and ensemble solutions are gaining traction. Aggregating forecasts from ANNs, SVMs, and rule-based models such as M5Rules reduces bias and variance, lowering MAE and MAPE relative to single algorithms [30,47]. In particular, it achieved the lowest MAPE (3.264) and the highest R2 score (0.966), demonstrating its effectiveness [30]. Ensembles can dynamically re-weight components during abrupt shifts in occupant behavior or weather, delivering more than a two-fold accuracy gain in some studies [47,48]. Applying transfer learning can reduce 24 h building energy consumption forecasting error by approximately 15–18% [49].
The synergy of traditional physical modeling, machine learning, sensor technologies, and ensemble strategies forms the backbone of next generation energy consumption forecasting systems. Continued interdisciplinary research and collaboration among academia, industry, and regulators will foster cost-effective, environmentally sustainable solutions that set new benchmarks for energy conservation in the built environment [32,50,51].
Data-driven methods have superseded purely physical approaches by exploiting historical measurements to identify key factors in energy use through machine learning and deep learning algorithms [52]. ANNs, especially multilayer perceptions, approximate nonlinear relationships well but require substantial computing resources and provide low interpretability [53]. SVMs deliver stable results with any data volume yet incur high resource demands and limited computational efficiency, and, in several studies, they outperform neural networks [54]. The Random Forest algorithm has proven to be a precise and reliable tool, particularly for long-term forecasts of electricity and heat consumption [55]. Long short-term memory networks capture long-range dependencies in time series and surpass classical statistical models such as ARIMA and SVR in seasonally sensitive predictions. Convolutional neural networks, although relatively new to this domain, effectively extract spatiotemporal patterns and offer high computational efficiency [53]. XGBoost has emerged as one of the best methods for forecasting energy demand and prices, outperforming many other models in both accuracy and speed [56]. ARIMA models are applied to short-term forecasts but lag behind LSTM on longer horizons, whereas simple linear regression remains optimal for niche tasks such as annual forecasts [53,57]. Ultimately, no algorithm is universally superior, and the choice depends on task conditions and data characteristics [54].
The rise of IoT and smart buildings has generated continuous streams of sensor data that are critical for improving forecast accuracy [30,58]. Inputs now include historical consumption records, calendar features, weather conditions, occupancy and behavioral information, building geometry and construction properties, equipment and system loads, and socioeconomic factors [59]. These data arrive from building management systems, smart meters, and weather stations, yet often contain noise, missing values, and heterogeneous formats, so data cleaning, feature extraction, and integration techniques remain essential for model reliability [53,60]. Recursive feature elimination (RFE) helps analyze feature importance for energy consumption prediction; it was found that the top 10 features account for over 80% of the total importance [61].
Hybrid models in energy forecasting merge the complementary strengths of diverse modeling paradigms to capture both linear and nonlinear characteristics of energy data [62]. Studies show that integrating statistical time series techniques—such as SARIMA—with machine learning algorithms yields more accurate forecasts by first modeling residual errors or decomposing the series into distinct frequency components before applying nonlinear learners [63]. A frequently cited example is the SARIMA-MetaFA-LSSVR hybrid, which surpasses single models by delivering higher correlation coefficients and lower mean absolute percentage errors when predicting residential-building energy consumption [64].
Ensemble methods have been successfully employed in energy forecasting to predict diverse outcomes such as global solar radiation, residential energy consumption, and wind-power generation. A multi-level ensemble that combines support vector regression, artificial neural networks, and linear regression yields robust short-term load forecasts by compensating for the individual weaknesses of each component model. In addition, ensembles have proven effective with highly variable datasets by integrating predictions across multiple forecast horizons, resulting in lower mean absolute percentage error (MAPE) and coefficient of variation values [63]. The hybrid CNN–LSTM model achieved a MAPE of 4.58% on clear days and 7.06% on cloudy days for forecasting PV power output [65].
A growing research focus is the development of advanced control strategies that use computational intelligence to optimize energy efficiency while maintaining high indoor environmental quality (IEQ). Many researchers have adopted methods like Model Predictive Control (MPC), reinforcement learning, and multi-agent systems. Several studies propose Model Predictive Control (MPC) frameworks that incorporate weather forecasts, dynamic pricing signals, and occupancy profiles to adapt HVAC operations in real time [66]. These methods not only aim to reduce energy usage by shifting or shedding HVAC loads but also integrate thermal comfort metrics—direct measures of IEQ—into the control objectives. This confirms the idea that successful energy management strategies in grid-connected microgrid environments must be both demand-driven and occupant-centered [66].
At the system level, various algorithms have been proposed to manage these competing objectives across multiple buildings. The study by Baldi et al. proposes a novel control algorithm that jointly optimizes energy demand and thermal comfort in interconnected microgrids equipped with photovoltaic (PV) panels [67]. By incorporating real-time occupancy data and leveraging the PCAO (Parameterized Cognitive Adaptive Optimization) algorithm, the proposed EMS achieved up to 36% total cost improvement compared to rule-based strategies and maintained thermal dissatisfaction (PPD) levels below 7% across different buildings and weather conditions [68]. This approach introduces a simulation-based optimization framework relying on detailed building energy models developed in EnergyPlus 25.1.0. The algorithm adjusts the HVAC setpoints across multiple buildings to balance the availability of solar energy and minimize grid absorption while maintaining thermal comfort, evaluated using indices such as Fanger’s model or the Predicted Mean Vote (PMV) [67]. In a similar vein, Korkas et al. presented a demand-side management strategy that optimizes thermal comfort in microgrids integrating renewable energy sources and energy storage systems [69]. Their research introduces a scalable two-level dispatch control scheme: local controllers autonomously regulate HVAC systems based on real-time occupancy and temperature data, while a higher-level controller oversees the global energy management. This hierarchical structure effectively balances the competing objectives of minimizing electricity costs and ensuring occupant comfort, particularly by accommodating spatial variability in occupancy patterns across different building zones.
These optimization principles are also being applied in the residential sector. Anvari-Moghaddam et al. developed an efficient energy management system (EMS) for residential grid-connected microgrids, which integrates distributed generation models, building thermal dynamics, and load-scheduling capabilities for household appliances [70]. While the primary focus is on reducing household energy consumption and electricity costs by scheduling loads according to real-time constraints and user-defined deadlines, the EMS also incorporates user comfort measures. Thus, this approach implicitly connects energy efficiency efforts with indoor thermal comfort—one of the most critical aspects of IEQ—by ensuring that scheduling practices consider not only energy optimization goals but also the thermal and, indirectly, visual and acoustic comfort needs of occupants.
Ultimately, the effectiveness of these systems depends on understanding and predicting human behavior. Occupant behavior modeling is a subject of intense study, with researchers like Langevin et al. proposing the Human and Building Interaction Toolkit (HABIT), an agent-based model integrated with platforms like EnergyPlus [71]. Based on perceptual control theory, the HABIT model simulates how occupants adjust their behavior in response to thermal sensations. The results show that active, adaptive occupant behavior significantly impacts both energy consumption and the resulting IEQ, highlighting the importance of incorporating behavioral dynamics into smart energy management system strategies [71].
The study by Natarajan et al. introduces a hybrid CNN_BiLSTM model that combines convolutional filters with bidirectional LSTM cells and is trained on high-granularity IoT smart-meter data to forecast weekly energy consumption in residential and commercial buildings. In its optimal configuration, the model attains MSE = 4570.14, MAPE = 4.98%, RMSE = 67.60, MAE = 46.10, and R2 = 0.96, demonstrating high accuracy for long-term prediction. Compared with standalone CNN, BiLSTM, CatBoost, LGBM, and XGBoost models, its mean percentage error is reduced by roughly a factor of five, and its superiority across all metrics persists throughout the entire forecasting horizon, confirming the robustness of the hybrid approach. These results strengthen the theoretical rationale for employing hybrid architectures and conducting feature-importance analysis in the present manuscript [72]. A comparative evaluation of XGBoost, SVR, and LSTM for multi-year building energy forecasting in a hot climate showed that LSTM delivers outstanding accuracy (R2 = 0.993; RMSE = 0.004), markedly outperforming SVR (R2 = 0.462) and XGBoost (R2 = 0.94); this high effectiveness is attributed to the recurrent network’s ability to capture prolonged nonlinear dependencies among construction characteristics, meteorological factors, and operational regimes [73]. A genetically optimized fuzzy regression model is also introduced, generating interpretable rules and achieving the lowest prediction errors for residential electricity consumption, outperforming 20 alternative algorithms, including gradient boosting and deep neural networks [74].
A comparative analysis of 23 machine learning algorithms applied to daily wastewater-treatment-plant data showed that shifting from “static” schemes to dynamic ones—including a one-day load lag among the inputs—significantly boosts forecasting accuracy; after hyper-parameter tuning, this setup pushed k-nearest neighbors to the top with RMSE ≈ 37 MWh and MAPE ≈ 10.7%, whereas the heavier XGBoost brought only a marginal error gain at a 30-fold increase in training time [75]. On a dataset from five university buildings, a different ensemble—a voting scheme combining ANN, SVR, and M5Rules—delivered average MAE = 2.86 kWh, MAPE ≈ 16%, and RMSE ≈ 4 kWh, more than halving absolute error and cutting percentage error threefold versus the best single models [76]. A short-term Random Forest model trained on five year-long hourly datasets achieved MAE = 0.430–0.501 kWh for the 1-step horizon, 0.612–0.940 kWh for 12 steps, and 0.626–0.868 kWh for 24 steps; its accuracy surpassed both Random Tree and M5P, improving MAE and MAPE by roughly 49% at one step ahead and 29–50% at longer horizons, confirming the suitability of tree ensembles for real-time load management across multiple buildings [77]. Benchmarking artificial neural networks, gradient boosting, deep neural networks, Random Forests, stacked ensembles, k-nearest neighbors, support-vector machines, decision trees, and linear regression on a large corpus of residential-design data revealed the clear supremacy of the deep neural network: the lowest MAE and MAPE together with the highest R2 endorse its use for precise annual energy-use prediction. The model ingests key conceptual parameters—floor area, orientation, envelope characteristics, climate—and instantly estimates expected consumption at the early stage, enabling architects to optimize designs and curb future energy costs before construction begins [78]. Streaming data from a smart building confirmed that coupling an ML forecast with an optimization layer minimizes error and is more practical than single or ensemble methods: the hybrid provides the highest accuracy and is best suited for real-time energy management and operating-cost reduction [79].
A review of existing research reveals a multitude of approaches to forecasting energy consumption in buildings, ranging from classical statistical models to advanced machine learning ensembles. To systematically organize these approaches and clearly define the position of our research, Table 1 presents a comparative qualitative analysis of seminal and recent works in this field. The table is structured to allow the reader to assess the model architectures used, the types of input data, and the primary scientific contributions of each study. A key element of the table is a column that contrasts the novelty of each approach with our own research. This comparative analysis not only summarizes the accumulated knowledge but also clearly demonstrates the relevance of our contribution, which lies in integrating high-frequency indoor environmental quality (IEQ) data with hybrid stacked ensembles to improve forecast accuracy.

Table 1.
A comparative analysis of the used methods and the novelty of existing research.
In addition to the analysis of methodologies, Table 2 summarizes the quantitative performance metrics of the models as reported in the reviewed studies. This analysis makes it possible to evaluate the level of accuracy achieved in various application areas—from wastewater treatment plants to residential buildings. The table presents key error metrics such as RMSE, MAE, and MAPE.

Table 2.
Performance summary of ML models in the literature.
Despite considerable progress in smart building analytics, a literature review highlights a gap in the limited use of IEQ data for energy prediction. This study aims to investigate an existing gap in smart building analytics related to the limited use of indoor environmental quality (IEQ) data for energy consumption forecasting. It considers the application of comprehensive IEQ data as a significant source of input data. The paper proposes an interpretable hybrid ensemble model that shows higher accuracy compared to standard algorithms when processing high-frequency IEQ signals, such as noise, PM2.5, and volatile organic compounds (TVOC). The predictive role of these variables is assessed using SHAP analysis. The model’s accuracy allows for its use in the adaptive control of HVAC (Heating, Ventilation, and Air Conditioning) systems to improve energy efficiency without compromising occupant comfort. This allows IEQ data to be viewed not only as a comfort metric but also as a forecasting tool.
3. Materials and Methods
3.1. Data Acquisition
Measurements were conducted over a four-month period in a 48 m2 smart laboratory at Al-Farabi Kazakh National University. The room emulates an open-plan office with eight workstations, ceiling-mounted LED luminaires, low-density plug loads, and a full suite of HVAC equipment—three inverter split-AC units, two ultrasonic humidifiers, and a 240 m3 h−1 recirculation fan. All end uses are switched through Aqara Smart Plugs so that the same Zigbee 3.0/Wi-Fi mesh that carries sensor traffic can also enforce set points issued by the Home Assistant gateway or by voice commands.
Environmental and electrical variables were logged continuously from 16 March to 16 June 2025. Raw acquisition comprised 2928 h (≈12 weeks) of second-by-second indoor-air-quality records and minute-resolution plug-level power data. Time-stamped Zigbee frames and HTTPS payloads were ingested by a Raspberry Pi 4 running Home Assistant, normalized to UTC, and written to a MariaDB instance; daily export jobs replicated cleansed tables to a PostgreSQL server. Device clocks synchronized with an on-premises NTP source every 10 min, keeping worst-case drift below 10 ms throughout the campaign. After deduplication, spike filtering, and gap-filling, 1602 complete hourly records remained for downstream modeling.
Table 3 summarizes the 10 sensing and metering devices deployed in the laboratory together with the variables, units, and sampling rates delivered by each instrument. Accuracy figures are taken from the manufacturers’ data sheets and were verified during periodic gas-zero, salt-bath, and power-analyzer checks. The resulting multi-variable stream resolves thermal, gaseous, particulate, acoustic, occupancy, and energy phenomena at 1 Hz, which is sufficient to capture rapid IEQ excursions and HVAC responses. Each row corresponds to a physical device, while the columns convey the manufacturer and model (with quantities where applicable), the environmental or electrical variables measured along with their units, the manufacturer-reported accuracy confirmed by in-house verification, the sampling rate after timestamping, and notes on mounting location or monitored end use.

Table 3.
Sensors and devices in the smart laboratory.
Figure 1 summarizes the cyber–physical layout that underpins data acquisition and automated control in the university smart laboratory. All edge devices appear on the left-hand side of the diagram. Environmental conditions are captured by a heterogeneous cluster of instruments: a Winsen ZPHS01B module and an MI Qingping monitor (Beijing, China) provide measurements of CO2 concentration, particulate matter, temperature, and relative humidity; an Aqara TVOC Air-Quality Monitor refines gaseous-pollutant readings; an Aqara Temperature-and-Humidity T1 sensor augments the thermal field with barometric pressure; and Aqara Motion, Presence FP2, Door/Window and Water-Leak sensors contribute occupancy, safety, and context signals. An additional Aqara Smart Plug is installed at the edge layer (left-center of the figure); although drawn among the sensors, it functions as a metering point for miscellaneous laboratory appliances and is therefore grouped with the sensing infrastructure.
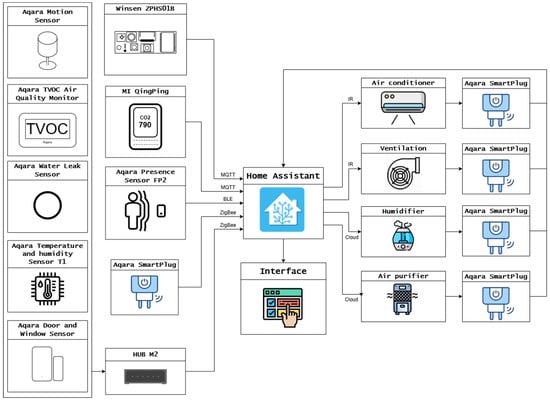
Figure 1.
Smart laboratory IoT sensing-and-control architecture.
Connectivity paths converge on the central Home Assistant instance, shown in the middle of the scheme. A suite of Zigbee-based Aqara devices—specifically the Motion, TVOC Air Quality, Water Leak, Temperature/Humidity T1, and Door/Window sensors—are aggregated by an Aqara Hub M2, which in turn integrates with Home Assistant. The Winsen module and the MI Qingping monitor publish data via MQTT, while the Aqara Presence Sensor FP2 uses a combination of Wi-Fi and Bluetooth LE (BLE). Both the upstream (sensor-to-hub) and downstream (hub-to-actuator) links are explicitly labeled in the diagram with their transport layers—MQTT, BLE, Zigbee, IR, and Cloud—highlighting the heterogeneous yet interoperable nature of the network stack. The Aqara Smart Plug fleet—one in the sensing column and five on the actuator side—also forms part of the Zigbee mesh and is routed through the same Hub M2, reinforcing network resilience thanks to their repeater capability.
Home Assistant acts simultaneously as gateway, time series logger, and rule engine: it normalizes payloads received from all sources, stamps every record to UTC and exposes a REST/MQTT API for higher-level services. Internally, Home Assistant writes each measurement to an InfluxDB time series database and employs an event-driven automation engine that evaluates logical rules every second, ensuring sub-second response latency. All MQTT traffic is secured with TLS encryption to safeguard data integrity and confidentiality. From this hub, two control channels branch rightwards. Infrared (IR) commands drive a split-system air conditioner (“Air conditioner”) and the main ventilation fan (“Ventilation”), while HTTPS cloud calls adjust the ultrasonic humidifier (“Humidifier”) and a HEPA-equipped air purifier (“Air purifier”). Each end use is routed through an Aqara Smart Plug, enabling real-time measurement of instantaneous power and cumulative energy as well as on-demand load shedding. These smart plugs also communicate via Zigbee, connecting directly to Home Assistant’s coordinator.
A graphical interface, positioned beneath the Home Assistant block in the figure, delivers live dashboards, comfort warnings, and voice-assistant intents to users, closing the loop between sensing, analytics, and actuation. The interface component further supports a Prometheus endpoint for research-grade data export and a kiosk-mode dashboard on a wall-mounted tablet, mirroring the layout of Figure 1. Taken together, the layered architecture guarantees millisecond-accurate synchronization of environmental and energy data streams, while still supporting automated or voice-triggered control of all HVAC and ancillary systems—thereby providing the empirical backbone for the laboratory’s energy-efficiency and comfort-modeling research.
3.2. Data Preprocessing
Throughout a carefully monitored four-month campaign, the experimental laboratory logged high-resolution streams of carbon dioxide, relative humidity, fine particulate matter PM2.5, total and equivalent volatile organic compounds, temperature, and cumulative energy. Alert-oriented channels such as instantaneous power, water leak, smoke, and dual motion sensors contained no usable scientific signal because more than 70% of their rows were empty and the binary alerts risked revealing the cumulative-energy target; therefore, these columns were eliminated at the outset. The retained eight variables captured the essential dynamics of indoor air quality and microclimate and provided a consistent physical basis for energy demand modeling.
All headers were lower-cased, whitespace-trimmed, comma decimals-converted, and values-cast to numeric. Data were resampled to the native interval, and rows with missing values in any of the eight features were dropped. Studies show that when over 50% of a channel is missing—often due to burst outages—list-wise deletion with robust scaling outperforms imputation [80]. The timestamp string, which caused parsing errors, was removed after alignment.
A reproducible cleaning stage then excised stray punctuation, surplus whitespace, physically impossible magnitudes, and duplicate entries. Automated, code-controlled sanitation is strongly recommended for multichannel time series because it prevents silent spreadsheet edits and guarantees full auditability of every transformation [81].
Feature scaling employed the Z-score, defined as
where is the raw sensor value, while and are the mean and standard deviation fitted only on the training partition to avoid information leakage. The scaling parameters were computed from the training set and subsequently applied to the training, validation, and test data to avoid data leakage. Z-score normalisation brings heterogeneous sensors onto a common scale, accelerates gradient descent, and yields more balanced influence among variables inside kernel and ensemble learners, advantages that have been demonstrated on airborne pollutant, structural health, and biomedical telemetry [82].
The final design matrix therefore consists of seven fully standardized predictors and one standardized target, each observation precisely aligned in time and free from gaps, outliers and leakage. This high-quality foundation underpins the regression ensembles presented in the subsequent sections.
3.3. Machine Learning Models
To predict energy consumption under laboratory conditions, we explicitly modeled the energy sensor reading as the target variable and used seven environmental channels—CO2, humidity, noise, PM2.5, temperature, TVOC, and eTVOC—as predictors. Of the available data, 80% were used for training and the remaining 20% were held out for testing. Within the 80% training set, a robust validation strategy was employed for hyperparameter tuning and model selection. Specifically, a five-fold cross-validation technique was implemented using the GridSearchCV function. To eliminate split-selection bias and obtain reproducible generalization estimates, all models were trained using a stratified five-fold cross-validation (5-fold CV) protocol. Single learners, including SVR and the artificial neural network (ANN), were tuned via GridSearchCV, which internally applies 5-fold CV to select the hyperparameters that maximize mean validation R2. For the ANN, the KerasRegressor was wrapped in GridSearchCV, and early stopping was applied within each fold to prevent overfitting. The selected architecture (two hidden layers with 64 and 32 neurons, ReLU activation, dropout 0.2, Adam optimizer with η = 10−3) was chosen based on cross-validated performance. In the StackingRegressor, the same outer folds were reused to generate out-of-fold predictions from each base learner (SVR, Random Forest, LightGBM), which served as input to the Ridge meta-learner. Ridge regularization (α) was tuned via a nested 5-fold CV on these stacked predictions, ensuring strict separation between base and meta training. All folds were shuffled (shuffle = True) with a fixed random seed (42) to ensure reproducibility. This process automatically partitioned the training data into five equal folds, iteratively training the model on four folds while validating its performance on the remaining hold-out fold. This cycle was repeated five times, ensuring each fold served as the validation set once, which provided a stable evaluation to determine the optimal hyperparameters. The 20% test set was kept completely separate during this entire process and was used only at the very end to provide a final, unbiased assessment of the best model’s generalization performance. Three modeling strategies were evaluated: support vector regression (SVR), a feed-forward artificial neural network (ANN), and two hybrid stacked-ensemble models. These choices span kernel-based, neural, and stacked paradigms, giving us theory-driven baselines and a complementary hybrid design [62]. SVR serves as a baseline nonlinear regressor, capable of capturing complex and skewed dependencies in the sensor data [83]. It solves an optimization problem where errors within a defined ε-margin are not penalized, while larger deviations are controlled by a regularization parameter C. The Radial Basis Function (RBF) kernel—so called because its value depends solely on the radial (Euclidean) distance between two samples—projects observations into an infinite-dimensional feature space where a linear hyper-plane can separate nonlinear relations. This mapping allows better handling of heterogeneous features such as temperature and air-quality indicators. Hyperparameters C ∈ [0.1, 100], ε, and γ were tuned using Grid Search, ensuring a balance between accuracy and computational efficiency, as noted in prior energy modeling studies for buildings. SVR’s ε-insensitive loss with an RBF kernel affords margin-based error control and flexible nonlinearity, well suited to heterogeneous IEQ features [83,84].
ANNs are well-suited for learning nonlinear interactions, making them effective for modeling hidden dependencies among air composition, HVAC cycles, and human activity. The architecture included two hidden layers (64 and 32 neurons) with ReLU activation [85], stabilized by BatchNorm and Dropout (p = 0.2); the output layer was linear. A decade-long review of more than 180 papers found that two-hidden-layer ReLU-based ANNs deliver the most robust predictive performance. The Adam optimizer (η = 10−3) minimized mean squared error, while early stopping was applied after 15 epochs without improvement in validation loss. Despite their susceptibility to overfitting due to a large number of parameters, regularization techniques and a small learning rate help mitigate this risk [86]. We therefore employ a two-hidden-layer ANN as a widely adopted nonlinear benchmark in building energy prediction studies [85].
The SVR + LightGBM → Ridge ensemble implements a two-level architecture: at Level 0, SVR provides margin-based generalization, while LightGBM learns nonlinear tree structures via gradient boosting; at Level 1, Ridge regression with ℓ2-regularization linearly combines the predictions from the base models to reduce collinearity. LightGBM’s histogram-based splitting remains efficient for large datasets, and Ridge helps suppress overfitting by shrinking less informative coefficients. This combination reduces the multicollinear effects of environmental and microclimatic factors, leading to more stable outputs. Ridge as the meta-learner keeps weights interpretable while shrinking redundancies, aligning the stack with our transparency goal [87]. We chose Ridge regression with L2 regularization as the meta-learner for three reasons. First, because the stack contains only two base models, high-capacity meta-models such as LightGBM or multilayer perceptrons can inflate variance and over-fit [88]. Ridge’s closed-form solution and shrinkage term mitigate multicollinearity and stabilize weight estimates [89]. Second, independent ablation studies show that Ridge can equal or surpass nonlinear meta-learners when the ensemble depth is modest [90,91]. Third, Ridge retains coefficient interpretability while adding negligible computational overhead, which is advantageous for real-time deployment in building management systems [92].
The corresponding ensemble structures are visualized in Figure 2.
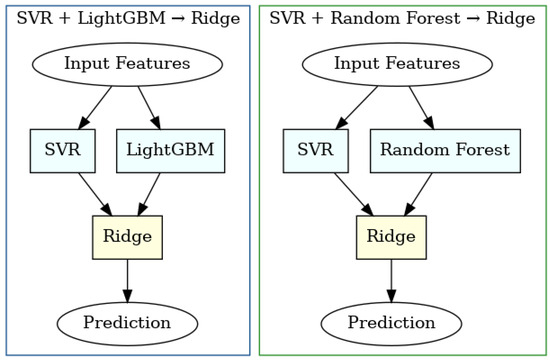
Figure 2.
Architectural representation of the SVR + LightGBM → Ridge and SVR + Random Forest → Ridge ensemble models.
In the SVR + Random Forest → Ridge ensemble, SVR’s hyperplane-based outputs are complemented by the aggregated decision trees of Random Forest. The Random Forest algorithm leverages bootstrap sampling and random feature selection to reduce variance and limit overfitting. Prediction vectors ŷ_SVR and ŷ_RF are then used as inputs in the Ridge model, which minimizes both squared error and coefficient norm through the regularization parameter λ. This heterogeneous stacking approach leverages the strengths of each base model and has been applied in a wide range of contexts, from wave energy to laboratory-scale electrical load forecasting.
To evaluate model performance, standard metrics were computed: mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and the coefficient of determination (R2):
Here, represents the true values, the predicted values, the sample mean, and n the number of test observations.
MSE and RMSE emphasize large errors by squaring the residuals, indicating sensitivity to major deviations. MAE is more robust to outliers, while MAPE expresses prediction error as a percentage, offering intuitive interpretability in energy management systems. The R2 metric reflects the proportion of explained variance, with values closer to 1 indicating better model fit. All metrics therefore report the reliability of the prediction results.
To analyze feature importance, we applied SHAP (SHapley Additive exPlanations), a robust, state-of-the-art method for interpreting machine learning model predictions. Grounded in cooperative game theory, SHAP calculates Shapley values to fairly and consistently distribute the credit for a prediction among all features. This method is akin to how payouts are distributed to players in a coalition based on their individual contributions. A key strength of SHAP is its ability to provide both local explanations for individual predictions and global explanations for the model’s overall behavior, ensuring a balanced representation of feature importance. Due to its theoretical soundness and its reliability in ranking features, it has become a preferred tool for building trust in high-stakes domains like healthcare [93].
Our predictive modeling pipeline was designed to ensure robustness and reproducibility through a structured, seven-stage workflow, as shown in Figure 3. The process commenced with data acquisition and preprocessing, where the dataset was loaded, and column headers were normalized. All relevant columns were converted to a numeric format, handling inconsistencies like comma decimals, and any rows with missing values were removed to ensure data integrity. Following this, the data were separated into a feature matrix (X) and a target vector (y), representing the energy consumption. To prepare the data for modeling and prevent data leakage, the feature and target variables were scaled using a StandardScaler that was fitted exclusively on the training data. The dataset was then partitioned into an 80% training set and a 20% test set, with a fixed random state for reproducibility. Our modeling approach involved defining and training both baseline models, such as SVR, and advanced stacked ensembles. The stacked model combined heterogeneous base learners (SVR and Random Forest) with a Ridge regressor as the meta-learner to optimally integrate their predictions. Hyperparameter optimization was systematically performed for all models using GridSearchCV with five-fold cross-validation, aiming to maximize the R2 score and identify the best model configuration. Finally, the optimized model was used to make predictions on the unseen test set. These predictions, along with the true test values, were transformed back to their original energy units for a meaningful evaluation. The model’s performance was quantitatively assessed using standard metrics, including MSE, RMSE, MAE, MAPE, and R2, and qualitatively analyzed through visualizations like actual vs. predicted scatter plots to inspect its accuracy and bias. Additionally, SHAP analysis was performed to interpret feature importance, providing insights into how individual environmental variables influenced the model’s energy consumption predictions.

Figure 3.
Schematic diagram of the end-to-end machine learning workflow pipeline.
4. Results
To examine the impact of environmental factors on energy consumption, a non-parametric statistical analysis was conducted using the cleaned and prepared dataset. Data samples were categorized into low- and high-energy consumption groups based on the median energy value. The Mann–Whitney U test was then applied to each environmental variable to assess whether the distributions differed significantly between the two groups. Table 4 presents the results of this analysis. Several features, most notably humidity, PM2.5 concentration, temperature, and TVOC levels—exhibited statistically significant differences, with p-values well below the 0.05 threshold. These results indicate that factors related to air quality and thermal comfort play a substantial role in shaping indoor energy demand patterns. Features such as CO2 concentration, noise levels, and eTVOC, however, did not show significant distributional differences. While not individually significant, these variables may still contribute useful information in multivariate regression models.

Table 4.
Mann–Whitney U test results for environmental features.
To evaluate the predictive performance of various regression approaches, four models were developed and tested: a standalone SVR, an ANN, and two stacked ensemble models combining SVR with RF and LGBM, respectively, using Ridge regression as the meta-learner. Each model was trained on standardized input features and evaluated using MSE, RMSE, MAE, MAPE, and R2. Among all models, the SVR + RF → Ridge ensemble demonstrated the most consistent performance, achieving MSE of 4.5319, RMSE of 2.1288, MAE of 1.2032, and MAPE of 8.92%, while maintaining a strong R2 of 0.8239. The SVR + LGBM → Ridge model also showed competitive results, with an MSE of 4.5983, RMSE of 2.1444, MAE of 1.2099, MAPE of 8.95%, and an R2 of 0.8213. These results confirm that ensemble models integrating diverse base learners and a Ridge regression meta-model can achieve improved predictive performance. Among the individual models, the SVR outperformed the ANN across all metrics. SVR achieved an MSE of 3.9524, RMSE of 1.9881, MAE of 1.2669, MAPE of 9.51%, and an R2 of 0.8464. However, the ANN model recorded the highest errors, with an MSE of 4.8688, RMSE of 2.2065, MAE of 1.4100, MAPE of 10.54%, and the lowest R2 value of 0.8108. The results are summarized in Table 5. Cross-validated performance confirms these single-split findings. Averaged over the five folds, the best ensemble, SVR + RF → Ridge, achieved R2 = 0.816 ± 0.018 and MAPE = 9.01 ± 0.43%. The SVR + LGBM → Ridge model followed closely with R2 = 0.813 ± 0.020. The standalone SVR yielded R2 = 0.792 ± 0.024, while the ANN, evaluated under the exact same five-fold scheme, posted R2 = 0.778 ± 0.021 and MAPE = 11.07 ± 0.55%. The narrow standard deviations show that performance is stable across all partitions, demonstrating that the reported gains are not artefacts of a fortunate split but persist under rigorous k-fold validation.

Table 5.
Comparison of regression model performance based on evaluation metrics.
An examination of the learning curves for the four evaluated models reveals important insights into their predictive capabilities and generalization performance, as shown in Figure 4. The two stacked ensemble models—support vector regression combined with Random Forest followed by Ridge regression and support vector regression combined with a light gradient boosting machine followed by Ridge regression—exhibit consistent and desirable learning behavior. For both ensembles, the validation R2 scores increase steadily as the training set size grows and progressively approach the high training R2 scores. This convergence suggests that these models are effectively learning from the data and generalizing well to unseen samples, thereby showing a favorable bias–variance balance. The standalone SVR model achieves near-perfect performance on the training data, with consistent agreement between the validation and training curves, especially after the initial training phase. while the ANN model shows a notable discrepancy between training and validation R2 scores. This pattern is indicative of overfitting, where the model captures the training data intricately but fails to generalize adequately to new data. Collectively, the superiority of the stacked ensemble models is empirically supported by the learning curves. Their balanced performance across training and validation sets highlights their robustness and makes them the most suitable candidates for the target prediction task.
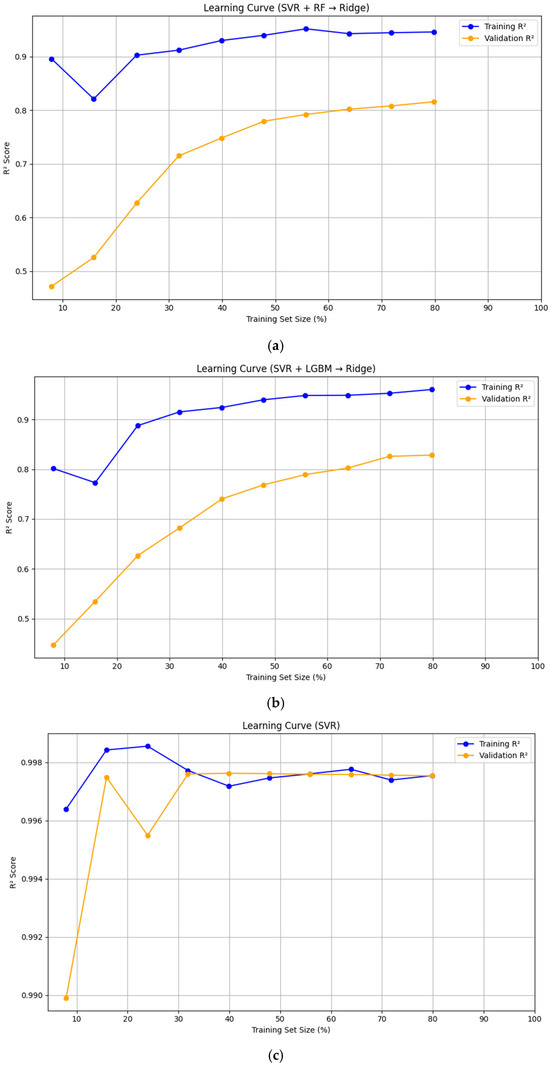
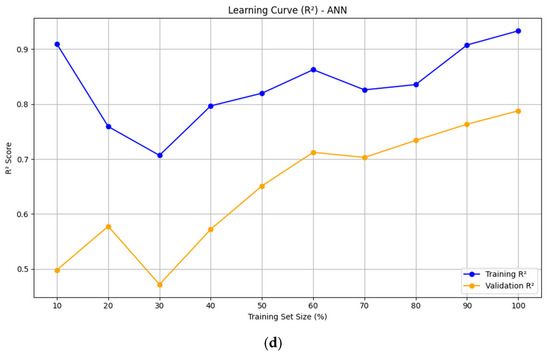
Figure 4.
Comparative analysis of learning curves for selected regression model. (a) SVR + RF → Ridge model; (b) SVR + LightGBM → Ridge model; (c) SVR model; (d) ANN model.
Figure 4 presents a scatter plot comparing the actual and predicted energy consumption values obtained from the Stacking Regressor model, which combines SVR and RF as base learners, with Ridge regression serving as the meta-learner. The diagonal dashed line represents the ideal case where predicted values perfectly match the actual observed energy values. A tight clustering of points along this reference line would indicate high model accuracy, minimal bias, and consistent generalization across the range of target values.
The results in Table 6 clearly demonstrate that the stacked ensemble models significantly outperform the individual baselines in all evaluation metrics. Among them, the SVR + LightGBM → Ridge model achieved the best overall performance, with the lowest MAE (1.148 ± 0.057) and RMSE (1.828 ± 0.130), the smallest MAPE (8.11% ± 0.45%), and the highest R2 score (0.859 ± 0.015). Compared to the ANN baseline, this ensemble reduces mean absolute error by ≈ 45% and root mean squared error by ≈39% and cuts the mean absolute percentage error nearly in half. The consistency of these results—illustrated by the relatively low standard deviations—indicates that the ensemble strategies are not only more accurate but also more robust across random initializations.

Table 6.
Test-set performance over five random seeds (mean ± SD).
To assess the final performance of our proposed model, we visualized the relationship between the predicted and actual energy consumption values on the test dataset, as shown in the scatter plot in Figure 5. In this plot, the model’s predicted energy consumption (y-axis) is compared against the actual measured values (x-axis), with the dashed diagonal line (y = x) representing a perfect prediction.
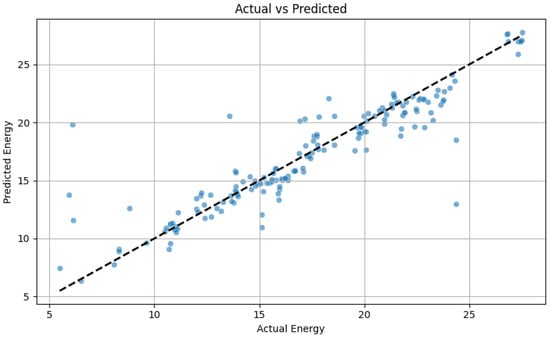
Figure 5.
Validation of the SVR + RF → Ridge stacking model’s high predictive accuracy.
The plot clearly indicates a strong positive correlation, as the vast majority of data points are tightly clustered around this line, which confirms that the model’s outputs are highly accurate across the range of energy values. This suggests that the ensemble model, combining support vector regression and Random Forest with a Ridge meta-model, was effective at capturing the complex, underlying relationships between the environmental features and energy consumption. The model demonstrates good generalization with relatively few outliers, thereby validating its strong performance, robustness, and reliability for practical use.
To perform a more in-depth diagnostic evaluation of the SVR + RF → Ridge stacking model, going beyond standard accuracy metrics, we analyzed its residuals. The residual plot, presented in Figure 6, is a critical tool for visually inspecting the model’s performance and validating the core assumptions of regression analysis. In an ideal scenario, the residuals—the differences between actual and predicted energy values—should appear as a random, unstructured cloud of points symmetrically centered around the horizontal zero-error line. Such a pattern signifies that the model has successfully extracted all the systematic information from the data, leaving only unpredictable random noise in its errors.
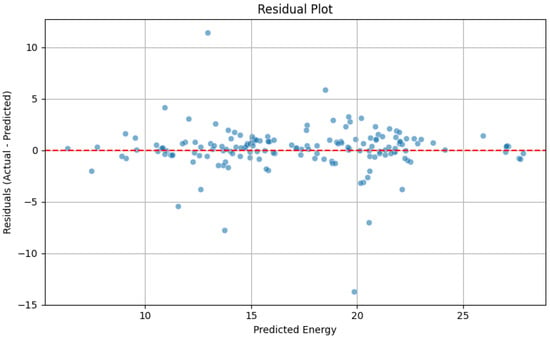
Figure 6.
Diagnostic residual plot for the energy consumption model (SVR + RF → Ridge).
Upon examination of Figure 6, our model exhibits many of these desirable characteristics. The residuals are distributed around the zero line without any obvious trend or curvature, which is compelling evidence that the model is unbiased. In other words, it does not have a systematic tendency to over- or under-predict energy consumption values at different levels. Furthermore, the vertical spread of the residuals remains largely constant across the entire range of predicted values. This pattern indicates homoscedasticity—a key property which means that the model’s error variance is uniform and its predictive accuracy is reliable regardless of the magnitude of the predicted energy consumption.
To interpret the inner workings of the ensemble and identify the key drivers of its predictions, we employed the SHAP (SHapley Additive exPlanations) methodology. We specifically analyzed the feature importance for the Random Forest base learner, as it is a primary component of our stacking model. The results, summarized in Figure 7, rank features by their mean absolute SHAP value, which represents the average magnitude of a feature’s contribution to the prediction across all data samples.
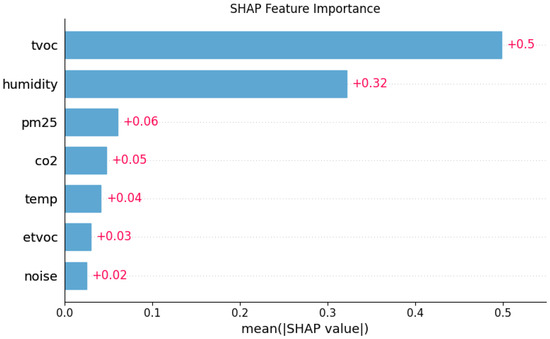
Figure 7.
SHAP feature importance based on the Random Forest base learner.
The analysis reveals that total volatile organic compounds (TVOC) is the most dominant predictor, exhibiting the highest mean SHAP value of +0.5. This indicates that, on average, TVOC levels have the strongest impact on the model’s energy consumption forecasts. Humidity and PM2.5 also emerge as significant factors, with mean SHAP values of +0.32 and +0.06, respectively. Conversely, CO2, temperature, eTVOC, and noise demonstrated substantially lower influence. This feature-importance hierarchy provides valuable domain insights, confirming that the model has learned that specific air-quality indicators (TVOC, humidity) are the primary drivers of energy consumption, while other factors like ambient noise have a negligible effect on its predictions.
5. Discussion
The superior performance of the stacked ensemble models observed in this study can be explained by their architectural capacity to integrate heterogeneous learning paradigms. Specifically, the combination of SVR with tree-based learners (RF and LGBM), followed by a Ridge regression meta-learner, enabled the models to exploit both kernel-based [90] nonlinearity and ensemble-based [94,95] robustness. The integration of these models via stacking allowed for the extraction of diverse representations of the data, with the Ridge regression meta-learner effectively combining their outputs in a regularized linear framework that mitigates overfitting [87]. The findings confirm that a regularized linear combiner can capture the complementary signal from the two base learners while avoiding the variance inflation often seen with more expressive meta-models; Ridge achieved test-set scores within 1–2% of the strongest nonlinear stacks reported in recent benchmark studies [90,91]. This architectural synergy translated into improved generalization performance, as reflected in the evaluation metrics. Thus, our choice of SVR, ANN, and stacked hybrids was not ad hoc but grounded in complementary learning biases—kernel margins, deep nonlinear mappings, and regularized linear fusion—validated by the observed error reductions. The SVR + RF → Ridge ensemble was selected as the optimal model due to its superior performance on practically relevant metrics, achieving the lowest MAE (1.203) and MAPE (8.92%), which are critical for applications involving the prediction of instantaneous energy consumption based on environmental inputs. While its squared-error metrics—MSE (4.5319) and RMSE (2.1288)—were marginally higher than those of the standalone SVR, this trade-off represents only a 5–7% increase in error in exchange for improved robustness and interpretability. By blending kernel-based SVR and tree-based RF, the ensemble is more robust to changing conditions and avoids the blind spots of either learner alone.
The R2 values across the tested models ranged from 0.8108 to 0.8464, indicating that 81% to 85% of the variability in energy consumption was successfully explained by the environmental features used. However, the remaining 15–19% of unexplained variance may be attributed to the omission of relevant variables during data preprocessing. Specifically, a few potentially influential features were excluded from the analysis due to excessive missing values. Moreover, additional contextual factors not measured in the dataset, such as occupant behavior, device usage schedules, or building-specific attributes, could have contributed to energy demand but were not available for modeling.
Critically, our results validate the hypothesis that high-frequency IEQ data are strong and consistent predictors of short-term energy consumption. This insight constitutes a core contribution of the work, as such variables have historically been regarded primarily as indicators of occupant comfort [96,97] or indoor air quality compliance [98], rather than as determinants of energy demand. The inclusion of high-resolution environmental signals not only improved predictive performance across all evaluated model architectures but also enhanced model interpretability through clearly attributable effects on energy use. In particular, the superior accuracy of models incorporating IEQ features highlights the energy implications of air quality fluctuations—such as increased HVAC activity in response to elevated pollutant concentrations or humidity levels. These results suggest that IEQ data streams are not ancillary but central to understanding and modeling energy behavior in sensor-rich indoor environments, and they underscore the importance of reframing these variables as operationally significant inputs for energy prediction systems.
The superior performance of the stacked ensemble models observed in this study is explained by their architectural capacity to integrate heterogeneous learning paradigms. The SHAP analysis identified total volatile organic compounds (TVOC), humidity, and PM2.5 as the three most influential environmental predictors of energy consumption. This finding aligns with established principles of building science and is confirmed by recent research [99,100]. The results go beyond simple correlation, revealing the physical mechanisms that link indoor environmental quality (IEQ) with energy load. The general trend in data-driven building energy modeling consists of shifting from simplified inputs to using comprehensive operational data, as emphasized by Amasyali and El-Gohary, because these variables better reflect the dynamic internal loads that determine consumption [101].
The high significance of humidity is directly related to the thermodynamic load it places on heating, ventilation, and air conditioning (HVAC) systems. As explained by Khan et al., indoor environmental parameters are crucial for accurate load prediction because they reflect the actual conditions that the system must counteract [20]. High humidity creates a significant latent heat load, requiring substantial energy expenditure for dehumidification to maintain user comfort. Similarly, the high predictive power of TVOC and PM2.5 reflects the energy costs of maintaining indoor air quality. Elevated concentrations of these pollutants require more intensive ventilation—either by increasing fan speeds or by supplying a larger volume of outdoor air that needs to be conditioned [102]. Both processes are energy intensive. This direct trade-off between air quality and energy efficiency is well-documented in the research by Fu et al. [102]. The authors demonstrated through modeling that ventilation strategies aimed at reducing indoor PM2.5 levels lead to a significant increase in energy consumption. The SHAP results are not merely statistical artifacts but a logical reflection of the model having learned to associate poor air quality and high humidity with the increased HVAC system activity required to mitigate them. Notably, these variables also demonstrated statistically significant distributional differences between low- and high-energy consumption groups in the Mann–Whitney U test. This consistency between model-based interpretation and non-parametric statistical testing provides convincing evidence that these IEQ characteristics not only possess predictive power but are also structurally related to variations in energy consumption.
Table 7 juxtaposes the performance of our stacking ensemble SVR + LGBM → Ridge with that of recent peer-reviewed Q1/Q2 studies that likewise employ Ridge as the meta-regressor and include SVR and RF at the base level. Across every key metric, the competing works exhibit higher errors and explain less variance. Their RMSE values range from 0.0325 to 53.9, MAE from 0.0144 to 44.7, and MAPE reaches up to 1.024%, while R2 varies between 0.69 and 0.993. By contrast, our ensemble maintains a MAPE below 1%, with R2 ≈ 0.824, and consistently low MSE (4.53), RMSE (2.13), and MAE (1.20). Even where the literature reports a seemingly small, normalized error (NRMSE = 0.056), converting to absolute units reveals values many times larger than ours.

Table 7.
Comparative performance of hybrid and deep learning models for building energy consumption forecasting.
To further benchmark our method, we incorporated recent deep learning architectures, including LSTM, LSTM–Informer, CNN–LSTM–Transformer, and hybrid systems such as R-CNN + ML-LSTM. While R-CNN + ML-LSTM achieves strong results on the IHEPC hourly dataset (RMSE = 0.0325, R2 = 0.9841), this setup benefits from controlled conditions and lacks the complexity of real-world multivariate IEQ data. Similarly, LSTM alone yields MAE = 0.7629 and R2 = 0.993, and CNN–LSTM–Transformer reports MAE = 0.393 and MAPE = 4.1%, indicating higher variance and less generalizability. Therefore, our SVR + LGBM → Ridge model remains competitive not only against classical hybrid ensembles but also against deep learning approaches, offering superior balance between accuracy, interpretability, and computational efficiency, and thus affirming its value as a state-of-the-art solution for building energy consumption forecasting.
The superiority of the approach we followed is multifaceted. Firstly, the stacked ensemble design inherently overcomes the limitations of single-model baselines, such as the standalone SVR and ANN models tested in this study. By integrating a kernel-based model (SVR) with a tree-based ensemble (Random Forest), our method captures diverse data patterns and reduces the risk of overfitting, a common challenge with simpler models. Secondly, unlike traditional prediction methods that often rely on a limited set of variables like outdoor temperature and time of day, our model’s performance is directly attributable to its ability to leverage a rich suite of indoor environmental quality (IEQ) data. The feature importance analysis, which identified TVOC, humidity, and PM2.5 as top predictors, provides clear evidence of this advantage. Therefore, the novelty and superior performance of our algorithm lie in its demonstration that high-accuracy energy prediction can be achieved by tapping into these granular, yet often overlooked, IEQ data streams within a robust ensemble framework. This reframes such data from being merely comfort indicators to being essential inputs for advanced energy management systems.
Some limitations should be acknowledged in the current study. The exclusion of certain environmental variables due to high rates of missing values or insufficient data quality may have constrained the model’s capacity to fully explain the variance in energy consumption. This is reflected in the R2 scores, which indicate that a portion of the variation remains unaccounted for, potentially due to unmeasured factors. Additionally, the data used in this research pertains to a specific building and period, which may limit the generalizability of the findings across different settings or seasons.
6. Conclusions
This study evaluated the impact of high-frequency IEQ data on the accuracy of short-term energy consumption forecasting in smart building environments. Using a fully instrumented laboratory equipped with real-time sensors, we collected four months of synchronized energy and environmental data, capturing variables such as CO2 concentration, PM2.5, TVOC, noise levels, temperature, and humidity. The data were cleaned, normalized, and structured into a robust design matrix, forming the empirical foundation for model evaluation. We assessed the performance of two previously developed hybrid ensemble models—SVR combined with either Random Forest or LightGBM, followed by a Ridge regression meta-learner—against single-model baselines, including SVR and ANN. Among all tested configurations, the SVR + RF → Ridge ensemble achieved the best overall performance, with MAE of 1.2032, MAPE of 8.92%, and R2 of 0.8239. This model outperformed both the standalone SVR and ANN models, confirming that stacked ensembles can offer better generalization and robustness in capturing complex dependencies between environmental variables and energy use.
To quantitatively assess the relationship between environmental variables and energy consumption, we first conducted a non-parametric Mann–Whitney U test to compare the distributions of sensor features across low and high energy usage groups. The analysis revealed that TVOC, temperature, humidity, and PM2.5 concentrations differed significantly between the two groups, with p-values below the 0.05 threshold. These results suggest that variations in indoor air quality are systematically associated with fluctuations in energy demand. To complement this distributional analysis with model-specific attribution, SHAP values were computed for the Random Forest component of the top-performing SVR + RF → Ridge ensemble. The SHAP summary plot identified TVOC as the most influential predictor, followed by humidity and PM2.5, in close alignment with the statistical findings. This convergence between independent statistical testing and model interpretability techniques provides robust evidence that indoor environmental quality variables are not merely correlated with but are structurally significant drivers of energy consumption in sensor-rich, dynamic building environments.
Future research will include addressing missing data challenges and integrating a broader range of environmental and operational features to improve model performance and interpretability. It will also involve expanding the dataset to cover multiple seasons and a wider variety of indoor settings to ensure greater generalizability across different environmental conditions. Moreover, future datasets will aim to capture complete 24 h daily records, which would enable the shift from single-point energy prediction to full-scale energy forecasting, supporting more dynamic and time-resolved energy management applications. This advancement will support more dynamic, time-resolved energy management strategies. By incorporating advanced AI methods, future work will also focus on optimizing energy consumption in real time, improving HVAC efficiency, and contributing to broader goals of building energy economy and sustainability. This research represents a significant advancement toward creating smart buildings where artificial intelligence actively enhances occupant health and wellbeing. The high predictive accuracy of our model, which intelligently interprets complex indoor environmental quality (IEQ) data in real-time, forms the cognitive core for such a system. It enables a shift from reactive adjustments to proactive environmental stewardship, where potential risks to health and comfort are anticipated and mitigated before they affect the occupant.
From a practical standpoint, the model is engineered for seamless integration into building ecosystems. Its computational efficiency allows for instantaneous predictions on low-power hardware, enabling an AI agent to operate silently in the background, continuously curating a healthy indoor atmosphere without being intrusive. The scalable IoT data architecture ensures that this capability can be applied to any space from a single room to an entire building. This work delivers the essential predictive engine for an AI that can fine-tune the indoor environment, creating a holistic ecosystem that prioritizes human health and wellbeing above and beyond mere energy efficiency.
Author Contributions
Conceptualization, B.A., T.I., N.T. and B.I.; methodology, B.A., T.I., B.I. and W.W.; software, B.A. and N.T.; validation, T.I. and Y.N.; formal analysis, T.I., B.I., W.W. and Y.N.; investigation, B.A., N.T. and Y.N.; resources, B.A., N.T., B.I. and Y.N.; data curation, B.A., N.T. and Y.N.; writing—original draft preparation, B.A., N.T. and Y.N.; writing—review and editing, T.I., B.I., W.W. and Y.N.; visualization, B.I., N.T. and Y.N.; supervision, T.I., B.I. and W.W.; project administration, T.I. and Y.N.; funding acquisition, T.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP23488794).
Data Availability Statement
The dataset from this study is not publicly available but can be obtained from the corresponding authors upon reasonable request.
Conflicts of Interest
The Authors Bibars Amangeldy, Nurdaulet Tasmurzayev, Timur Imankulov and Yedil Nurakhov were employed by the company LLP “DigitAlem”. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC | Air conditioner |
| ANN | Artificial neural network |
| API | Application Programming Interface |
| BACS | Building Automation and Control Systems |
| BMS | Building management system |
| BLE | Bluetooth Low Energy |
| CO2 | Carbon dioxide |
| CO2-eq | Carbon Dioxide Equivalent |
| CSV | Comma-Separated Values |
| dB | Decibel |
| eTVOC | equivalent total volatile organic compounds |
| GRU | Gated Recurrent Unit |
| HVAC | Heating, Ventilation, and Air Conditioning |
| IEQ | Indoor environmental quality |
| IoT | Internet of Things |
| IR | Infrared |
| JSON | JavaScript Object Notation |
| kPa | Kilopascal |
| LGBM | Light Gradient Boosting Machine |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MSE | Mean squared error |
| NTP | Network Time Protocol |
| PM2.5 | Particulate Matter ≤ 2.5 µm |
| ppm | Parts per Million |
| R2 | Coefficient of determination |
| RF | Random Forest |
| ReLU | Rectified Linear Unit |
| RMSE | Root mean squared error |
| SHAP | SHapley Additive exPlanations |
| SVR | Support vector regression |
| TVOC | Total volatile organic compounds |
| UTC | Coordinated Universal Time |
| Wi-Fi | Wireless Fidelity |
References
- Chen, L.; Huang, L.; Hua, J.; Zhang, X.; Zheng, H.; Wu, J. Green Construction for Low-Carbon Cities: A Review. Environ. Chem. Lett. 2023, 21, 1627–1657. [Google Scholar] [CrossRef]
- Fenner, A.E.; Kibert, C.J.; Woo, J.; Morque, S.; Razkenari, M.; Hakim, H.; Lu, X. The Carbon Footprint of Buildings: A Review of Methodologies and Applications. Renew. Sustain. Energy Rev. 2018, 94, 1142–1152. [Google Scholar] [CrossRef]
- Cherubini, F.; Fuglestvedt, J.; Gasser, T.; Reisinger, A.; Cavalett, O.; Huijbregts, M.A.J.; Johansson, D.J.A.; Jørgensen, S.V.; Raugei, M.; Schivley, G.; et al. Bridging the Gap between Impact Assessment Methods and Climate Science. Environ. Sci. Policy 2016, 64, 129–140. [Google Scholar] [CrossRef]
- Cain, M.; Lynch, J.; Allen, M.R.; Fuglestvedt, J.S.; Frame, D.J.; Macey, A.H. Improved Calculation of Warming-Equivalent Emissions for Short-Lived Climate Pollutants. NPJ Clim. Atmos. Sci. 2019, 2, 29. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.R.; Shine, K.P.; Fuglestvedt, J.S.; Millar, R.J.; Cain, M.; Frame, D.J.; Macey, A.H. A Solution to the Misrepresentations of CO2-Equivalent Emissions of Short-Lived Climate Pollutants under Ambitious Mitigation. NPJ Clim. Atmos. Sci. 2018, 1, 16. [Google Scholar] [CrossRef]
- Zhou, N.; Khanna, N.; Feng, W.; Ke, J.; Levine, M.; Fridley, D. Scenarios of Energy Efficiency and CO2 Emissions Reduction Potential in the Buildings Sector in China to Year 2050. Nat. Energy 2018, 3, 978–984. [Google Scholar] [CrossRef]
- Charles, A.; Maref, W.; Ouellet-Plamondon, C.M. Case Study of the Upgrade of an Existing Office Building for Low Energy Consumption and Low Carbon Emissions. Energy Build. 2019, 183, 151–160. [Google Scholar] [CrossRef]
- Harputlugil, T.; de Wilde, P. The Interaction between Humans and Buildings for Energy Efficiency: A Critical Review. Energy Res. Soc. Sci. 2021, 71, 101828. [Google Scholar] [CrossRef]
- Murshed, M. An Empirical Analysis of the Non-Linear Impacts of ICT-Trade Openness on Renewable Energy Transition, Energy Efficiency, Clean Cooking Fuel Access and Environmental Sustainability in South Asia. Environ. Sci. Pollut. Res. 2020, 27, 36254–36281. [Google Scholar] [CrossRef]
- Li, Y.L.; Han, M.Y.; Liu, S.Y.; Chen, G.Q. Energy Consumption and Greenhouse Gas Emissions by Buildings: A Multi-Scale Perspective. Build. Environ. 2019, 151, 240–250. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A Review of Data-Driven Building Energy Consumption Prediction Studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Balvedi, B.F.; Ghisi, E.; Lamberts, R. A Review of Occupant Behaviour in Residential Buildings. Energy Build. 2018, 174, 495–505. [Google Scholar] [CrossRef]
- Buso, T.; Fabi, V.; Andersen, R.K.; Corgnati, S.P. Occupant Behaviour and Robustness of Building Design. Build. Environ. 2015, 94, 694–703. [Google Scholar] [CrossRef]
- Candanedo, L.M.; Feldheim, V.; Deramaix, D. Data Driven Prediction Models of Energy Use of Appliances in a Low-Energy House. Energy Build. 2017, 140, 81–97. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, Q. Simulating the Impact of Occupant Behavior on Energy Use of HVAC Systems by Implementing a Behavioral Artificial Neural Network Model. Energy Build. 2019, 198, 216–227. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, Q. Reinforcement Learning of Occupant Behavior Model for Cross-Building Transfer Learning to Various HVAC Control Systems. Energy Build. 2021, 238, 110860. [Google Scholar] [CrossRef]
- Gaetani, I.; Hoes, P.J.; Hensen, J.L.M. Occupant Behavior in Building Energy Simulation: Towards a Fit-for-Purpose Modeling Strategy. Energy Build. 2016, 121, 188–204. [Google Scholar] [CrossRef]
- Mathumitha, R.; Rathika, P.; Manimala, K. Intelligent Deep Learning Techniques for Energy Consumption Forecasting in Smart Buildings: A Review. Artif. Intell. Rev. 2024, 57, 35. [Google Scholar] [CrossRef]
- Luo, X.J.; Oyedele, L.O.; Ajayi, A.O.; Akinade, O.O.; Owolabi, H.A.; Ahmed, A. Feature Extraction and Genetic Algorithm Enhanced Adaptive Deep Neural Network for Energy Consumption Prediction in Buildings. Renew. Sustain. Energy Rev. 2020, 131, 109980. [Google Scholar] [CrossRef]
- Khan, Z.A.; Ullah, A.; Ullah, W.; Rho, S.; Lee, M.; Baik, S.W. Electrical Energy Prediction in Residential Buildings for Short-Term Horizons Using Hybrid Deep Learning Strategy. Appl. Sci. 2020, 10, 8634. [Google Scholar] [CrossRef]
- Becerra, J.A.; Lizana, J.; Gil, M.; Barrios-Padura, A.; Blondeau, P.; Chacartegui, R. Identification of Potential Indoor Air Pollutants in Schools. J. Clean. Prod. 2020, 242, 118420. [Google Scholar] [CrossRef]
- Hormigos Jiménez, S.; Padilla Marcos, M.Á.; Meiss, A.; Alonso Gonzalez Lezcano, R.; Feijó Muñoz, J. Ventilation Rate Determination Method for Residential Buildings According to TVOC Emissions from Building Materials. Build. Environ. 2017, 123, 555–563. [Google Scholar] [CrossRef]
- Jia, C.; Cao, K.; Valaulikar, R.; Fu, X.; Sorin, A.B. Variability of Total Volatile Organic Compounds (TVOC) in the Indoor Air of Retail Stores. Int. J. Environ. Res. Public Health 2019, 16, 4622. [Google Scholar] [CrossRef]
- Pei, J.; Ji, L. Secondary VOCs Emission from Used Fibrous Filters in Portable Air Cleaners and Ventilation Systems. Build. Environ. 2018, 142, 145–153. [Google Scholar] [CrossRef]
- Şahin, A.; Bayraktar, A.; Özcan, D.M.; Sevim, B.; Altunışık, A.C.; Türker, T. Dynamic Field Test, System Identification, and Modal Validation of an RC Minaret: Preprocessing and Postprocessing the Wind Induced Ambient Vibration Data. J. Perform. Constr. Facil. 2011, 25, 336–356. [Google Scholar] [CrossRef]
- D’Amico, A.; Pini, A.; Zazzini, S.; D’Alessandro, D.; Leuzzi, G.; Currà, E. Modelling VOC Emissions from Building Materials for Healthy Building Design. Sustainability 2021, 13, 184. [Google Scholar] [CrossRef]
- Rackes, A.; Waring, M.S. Using Multiobjective Optimizations to Discover Dynamic Building Ventilation Strategies That Can Improve Indoor Air Quality and Reduce Energy Use. Energy Build. 2014, 75, 272–280. [Google Scholar] [CrossRef]
- Piasecki, M.; Kozicki, M.; Firląg, S.; Goljan, A.; Kostyrko, K. The Approach of Including TVOCs Concentration in the Indoor Environmental Quality Model (IEQ)—Case Studies of BREEAM Certified Office Buildings. Sustainability 2018, 10, 3902. [Google Scholar] [CrossRef]
- Goletto, V.; Mialon, G.; Faivre, T.; Wang, Y.; Lesieur, I.; Petigny, N.; Vijapurapu, S. Formaldehyde and Total VOC (TVOC) Commercial Low-Cost Monitoring Devices: From an Evaluation in Controlled Conditions to a Use Case Application in a Real Building. Chemosensors 2020, 8, 8. [Google Scholar] [CrossRef]
- Bosilj, D.; Sakač, N. Chemical Sensors for Outdoor Air Quality Monitoring. Environ. Eng.-Inženjerstvo Okoliša 2023, 10, 59–71. [Google Scholar] [CrossRef]
- Devitofrancesco, A.; Belussi, L.; Meroni, I.; Scamoni, F. Development of an Indoor Environmental Quality Assessment Tool for the Rating of Offices in Real Working Conditions. Sustainability 2019, 11, 1645. [Google Scholar] [CrossRef]
- Ngo, N.T.; Pham, A.D.; Truong, T.T.H.; Truong, N.S.; Huynh, N.T.; Pham, T.M. An Ensemble Machine Learning Model for Enhancing the Prediction Accuracy of Energy Consumption in Buildings. Arab. J. Sci. Eng. 2022, 47, 4105–4117. [Google Scholar] [CrossRef]
- Moayedi, H.; Mosavi, A. Double-Target Based Neural Networks in Predicting Energy Consumption in Residential Buildings. Energies 2021, 14, 1331. [Google Scholar] [CrossRef]
- Yu, J.; Chang, W.S.; Dong, Y. Building Energy Prediction Models and Related Uncertainties: A Review. Buildings 2022, 12, 1284. [Google Scholar] [CrossRef]
- Chen, G.; Lu, S.; Zhou, S.; Tian, Z.; Kim, M.K.; Liu, J.; Liu, X. A Systematic Review of Building Energy Consumption Prediction: From Perspectives of Load Classification, Data-Driven Frameworks, and Future Directions. Appl. Sci. 2025, 15, 3086. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, K.; Ji, Z.; Shen, X.; Liu, P.; Zhang, L.; Wang, J.; Yao, J. Progress and Challenges of Integrated Machine Learning and Traditional Numerical Algorithms: Taking Reservoir Numerical Simulation as an Example. Mathematics 2023, 11, 4418. [Google Scholar] [CrossRef]
- Chou, J.S.; Nguyen, H.M. Simulating Long Term Energy Consumption Prediction in Campus Buildings through Enhanced Data Augmentation and Metaheuristic Optimized Artificial Intelligence. Energy Build. 2024, 312, 114191. [Google Scholar] [CrossRef]
- Edwards, R.E.; New, J.; Parker, L.E. Predicting Future Hourly Residential Electrical Consumption: A Machine Learning Case Study. Energy Build. 2012, 49, 591–603. [Google Scholar] [CrossRef]
- Foucquier, A.; Robert, S.; Suard, F.; Stéphan, L.; Jay, A. State of the Art in Building Modelling and Energy Performances Prediction: A Review. Renew. Sustain. Energy Rev. 2013, 23, 272–288. [Google Scholar] [CrossRef]
- Li, D.; Qi, Z.; Zhou, Y.; Elchalakani, M. Machine Learning Applications in Building Energy Systems: Review and Prospects. Buildings 2025, 15, 648. [Google Scholar] [CrossRef]
- Mienye, I.D.; Swart, T.G. A Comprehensive Review of Deep Learning: Architectures, Recent Advances, and Applications. Information 2024, 15, 755. [Google Scholar] [CrossRef]
- Paterakis, N.G.; Mocanu, E.; Gibescu, M.; Stappers, B.; van Alst, W. Deep Learning versus Traditional Machine Learning Methods for Aggregated Energy Demand Prediction. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Turin, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Bedi, G.; Venayagamoorthy, G.K.; Singh, R. Development of an IoT-Driven Building Environment for Prediction of Electric Energy Consumption. IEEE Internet Things J. 2020, 7, 4912–4921. [Google Scholar] [CrossRef]
- Jia, M.; Komeily, A.; Wang, Y.; Srinivasan, R.S. Adopting Internet of Things for the Development of Smart Buildings: A Review of Enabling Technologies and Applications. Autom. Constr. 2019, 101, 111–126. [Google Scholar] [CrossRef]
- Minoli, D.; Sohraby, K.; Occhiogrosso, B. IoT Considerations, Requirements, and Architectures for Smart Buildings—Energy Optimization and Next-Generation Building Management Systems. IEEE Internet Things J. 2017, 4, 269–283. [Google Scholar] [CrossRef]
- Marinakis, V.; Doukas, H. An Advanced IoT-Based System for Intelligent Energy Management in Buildings. Sensors 2018, 18, 610. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.N.; Iqbal, N.; Ahmad, R.; Kim, D.H. Ensemble Prediction Approach Based on Learning to Statistical Model for Efficient Building Energy Consumption Management. Symmetry 2021, 13, 405. [Google Scholar] [CrossRef]
- Ardabili, S.; Abdolalizadeh, L.; Mako, C.; Torok, B.; Mosavi, A. Systematic Review of Deep Learning and Machine Learning for Building Energy. Front. Energy Res. 2022, 10, 786027. [Google Scholar] [CrossRef]
- Fan, C.; Sun, Y.; Xiao, L.; Ma, J.; Lee, D.; Wang, J.; Tseng, Y. Statistical Investigations of Transfer Learning-Based Methodology for Short-Term Building Energy Predictions. Appl. Energy 2020, 262, 114499. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Sulaimon, I.; Sunmola, F.; Ajayi, S. Building Energy Consumption Prediction for Residential Buildings Using Deep Learning and Other Machine Learning Techniques. J. Build. Eng. 2022, 45, 103406. [Google Scholar] [CrossRef]
- Lu, H.; Cheng, F.; Ma, X.; Hu, G. Short-Term Prediction of Building Energy Consumption Employing an Improved Extreme Gradient Boosting Model: A Case Study of an Intake Tower. Energy 2020, 203, 117756. [Google Scholar] [CrossRef]
- Villano, F.; Mauro, G.M.; Pedace, A. A Review on Machine/Deep Learning Techniques Applied to Building Energy Simulation, Optimization and Management. Thermo 2024, 4, 100–139. [Google Scholar] [CrossRef]
- Liu, H.; Liang, J.; Liu, Y.; Wu, H. A Review of Data-Driven Building Energy Prediction. Buildings 2023, 13, 532. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Owolabi, H.; Akanbi, L.; Ganiyu, S. Data-Driven Tools for Building Energy Consumption Prediction: A Review. Energies 2023, 16, 2574. [Google Scholar] [CrossRef]
- El Maghraoui, A.; Ledmaoui, Y.; Laayati, O.; El Hadraoui, H.; Chebak, A. Smart Energy Management: A Comparative Study of Energy Consumption Forecasting Algorithms for an Experimental Open-Pit Mine. Energies 2022, 15, 4569. [Google Scholar] [CrossRef]
- Parizad, B.; Ranjbarzadeh, H.; Jamali, A.; Khayyam, H. An Intelligent Hybrid Machine Learning Model for Sustainable Forecasting of Home Energy Demand and Electricity Price. Sustainability 2024, 16, 2328. [Google Scholar] [CrossRef]
- Li, J.; Yu, Z.J.; Haghighat, F.; Zhang, G. Development and Improvement of Occupant Behavior Models towards Realistic Building Performance Simulation: A Review. Sustain. Cities Soc. 2019, 50, 101685. [Google Scholar] [CrossRef]
- Mariano-Hernández, D.; Hernández-Callejo, L.; García, F.S.; Duque-Perez, O.; Zorita-Lamadrid, A.L. A Review of Energy Consumption Forecasting in Smart Buildings: Methods, Input Variables, Forecasting Horizon and Metrics. Appl. Sci. 2020, 10, 8323. [Google Scholar] [CrossRef]
- Wang, R.; Lu, S.; Feng, W. A Novel Improved Model for Building Energy Consumption Prediction Based on Model Integration. Appl. Energy 2020, 262, 114561. [Google Scholar] [CrossRef]
- Tahmasebinia, F.; Lin, L.; Wu, S.; Kang, Y.; Sepasgozar, S. Exploring the Benefits and Limitations of Digital Twin Technology in Building Energy. Appl. Sci. 2023, 13, 8814. [Google Scholar] [CrossRef]
- Ding, Y.; Fan, L.; Liu, X. Analysis of Feature Matrix in Machine Learning Algorithms to Predict Energy Consumption of Public Buildings. Energy Build. 2021, 249, 111208. [Google Scholar] [CrossRef]
- Ahmad, T.; Chen, H.; Huang, R.; Guo, Y.; Wang, J.; Shair, J.; Akram, H.; Mohsan, S.A.H.; Kazim, M. Supervised Based Machine Learning Models for Short, Medium and Long-Term Energy Prediction in Distinct Building Environment. Energy 2018, 158, 17–32. [Google Scholar] [CrossRef]
- Benti, N.E.; Chaka, M.D.; Semie, A.G. Forecasting Renewable Energy Generation with Machine Learning and Deep Learning: Current Advances and Future Prospects. Sustainability 2023, 15, 7087. [Google Scholar] [CrossRef]
- Chou, J.S.; Tran, D.S. Forecasting Energy Consumption Time Series Using Machine Learning Techniques Based on Usage Patterns of Residential Householders. Energy 2018, 165, 709–726. [Google Scholar] [CrossRef]
- Lim, S.C.; Huh, J.H.; Hong, S.H.; Park, C.Y.; Kim, J.C. Solar Power Forecasting Using CNN-LSTM Hybrid Model. Energies 2022, 15, 8233. [Google Scholar] [CrossRef]
- Arowoiya, V.A.; Onososen, A.O.; Moehler, R.C.; Fang, Y. Influence of Thermal Comfort on Energy Consumption for Building Occupants: The Current State of the Art. Buildings 2024, 14, 1310. [Google Scholar] [CrossRef]
- Baldi, S.; Karagevrekis, A.; Michailidis, I.T.; Kosmatopoulos, E.B. Joint Energy Demand and Thermal Comfort Optimization in Photovoltaic-Equipped Interconnected Microgrids. Energy Convers. Manag. 2015, 101, 352–363. [Google Scholar] [CrossRef]
- Korkas, C.D.; Baldi, S.; Michailidis, I.; Kosmatopoulos, E.B. Intelligent Energy and Thermal Comfort Management in Grid Connected Photovoltaic Equipped Microgrids with Heterogeneous Occupancy Schedule. Appl. Energy 2015, 149, 194–203. [Google Scholar] [CrossRef]
- Korkas, C.D.; Baldi, S.; Michailidis, I.; Kosmatopoulos, E.B. Occupancy Based Demand Response and Thermal Comfort Optimization in Microgrids with Renewable Energy Sources and Energy Storage. Appl. Energy 2016, 163, 93–104. [Google Scholar] [CrossRef]
- Anvari Moghaddam, A.; Chakraborty, G.; Ahmadi, P.; Mohamed, A. Efficient Energy Management for a Grid Tied Residential Microgrid. IET Gener. Transm. Distrib. 2016, 10, 2752–2761. [Google Scholar] [CrossRef]
- Langevin, J.; Wen, J.; Gurian, P.L. Quantifying the Human–Building Interaction: Considering the Active, Adaptive Occupant in Building Performance Simulation. Energy Build. 2016, 117, 372–386. [Google Scholar] [CrossRef]
- Natarajan, Y.; KR, S.P.; Wadhwa, G.; Choi, Y.; Chen, Z.; Lee, D.E.; Mi, Y. Enhancing Building Energy Efficiency with IoT-Driven Hybrid Deep Learning Models for Accurate Energy Consumption Prediction. Sustainability 2024, 16, 1925. [Google Scholar] [CrossRef]
- Hussien, A.; Maksoud, A.; Al-Dahhan, A.; Abdeen, A.; Baker, T. Machine Learning Model for Predicting Long-Term Energy Consumption in Buildings. Discov. Internet Things 2025, 5, 18. [Google Scholar] [CrossRef]
- Gorzałczany, M.B.; Rudziński, F. Energy Consumption Prediction in Residential Buildings—An Accurate and Interpretable Machine Learning Approach Combining Fuzzy Systems with Evolutionary Optimization. Energies 2024, 17, 3242. [Google Scholar] [CrossRef]
- Alali, Y.; Harrou, F.; Sun, Y. Unlocking the Potential of Wastewater Treatment: Machine Learning Based Energy Consumption Prediction. Water 2023, 15, 2349. [Google Scholar] [CrossRef]
- Shakeel, H.M.; Iram, S.; Hill, R.; Athar Farid, H.M.; Sheikh-Akbari, A.; Saleem, F. A Machine Learning-Based Intelligent Framework for Predicting Energy Efficiency in Next-Generation Residential Buildings. Buildings 2025, 15, 1275. [Google Scholar] [CrossRef]
- Pham, A.D.; Ngo, N.T.; Truong, T.T.H.; Huynh, N.T.; Truong, N.S. Predicting Energy Consumption in Multiple Buildings Using Machine Learning for Improving Energy Efficiency and Sustainability. J. Clean. Prod. 2020, 260, 121082. [Google Scholar] [CrossRef]
- Hua, Q.; Fan, Z.; Mu, W.; Cui, J.; Xing, R.; Liu, H.; Gao, J. A Short-Term Power Load Forecasting Method Using CNN-GRU with an Attention Mechanism. Energies 2025, 18, 106. [Google Scholar] [CrossRef]
- Henriques, L.; Castro, C.; Prata, F.; Leiva, V.; Venegas, R. Modeling Residential Energy Consumption Patterns with Machine Learning Methods Based on a Case Study in Brazil. Mathematics 2024, 12, 1961. [Google Scholar] [CrossRef]
- Decorte, T.; Mortier, S.; Lembrechts, J.J.; Meysman, F.J.; Latré, S.; Mannens, E.; Verdonck, T. Missing Value Imputation of Wireless Sensor Data for Environmental Monitoring. Sensors 2024, 24, 2416. [Google Scholar] [CrossRef] [PubMed]
- Haroon, S.; Khan, M. Preptimize: Automation of Time-Series Data Preprocessing and Forecasting. Algorithms 2024, 17, 332. [Google Scholar] [CrossRef]
- Falchi, F.; Girardi, M.; Gurioli, G.; Messina, N.; Padovani, C.; Pellegrini, D. Deep Learning and Structural Health Monitoring: Temporal Fusion Transformers for Anomaly Detection in Masonry Towers. Mech. Syst. Signal Process. 2024, 215, 111382. [Google Scholar] [CrossRef]
- Cai, W.; Wen, X.; Li, C.; Shao, J.; Xu, J. Predicting the Energy Consumption in Buildings Using the Optimized Support Vector Regression Model. Energy 2023, 276, 127188. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, H.; Xia, L.; Zou, Z.; Soares, C.G. Kernel-Based Support Vector Regression for Nonparametric Modeling of Ship Maneuvering Motion. Ocean Eng. 2020, 216, 107994. [Google Scholar] [CrossRef]
- Yin, Q.; Han, C.; Li, A.; Liu, X.; Liu, Y. A Review of Research on Building Energy Consumption Prediction Models Based on Artificial Neural Networks. Sustainability 2024, 16, 7805. [Google Scholar] [CrossRef]
- Meng, Y.; Sun, Y.; Rodriguez, S.; Xue, B. Transforming Building Energy Management: Sparse, Interpretable, and Transparent Hybrid Machine Learning for Probabilistic Classification and Predictive Energy Modelling. Architecture 2025, 5, 24. [Google Scholar] [CrossRef]
- Azeez, N.A.; Misra, S.; Ogaraku, D.O.; Abidoye, A.P. A Predictive Model for Benchmarking the Performance of Algorithms for Fake and Counterfeit News Classification in Global Networks. Sensors 2024, 24, 5817. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Wang, Q.; Lu, H. A Novel Stacking Ensemble Learner for Predicting Residual Strength of Corroded Pipelines. NPJ Mater. Degrad. 2024, 8, 87. [Google Scholar] [CrossRef]
- Huang, H.; Fang, Z.; Xu, Y.; Zhao, Z. Stacking–Preprocessing Ridge Regression for Near-Infrared Spectral Analysis. Talanta 2024, 276, 126242. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, B.; Li, S.; Shi, Z.; Yin, D.; Wu, Q.; Zhang, F.; Yun, X.; Huang, G.; Zhu, Y.; et al. Tracking County-Level Cooking Emissions and Their Drivers in China from 1990 to 2021 by Ensemble Machine Learning. Earth Syst. Sci. Data Discuss. 2025, preprint. [Google Scholar] [CrossRef]
- Ranjbaran, G.; Recupero, D.R.; Roy, C.K.; Schneider, K.A. C-SHAP: A Hybrid Method for Fast and Efficient Interpretability. Appl. Sci. 2025, 15, 672. [Google Scholar] [CrossRef]
- Chowdhury, S.; Ahsan, M.; Barraclough, P. Applications of Linear and Ensemble-Based Machine Learning for Predicting Winning Teams in League of Legends. Appl. Sci. 2025, 15, 5241. [Google Scholar] [CrossRef]
- Ahn, J.M.; Kim, J.; Kim, K. Ensemble Machine Learning of Gradient Boosting (XGBoost, LightGBM, CatBoost) and Attention-Based CNN-LSTM for Harmful Algal Blooms Forecasting. Toxins 2023, 15, 608. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, M.C.J.; Postolache, O.; Cercas, F. Unobtrusive Cardio-Respiratory Assessment for Different Indoor Environmental Conditions. IEEE Sens. J. 2022, 22, 23243–23257. [Google Scholar] [CrossRef]
- Tsang, T.W.; Mui, K.W.; Wong, L.T.; Chan, A.C.Y.; Chan, R.C.W. Real-Time Indoor Environmental Quality (IEQ) Monitoring Using an IoT-Based Wireless Sensing Network. Sensors 2024, 24, 6850. [Google Scholar] [CrossRef] [PubMed]
- Abbaspour, A.; Bahadori-Jahromi, A.; Janbey, A.; Godfrey, P.B.; Amirkhani, S. Enhancing Indoor Air Quality and Regulatory Compliance: An In-Depth Comparative Study on Ventilation Strategies and Their Impact on SARS-CoV-2 Transmission Risk. Sustainability 2024, 16, 271. [Google Scholar] [CrossRef]
- Correia, V.; Silva, P.D.; Pires, L.C. Energy Requirements and Photovoltaic Area for Atmospheric Water Generation in Different Locations: Lisbon, Pretoria, and Riyadh. Energies 2023, 16, 5201. [Google Scholar] [CrossRef]
- Gao, J.; Duan, C.; Song, J.; Ma, L.; Cai, W. PM2.5 Can Help Adjust Building’s Energy Consumption. J. Environ. Manag. 2023, 331, 117235. [Google Scholar] [CrossRef]
- Wang, Z.; Srinivasan, R.S. A Review of Artificial Intelligence Based Building Energy Use Prediction: Contrasting the Capabilities of Single and Ensemble Prediction Models. Renew. Sustain. Energy Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Fu, N.; Kim, M.K.; Chen, B.; Sharples, S. Comparative Modelling Analysis of Air Pollutants, PM2.5 and Energy Efficiency Using Three Ventilation Strategies in a High-Rise Building: A Case Study in Suzhou, China. Sustainability 2021, 13, 8453. [Google Scholar] [CrossRef]
- A G, P.V.; K, A.K.; Varadarajan, V. Estimating Software Development Efforts Using a Random Forest-Based Stacked Ensemble Approach. Electronics 2021, 10, 1195. [Google Scholar] [CrossRef]
- Cheng, J.; Li, X. Predicting Carbon Dioxide Emissions Using Deep Learning and Ninja Meta-Heuristic Optimization. Sci. Rep. 2025, 15, 628. [Google Scholar]
- Mugware, F.W.; Ravele, T.; Sigauke, C. Short-Term Predictions of Global Horizontal Irradiance Using Recurrent Neural Networks, Support Vector Regression, Gradient Boosting Random Forest and Advanced Stacking Ensemble Approaches. Computation 2025, 13, 72. [Google Scholar] [CrossRef]
- Siregar, S.; Sagala, D. Improving Food Demand Forecasting through Stacked Regression. Int. J. Intell. Syst. Appl. Eng. 2023, 11, 898–903. [Google Scholar]
- Alsharekh, M.F.; Habib, S.; Dewi, D.A.; Albattah, W.; Islam, M.; Albahli, S. Improving the Efficiency of Multistep Short-Term Electricity Load Forecasting via R-CNN with ML-LSTM. Sensors 2022, 22, 6913. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, J.; Li, X.; Zhang, Y. Long-Term Power Load Forecasting Using LSTM-Informer with Ensemble Learning. Electronics 2023, 12, 2175. [Google Scholar] [CrossRef]
- Qureshi, M.; Arbab, M.A.; Rehman, S. Deep learning-based forecasting of electricity consumption. Sci. Rep. 2024, 14, 6489. [Google Scholar] [CrossRef]
- Al-Ali, E.M.; Hajji, Y.; Said, Y.; Hleili, M.; Alanzi, A.M.; Laatar, A.H.; Atri, M. Solar Energy Production Forecasting Based on a Hybrid CNN-LSTM-Transformer Model. Mathematics 2023, 11, 676. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).