Imbalance Charge Reduction in the Italian Intra-Day Market Using Short-Term Forecasting of Photovoltaic Generation

Abstract

In the Italian intra-day electricity market (MI-XBID), where energy positions can be adjusted up to one hour before delivery, imbalance charges due to forecast errors from non-programmable renewable sources represent a critical issue. This work focuses on photovoltaic (PV) systems, whose production variability makes them particularly sensitive to forecast accuracy. To address these challenges, a comprehensive methodology for assessing and mitigating imbalance penalties by integrating a short-term PV forecasting model with a battery energy storage system is proposed. Unlike conventional approaches that focus exclusively on improving statistical accuracy, this study emphasizes the economic and regulatory impact of forecast errors under the current Italian imbalance settlement framework. A hybrid physical-artificial neural network is developed to forecast PV power one hour in advance, combining historical production data and clear-sky irradiance estimates. The resulting imbalances are analyzed using regulatory tolerance thresholds. Simulation results show that, by adopting a control strategy aimed at maintaining the battery’s state of charge around 50%, imbalance penalties can be completely eliminated using a storage system sized for just over 2 equivalent hours of storage capacity. The methodology provides a practical tool for market participants to quantify the benefits of storage integration and can be generalized to other electricity markets where tolerance bands for imbalances are applied.

1. Introduction

Renewable energy has made significant progress, particularly in the solar PV and wind sectors, where production and installation costs have substantially decreased. These dynamics persist, fostering investment from both public and private actors and contributing to further cost reductions and improved productivity levels [1]. In line with this trend, the International Energy Agency projects that PV energy will become the leading source in the renewable energy mix by 2030 [2]. In this context, system integration has become a key topic in public policy discussions, with particular focus on forecasting errors. In fact, inaccurate PV power forecasts can lead to power imbalances, compromising grid stability, disrupting market efficiency, and complicating real-time load management.

In response to these emerging challenges, the European regulatory framework has evolved to enhance market efficiency and flexibility. A key advance is the Regulation (EU) 2015/1222 (CACM), which established the Single Intra-Day Coupling (SIDC) to facilitate more dynamic and integrated intraday electricity trading across member states. This regulation introduced continuous trading in intra-day markets (IDM) with closure at least one hour before delivery (H-1), contingent upon the availability of sufficient cross-border transmission capacity. The SIDC was implemented through the Cross-Border Intraday (XBID) project, operational in Central Europe since 2018. Italy joined the SIDC in September 2021, aligning its IDM with the European framework. This integration allowed Italian market participants to access continuous cross-border trading until H-1 and led to a reorganization of the national IDM [3]. This shift in regulatory and operational paradigms has been further amplified by the widespread deployment of non-programmable renewable energy sources (NP-RES), which has redirected attention from day-ahead markets (DAM), where prices are primarily influenced by generation costs, to IDM, where pricing dynamics are increasingly driven by real-time grid conditions and system imbalances. As a result, dispatching users, and in particular wholesalers, must adopt strategies and tools to manage the variability between scheduled and actual injections, minimizing the risk of imbalances. In this context, increasingly accurate PV power forecasting methods were explored and adopted by load-serving entities and balancing authorities to optimize both market and system operations [4]. A wide range of forecasting approaches has been proposed in the literature, including regression methods, artificial intelligence techniques, numerical weather prediction models, local sensing, and hybrid systems [5,6,7,8,9,10]. Among these, hybrid forecasting models have gained increasing attention due to their ability to combine the strengths of physical and data-driven approaches [7,9,10]. However, the aforementioned studies focused on short-term PV power forecasting do not address any aspects related to the IDM. Consequently, they overlook market-specific regulations and do not evaluate the impact of forecast errors on imbalance costs or trading strategies within the MI-XBID framework.

Some studies have proposed forecasting tools aimed at supporting participation in the IDM, to improve trading strategies and reduce forecast uncertainty [11,12,13,14,15]. However, these works typically focus on the development of forecasting models without considering the specific regulatory frameworks that govern IDM operations. In most cases, performance is evaluated solely using statistical error metrics such as normalized Root Mean Square Error (nRMSE) and Mean Absolute Error (MAE), without assessing how forecast errors relate to market rules and imbalance settlement mechanisms. This highlights a broader limitation in the PV forecasting literature, where minimizing prediction errors is often prioritized over evaluating their financial implications. Moreover, there are some important aspects from the perspective of market bidding strategies to be investigated. In detail, it is necessary to understand whether more accurate forecasting models, measured through statistical error metrics, lead to greater economic benefits for market participants and compliance with market rules. Therefore, it is necessary to investigate the relationship between forecast errors and imbalance penalties. To date, only a limited number of studies have addressed this issue in depth [4,16,17,18,19,20]. The reviewed contributions adopt different perspectives. Some works, such as [17,20], focus on optimizing forecasting accuracy and bidding strategies specifically for the DAM, often within incentive-based regulatory frameworks. Other studies, like [21], explore speculative trading strategies in IDM, leveraging forecast errors for arbitrage without considering physical constraints or storage. Papers like [4,19] assess the economic value of forecasts or the long-term implications of market design, emphasizing profit maximization rather than imbalance mitigation. Among the reviewed works, only [18] explicitly refers to the Italian electricity market; however, it is based on a regulatory context from 2015, which no longer reflects the current structure of the Italian imbalance settlement system.

To the best of the authors’ knowledge, forecasting in the context of the MI-XBID continuous trading session, particularly relevant in the Italian IDM, has not been further investigated in recent literature.

The present study addresses this gap by providing a methodology that allows for reducing charge imbalances in the Italian IDM, which is based on the use of a hybrid neural network model, called Hybrid Physical-Artificial Neural Network (HPANN) [21], to short-term forecast the power output of PV plants, with a forecast horizon of 1 h. Specifically, the Clear Sky solar radiation Model (CSM) is used as an input to the ANN to enhance the model’s predictive performance. This type of model estimates the amount of solar radiation reaching the Earth’s surface under cloud-free conditions, providing a theoretical upper limit that helps improve the forecasting performance [22]. Moreover, in order to reduce imbalances and thus avoid penalties, the methodology involves the use of a battery with a suitable capacity value and a control charge/discharge strategy. By tackling the challenges posed by short-term market participation, this approach promotes a more sustainable, flexible, and decarbonized electricity system, in line with the objectives of the energy transition. Unlike many contributions that focus solely on statistical accuracy or speculative strategies, this work is among the few that assess forecasting models in real-world operational contexts, explicitly accounting for the latest imbalance settlement mechanisms currently in force in the Italian electricity market.

The paper is structured as follows. Section 1 presents a preliminary analysis of the problem and provides a concise review of relevant literature, highlighting the research gap that this study aims to address. Section 2 offers a more detailed examination of short-term PV power forecasting approaches and IDM-oriented methodologies. Section 3 describes the structure and regulatory framework of the Italian electricity market. Section 4 outlines the proposed methodology for evaluating and mitigating imbalance charges. Section 5 presents the case study, including the dataset, the design of the HPANN, and the results obtained by integrating a battery storage system to reduce imbalances. Finally, Section 6 provides the conclusions of the study.

2. Short-Term PV Power Forecasting and IDM-Oriented Methodologies

This section focuses on works addressing short-term PV power forecasting, with special attention to studies explicitly aimed at supporting participation in the IDM. The section explores various forecasting methodologies that have been proposed for IDM applications, evaluating their accuracy, implementation strategies, and limitations in terms of market integration and economic impact assessment.

Recent review articles on PV power forecasting [5,6,7,8,9,10] revealed that, among the various forecasting methods available, hybrid approaches consistently offer the best performance in terms of accuracy and reliability. In particular, deep neural networks with ensemble techniques or hybrid techniques supersede the traditional approaches of PV power forecasting in terms of efficiency and accuracy [10]. In [7], a comprehensive review of supervised machine-learning (ML) for PV power forecasting highlighted that hybrid forecasting methods are more prevalent and generally outperform conventional approaches. Similarly, Ref. [9], which presents a state-of-the-art review of the five most popular and advanced ANN models for PV power forecasting, highlights that hybrid models demonstrate superior performance over standalone approaches in terms of accuracy, resilience, and flexibility. In particular, a hybrid approach, such as an ANN combined with a physical model, similar to the approach employed in this work, can offer more precise and reliable predictions under both stable and variable weather conditions across different time horizons [10].

Among the various forecasting techniques analyzed in the literature, particular attention has been devoted to Artificial Neural Networks (ANNs) [5,8,10,23], which are widely recognized for their effectiveness in modeling the nonlinear behavior of PV systems and enabling accurate short-term PV power predictions. In [8], the accuracy of two prediction models has been compared: the ML model, most applied through ANNs and deep-learning (DL) models with Long-Short Term Memory (LSTM) networks. The analysis of the results in the case of three short-term prediction horizons (1, 15, and 60 min) showed that LSTM models obtain better overall prediction accuracy, except for the 60 min prediction horizon, where the accuracy of the two methods is comparable, with a nRMSE < 10%. This shows how ANNs and DL networks can both be used for PV power forecasting with a forecast horizon of one hour without losing performance. However, the choice between these two architectures depends on the specific application needs. Notably, ML methods are widely applied in industrial settings to develop data-driven models of nonlinear systems or plants [23] due to their ability to approximate with the desired accuracy any nonlinear function based on a suitable set of experimental data [5].

However, several factors can be considered to make ANN an effective and practical solution compared to other ML algorithms. Some reasons are [8,10]:

• the ability to model complex non-linearities;
• robustness and adaptability, ANNs can operate under different operating and environmental conditions, making them adaptable to variations in input data;
• computational efficiency, traditional ANNs require far fewer computational resources than other DL algorithms;
• simplified implementation, the almost simple structure of ANNs facilitates their implementation and maintenance, making them a practical choice for industrial applications where simplicity and reliability are crucial;
• better performance with limited data, ANNs typically require fewer training samples than other DL approaches to reach convergence.

These features are particularly useful when historical data is sparse or noisy, a common challenge in PV forecasting. For these reasons, using an ANN for the forecast of PV power generation is a choice that balances accuracy, computational efficiency, and simplicity of implementation, making it a practical and effective solution for applications in the Italian continuous IDM. The MI-XBID market, in fact, requires adjustments to energy bids close to the time of delivery to mitigate imbalances. The lightweight nature of ANNs makes them more practical for integration into energy trading platforms that require fast computation and regular model retraining.

Beyond general forecasting approaches, only a subset of recent studies have focused on developing predictive models specifically designed to support participation in the IDM [11,12,13,14,15] to improve trading strategies and mitigate the impact of forecast uncertainty on market operations. In [11], a forecasting tool based on DL models (CNN and Transformer) has been proposed. It aimed to support the participation of PV plants in energy markets (DAM and IDM), achieving an accuracy improvement of up to 32.45% in the forecasting of energy produced due to the use of the Transformer model and the limited use of only two meteorological inputs (cloud cover and temperature), with better results for the aggregate forecast than for individual plants. In [12], a hybrid ensemble model for intra-day PV power forecasting (1–6 H ahead) has been tested on two Austrian sites. The model achieves an nRMSE equal to 8.4% and a normalized MAE equal to 5.3% for one H-1 forecast, outperforming benchmark models across all tested horizons. The study developed in [13] is based on a probabilistic H-1 solar power forecasting model for a 317 kW PV plant in Poland, comparing four LSTM-based architectures. The LSTM-Autoencoder model was found to be the most reliable, achieving an average RMSE of 15.59 kW (4.9% of peak power) and an average MAE of 8.36 kW (2.6%) over 100 runs. Study [15] proposed an intra-day PV power forecasting strategy for Virtual Power Plants (VPP) based on the LSTM—recurrent neural networks (LSTM-RNNs) and an indirect approach in which the irradiance is forecasted first and the output power is calculated by using the PV model. The global MAE committed was 137.21 W in a PV facility of 2.97 kWp. In [15], a probabilistic model has been used for forecasting PV power. The model can be well-suited for trading in DAM and IDM since it is based on an advanced version of the Analog Ensemble method that enables performance comparable to state-of-the-art methods, but with significantly shorter computation time. Although all these studies propose forecasting models for IDM applications, they generally assess performance using statistical error metrics such as nRMSE and MAE, without considering market rules or imbalance settlement mechanisms.

This reflects a common limitation in the literature, where prediction accuracy is prioritized over an evaluation of the actual market impact. Yet, from a market perspective, the link between forecast accuracy and charge imbalance costs is not always linear [16] and has been explored in only a few contributions [4,16,17,18,19,20]. Specifically, in [4], the role of power forecasting models in smart micro-grids was investigated by introducing a profit forecasting technique as a key driver of micro-grid deployment success, and presented the liberalized electricity market based on blockchain technologies as a new paradigm promoted by micro-grids with specific regard to regulations and standards. However, the approach is more oriented toward profit optimization through market mechanisms rather than the reduction of penalties resulting from forecast-realization discrepancies. In [16], the authors determine the impact of PV power forecasting in the Iberian DAM. The study investigates several day-ahead forecasting models for a 1.86 MW PV plant, testing different input configurations and methodologies. The most effective model, an SVR trained with numerical weather prediction (NWP) data, achieved an nRMSE of 22.54% and delivered the highest economic return. Specifically, it generated an annual forecasting value of €4788 compared to a two-day persistence baseline in the Iberian DAM. However, authors concluded that certain models with slightly higher error metrics also produced greater profits, highlighting the need to consider market dynamics, not just forecast accuracy, when assessing the true economic value of prediction models. Finally, they did not analyze the IDM. In [17], the forecasting of the power output of a PV system located in Apulia, South East of Italy, at different forecasting horizons has been presented. An analysis has been carried out to evaluate the imbalance penalties associated with three forecasting models. This study dates back to 2015, a period in which the regulatory context differed substantially from today’s framework. The work [18] investigated the expected cost of inaccurate forecasts in the Scandinavian energy markets and how the past, present, and future energy market and imbalance settlement structures impact the value of the forecast and incentive for producers to provide accurate forecasts. Forecasts have been generated by the smart persistence model and a state-of-the-art NWP model from the European Centre for Medium-Range Weather Forecasts. The results have shown that for the IDM, both forecast models achieve high accuracy. Moreover, the estimated income and income losses are dependent on the electricity mix of the bidding areas. In addition, the transition from the dual-price to the single-price imbalance settlement structure reduces the value of providing accurate forecasts. However, this work focuses on long-term economic implications and is based on incentive market models. Another relevant contribution in the field of optimal energy market participation by distributed energy resources is presented in [19]. It is focused on the optimal bidding strategy, that is, the amount of power the VPP commits to supply. A multistage stochastic optimization model for a VPP operating in the South Korean DAM has been developed. The study is set in an incentive-based market, where rewards are given for accurate delivery within defined limits. The model updates intraday decisions every three hours and uses heuristics to ensure real-time applicability. Compared to the present study, the approach proposed in [19] targets the DAM bidding process. Although both papers address the problem of forecast uncertainty and its economic consequences in IDM, the Italian framework is based on penalizing imbalances, while the South Korean one is based on incentivizing the system. Overall, although the aims differ, both contributions highlight the importance of advanced forecasting models and optimization strategies to mitigate the impact of uncertainty in RES-based systems. An important contribution is also given by [20], where the authors investigated speculative trading strategies in the German continuous IDM, exploiting forecast errors of RESs to generate arbitrage profits without relying on physical assets. Their approach uses a parametric policy triggered by intraday forecast updates of aggregated VRES output and evaluates a trading strategy based on detailed limit order book data. Results show that the strategy yields significant profits, highlighting inefficiencies in the IDM and suggesting a potential “arms race” in forecast quality. Their work does not account for physical imbalances or storage dynamics, but it is based purely on price signals.

3. Structure and Regulatory Framework of the Italian Electricity Market

To understand the dynamics of power imbalances and their management, it is essential to first examine the structure and functioning of electricity markets, as well as the relevant regulatory frameworks that govern them.

The Italian IDM operates as the second phase of the spot electricity market, beginning after the closure of the DAM [3]. It enables market participants to adjust their injection or withdrawal schedules by submitting buy and sell offers up to one hour before physical energy delivery. Like the DAM, the IDM adopts a zonal structure, thereby accounting for transmission constraints between market zones. Historically, the IDM was composed of seven auction sessions that allowed energy trading up to four hours before delivery, with clearing achieved through the intersection of supply and demand curves. Since September 2021, Italy has been integrated into the SIDC, which introduced continuous cross-border trading via the MI-XBID platform. As a result, the Italian IDM now follows a hybrid model combining continuous trading, available from 15:30 of the previous day until one hour before delivery, with three daily auction sessions. During auction windows, continuous trading is temporarily suspended 50 min before closure. In continuous trading, unlike the auction-based mechanism, the Italian Market Operator does not act as a central counterparty, allowing market participants to trade bilaterally across European bidding zones, contingent on available transmission capacity.

Each dispatching user is required to submit a schedule regarding their energy injections into the grid (for plants with a capacity below 10 MVA, the schedule is submitted in aggregated form). This schedule is traded on the DAM, can be modified on the IDM, and may be further adjusted on the Dispatching Services Market (DSM), though this last modification applies only to units authorized to participate in the DSM and therefore excludes RESs.

At the end of the market processes, the final schedule is referred to as “Programma Vincolante Modificato e Corretto” (PVMC), that is, “Modified and Corrected Binding Schedule”. This is the schedule that the dispatching user is obligated to follow. The difference between the actual injected energy and the PVMC is known as the imbalance. This imbalance, measured in MWh, can be either positive or negative. A positive imbalance occurs when the injected energy exceeds the scheduled amount, meaning the producer delivers more electricity than planned. A negative imbalance, on the other hand, occurs when the actual injection is lower than scheduled, resulting in a shortfall that the system operator must compensate through upward balancing actions. In both cases, the dispatching user is financially responsible for the imbalance: they either receive a lower remuneration for excess energy (in the case of a positive imbalance) or are required to pay an imbalance charge for the missing energy (in the case of a negative imbalance), based on the applicable imbalance pricing rules.

The current imbalance settlement framework in Italy provides for three distinct pricing regimes, depending on the type of generation unit, even when these units belong to the same imbalance pricing zone [24]. Enabled units are those authorized to participate in the DSM and are subject to a dual-pricing mechanism [25] that reflects both the unit’s imbalance and the macro-zonal system imbalance. In contrast, non-enabled units, which include most renewable energy plants, are not allowed to participate in the DSM and are instead subject to a single-pricing scheme, where the imbalance price depends solely on the overall zonal imbalance. Within this latter category, NP-RES, such as PV, are treated with additional specificity: two alternative settlement options are provided, which must be selected annually by each dispatching user [26].

Under Option I, which is standard single-pricing without tolerance bands, the entire imbalance is valued at market prices according to the conventional rules for non-enabled units. This option does not provide any differentiation for NP-RES and can expose producers to high financial risks.

Conversely, Option II, specifically designed for NP-RES, introduces tolerance bands that define a range around the scheduled production, within which deviations are treated differently. The tolerance band widths (α) are expressed as a percentage of the final corrected binding schedule (PVMC), and their width depends on the energy source and plant size, as follows:

-

Wind plant with a peak power greater than 10 MW: α = 49% of PVMC;

-

Solar plant with a peak power greater than 10 MW: α = 31% of PVMC;

-

Wind plant with a peak power lower than or equal to 10 MW: α = 8% of PVMC;

-

Solar plant with a peak power lower than or equal to 10 MW: α = 8% of PVMC;

-

Run-of-river hydro: α = 8% of PVMC;

-

Other NP-RESs: α = 1.5% of PVMC.

This option can be considered a hybrid model due to the presence of the zonal balancing component, which adjusts the applied price based on the sign of the unit’s imbalance [24]. Specifically, the current regulation for non-enabled units powered by NP-RES that adopt Option 2 defines the following imbalance pricing mechanisms.

• For imbalance volumes exceeding α of PVMC, the pricing rule of non-enabled units is applied. In detail, the imbalance price is defined as the minimum (maximum) between the zonal price determined in the DAM and the weighted average of accepted purchase (sale) offers in real time on the Balancing Market (BM). The purpose is the balance during the settlement period and within the macro-zone, when the macro-zonal imbalance is positive (negative).
• For imbalance volumes within the tolerance band, the price is equal to the zonal DAM price plus a zonal equalizing component. This equalizing component is calculated to ensure the financial neutrality of the imbalance settlement for NP-RES units and is applied to the absolute value of each Balance Responsible Party’s imbalance, regardless of its direction.

Consequently, when NP-RES units opt for Option II, and therefore with lower financial risks compared to Option I, imbalances within the tolerance band result in lower economic impact for the producer than imbalances outside the band. However, the specific cost of imbalance varies hour by hour and depends on the sign and amount of the overall system imbalance.

4. Methodology

The methodology proposed in this study aims to evaluate and reduce power imbalances in the IDM.

First, the training stage is executed, and the following different input variables are selected and preprocessed according to their characteristics and time dynamics.

• G_POA: irradiance on the plane of the array. The historical G_POA data with a 15-min resolution is used as input to capture short-term variability, in particular, 8 values have been used, covering the last 2 h (H-3 to H-1) before the forecast time. Only values greater than 0 are used (to exclude night hours). If a value is zero, the last non-zero value is repeated in order to maintain a consistent number of input values for the model. Several configurations have been tested, including those that retained zero values, but the adopted approach led to the best forecasting performance.
• T_mod: module temperature. Hourly values are used, as temperature changes more slowly over time and is non-zero even at night. In particular, 4 values have been considered, covering the last 4 h before H.
• CSM: it estimates ground-level solar irradiance under cloud-free atmospheric conditions [22]. It is based on factors such as solar elevation angle, site altitude, aerosol content, water vapor, and other atmospheric parameters. The hourly value at the target forecast time is used (H), since it is a calculated value and it serves as a reference upper bound for solar irradiance at that specific hour.

Several combinations of input variables were tested, considering the available quantities, different time resolutions, and varying numbers of samples for each quantity. The final configuration was selected as it provided the best forecasting performance among all tested scenarios. The output is the hourly AC power, P_AC, aligned with the time granularity used in the IDM. Data from sunrise (t_Sunrise) and sunset (t_Sunset) have been considered.

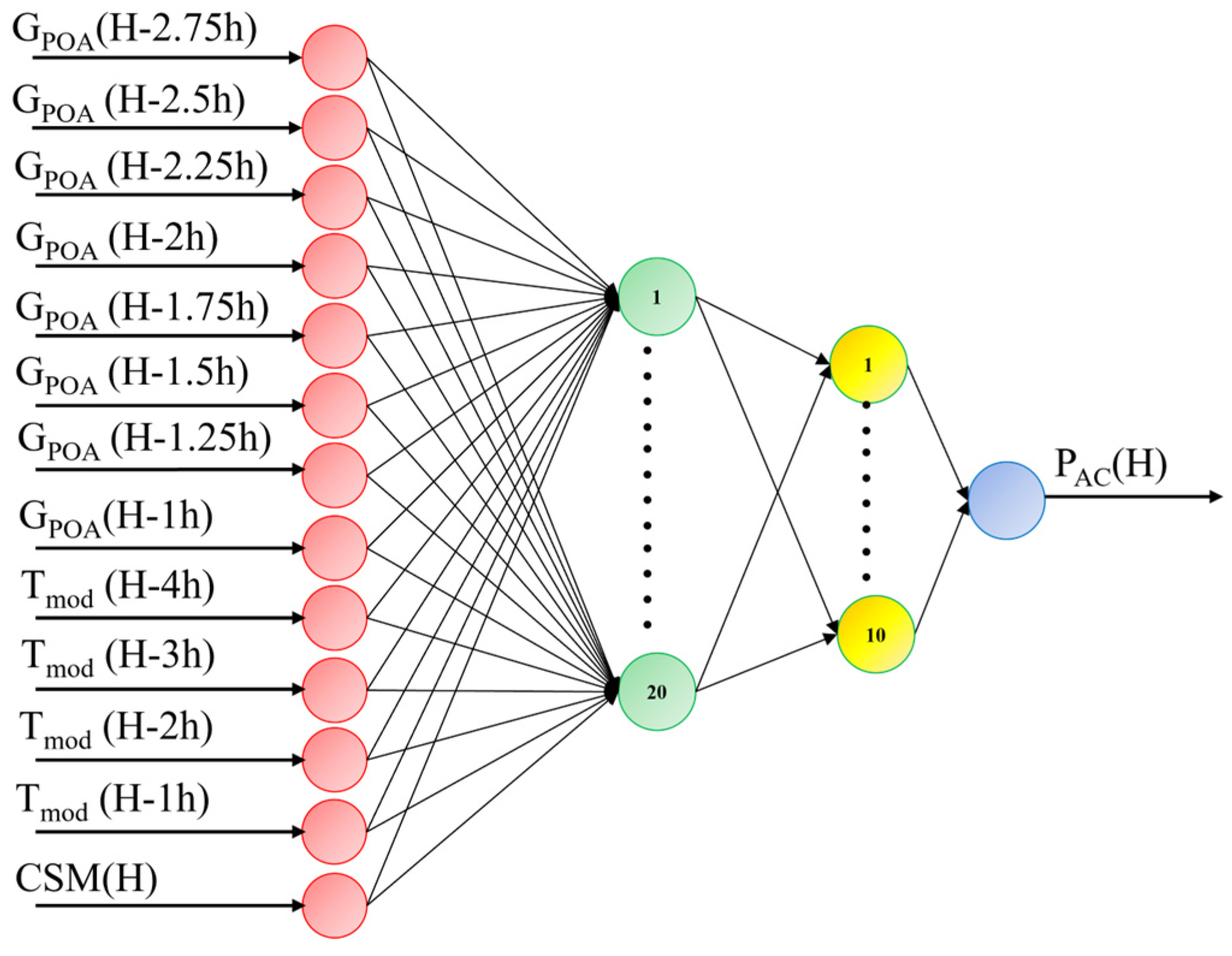
Figure 1 illustrates the structure of the HPANN, including the selected input variables and the output target used for the forecasting model.

Table 1. Input-Output Configuration example considering a generic day where t_Sunrise is 8:00 a.m.

Forecast Target (Output)	GPOA Input (15-min)	Tmod Input (Hourly)	Clear Sky Irradiance
PAC at 9:00	GPOA at 8:00 repeated 8 times (8 values)	Tmod from 5:00 to 8:00	CSM at 9:00
PAC at 10:00	GPOA at 8:00, GPOA at 8:15, GPOA at 8:30 and GPOA at 8:45 repeated twice (8 values)	Tmod from 6:00 to 9:00	CSM at 10:00
PAC 11:00	GPOA from 8:00 to 09:45 (8 values)	Tmod from 7:00 to 10:00	CSM at 11:00
PAC 11:00+h	GPOA from 8:00+h to 09:45+h (8 values)	Tmod from 7:00+h to 10:00+h	CSM at 11:00+h

illustrates the input configuration used for a typical day with sunrise at 8:00 a.m.: when forecasting P_AC one hour after sunrise, the model uses 8 repeated G_POA values (all non-zero) as input; two hours after sunrise, only 4 non-zero G_POA values are available, which are therefore each repeated twice; from three hours after sunrise onward, all G_POA values are non-zero and can be directly used as distinct inputs.

The input variables have been selected from the available dataset, which includes parameters typically monitored in utility-scale PV systems. Specifically, solar irradiance and module/environmental temperature, which are widely recognized as the most influential climatic variables affecting PV power output [27], have been used as inputs.

After the training HPANN stage, the methodology is structured, comprising the following steps.

• Forecasting stage. The AC power (P_AC) output of the PV plant is forecasted one hour ahead using an HPANN model trained on historical data.
  The forecasting performance is first assessed using standard statistical error metrics:
  • nRMSE [%] [10]: $nRMSE={\displaystyle \frac{\sqrt{{\sum }_{\mathrm{i}=1}^{\mathrm{M}}{\left(P_{PV\_meas}-P_{est}\right)}^2}}{\overline{\mathrm{y}}}}$;
  • normalized Mean Bias Error (nMBE) [28]: $nMBE={\displaystyle \frac{{\sum }_{i=1}^M{P_{PV\_meas}-P}_{est}}{N·\overline{y}}}$;
  • Coefficient of determination (R²) [28]: $R^2=1-{\displaystyle \frac{{\sum }_{i=1}^M{\left(P_{PV\_meas}-P_{est}\right)}^2}{{\sum }_{i=1}^M{\left(P_{PV\_meas}-\overline{y}\right)}^2}}$
  where P_{PV_meas} and P_est are the measured and forecasted values of P_AC, respectively; $\overline{y}$ is the mean of the measured values of P_AC and M is the total number of considered data. It is important to note that the exclusion of nighttime data, by considering only the period from sunrise to sunset, affects the computed values of the statistical performance metrics, since including zero values would artificially reduce the error between the measured and forecasted data.
  In addition, visual tools are employed, including scatter plots, error histograms, and normal probability plots, to enable a more comprehensive and nuanced evaluation of forecasting accuracy and bias. This multi-level analysis is particularly relevant for assessing the model’s suitability in market applications, where both the magnitude and the direction of forecast errors can have significant economic implications.
• Definition of tolerance bands. Upper and lower tolerance thresholds are established according to regulatory standards, computed as ±α·P_est.
• Error evaluation. At each time step, the error between the measured and forecasted P_AC is calculated as:

  $${error}_i=P_{PV\_meas}-P_{est}$$

  (1)

  The error is then compared against the tolerance band. If it falls outside this range, it is flagged as a high-cost imbalance, positive if ${error}_i>\alpha ·P_{est}$, or negative if ${error}_i<-\alpha ·P_{est}$.
• Battery modelling. A simple battery model based on the Coulomb Counting Method [29] is adopted to estimate the state of charge (SoC). It expresses the SoC as a function of energy, rather than just current, thus allowing a more direct representation of the remaining energy, and accounts for variations in the battery’s voltage. The implemented model ensures that the battery operates within technical limits, including SoC boundaries (SoC_min and SoC_max), charge/discharge efficiencies (η_ch and η_dish), and depth of discharge (DoD). DoD is the percentage of the nominal battery capacity, E_c, actually usable. The SoC is updated at each time step based on the net energy exchanged in a 1-h period. 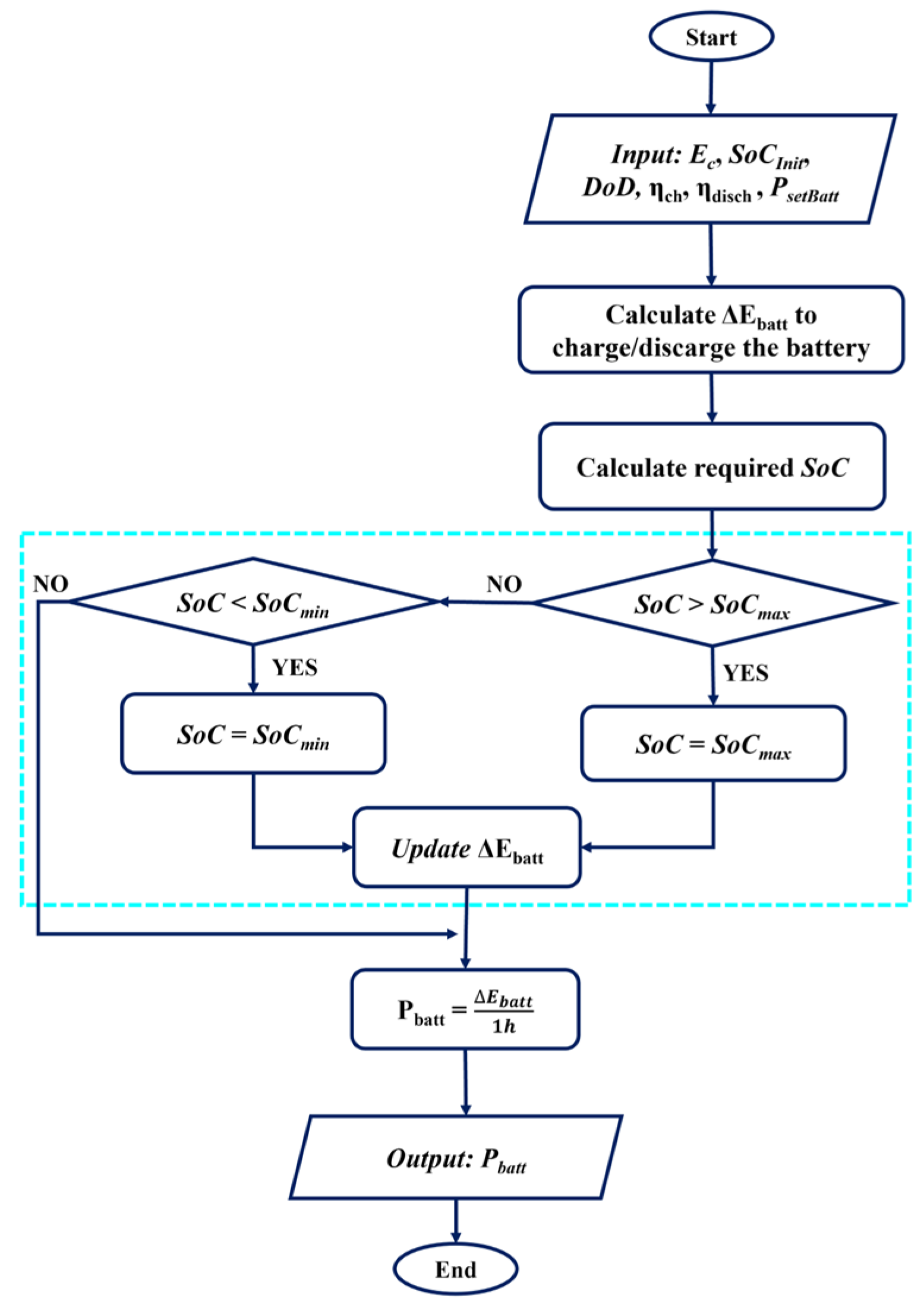Figure 2 illustrates the flow chart of the Battery function used in the flow chart of the first and second battery strategy considered for imbalance mitigation (Figure 3 and Figure 4), where:
  • E_setbatt is the energy requested (to be provided) from (to) the battery; thus, when E_setbatt is positive (negative), the battery should be discharged (charged);
  • ΔE_batt represents the energy actually supplied (provided) by the battery.
  In Figure 2, a first evaluation of ΔE_batt is performed considering E_setbatt, η_ch, and η_dish. Then the SoC necessary to meet E_setbatt is evaluated. The blocks in the light blue rectangle ensure that the battery operates within SoC boundaries (SoC_min and SoC_max). If the required energy would exceed the battery’s operational boundaries, the energy setpoints (ΔE_batt) are reduced accordingly.
• Battery compensation strategy. When an imbalance may occur, a battery is used to compensate for the deviation. Hour by hour, the battery is charged (discharged) based on whether the forecasted P_AC, P_est, underestimates (overestimates) the measured P_AC value, P_{PV_meas}, while handling the battery’s operational boundaries. Two battery compensation strategies have been considered and analyzed in this paper. Both are based on two distinct power values: the forecasted power, P_est, which represents the estimated production derived from short-term forecasting models, and the declared power, P_decl, which corresponds to the value submitted to the market and used for imbalance settlement calculations. In the following paragraphs, the two strategies will be analyzed in detail:
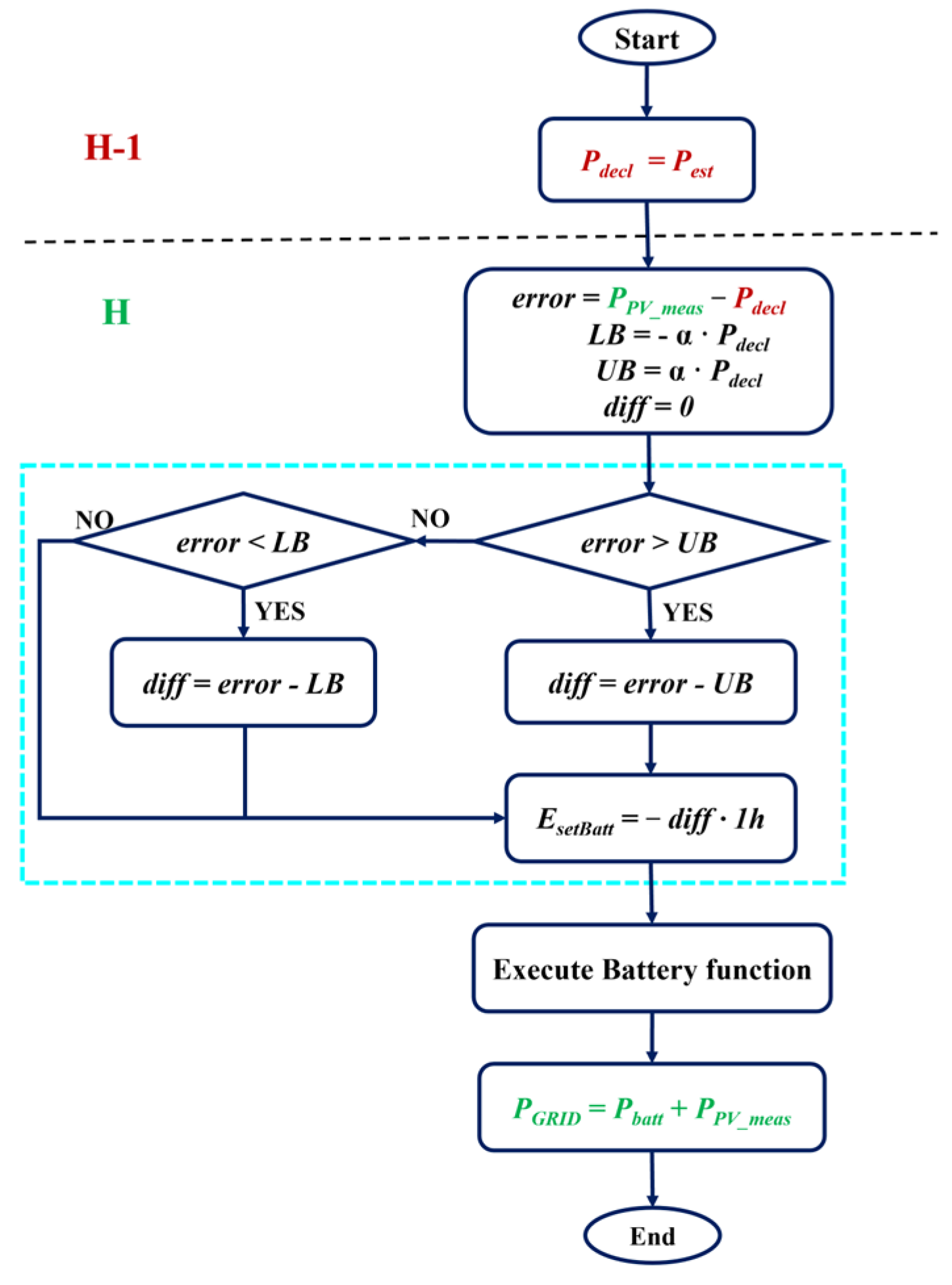
  • The first strategy applies a direct correction, using an energy battery setpoint, E_setbatt, equal to the portion of the variable error, defined as the difference between P_{PV_meas} and P_decl (which in this case is equal to P_est) that exceeds the tolerance threshold (±α·P_decl). Figure 3 shows the flow chart of the first battery compensation strategy. In particular, the variables shown in red refer to quantities computed at time H-1, whereas those in green at time H. The blocks inside the light blue rectangle allow setting E_setbatt based on the forecast error and the lower/upper bounds (LB, UB), such that the battery is charged (negative E_setbatt) when there is a positive imbalance, and discharged (positive E_setbatt) in case of negative imbalance. Then the Battery function (Figure 2) is executed to calculate ΔE_batt and consequently P_batt, which is the power supplied by/provided to the battery. Finally, the power injected into the grid (P_GRID) is computed.
  • The second battery compensation strategy differs from the previous one only in P_decl calculation: in this case, P_decl depends on the forecasted and the energy stored in the battery at H-1. More specifically, the strategy tries to keep the battery SoC always close to 50%. This approach improves the ability of the battery to compensate for many consecutive underestimations or overestimations due to forecasting errors. Therefore, the declared power is greater than the forecasted one when the SoC exceeds 50%, while it is lower than the forecasted power if the SoC is below 50%. Different from the previous greedy battery compensation strategy, this strategy improves the long-term consistency and reliability of imbalance mitigation and better ensures compliance with tolerance thresholds. Figure 4 shows the flow chart of the second battery compensation strategy. In particular, the variables shown in red refer to quantities computed at time H-1, whereas those in green at time H. P_N is the nominal power of the PV system, while P_B is the power that must be supplied to/provided by the battery in order to restore the SoC to 50%. It is worth noticing that P_B, computed at H-1, is different from the actual power P_batt, which is supplied to/provided by the battery at time H.

Finally, Figure 5 presents a block diagram illustrating the proposed methodology. First, the Clear Sky Model (CSM) is computed based on the latitude (lat), longitude (log), date, and specific time (H) corresponding to the P_AC to be forecasted. This value, along with the other inputs, which are G_POA and T_mod from H-1 and preceding, is the input of the HPANN model, which provides P_est. Then the declared power is evaluated according to the battery strategy and notified to the market. At hour H, the actual power output of the PV system is measured, P_{PV_meas}. Based on the comparison between the measured and estimated values, the battery is charged or discharged according to compensation strategies (Figure 2 and Figure 3), to try to ensure that the power supplied to the grid (P_GRID) implies a charge imbalance within the tolerance threshold or is entirely eliminated.

The proposed methodology can be used to assess the impact of different forecasting methods, battery sizes, and compensation strategies on charge imbalances. This enables the selection of the best forecasting method for the specific PV system, valuable insights into the optimal battery capacity required to reduce or eliminate imbalances, for different forecasting approaches, and compensation strategies.

To this aim, an energetic imbalance characterization is introduced to analyze the effectiveness of the forecasting method. As described in Section 3, the economic implications of the application of the proposed methodology, in the Italian IDM context, are highly dependent on the following prices: zonal DAM, zonal BM, and the balancing component that depend on the behavior of the other NP-RES power systems that are in the same zone. Therefore, the economic evaluation is highly affected by the volatility of such prices. On the other hand, the precise description of the imbalance charge rules in Italy is important to understand how the different prices can affect the economic results. Under this consideration, in this paper, only their energetic evaluation is performed. This approach is more useful because it can also be applied in other countries that use imbalance bands. Specifically, to analyze positive and negative imbalances:

$$imb={P_{GRID} - P}_{decl}$$

(2)

two key parameters are evaluated: the percentage of occurrences that the upper and lower thresholds are exceeded,

$${freq}_P={\displaystyle \frac{P}{M}}·100 if imb>\alpha ·P_{decl}$$

(3)

$${freq}_N={\displaystyle \frac{N}{M}}·100 if imb<-\alpha ·P_{decl}$$

(4)

and the total imbalance energy (positive and negative), normalized with respect to $P_{GRID}$

$$EIP={\displaystyle \frac{\left({\sum }_{i=1}^P{imb}_i-\alpha ·P_{decl}\right)·1h}{\left({\sum }_{i=1}^M{P}_{GRID}\right)·1h}}={\displaystyle \frac{{\sum }_{i=1}^P{imb}_i-(-\alpha ·P_{decl})}{{\sum }_{i=1}^M{P}_{GRID}}}if imb>\alpha ·P_{decl}$$

(5)

$$EIN={\displaystyle \frac{\left({\sum }_{i=1}^N{imb}_i-(-\alpha ·P_{decl})\right)·1h}{\left({\sum }_{i=1}^M{P}_{GRID}\right)·1h}}={\displaystyle \frac{{\sum }_{i=1}^N{imb}_i-(-\alpha ·P_{decl})}{{\sum }_{i=1}^M{P}_{GRID}}}if imb<-\alpha ·P_{decl}$$

(6)

where P is the number of hours exceeding the upper thresholds, N is the number of hours exceeding the lower thresholds, while M the total number of considered hours.

Moreover, by applying the proposed methodology and computing the key parameters over a representative set of historical data, it is possible to analyze imbalance behavior, determine the need for a storage system, and assess the impact of different battery sizes on imbalance mitigation.

5. Case Study

The data used in this study are from the EURAC PV system [30], which was installed at the airport of Bolzano, Italy, in 2010.

Table 2. Main characteristics of the EURAC PV system.

PV Cell Technology	Polycrystalline
PV nominal power	4.20 kWp
Tilt angle	30°
Azimuth angle	8.5°

summarizes the main characteristics of the PV power system.

A weather station is installed in close proximity to the test side to record various meteorological parameters. All data have been recorded over an 8-year period, spanning from February 2011 to January 2019, with a 15-min resolution.

The available measured quantities are:

-

ambient temperature, T_amb, [°C];

-

T_mod, [°C];

-

G_POA, [W/m²];

-

wind speed, ω, [m/s];

-

wind direction, dir, [°];

-

DC power, P_DC, [W];

-

P_AC, [W].

To ensure the reliability of the data and the effectiveness of the model, various pre-processing techniques have been applied to address missing entries, temporal inconsistencies, resolution differences, and feature scaling.

• Treatment of Missing Data. Only days with a percentage of 80% of available data have been considered, obtaining a subset of 2802 days. Gaps in the dataset, caused by sensor issues or environmental factors, have been filled using linear interpolation, preserving the continuity and underlying patterns of the time series.
• Temporal Alignment. Ground-based sensor data have been synchronized into a consistent 15 min interval using timestamp-based interpolation and merging. Solar radiation and power data have been compared to the CSM-generated data for synchronization.
• Feature Scaling. Min-Max normalization (scaling values between 0 and 1) was applied to prevent features with larger numerical ranges from overshadowing those with smaller ranges.

5.1. Hybrid Model to Forecast the PV Power Generation

In this section, the design of the HPANN model [21], based on an ANN and the CSM, used for the (H-1) P_AC forecasting, is described in detail. The number of inputs and their respective time resolutions have been determined through a trial-and-error approach, aiming to balance forecasting accuracy and model simplicity. The designed MLP neural network consists of a two-hidden-layer structure comprising 20 and 10 neurons [21]. Training performance is quantified using the Mean Squared Error (MSE) metric. A maximum of 500 training epochs is allowed, with early stopping based on a validation check criterion set to 10 consecutive failures. Both the hidden and output layers employ a radial basis activation function. The learning process is governed by the Levenberg-Marquardt backpropagation algorithm, which also handles weight and bias updates through its optimization strategy. The selection of key hyperparameters, such as training duration, hidden layer size, number of neurons in the hidden layer, and learning rate, was performed through empirical tuning based on trial-and-error experimentation. For example, for the selection of the number of hidden layers, 1 to 3 hidden layers have been tested, considering that an insufficient number of hidden layers may lead to underfitting, limiting the model’s ability to capture complex patterns, while an excessive number can cause overfitting and increase computational complexity without guaranteeing performance improvements. In order to choose the number of neurons, based on empirical heuristics such as the geometric and arithmetic means of the input and output layer sizes, a range of 5 to 30 neurons has been tested for the first hidden layer and 5 to 15 for the second. The final configuration with two hidden layers, with 20 and 10 neurons, respectively, yielded the best forecasting accuracy. This structure provides adequate ability to model complex nonlinear relationships in the data, while empirical tuning combined with validation-based early stopping was employed to reduce the risk of overfitting. While this heuristic method, based on a trial-and-error approach, lacks formal optimization guarantees, it remains a commonly adopted strategy for configuring ANNs in practical applications, particularly when the dimensionality of the search space is manageable and domain-specific expertise can guide the search. Nevertheless, future work may benefit from the integration of more systematic tuning strategies, such as metaheuristic optimization algorithms (e.g., genetic algorithms, Bayesian optimization), to further improve forecasting performance [31].

Among the available data, those relating to the first seven years of measurement have been used for network training, while the data relating to the last year (2018) were used for the test. Only data from sunrise to sunset has been considered. All network modeling procedures have been developed and trained using the MATLAB^® environment (version R2024b).

5.2. Impact of Battery Compensation Strategy and Size on Imbalance

Firstly, the experimental results obtained with the HPANN method, on the available data set, are reported. In

Table 3. Statistical coefficients obtained using a Smart persistence model and the HPANN to forecast the P_AC.

Model	nRMSE	nMBE	R2
Smart persistence	31.10%	2.07%	0.84
HPANN	25.95%	0.73%	0.90

, values of statistical coefficients obtained using the HPANN to forecast the P_AC are reported. To provide a benchmark, the table also shows the results obtained using a naïve forecasting approach based on the smart persistence method [32].

The tolerance, α, for the NP-RES unit analyzed in this paper is equal to 8% according to the Italian IDM. This implies that, in order to limit imbalance charges, the forecast error (as defined in Equation (1)) must satisfy the condition −α · $P_{est}$ ≤ error_i ≤ α · $P_{est}$, with α = 0.08. Figure 6 illustrates the comparison between P_{PV_meas} and P_est values, together with the corresponding forecast error and the tolerance thresholds ± α · $P_{est}$. For the sake of clarity, only a winter month (Figure 6a) and a summer month (Figure 6b) are reported.

As can be seen from Figure 6, the allowable error range is very narrow, making it likely for the error to fall outside of it, especially when solar irradiance is low (at sunrise and sunset hours and on cloudy days), where the economic impact remains limited.

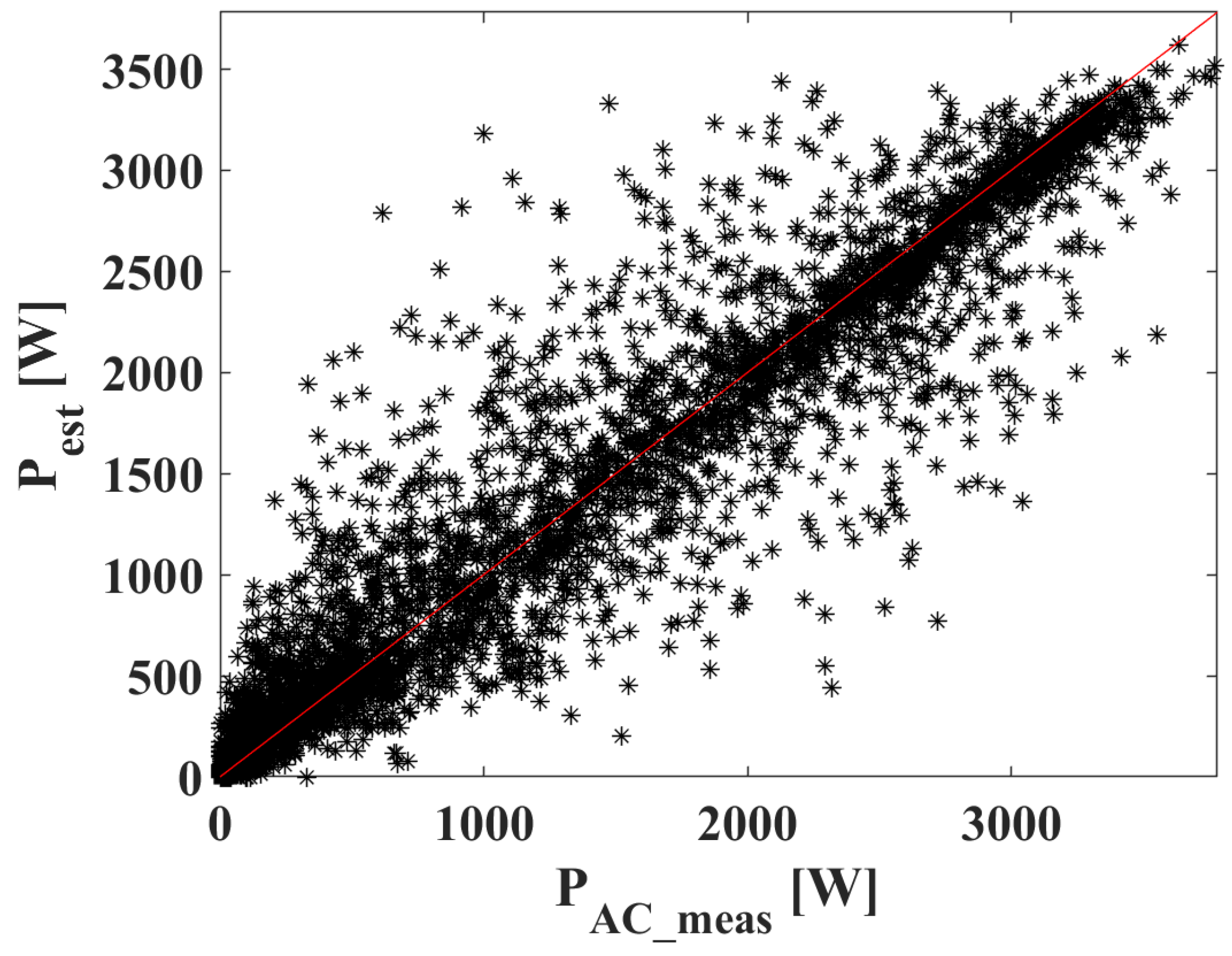
To better understand the results, the measured vs. forecasted data is reported in Figure 7. It can be observed that the PV power forecasting in the desired time horizon is quite satisfactory. Moreover, this plot allows a visual evaluation of overestimations and underestimations, helping to identify systematic prediction biases.

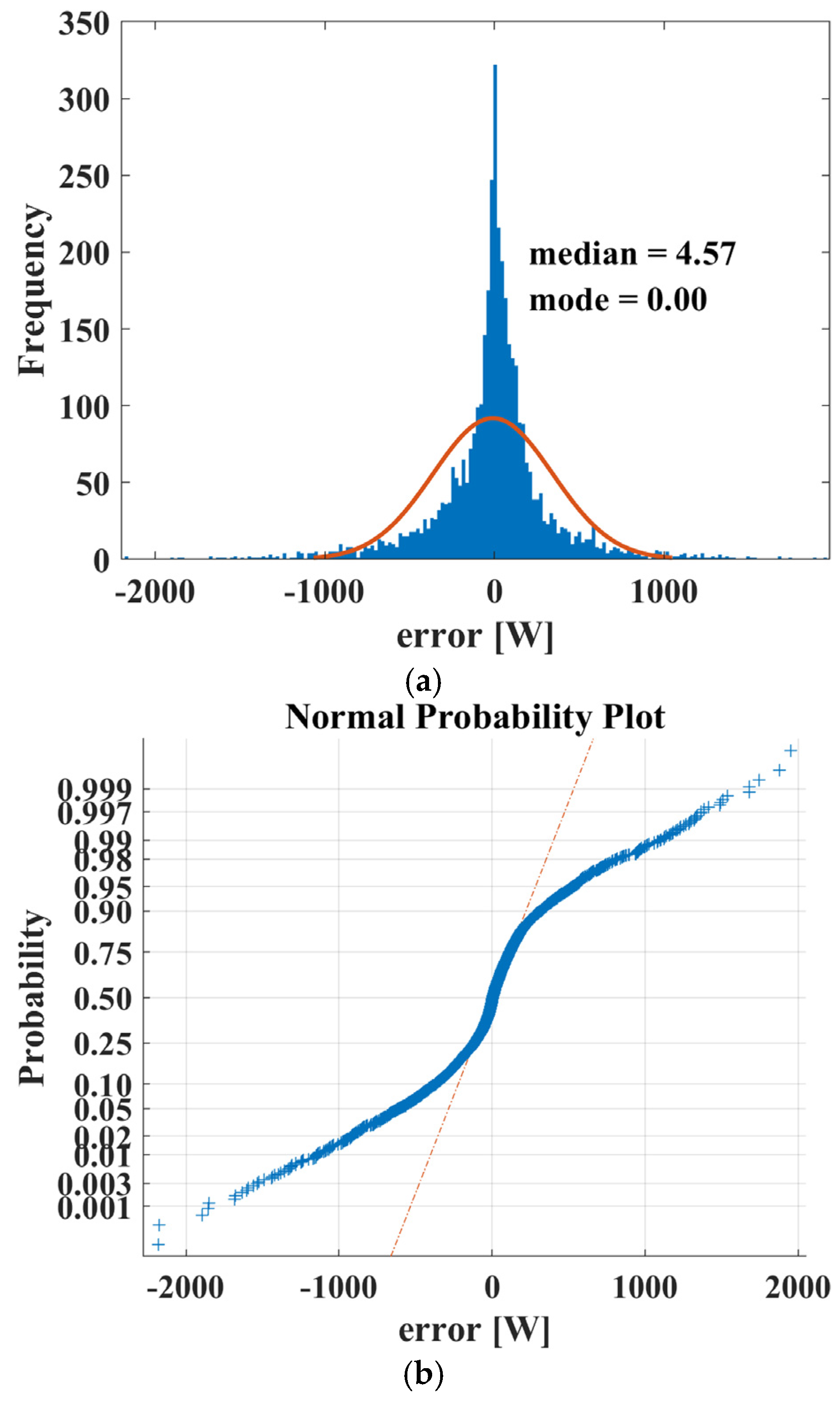
In order to analyze the distribution of data, Figure 8 shows the histogram and the Normal Probability plot of the error (Equation (1)).

The histogram in Figure 8a shows a positive skewed distribution, with a mode at 0, indicating a peak at zero, while the median at 4.57 suggests that most values lie above zero. This implies a tendency toward underestimation in predictions, as positive median values suggest that actual values are often higher than forecasted.

Then, to perform an energetic characterization of the forecast errors, the results of the two key parameters used to analyze imbalances, namely, the percentage of occurrences and the total imbalance energy, without considering the use of a storage system, are presented in the first row of

Table 4. Positive and negative key parameters considering imbalances outside the tolerance band, when no battery is used (first row) and when the first battery compensation strategy is used.

Ec [Wh]	freqP [%]	freqN [%]	EIP [%]	EIN [%]
0	29.8393	35.5267	4.8408	−5.9054
4000	3.188	13.1089	0.4334	−2.0337
8000	0.7651	10.8391	0.1234	−1.742
12,000	0.2805	10.278	0.0536	−1.6577
16,000	0.0255	9.8444	0.0024	−1.5899
17,000	0	9.7679	0	−1.5821
17,200	0	9.7679	0	−1.581
17,400	0	9.7424	0	−1.5799
17,600	0	9.7169	0	−1.5787
17,800	0	9.6914	0	−1.5776
18,000	0	9.6659	0	−1.5765

. It can be observed that the percentage of occurrences exceeding the upper threshold is lower than that of the lower threshold, indicating that negative imbalances are more frequent. Without using a storage system, the quantity error (Equation (1)) corresponds to the quantity imb (Equation (2)).

To reduce imbalances and consequently penalties, a battery can be employed that charges or discharges to limit the imbalance, especially when it exceeds the thresholds. The following parameter values have been used in the battery model described in Section 4: η_ch = η_disch = 0.94; DoD = 0.8; SoC_min = 10%; SoC_max = 90% and initial SoC, SoC_Init = 50% and Δt is one hour.

Simulations are conducted across a range of battery sizes to evaluate the effectiveness of each compensation strategy. For every configuration, the percentage of occurrences and the total imbalance energy of the forecast errors exceeding the tolerance band are computed. This enables the identification of the minimum battery capacity required to significantly reduce or completely eliminate imbalance occurrences, thus allowing more reliable and penalty-free operation in the IDM. In particular, in Table 4, the values of freq_P, freq_N, EIP, and EIN, considering $\left|{imb}_i\right|<\alpha ·P_{decl}$ and using the first battery compensation strategy, are shown as E_c changes.

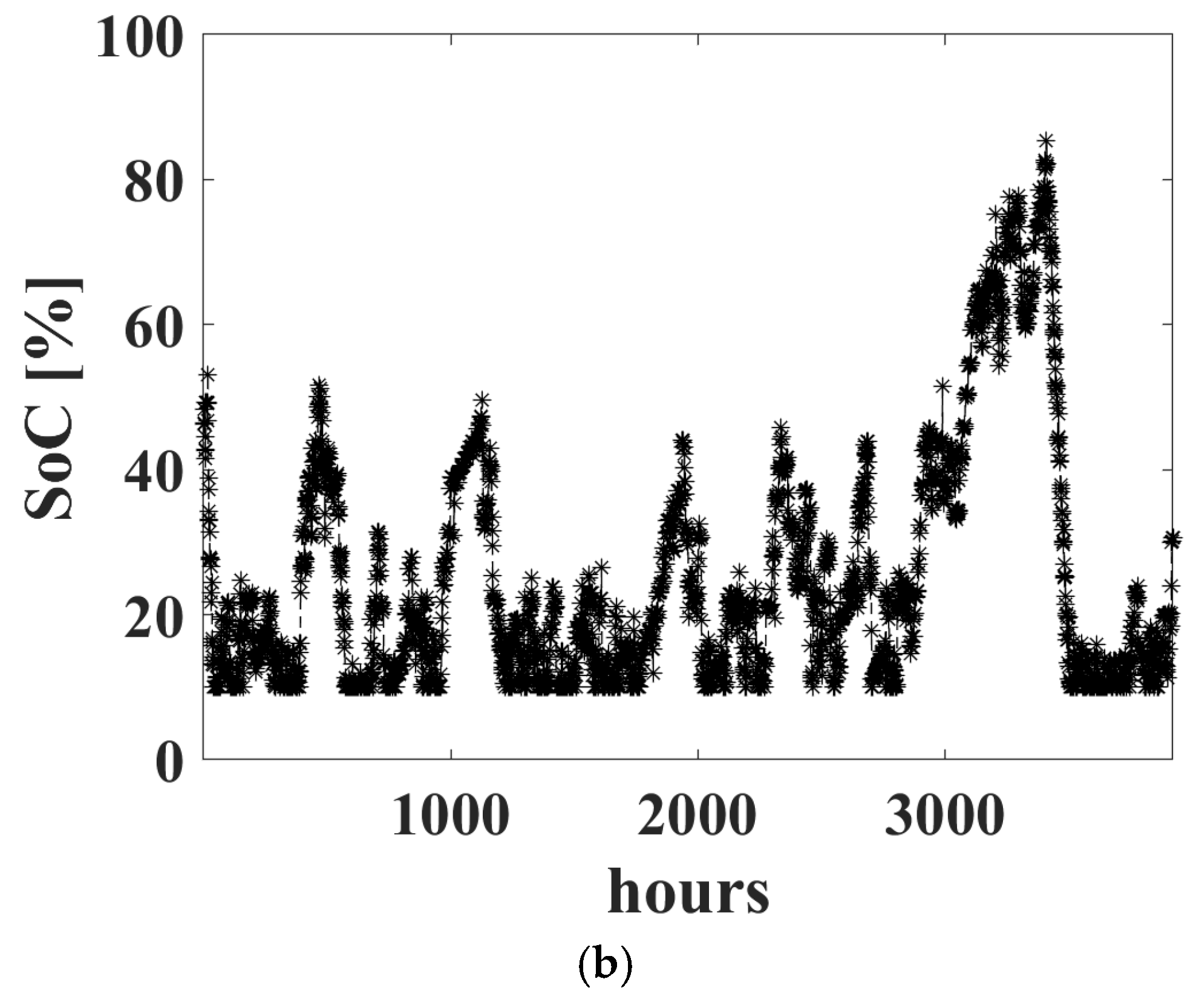
As it is possible to note, beyond a certain value of E_c, further increases do not provide additional benefits. This is because, in the scenario analyzed here, negative imbalances exceed positive ones, causing the battery’s SoC to remain frequently near its lower limit, as can be seen from Figure 9, which shows the SoC in the case of a battery with a capacity equal to 4 kWh (Figure 9a) is used and using a battery with a capacity equal to 18 kWh, that is, approximately 4 equivalent hours (Figure 9b).

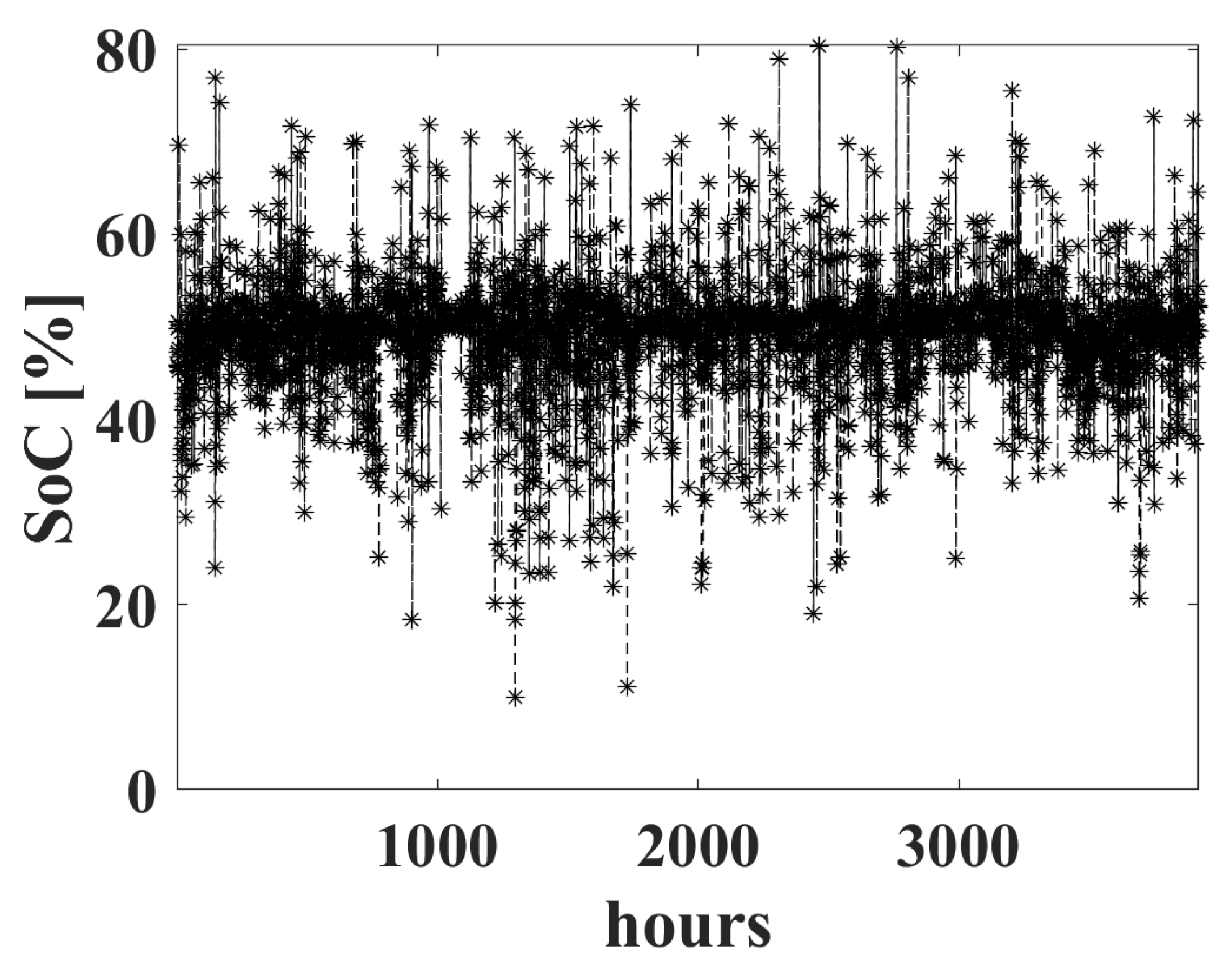
To prevent such behavior and completely eliminate imbalances outside the tolerance band and thus the associated penalties, the second battery compensation strategy has been proposed, which aims to keep the battery’s SoC around 50% at all times. This strategy allowed for the elimination of power imbalances outside the tolerance band $\left|{imb}_i\right|<\alpha ·P_{decl}$, (with α = 8%) using a battery with a capacity E_c = 7.2 kWh, that is, a bit more than 1.7 equivalent hours, as shown in

Table 5. Positive and negative key parameters considering imbalances outside the tolerance band ($\left|{imb}_i\right|<\alpha ·P_{decl}$, with α = 8%) when the second battery compensation strategy is used.

Ec [Wh]	freqP [%]	freqN [%]	EIP [%]	EIN [%]
4000	0.204	0.5356	0.0417	−0.1075
5000	0.0765	0.153	0.0043	−0.03
6000	0	0.051	0	−0.0113
7000	0	0.0255	0	−0.0011
7100	0	0.0255	0	−0.0006
7200	0	0	0	0

. In Figure 10, it is possible to note that using this strategy, the SoC remains always around 50%.

As discussed in Section 3, although imbalance penalties within the tolerance band are lower than those applied outside the band, in this study, the proposed methodology was also applied to completely eliminate all imbalances, including those within the tolerance band, by setting α equal to 0. This approach ensures the full elimination of penalties in order to assess the maximum potential benefit achievable through the proposed methodology. The results are presented in

Table 6. Positive and negative key parameters to obtain $\left|{\mathrm{i}\mathrm{m}\mathrm{b}}_{\mathrm{i}}\right|=0$ when the second battery compensation strategy is used.

Ec [Wh]	freqP [%]	freqN [%]	EIP [%]	EIN [%]
4000	0.4081	0.9946	0.0483	−0.2239
5000	0.051	0.4081	0.0048	−0.0773
6000	0	0.102	0	−0.0255
7000	0	0.051	0	−0.0113
8000	0	0.0255	0	−0.0035
8100	0	0.0255	0	−0.003
8200	0	0.0255	0	−0.0024
8300	0	0.0255	0	−0.0018
8400	0	0.0255	0	−0.0013
8500	0	0.0255	0	−0.0007
8600	0	0.0255	0	−0.0001
8700	0	0	0	0

.

Table 6 illustrates that imbalances can be fully eliminated by employing a battery with a capacity of 8.7 kWh, which corresponds to slightly more than 2 equivalent hours of storage.

6. Conclusions

This study presented a methodology designed to support the participation of PV systems in the Italian IDM, with a specific focus on the reduction of imbalance charges. To address this issue, an HPANN model has been developed to predict PV output one hour ahead, achieving a normalized RMSE of 25.95% (only daytime data have been considered, excluding zero nighttime values, to avoid artificially reducing forecast errors) and demonstrating robustness under various operating conditions. However, while accurate forecasting remains important, the results highlight that high accuracy alone, measured by metrics like nRMSE or MAE, does not always translate into good economic performance. In this regard, the core contribution of this work lies in proposing a methodology to reduce imbalance in an actual intra-day market. HPANN has been integrated with a storage system, demonstrating how a proper strategy of battery use can mitigate or totally avoid imbalance cost due to the forecasting models. Simulation results revealed that a simple battery model, combined with an optimized control strategy that tries to keep the state of charge close to 50%, can completely eliminate imbalance penalties when the battery capacity of the storage system is set to slightly more than 2 equivalent hours.

Overall, the proposed methodology can support decision-making for PV plant operators by quantifying the real impact of forecast errors and identifying optimal storage requirements. While this work is tailored to the Italian MI-XBID market, the general structure of the proposed methodology can be extended to other market contexts where tolerance thresholds or imbalance penalties are applied. Future developments may include the adoption of alternative forecasting techniques to evaluate their influence on imbalance dynamics, as well as the implementation of more advanced battery management strategies based on optimization algorithms to further enhance system efficiency and economic performance. Moreover, an in-depth economic assessment of the benefits provided by the storage system, in terms of avoided imbalance penalties, should be conducted to quantify the added value of battery integration and guide investment decisions in real market conditions.