Abstract
Governments worldwide have set ambitious targets for decarbonising energy grids, driving the need for increased renewable energy generation and improved energy efficiency. One key strategy for achieving this involves enhanced energy management in buildings, often using machine learning-based forecasting methods. However, such methods typically rely on extensive historical data collected via costly sensor installations—resources that many buildings lack. This study introduces a novel forecasting approach that eliminates the need for large-scale historical datasets or expensive sensors. By integrating custom-built models with existing energy data, the method applies calculated weighting through a distance matrix and accuracy coefficients to generate reliable forecasts. It uses readily available building attributes—such as floor area and functional type to position a new building within the matrix of existing data. A Euclidian distance matrix, akin to a K-nearest neighbour algorithm, determines the appropriate neural network(s) to utilise. These findings are benchmarked against a consolidated, more sophisticated neural network and a long short-term memory neural network. The dataset has hourly granularity over a 24 h horizon. The model consists of five bespoke neural networks, demonstrating the superiority of other models with a 610 s training duration, uses 500 kB of storage, achieves an R2 of 0.9, and attains an average forecasting accuracy of 85.12% in predicting the energy consumption of the five buildings studied. This approach not only contributes to the specific goal of a fully decarbonized energy grid by 2050 but also establishes a robust and efficient methodology for maintaining standards with existing benchmarks while providing more control over the method.
1. Introduction and Literature Survey
To achieve optimised energy management for public buildings, the precise forecasting of energy consumption is imperative. This optimisation facilitates strategic decision-making regarding when to procure, sell, and store energy, considering the anticipated energy generation from on-site renewable sources. Given the UK national grid’s commitment to reducing carbon emissions by 78% by 2035 [1], effective energy management and demand-side response have become crucial components of the overarching strategy.
The challenge in energy forecasting is underscored by the sheer volume of non-domestic buildings in the UK, which numbered 1.7 million in 2022 [2]. Traditional forecasting methods for each building necessitate extensive data collection, posing a logistical challenge. Machine learning algorithms (MLAs) present a promising avenue for addressing this challenge, with neural networks emerging as particularly effective. Neural networks exhibit superior accuracy compared to benchmark MLAs, allowing them to discern intricate relationships between variables, albeit at a higher computational cost. Long Short-Term Memory (LSTM) networks, a type of recurrent neural network, excel in forecasting energy consumption for commercial buildings. LSTMs effectively capture temporal dependencies in hourly data, enabling accurate predictions by retaining and selectively updating information over extended time periods, crucial for modelling the dynamic and complex nature of energy usage in commercial settings.
The focus of this research is on non-domestic office buildings, chosen due to the substantial number of new constructions. In 2023 offices comprised 20.26% of all buildings out of 10 categories [2,3]. The combination of neural networks and Bayesian optimisation in forecasting energy consumption for these office buildings holds promise for advancing optimised energy management strategies in the broader context of the UK’s carbon reduction initiatives.
Types of MLAs for forecasting the energy consumption of non-domestic buildings include Random Forest (RF) [4], Support Vector Machine (SVM) [5], Linear Regression (LR) [6], and Neural Networks (NNs) [7]. RFs are more capable with less data, due to the ability to split datasets up and retrain the model, but they often miss complex relationships due to the simplicity of the model. SVMs can be better if they have sufficient data, and not too many inputs (usually less than four) due to the large complexity of the models when given more inputs. The LR can be a good benchmark to see how other algorithms are performing as they are the simplest. The NN is more robust than the SVM and is more accurate when calculating complex relationships than the RF, so they are the most commonly used MLAs. A more complex NN called a long-short-term-memory (LSTM) was previously used to forecast the short-term energy consumption of non-domestic buildings [8], microgrid energy management [9], and long-term energy consumption [10]. These models can have higher accuracies than the standard NN if they are designed correctly. Although these models are all different, they require historical energy data to calculate relationships between training data and the target data, meaning they have not previously been used without historical data. If they cannot be used without historical data, then a machine learning forecasting model cannot be used on a new building without any historical data and the energy management cannot be optimised through machine learning methods.
Input features are important to reinforcement learning [11] and can have high importance on the output of the model, with different feature selection algorithms existing [12,13,14]. Maximum Relevance, Minimum Redundance (MRMR) was previously used to calculate how important a given feature is to the target variable, but also how it is affected by other input variables. This allows the models to be made more efficient than with other feature selection methods [15].
In the realm of optimising machine learning algorithms, Bayesian optimisation stands out. This algorithm distinguishes itself by its ability to construct a surrogate model, providing guidance on adjusting MLA parameters. This approach expedites convergence times and reduces computational requirements, making Bayesian optimisation a valuable tool in developing accurate MLAs for energy forecasting [16].
Neural networks show higher accuracy among other machine learning forecasting methods for energy parameters of singular and clusters of non-domestic buildings, between 0.8% error and 13.26% error [17,18,19,20,21,22]. More focused parameters such as the HVAC consumption [23] or the cooling consumption [24] can be forecasted with 5.31 root-mean-squared-error and 0.4% mean-actual-percentage-error, respectively. This is due to the complexity of the NN; they can have higher training times and require more computational power than other algorithms [25], but they often have higher forecasting accuracy [26]. To optimise efficiency of the NN with regard to accuracy, Bayesian optimisation is used to decrease the error of a NN by 67% compared to no optimisation [27]. The dataset lengths required are explained in Table 1.

Table 1.
The dataset lengths required to use machine learning forecasting of the energy parameters.
There are a variety of required datasets, depending on how complex the energy consumption relationships are, but they all require more than a month, or even six months of data which is consistent with all previous research. Although these methods prove useful when historical data is already known, they cannot be used where there is no data at all.
From previous research, there is clear evidence of machine learning applications for commercial energy demand forecast for both individual, and for multiple buildings at a time. The previous work requires to have a different algorithm for individual or sets of buildings. This means data must be collected for the buildings, and their energy parameters cannot be optimised through machine learning methods initially. The current problem is that there are no reliable methods of forecasting the energy consumption of non-domestic buildings without any previous collected data. The energy consumption patterns of all buildings in previous work vary with function, size location, and other factors. What can be certain though is that climate is a large contributor to this. This can be seen from the data collected in this research; in the summer, consumption increases due to coolers being used, and in the winter, the heating is used more. Mild climates promote lower energy consumption. This pattern is affected largely by occupation too. Lower occupancy results in lower energy consumption, due to certain rooms not being conditioned and therefore the energy consumption is lower.
No aggregated methods exist to forecast for a single building with no historical data. Instead, they are used for groups of buildings such as a university campus. This leaves a research gap which this study aims to address.
There is a clear research gap in which MLAs have not been used to forecast the energy parameters of a building in which there is no data. Instead, they are commonly used to forecast for a building that has historical data, or for groups of buildings. If the target building has functional similarities with other buildings in which the data is already acquired, then the MLA models from the other buildings may be used to forecast the energy consumption of the target building. This could provide a good rise for MLA applications in energy management which is shown in previous research to improve energy efficiency and reduce carbon emissions. If a machine learning model cannot be applied to a building with no historical data, then energy management cannot be optimised through machine learning methods, and the building is less energy efficient than it could be if it did have historical data. The aim of this research is to develop a method of combining multiple machine learning models that can forecast the energy consumption of a new building with no historical data. This allows the building’s energy consumption to be forecasted and thus the energy can be optimally managed, reducing carbon emissions, something which the previously mentioned applications have not performed.
To test this, the developed neural networks for the five buildings in which the data is known are used to forecast their respective energy consumption data, but with the input parameters (such as weather forecast) of the target building. The target building’s data is withheld from the model, so it has not seen the target building data before. The output of the proposed method gives a forecast of the target building’s energy consumption which is then compared to the actual target building’s energy consumption and the accuracy and other statistical tests are completed. This provides a method in which a building’s energy consumption can be forecasted without any historical data from that building being collected and thus filling the research gap.
The list of abbreviations used in this study are described in Abbreviations section.
2. Methodology and Derivation of Aggregated Neural Networks
The aggregation of multiple machine learning models provides at a high level, a robust single model that can provide accurate forecasts of energy consumption for the specified building, even without previous collected historical energy consumption data. In further detail though, the single model is actually compiled of multiple bespoke models from nine different buildings in England, and when a new building’s energy forecast is needed, buildings with similar data will be used to produce a forecast from the neural networks. The bespoke models refer to a single model for a single building, meaning it only takes data for a specific building and only forecasts data for the same, specific building. This results in the target building’s energy consumption being forecasted, but by combining the forecasts of the neural networks of the historical buildings in which the data is known, instead of the current method of waiting until enough data is collected. The distance matrix is a matrix of Euclidian distances of some of the buildings which largely affect energy consumption. This allows the buildings to be separated by these features, concluding which existing buildings are most similar to the target building. An accuracy coefficient is calculated to diminish the specific neural network’s forecast on the final forecast from the entire model. This means that if a neural network for building 1 has an accuracy of 80%, it will have less effect on the final forecast than a neural network for building 2 which may have an accuracy of 90%, for example. A larger and more complex NN and a LSTM-NN are also developed to compare the results of the proposed model. The steps to producing this method are as follows:
- Develop the aggregated neural networks, a single NN, and a LSTM NN from the existing five non-domestic buildings and measure the forecasting accuracy.
- Rank the aggregated neural networks in the distance matrix based on the distance from the target building. Calculate the average difference in energy consumption between the forecast and the actual building to reduce error. Calculate an accuracy coefficient. Multiplying each value by an accuracy coefficient diminishes its influence on the ultimate forecast.
- Calculate the neural network forecasts after they have been processed through the distance matrix, the accuracy coefficient, and the average energy consumption difference to determine a final outcome from the proposed method.
- Determine the accuracy of the developed models, with a comparison of each model and how they function.
This is explained through Figure 1.
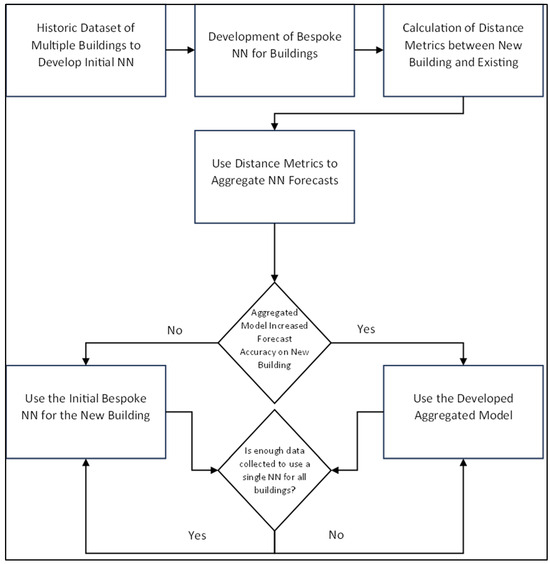
Figure 1.
The flow of the methodology proposed in this work.
The first block is for data collection and distance matrix calculations. The second block is for forecasting manipulation with the distance matrix and accuracy coefficient. The historical dataset is used to train bespoke NNs for each building they correspond to, but it is not used for the target building. The accuracy of the forecasts and the distance from the distance matrix is measured. Each bespoke NN is given the new building’s input data (weather forecast in this instance) and a forecast is calculated. The average difference between the energy consumptions between the two buildings is removed to push the forecast closer to the target. Each forecast is then multiplied by the distance matrix value and the accuracy coefficient which reduces the effect that less accurate and larger distance forecasts have on the ultimate forecast. If there is enough data for to develop a single NN for multiple buildings or for the single new building to produce accurate forecasts, the aggregated method is no longer necessary.
2.1. Data Processing and Developing Initial Neural Networks
The data collected from the five non-domestic buildings consists of hourly resolutions of between six months and 16 months of data, depending on the building. Five buildings are used to develop the models, and a single test building is used to test the model. For the training set, three are in London, one in Southampton, and one in Manchester, and the test building is in London. They are all office buildings, but the ranges of building age, floor space, total floors, average energy consumption, and energy rating are 12–160 years, 1.2–64.4 km2, 4–17 floors, 8–235 kWh, and 52–100 energy rating score, respectively. They all have similar working patterns such that they peak at roughly 9 am, 1 pm, and 5 pm due to the occupancy, but this variance in energy consumption between buildings at any time mean they cannot be forecasted without appropriate methods. They are made from glass, brick, and concrete, depending on the building.
The buildings are located in London, Manchester, and Leeds in the United Kingdom, consisting of a two law firms, two banks, and a shared office space.
The NN are optimised through Bayesian optimisation to ensure they have the highest accuracy and to reduce unnecessary computational power use. There are five cross-validation folds, and they are all built from between two layers and four layers, all using rectified linear unit (ReLU) activation functions, and each layer has between two and six neurons. Bayesian optimisation is achieved through measuring various parameters in 10 iterations defined in Table 2.

Table 2.
The parameters search space among multiple and single neural networks.
Table 2, showing the parameters initially used to determine the search space for the optimiser.
Data is collected from energy meters installed in each building and the weather data is collected through local climate sensors. All data is stored in online databases and is accessed through an API. It contains all of the data used in this work at 1.4 MB after processing. It uses a HTTP protocol, has a JSON data format, has an API key to keep the data secure, and exports the file as a csv file to be used by the Python 3.12 programming language in the Spyder software. The training dataset includes energy demand, time of day, day of week, outdoor air temperature, outdoor wind speed, outdoor humidity, and precipitation. There are 50,000 iterations of seven inputs, totalling 350,000 datapoints. There are less than 3000 missing datapoints, but these are linearly interpolated to retain as much data as possible. Any clear outlying data, outside of 90% of the mean is removed. Maximum Relevance, Minimum Redundance (MRMR) feature selection is used to remove any features that are not important to the forecast of the energy consumption of the individual buildings. It keeps 80% of the inputs and removes the 20% with the less importance. This allows the NN to train faster and improves accuracy as it is training on the more important data.
The data is illustrated through Table 3.

Table 3.
The input data for training the machine learning models in this study.
Table 3, showing a benchmark comparison of the forecasts of energy consumption between different machine learning models is mean-actual-percentage-error. This is one of the comparisons used in this study.
The accuracy of the developed model is measured through mean-actual-percentage-error (MAPE), calculated with Equation (1).
where ‘’ is the number of forecast values, and ‘’ and ‘’ are actual and forecasted values for observation . This method of output accuracy allows even comparisons across a wide range of building sizes and functions.
The accuracy of the NN is used to calculate an accuracy coefficient. If an accuracy is below expected, with regard to the rest of the accuracies of the NN, then it can be multiplied to reduce the effect that it has on the target building’s energy forecast.
2.2. Ranking Neural Networks in the Distance Matrix
The categorical data from all the buildings for the NNs is illustrated in Figure 2.
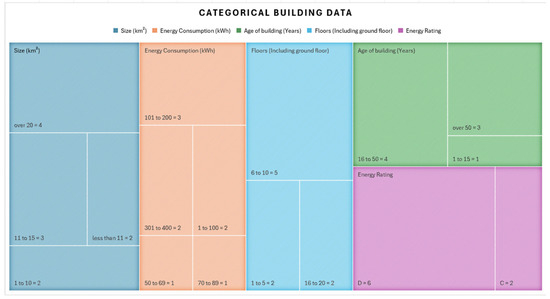
Figure 2.
Showing how the categorical data is split and how many buildings fit each category. There are no two buildings that fit each category the same. These are datasets that reflect accessible features that make up the building’s composition, affecting the energy consumption. The size of the floor space and total floors affect the energy consumption of the HVAC, the age of the building and energy rating affect insulation variously.
The distance matrix values are calculated by normalising the datasets per category of all observed buildings. The floor space ranges from 1.2 to 64.4 km2, the building age ranges from 14 to 160 years old, the total floors range from 4 to 17, the energy use ranges from 8 to 465 kWh, the energy performance grade is from 52 to 96, and the climate sum ranges from 106.0125 to 107.9472. The data is normalised as they all have different values such as total floors (1–15) being lower than energy consumption (1 kWh–400 kWh). This ensures that features with higher average values do not outweigh features with low average values that are measured differently. This data is then normalised through the following equations.
The distance between each building per category can be calculated through Equation (2).
where ‘’ is the average distance between the new building and each existing building, ‘’ is the total number of other buildings, ‘’ is the value of the new building per category, and ‘’ is the value of an existing building per category.
The calculated distances are then normalised through Equation (3).
where ‘’ is the original distance value, and ‘’ and ‘’ are the minimum and maximum values of the building data.
For the five buildings and six categories, there are 30 distances to be calculated, equal to five average distances, which is the normalised data calculated in Equation (3). These average values of each category and building are described through Figure 2.
The distance matrix values for the various categories are illustrated in Figure 3.
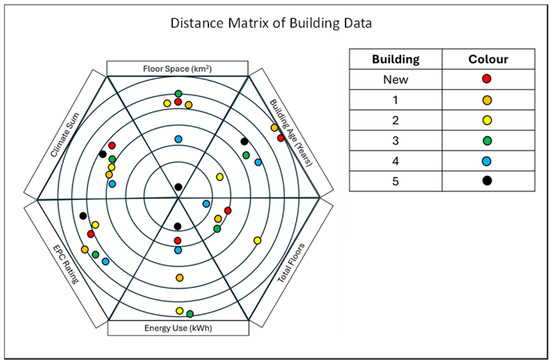
Figure 3.
Showing how the categories are used to create the distance matrix, consisting of floor space, building age, total floors, energy use, energy performance rating, and mean climate index.
The climate index is the sum of the average outdoor air temperature, outdoor wind speed, outdoor humidity, and precipitation over the year 2023 for the individual buildings. As some buildings have more extreme weather, the climate index increases, the internal energy consumers must work harder to maintain comfort, and therefore energy consumption increases. This relationship between the local climate and energy consumption is what is being addressed by splitting the buildings by the local climate index. The ‘New building’ or the ‘target buildings’ are an outlier on one occasion with the building age but present an average selection of variables for the rest of the data.
2.3. Employing and Attributing Significance Weights to Aggregate Neural Network Forecasts
As each office building in this work has similar features with one another, all existing buildings that have been collected can be used to forecast the energy consumption of the new building. This is achieved through employing the previously developed neural networks from other buildings, and then by multiplying the energy forecasts by the normalised distances calculated in Equation (2). The architecture is similar to that within the neural network, where each input value is assigned a weight to distribute importance among the network. This multiplies less valuable inputs by smaller numbers, and multiplies more valuable inputs by larger numbers. If the forecasts from the model are consistently over or under the actual historical values, the average errors can be stored and either subtracted or added to the forecast, improving the final accuracy. The average differences can be seen below.
The average difference per time of day between each existing building and the target building is calculated and then removed from each forecast. This is calculated through Equations (4)–(6).
where ‘’ and ‘’ are the average consumption at time ‘’ of the target building and the existing building. ‘’ and ‘’ are the number of datapoints for the target and existing building, ‘’ and ‘’ are the energy consumption of the target and existing building at a specified time of day. Once the average values for each building and each time of day are calculated, the difference can be removed from the existing building’s NN forecast.
where the energy consumption of the target building for the specified time and iteration ‘’ is adjusted ‘’. This is by subtracting the average difference between the target building and the existing building ‘’ for a specified time of day, from the NN forecast of the existing building ‘’. This ensures that buildings with different energy consumptions can be used to calculate the energy consumption forecast of a new building.
Finally, the weighted average from all NN forecasts can be calculated through Equation (7).
where ‘’ is the i-th value of the dataset, and ‘’ is the i-th weight corresponding to each NN as is calculated through Equation (2).
The weighted average of the NN is used to determine the optimal effect that each NN should have. This is achieved through a distance metric and an accuracy coefficient, both working the same way, and both improving the accuracy of the forecast. The input data is passed through the methodology presented previously, and the outcomes are explained next in the research.
3. Outcomes and Deliverables
There are an initial five buildings where all of the historical energy consumption, time, and weather data is available. A bespoke neural network has been developed per building and can forecast the energy consumption of between 5% and 40% error for hourly resolutions and a 24 h horizon. The aggregated neural network can forecast the energy consumption of the target buildings, but they are also used to forecast the energy consumption of the training buildings too, using the testing data from them set aside during training. This section is arranged by displaying the calculated matrix scores, then the initial neural network outputs, and finally the distance matrix multipliers and energy forecasts and accuracy are shown.
3.1. Distance Matrix Scores
The largest distance matrix score is the age of building two with a difference of 146 years compared to the target building. The smallest distance matrix is the total floors of building five as it matches the target building with four floors. The age of building one equalling one shows that this feature is furthest away from the target building, and building five having a total floor score of zero shows it is the closest in terms of feature similarity. The smallest other distance matrix is the energy performance rating of building four with a difference of 41 grades from the target building.
As shown in Table 4, the distance matrices are between zero and one, where one represents the variable of the existing building being the most similar to that of the target building, and zero being the furthest away.

Table 4.
The distance matrix scores between the new building one, and the already existing buildings one, two, three, four, and five after data standardisation.
Table 5, showing that the target building has the most similarities with the already-existing building four, and it has the least similarities with already-existing building three.

Table 5.
The average distance matrix scores between the new building one and the already-existing buildings one, two, three, four, and five.
3.2. Initial Neural Network Forecasts, Architectures, and Accuracy Coefficient Calculations
The already-existing building’s data is used to develop a bespoke NN, totalling five for this research. The NNs are trained and on various amounts of data depending on the building, but the target building has 1-year of randomised hourly data. The initial forecast accuracies and architectures are exhibited in this section. The architecture is illustrated in Table 6.

Table 6.
The architectures and mean-actual-percentage-errors of the initial developed neural networks for already-existing buildings one, two, three, four, and five, when forecasting their respective building’s energy consumption.
Table 6 shows the parameters used for the NN’s and that each building now has a bespoke NN that can forecast the energy consumption of the individual building that it is operating on. As each building has different environmental factors that affect the energy consumption, each NN is very different in regard to the parameter search space from Bayesian optimisation. They have not yet been used for the target building. The lowest error is from building three with 4.9923 MAPE and so it will have the largest accuracy coefficient to multiply the final output by. The largest error is from building five with 38.0303 MAPE and so it will have the smallest accuracy coefficient to multiply the final output by.
The accuracy of the single NN is explained through Table 7.

Table 7.
The average accuracy and architecture of the single neural network.
Table 7, showing the NN is trained with the 5 buildings’ data, where the value of energy consumption varies from 0 kWh to 700 kWh. It forecasts various buildings’ energy consumption with an error of 17.45% MAPE.
Table 8, showing the average optimised parameters of the LSTM-NN.

Table 8.
The average accuracy and architecture of the LSTM NN.
The accuracy coefficients are calculated by the standardisation of the forecast accuracies of the already-existing NN from buildings one, two, three, four, and five from Table 5 with Equation (4). These are presented in Table 9.

Table 9.
The normalised and transposed accuracy coefficients.
Once the input data from the new building is fed onto the already-existing NN, the forecasts can be multiplied by both the final distance matrix multiplier from Table 10 and the final accuracy coefficient. This ensures that the NNs with the highest errors have less effect on the final forecast than the NNs with the lowest errors.

Table 10.
Showing the average forecast errors between each building and the target building, the average error when the overall kWh difference is removed from each forecast, and then the average error when the positive or negative percentage error is removed per time series forecast.
3.3. Distance Matrix Multipliers and Accuracy Coefficient Improvements
The output energy forecasts of the initial NN can be used to represent the target building by multiplying the outputs by the distance matrix multiplier and the accuracy coefficient. The forecasts from the already-existing NNs are multiplied by the distance matrix multiplier and the accuracy coefficient to present a final forecast value. These values are presented in Table 10.
The NN from each building is activated and an energy consumption is forecasted, one by one from building one until building five. An example of this process in action can be explained through the following. Initially, the actual value of the target building at a specified time is 143 kWh. The forecasted values of the other NNs are 185, 123, 194, 210, and 71 kWh, respectively. The weighted average of the NN forecasts using Equation (2) and the values from Table 5 is 153.9 kWh which is closer than any other NN forecasts. This varies throughout the testing dataset, but the same principle is used. The average error between the forecasted and actual energy consumption for each time value of the day is calculated and removed from the forecasted value to improve accuracy further in the final column. Removing the average positive or negative error from the original error improves them by 1.7% across the five NNs.
The computational power, time taken to run, and the MAPE accuracy for each method are described through Table 11.

Table 11.
The total computational power for the single NN, the LSTM NN, and the aggregated NN when forecasting the energy consumption of the target buildings.
The accuracy of the ANN is further improved by removing the average positive or negative error from the forecasts as is described in Table 11. The aggregated NN is superior in time taken to train, space required, and with how much data is required to forecast the building’s energy consumption. The target building has 1 year of data to be tested with. This is significant to show that the results are trustworthy. A year of data includes all seasons and building functions throughout the year, giving a wider range for variables such as temperature, humidity, occupancy patterns, and energy consumption under diverse conditions. This comprehensive dataset allows the model to be robustly validated against a full cycle of operational and environmental influences, enhancing confidence in its predictive accuracy and generalizability beyond a single season or limited operational period. From 20 forecasts achieved, the average accuracy achieved from the ANN is 85.11% and the average accuracy achieved by the single NN is 82.96%. The average time taken to train is 641 s and 859 s for the ANN and NN, respectively. The average space required to store the model is 512 kB and 229 kB for the ANN and NN, respectively. More forecasts could have been achieved, and the results could change, but extending the number of forecasts does not produce a proportional increase.
4. Description and Interpretation of Results
For this investigation of energy consumption forecasting, three distinct models are implemented as follows: a Long Short-Term Memory network (LSTM) (last in Table 11), a single large Feedforward Neural Network (FFNN) (first in Table 11), and an Aggregated Neural Network (ANN) (second in Table 11). They are developed and tested on the five training buildings, and then tested on the target building. The results revealed that the ANN outperformed both the LSTM and the single NN, achieving an accuracy of 82.92%, while the LSTM and single NN achieved 82.55% and 76.7%, respectively. The accuracy of the developed model shows that when it has similar buildings in terms of the features selected in this study, it can produce an accurate forecast. It cannot be determined how accurate the forecasts would be for other building types or in very different climates. Factors that may greatly affect this are location—such as the UK is a wet and mild climate—size, and function. The buildings in this study are office buildings and so they consistently operate from 9 am until 5 pm, whereas industrial buildings, for example, would have extremely different operating patterns. The algorithms would not be able to forecast for a building in which there is a sparse similarity and if they have not seen any historical data before either.
The aim of this research is to develop a method to reduce or eliminate historical data needed to develop an accurate neural network to forecast the energy consumption of non-domestic buildings. Table 11 illustrates that the proposed method does not require historical data for the data used in this research, whereas the other models do require historical data.
4.1. Model Architecture and Complexity
The architecture of each model plays a pivotal role in its performance. The LSTM, designed to capture temporal dependencies, leverages memory cells to retain information over extended sequences. However, this architecture might not be well-suited for capturing complex relationships present in our diverse dataset, leading to a slightly lower accuracy compared to the Aggregated Neural Network.
The large FFNN, with its expansive hidden layers, may encounter challenges in learning intricate patterns within the dataset. Despite its capacity to model complex relationships, the potential for overfitting could be higher, affecting its overall accuracy. In contrast, the Aggregated Neural Network, constructed by combining multiple smaller neural networks, capitalises on the strengths of individual networks while mitigating the risk of overfitting. This adaptability to diverse patterns contributes to its superior accuracy.
Although this work shows the time taken to train the various methods, it does not show time taken to actually use the methods with regard to forecasting the energy consumption. The FFNN, the ANN, and LSTM can all forecast and aggregate the results where necessary within 10 s, so this is not a problem for situations such as with forecasting for a month or more of data.
4.2. Data Representation and Feature Importance
The representation of input features is crucial in energy consumption forecasting. The choice of features such as temperature, humidity, pressure, and wind speed, along with building-specific attributes, introduces a multidimensional aspect to the dataset. The Aggregated Neural Network may inherently excel at discerning intricate relationships among these features, resulting in superior accuracy.
Moreover, the aggregation of neural networks allows for specialised focus on subsets of features, enabling each sub-network to become an expert in understanding specific patterns. This modularized approach ensures that the overall model comprehensively captures the nuances present in the diverse features of our dataset.
The data required in the proposed method is more of that which might be necessary for previous methods mentioned in the literature review. This is because the distance matrix is needed to determine which buildings are most similar and different from the target building. This is a limitation as other data sources are required which building owners may not be willing to part with. Alternatively, the ability to work without historical energy consumption data whereas other models require this is a benefit.
The represented data includes all seasons of data, but the accuracy of the models throughout the seasons does not vary drastically with the season when they have historical data of a year or more. When there is an extreme change such as in Spring 2024 where the temperature increased for 2 weeks, the models’ forecasts become inaccurate due to not seeing the extreme temperature data before. The accuracy of the models drops when, for example, they have only been trained with the seasons of spring and summer, and they are trying to forecast for winter. This occurs because the temperature has dropped below a point which the model has seen before. All it can do is linearly calculate a forecast from the minimum temperature it has seen in the training data. This is often inaccurate due to the non-linear relationships between the training data and the energy consumption.
A logical problem arises through the operation of the buildings. For office buildings, they have the same operation, whereas if an industrial building were added into the distance matrix with no data, the forecast could be drastically different due to the building not operating the same as office buildings. In this circumstance, this would not be appropriate.
4.3. Computational Efficiency
While achieving the necessary accuracy, the Aggregated Neural Network consumes the least computational power among the three models. This efficiency is attributed to the hyperparameter tuning of the individual models. They can be controlled through defined Bayesian optimisation iterations, and each model can have a different selection of hyperparameters. This ensures there is less wasted computational complexity within the individual models than with the large FFNN that requires a model as complex as is necessary to calculate the most complex relationship with the dataset.
In contrast, the LSTM, with its sequential processing, incurs higher computational costs due to the necessity of processing data in a stepwise manner. The large FFNN, with its extensive hidden layers, demands considerable computational resources during training and prediction. The efficiency of the Aggregated Neural Network positions it as an attractive option for real-world applications where computational resources are a critical consideration.
4.4. Generalisation and Data Specificity
The dataset containing information from five different buildings, with a total of 16,329 data iterations, introduces a level of complexity and diversity. The Aggregated Neural Network’s ability to generalise well across various building characteristics and patterns suggests a robustness that the other models may struggle to achieve. For real-world deployment, the forecasting accuracy of the five buildings used for training is as important as the accuracy of the three testing buildings. The ANN has higher forecasting accuracy for the training building’s 20% of testing dataset aside.
In conclusion, the Aggregated Neural Network’s superior accuracy and computational efficiency can be attributed to its adaptability, modularized approach, and proficiency in capturing intricate relationships within the diverse dataset. This research underscores the importance of considering different neural network architectures for specific forecasting tasks, as model performance can significantly vary based on the dataset’s characteristics and the task at hand.
Although the proposed method does not require large historical datasets, it still requires there to be some information about the target building such as hourly energy consumption, age, location, etc. It still requires data about the building, but less data is required than for conventional methods of energy consumption forecasting.
The data in this work consists of only office buildings, but with a varied energy consumption and locations in the UK, from London to Leeds, showing variability in the data, and thus the generalisation of the proposed method. The large datasets in this work can be controlled through batch sizes of each NN. Although the batch size can be controlled, the actual data that is being used cannot and there is a chance that data will be missed from a specific building if it is limited. Therefore, when the large FFNN is forecasting a target building to the building with limited data, it has not learned the relationships to a high enough degree and cannot forecast accurately. The limited number of buildings does not favour the ANN method in this work. More buildings can be added to the model to provide more accurate average weighted outputs, and therefore more accurate forecasting.
5. Conclusions
In conclusion, this journal article introduces a novel machine learning approach for forecasting the energy demand of commercial buildings in the context of the UK government’s target for a fully decarbonized energy grid by 2050. The proposed method, an Aggregated Neural Network (ANN), combines bespoke models with pre-existing energy data to provide accurate energy consumption forecasts for both new and existing buildings.
The study addresses the challenge posed by the sheer volume of non-domestic buildings in the UK, highlighting the impracticality of traditional forecasting methods for each building due to extensive data collection requirements. The proposed model leverages available data such as floor space and function, positioning a new building within the matrix of existing data. A distance metric, similar to a K-nearest neighbour algorithm, is used to determine the appropriate neural network(s) to utilise.
Results indicate that the ANN outperforms Long Short-Term Memory (LSTM) networks and the NN in terms of accuracy. The ANN trains faster and gives more control than the other methods as each NN can be controlled independently instead of all of them as a whole. The ANN (85.12%) (500 kB) produces a higher accuracy than the FFNN (82.55%) (238 kB) and the LSTM (76.7%) (1100 kB) while requiring less space than the LSTM but more than the FFNN. The ANN also has faster training (610 s) than the FFNN (870 s) and LSTM (1620 s), respectively. This research emphasises the potential of the novel approach in providing accurate and insightful energy management strategies, contributing not only to the goal of a fully decarbonized energy grid by 2050 but also establishing a robust and efficient methodology that may be improved on by adding more data or by using more complex algorithms.
Future work could explore the scalability of the proposed model to a broader range of building types and regions. Additionally, refining the distance matrix calculations and exploring the model’s sensitivity to variations in input parameters could enhance its overall effectiveness. Furthermore, wider validation and testing will provide results on how well this can be generalised, allowing the application to more non-domestic buildings. Further research might also consider real-world implementation and validation of the proposed approach in diverse settings to assess its applicability and performance under different conditions. This work can be advanced further by gathering a larger set of buildings with larger differences, such as industrial buildings or buildings in largely different climates. More data regarding buildings allows the model to generalise further, but also to be more accurate, as logically, more buildings will be similar to the target building if enough data is gathered.
Author Contributions
Conceptualization, C.S. and A.A.; Methodology, C.S.; Software, C.S.; Validation, C.S. and A.A.; Investigation, C.S.; Resources, C.S.; Data curation, C.S.; Writing—original draft, A.A. and C.S.; Writing—review & editing, C.S. and A.A.; Visualization, C.S.; Supervision, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| ANN | Aggregated Neural Network |
| FFNN | Feed-Forward Neural Network |
| NN | Neural Network |
| LSTM | Long-Short Term Memory |
| MAPE | Mean-Actual-Percentage-Error |
References
- UK Enshrines New Target in Law to Slash Emissions by 78% by 2035. Available online: https://www.gov.uk/government/news/uk-enshrines-new-target-in-law-to-slash-emissions-by-78-by-2035#:~:text=The%20government%20is%20already%20working,a%20major%20economy%20to%20date (accessed on 15 July 2025).
- Available online: https://assets.publishing.service.gov.uk/media/66a7da1bce1fd0da7b592f0a/DUKES_2024_Chapter_5.pdf (accessed on 15 July 2025).
- The Non-Domestic National Energy Efficiency Data-Framework 2023. Available online: https://assets.publishing.service.gov.uk/media/64e62d47db1c07000d22b345/nd-need-2023-report.pdf (accessed on 15 July 2025).
- Ahmad, T.; Chen, H. Nonlinear autoregressive and random forest approaches to forecasting electricity load for utility energy management systems. Sustain. Cities Soc. 2019, 45, 460–473. [Google Scholar] [CrossRef]
- Saxena, N.; Kumar, R.; Rao, Y.K.S.S.; Mondloe, D.S.; Dhapekar, N.K.; Sharma, A.; Yadav, A.S. Hybrid KNN-SVM machine learning approach for solar power forecasting. Environ. Chall. 2024, 14, 100838. [Google Scholar] [CrossRef]
- Ciulla, G.; D’Amico, A. Building energy performance forecasting: A multiple linear regression approach. Appl. Energy 2019, 253, 113500. [Google Scholar] [CrossRef]
- Fathi, S.; Srinivasan, R.; Fenner, A.; Fathi, S. Machine learning applications in urban building energy performance forecasting: A systematic review. Renew. Sustain. Energy Rev. 2020, 133, 110287. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, R.; Cao, J.; Tan, J. A CNN and LSTM-based multi-task learning architecture for short and medium-term electricity load forecasting. Electr. Power Syst. Res. 2023, 222, 109507. [Google Scholar] [CrossRef]
- Jahani, A.; Zare, K.; Khanli, L.M. Short-term load forecasting for microgrid energy management system using hybrid SPM-LSTM. Sustain. Cities Soc. 2023, 98, 104775. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Rajasekar, E.; Natarajan, S.; McCullen, N. A comparative assessment of SARIMA, LSTM RNN and Fb Prophet models to forecast total and peak monthly energy demand for India. Energy Policy 2022, 168, 113097. [Google Scholar] [CrossRef]
- Ramos, D.; Faria, P.; Gomes, L.; Campos, P.; Vale, Z. Selection of features in reinforcement learning applied to energy consumption forecast in buildings according to different contexts. Energy Rep. 2022, 8, 423–429. [Google Scholar] [CrossRef]
- Al-Yaseen, W.L.; Idrees, A.K.; Almasoudy, F.H. Wrapper feature selection method based differential evolution and extreme learning machine for intrusion detection system. Pattern Recognit. 2022, 132, 108912. [Google Scholar] [CrossRef]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol 2005, 3, 185–205. (In English) [Google Scholar] [CrossRef]
- Qiao, Q.; Yunusa-Kaltungo, A.; Edwards, R.E. Developing a machine learning based building energy consumption prediction approach using limited data: Boruta feature selection and empirical mode decomposition. Energy Rep. 2023, 9, 3643–3660. [Google Scholar] [CrossRef]
- Zhao, Z.; Anand, R.; Wang, M. Maximum Relevance and Minimum Redundancy Feature Selection Methods for a Marketing Machine Learning Platform. arXiv 2009. [Google Scholar] [CrossRef]
- Joy, T.T.; Rana, S.; Gupta, S.; Venkatesh, S. Fast hyperparameter tuning using Bayesian optimization with directional derivatives. Knowl.-Based Syst. 2020, 205, 106247. [Google Scholar] [CrossRef]
- Mariano-Hernández, D.; Hernández-Callejo, L.; Solís, M.; Zorita-Lamadrid, A.; Duque-Perez, O.; Gonzalez-Morales, L.; Santos-García, F. A Data-Driven Forecasting Strategy to Predict Continuous Hourly Energy Demand in Smart Buildings. Appl. Sci. 2021, 11, 7886. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Li, Y. Electrical Energy Demand Forecasting Model Development and Evaluation with Maximum Overlap Discrete Wavelet Transform-Online Sequential Extreme Learning Machines Algorithms. Energies 2020, 13, 2307. [Google Scholar] [CrossRef]
- Moon, J.; Park, J.; Hwang, E.; Jun, S. Forecasting power consumption for higher educational institutions based on machine learning. J. Supercomput. 2018, 74, 3778–3800. [Google Scholar] [CrossRef]
- Lin, J.; Fernández, J.A.; Rayhana, R.; Zaji, A.; Zhang, R.; Herrera, O.E.; Liu, Z.; Mérida, W. Predictive analytics for building power demand: Day-ahead forecasting and anomaly prediction. Energy Build. 2022, 255, 111670. [Google Scholar] [CrossRef]
- Pallonetto, F.; Jin, C.; Mangina, E. Forecast electricity demand in commercial building with machine learning models to enable demand response programs. Energy AI 2022, 7, 100121. [Google Scholar] [CrossRef]
- Gao, Z.; Yu, J.; Zhao, A.; Hu, Q.; Yang, S. A hybrid method of cooling load forecasting for large commercial building based on extreme learning machine. Energy 2022, 238, 122073. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R. Deep learning forecasting for electric demand applications of cooling systems in buildings. Adv. Eng. Inform. 2022, 53, 101674. [Google Scholar] [CrossRef]
- Ahmad, T.; Chen, H. Short and medium-term forecasting of cooling and heating load demand in building environment with data-mining based approaches. Energy Build. 2018, 166, 460–476. [Google Scholar] [CrossRef]
- Sala-Cardoso, E.; Delgado-Prieto, M.; Kampouropoulos, K.; Romeral, L. Activity-aware HVAC power demand forecasting. Energy Build. 2018, 170, 15–24. [Google Scholar] [CrossRef]
- Mohammadi, M.; Talebpour, F.; Safaee, E.; Ghadimi, N.; Abedinia, O. Small-Scale Building Load Forecast based on Hybrid Forecast Engine. Neural Process. Lett. 2018, 48, 329–351. [Google Scholar] [CrossRef]
- Munem, M.; Bashar, T.M.R.; Roni, M.H.; Shahriar, M.; Shawkat, T.B.; Rahaman, H. Electric Power Load Forecasting Based on Multivariate LSTM Neural Network Using Bayesian Optimization. In Proceedings of the 2020 IEEE Electric Power and Energy Conference (EPEC), Edmonton, AB, Canada, 9–10 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).