Risk and Uncertainty in Geothermal Projects: Characteristics, Challenges and Application of the Novel Reverse Enthalpy Methodology

Abstract

A reliable geothermal risk assessment methodology is key to any business decision. To be effective, it must be based on widely accepted principles, be easy to apply, be auditable, and produce consistent results. In this paper, we review the key characteristics of a geothermal project and propose a novel approach derived from risk and uncertainty definitions used in the hydrocarbon industry. According to the proposed methodology, the probability of success is assessed by estimating three different components. The first is the geological probability of success, which is the likelihood that the geological model on which the geothermal project is based is correct and that the key fundamental geological elements are present. The second, the temperature threshold, is defined as the probability that the fluid is above a certain reference value. Such a reference value is the one used to design the development. Such a component, therefore, depends on the end use of the geothermal resource. The third component is the commercial probability of success and estimates the chance of a project being commercially viable using the Reverse Enthalpy Methodology. Geothermal projects do not have a single parameter that represents their monetary value. Therefore, in order to estimate it, it is necessary to make an initial assumption that can be revisited later in an iterative manner. The proposed methodology works with either the capital expenditure of the geothermal facility (power plant or direct thermal use) or the drilling cost as the initial assumption. Varying the other parameter, it estimates the probability of having a net present value (NPV) higher than zero.

1. Introduction

This article is a revised and expanded version of a paper entitled Risk and Uncertainty Assessment for Geothermal Projects using Reverse Enthalpy Methodology, which was presented at the European Geothermal Congress 2025—EGEC 2025, Zurich, Switzerland, 6–10 October 2025 [1].

Geothermal development projects are subject to a wide range of risks that could affect their viability. These include operational, environmental, regulatory, and financial risks. These factors are critical to project success and are usually evaluated using sensitivity analysis. However, this paper focuses specifically on exploration risk and subsurface uncertainty, which are particularly important during the early stages of project development. The two most critical parameters governing the economic feasibility of a geothermal project are uncertainty regarding reservoir temperature and sustainable productivity. Unlike other types of risk, subsurface uncertainties directly impact resource classification, investment decisions and long-term performance expectations. This necessitates a dedicated, geo-scientifically rigorous assessment framework.

Several excellent studies in the literature focus on defining risk and uncertainty in geothermal projects, often attempting to adapt risk assessment principles that were originally developed for the oil and gas industry [2,3,4,5,6,7,8,9,10].

In this paper, we propose a consistent and integrated methodology for assessing geological risk and uncertainty, as well as the commercial probability of success (PoS), in geothermal projects. Inspired by established practices in the hydrocarbon industry, our approach involves systematically analysing and evaluating critical parameters through a multi-stage process. Based on these principles, we present the Reverse Enthalpy Methodology (REM), which is specifically designed for the unique characteristics of geothermal developments. The key advantage of this methodology is its ability to quantify the relationship between subsurface risk and project economic performance, as measured by net present value (NPV). This comprehensive framework provides a more coherent, project-specific risk assessment and effectively bridges a gap in current evaluation models, which is particularly valuable in contexts in which data are scarce or in the early stages of geothermal exploration.

In principle, the approach can be applied to all types of geothermal fields, whether conventional or EGS (Enhanced Geothermal Systems), for any use, including direct heat or power generation. It is also fully compatible with the PRMS and UNECE classification systems [11,12,13,14]. A key benefit of the approach is that it allows self-consistent comparison and ranking of a portfolio of multiple geothermal project opportunities pre-drill, even if they have very different technology deployments or development cases. While many historical treatments have considered the technical risks of geothermal projects at various stages of maturity, the ability to derive and compare the likelihood of commercial success for many projects of varying investment, technology, maturity, and development case is transformative for geothermal portfolio management and scalability.

2. Geological Risk, Uncertainty, and Probability of Commercial Success

In this section, we present the key principles of the oil and gas industry so that they can be most effectively adapted to the very different characteristics of the geothermal context.

2.1. Exploration Geological Risk

In the petroleum industry, the concept of geological risk is often defined as the probability of drilling a well and not finding flowable hydrocarbons [15,16,17]. This risk in a hydrocarbon context is directly related to the presence or absence of the fundamental geological elements of a hydrocarbon field. The absence of one of these fundamental elements (source rock, reservoir, etc.) or the wrong timing is sufficient to prevent the accumulation of hydrocarbons. Geological risk is therefore represented by a binary distribution: success or failure. Note that colloquially, we talk about risk, but when we evaluate a project, we calculate the probability of geological success (Pg). The conversion is straightforward:

Pg = 100% − risk

(1)

Providing an exhaustive description of the methodology for calculating Pg according to the oil and gas industry’s best practices is beyond the scope of this paper. Further details can be found in Rose (2001) [16] and Cook (2021) [17], as well as in the extensive bibliographies of these two key references. However, a brief overview of how such a calculation is performed is provided below. Pg is estimated by systematically gathering and refining judgements from exploration team members. To remove as much subjectivity as possible from the estimation, the judgements are subjected to a peer review process by independent experts through multiple rounds of review. This method facilitates a convergence of informed opinions on key geological elements. This approach enhances transparency in risk assessment and provides a defensible basis for investment decisions, particularly in situations in which direct measurements are limited or ambiguous.

2.2. Uncertainties and Probability Distribution Function

Uncertainty signals a lack of knowledge about the extent or magnitude of a parameter. In relation to recoverable hydrocarbons, uncertainty is represented by the question following: have we found a very small quantity of hydrocarbons or a huge quantity? Probability distribution functions (PDFs) are a powerful and widely used method for describing uncertainty. They provide a complete characterisation of uncertainty by assigning a probability to each possible value a parameter can take. This probabilistic representation not only defines the range of possible values but also conveys essential statistical information, such as the central tendency (mean, median, and mode) and the spread (variance and standard deviation), enabling a comprehensive understanding of both the expected value and the variability of the parameter. The standard deviation, variance, and P10/P90 ratio of the PDF are all common and effective measures of the uncertainty level. The Monte Carlo method combines multiple PDFs of different parameters with defined relationships between them to model complex uncertainties. PDFs can be described loosely by the shape they take and the best approximating mathematical functions corresponding to that shape. In a “normal” distribution, the mean, P50, and mode are the same, but in a “lognormal” curve, the mean is higher than the P50 and much higher than the mode. In nature, simple parameters tend to have a normal distribution [18]. More complex variables that depend on a multiplication of individual distributions—including resource volumes in the geosciences—tend to be lognormal by virtue of the central limit theorem [18,19]. The cumulative distribution function (CDF) can be used instead as an equivalent (Figure 1). A CDF is simply a different way of presenting a given PDF. In a CDF, “P50” defines the value around which 50% of the outcomes are higher and 50% are lower. Similarly, “P10” has 10% of the values higher and 90% lower, and finally, “P90” has 90% of the values higher, and so on. Note that institutional conventions may differ, with P(x) and P(100 − x) definitions interchanged (e.g., P90 and P10, etc.). The CDF is an effective tool because it reveals, at a glance, the probability of achieving a result less than or greater than a certain threshold value.

A comprehensive description of the methodology for constructing a cumulative distribution function (CDF) in alignment with best practices established by the oil and gas industry lies beyond the scope of this paper. For an in-depth treatment of the topic, the reader is referred to the papers by Rose (2001) and Cook (2021), both of which offer extensive bibliographies that further support the subject. Nevertheless, a concise summary of the key steps involved in the calculation is presented below. In general, a cumulative distribution function (CDF) can be derived directly from empirical data or estimated using expert geological judgement. When constructing a CDF from an analogue dataset, the relative frequency of observed values is interpreted as a proxy for their probability, based on the assumption that values that occur more frequently are also more probable. However, this method is only valid when the dataset is representative of the parameter of interest and reflects the same geological conditions. If an appropriate dataset is unavailable, a CDF can be developed based on the geoscientist’s conceptual understanding of, and expert knowledge about, the geological system. The first step is to select a suitable theoretical distribution, typically either normal or lognormal, depending on the nature of the parameter. These distributions can be easily defined using commercially available software, which requires two input parameters, such as P10, P50, or P90, or statistical moments like the mean and standard deviation. A knowledgeable geoscientist can then adjust these inputs iteratively until the resulting CDF aligns with their expectations, is consistent with known geological constraints, and reflects expert interpretation. As with Pg estimation, to minimise subjectivity in the estimation process, the assessments undergo iterative, structured peer review by independent experts.

2.3. Probability of Commercial Success

In the oil and gas industry, the volume of recoverable hydrocarbons in a field is the key variable in determining the value of a project. Larger fields are proportionally more profitable. This is due to economies of scale: the cost per barrel of oil produced decreases as the size of the field increases. The resource distribution for an exploration prospect includes possible results that are too small to be commercial.

A CDF is therefore characterised by a portion that is commercial and a portion that is not. These two portions can be distinguished by calculating the minimum commercial field size (MCFS) of an exploration project (Figure 2) [16,17]. The MCFS is the volume of resources that has a net present value (NPV) of zero: the “breakeven” value. All possible results greater than the MCFS are commercially viable and have an NPV greater than zero. NPV is a term that incorporates the time value of money—and associated “discount rates”—which vary with company ambitions and interest rates in different locations.

The probability of finding resources equal to or larger than the MCFS is defined as the probability of commercial success (Pc).

2.4. Overall Probability of Success of an Exploration Oil and Gas Project

Thus, Pg (as seen in Section 2.1) is the probability of making a discovery, while Pc is the probability that such a discovery is large enough to have an NPV equal to or greater than zero [17]. Therefore, the probability of finding a commercial amount of hydrocarbon is the combined probability of Pg and Pc:

Total PoS of an exploration project = Pg × Pc

(2)

Similar to an oil and gas exploration project, such an approach can be used to estimate the PoS of a geothermal exploration project. However, defining the right parameter to use to estimate it is not as straightforward as in the hydrocarbon industry. This issue is discussed in the following sections.

3. Framing Risk and Uncertainty of a Geothermal Project

Geothermal energy is a renewable energy source that harnesses heat from the Earth’s interior. Some geothermal exploitations utilise water or steam fluids already present within rocks (hydrothermal), and others rely on the heat of drier rocks and either engineered permeability or conduction of heat into fluids in a wellbore (petrothermal). We address the hydrothermal case in this paper as the one with the most generically applicable set of risk elements, but the principles can be applied to petrothermal applications.

From a hydrothermal reservoir, hot fluids are produced to the surface through wells and used to generate electricity or provide direct heating. To apply the above principles, we differentiate elements to be considered in the risk system and those parameters affecting the level of uncertainty of the geothermal project.

3.1. Key Premises and Assumptions of the Risk System

3.1.1. Key Geological Elements

The importance of key geological elements such as fluid temperature and chemistry, reservoir permeability, sealing properties, etc., in geothermal systems varies depending on the development chosen.

For a given geology, the temperature of the geothermal fluid (for a single-phase geothermal system) may be a key risk factor for power development, but not for direct heat use. The “PoS must therefore be estimated as a function of the end use”. There is no single universal PoS for the project; there are as many as there are development scenarios. In some cases, the absence of one of these elements can lead to the complete failure of the project. In other cases, the cause of failure is not the total absence of the element, but “not enough presence” (e.g., insufficient reservoir permeability). Heat is the primary and unambiguous requirement, and beyond its mere presence, we need a replenishable flow of heat over the life of a geothermal project. Without this, there is no geothermal project. However, the presence of an “anomalous” heat source is not always essential for geothermal development. Convective intra-reservoir fluid flow can result in a geothermal field even in the absence of a crustal thermal anomaly. Alternatively, a generous financial incentive (e.g., a high feed-in tariff) may also influence the range of geothermal gradients that can be developed. Anomalously high heat flow helps geothermal development, but it is not always a prerequisite. There are many examples in which average heat flow is sufficient [20,21,22].

The importance of the remaining components—the aquifer, reservoir, seal, and favourable structural framework (Figure 3)—can vary. Water is essential as the primary heat carrier in any hydrothermal application of geothermal energy. However, with the advent of EGS and closed-loop systems [23,24,25], it is possible to consider the artificial introduction of fluids as heat carriers that are not already present in the system. In such cases, the initial presence of in situ reservoir water can be considered non-essential. In some geothermal settings, such as an intra-reservoir convecting water cell, a topography-driven advection flow, or a steam-dominated geothermal fluid, there is also a need for a confinement system with a seal and an overall favourable structural setting that acts as a trap. Other settings may be less reliant on a seal aspect.

3.1.2. Risk Factors for a Geothermal Project

To identify critical factors for success in a geothermal exploration project, we reviewed existing look-back studies. The causes of geothermal well failure are risk factors that affect future success. Few published studies provide the overall success rate of geothermal projects [26,27,28,29,30], but the International Finance Corporation report “Success of Geothermal Wells: a global study” provides useful insights [31]. Among the various reasons for failure highlighted in the 2013 IFC report [31], the following risk factors form the basis of the proposed risk system:

• Inadequate temperature;
• Inadequate well deliverability (reservoir permeability);
• Unacceptable geothermal fluid chemistry (e.g., too much non-condensable gas—CO₂, corrosive or scale forming).

3.1.3. Failure as Inability to Reach a Threshold

IFC (2013) noted in their report that “a dry well is a rarity—almost all wells flow to some extent” and “a well was only considered successful if the capacity was above a certain threshold” [31]. This is a key observation incorporated in the proposed system. In our experience, although there are many cases in which the success/failure distribution follows the typical oil and gas binary distribution (e.g., incorrect overall geological model, well drilled in recharge zone, etc.), there are many others in which the definition of “success” is more ambiguous, as per the IFC (2013) description [31]. In particular, the success of a project is often linked to the probability of having a flow rate per well and/or a fluid temperature above a certain threshold. The values of both parameters can be represented in terms of a CDF that describes the uncertainty. The CDF may be determined—either analytically or empirically—according to the procedure briefly described in Section 2.2. Such a threshold is a value somewhere on the CDF. The risk can be calculated once the shape of the CDF and the threshold are known. We call this “uncertainty-risk translation” and the corresponding probability “threshold risk”. The method of translating CDF uncertainty into risk described for Pc (Section 2.3) can also be used in this technical threshold case. Section 4.6 and Section 4.7 give examples of threshold risk assessments for fluid temperature and well deliverability.

3.2. Parameters Affecting the Uncertainty of a Geothermal Project

The volume of recoverable hydrocarbons in barrels of oil equivalent is the parameter that best defines a hydrocarbon field and describes the uncertainty in the value of an oil and gas project. In geothermal, there is no single, universally accepted equivalent parameter for reporting geothermal resources. Most existing methods for evaluating a geothermal resource focus on defining the heat of the system. Multiplying this by a heat recovery factor and a conversion efficiency value, they define the equivalent MWe capacity of the system. In our view, such a methodology is excellent for describing the potential of an area/region or for verifying that the proposed development can be safely supported by the regional heat system. However, the weakest link in these methodologies is that they do not address an aquifer’s ability to provide the well flow rates needed to sustain a geothermal plant through its project life.

To simplify the explanation of the proposed methodology, we assume a single-phase geothermal fluid, which allows us to use temperature instead of enthalpy. For two-phase systems, the proposed methodology is still applicable but requires consideration of the overall fluid flow rate and enthalpy, rather than the fluid flow rate and temperature. The applicability of the proposed methodology to two-phase systems is discussed briefly in Section 5.3 (Critical Factors of REM).

In a single-phase, low-to-medium enthalpy system, the recoverable thermal power (Pth) is given by the following equation [32,33]:

Pth = c_p × ṁ × (T_wh − T_ref) = c_p × ṁ × ΔT_wh−ref

(3)

where

• Pth is the recoverable thermal power;
• c_p is the heat capacity of the fluid;
• ṁ is the extractable mass flow rate;
• T_wh is the temperature of the produced fluid at the wellhead;
• T_ref is the reference temperature (usually the reinjection temperature);
• ΔT_wh−ref is the temperature differential.

Equation (3) illustrates the key parameters that underpin the exploitation of such a resource. Firstly, T_wh (fluid wellhead temperature) determines the type of energy use (e.g., power generation, direct heat usage, or thermal bath). High-enthalpy systems are characterised by higher efficiency in converting heat to power, which makes it possible to generate electricity there (Figure 4). The amount of thermal power extracted per unit mass is determined by Δ T_(wh−ref), where T_ref depends on the geochemistry of the fluids: the temperature of the reinjected fluids is chosen to avoid chemical precipitation and scaling problems. Finally, the total amount of extractable thermal power heat energy per unit time depends on the mass flow rate (ṁ) and the temperature differential Δ T_(wh−ref)). Equation (3)’s multivariate nature captures flow and temperature as the critical parameters, particularly when we convert thermal power into electricity.

Figure 5 conceptually shows the relationship between these two parameters for a 20 MW binary plant. The graph is not a straight line: higher-temperature fluids are more efficient at generating electricity than lower-temperature fluids (Figure 6) [34,35,36].

They require proportionally less “heat” to produce the same amount of electricity. Temperature and flow rate must always be considered together. If the temperature of an exploration well is lower than expected, such a deficit can be compensated by increasing the flow rate. A higher flow rate can be achieved by bringing more wells into production if the geothermal aquifer can support it. Conversely, if the fluid temperature is higher than expected, fewer wells can be drilled to supply the chosen plant, resulting in a better economic return on the project.

In theory, the amount of thermal power Pth of Equation (3) converted for a binary plant in electrical power, according to the graph reported in Figure 6, could be used to represent the value of a geothermal project in a similar way to recoverable hydrocarbons in an oil and gas project. It combines flow rate with fluid temperature but leaves a high degree of ambiguity. Figure 7 illustrates this ambiguity very well; it shows the relationship between temperature and CAPEX (capital expenditure) per MW of installed capacity for three different sizes of binary plants. At lower temperatures, the CAPEX per MW increases significantly. Figure 6 and Figure 7 were developed by the author based on calibration points obtained from studies constrained by commercial confidentiality.

Furthermore, a combination of low temperature and high flow will have a very low efficiency, requiring a large number of wells, making the project uneconomic (Figure 5 and Figure 6). Therefore, Pth alone, without knowing its temperature, is meaningless in terms of representing the value of the project. In practice, a geothermal power project is unlikely to be economically viable at temperatures below 140 °C unless the reservoir is very productive or the subsidy is very generous.

We conclude that temperature and flow rate per well must be considered together, but at the same time, they must be analysed separately to assess their different impacts on the value of the project.

4. The Proposed Risking System

4.1. The Components of the Probability of Success of an Exploration Geothermal Project

In line with the key premises described so far, we define geothermal risk as “the probability that one or more of the key parameters (i.e., fluid temperature, fluid chemistry and well deliverability) are “absent” or “worse” than expected, such that the associated development case is not applicable as intended.”

Therefore, PoS considers two distinct types of components:

• A Geothermal Geological PoS (Pg) related to the “absence” of one or more of the key elements, possibly due to a fundamental misinterpretation of geology and/or a completely unexpected geological condition. This component follows the typical binary success/failure distribution of an oil and gas exploration project. In general, Pg is independent of the development scheme chosen, but it depends on the geology of the area. We have identified three elements of Pg: the thermal model, fluid flow model, and geothermal fluids composition model. Pg can be estimated using the oil and gas approach, which is briefly described in Section 2.1.
• A threshold risk of the key parameters: the case of “worse” than expected (lower than the threshold) value described in Section 3.1.3. The proposed methodology applies the “worse than” approach to the inadequate temperature, inadequate flow rate, and adverse fluid composition risk elements. However, only the temperature and unfavourable fluid composition risk elements are assessed as standalone parameters. The advent of the binary power plant has reduced the importance of adverse fluid composition risk, which will be discussed later. In the proposed approach, the risk associated with the uncertainty of well deliverability is addressed in the calculation of Pc using REM, as lower fluid temperature can have a make-or-break effect on geothermal development, whereas lower well deliverability can be mitigated, within reasonable limits, by drilling more wells. More wells will affect the economics of the project and will thus be factored into Pc, but this will not stop the project if it is robust enough. Section 4.6 gives an example of threshold risk assessments for fluid temperature, while Section 4.7 and Section 5 show how the flow rate threshold risk is considered using REM.

4.2. Inadequate Temperature—Colder than Expected

A well may deliver fluids colder than expected for a variety of reasons, some linked to the geological model risk, some others due to threshold risk—i.e., local variations in a key parameter below a critical threshold. We list some possible causes of failure as examples. They are not exhaustive, and there may be others specific to the local geology of the area. Their probability of occurrence must be considered in the risk assessment and combined in Pg, as described in the dedicated subsection. They include:

• Elements related to Pg.
  • An incorrect overall geological and thermal model of the system.
  • The well may be drilled into the “cold” part of the aquifer recharge zone, which may be the result of an incorrect aquifer model.
  • Lack of sealing of the hot fluid circulation system, allowing heat loss.
  • The well may be drilled completely outside the heat anomaly.
  • Lack of intra-reservoir convection cells, i.e., no thick vertically connected reservoir or no intra-reservoir seal.
  • Lack of a favourable structural setting. A heat source is present, but the overall structural setting does not allow the heat to be confined and instead allows it to dissipate.
• Elements related to the threshold risk.
  • Geothermal fluids may mix with cooler surface meteoric water.
  • Partial development of intra-reservoir convection cells, i.e., a limited thick vertically connected reservoir or lack of a very efficient intra-reservoir seal.
  • The well may be drilled in a peripheral area of the heat anomaly.

Note that some of the examples in the two lists are very similar. Special care should be taken to avoid “double-risking” errors, i.e., by capturing any one feature in one risk element only.

4.3. Inadequate Well Deliverability (Reservoir Permeability)

In most cases, any lack of geothermal fluids is due to a lack of permeability—a very common reason for well failure. We distinguish two scenarios. Firstly, a poor choice of reservoir that is not suitable for geothermal development anywhere in the geological region, in which case this risk should be captured as a geothermal model risk. Secondly, the reservoir is, in principle, acceptable, but the well has penetrated a locally poor part of it. This is represented by the following question: if we drill a second well, do we have a chance of a significantly better permeability? This is an especially common situation in fractured reservoirs. To assist the decision-making process and to improve risk estimation, we propose the adoption of the Dry Hole Tolerance (DHT) approach described in the following subsection.

Note that for an EGS project, where artificial fracturing is used to achieve the required permeability and extract the heat from a suitable volume of thermal reservoir, the same applies: if the fracturing does not provide the desired flow rates, we distinguish regional and local factors—is this a function of the local site or the lithology and structural setting (stress regime) in general? Similarly, we can also consider the strength or weakness of the aquifer pressure affecting the performance of the geothermal field according to regional or local influences. Usually, this is not a make-or-break issue, except rarely for highly geopressurised systems. It is typically captured within uncertainties according to our proposed methodology, rather than in the risk of failure.

The Dry Hole Tolerance Approach (DHT)

We already noted that it is rare for a geothermal well to be completely “dry” and that the success or failure of a well is typically defined by the achievement of a threshold flow rate. A well may fail to flow at such a threshold rate due to site-specific variations rather than regional inadequacies. In such a case, the reservoir is generally acceptable, but there are some local negative variations that are difficult to predict. This may be due to a local absence of fractures, local variation in the primary sediment, local diagenetic processes, or other factors. In other words, we can say that it is due to “bad luck”. This is analogous to the play-based exploration approach used in oil and gas exploration: the regional presence of a permeable reservoir is related to the play and described by play risk, while local factors affecting reservoir presence or quality are prospect-specific and described by local risk. To evaluate this type of geothermal project dominated by local reservoir variability, the “dry hole tolerance” (DHT) approach, as applied in play-based exploration [37], can be used.

In the exploration phase, the DHT approach defines the reservoir’s “chance of success” as the composite probability of drilling at least one successful well within the “maximum number” of dry hole tolerances. This maximum number of dry holes, as defined by DHT, is the maximum number of unsuccessful wells that project management can accept, based on an economic evaluation, before stopping the project and declaring it a failure. Inherent in the approach is the recognition that the importance of permeability-controlled well deliverability in geothermal exploration means that failure is harder to definitively conclude on the basis of one well, compared with hydrocarbon exploration. It is easier to walk away from a system prematurely, while significant potential remains. We wish to avoid this in geothermal systems, since the greater permeabilities required for success are inherently more restricted to begin with, without also prematurely discarding those being considered.

To demonstrate the method, we use a fractured reservoir example, but it is not limited to this application. A geologist, after careful study of a fractured reservoir, might expect one successful well for every three wells drilled (success chance of 0.33). The executive, based on the economic assessment, then sets a dry hole tolerance of three wells. If three consecutive dry holes are drilled in this geothermal system, the project is stopped and declared a failure. Assuming that the wells are completely independent of each other, the probability of drilling three dry holes in such a case would be 0.036 (0.33 raised to the third power) or ~4%, and the probability of drilling at least one successful well would be 0.964 or ~96%. Where there are well dependencies and the outcome of one well affects the chance of others, a simple dry hole tolerance approach is not applicable. However, full consideration of dependencies would be complex and of limited practical value for a problem rooted in the relative independence of reservoir parameters. Near independence is a sufficient assumption.

Such an approach is particularly useful during the appraisal phase when an encouraging first well is followed by one or two dry wells. In this case, the chance of success of the reservoir is the probability of proving the required cumulative geothermal fluid flow for the chosen development with a drilling sequence that includes the dry holes established using the DHT approach. This analysis helps to identify, in a clear and transparent decision process, the right time to stop. Conversely, it also diminishes the risk of missing an opportunity and “walking away too soon”. The DHT is particularly useful when used in conjunction with option one of the REM, as presented later in Section 5.1. This provides an estimate of the commercial probability of success based on the maximum drilling cost (maximum number of wells) that makes the project NPV = 0. Therefore, the DHT and REM option one estimate the probability of completing a successful drilling programme and its impact on the commercial PoS.

4.4. Adverse Geothermal Fluid Composition

A well may fail due to an unfavourable fluid that deviates significantly from expectations, affecting the feasibility of plant operation or the ability to comply with local environmental regulations. Such results are rare but not unknown. These include the presence of hydrocarbons, a brine with a particularly high dissolved solids content, or a high level of non-condensable gases (typically CO₂ and H₂S). Wells drilled in a valid geothermal field may be considered failures if drilled within the CO₂ gas cap [38], although wells targeting the water part of the field could be developed. 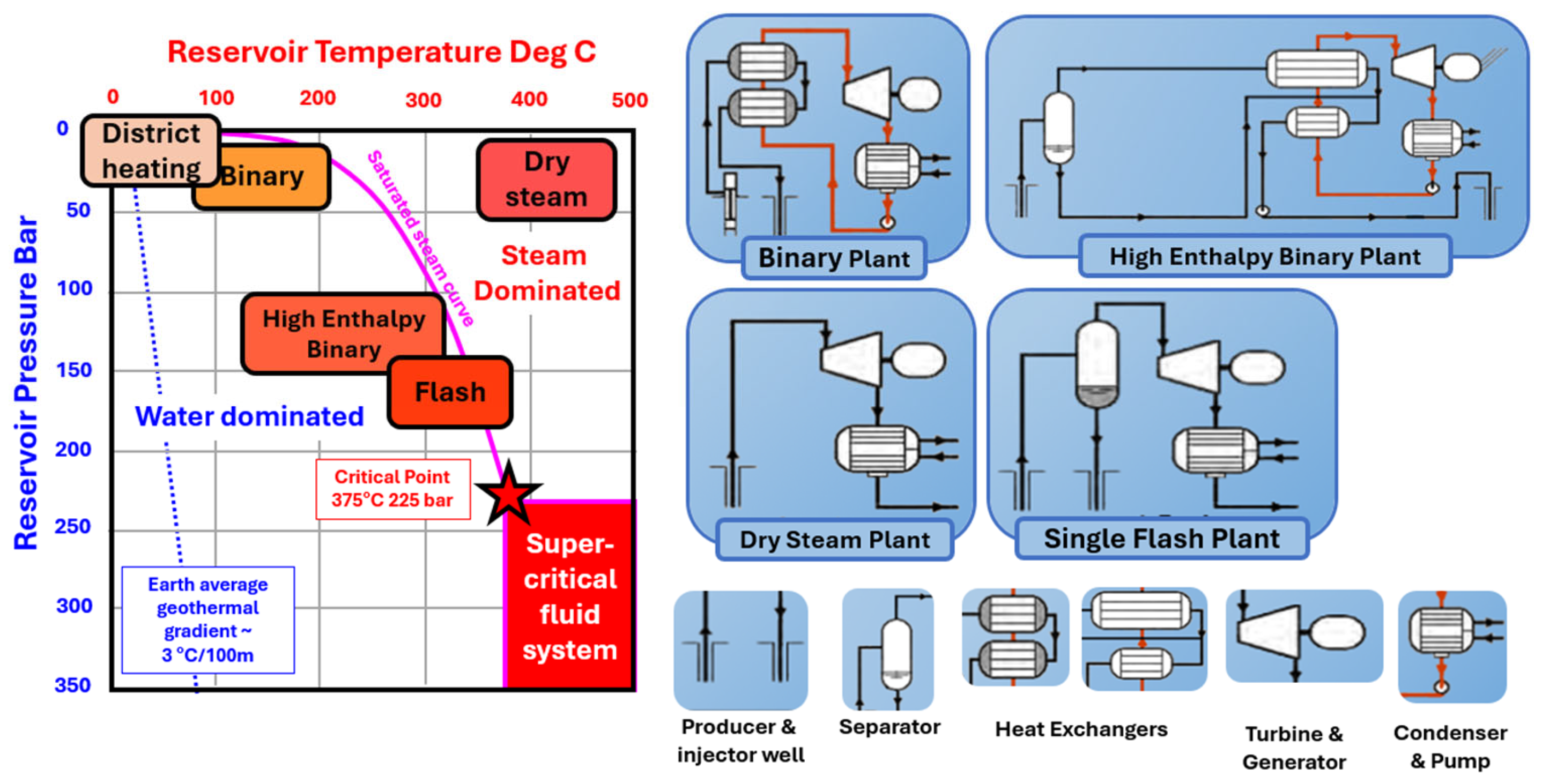In general, the development of binary power plant technology has increased the variety of geothermal fluids that can be commercially exploited and has significantly reduced operational and environmental impacts [39]. Using heat exchangers, such plants physically separate the fluids used in each surface plant from the reservoir fluids used to transport heat to the surface, reducing the impact of adverse reservoir chemistries. Nevertheless, it remains prudent to evaluate this type of failure.

An adverse fluid composition risk can be included in the PoS of the project either as part of Pg or as a threshold risk. It depends on the type and quantity of adverse elements present in the fluids and on pertinent local laws and regulations. It should be included in Pg if its mere presence does not allow the development of a geothermal project. Conversely, it should be treated as a threshold risk if the development of such a project requires the content of such an adverse element in the fluids to be below a certain level.

A completely different way of dealing with such a risk is to include the cost of mitigating the presence of this adverse element in the development cost. In this case, it should only be included in the economics and not in Pg or threshold risk to avoid double-risking error. In our experience, this last approach works best. The development of the binary plant has increased the variety of fluid types suitable for geothermal development, greatly reducing the risk of a project failing for this reason. We continue to treat fluid composition as a “threshold risk” for the sake of completeness, but in practice, temperature threshold risk is usually the main risk.

4.5. Combining Geological Risk and Threshold Risks in the Exploration PoS

So far, we have defined the overall geological PoS (Pg) and the threshold risks for the fluid temperature and adverse fluid (if not included in the fluid adverse composition threshold PoS or the development cost, as described above) composition. The well deliverability threshold risk is instead captured in the REM methodology when estimating Pc.

A key issue in the proposed approach is how we integrate individual geological risk elements into Pg. The geological risk combines the thermal geological model, the fluid flow geological model, and the geothermal fluid composition model¹. If one or more of these are incorrect, the geothermal system will fail.

Therefore:

Pg = fluid flow model PoS × thermal model PoS × geo-fluid composition model PoS

(4)

However, the same unexpected geological result may adversely affect more than one key geothermal element. For example, a poorly developed regional fracture network will affect the fluid flow model, but it may also prevent the formation of the intra-reservoir convective cycle, negatively affecting the thermal model. If this potential negative geological outcome is included in both of the regional risk elements, the risk is unduly doubled. If the key regional geothermal elements share one or more common risk factors (i.e., the same possible cause of failure), only the riskiest key element (lowest PoS) should be taken once and included in Pg to avoid double-risking.

Finally, in the proposed risk system, the overall exploration PoS is

Exploration PoS = Pg × temperature Pthr × adverse composition Pthr

(5)

where Pthr is the threshold PoS (if not included in Pg or in the development cost as described above).

4.6. Example of Geological Risk Assessment—Mt Lepini and Pontina Plain, Italy

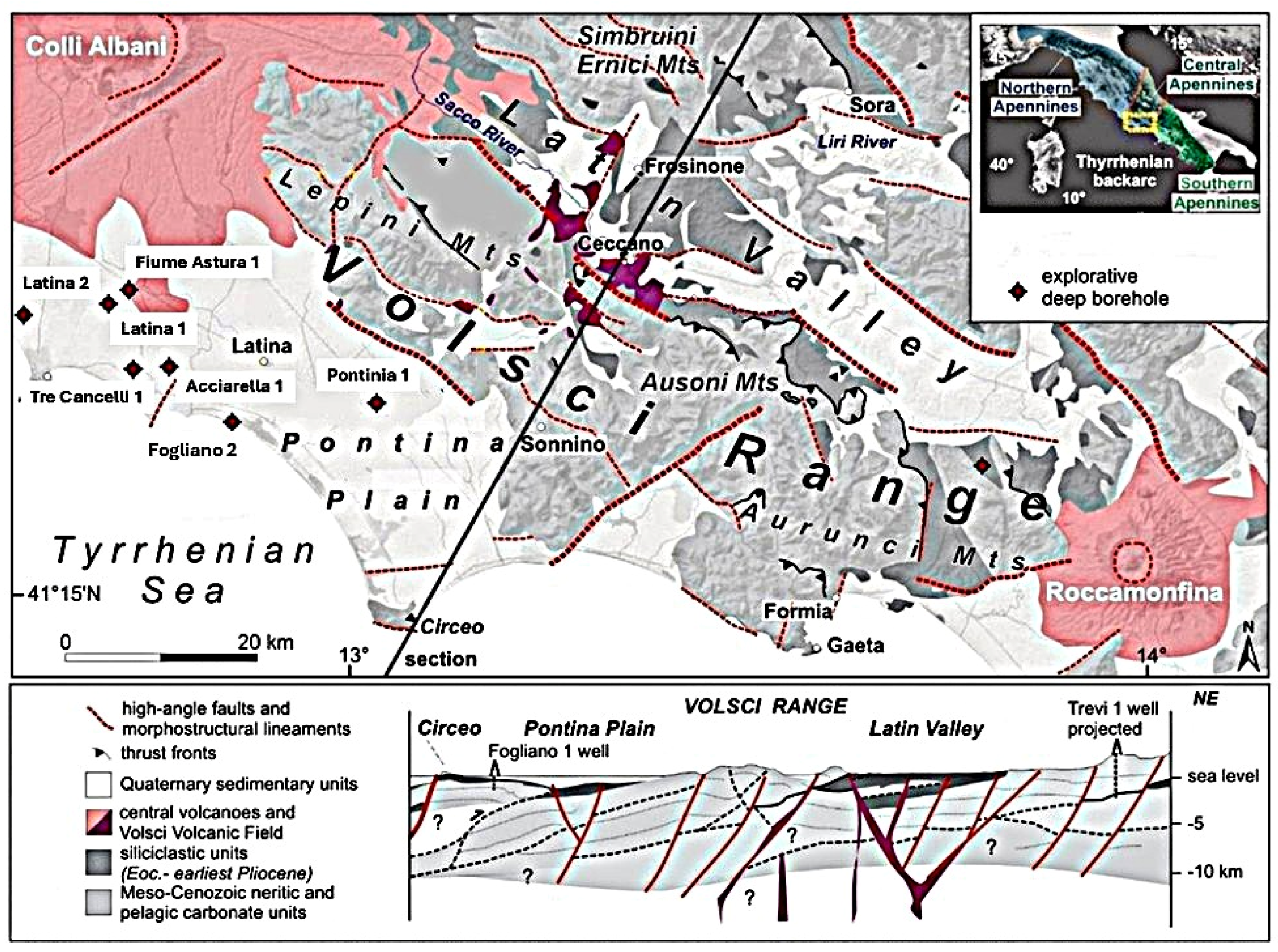
As an example of the Pg assessment, we present a simplified geological case of the Mt Lepini–Pontina Plain area in southern Latium (Italy). A more comprehensive and detailed geological description of the area can be found in Gori et al. 2024 [40]. The area represents a low-enthalpy geothermal system within the Apennine–Tyrrhenian back-arc system. It was affected by a compression phase in the Upper Tortonian, followed by a Plio-Quaternary extension phase. The geo-structural setting is shown in Figure 8 and Figure 9, reprinted from Gori et al. 2024 [40]. The area is a NW–SE trending antiformal stack of thick Mesozoic carbonate platform sediments that have been thrust to the east. To the west, a major normal fault separates it from the adjacent Pontina Plain. Sediments outcropping from the Monte Circeo promontory and Zannone Island and encountered in the Fogliano 1 and 2 wells demonstrate a NW–SE platform-to-pelagic carbonate transition in the west of the area. Oil and gas wells reveal thick carbonate sediments overlain by an “undefined” siliciclastic allochthonous unit and a syn- and post-rift clastic sequence of the Plio-Quaternary age.

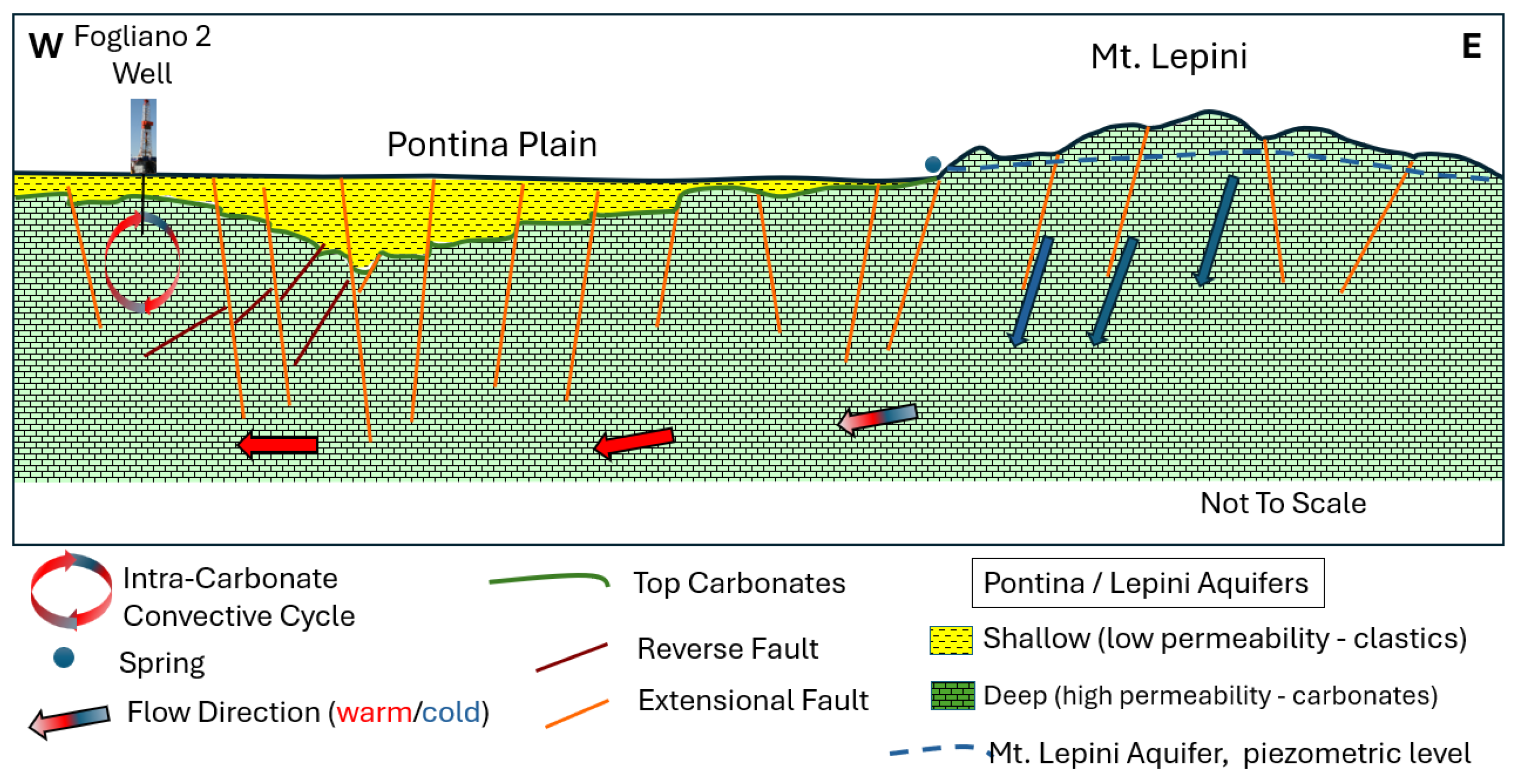
The geothermometers of local springs indicate a relatively low maximum temperature of 95 °C [40]. Nevertheless, the Fogliano 2 borehole recorded a temperature of 65 °C at a depth of 1000 m.bsl. within the carbonate sediments [41]. Such a relatively high temperature gradient is interpreted as a combination of (i) advective deep water circulation due to the high topographic recharge zone of Mt Lepini and (ii) the intra-reservoir convective cycle (Figure 10).

The Pontina Plain is an agricultural area, and geothermal resources could be developed to heat greenhouses in the area. The geothermal geological model is relatively well constrained and is shown in Figure 9 and Figure 10. The only critical element identified is the chance of warm water mixing with shallower cold water. This risk is only present in the area closer to Mt Lepini, where structural complexity is higher. The area of interest is to the west, and the reservoir is expected to be at 1000 m b.s.l.

According to this understanding, the low overall regional risk associated with the thermal geological model can be captured as a local threshold risk to avoid double-risk errors. We have therefore used 100% as Pg. This recognises the chance of a reservoir with some measure of fluid and heat certainly being present.

To generate the temperature CDF, we used available well data, geothermometer data, and regional knowledge of the area. The well data were mainly collected from the literature [41,42], and in most cases, it was not clear whether they were stabilised and, more generally, whether they were reliable. All five wells shown in Figure 9 and Figure 11 stopped in the overburden without reaching the reservoir.

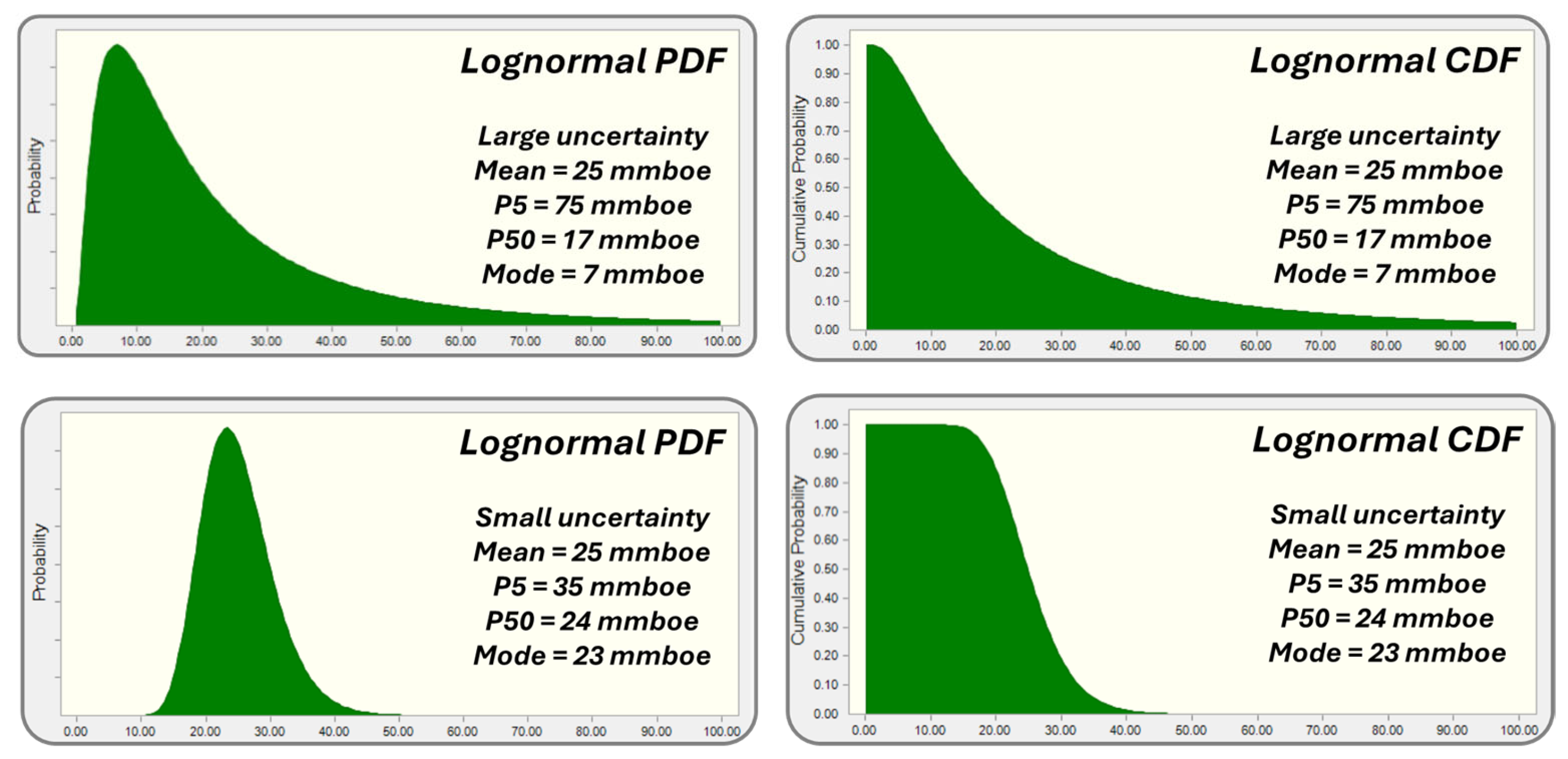
We applied the methodology described in Section 2.2 to construct a cumulative distribution function (CDF) for geothermal fluid temperatures. A lognormal distribution was selected to represent the data, as it more accurately captures the complex and multi-parametric characteristics of the geological system under investigation.

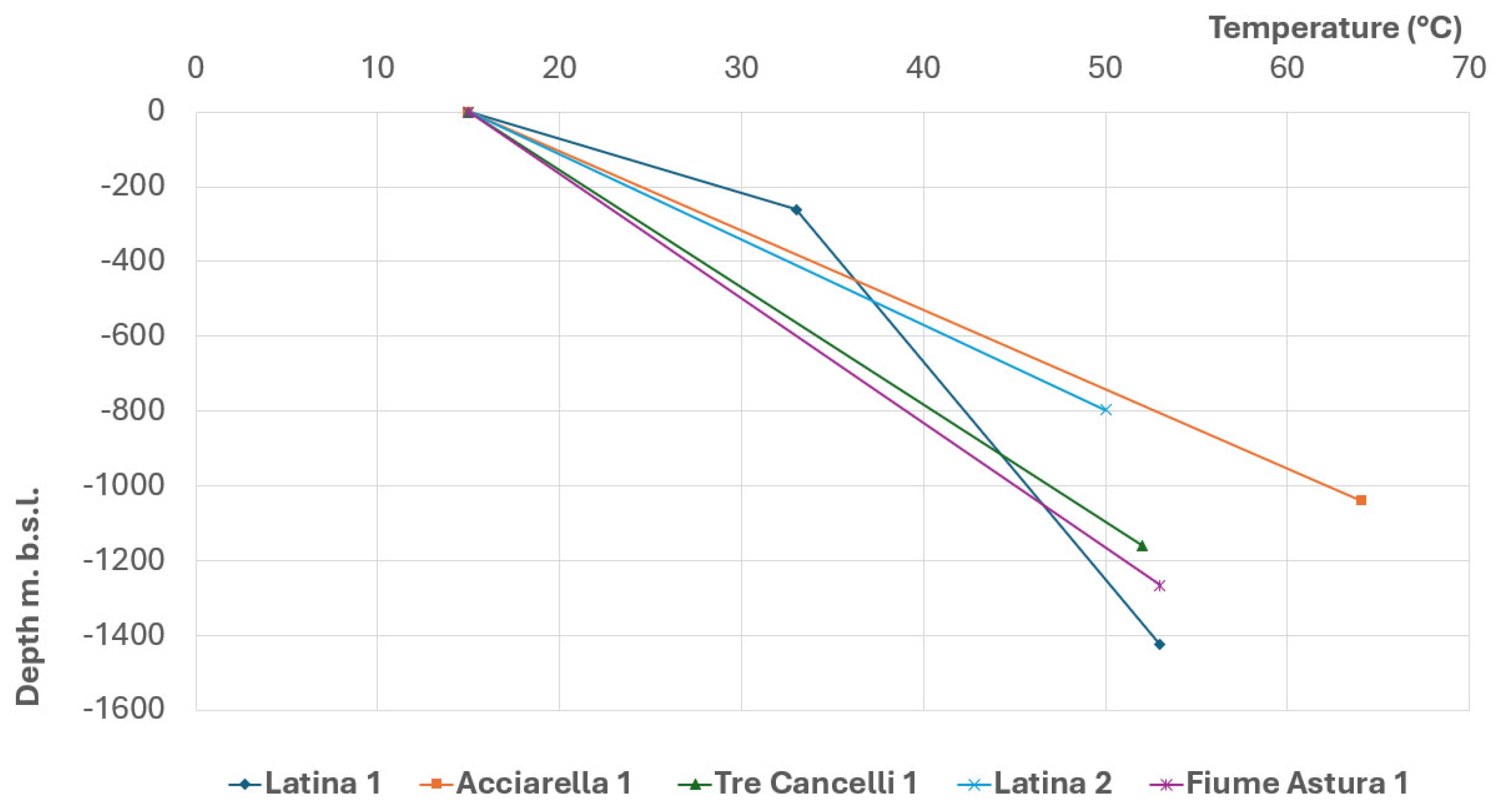
For the lower bound of the distribution, a temperature of 45 °C at 1000 m below sea level was adopted. This value is considered a reasonable estimate of the conductive geothermal gradient in the absence of convective heat transfer. It is supported by borehole temperature data from Latina 1, Torre Astura 1, and Tre Cancelli 1 (see Figure 11).

In contrast, the significantly higher geothermal gradients observed in the Latina 2 and Acciarella 1 wells are interpreted as evidence of intra-reservoir convective heat transport. These convective processes are likely associated with structural highs within the carbonate platform, possibly located below the total depth (TD) reached by the aforementioned boreholes. Although the choice of 45 °C as the minimum temperature may appear conservative—especially when compared to the elevated temperatures measured in the Fogliano 2, Latina 2, and Acciarella 1 wells—it was intentionally selected to reflect a cautious approach that accounts for temperature uncertainty and geological risk.

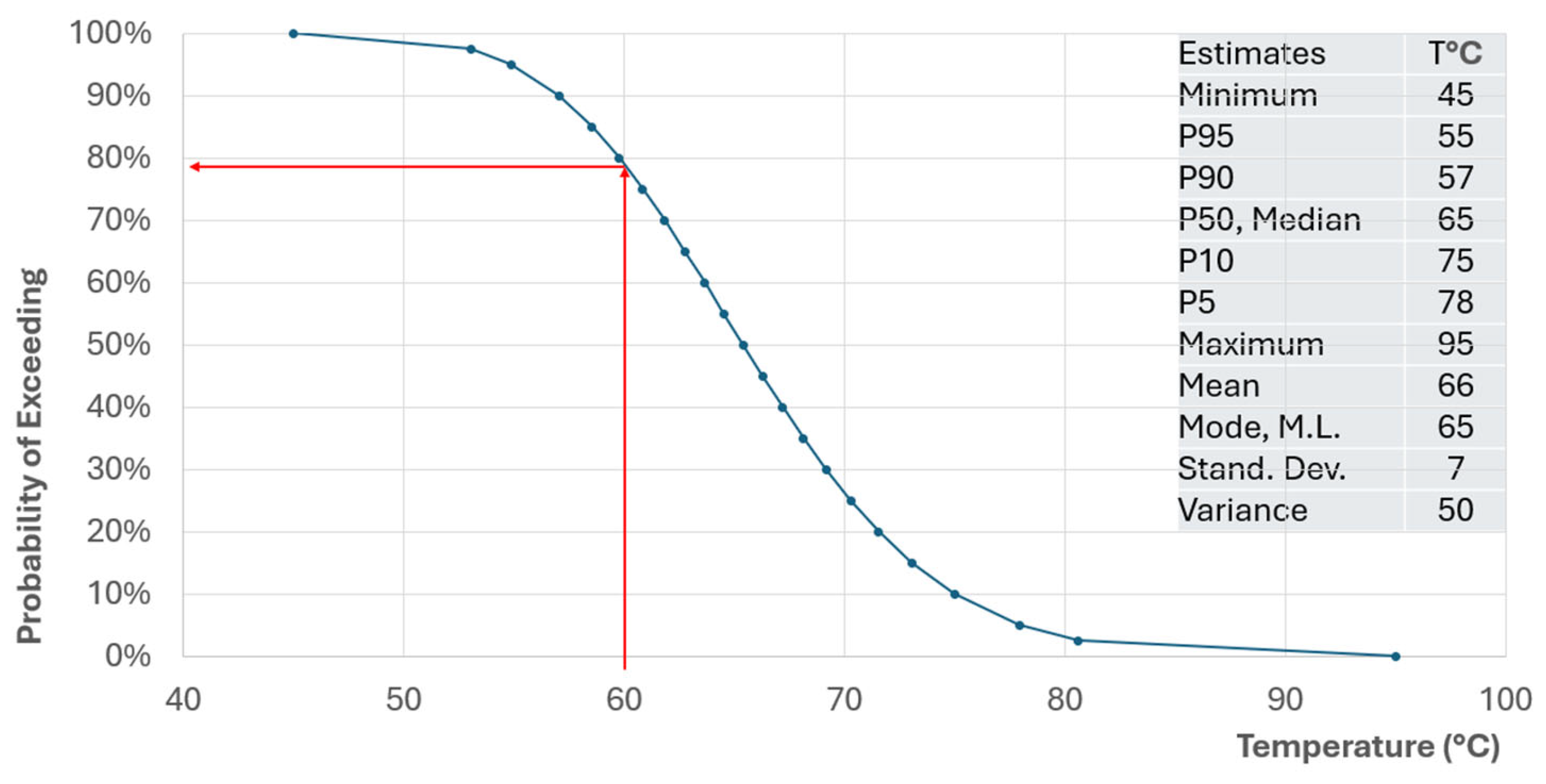
For the upper bound of the distribution, we adopted a value of 95 °C, based on results from geothermometric analyses. The resulting lognormal CDF, defined by these two calibration points (45 °C and 95 °C), is nearly symmetrical. Both the median (P50) and the mode cluster around 65 °C, which is consistent with the temperature data measured in the Fogliano 2 well (Figure 12).

On the basis of such a CDF, a value of 60 C has been selected as the reference temperature for the conceptual development of this project. This value is just below P80. Therefore, a well drilled in a carbonate reservoir in this area at 1000 m b.s.l. has a CDF-estimated 80% chance of finding a geothermal fluid with a temperature of 60 C or higher. This is the PoS threshold for fluid temperature. However, as a Pg of 100% was used, from Equations (4) and (5), this 80% value also becomes the exploration PoS of the project. We believe that this value adequately represents the risk of the area, also because the Fogliano 2 well is a very old well, and there are some discrepancies in the literature on the TD temperature and doubts about its reliability [41].

4.7. Example of a Well Deliverability Cumulative Distribution Function

As mentioned, the REM captures the well deliverability threshold risk when estimating Pc. To conclude our presentation on how CDFs are constructed, we demonstrate how to construct the well deliverability CDF, even though this element will be used later.

As an example of the construction of a cumulative distribution function for well deliverability, we continue with the Pontina–Mt Lepini geological case, already used for the evaluation of the exploration PoS. The reservoir is the Mesozoic platform carbonate sediment of the Latium–Abruzzi platform and adjacent deep-water carbonate paleogeographical units. Only two wells have been tested in the area of interest: the Pontinia 1 and Fogliano 2 wells, drilled in 1935 (estimated) and 1953 and flowing at rates of 280 and 190 m³/h, respectively. There is no information on the quality of these tests, but a higher flow rate is likely achievable with today’s technologies. In order to understand the overall capacity of this aquifer, we have qualitatively reviewed the available parameters, including the following:

• Total average cumulative aquifer flow rate: 13–15 m³/s (in four main spring systems);
• Hydraulic gradient: 5–6 m/km;
• Linear drainage front: about 25 km;
• Average transmissivity: 10⁻¹ m²/s [40].

In our experience, such parameters indicate a first-class aquifer. Such good reservoir quality is interpreted as being due to a hypogenic karst process affecting the whole area [43].

To generate the cumulative distribution function (CDF) of well deliverability for the hypothetical wells, we adopted the methodology outlined in Section 2.2. Consistent with the approach used for the temperature CDF, we modelled the well deliverability using a log-normal distribution, as this more effectively captures the inherent variability and complexity of subsurface flow conditions. The lognormal curve was calibrated based on two reference values: the flow rate measured at the Fogliano 2 well (used as the P90 value) and the maximum documented flow rate from a geologically comparable reservoir (confidential data), used as the P10 value, equating to 800 m³/h [44,45]. The resulting CDF, presented in Figure 13, yields a P50 value of approximately 400 m³/h. Notably, the mode of the distribution closely aligns with the flow rate observed in the Pontinia 1 well.

5. Reverse Enthalpy Methodology and the Probability of Commercial Success of a Geothermal Project

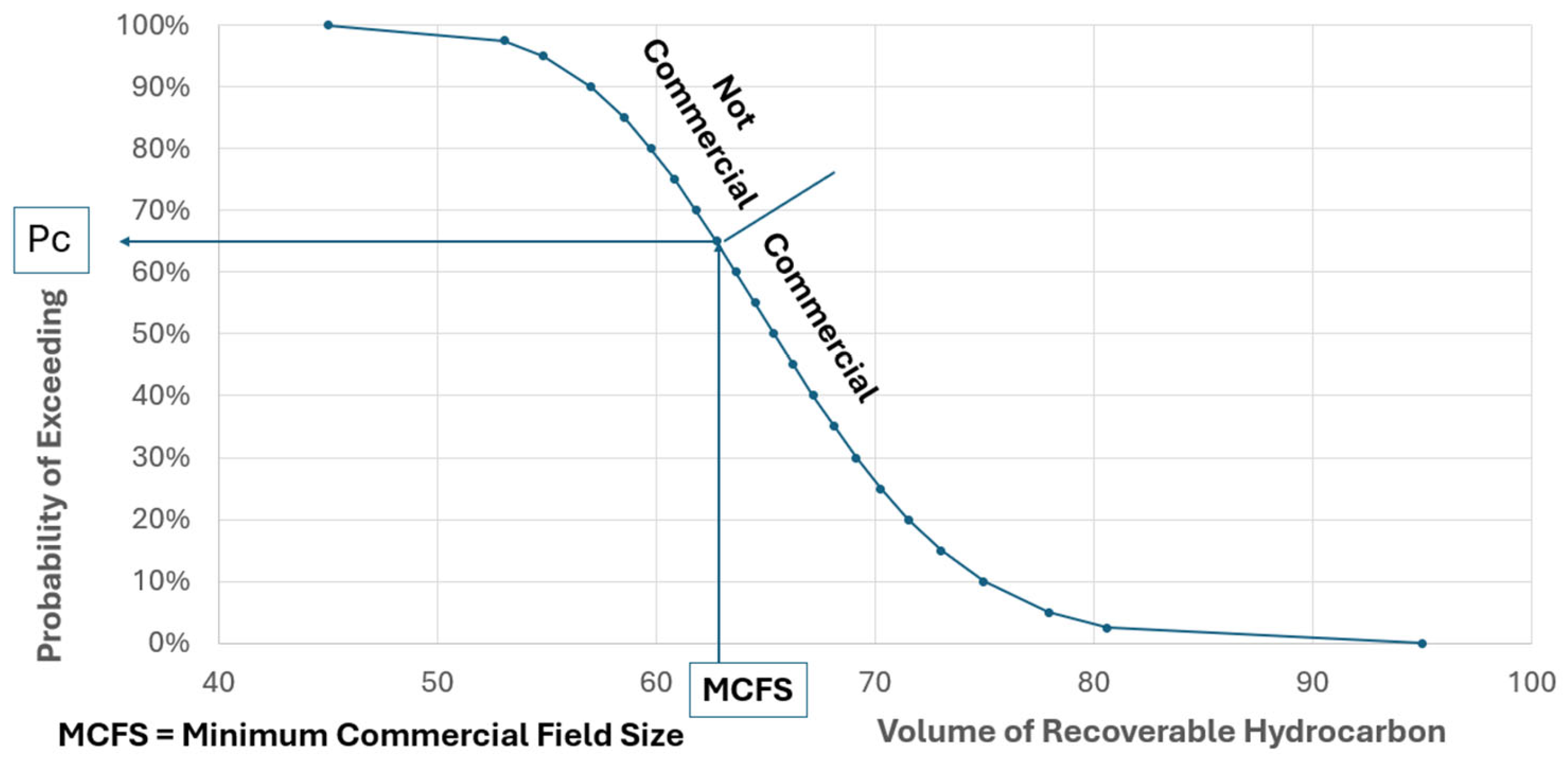
One of the main objectives of this paper is to provide a methodology that can be used to assess the Pc of a geothermal exploration project. Pc is the probability that such a discovery would be commercial, in other words, that it would have a positive net present value (NPV) at the company’s discount rate. Pc depends not only on technical parameters, such as fluid temperature, flow rate per well, and development costs, but also on other parameters, such as energy costs, fiscal terms, subsidies, and so on. In general, the uncertainties of these parameters are captured in the economic sensitivity analysis, and their discussion and analysis are beyond the scope of this paper and will not be discussed further. Note that this definition of commercial success for Pc makes no assessment of commercial competitiveness, only NPV-defined profitability. From an operator’s perspective, this NPV-based Pc is what is needed. From the customer’s point of view, it is also relevant to see which of the competing options offers not just profit but the most profit. This assessment is beyond the scope of this paper, but we note that the derivation of Pc is crucial to enable such further comparison.

According to the proposed approach, each technical parameter or component of the geothermal project is systematically analysed and evaluated. After verifying the presence or absence of key geological elements within the geological probability of success (Pg ) and assessing whether temperature and fluid conditions meet the minimum thresholds (i.e., are “sufficient” and “tolerable”), the remaining elements to be evaluated are well deliverability and the commercial probability of success (Pc). These aspects are addressed in the third and final phase of the overall probability of success (PoS) assessment through the application of the Reverse Enthalpy Methodology (REM).

As detailed in Section 2.3, Pc is estimated following best practices from the oil and gas sector. This involves identifying a parameter that accurately represents the monetary value of the project and analysing its cumulative distribution function (CDF). Pc is then derived by locating the point on the CDF where the net present value (NPV) of the project equals zero.

Within the REM framework, two alternative approaches are proposed for estimating the Pc component:

Option 1—Assuming a predefined geothermal facility type and installed capacity: In this scenario, the facility’s capital expenditure (CAPEX) and projected revenues are treated as input variables. Consequently, the total drilling cost becomes the only unknown. By determining the value of drilling cost that results in a project NPV of zero and plotting it on its corresponding CDF, the commercial probability of success (Pc) can be estimated.

Option 2—Assuming a predefined number of wells: In this case, the total drilling cost is treated as a known input. The CAPEX of the facility and the expected revenues—both of which depend on the facility type and its capacity—are considered unknowns. The minimum capacity (for a given facility type) required to achieve an NPV of zero is then calculated. This value is subsequently used to estimate Pc by referencing its position on the relevant CDF.

The two cases are described in more detail below. In both cases, the type and capacity of the geothermal facility and the number of wells can be subsequently adjusted iteratively until a satisfactory overall risk is achieved.

We use the term “a priori” to emphasise that the initial type, technology, and capacity of the geothermal facility, or the number of wells, are chosen at an early stage of the assessment, also for non-technical reasons. In most cases, the capacity of the geothermal facility is dictated by a phased derisking and development strategy (pilot/demonstration, main development, further expansion), regulatory requirements, or operation and maintenance strategy, etc.

On the other hand, the total number of wells is affected not only by geological constraints, such as the minimum distance between production and reinjection wells, but also by logistical and administrative constraints (e.g., the licence is too small and/or unsuitable due to topography, national park, houses, water for drilling, etc.). Therefore, in some cases, there may be many restrictions on the suitable well pad, to the point where the number of drillable wells is not a variable but a fixed number.

Although the choice between option one and option two of the REM may be dictated by “non-technical” reasons, these two approaches provide a different focus and perspective on risk. Option one, which focuses on total drilling costs, provides important information on how many possible negative-result wells the project can absorb before becoming economically negative (NPV < 0). Such information is an important corollary to the DHT approach, as noted above. The second option, which focuses instead on the geothermal facility, can be used to define the P90, P50, and P10 cases.

5.1. REM Option One—Focussing on Drilling CAPEX

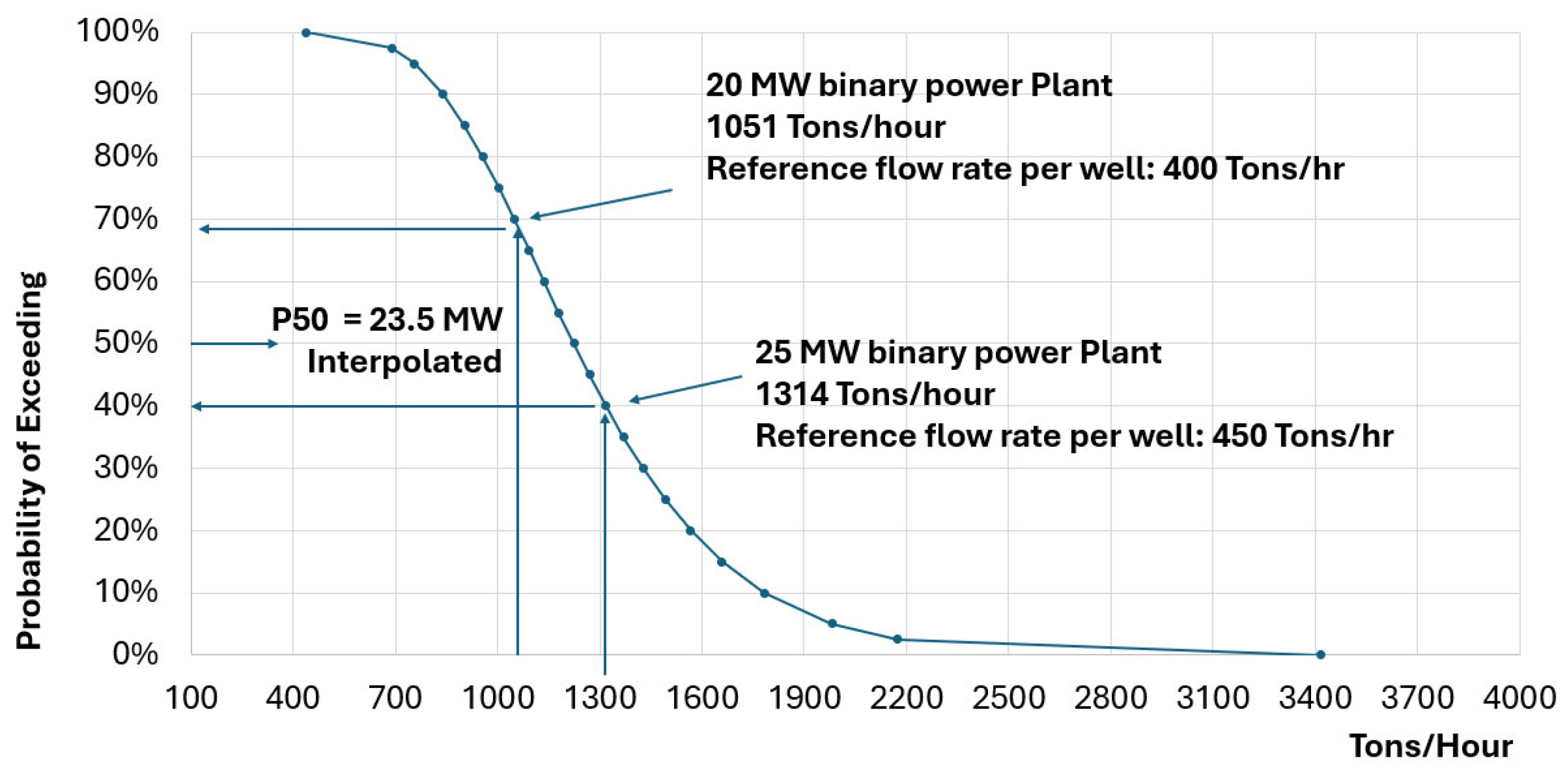
The starting point for REM option 1 and its relative Pc (hereafter named respectively REMd and Pcd, where d stands for drilling) is the flow rate of geothermal fluids required to feed the “a priori” defined facility. In the example of Figure 13, Figure 14, Figure 15 and Figure 16, a 20 MW binary plant was selected, and a temperature of the geothermal fluid of 180 °C without the need for ESPs (electric submersible pumps) to produce the fluid was assumed. A total flow rate of 1051 Tons/h (@ 180 °C geothermal fluid) was estimated to supply the plant’s needs. 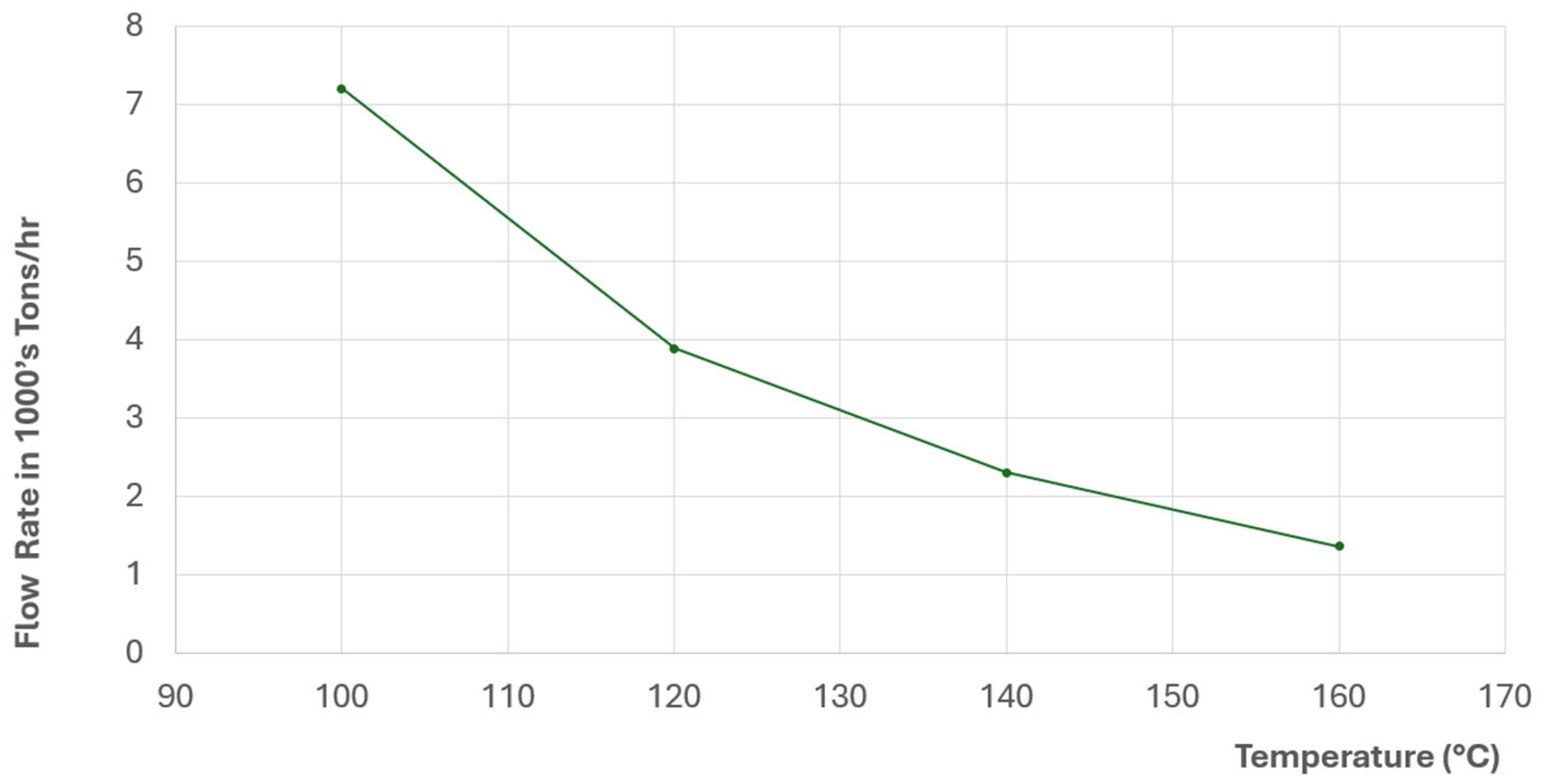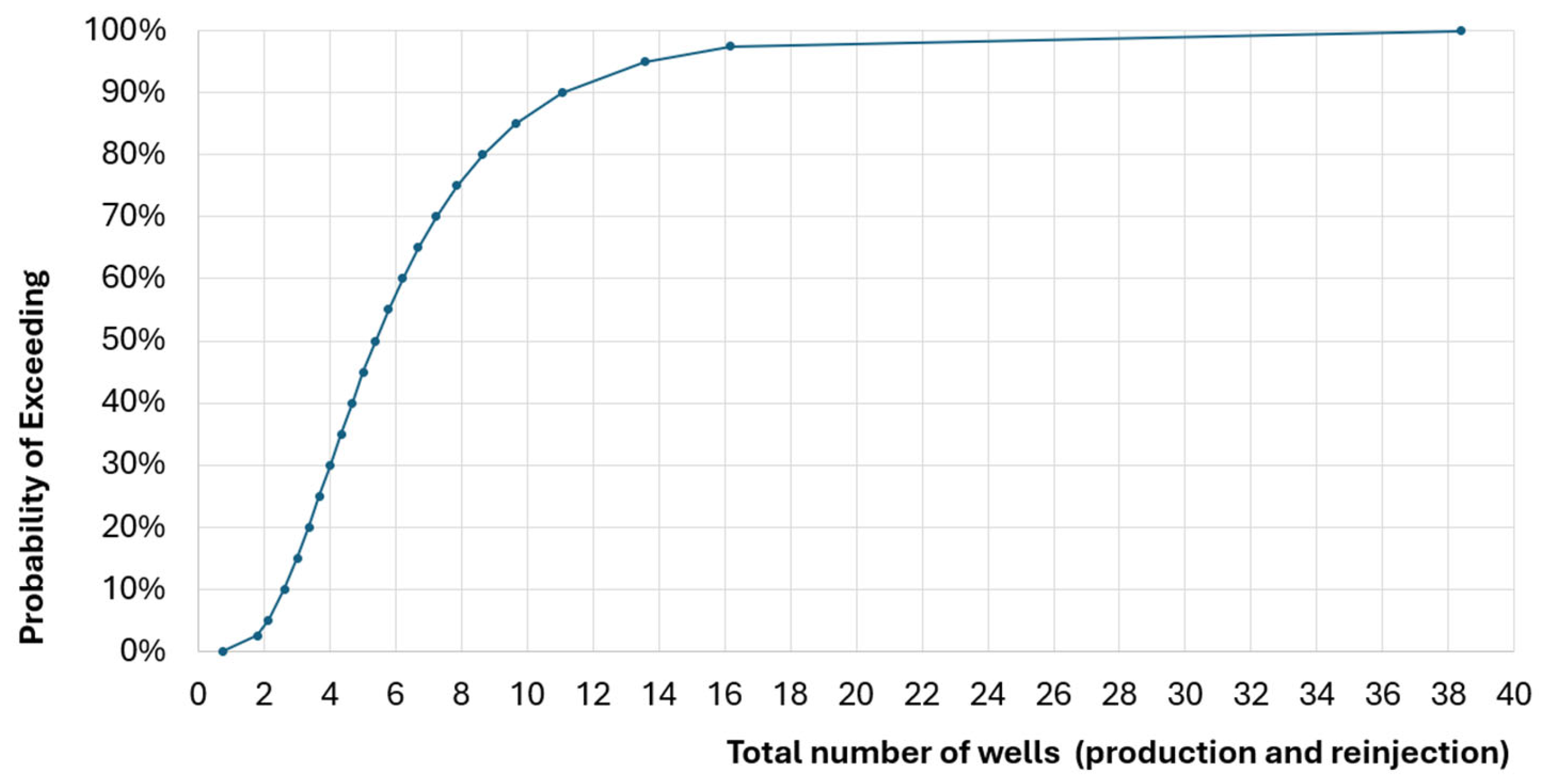In the second step, the well deliverability CDF is converted into the CDF of the number of wells required to develop such a plant (Figure 14). This CDF is simply obtained by dividing the flow rate required to supply such a plant by the well deliverability. The P10 case would require fewer wells because it is based on a high P10 well deliverability, whereas the P90 case would require many more wells because it is based on a low P90 well deliverability. Figure 15 shows the total number of wells, including injection wells and possibly abandoned exploration wells.

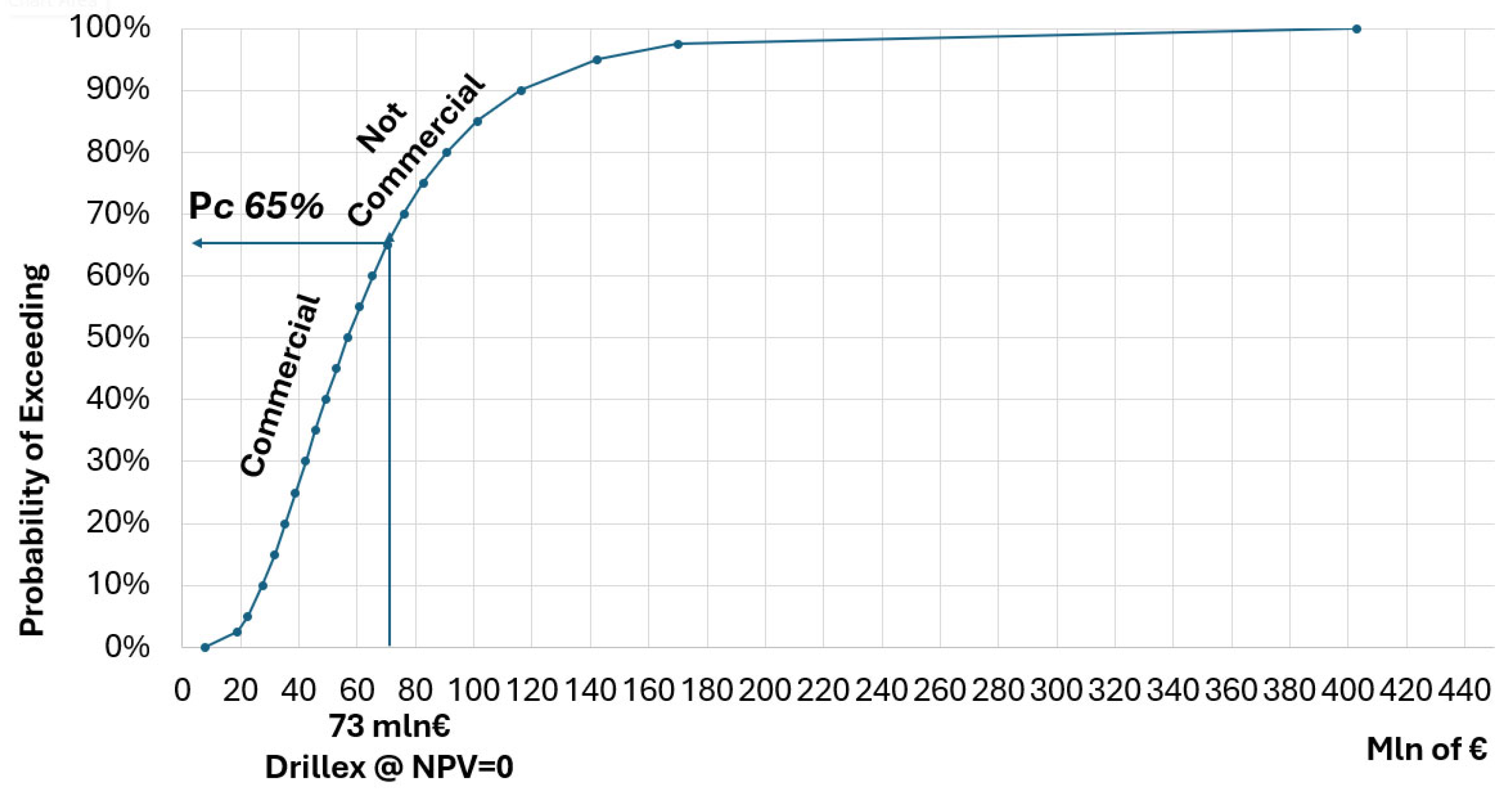
Once the well costs have been estimated, the CDF of the number of wells required to develop the project can be converted to the total drilling cost CDF of such a project. This drilling cost must include the cost of the re-injection wells and the cost of the fluid gathering system, as reported in Figure 16. The drilling costs reported at the upper end of the curve will generally be too high for the project to be economically viable. This is primarily due to poor well deliverability, necessitating the drilling of an excessive number of wells and significantly increasing overall drilling expenditure.

We can therefore define a threshold at which the drilling cost makes the total NPV of the project equal to zero. Above this value, the project is not economically viable because the drilling costs are too high (too many wells needed to develop it) and would kill it. Below this, the NPV would be positive. The probability of being below this value is the defined probability of commercial success. In our example, the threshold drilling cost value that makes the NPV of the project equal to zero is EUR 65 MM, corresponding to a Pcd of 65%. In simple terms, this threshold indicates the maximum amount of drilling cost (maximum number of wells) that can be undertaken without making the project uneconomic.

Alternatively, it may be that initial iterations of the development case produce an unacceptably low Pcd. In such cases, further iterations can be attempted, perhaps with different technology or a different use of heat, until an acceptable Pcd is achieved. On the other hand, if the first REM iteration shows an extremely high Pcd, this may mean that the expected deliverability of the wells could support a larger facility or a more profitable type of development. Again, the development case can be adjusted iteratively until a comfortable level of risk is achieved.

5.2. REM Option Two—Focussing on Facility CAPEX

Following the same logic as the proposed REMd, Pc can instead be determined based on well deliverability and CAPEX of the geothermal plant. In this case, we call it REMf and Pcf (f stands for facility). The recommended workflow starts by determining the a priori number of wells based on technical and non-technical factors. Subsequently, the CDFs of the individual wells are aggregated using the Monte Carlo method to produce the total CDF of geothermal fluid deliverability (Figure 17).

According to REMf, drilling costs (including production and reinjection wells and fluid gathering systems) become an input rather than an output of the assessment. Therefore, the facility cost and revenue are the only remaining variables. It is therefore possible to estimate the minimum capacity of a geothermal plant that will make the NPV = 0. In fact, a smaller development will reduce the total CAPEX of the plant, as well as the electricity produced and therefore the revenue. Considering that larger plants are proportionally more cost-efficient and therefore cheaper per unit of energy produced than smaller ones, reducing the capacity of the plant will progressively reduce the NPV until it reaches 0 (Figure 18). The flow rate required to supply the corresponding NPV = 0 plant, plotted against the total well deliverability CDF, gives Pcf according to REMf.

In addition, the total geothermal fluid deliverability CDF can be used to estimate the P90, P50, and/or P10 facility cases as shown in Figure 19. It is important to note that these values do not represent the overall potential of the project but the potential assuming a particular number of wells. If this assumption is changed, these values will be changed accordingly.

The calculation of Pcf based on the CAPEX of the facility is fully equivalent to the Pcd calculated using the drilling CAPEX. In general, we prefer to focus on drilling because it is the most critical parameter, and it is important to correctly communicate its variability and risk to the decision maker using the Pcd and DHT approach.

However, Pcd can also be applied in the early stage of REM to constrain the right choice of the “commercial a priori” facility.

Such an iterative process of adjusting the development case with respect to either Pcd or Pcf using REM should lead to a risk-optimised development case.

Such an approach is inherently well suited to long-term planning because it recognises that success is a function of the development plan and incorporates flexibility to make best use of what is available on present-day commercial terms. It also sensibly empowers corporate multi-project portfolio approaches to geothermal energy. Organisations with the flexibility to deploy different development plans for different usage are best placed to take advantage of results from any one location, but only if they can consistently define a Pc across multiple diverse geothermal projects—something that REM enables and that has been historically difficult.

5.3. Critical Factors of REM

The construction of the geothermal fluid temperature and well deliverability CDF is the most critical task in the proposed approach. In particular, the estimation of well deliverability can be a major challenge in new areas. There may be wells in areas of medium to low enthalpy where oil and gas exploration has taken place. However, they can be misleading. Rarely has an oil and gas company properly tested a “water” wet reservoir. To minimise costs, operations are stopped as soon as the nature of the fluids is established, without further assessment of the reservoir properties. Typically, only the top of the trap is tested, where the buoyant hydrocarbons are anticipated, and this often does not coincide with the best part of the reservoir. Furthermore, when testing a geothermal well, logistical problems can prevent a high-performing well from being properly tested. The amount of fluid that needs to be stored and disposed of can be phenomenal, making it impractical. Even in the case of an injection test, the amount of water required can be prohibitive. As a result, there are only a few cases in which a high deliverability of the reservoir has been easily established [46]. To overcome such difficulties, we recommend a 360-degree approach, starting from the geology, understanding the reliability of the data, and using data from other disciplines, such as hydraulic conductivity or permeability from the hydrogeological study.

Note that the use of the CDF differs from the oil and gas industry standard, where, in general, PDFs are used in Monte Carlo simulations. In the proposed methodology, CDFs are used to more easily estimate the threshold risk. The aim is to correctly estimate the probability of threshold reference values required for geothermal fluid temperature and well deliverability, i.e., the values enabling feasible development for the designated usage. If we enter a reference value such as P50 as the threshold required (temperature or well deliverability), by definition, we end up with a threshold risk of 50%. It takes some practice and experience to estimate and apply correctly. In general, it is recommended to use the low (P90 or minimum) and high (P10 or maximum) values as calibration points and then check if the P50 value correctly represents what is understood about the parameter’s most likely value. Once the distribution’s curves are calibrated by drilling new wells, the reference values can be reassessed.

As mentioned earlier, REM can also be applied to higher-enthalpy, multiphase, complex systems. It is a methodology for analysing data and calculating the probability of commercial success. As its name suggests, it was originally developed for high-enthalpy applications; unfortunately, due to confidentiality, these cases cannot be presented in this paper. In such more complex systems, the same approach was used, based on enthalpic fluid content and overall fluid well deliverability rather than temperature and water flow rate. In such a case, Equation (3), reported in Section 3.2, becomes [32,33]:

Pth = ṁ × Δh

(6)

where

• Pth is the thermal power (heat transfer rate);
• ṁ is the mass flow rate;
• Δh is the difference in specific enthalpy between the inlet and the outlet.

5.4. Integration of the Proposed Methodology with Geothermal Reservoir Modelling

The proposed methodology provides a structured framework for combining multidisciplinary data, geological interpretations and technical studies in order to evaluate the geological and commercial risks associated with geothermal development.

A key element in reinforcing the robustness of this risk assessment is the integration of a numerical geothermal reservoir model. Reservoir modelling is a critical tool for simulating subsurface processes, evaluating fluid flow and heat transport, and forecasting the long-term performance of the geothermal system. It enables conceptual models to be validated against observed data and provides quantitative predictions on key parameters such as well deliverability, reservoir sustainability, and thermal decline over time.

Incorporating a robust reservoir model within the proposed methodology substantially increases confidence in risk estimations. It enables developers and stakeholders to transition from qualitative assessments to a data-driven approach. Conversely, risk evaluations lacking the support of detailed reservoir simulations are inherently more speculative, particularly when dealing with uncertainties concerning production capacity, reservoir lifespan, and the effectiveness of reinjection strategies.

Therefore, integrating reservoir modelling is a fundamental enhancement of the methodology, ensuring that the estimated geological and commercial risks reflect the actual behaviour of the geothermal system as closely as possible.

5.5. Overall Probability of Success of a Geothermal Project

Similarly to an exploration oil and gas project (Equation (2)), we can define an overall PoS for an exploration geothermal project:

Total PoS of a geothermal exploration project = Pg × Threshold PoS × Pc (Pcf or Pcd)

(7)

where threshold PoS includes temperature threshold PoS and fluid adverse composition PoS if the latter is not already included in Pg or in the development cost (see Section 4.4).

Prior to the drilling of a first exploration well, the presence of a geothermal system is not 100% certain. At this pre-drill stage, there is still an associated risk related to the presence or absence of one or more geological key elements (Pg) and related to the fluid temperature threshold PoS, as already defined in Section 4.5. The presence of this latter factor is one of the major deviations from the typical oil and gas risk system. Such an element better captures the multiple “not good enough” aspects that can characterise geothermal systems compared to oil and gas. On the other hand, a project under appraisal will, by definition, be characterised by a Pg and a threshold fluid temperature of 100%, while Pc will be less than this value due to the risk of not having a high enough flow rate to sustain the development of the project. By contrast, a mature and commercial project ready for development would have Pg, threshold PoS, and Pc at 100%.

Therefore, these parameters together facilitate a better definition of the maturity of the project and the possible implementation of a scheme equivalent to PRMS for prospective and contingent resources and reserves [11].

5.6. Future REM Development

A key area for future development is extending the methodology to a wider range of geothermal project types, particularly those involving lower-permeability reservoirs, unconventional resources and high-enthalpy systems with limited natural fluid content.

Among unconventional geothermal concepts, EGS is one of the most technically challenging yet potentially transformative. In principle, the Reverse Enthalpy Methodology can be applied to EGS, as the fundamental principles remain valid. However, a few modifications must be introduced to make it fully applicable to this type of development.

In particular, it is crucial to incorporate a third cumulative distribution function (CDF) to capture the uncertainty in the volume of hot rock that is effectively fractured and hydraulically connected to the well system through stimulation or fracking. While traditional CDFs in the Reverse Enthalpy framework relate to subsurface temperature and fluid productivity, the fractured volume in EGS serves as a proxy for both thermal reservoir size and long-term resource sustainability.

This parameter cannot be overlooked. While achieving a high initial flow rate through artificial stimulation may demonstrate technical feasibility, this alone does not ensure long-term project viability. The fractured volume must be large enough to maintain high flow rates at a nearly constant temperature throughout the expected operational life of the project. Without this, thermal breakthrough and the rapid cooling of the production fluid would jeopardise economic returns and system reliability.

Considering the early stage of this type of project, more research and methodological refinement are needed.

Future research should therefore focus on quantifying the spatial extent and connectivity of the stimulated rock volume more accurately and integrating this with thermal modelling to define the third CDF.

6. Conclusions—Empowering Geothermal Project Investment

The proposed risk system addresses the concept of risk and uncertainty as developed in the oil and gas industry, significantly modified for geothermal applications. The historical principles are simple, clear, and well established through proven practical use. They are also very familiar to most geoscientists. They do, however, need to be applied properly. Geothermal and oil and gas may seem very similar, and both are rooted in subsurface analysis, but there are many aspects that combine to make them very distinct in practice. The differences must be well understood and carefully managed.

Unlike oil and gas systems, geothermal success at the development and production stage is much more highly dependent on two key parameters—the temperature of the geothermal fluids and flow rate. It is not that flow rate is unimportant in hydrocarbon projects, but the value of the commodity facilitates success for lower thresholds and more widespread values of flow rate than is normal for geothermal heat exploitation. Flow rate in hydrothermal (and EGS) systems is typically controlled by well-site-scale differences in permeability-related performance that are difficult to fully resolve without extended and expensive data sets. Progressing geothermal projects in regions where these data are initially absent or prohibitively expensive is difficult.

The proposed system is designed to be embedded in the assessment of commercial viability for a geothermal project. It presents a logical approach to this uncertainty based on an iteratively derived plant capacity. The successive iterations of analysis determine the likelihood of acceptable NPV-positive well counts. This empowers executives to assess whether such well counts and the chance of commercial success are sufficient to embark on a project and how much drilling without success should be tolerated before walking away. We believe that providing confidence in a logical approach to geothermal project uncertainty, particularly in areas immature for exploration, presents a key tool and a new approach to activating geothermal portfolio opportunity—one that is well suited to both commercial optimisation of geothermal resources in multiple uses and the effective management of geothermal project portfolios that allow an effective energy transition from fossil fuel dominance demands.