Optimal Configuration of Distributed Pumped Storage Capacity with Clean Energy
Abstract
1. Introduction
2. Construction of Clean Energy System
2.1. Electricity Purchase Billing Rules and System Structure Operation Mechanism
2.2. Basin Network Hydraulic Connection Coupling Characteristic Matrix
- (1)
- Type vector of hydropower station
- (2)
- Water area correlation matrix
- (3)
- Correlation matrix between hydropower station and pumped storage
2.3. Capacity Optimization Configuration Framework of Distributed Pumped Storage Power Station with Clean Energy System
3. Two-Layer Optimal Allocation Model of Distributed Pumped Storage Capacity with Clean Energy System
3.1. Upper Distributed Pumping Capacity Configuration Model
3.1.1. Objective Function
3.1.2. Constraints
- (1)
- Pumping storage unit installed capacity constraints
- (2)
- The storage capacity constraint of pumped storage power station
3.2. Operation Optimization of Lower Clean Energy System
3.2.1. Objective Function
3.2.2. Constraint Conditions
- (1)
- Output power constraint
- (2)
- System power balance
- (3)
- Sectional constraints [23]
- (4)
- Operation constraints of pumped storage power station
- (5)
- Operation constraints of hydropower station in basin
- (6)
- Constraints of hydropower station output and upper and lower limits of reservoir capacity
- (7)
- Reservoir capacity constraint of pumped storage power station
- (8)
- Spatial coupling relationship constraint of hydropower station
- (9)
- Reservoir balance of hydropower station in basin
- (10)
- Hydropower station power generation flow constraints
- (11)
- Discharge constraint of small hydropower
- (12)
- Reservoir capacity constraints at the beginning and end of scheduling
- (13)
- Purchase and sale of electricity mutually exclusive constraints
- (14)
- Purchasing and selling power transmission constraints
- (15)
- Load power constraint
4. Model Solving
4.1. Model Transformation
4.2. Solving Process
- 1.
- Initialize the parameters, divide the time slice in the scheduling period, describe the probability characteristics of the wind power, photovoltaic power, and load according to the distribution function proposed in reference [20], input the wind and solar load forecasting curve, and describe the engineering parameters and capacity constraints of the pumped storage power station.
- 2.
- Initialize the variables of the ADMM algorithm, including the Lagrange multiplier, penalty coefficient, and initial solution of the upper-layer pumped storage capacity configuration scheme problem.
- 3.
- The operational cost optimization model are established for each time slice, and the CPLEX solver is used to solve it. Operation strategies such as hydropower output, pumped storage power, and storage capacity in this period are obtained, and the boundary parameters and their corresponding dual variables with other periods are calculated.
- 4.
- CPLEX solves the pumped storage capacity allocation problem, updates the pumped storage capacity, coordinates the storage capacity continuity constraints for each time period, and updates the dual variables and boundary parameters.
- 5.
- The convergence of the dual variable in the current iteration is determined. If the convergence accuracy is satisfied, the optimal capacity configuration and full-time operation strategy of the pumped storage power station are the output. Otherwise, Step 3 is returned, and iterative optimization is continued. The updated boundary parameters and dual variables are transmitted for the next round of the solution.
5. Example Analysis
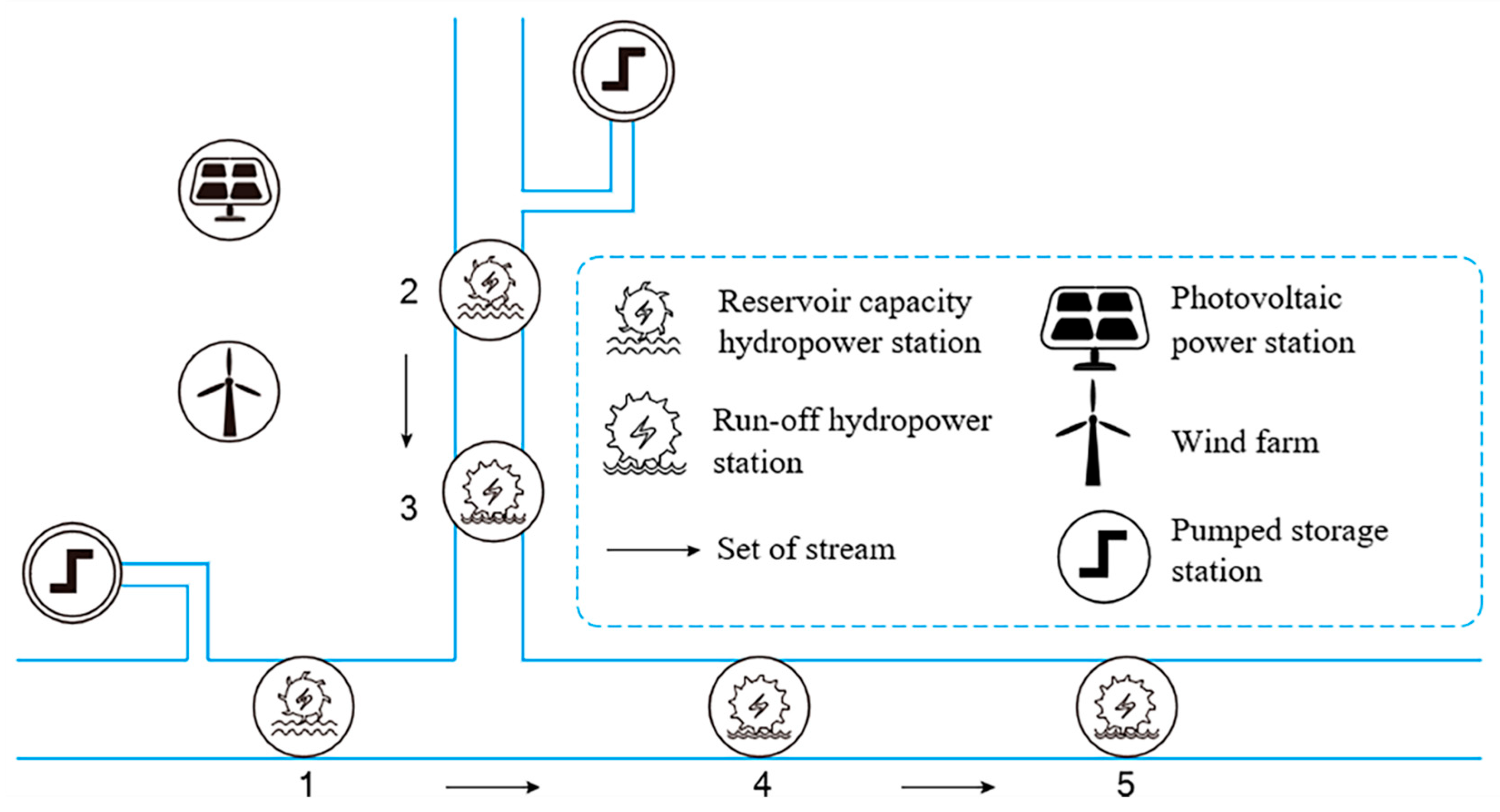
5.1. Example Setting
5.2. Analysis of Example Results
5.2.1. Capacity Configuration Result Analysis
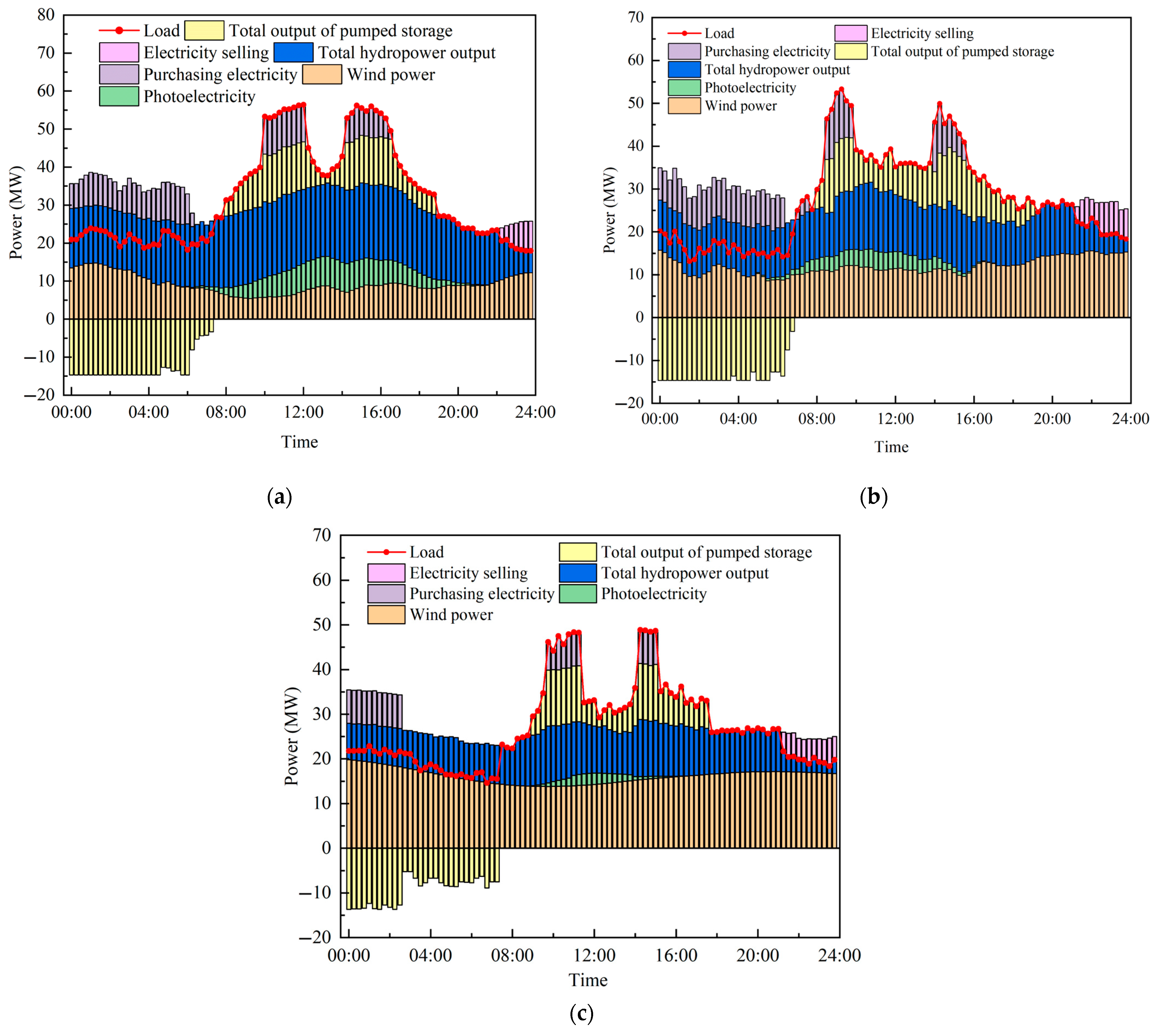
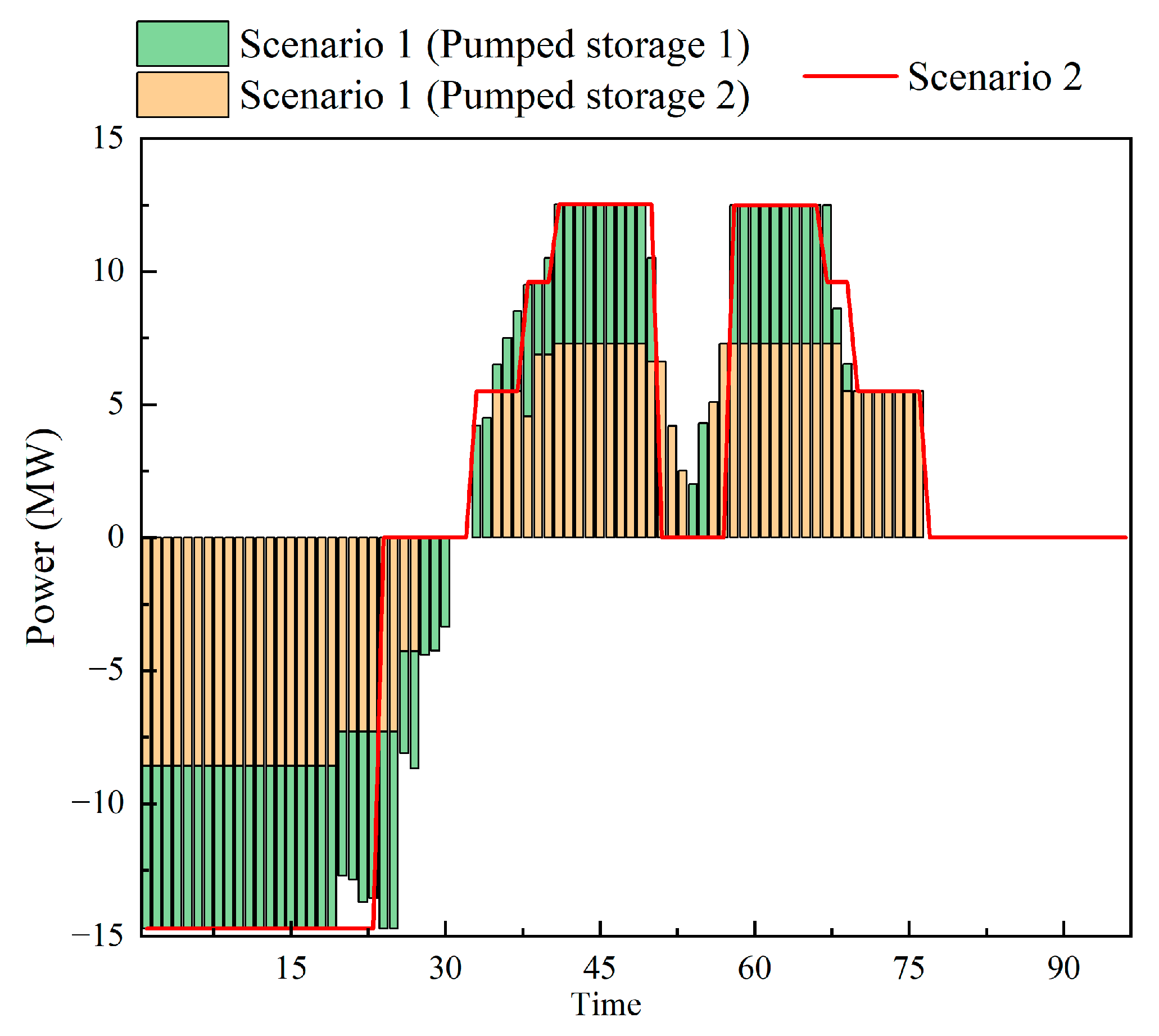
5.2.2. Impact of Distributed Pumped Storage on System Operation
5.2.3. The Influence of Capacity Configuration on the Optimization Results
6. Conclusions
- (1)
- The construction of a distributed pumped storage power station can give full flexibility to its regulation. In a period of low load, it can effectively absorb excess clean energy and reduce the system’s power sales to the higher power grid. During the peak load period, energy storage is released to reduce the demand for electricity and thus the electricity purchased from the superior power grid, thereby improving the overall economy of industrial users during operation.
- (2)
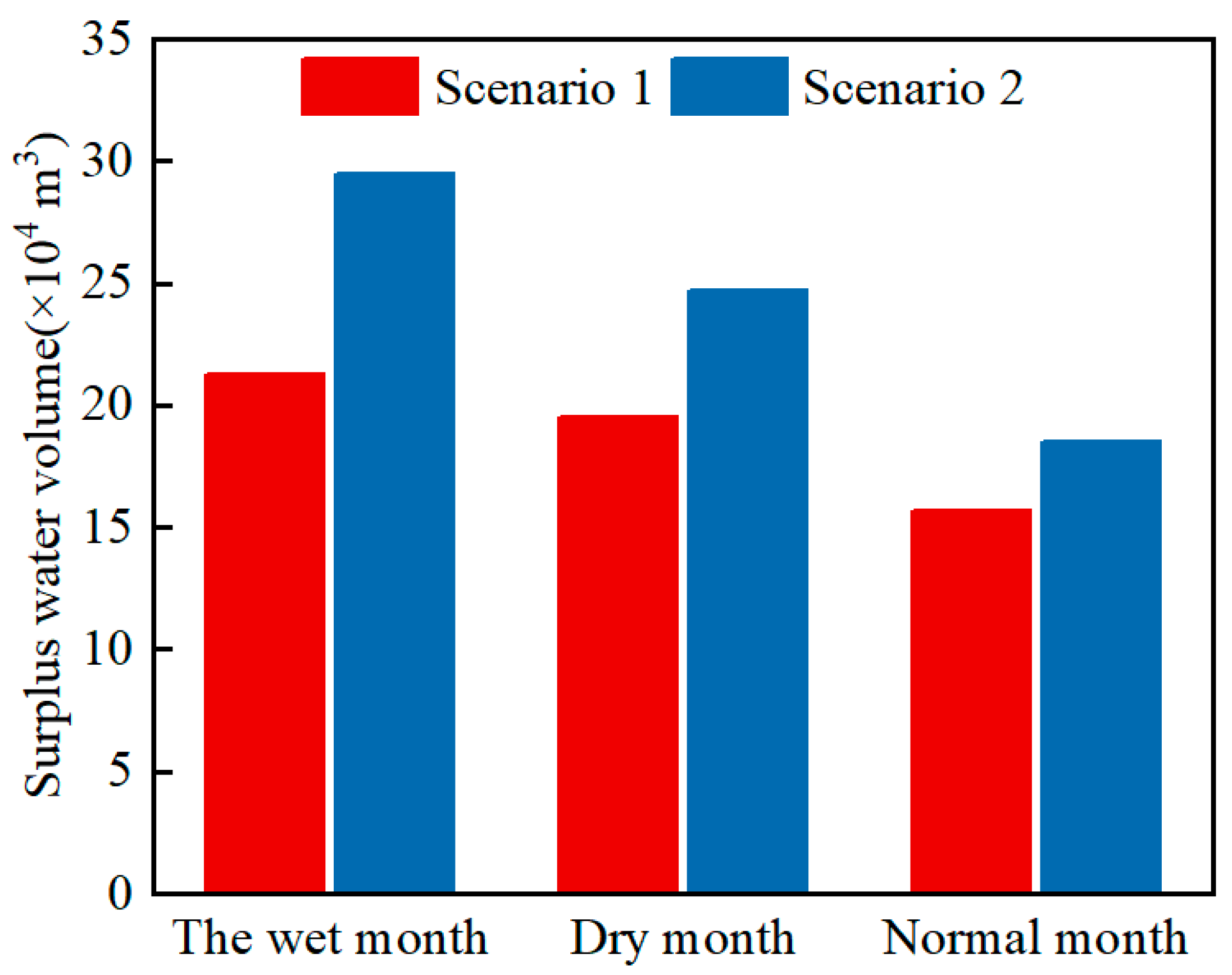
- Compared with the construction of a centralized pumped storage power station, the distributed pumped storage power station combined with the hydraulic coupling characteristics of the basin can flexibly adjust the water resource allocation in the region, effectively reduce the water abandonment phenomenon of the hydropower station, and improve the consumption level of clean energy to further improve the comprehensive operation efficiency of the system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IEA. World Energy Outlook 2022; IEA: Paris, France, 2022. [Google Scholar]
- Li, C.; Wang, N.; Shen, X.; Zhang, Y.; Yang, Z.; Tong, X.; Maréchal, F.; Wang, L.; Yang, Y. Energy Planning of Beijing Towards Low-Carbon, Clean and Efficient Development in 2035. CSEE J. Power Energy Syst. 2024, 10, 913–928. [Google Scholar] [CrossRef]
- Liu, S.; Ye, W.; Wu, Y.; Ye, Z. An Improved Tiered Electricity Pricing Scheme Considering Energy Saving and Carbon Reduction, Cross-Subsidy Handling, and User Demands. Energies 2025, 18, 2610. [Google Scholar] [CrossRef]
- Blasuttigh, N.; Negri, S.; Massi Pavan, A. Optimal ATECO-Based Clustering and Photovoltaic System Sizing for Industrial Users in Renewable Energy Communities. Energies 2025, 18, 763. [Google Scholar] [CrossRef]
- Gan, W.; Ai, X.; Fang, J.; Yan, M.; Yao, W.; Zuo, W.; Wen, J. Security constrained co-planning of transmission expansion and energy storage. Appl. Energy 2019, 239, 383–394. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, Y.; Wang, B. Review on market implementation and scheduling model considering flexibility mining of differentiated industrial high energy load. J. Electr. Technol. 2025, 2025, 2043–2062+2161. [Google Scholar]
- Liu, S.; Xu, J.; Xing, C.; Liu, Y.; Tian, E.; Cui, J.; Wei, J. Study on Dynamic Pricing Strategy for Industrial Power Users Considering Demand Response Differences in Master–Slave Game. Sustainability 2023, 15, 12265. [Google Scholar] [CrossRef]
- Wan, Q.; Liu, W. Robust interval optimization scheduling for direct power purchase of large users considering wind load uncertainty. Sol. Energy J. 2022, 2022, 347–355. [Google Scholar]
- Hu, D.; Wang, T. Optimizing Power Demand Side Response Strategy: A Study Based on Double Master–Slave Game Model of Multi-Objective Multi-Universe Optimization. Energies 2023, 16, 4009. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, C.; Li, Z.; Yin, S.; Xie, A.; Wang, P.; Ding, Y. The Impact of Participation Ratio and Bidding Strategies on New Energy’s Involvement in Electricity Spot Market Trading under Marketization Trends—An Empirical Analysis Based on Henan Province, China. Energies 2024, 17, 4463. [Google Scholar] [CrossRef]
- National Energy Administration of the People’s Republic of China. Medium and Long-Term Development Plan of Pumped Storage (2021–2035); National Energy Administration of the People’s Republic of China: Beijing, China, 2021.
- Legacy, M.R.J.; Wyk, E.V.; Brinkerhoff, J. Pumped Hydro Energy Storage: A Multi-Reservoir Continuous Supply Hydroelectric Generation and Storage System. In Proceedings of the 2024 IEEE Electrical Energy Storage Application and Technologies Conference (EESAT), San Diego, CA, USA, 29–30 January 2024; pp. 1–4. [Google Scholar]
- Wang, X.; Li, G.; Ji, S. Research on capacity optimization configuration of complementary power generation system considering wind-solar uncertainty. J. Power Eng. 2024, 2024, 1750–1759. [Google Scholar]
- Yao, J.; Wang, M.; Zhao, H. Optimal allocation of pumped storage capacity of local power grids considering cost recovery. Hydroelectr. Energy Sci. 2022, 2022, 208–211+197. [Google Scholar]
- Liu, B.; Zhou, B.; Yang, D.; Yang, Z.; Cui, M. Optimal capacity planning of combined renewable energy source-pumped storage and seawater desalination systems. Glob. Energy Interconnect. 2019, 2, 310–317. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Z.; Mandapaka, P.V.; Lo, E.Y.M. Risk-averse restoration of coupled power and water systems with small pumped-hydro storage and stochastic rooftop renewables. Appl. Energy 2023, 339, 120953. [Google Scholar] [CrossRef]
- Jing, H.; Zhao, H.; Yao, W. Flexible resource planning for new energy power generation systems with distributed pumped storage. Electr. Power Autom. Equip. 2023, 2023, 117–123+173. [Google Scholar]
- Xu, Q.; Shi, C.; Jing, H. Joint planning of transmission network and distributed pumped storage for new power systems. Power Syst. Prot. Control 2024, 2024, 128–137. [Google Scholar]
- Williams, M.-J.; Chang, C.-K. The Optimal Integration of Virtual Power Plants for the South African National Grid Based on an Energy Mix as per the Integrated Resource Plan 2019: A Review. Energies 2024, 17, 6489. [Google Scholar] [CrossRef]
- Seward, W.; Qadrdan, M.; Jenkins, N. Quantifying the value of distributed battery storage to the operation of a low carbon power system. Appl. Energy 2022, 305, 117684. [Google Scholar] [CrossRef]
- Brusco, G.; Menniti, D.; Pinnarelli, A.; Sorrentino, N. Renewable Energy Community with distributed storage optimization to provide energy sharing and additional ancillary services. Sustain. Energy Grids Netw. 2023, 36, 101173. [Google Scholar] [CrossRef]
- Muqbel, A.; Al-Awami, A.T.; Parvania, M. Optimal Planning of Distributed Battery Energy Storage Systems in Unbalanced Distribution Networks. IEEE Syst. J. 2022, 16, 1194–1205. [Google Scholar] [CrossRef]
- Duan, J.; Liu, F.; Yang, Y. Optimal operation for integrated electricity and natural gas systems considering demand response uncertainties. Appl. Energy 2022, 323, 119455. [Google Scholar] [CrossRef]
- Zhao, Z.; Yu, Z.; Kang, Y.; Wang, J.; Cheng, C.; Su, H. Hydro-photovoltaic complementary dispatch based on active regulation of cascade hydropower considering multi-transmission channel constraints. Appl. Energy 2025, 377, 124573. [Google Scholar] [CrossRef]
- Li, Y.; Hong, F.; Ge, X.; Zhang, X.; Zhao, B.; Wu, F. Optimal Capacity Configuration of Pumped-Storage Units Used to Retrofit Cascaded Hydropower Stations. Energies 2023, 16, 8049. [Google Scholar] [CrossRef]
- Li, Y.; Li, O.; Wu, F.; Ma, S.; Shi, L.; Hong, F. Multi-Objective Capacity Optimization of Grid-Connected Wind–Pumped Hydro Storage Hybrid Systems Considering Variable-Speed Operation. Energies 2023, 16, 8113. [Google Scholar] [CrossRef]
- Zhai, H.; Fan, W.; Zhang, Y. Research on the Two-Part Tariff Mechanism of Pumped Storage Power Stations: Analysis Based on the Construction of Pricing Calculation Models for Electricity Price Profit and Capacity Price. Price Theory Pract. 2022, 09, 178–182. [Google Scholar]
- Liu, Z.; Zhang, L.; Kou, P. Capacity Optimization Configuration of grid-connected Wind Power—Photovoltaic—pumped storage—Battery System. J. Power Eng. 2023, 43, 1151–1159. [Google Scholar] [CrossRef]
- Luo, B.; Chen, Y.; Miao, S. A joint short-term operation model for wind power and hybrid pumped-storage hydropower plant. J. Hydraul. Eng. 2023, 54, 955–966. [Google Scholar]
- Pan, P.; Chen, G.; Shi, H.; Zha, X.; Huang, Z. Distributed Robust Optimization Method for Active Distribution Network with Variable-Speed Pumped Storage. Electronics 2024, 13, 3317. [Google Scholar] [CrossRef]
- Zhong, H.; Liu, H.; Shi, Y. Optimal allocation of pumped storage reservoir capacity considering the aggregation effect of small hydropower and agricultural irrigation. Power Syst. Prot. Control 2025, 53, 1–13. [Google Scholar] [CrossRef]
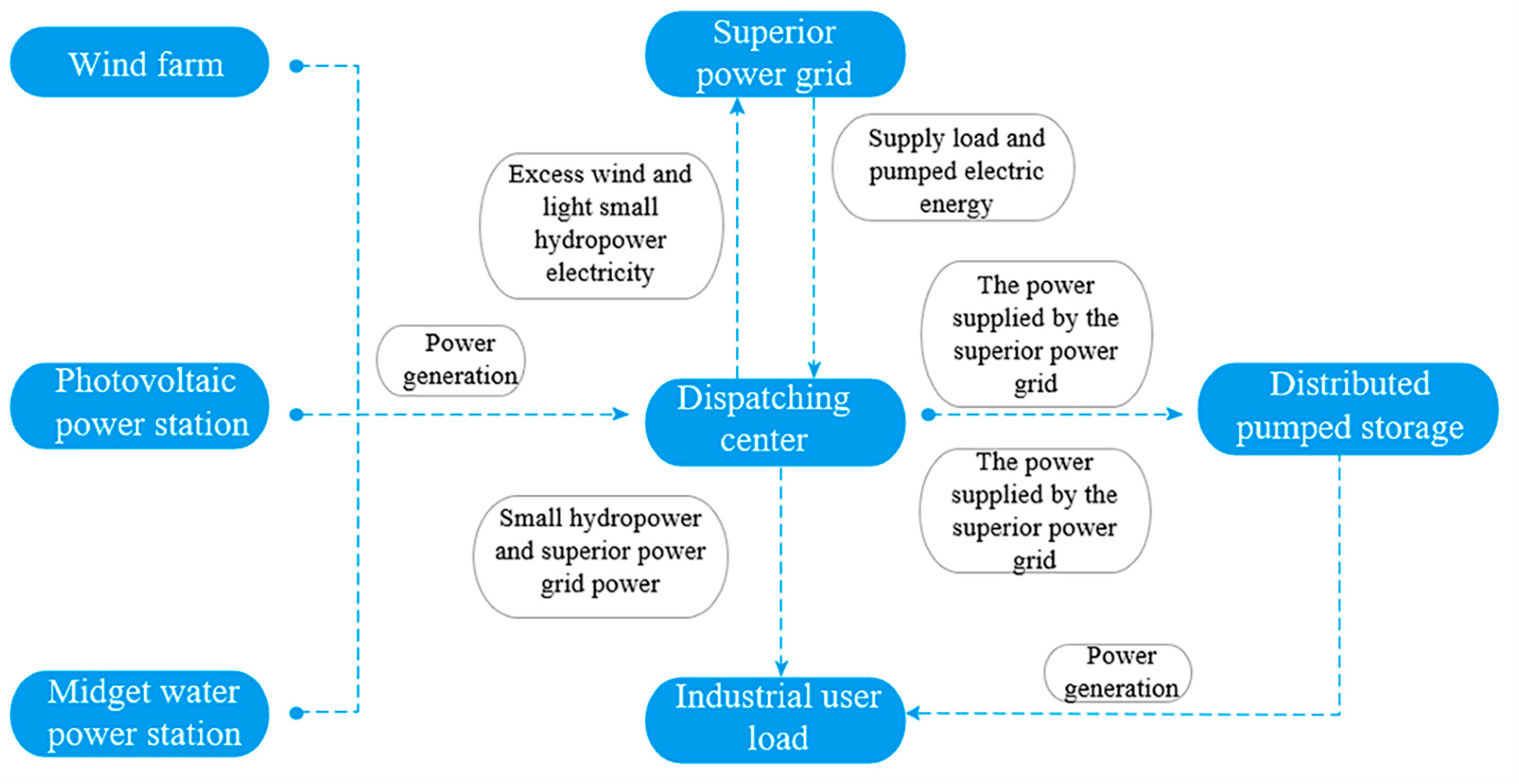
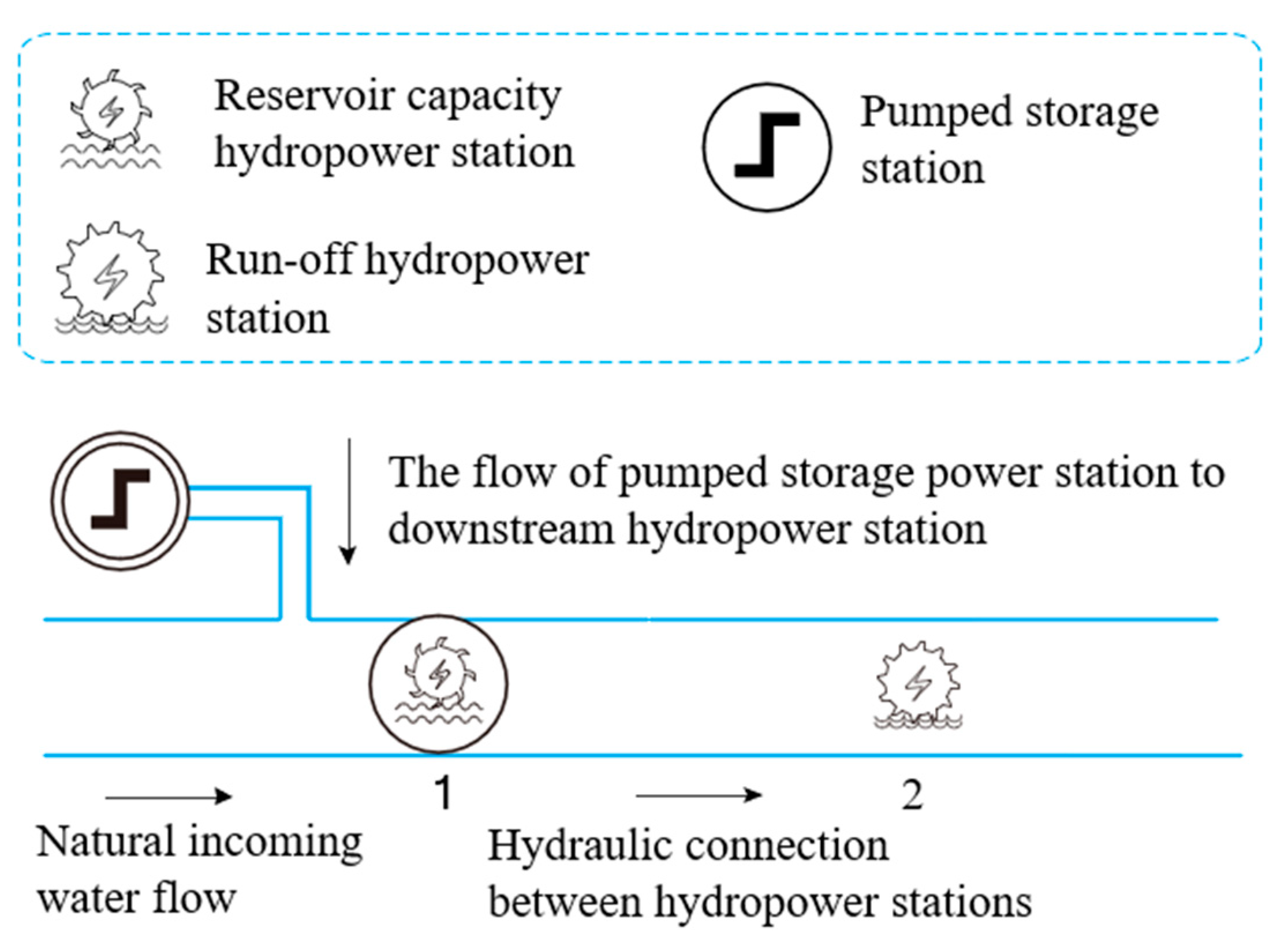
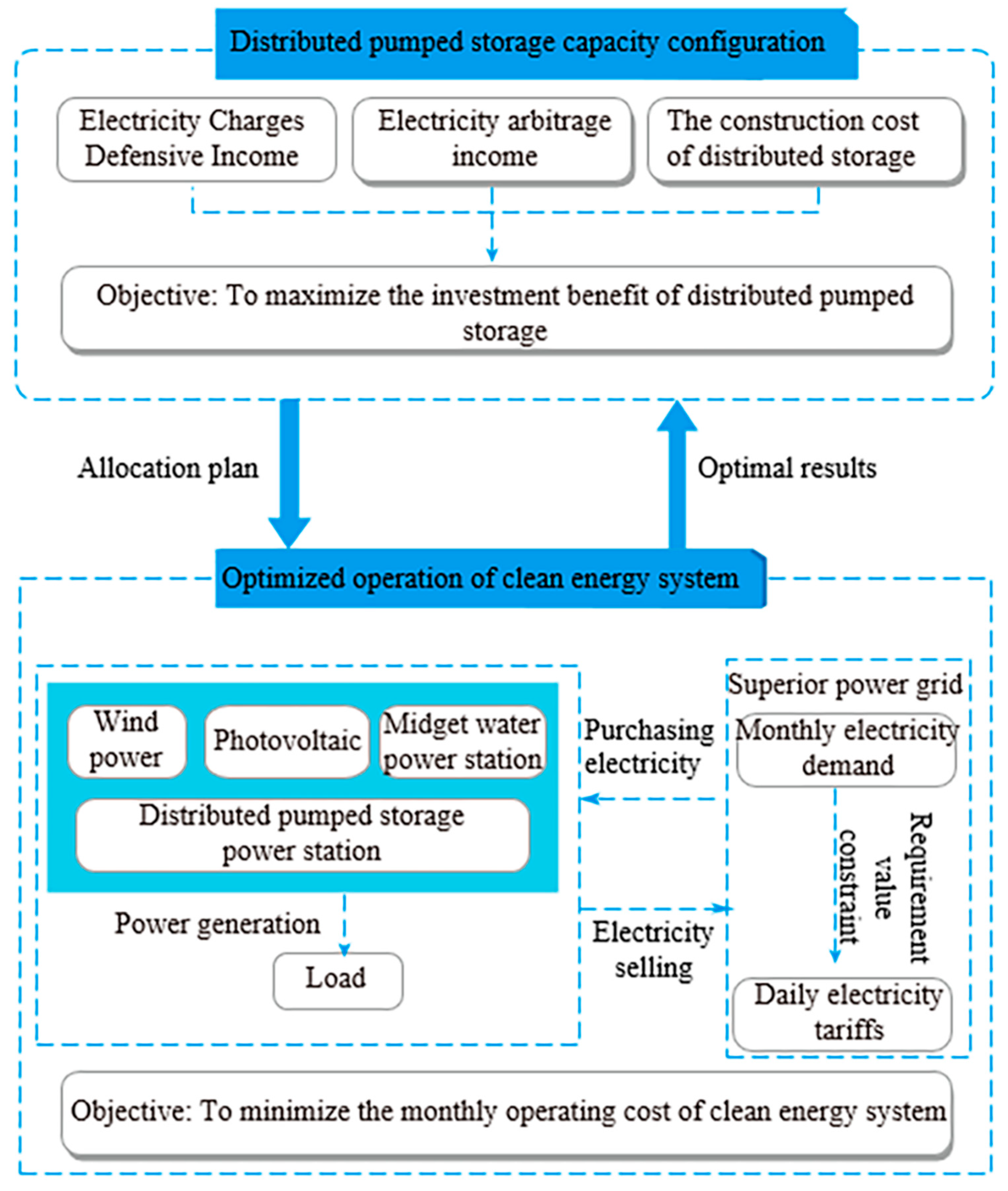
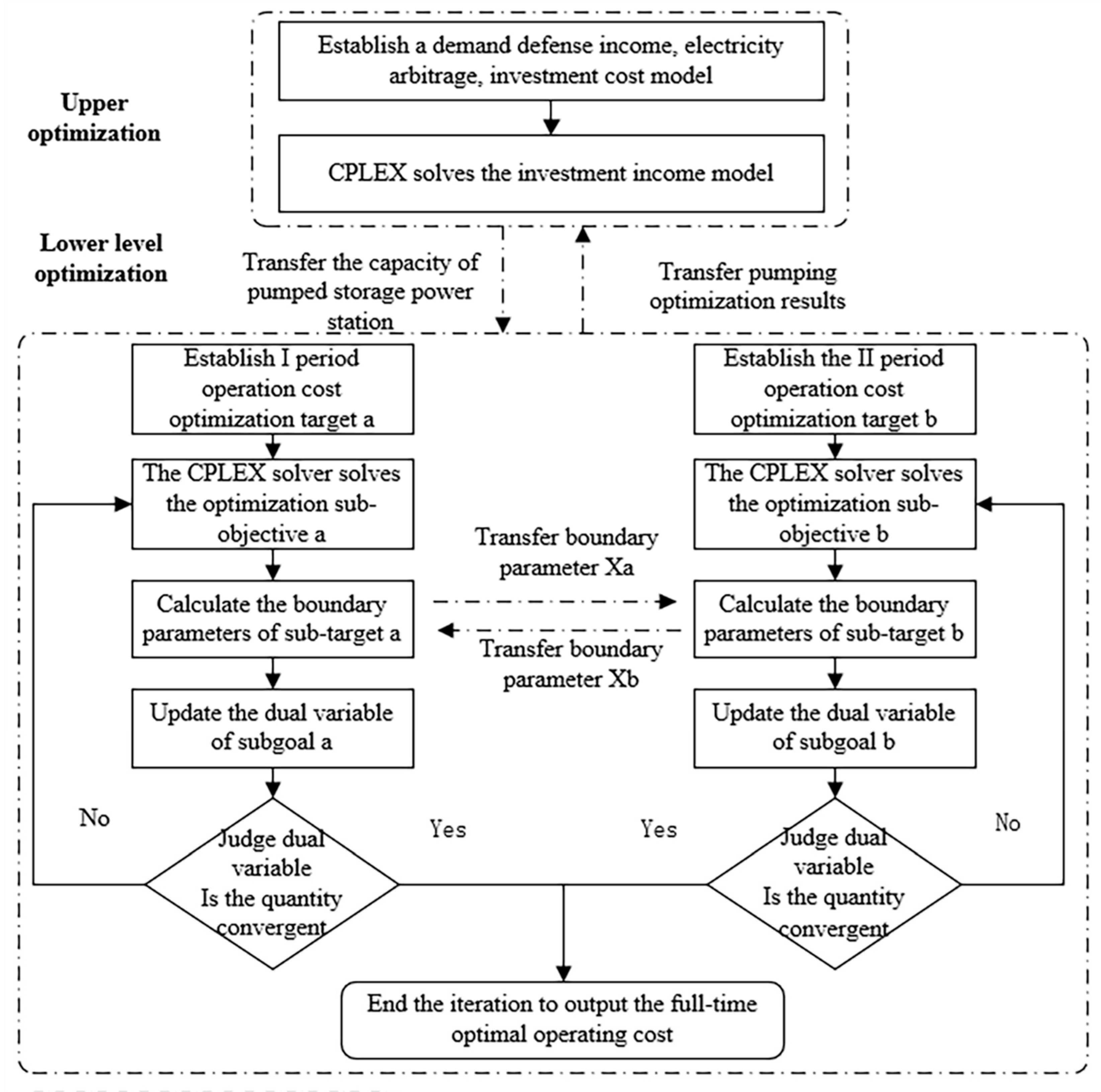

| Electrovalence | Time Interval | Electricity Purchase Price (RMB/KW·h) | Electricity Sales Price (RMB/KW·h) |
|---|---|---|---|
| Valley price | 0:00~8:00 | 0.3139 | 0.1567 |
| Flat peak electricity price | 12:00~17:00 21:00~24:00 | 0.6418 | 0.3205 |
| Peak load price | 8:00~12:00 17:00~21:00 | 1.0697 | 0.4803 |
| Power Station Number | Efficiency | Installed Capacity (MW) | Type of Hydropower Station | Maximum Storage Capacity (×104 m3) |
|---|---|---|---|---|
| 1 | 0.93 | 7.00 | Reservoir capacity hydropower station | 35.20 |
| 2 | 0.88 | 5.00 | Reservoir capacity hydropower station | 22.10 |
| 3 | 0.94 | 3.52 | Run-off hydropower station | 0 |
| 4 | 0.90 | 3.26 | Run-off hydropower station | 0 |
| 5 | 0.93 | 4.20 | Run-off hydropower station | 0 |
| Parameter | Numerical Value |
|---|---|
| (RMB/kW) | 2100 |
| [RMB/(m3/year)] | 14 |
| [RMB/(kW/year)] | 21 |
| (RMB/kW) | 2100 |
| (RMB/m3) | 500 |
| (10,000 RMB) | 40 |
| (10,000 RMB) | 50 |
| 0.05 | |
| (×104 m3) | 35.20 |
| (MW) | 50 |
| (×104 m3) | 100 |
| (Year) | 25 |
| (MW) | 45.72 |
| (MW) | 45.72 |
| (MW) | 20.52 |
| Parameter | Pumped Storage Station 1 | Pumped Storage Station 2 |
|---|---|---|
| Installed capacity (MW) | 8.58 | 6.12 |
| Storage capacity (×104 m3) | 78.00 | 59.00 |
| State | Maximum Power Purchase (MW) | Electricity Charge (10,000 RMB/Month) | Electricity Demand (10,000 RMB/Month) | Electricity Sales Revenue (10,000 RMB/Month) | Operating Cost (10,000 RMB/Month) | |
|---|---|---|---|---|---|---|
| Wet month | Not configured | 21.39 | 365.41 | 85.56 | 30.15 | 420.82 |
| Configuration | 9.91 | 154.94 | 39.64 | 10.18 | 184.40 | |
| Dry month | Not configured | 21.05 | 224.17 | 84.20 | 45.35 | 259.02 |
| Configuration | 7.53 | 70.79 | 30.12 | 13.49 | 87.42 | |
| Normal month | Not configured | 25.14 | 303.98 | 100.56 | 38.82 | 365.72 |
| Configuration | 11.53 | 127.59 | 46.12 | 18.27 | 155.44 |
| Annual Investment Cost (10,000 RMB) | Annual Electricity Purchase Cost (10,000 RMB) | Annual Electricity Sales Revenue (10,000 RMB) | |
|---|---|---|---|
| Scenario 1 | 539.50 | 1876.81 | 167.76 |
| Scenario 2 | 490.32 | 2139.35 | 190.15 |
| Centralized Pumped Storage | Distributed Pumped Storage | |
|---|---|---|
| Cost effectiveness | The annual electricity purchase cost is 21.3935 million RMB | The annual electricity purchase cost is 18.7681 million RMB |
| Operational flexibility | The regulation capacity of a single power station is limited | Multi-power station cooperative scheduling, as shown in Figure 7 |
| Effect on abandoned water | Abandoned water in wet, normal, and dry months amounted to 295,000 m3, 247,000 m3, and 182,000 m3 | Amount of abandoned water decreased by 27.79%, 21.05%, and 15.34% in wet, normal, and dry months |
| Total Capacity of Pumped Storage | System Annual Operating Cost (10,000 RMB) | Pumped Storage Annual Investment Benefit (10,000 RMB) |
|---|---|---|
| 0.5 | 1995.66 | 1023.54 |
| 0.75 | 1845.32 | 1153.01 |
| 1709.41 | 1280.04 | |
| 1.25 | 1827.21 | 1132.42 |
| 1.5 | 1874.32 | 1085.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhong, H.; Li, X.; Hu, W.; Ouyang, Z. Optimal Configuration of Distributed Pumped Storage Capacity with Clean Energy. Energies 2025, 18, 3896. https://doi.org/10.3390/en18153896
Wang Y, Zhong H, Li X, Hu W, Ouyang Z. Optimal Configuration of Distributed Pumped Storage Capacity with Clean Energy. Energies. 2025; 18(15):3896. https://doi.org/10.3390/en18153896
Chicago/Turabian StyleWang, Yongjia, Hao Zhong, Xun Li, Wenzhuo Hu, and Zhenhui Ouyang. 2025. "Optimal Configuration of Distributed Pumped Storage Capacity with Clean Energy" Energies 18, no. 15: 3896. https://doi.org/10.3390/en18153896
APA StyleWang, Y., Zhong, H., Li, X., Hu, W., & Ouyang, Z. (2025). Optimal Configuration of Distributed Pumped Storage Capacity with Clean Energy. Energies, 18(15), 3896. https://doi.org/10.3390/en18153896






