Fluid Dynamics Analysis of Flow Characteristics in the Clearance of Hydraulic Turbine Seal Rings
Abstract
1. Introduction
2. Theoretical Model Analysis
2.1. Flow Model Establishment
2.2. Flow Characterization
2.2.1. Tangential Velocity Distribution
2.2.2. Axial Velocity Distribution
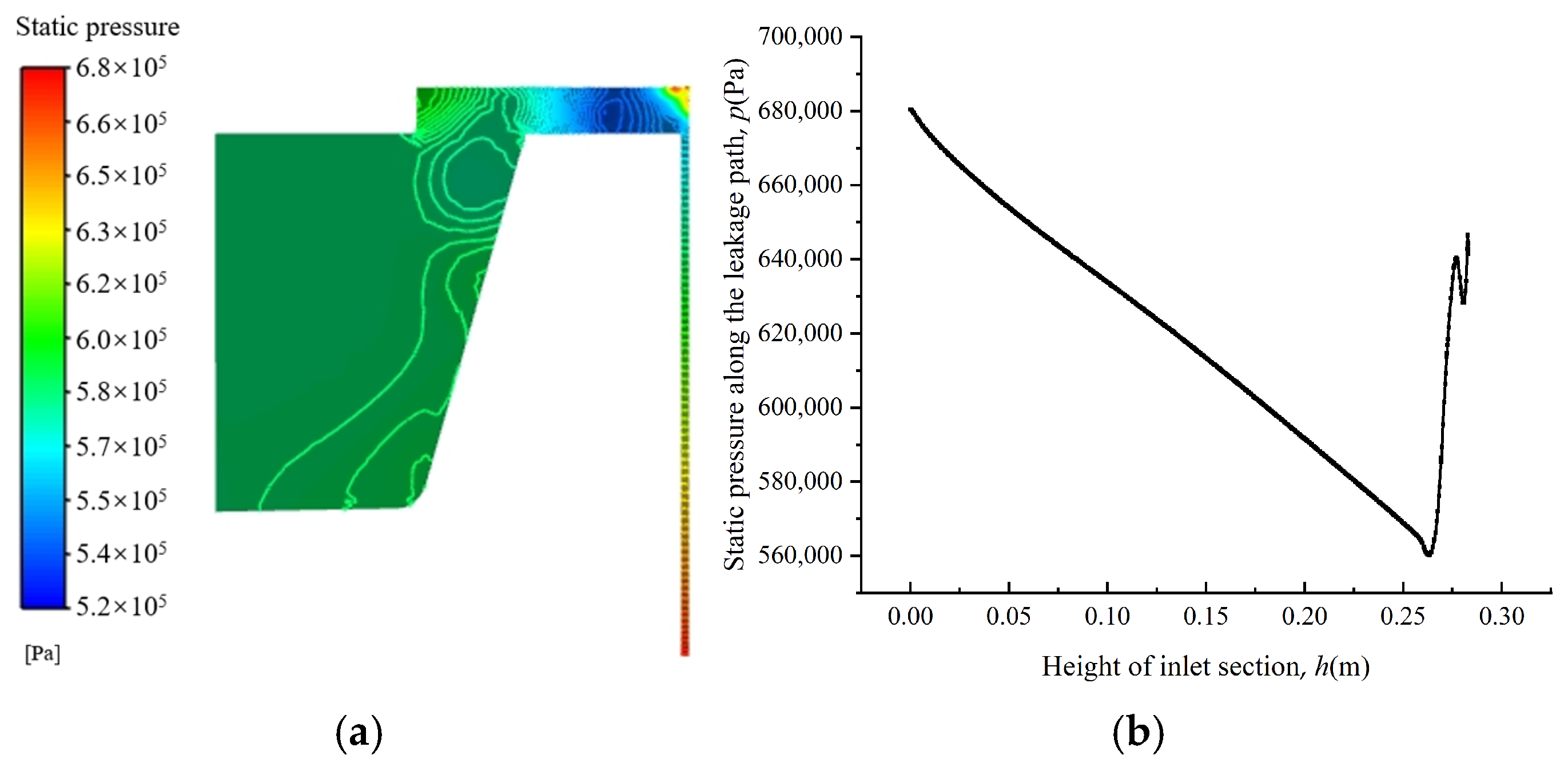
2.2.3. Pressure Distribution
- (1)
- Axial pressure
- (2)
- Radial pressure
2.3. Flow Stability Analysis at Multiple Scales
3. Numerical Simulation
3.1. Computational Model
3.2. Solver Setup
3.3. Result
3.3.1. Shear-Driven Flow Characteristics
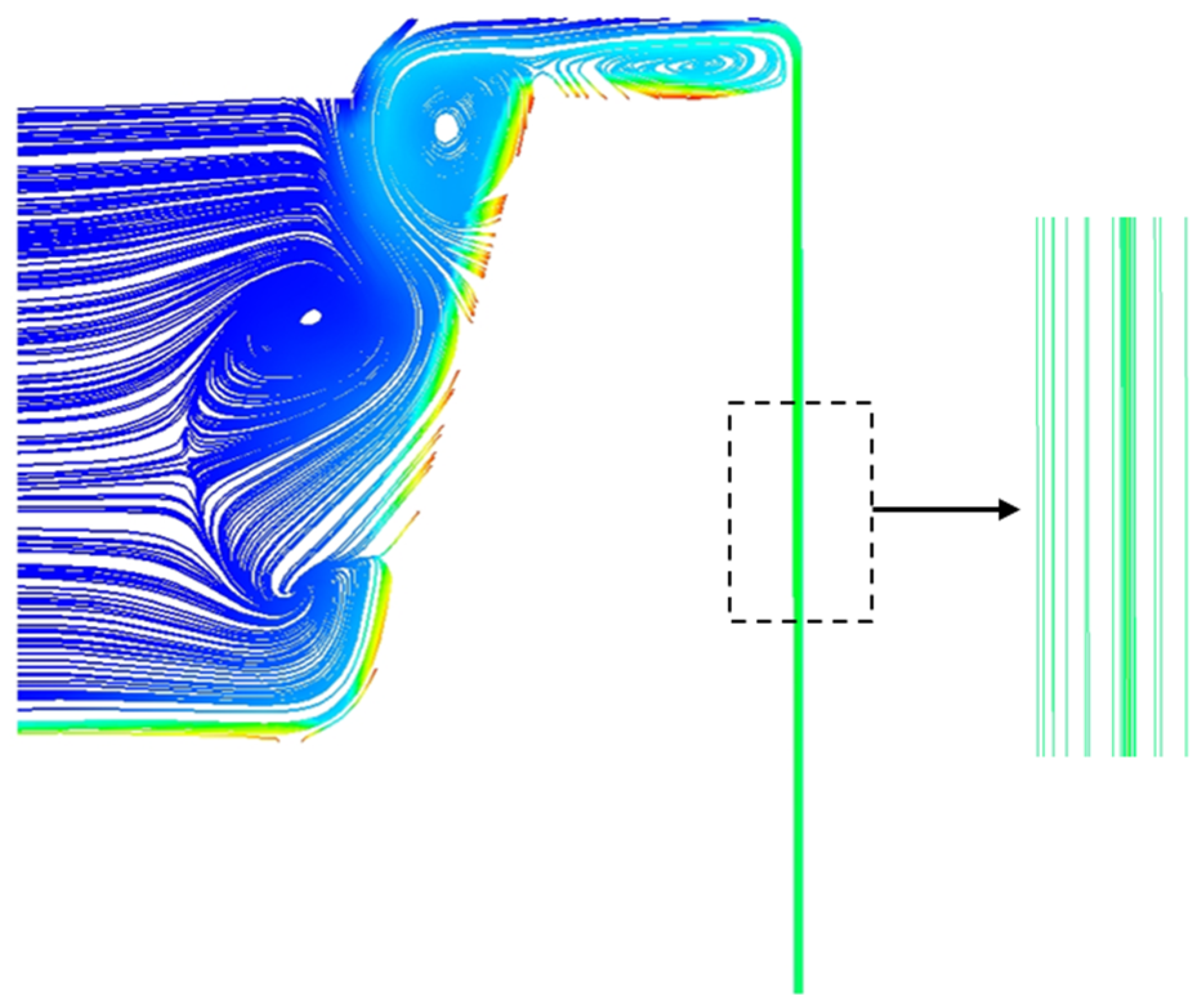
3.3.2. Influence of Short Channel Height on Flow Development
3.3.3. Rotation-Induced Vortices and Flow Instability
3.3.4. Pressure Pulsations and Flow Instability
3.4. Discussion
4. Conclusions and Outlook
4.1. Conclusions
- The CFD simulations not only validate the accuracy of the theoretical analysis but also enrich understanding of flow field characteristics through visualization. The simulation results demonstrate non-parabolic axial velocity distributions, spiral streamline trajectories, and a low-pressure zone in the upper-crown cavity, confirming the presence of vortices and the restrictive effect of short channels on flow development. The “U”-shaped distribution of turbulent kinetic energy and the dynamic variations in pressure fluctuations further reveal the rotation-induced turbulence enhancement effect, providing a powerful tool for the quantitative analysis of complex flow fields.
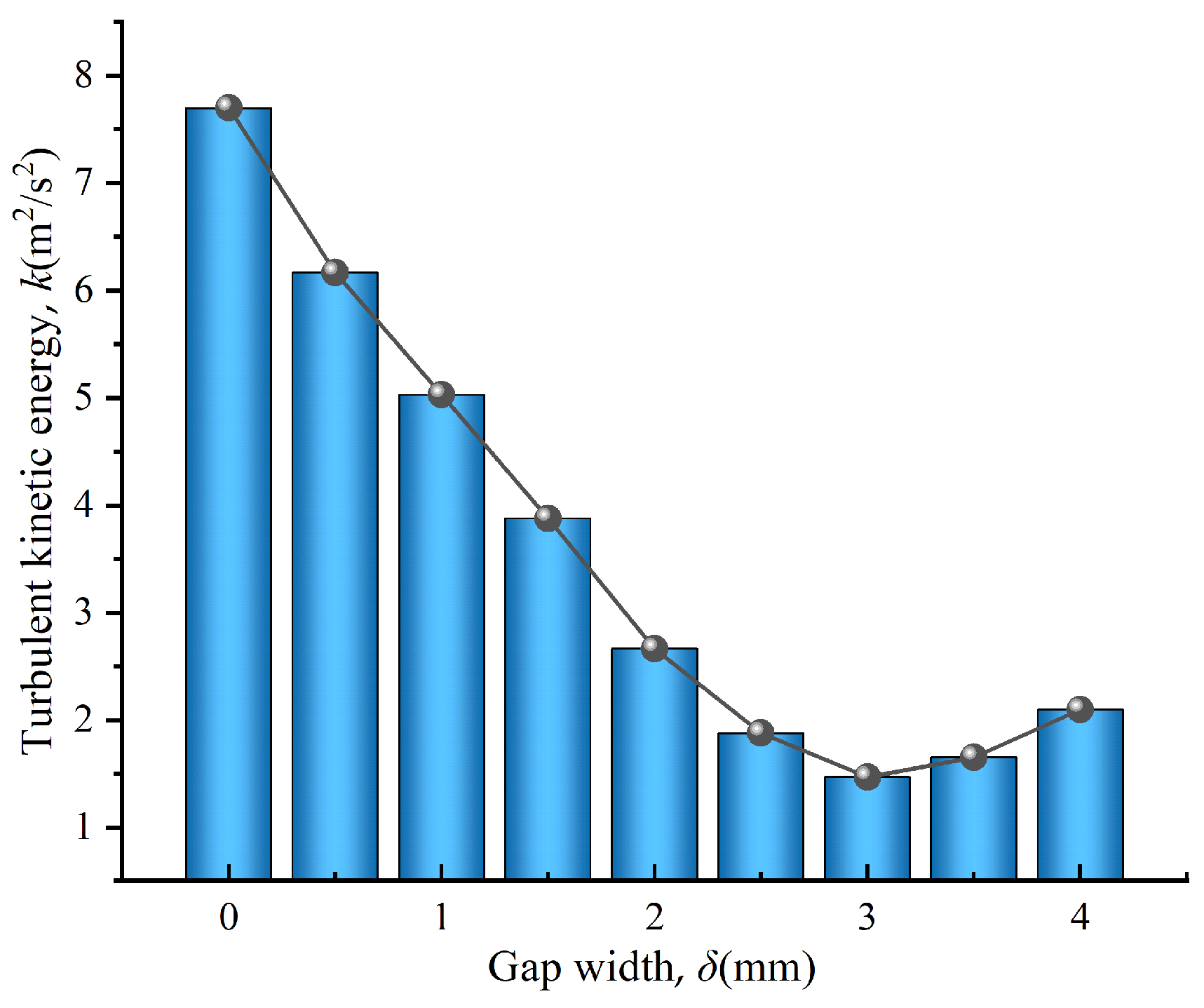
- The high-speed rotation of the inner wall is the dominant factor in the flow field within the gap. The theoretical analysis derived a nearly linear distribution of tangential velocity with a shear rate as high as 9250 s−1. CFD simulations further revealed an inverted “S”-shaped nonlinear distribution of tangential velocity along the radial direction, deviating from the linear characteristics of classical Couette flow. This phenomenon is attributed to the combined effects of turbulent diffusion and centrifugal force-induced secondary flows, highlighting the significant reshaping effect of rotation on boundary layer flow. Additionally, the streamline trajectories exhibited a spiral ascending flow pattern, particularly near the rotating wall, where the peak turbulent kinetic energy reaches 7.7 m2/s2, confirming the presence of complex vortex structures and turbulence enhancement induced by rotation. These findings provide new insights into understanding energy dissipation and leakage control in the internal flow of rotating machinery.
- This study incorporated the multi-scale effects introduced by the short channel height and high-speed rotation into the analytical framework and employed a modified Taylor number to assess flow stability. The results indicate that although the short channel geometry suppresses the formation of complete Taylor vortices, local small-scale vortices and flow instabilities still persist, particularly near the inner wall. Spectral analysis showed that the dominant frequency of pressure fluctuations is highly correlated with the rotational frequency of 1.27 Hz, and the amplitude decreases with increasing channel height, revealing the regulatory mechanism of the coupling between rotation and geometric constraints on flow stability.
4.2. Future Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mao, X.; Zhong, P.; Li, Z.; Liu, Z.; Hu, J.; Yan, J. Development and application of modified partially averaged Navier Stokes in the internal flow field of a Francis turbine. Phys. Fluids 2025, 37, 037122. [Google Scholar] [CrossRef]
- International Energy Agency. World Energy Outlook 2022; International Energy Agency: Paris, France, 2022. [Google Scholar]
- Rijal, M.; Neopane, H.; Chitrakar, S.; Pandey, A.; Dev, J. Numerical study of erosion on labyrinth seals of Francis turbine. J. Phys. Conf. Ser. 2023, 2629, 012021. [Google Scholar] [CrossRef]
- Zhou, D.; Chen, H.; Zhang, J.; Jiang, S.; Gui, J.; Yang, C.; Yu, A. Numerical Study on Flow Characteristics in a Francis Turbine during Load Rejection. Energies 2019, 12, 716. [Google Scholar] [CrossRef]
- Dörfler, P.; Sick, M.; Coutu, A. Flow-Induced Pulsation and Vibration in Hydroelectric Machinery: Engineer’s Guidebook for Planning, Design and Troubleshooting; Springer: London, UK, 2013. [Google Scholar] [CrossRef]
- Ohiemi, I.E.; Yang, S.; Singh, P.; Li, Y. Experimental investigation on the effect of axial gap on performance and unsteady pressure pulsations of low head axial flow hydraulic turbine. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Tang, B.; Liao, J.; Zhao, Z.; Deng, Q.; Li, J.; Feng, Z. Windage and Leakage Losses in Impeller Back Gap and Labyrinth Seal Cavities of Supercritical CO2 Centrifugal Compressors. Appl. Sci. 2025, 15, 3678. [Google Scholar] [CrossRef]
- Cui, J.; Tang, H. A review on flow instability in hydro-viscous drive. Phys. Fluids 2024, 36, 041301. [Google Scholar] [CrossRef]
- Xie, Y.; Du, Q.; Xie, L.; Wang, Z.; Li, S. Onset of turbulence in rotor-stator cavity flows. J. Fluid Mech. 2024, 991, A3. [Google Scholar] [CrossRef]
- Martinand, D.; Serre, E.; Lueptow, R.M. Absolute and convective instability of cylindrical Couette flow with axial and radial flows. Phys. Fluids 2009, 21, 104102. [Google Scholar] [CrossRef]
- Nagata, M. Taylor-Couette flow in the narrow-gap Limit. Philos. Trans. R. Soc. A 2023, 381, 20220134. [Google Scholar] [CrossRef]
- Cotrell, D.L.; McFadden, G.B. Axial flow effects on the stability of circular Couette flow with viscous heating. Phys. Fluids 2006, 18, 084106. [Google Scholar] [CrossRef]
- Trivedi, C. Time-dependent inception of vortex rings in a Francis turbine during load variation: Large eddy simulation and experimental validation. J. Hydraul. Res. 2020, 58, 790–806. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Dahlhaug, O.G. Numerical Techniques Applied to Hydraulic Turbines: A Perspective Review. Appl. Mech. Rev. 2016, 68, 010802. [Google Scholar] [CrossRef]
- Moore, J.J. Three-dimensional CFD rotordynamic analysis of gas labyrinth seals. J. Vib. Acoust. 2003, 125, 427–433. [Google Scholar] [CrossRef]
- Ding, J. Numerical Simulation and Experiment of Gas Film Flow Field on the Surface of Floating Ring Micro Groove Hydrodynamic Seal. Ph.D. Thesis, Lanzhou University of Technology, Lanzhou, China, 2019. [Google Scholar]
- Schiffer, J.; Benigni, H.; Jaberg, H.; Schneidhofer, T.; Ehrengruber, M. Numerical simulation of the flow in a Francis turbine including the runner seals on crown and band side. IOP Conf. Ser. Earth Environ. Sci. 2015, 26, 012022. [Google Scholar] [CrossRef]
- Kim, J.-H.; Ahn, J. Large Eddy Simulation of Leakage Flow in a Stepped Labyrinth Seal. Processes 2021, 9, 2179. [Google Scholar] [CrossRef]
- Nicoli, A.; Johnson, K.; Jefferson-Loveday, R. Computational modelling of turbulent taylor-couette flow for bearing chamber applications: A comparison of unsteady Reynolds-averaged Navier-Stokes models. Proc. Inst. Mech. Eng. Part A J. Power Energy 2022, 236, 985–1005. [Google Scholar] [CrossRef]
- Safari, A.; Saidi, M.H.; Salavatidezfouli, S.; Ma, W.; Yao, S. A comprehensive experimental and numerical study of Taylor-Couette flow on superhydrophobic surfaces. AIP Adv. 2025, 15, 055012. [Google Scholar] [CrossRef]
- Jia, X.; Zhang, H.; Zheng, Q.; Fan, S.; Tian, Z. Investigation on Rotor-Labyrinth Seal System with Variable Rotating Speed. Int. J. Turbo Jet Eng. 2020, 37, 209–219. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Y.; Qu, X.; Huo, G.; Zhao, Z. Simulation and Flow Analysis of the Hole Diaphragm Labyrinth Seal at Several Whirl Frequencies. Energies 2022, 15, 379. [Google Scholar] [CrossRef]
- Zheng, K.; Ma, H.; Sun, H.; Qin, J. Investigation of Flow Characteristics in Rotating Distributary and Confluence Cavities. Energies 2025, 18, 1287. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, L.; Sun, J.; Liu, M.; Liao, T.; Hu, X. Research on Micro Gap Flow Field Characteristics of Cylindrical Gas Film Seals Based on Experimental and Numerical Simulation. Aerospace 2024, 11, 40. [Google Scholar] [CrossRef]
- Perini, M.; Binder, N.; Bousquet, Y.; Schwartz, E. Rotating Instabilities in Shrouded Low Pressure Turbine at Design and Off-Design Conditions. J. Turbomach. 2023, 145, 111006. [Google Scholar] [CrossRef]
- Demay, Y.; Iooss, G.; Laure, P. The Couette Taylor Problem in the Small Gap Approximation. In Ordered and Turbulent Patterns in Taylor-Couette Flow; Andereck, C.D., Hayot, F., Eds.; NATO ASI Series; Springer: Boston, MA, USA, 1992; Volume 297. [Google Scholar] [CrossRef]
- Munson, B.R.; Young, D.F.; Okiishi, T.H.; Huebsch, W.W. Fundamentals of Fluid Mechanics, 8th ed.; Wiley: Hoboken, NJ, USA, 2018; ISBN 978-1-119-40787-3. [Google Scholar]
- Taylor, G.I. The Stability of a Viscous Liquid Contained Between Two Rotating Cylinders. Philos. Trans. R. Soc. Lond. A 1923, 223, 289–343. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Dover Publications: New York, NY, USA, 1981; p. 24. [Google Scholar]
- Mao, X.; Liu, Z.; Li, T.; Mao, G.; Chen, D. A brief review of numerical solving methods for internal fluid of pumped storage unit. Int. J. Energy Res. 2020, 44, 7549–7566. [Google Scholar] [CrossRef]
- Gavrilov, A.; Ignatenko, Y. Numerical Simulation of Taylor-Couette-Poiseuille Flow at Re = 10,000. Fluids 2023, 8, 280. [Google Scholar] [CrossRef]


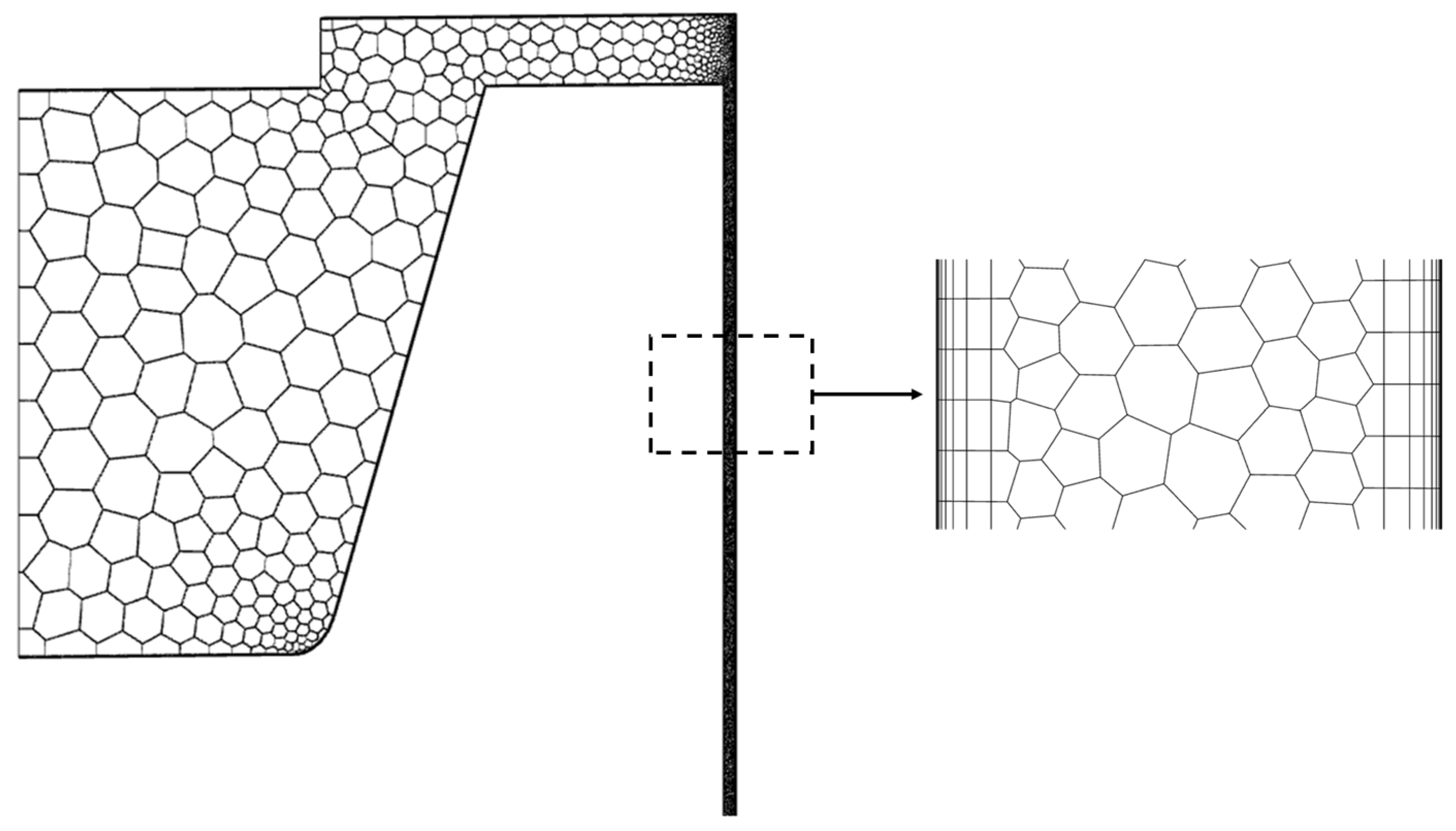
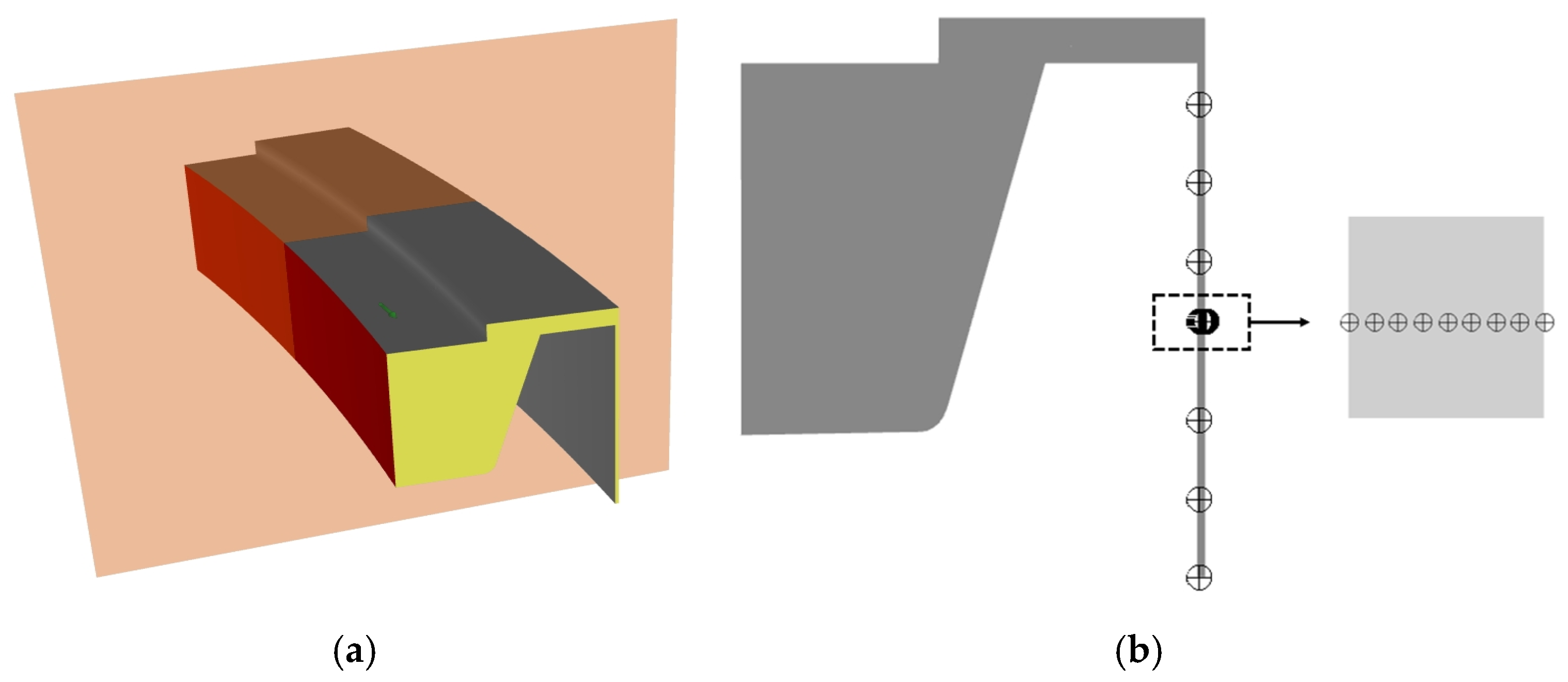




| Measurement Parameters | Coarse | Medium | Fine | e21 (%) | GCI21 (%) |
|---|---|---|---|---|---|
| Y-Velocity at Point 1 (m/s) | 10.2148 | 9.38755 | 9.03785 | 3.869 | 3.54 |
| Y-Velocity at Point 2 (m/s) | 2.70661 | 3.06686 | 3.08544 | 0.602 | 0.041 |
| Y-Velocity at Point 3 (m/s) | 0.286973 | 0.385668 | 0.390028 | 1.118 | 0.065 |
| Mass Flow Rate at inlet (kg/s) | 54.73 | 53.97 | 53.58 | 0.728 | 0.96 |
| Mass Flow Rate at outlet (kg/s) | 54.73 | 53.97 | 53.58 | 0.728 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Wu, W.; Deng, J.; Xue, B.; Xu, L.; Xie, B.; Wang, Y. Fluid Dynamics Analysis of Flow Characteristics in the Clearance of Hydraulic Turbine Seal Rings. Energies 2025, 18, 3726. https://doi.org/10.3390/en18143726
Chen L, Wu W, Deng J, Xue B, Xu L, Xie B, Wang Y. Fluid Dynamics Analysis of Flow Characteristics in the Clearance of Hydraulic Turbine Seal Rings. Energies. 2025; 18(14):3726. https://doi.org/10.3390/en18143726
Chicago/Turabian StyleChen, Leilei, Wenhao Wu, Jian Deng, Bing Xue, Liuming Xu, Baosheng Xie, and Yuchuan Wang. 2025. "Fluid Dynamics Analysis of Flow Characteristics in the Clearance of Hydraulic Turbine Seal Rings" Energies 18, no. 14: 3726. https://doi.org/10.3390/en18143726
APA StyleChen, L., Wu, W., Deng, J., Xue, B., Xu, L., Xie, B., & Wang, Y. (2025). Fluid Dynamics Analysis of Flow Characteristics in the Clearance of Hydraulic Turbine Seal Rings. Energies, 18(14), 3726. https://doi.org/10.3390/en18143726







