Regional Disparities, Spatial Effects, and the Dynamic Evolution of Distorted Energy Prices in China

Abstract

The distortion of energy prices has become an important obstacle to the high-quality development of China’s economy. Moreover, energy price distortions are not merely a domestic issue. They may trigger carbon leakage by diverting emissions-intensive production to countries with cheaper energy. Although the existing literature has extensively examined the effects of energy price distortions, two significant research gaps remain. First, most studies treat energy price distortions merely as an influencing factor, lacking a systematic analysis that places it at the core. Second, the spatial correlation characteristics of energy price distortions are often overlooked. This study measures the degree of energy price distortions across Chinese provinces from 2000 to 2022 and employs methods such as the Global Moran’s I, Local Moran’s I, and kernel density estimation to systematically analyze the spatial correlation, spatial distribution of coordination indices, and dynamic evolution patterns of these distortions. The results reveal that: (1) the overall degree of energy price distortions in China exhibited a trend of rising first and then declining, with significant regional disparities; (2) the regional gap followed an “expansion-contraction” trajectory; (3) there is notable spatial autocorrelation, with high-distortion areas concentrated in Northeast China, the middle reaches of the Yellow River, and Northwest China; and (4) the dynamic evolution suggests that distortion levels in high- and medium-value regions may continue to decline, while those in low-value regions may increase. This study fills a critical gap in the systematic spatial analysis of energy price distortions and provides new empirical evidence and policy insights for advancing market-oriented reforms in energy markets.

1. Introduction

As a global economic phenomenon, energy price distortion is widespread in developing countries and transitional economies. International experience indicates that government intervention in energy markets, lagging factor market reforms, and market monopolies often result in energy prices that fail to reflect the true scarcity of resources and the environmental externalities they generate [1,2]. Such distortions not only lead to inefficiencies in resource allocation but also transmit through price signals to influence industrial structure, energy consumption patterns, and carbon emission intensity, becoming a key obstacle to green economic transformation. Although energy price distortions are common, their manifestations and underlying mechanisms vary significantly across economies. As the world’s largest energy consumer and carbon emitter, China presents a particularly distinctive case. Price liberalization marked the decisive turning point in China’s shift from a command economy to a market-oriented one. Under central planning, resources were misallocated, goods were perennially scarce, and the entire economic engine was in need of overhaul. Reformers, therefore, had to find a breakthrough powerful enough to reset incentives yet subtle enough to avoid social upheaval. After limited experiments in tax and fiscal policy, they zeroed in on prices, the economy’s most fundamental signal. A transparent, flexible price-formation mechanism could unlock efficient resource allocation, spur production, and guide consumption far more effectively than any decree. Nowhere is this signal more critical than in energy. When energy prices are distorted, consumption habits warp, investment skews, and carbon footprints balloon. China’s ascent to the leading global user of energy and source of carbon emissions is therefore at odds with its new blueprint for green, productivity-led growth, and it magnifies vulnerabilities in national energy security. Correcting these price signals is no longer just an economic tweak; it is a strategic imperative for sustainable development.

As China’s market reforms deepen, price signals now govern the allocation of most final goods, yet factor-market reforms remain comparatively lagging. The central government continues to set prices for seven categories—including transmission and distribution tariffs, as well as oil and gas pipeline transportation—thereby preserving multiple pricing regimes within a single economy and inevitably generating energy-price distortions. The coexistence of planned- and market-based mechanisms produces two distinct forms of distortion: policy-induced distortions, rooted in market imperfections, and market-induced distortions, stemming from sub-optimal policy design. Although existing research has examined these distortions extensively, most studies treat them chiefly as explanatory variables that influence other outcomes. The largest body of work explores how distorted energy prices affect improvements in energy efficiency and factor substitution. For instance, Xu et al. [3] developed an extended vintage-capital model under imperfect factor markets and showed that distorted factor prices reshape the accumulation of high-efficiency capital vintages, thereby altering energy demand and CO₂ emissions. Wang et al. [4] argued that, amid China’s rapid development, distorted energy prices have become a principal obstacle to energy conservation and emission reduction. Sun et al. [5] introduced a joint-frontier parametric linear programming method based on the Shephard energy-distance function to measure total-factor energy efficiency in manufacturing and to derive shadow energy prices through cost minimization.

In light of the above, this study focuses on 30 Chinese provinces, and, based on a scientifically constructed measure of energy price distortions, employs multiple quantitative methods to clarify regional disparities and the dynamic evolution of their distribution. Compared with the existing literature, this paper makes several novel contributions. First, it provides a rigorous measurement of energy price distortion. While previous studies have primarily conducted qualitative analyses or relied on single-indicator case studies, this research draws on the fundamental connotations and characteristics of energy price distortion and utilizes the Cobb-Douglas (C-D) production function to comprehensively estimate provincial-level distortions across China. Second, it accurately identifies regional disparities in distortion levels. Although current research acknowledges the imbalance and inadequacy of energy price distortion, little attention has been paid to the extent and sources of these disparities. To address this gap, this study introduces the Theil index and its decomposition method to clarify the magnitude and sources of regional variation, offering valuable insights for reforming China’s energy pricing system. Third, it investigates the dynamic evolution of energy price distortion from a multidimensional perspective. Moving beyond the limitations of static analysis, the study incorporates both temporal and spatial dimensions by applying stochastic kernel density estimation and Markov chain analysis to capture the dynamic shifts in relative positions and state transition probabilities of distortion levels, aiming to provide empirical evidence and systematic understanding to support energy pricing reform.

The remainder of this paper is organized as follows. Section 2 reviews the relevant literature; Section 3 details the research methodology and data; Section 4 reports the empirical results; and Section 5 offers conclusions and policy recommendations.

2. Literature Review and Theoretical Framework

2.1. Literature Review

(1)

Measurement Methods of Energy Price Distortion

The production function approach, shadow pricing, and frontier analysis are the three primary methodologies used to estimate energy price distortion. Compared to the other two, the production function method is widely adopted due to its ease of data acquisition, simplicity in model construction, and its ability to directly reveal the gap between marginal prices and marginal productivity. Sun et al. [5] developed a joint frontier model based on the Shephard energy distance function to measure total-factor energy efficiency in China’s manufacturing sector, deriving shadow energy prices through cost minimization. Wu et al. [6] focused on China’s heavy industry and used the price gap method to estimate absolute price distortions across multiple energy types—including coal, oil, and natural gas—over the period 2003–2019. Ju et al. [2] applied a path analysis framework to construct three distortion indicators across five energy types. He found that although China’s energy pricing system has undergone partial marketization, significant distortions remain. Relative and dynamic distortions were found to promote economic growth, while absolute distortions constrained it. Moreover, achieving carbon reduction goals depends on reducing such distortions. Ouyang and Sun [1] employed a shadow pricing model combined with stochastic frontier analysis (SFA) to compare actual and shadow prices in China’s industrial sector, identifying allocative inefficiencies and potential energy savings. Ju et al. [7] and Sha et al. [8] proposed a theoretical energy pricing method based on marginal opportunity cost, decomposing the theoretical price into the marginal costs of production, utilization, and externalities. They used this framework to estimate distortions in coal, oil, and other energy types, establishing a broader framework for analyzing energy market distortions. Qiao et al. [9] adopted a ratio-based method to estimate capital and labor price distortions at the firm level. Capital distortion was estimated by comparing actual capital costs with the theoretical interest rate, while labor distortion was measured as the ratio of per capita labor cost to the industry average wage. Based on observed market prices, this approach reflects deviations from ideal resource allocation and is a typical method for measuring relative price distortion. Sun et al. [10] incorporated ecological efficiency, estimated using a bootstrap-DEA method, as an indicator of China’s environmental performance, and used a translog production function to estimate factor price distortions. Zhang et al. [11] proposed a production function model with time-varying elasticity and used a factor income share approach based on national accounts to estimate capital and labor price distortions. They argue that this method captures temporal variation more effectively than the C-D or translog models. Peng, Zhang, and Xu [12] used a non-radial directional distance function to investigate the effect of energy price distortion on energy efficiency in China, introducing a spatial correlation perspective and confirming that distortion significantly affects energy efficiency. Wang et al. [13] developed a translog production function combined with a stochastic frontier analysis model (SFA), using cities as the unit of analysis to evaluate total-factor energy efficiency and energy price distortion in China’s high-energy-consuming industries during 2003–2019.

(2)

Economic Impacts of Energy Price Distortion

Energy price distortion is more than a market anomaly as it profoundly affects macroeconomic outcomes. This section reviews its economic impacts, focusing on efficiency, resource allocation, and industrial structure, and explores the mechanisms through which these effects occur. Most existing studies focus on specific dimensions of energy price distortion, particularly its effects on efficiency and resource allocation. Xu and Tan [14] examined the implications of eliminating energy misallocation in China, concluding that correcting energy price distortions could significantly increase economic output and contribute to global energy savings. Wang et al. [13] employed a translog production function and stochastic frontier analysis (SFA) to investigate the impact of energy price distortion on total-factor energy efficiency (TFEE) in energy-intensive industries across Chinese cities. Their results showed that energy price distortion significantly suppresses efficiency improvements. Zamani et al. [15], using translog cost function estimation based on Iranian manufacturing data from 2006–2018, found that rising energy prices reduce energy intensity and enhance energy and labor efficiency, while having only minor effects on capital and material inputs. These studies indirectly support the view that market-oriented pricing and the reduction of distortions enhance both resource allocation efficiency and energy utilization. In addition, some research examines the broader systemic and macroeconomic effects of energy price distortion. Kirikkaleli and Darbaz [16], using Toda-Yamamoto causality, Fourier Toda, and Spectral BC tests, identified a bidirectional causality between energy prices and the food price index across different frequency domains. Punzi [17] employed a dynamic stochastic general equilibrium (DSGE) model of a small open economy to assess how energy price uncertainty affects macroeconomic variables. Croonenbroeck and Hüttel [18] proposed a simplified method to quantify the efficiency loss resulting from forecast errors in renewable energy prices. Their findings suggest that price forecast errors significantly impair resource allocation efficiency, particularly in volatile energy types such as solar power, while the effects for wind power were negligible. Furthermore, they observed time-dependent patterns in efficiency loss, underscoring the importance of improving forecast accuracy to reduce deadweight losses in energy allocation.

(3)

Environmental Impacts of Energy Price Distortion

With the growing global awareness of environmental protection, the environmental impacts of energy price distortion have increasingly become a focus of academic research. This section reviews how energy price distortion affects the environment directly or indirectly by influencing energy consumption patterns, carbon emission intensity, and related pathways. Scholars have explored the structural implications of energy price distortion. At the industrial sector level, accelerating the marketization of factor prices, particularly energy, is considered essential for advancing green industrial transformation and achieving China’s “dual carbon” goals. Xu et al. [3], Li Ke et al. [19], and Gao et al. [20] demonstrated that correcting price distortions not only improves energy efficiency and emission performance but also unlocks substantial growth potential for high-quality industrial development. Xu et al. estimated that eliminating distortions in energy and other factor prices could reduce industrial coal consumption by approximately 225 million tonnes and CO₂ emissions by 793 million tonnes annually, along with a reduction in air pollution. Li Ke, Xu Chang, and Tang Liwei found that mitigating distortions—especially in competitive energy markets—substantially increases industrial green total-factor productivity (GTFP), with the most urgent needs observed in eastern provinces and those under economic or fiscal pressure. Gao et al. further estimated that fully eliminating capital and energy market distortions could yield a 10% annual increase in green industrial development potential, with greater gains in central and western China. At the sectoral level, Gao et al. [21] showed that energy price distortion contributes to inefficient industrial structures, affecting both energy consumption intensity and carbon emission intensity. Wang, Bai, and Xie [22] estimated the extent of distortion in China’s oil pricing between 2004 and 2016, identifying positive price distortion in the transport sector. Their findings revealed significant substitution effects between oil, coal, and electricity, moderated by factor substitutability.

A systematic review of existing studies reveals several key research gaps that remain to be addressed. First, there are limitations related to data availability. Most current research relies on provincial-level or industry-level data [12], lacking long-term, high-frequency, and interprovincially comparable datasets. Some studies [10] estimate energy prices using proxy variables, which may introduce measurement bias. Second, there is a noticeable geographic coverage bias. Existing findings are predominantly concentrated in economically developed eastern regions [13], with insufficient attention to energy-rich areas in central and western China, making it difficult to reveal spatial heterogeneity across the entire territory. Third, there is a mismatch in the time dimension. Many studies are limited to data before 2019 [6] and fail to capture the structural shifts in the energy pricing mechanism that have occurred following the implementation of the “dual carbon” policy. To address these issues, this study focuses on 30 provinces in China. Based on a scientifically constructed measure of energy price distortion, the study investigates the imbalance and inadequacy of energy price distortions across regions. It introduces the Theil index and its decomposition method to clarify the extent and sources of regional disparities, and examines the dynamic evolution of the distribution of distortion levels from multiple dimensions. The aim is to provide empirical evidence and generalizable insights to support energy pricing reform.

(4)

Spatial Analysis of Energy Price Distortion

In recent years, spatial econometric approaches have been widely applied in the study of energy pricing and resource allocation. Methodologically, spatial econometrics is grounded in solid theoretical foundations. As noted by Anselin [23], spatial econometric models are effective in identifying spatial dependence and heterogeneity among variables. Following Chen et al. [24], we first employed Moran’s I test to confirm the spatial autocorrelation of energy price distortion, which aligns with the five fundamental principles of spatial econometrics proposed by Paelinck et al. [25]. For model selection, we adopted the spatial modeling framework suggested by Baltagi et al. [26] and ultimately employed the Spatial Lag Model (SLM) to capture the spatial spillover effects of energy price distortion.

Regarding the spatial analysis of energy price distortion, Elhorst [27] provided a systematic overview of spatial panel data models, offering a methodological foundation for studying spatial effects in energy pricing. In cross-country research, Wu et al. [28] employed a Spatial Durbin Model to reveal the suppressive effects of energy prices on both local and neighboring countries’ carbon emissions in the EU. Burnett et al. [29] applied a spatial panel data model to examine spatial dependence in U.S. energy markets and found significant negative spatial spillover effects of energy prices across states. At the methodological level, the seminal work by LeSage and Pace [30] provides theoretical guidance for constructing spatial weight matrices in energy price research. The Generalized Spatial Two-Stage Least Squares (GS2SLS) method, developed by Kelejian et al. [31], is widely used to address endogeneity in studies of energy markets. For instance, Hua et al. [32] applied this method to examine the spatial impact of technology market development on energy efficiency. In the Chinese context, Zhang et al. [33] adopted the Dagum Gini coefficient decomposition and spatial Markov chain methods to explore the dynamic spatial distribution of energy price distortions in the industrial sector. Their findings showed that energy distortions were more pronounced than labor distortions, with east-west disparities and spatial proximity identified as key drivers of this evolution. Peng et al. [12] used a spatial panel model to assess the impact of energy price distortions on energy efficiency, finding that distortions not only significantly reduced local energy efficiency but also generated spatial spillover and signaling effects in neighboring provinces, demonstrating strong spatial dependence. Additionally, Li et al. [34], using Geographically Weighted Regression (GWR), demonstrated that spatial heterogeneity implies that energy pricing policies should be tailored to the industrial structure and technological foundation of each region to maximize both economic and environmental benefits.

2.2. Theoretical Framework

The formation of energy misallocation can be examined from both the supply and demand sides. On the supply side, low energy efficiency in production results in a marginal output value of energy that is significantly lower than its total cost of use. On the demand side, factors such as price controls may cause energy prices to diverge from their true value, leading to overconsumption [3]. During China’s industrialization, many enterprises operated inefficiently due to technological limitations characteristic of specific stages of development. To maintain economic growth, government authorities implemented relatively loose environmental regulations during particular historical periods. This policy stance effectively encouraged an extensive growth model. Under such conditions, enterprises only bore the explicit costs of energy, while negative externalities—such as environmental pollution—were shifted onto society. As a result, the marginal output of energy remained far below its full social cost over the long term, ultimately causing distortions in resource allocation [4].

The evolution of environmental regulation policy in China has exhibited a clear pattern of institutional innovation. Rather than merely resorting to administrative price increases, policymakers sought to internalize environmental externalities, thereby restructuring the cost framework faced by enterprises. This policy design forced firms to make one of three choices: optimize their energy consumption patterns, implement energy-saving technological upgrades, or exit the market altogether. As a result, the institutional arrangement achieved a dual policy objective: maintaining relative stability in nominal energy prices while significantly improving energy use efficiency, thereby enhancing the overall efficiency of resource allocation [5].

From a regional perspective, the central government has taken a cautious stance on energy price marketization reforms out of concern for public welfare and livelihood protection. This cautious approach has led to a nationwide trend of energy price convergence. In theory, under perfect competition, firms should make production decisions such that the marginal output of energy equals its cost of use, in which case regional differences in pricing should not exist [35]. However, due to the heterogeneous environmental carrying capacities across regions and in light of limited autonomy over price regulation, local governments have adjusted enterprise energy costs by applying varying intensities of environmental regulation. This policy practice has resulted in significant regional differentiation in the implicit cost of energy use. To adapt to these institutional changes, firms at the micro level have had to improve energy productivity through technological innovation, aligning their operations with region-specific energy cost structures. At the macro level, this has ultimately manifested as regional disparities in energy allocation efficiency [36].

Based on the preceding literature review and theoretical framework, this study proposes the following hypotheses:

H1. 

Energy price distortions in China display significant regional disparities, following a spatial pattern of higher distortion in the east and lower distortion in the west.

H2. 

Energy price distortions exhibit significant spatial dependence, characterized by high-high and low-low clustering.

H3. 

The spatial effects of energy price distortions reflect a pattern of club convergence, whereby regions with similar levels of distortion tend to cluster together.

3. Research Methodology and Data Processing

3.1. Research Methodology

This study follows a “measurement-analysis-validation” research framework and consists of the following steps: (1) Measurement of energy price distortion: A provincial-level distortion index is constructed based on the C-D production function. (2) Decomposition of regional disparities: The Theil index is employed to examine spatial and temporal differences. (3) Test of spatial effects: Global and local Moran’s I indices are used to identify spatial clustering patterns. (4) Analysis of dynamic evolution: Kernel density estimation and Markov chain models are combined to forecast evolving trends. (5) Robustness Checks: Robustness tests on the convergence mechanism to verify the stability and consistency of the findings.

(1)

C-D Production Function

To capture the economic essence of factor-market distortions and to trace their temporal dynamics, this study adopts the production-function approach to evaluate provincial energy-price distortions. Grounded in the classical marginal principle, the method compares a factor’s observed price with its marginal revenue product to infer the degree of distortion. The C-D production function is widely used in long-term analyses of factor distortions due to its transparency, decomposability, and the ease of marginal product calculation [37,38]. In this study, the assumption of constant returns to scale is relaxed to improve the model’s adaptability to regional heterogeneity in China. The choice of the C-D function over the translog specification is based on the following considerations. First, the use of fixed elasticity coefficients in the C-D function simplifies parameter estimation and helps avoid the multicollinearity often introduced by interaction terms in translog models, making it particularly suitable for long-term panel data at the provincial level. Second, while the translog function provides greater flexibility in capturing time-varying elasticities of factor substitution, the primary objective of this study is to measure the relative degree of energy price distortion, rather than to track changes in elasticity over time. Third, the translog function requires higher data quality and a larger sample size, while provincial-level energy price data in China are subject to frequent adjustments in statistical definitions and classification standards. These inconsistencies undermine data comparability and reliability, thereby limiting the applicability of the translog specification in this context. The procedure begins by assuming that each province operates under a C-D technology, such that its production function is specified as:

$$Y_{it}=A_{it}\cdot K_{it}^{\alpha }{L}_{it}^{\beta }{E}_{it}^{\gamma }$$

(1)

Taking the natural logarithm of both sides of Equation (1) produces the linearized specification:

$$\ln Y_{it}=\ln A_{it}+\alpha \ln K_{it}+\beta \ln L_{it}+\gamma \ln E_{it}+{\mu }_{it}$$

(2)

Drawing on the shadow price model proposed by Ouyang and Sun [1] and integrating the price distortion measurement framework developed by Ju et al. [7], this study measures the degree of energy price distortion by comparing actual energy prices with their marginal revenue product. Given the marked heterogeneity in provincial development stages, the constant-returns-to-scale assumption is relaxed, permitting $\alpha +\beta +\gamma \ne 1$. Building on Equations (1) and (2), the marginal revenue product of energy for each province in year t can be further expressed as:

$$MR{P}_{E_{it}}=\gamma \cdot {\displaystyle \frac{Y_{it}}{E_{it}}}\hspace{1em}$$

(3)

In Equation (3), $i$ indexes provinces and $t$ denotes years. Comparing the observed energy price $P_{E_{it}}$ with its marginal revenue product $MR{P}_{E_{it}}$ yields the annual energy-price distortion for each province, expressed as:

$$Dis{t}_{E_{it}}={\displaystyle \frac{P_{E_{it}}-MR{P}_{E_{it}}}{MR{P}_{E_{it}}}}$$

(4)

The energy-price distortion index $Dis{t}_{E_{it}}$ captures the deviation of a province’s actual energy price from its market-equilibrium level in year t. When $Dis{t}_{E_{it}}>0$, meaning the observed price exceeds the marginal revenue product of energy, production units typically curb energy demand, substitute toward capital or labor, or enhance energy-use efficiency to conserve energy. Conversely, $Dis{t}_{E_{it}}<0$ indicates that the observed price lies below the equilibrium benchmark, suggesting scope for profitable expansion of energy input. Nonetheless, as energy consumption rises, the marginal return to additional energy diminishes, and its utilization efficiency correspondingly declines.

(2)

Theil T Index (GE(1))

This study employs the Theil T index, a member of the Generalized Entropy Index family, to measure energy distortion. Originally introduced by Theil [39], this method has been widely adopted in the analysis of regional disparities [40]. The Theil index is a measure of regional disparities, with larger values indicating greater differences. It is decomposable and can distinguish between within-region and between-region disparities. Energy distortion typically appears when certain regions or industries draw disproportionately on high-efficiency or low-cost energy, undermining economy-wide allocation. To capture this phenomenon, we apply the generalized entropy index GE(1). Unlike many alternative inequality measures, GE1 is especially sensitive to areas with extreme distortion, sharply illuminating the “resource-misallocation” pattern of excessive energy use. Further, its additivity and decomposability allow us to separate total distortion into between-region and within-region components, revealing the precise origins and structural contours of the problem. GE(1) strikes a balance between the sensitivity of GE(0) to low distortions and the tendency of GE(2) to overweight extremely high distortions, making it well-suited for capturing resource misallocation, where excessive energy possession by certain regions is a key concern. The additive decomposability of GE(1) provides clear, policy-relevant insights, whereas GE(2)’s use of squared terms may exaggerate outliers, and GE(0) may underrepresent areas with high levels of distortion. GE(1) is widely used in regional disparity studies, ensuring consistency and comparability with existing literature on China’s spatial heterogeneity. The corresponding computational formula is presented below.

$$T_t={\displaystyle \frac{1}{k}}{\displaystyle \sum _{i=1}^k\left(\frac{E_{it}}{\overline{E_t}}\times \ln \frac{E_{it}}{\overline{E_t}}\right)}$$

(5)

In Equation (5), $T_t$ takes values in the interval [0, 1] and rises monotonically with the severity of energy-price distortion. Values approaching 0 indicate convergence in provincial distortion levels, whereas values nearing 1 signal pronounced inter-provincial disparities. Here, $n$ denotes the number of provinces, $E_{it}$ denotes the energy-price distortion of province $i$, and $\overline{E}$ refers to the national mean.

$$T_{jt}={\displaystyle \frac{1}{n_j}}{\displaystyle \sum _{i=1}^{n_j}\left(\frac{E_{ijt}}{\overline{E_{jt}}}\times \ln \frac{E_{ijt}}{\overline{E_{jt}}}\right)}$$

(6)

In Equation (6), $T_{jt}$ denotes the overall Theil index for region $j$; $n_j$ is the number of provinces in region $j$; $E_{ijt}$ represents the energy-price distortion level of province $i$ within region $j$; and $\overline{E_{jt}}$ is the mean distortion level for region $j$.

$$T_t=T_{wt}+T_{bt}={\displaystyle \sum _{j=1}^8\left(\frac{n_j}{n}\times \frac{{\overline{E}}_{jt}}{\overline{E_t}}\times T_{jt}\right)}+{\displaystyle \sum _{j=1}^8\left(\frac{n_j}{n}\times \frac{{\overline{E}}_{jt}}{\overline{E_t}}\times \ln \frac{{\overline{E}}_{jt}}{\overline{E_t}}\right)}$$

(7)

In Equation (7), the overall Theil index for digital-rural development is decomposed into a within-region component $T_{wt}$ and a between-region component $T_{bt}$. The terms ${\displaystyle \frac{T_{wt}}{T_t}}$ and ${\displaystyle \frac{T_{bt}}{T_t}}$ denote the respective contribution shares of these two components to the national disparity, while ${\displaystyle \frac{E_{jt}}{E_t}}\times {\displaystyle \frac{T_{j_t}}{T_t}}$ captures the share of each region in the aggregated within-region inequality. The expression $E_{jt}$ is the sum of energy-price distortions for all provinces in region $j$, and $E_t$ is the corresponding national total.

3.2. Data Processing

The calculation of the marginal revenue product of energy relies primarily on data from standard statistical yearbooks. Provincial-level GDP, labor input, and capital stock are sourced from successive editions of the China Statistical Yearbook, while energy consumption figures are sourced from the China Energy Statistical Yearbook. Given the lack of officially published energy price data, researchers typically estimate them by inflating benchmark prices from 2003, as reported for 36 large and medium-sized cities in the China Price Yearbook 2004. However, this approach has notable limitations: the range of energy types is incomplete, and the selected cities do not adequately represent all 30 provinces. To enhance accuracy, this study adopts an alternative estimation method based on data from the Compilation of Data from the Third National Industrial Census. Compared with existing studies, our method covers more provinces and energy types, thereby enhancing representativeness. The process involves three main steps. First, the census provides both energy consumption volumes and corresponding prices for each province in 2000; multiplying these yields the total energy cost per province. Second, energy consumption is converted into standard coal equivalents, enabling the derivation of uniform provincial energy prices for 2000. Third, annual provincial energy prices for 2001–2022 are estimated by adjusting the 2000 baseline using the yearly Fuel and Power Price Index. To ensure the validity of the model specification, we conducted panel data diagnostics using the LLC, IPS, and Fisher-ADF tests to examine variable stationarity. The results show that the null hypothesis of a unit root for energy price distortion is rejected at the 1% significance level, indicating that the variable is stationary.

4. Empirical Analysis

4.1. Baseline Measurements

Table 1. Regional Energy Price Distortion Indices.

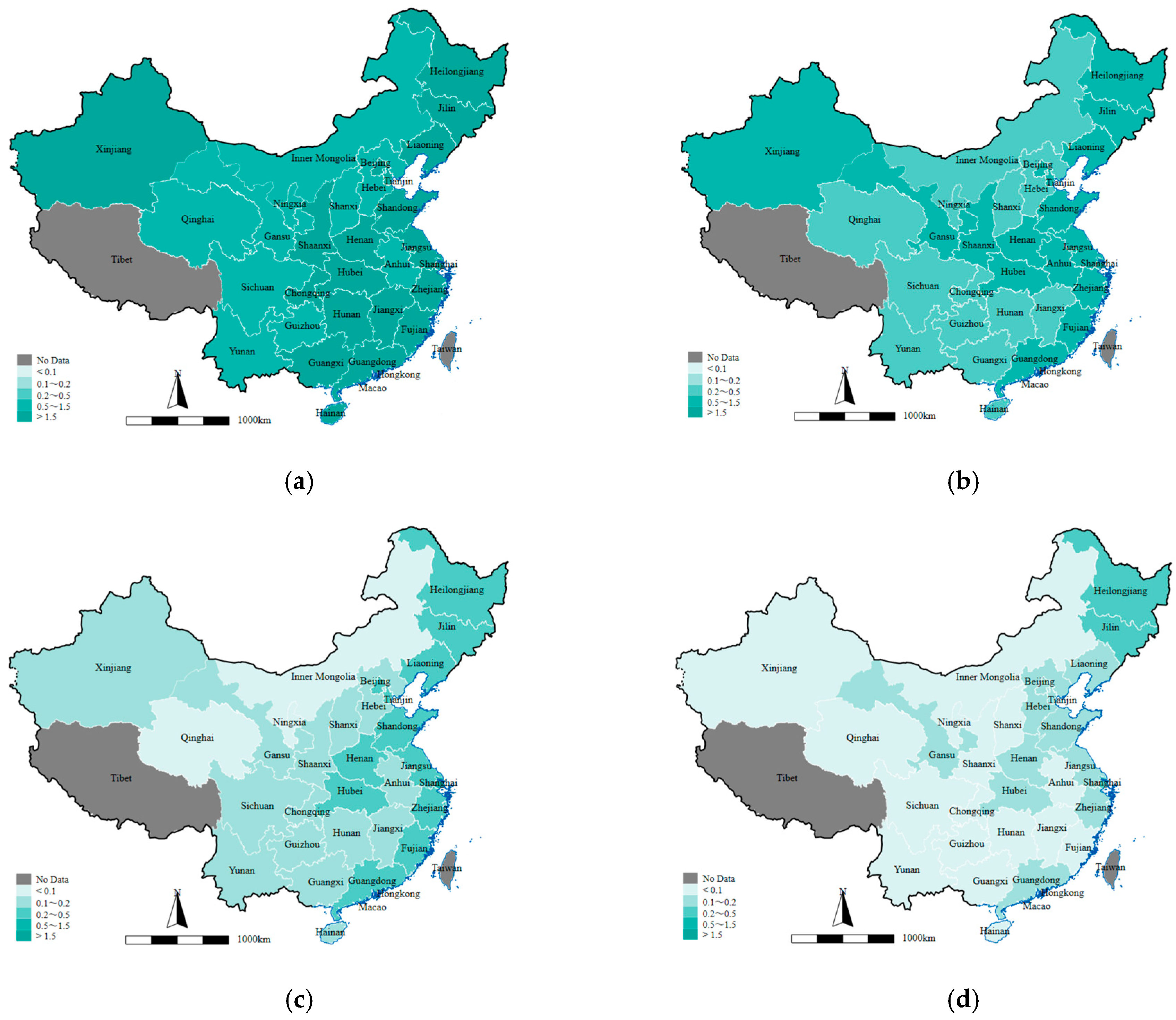
Area	2000	2008	2016	2022	Mean	Area	2000	2008	2016	2022	Mean
China	2.030	0.552	0.232	0.115	0.620	Henan	1.944	0.558	0.283	0.194	0.636
Liaoning	2.233	0.833	0.414	0.162	0.855	Shaanxi	1.910	0.501	0.173	0.088	0.541
Jilin	2.497	0.729	0.444	0.223	0.842	Middle Yellow River	5.894	1.568	0.652	0.372	1.739
Heilongjiang	1.664	0.864	0.410	0.222	0.778	Anhui	1.420	0.505	0.190	0.091	0.506
Northeast Comprehensive	6.394	2.427	1.268	0.607	2.474	Jiangxi	1.552	0.494	0.187	0.083	0.509
Beijing	2.056	0.643	0.314	0.157	0.707	Hubei	2.153	0.609	0.296	0.144	0.700
Tianjin	3.324	0.832	0.268	0.140	0.952	Hunan	1.599	0.341	0.170	0.084	0.432
Hebei	1.395	0.460	0.173	0.112	0.482	Middle Yangtze	6.724	1.948	0.843	0.401	2.147
Shandong	2.560	0.562	0.245	0.133	0.713	Guangxi	1.713	0.486	0.193	0.086	0.538
Northern Coast	9.335	2.497	1.001	0.543	2.854	Chongqing	1.618	0.320	0.147	0.066	0.422
Shanghai	4.422	1.136	0.554	0.270	1.352	Sichuan	1.419	0.351	0.170	0.080	0.414
Jiangsu	4.324	0.908	0.368	0.178	1.182	Guizhou	0.643	0.266	0.112	0.053	0.246
Zhejiang	3.288	0.750	0.317	0.141	0.904	Yunnan	1.335	0.375	0.142	0.061	0.405
Eastern Coast	12.034	2.793	1.240	0.589	3.439	Southwest	6.728	1.799	0.764	0.345	2.025
Fujian	2.793	0.547	0.212	0.095	0.743	Gansu	1.243	0.520	0.199	0.121	0.499
Guangdong	3.983	0.761	0.329	0.164	1.018	Qinghai	1.190	0.313	0.093	0.066	0.343
Hainan	1.926	0.396	0.122	0.048	0.490	Ningxia	0.993	0.252	0.082	0.026	0.235
Southern Coast	8.702	1.703	0.663	0.307	2.252	Xinjiang	1.673	0.750	0.168	0.077	0.608
Shanxi	0.788	0.308	0.110	0.061	0.276	Greater Northwest	5.099	1.835	0.542	0.290	1.685
Inner Mongolia	1.253	0.201	0.086	0.029	0.287

Note: Means in the table are arithmetic averages over the period 2000–2022.

reports provincial energy-price distortion indices for 2000–2022 and reveals three main patterns. First, at the national level, distortion has fallen sharply, dropping from 2.030 in 2000 to 0.115 in 2022, causing a 94.33% decline. Second, all eight economic regions exhibit a similar downward trajectory, yet their distortion levels differ markedly. Ranked from highest to lowest, the ordering is: East Coastal, North Coastal, Northeast Comprehensive, South Coastal, Middle Yangtze, Southwest, Middle Yellow River, and the Greater Northwest. The East and North Coastal regions display notably higher distortion than all others, while the Middle Yellow River and Greater Northwest show the lowest levels. Third, at the provincial scale, Shanghai, Jiangsu, Guangdong, Tianjin, and Zhejiang lead the distortion ranking, clustering within the East, North, and South Coastal zones. This pattern suggests that economically advanced or policy-favored areas more readily obtain low-cost energy through administrative intervention or market power, thereby exacerbating price distortion. These regions often benefit from subsidized electricity tariffs, preferential energy supply, and large firms that secure discounted prices, preventing energy prices from reflecting true supply-demand conditions and resource scarcity. Consequently, energy becomes over-allocated to energy-intensive, not necessarily efficient industries, hindering clean-energy uptake and efficiency gains and imposing a clear allocative-efficiency loss.

Figure 1 illustrates a clear decline in nationwide energy price distortions and a convergence of regional disparities between 2000 and 2022. Two notable trends emerge. First, the spatial concentration of high-distortion “hot spots” diminished significantly: in 2000, the most severe distortions (shown in dark green) were concentrated along the eastern coast as well as in Xinjiang, Gansu, and Liaoning. By 2022, however, all provinces had shifted into medium- or low-distortion categories, with top-tier distortion levels nearly disappearing. Second, the historical “east-high/west-low” gradient narrowed considerably. Initially, distortions were most pronounced in the East Coast and Northeast, while the major inland energy-producing provinces remained relatively stable. In the later years, distortions declined most rapidly in the coastal regions, while those in the northwest also receded, significantly reducing the east-west disparity. These trends suggest that market-oriented reforms—such as the liberalization of electricity, natural gas, and refined oil prices, the development of a unified national power market, and the implementation of carbon-trading pilot programs—have effectively curtailed distortionary administrative subsidies.

4.2. Regional Disparities

Using the Theil index, we quantify nationwide, within-region, and between-region differences in energy price distortions and compute each region’s contribution to the aggregate disparity, thereby revealing the spatial pattern and temporal dynamics of distortion.

Figure 2 indicates a “narrowing-widening” trajectory for regional gaps in distortion from 2000 to 2022. Specifically, both absolute distortion levels and their regional dispersion declined during 2000–2008, surged sharply over 2008–2016, and then leveled off during 2016–2022. Over the entire sample period, the amplitude of fluctuation in the between-region component is a modest 1.03%, whereas the within-region component swings by 90.11%. Hence, the inter-regional gap remains comparatively stable—albeit with a slight upward drift—while intra-regional inequality is far more volatile; even so, the magnitude of the between-region disparity consistently exceeds that of the within-region component. Ranking the volatility of provincial distortion by region yields the following order (high to low): Greater Northwest, East Coast, Middle Yellow River, South Coast, Middle Yangtze, Northeast Comprehensive, Southwest, and North Coast.

As shown in

Table 2. Regional Theil Index and Contribution Rates of Energy-Price Distortion.

Year		2000	2008	2016	2022	Change
Between-Region Gap and Contribution (%)		0.0757	0.0508	0.0839	0.0765	0.0008
		(71.76)	(62.08)	(70.23)	(57.45)	(−14.31)
Within-Region Gap and Contribution (%)	Northeast Comprehensive	0.0137	0.0026	0.0007	0.0102	−0.0035
		(1.36)	(0.47)	(0.10)	(1.34)	(−0.02)
	Northern Coast	0.0465	0.0234	0.0216	0.0071	−0.0394
		(6.76)	(4.31)	(2.60)	(0.83)	(−5.93)
	Eastern Coast	0.0085	0.0144	0.0294	0.0371	0.0286
		(1.58)	(2.97)	(4.38)	(4.75)	(3.17)
	Southern Coast	0.0423	0.0347	0.0752	0.1101	0.0678
		(5.74)	(4.36)	(5.98)	(7.35)	(1.61)
	Middle Yellow River	0.0572	0.0709	0.105	0.2105	0.1533
		(5.25)	(6.59)	(8.22)	(17.05)	(11.80)
	Middle Yangtze	0.0133	0.0201	0.026	0.0299	0.0166
		(1.39)	(2.89)	(2.63)	(2.61)	(1.22)
	Southwest	0.0449	0.02	0.016	0.0156	−0.0293
		(4.70)	(2.65)	(1.47)	(1.17)	(−3.53)
	Greater Northwest	0.0183	0.0892	0.0676	0.1178	0.0995
		(1.45)	(12.07)	(4.40)	(7.43)	(5.98)
	Within-Region Total	0.0298	0.031	0.0356	0.0566	0.0268
		(28.24)	(37.92)	(29.77)	(42.55)	(14.31)
Overall Gap		0.1055	0.0818	0.1195	0.1331	0.0166

Note: Numbers in parentheses indicate contribution rates (%).

, the contributions of between-region and within-region disparities to energy-price distortion exhibit an inverse relationship, with the between-region contribution consistently exceeding the within-region component throughout the observation period.

Specifically, ranking regions by their within-region contribution in descending order yields: Middle Yellow River, Greater Northwest, South Coast, East Coast, Middle Yangtze, Northeast Comprehensive, Southwest, and North Coast. Within-region inequality continues to widen in the East Coast, South Coast, Middle Yellow River, and Middle Yangtze regions; in contrast, it has declined in the Northeast Comprehensive, North Coast, and Southwest. In the Greater Northwest, within-region disparity initially widened before narrowing, but remains slightly above its initial level.

Meanwhile, the between-region gap has displayed “convergence” or “club convergence” since its peak. As national reforms in energy pricing and market liberalization have advanced, the earlier spikes in interregional distortion have been suppressed, and regions have begun to align more closely in both pricing mechanisms and allocative efficiency—hallmarks of club convergence. Moreover, the divergent trajectories of within-region disparities reflect heterogeneity in reform progress and market structures: differences in resource endowments, industrial composition, and policy enforcement have allowed internal gaps to expand in certain areas. These patterns underscore the need for targeted, region-specific policy interventions to foster coordinated development within regions.

This table highlights three distinct features of regional disparities in energy price distortion across China from 2000 to 2022. The first feature is a reversal in the relative contributions of interregional and intraregional disparities. Specifically, the contribution of interregional differences declined from 71.76% to 57.45%, while that of intraregional differences rose from 28.24% to 42.55%. This shift indicates that disparities among provinces, rather than between broader regions, have increasingly become the primary source of variation. The second feature is pronounced regional heterogeneity. For example, the contribution of internal disparities within the middle reaches of the Yellow River jumped from 5.25% to 17.05%, reflecting a widening policy implementation gap among major energy-producing provinces such as Shanxi and Shaanxi. This growing divergence can be attributed to three main factors. First, the lock-in effect of policy bias—with over 80% of energy enterprises being state-owned and receiving substantial subsidies—has weakened price signals and market responsiveness. Second, structural constraints in resource endowment play a role. Provinces such as Shanxi and Xinjiang, which serve as major energy suppliers, remain affected by legacy mechanisms of planned pricing, leading to persistently higher distortion levels compared to energy-consuming provinces. Third, uneven market integration across regions has resulted in mismatches between supply and demand, further exacerbating spatial disparities in energy pricing. The third feature is the stage-specific nature of distortion trends. Since 2016, the overall Theil index has shown signs of stabilization (rising modestly from 0.1195 to 0.1331), suggesting that efforts to develop a unified national electricity market during the 13th Five-Year Plan have yielded some success. Nevertheless, interprovincial disparities remain above 2008 levels, indicating that ongoing reforms have not yet fully addressed the historical legacy of price distortions.

4.3. Spatial Distribution

To reveal the geographic-spatial distribution of China’s energy-price distortion, this study takes a spatial-econometric perspective and employs the global Moran’s I statistic and Moran scatterplots to examine spatial autocorrelation and clustering. Moran’s I ranges from −1 to 1 and measures spatial autocorrelation, with positive values indicating the clustering of similar values and negative values indicating the clustering of dissimilar values. To analyze the spatial effects of energy price distortion, this study first constructs a spatial weight matrix W. Considering that geographically adjacent regions are more likely to exhibit spatial interactions, we define the spatial weights using a binary contiguity matrix.

Table 3. Global Moran’s I for Energy-Price Distortion in China.

Year	Moran’s I	p-Value	Year	Moran’s I	p-Value
2000	0.401 ***	0.000	2012	0.271 ***	0.006
2001	0.427 ***	0.000	2013	0.251 ***	0.010
2002	0.388 ***	0.000	2014	0.271 ***	0.006
2003	0.378 ***	0.000	2015	0.277 ***	0.005
2004	0.389 ***	0.000	2016	0.277 ***	0.005
2005	0.330 ***	0.001	2017	0.133 *	0.078
2006	0.296 ***	0.003	2018	0.269 ***	0.006
2007	0.282 ***	0.005	2019	0.260 ***	0.008
2008	0.260 ***	0.008	2020	0.248 ***	0.010
2009	0.282 ***	0.005	2021	0.230 **	0.015
2010	0.258 ***	0.009	2022	0.203 **	0.026
2011	0.253 ***	0.009

Notes: *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels, respectively.

shows that Moran’s I for energy-price distortion is statistically positively significant at the 1% level throughout 2000–2022, implying strong spatial autocorrelation and a broad clustering tendency across regions. The global Moran’s I remains positive and relatively stable over this period, yet exhibits a downward trend overall. This decline suggests that, although spatial clustering persists, its intensity is weakening. The spatial dependence of energy-price distortion has diminished over time, though a certain degree of spatial linkage still remains. Such a trajectory indicates that the spatial distribution of distortion is gradually optimizing, interregional differences are narrowing, and the pattern is moving toward a more balanced state. This evolution not only reflects progress toward integrated energy markets but also demonstrates a coordinated improvement in distortion levels across regions.

While the global Moran’s I captures the overall spatial autocorrelation of energy-price distortion, it may obscure inter-regional clustering patterns. To address this limitation, we employ the local Moran’s I to directly visualize each region’s distortion value and its spatial lag. In Figure 3, the horizontal axis represents the local distortion, while the vertical axis reflects its spatially lagged value. The four quadrants correspond to distinct spatial clustering patterns: HH (high-high) and LL (low-low) indicate positive spatial correlation (clustering), whereas LH (low-high) and HL (high-low) suggest negative spatial correlation (spatial heterogeneity).

The observed decline in Moran’s I index can be attributed to three main factors. First, the progressive weakening of local governments’ administrative intervention in energy pricing—due to the electricity market reform initiated after 2003, the launch of carbon trading pilots in 2015, and the construction of a unified national electricity market starting in 2017—has reduced the spatial correlation of price distortions stemming from policy discrepancies across regions. Second, the development of ultra-high-voltage (UHV) transmission networks and cross-regional energy delivery initiatives such as the “West-to-East Power Transmission” project has facilitated the broader optimization of energy resource allocation, thereby diminishing the homogeneity of distortions among geographically adjacent areas. Third, the gradual removal of interprovincial barriers to the mobility of energy resources, along with the initial operation of the national carbon market, has led to increasingly market-oriented price signals and the gradual emergence of “club convergence” patterns in regional price distortions.

Figure 3 reveals that, in all four benchmark years (2000, 2008, 2016, and 2022), most provinces fall into the HH and LL quadrants, indicating a persistent pattern of positive spatial autocorrelation in energy-price distortion.

Table 4. Provincial Distribution across Moran Scatterplot Quadrants for Energy-Price Distortion.

Quadrant	I	II	III	IV
2000	Shanghai, Jiangsu, Zhejiang, Fujian, Shandong, Beijing	Hainan, Anhui, Jiangxi, Hebei	Shanxi, Guizhou, Inner Mongolia, Ningxia, Qinghai, Yunnan, Sichuan, Xinjiang, Chongqing, Shaanxi, Gansu, Henan, Heilongjiang, Guangxi, Hunan	Liaoning, Hubei, Tianjin, Guangdong, Jilin
2008	Shanghai, Jiangsu, Zhejiang, Jilin, Beijing, Tianjin, Shandong	Inner Mongolia, Qinghai, Hebei, Jiangxi, Fujian, Anhui, Hainan	Shanxi, Chongqing, Ningxia, Guizhou, Sichuan, Yunnan, Hunan, Guangxi, Shaanxi, Gansu	Liaoning, Guangdong, Heilongjiang, Xinjiang, Hubei, Henan
2016	Shanghai, Jiangsu, Zhejiang, Jilin, Heilongjiang, Liaoning, Shandong, Tianjin	Hainan, Anhui, Fujian, Jiangxi, Inner Mongolia, Hebei	Qinghai, Chongqing, Guizhou, Yunnan, Ningxia, Gansu, Sichuan, Shaanxi, Guangxi, Xinjiang, Shanxi, Hunan	Beijing, Henan, Hubei, Guangdong
2022	Shanghai, Jiangsu, Jilin, Heilongjiang, Liaoning, Beijing, Tianjin, Zhejiang, Shandong	Hainan, Anhui, Fujian, Jiangxi, Inner Mongolia, Hebei	Ningxia, Guizhou, Yunnan, Qinghai, Xinjiang, Chongqing, Shaanxi, Shanxi, Hunan, Guangxi, Sichuan	Henan, Hubei, Guangdong, Gansu

details the spatial distribution of provinces across the four quadrants of the Moran scatterplot for energy-price distortion during 2000–2022. The third quadrant (LL) consistently contains the largest share of provinces, and its spatial footprint remains relatively stable. Specifically, 18 provinces fell into LL in 2000; this number declined to 11 in 2008, rose to 15 in 2016, and stood at 12 in 2022. These provinces are mainly located in the Middle Yellow River, Southwest, Northwest, and Middle Yangtze regions—areas that are relatively underdeveloped or resource-dependent—and exhibit strong positive spatial autocorrelation. In contrast, economically advanced regions such as the East Coast, South Coast, North Coast, and Northeast predominantly lie in the other quadrants of the Moran scatterplot. In less developed and resource-based areas, energy supply structures tend to be homogeneous and subject to tighter policy controls, producing more concentrated and stable distortion patterns. Conversely, in developed regions where market mechanisms are more mature, energy-price distortions display a more diversified and dynamic spatial configuration.

Table 4 discusses the evolution of quadrant distributions, which demonstrates a pronounced pattern of spatial polarization. Eastern provinces such as Shanghai and Jiangsu consistently remained in the first quadrant (HH), with spatial lag coefficients exceeding 0.7 (p < 0.05), forming a “high-distortion club.” The number of provinces in the third quadrant (LL) decreased from 18 to 12, with western provinces such as Xinjiang and Qinghai experiencing a decline in Moran’s I values by between 0.08 and 0.22. This indicates that the Western Development Strategy has weakened the spatial clustering of low-distortion areas. In 2022, provinces such as Guangdong and Gansu appeared in the fourth quadrant (HL), suggesting that some economically developed regions have taken the lead in reducing distortions through market-oriented reforms.

4.4. Dynamic Evolution

The above analysis demonstrates that China’s energy-price distortions exhibit significant spatial heterogeneity. To explore their temporal trajectories and variation characteristics, this study applies a Gaussian kernel estimation to uncover dynamic trends in regional distortion, providing a basis for future forecasting. In light of China’s socioeconomic development and regional characteristics, the 30 provincial-level units are categorized into Eastern, Central, and Western regions to better reflect differences in economic structure, resource endowment, policy environment, and energy-consumption habits. This classification facilitates the identification of interregional heterogeneity and clustering in distortion and enables targeted analysis of each region’s dynamic evolution. We select cross-sectional data for 2000, 2008, 2016, and 2022, and use their kernel density curves to examine how distortion evolves in each region and its influence on the overall pattern.

Figure 4a–d presents three-dimensional kernel density plots of energy-price distortion for China as a whole and its three major regions.

(1) Location Shift: Over time, the distribution curves for both the national aggregate and each region consistently shift leftward, indicating a steady decline in energy-price distortion. This trend suggests that distortions are easing and gradually approaching zero, reflecting the improved functioning of energy markets.

(2) Dispersion Pattern: The absolute dispersion of distortion levels varies across regions and over time. Nationally, the peak of the density curve rises while its width narrows, indicating a convergence of distortion levels across provinces. In the Western region, the peak height increases with some fluctuations, suggesting that although distortion is declining, regional coordination is strengthening and distortion levels are becoming more concentrated. The Eastern region exhibits the widest distribution, reflecting substantial interprovincial variation and greater volatility.

(3) Tail Behavior: The distribution curves exhibit right-skewed tails at both national and regional levels, indicating that certain provinces continue to experience relatively high levels of distortion. This long-tail phenomenon is most evident in the Eastern region, where pockets of high distortion remain prominent.

(4) Peak Structure: The Central region transitions from a bimodal to a unimodal distribution, signaling that the initial polarization in distortion levels has eased and values are becoming more balanced. In the Eastern region, a multimodal distribution—indicative of distinct tiers of distortion—gradually evolves into a single peak, suggesting increasing concentration and stability in the region’s distortion profile.

The underlying drivers of the “east-high, west-low” gradient in energy price distortion can be summarized in three main dimensions. First, eastern provinces initially attracted energy-intensive industries by offering tax incentives and electricity subsidies, which led to a persistent deviation of energy prices from marginal costs. In contrast, resource-rich western provinces such as Shaanxi and Xinjiang, which rely heavily on fiscal revenues from resource-based taxes, tend to maintain lower energy prices to sustain local industrial development. Second, although the eastern region is more economically advanced, its energy sector is often characterized by stronger administrative monopolies. In comparison, western provinces have progressively promoted market-based pricing through mechanisms such as the “West-to-East Electricity Transmission” program, thereby enhancing interregional energy integration and pricing flexibility. Third, the eastern region is dominated by export-oriented manufacturing, where energy demand is relatively inelastic and highly sensitive to price changes, making it more susceptible to policy interventions. Conversely, the West enjoys an abundance of coal, wind, and solar resources, resulting in lower energy supply costs and fewer institutional barriers to implementing market-oriented reforms.

To further investigate the transition dynamics across different levels of energy-price distortion, this study employs Markov-based transition probabilities, detailed in

Table 5. Traditional and Spatial Markov Transition Probability Matrices.

	Neighborhood Context	t/(t + 1)	I	II	III	Observations
Traditional		I	0.9944	0.0000	0.0056	178
		II	0.1408	0.8592	0.0000	206
		III	0.0036	0.1087	0.8877	276
Spatial	I	I	1.0000	0.0000	0.0000	126
		II	0.3243	0.6757	0.0000	37
		III	0.0000	0.0000	0.0000	0
	II	I	1.0000	0.0000	0.0000	49
		II	0.1181	0.8819	0.0000	127
		III	0.0000	0.2889	0.7111	45
	III	I	0.6667	0.0000	0.3333	3
		II	0.0476	0.9524	0.0000	42
		III	0.0043	0.0736	0.9221	231

. All three distortion categories demonstrate strong persistence: self-transition probabilities are 99.44% for Type I (low distortion), 85.92% for Type II (moderate distortion), and 88.77% for Type III (high distortion). Notably, downward transitions are more likely than upward ones, suggesting a general trend toward stabilization and improvement over time.

A more detailed analysis reveals that the distortion level of surrounding areas significantly influences local transitions: Low-distortion neighborhoods (I): Local low-distortion regions exhibit exceptional stability, with self-transition probabilities above 99.44%. Moderate-distortion areas in these neighborhoods have a 32.43% chance of improving to low distortion—more than double the baseline probability (14.08%)—indicating that favorable surroundings promote improvement. Moderate-distortion neighborhoods (II): Low-distortion areas remain stable, while 28.89% of high-distortion areas shift downward to moderate distortion, compared to a baseline of 10.87%. This suggests that a moderate environment can effectively suppress more severe distortion. High-distortion neighborhoods (III): A striking 33.33% of low-distortion areas transition upward to high distortion, while high-distortion areas show a self-transition probability of 92.21%, indicating increased persistence and a strong assimilation effect. These findings underscore the critical role of spatial context: low-distortion areas remain resilient in favorable environments, while high-distortion neighborhoods exert a contagious “escalation” effect on their surroundings, reinforcing localized patterns of inefficiency.

Table 5 analyzes the transition probability matrix and reveals three key patterns in the evolution of energy price distortions. First, the self-transition probability for the high-distortion state reaches 88.77%, which is higher than that for the low-distortion state, suggesting the existence of a “high-distortion trap,” though weaker than expected. Second, provinces neighboring high-distortion regions face a 33.33% probability of worsening, whereas only 14.08% of high-distortion provinces improve when surrounded by low-distortion neighbors. This indicates that negative spillover effects outweigh positive diffusion, as reflected in the differences in coefficients. Third, provinces in a medium-distortion state have a 32.43% probability of improving when located near low-distortion areas, significantly higher than in neutral environments (14.08%). This highlights the potential of regional coordinated reform as a breakthrough strategy and underscores the importance of implementing preventive measures in areas where energy prices have not yet experienced serious distortions. Meanwhile, provinces already in a low-distortion state should maintain their existing policy frameworks while exploring further opportunities to optimize energy pricing mechanisms. For provinces still in high or medium-distortion states, policymakers should carefully consider the long-term impacts and sustainability of interventions, avoiding short-term actions or excessive administrative interference.

4.5. Robustness Checks

Club convergence refers to the phenomenon where economic variables (such as income or productivity) exhibit convergence trends within specific subgroups or “clubs.” However, this convergence is limited to these subgroups and does not extend across the entire sample. In other words, certain regions with similar economic or social backgrounds tend to follow comparable growth patterns. To verify the robustness of our findings, we adopt the grouped α-convergence test method proposed by Barro and Sala-i-Martin [41] and Quah [42,43]. This method groups the sample based on distortion values, revealing whether convergence exists within each subgroup and analyzing the dynamic convergence patterns between groups. In our analysis, we use the same classification approach as in the Markov chain grouping and conduct convergence tests within each subgroup. Unlike the preliminary analysis based on the Markov chain transition matrix, the grouped α-convergence test directly quantifies the strength and robustness of convergence and statistically validates the significance of convergence trends within each group. When combined with Markov chain analysis, the grouped α-convergence test provides a more systematic and robust analytical framework.

Table 6. Convergence Trends in Different Distortion Groups.

Group	Coefficient	t-Value	p-Value	Convergence Pattern
High Distortion	−0.033 ***	−7.79	0.000	Convergence
Medium Distortion	−0.017 ***	−10.16	0.000	Convergence
Low Distortion	−0.015 ***	−10.90	0.000	Convergence

Notes: *** indicate statistical significance at the 1% level.

reports the empirical results, showing that the high-, medium-, and low-distortion groups all exhibit significant convergence. Specifically, the convergence coefficients are −0.033 for the high-distortion group, −0.017 for the medium-distortion group, and −0.015 for the low-distortion group, with p-values less than 0.01 for all groups. This confirms convergence within each group at the 1% significance level. These findings support the club convergence hypothesis, demonstrating that economic variables within each distortion group follow consistent convergence patterns. The grouped α-convergence test further confirms the presence of club convergence within each subgroup, enhancing the robustness of our conclusions and providing strong empirical support for related policy formulation.

5. Conclusions and Recommendations

Unlike previous studies that mainly focus on the determinants of energy price distortions, this study investigates their spatiotemporal dynamics, providing new evidence for understanding the marketization process of China’s energy sector. It reveals a “gradient lock-in” effect, where the negative spillovers from high-distortion provinces exert significantly stronger influences on surrounding regions than the positive diffusion effects from low-distortion areas. This supports the existence of a “policy-driven convergence” pattern, which is distinctive to transitional economies and differs from the natural convergence paths observed in developed markets. Additionally, by utilizing the decomposability of the Theil index, this study quantifies the dominant role of interregional disparities in contributing to overall distortion, offering a more refined structural explanation than traditional descriptive analysis. Based on estimates of energy-price distortion across 30 Chinese provinces from 2000 to 2022, this study employs the Theil index and spatial econometric methods to analyze regional disparities and spatial effects. In addition, kernel density estimation and a Markov chain model are used to assess the dynamic evolution of energy-price distortion in China. The main conclusions are as follows:

Energy price distortion in China has declined substantially, exhibiting a distinct “high in the east, low in the west” spatial pattern. From 2000 to 2022, the national distortion index decreased by 94.33%, indicating a significant retreat in price distortions and a steady progression toward more rational, market-based pricing mechanisms. Although the east-west divergence has narrowed over time, regional heterogeneity remains pronounced. The East and North Coastal regions continue to exhibit the highest distortion levels, largely due to policy biases and market concentration in economically developed areas. In contrast, regions such as the Middle Yellow River and the Greater Northwest report lower distortion levels, reflecting differences in economic development and the efficiency of energy resource allocation.

The evolution of regional disparities follows a “narrowing-widening-stabilizing” trajectory. Specifically, the regional gap narrowed between 2000 and 2008, widened rapidly from 2008 to 2016, and stabilized thereafter. The contribution of interregional disparities to overall distortion consistently exceeds that of intraregional differences. However, volatility within regions remains substantial, reflecting uneven progress in market reforms and divergent institutional conditions. In some cases, internal disparities in distortion have even expanded.

Energy price distortion displays significant positive spatial autocorrelation and clustering. Although the strength of these spatial effects has declined over time, indicating a gradual movement toward spatial equilibrium, a moderate degree of spatial dependence still persists. Local Moran’s I statistics further indicate the presence of stable high-high and low-low clusters in resource-dependent and less-developed regions, while economically advanced areas exhibit more heterogeneous and dynamic spatial patterns.

Energy price distortion has continued to decline across the country and in all major regions, accompanied by a gradual narrowing of regional disparities. In the Central region, the previous pattern of polarization has diminished, resulting in a more balanced, unimodal distribution. In the Western region, distortion has become more concentrated, whereas the Eastern region exhibits the highest volatility, along with a pronounced right-skewed tail, indicating that severe distortion persists in some provinces. Markov analysis confirms that distortion states are highly stable, with downward transitions occurring more frequently than upward shifts, suggesting a steady improvement under stable conditions. Moreover, spatial neighborhood effects remain significant, exhibiting a clear pattern of club convergence.

Based on the findings above, several targeted policy recommendations are proposed:

Further advance market-oriented energy pricing reforms, with a focus on mitigating distortions in the Eastern Coastal region. Reform efforts should prioritize accelerating the transition toward market-based pricing by phasing out policy subsidies and administrative controls, strengthening market competition, and preventing large enterprises from leveraging monopolistic advantages to obtain artificially low energy prices. Prices should more accurately reflect supply-demand dynamics and the scarcity of energy resources.

Implement regionally differentiated reform strategies to promote balanced intra-regional development. In regions with pronounced internal disparities—such as the Middle Yellow River, Greater Northwest, and South Coast—reform measures should be tailored to local resource endowments, industrial structures, and policy implementation capacities. Differentiated pricing strategies can enhance allocative efficiency and reduce internal distortion gaps. For the eastern coastal regions, it is recommended to gradually phase out electricity subsidies for energy-intensive industries, implement market-based pricing mechanisms, and strengthen antitrust regulation. For the central and western regions, it is advisable to establish regional energy trading centers, improve grid interconnectivity, and provide financial support to facilitate the energy transition.

Enhance spatially coordinated governance to optimize regional clustering effects. Leveraging insights from spatial economic analysis, interregional cooperation, and policy alignment should be strengthened to contain distortion spillovers caused by spatial clustering. Cross-regional regulatory mechanisms and information-sharing platforms can support greater policy consistency and promote the integration of national energy markets. To address potential resistance from local protectionism, it is recommended that energy marketization be incorporated into the performance evaluation systems of local governments.

Support structural transformation and energy diversification in resource-based and less-developed regions. These areas should receive targeted support to broaden their energy supply mix, promote clean energy deployment, and foster innovation. Reducing dependence on single energy sources will improve market flexibility and support the rationalization of pricing mechanisms.

Establish a dynamic monitoring and evaluation framework. By integrating spatiotemporal data, kernel density estimation, and spatial diagnostics, authorities can regularly track the evolution of energy-price distortion across regions, identify high-risk areas early, and adjust policy responses accordingly. This will ensure the sustained and adaptive advancement of energy pricing reform. These recommendations take into account regional disparities and the gradual nature of reform. For instance, electricity pricing reforms can be piloted in free trade zones before being gradually expanded nationwide.

Develop a tiered and progressive regional coordination mechanism to overcome administrative boundary constraints through a three-level framework of “intra-provincial reform, regional cooperation, and cross-regional coordination.” The plan includes establishing a unified regional electricity market with a “contract + spot” trading model and reserving 15% of capacity for inter-provincial transactions. It also calls for an interconnected pipeline network based on the “beneficiary pays” principle to support cross-provincial infrastructure development. A federated learning–based data platform will enable real-time load sharing at 15-min intervals. Supporting measures include legal revisions, incentive mechanisms, and a dynamic evaluation system. The implementation follows a three-phase roadmap, aiming to establish nationally unified market rules by 2030 and to achieve policy synergy through institutional innovation rather than geographic restructuring.