Economic Growth and Energy Consumption in Thailand: Evidence from the Energy Kuznets Curve Using Provincial-Level Data
Abstract
1. Introduction
1.1. Energy Kuznets Curve Theory
1.2. Socioeconomic Factors Affecting Energy Consumption
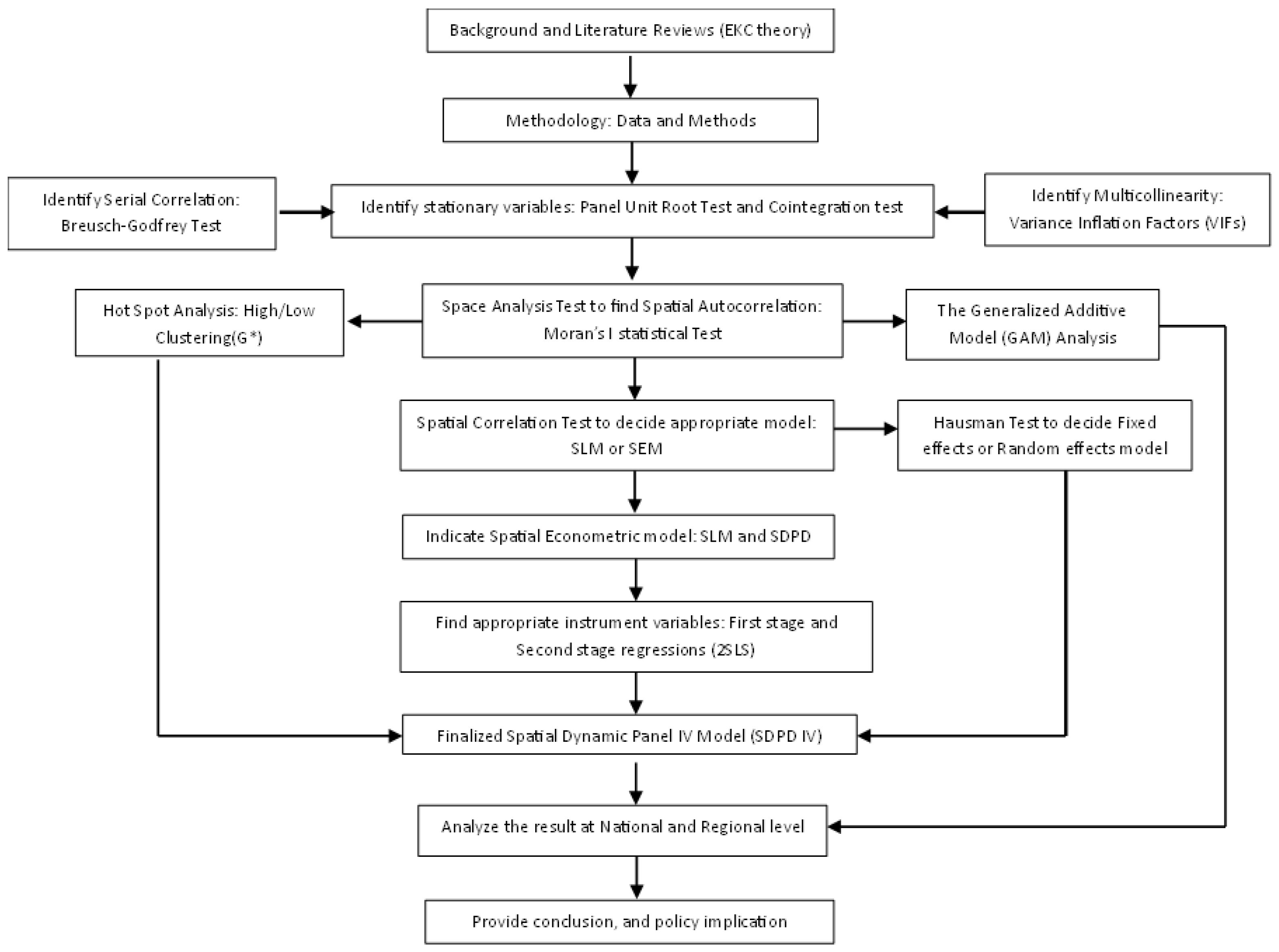
2. Materials and Methods
2.1. Model
2.2. Moran’s I Statistical Test
2.3. High/Low Clustering (G*) (Hot Spot Analysis)
2.4. LM Test for Spatial Dependence (LM-Lag, LM-Error), LM Test for Random Effects, LM Test for Serial Correlation
2.5. Spatial Panel Lag Model (SLM)
2.6. Spatial Dynamic Panel Lag Instrumental Variables Fixed-Effects Model (SDPD IV)
2.7. The Generalized Additive Model (GAM)
3. Results
3.1. Hot Spot Analysis Results
3.2. Spatial Dynamic Panel Econometric Model Results (SLM, SDPD IV)
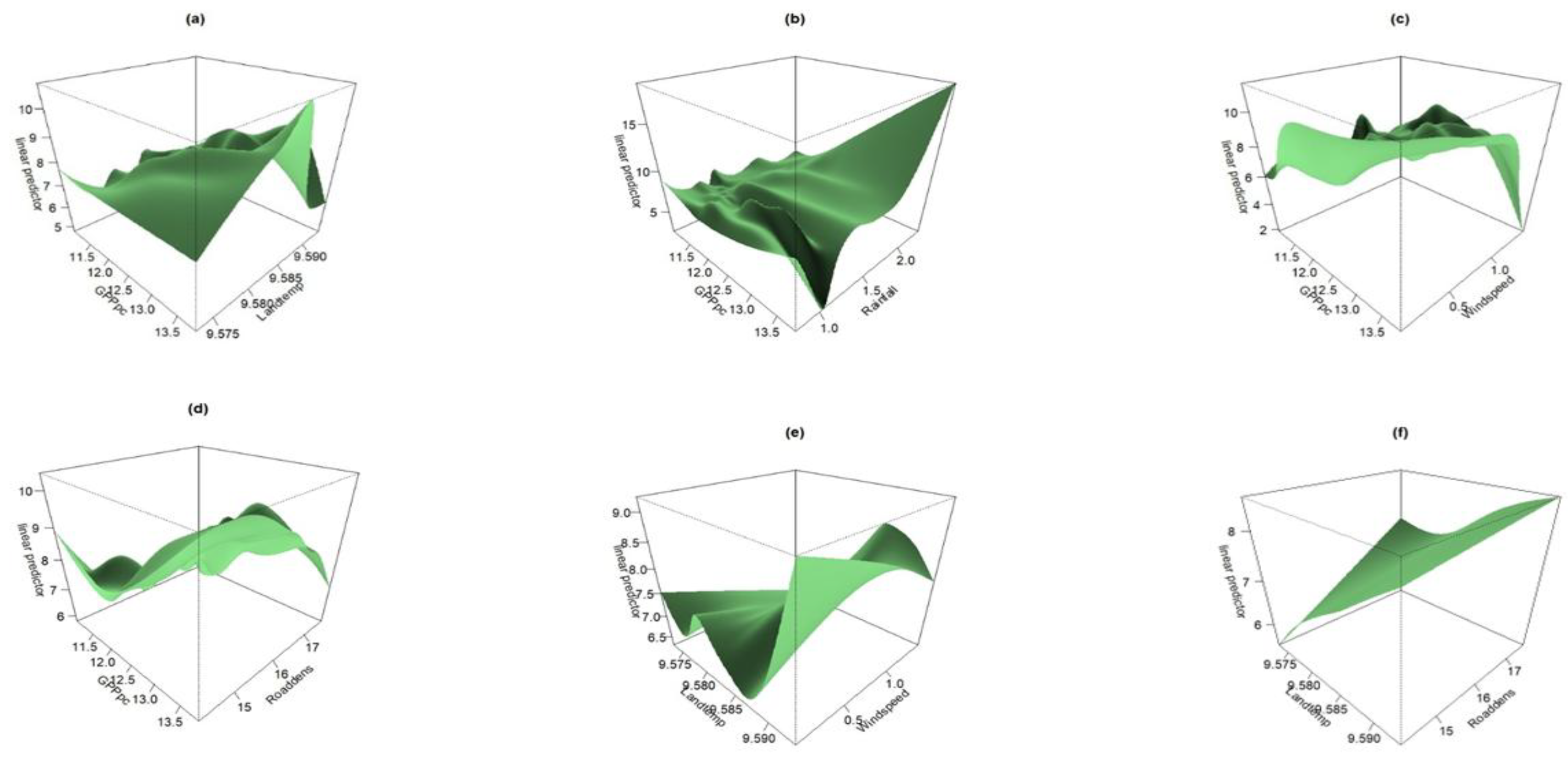
3.3. GAM Analysis Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Whole Region | ||||
|---|---|---|---|---|
| Level | First Difference | |||
| LLC | IPS | LLC | IPS | |
| Energycons_pc | −20.843 *** | −5.099 *** | −32.089 *** | −8.568 *** |
| GPPpc | −41.192 *** | −4.535 *** | −36.113 *** | −4.585 *** |
| GPPpc2 | −46.642 *** | −4.546 *** | −36.768 *** | −4.578 *** |
| Pop_dens | −1.1 × 102 *** | 4.317 | −3.3 × 103 *** | −7.257 *** |
| Landtemp_night | −74.822 *** | −4.932 *** | −1.2 × 102 *** | −6.653 *** |
| Rainfall | −24.257 *** | −6.548 *** | −14.518 *** | −6.081 *** |
| Windspeed | −31.093 *** | −4.568 *** | −67.697 *** | −8.924 *** |
| Roaddens | −13.813 *** | −3.645 *** | −45.701 *** | −7.309 *** |
| Bangkok and Vicinity, Central, Eastern, Western Region (BKK&VIC, CE, EA, WE) | ||||
| Level | First difference | |||
| LLC | IPS | LLC | IPS | |
| Energycons_pc | −13.999 *** | −2.068 | −30.020 *** | −4.375 *** |
| GPPpc | −34.520 *** | −2.682 *** | −95.010 *** | −2.676 *** |
| GPPpc2 | −40.884 *** | −2.691 *** | −99.332 *** | −2.672 *** |
| Pop_dens | −75.664 *** | 1.532 | −8.6 × 103 *** | −4.316 *** |
| Landtemp_night | −13.322 *** | −3.644 *** | −0.961 | −4.528 *** |
| Rainfall | −14.845 *** | −2.770 *** | −0.203 | −1.784 |
| Windspeed | −19.331 *** | −3.221 *** | −42.500 *** | −4.994 *** |
| Roaddens | −10.677 *** | −2.908 *** | −22.670 *** | −4.249 *** |
| Northeastern Region (NE) | ||||
| Level | First difference | |||
| LLC | IPS | LLC | IPS | |
| Energycons_pc | −8.409 *** | −3.063 *** | −7.952 *** | −4.599 *** |
| GPPpc | −20.121 *** | −2.572 ** | −32.806 *** | −2.892 *** |
| GPPpc2 | −18.695 *** | −2.570 ** | −43.748 *** | −2.884 *** |
| Pop_dens | 1.638 | 3.212 | −1.5 × 102 *** | −4.104 *** |
| Landtemp_night | −64.689 *** | −2.537 * | −94.600 *** | −2.384 |
| Rainfall | −11.857 *** | −4.045 *** | −25.310 *** | −4.292 *** |
| Windspeed | −15.992 *** | −3.280 *** | −13.360 *** | −5.065 *** |
| Roaddens | −6.294 *** | −2.565 ** | −6.463 *** | −3.687 *** |
| Northern Region (NO) | ||||
| Level | First difference | |||
| LLC | IPS | LLC | IPS | |
| Energycons_pc | −13.889 *** | −2.343 | −12.131 *** | −4.241 *** |
| GPPpc | −22.972 *** | −1.821 | −14.358 *** | −1.740 |
| GPPpc2 | −23.102 *** | −1.834 | −13.084 *** | −1.738 |
| Pop_dens | −25.097 *** | 1.390 | −2.9 × 102 *** | −3.704 *** |
| Landtemp_night | −72.246 *** | −2.279 | −37.632 *** | −2.454 |
| Rainfall | −15.180 *** | −2.761 *** | 11.471 | −2.645 ** |
| Windspeed | −12.966 *** | 0.047 | −47.949 *** | −3.683 *** |
| Roaddens | −5.660 *** | −0.196 | −28.630 *** | −3.445 *** |
| Southern Region (SO) | ||||
| Level | First difference | |||
| LLC | IPS | LLC | IPS | |
| Energycons_pc | −7.532 *** | −2.899 *** | −12.988 *** | −3.962 *** |
| GPPpc | −3.985 *** | −1.903 | −50.419 *** | −1.732 |
| GPPpc2 | −3.951 *** | −1.901 | −54.422 *** | −1.735 |
| Pop_dens | −6.109 *** | 2.666 | −4.0 × 102 *** | −2.148 |
| Landtemp_night | 0.504 | −1.057 | 3.258 | −3.881 *** |
| Rainfall | −4.052 *** | −3.705 *** | −6.460 *** | −3.785 *** |
| Windspeed | −13.483 *** | −2.456 | −28.477 *** | −4.011 *** |
| Roaddens | −4.817 *** | −1.303 | −26.790 *** | −3.149 *** |
Appendix B
| Models | Breusch–Godfrey F-Stat. | VIFs Mean | |
|---|---|---|---|
| Whole region | 0.255 | 1.75 | |
| BKK&VIC, CE, EA, WE | 0.000 | *** | 2.41 |
| NE | 0.000 | *** | 1.65 |
| NO | 0.000 | *** | 2.27 |
| SO | 0.000 | *** | 1.92 |
Appendix C
| LnEnergy cons_pc | LnGPPpc | LnGPPpc2 | LnPop_dens | LnRoad dens | LnLandtemp _night | LnRainfall | LnWindspeed | |
|---|---|---|---|---|---|---|---|---|
| LnEnergycons_pc | 1.000 | |||||||
| LnGPPpc | 0.921 | 1.000 | ||||||
| LnGPPpc2 | 0.917 | 0.999 | 1.000 | |||||
| LnPop_dens | 0.520 | 0.550 | 0.552 | 1.000 | ||||
| LnRoaddens | 0.044 | 0.084 | 0.082 | −0.056 | 1.000 | |||
| LnLandtemp_night | 0.552 | 0.542 | 0.538 | 0.674 | −0.236 | 1.000 | ||
| LnRainfall | −0.114 | −0.009 | −0.008 | −0.022 | −0.217 | −0.088 | 1.000 | |
| LnWindspeed | 0.279 | 0.213 | 0.217 | 0.563 | −0.062 | 0.507 | −0.102 | 1.000 |
Appendix D
| Whole Region (n = 616) | ||||
|---|---|---|---|---|
| Min | Max | Mean | Std. | |
| Energycons_pc (kWh/person) | 488.41 | 11,335.86 | 2151.62 | 1906.60 |
| GPPpc (baht/person) | 49,296.39 | 1,060,571.10 | 163,114.05 | 148,340.36 |
| Pop_dens (unit/km2) | 17.86 | 5776.47 | 303.59 | 751.09 |
| Roaddens (length) | 564,563.62 | 44,665,593.00 | 7,992,667.82 | 6,299,861.39 |
| Landtemp_night (Celcius) | 14,316.81 | 14,668.83 | 14,498.34 | 70.42 |
| Rainfall (mm/y) | 1.97 | 11.92 | 4.86 | 1.87 |
| Windspeed (m/s) | 1.00 | 4.77 | 2.30 | 0.72 |
| BKK&VIC, CE, EA, WE (n = 208) | ||||
| Energycons_pc (kWh/person) | 1144.30 | 11,335.86 | 3860.83 | 2320.39 |
| GPPpc (baht/person) | 63,731.97 | 1,060,571.10 | 277,110.95 | 200,107.08 |
| Pop_dens (unit/km2) | 42.12 | 5776.47 | 660.68 | 1199.79 |
| Roaddens (length) | 607,745.85 | 26,271,510.00 | 6,916,773.18 | 5,024,772.79 |
| Landtemp_night (Celcius) | 14,424.08 | 14,668.83 | 14,552.61 | 55.07 |
| Rainfall (mm/y) | 1.97 | 10.47 | 4.27 | 1.40 |
| Windspeed (m/s) | 1.60 | 3.49 | 2.59 | 0.48 |
| NE (n = 160) | ||||
| Energycons_pc (kWh/person) | 528.91 | 2507.83 | 981.53 | 367.97 |
| GPPpc (baht/person) | 48,296.39 | 134,338.26 | 78,464.42 | 17,647.38 |
| Pop_dens (unit/km2) | 50.68 | 162.20 | 111.68 | 23.82 |
| Roaddens (length) | 564,563.92 | 44,665,593.00 | 10,118,021.27 | 8,307,641.85 |
| Landtemp_night (Celcius) | 14,335.12 | 14,531.52 | 14,446.47 | 42.19 |
| Rainfall (mm/y) | 2.54 | 8.98 | 4.54 | 1.09 |
| Windspeed (m/s) | 1.26 | 4.13 | 2.72 | 0.66 |
| NO (n = 136) | ||||
| Energycons_pc (kWh/person) | 488.41 | 3559.13 | 1303.96 | 591.44 |
| GPPpc (baht/person) | 53,692.75 | 232,558.92 | 103,838.57 | 32,960.50 |
| Pop_dens (unit/km2) | 17.86 | 123.02 | 69.84 | 27.09 |
| Roaddens (length) | 1,650,247.80 | 34,436,118.00 | 9,113,139.56 | 5,827,785.85 |
| Landtemp_night (Celcius) | 14,316.81 | 14,593.78 | 14,454.02 | 67.63 |
| Rainfall (mm/y) | 2.56 | 5.64 | 3.78 | 0.69 |
| Windspeed (m/s) | 1.00 | 2.53 | 1.50 | 0.37 |
| SO (n = 112) | ||||
| Energycons_pc (kWh/person) | 521.67 | 5089.04 | 1678.24 | 947.59 |
| GPPpc (baht/person) | 53,802.99 | 422,668.67 | 144,310.91 | 76,855.01 |
| Pop_dens (unit/km2) | 60.58 | 1099.11 | 198.42 | 246.66 |
| Roaddens (length) | 887,209.69 | 16,903,140.00 | 5,593,965.81 | 3,959,558.91 |
| Landtemp_night (Celcius) | 14,450.81 | 14,606.54 | 14,525.49 | 33.34 |
| Rainfall (mm/y) | 4.58 | 11.92 | 7.73 | 1.69 |
| Windspeed (m/s) | 1.21 | 4.77 | 2.16 | 0.64 |
Appendix E
| Whole Region | BKK&VIC, CE, EA, WE | NE | NO | SO | |
|---|---|---|---|---|---|
| Pedroni Test | Test Statistics | Test Statistics | Test Statistics | Test Statistics | Test Statistics |
| Panel PP-Statistic | −18.779 *** | −13.317 *** | −4.094 *** | −12.626 *** | −9.917 *** |
| Panel ADF-Statistic | 24.378 *** | 11.672 *** | 14.820 *** | 12.344 *** | 9.950 *** |
| Kao Test | Test Statistics | Test Statistics | Test Statistics | Test Statistics | Test Statistics |
| Panel ADF-Statistic | 3.346 *** | 1.710 ** | 3.088 *** | 1.697 ** | −0.800 |
Appendix F
| Whole Region (n = 616) | |||
|---|---|---|---|
| First Stage | R-sq | F-Stat | Endogeneity |
| LnGPPpc | 0.999 | 22.230 | 0.000 |
| LnGPPpc2 | 0.999 | 20.039 | 0.000 |
| LnPop_dens | 0.587 | 132.811 | 0.000 |
| LnRoaddens | 0.204 | 46.058 | 0.000 |
| BKK&VIC, CE, EA, WE (n = 208) | |||
| First stage | R-sq | F-stat | Endogeneity |
| LnGPPpc | 0.999 | 0.264 | 0.000 |
| LnGPPpc2 | 0.999 | 0.220 | 0.000 |
| LnPop_dens | 0.722 | 118.838 | 0.398 |
| LnRoaddens | 0.197 | 7.459 | 0.000 |
| NE (n = 160) | |||
| First stage | R-sq | F-stat | Endogeneity |
| LnGPPpc | 0.999 | 8.867 | 0.142 |
| LnGPPpc2 | 0.999 | 8.924 | 0.159 |
| LnPop_dens | 0.349 | 23.208 | 0.047 |
| LnRoaddens | 0.485 | 8.280 | 0.000 |
| NO (n = 136) | |||
| First stage | R-sq | F-stat | Endogeneity |
| LnGPPpc | 0.999 | 11.080 | 0.253 |
| LnGPPpc2 | 0.999 | 11.346 | 0.258 |
| LnPop_dens | 0.451 | 11.221 | 0.083 |
| LnRoaddens | 0.413 | 19.342 | 0.198 |
| SO (n = 112) | |||
| First stage | R-sq | F-stat | Endogeneity |
| LnGPPpc | 0.999 | 4.180 | 0.009 |
| LnGPPpc2 | 0.999 | 3.947 | 0.010 |
| LnPop_dens | 0.564 | 29.308 | 0.001 |
| LnRoaddens | 0.286 | 7.812 | 0.015 |
Appendix G
| BKK&VIC, CE, EA, WE | ||||
|---|---|---|---|---|
| GPP per Capita (USD) | ||||
| USD 2755 | USD 3675 | USD 6125 | USD 6130 | |
| Energycons_pc | −0.510 | −0.326 | −0.001 | 0.000 |
| NE | ||||
| USD 1990 | USD 2145 | USD 2755 | USD 2785 | |
| Energycons_pc | −0.316 | −0.245 | −0.003 | 0.008 |
References
- World Bank. Electric Power Consumption (kWh Per Capita); World Bank Group: Washington, DC, USA, 2022; Available online: https://data.worldbank.org/indicator/EG.USE.ELEC.KH.PC?end=2023&name_desc=false&start=2023&year=2022 (accessed on 30 March 2025).
- World Bank. Electricity Production From Oil Sources (% of Total); World Bank Group: Washington, DC, USA, 2022; Available online: https://data.worldbank.org/indicator/EG.ELC.PETR.ZS?end=2023&name_desc=false&start=2023&year=2022 (accessed on 30 March 2025).
- World Bank. Combustible Renewables and Waste (% of Total Energy); World Bank Group: Washington, DC, USA, 2022; Available online: https://data.worldbank.org/indicator/EG.USE.CRNW.ZS?end=2023&name_desc=false&start=2023&year=2022 (accessed on 30 March 2025).
- Tunpaiboon, N. Business/Industry Trends 2025–2027: Electricity Generation Business; Krungsri Research: Bangkok, Thailand, 2024; Available online: https://www.krungsri.com/th/research/industry/industry-outlook/energy-utilities/power-generation/io/power-generation-2025-2027 (accessed on 29 March 2025).
- EPPO. Electricity Consumption by Sectors 2015–2022; Energy Policy and Planning Office: Bangkok, Thailand, 2022; Available online: https://www.eppo.go.th/index.php/en/en-energystatistics/electricity-statistic/Electricity%20Consumption%20for%20the%20Whole%20Country%20(Classified%20by%20Sector) (accessed on 30 March 2025).
- Phadkantha, R.; Yamaka, W. The nonlinear impact of electricity consumption on economic growth: Evidence from Thailand. Energy Rep. 2022, 8, 1315–1321. [Google Scholar] [CrossRef]
- EPPO. Growth Rate of Electricity Demand and Economic Growth 2015-2022; Energy Policy and Planning Office: Bangkok, Thailand, 2022; Available online: https://www.eppo.go.th/index.php/en/en-energystatistics/electricity-statistic/Power%20Generation%20Classified%20by%20Fuel%20Type%20(Detail)%20-%20Graph (accessed on 30 March 2025).
- EPPO. Power Generation (GWh) by Fuel 2015–2022; Energy Policy and Planning Office: Bangkok, Thailand, 2022; Available online: https://www.eppo.go.th/index.php/en/en-energystatistics/electricity-statistic/Power%20Generation%20Classified%20by%20Fuel%20Type (accessed on 30 March 2025).
- Chokchaichamnankit, S. Energy Projects Under the ASEAN Economic Community; Thai Climate Justice Organization: Chiang Mai, Thailand, 2012; Available online: https://www.thaiclimatejustice.org/sites/default/files/2012-08_โครงการด้านพลังงานภายใต้ประชาคมเศรษฐกิจอาเซียน.pdf (accessed on 3 January 2025).
- EGAT. Get to Know ASEAN Electricity; Electricity Generating Authority of Thailand: Nonthaburi, Thailand, 2016; Available online: https://www.thaigov.go.th/uploads/document/66/2017/02/pdf/Coal_power_plant_5.pdf (accessed on 30 March 2025).
- Fiscal Policy Office. Regional Fiscal Economic Report for November 2022; Fiscal Policy Office: Bangkok, Thailand, 2022; Available online: https://www.fpo.go.th/main/Economic-report/Monthly-regional-economic-situation/17261.aspx (accessed on 3 January 2025).
- NESDC. Gross Regional and Provincial Product (GPP); Office of the National Economic and Social Development Council: Bangkok, Thailand, 2022; Available online: https://www.nesdc.go.th/nesdb_en/more_news.php?cid=156&filename=index (accessed on 3 January 2025).
- EPPO. Electricity Consumption Per Capita; Energy Policy and Planning Office: Bangkok, Thailand, 2022; Available online: https://www.eppo.go.th/index.php/en/en-energystatistics/electricity-statistic/Electricity%20Consumption%20in%20PEA%20Area%20(Classified%20by%20Sector) (accessed on 30 March 2025).
- Arouri, M.; Shahbaz, M.; Onchang, R.; Islam, F.; Teulon, F. Environmental Kuznets curve in Thailand: Cointegration and causality analysis. J. Energy Dev. 2013, 39, 149–170. [Google Scholar]
- Azam, M.; Khan, A.Q.; Zaman, K.; Ahmad, M. Factors determining energy consumption: Evidence from Indonesia, Malaysia and Thailand. Renew. Sustain. Energy Rev. 2015, 42, 1123–1131. [Google Scholar] [CrossRef]
- Kyophilavong, P.; Shahbaz, M.; Anwar, S.; Masood, S. The energy-growth nexus in Thailand: Does trade openness boost up energy consumption? Renew. Sustain. Energy Rev. 2015, 46, 265–274. [Google Scholar] [CrossRef]
- Maneejuk, N.; Ratchakom, S.; Maneejuk, P.; Yamaka, W. Does the environmental Kuznets curve exist? An international study. Sustainability 2020, 12, 9117. [Google Scholar] [CrossRef]
- Phrakhruopatnontakitti, P.; Watthanabut, B.; Jermsittiparsert, K. Energy consumption, economic growth and environmental degradation in 4 Asian Countries: Malaysia, Myanmar, Vietnam and Thailand. Int. J. Energy Econ. Policy 2020, 10, 529–539. [Google Scholar] [CrossRef]
- Maneejuk, P.; Yamaka, W.; Sriboonchitta, S. Does the Kuznets curve exist in Thailand? A two decades’ perspective (1993–2015). Ann. Oper. Res. 2021, 300, 545–576. [Google Scholar] [CrossRef]
- Kuznets, S. International differences in capital formation and financing. In Capital Formation and Economic Growth; Princeton University Press: Princeton, NJ, USA, 1955; pp. 19–111. [Google Scholar]
- Grossman, G.M.; Krueger, A.B. Economic Growth and the Environment. Q. J. Econ. 1995, 110, 353–377. [Google Scholar] [CrossRef]
- Stern, D.I. The environmental Kuznets curve after 25 years. J. Bioeconom. 2017, 19, 7–28. [Google Scholar] [CrossRef]
- Panayotou, T. Demystifying the environmental Kuznets curve: Turning a black box into a policy tool. Environ. Dev. Econ. 1997, 2, 465–484. [Google Scholar] [CrossRef]
- Stern, D.I. The rise and fall of the environmental Kuznets curve. World Dev. 2004, 32, 1419–1439. [Google Scholar] [CrossRef]
- Suri, V.; Chapman, D. Economic growth, trade and energy: Implications for the environmental Kuznets curve. Ecol. Econ. 1998, 25, 195–208. [Google Scholar] [CrossRef]
- Lorente, D.; Alvarez-Herranz, A. An approach to the effect of energy innovation on environmental Kuznets curve: An introduction to inflection point. Bull. Energy Econ. 2016, 4, 224–233. [Google Scholar]
- Dasgupta, S.; Laplante, B.; Wang, H.; Wheeler, D. Confronting the environmental Kuznets curve. J. Econ. Perspect. 2002, 16, 147–168. [Google Scholar] [CrossRef]
- Ang, J.B. CO2 emissions, energy consumption, and output in France. Energy Policy 2007, 35, 4772–4778. [Google Scholar] [CrossRef]
- Halicioglu, F. An econometric study of CO2 emissions, energy consumption, income and foreign trade in Turkey. Energy Policy 2009, 37, 1156–1164. [Google Scholar] [CrossRef]
- Chandran, V.; Tang, C.F. The impacts of transport energy consumption, foreign direct investment and income on CO2 emissions in ASEAN-5 economies. Renew. Sustain. Energy Rev. 2013, 24, 445–453. [Google Scholar] [CrossRef]
- Al-Mulali, U.; Saboori, B.; Ozturk, I. Investigating the environmental Kuznets curve hypothesis in Vietnam. Energy Policy 2015, 76, 123–131. [Google Scholar] [CrossRef]
- Pablo-Romero, M.d.P.; De Jesús, J. Economic growth and energy consumption: The energy-environmental Kuznets curve for Latin America and the Caribbean. Renew. Sustain. Energy Rev. 2016, 60, 1343–1350. [Google Scholar] [CrossRef]
- Kurniawan, R.; Managi, S. Coal consumption, urbanization, and trade openness linkage in Indonesia. Energy Policy 2018, 121, 576–583. [Google Scholar] [CrossRef]
- Nguyen, K.H.; Kakinaka, M. Renewable energy consumption, carbon emissions, and development stages: Some evidence from panel cointegration analysis. Renew. Energy 2019, 132, 1049–1057. [Google Scholar] [CrossRef]
- Hien, P. Excessive electricity intensity of Vietnam: Evidence from a comparative study of Asia-Pacific countries. Energy Policy 2019, 130, 409–417. [Google Scholar] [CrossRef]
- Kibria, A.; Akhundjanov, S.B.; Oladi, R. Fossil fuel share in the energy mix and economic growth. Int. Rev. Econ. Financ. 2019, 59, 253–264. [Google Scholar] [CrossRef]
- Shahzad, Q.; Aruga, K. Spatial effect of economic performance on the ecological footprint: Evidence from Asian countries. Environ. Dev. Sustain. 2024. [Google Scholar] [CrossRef]
- Ozcan, B. The nexus between carbon emissions, energy consumption and economic growth in Middle East countries: A panel data analysis. Energy Policy 2013, 62, 1138–1147. [Google Scholar] [CrossRef]
- Wang, S.S.; Zhou, D.Q.; Zhou, P.; Wang, Q. CO2 emissions, energy consumption and economic growth in China: A panel data analysis. Energy Policy 2011, 39, 4870–4875. [Google Scholar] [CrossRef]
- Dyrstad, J.M.; Skonhoft, A.; Christensen, M.Q.; Ødegaard, E.T. Does economic growth eat up environmental improvements? Electricity production and fossil fuel emission in OECD countries 1980–2014. Energy Policy 2019, 125, 103–109. [Google Scholar] [CrossRef]
- Deichmann, U.; Reuter, A.; Vollmer, S.; Zhang, F. The relationship between energy intensity and economic growth: New evidence from a multi-country multi-sectorial dataset. World Dev. 2019, 124, 104664. [Google Scholar] [CrossRef]
- Borozan, D. Unveiling the heterogeneous effect of energy taxes and income on residential energy consumption. Energy Policy 2019, 129, 13–22. [Google Scholar] [CrossRef]
- Aruga, K. Investigating the energy-environmental Kuznets Curve hypothesis for the Asia-Pacific region. Sustainability 2019, 11, 2395. [Google Scholar] [CrossRef]
- Srisaringkarn, T.; Aruga, K. The Spatial Impact of PM2.5 Pollution on Economic Growth from 2012 to 2022: Evidence from Satellite and Provincial-Level Data in Thailand. Urban Sci. 2025, 9, 110. [Google Scholar] [CrossRef]
- Aslanidis, N.; Xepapadeas, A. Smooth ‘Inverted-V-Shaped’ & Smooth ‘N-Shaped’ Pollution-Income Paths; University of Crete: Rethymno, Greece, 2004. [Google Scholar]
- Sinha Babu, S.; Datta, S.K. The relevance of environmental Kuznets curve (EKC) in a framework of broad-based environmental degradation and modified measure of growth–a pooled data analysis. Int. J. Sustain. Dev. World Ecol. 2013, 20, 309–316. [Google Scholar] [CrossRef]
- Mahmood, H.; Alkhateeb, T.T.Y.; Tanveer, M.; Mahmoud, D.H. Testing the energy-environmental Kuznets curve hypothesis in the renewable and nonrenewable energy consumption models in Egypt. Int. J. Environ. Res. Public Health 2021, 18, 7334. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Wang, B.; Wang, Z. Role of renewable energy and non-renewable energy consumption on EKC: Evidence from Pakistan. J. Clean. Prod. 2017, 156, 855–864. [Google Scholar] [CrossRef]
- Marques, A.C.; Fuinhas, J.A.; Leal, P.A. The impact of economic growth on CO2 emissions in Australia: The environmental Kuznets curve and the decoupling index. Environ. Sci. Pollut. Res. 2018, 25, 27283–27296. [Google Scholar] [CrossRef]
- Mahmood, H. The effects of natural gas and oil consumption on CO2 emissions in GCC countries: Asymmetry analysis. Environ. Sci. Pollut. Res. 2022, 29, 57980–57996. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models; Springer Science & Business Media: Dordrecht, The Netherland, 1988. [Google Scholar]
- Wang, Y.; Li, K.; Xu, X.; Zhang, Y. Transport energy consumption and saving in China. Renew. Sustain. Energy Rev. 2014, 29, 641–655. [Google Scholar] [CrossRef]
- Neves, S.A.; Marques, A.C.; Fuinhas, J.A. Is energy consumption in the transport sector hampering both economic growth and the reduction of CO2 emissions? A disaggregated energy consumption analysis. Transp. Policy 2017, 59, 64–70. [Google Scholar] [CrossRef]
- Auffhammer, M.; Mansur, E.T. Measuring climatic impacts on energy consumption: A review of the empirical literature. Energy Econ. 2014, 46, 522–530. [Google Scholar] [CrossRef]
- Brown, C.; Meeks, R.; Ghile, Y.; Hunu, K. An Empirical Analysis of the Effects of Climate Variables on National Level Economic Growth; World Bank Policy Research Working Paper; World Bank: Washington DC, USA, 2010; Available online: https://ssrn.com/abstract=1645727 (accessed on 22 May 2025).
- Henseler, M.; Schumacher, I. The impact of weather on economic growth and its production factors. Clim. Change 2019, 154, 417–433. [Google Scholar] [CrossRef]
- Iamtrakul, P.; Chayphong, S. Factors affecting the development of a healthy city in Suburban areas, Thailand. J. Urban Manag. 2023, 12, 208–220. [Google Scholar] [CrossRef]
- Khanthavit, A. Instrumental-Variable Estimation of Bangkok-Weather Effects in the Stock Exchange of Thailand. Asian Acad. Manag. J. Account. Financ. 2017, 13, 83–111. [Google Scholar] [CrossRef]
- Nunta, J.; Sahachaisaeree, N. Cultural landscape, urban settlement and dweller’s perception: A case study of a vernacular village in Northern Thailand. Procedia-Soc. Behav. Sci. 2012, 42, 153–158. [Google Scholar] [CrossRef]
- Sarkodie, S.A.; Ahmed, M.Y.; Owusu, P.A. Ambient air pollution and meteorological factors escalate electricity consumption. Sci. Total Environ. 2021, 795, 148841. [Google Scholar] [CrossRef]
- Siriwashiraporn, A. Factors Affecting the Existence of Traditional Settlement of Pak Klong Wat Pradu Community, Samut Songkhram and Ratcha Buri Provinces; Chulalongkorn Univeristy: Bangkok, Thailand, 2007. [Google Scholar]
- Soytong, P.; Janchidfa, K.; Chayhard, S.; Phengphit, N. Analysis of Climate Change Impacts on Water Resource, Urban, and Human Settlements in Eastern Thailand: Geo-Informatics Approach for Climate Change Studies; Faculty of Geoinformatics, Burapha University: Chon Buri, Thailand, 2019; Available online: http://dspace.lib.buu.ac.th/xmlui/handle/1234567890/3888 (accessed on 22 May 2025).
- Wan, W.; Wang, J. The Impact of Weather on Economic Growth: County-Level Evidence from China. Sustainability 2024, 16, 9988. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, K.; Hu, W.; Zhu, B.; Wang, P.; Wei, Y.-M. Exploring the climatic impacts on residential electricity consumption in Jiangsu, China. Energy Policy 2020, 140, 111398. [Google Scholar] [CrossRef]
- Moran, P.A. The interpretation of statistical maps. J. R. Stat. Society. Ser. B (Methodol.) 1948, 10, 243–251. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Baltagi, B.H. A Companion to Theoretical Econometrics(Chapter Fourteen Spatial Econometrics); Wiley Online Library: Hoboken, NJ, USA, 2001. [Google Scholar]
- Elhorst, J.P. Unconditional maximum likelihood estimation of linear and log-linear dynamic models for spatial panels. Geogr. Anal. 2005, 37, 85–106. [Google Scholar] [CrossRef]
- Yu, J.; De Jong, R.; Lee, L.-f. Quasi-maximum likelihood estimators for spatial dynamic panel data with fixed effects when both n and T are large. J. Econom. 2008, 146, 118–134. [Google Scholar] [CrossRef]
- Elhorst, J.P. Spatial Econometrics: From Cross-Sectional Data to Spatial Panels; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar] [CrossRef]
- Bouayad-Agha, S.; Vedrine, L. Estimation strategies for a spatial dynamic panel using GMM. A new approach to the convergence issue of European regions. Spat. Econ. Anal. 2010, 5, 205–227. [Google Scholar] [CrossRef]
- Kripfganz, S.; Sarafidis, V. Estimating Spatial Dynamic Panel Data Models with Unobserved Common Factors in Stata. J. Stat. Softw. 2025. [Google Scholar] [CrossRef]
- Murshed, M. Are Trade Liberalization policies aligned with Renewable Energy Transition in low and middle income countries? An Instrumental Variable approach. Renew. Energy 2020, 151, 1110–1123. [Google Scholar] [CrossRef]
- Chen, X.; Chen, M. Energy, environment and industry: Instrumental approaches for environmental regulation on energy efficiency. Environ. Impact Assess. Rev. 2024, 105, 107439. [Google Scholar] [CrossRef]
- Siddiquee, M.; Ahamed, R. Exploring water consumption in Dhaka city using instrumental variables regression approaches. Env. Process 2020, 7, 1255–1275. [Google Scholar] [CrossRef]
- Karmaker, S.C.; Barai, M.K.; Sen, K.K.; Saha, B.B. Effects of remittances on renewable energy consumption: Evidence from instrumental variable estimation with panel data. Util. Policy 2023, 83, 101614. [Google Scholar] [CrossRef]
- Li, L.; Sun, W.; Hu, W.; Sun, Y. Impact of natural and social environmental factors on building energy consumption: Based on bibliometrics. J. Build. Eng. 2021, 37, 102136. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized additive models. Stat. Sci. 1986, 1, 297–310. [Google Scholar] [CrossRef]
- Bank of Thailand. Thai Economic Condition Report for 2022; Bank of Thailand: Bangkok, Thailand, 2022; Available online: https://www.bot.or.th/content/dam/bot/documents/th/thai-economy/state-of-thai-economy/annual-report/annual-econ-report-th-2565.pdf (accessed on 10 January 2025).
- NESDC. Thai Economic Performance in Q4 and 2022 and Outlook for 2023 (English Edition); Office of the National Economic and Social Development Council: Bangkok, Thailand, 2022; Available online: https://www.nesdc.go.th/nesdb_en/article_attach/65Q4%20Press%20Eng%20Q4-2022%20(2102%2015.46).pdf (accessed on 10 January 2025).
- Trakulchavalit, C. A Comparative Study on Housing and Behavior of Graduated From USA UK and Japan; Chulalongkorn University: Bangkok, Thailand, 1998. [Google Scholar]
- Chevaporanapiwat, C. Factors Affecting Changes in Human Settlements in Bang Lum-Poo District; Chulalongkorn University: Bangkok, Thailand, 2001. [Google Scholar]
- Algarni, S.; Tirth, V.; Alqahtani, T.; Alshehery, S.; Kshirsagar, P. Contribution of renewable energy sources to the environmental impacts and economic benefits for sustainable development. Sustain. Energy Technol. Assess. 2023, 56, 103098. [Google Scholar] [CrossRef]
- Aruga, K.; Islam, M.M.; Jannat, A. Assessing the CO2 emissions and energy source consumption nexus in Japan. Sustainability 2024, 16, 5742. [Google Scholar] [CrossRef]
- Dincer, I. Renewable energy and sustainable development: A crucial review. Renew. Sustain. Energy Rev. 2000, 4, 157–175. [Google Scholar] [CrossRef]
- Mohtasham, J. Renewable energies. Energy Procedia 2015, 74, 1289–1297. [Google Scholar] [CrossRef]
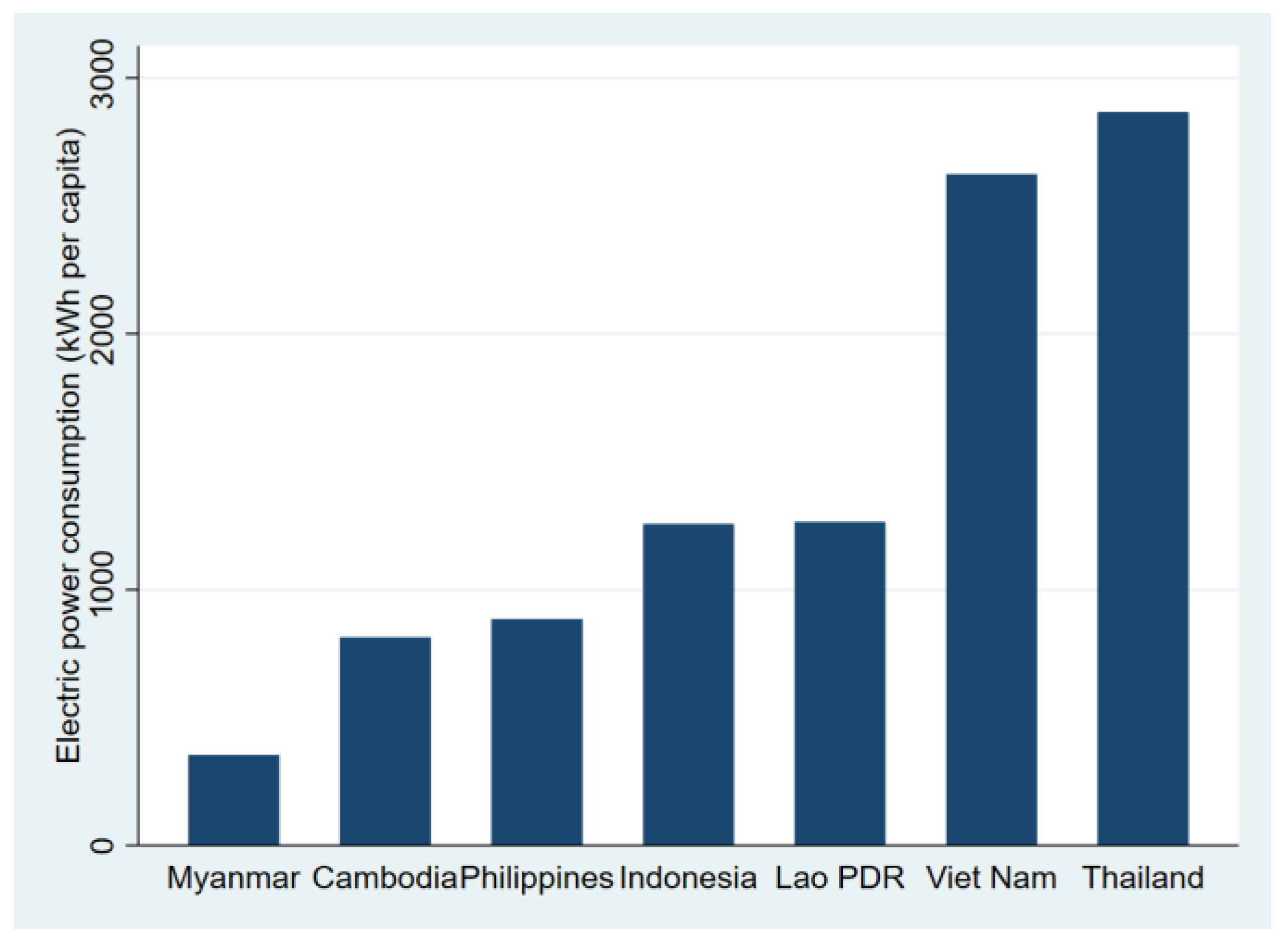
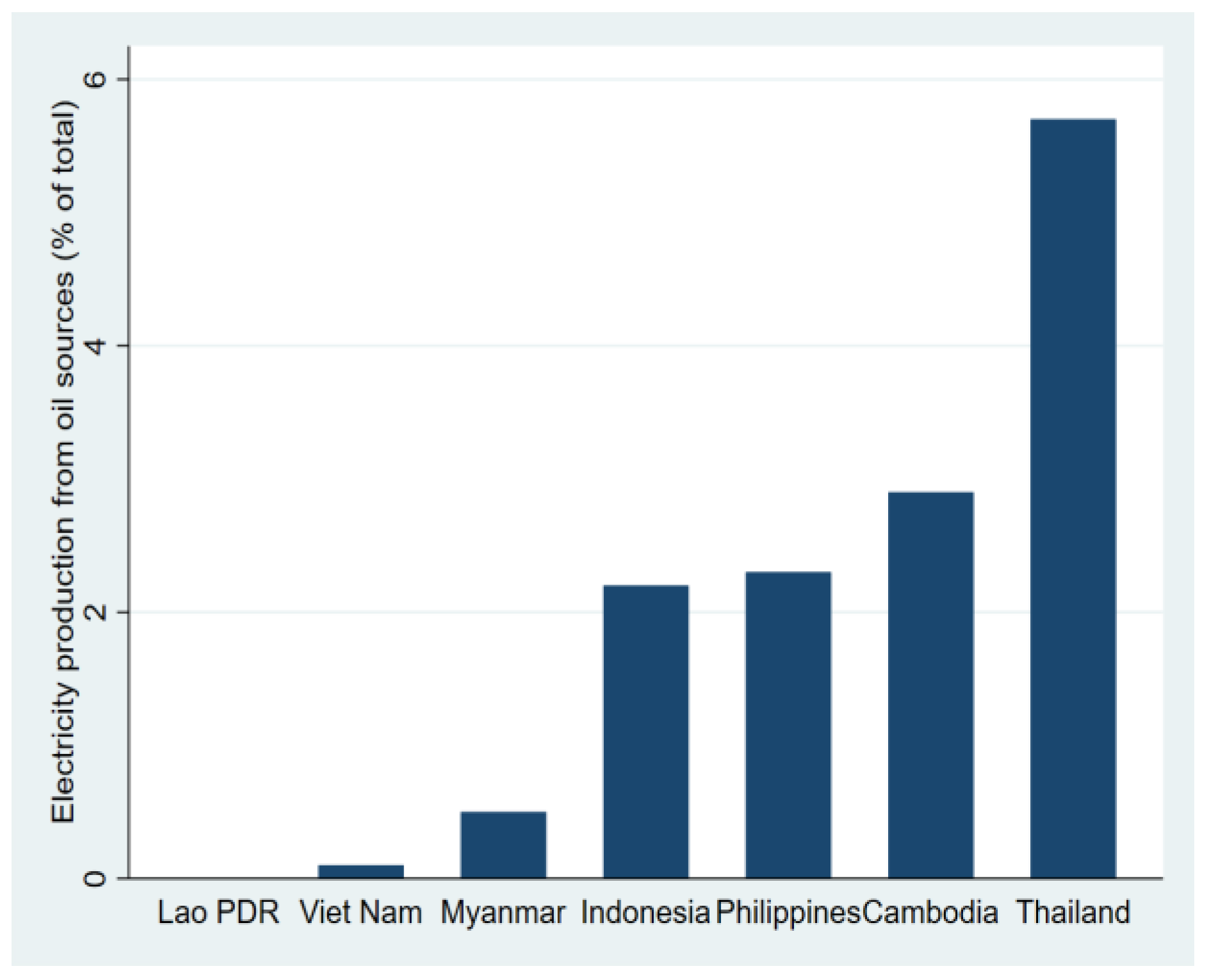
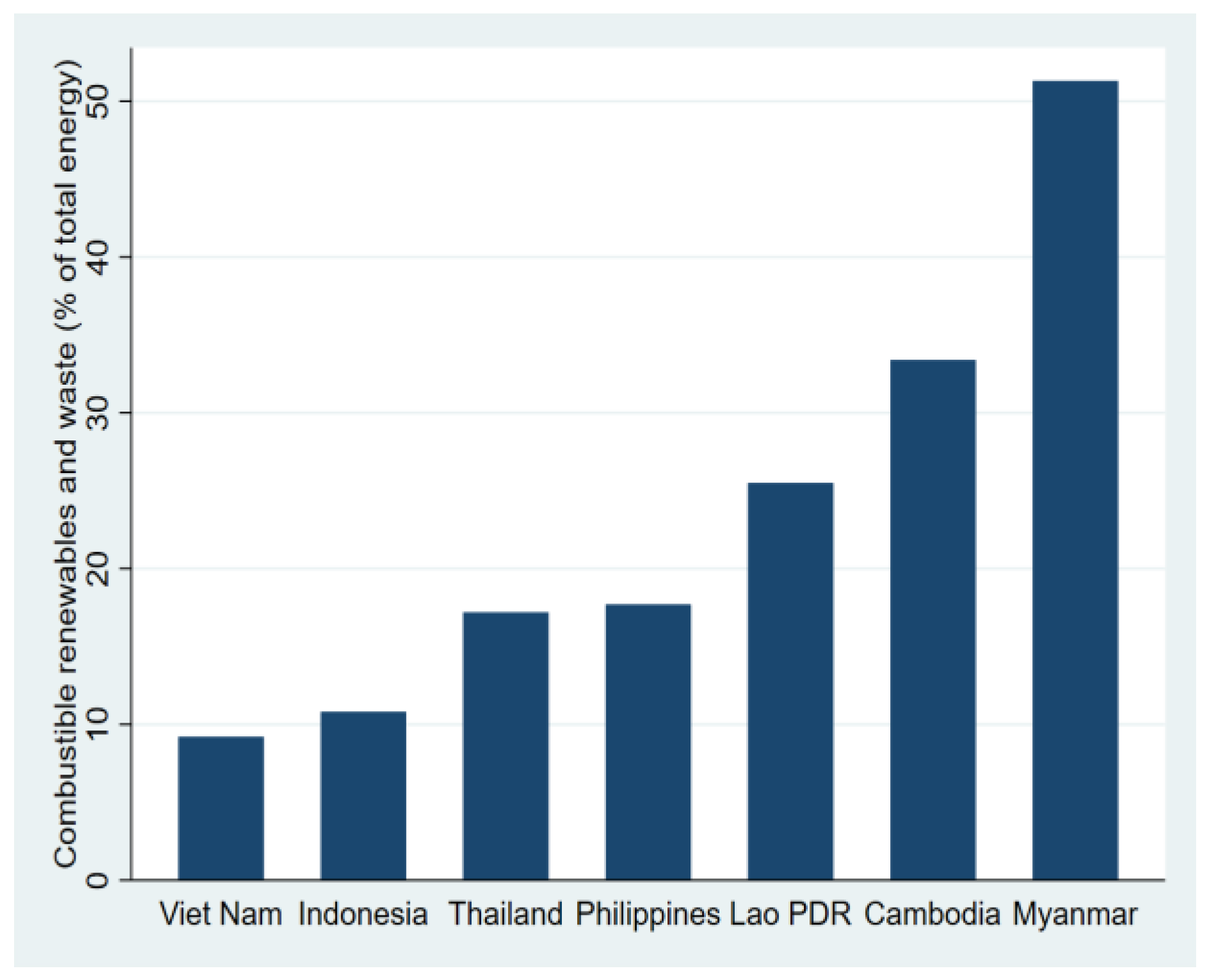

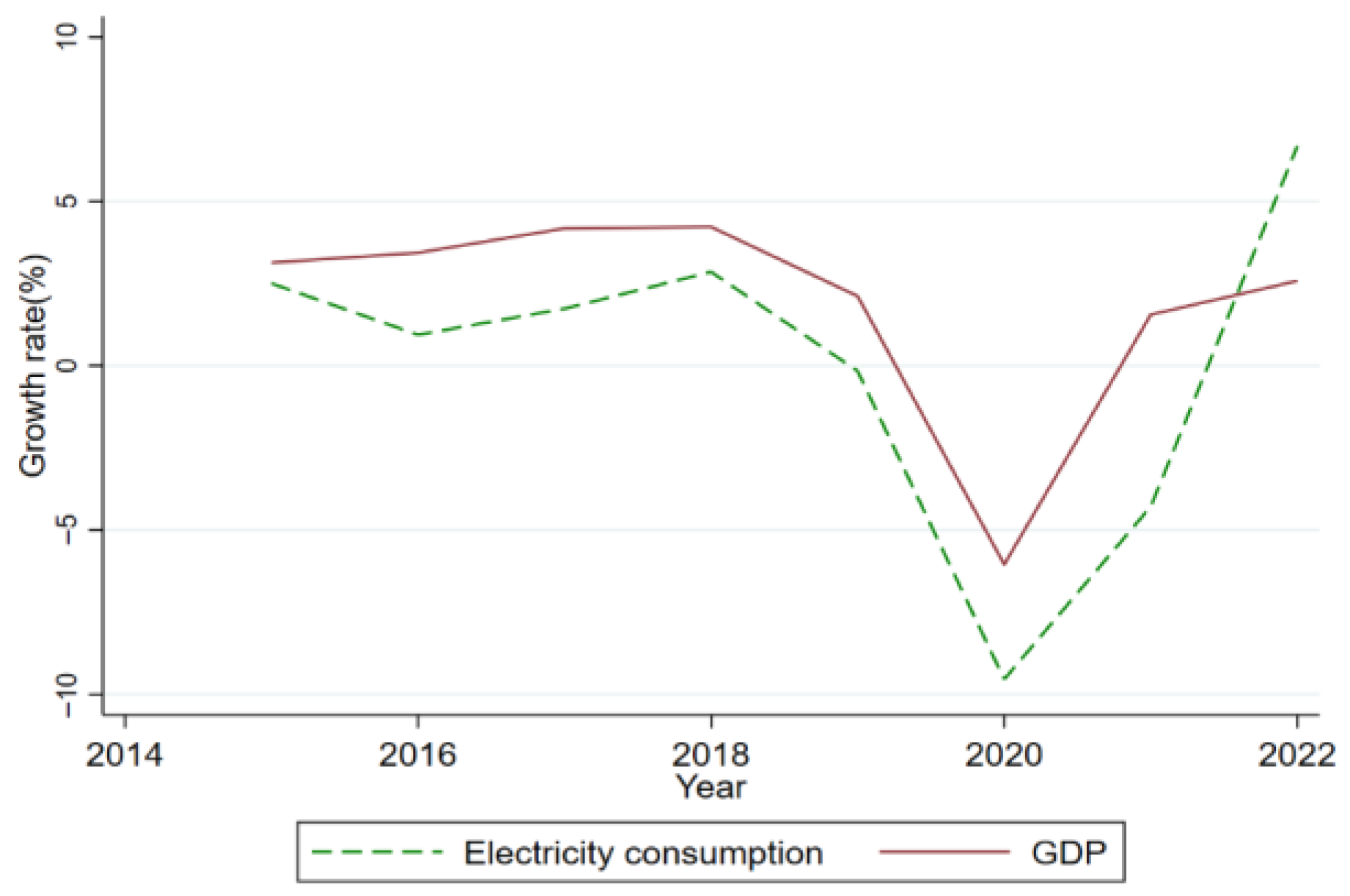
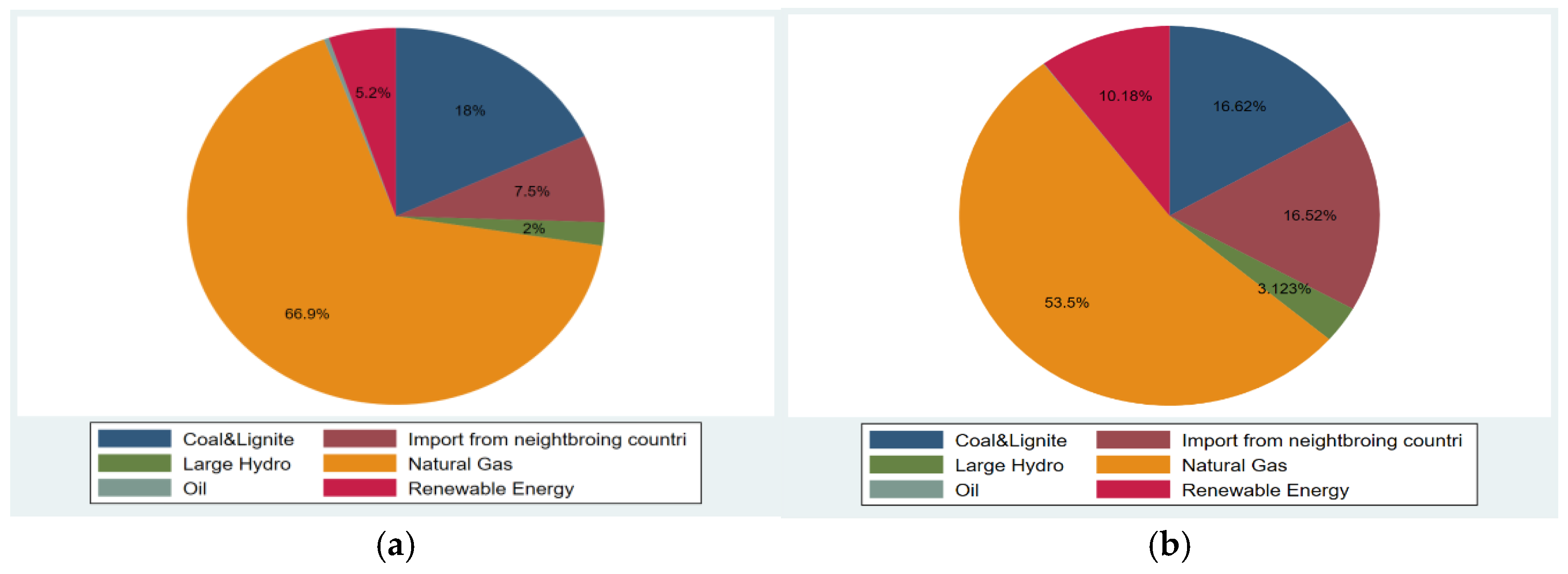


| Regions | 2022 GRP | 2022 GRP per Capita | 2022 Average Energy Consumption (GWh) | 2022 Average Energy Consumption (per Capita) (kWh/person) |
|---|---|---|---|---|
| Northeastern (NE) | USD 498 billion | USD 2724 | 1,162,050,000 | 1101 |
| Northern (NO) | USD 373 billion | USD 3329 | 990,185,072 | 1436 |
| Southern (SO) | USD 394 billion | USD 4053 | 1,207,050,000 | 1688 |
| Bangkok and Vicinity (BKK&VIC) | USD 2.2 trillion | USD 13,210 | 7,554,832,704 | 3861 |
| Integrated Regions | ||||
| BKK&VIC, CE, EA, WE | USD 3.6 trillion | USD 40,857 | 5,212,023,913 | 3970 |
| EKC Patterns | Authors | Dependent Variables | Independent Variables |
|---|---|---|---|
| Monotonically rising curve | Dasgupta, et al. [27], Ang [28], Halicioglu [29], Chandran and Tang [30], Al-Mulali, et al. [31], Pablo-Romero and De Jesús [32] | Energy use, annual emissions of CO2 | Gross value added per capita (GVApc), share of agriculture employment, foreign direct investment (FDI), transport energy consumption, labor force, exports and imports |
| Inverted U-shape | Suri and Chapman [25], Kurniawan and Managi [33], Nguyen and Kakinaka [34], Hien [35], Kibria, et al. [36], Maneejuk, et al. [17], Shahzad and Aruga [37] | Energy per capita, coal consumption, renewable energy consumption, non-renewable energy consumption, electricity consumption, CO2 emission | Real GDP, manufacturing value added (MVA), industrial value added (IVA), import, export, urbanization, share of secondary industry value added, trade openness, real oil price in country, fossil fuel share, population density |
| U-shape | Ozcan [38], Chandran and Tang [30], Wang, et al. [39], Dyrstad, et al. [40], Deichmann, et al. [41], Borozan [42], Aruga [43], Srisaringkarn and Aruga [44] | Electricity production, energy intensity, energy consumption in households per capita, annual emissions of CO2, SO2, suspended particulate matter | GDP, non-fossil energy, fossil energy, percentage of total energy consumption used in industry, transport, residential, services, agriculture and nonenergy use, energy taxes, energy prices, tertiary education, risk of poverty, climate conditions, population density |
| N-shape | Grossman and Krueger [21], Aslanidis and Xepapadeas [45], Sinha Babu and Datta [46], Mahmood, et al. [47] | Primary energy, oil, natural gas, coal consumption, hydroelectricity consumption, air quality index | GRP per capita, GRP, GRP square, GRP cubic, temperature, import shares, share of the tertiary industry, environmental degradation index and population |
| Types | Variables | Descriptions | Years | Sources | Expected Sign | References |
|---|---|---|---|---|---|---|
| Dependent Variable | A variable that represents a province’s economic activity using electricity consumption per capita as an indicator (kWh/person) | 2015–2022 | Metropolitan Electricity Authority (MEA), Provincial Electricity Authority (PEA), and Electricity Generating Authority of Thailand (EGAT) | |||
| Independent Variables | A variable that represents economic growth per capita in each province; reflects the level of economic output per person in that province (baht/person) | 2015–2022 | Office of the National Economic and Social Development Council (NESDC) | +/− | [30,38,43,44] | |
| A variable that represents a province’s population density; indicates how many people live per unit of area in that province (unit/km2) | 2015–2022 | Office of the National Economic and Social Development Council (NESDC) | + | [33,36,41] | ||
| A variable that represents the road density of a province in a given year (length) | 2015–2022 | Geofabrik | + | [30,52,53] | ||
| Instrumental Variables | A variable that represents a province’s land surface temperature at night; indicates how high the surface temperature is during nighttime in that province (Celcius) | 2015–2022 | MOD11A1.061 Terra Land Surface Temperature and Emissivity Daily Global 1km; bands: LST_Night_1km | [54,55,56,57,58,59,60,61,62,63,64] | ||
| A variable that shows the average annual rainfall in a province (mm/y) (millimeters/year) | 2015–2022 | CHIRPS Daily: Climate Hazards Center InfraRed Precipitation With Station Data (Version 2.0 Final); bands: precipitation | [54,55,56,57,58,59,60,61,62,63,64] | |||
| A variable that shows the average annual wind speed and direction in a province (m/s) (meters per second) | 2015–2022 | GLDAS-2.1: Global Land Data Assimilation System; bands: Wind_f_inst | [54,55,56,58,60,63,64] |
| Variable: Energy Consumption per Capita (Energycons_pc) | Whole Region | BKK&VIC, CE, EA, WE | NE | NO | SO |
|---|---|---|---|---|---|
| Moran’s I | 0.658 | 0.932 | 0.961 | 0.884 | 0.994 |
| E(I) | −0.013 | −0.013 | −0.013 | −0.013 | −0.013 |
| SE(I) | 0.088 | 0.091 | 0.094 | 0.094 | 0.089 |
| Z(I) | 7.690 | 10.419 | 10.363 | 9.507 | 11.269 |
| p-value | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| Tests | Statistic | df | p-Value |
|---|---|---|---|
| Moran’s I | 2.554 | 1 | 0.011 |
| Spatial Error | |||
| Lagrange multiplier | 1.406 | 1 | 0.236 |
| Robust Lagrange multiplier | 1.212 | 1 | 0.271 |
| Spatial Lag | |||
| Lagrange multiplier | 2.154 | 1 | 0.142 |
| Robust Lagrange multiplier | 1.961 | 1 | 0.161 |
| Variables: LnEnergycons_pc | Static Spatial Panel Lag Model (Whole Region) | Spatial Dynamic Panel Lag IV Model (Whole Region) | ||||||
|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | |||||
| LnEnergycons_pc(−1) | na | −0.074 (−1.13) | −0.087 (−1.36) | −0.081 (−1.36) | ||||
| LnGPPpc | 2.060 (4.75) | *** | 0.372 (5.53) | *** | −1.979 (−2.04) | ** | ||
| LnGPPpc2 | −0.070 (−3.92) | *** | 0.016 (6.07) | *** | 0.096 (2.44) | ** | ||
| LnPop_dens | −0.753 (−8.42) | *** | 13.117 (1.62) | 9.108 (1.69) | * | 6.336 (2.06) | ** | |
| LnLandtemp_night | −2.572 (−2.10) | ** | na | na | na | |||
| LnRainfall | 0.013 (1.01) | na | na | na | ||||
| LnWindspeed | 0.012 (0.46) | na | na | na | ||||
| LnRoaddens | 0.023 (3.86) | *** | 0.023 (1.50) | 0.023 (1.52) | 0.017 (1.09) | |||
| COVID | −0.001 (−0.06) | 0.011 (1.75) | * | 0.011 (1.78) | * | 0.006 (0.84) | ||
| Spatial rho | 0.336 (7.39) | *** | 0.372 (2.48) | ** | 0.347 (2.34) | ** | 0.327 (2.02) | ** |
| Obs | 616 | 462 | 462 | 462 | ||||
| Instruments nb. | 18 | 18 | 18 | |||||
| Hansen J | 14.147 | 13.768 | 10.450 | |||||
| (Hansen J p-value) | (0.291) | (0.316) | (0.490) | |||||
| AIC | −1840.591 | |||||||
| BIC | −1796.359 | |||||||
| RMSE | 20.889 | 12.703 | 8.857 | 6.225 | ||||
| MAE | 20.862 | 9.302 | 6.678 | 4.860 | ||||
| Variables: LnEnergycons_pc | BKK&VIC, CE, EA, WE | Variables | NE | ||||
|---|---|---|---|---|---|---|---|
| Coef. | Z-Stat | Coef. | Z-Stat | ||||
| Intercept | 48.986 | *** | 3.33 | Intercept | 58.134 | *** | 2.79 |
| LnEnergycons_pc(−1) | 0.495 | *** | 4.43 | LnEnergycons_pc(−1) | 0.151 | *** | 3.38 |
| LnGPPpc | −7.788 | *** | −5.53 | LnGPPpc | −10.977 | *** | −2.79 |
| LnGPPpc2 | 0.319 | *** | 5.63 | LnGPPpc2 | 0.481 | *** | 2.76 |
| LnPop_dens | −0.353 | −0.91 | LnPop_dens | 1.144 | 0.86 | ||
| LnRoaddens | 0.022 | * | 1.72 | LnRoaddens | 0.010 | *** | 3.44 |
| Spatial rho | 0.631 | *** | 2.61 | Spatial rho | 0.787 | *** | 7.21 |
| Obs | 156 | Obs | 120 | ||||
| Instruments nb. | 18 | Instruments nb. | 18 | ||||
| Hansen J | 10.063 | Hansen J | 10.634 | ||||
| (Hansen J p-value) | 0.611 | (Hansen J p-value) | 0.561 | ||||
| Variables | NO | Variables | SO | ||||
| Coef. | Z-stat | Coef. | Z-stat | ||||
| Intercept | −29.319 | −0.67 | Intercept | −3.996 | −0.65 | ||
| LnEnergycons_pc(−1) | 0.297 | *** | 3.77 | LnEnergycons_pc(−1) | 0.051 | 0.37 | |
| LnGPPpc | 4.889 | 1.23 | LnGPPpc | 0.531 | 0.34 | ||
| LnGPPpc2 | −0.211 | −1.24 | LnGPPpc2 | −0.011 | −0.17 | ||
| LnPop_dens | 0.251 | 1.11 | LnPop_dens | 0.653 | 0.71 | ||
| LnRoaddens | 0.025 | ** | 2.06 | LnRoaddens | 0.034 | *** | 3.92 |
| Spatial rho | 0.731 | *** | 5.87 | Spatial rho | 0.411 | *** | 4.46 |
| Obs | 102 | Obs | 84 | ||||
| Instruments nb. | 17 | Instruments nb. | 14 | ||||
| Hansen J | 8.201 | Hansen J | 7.327 | ||||
| (Hansen J p-value) | 0.695 | (Hansen J p-value) | 0.502 | ||||
| Whole Region (n = 462) | |||||||
|---|---|---|---|---|---|---|---|
| Variables | Short-Run Effect | Z-Stat | Long-Run Effect | Z-Stat | |||
| Direct | LnGPPpc | −2.012 | ** | −2.04 | −1.856 | ** | −1.98 |
| LnGPPpc2 | 0.097 | ** | 2.44 | 0.090 | ** | 2.35 | |
| LnPop_dens | 6.444 | ** | 2.08 | 5.943 | ** | 2.10 | |
| LnRoaddens | 0.017 | 1.09 | 0.016 | 1.11 | |||
| COVID | 0.006 | 0.84 | 0.005 | 0.84 | |||
| Indirect | LnGPPpc | −0.701 | −1.15 | −0.582 | −1.11 | ||
| LnGPPpc2 | 0.034 | 1.23 | 0.028 | 1.19 | |||
| LnPop_dens | 2.246 | 1.37 | 1.864 | 1.35 | |||
| LnRoaddens | 0.006 | 0.89 | 0.005 | 0.87 | |||
| COVID | 0.002 | 0.66 | 0.002 | 0.67 | |||
| Total | LnGPPpc | −2.713 | * | −1.87 | −2.438 | * | −1.82 |
| LnGPPpc2 | 0.131 | ** | 2.19 | 0.118 | ** | 2.11 | |
| LnPop_dens | 8.690 | ** | 2.12 | 7.801 | ** | 2.13 | |
| LnRoaddens | 0.023 | 1.06 | 0.021 | 1.09 | |||
| COVID | 0.008 | 0.80 | 0.007 | 0.81 | |||
| Estimated Degrees of Freedom | F-Statistic | p-Value | |
|---|---|---|---|
| GPPpc-Landtemp_night | 56.4 | 39.6 | <0.01 |
| GPPpc-Rainfall | 65.5 | 35.3 | <0.01 |
| GPPpc-Windspeed | 76.0 | 10.6 | <0.01 |
| GPPpc-Roaddens | 71.5 | 247.5 | <0.01 |
| Landtemp_night-Windspeed | 11.7 | 4.9 | <0.01 |
| Landtemp_night-Roaddens | 5.1 | 8.8 | <0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srisaringkarn, T.; Aruga, K. Economic Growth and Energy Consumption in Thailand: Evidence from the Energy Kuznets Curve Using Provincial-Level Data. Energies 2025, 18, 3980. https://doi.org/10.3390/en18153980
Srisaringkarn T, Aruga K. Economic Growth and Energy Consumption in Thailand: Evidence from the Energy Kuznets Curve Using Provincial-Level Data. Energies. 2025; 18(15):3980. https://doi.org/10.3390/en18153980
Chicago/Turabian StyleSrisaringkarn, Thanakhom, and Kentaka Aruga. 2025. "Economic Growth and Energy Consumption in Thailand: Evidence from the Energy Kuznets Curve Using Provincial-Level Data" Energies 18, no. 15: 3980. https://doi.org/10.3390/en18153980
APA StyleSrisaringkarn, T., & Aruga, K. (2025). Economic Growth and Energy Consumption in Thailand: Evidence from the Energy Kuznets Curve Using Provincial-Level Data. Energies, 18(15), 3980. https://doi.org/10.3390/en18153980







