Analysis of Aerodynamic Heating Modes in Thermochemical Nonequilibrium Flow for Hypersonic Reentry
Abstract
1. Introduction
2. Mathematical and Physical Models
2.1. Governing Equations
2.2. Thermodynamic Properties
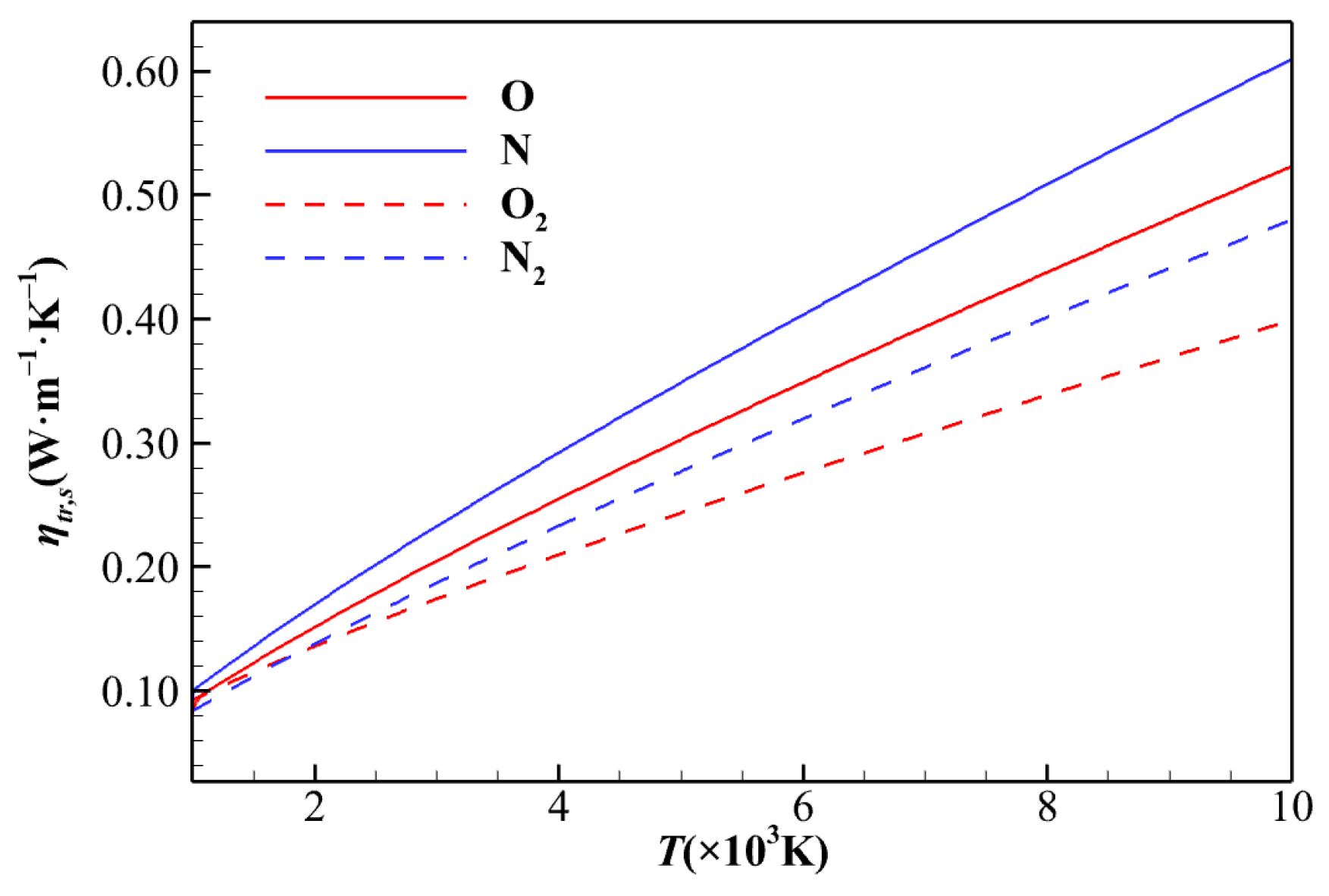
2.3. Transport Properties
2.4. Identification of Different Heat Transfer Modes
2.5. Flow Solver
3. Validation
4. Results and Analysis
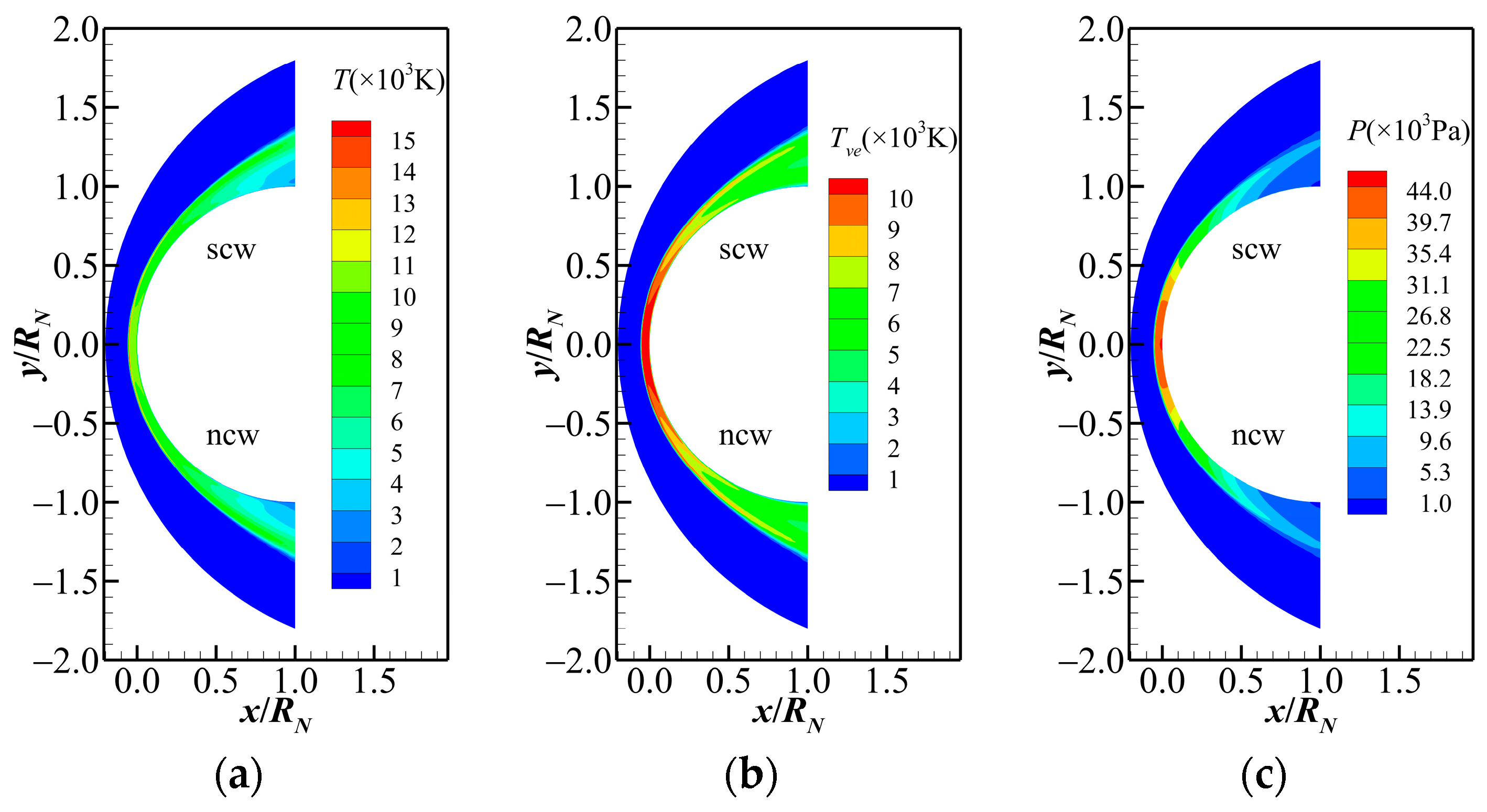
4.1. Flow Characteristics
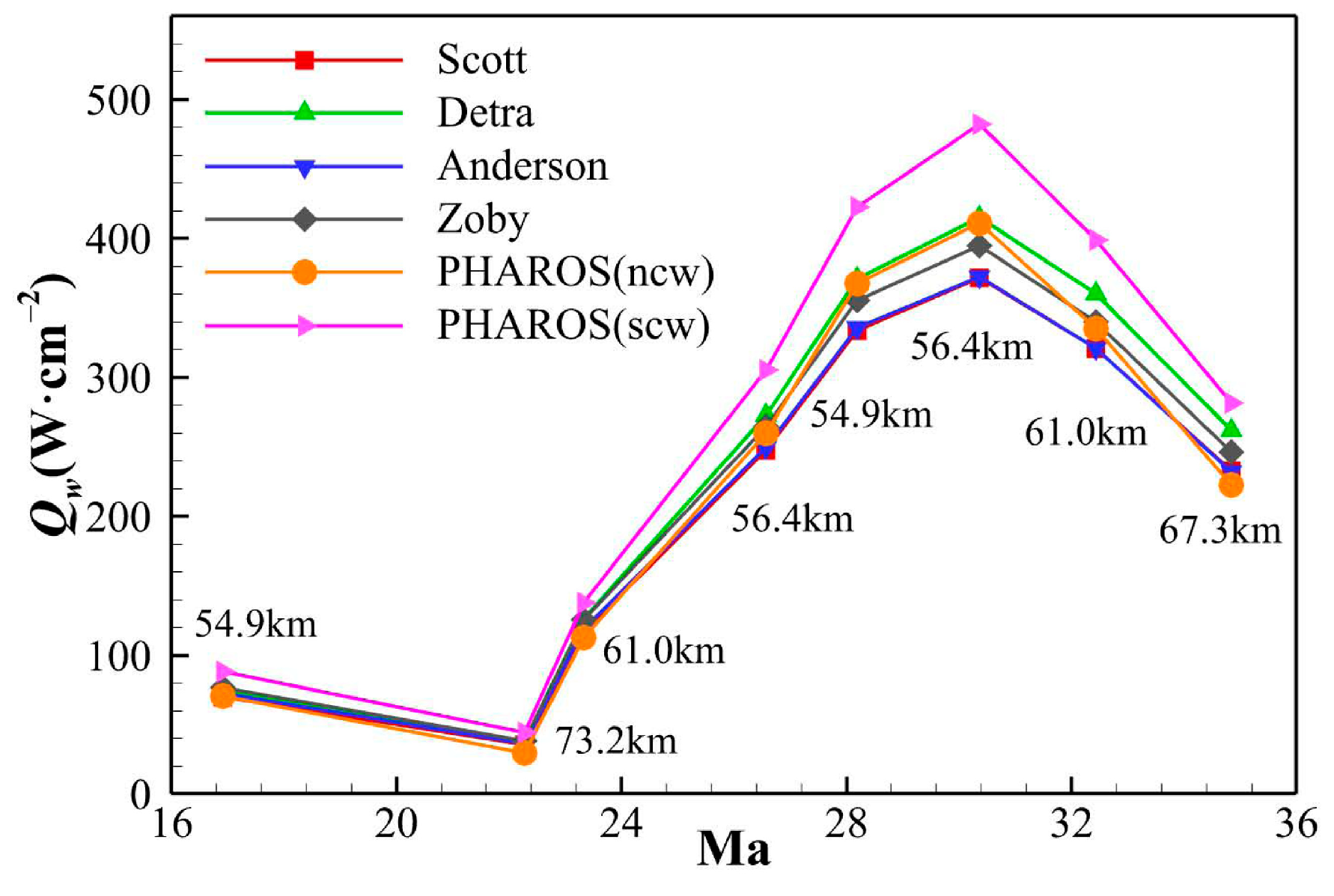
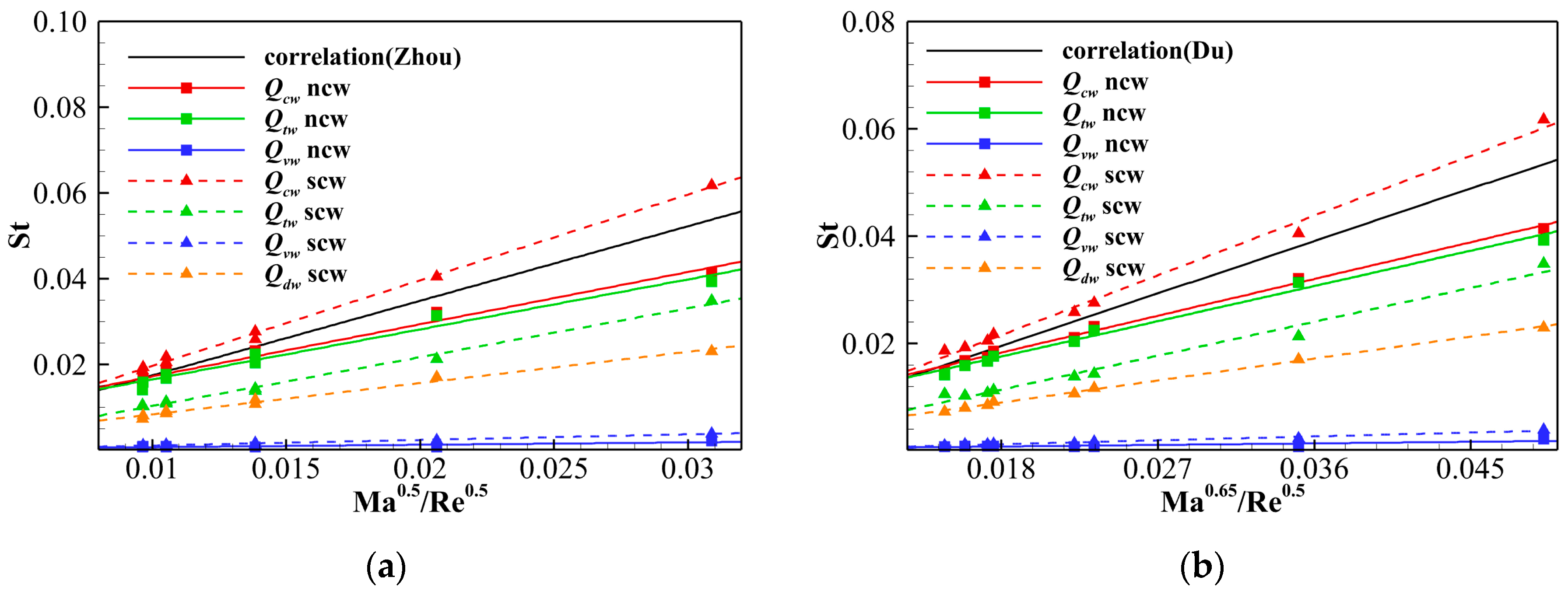
4.2. Assessment on Engineering Correlations of Stagnation Point Heat Flux
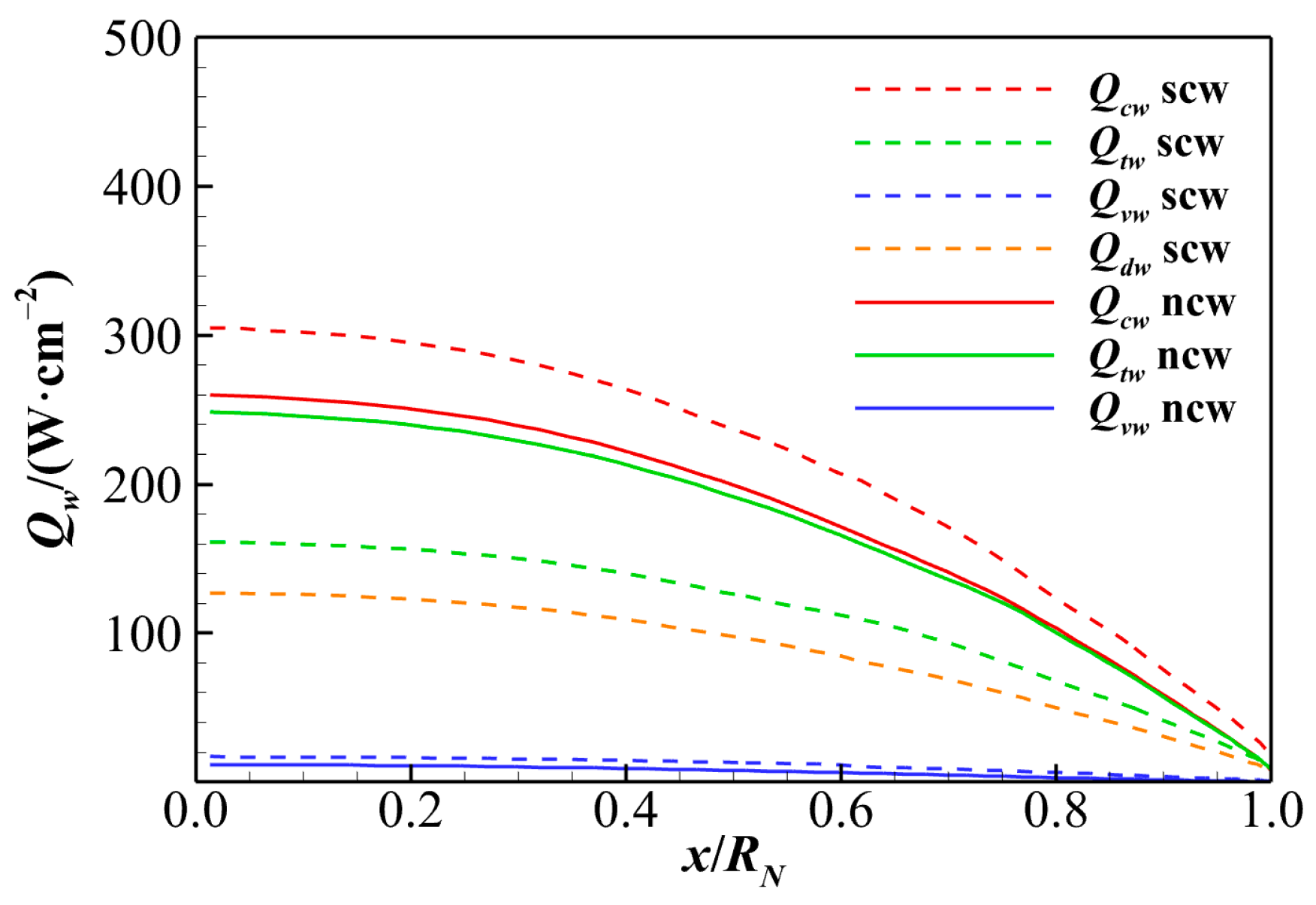
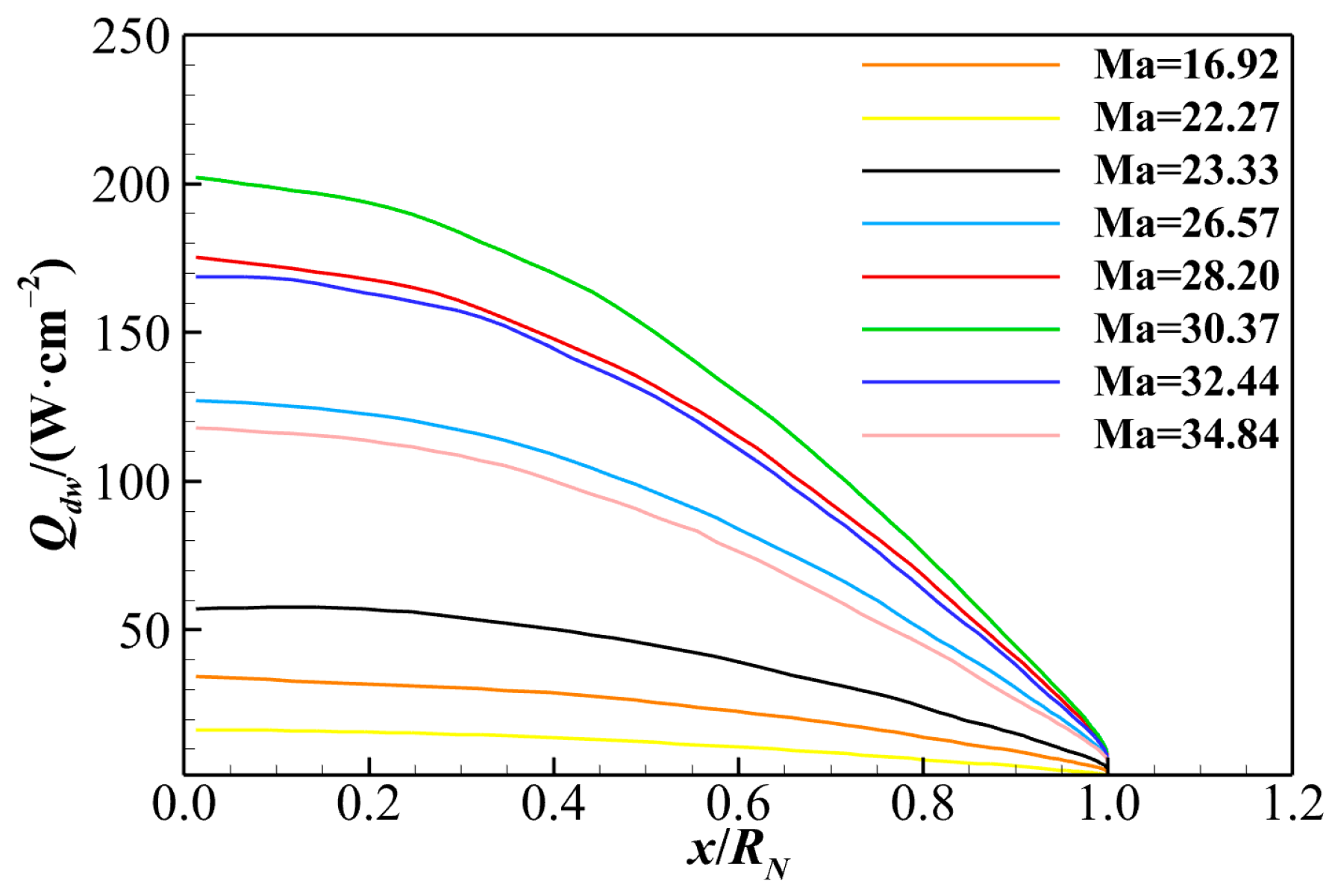
4.3. Super-Catalytic and Non-Catalytic Wall Heat Fluxes
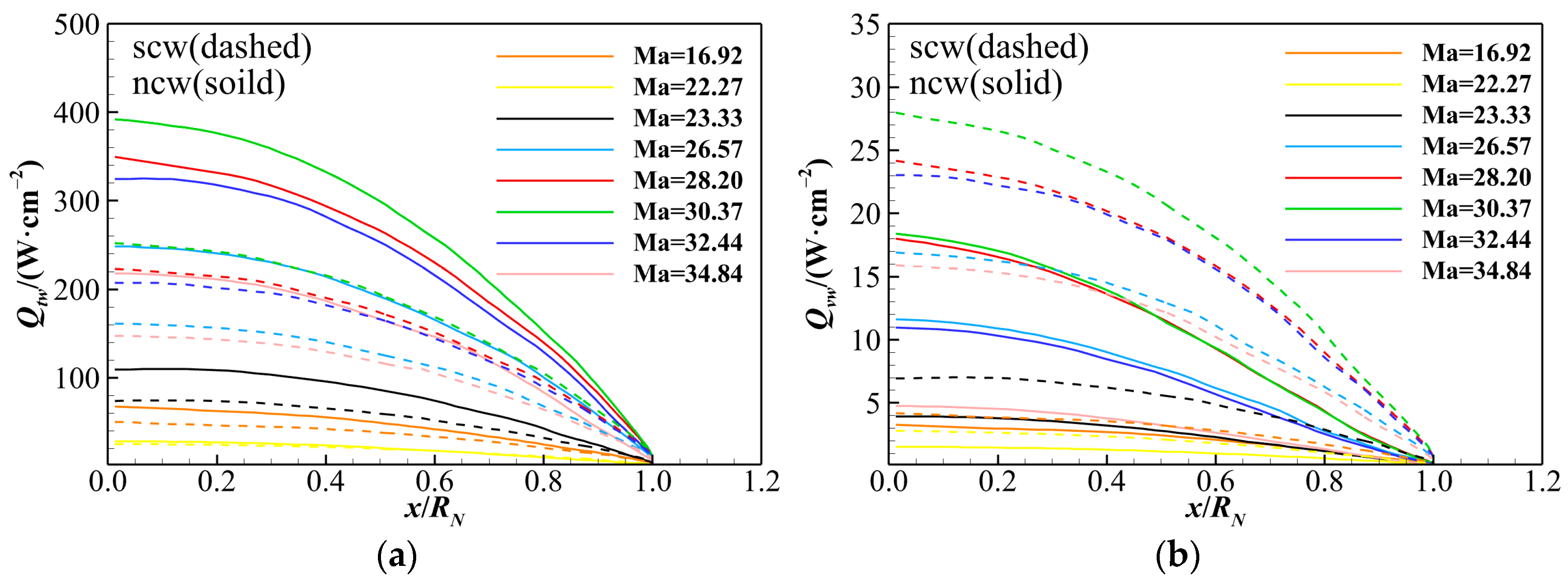
4.4. Identification of Different Heat Transfer Modes
5. Conclusions
- (1)
- A thin shock layer forms ahead of the sphere, leading to internal energy excitations and chemical reaction among air species. Significant thermochemical nonequilibrium effects occur within a short distance behind the shock. At the same flight altitude, the strength of the thermodynamic nonequilibrium effect increases with rising Mach number. The wall catalytic condition influences the reaction processes and species composition near the wall but has minimal impact on the main flow field.
- (2)
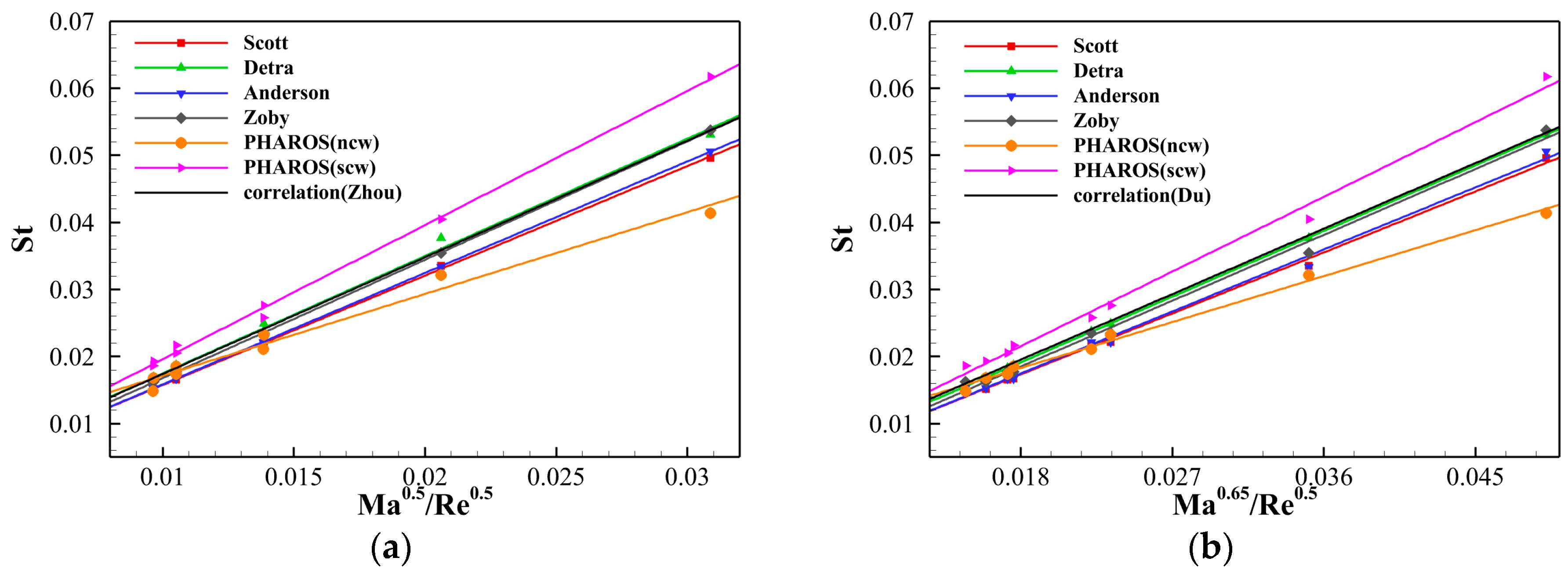
- The stagnation point heat transfers calculated using several simplified engineering correlations and the in-house solver PHAROS are compared, showing both quantitative and qualitative consistency. The stagnation point heat flux is then converted into a Stanton number and correlated with Reynolds and Mach numbers, referring to the relations proposed by Zhou et al. [36] and Du et al. [37]. All stagnation point Stanton numbers, whether from the engineering correlations or PHAROS, maintain a linear relationship with Re and Ma. However, when thermochemical nonequilibrium effects are included, the proportional coefficients should be adjusted as 2.000 (scw)/1.219 (ncw) and 1.237 (scw)/0.761 (ncw) in the Zhou et al. [36] and Du et al. [37] relations, respectively. Furthermore, the different heat transfer modes are also evaluated in the linear relations of St with Ma0.5/Re0.5 or Ma0.65/Re0.5, and the individual proportional coefficient for each mode are determined.
- (3)
- The contributions of different heat transfer modes to total heat flux are analyzed in dimensionless terms. Due to the extremely low vibrational–electronic thermal conductivity, the vibrational–electronic heat transfer constitutes only about 5% of the total heat flux under both catalytic wall conditions. The translational–rotational heat transfer accounts for approximately 95% of total aerodynamic heating under the non-catalytic wall condition. In the case of a super-catalytic wall, translational–rotational and chemical reaction heat transfers are roughly 55% and 40%, respectively. Therefore, special attention should be given to translational–rotational and chemical diffusion heat transfer modes when predicting aerodynamic heating for hypersonic reentry.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PHAROS | Parallel hypersonic aerothermodynamics and radiation optimized solver |
| CFD | Computational fluid dynamics |
| N-S | Navier–Stokes |
| DSMC | Direct simulation Monte Carlo |
| NCCR | Nonlinear coupled constitutive relations |
| StS | State to state |
| CLN | Constant Lewis number |
| scw | Super-catalytic wall |
| ncw | Non-catalytic wall |
References
- Bertin, J.J.; Cummings, R.M. Critical Hypersonic Aerothermodynamic Phenomena. Annu. Rev. Fluid Mech. 2006, 38, 129–157. [Google Scholar] [CrossRef]
- Anderson, J.D. Hypersonic and High Temperature Gas Dynamics, 2nd ed.; AIAA: Reston, VA, USA, 2006; pp. 13–23. [Google Scholar]
- Candler, G.V. Rate Effects in Hypersonic Flows. Annu. Rev. Fluid Mech. 2019, 51, 379–402. [Google Scholar] [CrossRef]
- Knight, D.; Chazot, O.; Austin, J.; Badr, M.A.; Candler, G.; Celik, B.; de Rosa, D.; Donelli, R.; Komives, J.; Lani, A. Assessment of predictive capabilities for aerodynamic heating in hypersonic flow. Prog. Aerosp. Sci. 2017, 90, 39–53. [Google Scholar] [CrossRef]
- Massimi, H.S.; Shen, H.; Wen, C.-Y.; Chen, Y.-S.; Liang, S.-M. Numerical analysis of hypersonic flows around blunt-nosed models and a space vehicle. Aerosp. Sci. Technol. 2015, 43, 360–371. [Google Scholar] [CrossRef]
- Guo, J.; Wang, X.; Li, S. Investigation of high enthalpy thermochemical nonequilibrium flow over spheres. Phys. Fluids 2024, 36, 016122. [Google Scholar] [CrossRef]
- Lee, J.-H. Basic governing equations for the flight regimes of aeroassisted orbital transfer vehicles. In Proceedings of the 19th Thermophysics Conference, Snowmass, CO, USA, 25–28 June 1984; p. 1729. [Google Scholar]
- Gnoffo, P.A. Conservation Equations and Physical Models for Hypersonic Air Flows in Thermal and Chemical Nonequilibrium; NASA-TP-2867; NASA Langley Research Center: Washington, DC, USA, 1989. [Google Scholar]
- Park, C. Assessment of a two-temperature kinetic model for dissociating and weakly ionizing nitrogen. J. Thermophys. Heat Transf. 1988, 2, 8–16. [Google Scholar] [CrossRef]
- Park, C. Assessment of two-temperature kinetic model for ionizing air. J. Thermophys. Heat Transf. 1989, 3, 233–244. [Google Scholar] [CrossRef]
- Surzhikov, S.; Shang, J. Kinetic models analysis for super-orbital aerophysics. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 7–10 January 2008; p. 1278. [Google Scholar]
- Ghezali, Y.; Haoui, R.; Chpoun, A. Effect of rotational nonequilibrium behind a normal shock wave in oxygen and nitrogen flow. Therm. Sci. Eng. Prog. 2020, 19, 100601. [Google Scholar] [CrossRef]
- Gupta, R.N.; Yos, J.M.; Thompson, R.A.; Lee, K.-P. A Review of Reaction Rates and Thermodynamic and Transport Properties for an 11-Species Air Model for Chemical and Thermal Nonequilibrium Calculations to 30,000 K; NASA-RP-1232; NASA Langley Research Center: Washington, DC, USA, 1990. [Google Scholar]
- Park, C. Review of chemical-kinetic problems of future NASA missions. I-Earth entries. J. Thermophys. Heat Transf. 1993, 7, 385–398. [Google Scholar] [CrossRef]
- Dunn, M.G.; Kang, S. Theoretical and Experimental Studies of Reentry Plasmas; NASA-CR-2232; NASA Langley Research Center: Washington, DC, USA, 1973. [Google Scholar]
- Zhenxun, G.; Chongwen, J.; Chun-Xuan, L. Review of numerical simulation methods for hypersonic and high-enthalpy non-equilibrium flow. Adv. Mech. 2023, 53, 561–591. [Google Scholar]
- Boyd, I. Nonequilibrium chemistry modeling in rarefied hypersonic flows. In Proceedings of the 33rd Thermophysics Conference, Norfolk, VA, USA, 28 June–1 July 1999; p. 3634. [Google Scholar]
- Boyd, I.D. Rotational and vibrational nonequilibrium effects in rarefied hypersonic flow. J. Thermophys. Heat Transf. 1990, 4, 478–484. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhao, W.; Jiang, Z.; Chen, W. Numerical simulation of hypersonic reaction flows with nonlinear coupled constitutive relations. Aerosp. Sci. Technol. 2021, 112, 106591. [Google Scholar] [CrossRef]
- Shuhua, Z.; Zhenyu, Y.; Wenwen, Z.; Weifang, C. Numerical simulation of hypersonic thermochemical nonequilibrium flows using nonlinear coupled constitutive relations. Chin. J. Aeronaut. 2023, 36, 63–79. [Google Scholar]
- Kim, M.; Gülhan, A.; Boyd, I.D. Modeling of electron energy phenomena in hypersonic flows. J. Thermophys. Heat Transf. 2012, 26, 244–257. [Google Scholar] [CrossRef]
- Hao, J.; Wang, J.; Lee, C. Numerical study of hypersonic flows over reentry configurations with different chemical nonequilibrium models. Acta Astronaut. 2016, 126, 1–10. [Google Scholar] [CrossRef]
- Jianlong, Y.; Meng, L. Numerical analysis of hypersonic thermochemical non-equilibrium environment for an entry configuration in ionized flow. Chin. J. Aeronaut. 2019, 32, 2641–2654. [Google Scholar]
- He, Q.-S.; Sun, S.-R.; Cao, X.; Jia, H.; Du, Y.-W.; Wang, H.-X. Non-equilibrium modeling on the aerothermodynamic characteristics of hypersonic inflatable reentry vehicle. Aerosp. Sci. Technol. 2023, 141, 108524. [Google Scholar] [CrossRef]
- Yu, M.; Qiu, Z.; Zhong, B.; Takahashi, Y. Numerical simulation of thermochemical non-equilibrium flow-field characteristics around a hypersonic atmospheric reentry vehicle. Phys. Fluids 2022, 34, 126103. [Google Scholar] [CrossRef]
- Chen, S.; Hu, Y.; Sun, Q. Study of the coupling between real gas effects and rarefied effects on hypersonic aerodynamics. In AIP Conference Proceedings; American Institute of Physics: Melville, NY, USA, 2012; pp. 1515–1521. [Google Scholar]
- Hong, Q.; Hao, J.; Uy, K.C.K.; Wen, C.-Y.; Sun, Q. Thermochemical nonequilibrium effects on high-enthalpy double-wedge flows. Phys. Fluids 2022, 34, 063607. [Google Scholar] [CrossRef]
- Zhao, W.; Yang, X.; Wang, J.; Zheng, Y.; Zhou, Y. Evaluation of Thermodynamic and Chemical Kinetic Models for Hypersonic and High-Temperature Flow Simulation. Appl. Sci. 2023, 13, 9991. [Google Scholar] [CrossRef]
- Hao, J.; Wang, J.; Lee, C. State-specific simulation of oxygen vibrational excitation and dissociation behind a normal shock. Chem. Phys. Lett. 2017, 681, 69–74. [Google Scholar] [CrossRef]
- Fay, J.A.; Riddell, F.R. Theory of Stagnation Point Heat Transfer in Dissociated Air. J. Aerosp. Sci. 1958, 25, 73–85. [Google Scholar] [CrossRef]
- Lees, L. Laminar Heat Transfer Over Blunt-Nosed Bodies at Hypersonic Flight Speeds. J. Jet Propuls. 1956, 26, 259–269. [Google Scholar] [CrossRef]
- Scott, C.; Ried, R.; Maraia, R.; Li, C.-P.; Derry, S. An AOTV aeroheating and thermal protection study. In Proceedings of the 19th Thermophysics Conference, Snowmass, CO, USA, 25–28 June 1984; p. 1710. [Google Scholar]
- Detra, R.; Hidalgo, H. Generalized heat transfer formulas and graphs for nose cone re-entry into the atmosphere. ARS J. 1961, 31, 318–321. [Google Scholar] [CrossRef]
- Zoby, E.; Moss, J.; Sutton, K. Approximate convective-heating equations for hypersonic flows. J. Spacecr. Rocket. 1981, 18, 64–70. [Google Scholar] [CrossRef]
- Viviani, A.; Pezzella, G. Aerodynamic and Aerothermodynamic Analysis of Space Mission Vehicles; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Zhou, B.; Yi, X.; Wang, Z.; Li, Z. Aerothermal Heating Correlations at Stagnation Point/Line in Low-Enthalpy Hypersonic Flow. AIAA J. 2023, 61, 1435–1439. [Google Scholar] [CrossRef]
- Du, T.; Chen, M.K.; Li, H.L.; Zhang, Y.L.; Shen, D. Suitability Analysis on Correlation Relation of Aerothermodynamics Entry Environment for Hypersonic Flying Vehicles. J. Astronaut. 2018, 39, 1039–1046. [Google Scholar]
- Tauber, M.E. A review of high-speed, convective, heat-transfer computation methods. In Proceedings of the Missile Aerodynamics Conference, Monterey, CA, USA, 31 October–2 November 1989. [Google Scholar]
- Yang, X.; Wang, J.; Zhou, Y.; Sun, K. Assessment of Radiative Heating for Hypersonic Earth Reentry Using Nongray Step Models. Aerospace 2022, 9, 219. [Google Scholar] [CrossRef]
- Lee, M.G. Numerical prediction of enhanced heat flux due to shock-on-shock interaction in hypersonic nonequilibrium flow. Int. J. Numer. Methods Heat Fluid Flow 1999, 9, 114–135. [Google Scholar] [CrossRef]
- Hao, J.; Wang, J.; Lee, C. Assessment of vibration–dissociation coupling models for hypersonic nonequilibrium simulations. Aerosp. Sci. Technol. 2017, 67, 433–442. [Google Scholar] [CrossRef]
- Hao, J.; Wang, J.; Lee, C. Development of a Navier—Stokes Code for Hypersonic Nonequilibrium Simulations. In Proceedings of the 21st AIAA International Space Planes and Hypersonics Technologies Conference, Xiamen, China, 6–9 March 2017; p. 2164. [Google Scholar]
- Vincenti, W.G.; Kruger, C.H., Jr.; Teichmann, T. Introduction to Physical Gas Dynamics; American Institute of Physics: Melville, NY, USA, 1966. [Google Scholar]
- Blottner, F.G.; Johnson, M.; Ellis, M. Chemically Reacting Viscous Flow Program for Multi-Component Gas Mixtures; Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 1971. [Google Scholar]
- Wilke, C.R. A viscosity equation for gas mixtures. J. Chem. Phys. 1950, 18, 517–519. [Google Scholar] [CrossRef]
- Gosse, R.; Candler, G. Diffusion flux modeling: Application to direct entry problems. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 10–13 January 2005; p. 389. [Google Scholar]
- MacCormack, R.W.; Candler, G.V. The solution of the Navier-Stokes equations using Gauss-Seidel line relaxation. Comput. Fluids 1989, 17, 135–150. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. J. Comput. Phys. 1997, 135, 229–248. [Google Scholar] [CrossRef]
- Wright, M.J.; Candler, G.V.; Bose, D. Data-Parallel Line Relaxation Method for the Navier-Stokes Equations. AIAA J. 1998, 36, 1603–1609. [Google Scholar] [CrossRef]
- Hao, J.; Wang, J.; Gao, Z.; Jiang, C.; Lee, C. Comparison of transport properties models for numerical simulations of Mars entry vehicles. Acta Astronaut. 2017, 130, 24–33. [Google Scholar] [CrossRef]
- Scalabrin, L.C. Numerical Simulation of Weakly Ionized Hypersonic Flow over Reentry Capsules; Citeseer: University Park, PA, USA, 2007. [Google Scholar]
- Chen, G.; Chen, W.; Lu, S.; Sun, M.; Song, R.; Sun, B. Study on the influence of high-temperature thermochemical nonequilibrium effects on the flow field characteristics around shaped wing. Phys. Fluids 2024, 36, 096129. [Google Scholar] [CrossRef]
- Surzhikov, S.T. Radiative gasdynamics of the nose surface of the Apollo-4 command module at its superobrital reentry. Fluid Dyn. 2018, 52, 815–831. [Google Scholar] [CrossRef]
- Papadopoulos, P.; Venkatapathy, E.; Prabhu, D.; Loomis, M.P.; Olynick, D. Current grid-generation strategies and future requirements in hypersonic vehicle design, analysis and testing. Appl. Math. Model. 1999, 23, 705–735. [Google Scholar] [CrossRef]
- Bose, D.; Brown, J.L.; Prabhu, D.K.; Gnoffo, P.; Johnston, C.O.; Hollis, B. Uncertainty Assessment of Hypersonic Aerothermodynamics Prediction Capability. J. Spacecr. Rocket. 2013, 50, 12–18. [Google Scholar] [CrossRef]
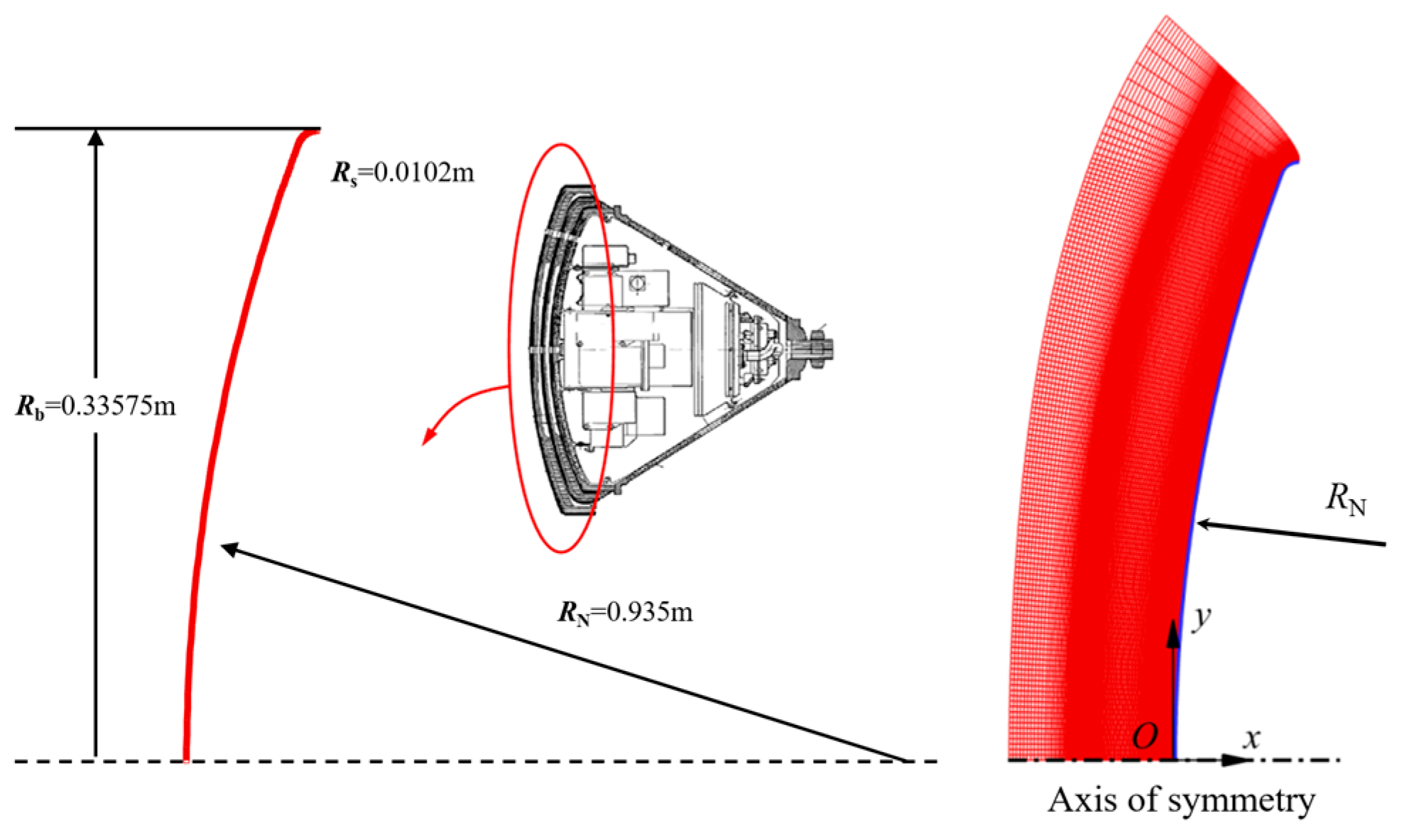
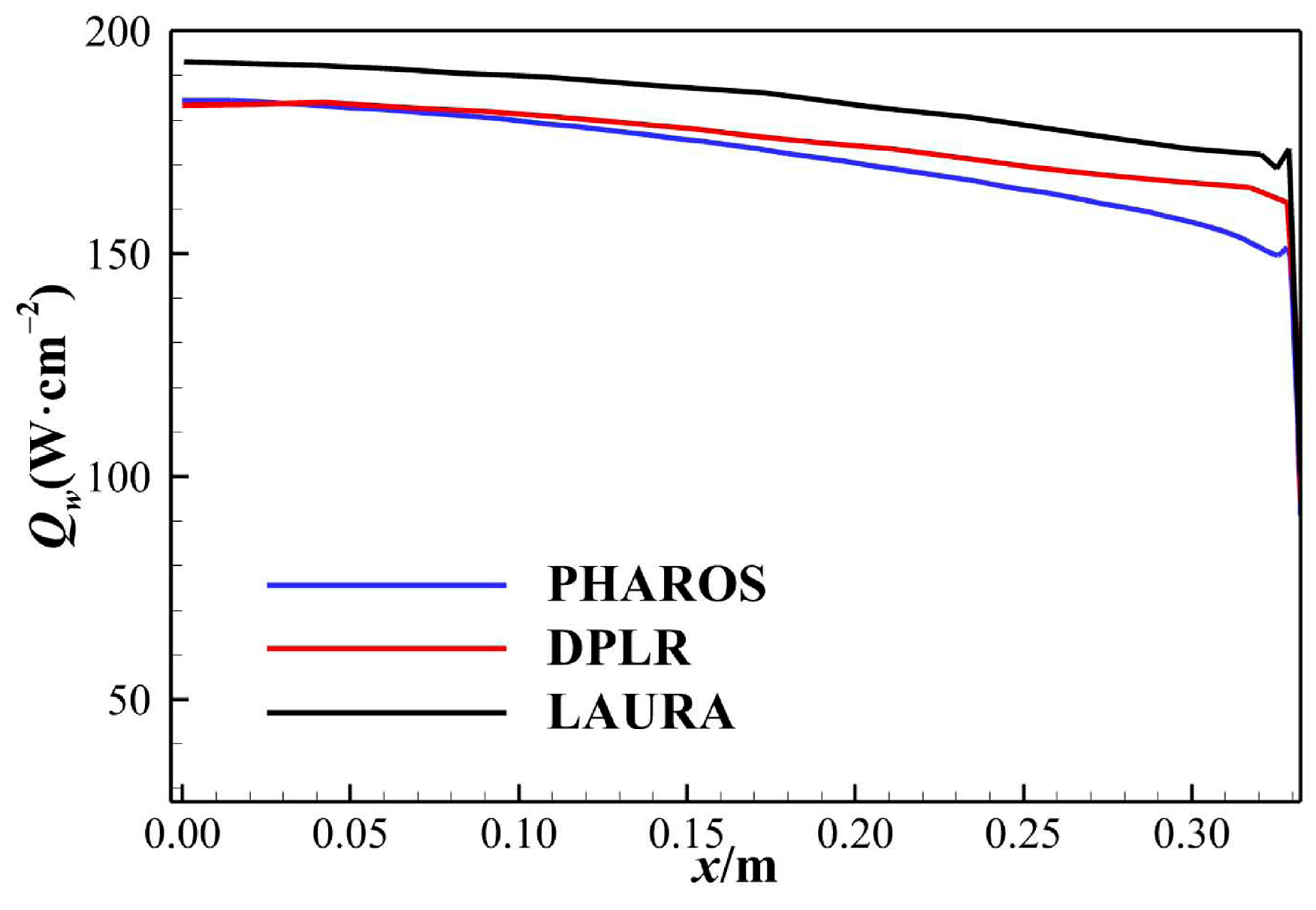

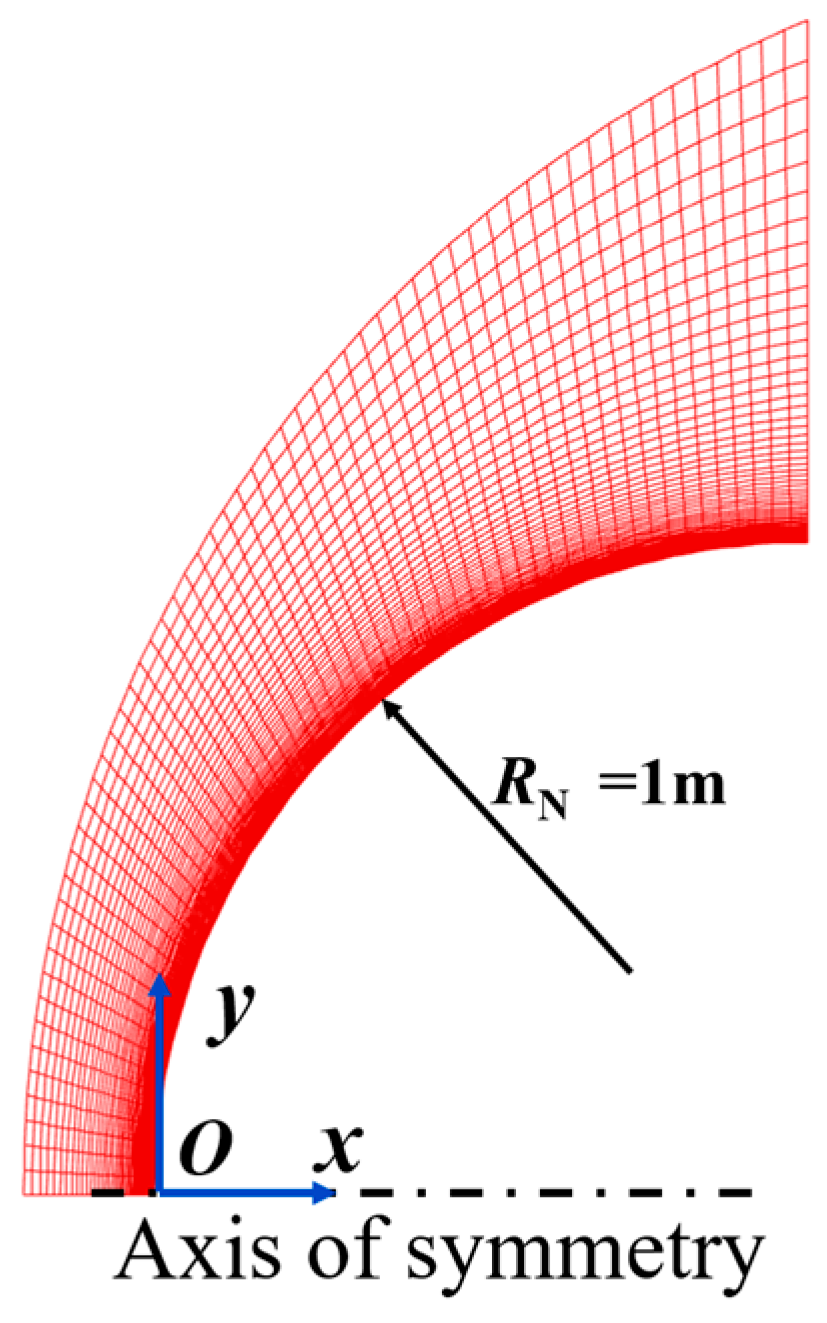




| No. | t/s | H/km | V∞/(km∙s−1) | Re | Ma | T∞/K | p∞/Pa | ρ∞/(kg·m−3) |
|---|---|---|---|---|---|---|---|---|
| 1 | 56 | 67.3 | 10.50 | 82,033.4 | 34.84 | 226 | 7.80 | 1.20 × 10−4 |
| 2 | 63 | 61.0 | 10.20 | 169,131.6 | 32.44 | 246 | 19.20 | 2.73 × 10−4 |
| 3 | 73 | 56.4 | 9.76 | 274,126.9 | 30.37 | 257 | 35.30 | 4.79 × 10−4 |
| 4 | 82 | 54.9 | 9.15 | 302,733.3 | 28.20 | 262 | 43.10 | 5.73 × 10−4 |
| 5 | 93 | 56.4 | 8.54 | 239,861.0 | 26.57 | 257 | 35.30 | 4.79 × 10−4 |
| 6 | 118 | 61.0 | 7.32 | 121,778.0 | 23.33 | 245 | 19.20 | 2.73 × 10−4 |
| 7 | 209 | 73.2 | 6.50 | 23,347.1 | 22.27 | 212 | 3.18 | 5.23 × 10−5 |
| 8 | 423 | 54.9 | 5.49 | 182,274.0 | 16.92 | 262 | 43.10 | 5.75 × 10−4 |
| Ma | scw ∆Ttr/∆xcell | ncw ∆Ttr/∆xcell | scw ∆Tve/∆xcell | ncw ∆Tve/∆xcell |
|---|---|---|---|---|
| 16.92 | 2.904 × 10−4 | 3.446 × 10−4 | 2.595 × 10−3 | 2.753 × 10−3 |
| 22.27 | 1.451 × 10−4 | 1.344 × 10−4 | 2.247 × 10−3 | 2.430 × 10−3 |
| 23.33 | 4.351 × 10−4 | 5.569 × 10−4 | 3.145 × 10−3 | 3.003 × 10−3 |
| 26.57 | 2.609 × 10−3 | 3.203 × 10−3 | 4.088 × 10−3 | 4.095 × 10−3 |
| 28.20 | 3.353 × 10−3 | 4.148 × 10−3 | 4.655 × 10−3 | 4.765 × 10−3 |
| 30.37 | 3.682 × 10−3 | 4.497 × 10−3 | 4.937 × 10−3 | 4.808 × 10−3 |
| 32.44 | 3.169 × 10−3 | 3.863 × 10−3 | 4.598 × 10−3 | 4.050 × 10−3 |
| 34.84 | 2.434 × 10−3 | 2.787 × 10−3 | 4.018 × 10−3 | 3.265 × 10−3 |
| Ma | 16.92 | 22.27 | 23.33 | 26.57 | 28.20 | 30.37 | 32.44 | 34.84 | |
|---|---|---|---|---|---|---|---|---|---|
| Sttw/Stcw | ncw | 95.4 | 94.9 | 96.5 | 95.5 | 95.1 | 95.5 | 96.7 | 97.9 |
| Stvw/Stcw | 4.6 | 5.1 | 3.5 | 4.5 | 4.9 | 4.5 | 3.3 | 2.1 | |
| Sttw/Stcw | scw | 56.4 | 56.5 | 53.5 | 52.8 | 52.8 | 52.3 | 51.9 | 52.4 |
| Stvw/Stcw | 4.7 | 6.2 | 5.0 | 5.5 | 5.7 | 5.8 | 5.8 | 5.7 | |
| Stdw/Stcw | 38.9 | 37.3 | 41.5 | 41.7 | 41.5 | 41.9 | 42.3 | 41.9 | |
| Relations | Catalytic Wall | Original | Modified | Heat Transfer Mode | ||
|---|---|---|---|---|---|---|
| Qtw | Qvw | Qdw | ||||
| St = C·Ma0.5 Re−0.5 (Zhou et al. [36]) | scw | 1.740 | 2.000 | 1.140 | 0.131 | 0.730 |
| ncw | 1.740 | 1.219 | 1.166 | 0.055 | \ | |
| St = C·Ma0.65 Re−0.5 (Du et al. [37]). | scw | 1.085 | 1.237 | 0.702 | 0.081 | 0.455 |
| ncw | 1.085 | 0.761 | 0.730 | 0.033 | \ | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Zhao, W.; Dong, X.; Zhang, Z.; Wang, J.; Yang, X.; Zhang, S.; Hao, J.; Sun, K. Analysis of Aerodynamic Heating Modes in Thermochemical Nonequilibrium Flow for Hypersonic Reentry. Energies 2025, 18, 3417. https://doi.org/10.3390/en18133417
He S, Zhao W, Dong X, Zhang Z, Wang J, Yang X, Zhang S, Hao J, Sun K. Analysis of Aerodynamic Heating Modes in Thermochemical Nonequilibrium Flow for Hypersonic Reentry. Energies. 2025; 18(13):3417. https://doi.org/10.3390/en18133417
Chicago/Turabian StyleHe, Shuai, Wei Zhao, Xinyue Dong, Zhuzhu Zhang, Jingying Wang, Xinglian Yang, Shiyue Zhang, Jiaao Hao, and Ke Sun. 2025. "Analysis of Aerodynamic Heating Modes in Thermochemical Nonequilibrium Flow for Hypersonic Reentry" Energies 18, no. 13: 3417. https://doi.org/10.3390/en18133417
APA StyleHe, S., Zhao, W., Dong, X., Zhang, Z., Wang, J., Yang, X., Zhang, S., Hao, J., & Sun, K. (2025). Analysis of Aerodynamic Heating Modes in Thermochemical Nonequilibrium Flow for Hypersonic Reentry. Energies, 18(13), 3417. https://doi.org/10.3390/en18133417








