Practices and Considerations in Wind Data Processing for Accurate and Efficient Wind Farm Energy Calculation
Abstract
1. Introduction
- Section 2 analyses the traditional method for the estimation of the Weibull parameters and proposes a new procedure to derive them.
- Section 3 explores the effect of wind speed binning on AEP calculation, concluding that the traditional speed binning of 1 m/s is not always the best choice for accuracy nor speed.
- Section 4 demonstrates that is possible to halve the number of calculations for symmetrical wind farm layouts for any layout type (with minimal error).
- Section 5 shows that the traditional preprocessing of wind conditions into 12 sectors leads to inconsistent results and proposes a sectorization with a higher number of sectors. If historical data are not available, wind data should be interpolated to increase the number of sectors.
- Section 6 presents an alternative visualization of wind resource potential, using a one-dimensional plot to illustrate the expected energy output from each direction.
Input Data
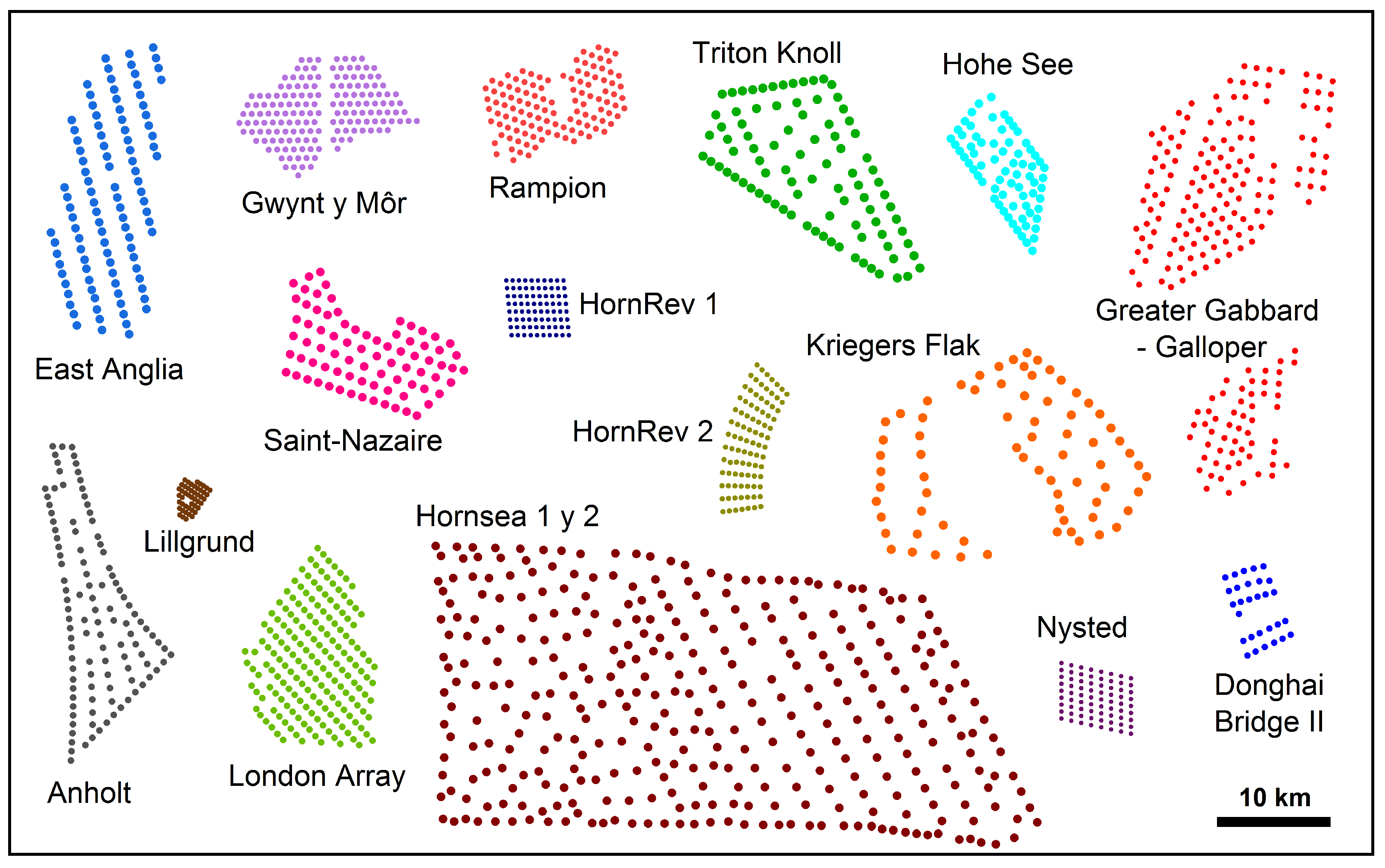
- General characteristics of the wind farms. Found in the Excel fileOffshore Wind Farms.xlsx, which includes data from 28 offshore wind farms.
- Concession areas. Contained in the file concession_area.m.
- Turbine positions at each wind farm. Contained in the file position_turbines.m.
- Turbine curves. Curves for power and Power factor (Cp), and when available, also for Ct, found in DataTurbines.m.
2. Deducing the Optimal Weibull Parameters from Time Series Data
2.1. Introduction and State of the Art
2.2. Method
- Histograms based on historical data: This method starts with a database containing measurements of wind direction and speed taken every ten minutes, following the IEC 61400-12-2:2022 standard [13]. During data processing, the measurements are grouped into bins for both wind speed and wind direction. Regarding wind speed, the wind speed bins typically have a size = 0.5 m/s as indicated by the IEC 61400-12-1:2022 standard, or 1 m/s as is common in research studies [14]. For the wind direction, greater representativeness of the wind conditions is achieved by grouping every 1 deg, although the IEC 61400-12-3:2022 standard specifies a bin size = 10 deg. At the final stage of the data processing, a matrix is filled with the frequency of occurrence for each wind direction and speed interval, with and defined in (4) and (5), respectively.This method is appropriate when historical data is available. However, most existing research studies do not have access to such detailed data for the site under study.
- Wind condition sectorization and Weibull distribution fitting by sector: this method starts by dividing the polar map into ns sectors, typically 12. Then, a two-parameter Weibull distribution is fitted to best represent the frequency of occurrence of each wind speed within each sector. This method results, on one hand, in a wind rose with ns sectors showing the frequency of wind occurrence per sector, and on the other hand, it provides the A and k values of the Weibull distribution fitted for each sector. This description of historical data is very manageable and is preferred by researchers, despite being less representative of reality.By defining the probability that the wind comes from sector s, given by the Windbull distribution () and the probability that the wind comes from sector s, given by the wind rose () asthe expression for the estimated average power yieldswhere is the ceiling of · and allows for the deduction of the sector s to which the wind direction belongs.
2.3. Results
2.4. Conclusions
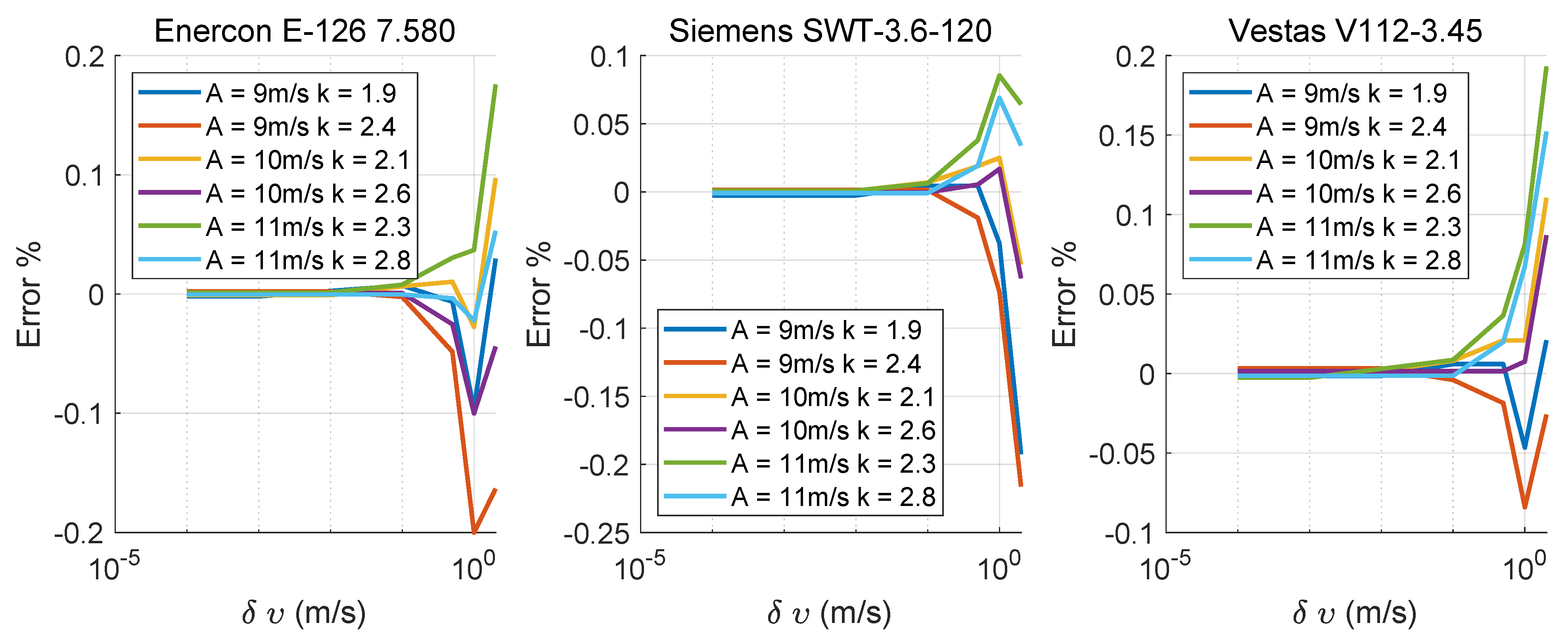
3. Effect of Wind Speed Binning on AEP Calculation
3.1. Introduction and State of the Art
3.2. Method
3.3. Results
3.4. Conclusion and Discussion
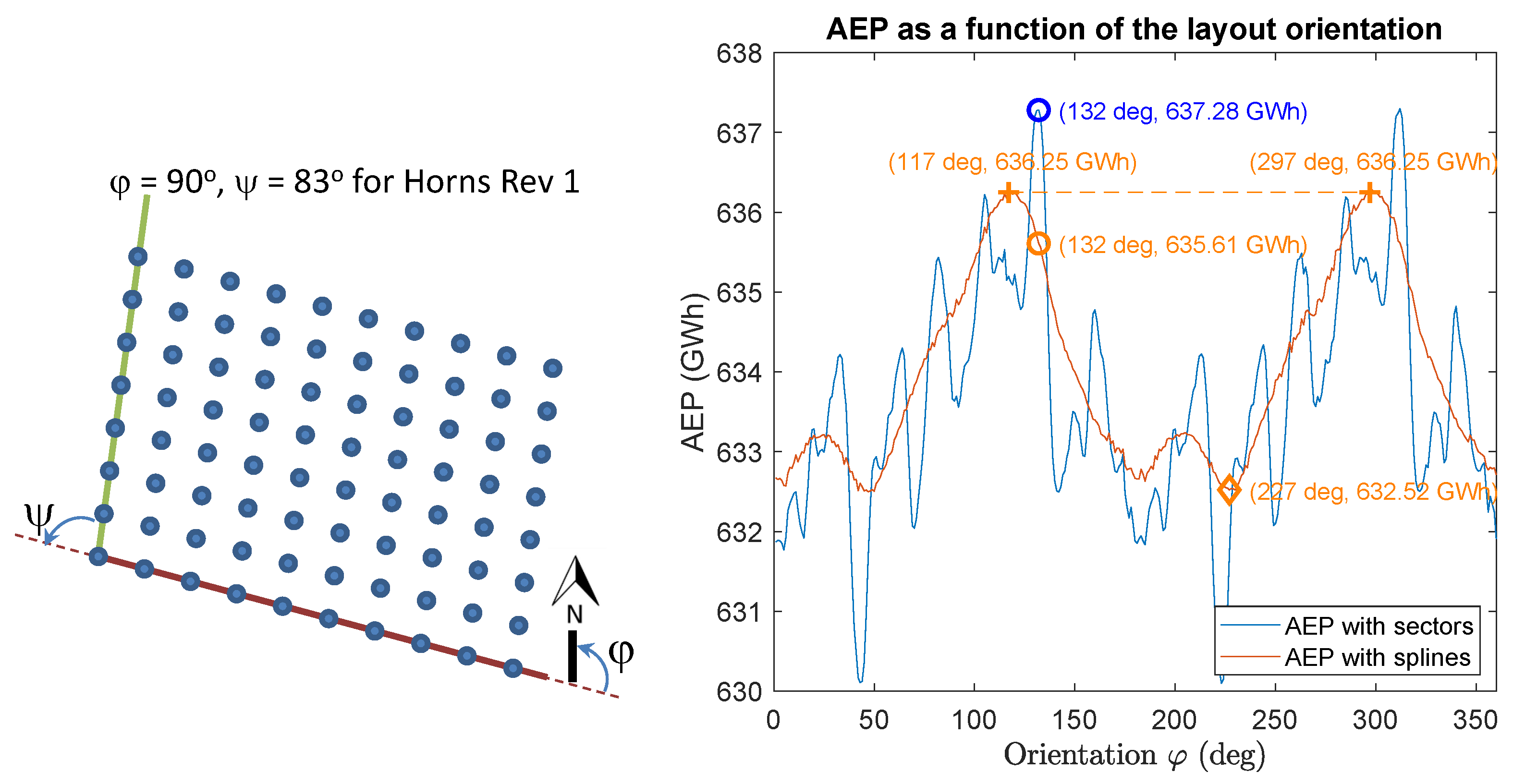
4. Exploiting Symmetrical Layouts to Accelerate the AEP Evaluation
4.1. Introduction and State of the Art
4.2. Method
4.3. Results
4.4. Conclusions
5. Effect of the Number of Wind Rose Sectors on AEP Calculation
5.1. Introduction and State of the Art
5.2. Method
5.3. Result
5.4. Conclusion and Discussion
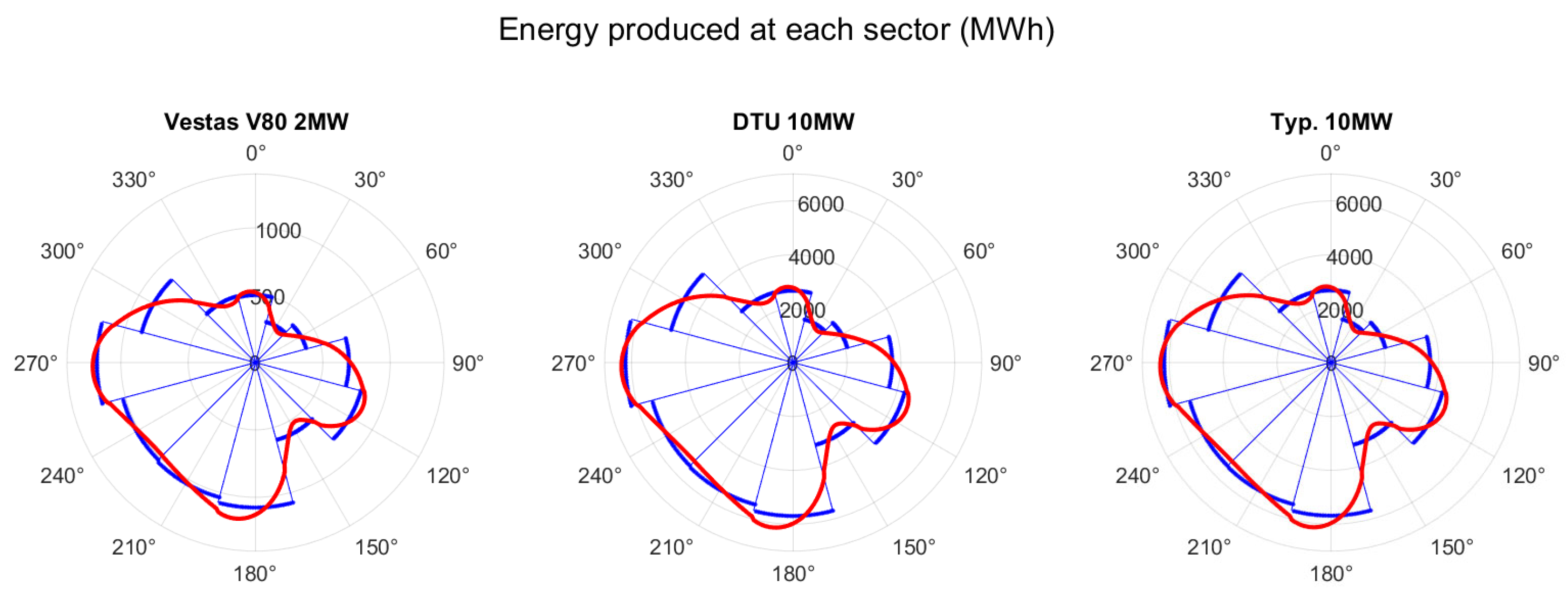
6. The Energy Rose: A Novel Representation of Wind Resource Potential
6.1. Introduction
6.2. Method
6.3. Results
6.4. Conclusions
7. Discussion
8. Conclusions
- The parameters of the Weibull distribution, which are typically derived using purely statistical tools to represent the actual frequency of wind speeds, often lead to significant errors in the estimation of AEP, usually underestimating it. This study proposes using a typical power curve (such as that of the DTU 10 MW reference turbine) to determine the Weibull parameters that best fit the power output derived from historical data.
- Most studies that conduct a thorough evaluation of AEP across the full wind speed range between uci and uco use a discretization of 1 m/s. This work proposes either using Equation (17) or assessing the error introduced by discretizations of 0.5 m/s and 2 m/s, with the goal of improving accuracy or reducing the CT.
- Many studies confuse the terms direction bin (related to the discretization used in AEP evaluation) and sector (related to the classification of wind data from historical records). While it is intuitive that a coarser direction binning (larger ) will introduce greater errors, a coarser sectorization (larger ) can also result not only in errors, but in an unrealistic representation of the wind farm’s behavior depending on the relative orientation of its turbines.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AEP | Annual Energy Production |
| OWF | Offshore wind farm |
| WF | wind farm |
| HR1 | Horns Rev 1 |
| nt | number of turbines |
| ns | number of sectors |
| uci | cut-in speed |
| uco | cut-out speed |
| density of probability at wind direction and wind speed v | |
| Pc | electric power given by the turbine manufacturer’s power curve |
| Cp | Power factor |
| CT | computational time |
| wind direction, in deg | |
| u | free stream wind speed in m/s |
| wind speed in m/s at turbine t taking into account wake effect | |
| probability that the wind comes from sector s, given by the wind rose | |
| probability that the wind comes from sector s, given by the Windbull distribution | |
| A | scale factor of the Weibull distribution |
| k | shape factor of the Weibull distribution |
| wind speed bin size in m/s | |
| wind direction bin size in deg | |
| sector size |
References
- Gonzalez-Rodriguez, A.; Serrano-González, J.; Burgos-Payán, M.; Riquelme-Santos, J. Realistic optimization of parallelogram-shaped offshore wind farms considering continuously distributed wind resources. Energies 2021, 14, 2895. [Google Scholar] [CrossRef]
- Herbert-Acero, J.F.; Probst, O.; Réthoré, P.E.; Larsen, G.C.; Castillo-Villar, K.K. A review of methodological approaches for the design and optimization of wind farms. Energies 2014, 7, 6930–7016. [Google Scholar] [CrossRef]
- Shakoor, R.; Hassan, M.Y.; Raheem, A.; Wu, Y.K. Wake effect modeling: A review of wind farm layout optimization using Jensen’s model. Renew. Sustain. Energy Rev. 2016, 58, 1048–1059. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, A.G.; Burgos-Payan, M.; Riquelme-Santos, J.; Serrano-González, J. Reducing computational effort in the calculation of annual energy produced in wind farms. Renew. Sustain. Energy Rev. 2015, 43, 656–665. [Google Scholar] [CrossRef]
- González Rodríguez, A.G. Projects in Matlab and C# Regarding the Wind Rose for the Evaluation of AEP. 2025. Available online: https://zenodo.org/records/15470904?preview=1 (accessed on 18 June 2025).
- International Standard IEC 61400-12-3:2022; Wind Energy Generation Systems—Part 12-3: Power Performance—Measurement Based Site Calibration. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- Serban, A.; Paraschiv, L.S.; Paraschiv, S. Assessment of wind energy potential based on Weibull and Rayleigh distribution models. Energy Rep. 2020, 6, 250–267. [Google Scholar] [CrossRef]
- Singh, K.; Bule, L.; Khan, M.G.; Ahmed, M.R. Wind energy resource assessment for Vanuatu with accurate estimation of Weibull parameters. Energy Explor. Exploit. 2019, 37, 1804–1832. [Google Scholar] [CrossRef]
- Chaurasiya, P.K.; Ahmed, S.; Warudkar, V. Comparative analysis of Weibull parameters for wind data measured from met-mast and remote sensing techniques. Renew. Energy 2018, 115, 1153–1165. [Google Scholar] [CrossRef]
- El-Bshah, A.; Al-Wesabi, F.N.; Al-Kustoban, A.M.; Alamgeer, M.; Nemri, N.; Eltahir, M.M.; Mahgoub, H.; Negm, N. Resource assessment of wind energy potential of Mokha in Yemen with weibull speed. Comput. Mater. Contin. 2021, 69, 1123–1140. [Google Scholar] [CrossRef]
- Raichle, B.W.; Carson, W.R. Wind resource assessment of the Southern Appalachian Ridges in the Southeastern United States. Renew. Sustain. Energy Rev. 2009, 13, 1104–1110. [Google Scholar] [CrossRef]
- Abbas, G.; Ali, A.; Othman, M.T.B.; Nawaz, M.W.; Rehman, A.U.; Hamam, H. A novel energy pattern factor-based optimized approach for assessing Weibull parameters for wind power applications. Sci. Rep. 2025, 15, 37. [Google Scholar] [CrossRef]
- International Standard IEC 61400-12-2:2022; Wind Energy Generation Systems—Part 12–2: Power performance of electricity producing wind turbines based on nacelle anemometry. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- Wais, P. A review of Weibull functions in wind sector. Renew. Sustain. Energy Rev. 2017, 70, 1099–1107. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, A.G.; Roldan-Fernandez, J.M.; Serrano-Gonzalez, J.; Muñoz-Díez, J.V. Gradient Descent Algorithm with Greedy Repositioning Using Power Deficit Aggregation of Wakes to Accelerate the Offshore Wind Farm Layout Optimization Problem in Irregular Concession Areas. Appl. Sci. 2024, 14, 11331. [Google Scholar] [CrossRef]
- Troen, I.; Petersen, E.L. European Wind Atlas; Risø National Laboratory: Roskilde, Denmark, 1989. [Google Scholar]
- International Standard IEC 61400-12-6:2022; Wind Energy Generation Systems—Part 12–6: Measurement Based Nacelle Transfer Function of Electricity Producing Wind Turbines. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- International Standard IEC 61400-12-1:2022; Wind Energy Generation Systems—Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- Feng, J.; Shen, W.Z. Solving the wind farm layout optimization problem using random search algorithm. Renew. Energy 2015, 78, 182–192. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, A.G.; Serrano-Gonzalez, J.; Burgos-Payan, M.; Riquelme-Santos, J. Multi-objective optimization of a uniformly distributed offshore wind farm considering both economic factors and visual impact. Sustain. Energy Technol. Assess. 2022, 52, 102148. [Google Scholar] [CrossRef]
- Ghaisas, N.S.; Archer, C.L. Geometry-based models for studying the effects of wind farm layout. J. Atmos. Ocean. Technol. 2016, 33, 481–501. [Google Scholar] [CrossRef]
- Al-Yahyai, S.; Charabi, Y.; Gastli, A. Geometrical Approach for Wind Farm Symmetrical Layout Design Optimization. In Proceedings of the 2015 IEEE 8th GCC Conference & Exhibition, Muscat, Oman, 1–4 February 2015. [Google Scholar]
- Neubert, A.; Shah, A.; Schlez, W. Maximum Yield From Symmetrical Wind Farm Layouts. In Proceedings of the 10th Wind Energy Conference-DEWEK, Bremen, Germany, 17–18 November 2010; Volume 98, pp. 1–4. [Google Scholar]
- Turner, S.D.; Romero, D.A.; Zhang, P.Y.; Amon, C.H.; Chan, T.C. A new mathematical programming approach to optimize wind farm layouts. Renew. Energy 2014, 63, 674–680. [Google Scholar] [CrossRef]
- van der Laan, M.P.; Andersen, S.J.; Réthoré, P.E.; Baungaard, M.; Sørensen, J.N.; Troldborg, N. Faster wind farm AEP calculations with CFD using a generalized wind turbine model. J. Phys. Conf. Ser. 2022, 2265, 022030. [Google Scholar] [CrossRef]
- Jaganath, M.M.; Ray, S.; Choudhury, N.B. Optimal placement of wind turbines: A techno-economic analysis using real-time wind speed data and metaheuristic algorithms. Int. J. Energy Water Resour. 2025. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z. Modelling wind for wind farm layout optimization using joint distribution of wind speed and wind direction. Energies 2015, 8, 3075–3092. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z.; Xu, C. Multi-Objective Random Search Algorithm for Simultaneously Optimizing Wind Farm Layout and Number of Turbines. J. Phys. Conf. Ser. 2016, 753, 032011. [Google Scholar] [CrossRef]
- Hou, P.; Enevoldsen, P.; Hu, W.; Chen, C.; Chen, Z. Offshore wind farm repowering optimization. Appl. Energy 2017, 208, 834–844. [Google Scholar] [CrossRef]
- Kirchner-Bossi, N.; Porté-Agel, F. Wind farm area shape optimization using newly developed multi-objective evolutionary algorithms. Energies 2021, 14, 4185. [Google Scholar] [CrossRef]
- Diaz, G.P.N.; Saulo, A.C.; Otero, A.D. Full wind rose wind farm simulation including wake and terrain effects for energy yield assessment. Energy 2021, 237, 121642. [Google Scholar] [CrossRef]
- Deng, X.; Xu, W.; Xu, Y.; Shao, Y.; Wu, X.; Yuan, W.; Qin, Z. Offshore wind power in China: A potential solution to electricity transformation and carbon neutrality. Fundam. Res. 2024, 4, 1206–1215. [Google Scholar] [CrossRef]
- Greenberg, D.; Byalsky, M.; Yahalom, A. Valuation of Wind Energy Turbines Using Volatility of Wind and Price. Electronics 2021, 10, 1098. [Google Scholar] [CrossRef]
- Alonzo, B.; Concettini, S.; Creti, A.; Drobinski, P.; Tankov, P. Profitability and Revenue Uncertainty of Wind Farms in Western Europe in Present and Future Climate. Energies 2022, 15, 6446. [Google Scholar] [CrossRef]
- Khan, M.A.; Iqbal, M.T. Evaluation of Wind Resources and the Effect of Market Price Components on Wind-Farm Income: A Case Study of Ørland in Norway. Energies 2018, 11, 2955. [Google Scholar] [CrossRef]


| v (m/s) | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 | 11.0 | 12.0 | 13.0 | 14.0 |
| P (kW) | 0 | 0 | 20 | 341 | 847 | 1595 | 2608 | 3928 | 5584 | 7437 | 9002 | 9718 |
| v (m/s) | 15.0 | 16.0 | 17.0 | 18.0 | 19.0 | 20.0 | 21.0 | 22.0 | 23.0 | 24.0 | 25.0 | |
| P (kW) | 9927 | 9983 | 9994 | 9995 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 |
| Sector | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7.96 | 7.50 | 7.80 | 7.56 | 8.49 | 8.65 | 9.07 | 10.02 | 9.89 | 10.05 | 9.01 | 7.58 | |
| 2.00 | 1.94 | 1.92 | 2.08 | 2.17 | 2.21 | 2.23 | 2.33 | 2.40 | 2.53 | 2.30 | 2.243 | |
| 7.50 | 7.60 | 7.80 | 7.70 | 8.60 | 8.70 | 9.80 | 10.70 | 9.80 | 10.50 | 8.90 | 7.50 | |
| 1.52 | 2.14 | 1.74 | 1.60 | 1.72 | 2.62 | 1.54 | 1.90 | 2.66 | 2.02 | 3.00 | 1.60 |
| Sector | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Turbine | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | RMS |
| Siemens Gamesa SG 3.6-120 MLE | −4.7 | 0.6 | 0.2 | 4.1 | 0.3 | 2.8 | 2.7 | 5.1 | 1.9 | 1.5 | 0.7 | 1.2 | 2.73 |
| Siemens Gamesa SG 3.6-120 sweep | 0.7 | −0.3 | 0.1 | 1.0 | 0.8 | −0.7 | 2.0 | 1.7 | 0.0 | 3.6 | −1.4 | 1.0 | 1.46 |
| Vestas V112/3450 MLE | −4.6 | 0.6 | 0.2 | 4.1 | 0.4 | 2.6 | 2.8 | 5.1 | 1.3 | 0.9 | 0.5 | 1.2 | 2.63 |
| Vestas V112/3450 sweep | 0.2 | −0.0 | 0.0 | 0.7 | 0.3 | −0.3 | 1.1 | 1.1 | −0.1 | 1.9 | −0.6 | 0.4 | 0.77 |
| Vestas V164-8.0 MLE | −10.4 | 1.6 | 0.9 | 8.5 | 1.9 | 5.7 | 6.9 | 11.4 | 0.4 | −0.5 | −0.1 | 2.2 | 5.80 |
| Vestas V164-8.0 sweep | −1.2 | 0.6 | −0.2 | −1.4 | −1.3 | 1.4 | −2.5 | −2.4 | −0.5 | −5.3 | 2.2 | −2.0 | 2.17 |
| DTU Reference 10 MW MLE | −13.7 | 2.4 | 0.6 | 12.4 | 1.5 | 6.8 | 9.3 | 15.4 | 1.0 | 0.4 | 0.7 | 3.4 | 7.81 |
| DTU Reference 10 MW sweep | −1.1 | 0.8 | −0.5 | 0.9 | −0.9 | 0.1 | 0.8 | 1.0 | −1.5 | −1.0 | 1.1 | −0.7 | 0.93 |
| Offshore Wind Farm | AEP (GWh) from (3) | AEP (GWh) from (22) | Deviation |
|---|---|---|---|
| Anholt | 1716.1370 | 1715.9920 | 0.0085% |
| Donghai Bridge II | 283.5456 | 283.5461 | 0.0002% |
| East Anglia | 3049.1824 | 3049.2454 | 0.0021% |
| Galloper | 966.5156 | 966.5302 | 0.0015% |
| Greater Gabbard | 1353.6965 | 1353.6401 | 0.0042% |
| Gwynt y Mor | 796.8648 | 796.8561 | 0.0011% |
| Hohe See | 2249.6075 | 2249.5682 | 0.0017% |
| Horns Rev1 | 633.7517 | 633.7517 | 0.0000% |
| Horns Rev2 | 1071.8195 | 1071.8195 | 0.0000% |
| Hornsea 1 | 5333.8664 | 5333.7726 | 0.0018% |
| Hornsea 2 | 5617.5984 | 5617.6035 | 0.0001% |
| Kriegers Flak | 740.6054 | 740.5905 | 0.0020% |
| Lillgrund | 207.7917 | 207.7773 | 0.0069% |
| London Array | 1972.7769 | 1972.7809 | 0.0002% |
| Nysted | 442.8121 | 442.8121 | 0.0000% |
| Rampion | 1175.3450 | 1175.3566 | 0.0010% |
| Saint Nazaire | 1320.0645 | 1320.0501 | 0.0011% |
| Triton Knoll | 2844.1055 | 2843.9149 | 0.0067% |
| Sector | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (%) | 7.42 | 4.07 | 5.13 | 7.82 | 8.33 | 6.32 | 10.90 | 10.23 | 12.12 | 10.03 | 11.70 | 5.93 |
| A | 8.71 | 9.36 | 9.29 | 10.27 | 10.89 | 10.49 | 10.94 | 11.23 | 9.93 | 11.94 | 9.17 | 10.31 |
| K | 2.08 | 2.22 | 2.41 | 2.37 | 2.51 | 2.75 | 2.61 | 2.51 | 2.33 | 3.35 | 2.58 | 2.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Rodriguez, A.G.; Riega-Medina, J.M.; Ruano-Ruano, I.; Muñoz-Diez, J.V. Practices and Considerations in Wind Data Processing for Accurate and Efficient Wind Farm Energy Calculation. Energies 2025, 18, 3402. https://doi.org/10.3390/en18133402
Gonzalez-Rodriguez AG, Riega-Medina JM, Ruano-Ruano I, Muñoz-Diez JV. Practices and Considerations in Wind Data Processing for Accurate and Efficient Wind Farm Energy Calculation. Energies. 2025; 18(13):3402. https://doi.org/10.3390/en18133402
Chicago/Turabian StyleGonzalez-Rodriguez, Angel Gaspar, Jose Manuel Riega-Medina, Ildefonso Ruano-Ruano, and Jose Vicente Muñoz-Diez. 2025. "Practices and Considerations in Wind Data Processing for Accurate and Efficient Wind Farm Energy Calculation" Energies 18, no. 13: 3402. https://doi.org/10.3390/en18133402
APA StyleGonzalez-Rodriguez, A. G., Riega-Medina, J. M., Ruano-Ruano, I., & Muñoz-Diez, J. V. (2025). Practices and Considerations in Wind Data Processing for Accurate and Efficient Wind Farm Energy Calculation. Energies, 18(13), 3402. https://doi.org/10.3390/en18133402








