Achieving Power-Noise Balance in Wind Farms by Fine-Tuning the Layout with Reinforcement Learning
Abstract
1. Introduction
2. Wind Farm Power and Noise
2.1. Power Production Calculation
2.2. Noise Evaluation Model
3. Wind Farm Layout Optimization
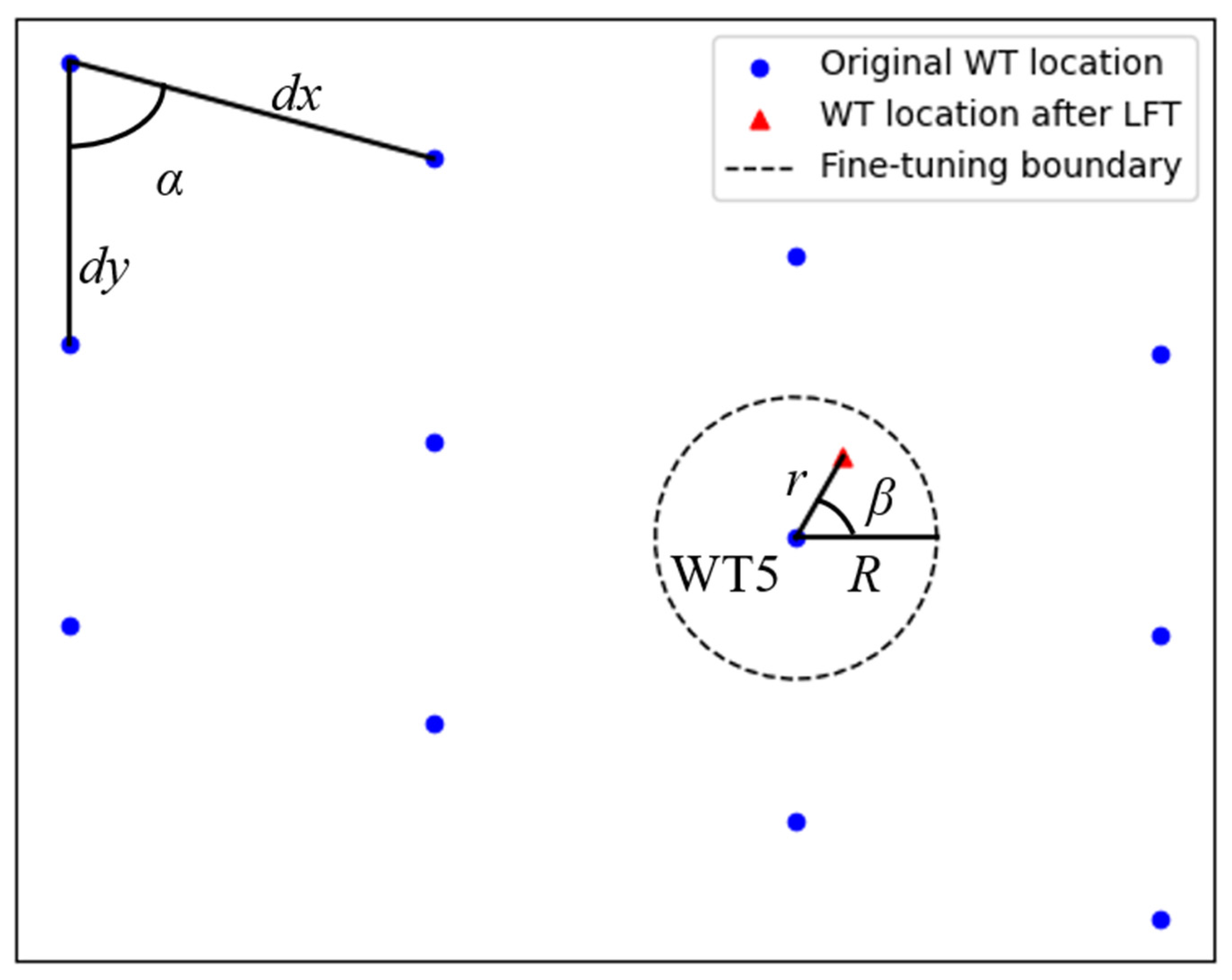
3.1. Wind Turbine Location Fine-Tuning
3.2. Problem Formula
4. RL-Based WFLO Model
4.1. Deep Q Learning Algorithm
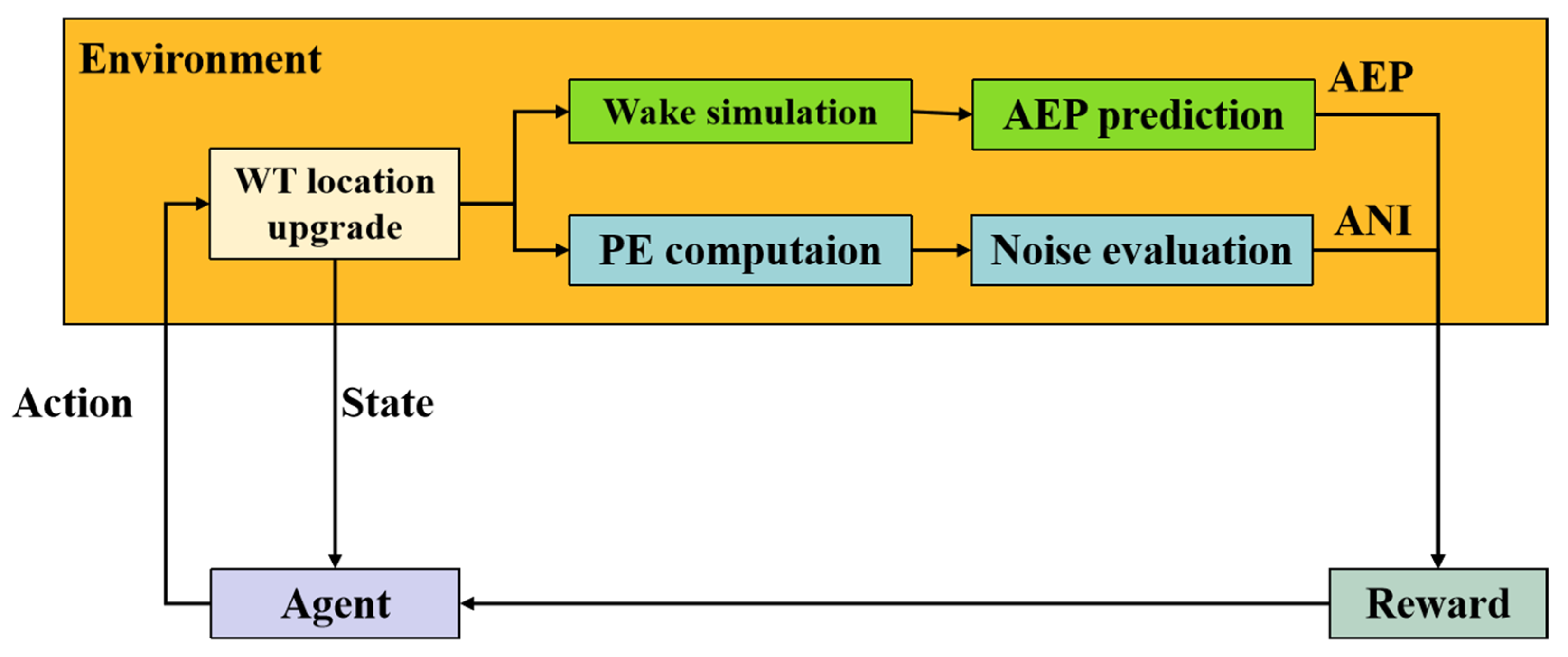
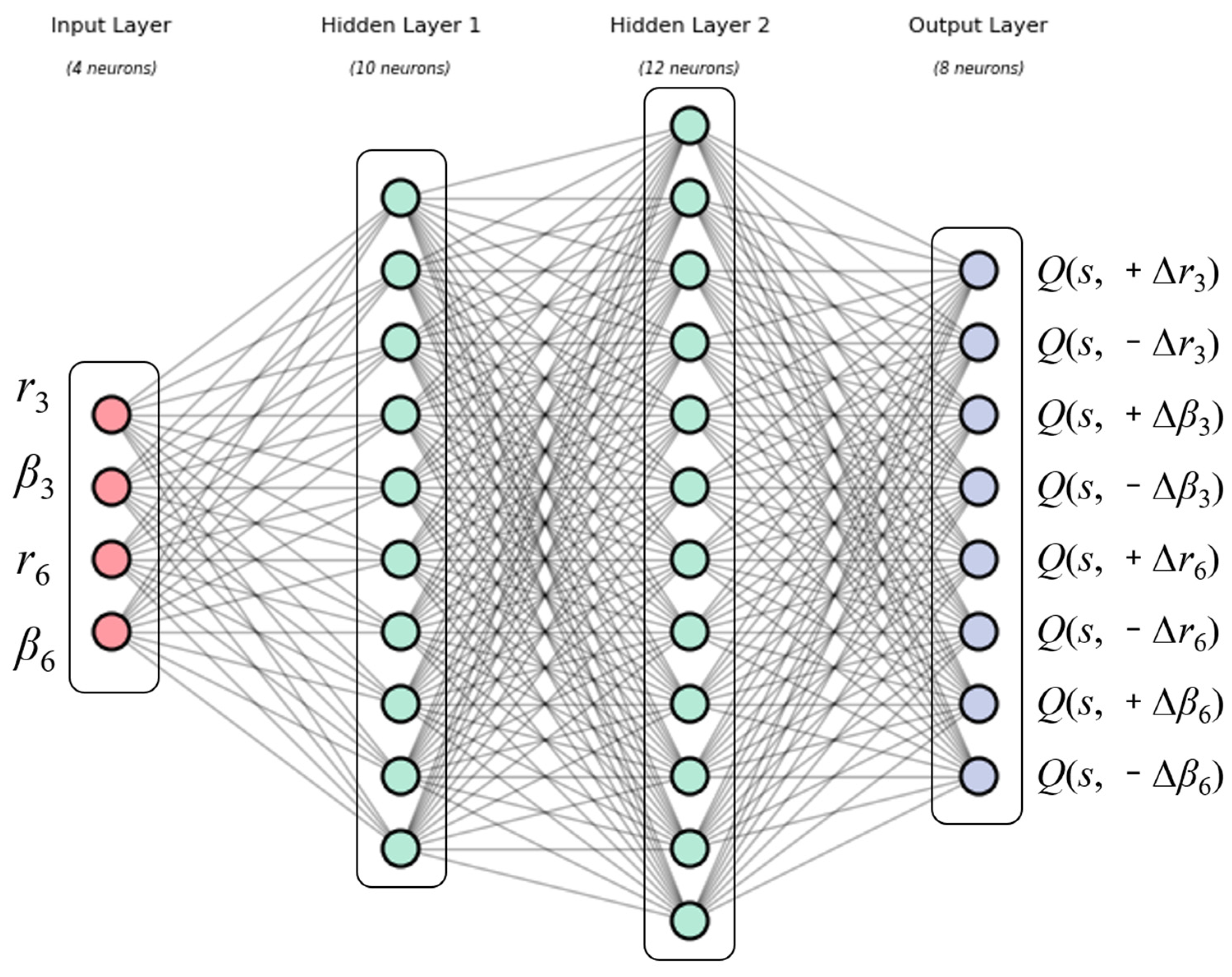
4.2. DQN-Based WFLO Framework
- State: The state s means the current location (rj, βj) (j = 1, 2, …, k) of k WTs under fine-tuning. The state is upgraded by a new action. To improve efficiency, the continuous region is discretized, the step intervals Δr and Δβ are set to 0.2D and 10°, respectively. These values were determined through empirical tests and calibrated against neighboring resolutions (Δr: 0.1D, 0.3D and 0.4D, Δβ: 5° and 15°). These resolution values were chosen based on an initial parameter sensitivity analysis. The guiding principle was to balance computational efficiency and result accuracy. The state is the WT location at the current step.
- Action: The action space encompasses the total available fine-tuning region, with each point being a potential WT location. For the fine-tuning region of k turbines, the action a = (±Δrj, ±Δβj) controls the movement of the turbines. The predefined fine-tuning circle sets the maximum displacement limit. The parameterization is defined by 8 variables (a radius step ±Δr and an angle step ±Δβ for two turbines).
- Reward: The value of GPN of a given wind farm layout represents the reward. Based on the current state and the original layout, the entire wind farm layout (xi, yi) (i = 1, 2, …, N) is created. Wake simulations and PE computations are then conducted to obtain total AEP generation and the noise influence area. Finally, rewards are calculated by combining the AEP improvement and noise area reduction.
5. Simulation Study
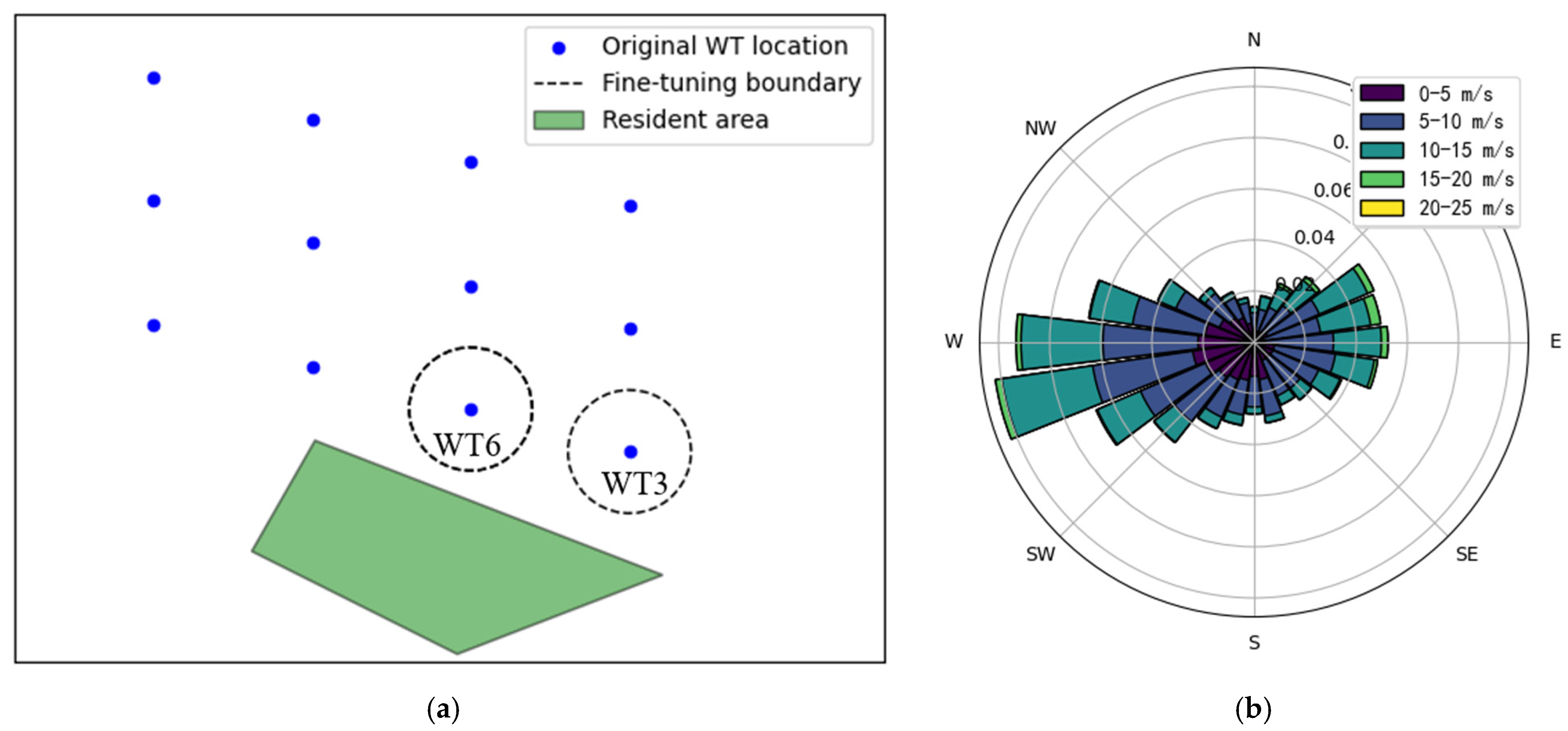
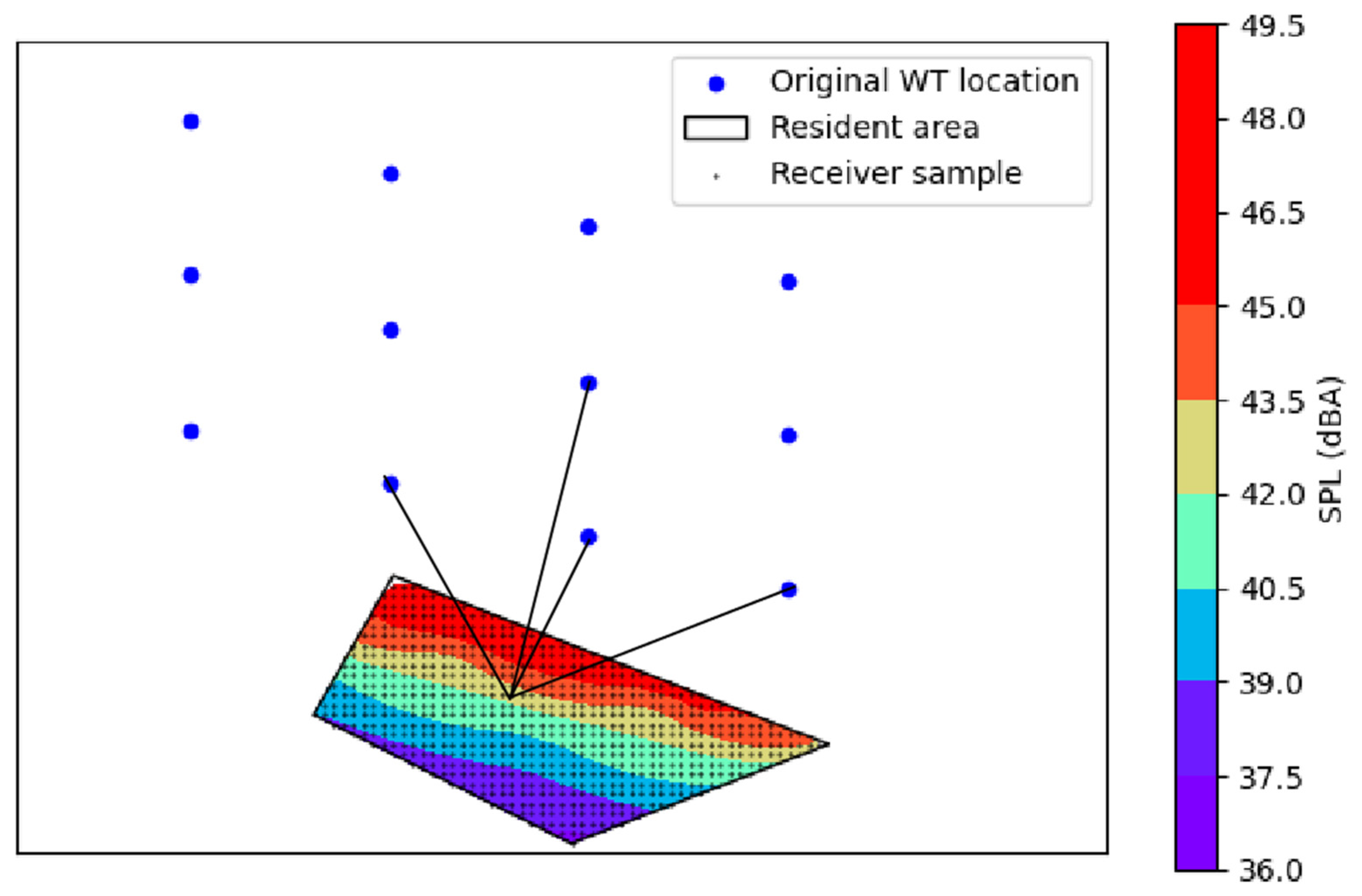
5.1. Wind Farm Description
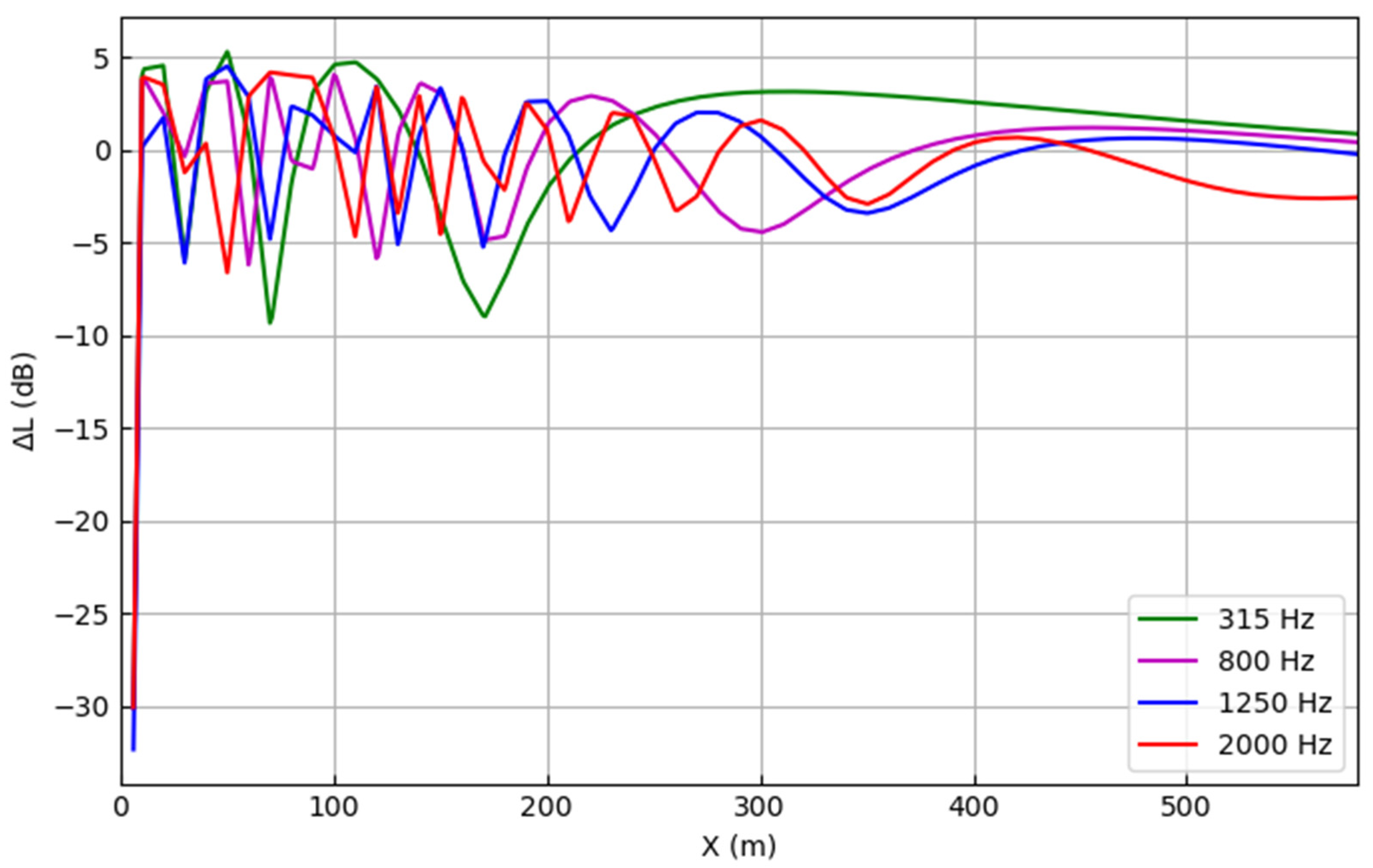
5.2. Noise Propagation Simulation
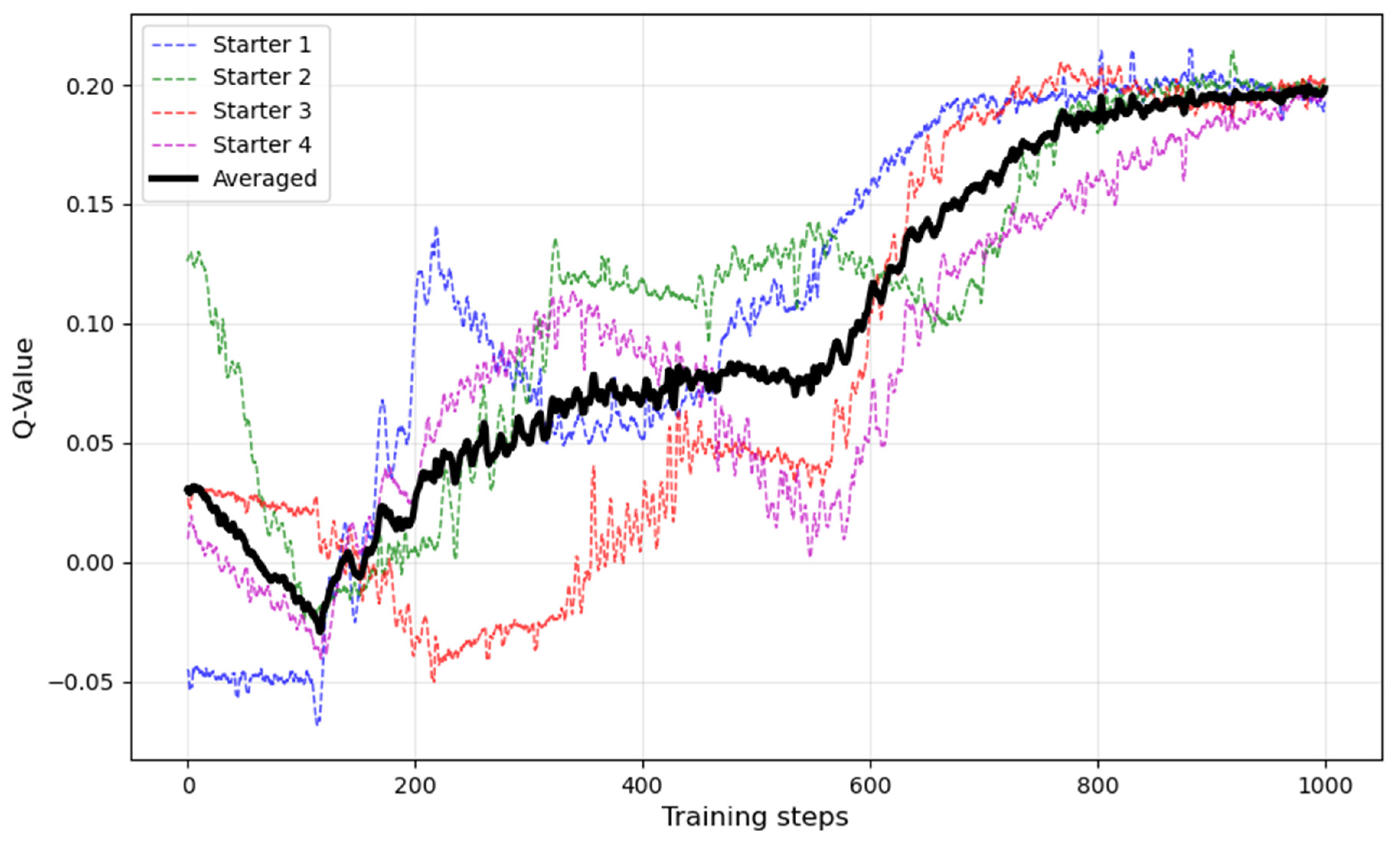
5.3. Building the DQN Agent
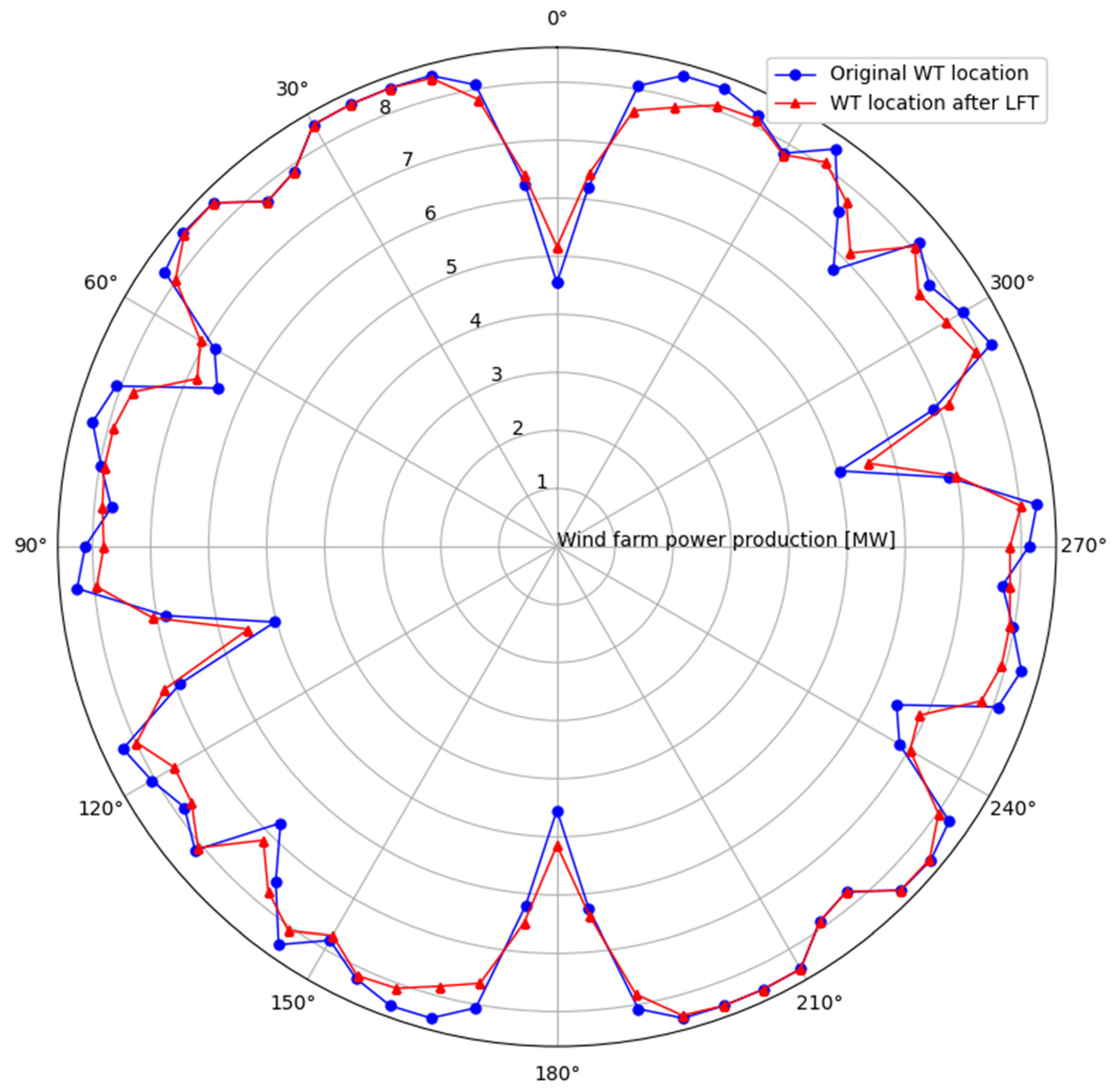
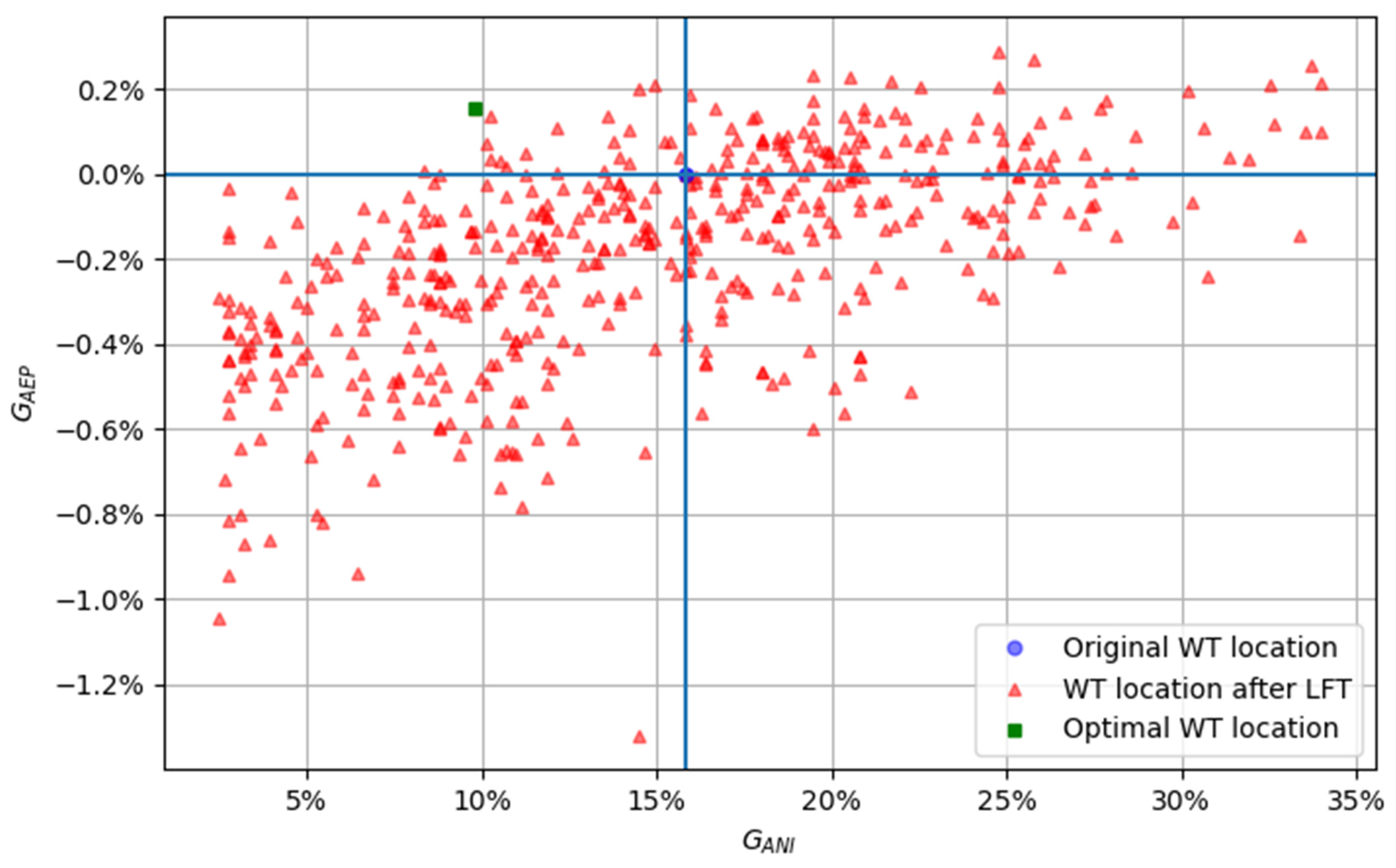
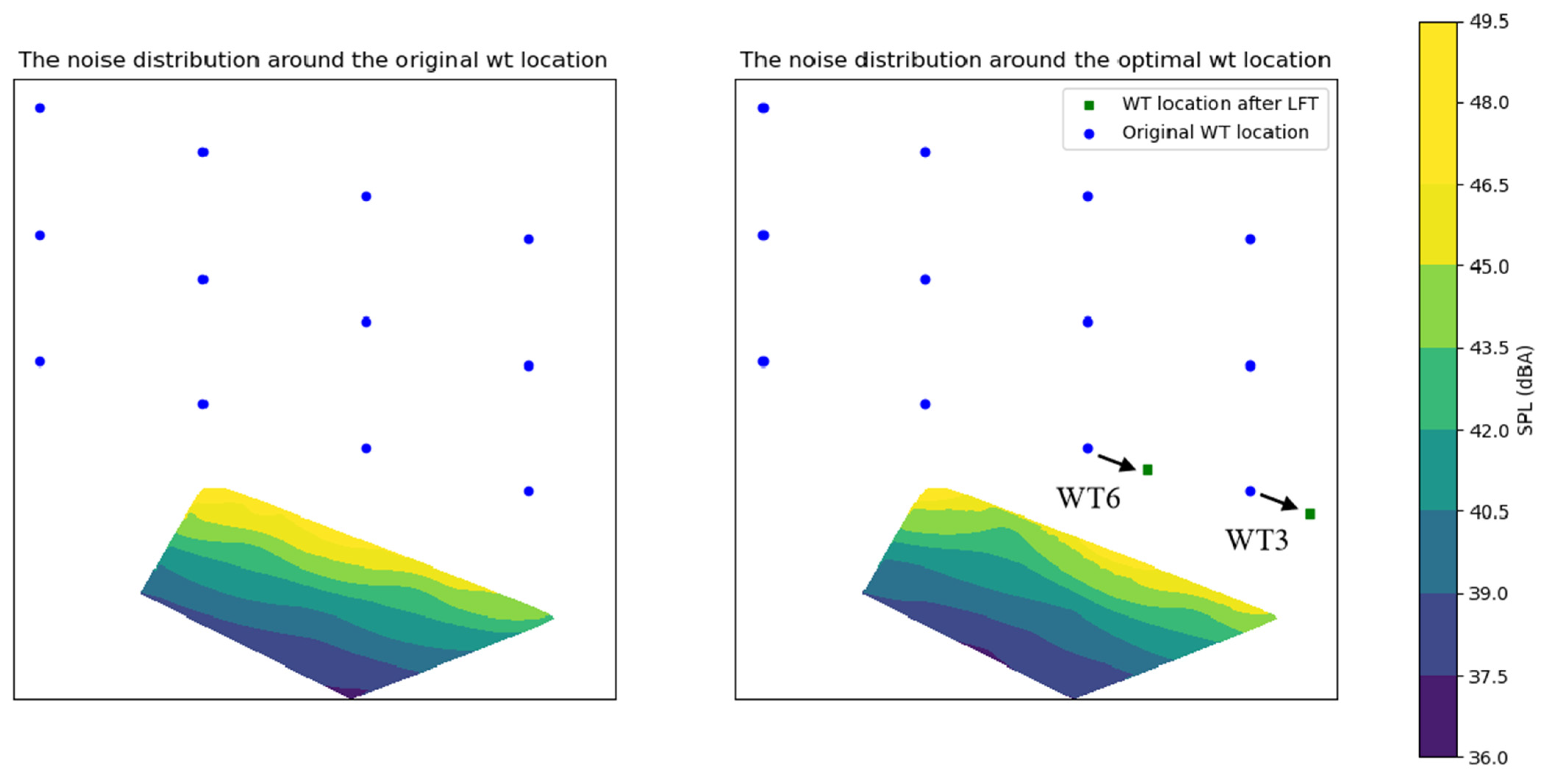
5.4. Optimization Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wisniewski, R.; Soleimanzadeh, M. An Optimization Framework for Load and Power Distribution in Wind Farms: Low Wind Speed. IFAC Proc. Vol. 2011, 44, 5561–5566. [Google Scholar] [CrossRef]
- Könecke, S.; Hörmeyer, J.; Bohne, T.; Rolfes, R. A New Base of Wind Turbine Noise Measurement Data and Its Application for a Systematic Validation of Sound Propagation Models. Wind. Energy Sci. Discuss. 2022, 8, 639–659. [Google Scholar] [CrossRef]
- Nyborg, C.M.; Fischer, A.; Thysell, E.; Feng, J.; Søndergaard, L.S.; Sørensen, T.; Hansen, T.R.; Hansen, K.S.; Bertagnolio, F. Propagation of Wind Turbine Noise: Measurements and Model Evaluation. J. Phys. Conf. Ser. 2022, 2265, 032041. [Google Scholar] [CrossRef]
- Josimović, B.; Bezbradica, L.; Manić, B.; Srnić, D.; Srebrić, N. Cumulative Impact of Wind Farm Noise. Appl. Sci. 2023, 13, 8792. [Google Scholar] [CrossRef]
- van Kuik, G.A.M.; Peinke, J.; Nijssen, R.; Lekou, D.; Mann, J.; Sørensen, J.N.; Ferreira, C.; van Wingerden, J.W.; Schlipf, D.; Gebraad, P.; et al. Long-Term Research Challenges in Wind Energy—A Research Agenda by the European Academy of Wind Energy. Wind Energy Sci. 2016, 1, 1–39. [Google Scholar] [CrossRef]
- Veers, P.; Bottasso, C.; Manuel, L.; Naughton, J.; Pao, L.; Paquette, J.; Robertson, A.; Robinson, M.; Ananthan, S.; Barlas, A.; et al. Grand Challenges in the Design, Manufacture, and Operation of Future Wind Turbine Systems; Aerodynamics and hydrodynamics. Wind. Energy Sci. 2022, 8, 1071–1131. [Google Scholar] [CrossRef]
- Willis, D.J.; Niezrecki, C.; Kuchma, D.; Hines, E.; Arwade, S.R.; Barthelmie, R.J.; DiPaola, M.; Drane, P.J.; Hansen, C.J.; Inalpolat, M.; et al. Wind Energy Research: State-of-the-Art and Future Research Directions. Renew. Energy 2018, 125, 133–154. [Google Scholar] [CrossRef]
- Zagubień, A.; Wolniewicz, K.; Szwochertowski, J. Analysis of Wind Farm Productivity Taking Wake Loss into Account: Case Study. Energies 2024, 17, 5816. [Google Scholar] [CrossRef]
- Howland, M.F.; Quesada, J.B.; Martínez, J.J.P.; Larrañaga, F.P.; Yadav, N.; Chawla, J.S.; Sivaram, V.; Dabiri, J.O. Collective wind farm operation based on a. predictive model increases utility-scale energy production. Nat. Energy 2022, 7, 818–827. [Google Scholar] [CrossRef]
- Silva, J.G.; Ferrari, R.; Wingerden, J.W.V. Wind farm control for wake-loss compensation, thrust balancing and load-limiting of turbines. Renew. Energy 2023, 203, 421–433. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z. Co-Optimization of the Shape, Orientation and Layout of Offshore Wind Farms. J. Phys. Conf. Ser. 2020, 1618, 042023. [Google Scholar] [CrossRef]
- Hasager, C.B.; Vincent, P.; Badger, J.; Badger, M.; Di Bella, A.; Peña, A.; Husson, R.; Volker, P.J.H. Using Satellite SAR to Characterize the Wind Flow around Offshore Wind Farms. Energies 2015, 8, 5413–5439. [Google Scholar] [CrossRef]
- Sickler, M.; Ummels, B.; Zaaijer, M.; Schmehl, R.; Dykes, K. Offshore Wind Farm Optimisation: A Comparison of Performance between Regular and Irregular Wind Turbine Layouts. Wind Energy Sci. 2023, 8, 1225–1233. [Google Scholar] [CrossRef]
- Tao, S.; Xu, Q.; Andrés Feijóo Zheng, G.; Zhou, J. Nonuniform wind farm layout optimization: A state-of-the-art review. Energy 2020, 209, 118339. [Google Scholar] [CrossRef]
- Hou, P.; Zhu, J.; Ma, K.; Yang, G.; Hu, W.; Chen, Z. A review of offshore wind farm layout optimization and electrical system design methods. J. Mod. Power Syst. Clean. Energy 2019, 7, 975–986. [Google Scholar] [CrossRef]
- Nyborg, C.M.; Fischer, A.; Réthoré, P.-E.; Feng, J. Optimization of Wind Farm Operation with a Noise Constraint. Wind Energy Sci. Discuss. 2022, 8, 255–276. [Google Scholar] [CrossRef]
- Réthoré, P.-E.; Fuglsang, P.; Larsen, G.C.; Buhl, T.; Larsen, T.J.; Madsen, H.A. TOPFARM: Multi-fidelity Optimization of Wind Farms. Wind. Energy 2014, 17, 1797–1816. [Google Scholar] [CrossRef]
- Pedersen, M.M.; Forsting, A.M.; van der Laan, P.; Riva, R.; Roman, L.A.; Risco, J.C.; Friis-Møller, M.; Quick, J.; Schøler Christiansen, J.P.; Réthoré, P.E.; et al. PyWake 2.5.0: An Open-Source Wind Farm Simulation Tool. DTU Wind, Technical University of Denmark. 2023. Available online: https://gitlab.windenergy.dtu.dk/TOPFARM/PyWake (accessed on 11 January 2025).
- Wu, X.; Hu, W.; Huang, Q.; Chen, C.; Jacobson, M.Z.; Chen, Z. Optimizing the Layout of Onshore Wind Farms to Minimize Noise. Appl. Energy 2020, 267, 114896. [Google Scholar] [CrossRef]
- Wolniewicz, K.; Zagubień, A.; Wesołowski, M. Energy and Acoustic Environmental Effective Approach for a Wind Farm Location. Energies 2021, 14, 7290. [Google Scholar] [CrossRef]
- Mittal, P.; Mitra, K. Micrositing under practical constraints addressing the energy-noise-cost trade-off. Wind Energy 2020, 23, 1905–1918. [Google Scholar] [CrossRef]
- Thomas, J.J.; Baker, N.F.; Malisani, P.; Quaeghebeur, E.; Sanchez Perez-Moreno, S.; Jasa, J.; Bay, C.; Tilli, F.; Bieniek, D.; Robinson, N.; et al. A comparison of eight optimization methods applied to a wind farm layout optimization problem. Wind Energy Sci. 2023, 8, 865–891. [Google Scholar] [CrossRef]
- Risco, J.C.; Rodrigues, R.V.; Friis-Møller, M.; Quick, J.; Pedersen, M.M.; Réthoré, P.-E. Gradient-Based Wind Farm Layout Optimization with Inclusion and Exclusion Zones. Wind. Energy Sci. 2024, 9, 585–600. [Google Scholar] [CrossRef]
- Stanley, A.P.J.; Ning, A. Massive Simplification of the Wind Farm Layout Optimization Problem. Wind. Energy Sci. 2019, 4, 663–676. [Google Scholar] [CrossRef]
- Kumar, M.; Sharma, A.; Sharma, N.; Sharma, F.B.; Bhadu, M.; Al-Quraan, A. Wind farm layout optimization problem using nature-inspired algorithms. J. Electr. Comput. Eng. 2024, 2024, 9406519. [Google Scholar] [CrossRef]
- Yang, K.; Deng, X.; Ti, Z.; Yang, S.; Huang, S.; Wang, Y. A Data-Driven Layout Optimization Framework of Large-Scale Wind Farms Based on Machine Learning. Renew. Energy 2023, 218, 119240. [Google Scholar] [CrossRef]
- Luo, Z.; Luo, W.; Xie, J.; Xu, J.; Wang, L. A New Three-Dimensional Wake Model for the Real Wind Farm Layout Optimization. Energy Explor. Exploit. 2022, 40, 701–723. [Google Scholar] [CrossRef]
- Li, Y.A. Deep Reinforcement Learning on Wind Power Optimization. In Proceedings of the 2022 International Conference on Networks, Communications and Information Technology (CNCIT), Beijing, China, 17–19 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 45–51. [Google Scholar]
- Yu, X.; Lu, Y. Reinforcement Learning-Based Multi-Objective Differential Evolution for Wind Farm Layout Optimization. Energy 2023, 284, 129300. [Google Scholar] [CrossRef]
- Bai, F.; Ju, X.; Wang, S.; Zhou, W.; Liu, F. Wind Farm Layout Optimization Using Adaptive Evolutionary Algorithm with Monte Carlo Tree Search Reinforcement Learning. Energy Convers. Manag. 2022, 252, 115047. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, W. A Teaching-Learning-Based Optimization Algorithm with Reinforcement Learning to Address Wind Farm Layout Optimization Problem. Appl. Soft Comput. 2024, 151, 111135. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z. Modelling Wind for Wind Farm Layout Optimization Using Joint Distribution of Wind Speed and Wind Direction. Energies 2015, 8, 3075–3092. [Google Scholar] [CrossRef]
- Salomons, E.M. Computational Atmospheric Acoustics; Springer Science Business Media, B.V.: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Gilbert, K.E. A numerically stable formulation of the Green’s function parabolic equation: Subtracting the surface-wave pole. JASA Express Lett. 2014, 137, EL8–EL14. [Google Scholar] [CrossRef]
- Barlas, E.; Zhu, W.J.; Shen, W.Z.; Andersen, S.J. Wind turbine noise propagation modelling: An unsteady approach. The science of making torque from wind. J. Phys. Conf. Ser. 2016, 753, 022003. [Google Scholar] [CrossRef]
- Barlas, E.; Zhu, W.J.; Shen, W.Z.; Dag, K.; Moriarty, P. Investigation of amplitude modulation noise with a fully coupled wind turbine noise source and advanced propagation model. In Proceedings of the International Conferences of Wind Turbine Noise, Rotterdam, The Netherlands, 2–5 May 2017. [Google Scholar]
- Barlas, E.; Zhu, W.J.; Shen, W.Z.; Sørensen, J.N.; Kelly, M.; Andersen, S.J. Effect of wind turbine wake on atmospheric sound propagation. Appl. Acoust. 2017, 122, 51–61. [Google Scholar] [CrossRef]
- ISO 9613-2:1996; Acoustics—Attenuation of Sound during Propagation Outdoors Part 2: General Method of Calculation. International Organization for Standardization: Geneva, Switzerland, 1996.
- Yang, Y.; Gao, Y.; Ding, Z.; Wu, J.; Zhang, S.; Han, F.; Qiu, X.; Gao, S.; Wang, Y.-G. Advancements in Q-learning Meta-heuristic Optimization Algorithms: A Survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2024, 14, e1548. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- King, J.; Fleming, P.; King, R.; Martínez-Tossas, L.A.; Bay, C.J.; Mudafort, R.; Simley, E. Control-Oriented Model for Secondary Effects of Wake Steering. Wind Energy Sci. 2021, 6, 701–714. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, W.J.; Shen, W.Z.; Barlas, E.; Sørensen, J.N.; Cao, J.; Yang, H. Development of an Efficient Numerical Method for Wind Turbine Flow, Sound Generation, and Propagation under Multi-Wake Conditions. Appl. Sci. 2019, 9, 100. [Google Scholar] [CrossRef]
- Leloudas, G.; Zhu, W.J.; Sørensen, J.N.; Shen, W.Z.; Hjort, S. Prediction and Reduction of Noise from a 2.3 MW Wind Turbine. J. Phys. Conf. Ser. 2007, 75, 012083. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Replay buffer capacity N | 200 |
| Reward discount factor γ | 0.1 |
| The ε-greedy policy ε | 0.8 |
| Learning rate | 0.002 |
| Batch size | 64 |
| Number of training episodes | 500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, G.; Zhu, W.; Zhang, Z.; Shen, W.; Chen, Z. Achieving Power-Noise Balance in Wind Farms by Fine-Tuning the Layout with Reinforcement Learning. Energies 2025, 18, 5019. https://doi.org/10.3390/en18185019
Guo G, Zhu W, Zhang Z, Shen W, Chen Z. Achieving Power-Noise Balance in Wind Farms by Fine-Tuning the Layout with Reinforcement Learning. Energies. 2025; 18(18):5019. https://doi.org/10.3390/en18185019
Chicago/Turabian StyleGuo, Guangxing, Weijun Zhu, Ziliang Zhang, Wenzhong Shen, and Zhe Chen. 2025. "Achieving Power-Noise Balance in Wind Farms by Fine-Tuning the Layout with Reinforcement Learning" Energies 18, no. 18: 5019. https://doi.org/10.3390/en18185019
APA StyleGuo, G., Zhu, W., Zhang, Z., Shen, W., & Chen, Z. (2025). Achieving Power-Noise Balance in Wind Farms by Fine-Tuning the Layout with Reinforcement Learning. Energies, 18(18), 5019. https://doi.org/10.3390/en18185019







