Abstract
Wind energy is paramount to the European Union’s decarbonization and electrification goals. As wind farms expand with larger turbines and more powerful generators, conventional ‘greedy’ control strategies become insufficient. Coordinated control approaches are increasingly needed to optimize not only power output but also structural loads, supporting longer asset lifetimes and enhanced profitability. Despite recent progress, the effective implementation of multi-objective wind farm control strategies—especially those involving yaw-based wake steering—remains limited and fragmented. This study addresses this gap through a structured review of recent developments that consider both power maximization and fatigue load mitigation. Key concepts are introduced to support interdisciplinary understanding. A comparative analysis of recent studies is conducted, highlighting optimization strategies, modelling approaches, and fidelity levels. The review identifies a shift towards surrogate-based optimization frameworks that balance computational cost and physical realism. The reported benefits include power gains of up to 12.5% and blade root fatigue load reductions exceeding 30% under specific scenarios. However, challenges in model validation, generalizability, and real-world deployment remain. AI emerges as a key enabler in strategy optimization and fatigue damage prediction. The findings underscore the need for integrated approaches that combine physics-based models, AI techniques, and instrumentation to fully leverage the potential of wind farm control.
1. Introduction
Wind energy plays a crucial role in meeting the European Union’s decarbonization and electrification goals [1]. Over the decades, wind turbines (WTs) have increased in size, featuring larger blades and more powerful generators, leading to higher energy production and reduced operational costs. Similarly, wind farms (WFs) have expanded, benefiting from economies of scale. These advancements not only aim to lower the levelized cost of energy (LCOE) but also enhance profitability for developers by reducing costs and improving efficiency, which directly impacts the financial viability of wind power projects.
However, with these developments come the challenge of effectively managing the collective control of WTs in a WF array. Key challenges include aerodynamic interactions causing wake effects, trade-offs between model fidelity and complexity, uncertainties in wind conditions and turbine parameters, and the growing complexity of data processing as WF’s scale up. The need for robust controllers, efficient data processing, and addressing multiple conflicting objectives further complicates WF controller designs [2].
Modern WFs are equipped with advanced monitoring and control systems to ensure safe, reliable operation. However, simultaneously optimizing multiple objectives, such as maximizing power generation, minimizing turbine loads, and adapting to fluctuating electricity prices, remains a challenge. To meet this, WF control is shifting from controlling turbines individually to adopting a more holistic approach [3].
One of the main challenges is wake interaction, where the slower, more turbulent flow behind a turbine’s rotor affects downstream turbines, causing power losses and accelerated structural degradation. Wake redirection control, which misaligns rotor planes with incoming wind via yaw actuators, has emerged as a promising method to mitigate wake losses. Accurate WF modelling is crucial to determine optimal misalignment angles [4,5].
While wake redirection control has been demonstrated through simulations and field experiments, most implementations have used open-loop approaches, relying on accurate models without real-time feedback. Moreover, the majority of existing studies have focused primarily on power maximization, often overlooking other critical objectives such as structural load reduction and turbine lifetime extension.
Closed-loop systems, in which control actions are adapted based on discrepancies between actual and desired outcomes, are becoming increasingly relevant—especially with the rise of dynamic wake control strategies, such as wake breakup and mixing, which demand real-time optimization [5]. Although some recent works have introduced closed-loop and adaptive control approaches, their validation through field experiments and their large-scale deployment remain limited.
Recent reviews have provided important foundations for WF control research. Andersson et al. [3] offer a broad classification of control strategies, highlighting wake steering as a promising technique while pointing to key limitations such as the lack of field validation and challenges in state estimation. Meyers et al. [4] identify four core areas—flow physics, algorithms and artificial intelligence (AI), validation, and co-design—as essential for advancing control strategies, especially towards closed-loop implementation and value-based optimization. Njiri et al. [6] focus on multi-objective turbine-level control, emphasizing the need to balance power efficiency and structural load reduction.
However, a focused review that connects yaw-based wake steering with multi-objective optimization—particularly frameworks that consider both power gains and fatigue mitigation—is still missing. As this topic continues to evolve rapidly, with increasing attention to real-world implementation and lifetime-aware control, the present study aims to fill that gap by collecting, comparing, and synthesizing recent contributions in the field. It offers an updated and comprehensive overview of yaw-based WF flow control and optimization strategies, with a particular focus on emerging multi-objective frameworks. While the term ‘flow control’ is commonly used to refer to techniques that regulate aerodynamic loads, such as trailing edge jets or plasma control, in the present context it refers specifically to wake flow control in WFs.
The present study follows a logical structure that begins with foundational concepts in wind farm control strategies and objectives, and then, it progresses through control architectures, modelling challenges, and fatigue prediction. It culminates in a structured synthesis of recent studies employing yaw-based wake steering for power and fatigue damage optimization, with emphasis on modelling approaches, optimization frameworks, and fidelity levels. The main innovative contributions of this review are as follows: (i) the consolidation and critical assessment of the recent literature specifically targeting multi-objective control strategies—particularly those that combine power gains and fatigue mitigation under yaw-based wake steering; and (ii) the identification of emerging technological enablers, such as surrogate models and AI, and their role in facilitating real-time optimization and model fidelity trade-offs. These contributions offer a timely perspective on the ongoing evolution in wind farm control, which increasingly moves beyond power-centric strategies towards lifetime-aware and economically informed operation.
This manuscript is structured to guide the reader through the key components that underpin yaw-based wake steering and its role in multi-objective wind farm optimization.
Section 2 lays the foundation by presenting core background concepts: the physics of wake interactions, the structure of wind turbine and farm-level control systems, and the primary objectives traditionally pursued in WF control—namely, power maximization and load mitigation.
Building on this foundation, Section 3 discusses the evolution from open-loop to closed-loop control strategies. It highlights the limitations of steady-state, model-driven approaches typically used in open-loop systems and reviews how feedback-based closed-loop control can address these shortcomings under realistic, time-varying conditions. The model-free approaches are also briefly discussed to acknowledge their potential for future applications.
Section 4 addresses the critical role of modelling in supporting both control accuracy and fatigue prediction. It includes detailed discussions of wake models, aero-structural models, and the use of digital twins. It also examines how fatigue assessment methods and instrumentation support more reliable multi-objective optimization frameworks.
Section 5 presents the core of the review: a focused analysis of yaw-based wake steering within multi-objective optimization frameworks. It synthesizes the literature that balances power output, structural load reduction, and economic performance while also discussing how artificial intelligence (AI) is being used to improve adaptability and reduce computational burden.
In Section 6, the review broadens in scope to include innovative wake control techniques beyond yaw-based strategies—such as wake mixing and rotor tilting—which show promise for future applications in dynamic control strategies or floating WFs, respectively. Section 7 then concludes with final remarks and outlines potential future research directions.
2. Control Strategies for Wind Farms: Background and Objectives
To reduce the LCOE and meet the demand of renewable energy, it is necessary to cluster WTs into WFs. WTs extract kinetic energy and convert it into mechanical energy and then into electrical energy. This process inevitably affects the upwind and downwind airflow of the WT [7].
2.1. Wake Physics as a Basis for Control Strategy Design
On the upwind side, known as the induction region, the main effect is the wind speed reduction. On the downwind side, the WT causes a ‘shadow’, called the wake, that affects the energy production of other downstream WTs [8].
The wake region can be divided into two main regions, as shown in Figure 1 [7]:
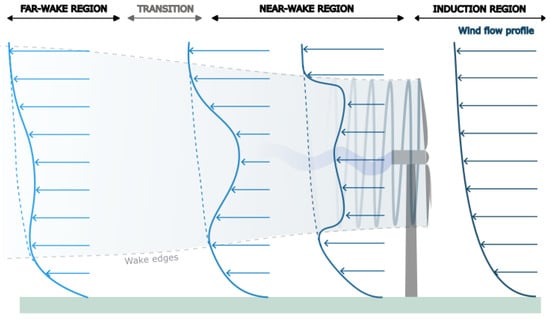
Figure 1.
Flow regions from the WT interactions. Note: The region upstream the WT is referred to as the induction region. However, to be precise, the velocity continues to decrease just after the turbine in the near-wake region.
- The near-wake region extends approximately 2–4 rotor diameters downstream of the turbine. This region is strongly influenced by the turbine’s shape and design, leading to a complex, non-uniform three-dimensional flow pattern.
- The far-wake region develops further downstream, where the influence of the turbine’s specific geometry diminishes. In this region, the mean flow characteristics can be estimated based on overall parameters such as thrust, power output, and prevailing inflow conditions.
Following the near-wake region, a transition region exists where the turbulence intensity builds up as tip vortices begin to break down and the shear layers expand. This region typically experiences the lowest mean velocity within the wake. As the shear layers meet and mix further downstream, the mean velocity starts to recover, and the turbulence intensity begins to decay [9].
For more details on wake flow, Porté-Agel et al. [7] present a review on recent theoretical, experimental, and computational research on WT and WF flows, with an emphasis on turbine wakes and their interactions with the atmospheric boundary layer (ABL).
The layout and configuration of the WF influence the feasible operation and control strategies, which subsequently impact the overall economic performance of the project [4]. One of the main challenges in the WF design is determining the best turbine arrangement that aligns with the site-specific wind conditions and the number of installed turbines. This allows an optimum space utilization and energy maximization, which, together with efficient WF control strategies, could lead to optimal WF management.
The present study focuses on the WF control rather than the system’s design, such as machine selection, sizing, or layout.
2.2. Wind Turbine and Wind Farm Control Overview
The WT is the functional unit of WFs and needs a control system to safely and efficiently generate power. The control system is usually designed to maximize annual energy production while minimizing turbine loads [10].
2.2.1. Control Systems and Operating Principles
Typically, besides the WF controller, there are two other main controller components in WTs (Figure 2) [10]:
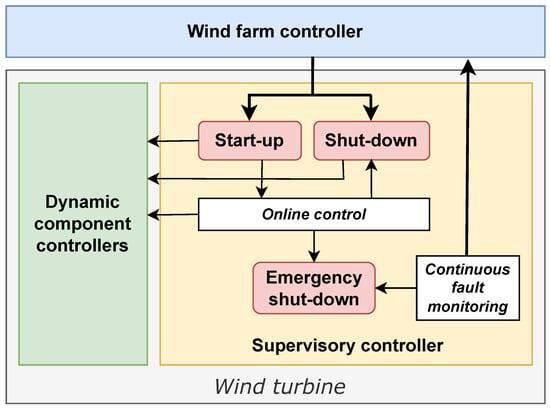
Figure 2.
Control system components: WF controller; and supervisory controller (i) and dynamic component controllers (ii). Adapted from [10].
- A supervisory controller for each wind turbine;
- A dynamic controller for the different subsystems of each wind turbine.
The first WT controller (1) handles responses to gradual and long-term variations in environmental and operational conditions, such as initiating or stopping the WT operation or sending commands to the dynamic control systems of the turbine. The second type of controller (2) performs continuous real-time modifications to the turbine’s actuators and subsystems in response to sudden fluctuations in operating conditions: for example, modifying the blade pitch angles or adjusting the position of a specific actuator.
Key control variables for turbine performance include the following: generator torque (), which regulates power conversion; blade pitch angle (), which adjusts aerodynamic responses to the wind; and yaw angle (), which orients the rotor to optimize energy capture. Instead of the generator torque, the tip–speed ratio ( or TSR) and the rotor rotational speed () can also be controlled [3]. The first () signifies the ratio of the blade tip’s speed to wind speed, and adjusting this parameter has a dominant effect on the turbine’s efficiency. The second () governs the rotational speed of the turbine’s blades, enabling dynamic power generation control by adapting to the wind’s specific characteristics at any given moment.
Wind turbine operation is divided into three control regions. In Region I, below the cut-in wind speed (), the turbine remains inactive due to insufficient wind. In Region II, between and the rated wind speed (), the turbine operates at variable speeds to maintain the optimal tip speed ratio (TSR), maximizing efficiency. In Region III, from to the cut-out speed (), the blade’s pitch is adjusted to limit power output, ensuring safe operation. Beyond , the turbine shuts down to prevent excessive loads.
At the wind farm level, WF controllers—also known as supervisory control and data acquisition (SCADA) systems—can start and stop WTs and coordinate the operation of many WTs. This functionality is achieved through communication with the individual supervisory controllers of each turbine [10].
2.2.2. Wind Farm Control Strategies
In a WF, the standard control strategy, known as ‘greedy control’, focuses on maximizing the power output of each WT individually, treating each turbine as a standalone unit without considering the presence of other turbines [2,11,12]. However, as WFs grow in size and number of turbines, particularly in offshore locations, the aerodynamic interactions increase, and demands for advanced control strategies, such as axial induction and yaw-based wake steering, emerge.
The first consists of optimizing the WF’s performance by adjusting the axial induction factor of individual turbines, typically achieved through changes in the blade’s pitch angle or derating [13]. Derating refers to the intentional reduction in a turbine’s power output below its maximum capacity by lowering the power set-point—typically done without changing the pitch angle, but rather by adjusting the generator torque or limiting the generator’s electrical output. The axial induction factor represents the decrease in wind speed caused by the turbine rotor, and it is directly linked to rotor thrust.
The second strategy—yaw-based wake steering control—involves adjusting the orientation or yaw angle of a WT to control the direction of its wake, aiming to optimize interactions between turbines and mitigate wake effects on downstream machines (Figure 3) [13]. While yaw-based control is the most advanced commercially established approach, challenges persist, particularly in understanding the intricate behaviour of wakes to yaw set-points and their sensitivity to atmospheric conditions. Deflected wakes exhibit asymmetry and a lateral flow component, impacting downstream turbines [4]. The interaction of yawed wakes with atmospheric factors like stratification and wind veer requires deeper investigation [14,15]. Researchers are actively developing wake models that incorporate steering effects and adapt to changing wake shapes [4,16]. The practical application of static yaw control involves balancing its capacity to decrease loading in downstream turbines against potential structural and loading impacts on various components of the yawed turbine itself [4].
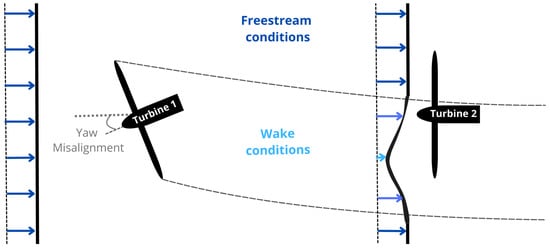
Figure 3.
Schematic representation of wake steering control due to yaw misalignment with the inflow.
2.3. Control Objectives: Achievements and Opportunities
The primary goal of WF control is to enhance operational efficiency, boost economic viability, and minimize maintenance and operational expenditures. The challenge is inherently multi-disciplinary, which is evident when examining the diverse specific control objectives, as outlined in the following [2,4,17,18]:
- Increasing energy extraction: In recent evaluations comprising both academic and industrial experts [17], increased energy production is given as the foremost benefit of flow control technology. This objective has been widely explored through various simulation models, aerodynamic experiments, and real-world field assessments, offering quantifiable gains in annual energy production (AEP) and revenue. Predicted gains vary widely based on factors like turbine technology, site conditions, and resource specifics. Confidence in predicted gains hinges on the complexity of WF flow models, sensor accuracy, and data analysis sophistication.
- Reducing structural loading: Flow control in WFs has the potential to mitigate structural loading on turbines by reducing local wake-added turbulence and redirecting wakes. Fewer studies focus on this goal when compared to increasing energy extraction. Reducing structural loads can have a substantial impact, potentially influencing layout, system cost distribution, and operational strategies. Evaluating the economic benefits of load reduction is complex due to its intricate links with component durability, residual lifespan, and operations and maintenance (O&M) expenses. Nonetheless, as explained by Meyers et al. [4], there are clear advantages in pre-construction, project development, and the possibility of extending the operational lifespan of existing turbines and wind farms.
- Power regulation for grid support and balancing: WF control can play an important role in grid stability and ancillary services, offering a nuanced approach. While lumping the farm into one power plant model is a common strategy, controlling wake interactions provides advantages for services requiring the regulation of active WF power outputs over longer time spans, i.e., longer than the flow time between two consecutive turbines. WF control can sustain WTs’ aggregated power within quality requirements set by transmission system operators. The implementation of flow control strategies, such as maximizing reserve power for compensation during downregulation, enhancing its value in the balancing market, minimizing fatigue loads, and supporting asset management under dynamic electricity prices, becomes crucial for efficient WF operation and revenue maximization.
- Other improvements: Ancillary services in WF control can be grouped into several categories. First, there are electrical support services like reactive power compensation and voltage regulation, which help maintain grid stability. Second, turbine protection services address issues unrelated to structural fatigue, such as preventing leading edge erosion, mitigating icing, and protecting power electronics from overheating. Finally, there are operational modelling services, which include efforts to reduce aerodynamic noise and mitigate environmental impacts, such as bird and bat collisions. Techniques such as turbine curtailment or shutdown, active pitching, and induction control are employed for these purposes. While these controls traditionally focus on individual turbines, their integration into a multi-objective WF control optimization can enhance overall performance, profitability, and environmental impact. Moreover, the integration of hybrid WFs [19], which produce both electricity for the grid and green hydrogen, is an emerging area of interest that can further enhance the sustainability and versatility of wind energy systems.
WF control holds significant promise for the wind energy sector, with the primary objective of maximizing operational efficiency, enhancing economic viability, and minimizing maintenance and operational costs. The consensus within the WF control community highlights increased energy production as the most crucial benefit, followed by the potential alleviation of turbine structural loads and the extension of their lifetime. Operations and maintenance (O&M) optimization is acknowledged as the third primary goal, while reducing environmental impacts, such as noise and wildlife collisions, is viewed as having the least perceived benefit. Achieving these goals poses challenges, including the need for accurate predictions of improvements, creating standardized validation tools, and addressing uncertainties regarding the efficiency of WF control. The WF control community acknowledges that overcoming these challenges will contribute to the broad adoption and integration of WF control into the wind energy landscape, paving the way for more sustainable and efficient WF operation and management [17].
While this section has presented the elementary architecture and strategic goals of WF control, the implementation of effective control relies heavily on how these strategies are executed. The following section explores the progression from traditional open-loop approaches to emerging closed-loop solutions, which aim to overcome key operational limitations.
3. From Open-Loop to Closed-Loop Control
Effective WF flow control depends on understanding physics and developing robust algorithms. These dictate how each WT operates in real time to optimize goals such as power production or load distribution. Control strategies are typically categorized as open-loop or closed-loop.
3.1. Open-Loop Control: A Standard Approach
Currently, open-loop control serves as the standard for WF flow control, with recent field experiments testing induction and wake steering [4,20].
These control algorithms employ a gain scheduling approach (Figure 4), where control gains are defined offline for different operating conditions, corresponding to steady-state models optimized for varying atmospheric conditions. These gains are then stored in LUTs and retrieved in real time for the current operating condition, considering external inputs like wind speed, direction, and turbulence levels [21]. In the scheme, the sensor and the influence of sensor noise are explicitly represented, showing how measurements are affected by noise in real-time operations. This ‘open-loop’ method, though effective in controlled testing environments, is dependent on accurate models and is susceptible to disturbances. To scale WF flow control to entire WFs with higher temporal resolutions and manage uncertainties, there is a need for robust feedback control that can accommodate inherent uncertainties in wind energy production [4].
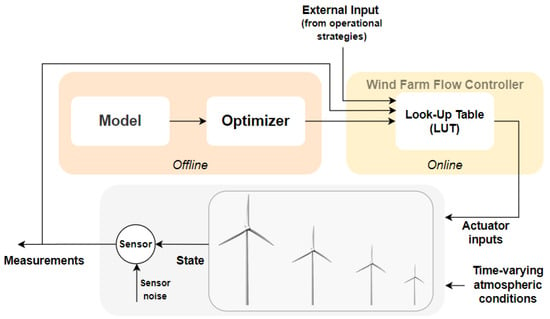
Figure 4.
Open-loop control scheme. Adapted from [4].
In [22], a simple open-loop control, unaffected by wind speed variations, was introduced to optimize power distribution among WTs in the farm, aligning with established practices in modern multi-megawatt WTs.
A notable example of open-loop wake steering implementation at a commercial level is Siemens Gamesa’s Wake Adapt system [23]. This system determines pre-calculated yaw offsets using engineering models (SGRE FLORIS) and stores them in a look-up table (LUT). The effectiveness of Wake Adapt has been validated through field experiments, including a swap test conducted in an offshore WF with 72 turbines over 14 months. The swap test is a field-based method used to measure the energy gain from Wake Adapt. It involves periodically switching Wake Adapt functionality on and off in a wind farm to collect two datasets: one with Wake Adapt active and one with it inactive. The measured energy benefit (+0.64%) closely matched the predicted gain (+0.65%), demonstrating the system’s accuracy in improving energy production.
Besides Siemens Gamesa’s Wake Adapt system, several academic field campaigns have tested open-loop control strategies. A study by Fleming et al. [24] reports an open-loop controlled field experiment to be implemented at the SWiFT facility in Texas, using three modified Vestas V27 WTs (Vestas Wind Systems A/S, Aarhus, Denmark). In a different study, Fleming et al. [25] extended this concept to an operational offshore WF in China, where commercial-scale turbines were programmed with predetermined yaw offsets derived from model optimization. Despite the short data collection window and limited control flexibility, power gains up to 29% were observed for specific turbine pairs, confirming the potential of wake steering in offshore environments. More recently, Simley et al. [26] conducted a three-month field campaign at a commercial land-based WF, using two turbines spaced 3.7 rotor diameters apart. Wake steering was achieved by modifying yaw signals via a control box, alternating between baseline and steering modes at regular intervals. The study quantified energy gains across different wind speed bins, finding the most pronounced improvements between 8 and 12 m/s and validating model predictions using FLORIS coupled with a wind direction variability model. All three studies rely on open-loop frameworks where yaw offsets are scheduled based on pre-computed strategies without real-time feedback or wake observations, offering valuable performance insights while also highlighting the need for closed-loop systems to better adapt to dynamic wind conditions.
The WF control strategies mentioned in Section 2.2.2, owing to their steady nature, are well suited for an open-loop framework. However, the emergence of dynamic strategies, exemplified by mixing wake control as discussed later in Section 6.1, implies a dynamic closed-loop control framework presented in Section 3.2.
3.2. Developments on Closed-Loop Control
Closed-loop control offers a dynamic, real-time approach to optimizing turbine performance. Unlike open-loop control, which relies on predetermined models, it enables more adaptive and responsive operations [2,4,5,27,28]. The need for closed-loop control arises from the inherent complexity of WF dynamics, where spatial and temporal variations demand continuous adjustments for optimal performance.
Closed-loop control, as illustrated in Figure 5, involves the integration of measurements obtained from various sources, such as sensors within turbines, meteorological mast, or LiDAR systems. These measurements feed into a real-time optimization framework, which, in turn, determines the next control action for individual turbines. The closed-loop approach requires a more accurate representation of the WF’s dynamic state, surpassing the limitations of steady-state models employed in open-loop systems.
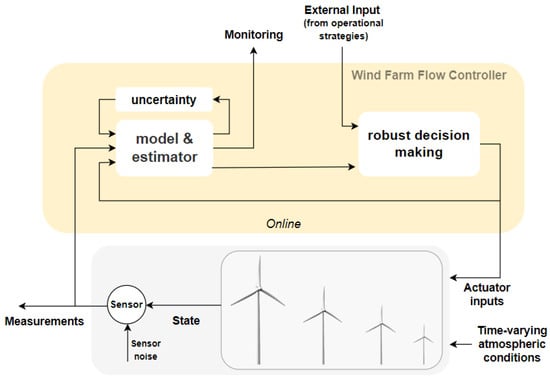
Figure 5.
Closed-loop control scheme. Adapted from [4].
The closed-loop paradigm encompasses several critical components, each contributing to the efficacy of the control strategy [4,5]:
- Internal model: At the core of closed-loop control is the internal model, which extrapolates and predicts the future behaviour of the WF based on possible control actions. Steady-state models and dynamic engineering models serve as internal models, capturing the essential first principles necessary for predicting wake behaviour and turbine interactions. More detailed models enable comprehensive system simulations, while simplified versions facilitate controller or estimator design, with the performance of the controlled system validated against the complete model (simulator).
- Estimation or data assimilation: The accurate awareness of the WF’s current state is crucial for effective closed-loop control. Estimation techniques, such as Kalman filters, are employed to combine available measurement data with the internal model, providing real-time insights into the flow field within the WF.
- Model calibration and adaptation: The continuous refinement of the internal model is realized through calibration and adaptation. These processes involve updating the first-principle model using real-time data, ensuring that it accurately represents the flow and turbine dynamics within the WF.
- Robust decision-making: The closed-loop control strategy relies on a robust decision-making process that optimizes actuator inputs over a specified horizon. The objective function, conditioned by the data-calibrated internal model, defines the best control parameters for each WT. Receding-horizon control is commonly employed, where decisions are made iteratively based on the evolving state of the WF.
While closed-loop control offers advantages in terms of adaptability and robustness, several challenges persist. The precision of the internal model, computational complexity, and the capacity to manage uncertainties are critical considerations. The evolving nature of WFs demands ongoing progress in theory, integrated design, and optimization methods. Additionally, the interplay between control engineering, optimization, and machine learning is essential for fully leveraging closed-loop control in WF operations [4].
An example of a closed-loop implementation of wake steering control is the field test carried out by Howland et al. [29], conducted at a utility-scale WF in Alberta, Canada. In this study, the control strategy combined a computationally efficient analytic wake model with site-specific calibration based on five years of SCADA data. Yaw misalignments were continuously optimized in real time using an analytic gradient ascent approach, updating control actions based on measured turbine performance. This closed-loop framework led to statistically significant power gains of up to 47% under specific wind conditions, while also reducing power variability by up to 72%. The results validated the potential of real-time wake steering to improve both the efficiency and reliability of WF power production.
In summary, closed-loop control represents a paradigm shift in WF control, utilizing real-time feedback to optimize performance under dynamic and unpredictable conditions. The integration of advanced modelling, state estimation, and robust decision-making processes positions closed-loop control as a key component of future WF flow estimation and control systems.
3.3. Note on Model-Free Control Approaches
Contrary to model-based control methods, as presented in Figure 4 and Figure 5, model-free methods operate without relying on analytical WF models. These approaches, driven by measurement data, seek to iteratively determine optimal control actions guided by user-defined objectives or reward functions. Although the present review does not delve deeply into specific techniques, it is important to note that a variety of model-free methods have been explored in the literature. These include, for example, a distributed learning algorithm utilizing game theory [30], decentralized optimization approaches [31], and the probabilistic optimization Bayesian Ascent (BA) algorithm [32].
Additionally, more recent model-free control techniques include extremum-seeking control (ESC), which continuously adjusts control parameters in real time to maximize power output. For instance, Salamah et al. [33] developed a sliding-mode-based extremum-seeking algorithm designed to optimize the setpoints of WT within a farm. This distributed control scheme, independent of wake model selection, combines a dynamic consensus algorithm with an ESC controller, allowing turbines to collaboratively maximize power production under varying wind conditions.
Reinforcement learning (RL) methods have also emerged as a promising approach for WF optimization [12]. These methods adapt to complex wake interactions and time-varying wind conditions by learning control policies through trial and error. RL provides a flexible and adaptive framework for managing nonlinear control challenges in WF.
While these methods show promise in maximizing power at the farm level, challenges remain, particularly in terms of robustness to fluctuating wind conditions and wake dynamics [2].
As the field moves towards more advanced and real-time control strategies, particularly those requiring closed-loop implementation, the demands on modelling fidelity and computational efficiency become increasingly significant. The following section examines the numerical and structural modelling frameworks that enable such control schemes and support multi-objective optimization.
4. Challenges of Numerical Modelling and Fatigue Prediction
The effectiveness of WF control depends on robust numerical modelling. Numerical models simulate the intricate physics of WTs and their interactions within a WF. The selection of a computational method and software involves a balance between accuracy and computational efficiency. Efficient methods complete simulations within an acceptable timeframe using standard computing equipment. In early design phases, simplified and computationally efficient approaches, such as linear frequency-domain solvers, are used for WT sizing. Mid-fidelity methods assess global dynamics, relying on engineering models incorporating coupled hydro-aero-servo-elastic solvers. According to De Kooning [34], enhancing the precision of numerical engineering tools remains an area for improvement. High-fidelity methods, applied in final design phases, provide in-depth analyses of specific load cases, like slamming events in offshore settings [35], using techniques like Computational Fluid Dynamics (CFDs). However, these methods often require significant computational resources and time to complete simulations, which can be impractical for large-scale or time-sensitive analyses. Additionally, high-fidelity software aids in refining coefficients for mid-fidelity engineering models [2,34].
There is a current trend towards high-level modulation, which is more advanced, aiming to create a virtual representation of the equipment. The next subsection presents the developments and challenges in wake modelling, i.e., WT interaction (Section 4.1). Following this, advancements in aero-structural modelling and fatigue assessment are discussed in Section 4.2 and Section 4.3, respectively. Finally, the concept of digital twins for individual WTs is introduced in Section 4.4.
4.1. Wake Modelling
The advancement of WF control has motivated focused research on wake models crucial for accurate predictions in various atmospheric conditions, inflow characteristics, turbulence, and wake dynamics [21]. These models, essential for WF control methods, are typically categorized as low-, medium-, and high-fidelity models based on their computational complexity and accuracy. The Jensen model represents a low-fidelity example, offering steady-state information but lacking temporal dynamics. Medium-fidelity models, like the WF Simulator, introduce dynamics with simplified Navier-–Stokes equations. High-fidelity models, including SOWFA and PALM, use large-eddy simulations for accuracy but demand higher computational resources [2].
Model development involves the meticulous analysis of field experiments, high-fidelity simulations, and the incorporation of empirical parameterizations [2]. Among the various modelling approaches, analytical wake models play a central role in WF control due to their simplicity and suitability for optimization tasks. Below, key analytical models are introduced, focusing on the widely adopted Gaussian wake model and its variants, which offer a suitable balance between accuracy and computational efficiency.
Analytical modelling offers a straightforward and effective approach for estimating the average velocity deficit in WT wakes. Some important examples, such as models by Jensen [36], Frandsen et al. [37], and Bastankhah and Porté-Agel [38], may not match the precision of advanced numerical simulations. However, their simplicity and low computational demands make them ideal for optimizing WF layout and control, especially in offshore settings. Optimization techniques like genetic algorithms and particle swarm optimization often demand numerous simulations, making analytical models practical [7].
One widely applied analytical model is the Gaussian wake model, which strikes a balance between computational efficiency and accuracy. This model is often used to predict the velocity deficit in a turbine’s wake, assuming a Gaussian distribution in both the lateral and vertical directions. The velocity deficit at any point (x, y, z) in the wake is described by the following equation [39]:
where is the freestream wind speed; C is the wake decay constant; and represent the wake width in the y and z directions, respectively; is the wake deflection.
The wake decay constant C can be defined as follows:
where is the initial momentum deficit at the rotor, which is related to the thrust coefficient by
Furthermore, Abkar and Porté-Agel [40] demonstrate that the wake expansion rates differ in the lateral (y) and vertical (z) directions due to wake meandering. The wake width in the y and z directions, and , grows according to the following relations [39]:
where D is the rotor diameter, is the location of wake initiation, and represent the lateral and vertical wake expansion rates, and are the initial wake widths, and is the yaw misalignment.
In WFs with multiple turbines, the wake from one turbine may overlap with the wake from others. The wake combination is typically performed using a quadratic superposition of velocity deficits from multiple sources [39,41]. For N turbines, the combined wake deficit is calculated as follows:
This approach accounts for the cumulative effect of wakes on downstream turbines, helping determine the total wind speed reduction experienced.
The power produced by a WT is closely linked to the wind speed at the rotor, which is reduced due to the wake effect. Using the power curve of the WT, the power output can be derived from the effective wind speed (i.e., the freestream wind speed minus the wake-induced velocity deficit):
where is the power output as a function of wind speed, and is the effective wind speed after accounting for wake effects.
These equations capture the primary mechanisms of wake behaviour in WFs, providing a foundation for modelling velocity deficits and wake interactions among turbines. However, to enhance predictive accuracy, several key parameters need further refinement. Specifically, wake growth rates in the lateral and vertical directions ( and ), wake deflection (), and the initial wake conditions ( and ) are areas of active research. Understanding the effects of ambient turbulence intensity, atmospheric stability, and secondary wake effects is essential, especially for the accurate modelling of wake meandering and recovery. Enhanced empirical data and field studies are critical for refining these variables, allowing more accurate predictions of power generation, wake impact, and load distribution across the WF.
Fleming et al. [42] explored the impact of flow structures, especially counter-rotating vortices, in WF control during wake steering. These vortices were identified as crucial in deforming wake shapes, explaining asymmetry in wake steering for varying yaw angles and influencing interactions between steered and downstream wakes. The concept of “secondary steering” was introduced, demonstrating how a steered wake can redirect the wake of a downstream turbine that is not yawed. Emphasizing the importance of incorporating these flow structures into engineering wake models for accurate WF control predictions, ongoing research aims to develop new models considering these vortices. In a more recent contribution, King et al. [39] introduced a model addressing the secondary effects of yaw misalignment in large turbine arrays. This model, known as the Gauss–curl hybrid (GCH), considers yaw-induced wake recovery and secondary wake steering in extensive arrays, unlike prior models that focused on the interaction between just two WTs. Validation through simulations for various turbine scenarios demonstrated the GCH model’s effectiveness, indicating its potential to substantially improve WF performance by manipulating flow through vortex-induced effects.
More recently, Lin et al. (2022) [43] developed two analytical wake velocity models, leveraging cosine and Gaussian shapes; these models outperformed established models, with a preference for the Gaussian variant due to improved accuracies in predicting wind speed distributions and available wind power. Additionally, Gao et al. [44] presented a novel three-dimensional Jensen–Gaussian vortex (3DJG) model that introduces a paradigm shift, eliminating the need for trial calculations and offering superior accuracy in predicting complex wake profiles.
In parallel with model development, several studies have focused on the validation and comparison of wake models to ensure their accuracy and reliability [45,46,47]. For instance, Annoni et al. [21] conducted a field campaign at the National Wind Technology Center, comparing field data with control-oriented wake models. The study, utilizing the FLORIS engineering tool, validated the Gaussian wake model for its accurate representation of wake characteristics. Furthermore, Rak et al. [45] provide an example of comparing various wake models for power maximization. The collaborative yaw-based wake steering strategy for an eight-turbine WF was investigated using different wake-deficit models, including the Jensen model, the Gaussian-shaped Bastankhah model, and its extension, the GCH model. The study emphasizes the potential of collaborative yaw-based control, with the GCH model showing significant promise in enhancing WF performance.
In large WF layouts, deep array effects refer to the complex interactions and wake overlap that occur downstream. This phenomenon, as investigated by Bay et al. [48], poses challenges for existing wake models, especially when it comes to accurately forecasting wake losses and the interactions between WT over large distances. Traditional wake superposition methods, often empirically derived, exhibit limitations in capturing the intricate dynamics associated with deep array effects, leading to underpredictions of total wake losses in the rear of large WFs. The discrepancies identified in prior studies, such as those by Hamilton et al. [49] and Doekemeijer et al. [50], underscore the need for improved modelling approaches. Bay’s research introduces the cumulative curl (CC) model, building on the GCH model, to enhance accuracy in predicting wake behaviour and power production, especially in scenarios involving numerous partial wakes and considerable distances downstream of WTs. The CC model exhibits superior performance in large WF simulations and offers a promising solution for addressing the challenges associated with deep array effects.
4.2. Aero-Structural Modelling
Structural modelling is essential for understanding fatigue and load behaviour in WTs throughout their operational life. It also guides material selection—steel is used in towers for strength, while composite materials like fiberglass are preferred in blades to reduce weight and ensure durability. Offshore turbines require even more robust designs to withstand wave loads and currents.
Different fidelity levels in aerodynamic and structural (aeroelastic) modelling are utilized to balance computational efficiency with accuracy. Depending on the simulation goals, these models can range from low-fidelity to high-fidelity tools. Low-fidelity models are often preferred during initial sizing and optimization tasks. Engineering tools, which fall under mid-fidelity models, are commonly applied in load analyses to evaluate both normal and extreme operational scenarios. In the later stages of design, high-fidelity models are typically used for in-depth analysis, especially to precisely calculate structural stresses. Additionally, a combined approach involving multiple fidelity levels can be implemented, where components from different fidelity models are integrated to improve the overall design workflow. For instance, more advanced tools can help refine simpler models or verify critical aspects of the design [51]. A deeper review of different aeroelastic tools and respective fidelity levels is given by Otter et al. [51].
For simpler and less detailed models, one-dimensional (1D) models are commonly employed due to their computational efficiency, facilitating rapid simulations of blade deformations and stresses. However, these methods may overlook complex aerodynamic interactions and nonlinear effects that are particularly evident in large and flexible turbine blades. These low-fidelity tools rely on simpler techniques, like the Blade Element Momentum (BEM) theory, to calculate unsteady aerodynamic forces, combined with one-dimensional structural models to predict WT deformations. However, these models need modifications to account for unsteady behaviour and three-dimensional effects. Although they work well for smaller turbines, their precision decreases when applied to larger WTs, especially those with significant blade tip deformations that exceed 10% of the blade’s radius [51,52].
Within mid-fidelity aeroelastic models, there are different tools, such as OpenFAST from NREL [53], HAWC2 developed by DTU Wind Energy [54], and Bladed from DNV GL [55]. One of the most used tools is the OpenFAST that is a time-domain numerical method for analysing fixed and floating horizontal-axis WTs. This tool integrates aerodynamics, hydrodynamics, control systems, and structural dynamics, and it has undergone extensive verification and validation throughout its development [56]. OpenFAST combines multiple interconnected codes, referred to as modules, enabling users to study the dynamic behaviour of various structures, including two- or three-bladed horizontal-axis WTs. It supports a range of configurations and inputs, including control strategies, mooring system designs, and environmental conditions like wind and sea states.
Structural-dynamic models for WTs with respect to the above-mentioned tools typically encompass components such as a tower, platform, nacelle, drivetrain, and rotor. These models serve as the interface for computing displacements, velocities, accelerations, and reaction loads based on inputs such as aerodynamic and hydrodynamic loads, controller commands, and substructure reactions. Multi-body hinges, where different rigid parts are connected through springs, and modal components are often combined, with the latter being utilized for components like blades and towers. In modal systems, Bernoulli–Euler beam theory is commonly applied to model bending behaviour, neglecting shear, axial, or torsional deformations. Assumptions may also include the use of isotropic materials with negligible mass or elastic offsets and small deflections for towers and beams [53,56]. In engineering tools, aerodynamic loads on the blades and tower typically rely on the BEM theory with empirical corrections. These corrections, such as Glauert’s empirical correction with Buhl’s modification and Prandtl’s tip loss, enhance the accuracy of load predictions.
The transition from simpler beam-type models or common engineering tools to Finite Element Method (FEM) modelling marks a shift towards greater fidelity and reliability in understanding a WT’s structural behaviour. While modal approaches provide valuable insights into the overall behaviour of WTs, FEM allows for a more detailed exploration of geometric and material effects, including buckling and nonlinear behaviour. This is especially relevant for longer blades of larger WTs, where the accurate prediction of structural stability is essential [57]. FEM involves discretizing a continuous structure into smaller, finite elements, allowing for the approximation of its behaviour under various conditions. The problem domain is divided into interconnected subdomains, or elements, where equations governing the behaviour of each element are derived based on physical laws and boundary conditions. These equations are then assembled into a system of algebraic equations and solved using FEM methods. Some of the most used tools are ANSYS (https://www.ansys.com, accessed on 25 April 2025) or ABAQUS (https://www.3ds.com/products-services/simulia/products/abaqus, accessed on 25 April 2025) [57,58].
4.3. Fatigue Prediction: Towards Reliable Multi-Objective Optimization
Reliable fatigue prediction is essential for incorporating structural load considerations into WF control strategies. This requires not only accurate aerodynamic and structural modelling but also robust methods for quantifying fatigue damage over time. The following subsection introduces the key metrics and assessment approaches used to evaluate fatigue loads in WTs, with a particular focus on their relevance for optimization frameworks.
4.3.1. Fatigue Damage Assessment
Fatigue assessment plays a crucial role in horizontal-axis WTs by enabling management for extended lifetime and desired robustness, particularly in remote locations with limited accessibility. Components are subjected to cyclic loading, leading to structural damage over time. Turbulence and gravitational/rotational imbalances are primary sources of cyclic loading, affecting critical components like blades, towers, and drive trains, thus accelerating structural damage. Additional factors such as wind shear, yawed inflow, and tower shadow contribute to the complexity of loading conditions [59].
Understanding fatigue behaviour involves utilizing S-N curves, which depict the relationship between stress levels and the number of cycles to failure. Various modelling approaches, such as Miner’s rule for damage accumulation or advanced numerical simulations, are employed to compute fatigue life and assess structural integrity. Challenges in this field include accurately capturing uncertainties in load conditions, developing sophisticated fatigue models for precise analysis, and implementing cost-effective maintenance strategies to mitigate fatigue-related issues effectively [60].
Fatigue life can be estimated using Miner’s rule, which accounts for cumulative damage. This is given by the following:
where is the number of cycles experienced at a given stress level, is the number of cycles to failure at that stress level, and D represents cumulative damage, with failure typically occurring when [61,62].
In wind turbine structural modelling, stress calculations at critical points like the tower base and blade root are essential for fatigue assessment. At the tower base, the total stress at any azimuth angle is calculated by combining the fore–aft and side-to-side bending moments as follows [63,64]:
where and are the side–side and fore–aft moments, and W is the section modulus derived from the cross-sectional properties of the tower. The section modulus is defined by the tower stiffness and material properties, indicating the cross-section’s resistance to bending.
The S-N curve, detailing the correlation between stress magnitude and the number of cycles until failure for steel structures, can be obtained with parameters from Eurocode 3 [65], which provides a two-region form tailored for fatigue analysis in steel towers.
For the blade root, stresses incorporate both bending and axial forces to account for rotational effects. The total stress at the blade root is given by [63,64,66]:
where and are the edgewise and flapwise moments, respectively, is the axial force, and and represent the edgewise and flapwise section moduli. Since axial forces fluctuate with the rotation, mean stress becomes significant in blade root fatigue calculations, unlike the tower base where axial loads are comparatively stable.
For the blade root, the Goodman relation and S-N curve are applied to calculate the cycles to failure, N, for each unique combination of stress range () and mean stress (mean) [64,67]:
where and are reduction factors, and are characteristic resistances, and is their average. The cumulative fatigue damage is calculated for each azimuth angle, with the maximum damage across the blade root perimeter identified. This approach to stress and fatigue analysis enables a comprehensive understanding of critical loads and lifespan impacts on turbine components.
4.3.2. Instrumentation for an Improved Assessment
Instrumentation plays a pivotal role in advancing the assessment and control strategies of WFs. As WTs evolve in size and power output, the adverse effects of structural loads become increasingly pronounced [6]. To navigate these challenges, a comprehensive framework on instrumentation and data processing is essential.
Observability, the dual of controllability, is central to this paradigm shift from open-loop to closed-loop control [4]. Controllability refers to the influence exerted by control actuators, such as the blade pitch system, on-flow states (e.g., wind speed and direction), and outputs (e.g., power generation). In contrast, observability determines how well flow states can be verified through a limited set of measurements. This interplay is particularly intricate in the context of high-dimensional nonlinear systems, such as WF flows [4].
Supervisory control and data acquisition (SCADA) systems serve as the structure of WT instrumentation [3]. SCADA records a vast number of parameters crucial for monitoring system conditions and designing control strategies. These include blade pitch position, yaw orientation, rotational speeds of the rotor and generator, electrical current in the generator, active and reactive power production, wind speed measured by anemometers, and wind direction. Additional sensors, including thermal cameras, acoustic emission transducers, and LiDAR systems, offer supplementary data for a holistic understanding of WF operation [3].
However, ensuring the accuracy of these data streams requires careful analysis to filter out potential errors. Sensor noise, as illustrated in Figure 4 and Figure 5, can obscure measurement accuracy and must be accounted for, alongside other influencing factors like sun position and temperature variations that may impact sensor performance and introduce measurement deviations [68]. The effective filtering and calibration of these signals are essential for a reliable assessment of WT conditions.
The challenges in instrumentation are multifaceted. Structural loads induced by aerodynamic forces, gyroscopic effects, and other factors necessitate a complex approach to access the actual fatigue damage on the turbine’s components [4]. The cyclic loads, particularly in large WTs, can lead to premature failure if not adequately mitigated. Moreover, the dynamic nature of wind behaviour, with both daily and seasonal patterns and stochastic properties, complicates the effective prediction of a turbine’s response to these loads [4].
Pacheco et al. [64] address such challenges by directly measuring strains on WTs and employing SCADA data. A method for evaluating fatigue damage progression over time is presented. This approach, rooted in strain measurements, allows a diagnostic of structural integrity, which is essential for making informed decisions on the decommissioning or life extension of WTs.
Hines et al. [69] conducted a study focused on the continuous monitoring of an offshore WT in the Block Island WF, situated off the coast of Rhode Island, USA. The work addressed the growing challenges in offshore wind energy, emphasizing the need for reliable structural monitoring due to harsh marine conditions and mechanical stress. The monitoring setup included both wired and wireless sensors, such as accelerometers, strain gauges, and inclinometers. Hines et al. highlighted the importance of such instrumentation for predictive maintenance, emphasizing the benefits of condition-based approaches over traditional strategies. This research is important for understanding and improving offshore WT performance, diagnosing faults, and setting a benchmark for structural health monitoring. The collected data and derived modal parameters form the foundational database that defines the benchmark structural characteristics of offshore WTs.
4.4. Digital Twins in Wind Farm Control: Beyond the Buzzword
The term digital twin is increasingly used across the wind energy sector, often as a buzzword applied broadly without clear definitions or a consistent understanding of its practical implications. While frequently invoked in research and industry reports, the concept is sometimes ambiguously presented, with limited discussion on how it can concretely enhance WT or WF control. To move beyond this superficial usage, it is essential to clarify what constitutes a true digital twin and how its implementation can support control strategies, monitoring, and decision-making in modern WFs.
The concept of a digital twin includes different levels: a digital model, a digital shadow, and a full digital twin [34]. A digital model refers to a virtual replica without automated information exchange. A digital shadow adds unidirectional automated data flow, whereas a digital twin necessitates two-way communication, enabling synchronization with the physical system. The practical implementation involves defining behaviours, creating models with required fidelity, and ensuring correct data stream coupling [34]. In WTs, numerical modelling is crucial. The challenge increases in floating offshore WTs (FOWTs), where coupling aerodynamics and hydrodynamics bring even more complexity. Tools like OpenFAST and OpenFOAM cater to different fidelity levels [51]. A broader literature review emphasizes the importance and state of the art of digital twins for WT and components, using various modelling techniques and enhancing condition monitoring and fault diagnosis [34,51].
5. Multi-Objective Optimization Through Yaw-Based Wake Steering
Building upon the foundations of control strategies, numerical modelling, and fatigue prediction presented in the previous sections, this section explores the integration of these elements through multi-objective optimization frameworks. Among the various WF flow control strategies, yaw-based wake steering has emerged as one of the most extensively studied and explored. While early work focused primarily on power maximization, more recent approaches incorporate structural load mitigation, economic objectives, and AI-enhanced strategies to address the complexities of real-world deployment. The following subsections present a structured review of these developments, beginning with the fundamental trade-off between power output and structural loads.
5.1. Balancing Power Output and Structural Loads
A key challenge in managing WT arrays is developing efficient collective control strategies that balance energy capture, structural load mitigation, system stability, and operational costs. The main optimization goals include minimizing fatigue loads and tracking power references, which are complex tasks due to the multitude of possible solutions. Various optimization methods, such as parametric programming, distributed model predictive control (DMPC), and data-driven multi-objective predictive controllers, have been explored to achieve power tracking and load reduction [2].
In recent years, significant advancements have been made in optimizing WF performance through yaw-based wake steering control strategies. Van Dijk et al. [70] explored the impact of yaw-misalignment on WF wake to enhance power production and reduce loads due to partial wake overlap. The framework integrated FLORIS and CCBlade models, employing a gradient-based optimizer to find optimal yaw settings. Similarly, Kanev et al. [13] investigated wake control’s potential to optimize the lifetime operation of WFs using the FarmFlow software (Energy Research Centre of the Netherlands (ECN), now part of TNO, The Hague, The Netherlands; https://www.tno.nl, accessed on 25 April 2025) and an optimization approach, exploring both pitch-based and yaw-based wake control. Their findings suggest that such strategies can increase yearly power production and reduce fatigue loads.
Bossanyi et al. [71] combined induction control and wake steering for WF energy and fatigue load optimization. The study introduced a steady-state optimization tool and a fast time-domain simulation model for testing WF controllers under realistic conditions. The results highlighted the potential benefits of combined power and yaw control, though ongoing validation efforts are necessary due to uncertainties in wake models. Reyes et al. [72] validated a lookup-table approach to modelling turbine fatigue loads under active wake control, proposing an efficient methodology for assessing farm loads. The study indicated that wake redirection could increase overall power production and decrease lifetime fatigue loads, although further validation is required due to uncertainties associated with real-time wind variations.
In another study, Lin et al. (2020) [73] optimized power and fatigue loads using large-eddy simulation data, revealing Pareto-optimal strategies that emphasize load mitigation alongside power maximization. More recently, addressing an offshore WF, Sun et al. [74] also proposed a multi-objective wake redirection control scheme that simultaneously maximizes power output and reduces fatigue loads. Using a fatigue assessment model derived from aero-elastic simulations [75], the scheme effectively evaluated fatigue damage on WTs subjected to yaw misalignment and wake interactions. Numerical results from the simulations of an offshore WF comprising nine NREL 5MW baseline turbines demonstrated that this control strategy could increase the overall power output by up to 12.5% while simultaneously reducing the fatigue loads of critical structures by up to 15.3%.
Building on previous findings, He et al. (2023) [76] added valuable insights by investigating optimal yaw strategies and fatigue analysis of WTs under combined wake and yaw control. They conducted a comprehensive fatigue analysis under various conditions and proposed a cost function for optimal yaw control. The findings suggest efficient yaw ranges in the direction defined as clockwise when viewed from upstream to downstream, contributing to the understanding of multi-objective active yaw control strategies.
More recently, Lucas Frutuoso et al. [77] focused on optimizing WF yaw control using a multi-objective approach for a real-world case study at the Tocha Wind Farm in Portugal. A direct multi-search (DMS) algorithm to balance power outputs and fatigue loads was applied. The study revealed that by optimizing yaw angles, power could improve by up to 4.6%, and damage equivalent moments (DEMs) at the blade root and tower base could improve by 5.7% and 84%, respectively. The research underscored the importance of considering multiple objectives to enhance WF performance and extend turbine lifespan, even though the effects of unsteady flow dynamics on fatigue need to be incorporated.
5.2. Economic Optimization and Lifetime Extension
Other recent works have focused on optimizing economic performance. In contrast to previous methods, Braunbehrens et al. [78] presented the first experimental results of a lifetime-aware WF control strategy aimed at maximizing economic performance while ensuring desired turbine lifetimes. Utilizing yaw-induced wake steering, the strategy balances power output and fatigue damage by integrating power and damage estimators. Tested with three model turbines in a wind tunnel, the strategy demonstrated improved economic performance compared to conventional greedy and maximum power strategies, with significant reductions in maintenance costs and increased overall profit, particularly under scenarios simulating pre-construction and mid-lifetime adjustments. The study highlighted gaps, such as the need for more comprehensive long-term simulations, validation with full-scale turbines, and the refinement of economic models for different turbine components and operational scenarios.
Requate et al. [79] developed an optimization method to maximize the economic value of WTs through the condition-based adaptation of power set-points, balancing load reduction and power generation to extend a turbine’s lifetime. By annually varying operating strategies selected from an initial multi-objective optimization Pareto front, the method demonstrated slight improvements in the net present value (NPV) over constant strategies. Three case studies illustrated increased economic value through this adaptive approach, emphasizing the balance between potential structural damage and energy outputs. The study acknowledged the need for further research to address uncertainties in damage calculations and to extend the method’s application to entire WFs.
While these recent contributions mark a promising step towards integrating economic and lifetime-aware objectives into WF control, several challenges remain. First, the true long-term economic impact of fatigue-optimized strategies has yet to be fully validated under real-world, full-scale conditions. Excessive dependence on simplified assumptions or short-term proxies—such as limited fatigue models or narrow operational conditions—may limit the confidence of industry stakeholders in adopting such methods. To ensure robust and scalable solutions, optimization frameworks must comprehensively address all operational regimes across the turbine’s lifetime, including periods of curtailment, extreme events, and maintenance cycles. Moreover, one of the key barriers to advancing lifetime-aware economic control lies in the need for accurate, computationally efficient fatigue prediction models that are compatible with control-oriented WF simulations. Without reliable structural modelling integrated into the optimization loop, it remains difficult to confidently quantify and balance the trade-offs between power extraction, load reduction, and economic return.
5.3. Integrating AI for Enhanced Control
Building on these advanced optimization techniques, artificial intelligence (AI) has emerged as a powerful tool for further enhancing WF control and performance. AI offers data-driven solutions to improve the responsiveness and robustness of WF control systems. In recent years, the integration of AI techniques, such as reinforcement learning (RL) and deep learning, has significantly advanced the capabilities of WF control systems.
Reinforcement learning (RL) has gained prominence for its ability to optimize control performance iteratively through trial and error. It enables WF controllers to adapt to complex, ‘black-box’ systems, a feat that is often unattainable with conventional control methods. RL has been employed to enhance various aspects of WF operations, from power generation maximization to the dynamic tracking of reference signals, as noted by Dong et al. [2].
Deep learning models, particularly neural networks, play a pivotal role in AI-driven WF control. These models facilitate handling high system complexities and extracting information from vast datasets without explicit reliance on analytical models. Meyers et al. [4] highlight the increasing application of complex statistical techniques, such as multilayered neural networks, in improving WF models and estimators, ultimately reducing uncertainties in predictions.
Several studies showcase the advantages of AI in optimizing WF layouts and mitigating turbine fatigue loads. For instance, He et al. (2022) [80] introduced a machine learning-based method for predicting fatigue loads under yaw control, contributing to ongoing efforts to balance power generation and structural performance. Pawar et al. [81] explored the application of deep learning to construct surrogate models for wake prediction, demonstrating computational efficiency in tasks like layout optimization and highlighting the potential of AI-driven models in enhancing WF design and performance.
Extending the use of AI to multi-objective control strategies, recent studies have focused on ANN-based (artificial neural network) surrogate models for fatigue prediction under yaw control. Guilloré et al. [82] introduced a surrogate load model based on sector-averaged inflow quantities and local control set-points to predict damage equivalent loads (DELs) for various turbine positions and control actions within a WF. The model achieved strong accuracy, with low scatter and root mean square percentage error (RMSPE) values across damage equivalent load (DEL) channels. It effectively predicted fatigue loads for control strategies like wake steering and induction control. They suggested that further validation with wind tunnel experiments and full field measurements is necessary to refine the surrogate model’s accuracy. Liew et al. [83] utilized aeroelastic simulations from HAWC2Farm to train surrogate models to predict turbine fatigue loads under various wake interactions. The study reported a 4.1% increase in annual energy production (AEP) through unconstrained optimization, emphasizing the importance of balancing power outputs with fatigue load considerations. They highlighted the need to address potential uncertainties in model predictions and ensure consistency between dynamic and steady-state simulations.
Expanding on these AI-based fatigue load predictions, Yang et al. (2025) [84] proposed a novel double-stage AI-based optimization framework that integrates an ANN yaw wake model with Bayesian machine learning to optimize both power generation and turbine lifetimes. Their study highlights the trade-off benefits of AI-driven yaw control, demonstrating that an 8% increase in WF lifetime can be achieved with less than 2% power loss. Furthermore, their findings emphasize the importance of incorporating load effects into yaw control strategies, particularly benefiting back-row turbines in wake interactions.
While AI offers remarkable opportunities for improving WF control, challenges persist, including high computational costs and the need for extensive data for model training. However, ongoing research continues to push the boundaries of AI applications in WF control and optimization, promising a future where advanced algorithms play a central role in maximizing the efficiency and reliability of wind energy production.
5.4. Literature Synthesis: Optimization and Modelling Approaches
Table 1 summarizes key studies on multi-objective optimization using yaw-based wake steering, with attention to optimization strategies, modelling approaches, and model fidelity. These studies reflect the growing interest in control strategies that simultaneously consider power output and fatigue load reduction—two objectives that are often conflicting and require careful balancing. Reported gains vary significantly depending on site conditions, turbine layouts, and modelling assumptions, with power increases reaching up to 12.5% and fatigue load reductions exceeding 30% in select scenarios.

Table 1.
Summary of optimization methods and modelling approaches on studies using yaw-based wake steering control for power and fatigue optimization. Ordered by publication year.
A closer examination reveals an apparent shift in methodology over time. While early studies typically relied on low-fidelity engineering models such as FLORIS to optimize yaw angles, recent works increasingly adopt medium-fidelity simulations, often using tools like FAST.Farm or high-fidelity aeroelastic codes to generate datasets for training surrogate models. This hybrid approach—calibrating lightweight models with high-fidelity outputs—offers a pragmatic balance between computational tractability and physical realism. However, the reliability of such surrogate-based frameworks hinges on their ability to generalize across operating conditions, which is not always validated in the literature. Among the most recent studies, only Lucas Frutuoso et al. [77] relied solely on a low-fidelity model (FLORIS). However, the authors explicitly acknowledged that unsteady wake dynamics and their effects on fatigue were not modelled, which limits the confidence in the study’s fatigue-related findings.
Optimization techniques also exhibit significant diversity. Several studies apply classical single-objective formulations—employing weighted combinations of power and load-related terms. In contrast, others adopt Pareto-based multi-objective frameworks that incorporate damage or economic metrics. The use of artificial intelligence, particularly reinforcement learning and surrogate-assisted optimization, is becoming more prevalent, yet challenges related to transparency, model interpretability, and generalizability remain.
Open-loop control continues to dominate the reviewed literature, primarily due to its simplicity and compatibility with existing SCADA infrastructure. However, these approaches typically rely on pre-computed yaw offset tables or surrogate models and lack the feedback mechanisms needed to adapt to real-time atmospheric variability or to support more innovative, dynamic control strategies (see Section 6). While a few studies have begun to explore closed-loop or adaptive controllers, the experimental validation of these approaches remains limited. As a result, most proposed methods remain at the proof-of-concept or simulation stage, and their readiness for large-scale field deployment is not yet demonstrated.
Moreover, only a minority of works attempt to integrate economic metrics such as LCOE or into the optimization framework. While studies by Braunbehrens et al. and Requate et al. represent recent efforts to address this gap, broader adoption of techno-economic modelling is needed. Without such integration, control strategies may remain misaligned with the long-term profitability and operational priorities of WF operators.
In summary, the recent literature demonstrates significant progress in the application of yaw-based control for multi-objective WF optimization. However, technical challenges persist. A lack of real-world validation for surrogate models, limited implementation of adaptive control architectures, and minimal integration of economic metrics all constrain the readiness of these strategies for commercial deployment. From a practical standpoint, different approaches may be more suitable depending on the project’s context. For example, onshore WFs with stable inflow conditions and comprehensive instrumentation may benefit from open-loop strategies using well-calibrated surrogate models. In contrast, offshore farms, where access is limited and mechanical fatigue is critical, may require closed-loop or adaptive frameworks that prioritize structural load reduction and long-term availability. Future research should focus on hybrid control architectures that combine AI-enhanced surrogate models with real-time feedback and robust multi-objective optimization. These systems should be verified not only through simulation but also in field conditions, enabling the more confident deployment of control strategies tailored to specific WF configurations and operational goals.
6. Beyond Yaw-Based Steering: Emerging Wake Control Approaches
This section extends beyond conventional methods like yaw-based wake steering explored in the present study, exploring novel strategies such as wake breakup and wake mixing and tilting. These innovative techniques focusing on wakes offer promising avenues for further advancements in WF control and optimization.
6.1. Wake Breakup and Mixing
Controlled wake breakup and mixing offer strategic benefits for optimizing wind farm performance, but achieving this requires a deep understanding of wake dynamics. Studies by Quaranta et al. [86] and Premaratne et al. [87] have made significant contributions towards enhancing wake diagnosis, which in turn could enable more precise control measures and greater WF efficiency [4].
Quaranta et al. [86] investigated the long-wave instability of helical vortices, and the study identifies patterns crucial for wake dynamics. The visualisation of an unperturbed helix and a rotor tip vortex with an initial perturbation can be found in the original source. This information is valuable for optimizing WF control strategies, especially in understanding vortex interactions and downstream effects.
Expanding on this, Premaratne et al. [87] characterized turbine wakes by focusing on a scaled WT model subjected to turbulent boundary layer wind. The study revealed the presence of tip vortices, and understanding the early breakup of these vortices is essential for formulating effective control measures. The study employs proper orthogonal decomposition (POD) analysis, offering insights into the coherent flow structures and aiding in the identification of dominant vortices. These findings provide a detailed understanding of wake behaviour and may contribute to the development of advanced WF control strategies.
Two distinct strategies for controlling wakes have emerged: the pulse and helix approaches [88,89]. The pulse method, exemplified by dynamic induction control, varies the thrust of WTs over a revolution to enhance wake mixing and reduce turbine-to-turbine interaction. While effective, this method introduces power and thrust fluctuations. Conversely, the helix approach utilizes individual pitch control to dynamically manipulate the wake, creating a helical wake through varying fixed-frame tilt and yaw moments. This promotes faster wake recovery with minimal fluctuations in power and thrust. The pulse method’s effectiveness depends heavily on frequency and amplitude, particularly for floating WTs, where turbine motion further impacts wake mixing. On the other hand, the helix approach has demonstrated strong results in increasing energy capture, outperforming static derating and dynamic induction control in terms of power and thrust stability. Its compatibility with existing individual pitch control systems suggests that it could be implemented quickly in the industry without the need for major turbine redesign [89].
Building on these strategies, Korb et al. [12] explored the application of reinforcement learning (RL) to WF control. Their study tuned the parameters of the helix approach, achieving a 6.8% increase in total power production. RL offers the advantage of learning optimal control policies through trial and error, enabling it to adapt to complex wake interactions and time-varying wind conditions, thus optimizing both power production and turbine efficiency.
6.2. Rotor Tilting
Traditional turbines lack built-in mechanisms for vertical wake steering. However, floating turbines can employ a technique called differential ballast control to dynamically adjust the platform’s attitude, influencing the vertical trajectory of the wake. This innovative approach offers an alternative means to optimize the performance of floating WTs, complementing the conventional rotor tilting method, also known as the ‘static pitch angle’ method [4,90,91].
Storm [92] highlights the benefits of rotor tilting for enhancing WF energy production. However, FLORIS simulations often overestimate power gains due to the absence of ground interaction modelling. Despite this, a case study indicated significant improvements in power production when combining rotor yaw and tilt.
Nanos et al. [91] explores a related concept—vertical wake deflection using active ballast control for offshore WTs. Their work, considering a cluster of two WTs and supported by wind tunnel experiments and LES (large eddy) simulations, demonstrates an approximate 8% increase in cluster power through controlled vertical wake redirection.
In summary, tilting for vertical wake deflection, or static pitch angle adjustment, presents a promising avenue for optimizing WF performance, though challenges such as model accuracy and ground interaction must be carefully addressed in future research.
7. Conclusions
This review has examined the recent advancements in wind farm control and optimization, focusing on yaw-based wake steering as a key strategy for improving both energy output and wind turbine durability. Drawing on studies from the past decade, the present study synthesized developments in optimization frameworks, control strategies, and modelling approaches, with particular attention to multi-objective formulations that include power production, fatigue mitigation, and economic value.
Reported gains across the literature indicate that yaw-based strategies can yield power output increases of up to 12.5% at the farm level, blade root fatigue load reductions exceeding 30%, and profit increases over 100% under certain conditions. However, these benefits are highly dependent on the fidelity of the underlying models, wind farm configuration, and atmospheric conditions. As such, while these figures demonstrate the potential of yaw control, they should not be considered universally applicable.
A critical insight from this review is the evolving role of modelling. Some early studies relied solely on low-fidelity models such as FLORIS, but recent approaches favour medium- or high-fidelity simulations to train surrogate models. This hybrid methodology strikes a balance between computational efficiency and physical realism but introduces new challenges regarding generalizability and site-specific calibration.
Optimization techniques have similarly diversified, ranging from classical weighted single-objective formulations to advanced Pareto-based methods that explicitly balance power and structural loading objectives. Notably, the integration of economic indicators—such as LCOE or NPV—remains limited, though recent work has begun to bridge this gap. These studies underscore the need for more robust techno-economic frameworks that can guide practical decision-making.
In terms of control architecture, open-loop strategies remain predominant due to their simplicity and compatibility with existing SCADA systems. Yet, their inability to adapt to real-time atmospheric variability limits reliability. Closed-loop and adaptive control methods show promise—particularly in dynamic environments—but remain largely confined to simulations or small-scale testing, with field validation still rare.
In summary, while the WF control topic has progressed considerably, several gaps remain: (i) insufficient experimental validation of advanced control strategies, (ii) limited integration of fatigue-aware and economic objectives in unified frameworks, and (iii) the need for reliable, control-oriented structural models. Addressing these challenges will be essential for translating current research into scalable, cost-effective solutions.
Ultimately, by combining physical insight, computational efficiency, and multi-objective trade-offs, future wind farm control strategies can better align with industry needs—enhancing both operational performance and long-term economic viability. These advancements also ensure the long-term sustainability of wind energy as a major contributor to global decarbonization efforts.
Author Contributions
Conceptualization, T.R.L.F. and R.C.; methodology, T.R.L.F.; software, T.R.L.F.; validation, R.C., R.B.S.P. and A.M.; formal analysis, R.C., R.B.S.P. and A.M.; investigation, T.R.L.F.; resources, R.C. and R.B.S.P.; data curation, T.R.L.F.; writing—original draft preparation, T.R.L.F.; writing—review and editing, R.C., R.B.S.P. and A.M.; visualization, R.C.; supervision, R.C. and R.B.S.P.; project administration, R.C. and R.B.S.P.; funding acquisition, R.C. and R.B.S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Foundation for Science and Technology (Fundação para a Ciência e Tecnologia, FCT) through scholarship 2024.01639.BD; project LAETA Base Funding (DOI:10.54499/UIDB/50022/2020) and project M4WIND (DOI:10.54499/2022.08120.PTDC); and national funds through FCT/MCTES (PIDDAC). Rui Castro was supported by national funds through FCT under project UIDB/50021/2020 (DOI:10.54499/UIDB/50021/2020).
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- IEA. World Energy Outlook 2022; International Energy Agency: Paris, France, 2022. [Google Scholar]
- Dong, H.; Xie, J.; Zhao, X. Wind farm control technologies: From classical control to reinforcement learning. Prog. Energy 2022, 4, 032006. [Google Scholar] [CrossRef]
- Andersson, L.E.; Anaya-Lara, O.; Dykes, K.; Fleming, P.; Gebraad, P.; Tande, J.O.; Merz, K.O. Wind farm control—Part I: A review on control system concepts and structures. IET Renew. Power Gener. 2021, 15, 2085–2108. [Google Scholar] [CrossRef]
- Meyers, J.; Bottasso, C.; Dykes, K.; Fleming, P.; Gebraad, P.; Giebel, G.; Göçmen, T.; van Wingerden, J.-W. Wind farm flow control: Prospects and challenges. Wind Energy Sci. 2022, 7, 2271–2306. [Google Scholar] [CrossRef]
- Doekemeijer, B.M.; van Wingerden, J.-W.; Fleming, P.A. A tutorial on the synthesis and validation of a closed-loop wind farm controller using a steady-state surrogate model. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 2825–2836. [Google Scholar]
- Njiri, J.G.; Söffker, D. State-of-the-art in wind turbine control: Trends and challenges. Renew. Sustain. Energy Rev. 2016, 60, 377–393. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-Turbine and Wind-Farm Flows: A Review. Bound.-Layer Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef] [PubMed]
- Sawant, M.; Thakare, S.; Rao, A.P.; Feijóo-Lorenzo, A.E.; Bokde, N.D. A Review on State-of-the-Art Reviews in Wind-Turbine- and Wind-Farm-Related Topics. Energies 2021, 14, 2041. [Google Scholar] [CrossRef]
- Neunaber, I.; Hölling, M.; Stevens, R.J.A.M.; Schepers, G.; Peinke, J. Distinct Turbulent Regions in the Wake of a Wind Turbine and Their Inflow-Dependent Locations: The Creation of a Wake Map. Energies 2020, 13, 5392. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind energy explained: Theory, design, and application. In Wind Energy Explained: Theory, Design, and Application, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 359–404. [Google Scholar]
- Deljouyi, N.; Nobakhti, A.; Abdolahi, A. Wind farm power output optimization using cooperative control methods. Wind Energy 2021, 24, 502–514. [Google Scholar] [CrossRef]
- Korb, H.; Asmuth, H.; Stender, M.; Ivanell, S. Exploring the application of reinforcement learning to wind farm control. J. Phys. Conf. Ser. 2021, 1934, 012022. [Google Scholar] [CrossRef]
- Kanev, S.K.; Savenije, F.J.; Engels, W.P. Active wake control: An approach to optimize the lifetime operation of wind farms. Wind Energy 2018, 21, 488–501. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. Influence of the Coriolis force on the structure and evolution of wind turbine wakes. Phys. Rev. Fluids 2016, 1, 063701. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Porté-Agel, F. Effects of Thermal Stability and Incoming Boundary-Layer Flow Characteristics on Wind-Turbine Wakes: A Wind-Tunnel Study. Bound.-Layer Meteorol. 2010, 136, 515–533. [Google Scholar] [CrossRef]
- Howland, F.H.; Dabiri, J.O. Influence of Wake Model Superposition and Secondary Steering on Model-Based Wake Steering Control with SCADA Data Assimilation. Energies 2021, 14, 52. [Google Scholar] [CrossRef]
- van Wingerden, J.W.; Fleming, P.A.; Göçmen, T.; Eguinoa, I.; Doekemeijer, B.M.; Dykes, K.; Lawson, M.; Simley, E.; King, J.; Astrain, D. Expert Elicitation on Wind Farm Control. J. Phys. Conf. Ser. 2020, 1618, 022025. [Google Scholar] [CrossRef]
- Kheirabadi, A.C.; Nagamune, R. A quantitative review of wind farm control with the objective of wind farm power maximization. J. Wind Eng. Ind. Aerodyn. 2019, 192, 45–73. [Google Scholar] [CrossRef]
- Lucas, T.R.; Ferreira, A.F.; Santos Pereira, R.B.; Alves, M. Hydrogen production from the WindFloat Atlantic offshore wind farm: A techno-economic analysis. Appl. Energy 2022, 15, 118481. [Google Scholar] [CrossRef]
- Doekemeijer, B.M.; Kern, S.; Maturu, S.; Kanev, S.; Salbert, B.; Schreiber, J.; Campagnolo, F.; Bottasso, C.L.; Schuler, S.; Wilts, F.; et al. Field experiment for open-loop yaw-based wake steering at a commercial onshore wind farm in Italy. Wind Energy Sci. 2021, 6, 159–176. [Google Scholar] [CrossRef]
- Annoni, J.; Fleming, P.; Scholbrock, A.; Roadman, J.; Dana, S.; Adcock, C.; Porté-Agel, F.; Raach, S.; Haizmann, F.; Schlipf, D. Analysis of control-oriented wake modeling tools using lidar field results. Wind Energy Sci. 2018, 3, 819–831. [Google Scholar] [CrossRef]
- Kim, H.; Kim, K.; Paek, I. Model Based Open-Loop Wind Farm Control Using Active Power for Power Increase and Load Reduction. Appl. Sci. 2017, 7, 1068. [Google Scholar] [CrossRef]
- Pena Martinez, J.J.; Coussy, J. Wake steering experiments in onshore and offshore wind farms. J. Phys. Conf. Ser. 2024, 2767, 092090. [Google Scholar] [CrossRef]
- Fleming, P.; Church, M.; Scholbrock, A.; Clifton, A.; Schreck, S.; Johnson, K.; Wright, A.; Gebraad, P.; Annoni, J.; Naughton, B.; et al. Detailed field test of yaw-based wake steering. J. Phys. Conf. Ser. 2016, 753, 052003. [Google Scholar] [CrossRef]
- Fleming, P.; Annoni, J.; Shah, J.J.; Wang, L.; Ananthan, S.; Zhang, Z.; Hutchings, K.; Wang, P.; Chen, W.; Chen, L. Field test of wake steering at an offshore wind farm. Wind Energy Sci. 2017, 2, 229–239. [Google Scholar] [CrossRef]
- Simley, E.; Fleming, P.; Girard, N.; Alloin, L.; Godefroy, E.; Duc, T. Results from a wake-steering experiment at a commercial wind plant: Investigating the wind speed dependence of wake-steering performance. Wind Energy Sci. 2021, 6, 1427–1453. [Google Scholar] [CrossRef]
- Doekemeijer, B.M.; van der Hoek, D.C.; van Wingerden, J.W. Closed-loop model-based wind farm control using FLORIS under time-varying inflow conditions. Renew. Energy 2020, 156, 719–730. [Google Scholar] [CrossRef]
- Campagnolo, F.; Petrovic, V.; Schreiber, J.; Nanos, E.M.; Croce, A.; Bottasso, C.L. Wind tunnel testing of a closed-loop wake deflection controller for wind farm power maximization. J. Phys. Conf. Ser. 2016, 753, 032006. [Google Scholar] [CrossRef]
- Howland, M.F.; Lele, S.K.; Dabiri, J.O. Wind farm power optimization through wake steering. Proc. Natl. Acad. Sci. USA 2019, 116, 14495–14500. [Google Scholar] [CrossRef]
- Marden, J.R.; Ruben, S.D.; Pao, L. A model-free approach to wind farm control using game theoretic methods. IEEE Trans. Control Syst. Technol. 2013, 21, 1207–1214. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, X. Decentralized model-free wind farm control via discrete adaptive filtering methods. IEEE Trans. Smart Grid 2018, 9, 2529–2540. [Google Scholar] [CrossRef]
- Park, J. Contextual Bayesian optimization with trust region (CBOTR) and its application to cooperative wind farm control in region 2. Sustain. Energy Technol. Assess. 2020, 38, 100679. [Google Scholar] [CrossRef]
- Salamah, Y.B.; Ozguner, U. Distributed Extremum-Seeking for Wind Farm Power Maximization Using Sliding Mode Control. Energies 2021, 14, 828. [Google Scholar] [CrossRef]
- De Kooning, J.D.M.; Stockman, K.; De Maeyer, J.; Jarquin-Laguna, A.; Vandevelde, L. Digital Twins for Wind Energy Conversion Systems: A Literature Review of Potential Modelling Techniques Focused on Model Fidelity and Computational Load. Processes 2021, 9, 2224. [Google Scholar] [CrossRef]
- Xu, S.; Xue, Y.; Zhao, W.; Wan, D. A Review of High-Fidelity Computational Fluid Dynamics for Floating Offshore Wind Turbines. J. Mar. Sci. Eng. 2022, 10, 1357. [Google Scholar] [CrossRef]
- Jensen, N.O. A Note on Wind Turbine Interaction; Risø-M-2411; Risoe National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
- Frandsen, S.T.; Barthelmie, R.; Pryor, S.; Rathmann, O.; Larsen, S.; Højstrup, J.; Thøgersen, M. Analytical modelling of wind speed deficit in large offshore wind farms. Wind Energy 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. A new analytical model for wind-turbine wakes. Renew. Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
- King, J.; Fleming, P.; King, R.; Martínez-Tossas, L.A.; Bay, C.J.; Mudafort, R.; Simley, E. Control-oriented model for secondary effects of wake steering. Wind Energy Sci. 2021, 6, 701–714. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. Influence of atmospheric stability on wind-turbine wakes: A large-eddy simulation study. Phys. Fluids 2015, 27, 035104. [Google Scholar] [CrossRef]
- Katic, I.; Højstrup, J.; Jensen, N.O. A Simple Model for Cluster Efficiency. In Proceedings of the EWEC’86, Rome, Italy, 7–9 October 1986; Volume 1, pp. 407–410. [Google Scholar]
- Fleming, P.; Annoni, J.; Churchfield, M.; Martinez-Tossas, L.A.; Gruchalla, K.; Lawson, M.; Moriarty, P. A simulation study demonstrating the importance of large-scale trailing vortices in wake steering. Wind Energy Sci. 2018, 3, 243–255. [Google Scholar] [CrossRef]
- Lin, J.W.; Zhu, W.J.; Shen, W.Z. New engineering wake model for wind farm applications. Renew. Energy 2022, 198, 1354–1363. [Google Scholar] [CrossRef]
- Gao, X.; Li, B.; Wang, T.; Sun, H.; Yang, H.; Li, Y.; Wang, Y.; Zhao, F. Investigation and validation of 3D wake model for horizontal-axis wind turbines based on field measurements. Appl. Energy 2020, 260, 114272. [Google Scholar] [CrossRef]
- Rak, B.P.; Santos Pereira, R.B. Impact of the wake deficit model on wind farm yield: A study of yaw-based control optimization. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104827. [Google Scholar] [CrossRef]
- Gao, X.; Li, Y.; Zhao, F.; Sun, H. Comparisons of the accuracy of different wake models in wind farm layout optimization. Energy Explor. Exploit. 2020, 38, 1725–1741. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Triantafyllou, P.; Stinis, P. Critical evaluation of Wind Turbines’ analytical wake models. Renew. Sustain. Energy Rev. 2021, 144, 110991. [Google Scholar] [CrossRef]
- Bay, C.J.; Fleming, P.; Doekemeijer, B.; King, J.; Churchfield, M.; Mudafort, R. Addressing deep array effects and impacts to wake steering with the cumulative-curl wake model. Wind Energy Sci. 2023, 8, 401–419. [Google Scholar] [CrossRef]
- Hamilton, N.; Bay, C.J.; Fleming, P.; King, J.; Martínez-Tossas, L.A. Comparison of modular analytical wake models to the Lillgrund wind plant. J. Renew. Sustain. Energy 2020, 12, 053311. [Google Scholar] [CrossRef]
- Doekemeijer, B.M.; Simley, E.; Fleming, P. Comparison of the Gaussian wind farm model with historical data of three offshore wind farms. Energies 2022, 15, 1964. [Google Scholar] [CrossRef]
- Otter, A.; Murphy, J.; Pakrashi, V.; Robertson, A.; Desmond, C. A review of modelling techniques for floating offshore wind turbines. Wind Energy 2022, 25, 831–857. [Google Scholar] [CrossRef]
- Sayed, M.; Klein, L.; Lutz, T.; Krämer, E. The impact of the aerodynamic model fidelity on the aeroelastic response of a multi-megawatt wind turbine. Renew. Energy 2019, 140, 304–318. [Google Scholar] [CrossRef]
- Jonkman, J.; Buhl, M.L., Jr. FAST User’s Guide; NREL/EL-500-38230; NREL: Golden, CO, USA, 2005. [Google Scholar]
- Larsen, T.J.; Hansen, A.M. How 2 HAWC2, the User’s Manual; Risø-R-1597; Risø: Roskilde, Denmark, 2019. [Google Scholar]
- Uchida, T.; Kawashima, Y. New Assessment Scales for Evaluating the Degree of Risk of Wind Turbine Blade Damage Caused by Terrain-Induced Turbulence. Energies 2019, 12, 2624. [Google Scholar] [CrossRef]
- Cordle, A.; Jonkman, J. State of the art in floating wind turbine design tools. In Proceedings of the International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Navadeh, N.; Goroshko, I.; Zhuk, Y.; Moghadam, F.E.; Fallah, A.S. Finite Element Analysis of Wind Turbine Blade Vibrations. Vibration 2021, 4, 310–322. [Google Scholar] [CrossRef]
- Hansen, M.O.L.; Sørensen, J.N.; Voutsinas, S.; Sørensen, N.; Madsen, H.A. State of the art in wind turbine aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2006, 42, 285–330. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Pereira, R.; Kotsonis, M. Fluctuations of angle of attack and lift coefficient and the resultant fatigue loads for a large Horizontal Axis Wind turbine. Renew. Energy 2017, 114-B, 904–916. [Google Scholar]
- Liao, D.; Zhu, S.-P.; Correia, J.; De Jesus, A.; Veljkovic, M.; Berto, F. Fatigue reliability of wind turbines: Historical perspectives, recent developments and future prospects. Renew. Energy 2022, 200, 724–742. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative Damage in Fatigue. J. Appl. Mech. 1945, 3, 159–164. [Google Scholar] [CrossRef]
- Thomsen, K. The Statistical Variation of Wind Turbine Fatigue Loads; Risø-R-1063(EN); Risø National Laboratory: Roskilde, Denmark, 1998. [Google Scholar]
- Oliveira, G. Vibration-Based Structural Health Monitoring of Wind Turbines. Ph.D. Thesis, FEUP, Porto, Portugal, 2016. [Google Scholar]
- Pacheco, J.; Pimenta, F.; Pereira, S.; Cunha, A.; Magalhães, F. Experimental evaluation of strategies for wind turbine farm-wide fatigue damage estimation. Eng. Struct. 2023, 285, 115913. [Google Scholar] [CrossRef]
- EN 1993-1-9; Eurocode 3. Design of Steel Structures—Part 1-9: Fatigue. European Committee for Standardization: Brussels, Belgium, 2005.
- Pimenta, F.; Ribeiro, D.; Róman, A.; Magalhães, F. Predictive model for fatigue evaluation of floating wind turbines validated with experimental data. Renew. Energy 2024, 223, 119981. [Google Scholar] [CrossRef]
- DNVGL-ST-0376; Standard: Rotor Blades for Wind Turbines. DNV GL AS: Bærum, Norway, 2015.
- Pacheco, J.; Guimarães, S.; Moutinho, C.; Marques, M.; Matos, J.C.; Magalhães, F. New strategies for optimized structural monitoring of wind farms: Experimental campaign. Wind Energy Sci. 2020, 5, 983–996. [Google Scholar] [CrossRef]
- Hines, E.M.; Baxter, C.D.P.; Ciochetto, D.; Song, M.; Sparrevik, P.; Meland, H.J.; Strout, J.M.; Bradshaw, A.; Hu, S.-L.; Basurto, J.R.; et al. Structural instrumentation and monitoring of the Block Island Offshore Wind Farm. Renew. Energy 2023, 202, 1032–1045. [Google Scholar] [CrossRef]
- van Dijk, M.T.; van Wingerden, J.W.; Ashuri, T.; Li, Y. Wind farm multi-objective wake redirection for optimizing power production and loads. Energy 2017, 121, 561–569. [Google Scholar] [CrossRef]
- Bossanyi, E. Combining induction control and wake steering for wind farm energy and fatigue loads optimisation. J. Phys. Conf. Ser. 2018, 1037, 032011. [Google Scholar] [CrossRef]
- Reyes, H.M.; Kanev, S.; Doekemeijer, B.; van Wingerden, J.W. Validation of a lookup-table approach to modeling turbine fatigue loads in wind farms under active wake control. Wind Energy Sci. 2019, 4, 549–561. [Google Scholar] [CrossRef]
- Lin, M.; Porté-Agel, F. Power Maximization and Fatigue-Load Mitigation in a Wind-Turbine Array by Active Yaw Control: An LES Study. J. Phys. 2020, 1618, 042036. [Google Scholar] [CrossRef]
- Sun, J.; Chen, Z.; Yu, H.; Qian, P.; Zhang, D.; Si, Y. Multi-Objective Offshore Wind Farm Wake Redirection Optimization for Power Maximization and Load Reduction. In Proceedings of the American Control Conference, Atlanta, GA, USA, 8–10 June 2022; pp. 5235–5240. [Google Scholar]
- Sun, J.; Chen, Z.; Yu, H.; Gao, S.; Wang, B.; Ying, Y.; Sun, Y.; Qian, P.; Zhang, D.; Si, Y. Quantitative evaluation of yaw-misalignment and aerodynamic wake induced fatigue loads of offshore wind turbines. Renew. Energy 2022, 199, 71–86. [Google Scholar] [CrossRef]
- He, R.; Yang, H.; Lu, L. Optimal yaw strategy and fatigue analysis of wind turbines under the combined effects of wake and yaw control. Appl. Energy 2023, 337, 120878. [Google Scholar] [CrossRef]
- Lucas Frutuoso, T.R.; Marante Pereira, M.; Santos Pereira, R.B.; Madeira, J.F.A.; Cintra, J. Exploring the Power and Loads Paradigm: Tocha Farm Case Study. J. Phys. Conf. Ser. 2024, 2767, 092102. [Google Scholar] [CrossRef]
- Braunbehrens, R.; Anand, A.; Campagnolo, F.; Bottasso, C.L. First experimental results on lifetime-aware wind farm control. J. Phys. Conf. Ser. 2024, 2767, 032042. [Google Scholar] [CrossRef]
- Requate, N.; Meyer, T.; Hofmann, R. Maximizing value through optimized annual selection of Pareto-optimal wind turbine operating strategies. J. Phys. Conf. Ser. 2024, 2767, 032045. [Google Scholar] [CrossRef]
- He, R.; Yang, H.; Sun, S.; Lu, L.; Sun, H.; Gao, X. A machine learning-based fatigue loads and power prediction method for wind turbines under yaw control. Appl. Energy 2022, 18, 120013. [Google Scholar] [CrossRef]
- Pawar, S.; Sharma, A.; Vijayakumar, G.; Bay, C.J.; Yellapantula, S.; San, O. Towards multi-fidelity deep learning of wind turbine wakes. Renew. Energy 2022, 200, 867–879. [Google Scholar] [CrossRef]
- Guilloré, A.; Campagnolo, F.; Bottasso, C.L. A control-oriented load surrogate model based on sector-averaged inflow quantities: Capturing damage for unwaked, waked, wake-steering and curtailed wind turbines. J. Phys. Conf. Ser. 2024, 2767, 032019. [Google Scholar] [CrossRef]
- Liew, J.; Riva, R.; Friis-Møller, M.; Madeira, J.F.A.; Göçmen, T. Wind Farm Control Optimisation Under Load Constraints Via Surrogate Modelling. J. Phys. Conf. Ser. 2024, 2767, 092039. [Google Scholar] [CrossRef]
- Yang, S.; Deng, X.; Li, Q. A joint optimization framework for power and fatigue life based on cooperative wake steering of wind farm. Energy 2025, 319, 134849. [Google Scholar] [CrossRef]
- Popko, W.; Thomas, P.; Sevinc, A.; Rosemeier, M.; Batge, M.; Braun, R.; Meng, F.; Horte, D.; Balzani, C. Iwes Wind Turbine iwt-7.5-164. rev 4; Fraunhofer Institute for Wind Energy Systems IWES: Bremerhaven, Germany, 2018. [Google Scholar]
- Quaranta, H.U.; Bolnot, H.; Leweke, T. Long-wave instability of a helical vortex. J. Fluid Mech. 2015, 780, 687–716. [Google Scholar] [CrossRef]
- Premaratne, P.; Tian, W.; Hu, H. A Proper-Orthogonal-Decomposition (POD) Study of the Wake Characteristics behind a Wind Turbine Model. Energies 2022, 15, 3596. [Google Scholar] [CrossRef]
- van den Berg, D.; de Tavernier, D.; van Wingerden, J.-W. The dynamic coupling between the pulse wake mixing strategy and floating wind turbines. Wind Energy Sci. 2023, 8, 849–864. [Google Scholar] [CrossRef]
- Frederik, J.A.; Doekemeijer, B.M.; Mulders, S.P.; van Wingerden, J.-W. The helix approach: Using dynamic individual pitch control to enhance wake mixing in wind farms. Energies 2020, 23, 1739–1751. [Google Scholar] [CrossRef]
- Harvey, M.; Strivens, S.; Evans, H.; Morris, A.; Wendt, F.; Matha, D.; Phillips, S.; Hawkes, G.; Sowman, J.; Borgarino, B.; et al. Floating Wind Joint Industry Programme, Phase IV Summary Report; Carbon Trust: London, UK, 2022. [Google Scholar]
- Nanos, E.M.; Letizia, S.; Clemente, D.J.B.; Wang, C.; Rotea, M.; Iungo, V.I.; Bottasso, C. Vertical wake deflection for offshore floating wind turbines by differential ballast control. J. Phys. Conf. Ser. 2020, 1618, 022047. [Google Scholar] [CrossRef]
- Storm, R.M. Wake Control Using Rotor Tilting: Optimizing Wind Farm Energy Production Through Vertical Wake Deflection. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).