Identification of Dielectric Response Parameters of Pumped Storage Generator-Motor Stator Winding Insulation Based on Sparsity-Enhanced Dynamic Decomposition of Depolarization Current

Abstract

Accurate diagnosis of the insulation condition of stator windings in pumped storage generator-motor units is crucial for ensuring the safe and stable operation of power systems. Time domain dielectric response testing is an effective method for rapidly diagnosing the insulation condition of capacitive devices, such as those in pumped storage generator-motors. To precisely identify the conductivity and relaxation process parameters of the insulating medium and accurately diagnose the insulation condition of the stator windings, this paper proposes a method for identifying the insulation dielectric response parameters of stator windings based on sparsity-enhanced dynamic mode decomposition of the depolarization current. First, the measured depolarization current time series is processed through dynamic mode decomposition (DMD). An iterative reweighted L1 (IRL1)-based method is proposed to formulate a reconstruction error minimization problem, which is solved using the ADMM algorithm. Based on the computed modal amplitudes, the dominant modes—representing the main insulation relaxation characteristics—are separated from spurious modes caused by noise. The parameters of the extended Debye model (EDM) are then calculated from the dominant modes, enabling precise identification of the relaxation characteristic parameters. Finally, the accuracy and feasibility of the proposed method are verified through a combination of simulation experiments and laboratory tests.

1. Introduction

With continuous advancement of the “dual carbon” goal, energy structure reform and low-carbon transformation of the power sector in China have been steadily deepening. The grid-connected capacity of new energy has grown rapidly, and the high proportion of renewable energy integration poses significant challenges to the safe and stable operation of the power system [1]. Against this backdrop, the peak-shaving, frequency regulation, phase-balancing, and emergency reserve functions of pumped storage power stations [2] play critical roles in ensuring the safe and stable operation of the new power system and have seen significant development in recent years. The functional role of pumped storage power stations requires their generator-motors to undergo frequent rapid starts and stops, as well as swift transitions between operating modes. This results in the stator windings of the units being subjected repeatedly to extreme electrical, mechanical, and thermal stresses [3,4]. The rapid degradation of the winding insulation system leads to the formation of defects, which further evolve and significantly increase the probability of sudden failures. A sudden failure of a pumped storage unit would result in substantial economic losses, with potentially severe and far-reaching consequences. Therefore, accurately diagnosing the insulation condition of pumped storage generator-motor stator windings is crucial for preventing sudden winding failures and ensuring the safe and stable operation of the power system.

Currently, commonly used on-site diagnostic methods for assessing stator winding insulation condition include insulation resistance testing, withstand voltage testing, impulse voltage testing, partial discharge testing, and dielectric loss factor (tan δ) measurement [5]. However, the test results of these methods often exhibit significant variability and provide limited insulation information, making it difficult to achieve accurate diagnosis of stator winding insulation condition. More importantly, the mainstream starting method for pumped storage units is variable-frequency starting, and the operating environment is characterized by substantial white noise and harmonic interference. Moreover, during routine maintenance of a unit within the power station, other units that are operating normally are not shut down, which places even higher demands on the robustness of the diagnostic methods. Therefore, there is an urgent need to develop a diagnostic method for stator winding insulation condition that is efficient, non-destructive, highly resistant to interference, and capable of providing comprehensive diagnostic information.

In recent years, dielectric response testing has gradually become an important method for assessing capacitive equipment such as transformer oil-paper insulation [6,7], cable insulation [8,9] and stator winding insulation [10] owing to its advantages of being efficient, non-destructive, highly resistant to interference, and capable of providing rich insulation condition information. Among them, the polarization and depolarization current (PDC) method in time domain dielectric response testing uses a DC voltage for measurement and offers advantages such as portable equipment, rapid testing, and rich diagnostic information. When a DC voltage is applied to the stator windings of a pumped storage generator-motor, the response characteristics of the insulation and its equivalent circuit exhibit pronounced capacitive behavior. Therefore, using the PDC method to test the stator windings of pumped storage generator-motors can effectively diagnose the insulation condition.

Overall, the key points for diagnosing the insulation condition of electrical equipment using the PDC method are: (1) performing equivalent modeling of the measured polarization and depolarization currents from the PDC testing device to construct the EDM; and (2) accurately identifying the branch characteristic parameters related to insulation conductivity and relaxation behavior based on the constructed EDM. The number of branches and their parameters are then used to calculate the electrical parameters of insulation, enabling accurate assessment of the insulation condition of the equipment [11]. Based on these two key diagnostic points, it is evident that accurately diagnosing the insulation condition of pumped storage generator-motor stator windings using time domain dielectric response testing hinges on two main aspects, detailed as follows:

(1)

Establishing an EDM that accurately represents the epoxy–mica composite insulation system of stator windings. At present, the process of constructing EDMs for the insulation of capacitive electrical equipment is largely based on expert experience, where the number of branches in the model is estimated using prior knowledge. This approach places high demands on the experience level of on-site testing personnel. To address this issue, the authors of ref. [12] propose construct-ing EDM by enumerating multiple branch numbers and fitting the current based on each model, then selecting the model with the highest fitting accuracy. Although this method partially addresses the issue of determining the number of branches, artificially setting the number of branches solely to achieve better fitting accuracy undermines the physical significance of each branch in the EDM. The authors of ref. [13] determined the number of branches in the model by differentiating the depolarization current and identifying the number of local maxima in the resulting differential curve. Although this method can automatically determine the number of branches in the model, it has drawbacks such as high computational complexity, a relatively intricate calculation process, and strong sensitivity to noise, making it unsuitable for rapid diagnostics in engineering field applications.

(2)

Precisely identifying the model parameters based on PDC test data. Currently, traditional approaches rely on fitting methods, where the expression of the polarization/depolarization current is derived from a predefined model, and fitting algorithms are then used to solve for the branch parameters. In recent years, intelligent optimization algorithms such as genetic algorithms (GAs) [14], the gray wolf optimizer (GWO) [15], and the Cuckoo search (CS) algorithm [16] have been increasingly adopted to improve fitting accuracy. However, although these methods can quickly find results with very high fitting accuracy, they still require manual setting of the branch number. As mentioned earlier, these approaches not only lose the physical significance of the EDM but also struggle to detect changes in the number of branches.

To address the challenge of achieving rapid and accurate insulation diagnostics for pumped storage generator-motor stator windings using the PDC method in field applications, the primary prerequisite is to construct an EDM with clear physical significance and to develop a highly robust parameter identification method. Therefore, this paper proposes a dielectric response parameter identification method based on sparsity-enhanced dynamic decomposition of the depolarization current. This method enables the automatic determination of the number of branches in the EDM while ensuring the physical interpretability of the results, effectively addressing the challenge faced by traditional methods in determining the appropriate number of branches. Moreover, the method demonstrates strong robustness, accurately identifying EDM branch parameters even under low signal-to-noise ratio (SNR) conditions. First, the depolarization current time series is subjected to modal decomposition based on the DMD algorithm to extract modal components at each order, each representing distinct physical characteristics. Subsequently, the IRL1 minimization method and ADMM are introduced to sparsify each modal component, enabling precise separation of dominant modes—representing the insulation relaxation characteristics—from spurious modes caused by noise interference. The model parameters are then calculated based on the dominant modes, achieving automatic determination of the number of branches in the EDM and precise identification of the model parameters. Finally, the accuracy of the proposed method is validated through simulation experiments using predefined model parameters and its performance is compared with that of traditional fitting methods. Additionally, the method is applied in the laboratory to diagnose the insulation condition of different stator bar samples, and the diagnostic results are compared with the microscopic morphology and performance characterization of the insulation, further verifying the effectiveness of the proposed approach.

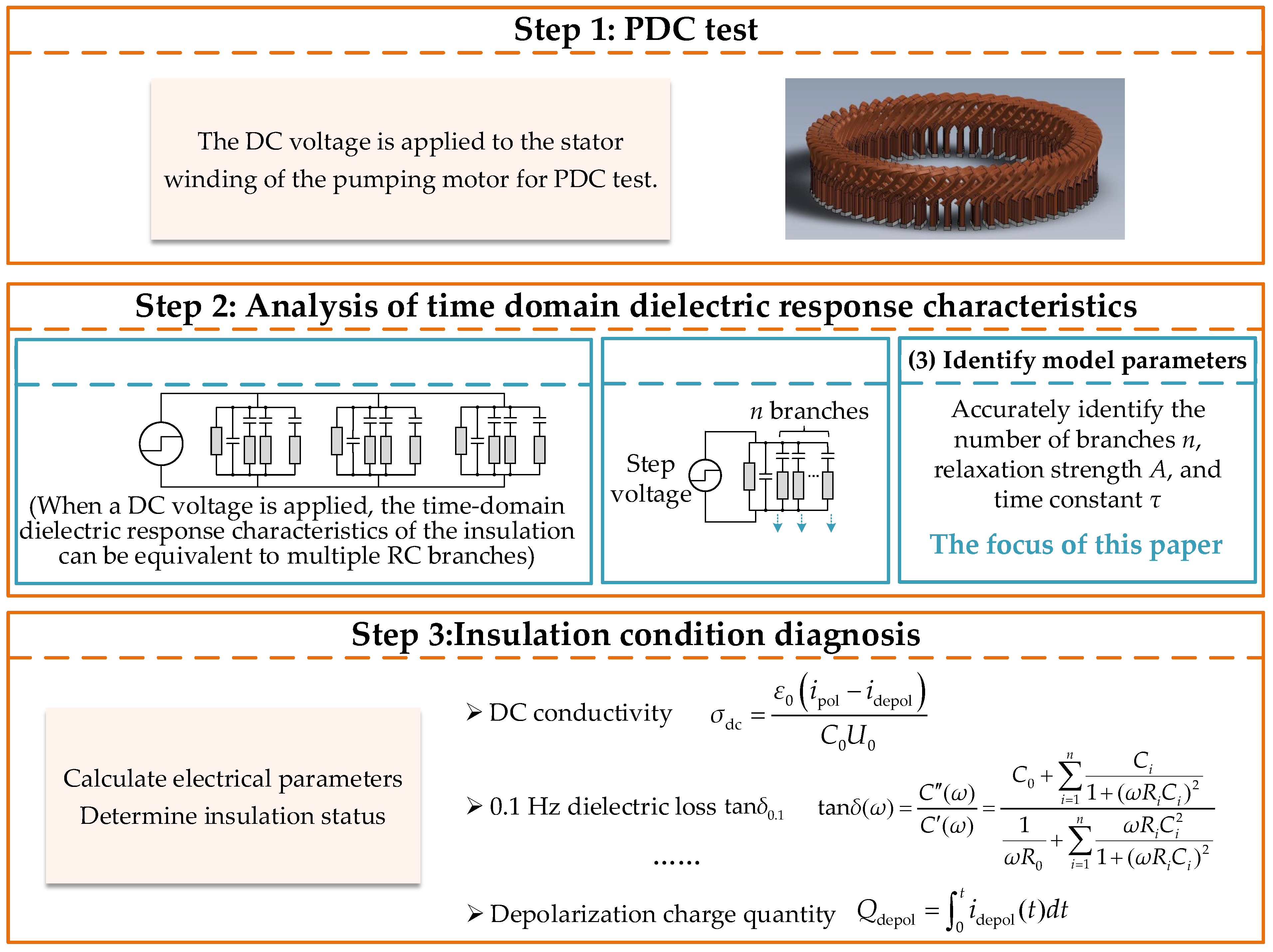
2. Principle of Diagnosing Stator Winding Insulation Condition Based on the PDC Method

The on-site diagnostic process for assessing the insulation condition of a single-phase stator winding in a pumped storage generator-motor using the PDC method is shown in Figure 1 and is described in detail below.

In the first step, DC voltage U₀ is applied to the single-phase stator winding of the pumped storage generator-motor to perform the PDC test, inducing polarization in the insulation. According to dielectric response theory, the polarization current i_pol can be expressed as follows:

$$i_{\mathrm{pol}}(t)=C_0{U}_0\left[{\displaystyle \frac{\sigma }{{\epsilon }_0}}+f(t)\right]$$

(1)

where C₀ is the geometric capacitance of the winding. U₀ is the polarization voltage. σ is the conductivity. ε₀ is the vacuum permittivity. f(t) is the dielectric response function of the winding insulation.

After applying polarization voltage U₀ for a duration of t_p, the voltage is removed, ending the polarization process and initiating the depolarization test. The measured depolarization current i_depol can be expressed as follows:

$$i_{\mathrm{depol}}(t)=C_0{U}_0\left[f(t)–f(t+t_p)\right]$$

(2)

where t_p is the polarization duration.

In the second step, after completing the PDC test, the polarization/depolarization currents are analyzed to obtain the time domain dielectric response characteristics of the stator winding. Accurate analysis of the time domain dielectric response hinges on constructing an EDM based on the physical properties of the insulation and precisely identifying the model parameters from the test data.

During the PDC test, each stator bar of the single-phase winding is subjected to the same DC voltage. The time domain dielectric response characteristics of the insulation can be equivalently represented by a multi-RC circuit composed of a series-parallel combination of resistors and capacitors, namely the EDM [17].

The single-phase stator winding consists of multiple stator bars connected in series and parallel, with insulating boxes used at the junctions to complete the insulation structure. Since the material of the insulating boxes is the same as that of the insulation, their time domain dielectric response characteristics do not differ significantly from those of the insulation. Therefore, the time domain dielectric response of the single-phase stator winding can be equivalently represented by the series-parallel combination of multiple EDMs, effectively forming a unified EDM for the entire winding.

The structure of the EDM is shown in Figure 2, where each branch of the model represents a specific type of relaxation or conduction process within the stator winding insulation system. R₀ represents the insulation resistance, corresponding to the conductive current component of the insulation under a DC electric field. C₀ is the geometric capacitance, representing the overall instantaneous polarization process of the insulation, which completes within a very short time. Each series branch of R_i and C_i represents a distinct type of relaxation process within the insulation. The relaxation time constant for each branch is τ_i = R_i × C_i.

After equivalently modeling the time domain dielectric response behavior of the stator winding insulation, the polarization current i_pol and the depolarization current i_depol can be expressed as follows:

$$i_{\mathrm{pol}}={\displaystyle \frac{U_0}{R_0}}+{\displaystyle \sum _{i=1}^n\frac{U_0}{R_i}{e}^{–\frac{t}{{\tau }_i}}}$$

(3)

$$i_{\mathrm{depol}}={\displaystyle \sum _{i=1}^n{A}_i{e}^{–\frac{t}{{\tau }_i}}}$$

(4)

$$A_i={\displaystyle \frac{U_0}{R_i}}\left(1–e^{–{\displaystyle \frac{t_p}{{\tau }_i}}}\right)$$

(5)

where A_i is the relaxation strength coefficient of branch i.

After equivalently modeling the time domain dielectric response characteristics of the single-phase stator winding, the key to diagnosing the insulation condition of the pumped storage generator-motor lies in determining the number of relaxation branches n with clear physical significance. Based on this, the relaxation strength coefficient A_i and relaxation time constant τ_i of each branch are then accurately solved using the noise-affected test data.

In the third step, electrical parameters are calculated based on the dielectric response characteristics—that is, using the branch number n and the branch parameters A_i and τ_i to compute key electrical quantities such as the DC conductivity σ_dc, the dielectric loss factor at 0.1 Hz tanδ_0.1, and the depolarization charge Q_depol. By analyzing changes in the model parameters and electrical parameters, accurate diagnosis of the stator winding insulation condition can be achieved. If errors occur in identifying n, A_i, and τ_i in the second step, the subsequent calculation of electrical parameters will be directly affected, making it impossible to accurately diagnose the insulation condition of the pumped storage generator-motor stator windings. Therefore, the focus of this study is to accurately identify the physically meaningful branch number n, relaxation strength coefficient A_i, and relaxation time constant τ_i from noise-contaminated test data.

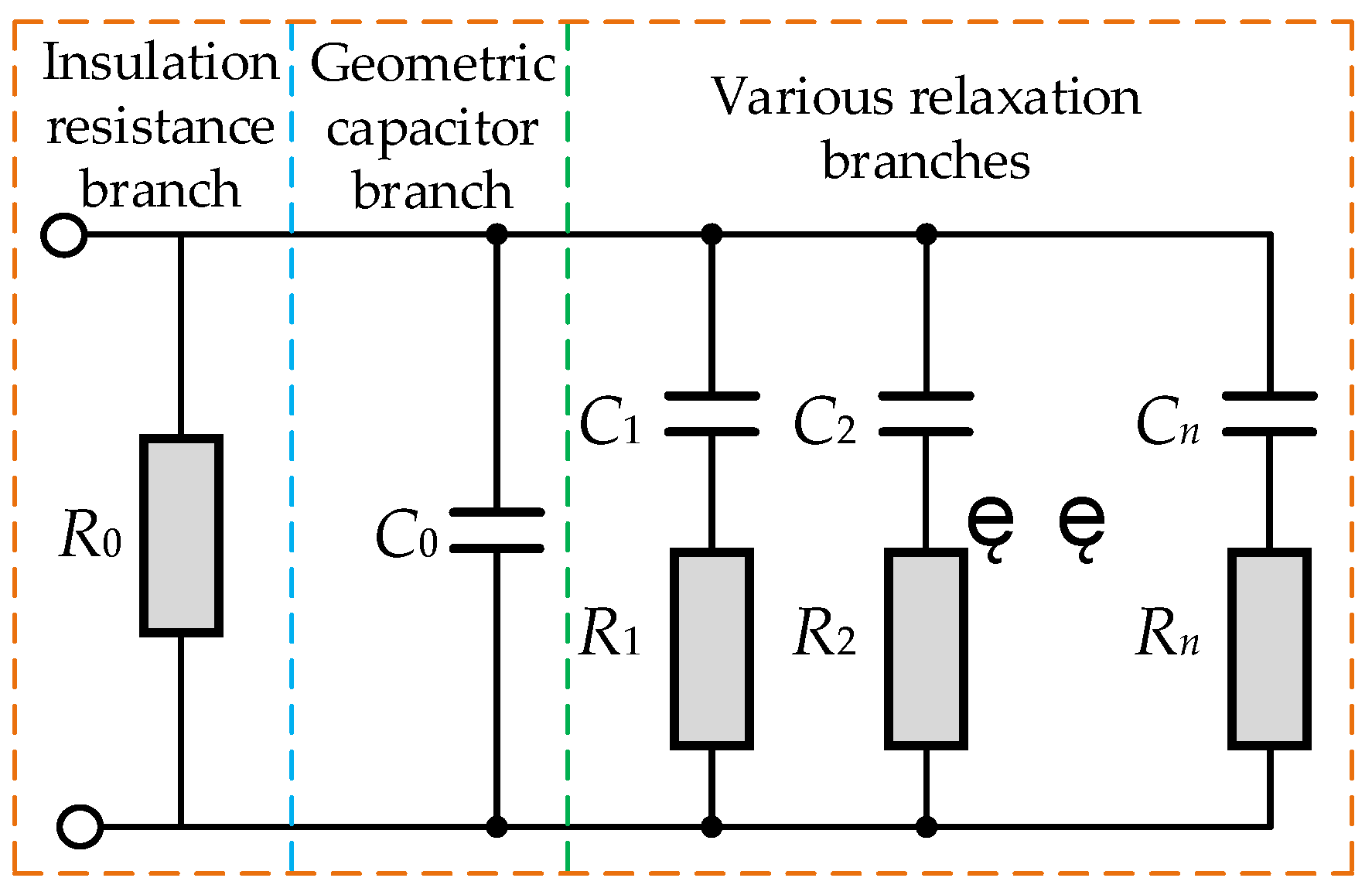
3. EDM Parameter Identification Method Based on Sparsity-Enhanced Dynamic Decomposition of Depolarization Current

Based on the measured polarization and depolarization current data, directly predicting the number of branches in the EDM may lead to errors in branch number identification due to the unclear physical meaning of each branch, making it difficult to accurately diagnose insulation condition. Therefore, this paper applies the DMD algorithm to process the depolarization current time series to obtain modal components with clear physical significance. Subsequently, the IRL1 minimization method and ADMM algorithm are applied to perform a sparsity enhancement on each modal component, enabling precise selection of the dominant modes that represent the insulation relaxation characteristics. These dominant modes correspond one-to-one with the branches of the EDM. By using the dominant modes to solve for the branch parameters, the method achieves joint and accurate identification of both the branch number and parameters of the EDM for the stator winding insulation of the pumped storage generator-motor.

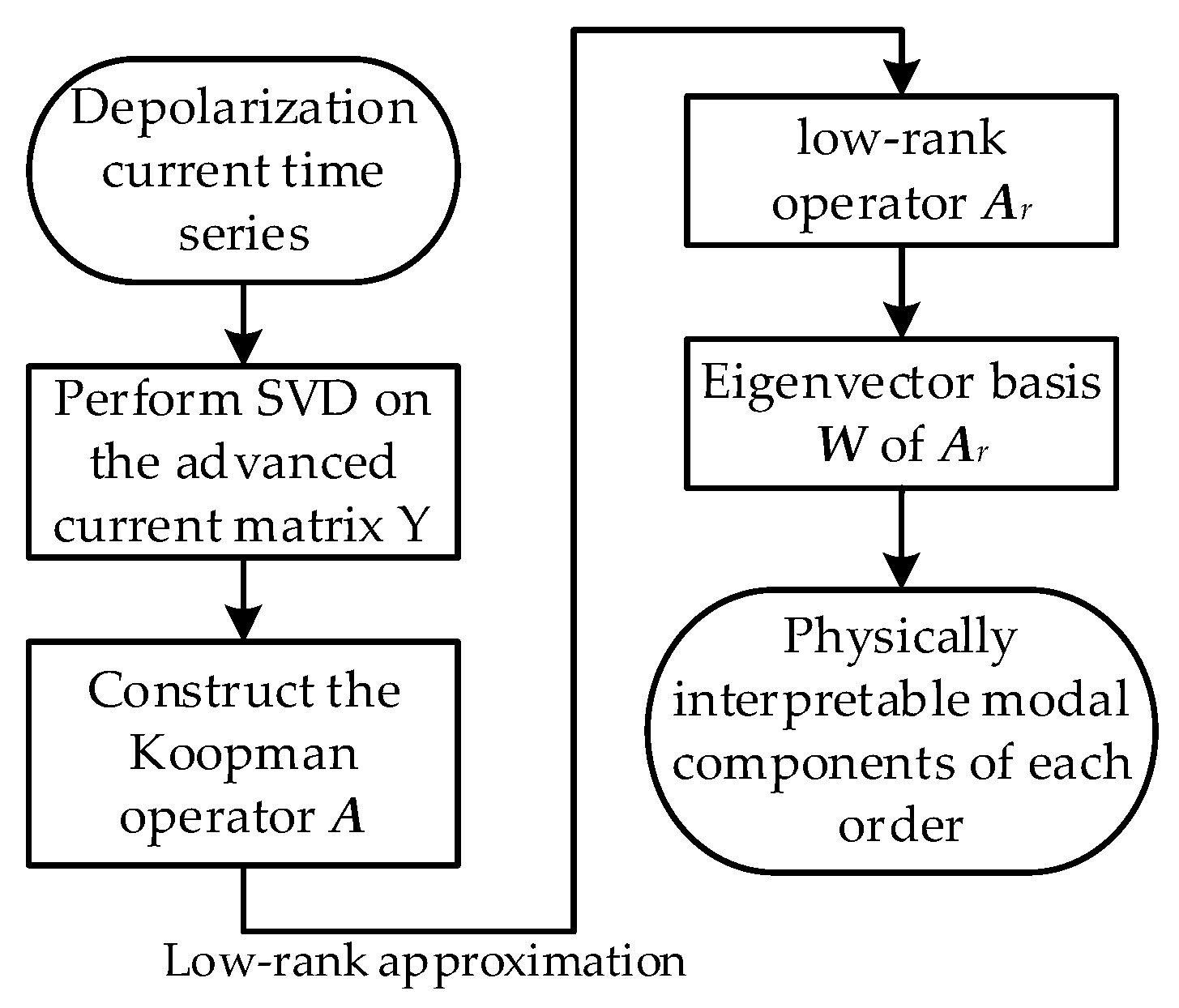
3.1. Dynamic Decomposition of the Depolarization Current Sequence

When performing on-site PDC testing of the stator windings of a pumped storage generator-motor, both polarization and depolarization current curves can be obtained. Either of these current time series can be used for subsequent processing to achieve insulation condition diagnosis. However, it is important to note that the on-site operating environment of pumped storage generator-motors typically involves high humidity and significant contamination. When applying DC voltage to a single-phase winding for PDC testing, using the polarization current for subsequent analysis may lead to large errors in insulation condition diagnosis due to substantial surface leakage currents on the stator bars. In addition, during on-site testing, the polarization current is more susceptible to low-frequency noise, temperature fluctuations, and residual charge effects [18]. Based on the above considerations, this study selects the depolarization current time series of the insulation of the pumped storage generator-motor stator winding for subsequent analysis.

The DMD algorithm was originally applied mainly to flow characteristic extraction problems in fluid mechanics [19]. Each mode obtained by the algorithm corresponds to a unique frequency, which in turn maps directly to a relaxation branch of the EDM, ensuring that the identified branches have clear physical significance [20].

Centering on the depolarization current time series y(t) (t = 1, 2, …, n) obtained from PDC testing, it is constructed into an m × (m + 1) Hankel matrix as follows:

$$\mathit{Y}=\left[\begin{array}{cccc}\mathit{y}\left(1\right)& \mathit{y}\left(2\right)& \dots & \mathit{y}\left(m+1\right)\\ \mathit{y}\left(2\right)& \mathit{y}\left(3\right)& \dots & \mathit{y}\left(m+2\right)\\ ⋮& ⋮& \ddots & ⋮\\ \mathit{y}\left(n–m\right)& \mathit{y}\left(n–m+1\right)& \dots & \mathit{y}\left(n\right)\end{array}\right]$$

(6)

The first m columns and the last m columns of the depolarization current matrix Y are taken to form the forward matrix Y₁ and the backward matrix Y₂, with their relationship expressed as in Equation (7):

$${\mathit{Y}}_2=\mathit{A}{\mathit{Y}}_1+{\mathit{\epsilon }}_0$$

(7)

where the high-order complex matrix A is the Koopman operator, the eigenvectors and eigenvalues of which contain the dynamic characteristics of the depolarization current, representing the relaxation behavior of the insulation of the pumped storage generator-motor stator windings. ε₀ is the residual matrix.

Performing singular value decomposition (SVD) on Y₁ and neglecting the residual matrix ε₀, the decomposition result is shown as follows:

$${\mathit{Y}}_1=\mathit{U}\mathit{\Sigma }{\mathit{V}}^{\ast }$$

(8)

where U is the left singular matrix, Σ is the singular value matrix, and V is the right singular matrix. Based on Equations (7) and (8), the Koopman operator A is computed as follows:

$$\mathit{A}={\mathit{U}}^{\ast }{\mathit{Y}}_2\mathit{V}{\mathit{\Sigma }}^{–1}$$

(9)

The depolarization test of stator windings typically lasts 10–30 min, and to ensure accuracy, the sampling rate is generally no less than 20 Hz. This results in extremely large data volumes per test, making direct computation of the Koopman operator A time consuming and unfavorable for fast on-site diagnostics. To speed up computation and prevent divergence, a low-rank approximation of the Koopman operator is applied. Since the noise magnitude during on-site testing is lower than that of the depolarization current, this rank truncation step partially eliminates noise effects, thereby improving the robustness of the method. Extensive testing and analysis show that using the terminal value of the depolarization current as the rank truncation threshold is sufficient for subsequent calculations. Assuming the rank truncation threshold is r, the low-rank operator A_r, which reflects the characteristics of matrix A, is constructed as follows:

$${\mathit{A}}_r={{\mathit{U}}_r}^{\ast }{\mathit{Y}}_2{\mathit{V}}_r{\mathit{\Sigma }}_r^{–1}$$

(10)

where U_r is the left singular matrix after rank truncation, Σ_r is the truncated singular value matrix, and V_r is the right singular matrix after rank truncation.

The eigenvalues and eigenvectors of A_r are solved as follows:

$${\mathit{A}}_r\mathit{W}=\mathit{W}\mathit{\Lambda }$$

(11)

where Λ is the diagonal matrix of eigenvalues of A_r and W is the matrix of eigenvectors of A_r. Based on the known eigenvalues and eigenvectors of A_r, the individual modes are constructed as follows:

$$\mathit{\Phi }={\mathit{Y}}_2\mathit{V}{\mathit{\Sigma }}^{–1}\mathit{W}=\left[\begin{array}{cccc}{\mathit{\varphi }}_1& {\mathit{\varphi }}_2& \cdots & {\mathit{\varphi }}_r\end{array}\right]$$

(12)

where Φ is the mode matrix and ϕ_i(i = 1, 2, …, r) are the individual dynamic modes.

It can be seen that each eigenvalue and eigenvector of A_r uniquely corresponds to a single-frequency mode, representing a specific relaxation characteristic of the stator winding insulation. Thus, the proposed method enables the construction of an EDM with physically meaningful branches.

In summary, the dynamic decomposition process of the depolarization current based on the DMD algorithm is illustrated in Figure 3. After forming the depolarization current sequence into a Hankel matrix, the forward current matrix Y₁ is subjected to SVD, followed by construction of the Koopman operator A. After applying low-rank approximation to A, physically meaningful modes are built directly from the eigenvectors of A_r.

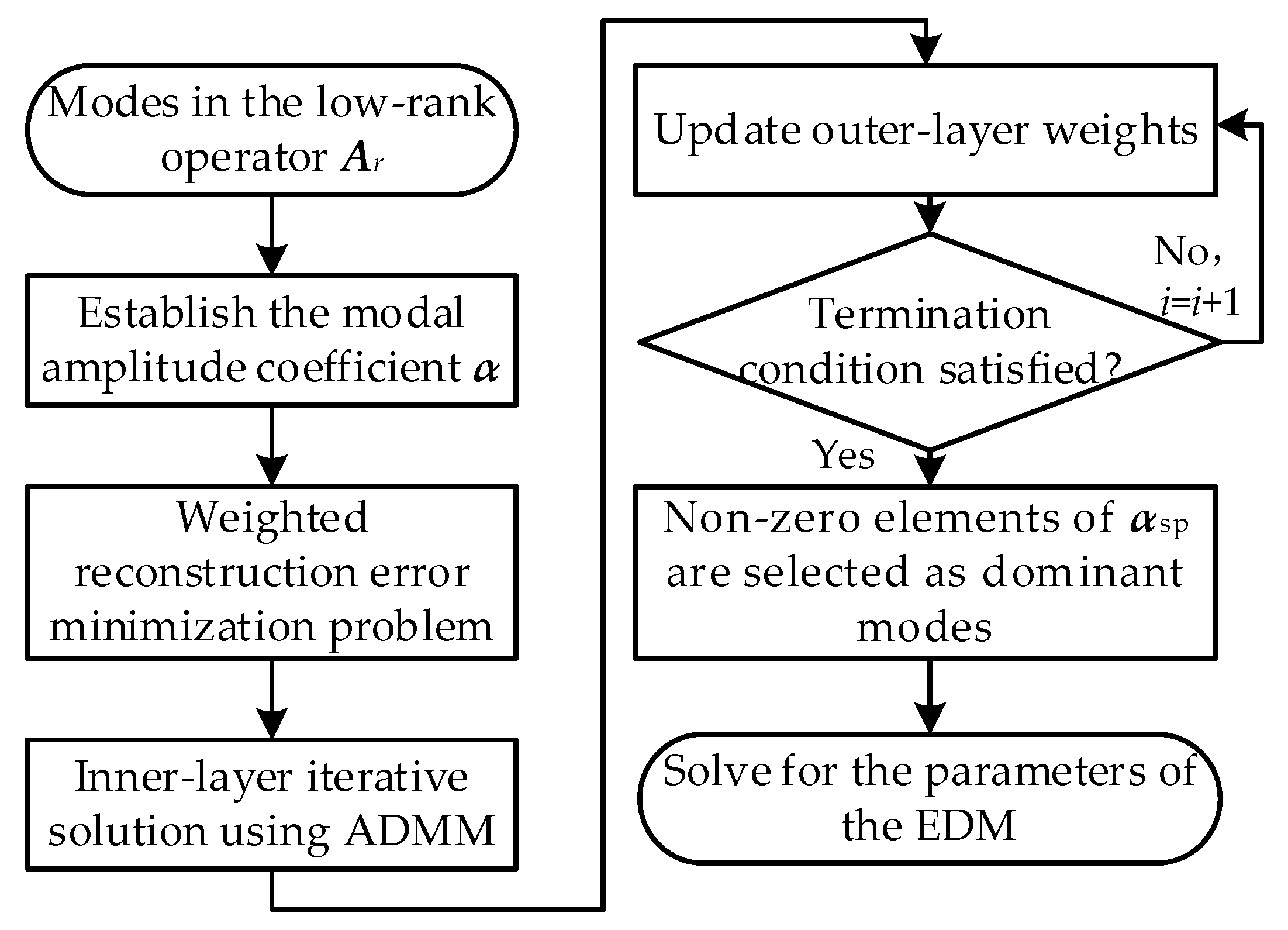
3.2. Sparsity Enhancement Method Based on the IRL1-ADMM Method

In Section 3.1, the DMD algorithm is used to achieve dynamic decomposition of the depolarization current, thereby constructing the EDM. However, during the modal decomposition process, a relatively large depolarization current endpoint value is selected as the truncation threshold to preserve the dominant modes, which causes the truncated modes to still contain false modes introduced by on-site noise. To enhance the robustness of the proposed testing method against on-site noise and to uniquely determine the branch number of the EDM, this study introduces L1 regularization with dynamically adjusted weights, constructing an optimization problem that minimizes reconstruction error to facilitate subsequent screening of each mode.

Based on the principles of the DMD algorithm, the expression for the forward depolarization current matrix Y₁ containing the modal amplitudes α_i is given by Equation (13):

$${\mathit{Y}}_1\approx \mathit{\Phi }{\mathit{D}}_{\alpha }{\mathit{V}}_{\mathrm{and}}={\left[\begin{array}{c}{\mathit{\varphi }}_{ 1}\\ {\mathit{\varphi }}_{ 2}\\ ⋮\\ {\mathit{\varphi }}_{ r}\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cccc}{\alpha }_1& & & \\ & {\alpha }_2& & \\ & & \ddots & \\ & & & {\alpha }_r\end{array}\right]\left[\begin{array}{cccc}1& {\lambda }_1& \dots & {\lambda }_1^{N-2}\\ 1& {\lambda }_2& \dots & {\lambda }_2^{N-2}\\ ⋮& ⋮& & ⋮\\ 1& {\lambda }_r& \dots & {\lambda }_r^{N-2}\end{array}\right]$$

(13)

where D_α= diag(α₁ α₂ … α_r) is the diagonal matrix of amplitude coefficients and V_and is the Vandermonde matrix that encapsulates the relaxation characteristics of insulation.

To specify the initial values of the amplitude coefficients and facilitate the preliminary separation of dominant and spurious modes, the reconstruction error in Equation (13) is defined as in Equation (14):

$$\begin{array}{l}\mathit{J}\left(\mathit{\alpha }\right)=\left|\right|{\mathit{Y}}_1-\mathit{\Phi }{\mathit{D}}_{\alpha }{\mathit{V}}_{\mathrm{and}}|{|}_F^2\\ \hspace{1em}=\mathrm{tr}({(\mathit{\Sigma }{\mathit{V}}^{\ast }-\mathit{W}{\mathit{D}}_{\alpha }{\mathit{V}}_{\mathrm{and}})}^{\ast }(\mathit{\Sigma }{\mathit{V}}^{\ast }-\mathit{W}{\mathit{D}}_{\alpha }{\mathit{V}}_{\mathrm{and}}))\\ \hspace{1em}={\mathit{\alpha }}^{\ast }\mathit{P}\mathit{\alpha }-{\mathit{q}}^{\ast }\mathit{\alpha }-{\mathit{\alpha }}^{\ast }\mathit{q}+s\end{array}$$

(14)

where P = (W*W)$\cdot$(V_andV_and*)^T represents element-wise multiplication of corresponding matrix entries. q = diag(V_andVΣ*W)^T. s = tr(Σ*Σ). α is the column vector composed of the truncated α_i(I = 1, 2, …, r), expressed as α = [α₁ α₂ … α_r]^T.

The minimum reconstruction error optimization problem is defined as follows:

$$\underset{\alpha }{\min } \mathit{J}\left(\mathit{\alpha }\right)$$

(15)

By solving Equation (15), the initial expression for α is obtained as shown in Equation (16):

$$\mathit{\alpha }={\mathit{P}}^{-1}\mathit{q}$$

(16)

Then, the IRL1 minimization method is introduced to enhance the sparsity of the approach, minimizing the deviation between the dominant modes and the relaxation information contained in the forward depolarization current matrix Y₁, with the formulated least absolute shrinkage and selection operator (LASSO) expressed as follows:

$$\underset{\alpha }{\min }{‖\mathit{Y}-\mathit{\Phi }\mathit{\alpha }‖}_2^2+\lambda {\displaystyle \sum _{i=1}^n{\mathsf{\omega }}_{\mathrm{i}}^{(\mathrm{k})}}|{\alpha }_i|$$

(17)

where λ is the regularization parameter, with larger values promoting higher sparsity in the method. After extensive computational testing and considering the trade-off between sparsity and computational efficiency, λ is set to 0.01 in this study. The expression for weight ω is:

$${\mathsf{\omega }}_i^{(k)}={\displaystyle \frac{1}{|{\alpha }_i^{(k–1)}|+ϵ}}$$

(18)

where ϵ > 0 is the smoothing parameter.

Subsequently, each weighted LASSO subproblem is solved using the ADMM approach, with the procedure described below.

(1)

Introducing the auxiliary variable z, reformulate Equation (19) as follows:

$$\underset{\alpha }{\min }{‖\mathit{Y}-\mathit{\Phi }\mathit{\alpha }‖}_2^2+\lambda {\displaystyle \sum _{i=1}^n{\omega }_i^{(k)}}| z_i |$$

(19)

The corresponding augmented Lagrangian function is:

$$\mathcal{L}(\mathit{\alpha },\mathit{z},\mathit{\mu })=||\mathit{Y}-\mathit{\Phi }\mathit{\alpha }|{|}_2^2+\lambda {\displaystyle \sum _{i=1}^n{w}_i^{(k)}}| z_i |+{\mathit{\mu }}^{\mathrm{T}}(\mathit{\alpha }-\mathit{z})+{\displaystyle \frac{\rho }{2}}||\mathit{\alpha }-\mathit{z}|{|}_2^2$$

(20)

where μ denotes the Lagrange multiplier and ρ > 0 is the penalty parameter of the augmented term.

(2)

Iteratively update α, z, and μ:

$$\left\{\begin{array}{c}{\mathit{\alpha }}^{t+1}=\underset{\alpha }{\mathrm{argmin}}\mathcal{L}(\mathit{\alpha },{\mathit{z}}^t,{\mathit{\mu }}^t)\\ {\mathit{z}}^{t+1}=\underset{\beta }{\mathrm{argmin}}\mathcal{L}({\mathit{\alpha }}^{t+1},\mathit{z},{\mathit{\mu }}^t)\\ {\mathit{\mu }}^{t+1}={\mathit{\mu }}^t+\rho ({\mathit{\alpha }}^{t+1}-{\mathit{z}}^{t+1})\end{array}\right.$$

(21)

(3)

Update the weights and repeat until the convergence criterion is satisfied. After the inner-layer ADMM converges, the weights are updated as follows:

$${\omega }_i^{(k+1)}={\displaystyle \frac{1}{|{\alpha }_i^{(k)}|+ϵ}}$$

(22)

Repeat the outer IRL1 iterations until the following convergence criterion is satisfied:

$${\displaystyle \frac{{‖{\mathit{\alpha }}^{(k)}-{\mathit{\alpha }}^{(k-1)}‖}_2}{{‖{\mathit{\alpha }}^{(k-1)}‖}_2}}<\delta$$

(23)

where δ is the convergence threshold. After extensive computational analysis and considering both computational complexity and efficiency, δ is set to 0.001 in this study.

The optimal solution α_sp can be obtained through the above solution process, as expressed in Equation (24):

$${\mathit{\alpha }}_{\mathrm{sp}}=\left[\begin{array}{cc}\mathit{I}& \mathbf{0}\end{array}\right]{\left[\begin{array}{cc}\mathit{P}& {\mathit{E}}^{\mathrm{T}}\\ \mathit{E}& \mathbf{0}\end{array}\right]}^{-1}\left[\begin{array}{c}\mathit{q}\\ \mathbf{0}\end{array}\right]$$

(24)

where I is the identity matrix, and E consists of unit column vectors for which the nonzero elements correspond to the zero components of α.

This paper employs the IRL1 method to enhance the sparsity of the solution and utilizes the ADMM to efficiently solve each weighted LASSO subproblem. By integrating the sparsity-promoting mechanism of IRL1 with the strong robustness of ADMM, the proposed approach significantly improves the identification accuracy of dominant modes within noisy signals.

Through the above iterative sparsity enhancement solution based on IRL1-ADMM, the optimal amplitude coefficients α_sp for each mode are constructed. In this process, the amplitude coefficients of spurious modes are effectively zeroed out, enabling precise separation of dominant modes—representing the insulation relaxation characteristics—from spurious modes caused by noise interference.

Based on the selected dominant modes, the parameters of the EDM for the stator winding insulation are calculated using Equations (25) and (26). By analyzing the variations in the number of branches n, the relaxation strength coefficient A_i, and the relaxation time constant τ_i, the insulation condition of the stator winding can be accurately diagnosed.

$${\tau }_i=-{\displaystyle \frac{T_s}{\ln \left({\lambda }_i\right)}}$$

(25)

$$\left[\begin{array}{c}\mathit{y}\left(1\right)\\ \mathit{y}\left(2\right)\\ ⋮\\ \mathit{y}\left(n\right)\end{array}\right]=\left[\begin{array}{cccc}1& 1& \dots & 1\\ {\lambda }_1& {\lambda }_2& \dots & {\lambda }_i\\ ⋮& ⋮& \ddots & ⋮\\ {\lambda }_1^{n-1}& {\lambda }_2^{n-1}& \dots & {\lambda }_i^{n-1}\end{array}\right]\left[\begin{array}{c}{A}_1\\ A_2\\ ⋮\\ A_i\end{array}\right]$$

(26)

where T_s is the sampling interval of the PDC test.

Overall, the sparsity-enhanced process of the depolarization current based on the IRL1-ADMM method is illustrated in Figure 4. Based on the modal components of the low-rank operator A_r from Section 3.1, the amplitude coefficients α are constructed. By solving the reconstruction error optimization problem based on the IRL1-ADMM method, the minimum reconstruction error is achieved when the termination condition is met. The dominant modes corresponding to the optimized amplitude coefficients α_sp are then used to calculate the parameters of the EDM, thereby realizing the joint and precise identification of both the branch number and parameters of the EDM of stator winding insulation.

4. Method Validation

To verify the accuracy and feasibility of the proposed method, this study employed a combination of simulation and experimental validation. For simulation verification, comparative tests were conducted using predefined branch parameters. For experimental verification, stator bar samples with different insulation conditions were prepared and tested in the laboratory. The insulation condition of each sample was diagnosed using the proposed method. The insulation of different samples was then taken for microscopic morphology and performance characterization. By comparing the insulation analysis results with the diagnostic outcomes of the proposed method, the accuracy and feasibility of the method were validated.

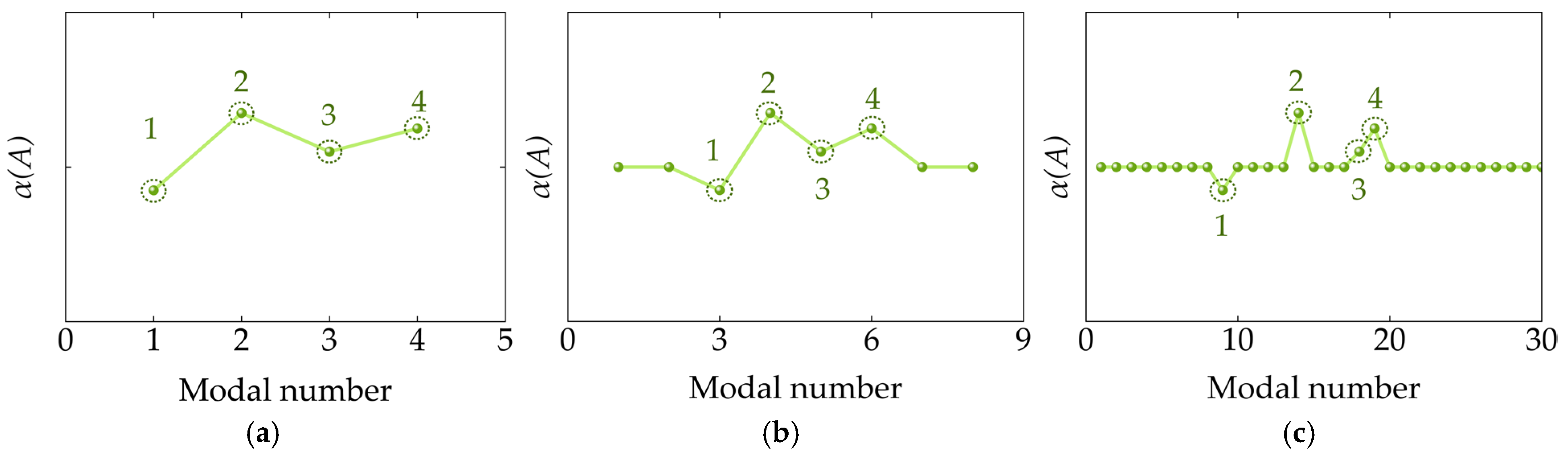
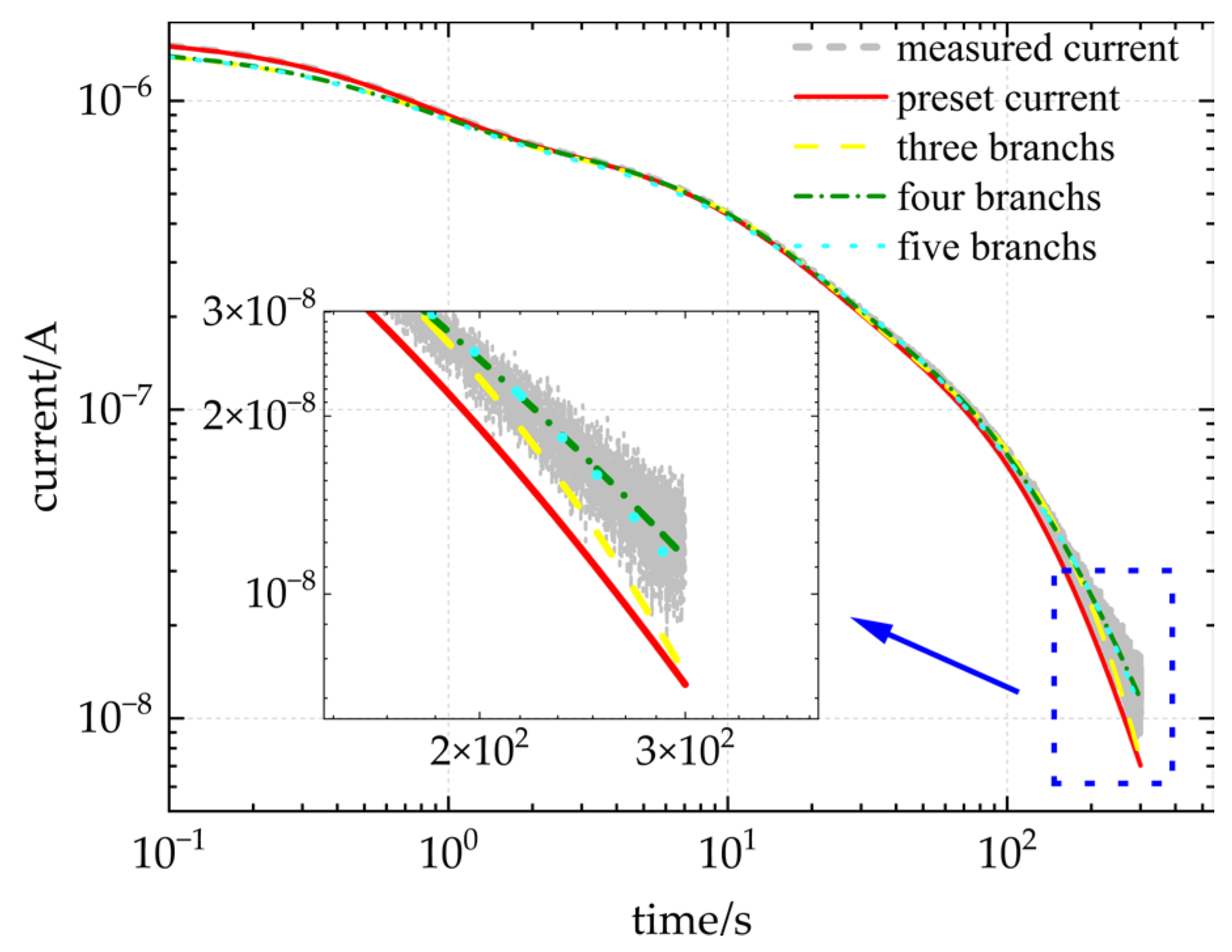
4.1. Simulation Validation

To verify the accuracy of the proposed method in identifying both the branch number and parameters of the EDM, depolarization current time series were generated using MATLAB R2024a for validation of branch identification performance. The typical polarization types in stator winding insulation include interfacial polarization, dipole orientation polarization, and space charge polarization. When insulation degrades, additional polarization types emerge, resulting in an increased number of branches in the EDM. Therefore, four branches were preset in this study to simulate the condition of insulation degradation with additional branches. The magnitudes of the preset parameters for each branch were configured based on typical polarization types of stator insulation, as detailed in

Table 1. The setup of branch parameters for depolarization current simulation in MATLAB.

Branch i	Relaxation Strength Ai/nA	Time Constant τi/s
1	40	150
2	240	60
3	510	10
4	850	0.6

. Additionally, to simulate the presence of strong noise interference during field testing at pumped storage power stations, random noise was added to the four-branch simulated current data, resulting in SNR values of 50 dB, 40 dB, and 30 dB.

Using the proposed method, depolarization current data under different SNR conditions were analyzed, and the identified branch parameters are summarized in

Table 2. Identification results of branch parameters under different noise conditions.

SNR	Branch i	Relaxation Strength Ai/nA	Time Constant τi/s
50 dB	1	38.498	155.765
	2	240.92	60.608
	3	511.566	10.002
	4	849.286	0.6
40 dB	1	42.176	150.691
	2	231.931	61.913
	3	499.291	10.083
	4	833.349	0.598
30 dB	1	46.755	152.273
	2	221.533	62.412
	3	523.936	10.021
	4	844.836	0.599

. The correspondence between α and the number of branches is shown in Figure 5. In Figure 5, the dominant modes are marked with circles, and the numbers indicate the indices of the dominant modes. At an SNR value of 50 dB, the terminal value of the depolarization current was approximately 7 nA, and the rank truncation threshold r was set to 7 nA. At SNR values of 40 dB and 30 dB, the terminal value of the depolarization current was approximately 8 nA, and the rank truncation threshold r was set to 8 nA. The results showed that, across all three noise levels, the method accurately determined the branch number n = 4, confirming the effectiveness of the approach in identifying the correct number of branches. As the SNR value decreased, deviations between the identified relaxation strength A, relaxation time constant τ, and their preset values gradually increased. The maximum deviation in relaxation strength A was observed for A₁ under the 30 dB condition, with a deviation of 16.88%. The maximum deviation in relaxation time constant τ occurred for τ₂ under the same 30 dB condition, with a deviation of 4.02%.

An analysis of these deviations indicated that the errors arose because the EDM parameters in Equations (25) and (26) were calculated using depolarization current data contaminated by noise. For instance, under the 30 dB SNR condition, the SNR at the tail end of the current dropped below −10 dB. Thus, even if either A or τ was identified perfectly, the other may still exhibit deviation due to signal distortion. Furthermore, when analyzing polarization types based on the EDM, classification typically relies on the relaxation time constant τ rather than A. Therefore, in model parameter identification, it is essential to prioritize the accuracy of τ. Even under 30 dB SNR, the proposed method successfully identified the correct number of branches, with the maximum deviation in τ remaining small (approximately 4%), which is fully acceptable for engineering applications.

To further quantify the branch identification performance of the proposed algorithm, the coefficient of determination R² and the mean absolute percentage error (MAPE) were introduced to measure the difference between the original data and the identified data. The coefficient of determination R² is a statistical indicator used to assess the goodness of fit between the identified and original data. Its calculation formula is given as follows, with a range from 0 to 1, with a higher R² value indicating a better fit:

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{\left|{\mathit{y}}_{\mathrm{measured}}\left(i\right)-\widehat{\mathit{y}}\left(i\right)\right|}^2}}{{{\displaystyle \sum _{i=1}^n\left|{\mathit{y}}_{\mathrm{measured}}\left(i\right)-\frac{1}{n}{\displaystyle \sum _{i=1}^n\widehat{\mathit{y}}\left(i\right)}\right|}}^2}}$$

(27)

Here, y_measured(i) represents the measured current data and y(i) denotes the identified current data.

The mean absolute percentage error (MAPE) is a statistical metric used to assess the accuracy of a prediction model, representing the absolute percentage error between the predicted and actual values. Its calculation formula is given as follows, with a smaller MAPE value indicating that the identification results are closer to the original data:

$$MAPE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|\frac{{\mathit{y}}_{\mathrm{preset}}\left(i\right)-\widehat{\mathit{y}}\left(i\right)}{{\mathit{y}}_{\mathrm{preset}}\left(i\right)}\right|}\times 100\%$$

(28)

Here, y_preset(i) represents the preset current data.

The calculated R² and MAPE values under different SNR conditions are shown in Figure 6. As the noise level increased, R² decreased, with the minimum value reaching 0.9990. Conversely, MAPE increased with rising noise levels, with a maximum of approximately 6%. Overall, as the noise amplitude increased, the identification error of the branch parameters gradually grew. However, even at an SNR value of 30 dB, the algorithm maintained excellent accuracy and robustness, demonstrating that the proposed method is clearly feasible for identifying the dielectric response parameters of stator winding insulation in engineering field applications.

In addition, the performance of the proposed method was compared with commonly used branch fitting methods [14,15,16]. The traditional branch fitting method was applied to identify parameters from current data with an SNR value of 30 dB. The results for different branch numbers are shown in Figure 7. The figure shows that traditional methods, which focus on achieving the best mathematical fit, naturally produce good fitting results. However, these methods often rely on manually setting the branch number to improve fitting accuracy. Although the fit may look good, the true branch number cannot be accurately determined. This can cause large errors in the identified parameters and may mislead insulation condition assessments. Therefore, such methods are not suitable for practical diagnostics during maintenance.

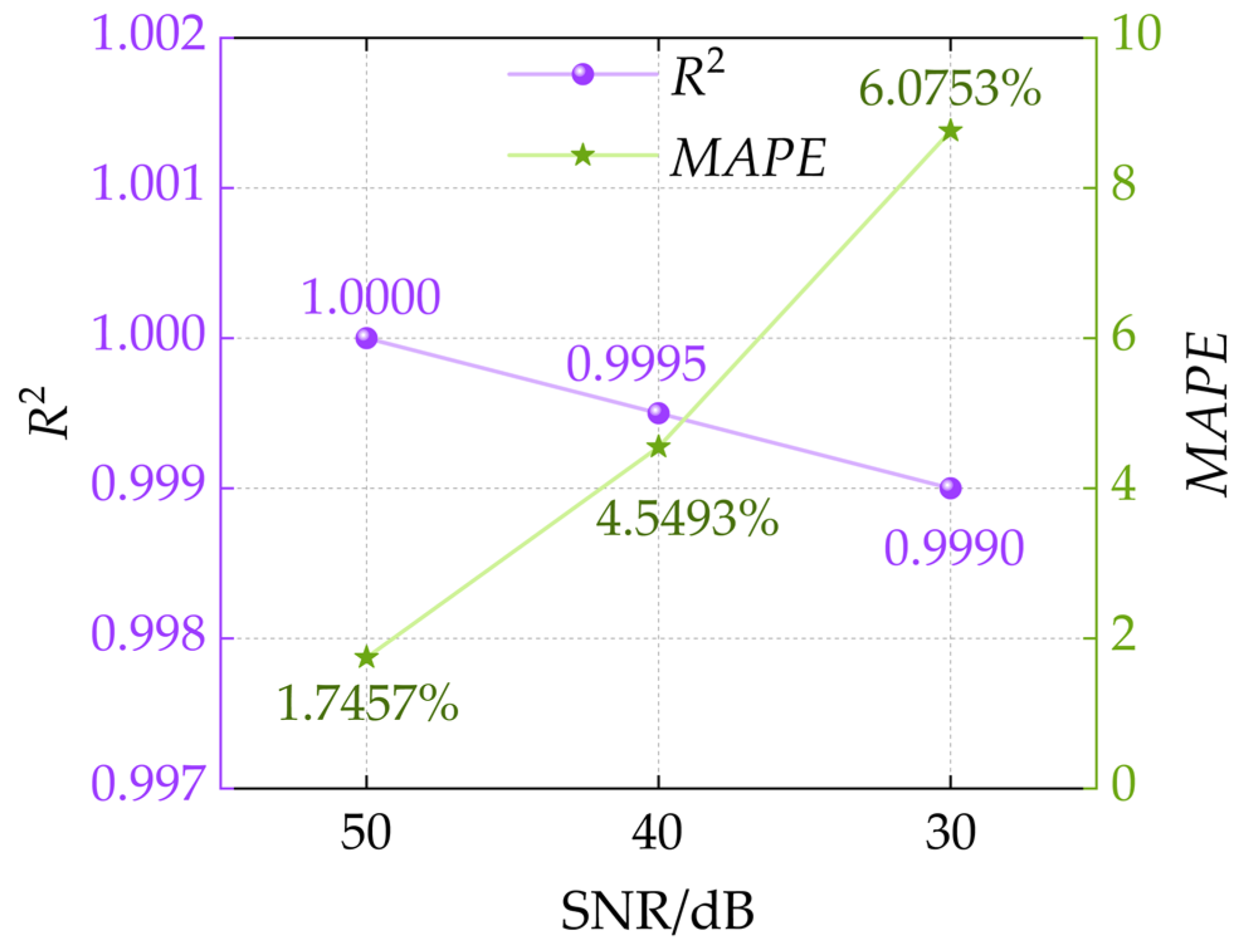
4.2. Experimental Validation

During on-site PDC testing, when a DC voltage is applied to a single-phase stator winding, the time domain dielectric response characteristics of the insulation can be equivalently modeled by an EDM comprising multiple branches, as illustrated in Figure 8. In practice, under DC voltage, the time domain dielectric response characteristics of a single stator bar can also be equivalently represented by an EDM with multiple branches; the main difference between the complete winding and a single bar lies in the number of branches and the magnitude of the branch parameters. To experimentally validate the accuracy and feasibility of the proposed method, and given the constraints of the testing environment, a single stator bar was tested in the laboratory using the PDC method. The proposed method was then applied for parameter identification to assess the insulation condition. Subsequently, samples were taken sequentially from the insulation of different specimens, and microscopic characterization as well as material performance testing methods were employed. The characterization results were then compared with the diagnostic outcomes obtained using the proposed method, validating its accuracy and feasibility.

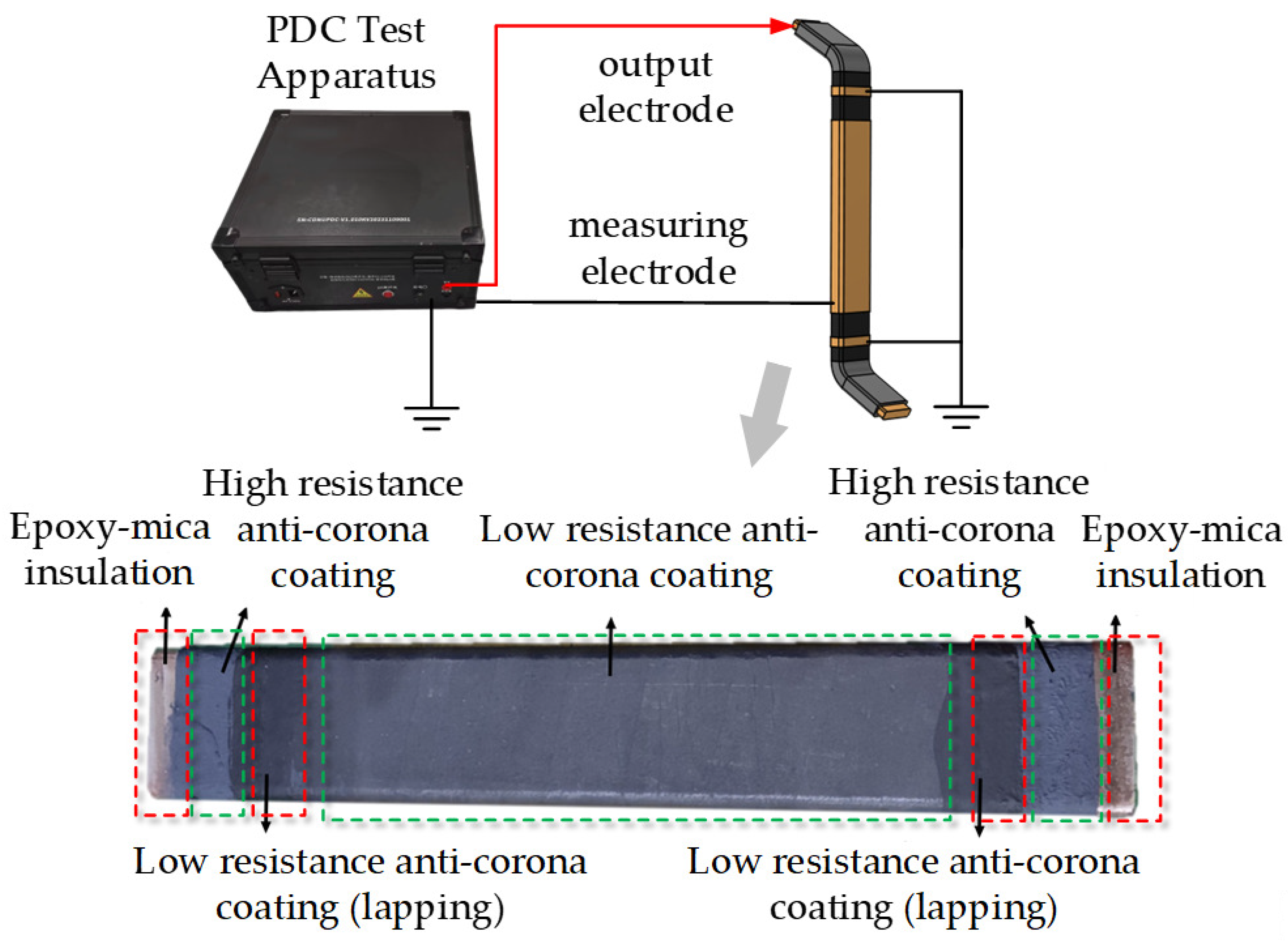
4.2.1. Experimental Sample Setup

A stator bar aging and testing platform was set up in the laboratory. The test samples were fabricated from newly manufactured stator bars of a pumped storage generator-motor, rated at 15.75 kV and 312 MW. The insulation consisted of an epoxy–mica composite, produced using a low-resin vacuum pressure impregnation (VPI) process, with the insulation classified as Class F. During the experiment, the slot section of the full-length stator bar was mechanically processed into short specimens of 50 cm in length, and the insulation corona protection structure of each sample was restored. A schematic of the short sample preparation is shown in Figure 9.

The low-resistance corona protection tape at both ends of each short sample was stripped for 8 cm. A 0.3-mm-thick layer of high-resistance corona protection paint was applied between 2 cm and 7 cm from the ends. After curing, a 0.3-mm-thick layer of low-resistance corona protection paint was coated between 5 cm and 9 cm from the ends as an overlap to prevent electric field distortion at the junction between the low-resistance tape and high-resistance paint from affecting the test results.

After preparation, the samples were placed in a thermostatic electric blast drying oven for thermal aging to simulate different insulation conditions of the stator bars, facilitating subsequent evaluation of their insulation status using the proposed method.

The drying oven used was model DHG-9640A, with the thermal aging temperature set at 180 °C. The aging durations for each stator bar are listed in

Table 3. The setup of the samples.

Sample Number	Sample Processing
#1	Thermal aging 0 days
#3	Thermal aging 10 days
#2	Thermal aging 20 days
#4	Thermal aging 30 days

. After aging, each sample was cooled to room temperature in a dry environment, and PDC testing was promptly carried out following the wiring configuration shown in Figure 9 to prevent moisture absorption from affecting the test results. The employed testing apparatus was a self-developed PDC testing device [21].

During testing, the copper conductor of the stator bar was connected to the high-voltage output terminal of the tester, while the central low-resistance corona coating was tightly wrapped with copper foil and connected to the measurement terminal. Shielding rings were installed at both ends and grounded to eliminate the influence of surface leakage currents on the test results. The PDC test was conducted with a polarization voltage of 1 kV, and both the polarization and depolarization times were set to 300 s.

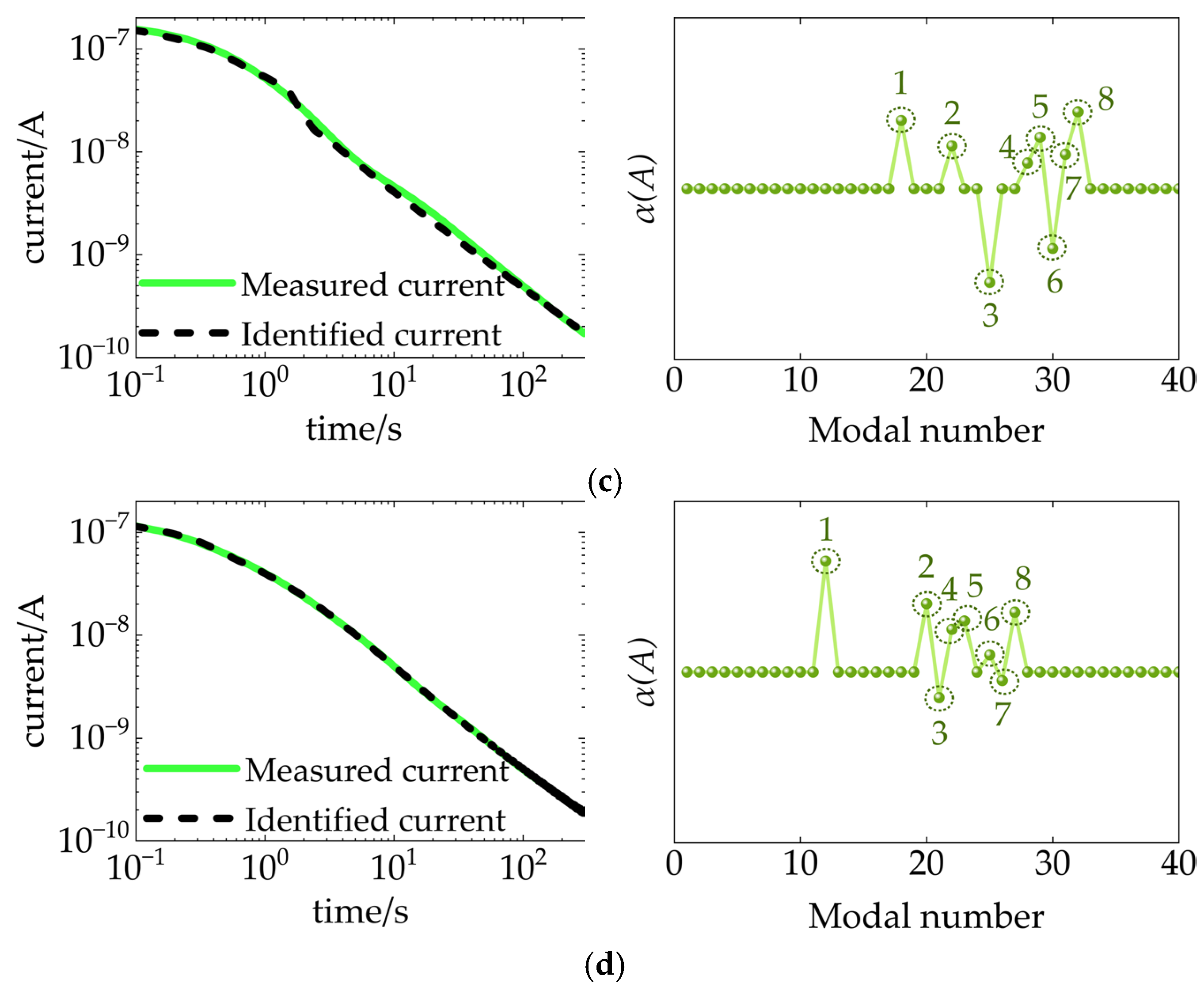
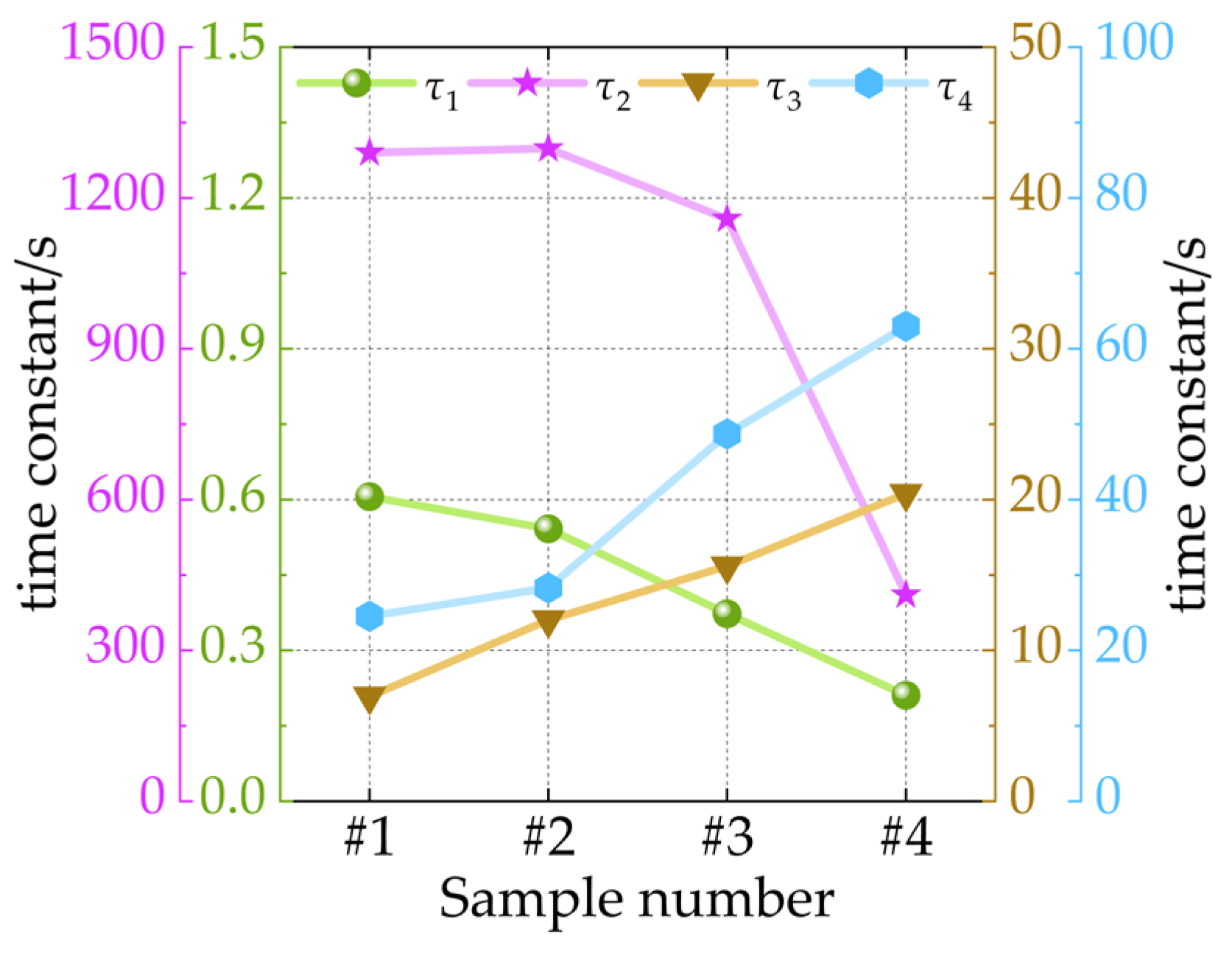
4.2.2. Insulation Condition Assessment

Based on the depolarization current time series obtained from the PDC tests of different samples, branch number and parameter identification were performed. The terminal value of the depolarization current for all sample groups was at the nanoampere level; therefore, the rank truncation threshold r was set to 1 nA. The depolarization current and branch identification results are shown in Figure 10. In Figure 10, the dominant modes are marked with circles, and the numbers indicate the indices of the dominant modes. It can be observed that the measured and identified currents for all samples exhibited a high degree of agreement, demonstrating the strong identification accuracy of the proposed method. The number of dominant modes retained using the proposed method directly corresponded to the number of branches in the EDM, eliminating the need for manual determination of branch numbers and thereby reducing the application threshold for this method in maintenance scenarios. Comparing the branch numbers of different samples, samples #1 and #2 exhibited six branches, while samples #3 and #4 showed an increase to eight branches, indicating the emergence of new polarization types within the insulation that warrant close attention. The additional branches had relatively small relaxation strength A and time constant τ values on the order of 100, suggesting they were most likely associated with interfacial polarization. This implied that slight delamination may have occurred in the epoxy–mica insulation systems of samples #3 and #4.

An analysis of the trends in the identified branch parameters for each sample was conducted. Due to space limitations, only the variations in the time constants of selected representative branches are presented here, as shown in Figure 11. τ₁ is the time constant corresponding to the branch with the largest relaxation strength, representing the dipolar polarization process within the insulation. τ₂ is the time constant of the branch with the longest relaxation time, which is closely related to the insulation condition [22]. τ₃ and τ₄ are time constants with values slightly lower than that of τ₂, typically in the range of 10¹~10², and are most likely associated with interfacial polarization. As shown in Figure 11, the values of τ₁ and τ₂ decreased progressively across samples #1, #2, #3, and #4. The reduction in τ₁ value indicated that dipolar polarization was more easily established, while the decrease in τ₂ value confirmed the continuous degradation of the stator bar insulation. By contrast, the values of τ₃ and τ₄ increased successively, suggesting a slower establishment of interfacial polarization, likely due to the worsening of delamination within the insulation. In summary, the diagnostic results for insulation condition were ranked as follows: #1 > #2 > #3 > #4.

To further quantify the identification errors across different samples, the R² values for each sample are calculated and shown in

Table 4. The R² values of the identification results for different samples.

Sample Number	R2
#1	0.9987
#3	0.9963
#2	0.9961
#4	0.9998

. It can be seen that, although the noise level varied during PDC testing of different samples, resulting in slight fluctuations in accuracy, all R² values remained above 0.9961. This demonstrated that the proposed method offers strong noise robustness and can meet the practical requirements for rapid insulation condition diagnostics of pumped storage generator-motor stator windings in field applications. Although the single stator bar used in the laboratory differs from the actual stator winding, in practice, once the time domain dielectric response of insulation under DC voltage is equivalently modeled using the EDM, the difference lies only in the number of model branches and the specific parameter values. This does not affect the applicability or effectiveness of the proposed method for diagnosing the insulation condition of stator windings.

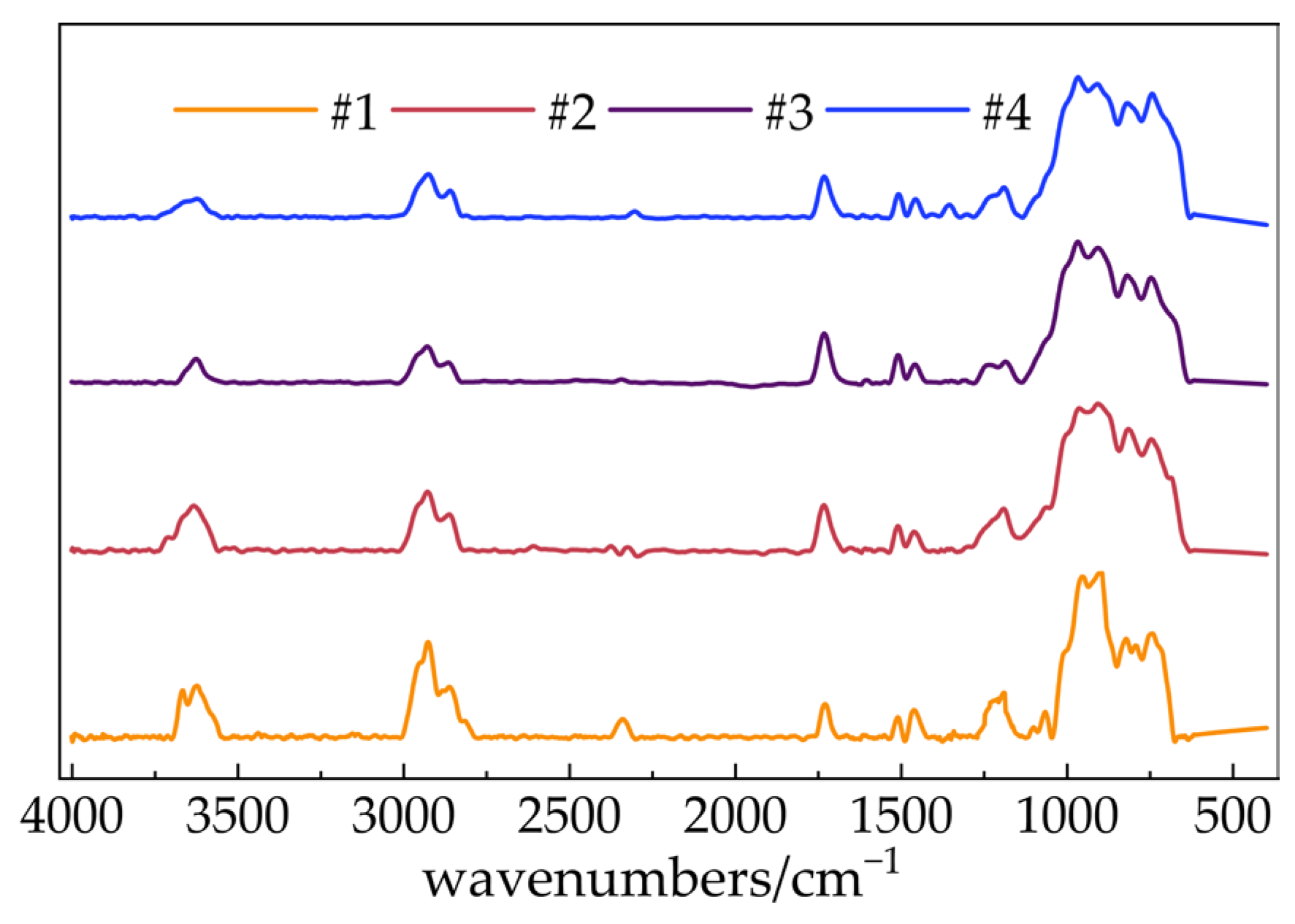
4.2.3. Material Performance Testing of Samples for Validation

Since the stator bars used in this study were newly manufactured, post-curing of the insulation may occur during the aging process, meaning that the insulation condition may initially improve before degrading. Therefore, it is not possible to directly assess the insulation condition of the stator bars based solely on aging duration. To reliably validate the accuracy of the insulation state assessment results in Section 4.2.2 using the proposed method, samples were taken from the insulation of stator bars #1, #2, #3, and #4 for scanning electron microscope (SEM) testing and Fourier-transform infrared spectroscopy (FTIR) analysis. The material performance characterization results were then compared with the assessment outcomes presented in Section 4.2.2 to verify the reliability of the proposed evaluation method.

The insulation samples obtained were coated with gold using a sputter coater, and their microstructure was characterized using a Phenomenon Pro scanning electron microscope (manufactured by Phenom-World B.V., Thermo Fisher Scientific, Eindhoven, The Netherlands). During testing, the accelerating voltage was set to 10 kV, and the magnification was 4000×. The characterization results are shown in Figure 12.

As shown in the figure, the surface morphology of sample #1’s insulation was very smooth, with only a small number of detached resin particles of small size. The adhesion between the epoxy resin and mica layers was good, indicating that the insulation was in good condition. For sample #2, the number of detached particles on the insulation surface increased, but the surface morphology remained smooth overall. The insulation condition was generally similar to that of sample #1, which was consistent with the conclusion in Section 4.2.2, where the number of branches did not change and the branch parameters showed only minor variations. For sample #3, SEM testing of the insulation showed that although the surface of a single insulation layer remained smooth, slight delamination had already occurred. This was consistent with the diagnostic results for sample #3 in Section 4.2.2, where two additional branches were identified, and the magnitude of the branch time constants strongly suggested that they corresponded to new interfacial polarization processes. For sample #4, testing revealed that its insulation exhibited pronounced delamination, with multiple strip-shaped depressions appearing on the surface of individual insulation layers. The insulation condition was the poorest among the samples, which was fully consistent with the diagnostic results obtained using the method proposed in this study. The SEM diagnostic results for all samples were consistent with the parameter identification results in Section 4.2.2, and the method proposed in this study successfully identified delamination phenomena in the insulation of the stator bars.

Further testing was carried out on the insulation samples using a Nicolet 6700 spectrometer (manufactured by Thermo Fisher Scientific, Madison, WI, USA) for FTIR. The light source was a mid-to-far infrared source, with air cooling, a resolution of 0.09 cm⁻¹, wavenumber accuracy of 0.01 cm⁻¹, and a spectral detection range of 400–4000 cm⁻¹. The test results are shown in Figure 13. It can be observed that within the tested spectral range, the main infrared absorption peaks of the epoxy-mica insulation system included the benzene ring C-H out-of-plane deformation vibration peak at 742.86 cm⁻¹, the epoxy ring vibration peak at 902.04 cm⁻¹, the -C=CH- characteristic absorption peak at 965.31 cm⁻¹, the C=O absorption peak between 1700–1750 cm⁻¹, the C-H symmetric stretching vibration peak at 2876 cm⁻¹, the C-H asymmetric stretching vibration peak at 2924 cm⁻¹, and the -OH characteristic absorption peak at 3621 cm⁻¹.

In this study, the C-H asymmetric stretching vibration peak (2924 cm⁻¹) and the C-H symmetric stretching vibration peak (2876 cm⁻¹) were used to qualitatively characterize the aging condition of the insulation in each stator bar sample. These two C–H bonds are among the primary structural components of the epoxy resin molecular chain. The intensities of these peaks intuitively reflect the degree of molecular chain scission in epoxy resin and thus serve as useful indicators of the insulation condition [23]. It can be clearly observed from the figure that the intensity of these characteristic peaks for samples #1, #2, #3, and #4 gradually decreased, indicating that the degree of molecular chain degradation in the epoxy resin followed the order #1 < #2 < #3 < #4. Accordingly, the results for the insulation condition were ranked as follows: #1 > #2 > #3 > #4. The diagnostic results of the infrared spectroscopy aligned well with the diagnostic outcomes obtained using the method proposed in Section 4.2.2, verifying the accuracy of the proposed method for identifying the dielectric response parameters of the insulation.

5. Conclusions

To address the urgent need for fast and accurate on-site diagnosis of the insulation condition of pumped storage generator-motor stator windings, and the challenge that although the existing PDC method is convenient for field testing it struggles to accurately determine the EDM, this paper proposes a dielectric response parameter identification method based on sparsity-enhanced dynamic decomposition of the depolarization current. The effectiveness of the proposed method is validated through simulation and laboratory testing, and the main conclusions are as follows:

(1)

To address the limitation of traditional methods in accurately determining the number of branches in the EDM, this study employs the DMD algorithm to decompose the depolarization current into distinct modes. The dominant modes are automatically extracted and used to determine the number of branches, thereby enabling precise identification of both the number and parameters of EDM branches. This approach effectively overcomes the reliance on extensive expert experience or the blind pursuit of fitting accuracy commonly seen in traditional methods.

(2)

Building on the dynamic decomposition of the depolarization current, this study proposes the use of the IRL1 method to construct a reconstruction error minimization problem, which is solved via the ADMM algorithm. This approach enables the precise selection of dominant modes and accurately determines the number of EDM branches even under low SNR conditions. As a result, the robustness of the proposed method against noise in field testing environments is significantly enhanced, enabling joint and accurate identification of both the model’s branch number and parameters. It effectively addresses the limitation of traditional methods, which fail to reliably identify the number of EDM branches under low SNR scenarios.