Assessment of Global and Detailed Chemical Kinetics in Supercritical Combustion for Hydrogen Gas Turbines
Abstract
1. Introduction
2. Materials and Methods
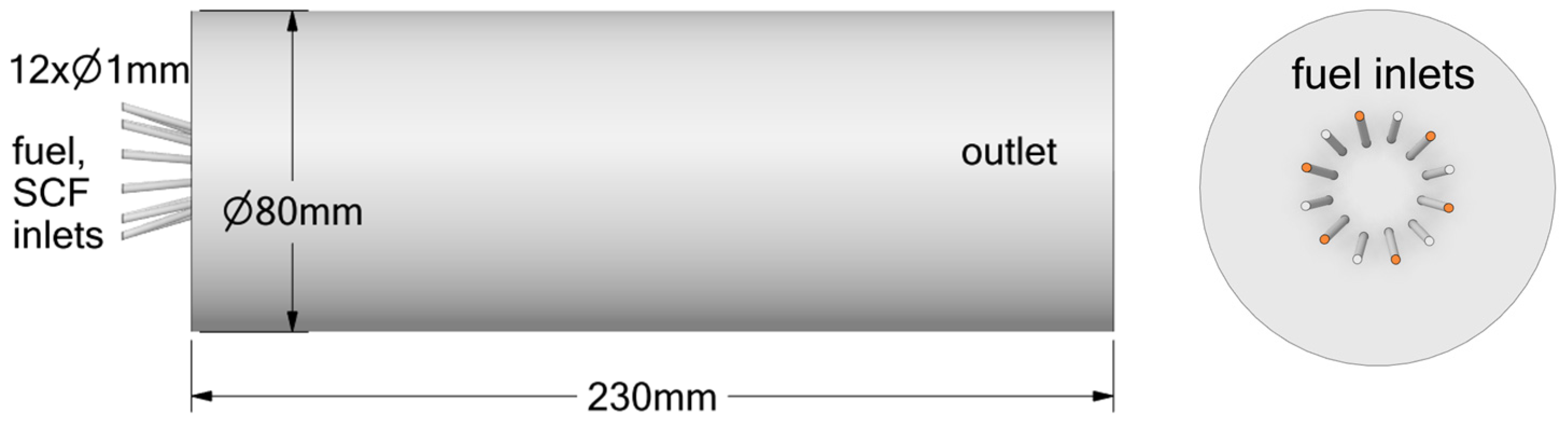
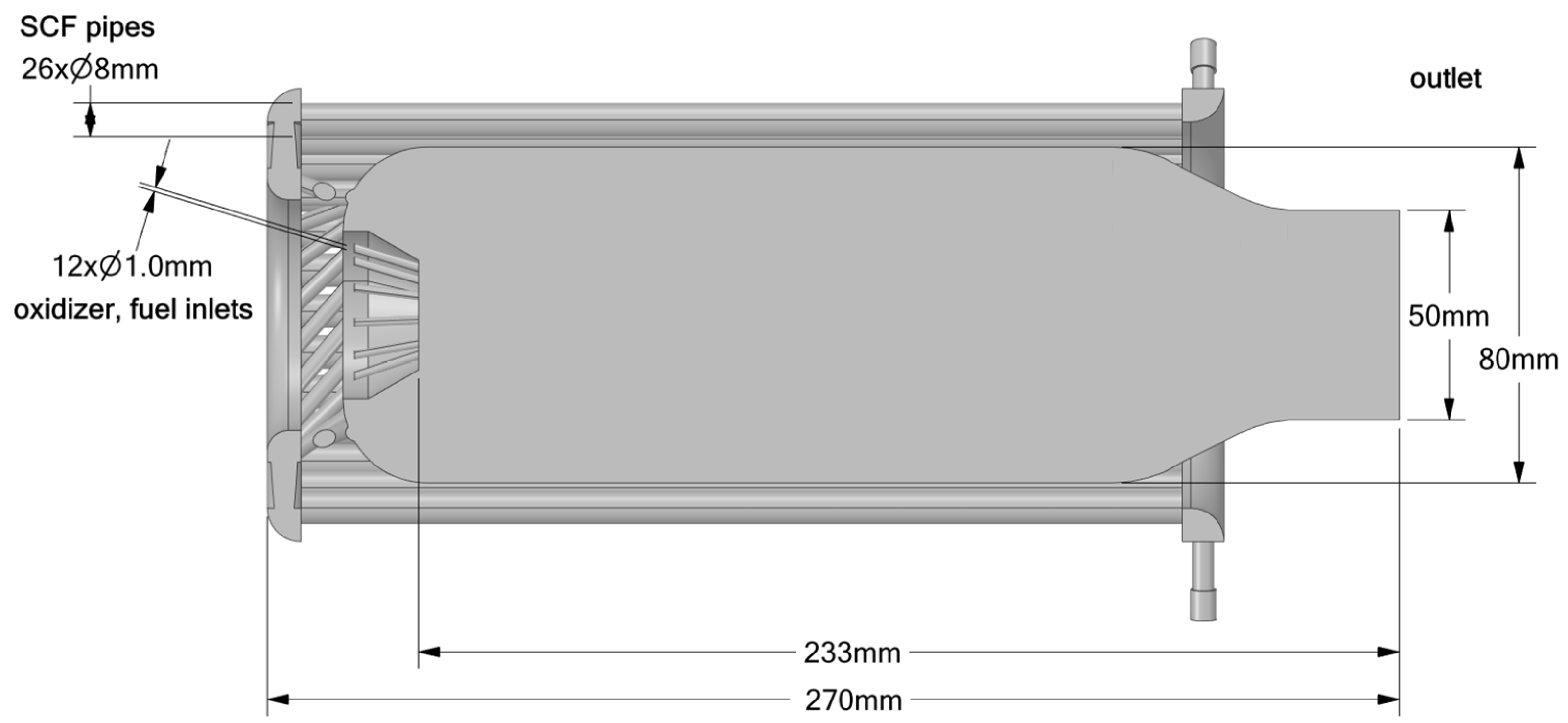
2.1. Study Geometries
2.2. Models and Boundary Conditions
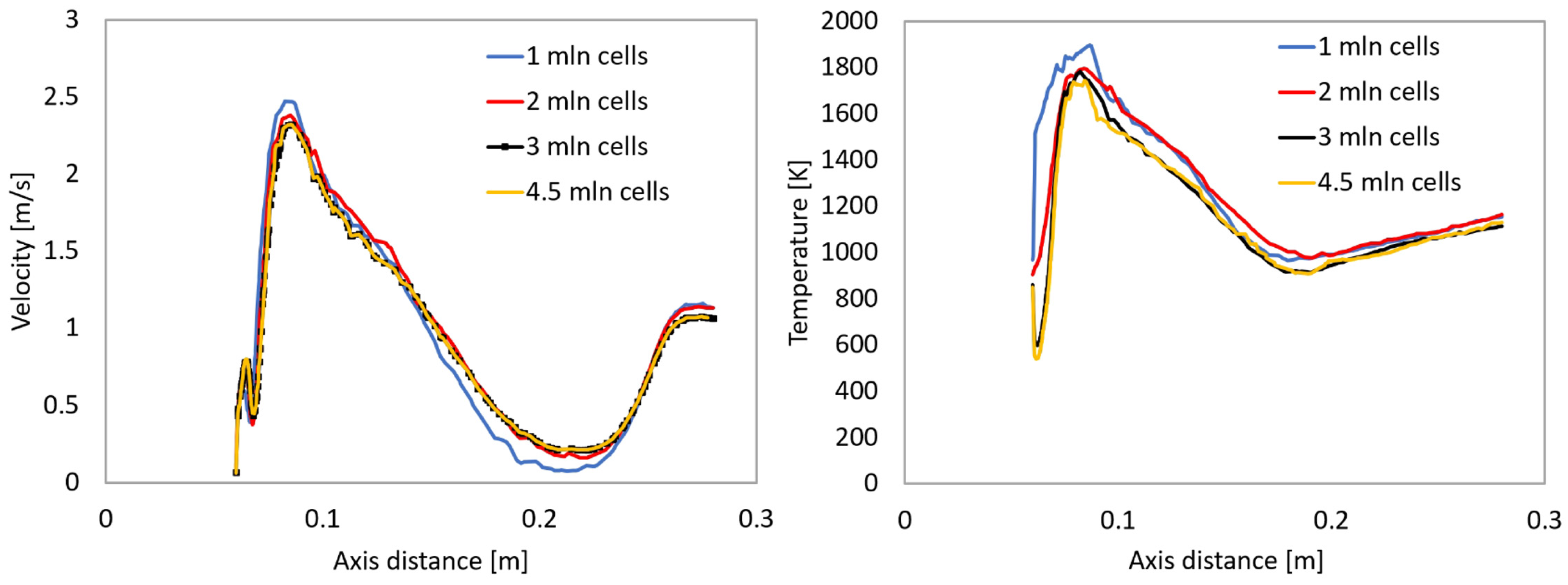
2.3. Mesh Independence Study
3. Results and Discussion
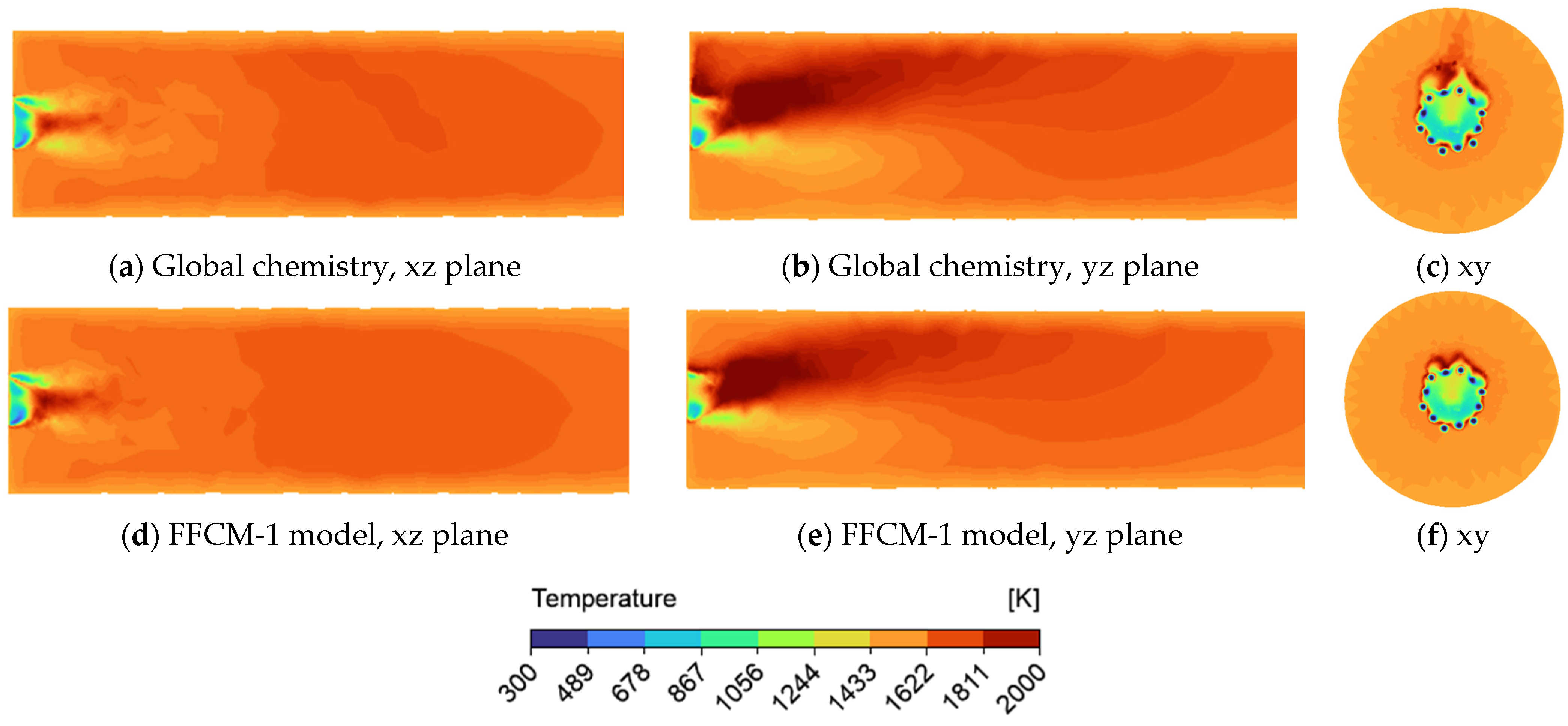
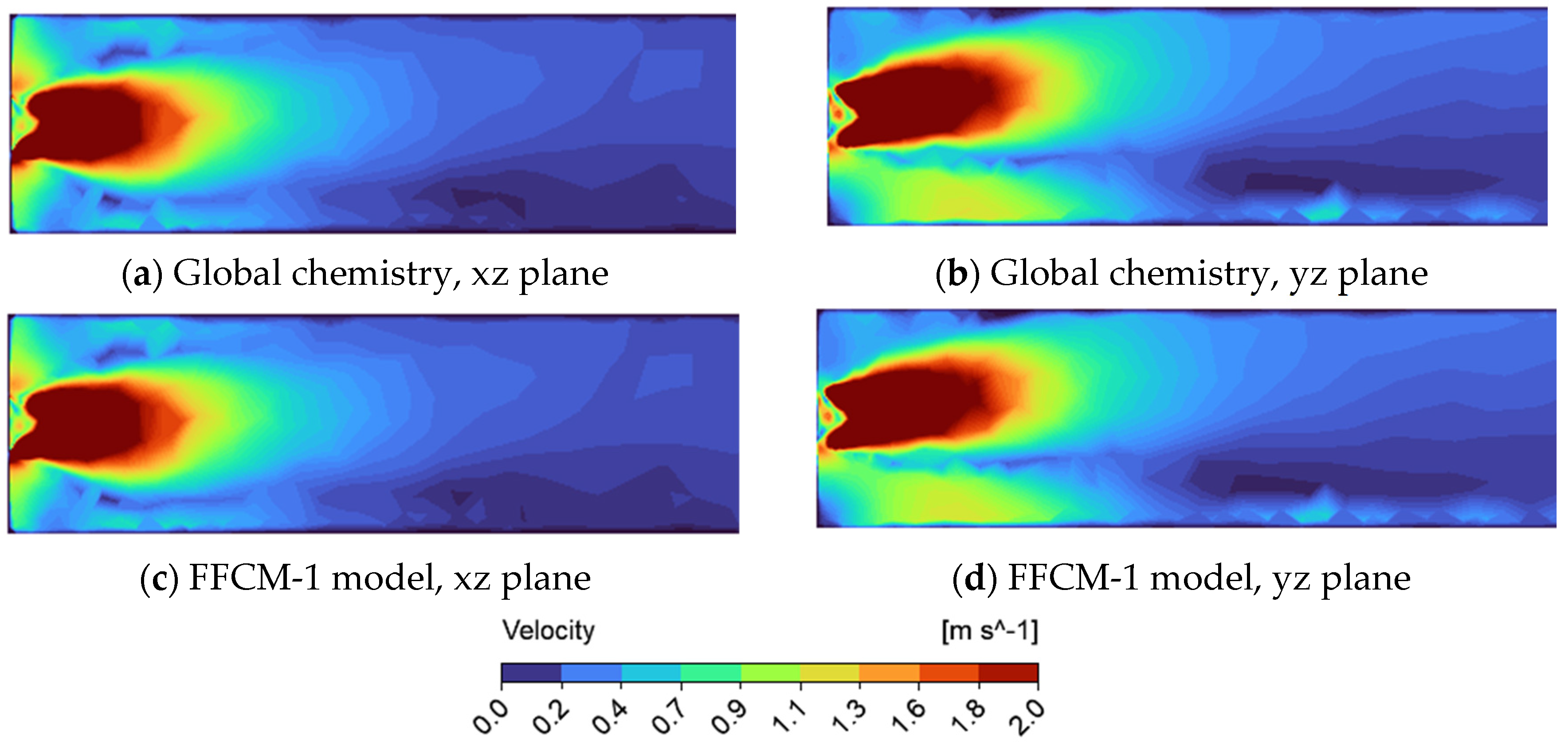
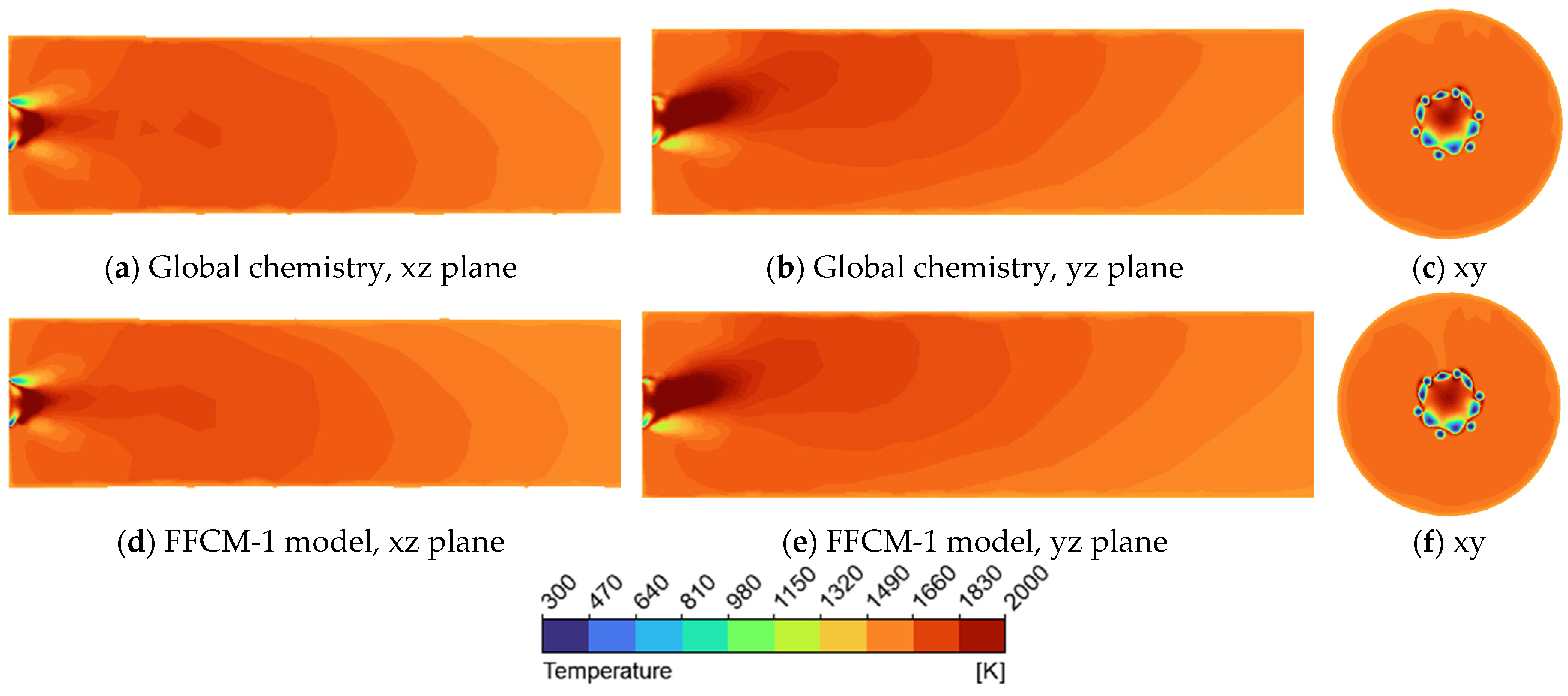
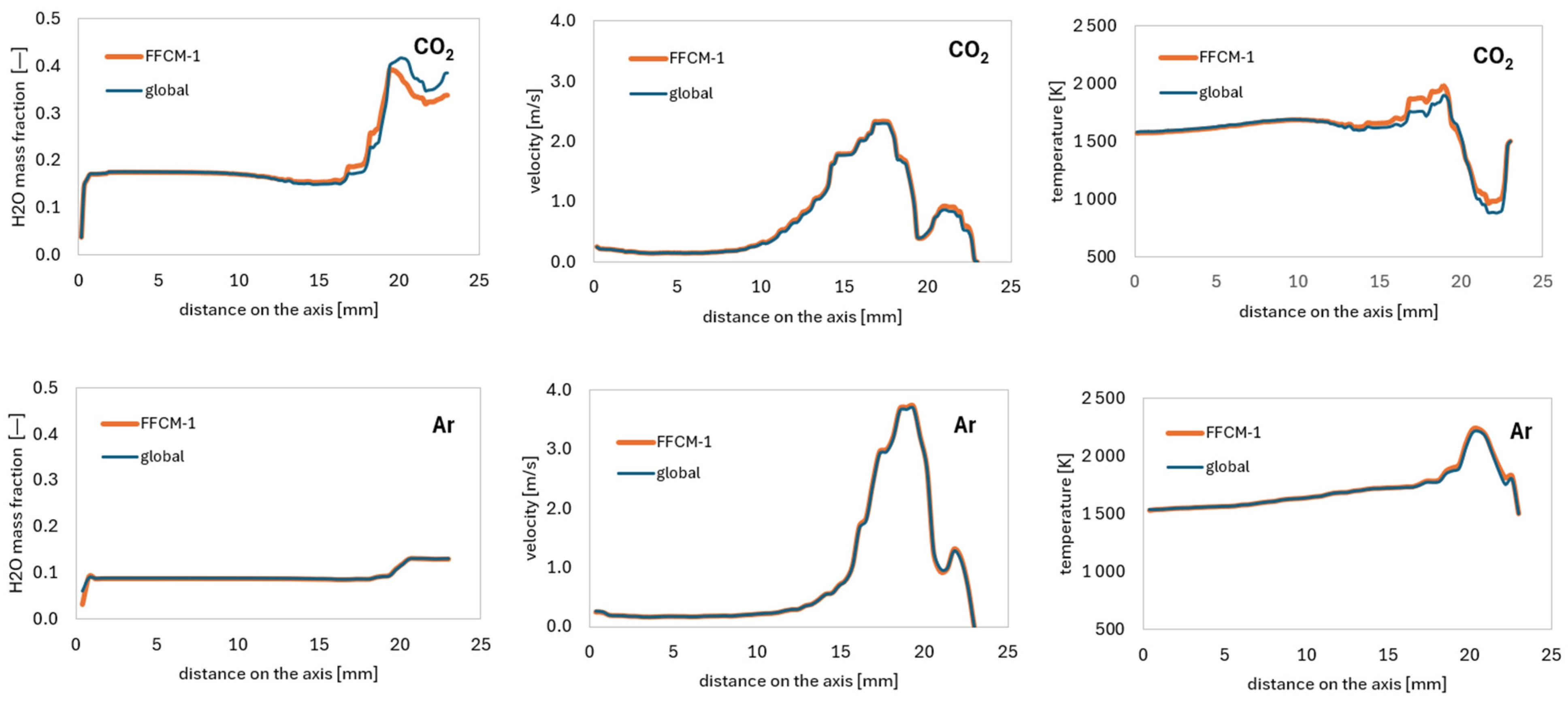
3.1. Comparison of Global and Detailed Chemistry Mechanism for Two Supercritical Working Fluids
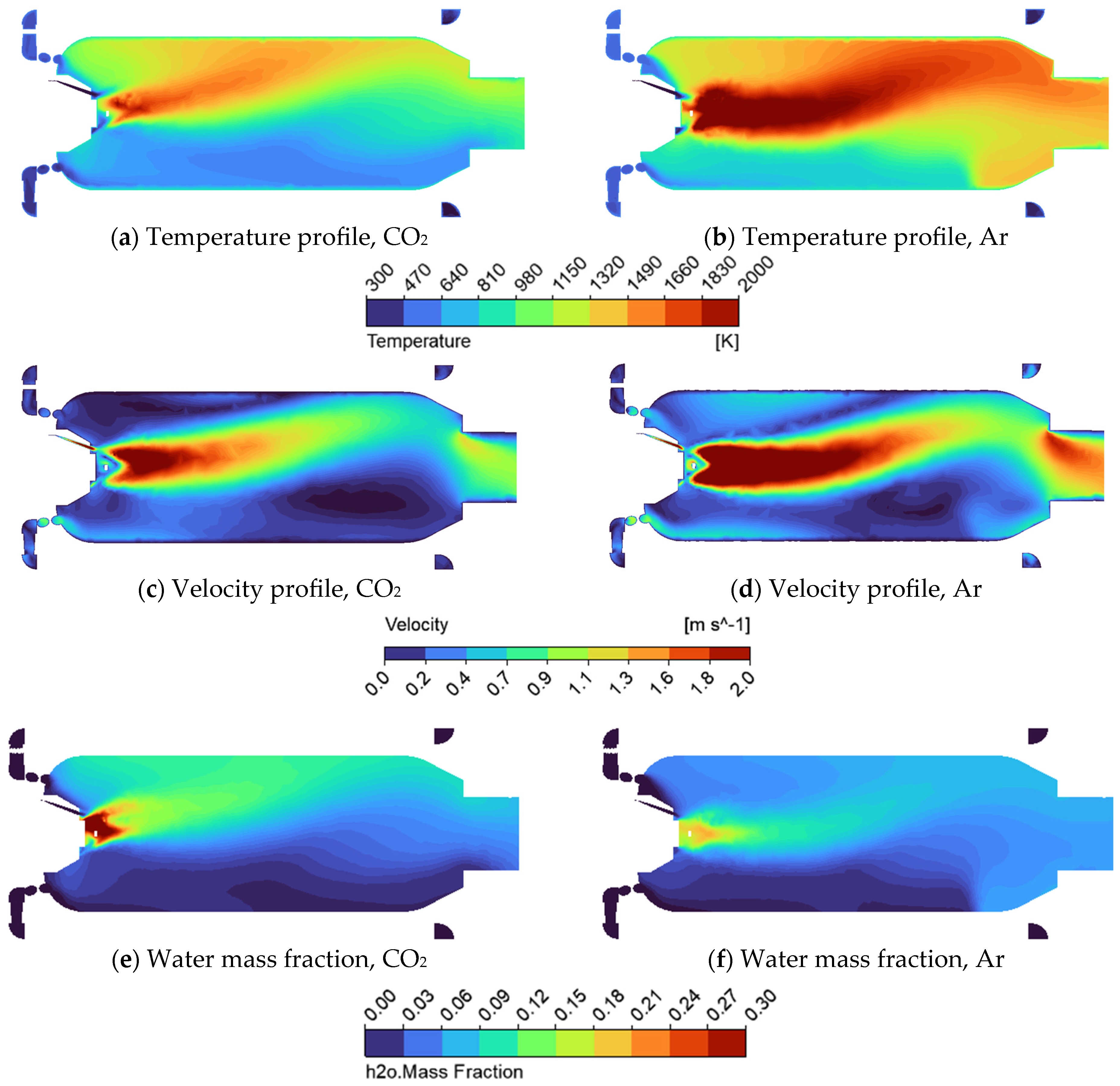
3.2. Combustion Behaviour in the Real Combustor for Supercritical Carbon Dioxide and Argon
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Mass flow rate, | |
| T | Temperature, |
| w | mass fraction, |
| Subscription | |
| out | outlet |
| H2O | water |
| O2 | oxygen |
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| FFCM-1 | Foundational Fuel Chemistry Model 1.0 |
| SCF | Super Critical Fluid |
| sAr | Supercritical argon |
| sCO2 | Supercritical carbon dioxide |
References
- The Glasgow Climate Pact–Key Outcomes from COP26. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-glasgow-climate-pact-key-outcomes-from-cop26 (accessed on 1 June 2025).
- Reale, F. The Allam Cycle: A Review of Numerical Modeling Approaches. Energies 2023, 16, 7678. [Google Scholar] [CrossRef]
- Chan, W.; Morosuk, T.; Li, X.; Li, H. Allam Cycle: Review of Research and Development. Energy Convers. Manag. 2023, 294, 117607. [Google Scholar] [CrossRef]
- Xie, M.; Chen, X.; Chen, L.; Zhou, M.; Liu, Y.; Zeng, L.; Shi, H.; Zhang, F.; Xie, S.; Zhao, Y. Evaluating the Feasibility of a Novel Allam Cycle for Co-Generating Power and Water in Hot Regions. Energy Convers. Manag. 2024, 309, 118447. [Google Scholar] [CrossRef]
- Rodríguez Hervás, G.; Petrakopoulou, F. Exergoeconomic Analysis of the Allam Cycle. Energy Fuels 2019, 33, 7561–7568. [Google Scholar] [CrossRef]
- Shao, J.; Choudhary, R.; Davidson, D.F.; Hanson, R.K.; Barak, S.; Vasu, S. Ignition Delay Times of Methane and Hydrogen Highly Diluted in Carbon Dioxide at High Pressures up to 300 Atm. Proc. Combust. Inst. 2019, 37, 4555–4562. [Google Scholar] [CrossRef]
- Conaire, M.Ó.; Curran, H.J.; Simmie, J.M.; Pitz, W.J.; Westbrook, C.K. A Comprehensive Modeling Study of Hydrogen Oxidation. Int. J. Chem. Kinet. 2004, 36, 603–622. [Google Scholar] [CrossRef]
- Beigzadeh, A.; Alabbad, M.; Liu, D.; Aljohani, K.; Hakimov, K.; Kashif, T.A.; Zanganeh, K.; Croiset, E.; Farooq, A. Reaction Kinetics for High Pressure Hydrogen Oxy-Combustion in the Presence of High Levels of H2O and CO2. Combust. Flame 2023, 247, 112498. [Google Scholar] [CrossRef]
- Allam, R.J.; Fetvedt, J.E.; Forrest, B.A.; Freed, D.A. The Oxy-Fuel, Supercritical CO2 Allam Cycle: New Cycle Developments to Produce Even Lower-Cost Electricity from Fossil Fuels Without Atmospheric Emissions. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. Volume 3B: Oil and Gas Applications; Organic Rankine Cycle Power Systems; Supercritical CO2 Power Cycles; Wind Energy. [Google Scholar]
- Allam, R.J.; Palmer, M.R.; Brown, G.W.; Fetvedt, J.; Freed, D.; Nomoto, H.; Itoh, M.; Okita, N.; Jones, C. High Efficiency and Low Cost of Electricity Generation from Fossil Fuels While Eliminating Atmospheric Emissions, Including Carbon Dioxide. Energy Procedia 2013, 37, 1135–1149. [Google Scholar] [CrossRef]
- White, M.T.; Bianchi, G.; Chai, L.; Tassou, S.A.; Sayma, A.I. Review of Supercritical CO2 Technologies and Systems for Power Generation. Appl. Therm. Eng. 2021, 185, 116447. [Google Scholar] [CrossRef]
- Weiland, N.; Thimsen, D. A Practical Look at Assumptions and Constraints for Steady State Modeling of SCO2 Brayton Power Cycles. In Proceedings of the 5th International Symposium—Supercritical CO2 Power Cycles, San Antonio, TX, USA, 28–31 March 2016. NETL-PUB-20271. [Google Scholar]
- Sasaki, T.; Itoh, M.; Maeda, H.; Tominaga, J.; Saito, D.; Niizeki, Y. Development of Turbine and Combustor for a Semi-Closed Recuperated Brayton Cycle of Supercritical Carbon Dioxide. In Proceedings of the ASME 2017 Power Conference Joint with ICOPE-17, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar] [CrossRef]
- Delimont, J.; Mcclung, A.; Portnoff, M. Direct Fired Oxy-Fuel Combustor for SCO2 Power Cycles: 1MW Scale Design and Preliminary Bench Top Testing. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar] [CrossRef]
- Delimont, J.; Mcclung, A.; Portnoff, M. Simulation of a Direct Fired Oxy-Fuel Combustor for sCO2 Power Cycles. In Proceedings of the 5th International Symposium—Supercritical CO2 Power Cycles, San Antonio, TX, USA, 28–31 March 2016; Available online: https://sco2symposium.com/papers2016/OxyFuel/116paper.pdf (accessed on 1 March 2025).
- Coogan, S.; Gao, X.; Mcclung, A. Evaluation of Kinetic Mechanisms for Direct Fired Supercritical Oxy-Combustion of Natural Gas. In Proceedings of the ASME Turbo Expo, Seoul, Republic of Korea, 13–17 June 2016. [Google Scholar] [CrossRef]
- Jin, S.; Deng, J.; Xie, K.; Liang, X.; Wang, C.; Ding, W.; Li, L. Knock Control in Hydrogen-Fueled Argon Power Cycle Engine with Higher Compression Ratio by Water Port Injection. Appl. Energy 2023, 349, 121664. [Google Scholar] [CrossRef]
- Wang, C.; Deng, J.; Ding, W.; Huang, Y.; Tang, Y.; Li, L. Thermodynamic Analysis of Employing Argon as the Diluent and Adding Hydrogen in an HCCI Ammonia Engine: Ignition Characteristics and Performances of Combustion and NO Emissions. Int. J. Hydrogen Energy 2024, 49, 293–300. [Google Scholar] [CrossRef]
- Oleś, S.; Mularski, J.; Pyka, D.; Pawlak-Kruczek, H.; Pozarlik, A. Optimization of Hydrogen Supercritical Oxy-Combustion in Gas Turbines. Fuels 2025, 6, 6. [Google Scholar] [CrossRef]
- Cameretti, M.C.; Tuccillo, R. Combustion Features of a Bio-Fuelled Micro-Gas Turbine. Appl. Therm. Eng. 2015, 89, 280–290. [Google Scholar] [CrossRef]
- Chakchak, S.; Hidouri, A.; Ghabi, A.; Chrigui, M.; Boushaki, T. Numerical Study of Turbulent Swirling Diffusion Flame Under Lean and Rich Conditions Using Turbulence Realizable K-Epsilon Model. Combust. Sci. Technol. 2023, 195, 1461–1482. [Google Scholar] [CrossRef]
- Hilbert, R.; Tap, F.; El-Rabii, H.; Thévenin, D. Impact of Detailed Chemistry and Transport Models on Turbulent Combustion Simulations. Prog. Energy Combust. Sci. 2004, 30, 61–117. [Google Scholar] [CrossRef]
- Chen, J.; Chen, G.; Zhang, A.; Deng, H.; Wen, X.; Wang, F.; Mei, Y. Experimental and Numerical Study on the Effect of CO2 Dilution on the Laminar Combustion Characteristics of Premixed CH4/H2/Air Flame. J. Energy Inst. 2022, 102, 315–326. [Google Scholar] [CrossRef]
- Smith, G.P.; Tao, Y.; Wang, H. Foundational Fuel Chemistry Model Version 1.0 (FFCM-1). Available online: https://web.stanford.edu/group/haiwanglab/FFCM1/pages/FFCM1.html (accessed on 1 March 2025).
- Burke, M.P.; Chaos, M.; Dryer, F.L.; Ju, Y. Negative Pressure Dependence of Mass Burning Rates of H2/CO/O2/Diluent Flames at Low Flame Temperatures. Combust. Flame 2010, 157, 618–631. [Google Scholar] [CrossRef]
- Hjärtstam, S.; Normann, F.; Andersson, K.; Johnsson, F. Oxy-Fuel Combustion Modeling: Performance of Global Reaction Mechanisms. Ind. Eng. Chem. Res. 2012, 51, 10327–10337. [Google Scholar] [CrossRef]
- Ba, J.; Wei, W.; Zhao, L.; Gang, X.; Dong, W.; Zhou, T. Numerical Simulation of Trans-/near-/Supercritical Injection Characteristics Based on Real Fluid Properties. Energy 2023, 278, 127767. [Google Scholar] [CrossRef]
- Hickey, J.-P.; Ihme, M. Supercritical Mixing and Combustion in Rocket Propulsion. Available online: https://web.stanford.edu/group/ctr/ResBriefs/2013/02_hickey.pdf (accessed on 6 May 2025).
- Bartle, K.D.; Clifford, A.A.; Shilstone, G.F. Estimation of Solubilities in Supercritical Carbon Dioxide: A Correlation for the Peng-Robinson Interaction Parameters. J. Supercrit. Fluids 1992, 5, 220–225. [Google Scholar] [CrossRef]
- Sodeifian, G.; Hsieh, C.M.; Tabibzadeh, A.; Wang, H.C.; Arbab Nooshabadi, M. Solubility of Palbociclib in Supercritical Carbon Dioxide from Experimental Measurement and Peng–Robinson Equation of State. Sci. Rep. 2023, 13, 2172. [Google Scholar] [CrossRef] [PubMed]
- ANSYS Inc. Ansys Fluent Theory Guide. Available online: https://dl.cfdexperts.net/cfd_resources/Ansys_Documentation/Fluent/Ansys_Fluent_Theory_Guide.pdf (accessed on 1 March 2025).

| Case # | Geometry | Mechanism | SCF | Pressure |
|---|---|---|---|---|
| 1 | Tube | FFCM-1 | CO2 | 110 bar |
| 2 | Tube | Global | CO2 | 110 bar |
| 3 | Tube | FFCM-1 | Ar | 73 bar |
| 4 | Tube | Global | Ar | 73 bar |
| 5 | Combustor | Global | CO2 | 110 bar |
| 6 | Combustor | Global | Ar | 110 bar |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oleś, S.; Mularski, J.; Pawlak-Kruczek, H.; Singh, A.K.; Pozarlik, A. Assessment of Global and Detailed Chemical Kinetics in Supercritical Combustion for Hydrogen Gas Turbines. Energies 2025, 18, 3380. https://doi.org/10.3390/en18133380
Oleś S, Mularski J, Pawlak-Kruczek H, Singh AK, Pozarlik A. Assessment of Global and Detailed Chemical Kinetics in Supercritical Combustion for Hydrogen Gas Turbines. Energies. 2025; 18(13):3380. https://doi.org/10.3390/en18133380
Chicago/Turabian StyleOleś, Sylwia, Jakub Mularski, Halina Pawlak-Kruczek, Abhishek K. Singh, and Artur Pozarlik. 2025. "Assessment of Global and Detailed Chemical Kinetics in Supercritical Combustion for Hydrogen Gas Turbines" Energies 18, no. 13: 3380. https://doi.org/10.3390/en18133380
APA StyleOleś, S., Mularski, J., Pawlak-Kruczek, H., Singh, A. K., & Pozarlik, A. (2025). Assessment of Global and Detailed Chemical Kinetics in Supercritical Combustion for Hydrogen Gas Turbines. Energies, 18(13), 3380. https://doi.org/10.3390/en18133380









