Abstract
This study examines how the frequency of an innovative energy harvester is tuned and how it behaves. This harvester transforms thermal energy into mechanical oscillations of two polyvinylidene fluoride (PVDF) piezoelectric beams, which produce electrical energy via a shape memory alloy (SMA) thread. The oscillation frequency is modified by two magnetic weights that are positioned symmetrically on the SMA thread and interact with stationary NdFeB permanent magnets. The SMA thread shifts laterally due to longitudinal thermal contraction and expansion induced by a constant-temperature heater. Temperature gradients above the heater trigger cyclical variations in the length of the SMA thread, leading to autonomous vibrations of the masses in both the vertical and horizontal planes. An experimental apparatus was constructed to analyze the harvester by tracking the motions of the masses and the voltages produced by the piezoelectric beams. Information was gathered regarding the correlation between output voltage and power with the consumer’s load resistance. These outcomes were confirmed using a multiphysics dynamic simulation that incorporated the interconnections among mechanical, thermal, magnetic, and electrical systems. The findings indicate that the use of permanent magnets increases the bending vibration frequency from 8.3 Hz to 9.2 Hz. For a heater maintained at 70 °C, this boosts the output power from 1.9 µW to 8.18 µW. A notable property of the considered energy harvester configuration is its ability to operate at cryogenic temperatures.
1. Introduction
Energy storage from oscillating sources is a promising solution for energy supplying of devices with low energy consumption [1,2,3,4]. Among the various sources of unexploited ambient energy, mechanical vibrations, optical radiation, and thermal energy are the most widely used [5,6,7]. The rapid response rate, which significantly influences the efficiency of the energy delivered by the mechanism, presents a challenge for actuators utilizing shape memory alloy (SMA) components. The duration required to attain phase transitions of these harvesters can be reduced. In other words, the response rate is limited by the time for heating and, in particular, the time required for temperature reduction of the SMA element actuator. Therefore, minimizing the duration required to attain the phase transformation temperature is essential to increase the reaction rate. One of the methods for improving the response speed of the SMA is to reduce the dimensions. A triggering rate of 1.6 kHz has been reported as the thickness of the shape memory alloy element approaches 1 μm. These are several orders of magnitude higher than the speeds typically associated with SMA actuators [8]. Nonetheless, actuation speed is influenced by multiple factors beyond the geometric sizes of the SMA element. For some actuators, the actuation speed may vary depending on alterations in the thermal cooling or heating response of the actuator. This means that even if actuators have close dimensions with respect to the SMA driving element, the dynamic response would be different depending on the change in the generalized inertia coefficient of the entire actuation system or the supplied power required for actuation [9,10]. Changing the chemical composition of the SMA in the actuator allows for the cyclic transformation of the SMA over a lower thermal range. Introducing a small quantity of titanium into the Cu-Zn-Al alloy substantially lowers the martensite phase temperature range [11].
The efficiency of energy harvesting in piezoelectric cantilever (PEC) devices depends on the magnitude of the frequency at which the mechanism oscillates [12,13]. To increase the energy harvesting efficiency, many methods have been proposed to optimize the energy harvesting by adjusting the oscillation frequency [14,15]. One approach to regulating the oscillation frequency involves employing multiple piezoelectric cantilevers with mechanical resonance frequencies strategically distributed across the target frequency spectrum, ensuring that at any given frequency, at least one cantilever vibrates near its resonance point. The widely adopted methodology for designing such a system is presented in [16,17]. The frequency configuration of the PEC can also be achieved by varying the magnitude of the generalized inertia coefficient of the beam [18] or the elastic properties of the PEC [19]. The stiffness of the PEC can be varied by changing the dimensions of the cantilever or its material characteristics. Some solution developments include the piezoelectric characteristics of the PECs and the properties of the electric diagram in the calculations [20]. Methods for frequency scaling [21,22], the implementation of non-linear methods [23,24,25], and introducing innovative elements such as inerters [26] have also been proposed.
Bouhedma et al. have presented a piezoelectric vibrational energy harvester whose frequency characteristics can be altered using magnets with an up-to-18% change [27]. To achieve high electrical power stability, a concept for a piezoelectric energy harvester that mimics the switch mechanism has been proposed. The extracted energy is increased by a collision between two magnets [28]. The dynamics of a bistable magnetic oscillator are controlled by the strength and polarization of the added magnets [29]. The extracted energy voltage reaches the highest value in nonlinear oscillations, with the output power improved by up to 600% compared to linear oscillations. The operational principle of vibrating energy harvesters with permanent magnets is reviewed, and questions of stability regarding magnets with different forces are discussed to increase the harvested power output [30]. The dynamic behavior of tri-stable energy harvesters with wide a frequency range employing magnetic coupling has been systematically analyzed [31]. In comparison to the bi-stable configuration, the investigations indicate that this harvester transitions more readily between its distinct states, enabling enhanced energy output across a broader frequency spectrum. A broadband nonlinear quin-stable energy harvester is considered [32]. Control over the piezoelectric energy generated is achieved by magnets usually deployed in a repulsive or attractive configuration [33]. The combined use of piezoelectric and electromagnetic transduction within this hybrid approach significantly improves the harvester’s energy output under identical external excitation conditions [34]. Moreover, the development of a new generation of devices is feasible through the utilization of materials and structures that exploit magnetoelectric effects. In ferromagnetic–ferroelectric layered composites, magnetoelectric coupling emerges from the interaction between magnetostrictive and piezoelectric responses occurring during ferroelectric phase transitions. The important advantage of magnetic field-based methods compared to mechanical methods is their remoteness and lack of contact. Ferrite-based composites hold significant potential for applications in sensing technologies, self-powered systems, electrically tunable microwave devices, and other advanced functional components [35]. Several reviews on piezoelectric energy harvesting have been published, most of them mainly focusing on biomedical applications [36], microelectromechanical systems (MEMS) [37], nanogenerators [38], materials, and energy harvesting from various sources [39].
In previous publications, the authors of this paper have developed and investigated a self-excited thermomechanical oscillator [40] and an energy harvester [41] in which the heat of a constant-energy heater is converted into vibrations of an SMA thread. Two masses are mounted on the SMA thread, which perform vibrations in two perpendicular directions: longitudinal and transverse. The longitudinal vibration is due to the contraction of the SMA thread when it approaches the heater. These contractions shorten the thread, and this causes it to move away from the heater and subsequently cool with elongation due to the inertial forces of the masses. The transverse vibrations are due to the relative movement of the thread from the SMA in the vertical direction and are caused by inertial forces and the weight of the masses, in addition to the contractions. The variation in Young’s modulus resulting from phase transitions of the SMA thread induces an additional, higher-frequency oscillation that superimposes onto the primary longitudinal vibrations. The energy harvester [41] implemented on this principle transforms the resulting oscillations through piezoelectric cantilevers mounted at the ends of the thread. Studies have shown that the vibrations have a pseudo-stochastic character due to the hysteresis of the relative martensitic fraction.
The aim of this of this work is to examine potential approaches for improving the generated power of the above-described self-excited thermal energy harvester by tuning the resonant frequency of the vibrating SMA thread using permanent magnets.
2. Architecture of the Vibration-Based Energy Harvester and Its Natural Frequency Tuning System
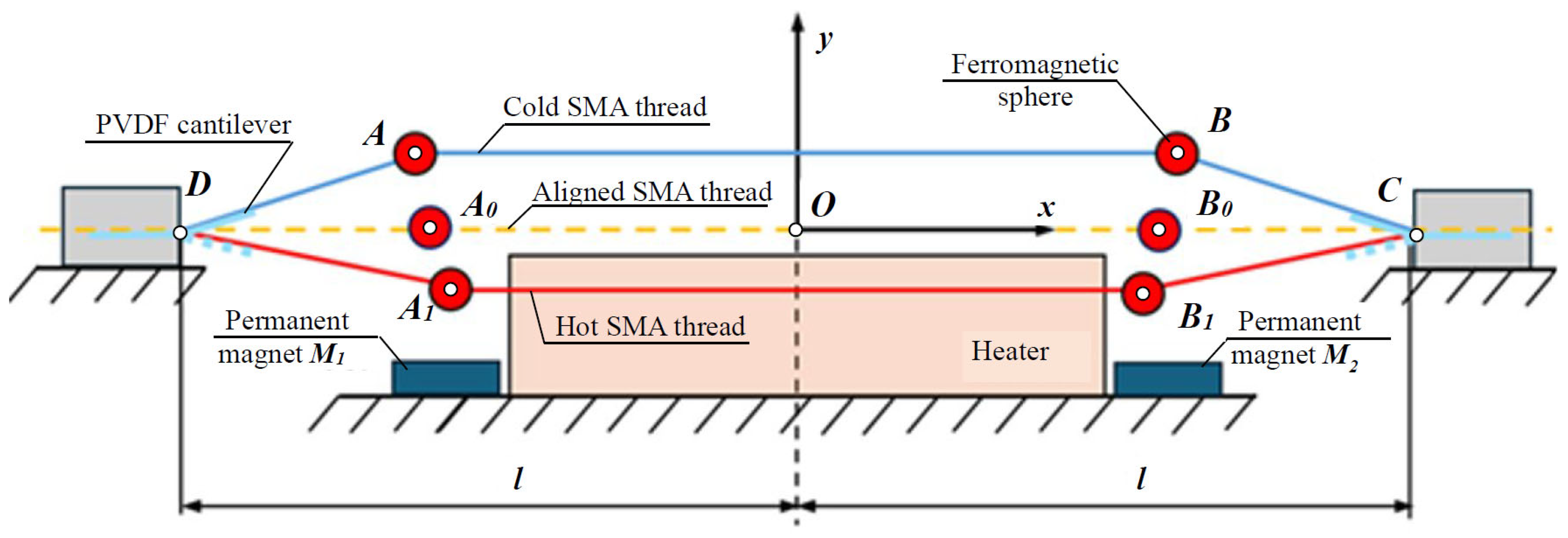
The thermoelectric energy harvester comprises a SMA thread anchored between two fixed supports, and , symmetrically positioned with respect to a stationary heater. Two identical spherical masses are rigidly attached to the wire in proximity to the heater, on which magnetic forces, due to symmetrically placed NdFeB magnets (M1 and M2), act. Located at the fixed termini of the SMA thread, two piezoelectric cantilevers are affixed via a heat-resistant foil, enabling them to track the bending deformation of the thread. The assembly maintains geometric symmetry relative to the y-axis of the reference coordinate system (Figure 1). The thread material is a shape memory alloy, Nitinol (NiTi), known by the trademark Flexinol® [42], manufactured from a slender PVDF sheet, which was integrated into the piezoelectric cantilevers.
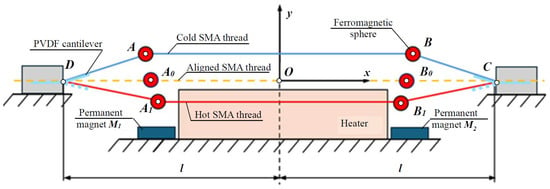
Figure 1.
Scheme of the thermoelectric energy harvester.
The operational principle of the energy harvester, as previously described, relies on thermal variations above the heater. Elevated temperatures near the heater surface induce contraction in the SMA thread, causing it to retract from the heated region. Upon entering the cooler zone, the SMA thread becomes more pliable and elongates under the inertial forces of the attached masses, drawing it back toward the heater and into the magnetic field’s active region. This thermomechanical cycle repeats continuously, generating periodic vibrations in the SMA thread and mass assembly. The resulting bending deformations near the fixed supports are transmitted to the piezoelectric cantilevers, which, in turn, convert the mechanical energy into electrical energy (see the Video in the Supplementary Materials).
3. Composing the Dynamical Model by Combining the Interactions of the Different Physical Domains
The spacing between the two anchors, D and C, is configurable, enabling the installation of the SMA thread under initial tension or initial slack. The geometric parameter notations correspond to those presented in Figure 1, and the methodology for analyzing the mechanical and thermal strains in the SMA thread and PVDF cantilevers aligns with the procedure outlined in [41].
3.1. Elsatic and Thermal Parameters of the SMA Thread and Bending of the Piezoelectric Cantilevers
The distance between the fixed points and is chosen, ; the half pre-strain is equal to
where is the applied length of the SMA thread before tensioning.
A relative length, , is introduced as
where and are the lengths of the thread sections if the ferromagnetic masses lie on the segment.
Considering the symmetric arrangement and uniformity of the distribution of the deformations along the entire length of the thread, the pre-strains and of the end sections and are equal and can be expressed as follows:
In this case, for the middle section, A0B0, its deformation can be written as follows:
Due to the specific symmetrical design shown in Figure 1, it can be proved that the middle-section thread moves parallel to the horizontal surface of the heater; therefore, its temperature is uniformly distributed. Since the end sections and are relatively far from the heater, they are assumed not to heat up and their temperature is low; i.e., they are cold sections with a temperature equal to that of the room. The deformation of the cold (or end) sections due to the displacement of the ferromagnetic weights and the initial tension for the symmetrical motion variant has the following form:
and
where the coordinates of the points , , , and are , , , , , , and , respectively.
Under the same conditions, for the middle section, deformation can be written as follows:
where . Since the end sections of the SMA thread are room temperature, which is smaller than the final martensitic temperature, Mf, of NiTi, the stiffness of these sections can be expressed by
where is the NiTi Young’s modulus of the martensite, and A is the cross-sectional area of the SMA thread.
For the stiffness of the middle section, it can be written as follows:
but since this section is subjected to varying temperatures that cause all phase transformations in NiTi, the Young’s modulus also transforms depending on the current phase. According to the model discussed in [43], this module can be represented by
where Young’s modulus , , , and are, respectively, the fully twined, partially twined, and detwinned martensite and austenite; is the yield strain of the twined martensite; is the minimum strain of the detwinned martensite; and
is the middle-section strain.
The relative martensite fraction is expressed as
where is the current temperature of the NiTi, and is the temperature, dependent on whether there is cooling or heating, calculated by the following:
In (12), the unit of the coefficient is temperature, calculated by the following expression:
where the transient NiTi temperatures, , , , and, , are the starting and final temperatures for austenite and martensite, respectively. The constants and were determined experimentally in [44].
The hysteresis model is presented in [43]. It is based on an analysis of the temperature fluctuation point, , at which a gradient change in the transient temperature occurs as .
Let us denote the derivatives of the transient temperature with respect to the time before the fluctuation point by and after the fluctuation point by .
In cases where
the parameter , called the scale factor, is determined by
and
If at the fluctuation temperature, , changes from cooling to warming, i.e.,
the scale factor takes the following form:
and
Similarly, sub-minor hystereses that occur in cases in which a minor hysteresis already appears are described, as well as a sub-minor temperature fluctuation that occurs during a transition. For these cases, approaches analogous to those described in [43] are used.
To simplify the general formulation of the problem, it is assumed that the temperature field above the heater in which the NiTi thread moves is stationary. In addition, we employ the simplifying assumption that the NiTi thread itself obtains a potential temperature from this field via dependence:
where coordinates and are determined experimentally [40]; is the maximum temperature in the NiTi thread obtained from the heater; is the experimentally determined length of a theoretical segment; and is the room temperature.
Considering (21) and the hysteresis theory of the relative martensitic fraction (12–20), it is seen that the Young’s modulus, , for the middle section is a potential function of the coordinates of the ferromagnetic masses and the temperature of the SMA thread, which is here also assumed to be a potential function. These properties facilitate the application of Lagrange equations of the second kind to the solution of the dynamics problem.
The bending of the piezoelectric beams due to the movement of the SMA thread is assumed to be as in [41], where the bent shape for the left cantilever is assumed to be a parabola of the following form:
and for the right cantilever, the bent shape is described with the parabola
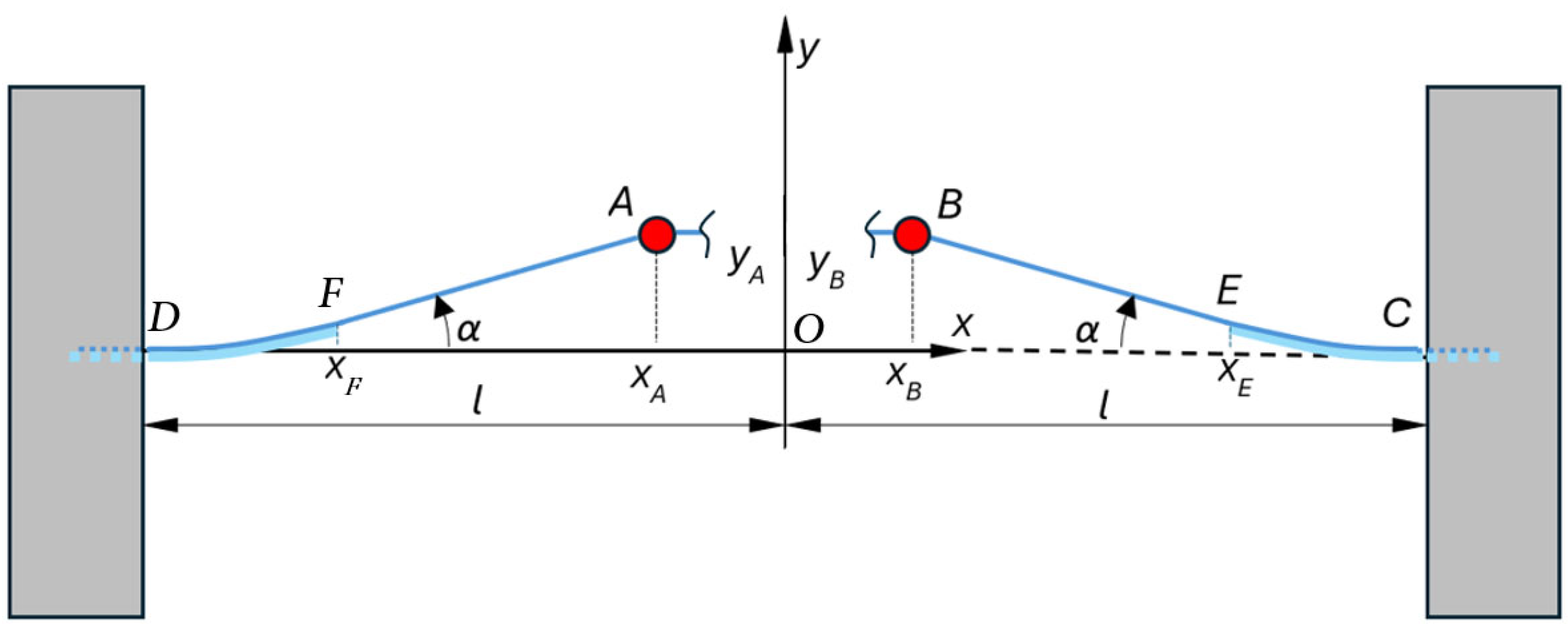
where is the piezoelectric cantilever length, and and are obtained based on the assumption that the angles of the cantilever and NiTi thread slopes at the fixation points coincide (Figure 2).
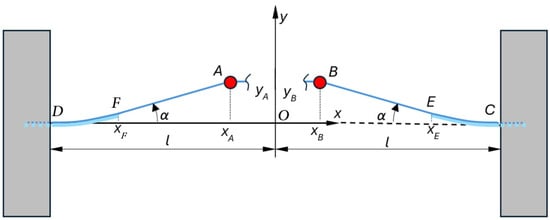
Figure 2.
Determination of the bending of piezoelectric cantilevers. This figure has been revised and adapted from [41].
In accordance with the assumptions on the shape of the bending, the following factors are found:
and
3.2. Determination of Magnetic Forces and Their Potential Energy
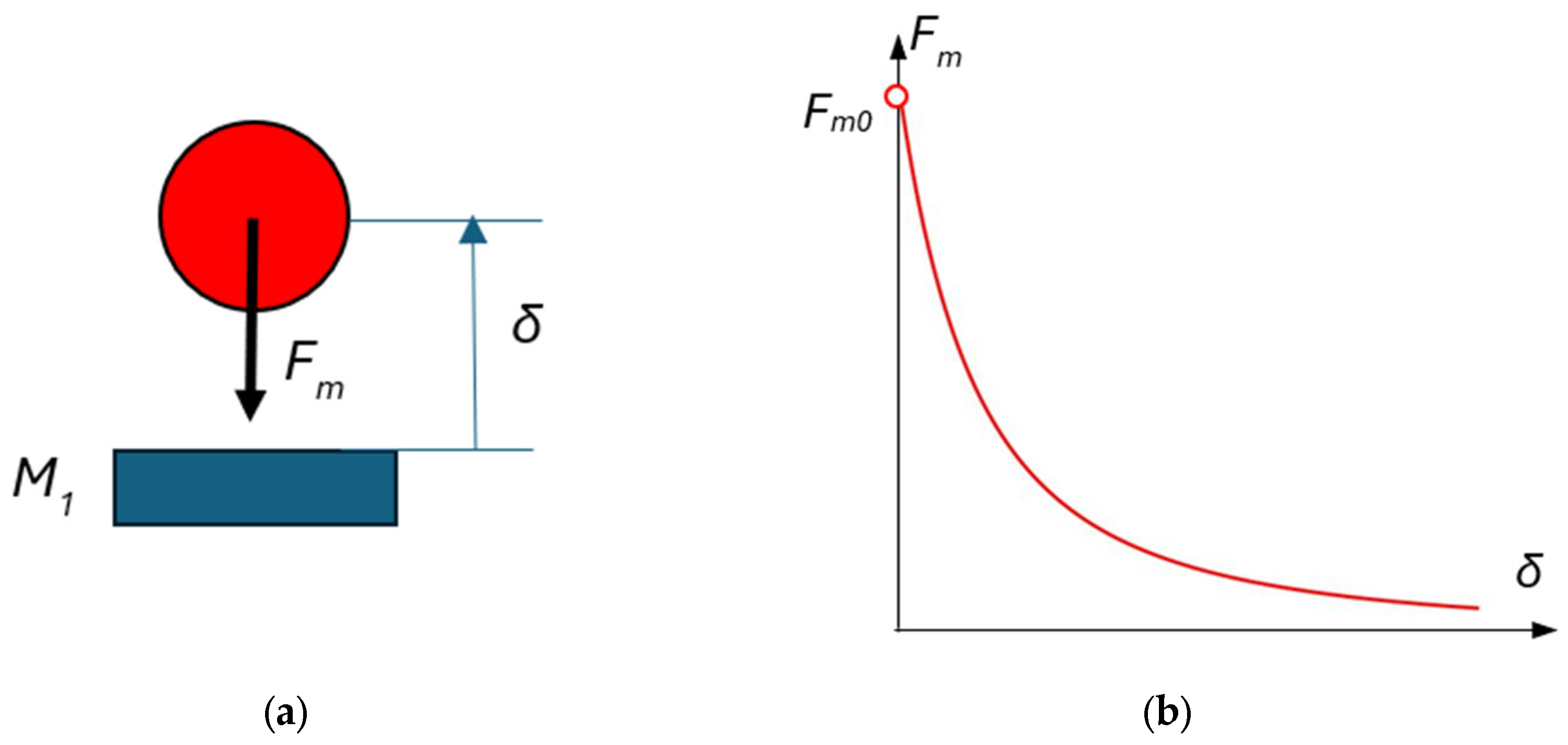
It is assumed that the magnetic force between a spherical ferromagnetic mass and a permanent magnet, as depicted in Figure 3a, is approximated by the following function:
where is the imaginary magnetic mass, is the imaginary initial gap, and is the distance between the upper surface of the permanent magnet and the sphere center. The same force function was determined in [45] based on numerical approximations and experiments.
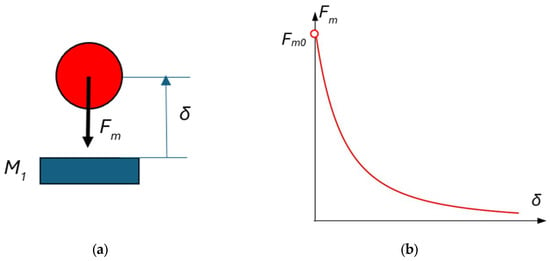
Figure 3.
Magnetic force between a permanent magnet and a spherical ferromagnetic mass: (a) problem statement; (b) graphical characteristics of the magnetic force.
The force function (26), also called the static magnetic force characteristic, has the graphical interpretation shown in Figure 3b. The magnetic force at a conditional zero gap (it is called conditional because the distance between the sphere and the magnet can practically never be zero because of the roughness and deviations of the shapes of the two surfaces) at = 0 is the initial magnetic force:
from which the unit of the imaginary magnetic mass [Nm2] is evident.
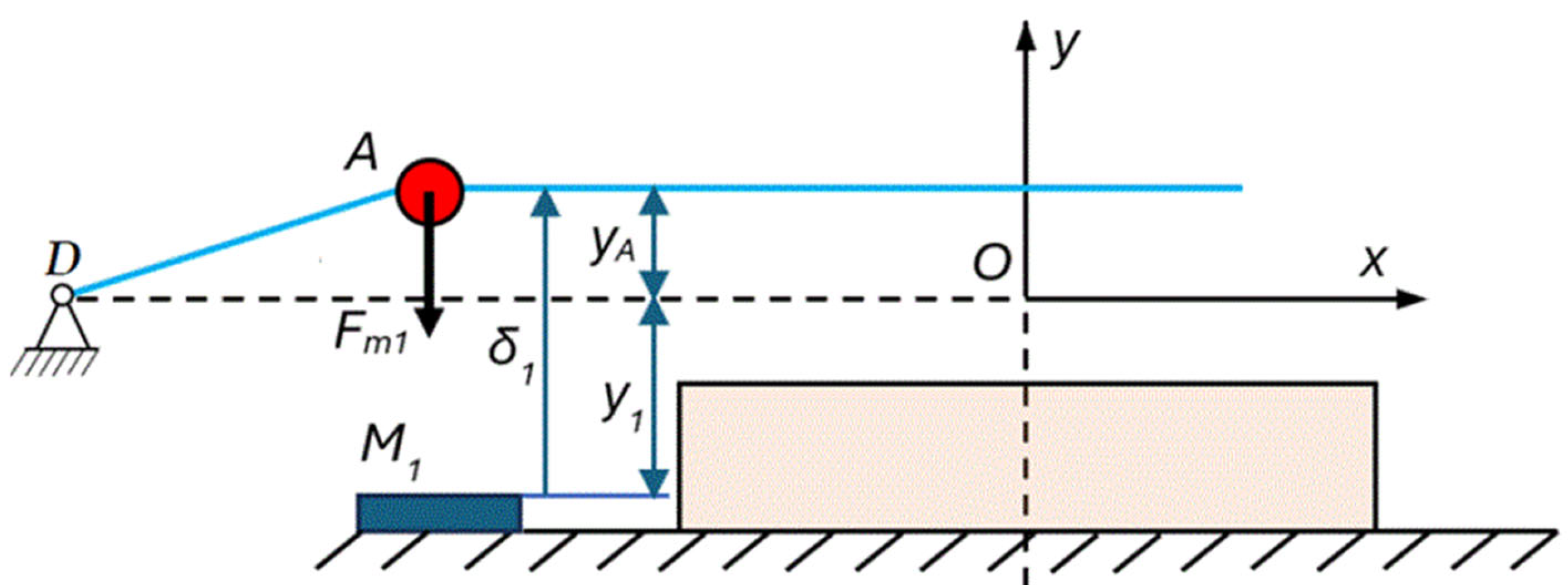
The application of Equation (26) to the energy harvester considered here is clarified by Figure 4. The current position of the ferromagnetic mass at point is located at position . The influence of the displacement of the masses along the axis on the magnetic forces is neglected.
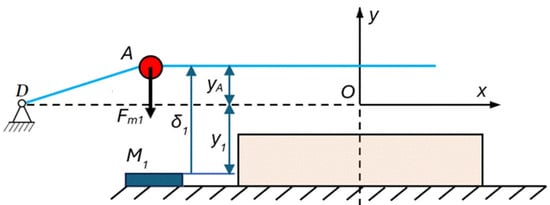
Figure 4.
The force of the permanent magnet located in the energy harvester acting on a ferromagnetic mass, A, mounted on a thread of SMA.
Taking into account that
according to (26), the left magnet M1 will exert the following force:
The right magnet will exert the same force because the coordinates of the two ferromagnetic masses are equal.
The potential energies of the two magnet forces are determined after integration
3.3. Derivation of the Lagrange Equations of the Second Kind
In the energy harvester investigated here, the two ferromagnetic masses move along the and axes; in addition, the two piezoelectric cantilever beams generate two different electric charges: of the left cantilever and of the right cantilever. This means that the total number of the generalized coordinates is six. The four mass coordinates, , , , and , are mechanical, and the two charges, and , are electrical.
Since the energy harvester is assumed to be in its symmetrical configuration, the following notations can be introduced: , , , , , and . Note that symmetry reduces the generalized coordinates from six to three: , , and . The symmetry also allows the following notations to be introduced: , , , , , , and .
The kinetic energy of the symmetric mechanical system is obtained in the following form:
where , and is the ferromagnetic sphere mass.
The potential energy (except the piezoelectric one) is the sum of the mechanical and the magnetic potential energy, expressed by
where
and
The piezoelectric energy, , according to [46], is derived in the following form:
where
and
is the length of the piezoelectric cantilever.
is the equivalent capacitance of the piezoelectric transducer; and are the piezoelectric charge coefficient of PVDF and the dielectric permittivity, respectively; is the piezoelectric cantilever compliance determined under a constant electric field; is the PVDF electromechanical coupling coefficient; , , and are the second moment of area, the width, and the thickness of the PVDF beam, respectively.
Based on the above results, the Lagrangian of the magnetoelectromechanical system is written in the following form:
The system of three coupled equations describing the multiphysics dynamics of the energy harvester is derived according to the Lagrange equations, which have the following forms:
where , , and .
The generalized forces, , for the considered case are
where is the gravity acceleration; and are the viscous resistance coefficients along the and axes, respectively; and is the resistance of the electric load.
Applying Equations (40) to (39), the following system is derived:
where
and
The middle-section Young’s modulus derivative for of SMA thread in question is calculated according to the following relation:
where the derivative of the relative martensite fraction considering (21) is
From (42), it follows that the magnetic system has a contribution that is expressed by a potential force of the following form:
This force, presented in Maclaurin’s series, leads to the following:
The factor in front of indicates that the magnetic system will increase the natural mechanical frequency of vibration along the coordinate.
The ODE system (42) can be solved numerically using Table 1.

Table 1.
Parameter values for the solution of the ODE system (42).
4. Experimental Studies on the Influence of Magnetic Tuning
The experimental investigations of the influence of the magnetic system on the natural frequency tuning were carried out using a dedicated experimental setup. The experimental setup is illustrated schematically in Figure 5a. A top-down view of the entire system is presented in Figure 5b. Figure 5c provides a detailed close-up of the left side of the energy harvester, featuring the PVDF cantilever (2), the horizontal position sensor (3), the ferromagnetic mass (4), the heater (5), and magnets (10). On the right side, Figure 5d displays an image of the energy harvester, highlighting the sphere (4), heater (5), vertical-position sensor (6), SMA thread (7), right support (8), and magnets (10).
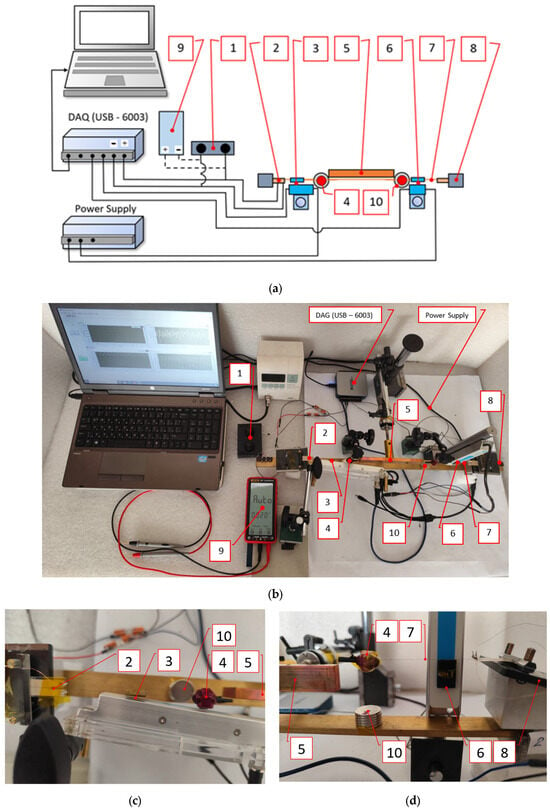
Figure 5.
Experimental setup of the thermoelectric energy harvester: (a) schematic and overall concept; (b) top view of the whole experimental setup; (c) partial view of the left side; (d) partial view of the right side of the energy harvester. (1) variable load resistors; (2) PVDF cantilever; (3) horizontal position sensor; (4) ferromagnetic mass; (5) heater; (6) vertical position sensor; (7) SMA thread; (8) right support; (9) ohmmeter; (10) permanent magnet stack.
In the experimental configuration, the energy harvester features a heater (5) positioned along the central strand of the CMA (7), with ferromagnetic spheres (4) directly influenced by NdFeB magnets (10). To monitor the movement, sensors are installed to measure horizontal displacement (3) and vertical displacement (6) of the masses. These sensors are of the DT1-028K/L model from MEAS Germany GmbH Dortmund. Variable load resistors (1) are connected in parallel with the outputs of the two piezoelectric beams (2), with their resistance being adjustable via an ohmmeter (9). The voltage signals from the piezoelectric elements and the displacement sensors are collected by a National Instruments DAQ USB-6003 data acquisition system then processed by a laptop running a LabVIEW (11) program to record the data into an Excel file.
In order to investigate the influence of magnets on the output voltage, two types of experiment were conducted. In the first, the results of the displacement along the two axes and the generated output voltage with the magnets removed were recorded. In the second type of experiment, the same signals were recorded but in the presence of magnets. In these experiments, the location and number of magnets was chosen to obtain the maximum output voltage.
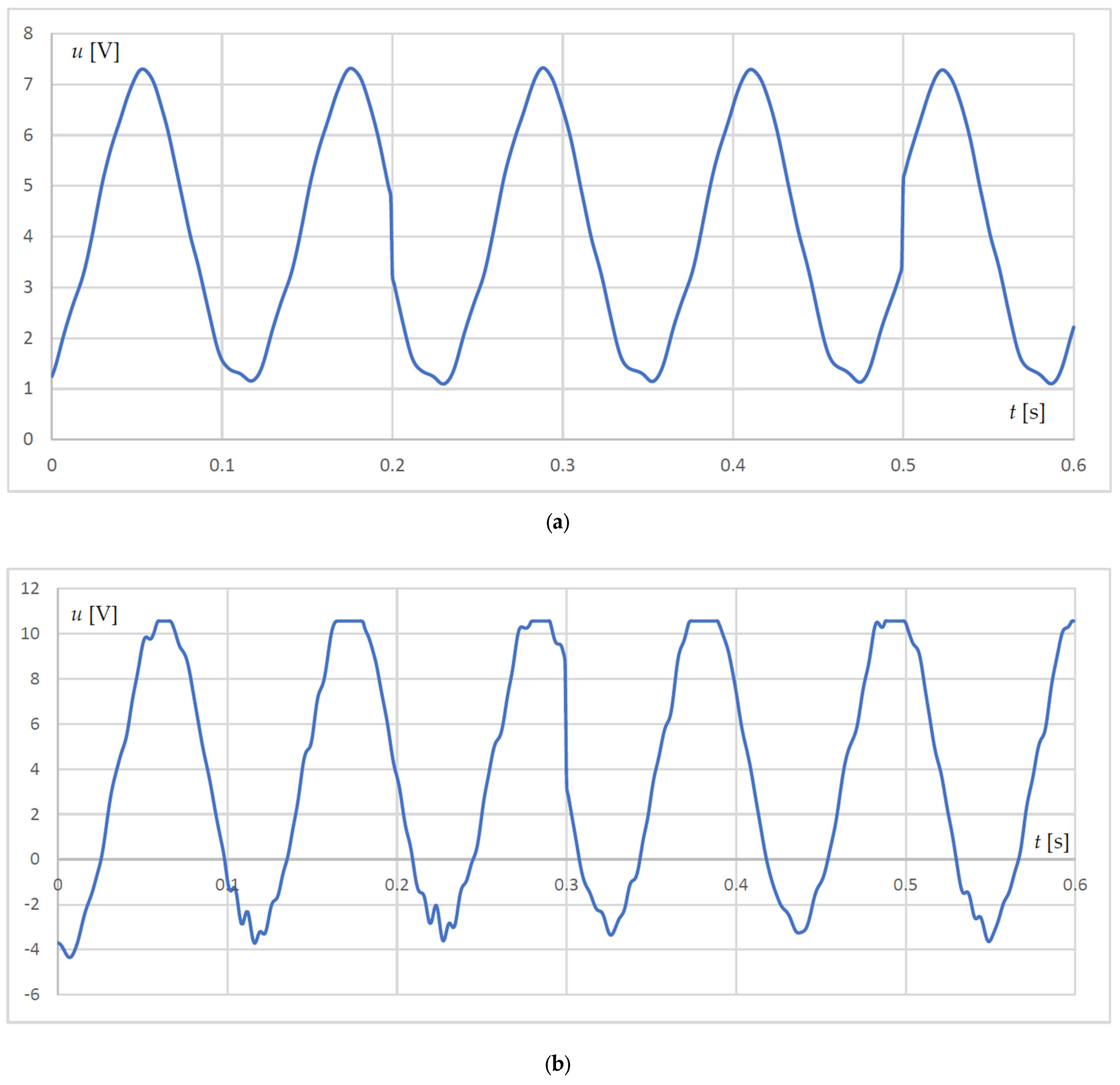
A comparison between the output voltages of the energy harvester without and with permanent magnets is shown in Figure 6. The plot of the resulting voltage without magnets is shown in Figure 6a, and the same output voltage but with magnets added is given in Figure 6b. It can be seen that the magnet increases the vibration frequency of the piezoelectric cantilevers and, furthermore, increases the magnitude of the generated output voltage.
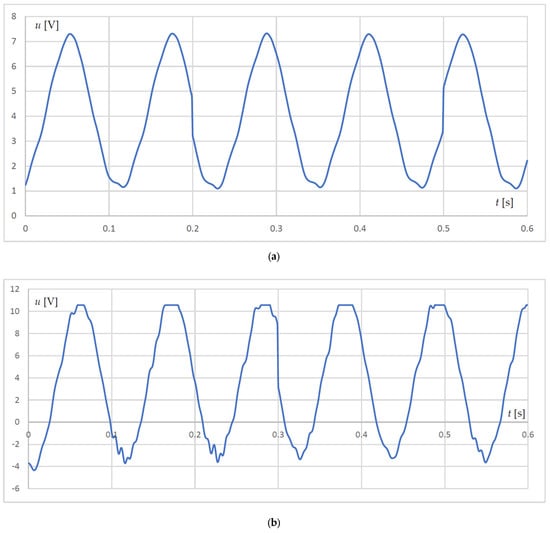
Figure 6.
Comparison between the output voltages obtained experimentally at heater temperature of 70 °C and a load resistor of 5.5 MOhms: (a) output voltage of the energy harvester without magnets; (b) output voltage of the energy harvester with magnets.
From the graphs, it is found that the magnets resulted in an increase in the output peak-to-peak voltage from 6.12 to 14.14 V, which is about a 130% increase in output voltage of the energy harvester with magnets. The magnets increased the output voltage frequency from 8.3 Hz to 9.2 Hz, which, in this case, is about an 11% increase in frequency.
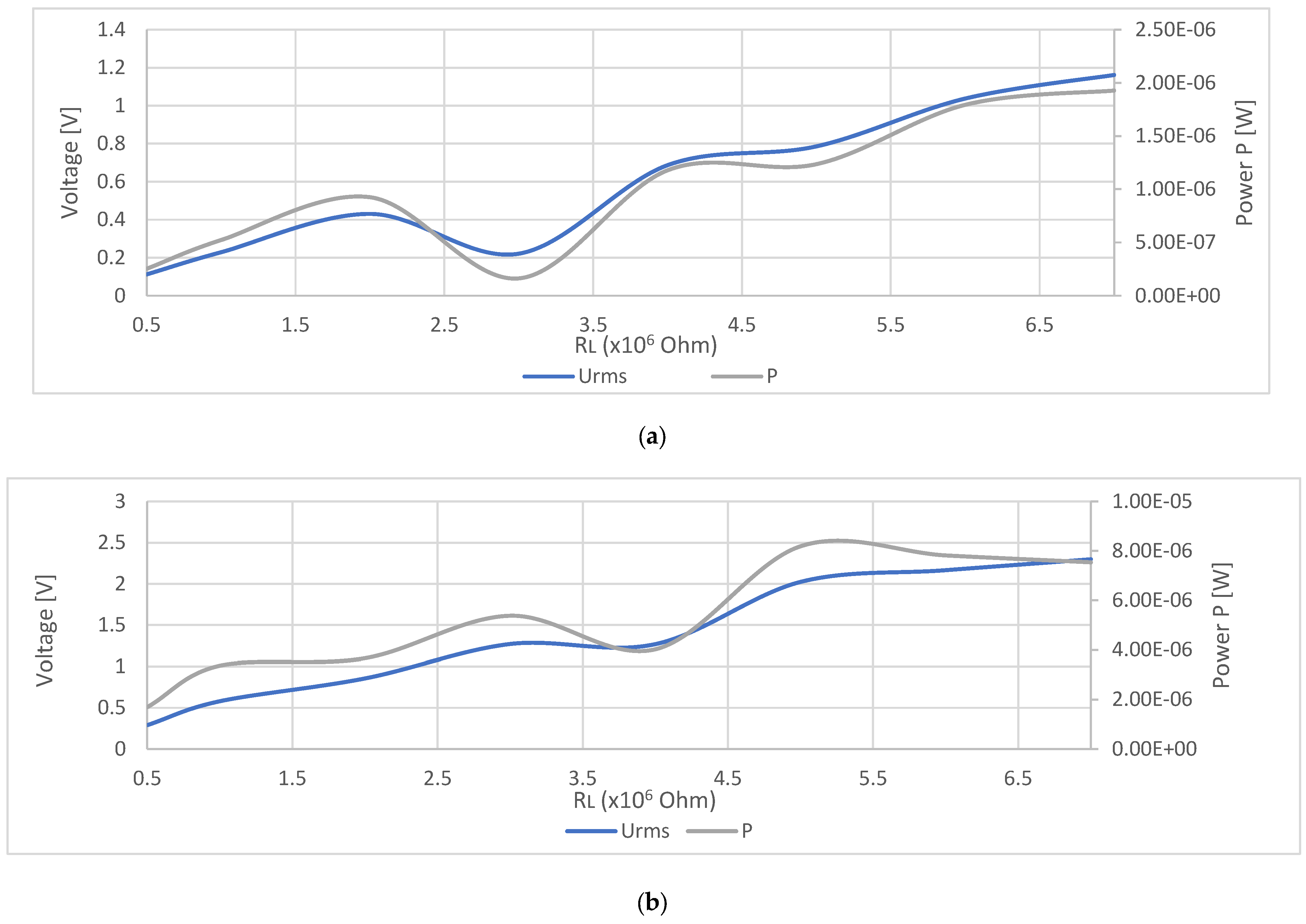
Figure 7 shows the output rms voltages and the power obtained experimentally at a heater temperature of 70 °C. From the comparisons that can be made from Figure 7a,b, it can be concluded that The maximum power, P = 1.9 µW, for the energy harvester without magnets is obtained at a load resistance of RL = 7 MOhms. For the energy harvester with magnets, the obtained maximum power is P = 8.18 µW at a load resistance of RL = 5 MOhms. This result shows that the magnets contributed to increasing the output optimum power by 330%.
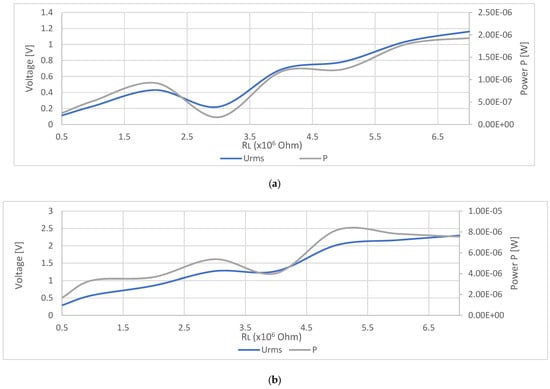
Figure 7.
Comparison between the output rms voltages and the power obtained experimentally at a heater temperature pg 70 °C: (a) output rms voltage and power of the energy harvester without magnets; (b) output rms voltage and power of the energy harvester with magnets.
5. Comparison of Theoretical and Experimental Data to Validate the Dynamic Model
The dynamical model consisting of the system of differentials (Equation (42)) differs from the model solutions in [41] in terms of the added potential magnetic energy. For the system’s solution, the same approach, based on the implicit fifth-order Euler method and the same initial conditions according to Table 1, was used.
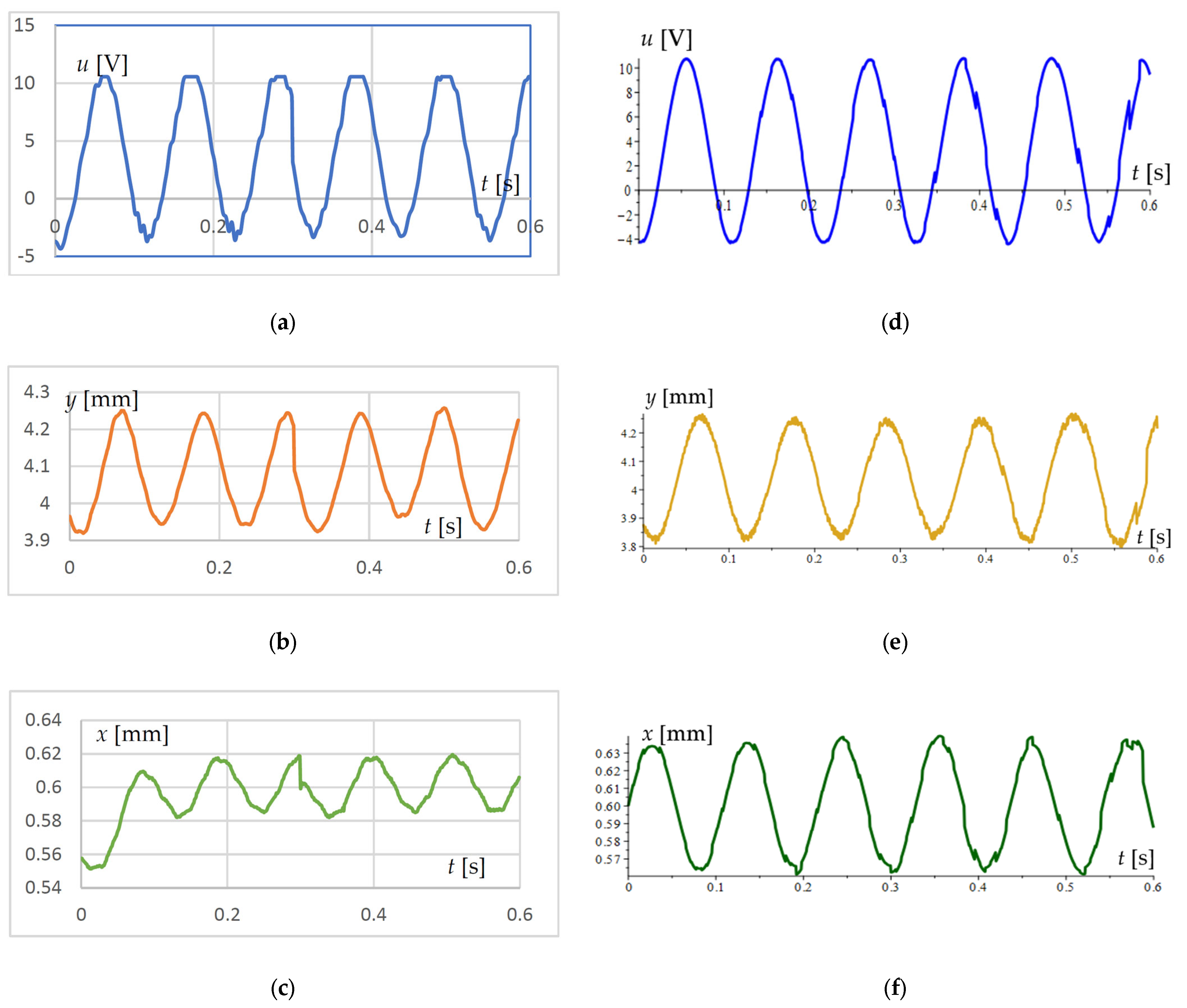
Figure 8a–c show the experimental results for the output voltage and the displacement of the spheres along the y-axis and x-axis, respectively. For comparison, Figure 8d–f show the results obtained from the solution of Equation (42).
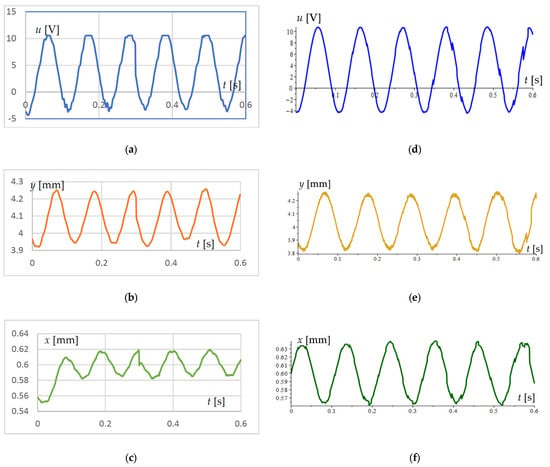
Figure 8.
Comparison of the experimental data with the theoretical predictions at a heater temperature of 70 °C and a load resistance of 500 MΩ: (a) experimental rms voltage; (b) experimental vertical displacement y of the ferromagnetic mass; (c) experimental horizontal displacement x of the ferromagnetic mass; (d) theoretically obtained rms voltage; (e) theoretically obtained vertical displacement y of the ferromagnetic mass; (f) theoretically obtained horizontal displacement x of the ferromagnetic mass;.
The numerical simulation results show a reasonably good confirmation of the experimental data. In analogous studies in [40], it was found that due to the multiple hystereses and the variable nature of the SMA thread heating, the vibrations have a pseudo-stochastic character that affects both the amplitudes and the frequencies and phases. The variation of the temperature modulus with respect to the Young’s modulus leads to a change in the frequencies of three types of oscillations: one thermal oscillation along the x-axis and two mechanical oscillations along both the x and y axes. The sum of the x-axis displacements is the cause of the modulated vibrations along this axis.
The displacement in Figure 8c differs from that in Figure 8f, especially in the interval of the time from 0 to 0.05 s. This difference is most likely due to the stochastic nature of the solution and the experimental results.
The system of ordinary differentials (Equation (42))is highly non-linear due to discontinuities on the right-hand sides of the functions caused by hysteresis. This makes them stiff and difficult to solve numerically. Attempts to use standard methods such as Runge–Kutta–Fehlberg 7(8) were unsuccessful, and a solution was only obtained by controlling the time step and number of iterations using the implicit Euler method [48] (see the Maple code form, Supplementary Materials).
It is well known that the phase transition temperatures of NiTi can vary widely depending on its chemical composition. For example, they can range from −150 °C to 150 °C [49]. Recent studies show that the cryogenic range is increasing. These studies suggest that the heat conversion method could be applicable at cryogenic temperatures. Having a “heater” operating in the low temperature range would create the necessary temperature distribution regardless of phase changes at low temperatures.
6. Conclusions
Unlike most thermal energy harvesters, which use temperature fluctuations over time, the innovative thermal energy harvester considered here converts the heat of a constant-temperature source, which generated a difference in the ambient temperature. This temperature distribution drives the oscillating SMA thread and a corresponding cantilever made of the piezoelectric material PVDF. In addition to smart materials such as the shape memory alloy Nitinol and the environmentally friendly piezoelectric material PVDF, two strong neodymium magnets are added to tune the natural frequency.
In a recently designed thermal energy harvesting device utilizing a (SMA) thread, a system of permanent magnets was added to influence the displacement of the ferromagnetic masses attached to the SMA threads. Since the heat source is at a constant temperature, thermal energy conversion is achieved via the self-excited vibrations of the SMA thread and the subsequent mechanoelectrical conversion by piezoelectric PVDF cantilevers. It has been shown, both experimentally and theoretically, that permanent magnets increase the natural vibration frequency of the system’s SMA thread and ferromagnetic masses.
Due to the influence of the permanent magnets, the thermal energy harvester’s output power rose from 1.9 µW to 8.18 µW, representing an approximately 330% increase. Additionally, the peak-to-peak voltage increased from 6.12 V to 14.14 V.
The experimental setup developed is capable of measuring vibration processes in real time, where no integration is required to determine the displacement. This is because the signal for the displacement along both axes is obtained from a non-contact inductive sensor, which only needs to be calibrated. If an inertial sensor such as an accelerometer were to be used, the double integration required to calculate the displacement would introduce large errors.
An interesting feature of the thermal energy harvester under consideration is that it can operate at cryogenic temperatures due to the wide temperature range over which the phase transformation of NiTi can be varied.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/en18133341/s1: Video S1: Magnetic Tuning of a Thermal Energy Harvester. File S2: Maple code of ODE system solution.
Author Contributions
Conceptualization, T.T., T.G., G.T. and I.Y.; methodology, T.T. and T.G.; software, T.T. and I.Y.; validation, I.Y.; formal analysis, G.T.; investigation, I.Y. and T.T.; resources, T.G.; data curation, T.G.; writing—original draft preparation, T.T. and I.Y.; writing—review and editing, G.T. and T.G.; visualization, T.T.; supervision, T.T.; project administration, G.T.; funding acquisition, G.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union—NextGenerationEU, through the National Recovery and Resilience Plan of the Republic of Bulgaria, project № BG-RRP-2.004-0005.
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tang, L.; Yang, Y.; Soh, C.K. Toward Broadband Vibration-Based Energy Harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 1867–1897. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, L.; Li, H. Vibration Energy Harvesting Using Macro-Fiber Composites. Smart Mater. Struct. 2009, 18, 115025. [Google Scholar] [CrossRef]
- Arnold, D.P. Review of Microscale Magnetic Power Generation. IEEE Trans. Magn. 2007, 43, 3940–3951. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Issues in Mathematical Modeling of Piezoelectric Energy Harvesters. Smart Mater. Struct. 2008, 17, 065016. [Google Scholar] [CrossRef]
- Adu-Manu, K.S.; Adam, N.; Tapparello, C.; Ayatollahi, H.; Heinzelman, W. Energy-Harvesting Wireless Sensor Networks (EH-WSNs). ACM Trans. Sens. Netw. 2018, 14, 1–50. [Google Scholar] [CrossRef]
- Shaikh, F.K.; Zeadally, S. Energy Harvesting in Wireless Sensor Networks: A Comprehensive Review. Renew. Sustain. Energy Rev. 2016, 55, 1041–1054. [Google Scholar] [CrossRef]
- Wei, C.; Jing, X. A Comprehensive Review on Vibration Energy Harvesting: Modelling and Realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Lee, H.; Kim, M.; Lee, G.; Kim, C.; Ahn, S. Shape Memory Alloy (SMA)-Based Microscale Actuators with 60% Deformation Rate and 1.6 KHz Actuation Speed. Small 2018, 14, 1801023. [Google Scholar] [CrossRef]
- AbuZaiter, A.; Nafea, M.; Mohamed Ali, M.S. Development of a Shape-Memory-Alloy Micromanipulator Based on Integrated Bimorph Microactuators. Mechatronics 2016, 38, 16–28. [Google Scholar] [CrossRef]
- Wang, Z.; Hang, G.; Wang, Y.; Li, J.; Du, W. Embedded SMA Wire Actuated Biomimetic Fin: A Module for Biomimetic Underwater Propulsion. Smart Mater. Struct. 2008, 17, 025039. [Google Scholar] [CrossRef]
- Kuo, T.Y.; Lin, H.S.; Lee, H.T. The Relationship between of Fracture Behaviors and Thermomechanical Effects of Alloy AA2024 of T3 and T81 Temper Designations Using the Center Crack Tensile Test. Mater. Sci. Eng. A 2005, 394, 28–35. [Google Scholar] [CrossRef]
- Li, T.; Chen, Y.H.; Ma, J. Frequency Dependence of Piezoelectric Vibration Velocity. Sens. Actuators A Phys. 2007, 138, 404–410. [Google Scholar] [CrossRef]
- Qiu, Y.; Sun, S.; Xu, C.; Wang, Y.; Tian, Y.; Liu, A.; Hou, X.; Chai, H.; Zhang, Z.; Wu, H. The Frequency-Response Behaviour of Flexible Piezoelectric Devices for Detecting the Magnitude and Loading Rate of Stimuli. J. Mater. Chem. C Mater. 2021, 9, 584–594. [Google Scholar] [CrossRef]
- Dechant, E.; Fedulov, F.; Fetisov, L.; Shamonin, M. Bandwidth Widening of Piezoelectric Cantilever Beam Arrays by Mass-Tip Tuning for Low-Frequency Vibration Energy Harvesting. Appl. Sci. 2017, 7, 1324. [Google Scholar] [CrossRef]
- Shi, G.; Yang, Y.; Chen, J.; Peng, Y.; Xia, H.; Xia, Y. A Broadband Piezoelectric Energy Harvester with Movable Mass for Frequency Active Self-Tuning. Smart Mater. Struct. 2020, 29, 055023. [Google Scholar] [CrossRef]
- Shahruz, S.M. Design of Mechanical Band-Pass Filters for Energy Scavenging. J. Sound. Vib. 2006, 292, 987–998. [Google Scholar] [CrossRef]
- Shahruz, S.M. Limits of Performance of Mechanical Band-Pass Filters Used in Energy Scavenging. J. Sound. Vib. 2006, 293, 449–461. [Google Scholar] [CrossRef]
- Cui, Y.; Mo, S.; Hu, W.; Lu, D. Effective Beam Mass of Diametrically Driven Self-Accelerating Beams in Photonic Lattices. Phys. Lett. A 2023, 489, 129159. [Google Scholar] [CrossRef]
- Staszak, N.; Gajewski, T.; Garbowski, T. Effective Stiffness of Thin-Walled Beams with Local Imperfections. Materials 2022, 15, 7665. [Google Scholar] [CrossRef]
- Xue, H.; Hu, Y.; Wang, Q. Broadband Piezoelectric Energy Harvesting Devices Using Multiple Bimorphs with Different Operating Frequencies. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2104–2108. [Google Scholar] [CrossRef]
- Chen, S.; Ma, L.; Chen, T.; Liu, H.; Sun, L.; Wang, J. Modeling and Verification of a Piezoelectric Frequency-up-Conversion Energy Harvesting System. Microsyst. Technol. 2017, 23, 2459–2466. [Google Scholar] [CrossRef]
- Žižys, D.; Gaidys, R.; Ostaševičius, V.; Narijauskaitė, B. Vibro-Shock Dynamics Analysis of a Tandem Low Frequency Resonator—High Frequency Piezoelectric Energy Harvester. Sensors 2017, 17, 970. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Kiziroglou, M.E.; Yates, D.C.; Yeatman, E.M. A Motion-Powered Piezoelectric Pulse Generator for Wireless Sensing via FM Transmission. IEEE Internet Things J. 2015, 2, 5–13. [Google Scholar] [CrossRef]
- Ibrahima, D.S.; Muthalif, A.G.A.; Saleh, T. A Piezoelectric Based Energy Harvester with Magnetic Interactions: Modelling and Simulation. Adv. Mat. Res. 2015, 1115, 549–554. [Google Scholar] [CrossRef]
- Upadrashta, D.; Yang, Y.; Tang, L. Material Strength Consideration in the Design Optimization of Nonlinear Energy Harvester. J. Intell. Mater. Syst. Struct. 2015, 26, 1980–1994. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Lee, H.P.; Yang, Y.; Zhang, X. A Review of the Inerter and Inerter-Based Vibration Isolation: Theory, Devices, and Applications. J. Franklin Inst. 2022, 359, 7677–7707. [Google Scholar] [CrossRef]
- Bouhedma, S.; Zheng, Y.; Lange, F.; Hohlfeld, D. Magnetic Frequency Tuning of a Multimodal Vibration Energy Harvester. Sensors 2019, 19, 1149. [Google Scholar] [CrossRef]
- Yang, C.-L.; Chen, K.-W.; Chen, C.-D. Model and Characterization of a Press-Button-Type Piezoelectric Energy Harvester. IEEE/ASME Trans. Mechatron. 2019, 24, 132–143. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear Energy Harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y.; Soh, C.-K. Improving Functionality of Vibration Energy Harvesters Using Magnets. J. Intell. Mater. Syst. Struct. 2012, 23, 1433–1449. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband Tristable Energy Harvester: Modeling and Experiment Verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Wang, W. Wideband Quin-Stable Energy Harvesting via Combined Nonlinearity. AIP Adv. 2017, 7, 045314. [Google Scholar] [CrossRef]
- Bouzelata, Y.; Kurt, E.; Uzun, Y.; Chenni, R. Mitigation of High Harmonicity and Design of a Battery Charger for a New Piezoelectric Wind Energy Harvester. Sens. Actuators A Phys. 2018, 273, 72–83. [Google Scholar] [CrossRef]
- Iqbal, M.; Khan, F.U. Hybrid Vibration and Wind Energy Harvesting Using Combined Piezoelectric and Electromagnetic Conversion for Bridge Health Monitoring Applications. Energy Convers. Manag. 2018, 172, 611–618. [Google Scholar] [CrossRef]
- Gupta, R.; Tomar, M.; Kumar, A.; Gupta, V. Performance of Magnetoelectric PZT/Ni Multiferroic System for Energy Harvesting Application. Smart Mater. Struct. 2017, 26, 035002. [Google Scholar] [CrossRef]
- Dąbrowska, A.; Greszta, A. Analysis of the Possibility of Using Energy Harvesters to Power Wearable Electronics in Clothing. Adv. Mater. Sci. Eng. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Tian, W.; Ling, Z.; Yu, W.; Shi, J. A Review of MEMS Scale Piezoelectric Energy Harvester. Appl. Sci. 2018, 8, 645. [Google Scholar] [CrossRef]
- Park, J.Y.; Salauddin, M.; Rasel, M.S. Nanogenerator for Scavenging Low Frequency Vibrations. J. Micromechanics Microengineering 2019, 29, 053001. [Google Scholar] [CrossRef]
- Kou, J.; Liu, Y.; Zhu, Y.; Zhai, J. Progress in Piezotronics of Transition-Metal Dichalcogenides. J. Phys. D Appl. Phys. 2018, 51, 493002. [Google Scholar] [CrossRef]
- Yotov, I.; Todorov, G.; Todorov, T. Study of Self-Excited Thermomechanical Oscillator with Shape Memory Alloys. Actuators 2024, 13, 182. [Google Scholar] [CrossRef]
- Yotov, I.; Todorov, G.; Gieva, E.; Todorov, T. Dynamics of a Self-Excited Vibrating Thermal Energy Harvester with Shape Memory Alloys and PVDF Cantilevers. Actuators 2024, 14, 8. [Google Scholar] [CrossRef]
- Dynalloy Inc. Technical Characteristics of Flexinol Actuator Wire. Available online: https://dynalloy.com/#smaller (accessed on 14 November 2024).
- Mitrev, R.; Todorov, T.; Fursov, A.; Ganev, B. Theoretical and Experimental Study of a Thermo-Mechanical Model of a Shape Memory Alloy Actuator Considering Minor Hystereses. Crystals 2021, 11, 1120. [Google Scholar] [CrossRef]
- Mitrev, R.; Todorov, T.S. A Case Study of Experimental Evaluation of the Properties of Shape Memory Alloy Wires. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2022; p. 060010. [Google Scholar] [CrossRef]
- Todorov, T.S.; Mitrev, R.P.; Tudjarov, B.N.; Nikolov, R.F. Qualitative Analysis of Oscillating Magnetomechanical System. IOP Conf. Ser. Mater. Sci. Eng. 2449 2019, 618, 012054. [Google Scholar] [CrossRef]
- Preumont, A. Mechatronics: Dynamics of Electromechanical and Piezoelectric Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Sessler, G.M. Piezoelectricity in Polyvinylidenefluoride. J. Acoust. Soc. Am. 1981, 70, 1596–1608. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Stöckel, D. Industrial Applications of Nickel-Titanium Shape Memory Alloys. In Proceedings of the ESOMAT 1989—Ist European Symposium on Martensitic Transformations in Science and Technology, Les Ulis, France, 9–10 March 1989; pp. 223–230. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).