Planning Scheme for Optimal PMU Location Considering Power System Expansion
Abstract
1. Introduction
2. Power System Expansion Planning
- 1.
- If the voltage and current on one side of the branch are known, the values on the other can be determined by applying Ohm’s Law.
- 2.
- ZIB and its repercussions: If only one bus is not observable, applying Kirchhoff’s Law of Currents makes the bus observable.
- 3.
- If the voltage phasors on both sides of a branch are known, the corresponding current phasors can be obtained.
2.1. Optimal PMU Placement Considering Redundancy and Observability Restrictions
2.2. Location of the Minimum Number of PMUs to Maximize Observability
2.3. Transmission Expansion Planning
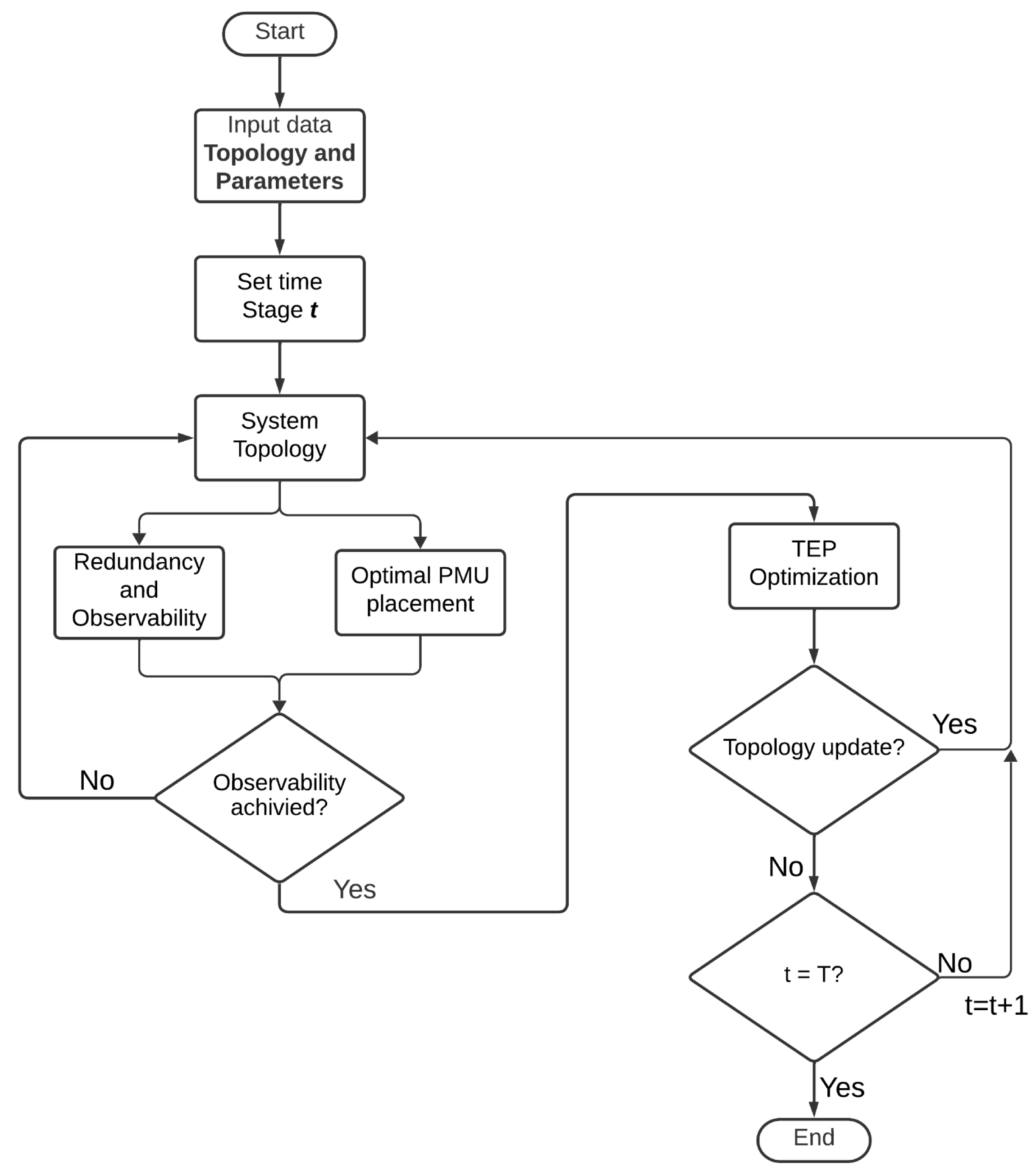
3. Problem Formulation and Methodology
| Algorithm 1: Optimal PMU location considering TEP |
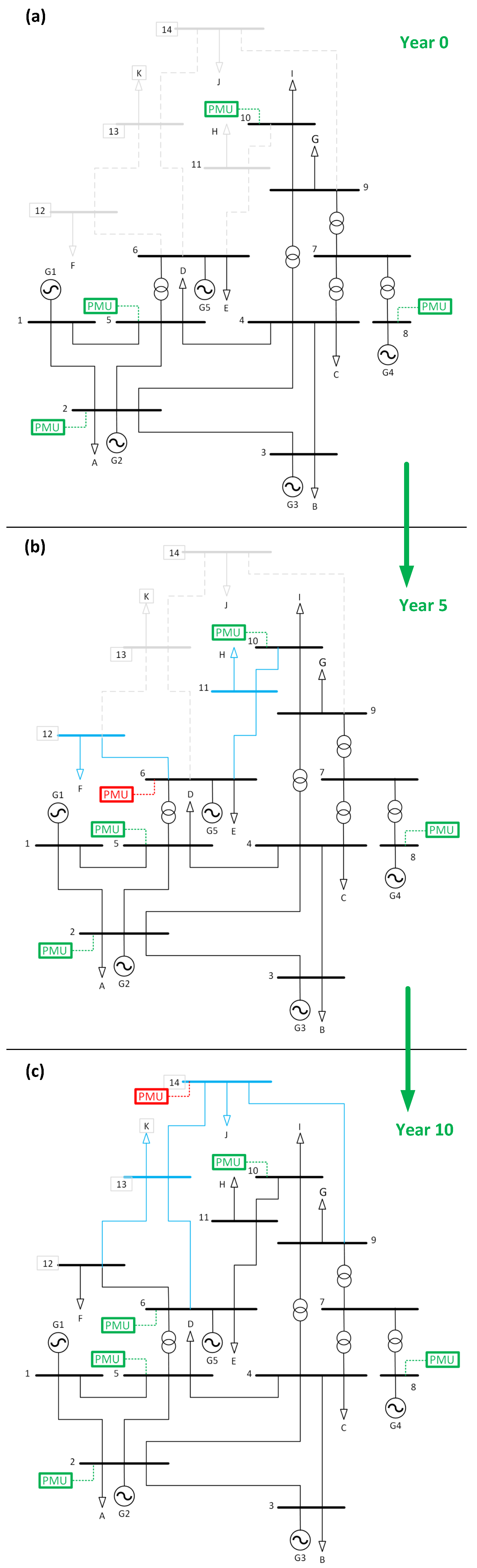
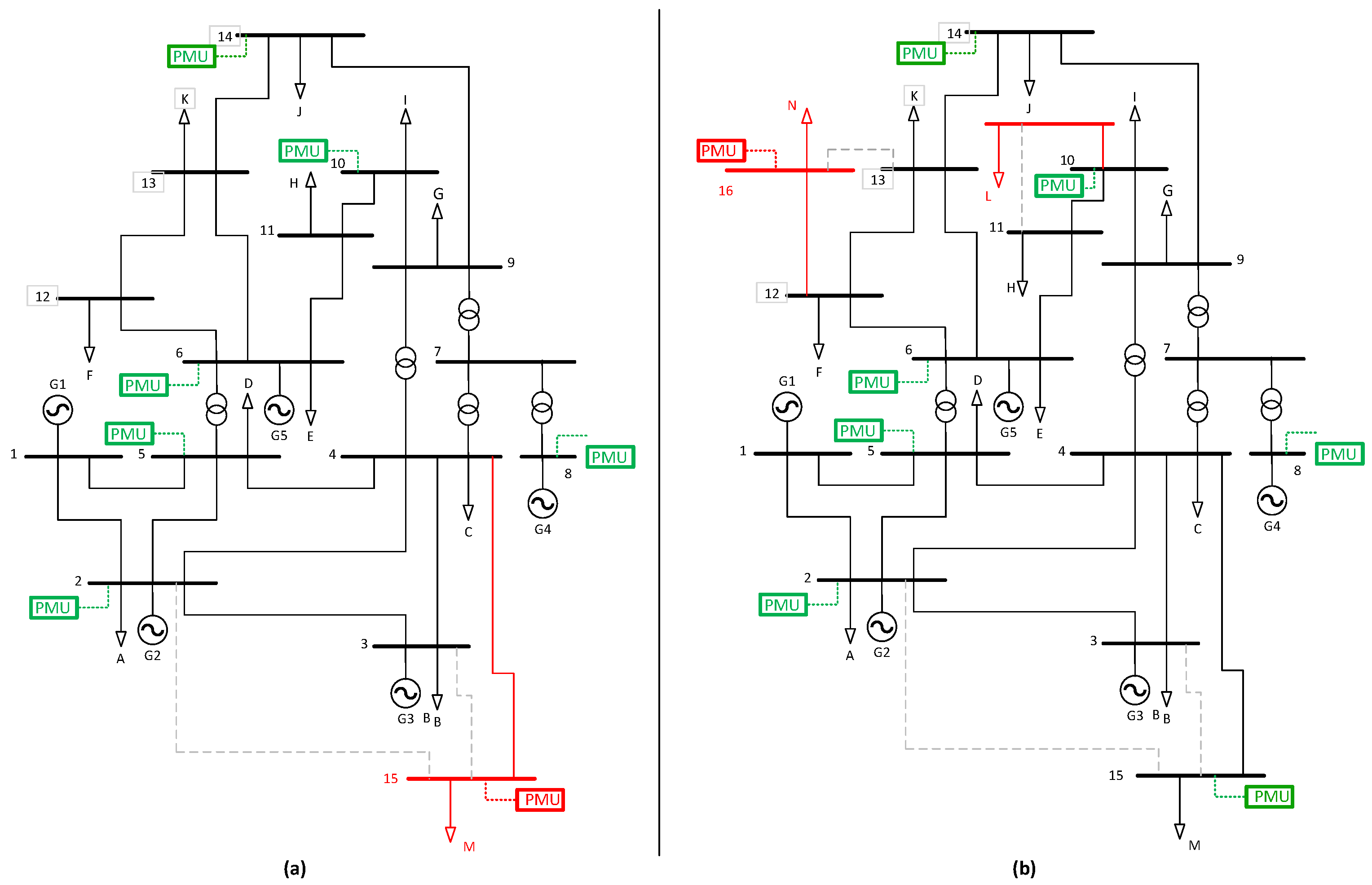
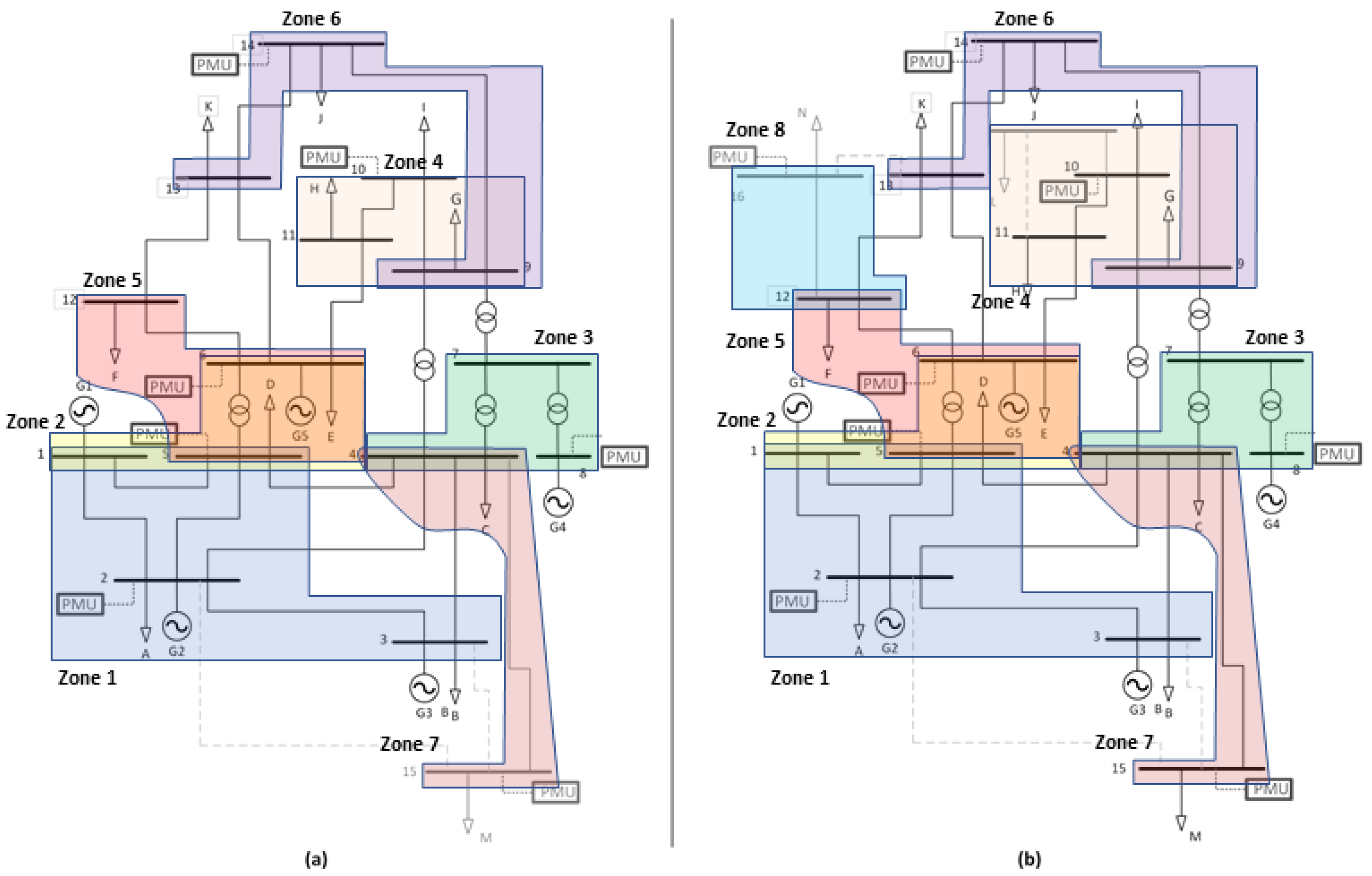
4. Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EPS connectivity matrix | |
| PMU implementation cost at node i | |
| PMU location binary variable at node i | |
| EPS observability percentage | |
| PMU quantity | |
| T | Planning period |
| Operation costs | |
| Investment costs | |
| generators set | |
| Nodes set | |
| Generation production costs | |
| Generator real power | |
| Initial state of the line between nodes | |
| Binary variable representing the status of the line | |
| Cost of the candidate line between nodes | |
| Power flow limit per line | |
| Maximum power flow limit per line | |
| Susceptance of the line between nodes | |
| Voltage angle at node i | |
| M | maximum line load capacity |
| Real power generated by the generator i | |
| Maximum active power limit of generators | |
| Minimum active power limit for generator | |
| Load shedding at node i | |
| Load at node i |
References
- Manousakis, N.M.; Korres, G.N.; Georgilakis, P.S. Taxonomy of PMU placement methodologies. IEEE Trans. Power Syst. 2012, 27, 1070–1077. [Google Scholar] [CrossRef]
- Ghamsari-Yazdel, M.; Esmaili, M.; Amjady, N. Optimal substation-based joint allocation of PMUs and measuring channels considering network expansion planning. Int. J. Electr. Power Energy Syst. 2019, 106, 274–287. [Google Scholar] [CrossRef]
- Aminifar, F.; Fotuhi-Firuzabad, M.; Safdarian, A.; Davoudi, A.; Shahidehpour, M. Synchrophasor Measurement Technology in Power Systems: Panorama and State-of-the-Art. IEEE Access 2014, 2, 1607–1628. [Google Scholar] [CrossRef]
- Mohanta, D.K.; Murthy, C.; Sinha Roy, D. A Brief Review of Phasor Measurement Units as Sensors for Smart Grid. Electr. Power Compon. Syst. 2016, 44, 411–425. [Google Scholar] [CrossRef]
- Johnson, T.; Moger, T. A critical review of methods for optimal placement of phasor measurement units. Int. Trans. Electr. Energy Syst. 2021, 31, 1–25. [Google Scholar] [CrossRef]
- Babu, R.; Raj, S.; Bhattacharyya, B. Weak bus-constrained PMU placement for complete observability of a connected power network considering voltage stability indices. Prot. Control Mod. Power Syst. 2020, 5, 28. [Google Scholar] [CrossRef]
- Carrión Galarza, D.F.; González Sánchez, J.W. Ubicación óptima de PMU considerando restricciones de contingencias N-1 en sistemas eléctricos de potencia. Enfoque UTE 2019, 10, 1–12. [Google Scholar] [CrossRef]
- Asgari, A.; Firouzjah, K.G. Optimal PMU placement for power system observability considering network expansion and N-1 contingencies. IET Gener. Transm. Distrib. 2018, 12, 4216–4224. [Google Scholar] [CrossRef]
- Aghaei, J.; Baharvandi, A.; Rabiee, A.; Akbari, M.A. Probabilistic PMU Placement in Electric Power Networks: An MILP-Based Multiobjective Model. IEEE Trans. Ind. Inform. 2015, 11, 332–341. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Korres, G.N. Optimal PMU arrangement considering limited channel capacity and transformer tap settings. IET Gener. Transm. Distrib. 2020, 14, 5816–5822. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Korres, G.N. Optimal PMU Placement for Numerical Observability Considering Fixed Channel Capacity-A Semidefinite Programming Approach. IEEE Trans. Power Syst. 2016, 31, 3328–3329. [Google Scholar] [CrossRef]
- Hanis, N.; Rahman, A.; Zobaa, A.F. Binary PSO Algorithm for Optimal PMUs Placement. IEEE Trans. Ind. Inform. 2017, 13, 3124–3133. [Google Scholar]
- Bae, J. Cost-Effective placement of phasor measurement units to defend against false data injection attacks on power grid. Energies 2020, 13, 3862. [Google Scholar] [CrossRef]
- Ali, Z.M.; Razavi, S.E.; Javadi, M.S.; Gandoman, F.H.; Abdel Aleem, S.H. Dual enhancement of power system monitoring: Improved probabilistic multi-stage PMU placement with an increased search space & mathematical linear expansion to consider zero-injection bus. Energies 2018, 11, 1429. [Google Scholar] [CrossRef]
- Bečejac, V.; Stefanov, P. Groebner bases algorithm for optimal PMU placement. Int. J. Electr. Power Energy Syst. 2020, 115, 105427. [Google Scholar] [CrossRef]
- Abd el Ghany, H.A. Optimal PMU allocation for high-sensitivity wide-area backup protection scheme of transmission lines. Electr. Power Syst. Res. 2020, 187, 106485. [Google Scholar] [CrossRef]
- Mohammadi, P.; Mehraeen, S.; Nazaripouya, H. Sensitivity analysis-based optimal PMU placement for fault observability. IET Gener. Transm. Distrib. 2021, 15, 737–750. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Chatterjee, S.; Roy, B.K.S. Optimal PMU placement solution: Graph theory and MCDM-based approach. IET Gener. Transm. Distrib. 2017, 11, 3371–3380. [Google Scholar] [CrossRef]
- Razavi, S.E.; Falaghi, H.; Esmaeel Nezhad, A.; Hadidian Moghaddam, M.J.; Gandoman, F.H. An Effective Approach for the Probabilistic and Deterministic Multistage PMU Placement Using Cuckoo Search: Iran’s National Power System. Iran. J. Sci. Technol.-Trans. Electr. Eng. 2020, 44, 237–252. [Google Scholar] [CrossRef]
- Saleh, A.A.; Adail, A.S.; Wadoud, A.A. Optimal phasor measurement units placement for full observability of power system using improved particle swarm optimisation. IET Gener. Transm. Distrib. 2017, 11, 1794–1800. [Google Scholar] [CrossRef]
- Gacitua, L.; Gallegos, P.; Henriquez-Auba, R.; Lorca, Á.; Negrete-Pincetic, M.; Olivares, D.; Valenzuela, A.; Wenzel, G. A comprehensive review on expansion planning: Models and tools for energy policy analysis. Renew. Sustain. Energy Rev. 2018, 98, 346–360. [Google Scholar] [CrossRef]
- Giral Ramírez, D.A.; Montoya Giraldo, O.D.; Vargas Robayo, C.Y.; Blanco Valbuena, D.F. Evaluación de modelos de programación lineal y no lineal para la planeación de sistemas de transmisión en el software GAMS. Tecnura 2021, 25, 16–50. [Google Scholar] [CrossRef]
- Bolaños Ocampo, R.A.; Correa Flórez, C.A. Planeamiento de la transmisión considerando seguridad e incertidumbre en la demanda empleando programación no lineal y técnicas evolutivas. Rev. Tecnura 2013, 18, 62. [Google Scholar] [CrossRef][Green Version]
- Palacios, J. Estado del arte de la planeación de expansión de sistemas de transmisión. I+D Tecnol. 2020, 16, 78–85. [Google Scholar] [CrossRef]
- Hamidpour, H.; Aghaei, J.; Pirouzi, S.; Niknam, T.; Nikoobakht, A.; Lehtonen, M.; Shafie-khah, M.; Catalão, J.P. Coordinated expansion planning problem considering wind farms, energy storage systems and demand response. Energy 2022, 239, 122321. [Google Scholar] [CrossRef]
- Zhao, J.H.; Dong, Z.Y.; Lindsay, P.; Wong, K.P. Flexible transmission expansion planning with uncertainties in an electricity market. IEEE Trans. Power Syst. 2009, 24, 479–488. [Google Scholar] [CrossRef]
- Vilaça, P.; Street, A.; Colmenar, J.M. A MILP-based heuristic algorithm for transmission expansion planning problems. Electr. Power Syst. Res. 2022, 208, 107882. [Google Scholar] [CrossRef]
- Escudero, P.; Carrión, D. Expansión de un sistema de transmisión mediante LOPF-AC Expansion of a transmission system using LOPF-AC. INGE CUC 2018, 14, 116–125. [Google Scholar] [CrossRef]
- Tejada-Arango, D.; López-Lezama, J.M.; Rider, M.J. Planeamiento de la expansión de la red de transmisión en sistemas eléctricos de potencia considerando reconfiguraciones de red. Inf. Tecnol. 2014, 25, 85–96. [Google Scholar] [CrossRef]
- Li, C.; Conejo, A.J.; Liu, P.; Omell, B.P.; Siirola, J.D.; Grossmann, I.E. Mixed-integer linear programming models and algorithms for generation and transmission expansion planning of power systems. Eur. J. Oper. Res. 2022, 297, 1071–1082. [Google Scholar] [CrossRef]
- Esmaili, M.; Ghamsari-Yazdel, M.; Amjady, N.; Chung, C.Y.; Conejo, A.J. Transmission Expansion Planning including TCSCs and SFCLs: A MINLP Approach. IEEE Trans. Power Syst. 2020, 35, 4396–4407. [Google Scholar] [CrossRef]
- Hemmati, R.; Hooshmand, R.A.; Khodabakhshian, A. State-of-the-art of transmission expansion planning: Comprehensive review. Renew. Sustain. Energy Rev. 2013, 23, 312–319. [Google Scholar] [CrossRef]
- Alhamrouni, I.; Khairuddin, A.; Ferdavani, A.; Salem, M. Transmission expansion planning using AC-based differential evolution algorithm. IET Gener. Transm. Distrib. 2014, 8, 1637–1644. [Google Scholar] [CrossRef]
- Carrión, D.; Francisco, J.; Paul, M. Revisión para la restauración optima de la operación del sistema eléctrico basado en criterios de calidad de energía y estabilidad. Rev. I+D Tecnol. 2021, 17, 9. [Google Scholar] [CrossRef]



| Reference | Methodology | Optimization Approach | Key Features | Advantages | Limitations |
|---|---|---|---|---|---|
| [1] | PMU placement taxonomy | Various (ILP, metaheuristics) | Comprehensive classification of methods | Broad overview, useful for method selection | Does not propose a new optimization model |
| [7] | PMU placement with N-1 contingencies | MILP | Based on Ecuadorian EPS | Realistic case constraints | No cost or staged planning |
| [8] | PMU placement with N-1 contingencies | MILP | Integrates reliability constraints | Practical for contingency analysis | No temporal expansion modeled |
| [9] | Probabilistic PMU placement | MILP (multi-objective) | Considers uncertainty in observability | Robust under system variability | Focused on static systems |
| [14] | Multi-stage PMU placement with expansion | Hybrid (mathematical + heuristic) | Accounts for network expansion | Introduces staging | Complexity increases with scale |
| [This paper] | PMU placement with expansion over time | MILP (stepwise planning) | Observability + redundancy + expansion | Adaptable, cost-aware, supports scheduling | Currently excludes contingencies and cyber-resilience |
| Year | # Nodes | # PMUs | Nodes with PMU | # Buses Observed |
|---|---|---|---|---|
| 0 | 10 | 4 | 2, 5, 8, 10 | 9 (90%) |
| 2 | 10 | 4 | 2, 5, 8, 10 | 10 (100%) |
| 4 | 10 | 4 | 2, 5, 8, 10 | 10 (100%) |
| 6 | 12 | 5 | 2, 5, 6, 8, 10 | 12 (100%) |
| 8 | 12 | 5 | 2, 5, 6, 8, 10 | 12 (100%) |
| 10 | 14 | 6 | 2, 5, 6, 8, 10, 14 | 14 (100%) |
| Year | # Nodes | # PMUs | Nodes with PMU | # Buses Observed |
|---|---|---|---|---|
| 12 | 14 | 6 | 2, 5, 6, 8, 10, 14 | 14 (100%) |
| 14 | 14 | 6 | 2, 5, 6, 8, 10, 14 | 14 (100%) |
| 16 | 15 | 7 | 2, 5, 6, 8, 10, 14, 15 | 15 (100%) |
| 18 | 15 | 7 | 2, 5, 6, 8, 10, 14, 15 | 15 (100%) |
| 20 | 17 | 8 | 2, 5, 6, 8, 10, 14, 15, 16 | 16 (100%) |
| Total Nodes | New Loads | Candidates Lines | New Lines |
|---|---|---|---|
| 14 | bus 15 45 kW | 2–15, 3–15, 4–15 | 4–15 |
| 15 | bus 16 8 kW | 12–16, 13–16 | 12–16 |
| 16 | bus 17 5 kW | 10–17, 11–17 | 10–17 |
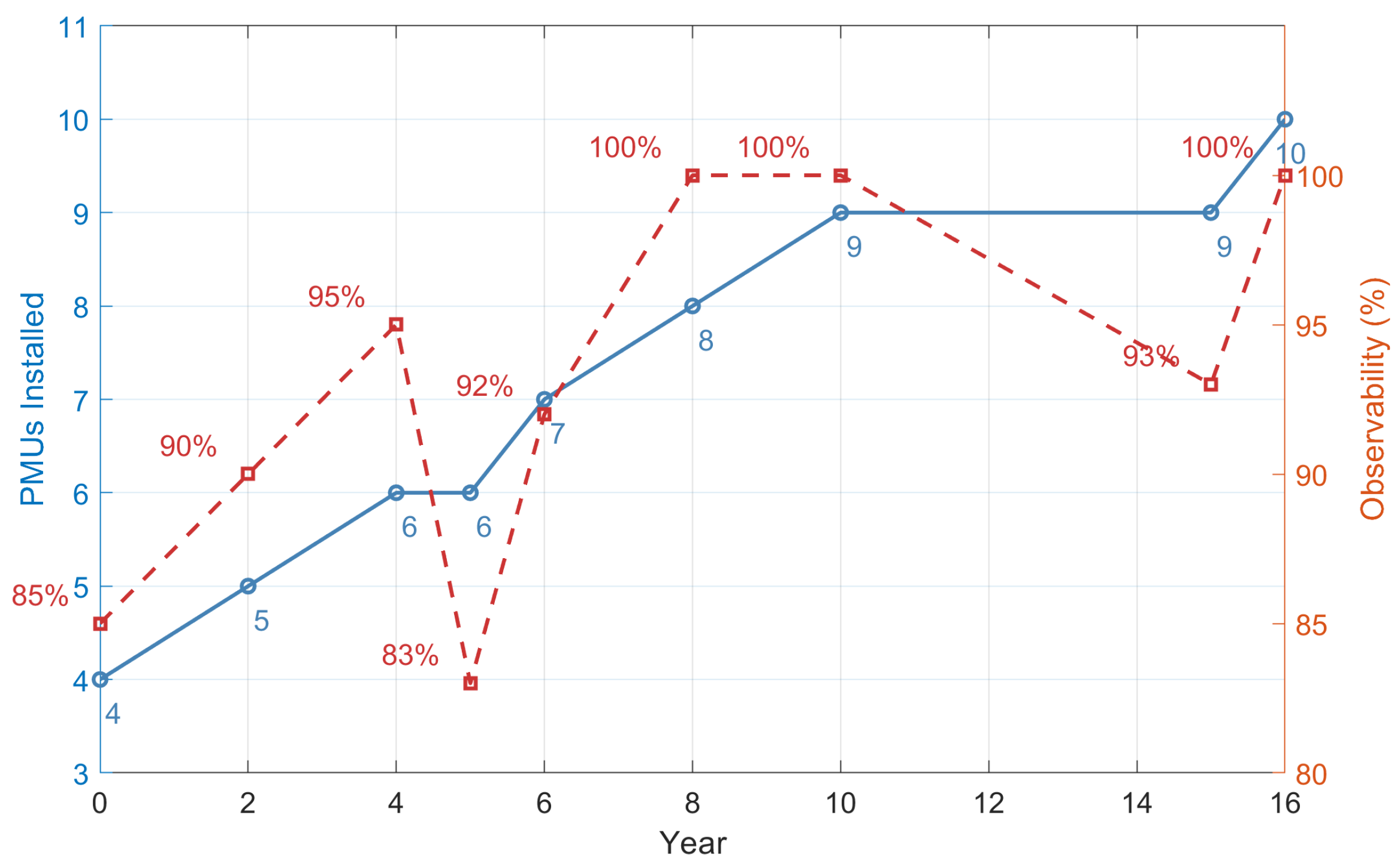
| Year | # Nodes | # PMUs | Nodes with PMU | # Buses Observed |
|---|---|---|---|---|
| 0 | 20 | 4 | 1, 6, 12, 19 | 17 (85%) |
| 2 | 20 | 5 | 1, 2, 6, 9, 12, 19 | 18 (90%) |
| 4 | 20 | 6 | 1, 2, 6, 9, 12, 19 | 19 (95%) |
| 5 | 24 | 6 | 1, 2, 6, 9, 12, 19 | 20 (83%) |
| 6 | 24 | 7 | 1, 2, 6, 9, 10, 12, 19 | 22 (92%) |
| 8 | 24 | 8 | 1, 2, 6, 9, 10, 12, 19, 23 | 24 (100%) |
| 10 | 28 | 9 | 1, 2, 6, 9, 10, 12, 19, 23, 25 | 28 (100%) |
| 15 | 30 | 9 | 1, 2, 6, 9, 10, 12, 19, 23, 25 | 28 (93%) |
| 16 | 30 | 10 | 1, 2, 6, 9, 10, 12, 19, 23, 25, 27 | 30 (100%) |
| Year | # Nodes | # PMUs | Nodes with PMU | # Buses Observed |
|---|---|---|---|---|
| 0 | 100 | 19 | 1, 7, 9, 11, 17, 21, 25, 28, 34, 37, 49 56, 59, 65, 70, 77, 80, 85, 94 | 86 (86%) |
| 1 | 100 | 21 | 1, 7, 9, 11, 17, 21, 25, 28, 34, 37, 49, 52 56, 59, 62, 65, 70, 71, 77, 80, 85, 94 | 90 (90%) |
| 2 | 100 | 23 | 1, 7, 9, 11, 17, 21, 25, 28, 34, 37, 45, 49 52, 56, 59, 62, 65, 70, 71, 77, 80, 85, 94 | 94 (94%) |
| 3 | 100 | 25 | 1, 7, 9, 11, 15, 17, 21, 25, 28, 34, 37, 45, 49 52, 56, 59, 62, 65, 70, 71, 77, 80, 85, 91, 94 | 97 (97%) |
| 4 | 100 | 27 | 1, 7, 9, 11, 15, 17, 21, 25, 28, 31, 34, 37, 40, 45 49, 52, 56, 59, 62, 65, 70, 71, 77, 80, 85, 91, 94 | 99 (99%) |
| 6 | 100 | 29 | 1, 7, 9, 11, 15, 17, 21, 25, 28, 31, 34, 37, 40, 45, 49, 52 56, 59, 62, 65, 70, 71, 77, 80, 85, 91, 94, 100, 101 | 101 (100%) |
| 8 | 100 | 30 | 1, 7, 9, 11, 15, 17, 21, 25, 28, 31, 34, 37, 40, 45, 49, 52 56, 59, 62, 65, 70, 71, 77, 80, 85, 87, 91, 94, 100, 101 | 105 (97%) |
| 8 | 100 | 31 | 1, 7, 9, 11, 15, 17, 21, 25, 28, 31, 34, 37, 40, 45, 49, 52, 56 59, 62, 65, 70, 71, 77, 80, 85, 87, 91, 94, 100, 101, 105 | 118 (100%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvajal, G.; Carrión, D.; Jaramillo, M. Planning Scheme for Optimal PMU Location Considering Power System Expansion. Energies 2025, 18, 3283. https://doi.org/10.3390/en18133283
Carvajal G, Carrión D, Jaramillo M. Planning Scheme for Optimal PMU Location Considering Power System Expansion. Energies. 2025; 18(13):3283. https://doi.org/10.3390/en18133283
Chicago/Turabian StyleCarvajal, Gandhi, Diego Carrión, and Manuel Jaramillo. 2025. "Planning Scheme for Optimal PMU Location Considering Power System Expansion" Energies 18, no. 13: 3283. https://doi.org/10.3390/en18133283
APA StyleCarvajal, G., Carrión, D., & Jaramillo, M. (2025). Planning Scheme for Optimal PMU Location Considering Power System Expansion. Energies, 18(13), 3283. https://doi.org/10.3390/en18133283









