A Simulation and a Computational Study on the Reliability Verification of Epoxy Resin Paper-Impregnated Bushings in Power Transformers
Abstract
1. Introduction
2. Simulation and Test Methods
2.1. Geometric Model
2.2. Mathematical Models
2.2.1. A Mathematical Model for Electric Field Simulation
2.2.2. A Mathematical Model for Seismic Performance
2.2.3. A Mathematical Model for Thermal Short-Circuit Current
2.2.4. A Mathematical Model for Thermal Field Simulation
2.3. Model Parameters and Boundary Conditions
2.4. Bushing Performance Test Methods
3. Results and Discussion
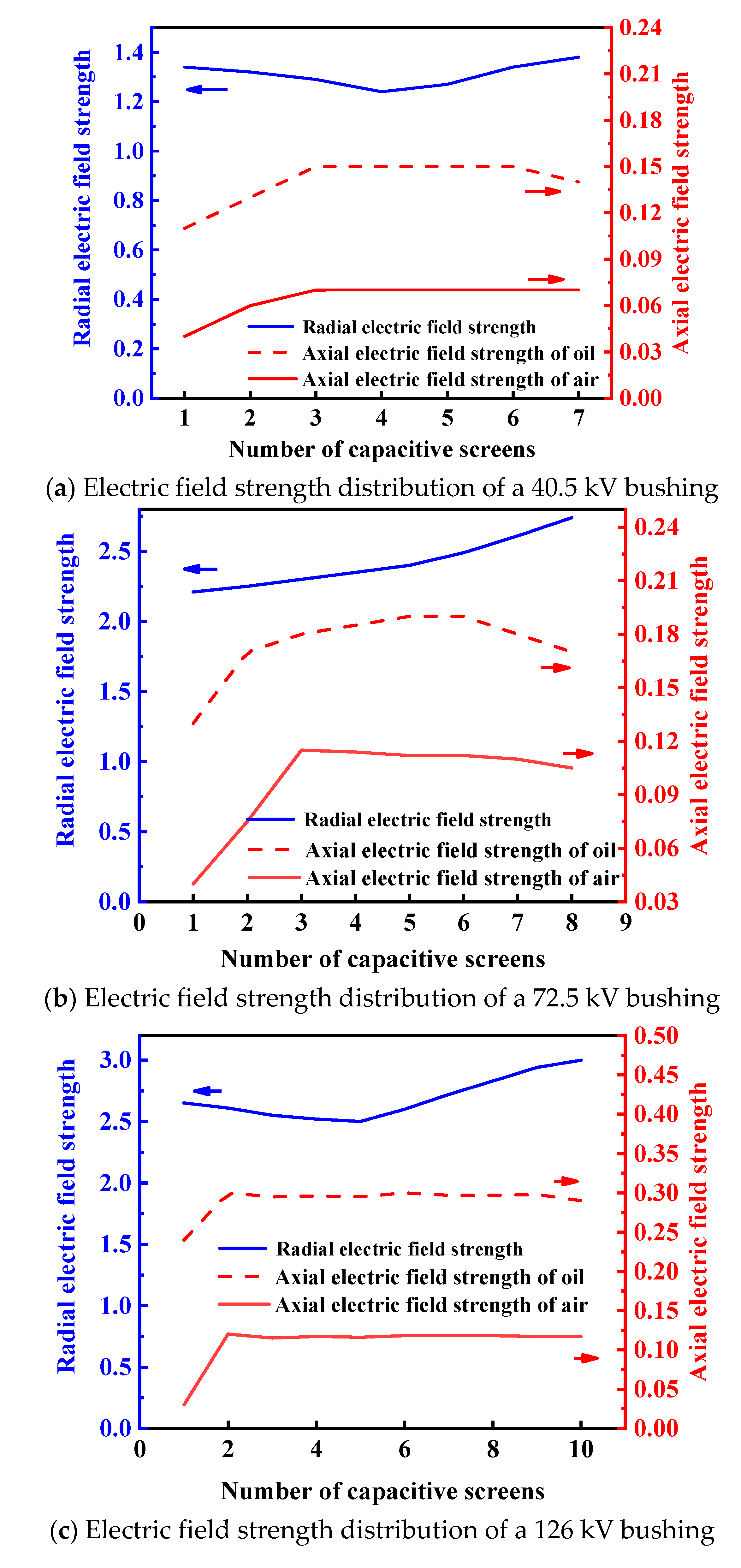
3.1. Simulation of Electric Field Strength in the Epoxy Core
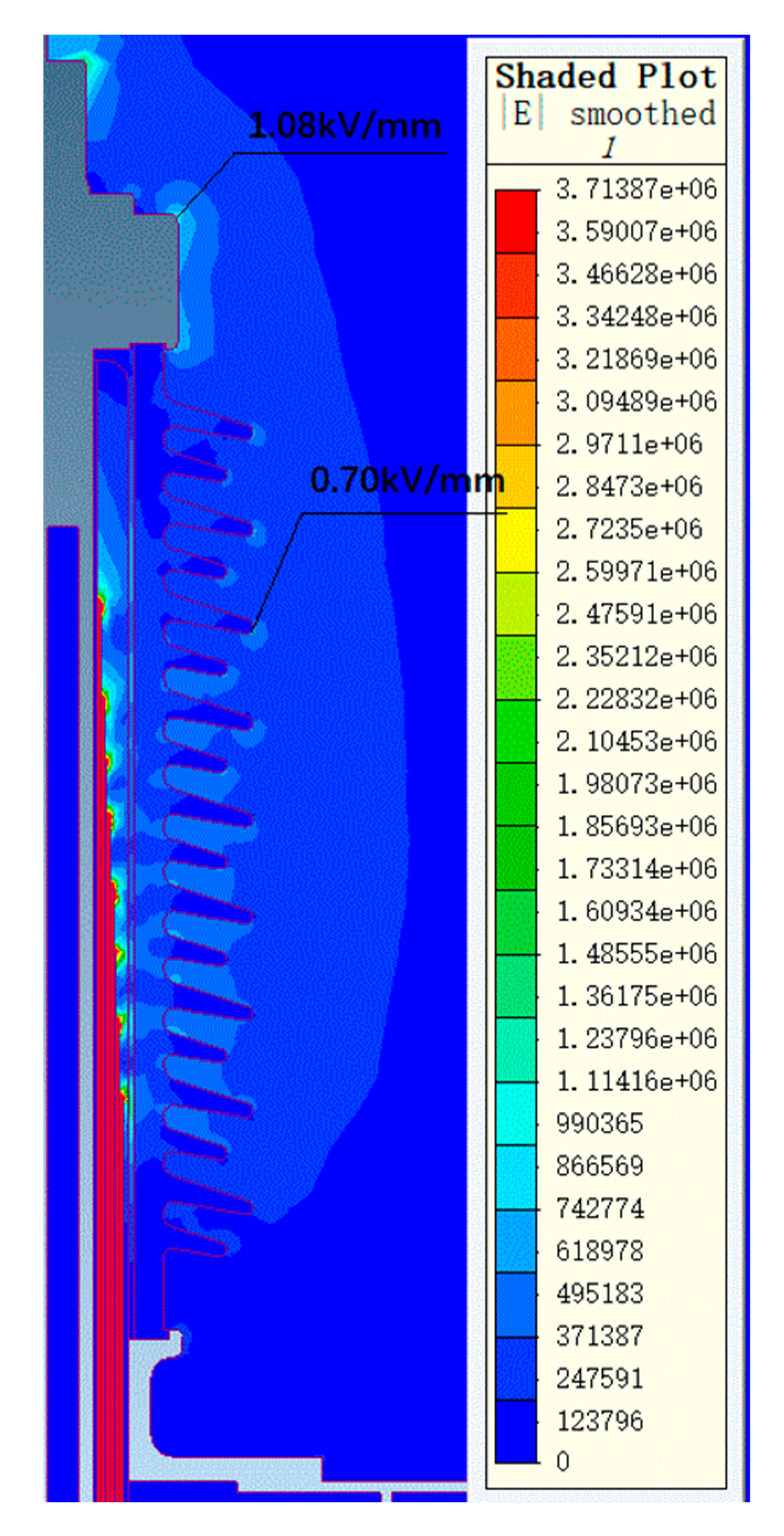
3.2. Bushing Electric Field Simulation
3.2.1. Simulation of the Bushing Electric Field Under Phase Voltage
3.2.2. Simulation of the Bushing Terminal Electric Field Under Power Frequency Voltage
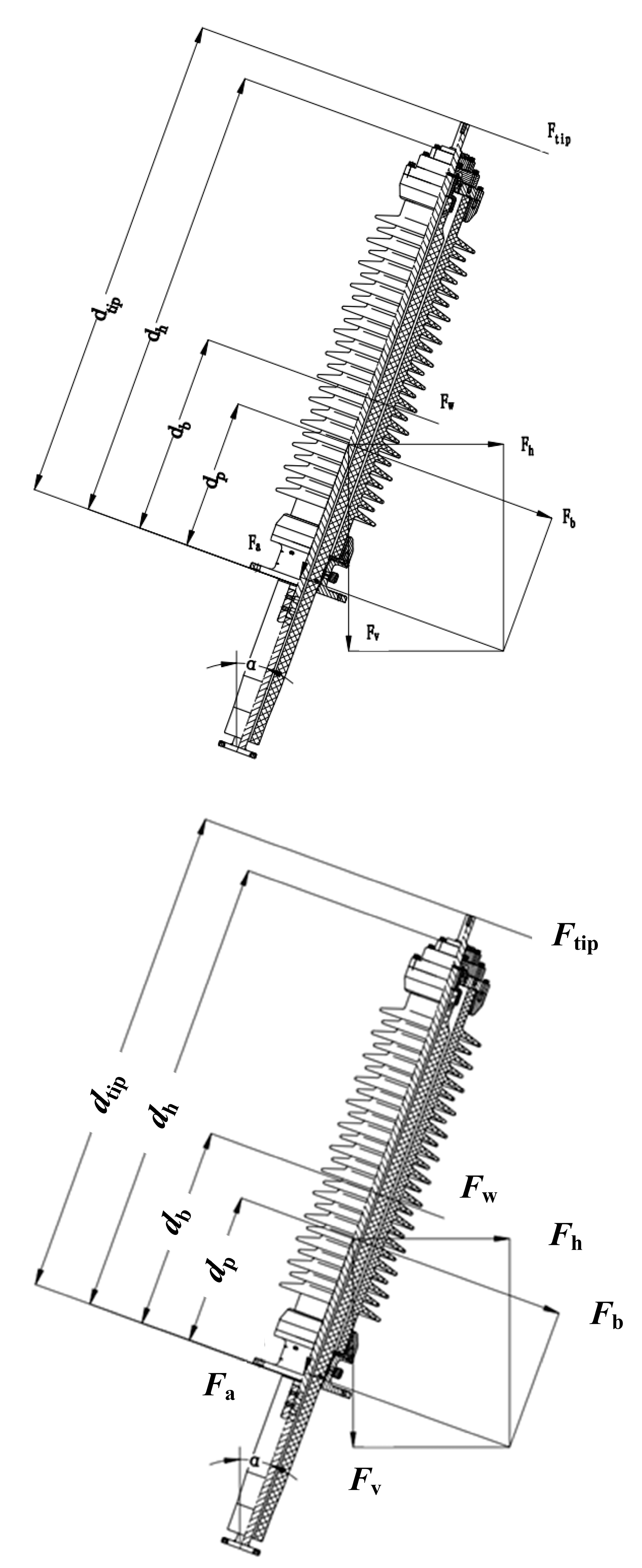
3.3. Seismic Performance Calculation
3.4. Thermal Short-Circuit Current Calculation of Bushings
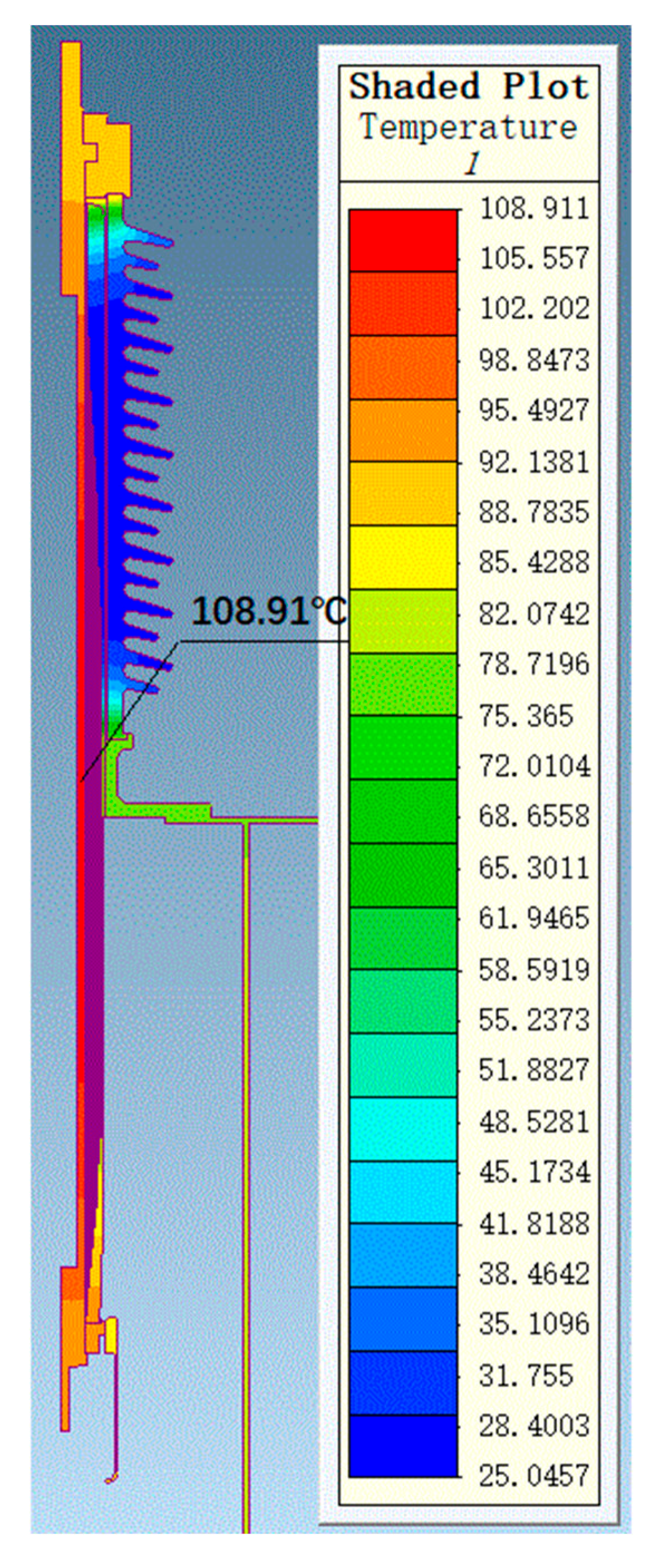
3.5. Bushing Thermal Field Simulation Calculation
3.6. Bushing Performance Testing
4. Conclusions
- 1
- The electric field strength distribution varies among bushings with different structures. The maximum radial electric field strengths for the 40.5 kV, 72.5 kV, and 126 kV bushings are 1.39 kV/mm, 2.86 kV/mm, and 3.0 kV/mm, respectively, all meeting the usage requirements. The maximum axial electric field strengths at both the oil end and air end of the bushing are below the allowable axial electric field strength, satisfying the usage requirements.
- 2
- The bushings with rated voltages of 40.5 kV, 72.5 kV, and 126 kV meet the 8-degree seismic resistance requirements and can effectively withstand the standard seismic intensity value Ith. They are also capable of withstanding the electromagnetic forces caused by dynamic stability currents, in compliance with standard specifications. The bushings demonstrate reliable operational capabilities under extreme scenarios.
- 3
- The thermal stability of the bushings under short-circuit conditions complies with national standards. The final conductor temperature in all cases is below 180 °C, providing sufficient safety margins. The thermal field simulation results indicate that the maximum temperature of the 72.5 kV bushing under a current of 2000 A is 109 °C, and the maximum temperature of the 126 kV bushing under a current of 1250 A is 98 °C, both satisfying engineering usage requirements.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, H.; Li, Y.; Luo, X.; Zhang, E.; Jing, J. Investigation on Hot Spot Temperature of Resin-Impregnated Paper High-Voltage Bushing Based Upon Dielectric Loss. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 1884–1892. [Google Scholar] [CrossRef]
- Shi, S.; Tian, H.; Xie, G.; Wang, Q.; Xie, T.; Pang, X.; Yang, G.; Liu, P.; Peng, Z. Insulation Degradation of Epoxy Resin Impregnated Paper Bushing Under Discharge Arc Ablation. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 2776–2784. [Google Scholar] [CrossRef]
- Shang, G.; Liu, X.; Shao, Y.; Chen, M.; Sun, Y.; Zhang, Q.; Tang, H.; Li, X. Insulation Degradation Characteristics and Phase-Field Simulation of Epoxy Resin for Valve-Side Bushing Under Strongly Coupled Electrothermal Field. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 615–624. [Google Scholar] [CrossRef]
- Li, L.; Li, Q.; Xu, S.; Liu, R.; Dong, M.; Ying, S.; Tian, J.; Xin, W.; Haddad, M.; Jiang, X. Electric Field Improvement for High-Voltage Bushings. Polymers 2023, 15, 40. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, S.; Jin, H.; Zhang, Z.; Wang, C.; Liu, P. A novel simulation of space charge decay dynamics after removing the voltage in epoxy resin composites. J. Phys. D Appl. Phys. 2025, 58, 035303. [Google Scholar] [CrossRef]
- Shang, G.; Sun, Y.; Tang, H.; Li, X.; Zhang, S.; Li, J.; Liu, X. Degradation mechanism for epoxy resins under combined electric, thermal and compressive stresses. Polym. Degrad. Stab. 2024, 230, 111038. [Google Scholar] [CrossRef]
- Lin, M.; Wu, G.; Liu, K.; Yan, X.; Tang, H. Review of Detection Methods for Typical Faults in Transformer Bushings. IEEE Electr. Insul. Mag. 2024, 40, 33–44. [Google Scholar] [CrossRef]
- Chen, M.; Liu, X.; Shao, Y.; Shang, G.; Zhang, Q.; Tang, H.; Liu, L. Degradation characteristics of insulation near aluminium foil edges inside dry-type bushing cores under electrothermal compound stress. High Volt. 2022, 7, 1153–1164. [Google Scholar] [CrossRef]
- Sun, H.; Yang, D.; Shi, W.; Sun, Y.; Liu, X. Influence of Multi-Order Harmonic Voltage on Degradation in Epoxy Resin Layer of High Voltage Valve Side Bushing. IEEE Trans. Dielectr. Electr. Insul. 2025, 3542002. [Google Scholar] [CrossRef]
- Elsadd, M.A.; Elsad, R.A.; Huwayz, M.A.; Mansour, S.A.; Zaky, M.S.; Elkalashy, N.I.; Izzularab, M.A. Improving the distribution system capability by incorporating ZnO nanoparticles into high-density polyethylene cable materials. Sci. Rep. 2024, 14, 25834. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Liao, J.; Tian, H.; Liu, P.; Peng, Z. Regularity analysis of the temperature distribution of epoxy impregnated paper converter transformer bushings. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3254–3264. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, H.; Peng, Z.; Liu, P.; Zhang, T.; Hu, W. 3-D coupled electromagnetic-fluid-thermal analysis of epoxy impregnated paper converter transformer bushings. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 630–638. [Google Scholar] [CrossRef]
- Yadav, S.; Chamorro, H.R.; Flores, W.C.; Mehta, R.K. Investigation of Improved Thermal Dissipation of ±800 kV Converter Transformer Bushing Employing Nano-Hexagonal Boron Nitride Paper Using FEM. IEEE Access 2021, 9, 149196–149217. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Li, K.; Ma, H.; Chen, P.; Huang, K. Analysis of Transformer GSB Bushing Fault Causes Based on Finite Element Simulation. J. Phys. Conf. Ser. 2024, 2800, 012002. [Google Scholar] [CrossRef]
- Zhu, W.; Xie, Q.; Lu, J. Seismic testing and fragility analysis considering material strength uncertainty of 1100 kV GFRP composite power transformer bushing. Case Stud. Constr. Mater. 2024, 21, e03564. [Google Scholar] [CrossRef]
- He, C.; Xie, Q.; Zhou, Y. Influence of flange on seismic performance of 1100-kV ultra-high voltage transformer bushing. Earthq. Spectra 2019, 35, 447–469. [Google Scholar] [CrossRef]
- Shi, Y.; Xie, G.; Wang, Q.; Li, X.; Yang, X.; Liu, P.; Peng, Z. Simulation analysis and calculation of electric field distribution characteristics of UHV wall bushing. Energy Rep. 2021, 7, 110–117. [Google Scholar] [CrossRef]
- IEC TS 61463; Bushings-Seismic Qualification. International Electrotechnical Commission: Geneva, Switzerland, 2016.
- GB/T 4109-2022; Insulated Bushings for Alternating Voltages Above 1000 V. Standards Press of China: Beijing, China, 2022.
- Lan, B.; Guo, N.; Li, J.; Tang, H.; Wang, X.; Ding, W. Multi-physical Field Coupling Simulation of DC Bushing Core Considering the Anisotropic Volume Conductivity of Resin Impregnated Paper. High Volt. Eng. 2025, 40, 900–912. [Google Scholar]
- IEC 60137:2017; Insulated Bushings for Alternating Voltages Above 1000 V. International Electrotechnical Commission: Geneva, Switzerland, 2017.
- GB/T 50260-2013; Code for Seismic Design of Electrical Installations. Standards Press of China: Beijing, China, 2013.
- Allahbakhshi, M.; Akbari, M. Heat analysis of the power transformer bushings using the finite element method. Appl. Therm. Eng. 2016, 100, 714–720. [Google Scholar] [CrossRef]
- Sitar, R.; Janic, Z.; Stih, Z. Improvement of thermal performance of generator step-up transformers. Appl. Therm. Eng. 2015, 78, 516–524. [Google Scholar] [CrossRef]
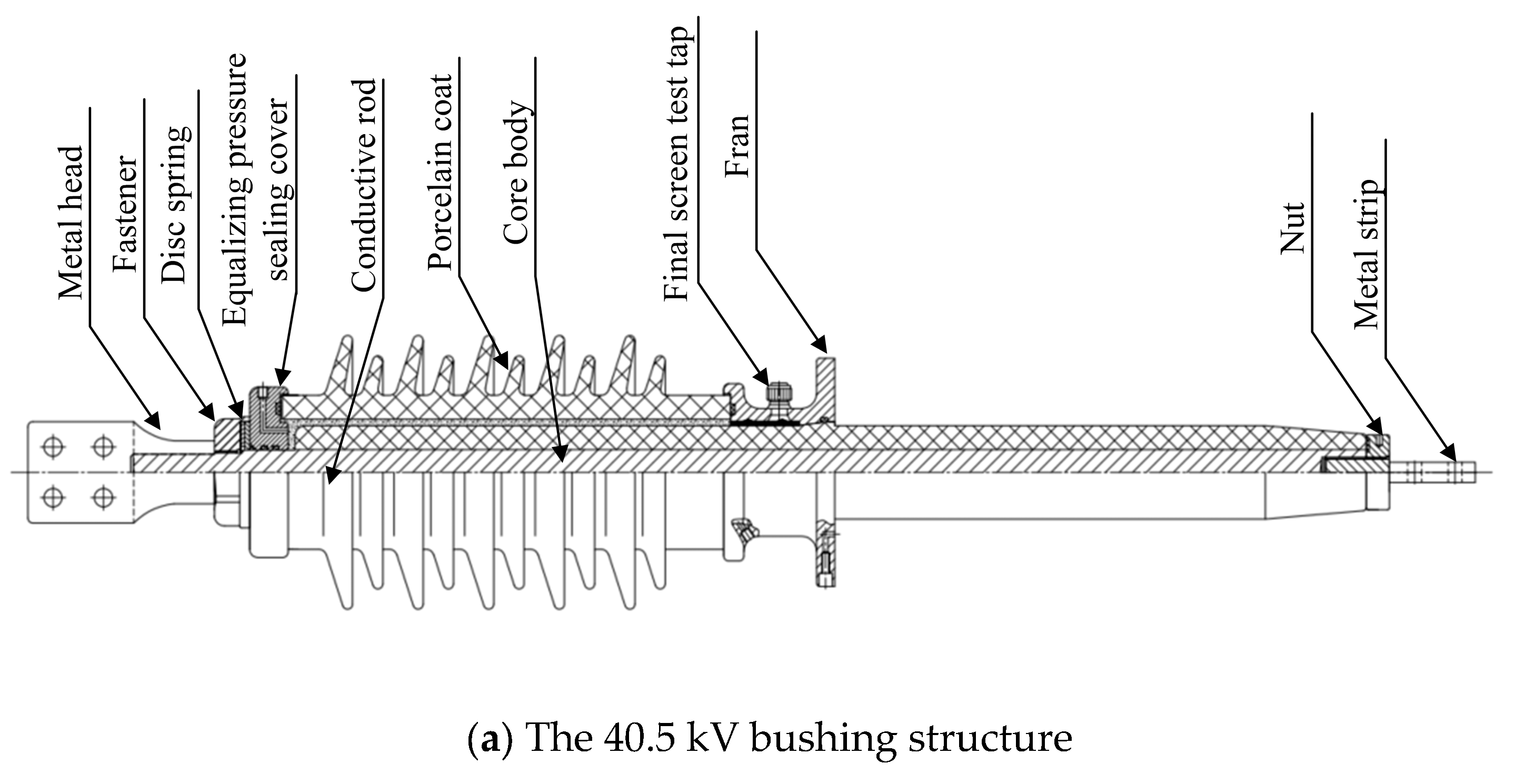
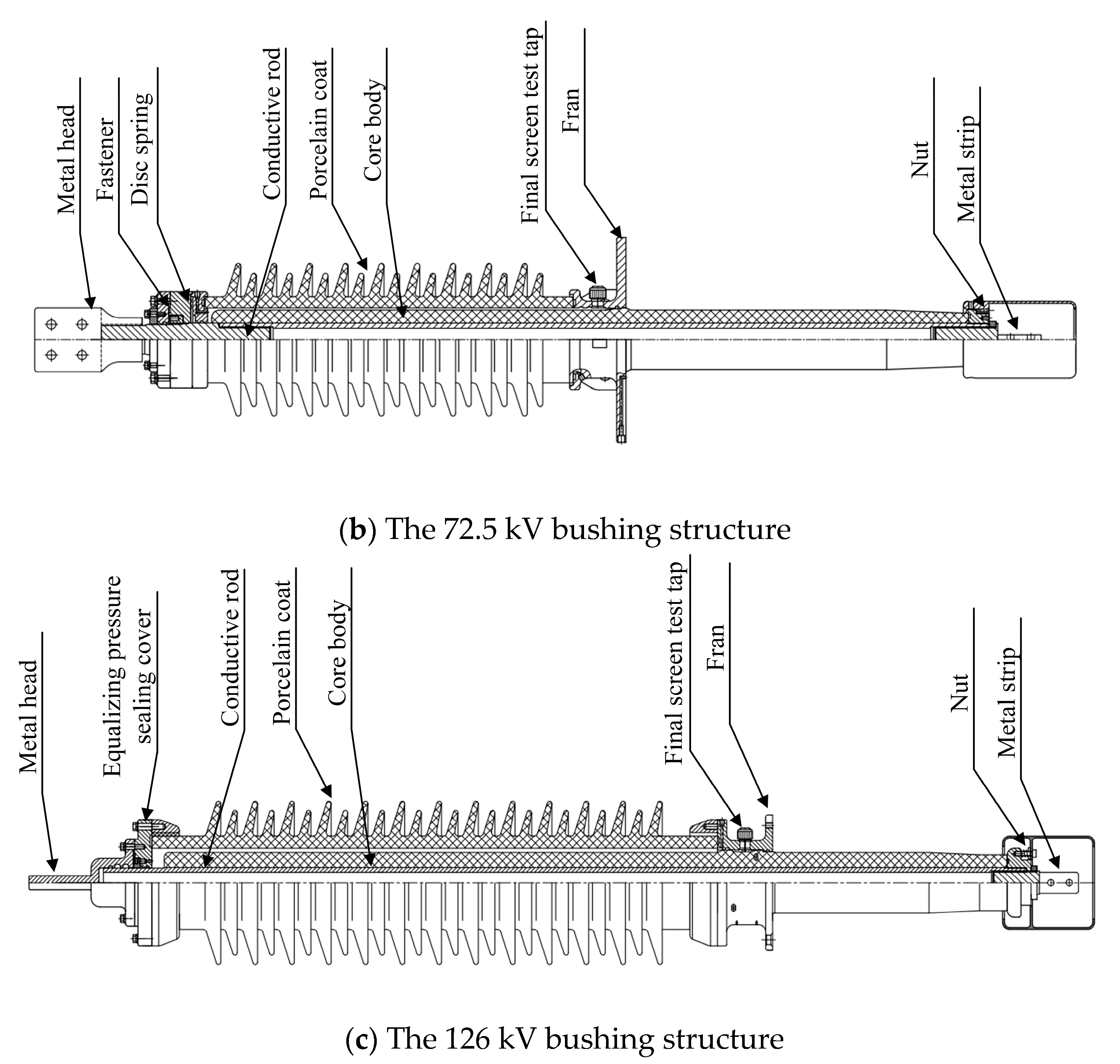
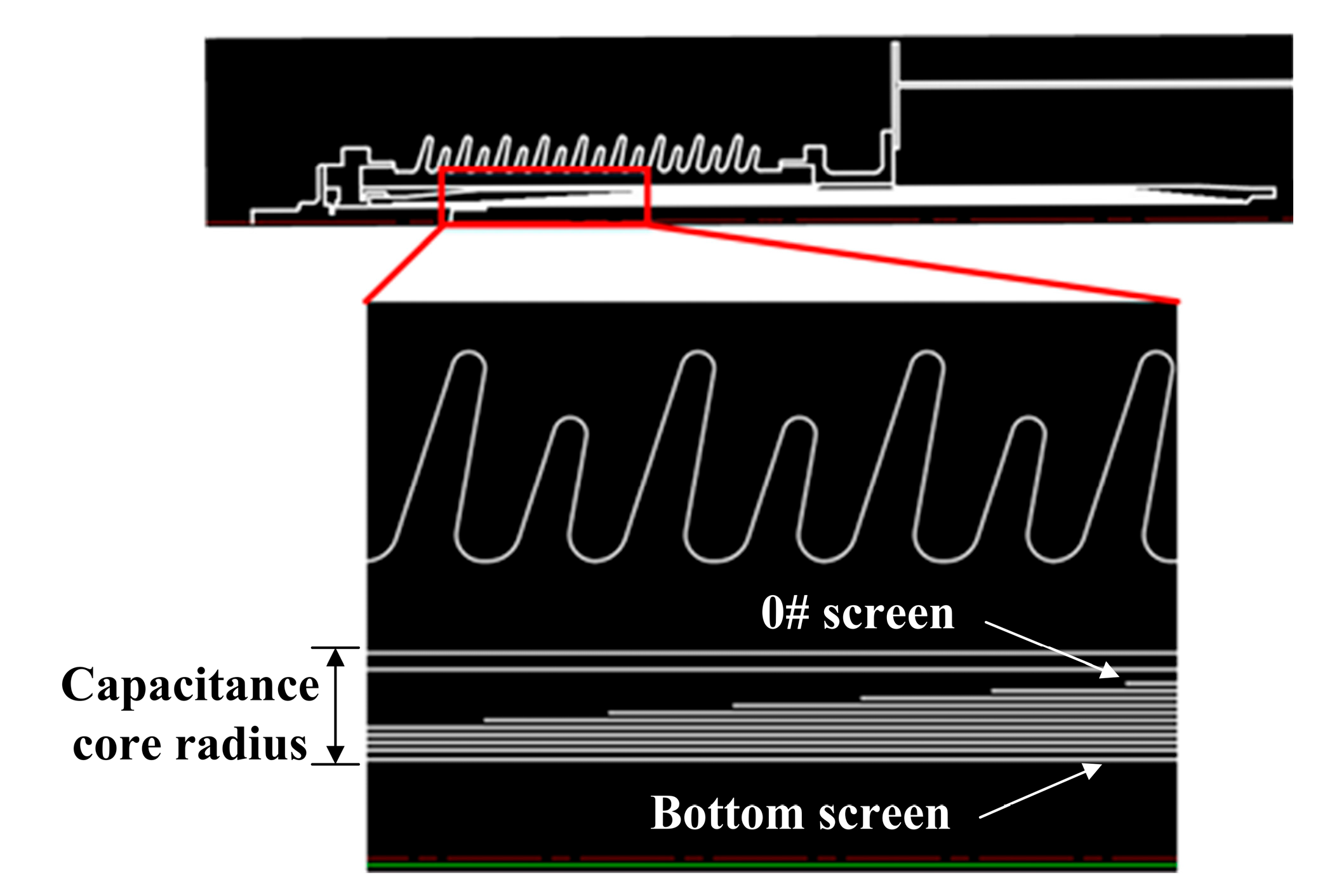



| Voltage Level | 40.5 kV | 72.5 kV | 126 kV | |
|---|---|---|---|---|
| Capacitance core radius (cm) | 4.6 | 11.6 | 13 | |
| Screen spacing (cm) | 0.25 | 0.225 | 0.225 | |
| Length of screen (cm) | 0 # | 114.7 | 147 | 185 |
| 1 # | 98.7 | 125.7 | 154.5 | |
| 2 # | 88.7 | 116.1 | 145.5 | |
| 3 # | 80.3 | 109.1 | 136.7 | |
| 4 # | 74 | 101.9 | 127.9 | |
| 5 # | 67.6 | 94.6 | 119.1 | |
| 6 # | 60.9 | 87 | 110.1 | |
| 7 # | 53.7 | 79 | 100.8 | |
| 8 # | / | 70.3 | 91.1 | |
| 9 # | / | / | 83.5 | |
| 10 # | / | / | 75.3 | |
| Modules | Boundary Conditions | Unit |
|---|---|---|
| Conductive rod, 0 # screen | high voltage | V |
| Other screens | floating potential | V |
| Bottom screen, flange | grounding | V |
| Air | 25 | °C |
| Oil | 85 | °C |
| Heat transfer coefficient | 5 | W/(m2·K) |
| Current of conductive rod | 2000 (72.5 kV) | A |
| 1250 (126 kV) |
| Materials | Density/(kg/m3) | Heat Conductivity/[W/(m·K)] | Constant Pressure Heat Capacity/[J/(kg·K)] | Conductivity/(S/m) | Relative Permittivity |
|---|---|---|---|---|---|
| Copper | 8.96 | 400 | 385 | 5.998 × 107 | 1 |
| Epoxy resin-impregnated capacitor core | 2.21 | 0.10 | 730 | 7 × 10−15 | 4.2 |
| Aluminum foil screen | 3.90 | 237 | 900 | 1 × 108 | 1 |
| Silicone rubber | 2.20 | 0.20 | 703 | 1 × 10−14 | 3.75 |
| Air domain | 1.29 | 0.25 | 1003 | 1 × 10−18 | 1 |
| Voltage Level (kV) | 40.5 | 72.5 | 126 |
|---|---|---|---|
| Seismic intensity (degrees) | 8 | 8 | 8 |
| agh | 0.3 g | 0.3 g | 0.3 g |
| agv | 0.15 g | 0.15 g | 0.15 g |
| mp (kg) | 78 | 130 | 220 |
| dp (mm) | 386 | 402 | 585 |
| A (°) | 0 | 0 | 0 |
| P (Pa) | 70 | 70 | 70 |
| De (mm) | 270 | 296 | 350 |
| Di (mm) | 230 | 256 | 310 |
| dh (mm) | 695 | 931 | 1530 |
| db (mm) | 498 | 506 | 666 |
| Fop (N) | 2000 | 2000 | 4000 |
| dtip (mm) | 880 | 1156 | 1625 |
| D (m) | 0.152 | 0.168 | 0.2 |
| D (m) | 0.105 | 0.125 | 0.148 |
| σ (MPa) | 50 | 50 | 50 |
| Voltage Level (kV) | 40.5 | 72.5 | 126 |
|---|---|---|---|
| Mbs (kN·m) | 0.66 | 1.15 | 2.84 |
| Mbw (kN·m) | 0.06 | 0.09 | 0.24 |
| Mbtip (kN·m) | 1.23 | 1.62 | 4.55 |
| M (kN·m) | 1.96 | 2.86 | 7.63 |
| MD (kN·m) | 13.5 | 16 | 27.5 |
| Voltage Level (kV) | 40.5 | 72.5 | 126 |
|---|---|---|---|
| θ0 (°C) | 120 | 120 | 120 |
| Ith (kA) | 31.25 | 50 | 31.25 |
| tth (s) | 2 | 2 | 2 |
| Ρ (μΩ·cm) | 7.1 | 1.85 | 2.83 |
| D (cm) | 4.5 | 6.5 | 6.5 |
| Voltage Level (kV) | 40.5 | 72.5 | 126 |
|---|---|---|---|
| St (cm2) | 15.9 | 22.96 | 17.27 |
| d (cm) | 1.895 | 0.969 | 1.198 |
| Se (cm2) | 15.5 | 16.8 | 17.3 |
| θf (°C) | 126 | 130 | 131 |
| Voltage Level (kV) | Power Frequency Withstand-Voltage Test (kV) | Power Frequency Wet Withstand-Voltage Test (s) | Lightning Impulse Full-Wave Test (kV) | Partial Discharge Test (pC) | Temperature Rise Test (°C) | Seismic Test |
|---|---|---|---|---|---|---|
| 40.5 | 105 | 60 | 250 | 1 | 75.8 | 0.3 g |
| 72.5 | 165 | 60 | 380 | 1 | 74.5 | 0.3 g |
| 126 | 305 | 60 | 650 | 1 | 72.4 | 0.3 g |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Tong, X.; Liu, L.; Dong, X.; Yan, T.; Tang, W.; Wang, L.; Cao, B.; Luo, Z. A Simulation and a Computational Study on the Reliability Verification of Epoxy Resin Paper-Impregnated Bushings in Power Transformers. Energies 2025, 18, 3239. https://doi.org/10.3390/en18133239
Liu D, Tong X, Liu L, Dong X, Yan T, Tang W, Wang L, Cao B, Luo Z. A Simulation and a Computational Study on the Reliability Verification of Epoxy Resin Paper-Impregnated Bushings in Power Transformers. Energies. 2025; 18(13):3239. https://doi.org/10.3390/en18133239
Chicago/Turabian StyleLiu, Daijun, Xiaobang Tong, Libao Liu, Xiaoying Dong, Tianming Yan, Wenkai Tang, Liming Wang, Bin Cao, and Zimin Luo. 2025. "A Simulation and a Computational Study on the Reliability Verification of Epoxy Resin Paper-Impregnated Bushings in Power Transformers" Energies 18, no. 13: 3239. https://doi.org/10.3390/en18133239
APA StyleLiu, D., Tong, X., Liu, L., Dong, X., Yan, T., Tang, W., Wang, L., Cao, B., & Luo, Z. (2025). A Simulation and a Computational Study on the Reliability Verification of Epoxy Resin Paper-Impregnated Bushings in Power Transformers. Energies, 18(13), 3239. https://doi.org/10.3390/en18133239






