A Dimensionless Number for Evaluating the Influence of Heat Conduction in the Gas Phase on Liquid Evaporation

Abstract

Heat conduction in the gas phase may influence liquid evaporation, yet a quantitative characterization of this effect still remains lacking. Here, through dimensionless analysis of the theoretical model for droplet evaporation, two limiting solutions were obtained for the droplet evaporation considering heat conduction in the gas phase. Based on these solutions, a dimensionless number, HCg, was introduced to evaluate the influence of heat conduction in the gas phase on liquid evaporation. Further analysis indicates that HCg is a function of the relative thermal conductivity of the surrounding air, the evaporative cooling number of the liquid, and the contact angle of the droplet. Analytical expressions for both HCg and the droplet evaporation rate were acquired by fitting the numerical simulations. These results show that the effect of gas-phase heat conduction can generally be neglected due to the typically small values of HCg but becomes significant in cases involving atmospheres with higher thermal conductivity, liquids with smaller evaporative cooling numbers, or droplets with larger contact angles. This work may provide a simple yet accurate criterion for estimating the effects of gas-phase heat conduction on liquid evaporation.

1. Introduction

The evaporation of sessile liquid droplets is a pivotal process in an extensive array of industrial and scientific domains, including ink-jet printing [1,2,3], medical diagnostics [4,5], DNA mapping [6,7,8], and heat pipe cooling technologies [9,10,11]. Consequently, it has garnered substantial research attention in recent years. In the early stages of research, the “isothermal model” (hereafter referred to as the ISO model) for droplet evaporation was first proposed [12,13,14,15]. In this model, the temperature at the droplet surface is assumed to be constant, and the vapor concentration is also constant, equal to the saturation concentration of the liquid. Furthermore, the evaporation from the liquid surface is considered to be controlled by vapor diffusion in the surrounding air. However, in reality, evaporation can cause a temperature drop at the liquid surface due to the latent heat of vaporization [16,17,18,19,20,21]. This evaporative cooling can, in turn, influence the evaporation process by reducing the saturation vapor concentration at the liquid’s free surface [22,23,24,25,26,27]. In this “evaporative cooling model” (hereafter referred to as the Ec model), liquid evaporation becomes a two-way coupled problem, and the cooling effect can significantly reduce the evaporation rate. To identify the transition from the isothermal case to the nonisothermal one, Sefiane and Bennacer [26] proposed a dimensionless number denoted as SB. Further, Xu and Ma [28] introduced another dimensionless number, Ec, to quantify the strength of the evaporative cooling effect.

At the liquid surface, the heat required to sustain evaporation can be supplied from both the underlying substrate [18,23,29,30] and the surrounding air [24,26,31,32]. Regarding the impact of the substrate on the evaporation, Girard et al. [29,30] found that the substrate temperature significantly influences droplet evaporation. Dunn et al. [23] showed that the evaporation rate is higher for substrates with higher thermal conductivities. Furthermore, Wang et al. [33] indicated that it is cooling at the droplet surface that couples the evaporation process to the underlying substrate and that the influence of the substrate on liquid evaporation largely depends on the strength of evaporative cooling, i.e., on the dimensionless number Ec.

With regard to the surrounding air, Sefiane and Bennacer [26] believed that thermal conduction in the gas phase can often be neglected due to its lower thermal conductivity compared to that of liquids and solids. However, Saada et al. [24,32] found that, on an ideally thermally insulating substrate, the energy required for evaporation may be predominantly supplied by the gas phase. To the best of our knowledge, the effects of heat conduction in the gas phase on liquid evaporation have not yet been fully understood, and a quantitative criterion for evaluating the influence of gas-phase heat conduction on liquid evaporation is still lacking.

In this paper, the theoretical model for the evaporation of sessile liquid droplets that considers heat conduction in the gas phase is compared with the ISO model and the Ec model. Based on these comparisons, a dimensionless number was defined to evaluate the effect of heat conduction in the gas phase on liquid evaporation. Analytical expressions for both the dimensionless number and the evaporation rate of sessile droplets when considering gas-phase heat conduction were obtained by fitting numerical data. The present work provides a simple yet accurate criterion for estimating the effects of heat conduction in the gas phase on liquid evaporation and thus may offer a better understanding of the evaporation process of sessile droplets.

2. Mathematical Model

Here, we consider a slowly evaporating liquid droplet with a contact line radius of R and a contact angle of θ resting on a flat isothermal substrate maintained at a constant temperature of T₀ (see Figure 1). The thermal conductivities of the liquid and the ambient air are denoted by k_L and k_G, respectively. Convective flows in both the liquid and the air are neglected, and heat transfer in both phases is assumed to occur solely via conduction. For quasi-steady diffusion-limited evaporation [16], the vapor concentration c in the air, the temperature T_G in the air, and the temperature T_L in the liquid all satisfy Laplace’s equation.

∇² c = 0, for z ≥ h_L(r),

(1)

The boundary conditions are as follows:

c = Hc₀, for z = ∞, r = ∞,

(2)

c = c₀, for z = h_L(r), r ≤ R,

(3)

∂ c/∂ n = 0, for z = 0, r > R,

(4)

where c₀ = c_sat(T₀) is the saturated vapor concentration of the liquid at temperature T₀, h_L(r) is the height of the droplet, H is the relative humidity of the ambient air, and n is the unit normal.

For the Ec model [28], the temperature dependence of the saturation vapor concentration is considered, and the heat required to sustain evaporation is assumed to come solely from the underlying substrate. Accordingly, the governing equations for the evaporation process become

∇² c = 0, for z ≥ h_L(r),

(5)

∇² T_L = 0, for 0 ≤ z ≤ h_L(r).

(6)

The boundary conditions are as follows:

c = Hc₀, for z = ∞, r = ∞,

(7)

c = c₀ + b (T_L − T₀), k_L ∇ T_L · n = H_L D ∇ c · n, for z = h_L(r), r ≤ R,

(8)

T_L = T₀, for z = 0, r ≤ R,

(9)

∂ c/∂ n = 0, for z = 0, r > R,

(10)

where b = dc_sat/dT, H_L is the latent heat of evaporation, and D is the diffusion coefficient of vapor in the atmosphere.

In the present model, heat conduction in the gas phase is also taken into account, and the governing equations for the evaporation process can be expressed as follows:

∇² c = 0, ∇² T_G = 0, for z ≥ h_L(r),

(11)

∇² T_L = 0, for 0 ≤ z ≤ h_L(r),

(12)

The boundary conditions are as follows:

c = Hc₀, T_G = T₀, for z = ∞, r = ∞,

(13)

c = c₀ + b (T_L − T₀), k_L ∇ T_L · n − k_G ∇ T_G · n = H_L D ∇ c · n, for z = h_L(r), r ≤ R,

(14)

T_L = T₀, for z = 0, r ≤ R,

(15)

∂ c/∂ n = 0, T_G = T₀, for z = 0, r > R,

(16)

The models proposed in this study were numerically solved using the commercial software COMSOL Multiphysics v5.2. The temperature T(r) and evaporation flux J(r) at the radial position r on the droplet surface were obtained, and the total evaporation rate of the droplet J_T was subsequently deduced. To ensure accurate numerical results, the mesh in the model was refined iteratively until the criteria ε₁ = (J_T,i+1 − J_T,i)/J_T,i < 0.005 and ε₂ = [T_i+1(r) − T_i(r)]/T_i(r) < 0.005 were satisfied, where J_T,_i is the total evaporation rate of the droplet, and T_i(r) is the surface temperature at r for the i-th finite element’s mesh refinement.

Since both the steady-state temperature and vapor concentration fields conform to Laplace’s equation, the vapor concentration field can be treated as a quasi-temperature field. Here, by choosing the scaling factors for non-dimensionalization as T₁ = (c − c₀)/[c₀ (1 − H)], T₂ = b (T_G − T₀)/c₀ (1 − H), and T₃ = b (T_L − T₀)/[c₀(1 – H)], Equations (11)–(16) can be rewritten in a dimensionless form as follows:

∇² T₁ = 0, ∇² T₂ = 0, for z₁ ≥ h₁ (r₁),

(17)

∇² T₃ = 0, for 0 ≤ z₁ ≤ h₁ (r₁),

(18)

T₁ = −1, T₂ = 0, for z₁ = ∞, r₁ = ∞,

(19)

T₁ = T₂ = T₃, ∂T₃/∂ n − k_RG(∂T₂/∂ n) = Ec (∂T₁/∂ n), for z₁ = h₁ (r₁), r₁ ≤ 1,

(20)

T₃ = 0, for r₁ = 0, r ≤ 1,

(21)

T₂ = 0, ∂ T₁/∂ n = 0, for z₁ = 0, r₁ > 1,

(22)

where r₁ = r/R, z₁ = z/R, h₁ (r₁) = h (r)/R; Ec = (H_LDb)/k_L is the evaporative cooling number, which denotes the strength of the evaporative cooling at the liquid surface [28,33]; and k_RG = k_G/k_L is the relative thermal conductivity of the surrounding air. From Equations (17)–(22), it can be easily seen that the evaporation of droplets with a given contact angle is completely determined by two dimensionless numbers, i.e., k_RG and Ec. This indicates that heat conduction in the gas phase and evaporative cooling at the liquid surface are coupled during the evaporation process, and the effects of heat conduction in the gas phase on liquid evaporation should be related to the evaporative cooling effect at the liquid surface.

3. Results and Discussion

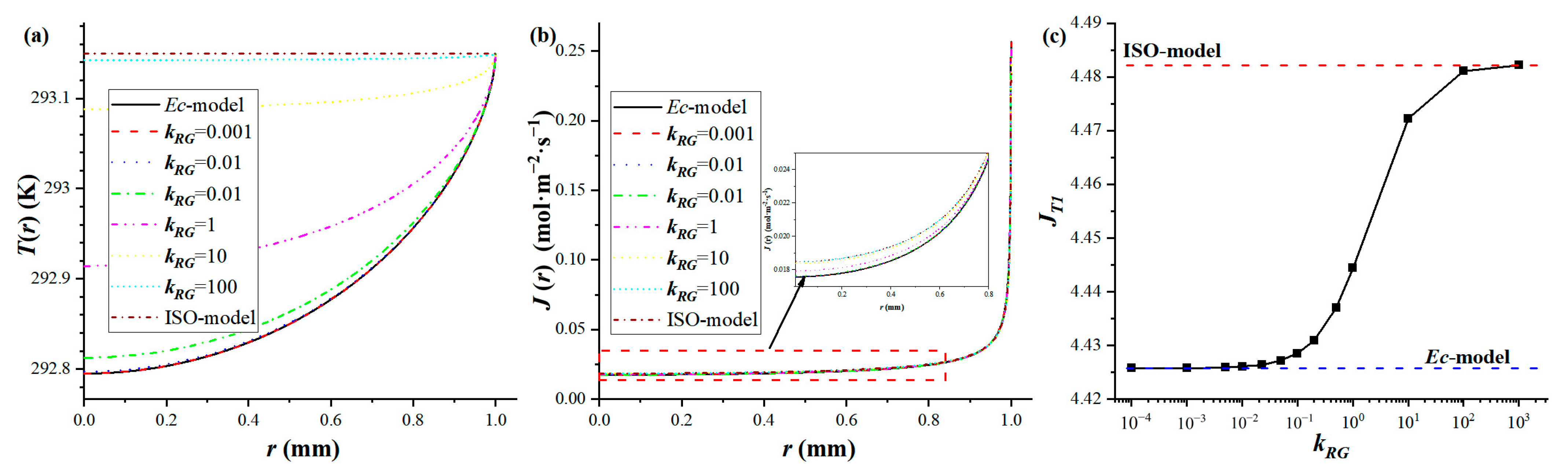
3.1. Limiting Solutions for Droplet Evaporation

From the above equations, two limiting solutions for the droplet evaporation can be deduced. When k_RG → 0, the heat conduction in the air can be neglected. Therefore, the present model regresses to the Ec model and the total evaporation rate of the droplet J_T → J_T,Ec, where J_T,Ec is the total evaporation rate in the Ec model (see Figure 2). When k_RG → ∞, gas-phase thermal conductivity becomes sufficiently large to ensure that the heat loss at the droplet surface due to evaporation can be promptly compensated by heat conduction in the gas phase. As a result, the evaporative cooling effect at the droplet surface can be neglected, and thus J_T → J_T,ISO, where J_T,ISO is the total evaporation rate in the ISO model (see Figure 2).

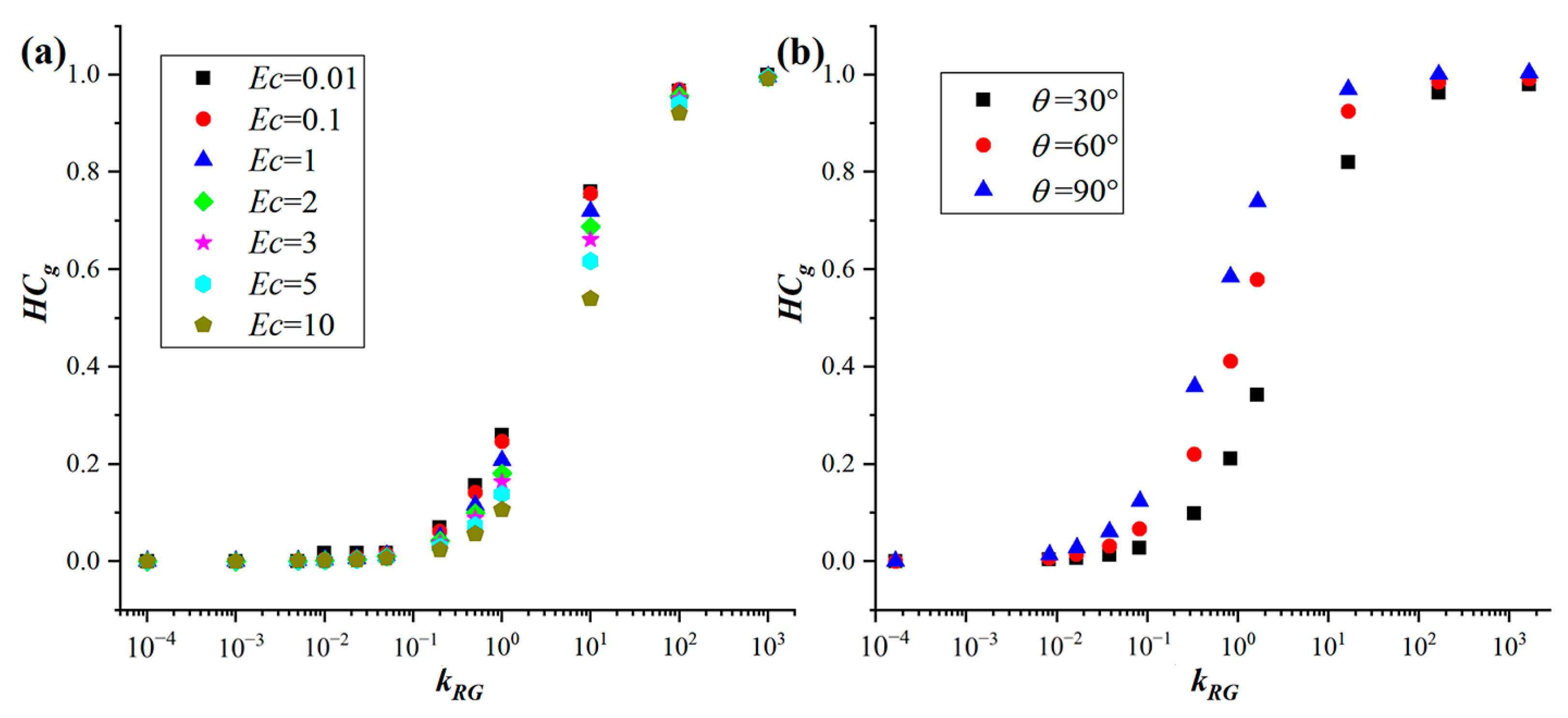
3.2. A Dimensionless Number Characterizing the Influence of Heat Conduction in Gas

As the heat transferred to the liquid surface through the gas phase is enhanced, the evaporative cooling effect at the liquid surface will decrease, and the evaporation rate increases from J_T,Ec to J_T,ISO (see Figure 2c). This indicates that the dimensionless number HCg = (J_T − J_T,Ec)/(J_T,ISO − J_T,Ec) can be used to evaluate the influence of gas-phase heat conduction on liquid evaporation. When gas-phase heat conduction has no influence on evaporation, J_T = J_T,Ec, and thus HCg = 0. As the effect of gas-phase heat conduction increases, HCg gradually increases from 0 to 1. When heat conduction in the air is so rapid that evaporative cooling at the liquid surface can be neglected, J_T = J_T,ISO, and therefore HCg = 1 (see Figure 2c).

Equations (17)–(22) indicate that the dimensionless number HCg should be a function of k_RG, Ec, and θ. To investigate the effects of these parameters on HCg, numerical simulations of droplet evaporation were performed over a wide range of k_RG (from 10⁻⁴ to 10³), Ec (from 0.01 to 10), and θ (30°, 60°, 90°). The results clearly show that HCg increases gradually from 0 to 1 as k_RG increases, which is in full agreement with the previous analysis (see Figure 3). For droplets with fixed θ and k_RG, an increase in Ec leads to a decrease in HCg (see Figure 3a). This behavior arises from the competition between evaporative cooling at the liquid surface and heat transfer in the gas phase: the former tends to lower the surface temperature, while the latter compensates for it. Furthermore, the numerical results indicate that increasing the contact angle θ results in a higher HCg (see Figure 3b). This can be attributed to the fact that, although increasing θ has little effect on the total evaporation rate [14], it lengthens the heat conduction path from the substrate to the liquid surface, thereby enhancing the evaporative cooling effect at the surface. Consequently, a larger temperature gradient develops in the gas phase. Combined with the increased surface area as θ increases, this leads to greater heat conduction from the gas phase to the liquid surface, thus strengthening the influence of gas-phase heat conduction on liquid evaporation.

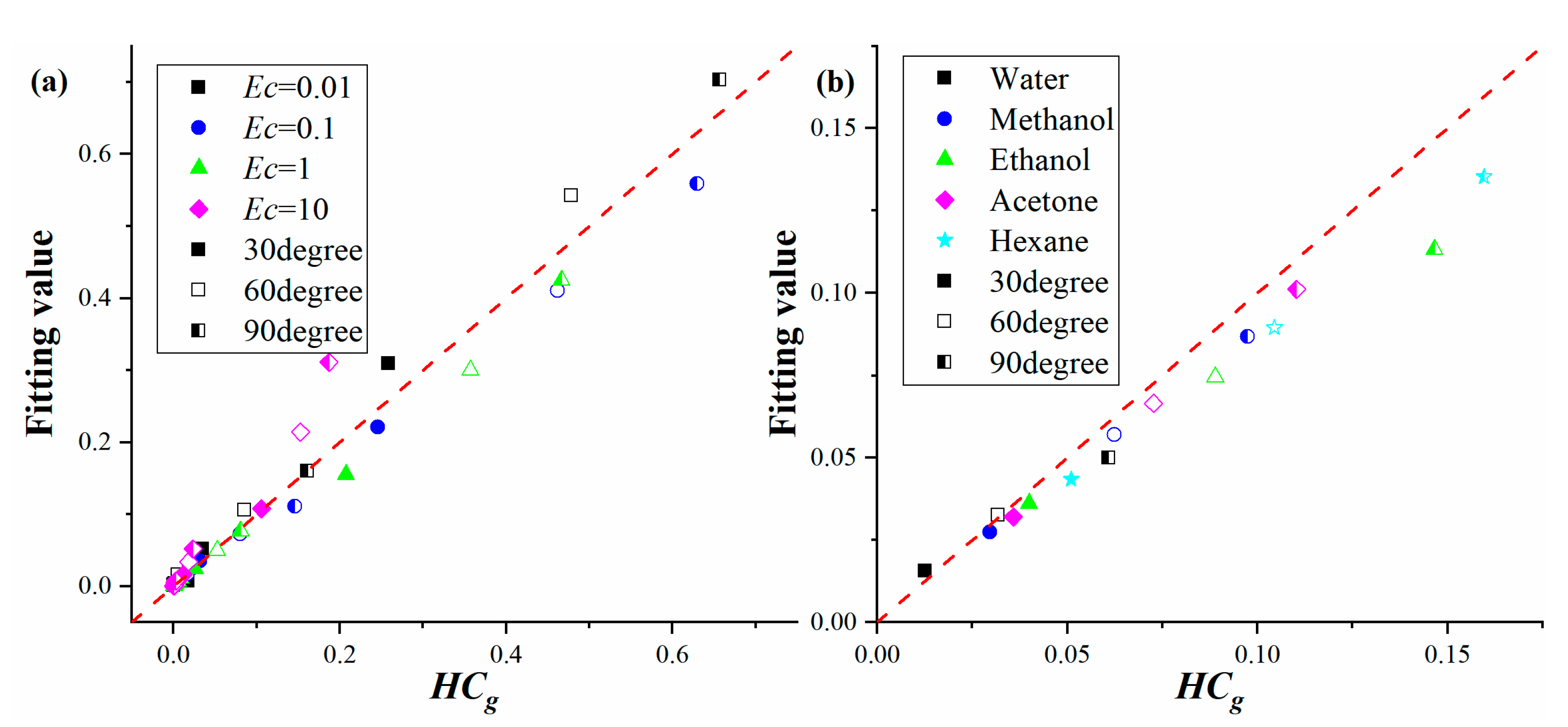
3.3. Analytic Expressions for HCg and the Droplet Evaporation Rate

To derive an analytical expression for HCg, numerical results of droplet evaporation over a wide range of k_RG (from 10⁻² to 10), Ec (from 0.01 to 10), and θ (30°, 60°, 90°), which covers normal circumstances, were fitted using OriginLab 2018. The fitting shows that the dimensionless number HCg can be well approximated by the equation below (see Figure 4a), and the coefficient of determination of the fitting is 0.9661.

HCg = 1 − exp{−0.34θ^1.08k_RG ^0.84Ec^−0.17}

(23)

Accordingly, the total evaporation rate of the droplet can be approximately expressed as follows:

J_T = J_T,Ec + (1 + exp{−0.34θ^1.08k_RG ^0.84Ec^−0.17}) (J_T,ISO − J_T,Ec)

(24)

To validate the accuracy of the fitting equation and to assess the influences of gas-phase heat conduction on liquid evaporation under normal circumstances, the evaporation of sessile droplets of five liquids (i.e., water, methanol, ethanol, acetone, and hexane, whose parameters are listed in

Table 1. Physical parameters for the liquid–air pairs.

Parameters	Unit	Water	Methanol	Acetone	Ethanol	Hexane
kL	kgms−3K−1	0.604	0.203	0.161	0.167	0.1167
ρL	kgm−3	998	790	788	785	655
CL	m2s−2K−1	4180	2530	2170	2438	2270
HL	m2s2	2.45 × 106	1.2 × 106	5.49 × 105	8.455 × 105	3.843 × 105
b	kgm−3K−1	1.11 × 103	9.47 × 10−3	2.84 × 10−2	7.08 × 10−3	3.41 × 10−2
c0	kgm−3	0.0194	0.186	0.637	0.1417	0.7022
D	m2s−1	2.44 × 10−5	1.5 × 10−5	1.06 × 10−5	1.19 × 10−5	7.32 × 10−6
kG	kgms−3K−1	0.023	0.023	0.023	0.023	0.023
Ec	1	0.10986	0.83970	1.02652	0.42656	0.82199
kRG	1	0.03808	0.11330	0.12772	0.14286	0.19709

) under ambient air with pressure set at 998 mbar was numerically simulated. The consistency between the dimensionless number HCg obtained from Equation (23) and that calculated directly from its definition using simulation results, i.e., HCg = (J_T − J_T,Ec)/(J_T,ISO − J_T,Ec), confirms the validity and applicability of the proposed analytical equation (see Figure 4b). In the figure, the x-axis represents the simulation data, and the y-axis represents the HCg calculated using Equation (23). All data were fitted using the equation y = x, yielding a coefficient of determination of 0.99612, which means the data are fitted well. The results also demonstrate that HCg is generally very small under normal conditions. For instance, for water droplets with a contact angle of 30°, the dimensionless number HCg is only 0.015. This suggests that the effect of gas-phase heat conduction on droplet evaporation can typically be neglected, which is consistent with the findings of Sefiane and Bennacer [26]. However, in certain cases, such as droplets with a smaller Ec, a larger k_RG, and a larger contact angle, the dimensionless number HCg can be relatively large. For example, for hexane droplets with a contact angle of 90°, HCg can reach up to 0.16. In such cases, the influence of gas-phase heat conduction becomes more pronounced and should be considered when modeling droplet evaporation.

4. Conclusions

In this study, a theoretical model for droplet evaporation that incorporates vapor diffusion in the air, evaporative cooling at the liquid surface, and heat conduction in both the liquid and the surrounding atmosphere was analyzed. The results indicate that droplet evaporation regresses to the Ec model when heat conduction in the air can be neglected and transitions to the ISO model when the evaporative heat loss at the liquid surface can be promptly compensated by heat transfer from the surrounding air. Based on these two limiting solutions, a dimensionless number, HCg, was presented to evaluate the influence of gas-phase heat conduction on liquid evaporation. Numerical simulations show that HCg gradually increases from 0 to 1 as the effect of gas-phase heat conduction becomes more significant.

Further, the effects of the thermal conductivity of the surrounding air, the evaporative cooling number, and the contact angle on HCg were investigated. Analytical expressions for HCg and the total evaporation rate of sessile droplets were obtained by fitting the numerical results, indicating that HCg can be well expressed as a function of these three variables. The results indicate that the influence of gas-phase heat conduction is usually negligible due to small HCg values but should be considered for atmospheres with higher thermal conductivity, liquids with smaller evaporative cooling numbers, or droplets with larger contact angles. Although convection in both the liquid and air was ignored, the model presented here can serve as a foundational framework for addressing more complicated situations. Despite its simple origin and limitations, this work provides a simple yet accurate criterion for estimating the effects of gas-phase heat conduction on liquid evaporation.