Correlational Analysis of Relationships Among Nodal Powers and Currents in a Power System
Abstract
1. Introduction
- Difference-based measures—a family of parameterized distances, called the Minkowski distance, Canberra distance, Hamming distance, and Gower’s coefficient.
- Correlation-based measures—the cosine measure, Pearson’s correlation measure, and Spearman’s correlation measure.
- k-Centers clustering (k-means, k-medians, k-medoids, and adaptive k-centers),
- Hierarchical clustering,
- Support vector machines,
- Support vector regression,
- Kohonen’s self-organizing maps (SOM).
- Developing an approach to planned analyses.
- Using the adopted approach, developing original methods allowing for solving Problem I and Problem C.
- Presentation of the properties of the proposed method.
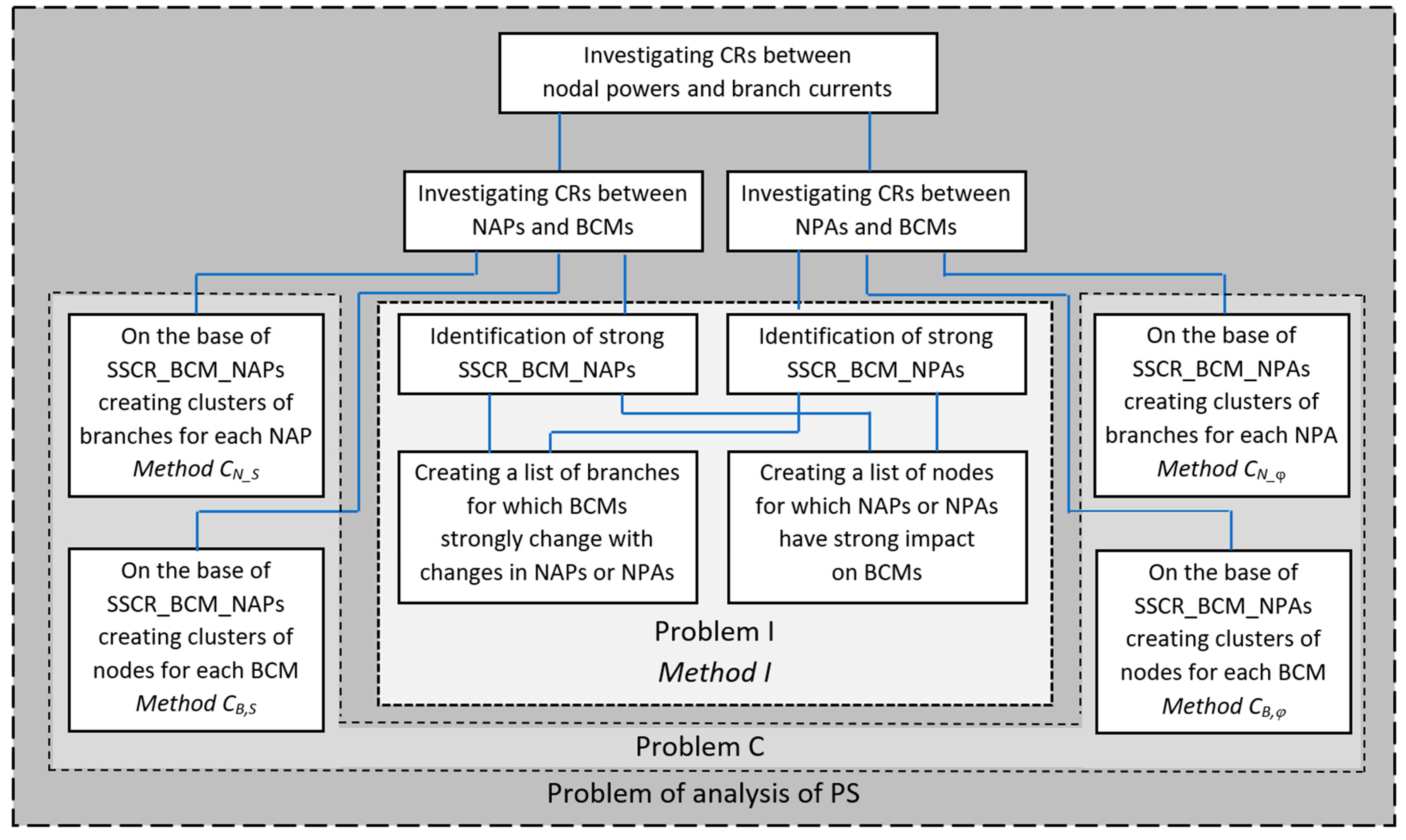
2. Correlational Approach to Solving the Considered Problems
3. Investigation of Correlational Relationships Between Distinguished Quantities
4. Proposed Methods
4.1. Method I—Method of Finding Branches with Currents Statistically Significantly Correlated with Nodal Powers and Indicating the Nodes at Which These Powers Are
- Step 0
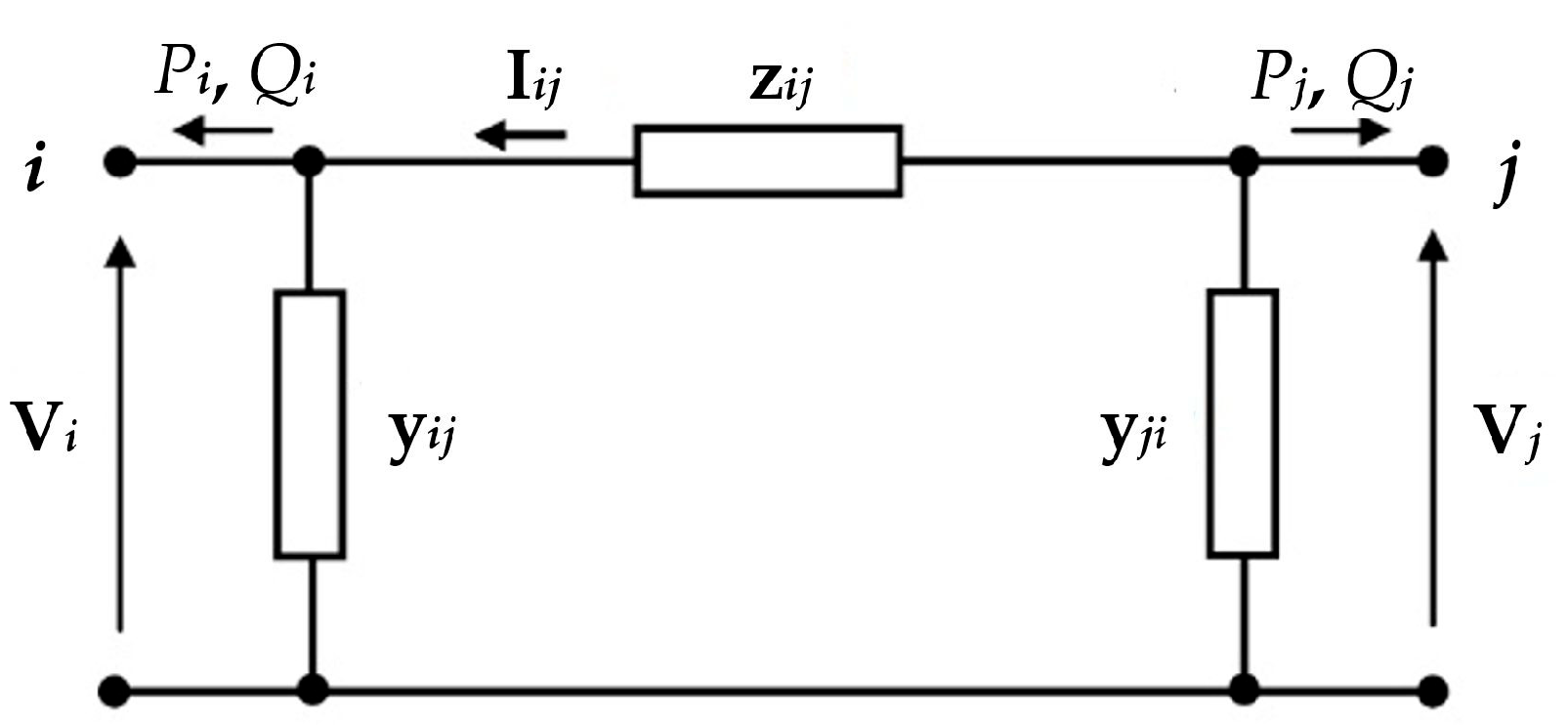
- Creation of datasets of magnitudes of individual currents at the ends of the PS branches:
- if current phasors are measured at the ends of the branches of the PS, then elements of the sets of observations of BCMs are measurements of the BCMs,
- if active and reactive power flows are measured at the ends of the branches of the PS, then elements of the set of observations of BCMs are results of calculations using Formula (1).
- Creation of datasets of NAPs and NPAs, calculated on the basis of active and reactive nodal powers in accordance with Formulas (10) and (11), respectively.
- Step 1
- Analyses of CRs between BCMs and NAPs:
- Calculation of KRCCs for CRs between magnitudes of the currents at the ends of the PS branches and NAPs.For each branch, among the two CRs between the magnitudes of currents at the branch ends and NAP Sk k ∈ {1, 2, …, n}, select the CR for which the absolute value of the KRCC is larger. The selected CR is the characteristic CR between the magnitude of the current on the considered branch and NAP Sk k ∈ {1, 2, …, n}.
- Creation of set , the elements of which are characteristic CRs between BCMs and NAPs.
- Analyses of CRs between BCMs and NPAs:
- Calculation of KRCCs for CRs between magnitudes of the currents at the ends of the PS branches and NPAs.For each branch, among the two CRs between the magnitudes of currents at the branch ends and NPA φk k ∈ {1, 2, …, n}, select the CR for which the absolute value of the KRCC is larger. The selected CR is the characteristic CR between the magnitude of the current on the considered branch and NPA φk k ∈ {1, 2, …, n}.
- Creation of set , the elements of which are characteristic CRs between BCMs and NPAs.
- Step 2
- Performing significance tests of all CRs from set .
- 2.
- Creating set , the elements of which are SSCRs between BCMs and NAPs, and these CRs are elements of set .
- 3.
- Performing significance tests of all CRs from set , using the statistic (13).
- 4.
- Creating set , the elements of which are SSCRs between BCMs and NPAs, and these CRs are elements of set .
- Step 3
- Creating sets and , being subsets of sets and , respectively. For each element of set as well as set , the absolute value of the KRCC is in the interval range.
- Step 4
- Creating ordered set containing branches, each of which is characterized by the fact that the current flowing on it has a magnitude that is in SSCRs belonging to set or set .The branches in set are arranged in decreasing order of the absolute values of the KRCCs for the CRs between BCMs and NAPs or for the CRs between BCMs and NPAs. The branch that is in the first position is the one on which there is a current with the magnitude remaining in the strongest CR with a specific NAP or a specific NPA. One branch appears only once in set . The position of a branch in set is determined by the maximal value of the absolute values of the KRCCs for CRs between BCMs and NAPs, as well as for CRs between BCMs and NPAs.
- Creating ordered set , containing nodes, each of which is characterized by the fact that the NAP at this node is in SSCRs belonging to set , or the NPA at this node is in SSCRs belonging to set .The nodes in set are arranged in decreasing order of the absolute values of the KRCCs for the considered CRs. The larger the position number of a node, the weaker the correlation between the NAP or NPA at this node and the corresponding BCM. A node appears only once in set at a position that is defined by the maximum value of the absolute values of KRCCs for CRs between the NAP at that node and BCMs, as well as for CRs between the NPA at that node and BCMs.
4.2. Methods of Clustering of the PS Based on the Investigation of Correlations Between the Distinguished Quantities
- Method CB,S and Method CB,φ—methods of clustering of the PS from the point of view of changes in individual BCMs as a consequence of changes in NAPs or NPAs, respectively.
- Method CN_S and Method CN_φ—methods of clustering of the PS from the point of view of changes in individual NAPs or NPAs impacting on changes in BCMs, respectively.
- If Y ∈ {S, φ}, the following statements will be treated as equivalent: (i) “cluster is associated with the magnitude of the current on branch bi_j” and “cluster is associated with branch bi_j”, and (ii) “cluster is associated with the NAP at node nk”, “cluster is associated with the NPA at node nk”, and “cluster is associated with node nk”.
- Superscript range denotes interval [th, 1], where th is a constant, limiting, from the bottom, the values of KRCCs of CRs between the quantities that are considered in the case of a cluster. Thus, th can be treated as a parameter of the PS clustering. A th threshold of 0 means that there is no lower bound on the previously mentioned KRCCs.
4.2.1. Method CB,S
- Step 0–Step 3
- Step 4
- Step 5
4.2.2. Method CB,φ
4.2.3. Method CN_S
- Step 0–Step 3
- Step 4
- Step 5
4.2.4. Method CN_φ
5. Case Study 1
5.1. IEEE 14-Bus Test System
5.2. IEEE 30-Bus Test System
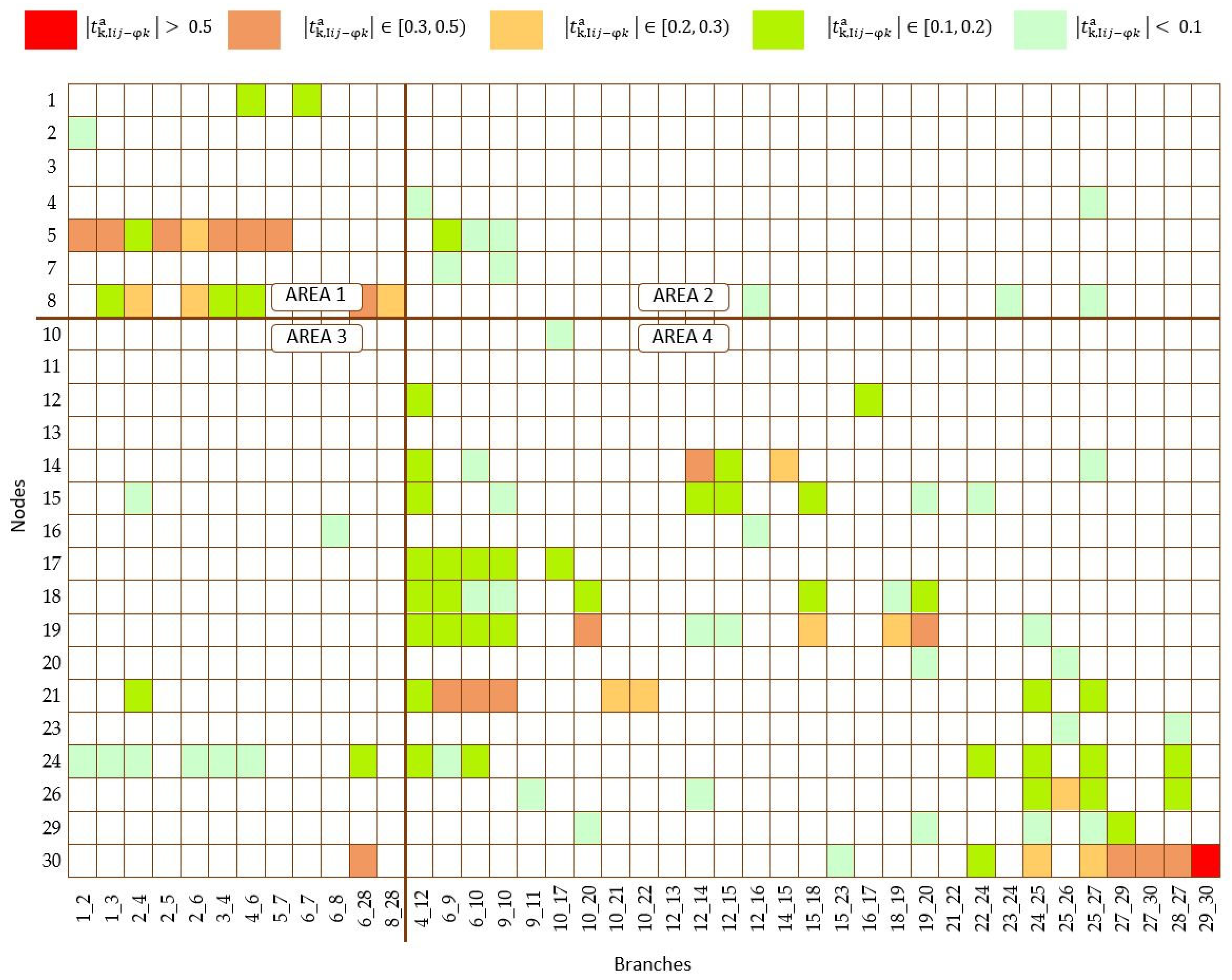
6. Case Study 2
7. Analyses of Results of Case Studies and Discussion
7.1. Taking into Account All Data—General Considerations
7.1.1. Correlational Relationships Between Branch–Current Magnitudes and Nodal Apparent Powers in the Case of TS14
- NAP S1 and the magnitudes of the current on the branches that were on the transition paths from node n1 to all nodes in HVP_TS,
- NAP S3 and the magnitudes of the current on the branches entering node n3 (i.e., branches b2_3 and b3_4) and on branch b1_2 (the KRCC for crI1_2-S3 is near to 0.5), which, together with branch b2_3, constitute the transition path between node n1 and node n3,
- NAP S8 and the magnitude of the current on the only branch connecting node n8 with the rest of TS14,
- NAP S12 and the magnitude of the current on the branch connecting node n12 with node n6.
7.1.2. Correlational Relationships Between Branch–Current Magnitudes and the Arguments of Nodal Powers in the Case of TS14
7.1.3. Impact of PS Size
7.2. Taking into Account Different Parts of the Possessed Data—General Considerations
- Taking into account sets , and one can ascertain that the number of SSCR_BCM_NAPs, for which KRCCs were in the interval [0.5, 1.0], decreased as the TS14 load level increased. In sets , , and , there was no SSCR for which the KRCC was in the interval [0.5, 1.0].
- Strong SSCRs (i.e., characterized by a KRCC greater than 0.5) observed for smaller amounts of data (Case l, Case m, or Case L) were also observed for larger amounts of data (Case a), but not vice versa. When looking for the most loaded branches in the PS, the largest possible number of PS operating states should be taken into account.
- It should be noted that in none of sets and Y = S, φ were there are any SSCRs for which absolute values of KRCCs were in the interval [0.0, 0.1). Such SSCRs were in sets Y = S, φ. The reasons for these facts should be sought in the fact that the number of PS states for which there were data used to determine the strength of CRs, qualified to sets Y = S, φ, was much larger than the number of PS states for which there were data used to determine the strength of CRs, qualified to sets or Y = S, φ.
- For the branches on which the currents had magnitudes that strongly changed with changes in NAPs, (i) if they were such in any of the cases Case l, Case m, and Case L, then they were also such in Case a, and (ii) constitute a set with a number of elements decreasing with increasing the load level of TS14 (Table 7).
- The above observation also applied to the nodes at which NAPs strongly affected BCMs.
- Branches b7_8, b2_3, and b3_4 were identified as those on which the currents had magnitudes that strongly changed with changes in NAPs regardless of the load level of TS. Two of those branches were connected to node n3 and one to node n8. There were reactive power sources in both of the mentioned nodes. It should also be noted that nodes n3 and n8 were identified as those nodes at which NAPs strongly affected BCMs regardless of the load level of TS14.
7.3. Clustering of TS14
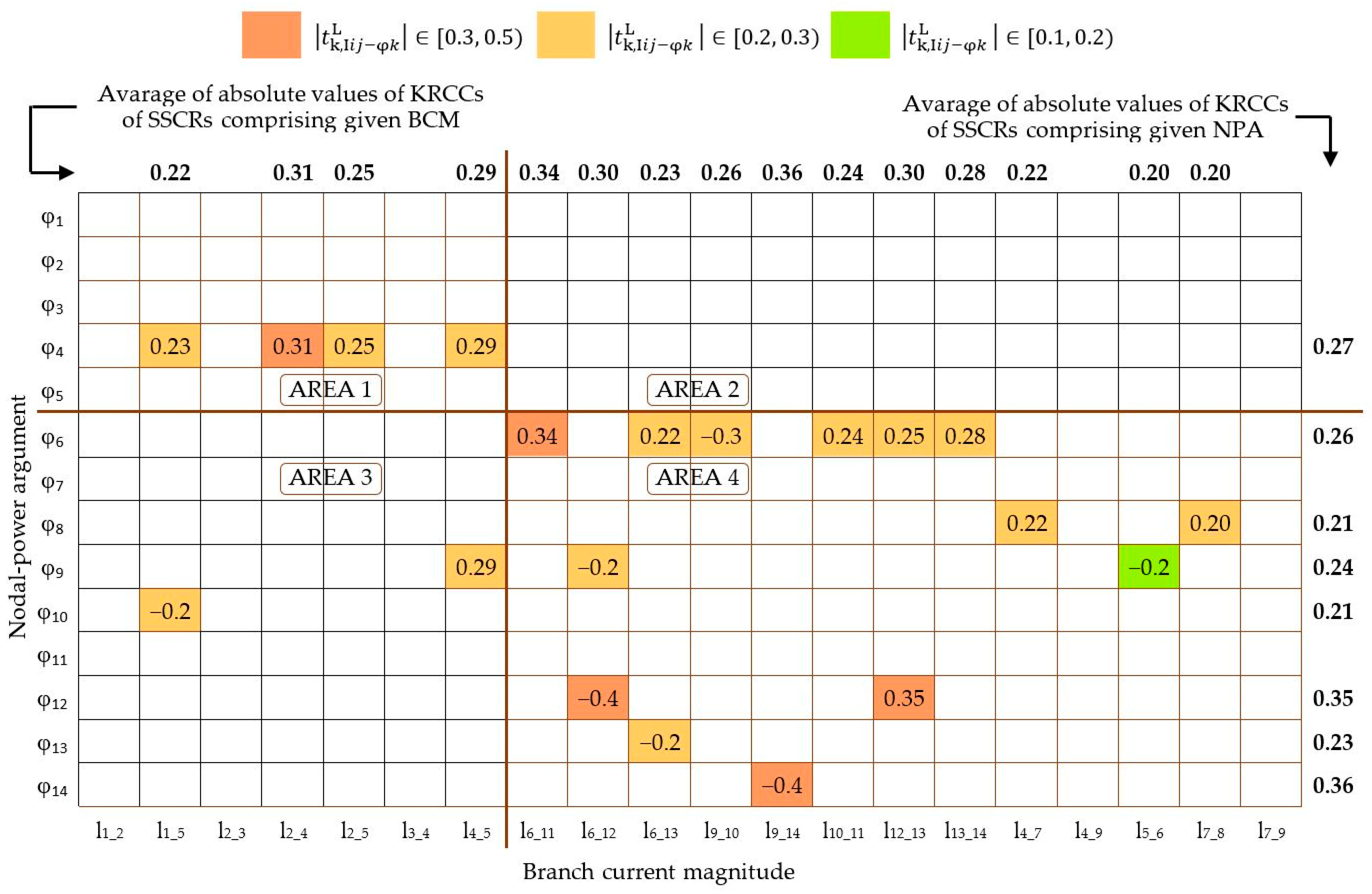
- the th parameter (Figure 4).
7.3.1. Clustering of PS from the Point of View of Changes in Individual BCMs as a Consequence of Changes in NAPs or NPAs—Method CB,S and Method CB,φ
- Among clusters i,j ∈ {1, 2, …, 14} i ≠ j, two clusters stood out from the others. They were and . Each of these clusters contained one node. It can be seen that:
- Branches b9_10 and b10_11 were branches on the transition path from node n9 to node n11. BCM I9_10 differed relatively little from I10_11.
- Branch b7_8, which was the only branch connecting node n8 with the rest of the TS14, entered node n7, with which branches b4_7 and b7_9 were incident. Branches b4_7 and b7_9 constituted the transition path between nodes n4 and n9. The difference between BCMs I4_7 and I7_9 was also small.
- 3.
- If TS14 clustering was performed using Method CB,S, then in Case a, the elements of the clusters associated with any branch in HVP_TS were nodes n1 and n3, and if branch b2_3 was omitted, then n4 was also such an element. It should be noted that n1 is a generation node and n3 is a node with a reactive power compensator. Node n4 is on the higher-voltage side of the transformer, being between HVP_TS and LVP_TS. There is no such node that is an element of every cluster associated with any branch in LVP_TS.
7.3.2. Clustering of PS from the Point of View of Changes in Individual NAPs or NPAs Impacting on Changes in BCMs—Method CN_S and Method CN_φ
- Regardless of the TS14 load level, Method CN_S did not provide a basis for defining clusters associated with nodes n2, n5, and n7. This is due to the fact that each of NAPs S2, S5, and S7 did not enter any SSCR. It should be emphasized that node n7 is an internal node of the three-winding transformer model and, as such, was not taken into account in the analyses that were carried out here. NAPs at nodes n2 and n5 did not have a significant impact on BCMs in TS14. The NAP at node n2 reached relatively high values, but in a significant number of operating states of TS14 it was lower than NAPs at nodes n1 and n3 simultaneously. Nodes n1 and n3 are neighboring nodes to node n2. In turn, in almost all operating states of TS14, the NAP at node n5 was lower than the NAPs at any neighboring node.
- In Case a, cluster included the largest number of branches (17 branches). Next were (14 branches) and (13 branches). Cluster was also distinguished by the number of branches on which currents had magnitudes remaining in strong SSCRs with NAP S1 (see Table 1). In this respect, the next node was node n3, then n8 and n12. In Case l and Case m, the cluster associated with node n1 was no longer in first place in the discussed ranking, appearing in second place, with the same number of considered branches as the cluster associated with node n3, but worse characteristics of the considered SSCRs. In Case L, the cluster associated with node n1 no longer had the branches with currents having magnitudes remaining in strong SSCRs with NAP S1. Cluster did not have a very large number of branches. The branches of cluster were mostly in HVP_TS. The numbers of branches in clusters and should be considered small. These branches were located primarily in LVP_TS. The clusters associated with nodes n3, n8, and n12 retained their importance regardless of the TS14 load level. The importance of a cluster was assessed based on the branches belonging to it that contained currents with magnitudes that were in strong SSCRs.In Section 7.1.1, the importance of nodes n1, n3, n8, and n12 in TS14 was discussed. The earlier-presented facts are a logical consequence of this importance.
- Regardless of the TS14 load level, Method CN_φ did not provide a basis for defining clusters associated with nodes n1, n7, and n11. The lack of a cluster associated with n1 resulted from the fact that it is the slack node. The case of node n7 was described earlier. NPAs at node n11 did not have a significant impact on BCMs in TS14. CRs with NPA φ11 were not SSCRs and, therefore, there was no basis for defining the cluster associated with node n11.
- In Case a, cluster included the most branches. The same number of branches was found in cluster . Considering the number of branches, the next clusters to be mentioned were , , and . The greater part of the branches of each of the mentioned clusters was in LVP_TS. The clusters including a smaller number of branches were and . These clusters were entirely in HVP_TS. It should be noted that nodes n9, n6, n8, and n3 were at important points of TS14. Nodes n9 and n6 were on the only transition paths between HVP_TS and LVP_TS on the LVP_TS side. Nodes n6, n8, and n3 are nodes with reactive power compensators. Nodes n13 and n14 are load nodes. In each of them, the average NAP was greater than the average NAP in every other node in LVP_TS except nodes n6 and n9.In Case l, Case m, and Case L, the clusters defined by Method CN_φ had sizes significantly different from those in Case a. When the TS14 load level changed, the cluster that stood out the most was the cluster associated with node n6. It had a relatively large size (the largest in comparison to other clusters) and changed little with changes in the TS14 load level. This means that NPA φ6 had a significant effect on BCMs regardless of the TS14 load level.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BCM | branch current magnitude |
| Case x | instance of a dataset characterized by the number of data and the interval of values of the power system active power losses; x ∈ {a, l, m, L} |
| Case l, Case m, Case L, | cases of low, medium, and large power system active power losses, respectively |
| Case a | a case involving Case l, Case m, and Case L at the same time |
| CR | correlational relationship |
| SSCR_BCM_NAP | statistically significant correlational relationship between a branch current magnitude and a nodal apparent power |
| SSCR_BCM_NPA | statistically significant correlational relationship between a branch current magnitude and a nodal power argument |
| HVP_TS | higher-voltage part of the test system |
| KRCC | Kendall’s rank correlation coefficient |
| LVP_TS | lower-voltage part of the test system |
| NAP | nodal apparent power |
| NPA | nodal power argument |
| PS | power system |
| SSCR | statistically significant correlational relationship |
| TS14 | IEEE 14-Bus Test System |
| TS30 | IEEE 30-Bus Test System |
| Symbols | |
| n | number of all nodes in a power system |
| nk | node k in a power system |
| bi_j | a branch between nodes ni and nj |
| a complex nodal power at node nk | |
| Sk | |
| an argument | |
| Pk | a nodal active power at node nk |
| Qk | a nodal reactive power at node nk |
| a complex voltage at node nk | |
| Vk | a magnitude of the voltage at node ni |
| a complex power flow on branch bi_j at end i | |
| Pij | active power flow on branch bi_j at end i |
| Qij | reactive power flow on branch bi_j at end i |
| Iij | a magnitude of the current on branch bi_j at node ni |
| an element of the power system admittance matrix | |
| rij, xij, | parameters of the π model of the branch i-j, i.e., a resistance, an inductive reactance, and a capacitive susceptance, respectively |
| zij = rij + j xij | |
| yij = j 0.5 bij | |
| m | number of measurement data |
| x | superscript indicating the use of data of Case x, where x ∈ {a, l, m, L} |
| crU-W | CR between quantities U and W |
| KRCC characterizing CR between quantities U and W | |
| z | a statistic used in significance tests |
| α | significance level |
| th | a constant, limiting, from the bottom, the values of KRCCs of CRs between the quantities that are considered in the case of a cluster |
| set of all characteristic CRs between BCMs and NAPs | |
| set of all characteristic SSCRs between BCMs and NAPs for Case x, x ∈ {a, l, m, L} | |
| set of all characteristic SSCRs between BCMs and NAPs for Case x, x ∈ {a, l, m, L}, when KRCCs for these SSCRs are in the interval range | |
| set of all characteristic CRs between BCMs and NPAs | |
| set of all characteristic SSCRs between BCMs and NPAs for Case x, x ∈ {a, l, m, L} | |
| set of all characteristic SSCRs between BCMs and NPAs for Case x, x ∈ {a, l, m, L}, when KRCCs for these SSCRs are in the interval range | |
| a cluster including PS nodes, at which there are NAPs in SSCRs with BCM Iij under the assumption that the absolute value of the KRCC of every such SSRC is in the interval range | |
| a cluster including PS nodes, at which there are NPAs in SSCRs with BCM Iij under the assumption that the absolute value of the KRCC of every such SSRC is in the interval range | |
| a cluster including PS branches, on which there are currents having magnitudes in SSCRs with NAP Sk under the assumption that the absolute value of the KRCC of every such SSRC is in the interval range | |
| a cluster including PS branches, on which there are currents having magnitudes in SSCRs with NPA φk under the assumption that the absolute value of the KRCC of every such SSRC is in the interval range | |
Appendix A. Use of the Proposed Methods in Case l
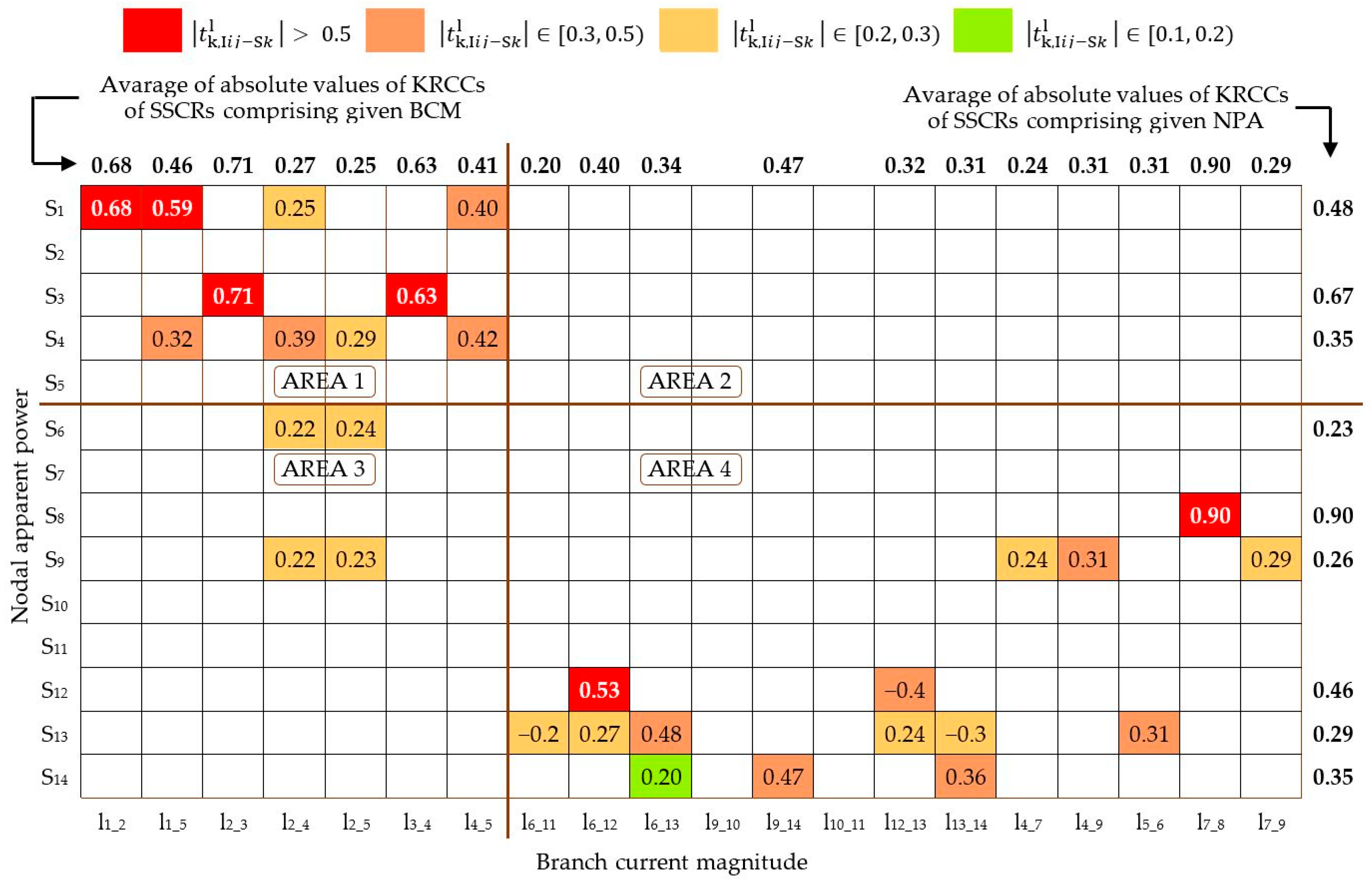
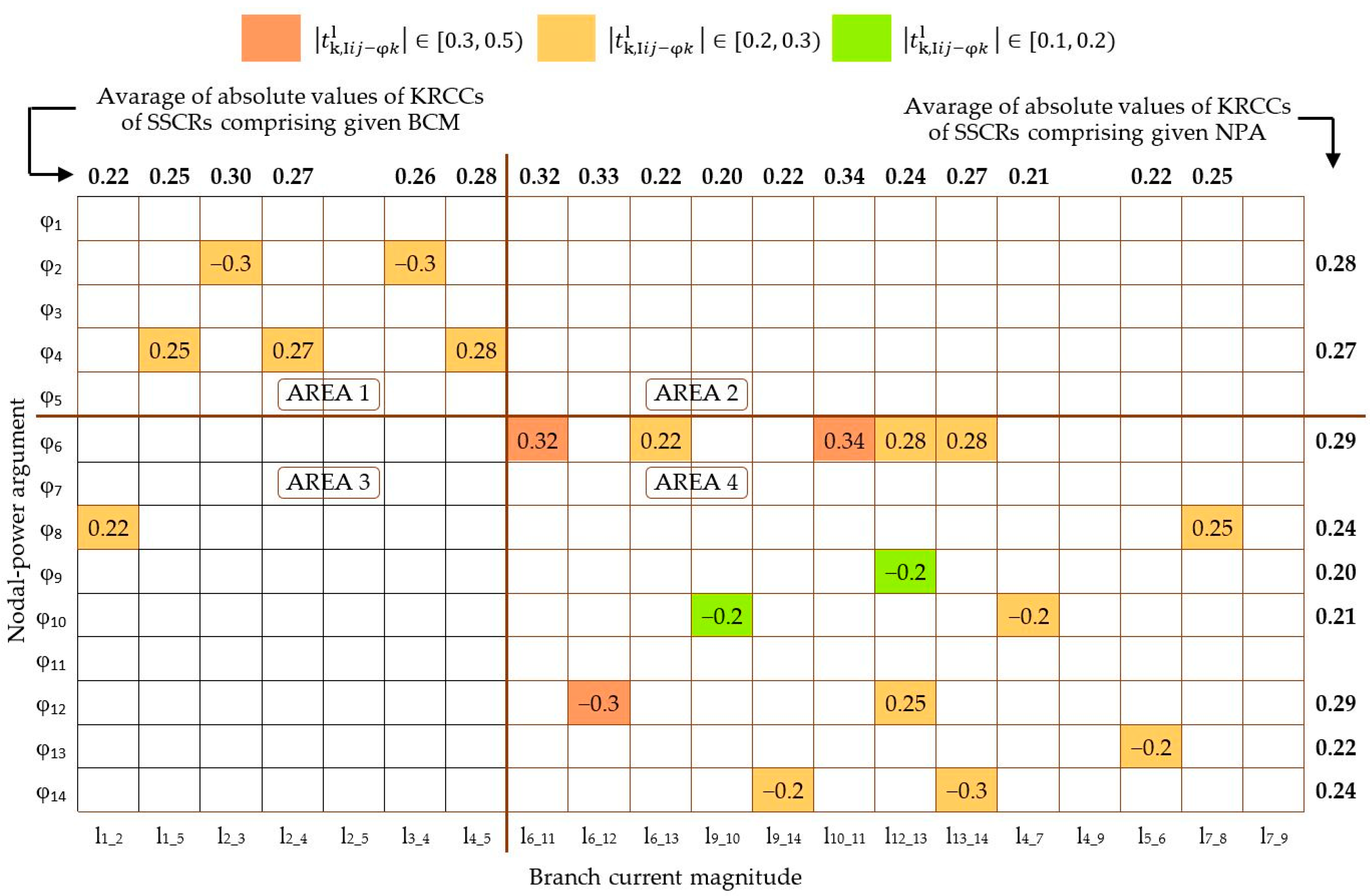
Appendix B. Use of the Proposed Method in Case m

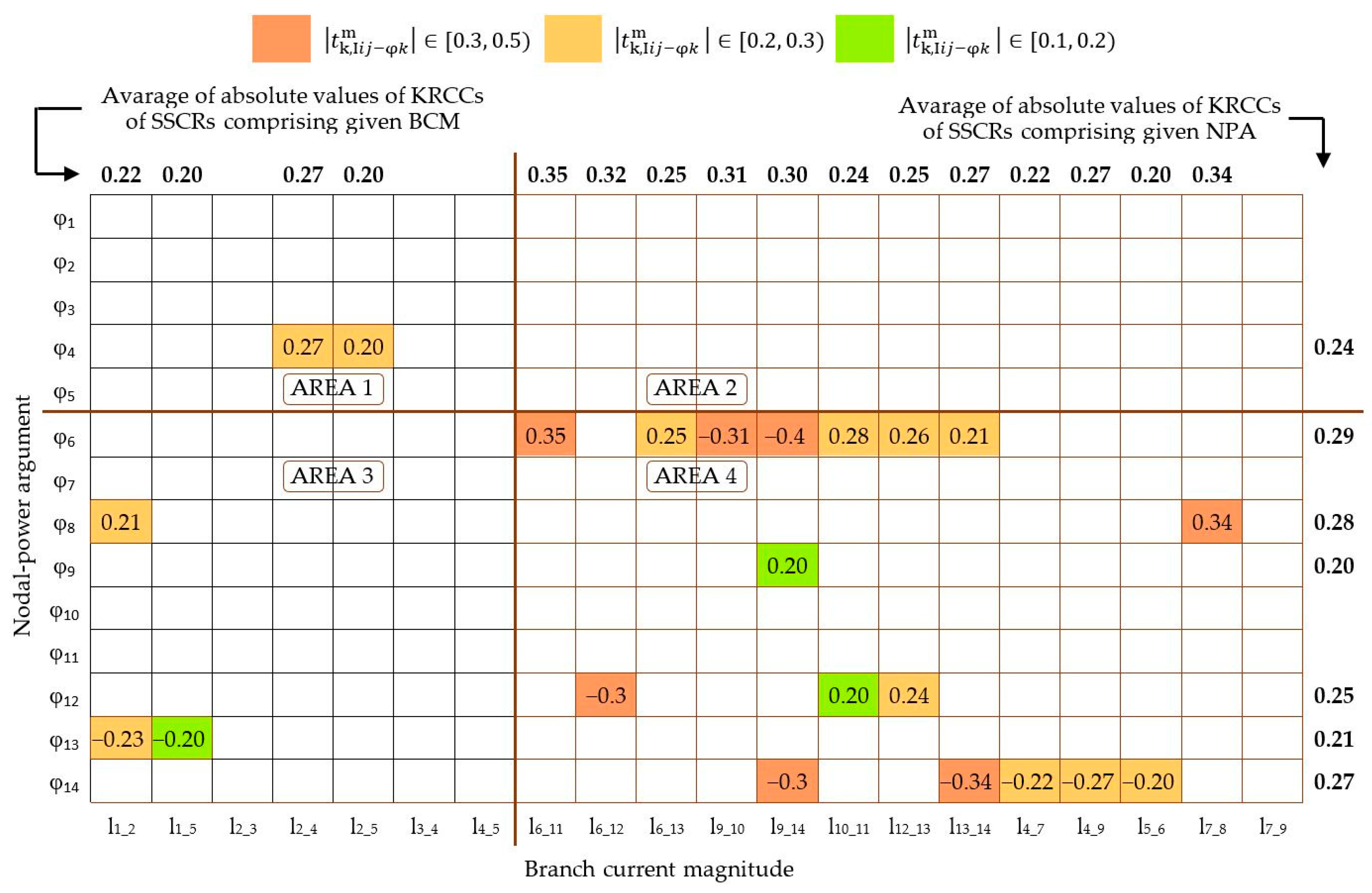
Appendix C. Use of the Proposed Method in Case L
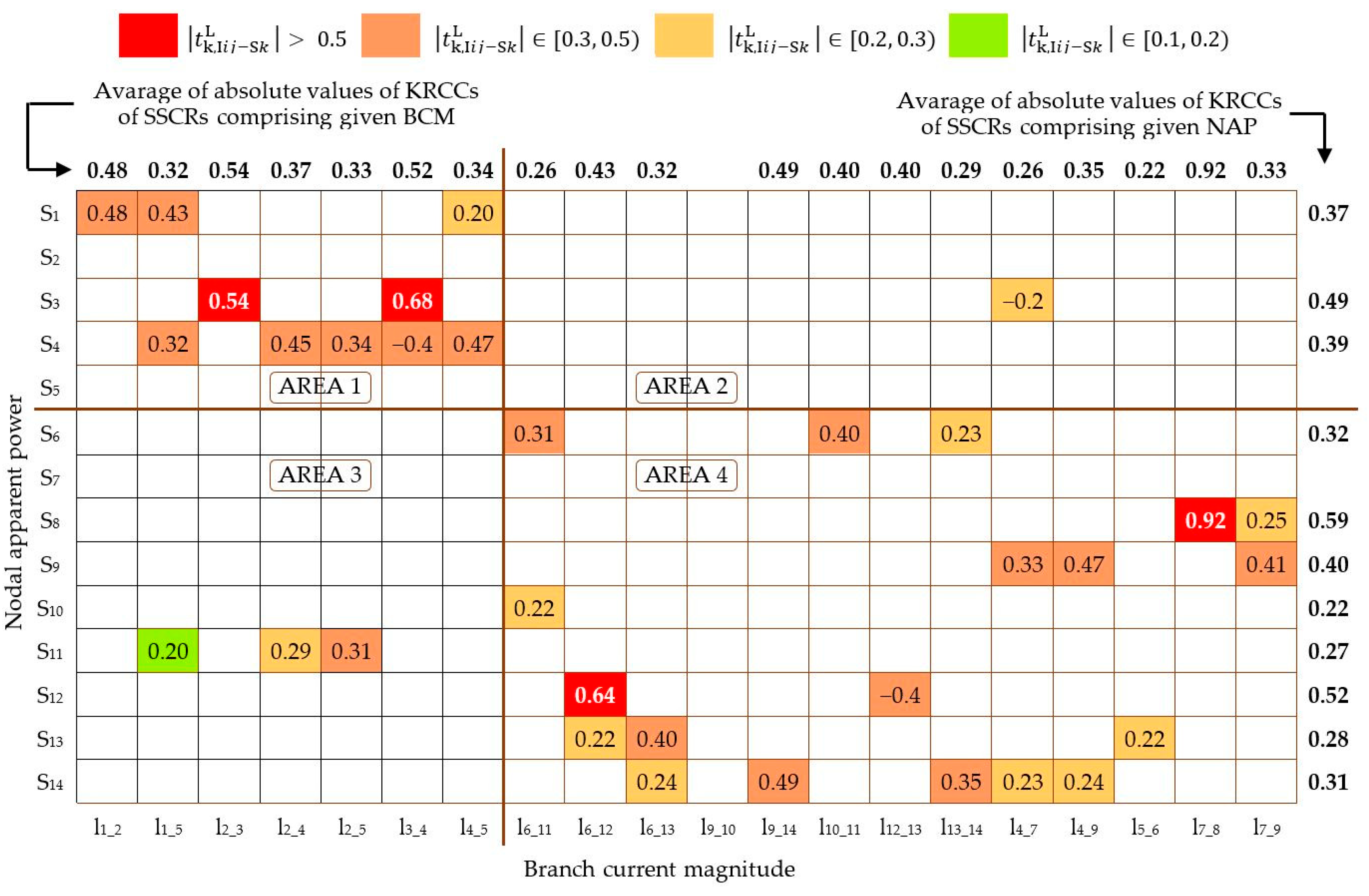
References
- Saric, A.T.; Stankovic, A.M. Model uncertainty in security assessment of power systems. IEEE Trans. Power Syst. 2005, 20, 1398–1407. [Google Scholar] [CrossRef]
- Stewart, G.W.; Sun, G.J. Matrix Perturbation Theory; Academic Press, Inc.: Boston, MA, USA, 1990. [Google Scholar]
- Jiang, X.; Chen, Y.C.; Domínguez-García, A.D. A set-theoretic framework to assess the impact of variable generation on the power flow. IEEE Trans. Power Syst. 2013, 28, 855–867. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.L.; Wang, Y.X.; Ding, R.; Zheng, Y.; Wang, Y.; Cheng, X.; Zha, X. Reactive Voltage Partitioning Method for the Power Grid With Comprehensive Consideration of Wind Power Fluctuation and Uncertainty. IEEE Access 2020, 8, 124514–124525. [Google Scholar] [CrossRef]
- Cichosz, P. Data Mining Algorithms: Explained Using R; John Wiley & Sons: Chichester, UK, 2015. [Google Scholar]
- Maimon, O.; Rokach, L. Data Mining and Knowledge Discovery, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Li, H.; Wang, J. From Soft Clustering to Hard Clustering: A Collaborative Annealing Fuzzy c-Means Algorithm. IEEE Trans. Fuzzy Syst. 2024, 32, 1181–1194. [Google Scholar] [CrossRef]
- Yin, H.; Aryani, A.; Petrie, S.; Nambissan, A.; Astudillo, A.; Cao, S. A Rapid Review of Clustering Algorithms. arXiv 2024, arXiv:2401.07389v1. [Google Scholar]
- Rajabi, A.; Eskandari, M.; Ghadi, M.J.; Li, L.; Zhang, J.; Siano, P. A Comparative Study of Clustering Techniques for Electrical Load Pattern Segmentation. Renew. Sustain. Energy Rev. 2020, 120, 109628. [Google Scholar] [CrossRef]
- Teichgraeber, H.; Brandt, A.R. Clustering Methods to Find Representative Periods for the Optimization of Energy Systems: An initial Framework and Comparison. Appl. Energy 2019, 239, 1283–1293. [Google Scholar] [CrossRef]
- Rocchetta, R. Enhancing the Resilience of Critical Infrastructures: Statistical Analysis of Power Grid Spectral Clustering and Post-Contingency Vulnerability Metrics. Renew. Sustain. Energy Rev. 2022, 159, 112185. [Google Scholar] [CrossRef]
- Okon, T.; Wilkosz, K. Diagnostics of reactive power flow in a power network. In Proceedings of the International Conference on Diagnostics in Electrical Engineering (Diagnostika), Pilsen, Czech Republic, 4–7 September 2018; pp. 1–4. [Google Scholar]
- Kosmala Neto, M.; Okon, T.; Wilkosz, K. Areas of Impact of Nodal Powers on Power Flows in a Power System. In Proceedings of the 24th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 15–17 May 2024; pp. 1–5. [Google Scholar]
- Power Systems Test Case Archive, 14 Bus Power Flow Test Case. Available online: https://labs.ece.uw.edu/pstca/pf14/pg_tca14bus.htm (accessed on 25 May 2025).
- Power Systems Test Case Archive, 30 Bus Power Flow Test Case. Available online: https://labs.ece.uw.edu/pstca/pf30/pg_tca30bus.htm (accessed on 25 May 2025).
- Trochim, W.M.; Donnelly, J.P.; Arora, K. Research Methods: The Essential Knowledge Base; Cengage Learning, Inc.: Boston, MA, USA, 2014. [Google Scholar]
- Okon, T.; Wilkosz, K. Propagation of Voltage Deviations in a Power System. Electronics 2021, 10, 949. [Google Scholar] [CrossRef]
- Okon, T.; Wilkosz, K. Analysis of the Influence of Nodal Reactive Powers on Voltages in a Power System. Energies 2023, 16, 1567. [Google Scholar] [CrossRef]
- Tao, S.; Xu, Q.; Peng, Y.; Xiao, X.; Tang, N. Correlation between injected power and voltage deviation at the integrating node of new energy source. In Proceedings of the 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), Dengfeng, China, 8–10 August 2011; pp. 7031–7034. [Google Scholar]
- Yang, X.; Song, D.; Liu, D.; Wang, F. Node grouping for low frequency oscillation based on Pearson correlation coefficient and its application. In Proceedings of the 2016 IEEE International Conference on Power System Technology (POWERCON), Wollongong, NSW, Australia, 28 September–1 October 2016; pp. 1–5. [Google Scholar]
- Zuo, J.; Xiang, M.; Zhang, B.; Hen, D.C.; Guo, H. Correlation data analysis for low-frequency oscillation source identification. In Proceedings of the 2017 4th International Conference on Systems and Informatics (ICSAI), Hangzhou, China, 11–13 November 2017; pp. 1466–1470. [Google Scholar]
- Chmielowiec, K.; Wiczynski, G.; Rodziewicz, T.; Firlit, A.; Dutka, M.; Piatek, K. Location of power quality disturbances sources using aggregated data from energy meters. In Proceedings of the 12th International Conference and Exhibition on Electrical Power Quality and Utilisation (EPQU), Cracow, Poland, 14–15 September 2020; pp. 1–5. [Google Scholar]
- Feng, D.; Zhou, S.; Wang, T.; Li, Y.; Liu, Y. A method for identifying major disturbance sources in a regional grid. In Proceedings of the IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Sprent, P.; Smeeton, N.C. Applied Nonparametric Statistical Methods, 3rd ed.; Chapman & Hall/CRC: New York, NY, USA, 2001. [Google Scholar]
- Gibbons, J.D.; Chakraborti, S. Nonparametric Statistical Inference, 4th ed.; Revised and Expanded; Marcel Dekker, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; LEA: New York, NY, USA, 1988. [Google Scholar]




| Strenght of Association | KRCC | |
|---|---|---|
| Positive | Negative | |
| Very small | <0.1 | >−0.1 |
| Small | [0.1, 0.3) | (−0.3, −0.1] |
| Medium | [0.3, 0.5) | (−0.5, −0.3] |
| Large | [0.5, 1.0] | [−1.0, −0.5] |
| Quantities in CRs | Number of SSCRs (%) |
|---|---|
| NAPs, BCMs | 34.29 |
| NPAs, BCMs | 30.48 |
| Sk | Iij | Sk | Iij | Sk | Iij | Sk | Iij | Sk | Iij | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S8 | l7_8 | 0.91 | S4 | l2_5 | 0.38 | S8 | l7_9 | 0.21 | S1 | l6_11 | 0.13 | S13 | l4_7 | 0.10 |
| S3 | l2_3 | 0.82 | S9 | l4_7 | 0.38 | S9 | l2_4 | 0.20 | S1 | l13_14 | 0.13 | S13 | l7_9 | 0.10 |
| S3 | l3_4 | 0.80 | S14 | l13_14 | 0.36 | S4 | l1_2 | 0.19 | S12 | l5_6 | 0.13 | S14 | l1_5 | 0.10 |
| S1 | l1_2 | 0.79 | S3 | l2_4 | 0.36 | S6 | l12_13 | 0.19 | S13 | l4_9 | 0.13 | S3 | l5_6 | 0.10 |
| S1 | l1_5 | 0.76 | S4 | l4_5 | 0.34 | S9 | l5_6 | 0.19 | S14 | l6_12 | 0.13 | S6 | l5_6 | 0.10 |
| S1 | l4_5 | 0.61 | S6 | l10_11 | 0.34 | S14 | l5_6 | 0.18 | S1 | l6_12 | 0.12 | S6 | l6_12 | 0.10 |
| S1 | l2_3 | 0.60 | S6 | l6_11 | 0.30 | S1 | l6_13 | 0.17 | S1 | l7_9 | 0.12 | S8 | l4_5 | 0.10 |
| S1 | l2_4 | 0.55 | S6 | l13_14 | 0.29 | S14 | l7_9 | 0.17 | S1 | l10_11 | 0.12 | S9 | l1_2 | 0.10 |
| S12 | l6_12 | 0.55 | S4 | l1_5 | 0.28 | S9 | l1_5 | 0.17 | S14 | l2_4 | 0.12 | S9 | l6_13 | 0.10 |
| S3 | l1_2 | 0.496 | S13 | l5_6 | 0.27 | S14 | l2_5 | 0.15 | S8 | l4_7 | 0.12 | S10 | l1_5 | 0.09 |
| S3 | l4_5 | 0.49 | S13 | l6_12 | 0.26 | S6 | l6_13 | 0.15 | S9 | l4_5 | 0.12 | S10 | l2_5 | 0.09 |
| S3 | l1_5 | 0.47 | S14 | l6_13 | 0.26 | S1 | l4_7 | 0.14 | S9 | l6_11 | 0.12 | S10 | l10_11 | 0.09 |
| S9 | l4_9 | 0.47 | S3 | l2_5 | 0.26 | S1 | l4_9 | 0.14 | S1 | l12_13 | 0.11 | S10 | l4_7 | 0.08 |
| S14 | l9_14 | 0.46 | S13 | l12_13 | 0.25 | S10 | l6_11 | 0.14 | S10 | l6_12 | 0.11 | S4 | l3_4 | −0.09 |
| S1 | l2_5 | 0.45 | S1 | l5_6 | 0.23 | S13 | l2_5 | 0.14 | S10 | l9_10 | 0.11 | S6 | l9_14 | −0.11 |
| S13 | l6_13 | 0.44 | S14 | l4_9 | 0.23 | S13 | l9_14 | 0.14 | S13 | l1_5 | 0.11 | S13 | l10_11 | −0.11 |
| S1 | l3_4 | 0.43 | S9 | l2_5 | 0.23 | S6 | l1_5 | 0.14 | S13 | l2_4 | 0.11 | S13 | l6_11 | −0.13 |
| S9 | l7_9 | 0.42 | S14 | l4_7 | 0.22 | S6 | l1_2 | 0.14 | S9 | l13_14 | 0.11 | S13 | l13_14 | −0.19 |
| S4 | l2_4 | 0.40 | S14 | l12_13 | 0.21 | S9 | l10_11 | 0.14 | S10 | l5_6 | 0.10 | S12 | l12_13 | −0.36 |
| φk | Iij | φk | Iij | φk | Iij | φk | Iij | φk | Iij | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| φ6 | l6_11 | 0.31 | φ4 | l1_5 | 0.17 | φ13 | l13_14 | 0.09 | φ10 | l9_10 | −0.11 | φ9 | l6_13 | −0.15 |
| φ8 | l7_8 | 0.29 | φ6 | l6_12 | 0.16 | φ8 | l6_11 | 0.09 | φ13 | l4_7 | −0.11 | φ14 | l6_13 | −0.16 |
| φ4 | l2_4 | 0.26 | φ3 | l1_5 | 0.15 | φ9 | l7_8 | −0.08 | φ13 | l4_9 | −0.11 | φ9 | l10_11 | −0.16 |
| φ6 | l12_13 | 0.26 | φ9 | l4_7 | 0.13 | φ10 | l7_9 | −0.09 | φ13 | l9_14 | −0.11 | φ9 | l12_13 | −0.16 |
| φ4 | l2_5 | 0.25 | φ2 | l1_2 | 0.12 | φ12 | l5_6 | −0.09 | φ5 | l1_2 | −0.11 | φ9 | l13_14 | −0.18 |
| φ6 | l10_11 | 0.25 | φ3 | l2_4 | 0.12 | φ13 | l1_5 | −0.09 | φ9 | l6_12 | −0.12 | φ9 | l6_11 | −0.19 |
| φ6 | l13_14 | 0.25 | φ8 | l2_3 | 0.12 | φ14 | l1_5 | −0.09 | φ13 | l2_5 | −0.13 | φ13 | l5_6 | −0.2 |
| φ3 | l2_3 | 0.24 | φ9 | l4_5 | 0.12 | φ9 | l3_4 | −0.09 | φ13 | l6_12 | −0.13 | φ6 | l9_14 | −0.21 |
| φ6 | l6_13 | 0.24 | φ4 | l1_2 | 0.11 | φ10 | l2_4 | −0.1 | φ14 | l2_5 | −0.13 | φ13 | l6_13 | −0.25 |
| φ12 | l12_13 | 0.23 | φ8 | l3_4 | 0.11 | φ13 | l2_4 | −0.1 | φ14 | l5_6 | −0.13 | φ14 | l13_14 | −0.25 |
| φ3 | l3_4 | 0.23 | φ8 | l4_5 | 0.11 | φ13 | l7_9 | −0.1 | φ10 | l4_7 | −0.14 | φ6 | l9_10 | −0.28 |
| φ4 | l4_5 | 0.22 | φ8 | l7_9 | 0.11 | φ14 | l2_4 | −0.1 | φ10 | l4_9 | −0.14 | φ14 | l9_14 | −0.3 |
| φ9 | l9_10 | 0.21 | φ6 | l1_5 | 0.1 | φ14 | l7_9 | −0.1 | φ13 | l12_13 | −0.14 | φ12 | l6_12 | −0.34 |
| φ9 | l9_14 | 0.18 | φ8 | l1_2 | 0.1 | φ5 | l1_5 | −0.1 | φ14 | l4_9 | −0.14 | |||
| φ3 | l1_2 | 0.17 | φ8 | l4_7 | 0.1 | φ10 | l2_5 | −0.11 | φ14 | l12_13 | −0.14 | |||
| φ3 | l4_5 | 0.17 | φ8 | l10_11 | 0.1 | φ10 | l5_6 | −0.11 | φ14 | l4_7 | −0.15 |
| Interval of System Active Power Losses, pu | TS14 Loading Level |
|---|---|
| [0.06, 0.13) | low |
| [0.13, 0.20) | medium |
| [0.20, 0.27] | large |
| Case x | Interval of System Active Power Losses pu | % | % | ||
|---|---|---|---|---|---|
| Case a | [0.06, 0.34] | 95 | 100.0 | 77 | 100.0 |
| Case l | [0.06, 0.13) | 29 | 30.53 | 20 | 25.97 |
| Case m | [0.13, 0.20) | 34 | 35.79 | 22 | 28.57 |
| Case L | [0.20, 0.27] | 33 | 34.74 | 20 | 25.97 |
| Case | Branches | Nodes |
|---|---|---|
| Case a | b7_8, b2_3, b3_4, b1_2, b1_5, b4_5, b2_4, b6_12 | n8, n3, n1, n12 |
| Case l | b7_8, b2_3, b1_2, b3_4, b1_5, b6_12 | n8, n3, n1, n12 |
| Case m | b7_8, b3_4, b2_3, b1_2, b1_5 | n8, n3, n1 |
| Case L | b7_8, b3_4, b6_12, b2_3 | n8, n3, n12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosmala Neto, M.; Okon, T.; Wilkosz, K. Correlational Analysis of Relationships Among Nodal Powers and Currents in a Power System. Energies 2025, 18, 3188. https://doi.org/10.3390/en18123188
Kosmala Neto M, Okon T, Wilkosz K. Correlational Analysis of Relationships Among Nodal Powers and Currents in a Power System. Energies. 2025; 18(12):3188. https://doi.org/10.3390/en18123188
Chicago/Turabian StyleKosmala Neto, Miguel, Tomasz Okon, and Kazimierz Wilkosz. 2025. "Correlational Analysis of Relationships Among Nodal Powers and Currents in a Power System" Energies 18, no. 12: 3188. https://doi.org/10.3390/en18123188
APA StyleKosmala Neto, M., Okon, T., & Wilkosz, K. (2025). Correlational Analysis of Relationships Among Nodal Powers and Currents in a Power System. Energies, 18(12), 3188. https://doi.org/10.3390/en18123188







