A Multimodal Interaction-Driven Feature Discovery Framework for Power Demand Forecasting
Abstract
1. Introduction
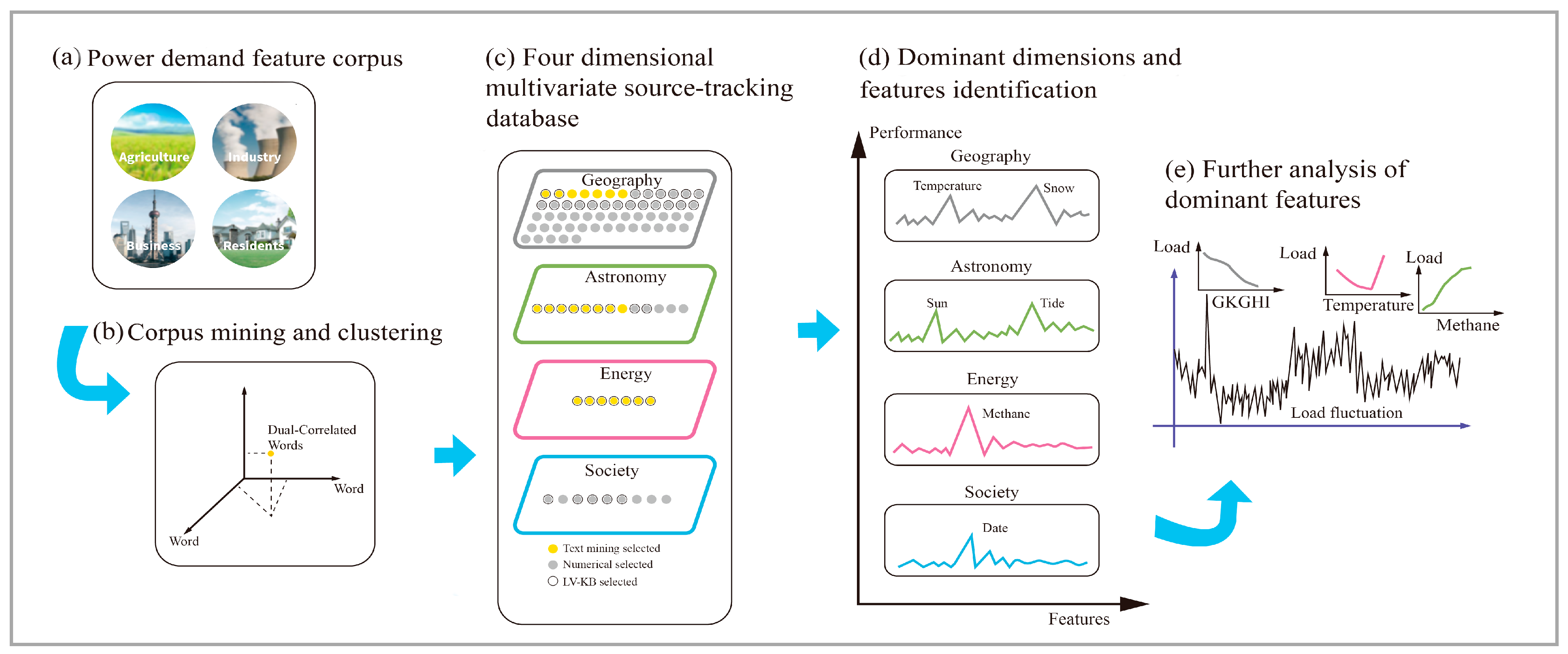
2. Discovery of Candidate Feature Set
2.1. Construction of Power Demand Feature Corpus
2.2. Text Mining on Power Demand Feature Corpus
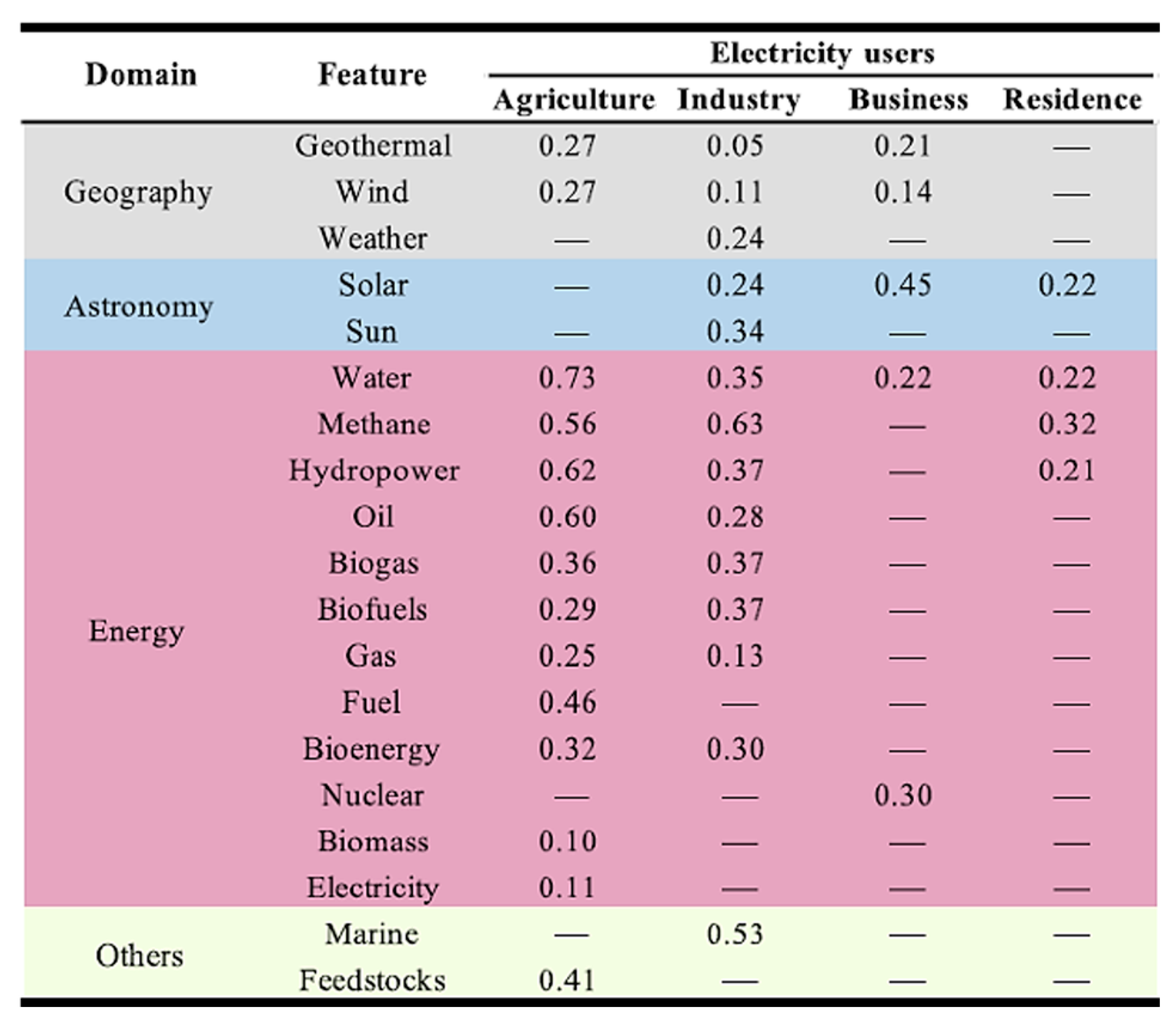
2.3. Creation of Candidate Feature-Type Set
3. Identification of Dominant Dimensions and Features
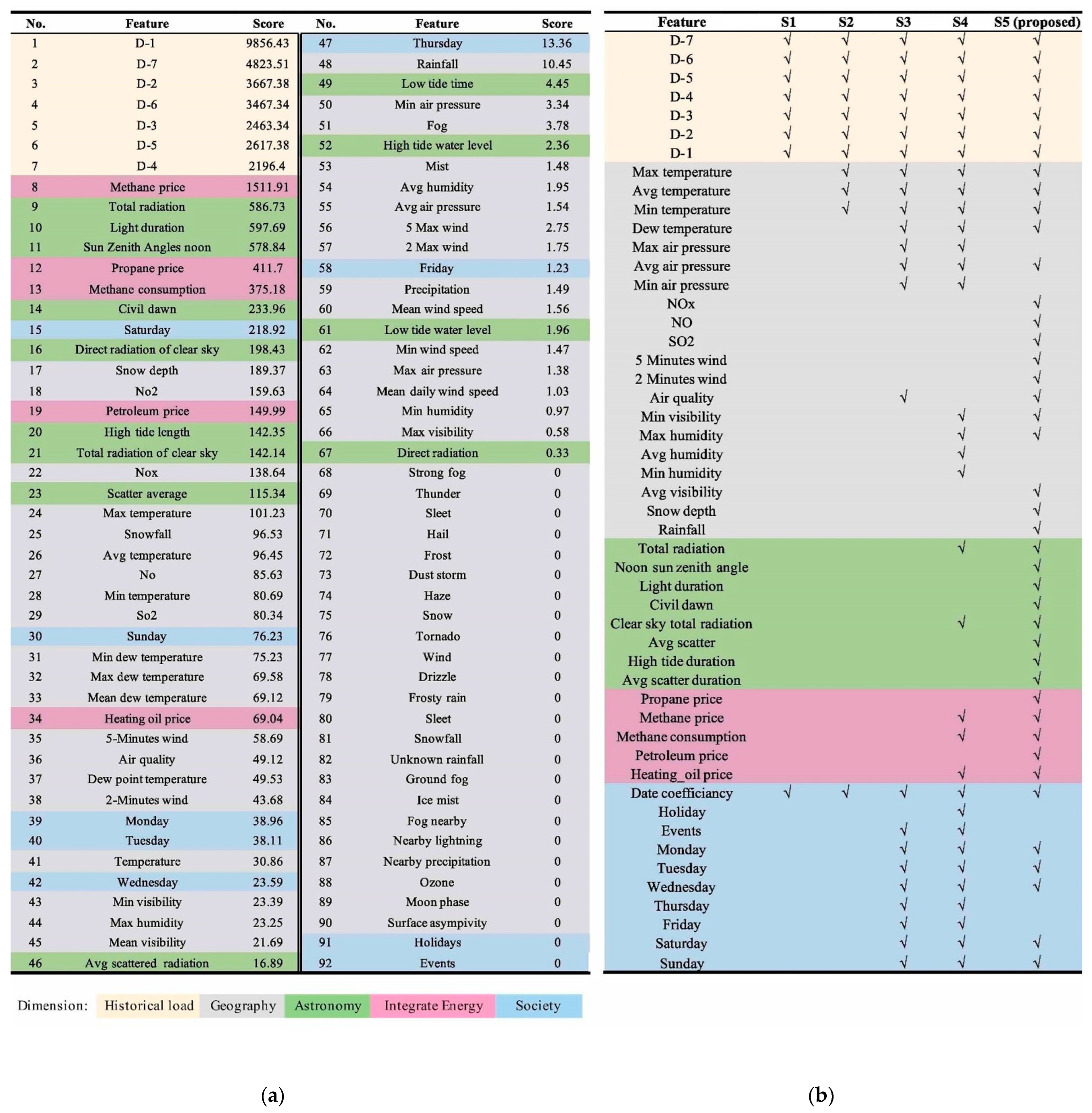
3.1. Feature Database Construction
3.2. Dominant Dimension Identification
3.3. Feature Identification
4. Forecasting Experiments and Performance Comparison of Proposed Features
4.1. Forecasting Experiments Overview
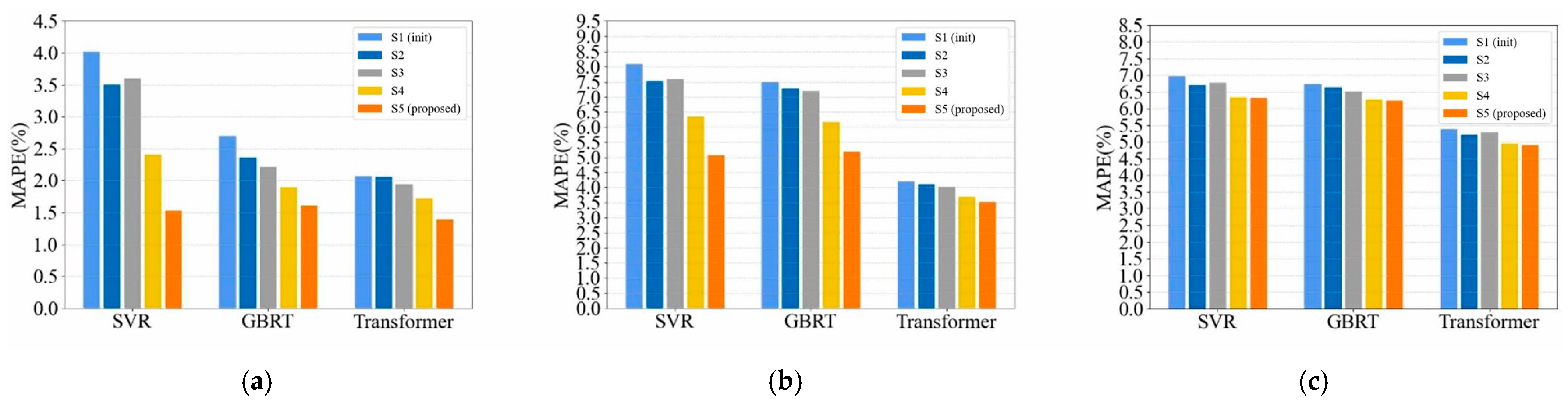
4.2. Comparison with the SoTA Feature Schemes
4.3. Summary
5. Further Analysis of Proposed Features
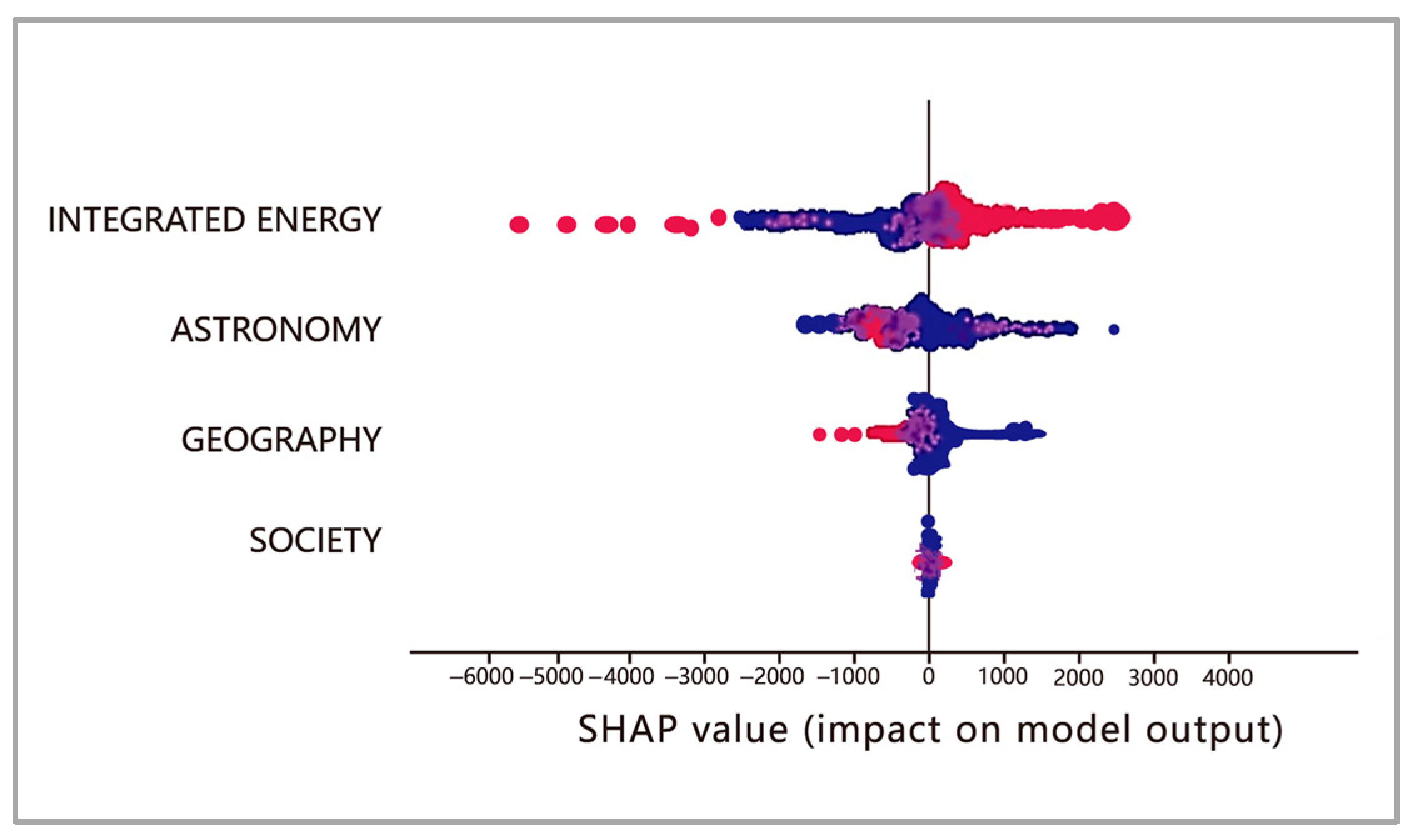
5.1. Sensitivity Analysis of Feature Contributions
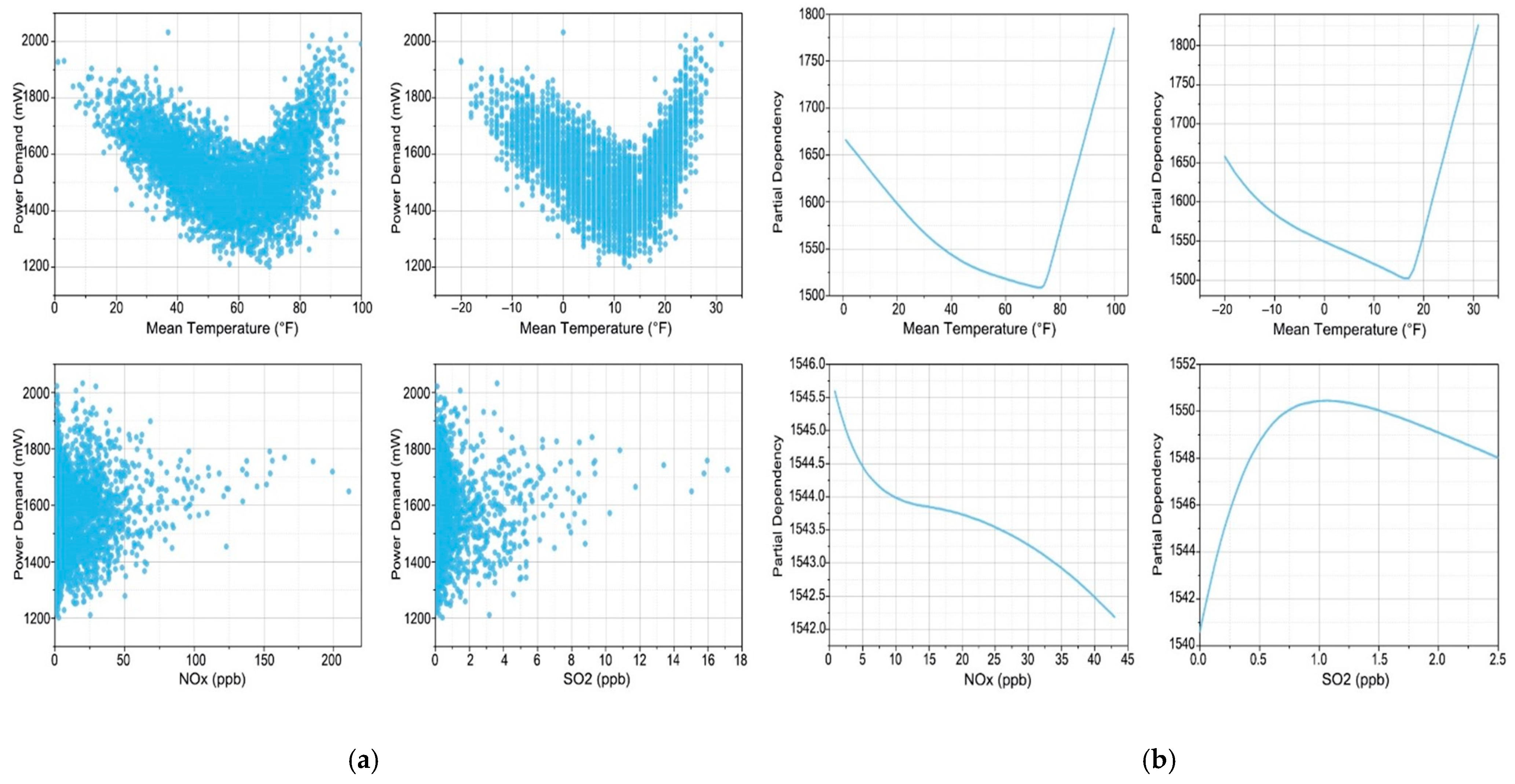
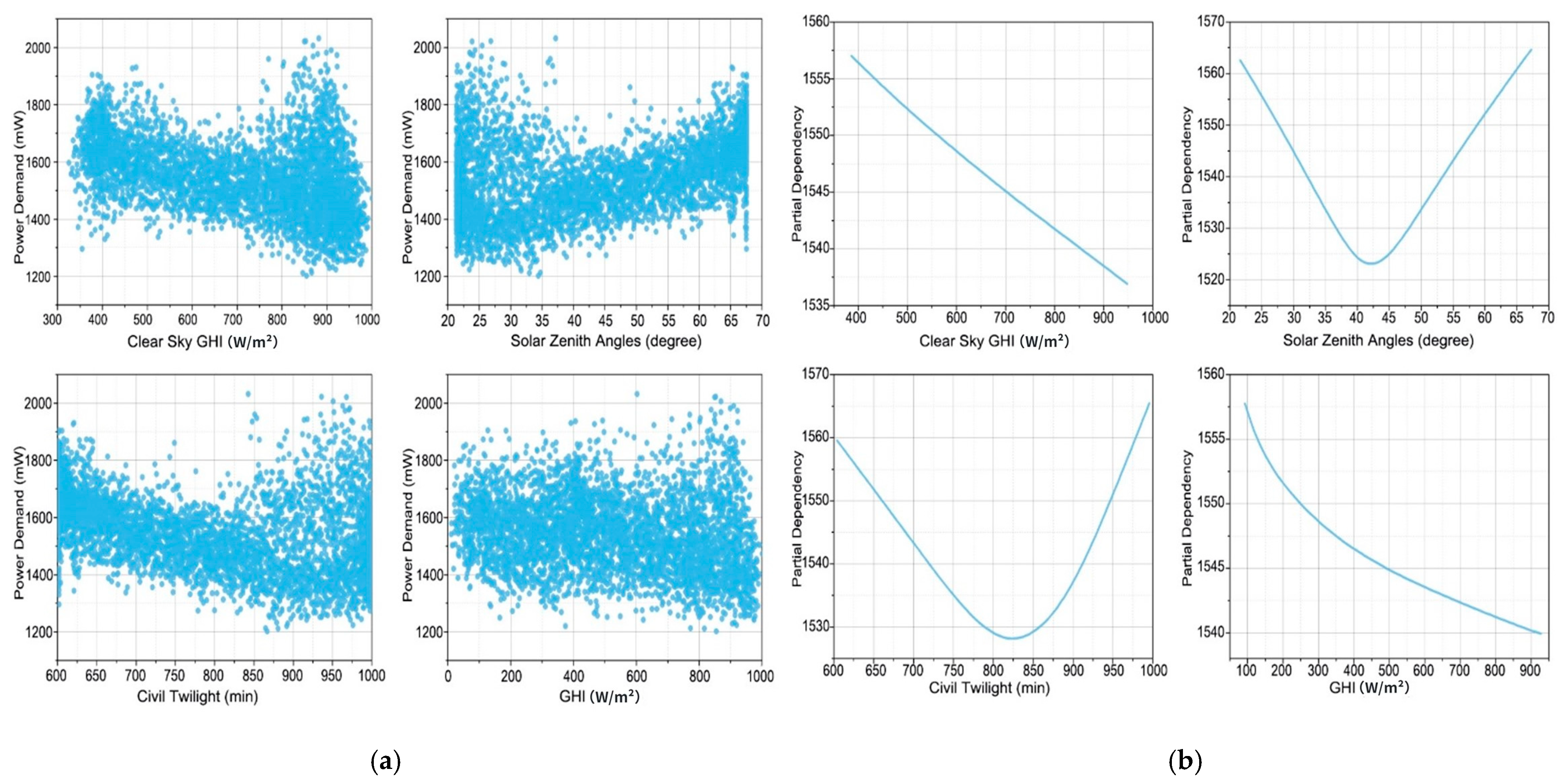
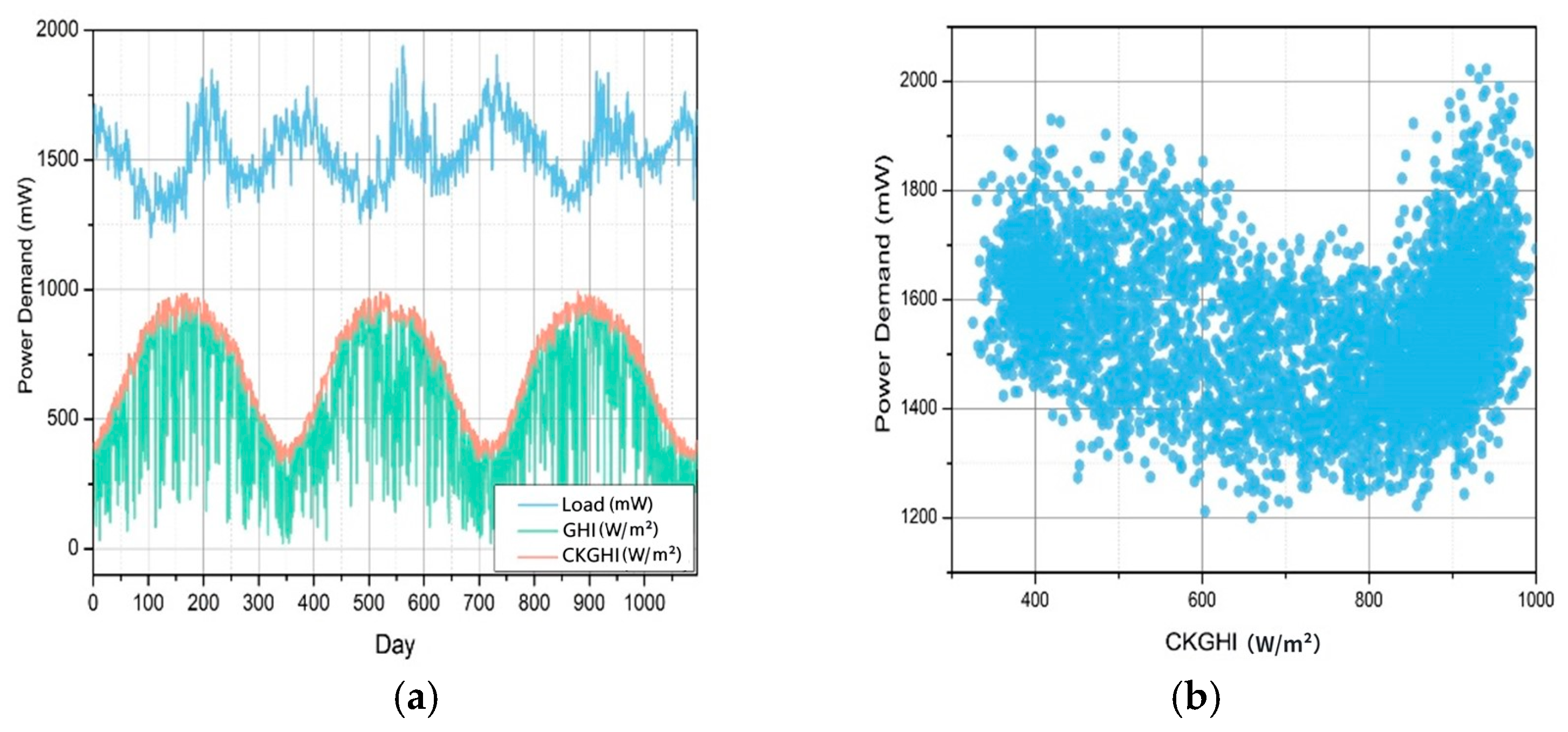
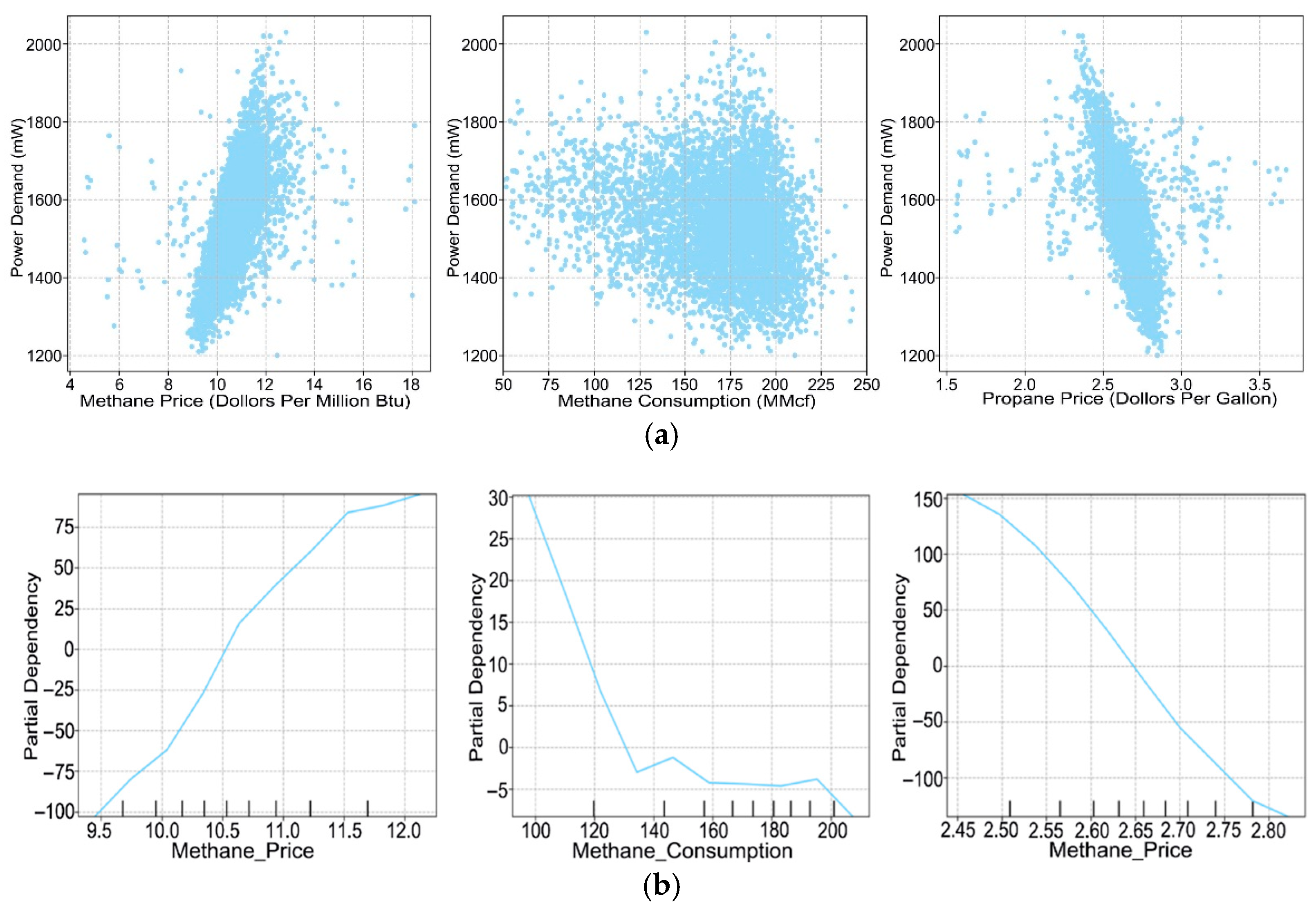
5.2. Dependency Relationship Analysis
5.3. Lagging Effect Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Texas Case
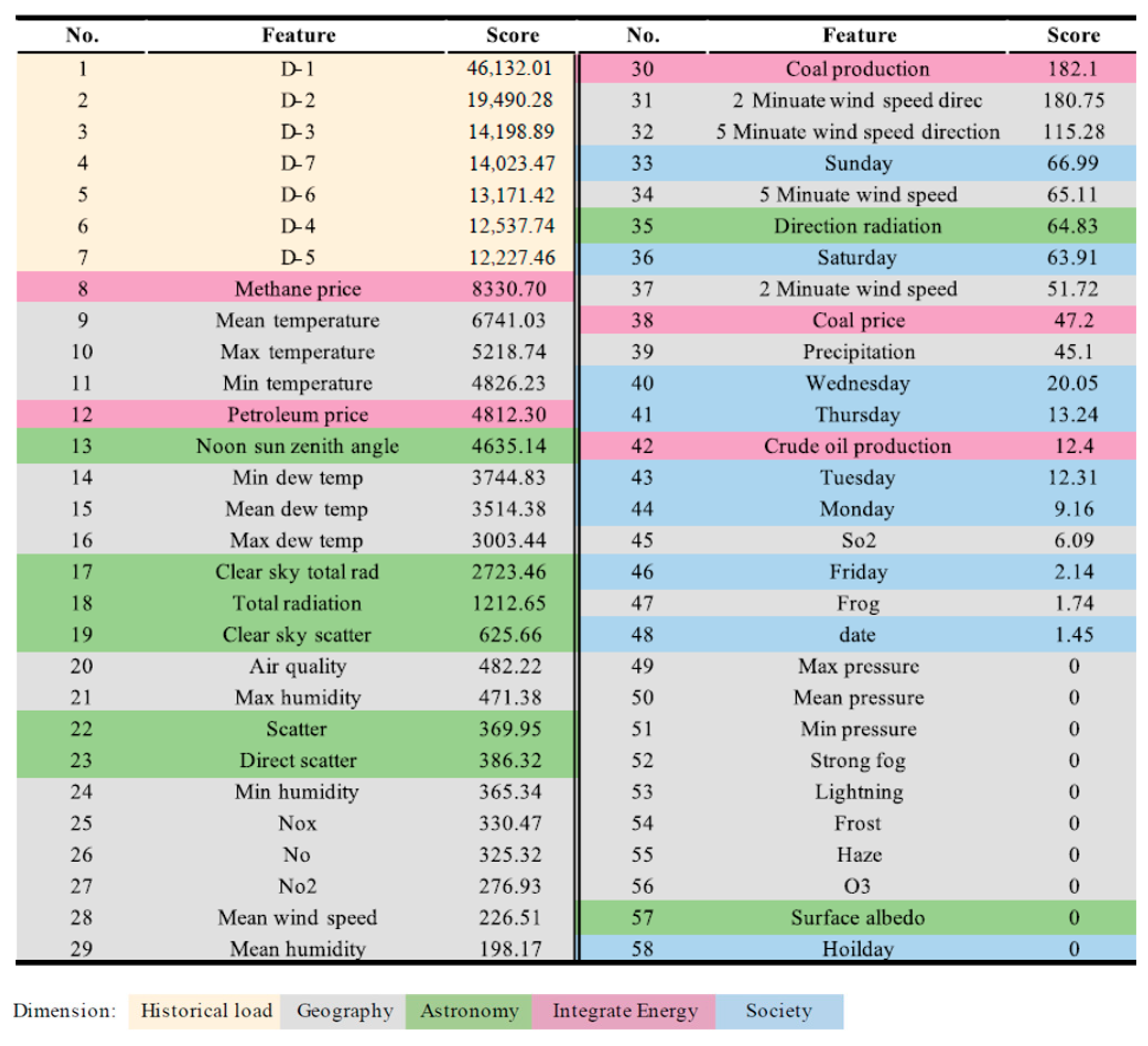
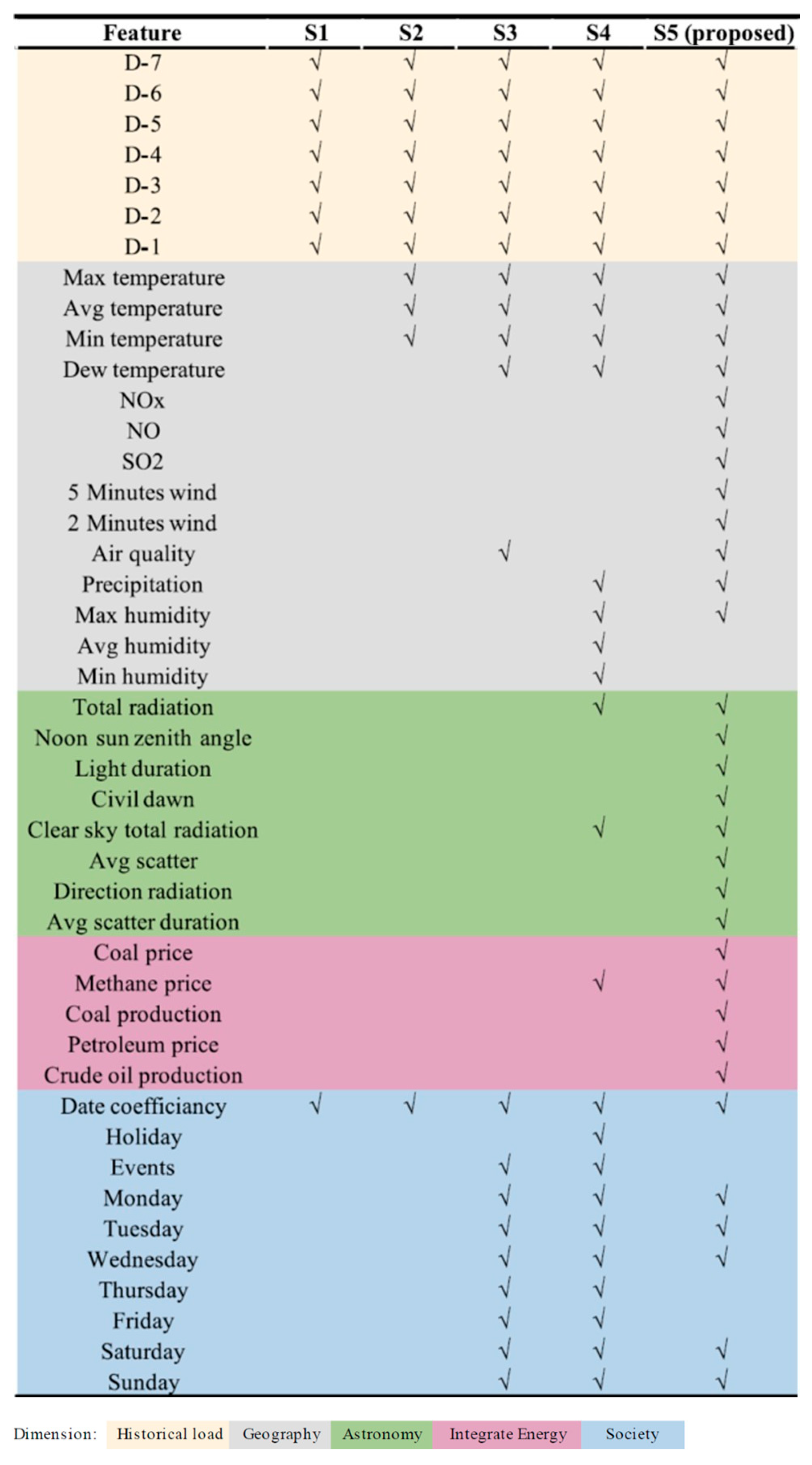
Appendix B. The NSW Case
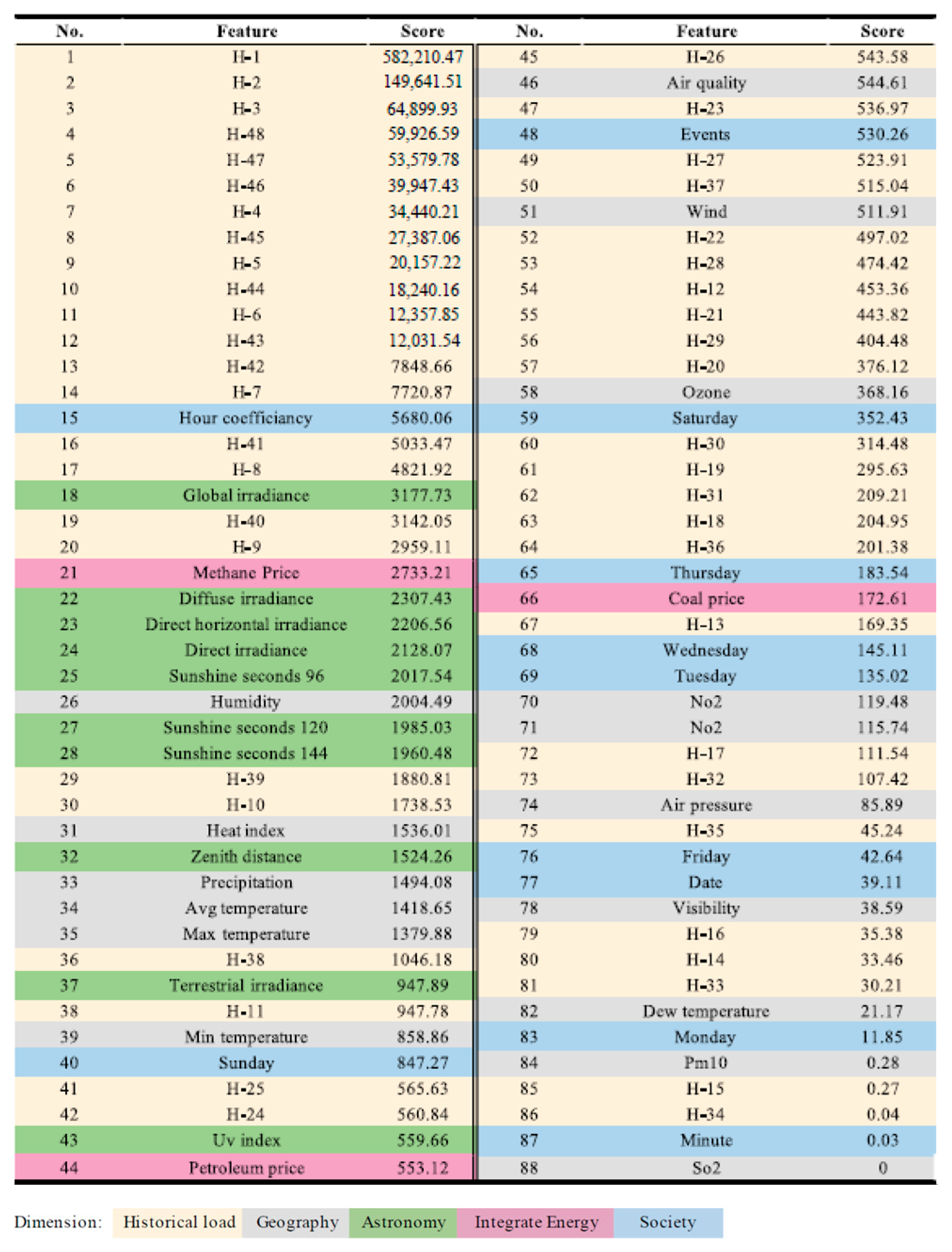
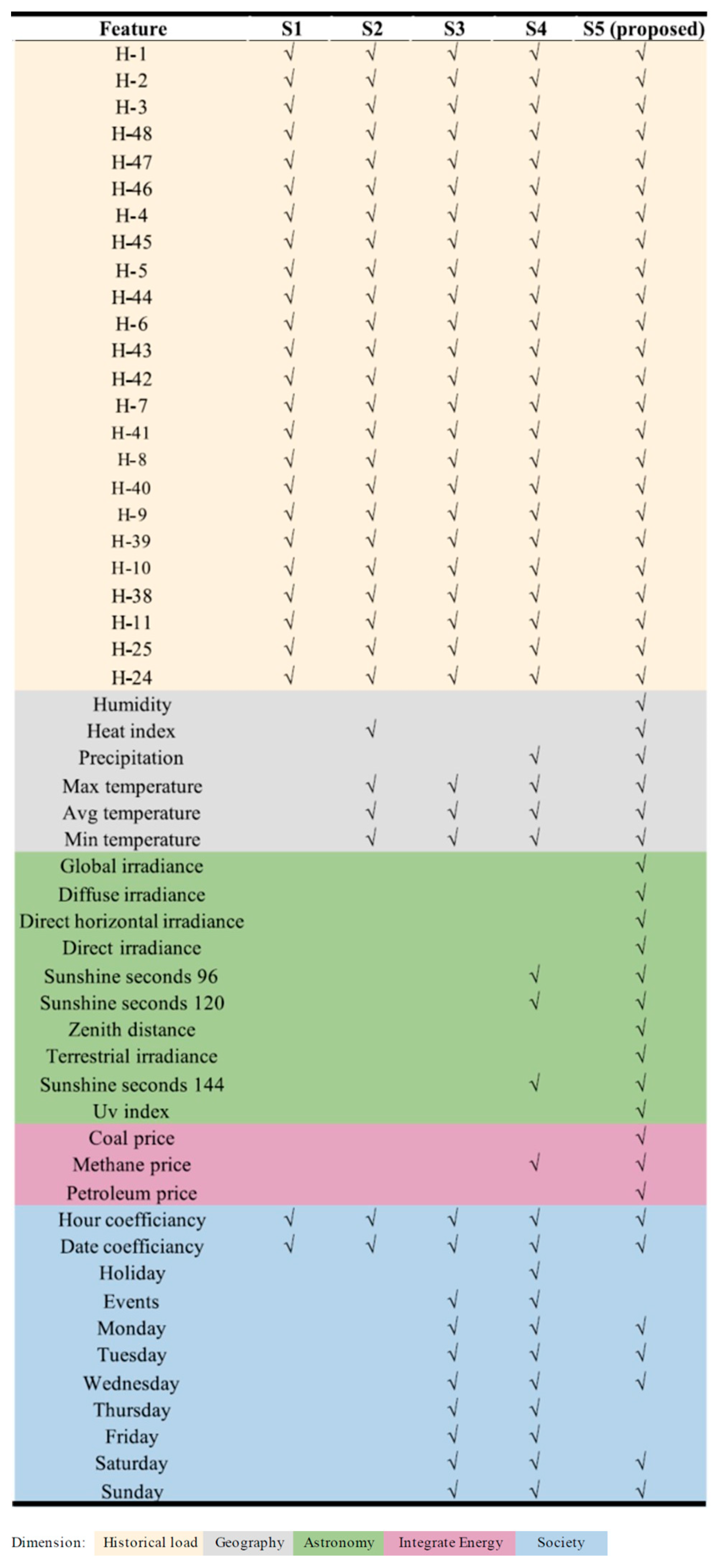
References
- Zhao, J.; Li, F.X.; Zhang, Q.W. Impacts of Renewable Energy Resources on the Weather Vulnerability of Power Systems. Nat. Energy 2024, 9, 1407–1414. [Google Scholar] [CrossRef]
- Saadaoui, A.; Ouassaid, M.; Maaroufi, M. Overview of Integration of Power Electronic Topologies and Advanced Control Techniques of Ultra-Fast EV Charging Stations in Standalone Microgrids. Energies 2023, 16, 1031. [Google Scholar] [CrossRef]
- Zhu, J.; Dong, H.; Zheng, W.; Li, S.; Huang, Y.; Xi, L. Review and Prospect of Data-Driven Techniques for Load Forecasting in Integrated Energy Systems. Appl. Energy 2022, 321, 119269. [Google Scholar] [CrossRef]
- Hafeez, G.; Khan, I.; Jan, S.; Shah, I.A.; Khan, F.A.; Derhab, A. A Novel Hybrid Load Forecasting Framework with Intelligent Feature Engineering and Optimization Algorithm in Smart Grid. Appl. Energy 2021, 299, 117178. [Google Scholar] [CrossRef]
- Bai, W.; Zhu, J.; Zhao, J.; Cai, W.; Li, K. An Unsupervised Multi-Dimensional Representation Learning Model for Short-Term Electrical Load Forecasting. Symmetry 2022, 14, 1999. [Google Scholar] [CrossRef]
- Zhou, M.; Jin, M. Holographic ensemble forecasting method for short-term power load. IEEE Trans. Smart Grid 2017, 10, 425–434. [Google Scholar] [CrossRef]
- Miraki, A.; Parviainen, P.; Arghandeh, R. Electricity demand forecasting at distribution and household levels using explainable causal graph neural network. Energy AI 2024, 16, 100368. [Google Scholar] [CrossRef]
- Abedinia, O.; Amjady, N.; Zareipour, H. A new feature selection technique for load and price forecast of electrical power systems. IEEE Trans. Power Syst. 2016, 32, 62–74. [Google Scholar] [CrossRef]
- Elahe, M.F.; Jin, M.; Zeng, P. Knowledge-based systematic feature extraction for identifying households with plug-in electric vehicles. IEEE Trans. Smart Grid 2022, 13, 2259–2268. [Google Scholar] [CrossRef]
- Xie, J.; Hong, T. Temperature scenario generation for probabilistic load forecasting. IEEE Trans. Smart Grid 2016, 9, 1680–1687. [Google Scholar] [CrossRef]
- Xie, J.; Chen, Y.; Hong, T.; Laing, T.D. Relative humidity for load forecasting models. IEEE Trans. Smart Grid 2016, 9, 191–198. [Google Scholar] [CrossRef]
- You, M.; Wang, Q.; Sun, H.; Castro, I.; Jiang, J. Digital twins based day-ahead integrated energy system scheduling under load and renewable energy uncertainties. Appl. Energy 2022, 305, 17899. [Google Scholar] [CrossRef]
- Son, H.; Kim, C. Short-term forecasting of electricity demand for the residential sector using weather and social variables. Resour. Conserv. Recycl. 2017, 123, 200–207. [Google Scholar] [CrossRef]
- Zeng, P.; Sheng, C.; Jin, M. A learning framework based on weighted knowledge transfer for holiday load forecasting. J. Mod. Power Syst. Clean Energy 2019, 7, 329–339. [Google Scholar] [CrossRef]
- Aguilar Madrid, E.; Antonio, N. Short-term electricity load forecasting with machine learning. Information 2021, 12, 50. [Google Scholar] [CrossRef]
- Zhu, R.; Guo, W.; Gong, X. Short-term load forecasting for CCHP systems considering the correlation between heating, gas and electrical loads based on deep learning. Energies 2019, 12, 3308. [Google Scholar] [CrossRef]
- Wang, S.; Wang, S.; Chen, H.; Gu, Q. Multi-energy load forecasting for regional integrated energy systems considering temporal dynamic and coupling characteristics. Energy 2020, 195, 116964. [Google Scholar] [CrossRef]
- Türkoğlu, A.S.; Erkmen, B.; Eren, Y.; Erdinç, O.; Küçükdemiral, İ. Integrated approaches in resilient hierarchical load forecasting via TCN and optimal valley filling based demand response application. Appl. Energy 2024, 360, 122722. [Google Scholar] [CrossRef]
- Wei, C.; Pi, D.; Ping, M.; Zhang, H. Short-term load forecasting using spatial-temporal embedding graph neural network. Electr. Power Syst. Res. 2023, 225, 109873. [Google Scholar] [CrossRef]
- Cheng, F.; Liu, H. Multi-step electric vehicles charging loads forecasting: An autoformer variant with feature extraction, frequency enhancement, and error correction blocks. Appl. Energy 2024, 376, 124308. [Google Scholar] [CrossRef]
- Bayoudh, K.; Knani, R.; Hamdaoui, F.; Mtibaa, A. A survey on deep multimodal learning for computer vision: Advances, trends, applications, and datasets. Vis. Comput. 2022, 38, 2939–2970. [Google Scholar] [CrossRef]
- Liu, Y.; Qiao, L.; Lu, C.; Yin, D.; Lin, C.; Peng, H.; Ren, B. OSAN: A one-stage alignment network to unify multimodal alignment and unsupervised domain adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, Canada, 18–22 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 3551–3560. Available online: https://openaccess.thecvf.com/content/CVPR2023/html/Liu_OSAN_A_One-Stage_Alignment_Network_To_Unify_Multimodal_Alignment_and_CVPR_2023_paper.html (accessed on 20 May 2024).
- Fan, L.; Krishnan, D.; Isola, P.; Katabi, D.; Tian, Y. Improving clip training with language rewrites. Adv. Neural Inf. Process. Syst. 2023, 36, 35544–35575. Available online: https://proceedings.neurips.cc/paper_files/paper/2023/file/6fa4d985e7c434002fb6289ab9b2d654-Paper-Conference.pdf (accessed on 20 May 2024).
- Dai, Y.; Yan, Z.; Cheng, J.; Duan, X.; Wang, G. Analysis of multimodal data fusion from an information theory perspective. Inf. Sci. 2023, 623, 164–183. [Google Scholar] [CrossRef]
- Turk, M. Multimodal interaction: A review. Pattern Recognit. Lett. 2014, 36, 189–195. [Google Scholar] [CrossRef]
- Xiao, S.; Chen, G.; Zhang, C.; Li, X. Complementary or substitutive? A novel deep learning method to leverage text-image interactions for multimodal review helpfulness prediction. Expert Syst. Appl. 2022, 208, 118138. [Google Scholar] [CrossRef]
- McEnery, T.; Brezina, V.; Gablasova, D.; Banerjee, J. Corpus linguistics, learner corpora, and SLA: Employing technology to analyze language use. Annu. Rev. Appl. Linguist. 2019, 39, 74–92. [Google Scholar] [CrossRef]
- Wang, Y.; Soler, J. Investigating predatory publishing in political science: A corpus linguistics approach. Appl. Corpus Linguist. 2021, 1, 100001. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.; Cheng, Y.; Zhang, Y. Learning deep generative clustering via mutual information maximization. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 6263–6275. [Google Scholar] [CrossRef]
- Amado, A.; Cortez, P.; Rita, P.; Moro, S. Research trends on Big Data in Marketing: A text mining and topic modeling based literature analysis. Eur. Res. Manag. Bus. Econ. 2018, 24, 1–7. [Google Scholar] [CrossRef]
- Eskici, H.B.; Koçak, N.A. A text mining application on monthly price developments reports. Cent. Bank Rev. 2018, 18, 51–60. [Google Scholar] [CrossRef]
- Jakawat, W.; Makkhongkaew, R. Graph clustering with K-nearest neighbor constraints. In Proceedings of the 2019 16th International Joint Conference on Computer Science and Software Engineering (JCSSE), Chonburi, Thailand, 10–12 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 309–313. [Google Scholar] [CrossRef]
- Zhang, F.; Fleyeh, H.; Wang, X.; Lu, M. Construction site accident analysis using text mining and natural language processing techniques. Autom. Constr. 2019, 99, 238–248. [Google Scholar] [CrossRef]
- Hughes-Cromwick, E.; Coronado, J. The value of US government data to US business decisions. J. Econ. Perspect. 2019, 33, 131–146. [Google Scholar] [CrossRef]
- Dixon, R.K.; McGowan, E.; Onysko, G.; Scheer, R.M. US energy conservation and efficiency policies: Challenges and opportunities. Energy Policy 2010, 38, 6398–6408. [Google Scholar] [CrossRef]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef]
- Liu, Z.; Ning, J.; Cao, Y.; Wei, Y.; Zhang, Z.; Lin, S.; Hu, H. Video swin transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 3202–3211. [Google Scholar] [CrossRef]
- Rajbhandari, Y.; Marahatta, A.; Ghimire, B.; Shrestha, A.; Gachhadar, A.; Thapa, A.; Chapagain, K.; Korba, P. Impact study of temperature on the time series electricity demand of urban nepal for short-term load forecasting. Appl. Syst. Innov. 2021, 4, 43. [Google Scholar] [CrossRef]
- Tang, X.; Chen, H.; Xiang, W.; Yang, J.; Zou, M. Short-term load forecasting using channel and temporal attention based temporal convolutional network. Electr. Power Syst. Res. 2022, 205, 107761. [Google Scholar] [CrossRef]
- Alipour, P.; Mukherjee, S.; Nateghi, R. Assessing climate sensitivity of peak electricity load for resilient power systems planning and operation: A study applied to the Texas region. Energy 2019, 185, 1143–1153. [Google Scholar] [CrossRef]
- Giannelos, S.; Moreira, A.; Papadaskalopoulos, D.; Borozan, S.; Pudjianto, D.; Konstantelos, I.; Sun, M.; Strbac, G. A Machine Learning Approach for Generating and Evaluating Forecasts on the Environmental Impact of the Buildings Sector. Energies 2023, 16, 2915. [Google Scholar] [CrossRef]
- Ahmar, A.S.; Botto-Tobar, M.; Rahman, A.; Hidayat, R. Forecasting the Value of Oil and Gas Exports in Indonesia using ARIMA Box-Jenkins. JINAV J. Inf. Vis. 2022, 3, 35–42. [Google Scholar] [CrossRef]
| Tasks | ST | S1 | S2 | ST-conf | S1-conf | S2-conf | Tasks | ST | S1 | S2 | ST-conf | S1-conf | S2-conf |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G | 0.1568 | 0.1564 | non | 0.0144 | 0.0347 | non | G + I | non | non | 0.0017 | non | non | 0.0445 |
| A | 0.1505 | 0.1531 | non | 0.0130 | 0.0291 | non | G + S | non | non | 0.0013 | non | non | 0.0594 |
| I | 0.6882 | 0.6882 | non | 0.0450 | 0.0668 | non | A + I | non | non | −0.0028 | non | non | 0.0440 |
| S | 0.0011 | 0.0011 | non | 0.0001 | 0.0030 | non | A + S | non | non | −0.0048 | non | non | 0.0571 |
| G + A | non | non | 0.0013 | non | non | 0.0505 | I + S | non | non | 0.0002 | non | non | 0.0058 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, Z.; Jin, M.; Zeng, P. A Multimodal Interaction-Driven Feature Discovery Framework for Power Demand Forecasting. Energies 2025, 18, 2907. https://doi.org/10.3390/en18112907
Ning Z, Jin M, Zeng P. A Multimodal Interaction-Driven Feature Discovery Framework for Power Demand Forecasting. Energies. 2025; 18(11):2907. https://doi.org/10.3390/en18112907
Chicago/Turabian StyleNing, Zifan, Min Jin, and Pan Zeng. 2025. "A Multimodal Interaction-Driven Feature Discovery Framework for Power Demand Forecasting" Energies 18, no. 11: 2907. https://doi.org/10.3390/en18112907
APA StyleNing, Z., Jin, M., & Zeng, P. (2025). A Multimodal Interaction-Driven Feature Discovery Framework for Power Demand Forecasting. Energies, 18(11), 2907. https://doi.org/10.3390/en18112907






