Abstract
The increasing integration of renewable energy sources (RESs) introduces significant uncertainties in both generation and demand, presenting critical challenges to the convergence, feasibility, and real-time performance of optimal power flow (OPF). To address these challenges, a multi-agent deep reinforcement learning (DRL) model is proposed to solve the OPF while ensuring constraints are satisfied rapidly. A heterogeneous multi-agent proximal policy optimization (H-MAPPO) DRL algorithm is introduced for multi-area power systems. Each agent is responsible for regulating the output of generation units in a specific area, and together, the agents work to achieve the global OPF objective, which reduces the complexity of the DRL model’s training process. Additionally, a graph neural network (GNN) is integrated into the DRL framework to capture spatiotemporal features such as RES fluctuations and power grid topological structures, enhancing input representation and improving the learning efficiency of the DRL model. The proposed DRL model is validated using the RTS-GMLC test system, and its performance is compared to MATPOWER with the interior-point iterative solver. The RTS-GMLC test system is a power system with high spatial–temporal resolution and near-real load profiles and generation curves. Test results demonstrate that the proposed DRL model achieves a 100% convergence and feasibility rate, with an optimal generation cost similar to that provided by MATPOWER. Furthermore, the proposed DRL model significantly accelerates computation, achieving up to 85 times faster processing than MATPOWER.
1. Introduction
The OPF problem refers to minimizing the power generation cost by appropriately scheduling the dispatchable generation while satisfying physical and engineering constraints of the power system [1]. In recent decades, the penetration of RESs such as photovoltaics and wind power has steadily increased. Under high levels of uncertainty, efficiently solving large-scale OPF problems with feasible solutions has emerged as one of the key challenges in modern power systems.
To deal with the intermittent and uncertain nature of RESs relating to their fluctuations in power output, stochastic OPF is introduced and more frequently solved to maintain the power balance [2]. To obtain the stochastic OPF solution, operators generate numerous load scenarios and solve each scenario with the basic OPF procedure. However, conventional iteration-based optimization methods such as the Newton method, simplex method, and interior-point method, and recently proposed advanced methods such as the point estimation method based on Gram–Charlier expansion [3] and sequential linear programming [4], require significant computational complexity and time consumption for large-scale RES power systems [5]. For instance, solving stochastic OPF for 1000 different load scenarios in a power system with hundreds of nodes typically takes >10 min, which is inadequate for real-time management in terms of the rapid RES fluctuations [6]. Meanwhile, most iteration-based optimization methods are model-based. The performance of model-based methods largely depends on the prior knowledge of electrical parameters of the power system model, which may be time-varying, inaccurate, and unavailable in practical scenarios [7]. In addition, due to the non-linear and non-convex nature of the OPF problem, finding feasible OPF solutions is an NP-hard problem and becomes a cornerstone of existing challenges [8].
The above challenges and the advancement of data-driven artificial intelligence (AI) techniques motivate the use of the DRL model to solve large-scale OPF problems in highly RES-penetrated power systems. Unlike existing adaptive methods such as DynaSLAM [9] with parameter adaptation, the DRL is a more effective method for adapting to entire complex and dynamic environments, e.g., the strong uncertainties of RES generation and load demand, through automatically optimizing reward and policies without manual intervention or prior rules. With the help of the online training and offline execution framework, the DRL method greatly reduces the computational burden to meet the real-time OPF requirement [10]. To guarantee the solution’s feasibility, recent works on DRL-based OPF methods have attempted various strategies to address the security constraints. Yan and et al. proposed a Lagrangian-based DRL approach to construct an augmented action-value function with a penalty on constraint violation [11]. Sayed et al. add a novel convex safety layer with the penalty convex–concave procedure into the DRL model [12]. Similarly, hybrid knowledge or expert knowledge safety layers are developed and combined with the DRL model to improve the solution feasibility in [7,13]. However, most existing DRL-based OPF methods adopt a single-agent architecture [14,15,16]. For large-scale RES power systems, the high-dimensional state and action spaces increase the risk of the dimensionality curse. To improve the scalability and mitigate the training complexity of DRL methods, strategies like multi-task attribution map [17] and the scalable graph DRL [18] are introduced. Additionally, the multi-agent DRL framework [19] presents a promising startegy for solving the large-scale OPF in multi-area power systems. For example, sub-regions and/or areas of the power system are identified according to geographical, administrative, or dispatching authority boundaries. Each agent of the multi-agent DRL framework is only responsible for generating the actions for one area of the power system, and all agents collaboratively share information to accomplish the optimization task for the entire system. The multi-agent DRL framework has been proven effective for the energy management of power systems [20,21] and the frequency or voltage control of microgrids or multi-area power systems [22,23,24]. Nevertheless, the multi-agent DRL framework applied specifically to OPF problems in multi-area power systems still warrants further investigation.
Moreover, in RES power systems, extracting critical spatiotemporal information from RES power output and power system structure to provide meaningful feature inputs for the DRL model is one of the key factors in ensuring its decision-making performance. Li et al. use attention neural networks to directly joint load profile and weather patterns with power dispatch and generation [5]. Gao et al. introduce a Bayesian deep neural network and conditional variational auto-encoder to generate random spatiotemporal source–load scenarios [25]. By integrating physics-informed rules or laws into deep learning models, the physics-informed neural network (PINN) [26,27] shows its great potential for enhancing the convergence and feasibility of OPF in RES power systems [28]. Additionally, the power system is a typical graph-structured system, where data are collected from non-Euclidean domains with interdependency among nodes. Graph neural networks (GNNs) demonstrate strong feature extraction capability in graph-structured systems, e.g., power systems [29,30]. Recent works show that the GNN remarkably improves the OPF performance by integrating the spatial features of power system topology and the temporal features of RESs’ power output time series [31,32,33].
In this paper, an H-MAPPO-based DRL model with a GNN feature extraction layer is proposed to solve the OPF. The main contributions are summarized below:
- The heterogeneous MAPPO (H-MAPPO) DRL model is proposed to address the OPF problem in multi-area power systems, significantly reducing training complexity and enhancing decision-making efficiency.
- A GNN layer is incorporated to extract spatiotemporal features of RES fluctuations and power grid topologies, enhancing the convergence and feasibility of OPF solutions.
- The performance of the proposed DRL model is validated using the RTS-GMLC test system, a near-real power system model with high spatial and temporal resolution and substantial RES penetration.
2. Problem Formulation
Under the steady-state operation and 3-ph balanced conditions [34], the OPF model can be formulated as follows:
where the quadratic cost function in Equation (1) is .
Markov Decision Process Formulation
In an N-bus power system composed of areas, assuming each area of the power system corresponds to an agent, and all agents collaboratively make decisions to achieve OPF for the entire system, the OPF problem can be formulated as an MDP with the main components of state space S, action space A, state transition probability matrix , and reward function R:
(1) State: At each time step t, the local observation of area is
where .
The global state space includes the local observation of all areas:
(2) Action: The action space is the set of all possible actions that each area of the power system can take under a given state. At each time step t, the local action space is defined as
The entire action space is defined as
(3) Reward: The reward function serves as a quantitative metric to assess the utility or value associated with a particular state and action pair, which is designed according to the optimization objective. As shown by Equations (1)–(10), the objective is power flow optimization, e.g., minimizing generation costs under system constraints. The corresponding reward function is defined as follows:
In Equation (16), . The OPF solution is converged and feasible when all constraints shown by Equations (2)–(10) are satisfied. The OPF solution is converged but infeasible when constraints (2)–(5) are satisfied and constraints (6)–(10) are violated. The OPF solution is non-convergent when constraints (2)–(5) are violated.
3. Deep Reinforcement Learning Foundations
DRL is an advanced method for solving MDP problems. The fundamental idea of DRL is to maximize the cumulative reward function assigned to a specific task through continuous interactions between the agent and the environment, e.g., power systems, ultimately learning the optimal strategy for performing the task. To address the challenge of efficient and stable DRL training for coordinating multiple agents in the power system’s OPF environment, the concept of a heterogeneous multi-agent system is introduced, along with the MAPPO algorithm. In addition, the GNN is introduced to extract the global spatial–temporal feature from the time series of state variables and the power grid topology, which will be used as part of the input of the DRL model.
3.1. Heterogeneous Multi-Agent System
In practical large-scale power systems, the power flow optimization strategy is often deployed across multiple areas of the power system. Each area includes different numbers of buses, dispatchable generation units, and transmission lines, requiring the adaptivity for non-uniform state and action spaces of individual DRL agents. The corresponding multi-agent system is the heterogeneous multi-agent system (H-MAS). The H-MAS structure is particularly critical for solving the OPF in multi-area power systems. First, compared with the homogeneous multi-agent DRL method, agents in H-MAS can adapt to non-uniform state and action spaces, enabling them to handle specific operational constraints and objectives. For example, each agent can independently adjust the power output of dispatchable generation units within its area while collaboratively optimizing global objectives, i.e., minimizing the total generation cost while satisfying the physical and engineering constraints of the multi-area power system. Second, the H-MAS naturally aligns with the decentralized nature of modern power systems, where each area operates autonomously but must coordinate with neighboring areas to ensure system-wide stability. During the training process, the DRL agents share global information about the multi-area power system and take action with local observations at the execution stage. While the OPF problem of the multi-area power system could theoretically be solved using a single-agent DRL method, the practical training process often suffers from the curse of dimensionality due to the growing state and action spaces in large-scale systems. In contrast, the H-MAS framework decomposes the OPF problem into smaller subproblems for each area, significantly reducing training difficulties and improving scalability for practical multi-area power systems.
3.2. Multi-Agent Proximal Policy Optimization
MAPPO is an extended algorithm of proximal policy optimization for the multi-agent system environment. The proximal policy optimization algorithm is a policy gradient approach, seeking to enhance policy performance by optimizing surrogate objective functions through stochastic gradient ascent and following interactions with the environment and data sampling [35]. By leveraging multiple samples for policy gradient estimation, PPO efficiently utilizes the collected data, enabling faster training and more streamlined update procedures. Furthermore, PPO carefully regulates policy modifications during the update phase to avoid large, destabilizing changes that could compromise training stability. With the MAPPO algorithm, the MDP problem is implemented by modeling each agent’s decision-making as a decentralized MDP with shared observations. During training, agents interact with the environment by observing states (or partial observations), taking actions based on their policies, and receiving rewards, following the MDP structure introduced in Section 2.
The MAPPO algorithm adopts a CTDE framework [36], making it particularly well suited for fully cooperative environments, e.g., the OPF scenario for the power system with multiple areas. In the CTDE framework, the central controller is only responsible for the training, collecting the global environment state information, as shown in Equation (13), to train the actor and critic networks of each agent. During the execution, agent m at time step t can obtain its local observation , as shown in Equation (12), and then, based on its actor network , take action , as shown in Equation (15). Due to the cooperative relationship between the agents in this paper, all agents share the same reward , as shown in Equation (16). The critic network collects and to generate a Q-value function to maximize the reward function.
The loss function of the actor network is formulated as follows:
In Equation (17), the importance sampling ratio is , representing the ratio of the new policy to the old policy. The clipping function limits the change between the old and new policies in the range , aiming to avoid the excessive modification of the objective value. The critic network is trained by the TD-error method [37] to maximize the loss function. The specific loss function is
The proposed DRL-based OPF method deploys the H-MAPPO algorithm. As a comparison baseline, the traditional interior-point method in MATPOWER is used. The interior-point method solves OPF by transforming the constrained optimization problem into a sequence of unconstrained subproblems using barrier functions. It handles inequality constraints, e.g., generation limits, by keeping iterates strictly feasible while gradually reducing a barrier parameter. The interior-point method follows the perturbed Karush–Kuhn–Tucker conditions, balancing optimality and feasibility until convergence.
3.3. Graph Neural Network
The GNN is an effective method for the representation learning of graph-structured data. The power system can be represented as a graph, enabling the use of GNNs to extract its spatiotemporal features. Let denote the graph of a power system, where and are the node and edge sets. The node and edge represent the bus and transmission line in the power system. The node feature vectors for are the input of the GNN. For each bus in the power system, the node feature includes the generation active power output and active load demand of that bus. In this paper, the GNN shares the same structure of the graph . GNNs use the graph structure and node features to extract a representation vector of each node, , the output of GNN. GNNs employ a neighborhood aggregation approach, where the representation vector of a node is derived by recursively collecting and transforming the representation vectors of its neighboring nodes [38]. Specifically, the GraphSAGE (Graph Sample and Aggregator) [39] is deployed, which is a GNN framework for learning node embeddings in large-scale graphs. The core idea of GraphSAGE is to generate node representations by sampling and aggregating features from a node’s local neighborhood, rather than learning individual embeddings for each node. By recursively aggregating information from sampled neighbors, GraphSAGE captures structural patterns. A modified mean-based aggregator with a convolutional function is used to sample and aggregate features:
In Equation (19), the input of GNN is a vector that includes the information about the adjacency matrix of the power grid, admittance of transmission lines, and loads of all nodes. The output of GNN is called the representation vector.
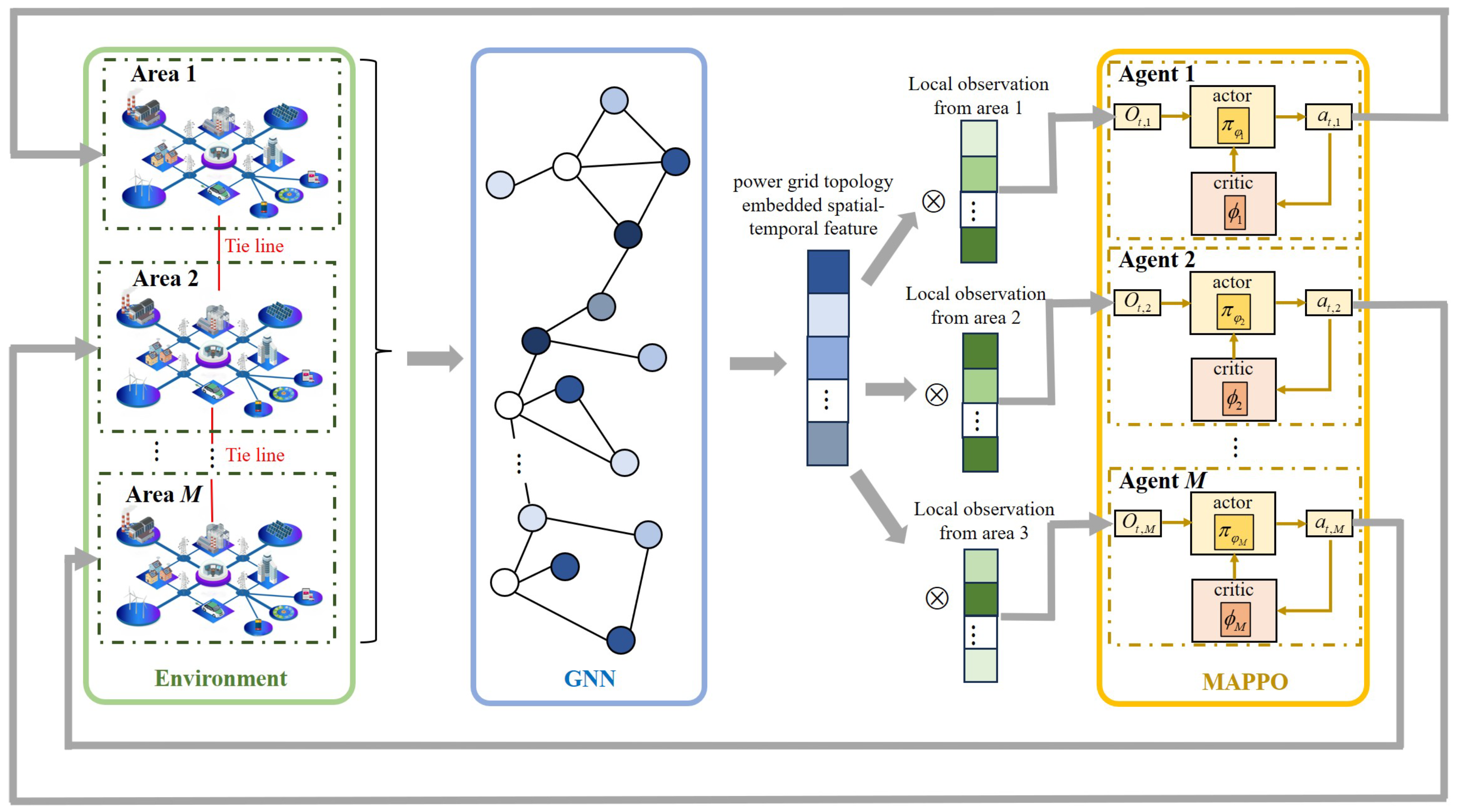
The overall architecture for power flow optimization based on H-MAPPO and GNN is illustrated in Figure 1. With the input including the adjacency matrix of the power grid, admittance of transmission lines, and loads of all nodes, the GNN is employed to extract the topology-embedded spatiotemporal features of the power grid. Subsequently, the features provided by the GNN are multiplied with the local observation from each area to form the inputs for H-MAPPO. Based on the inputs and the trained policy, H-MAPPO determines the action values for the next step, which is fed back into the power system to adjust generator outputs and achieve the OPF.
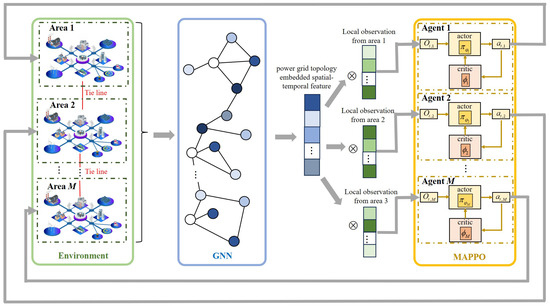
Figure 1.
The architecture of MAPPO- and GNN-based power flow optimization.
4. Simulation and Results
4.1. RTS-Grid Modernization Laboratory Consortium System
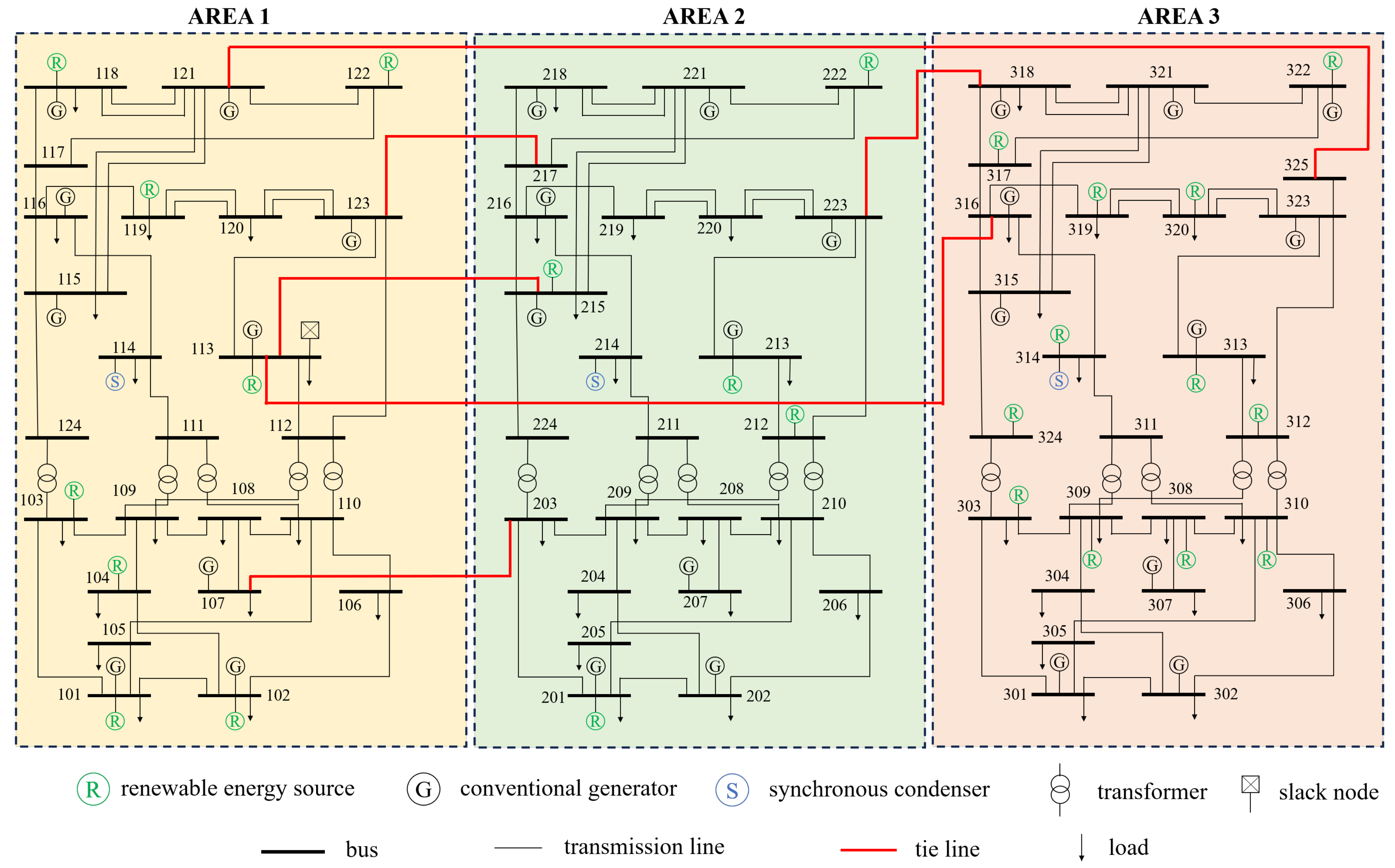
In 2019, the RTS-GMLC system was introduced as an updated version of the RTS-96 test system. The RTS-GMLC system aims to facilitate the study and analysis of challenges in modern power systems including the variability and uncertainty of generation fleets and the flexibility of dispatch processes such as unit commitment and economic dispatch under uncertainty. As shown in Figure 2, the RTS-GMLC system includes 73 buses, 158 generators, 121 branches, and 3 areas connected by 6 tie lines.
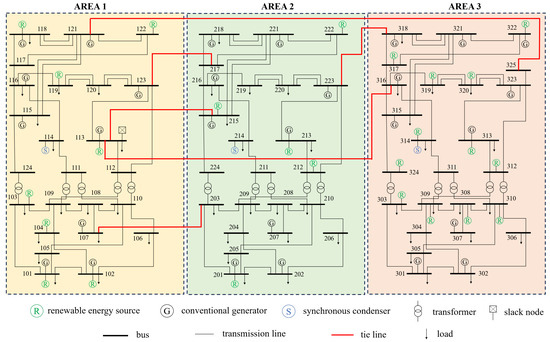
Figure 2.
Diagram of the RTS-GMLC system. Numbers around the buses indicate the bus indices of the RTS-GMLC system.
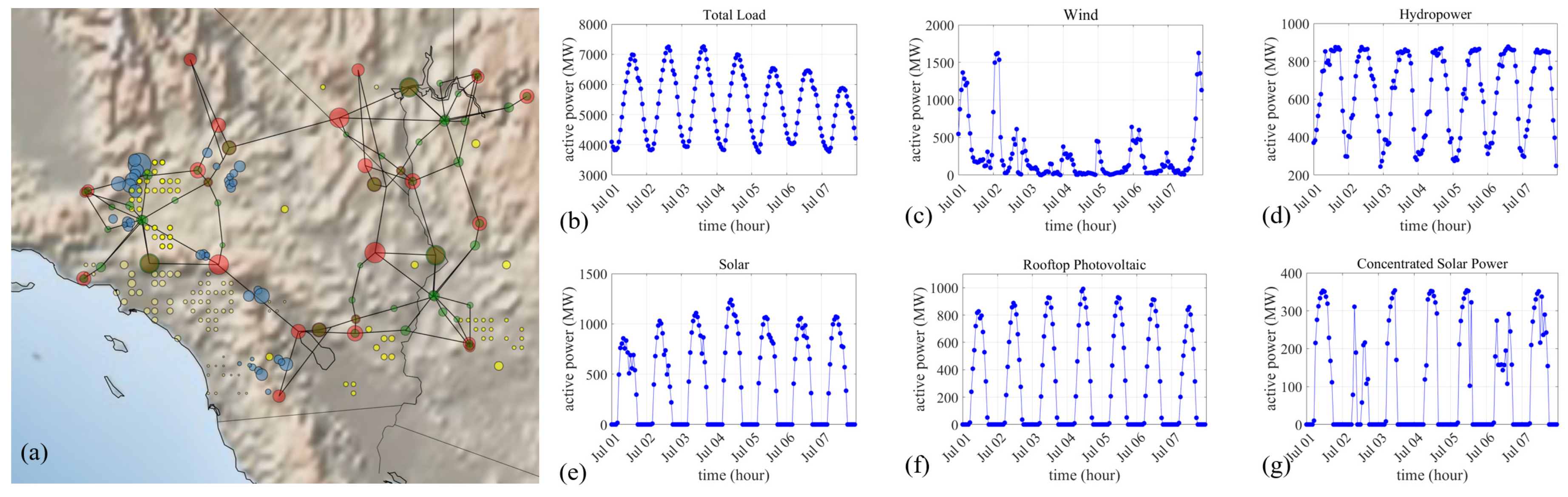
The RTS-GMLC system represents a high spatial and temporal resolution power system with high renewable penetration. For the RTS-GMLC system, monitoring, analysis, and control operations can be carried out with detailed generation, load, and grid topology data across both space and time. The high-resolution capability is essential for addressing the increasing complexity of power systems due to the integration of RESs. As shown in Figure 3a, the geographic location of the power network of the RTS-GMLC model is arbitrarily projected onto nearly 250 square miles in the southwestern United States. With the help of the data from balancing authorities and the Western Wind and Solar Integration Study 2 (WWSIS-2) dataset, the RTS-GMLC model provides a reference for load, solar, wind, rooftop photovoltaic, CSP, and hydrologic time-series [40]. The load and RES time series enable year-long simulations with hourly resolution, e.g., 24 data points each day. A one-week illustration of load and RES time series is shown in Figure 3b–g. Nevertheless, it should be noted that the RTS-GMLC system remains synthetic and does not represent a real-world power system [41].
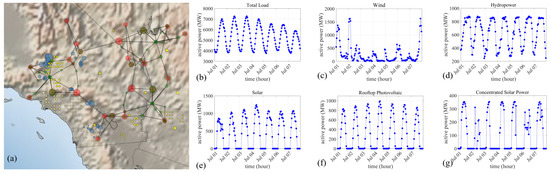
Figure 3.
Spatial–temporal data of the RTS-GMLC system. (a) The geographic location of the RTS-GMLC system. The circles in blue, yellow, and red indicate the locations of wind, solar and hydrologic resources. The green circles indicate the locations of loads. (b) The active power time series of the total load. (c) The active power time series of wind resources. (d) The active power time series of hydropower resources. (e) The active power time series of solar resources. (f) The active power time series of rooftop photovoltaic resources. (g) The active power time series of CSP resources.
4.2. Experimental Setup
The effectiveness and performance of the proposed DRL model are validated by the TRS-GMLC system. The proposed DRL model is realized with PyTorch (2.6.0). The training is conducted on a personal laptop with 13th Gen Intel(R) Core(TM) i9-13900H. The power system environment is built in MATLAB2024b with the MATPOWER toolbox. The load profile and power generation time series from 1 January 2021 to 31 December 2021 are available from the RTS-GMLC system repository [42], which are used to generate the training dataset. The training dataset includes 8784 samples, representing the one-year hourly power flow conditions. With the CTDE framework of the MAPPO, three DRL agents are used for the OPF task. Each agent corresponds to one area in the RTS-GMLC system shown in Figure 2. Each agent takes action on generation power adjustment for the corresponding area. The hyperparameters used to train the proposed DRL model are given in Table 1.

Table 1.
Summary of hyperparameters.
4.3. Results Analysis
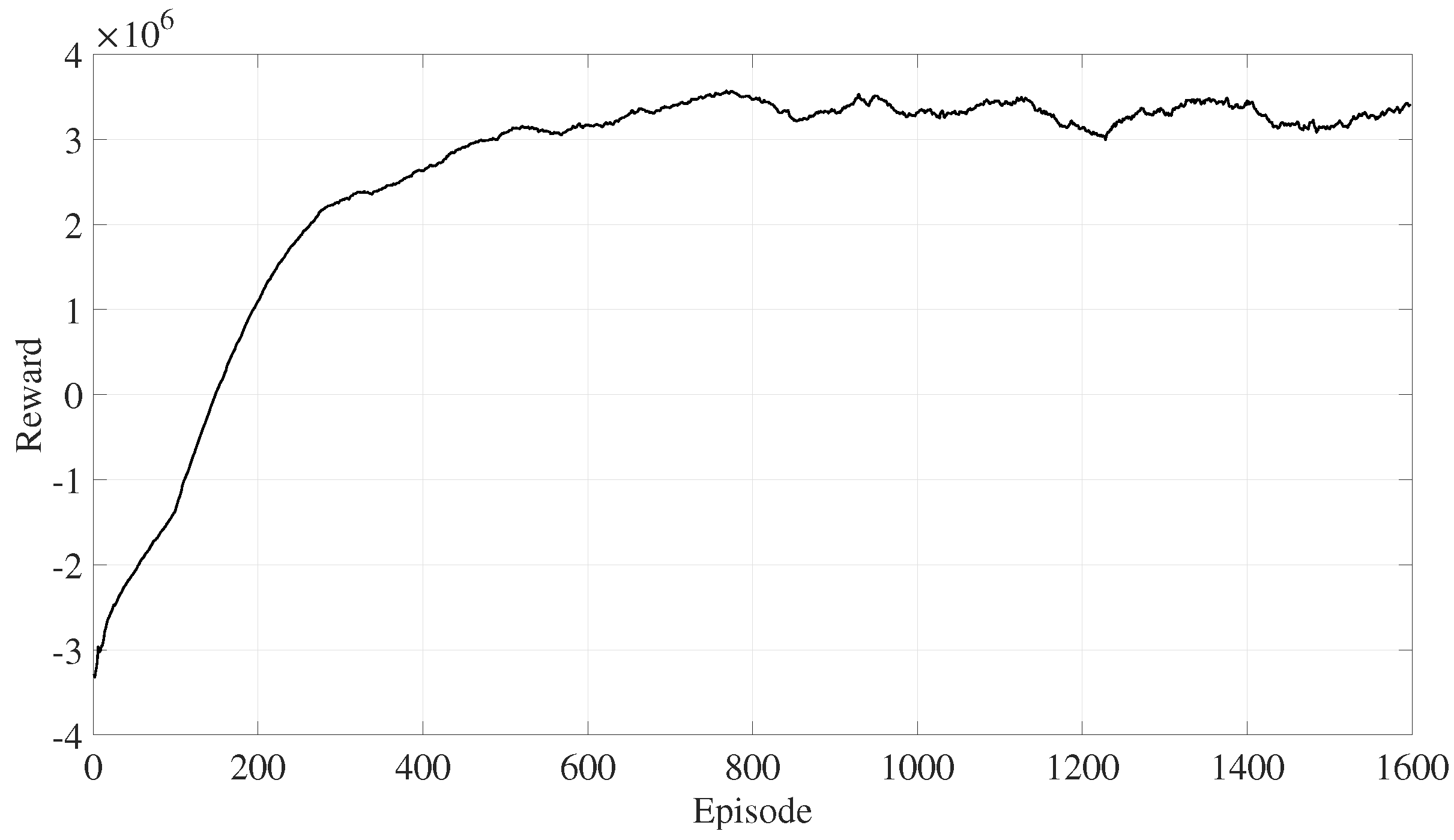
During the training process, the DRL model is updated once per episode with a batch of samples. The reward for an episode is the sum of rewards for all samples in the batch. As shown in Figure 4, the reward for each episode continuously increases and converges to a relatively high reward value after approximately 600 episodes.
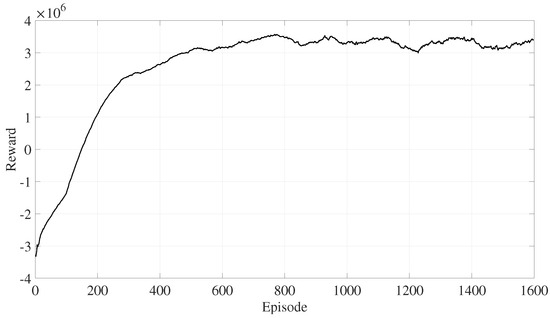
Figure 4.
Reward during the training stage.
Four metrics are used to evaluate the performance: convergence rate, feasibility rate, cost difference, and computing time. The OPF solution is convergent if it satisfies the constraints from Equations (2)–(5). The OPF solution is feasible if it meets all constraints from Equations (6)–(10). Practical power system operation requires OPF solutions that are both converged and feasible. As shown by Equations (20) and (21), the convergence rate and feasibility rate are defined as the ratio of converged and feasible OPF solutions to the total number of samples in the test dataset:
The cost difference refers to the difference between the generation costs determined by the DRL model and MATPOWER. Note that the cost difference is normalized by the generation cost given by MATPOWER. The computing time refers to the time for the DRL model or MATPOWER to obtain an OPF solution.
The performance is tested under scenario A and scenario B. For scenario A and scenario B, the test dataset includes = 2000 samples based on the load profile sampled within and of the default load uniformly at random, respectively. Note that compared with scenario A, the load sampling uncertainty is high in scenario B, increasing the mismatched power and difficulty in finding converged and feasible OPF solutions. In each scenario, the performance of the proposed DRL model after training is compared to that of MATPOWER. It can be found from Table 2 that, for scenario A with low load sampling uncertainty, the performance in terms of convergence, feasibility, and generation cost is similar between the proposed DRL model and MATPOWER, e.g., the convergence rate and feasibility rate are 100% for both proposed DRL model and MATPOWER, and the cost difference is 1.4% ± 0.75%. As shown by Table 3, for scenario B with high load sampling uncertainty, the convergence rate and feasibility rate of the proposed DRL model are still 100% with the similar generation cost given by MATPOWER (cost difference is 1.5% ± 0.75%), while the convergence rate and feasibility rate of the MATPOWER significantly decrease to 68.8%. In addition, for large-scale power systems with high RES penetration, the computational efficiency of OPF methods is essential to maintain power balance under rapid power fluctuations. The proposed DRL model shows a substantially fast decision-making performance. Specifically, for scenario A, the average computing time of the proposed DRL model is 6.7 ms, approximately 37× faster than MATPOWER, and for scenario B, the average computing time of the proposed DRL model is 6.8 ms, approximately 85× faster than MATPOWER. Finally, different random seeds are used to initialize the DRL training process. The corresponding convergence rate and feasibility rate are 100% with the DRL after training, demonstrating robustness against the stochastic nature of DRL algorithms.

Table 2.
Performance comparisons under scenario A.

Table 3.
Performance comparisons under scenario B.
5. Conclusions
For multi-area power systems with a high penetration of RESs, a DRL model using the H-MAPPO framework is proposed to solve the OPF problem. In the proposed DRL model, each agent is responsible for determining the power generation in one area of the power system while all agents collaboratively optimize the overall power flow across the whole power system. A GNN layer is integrated into the model to extract spatiotemporal features of RES fluctuations and grid topologies. The performance of the proposed DRL model is validated using the RTS-GMLC test system, and its results are compared to MATPOWER, which solves the OPF using the interior-point method. The proposed DRL model achieves a 100% convergence rate and feasibility rate. The optimized generation cost is comparable between the DRL model and MATPOWER. Furthermore, the DRL model demonstrates robustness in terms of convergence and feasibility even under high load sampling uncertainty. Additionally, the proposed DRL model exhibits significant computational efficiency, being up to 85 times faster than MATPOWER, thus meeting the real-time requirements for OPF tasks.
Author Contributions
Conceptualization, L.Z.; data curation, H.X.; formal analysis, L.Z. and R.C.; funding acquisition, X.C.; investigation, L.H. and L.L.; methodology, L.Z.; project administration, X.C.; resources, H.X.; software, L.Z. and L.H.; supervision, L.Z. and X.C.; validation, L.H.; visualization, L.L.; writing—original draft, L.H.; writing—review and editing, X.C. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is supported by the project “Research on Multi-sectional Power Flow Online Collaborative Optimization Strategies Based on Graph Neural Networks and Safe Reinforcement Learning (SGTYHT/23-JS-004)” founded by the East China Division, State Grid Corporation of China.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
Authors Liangcai Zhou, Linlin Liu and Hao Xu were employed by the company East China Division, State Grid Corporation of China. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations and Notations
The following abbreviations are used in this manuscript:
| OPF | optimal power flow |
| RES | renewable energy source |
| AI | artificial intelligence |
| DRL | deep reinforcement learning |
| GNN | graph neural network |
| MAPPO | multi-agent proximal policy optimization |
| H-MAPPO | heterogeneous multi-agent proximal policy optimization |
| MDP | Markov decision process |
| CTDE | centralized training and decentralized execution |
| GMLC | Grid Modernization Laboratory Consortium |
| CSP | concentrating solar power |
The following notations are used in this manuscript:
| total cost of power generation | |
| number of generators | |
| active power output of generator k at time t | |
| reactive power output of generator k at time t | |
| quadratic cost function | |
| , , and | coefficients of the cost function |
| net injection of the active power of the ith node at time t | |
| net injection of the reactive power of the ith node at time t | |
| and | sets of neighborhood of node i and node v |
| nodal voltage amplitude of the ith node at time t | |
| angle difference between node i and node j at time t | |
| and | conductance and susceptance of the branch |
| and | upper and lower bounds of the active power outputs of generator k |
| and | upper and lower bounds of the reactive power outputs of generator k |
| active power on the branch | |
| and | upper and lower bounds of active power on the branch |
| and | upper and lower bounds of the voltage amplitude at node i |
| set of transmission sections | |
| set of tie lines in the zth transmission section | |
| and | upper and lower bounds of active power across transmission section z |
| , , and | state space, action space, and state transition probability matrix of the MDP |
| reward function | |
| local observation of area m at time t | |
| M | total areas of the multi-area power system |
| vector of active power output of generators in area m at time t | |
| number of generators in area m | |
| power loss | |
| local observations of area m at time t | |
| local action of area m at time t | |
| active power output adjustment of generator i in area m at time t | |
| , , , and | positive constants of the reward function |
| mismatched power between total generation and total load | |
| loss function of the actor network | |
| importance sampling ratio | |
| clipping function | |
| advantage function | |
| loss function of the critic network | |
| discount factor | |
| r | return at time |
| evaluation of observation at time t | |
| representation vector of node v at the lth layer of GraphSAGE | |
| and | learnable weight matrices of GraphSAGE |
| elementwise mean function | |
| number of samples in the test dataset | |
| number of samples with converged OPF solutions | |
| number of samples with feasible OPF solutions |
References
- Skolfield, J.K.; Escobedo, A.R. Operations research in optimal power flow: A guide to recent and emerging methodologies and applications. Eur. J. Oper. Res. 2022, 300, 387–404. [Google Scholar] [CrossRef]
- Mitrovic, M.; Lukashevich, A.; Vorobev, P.; Terzija, V.; Budennyy, S.; Maximov, Y.; Deka, D. Data-driven stochastic AC-OPF using Gaussian process regression. Int. J. Electr. Power Energy Syst. 2023, 152, 109249. [Google Scholar]
- Chen, Y.; Guo, Z.; Li, H.; Yang, Y.; Tadie, A.T.; Wang, G.; Hou, Y. Probabilistic optimal power flow for day-ahead dispatching of power systems with high-proportion renewable power sources. Sustainability 2020, 12, 518. [Google Scholar] [CrossRef]
- Mhanna, S.; Mancarella, P. An exact sequential linear programming algorithm for the optimal power flow problem. IEEE Trans. Power Syst. 2021, 37, 666–679. [Google Scholar]
- Li, C.; Kies, A.; Zhou, K.; Schlott, M.; El Sayed, O.; Bilousova, M.; Stöcker, H. Optimal Power Flow in a highly renewable power system based on attention neural networks. Appl. Energy 2024, 359, 122779. [Google Scholar]
- Pan, X.; Chen, M.; Zhao, T.; Low, S.H. DeepOPF: A feasibility-optimized deep neural network approach for AC optimal power flow problems. IEEE Syst. J. 2022, 17, 673–683. [Google Scholar]
- Yi, Z.; Wang, X.; Yang, C.; Yang, C.; Niu, M.; Yin, W. Real-time sequential security-constrained optimal power flow: A hybrid knowledge-data-driven reinforcement learning approach. IEEE Trans. Power Syst. 2023, 39, 1664–1680. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Chiang, H.D. On the nonconvex feasible region of optimal power flow: Theory, degree, and impacts. Int. J. Electr. Power Energy Syst. 2024, 161, 110167. [Google Scholar]
- Bescos, B.; Fácil, J.M.; Civera, J.; Neira, J. DynaSLAM: Tracking, mapping, and inpainting in dynamic scenes. IEEE Robot. Autom. Lett. 2018, 3, 4076–4083. [Google Scholar] [CrossRef]
- Chen, X.; Qu, G.; Tang, Y.; Low, S.; Li, N. Reinforcement learning for selective key applications in power systems: Recent advances and future challenges. IEEE Trans. Smart Grid 2022, 13, 2935–2958. [Google Scholar]
- Yan, Z.; Xu, Y. Real-time optimal power flow: A lagrangian based deep reinforcement learning approach. IEEE Trans. Power Syst. 2020, 35, 3270–3273. [Google Scholar]
- Sayed, A.R.; Wang, C.; Anis, H.I.; Bi, T. Feasibility constrained online calculation for real-time optimal power flow: A convex constrained deep reinforcement learning approach. IEEE Trans. Power Syst. 2022, 38, 5215–5227. [Google Scholar]
- Chen, Y.; Du, Q.; Liu, H.; Cheng, L.; Younis, M.S. Improved Proximal Policy Optimization Algorithm for Sequential Security-Constrained Optimal Power Flow Based on Expert Knowledge and Safety Layer. J. Mod. Power Syst. Clean Energy 2023, 12, 742–753. [Google Scholar]
- Zhou, Y.; Lee, W.J.; Diao, R.; Shi, D. Deep reinforcement learning based real-time AC optimal power flow considering uncertainties. J. Mod. Power Syst. Clean Energy 2021, 10, 1098–1109. [Google Scholar]
- Zhou, Y.; Zhang, B.; Xu, C.; Lan, T.; Diao, R.; Shi, D.; Wang, Z.; Lee, W.J. A data-driven method for fast ac optimal power flow solutions via deep reinforcement learning. J. Mod. Power Syst. Clean Energy 2020, 8, 1128–1139. [Google Scholar]
- Perera, A.; Kamalaruban, P. Applications of reinforcement learning in energy systems. Renew. Sustain. Energy Rev. 2021, 137, 110618. [Google Scholar]
- Liu, S.; Luo, W.; Zhou, Y.; Chen, K.; Zhang, Q.; Xu, H.; Guo, Q.; Song, M. Transmission interface power flow adjustment: A deep reinforcement learning approach based on multi-task attribution map. IEEE Trans. Power Syst. 2023, 39, 3324–3335. [Google Scholar]
- Chen, J.; Yu, T.; Pan, Z.; Zhang, M.; Deng, B. A scalable graph reinforcement learning algorithm based stochastic dynamic dispatch of power system under high penetration of renewable energy. Int. J. Electr. Power Energy Syst. 2023, 152, 109212. [Google Scholar]
- Du, W.; Ding, S. A survey on multi-agent deep reinforcement learning: From the perspective of challenges and applications. Artif. Intell. Rev. 2021, 54, 3215–3238. [Google Scholar]
- Zhang, Q.; Dehghanpour, K.; Wang, Z.; Qiu, F.; Zhao, D. Multi-agent safe policy learning for power management of networked microgrids. IEEE Trans. Smart Grid 2020, 12, 1048–1062. [Google Scholar] [CrossRef]
- Jendoubi, I.; Bouffard, F. Multi-agent hierarchical reinforcement learning for energy management. Appl. Energy 2023, 332, 120500. [Google Scholar]
- Hu, D.; Ye, Z.; Gao, Y.; Ye, Z.; Peng, Y.; Yu, N. Multi-agent deep reinforcement learning for voltage control with coordinated active and reactive power optimization. IEEE Trans. Smart Grid 2022, 13, 4873–4886. [Google Scholar]
- Li, J.; Yu, T.; Zhang, X. Coordinated load frequency control of multi-area integrated energy system using multi-agent deep reinforcement learning. Appl. Energy 2022, 306, 117900. [Google Scholar]
- Yan, Z.; Xu, Y. A multi-agent deep reinforcement learning method for cooperative load frequency control of a multi-area power system. IEEE Trans. Power Syst. 2020, 35, 4599–4608. [Google Scholar]
- Gao, F.; Xu, Z.; Yin, L. Bayesian deep neural networks for spatio-temporal probabilistic optimal power flow with multi-source renewable energy. Appl. Energy 2024, 353, 122106. [Google Scholar]
- Noorizadegan, A.; Cavoretto, R.; Young, D.; Chen, C. Stable weight updating: A key to reliable PDE solutions using deep learning. Eng. Anal. Bound. Elem. 2024, 168, 105933. [Google Scholar]
- Zhang, R.; Xu, N.; Zhang, K.; Wang, L.; Lu, G. A parametric physics-informed deep learning method for probabilistic design of thermal protection systems. Energies 2023, 16, 3820. [Google Scholar] [CrossRef]
- Huang, B.; Wang, J. Applications of physics-informed neural networks in power systems-a review. IEEE Trans. Power Syst. 2022, 38, 572–588. [Google Scholar]
- Liao, W.; Bak-Jensen, B.; Pillai, J.R.; Wang, Y.; Wang, Y. A review of graph neural networks and their applications in power systems. J. Mod. Power Syst. Clean Energy 2021, 10, 345–360. [Google Scholar]
- Sun, P.; Huo, L.; Chen, X.; Liang, S. Rotor Angle Stability Prediction using Temporal and Topological Embedding Deep Neural Network Based on Grid-Informed Adjacency Matrix. J. Mod. Power Syst. Clean Energy 2023. [Google Scholar]
- Gao, M.; Yu, J.; Yang, Z.; Zhao, J. Physics embedded graph convolution neural network for power flow calculation considering uncertain injections and topology. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 15467–15478. [Google Scholar]
- Falconer, T.; Mones, L. Leveraging power grid topology in machine learning assisted optimal power flow. IEEE Trans. Power Syst. 2022, 38, 2234–2246. [Google Scholar] [CrossRef]
- Hansen, J.B.; Anfinsen, S.N.; Bianchi, F.M. Power flow balancing with decentralized graph neural networks. IEEE Trans. Power Syst. 2022, 38, 2423–2433. [Google Scholar] [CrossRef]
- Sayed, A.R.; Zhang, X.; Wang, G.; Wang, C.; Qiu, J. Optimal operable power flow: Sample-efficient holomorphic embedding-based reinforcement learning. IEEE Trans. Power Syst. 2023, 39, 1739–1751. [Google Scholar]
- Shixin, Z.; Feng, P.; Anni, J.; Hao, Z.; Qiuqi, G. The unmanned vehicle on-ramp merging model based on AM-MAPPO algorithm. Sci. Rep. 2024, 14, 19416. [Google Scholar] [CrossRef]
- Peng, R.; Chen, S.; Xue, C. Collaborative Content Caching Algorithm for Large-Scale ISTNs Based on MAPPO. IEEE Wirel. Commun. Lett. 2024, 13, 3069–3073. [Google Scholar]
- Liu, X.; Yin, Y.; Su, Y.; Ming, R. A multi-UCAV cooperative decision-making method based on an MAPPO algorithm for beyond-visual-range air combat. Aerospace 2022, 9, 563. [Google Scholar] [CrossRef]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1025–1035. [Google Scholar]
- Barrows, C.; Bloom, A.; Ehlen, A.; Ikäheimo, J.; Jorgenson, J.; Krishnamurthy, D.; Lau, J.; McBennett, B.; O’Connell, M.; Preston, E.; et al. The IEEE reliability test system: A proposed 2019 update. IEEE Trans. Power Syst. 2019, 35, 119–127. [Google Scholar]
- Karmakar, A.; Cole, W. Nodal Capacity Expansion Modeling with ReEDS: A Case Study of the RTS-GMLC Test System; Technical report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2024.
- Preston, G. Repository for the TRS-GMLC System. 2024. Available online: https://github.com/GridMod/RTS-GMLC (accessed on 7 December 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).