Quasi-Static Tractor Implement Model for Assessing Energy Savings in Partial Electrification
Abstract
1. Introduction
2. Methodology
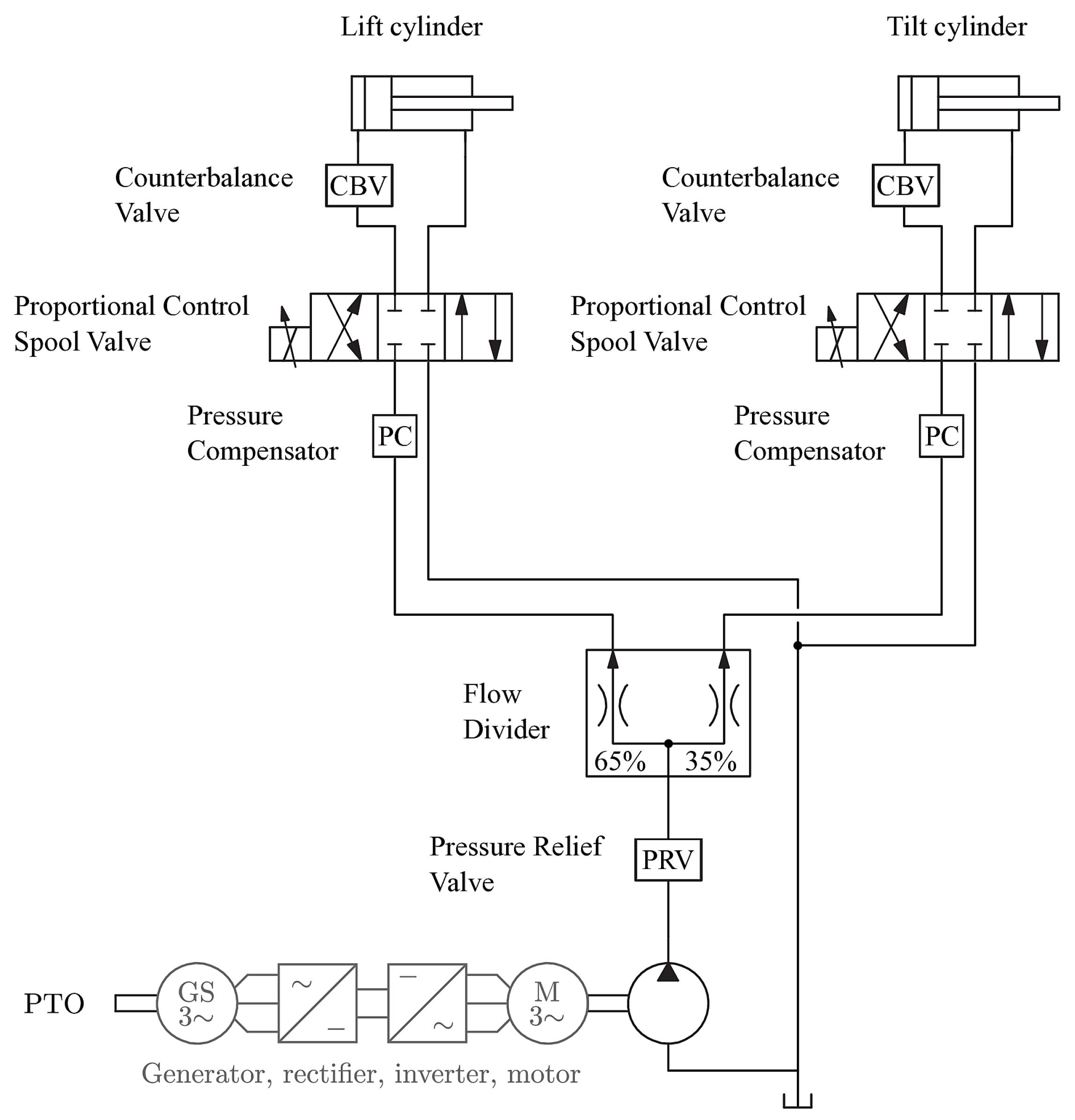
2.1. Tractor Implement Under Study
2.2. Experimental Tests Performed on the Implement
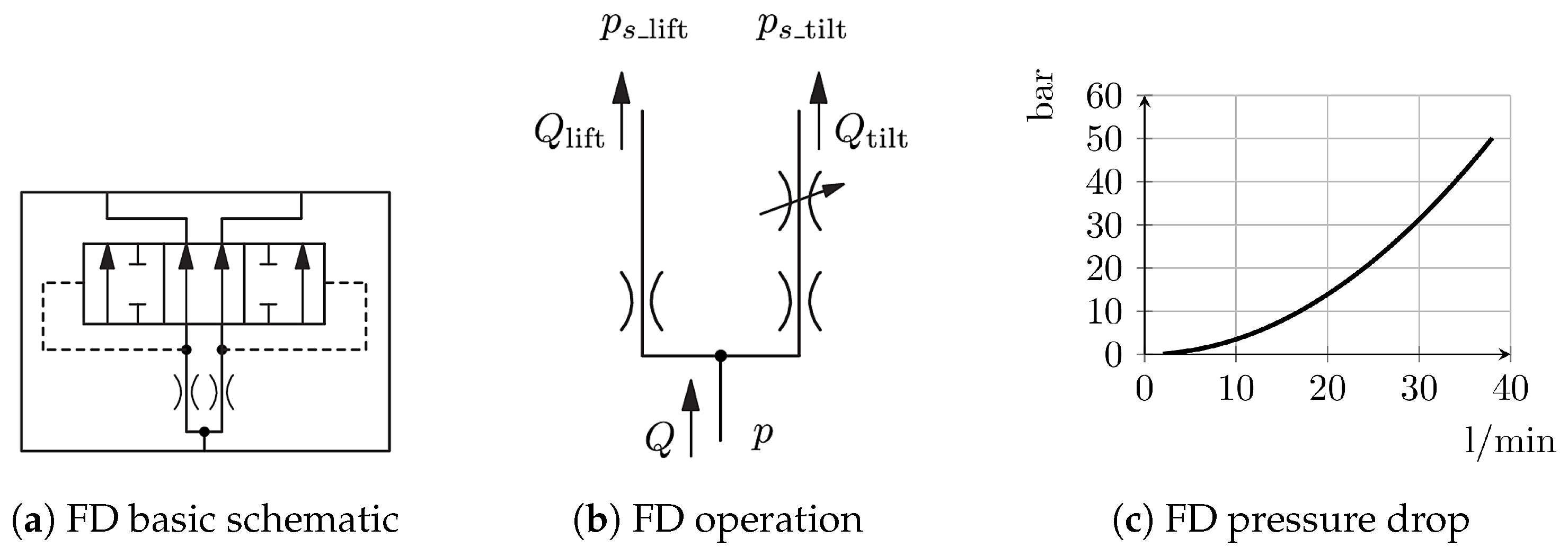
2.3. Quasi-Static Model of the Hydraulic Circuit
- Each valve’s metering orifice is modeled as a turbulent flow orifice, as commonly carried out in the literature [34].
- Identical parameters ( and in (1)) are used for both the flow paths of the control valve during extension (P-A and B-T) and retraction (P-B and A-T).
- Pressure drop through check valves is negligible when flow is permitted.
- Leakage, mechanical friction, and compressibility effects are considered negligible.
- Tank pressure is assumed to be zero.
- Actuator force and speed are known.
- A constant pressure drop is maintained across the inlet orifice (load sensing): during extension—− = ; during retraction—− = , where is the desired pressure margin, kept constant to ensure a unique correlation between valve spool displacement and flow rate.
- No regeneration occurs; all fluid leaving the cylinder goes to the tank.
- No energy recovery is considered.
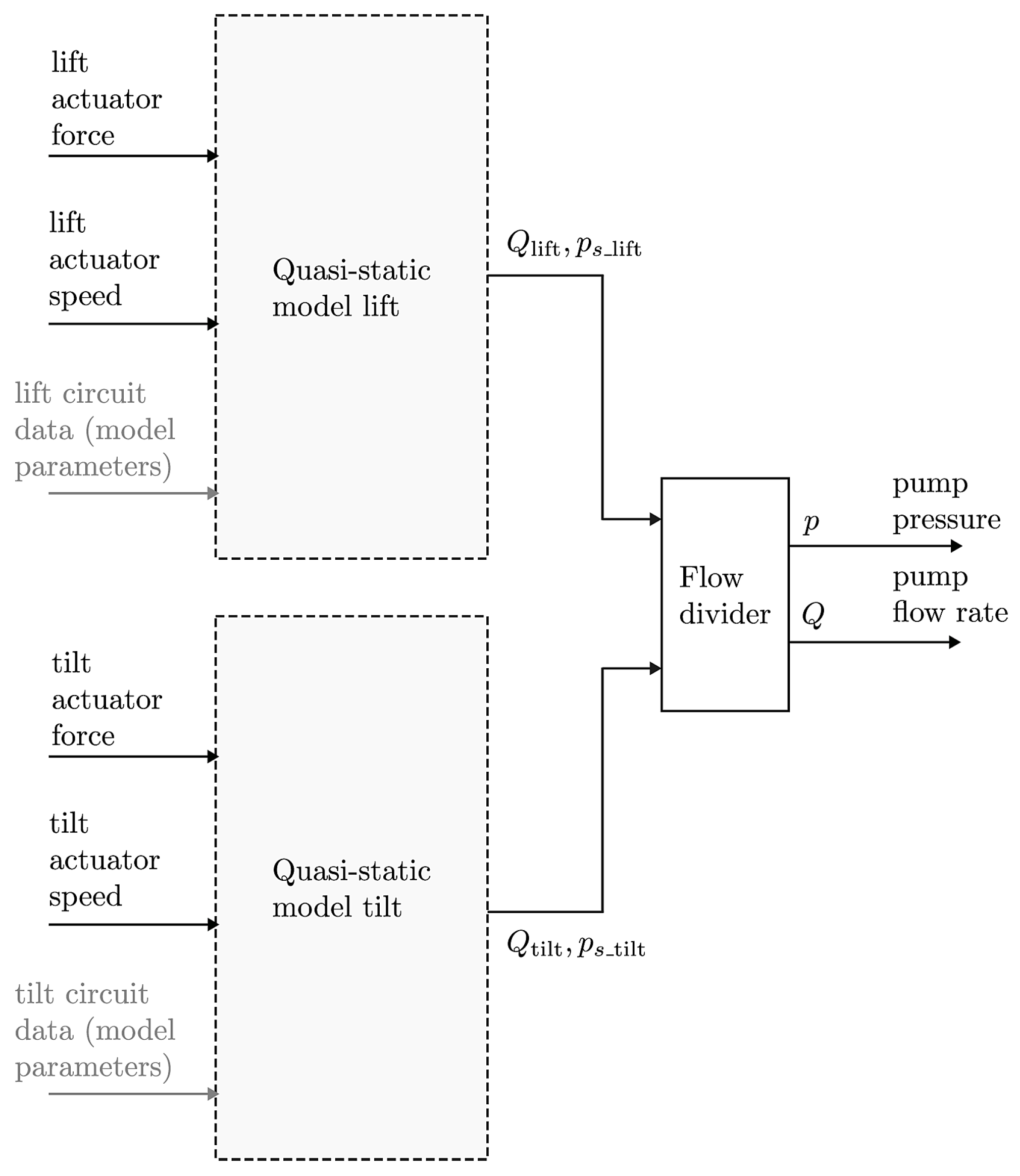
2.4. Extension of the Quasi-Static Model for Two Cylinders
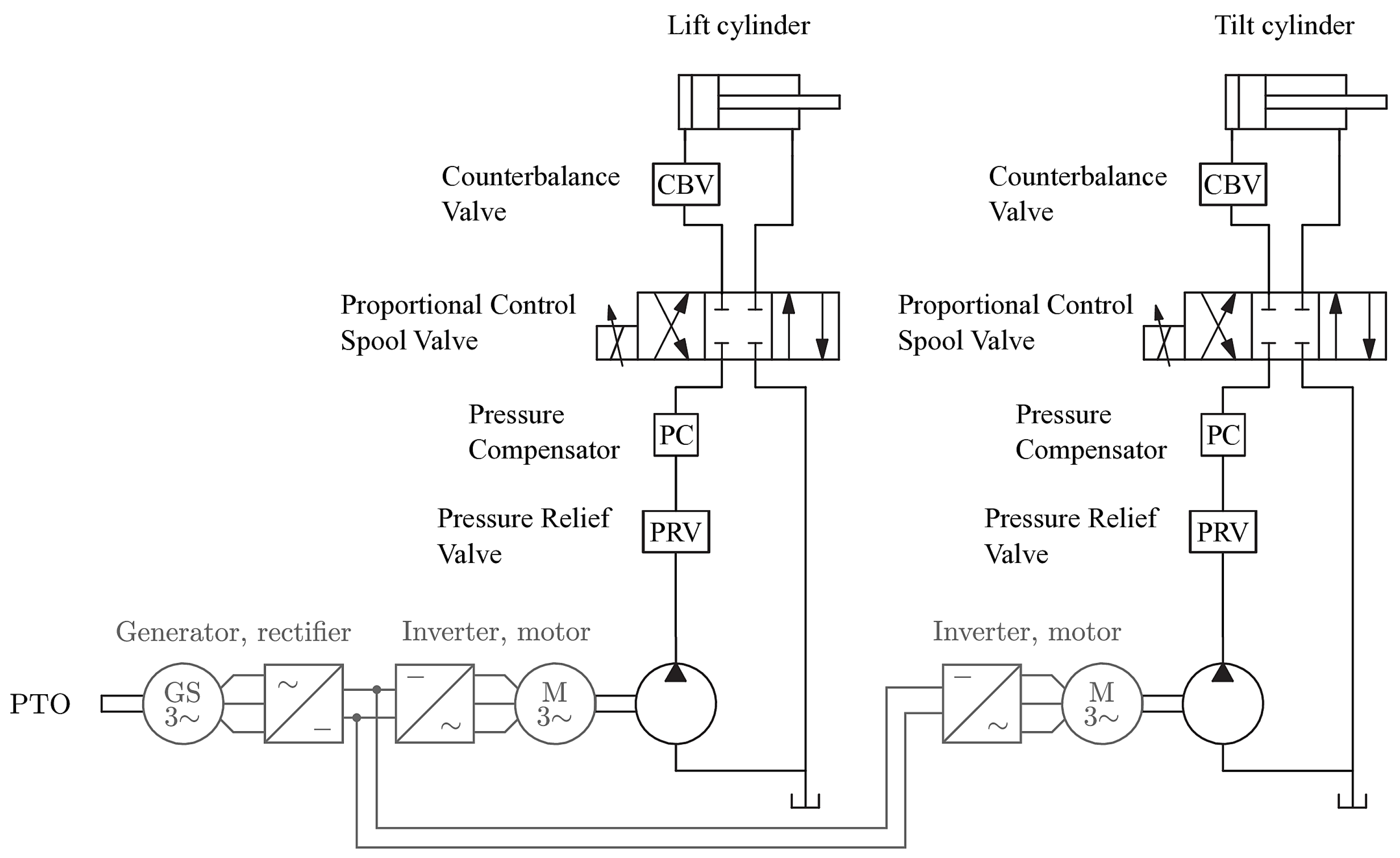
2.5. Proposed Electrification Schemes
- At fixed speed.
- At variable speed (first electrification scheme).
- At variable speed (second electrification scheme).
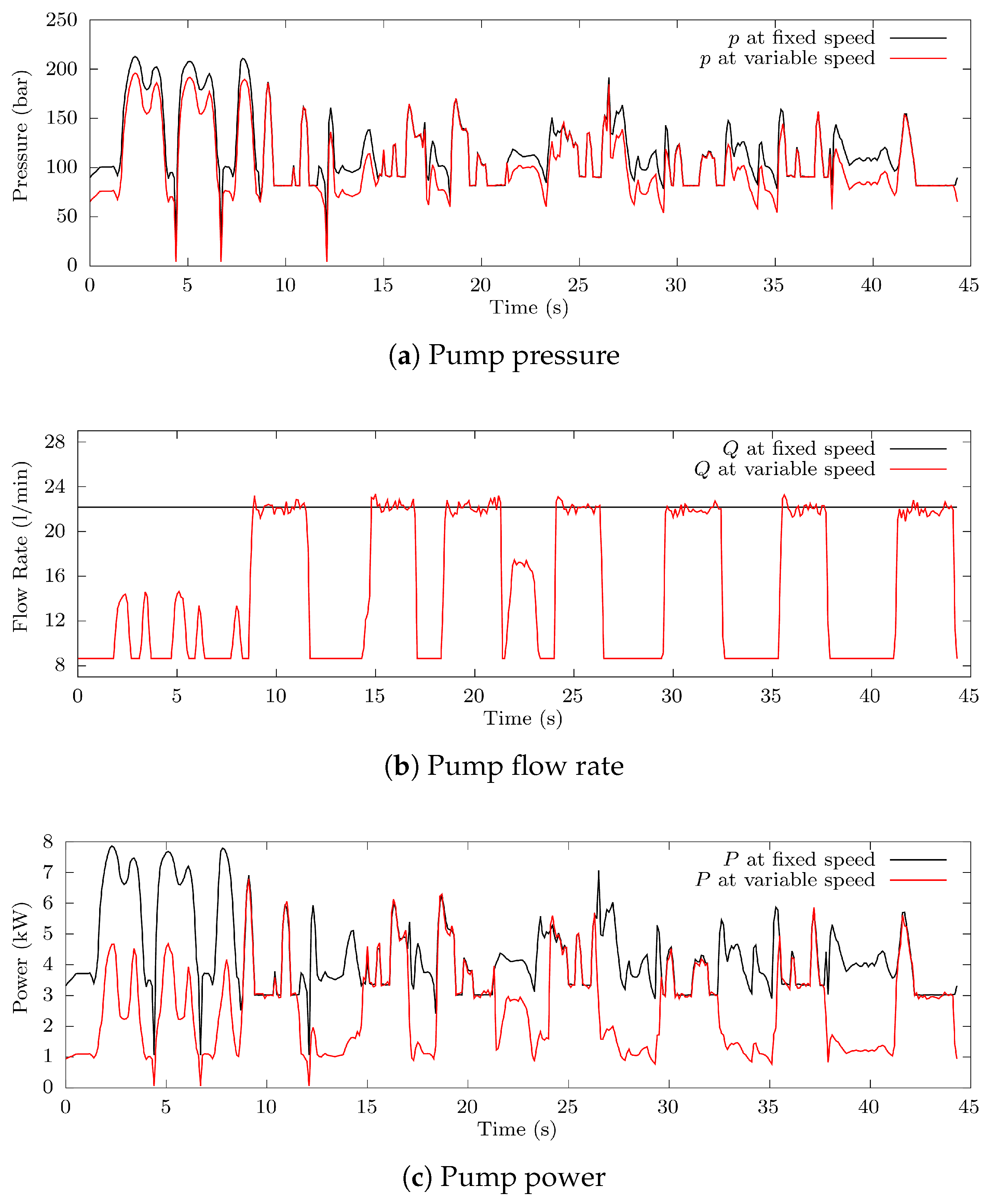
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moreda, G.P.; noz García, M.A.M.; Barreiro, P. High voltage electrification of tractor and agricultural machinery—A review. Energy Convers. Manag. 2016, 115, 117–131. [Google Scholar] [CrossRef]
- Scolaro, E.; Beligoj, M.; Estevez, M.P.; Alberti, L.; Renzi, M.; Mattetti, M. Electrification of Agricultural Machinery: A Review. IEEE Access 2021, 9, 164520–164541. [Google Scholar] [CrossRef]
- Un-Noor, F.; Wu, G.; Perugu, H.; Collier, S.; Yoon, S.; Barth, M.; Boriboonsomsin, K. Off-Road Construction and Agricultural Equipment Electrification: Review, Challenges, and Opportunities. Vehicles 2022, 4, 780–807. [Google Scholar] [CrossRef]
- Mocera, F.; Somà, A.; Martelli, S.; Martini, V. Trends and Future Perspective of Electrification in Agricultural Tractor-Implement Applications. Energies 2023, 16, 6601. [Google Scholar] [CrossRef]
- Buning, E.A. Electric drives in agricultural machinery—Approach from the tractor side. J. Agric. Eng. 2010, 47, 30–35. [Google Scholar]
- Tritschler, P.J.; Bacha, S.; Rullière, E.; Husson, G. Energy management strategies for an embedded fuel cell system on agricultural vehicles. In Proceedings of the The XIX International Conference on Electrical Machines—(ICEM 2010), Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Stempfer, G.; Bebeti, M.; Himmelsbach, R.; Volpert, B. Electrification in agricultural engineering technologies and synergies. Atzoffhighway Worldw. 2017, 10, 66–69. [Google Scholar] [CrossRef]
- Minav, T.; Lehmuspelto, T.; Sainio, P.; Pietola, M. Series Hybrid Mining Loader with Zonal Hydraulics. In Proceedings of the 10th International Fluid Power Conference, Dresden, Germany, 8–10 March 2016; pp. 211–224. [Google Scholar]
- Beligoj, M.; Scolaro, E.; Alberti, L.; Renzi, M.; Mattetti, M. Feasibility Evaluation of Hybrid Electric Agricultural Tractors Based on Life Cycle Cost Analysis. IEEE Access 2022, 10, 28853–28867. [Google Scholar] [CrossRef]
- Perez Estevez, M.A.; Melendez Frigola, J.; Armengol Llobet, J.; Alberti, L.; Renzi, M. Optimal design of a series hybrid powertrain for an agricultural tractor. Energy Convers. Manag. X 2024, 24, 100789. [Google Scholar] [CrossRef]
- Mattetti, M.; Annesi, G.; Intrevado, F.P.; Alberti, L. Investigating the efficiency of hybrid architectures for agricultural tractors using real-world farming data. Appl. Energy 2025, 377, 124499. [Google Scholar] [CrossRef]
- Renius, K.T. Fundamentals of Tractor Design; Springer Charm: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Stoss, K.J.; Sobotzik, J.; Shi, B.; Kreis, E.R. Tractor Power for Implement Operation-Mechanical, Hydraulic, and Electrical: An Overview. In Proceedings of the 2013 Agricultural Equipment Technology Conference, Kansas City, MO, USA, 28–30 January 2013; American Society of Agricultural and Biological Engineers (ASABE): St. Joseph, MI, USA, 2013. [Google Scholar]
- Gonzalez de-Soto, M.; Emmi, L.; Benavides, C.; Garcia, I.; Gonzalez de-Santos, P. Reducing air pollution with hybrid-powered robotic tractors for precision agriculture. Biosyst. Eng. 2016, 143, 79–94. [Google Scholar] [CrossRef]
- Engström, J.; Lagnelöv, O. An Autonomous Electric Powered Tractor–Simulation of All Operations on a Swedish Dairy Farm. J. Agric. Sci. Technol. 2018, 8, 182–187. [Google Scholar] [CrossRef]
- Lajunen, A.; Sainio, P.; Laurila, L.; Pippuri-Mäkeläinen, J.; Tammi, K. Overview of Powertrain Electrification and Future Scenarios for Non-Road Mobile Machinery. Energies 2018, 11, 1184. [Google Scholar] [CrossRef]
- Pickel, P. Electricity for tractors and tractor-implement systems. In Proceedings of the 29th Members Meeting, Hannover, Germany, 10–11 November 2019. [Google Scholar]
- Cisternas, I.; Velásquez, I.; Caro, A.; Rodríguez, A. Systematic literature review of implementations of precision agriculture. Comput. Electron. Agric. 2020, 176, 105626. [Google Scholar] [CrossRef]
- Prabhakaran, A.; Chithra Lekshmi, K.S.; Janarthanan, G. Advancement of data mining methods for improvement of agricultural methods and productivity. In Artificial Intelligence in Data Mining; Binu, D., Rajakumar, B.R., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 199–221. [Google Scholar]
- Belforte, G.; Deboli, R.; Gay, P.; Piccarolo, P.; Ricauda Aimonino, D. Robot Design and Testing for Greenhouse Applications. Biosyst. Eng. 2006, 95, 309–321. [Google Scholar] [CrossRef]
- Escolà, A.; Rosell-Polo, J.R.; Planas, S.; Gil, E.; Pomar, J.; Camp, F.; Llorens, J.; Solanelles, F. Variable rate sprayer. Part 1—Orchard prototype: Design, implementation and validation. Comput. Electron. Agric. 2013, 95, 122–135. [Google Scholar] [CrossRef]
- Bechar, A.; Vigneault, C. Agricultural robots for field operations: Concepts and components. Biosyst. Eng. 2016, 149, 94–111. [Google Scholar] [CrossRef]
- Comba, L.; Biglia, A.; Sopegno, A.; Grella, M.; Dicembrini, E.; Ricauda Aimonino, D.; Gay, P. Convolutional Neural Network Based Detection of Chestnut Burrs in UAV Aerial Imagery. In Proceedings of the AIIA 2022: Biosystems Engineering Towards the Green Deal, Palermo, Italy, 19–22 September 2022; Ferro, V., Giordano, G., Orlando, S., Vallone, M., Cascone, G., Porto, S.M.C., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 501–508. [Google Scholar]
- Hahn, K. High Voltage Electric Tractor-Implement Interface. SAE Int. J. Commer. Veh. 2008, 1, 383–391. [Google Scholar] [CrossRef]
- Rauch, N. Experiences and visions of an implement manufacturer. Agric. Eng. Today 2010, 35, 3–9. [Google Scholar]
- Rahe, F.; Resch, R. Electrification of Agricultural Machinery From the Perspective of an Implement Manufacturer. In Proceedings of the 9th AVL International Commercial Powertrain Conference 2017, Messe Congress Graz, Austria, 10–11 May 2017. [Google Scholar]
- Bals, R.; Jünemann, D.; Berghaus, A. Partial Electrification of an Agricultural Implement. Atzheavy Duty Worldw. 2019, 12, 38–41. [Google Scholar] [CrossRef]
- Varani, M.; Mattetti, M.; Molari, G. Performance Evaluation of Electrically Driven Agricultural Implements Powered by an External Generator. Agronomy 2021, 11, 1447. [Google Scholar] [CrossRef]
- Magnusson, J.; Eric, P. Electrifying Agricultural Implements: A Study of Design Implications of Electrification. Master’s Thesis, Jönköping University, Jönköping, Sweden, 2023. [Google Scholar]
- Tian, X.; Jenkins, R.; Lengacher, J.; Vacca, A.; Fiorati, S.; Pintore, F.; Cristofori, D. An Analysis of Mixed Hydraulic and Electric Configurations for the Actuation of Tractor Auxiliary and Implement Functions to Reduce Power Consumption. In Proceedings of the LAND.TECHNIK AgEng 2023, Hannover, Germany, 10 November 2023; pp. 1–14. [Google Scholar]
- Grossi, F.; Cittadella, M.; Biagiotti, L.; Mariniello, C. Improving Efficiency of Farming Tractor Implement by Electrification. In Proceedings of the 2024 IEEE Vehicle Power and Propulsion Conference (VPPC), Washington, DC, USA, 7–10 October 2024; pp. 1–6. [Google Scholar]
- Khatti, R.; Plate, J. Allis-Chalmers Load-Sensitive Hydraulic System for Tractor-Implement Control. Trans. ASABE 1974, 17, 851–855. [Google Scholar] [CrossRef]
- Beligoj, M.; Zava, M.; Alberti, L.; Termini, A. Hydraulics Decentralization on a Mobile Crane. In Proceedings of the 2022 Second International Conference on Sustainable Mobility Applications, Renewables and Technology (SMART), Cassino, Italy, 23–25 November 2022; pp. 1–9. [Google Scholar]
- Vacca, A.; Franzoni, G. Hydraulic Fluid Power: Fundamentals, Applications, and Circuit Design; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]


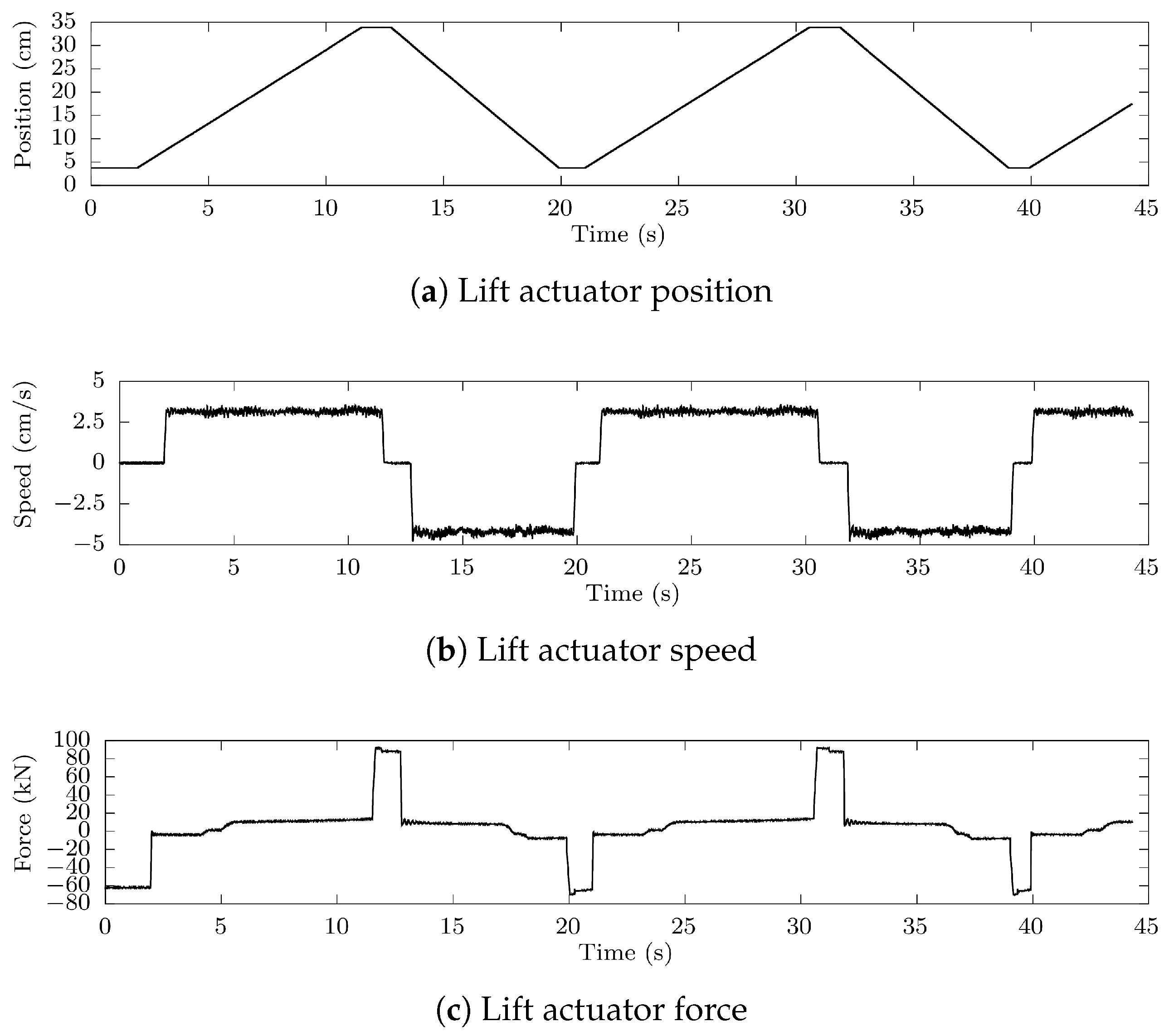
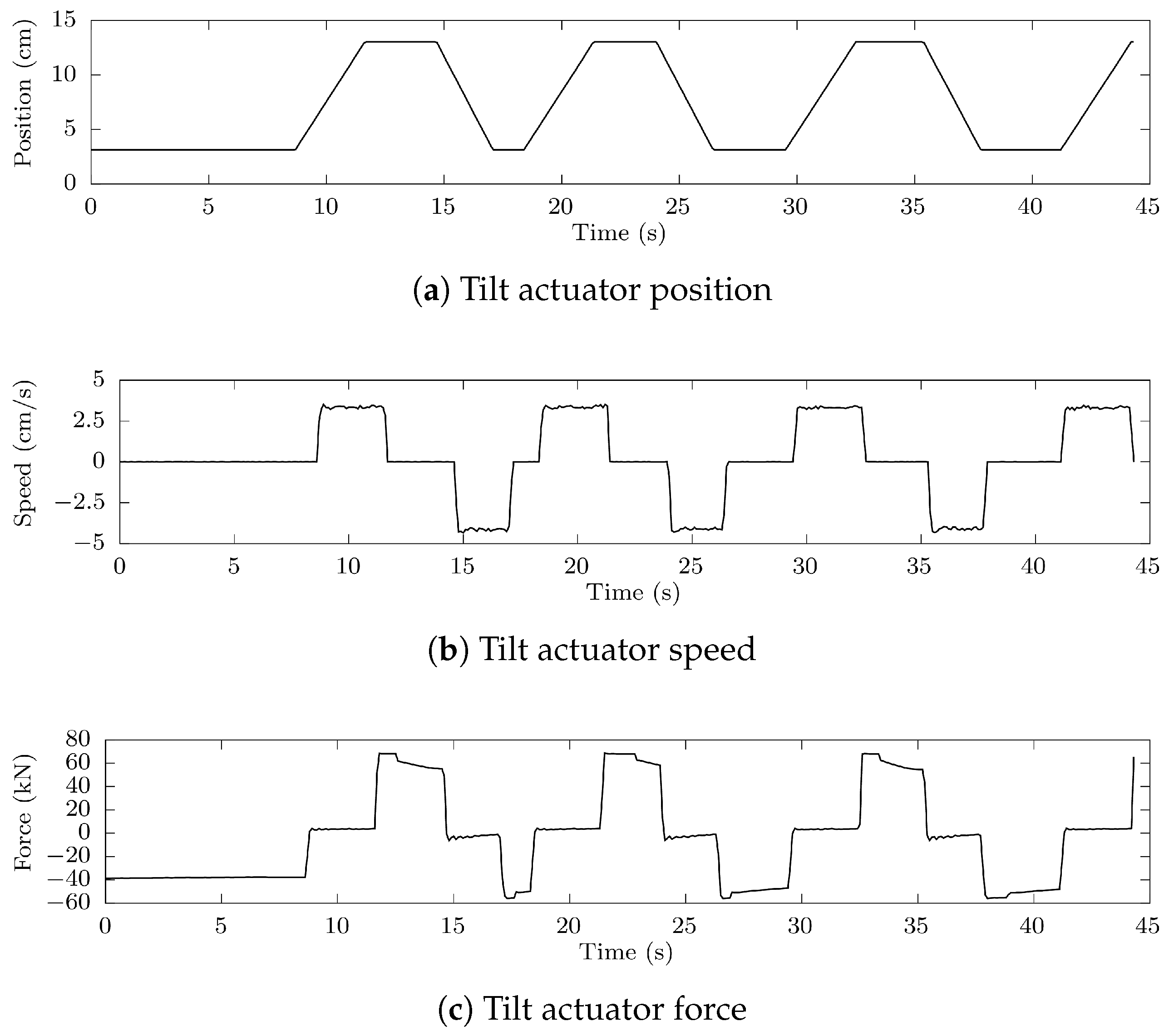
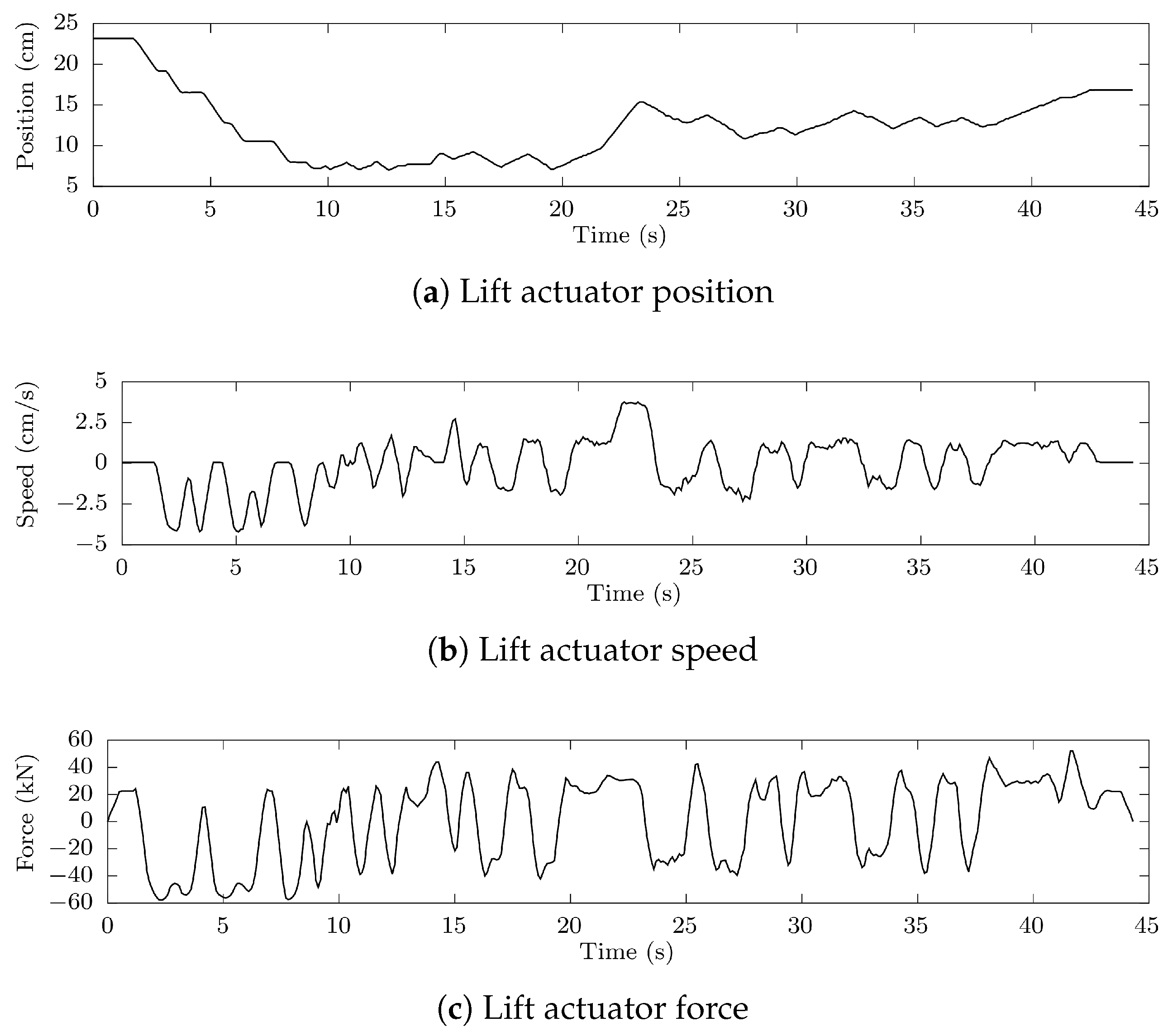


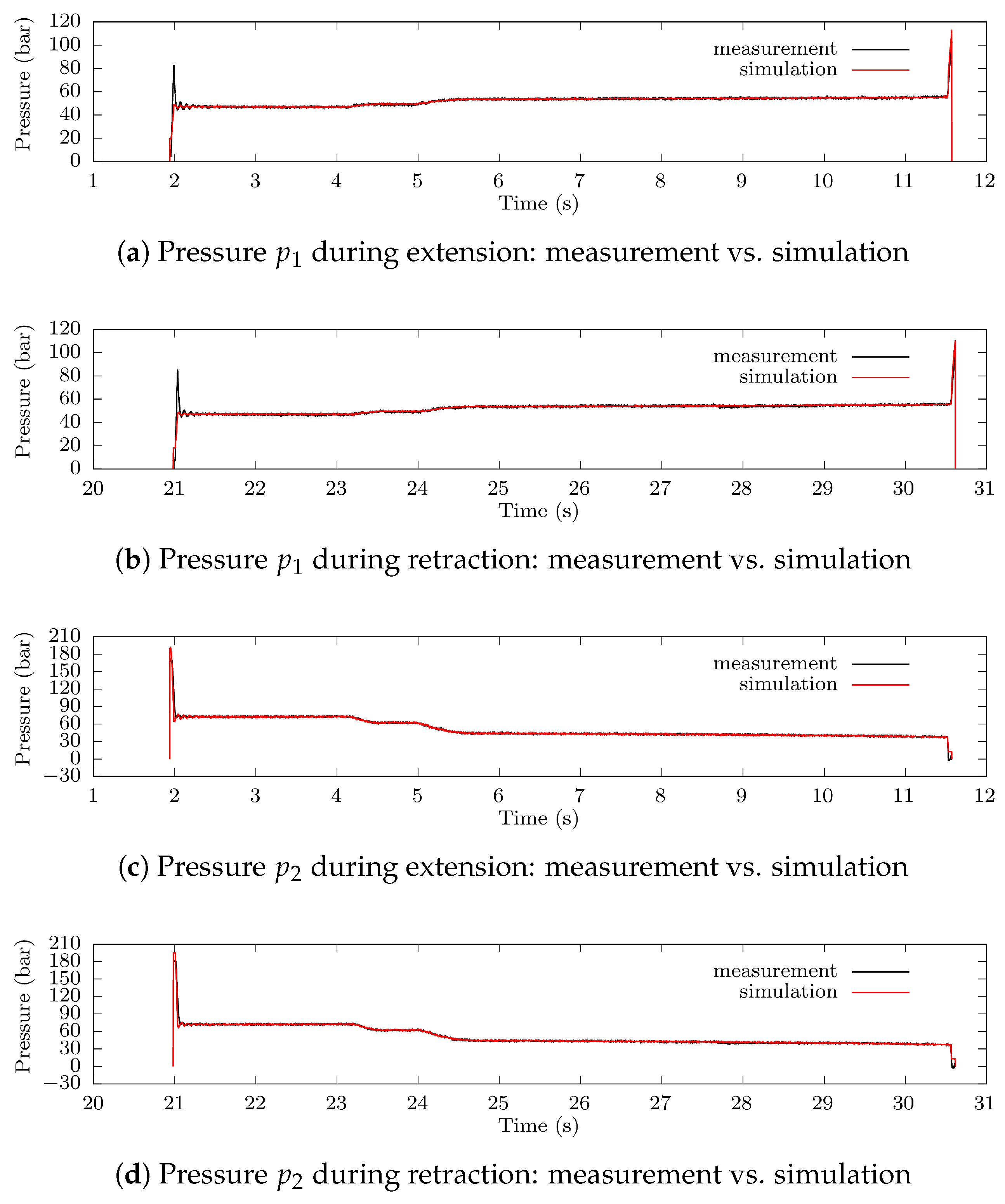
| Lift | Tilt | PTO Total Energy at Fixed Speed (Original Circuit) | PTO Total Energy at Variable Speed (First Electrification Scheme) | Energy Savings |
|---|---|---|---|---|
| Field test | Indoor test | 202.65 kJ | 157 kJ | 22.5% |
| Indoor test | Indoor test | 146.09 kJ | 132.76 kJ | 9.1% |
| Lift | Tilt | PTO Total Energy at Fixed Speed Centralized (Original Circuit) | PTO Total Energy at Variable Speed Decentralized (Second Electrification Scheme) | Energy Savings |
|---|---|---|---|---|
| Field test | Indoor test | 202.65 kJ | 94.36 kJ | 53.4% |
| Indoor test | Indoor test | 146.09 kJ | 80.31 kJ | 45% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berto, M.; Beligoj, M.; Alberti, L. Quasi-Static Tractor Implement Model for Assessing Energy Savings in Partial Electrification. Energies 2025, 18, 2766. https://doi.org/10.3390/en18112766
Berto M, Beligoj M, Alberti L. Quasi-Static Tractor Implement Model for Assessing Energy Savings in Partial Electrification. Energies. 2025; 18(11):2766. https://doi.org/10.3390/en18112766
Chicago/Turabian StyleBerto, Matteo, Matteo Beligoj, and Luigi Alberti. 2025. "Quasi-Static Tractor Implement Model for Assessing Energy Savings in Partial Electrification" Energies 18, no. 11: 2766. https://doi.org/10.3390/en18112766
APA StyleBerto, M., Beligoj, M., & Alberti, L. (2025). Quasi-Static Tractor Implement Model for Assessing Energy Savings in Partial Electrification. Energies, 18(11), 2766. https://doi.org/10.3390/en18112766








