A Trusted Sharing Strategy for Electricity in Multi-Virtual Power Plants Based on Dual-Chain Blockchain
Abstract
1. Introduction
2. Electricity Energy Trading Architecture and Optimization Model
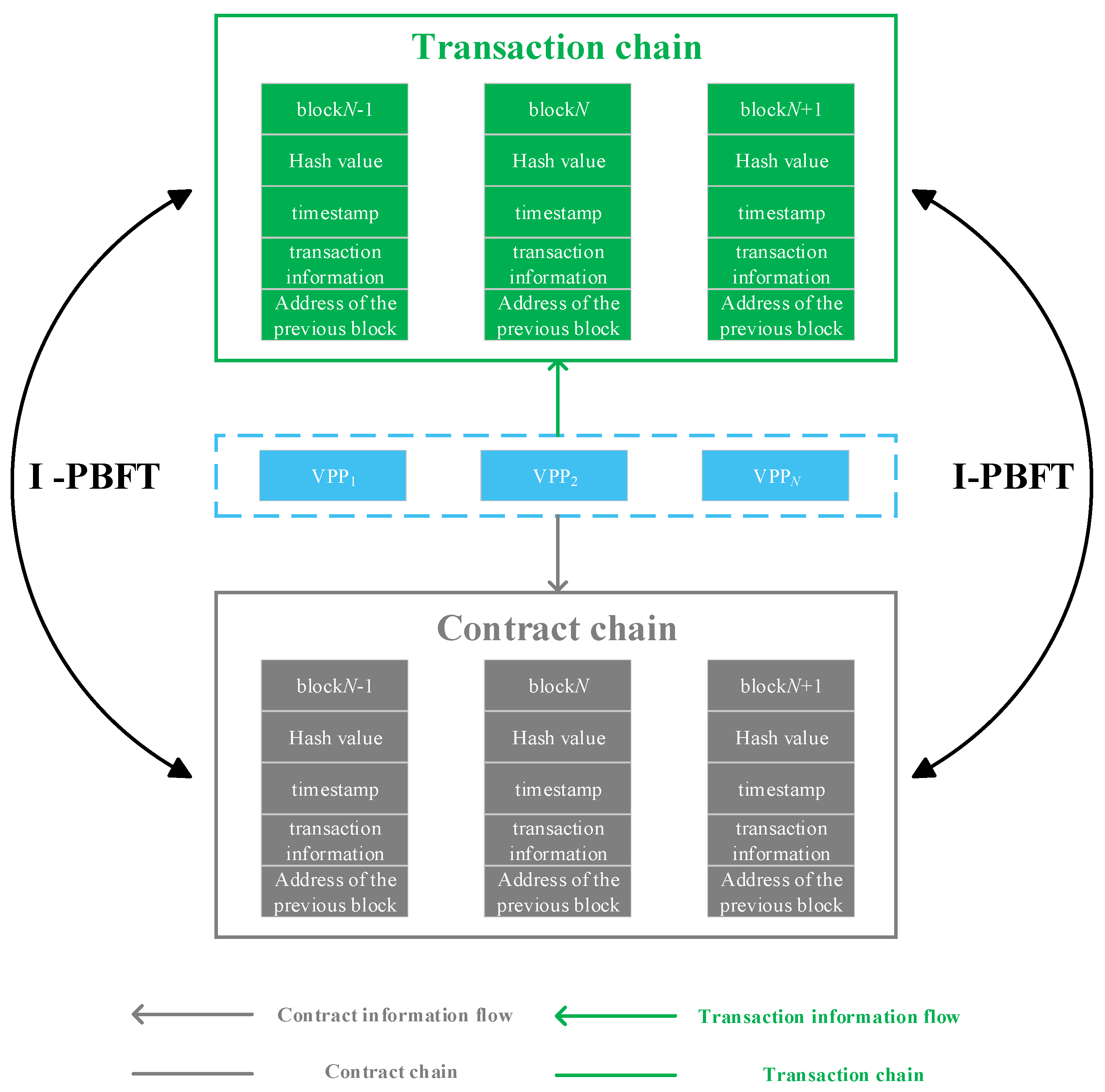
2.1. Dual-Chain Blockchain-Based Architecture for Electricity Trading
2.2. Multi-VPP Trading Decision Model
2.2.1. Single VPP Running Costs Models
2.2.2. Nash Negotiation-Based Multi-VPP Electricity Sharing Transaction Decision Modeling
3. Blockchain Implementation of Multi-VPP Power Sharing Transactions
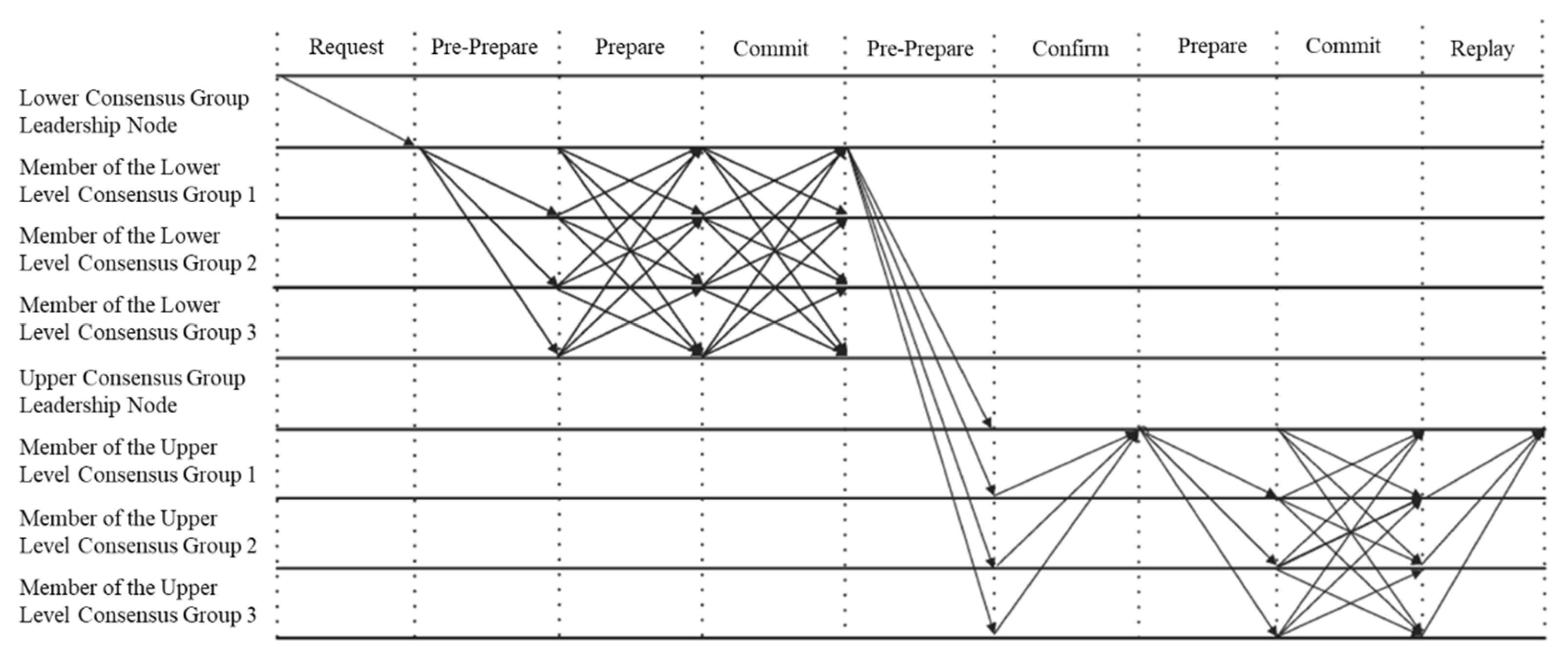
3.1. I-PBFT Consensus Algorithm Execution Process
3.1.1. Secret Key Negotiation Algorithm for Zero Knowledge Based Authentication
3.1.2. I-PBFT Consensus Algorithm Execution Process
3.1.3. I-PBFT Consensus Algorithm Attack Resistance Mechanism and Security Analysis
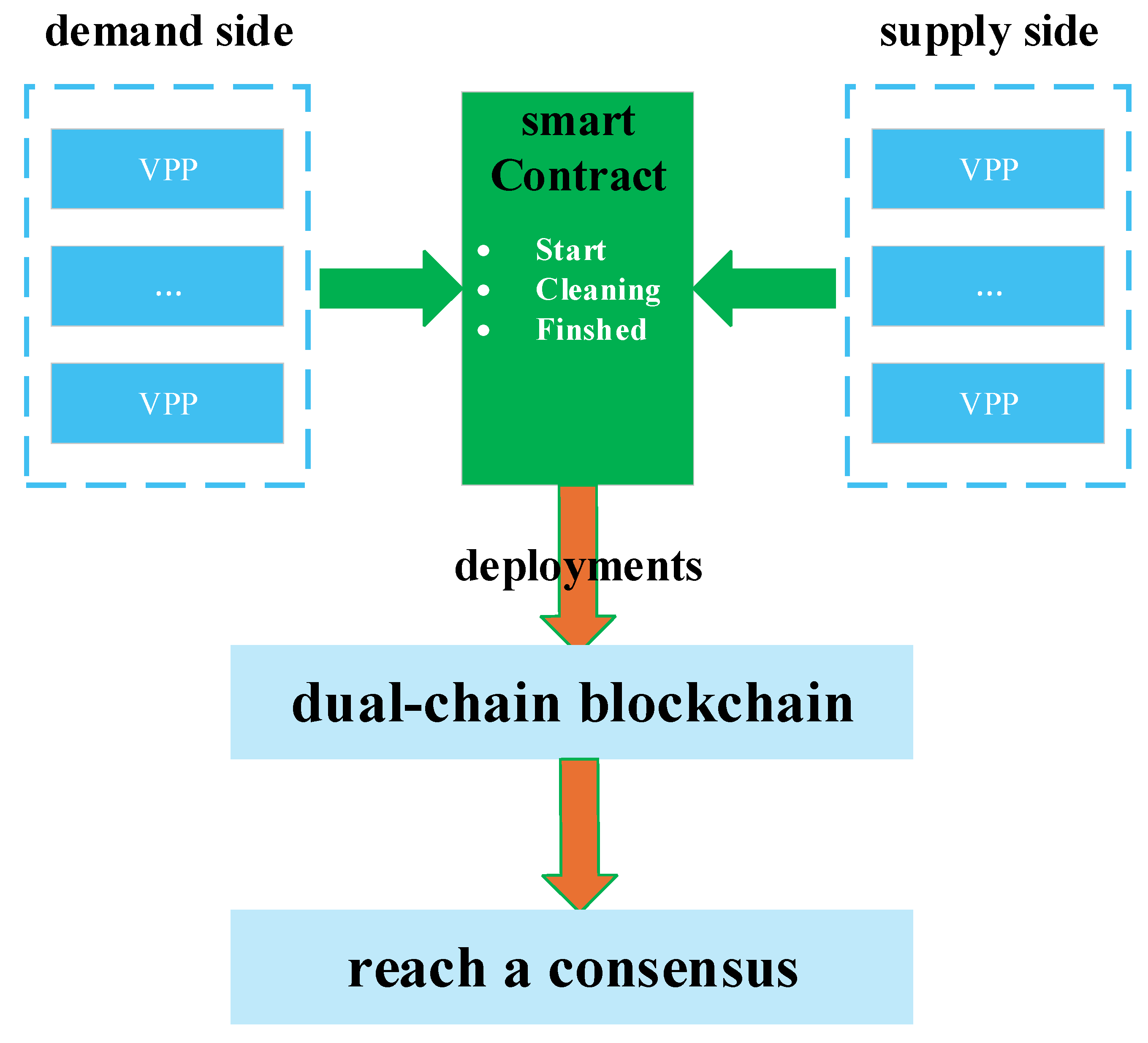
3.2. Smart Contract Design
4. Example Analysis
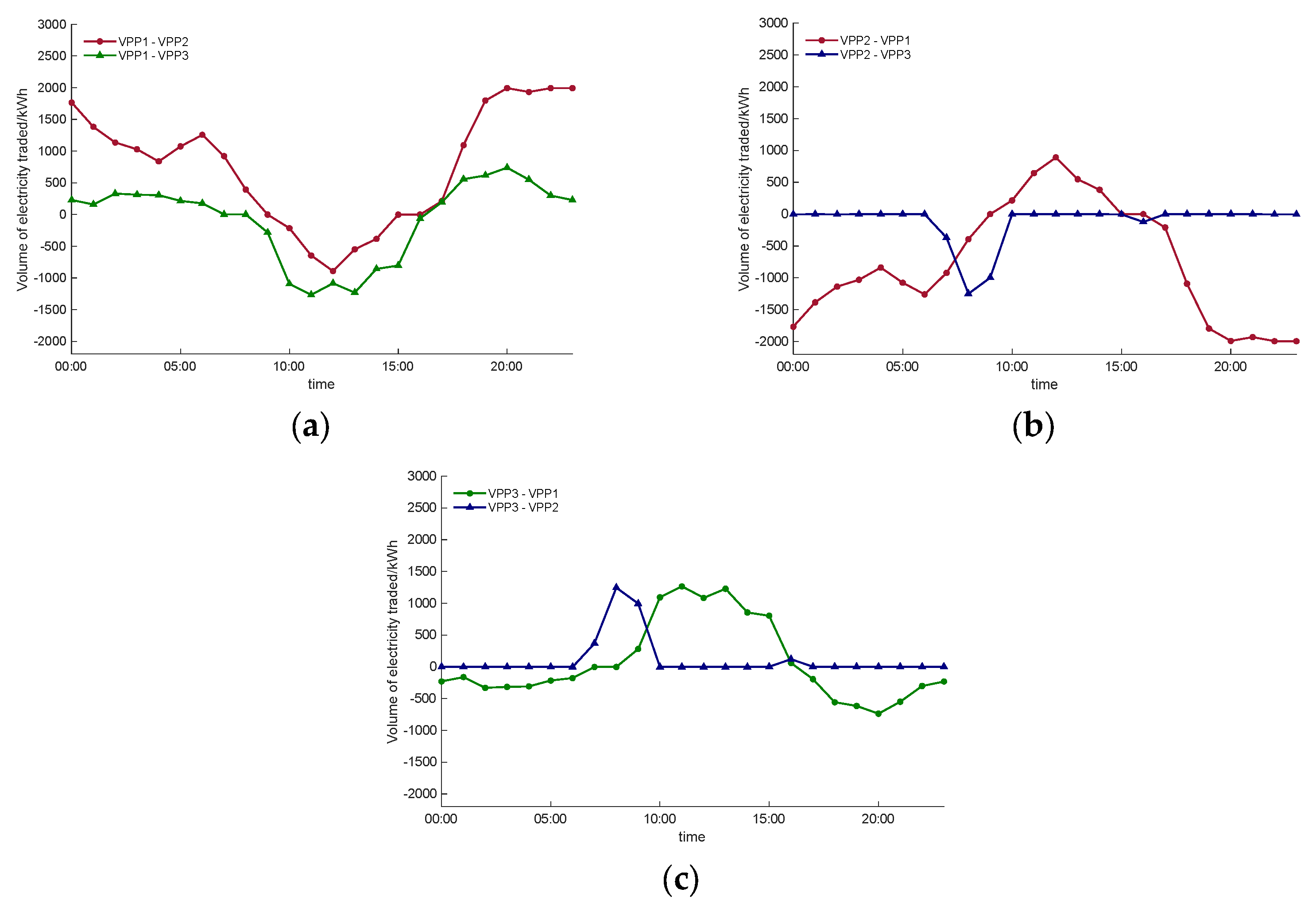
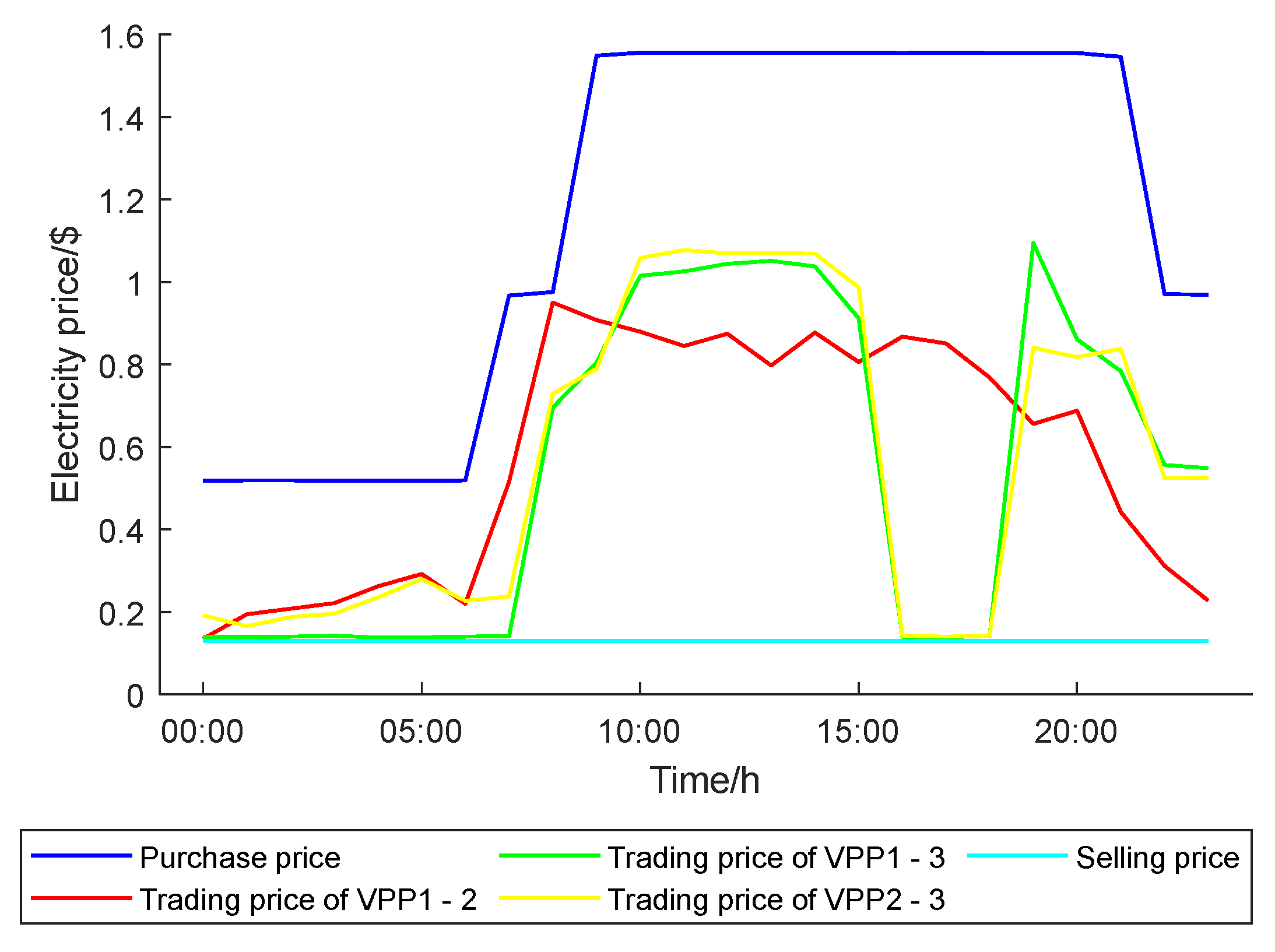
4.1. Clearance of Transactions
4.2. I-PBFT Consensus Process
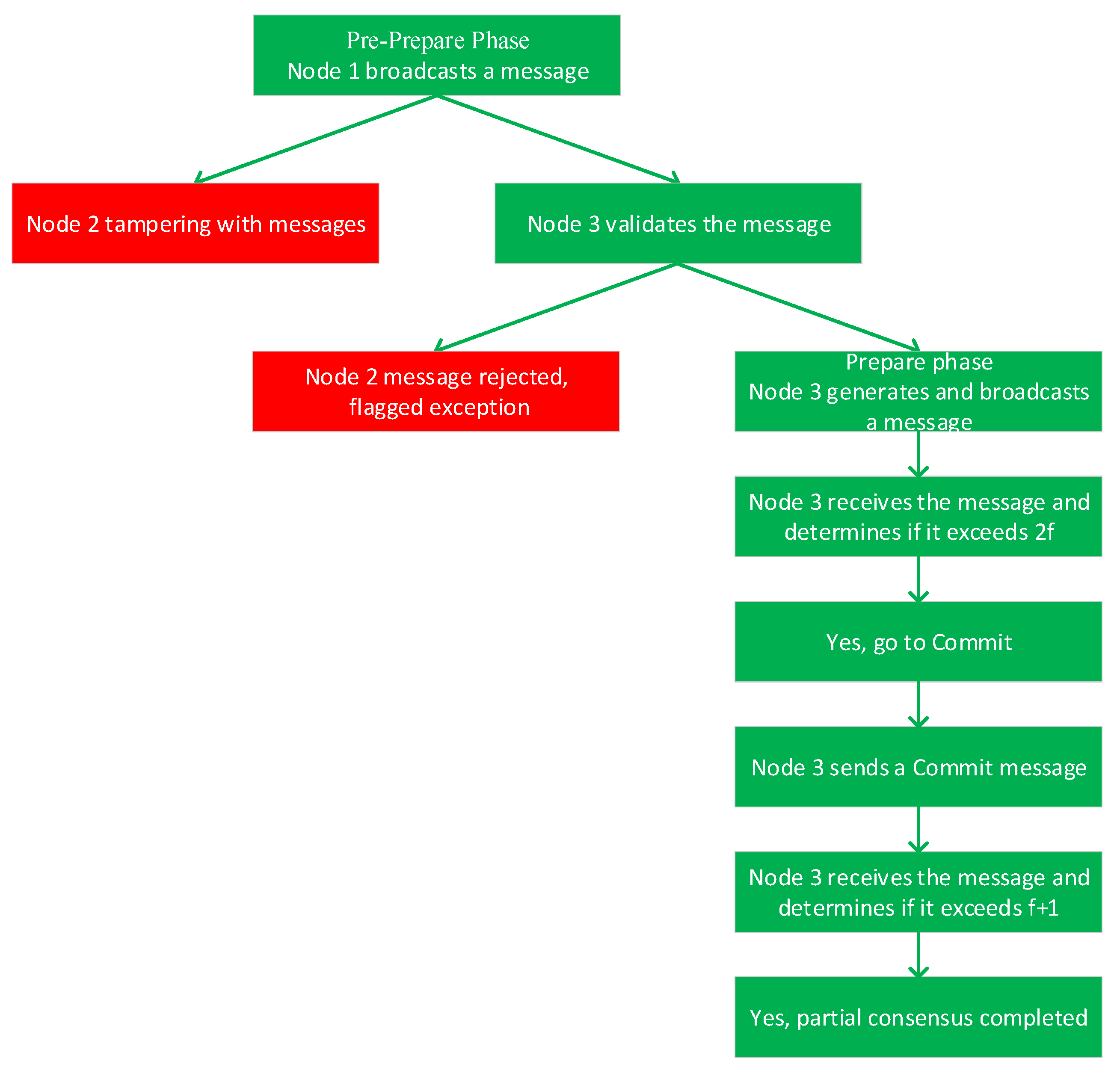
4.2.1. Analysis of Common Node Evil Scenarios
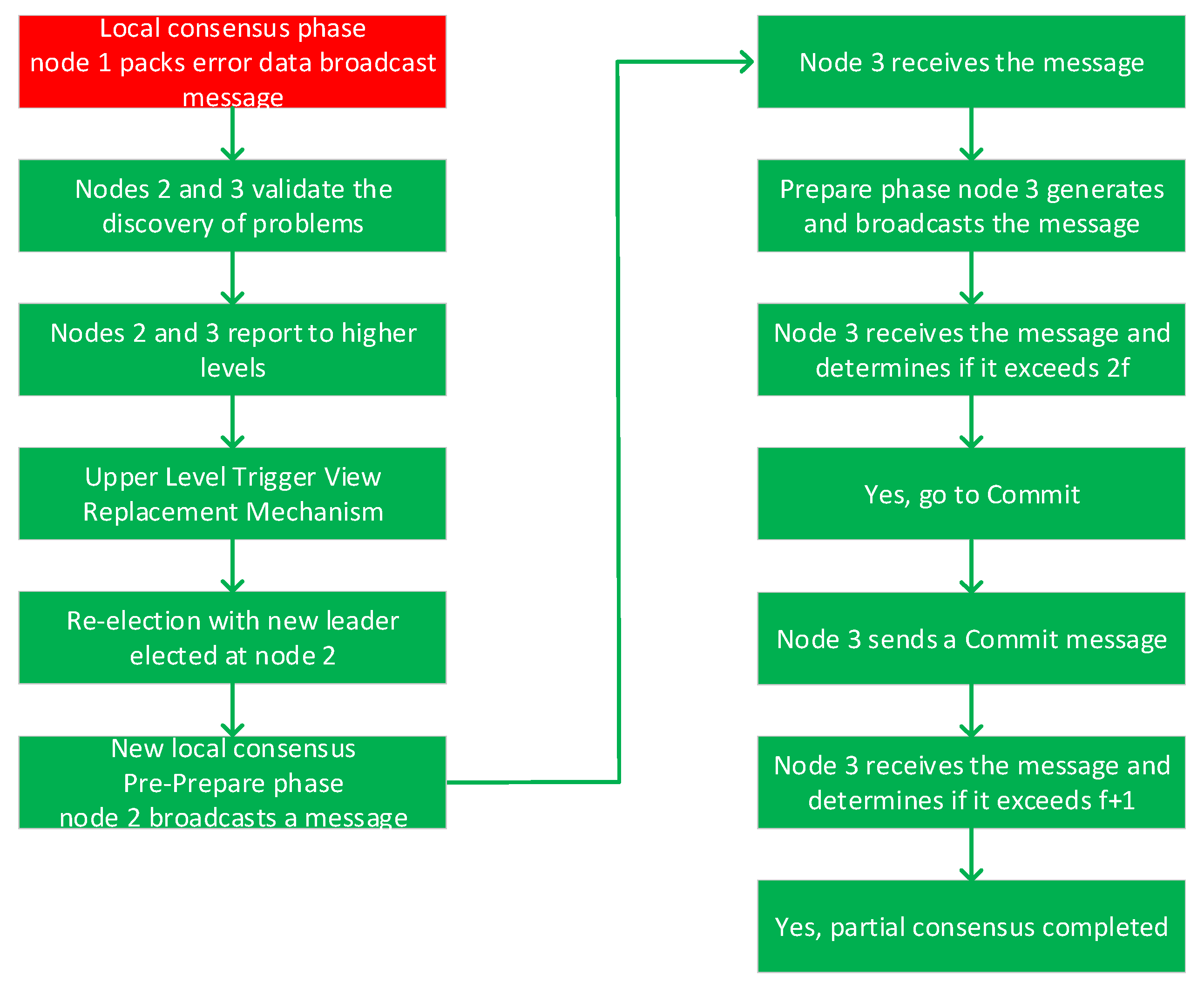
4.2.2. Leader Node Evil Scenario Analysis
4.2.3. Time Delay Analysis
4.2.4. Communications Overhead
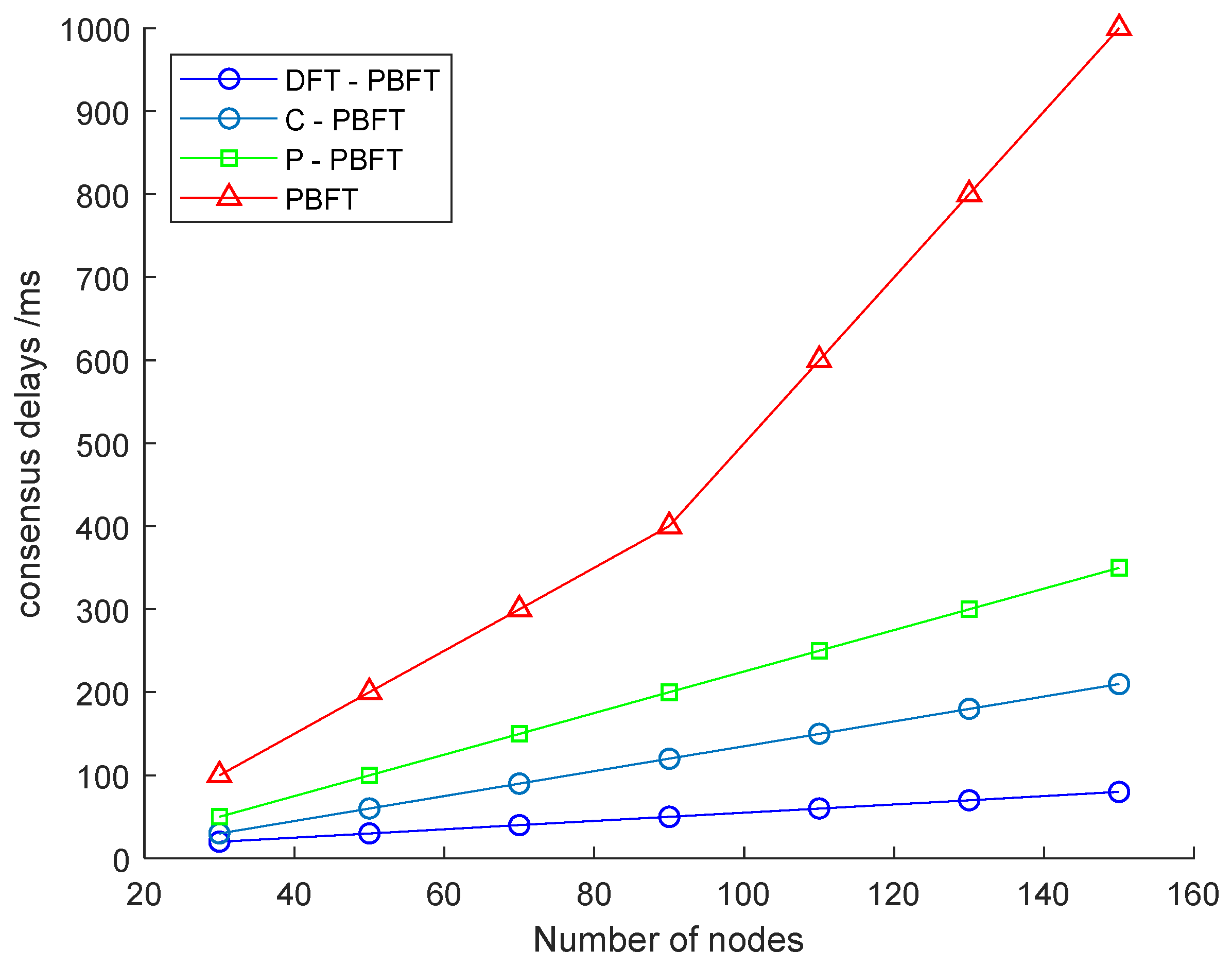
4.3. Comparative Analysis of Dual-Chain Blockchain Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, C.; Chen, Y.; Shi, K.; Wang, J.; Xiao, T. Distributed power trading among park microgrid-type virtual power plants based on trend distribution identification. Power Supply 2024, 41, 112–119. [Google Scholar] [CrossRef]
- Zuo, J.; Ai, Q.; Wang, W.; Zhao, J.; Yu, T.; Tao, W. Status Quo of Virtual Power Plant Standardization and Architecture Design. Power Syst. Autom. 1–13. Available online: https://http-kns_cnki_net.shiep.vpn358.com/kcms/detail/32.1180.TP.20250326.1417.002.html (accessed on 21 April 2025).
- Wang, D.; Ai, Q.; Yu, T.; Zuo, J.; Lu, Y.; Li, J. Technical Difficulties and Solutions for Trusted Transactions in Virtual Power Plants. Power Syst. Autom. 1–18. Available online: https://http-kns_cnki_net.shiep.vpn358.com/kcms/detail/32.1180.TP.20241030.1550.006.html (accessed on 21 April 2025).
- Liang, Y.; Zuo, J. Virtual power plant technology and outlook. New Power Syst. 2025, 3, 12–32. [Google Scholar] [CrossRef]
- Zuo, J.; Ai, Q.; Wang, D.; Wang, W.; Xu, C. Privacy-preserving trading strategies for virtual power plants in the power peaking market. Power Syst. Autom. 2024, 48, 149–157. [Google Scholar]
- Li, D.; Yang, K.; Guo, Q. A privacy-preserving settlement model for virtual power plant power transactions. Power Syst. Technol. 2024, 48, 3713–3723. [Google Scholar] [CrossRef]
- Zhang, L.; Bao, F. Research on Cooperative Operation of Multi-Virtual Power Plant Containing Distributed New Energy. Electr. Meas. Instrum. 1–9. Available online: https://http-kns_cnki_net.shiep.vpn358.com/kcms/detail/23.1202.th.20240621.1130.002.html (accessed on 21 April 2025).
- Zhao, Y.; Song, W.; Li, W.; Meng, Y.; Ma, G. Optimized operation method of multi-virtual power plant considering shared energy storage capacity allocation. Grid Clean Energy 2024, 40, 92–101. [Google Scholar]
- Cheng, X.; Wang, J.; Jin, Y.; Li, R.; Bao, Y.; Deng, H. Cooperative gaming strategy for multiple virtual power plants taking into account distribution network operation constraints. South. Power Grid Technol. 2023, 17, 119–131. [Google Scholar] [CrossRef]
- Zhu, Y.; Guo, J.; Zhou, Y.; Han, H.; We, Z. A multi-virtual power plant electricity-carbon P2P trading model considering carbon-green certificate market coupling. Power Autom. Equip. 2025, 45, 51–58. [Google Scholar] [CrossRef]
- Xu, H.; Tian, Y.; Zhao, Y.; Chai, Y.; Fang, Q. Optimal scheduling of multi-virtual power plant hybrid game considering green certificate-carbon trading. Intell. Power 2024, 52, 1–7+16. [Google Scholar]
- Liu, W.; Chen, Z.; Du, P.; Chen, J.; Li, B. A model of multi-virtual power plant participation in day-ahead power market bidding based on coalition game. Power Autom. Equip. 2024, 44, 135–142+150. [Google Scholar] [CrossRef]
- Han, H.; Xu, Y.; Wu, C.; Jiang, X.; Cao, S.; Zang, H.; Chen, S.; Wei, Z. Nash Equilibrium-Based Two-Stage Cooperative Operation Strategy for Multi-Microgrids Considering Uncertainty. In Protection and Control of Modern Power Systems; PSPC: Xuchang, China, 2024; Volume 9, pp. 42–57. [Google Scholar] [CrossRef]
- Bate, W.G. Blockchain and the Future of Tokenization. Res.-Technol. Manag. 2025, 68, 59–62. [Google Scholar] [CrossRef]
- Ping, J.; Yan, Z.; Chen, S.; Yao, L.; Qian, M. Coordinating EV charging via blockchain. J. Mod. Power Syst. Clean Energy 2020, 8, 573–581. [Google Scholar] [CrossRef]
- Alam, K.S.; Kaif, A.D.; Das, S.K. A blockchain-based optimal peer-to-peer energy trading framework for decentralized energy management with in a virtual power plant: Lab scale studies and large scale proposal. Appl. Energy 2024, 365, 123243. [Google Scholar] [CrossRef]
- Salehi, M.K.; Rastegar, M. Blockchain-enabled framework for transactive home energy management with cloud energy storage under uncertainties. Energy Build. 2024, 317, 17. [Google Scholar] [CrossRef]
- Sadri, H. AI-Driven Integration of Digital Twins and Blockchain for Smart Building Management Systems: A Multi-Stage Empirical Study. J. Build. Eng. 2025, 105, 112439. [Google Scholar] [CrossRef]
- Wang, H.; Fei, F.; Chen, K. A distributed scheduling strategy for virtual power plants based on energy blockchain. J. Syst. Manag. 2022, 31, 406–411. [Google Scholar]
- Zhou, B.; Zhang, Y.; Zang, T.; Cao, Q.; Zhang, Y.; Peng, H. Optimized operation of multi virtual power plant master-slave game based on blockchain. Power Syst. Autom. 2022, 46, 155–163. [Google Scholar]
- Ren, J.; Zhang, Q. Two-stage robust optimal scheduling of virtual power plant based on energy blockchain. Power Autom. Equip. 2020, 40, 23–33. [Google Scholar] [CrossRef]
- Wang, W.; Ai, Q.; Li, X.; Wang, D.; Chen, M. Master-slave multi-chain transaction matching mechanism for virtual power plant based on improved consensus algorithm. Power Eng. Technol. 2024, 43, 69–80. [Google Scholar]
- Liu, Y.; Fan, Y.; Bai, X.; Song, Y. Virtual power plant model and scheduling strategy based on optimized computational blockchain system. J. Electrotechnol. 2023, 38, 4178–4191. [Google Scholar] [CrossRef]
- Wu, J.; Lou, P.; Guan, M.; Huang, Y.; Zhang, W.; Cao, Y. Optimization strategy for power sharing operation of multiple microgrids based on asymmetric Nash negotiation. Grid Technol. 2022, 46, 2711–2723. [Google Scholar] [CrossRef]
- Fu, J.; Jing, C.; Du, M. Review and progress of DBSCAN research on spatial density clustering pattern mining method. Sci. Surv. Mapp. 2018, 43, 50–57. [Google Scholar]


| Program | Attack | Security |
|---|---|---|
| Traditional PBFT | sybil attacks + eclipse attacks | vulnerable |
| Schnorr + PBFT | sybil attacks + eclipse attacks | Dependent on complex interactions |
| I-PBFT | sybil attacks + eclipse attacks | defend against attack |
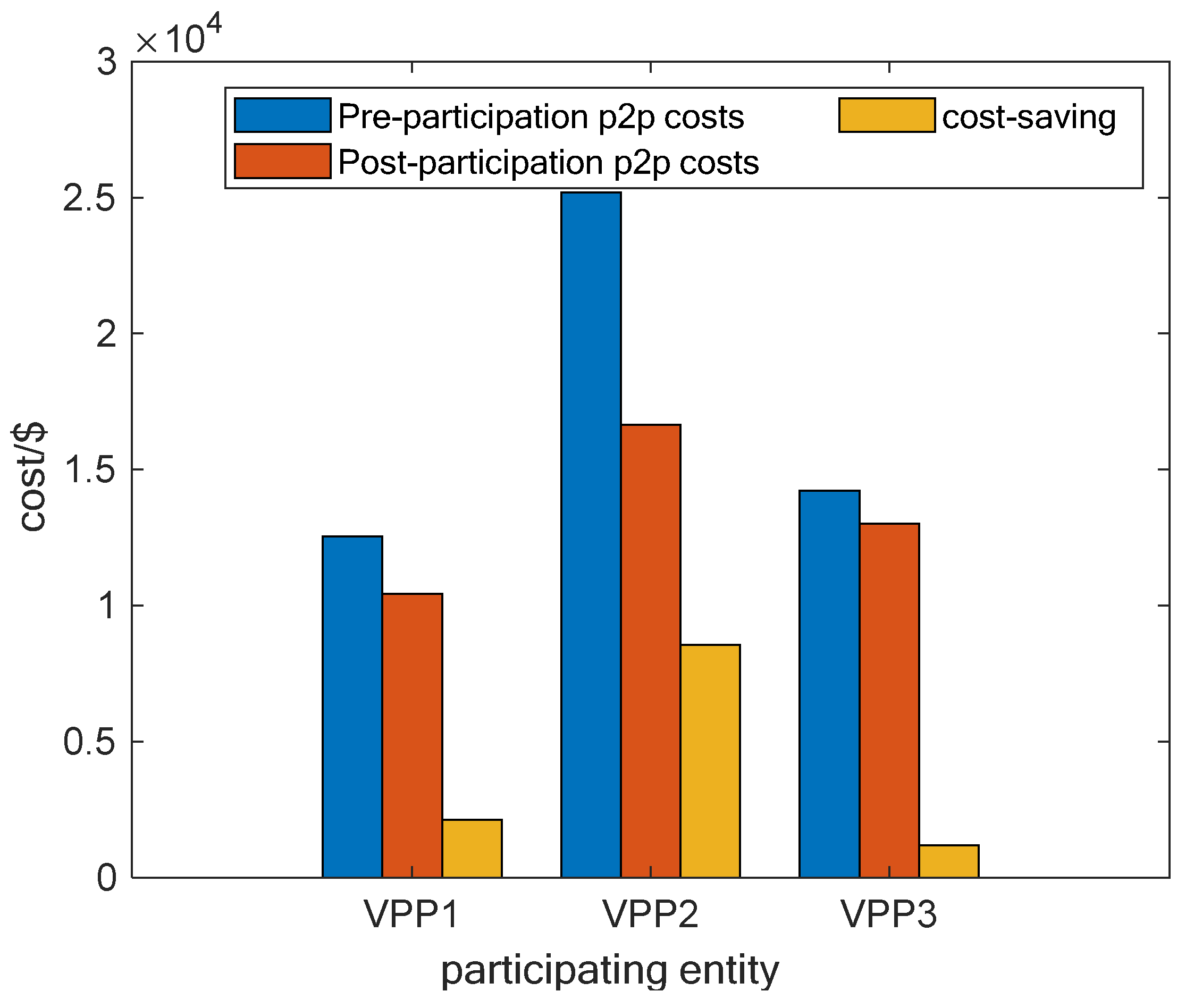
| VPP Number | Stand-Alone Operating Costs/$ | P2P Transaction Running Costs/$ |
|---|---|---|
| VPP1 | 12,553.2 | 10,423.5 |
| VPP2 | 25,183.14 | 16,633.6 |
| VPP3 | 14,208.61 | 13,020.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Zheng, C.; He, X.; Liu, X.; Zhai, S.; Lin, G.; Su, S.; Zhao, C.; Ai, Q. A Trusted Sharing Strategy for Electricity in Multi-Virtual Power Plants Based on Dual-Chain Blockchain. Energies 2025, 18, 2741. https://doi.org/10.3390/en18112741
Huang W, Zheng C, He X, Liu X, Zhai S, Lin G, Su S, Zhao C, Ai Q. A Trusted Sharing Strategy for Electricity in Multi-Virtual Power Plants Based on Dual-Chain Blockchain. Energies. 2025; 18(11):2741. https://doi.org/10.3390/en18112741
Chicago/Turabian StyleHuang, Wei, Chao Zheng, Xuehao He, Xiaojie Liu, Suwei Zhai, Guobiao Lin, Shi Su, Chenyang Zhao, and Qian Ai. 2025. "A Trusted Sharing Strategy for Electricity in Multi-Virtual Power Plants Based on Dual-Chain Blockchain" Energies 18, no. 11: 2741. https://doi.org/10.3390/en18112741
APA StyleHuang, W., Zheng, C., He, X., Liu, X., Zhai, S., Lin, G., Su, S., Zhao, C., & Ai, Q. (2025). A Trusted Sharing Strategy for Electricity in Multi-Virtual Power Plants Based on Dual-Chain Blockchain. Energies, 18(11), 2741. https://doi.org/10.3390/en18112741






